Математика. НОД и НОК: наибольший общий делитель и наименьшее общее кратное
Множество делителей
Рассмотрим такую задачу: найти делитель числа $140$. Очевидно, что у числа $140$ не один делитель, а несколько. В таких случаях говорят, что задача имеет множество решений. Найдем их все. Прежде всего разложим данное число на простые множители:
$140 = 2 \cdot 2 \cdot 5 \cdot 7$.
Теперь мы без труда можем выписать все делители. Начнем с простых делителей, то есть тех, которые присутствуют в разложении, приведенном выше:
$2, ~5, ~7$.
Затем выпишем те, которые получаются попарным умножением простых делителей:
$2\cdot 2 = 4, ~~~2\cdot 5 = 10, ~~~2\cdot 7 = 14, ~~~5\cdot 7 = 35$.
Затем — те, которые содержат в себе три простых делителя:
$2\cdot 2\cdot 5 = 20, ~~~2\cdot 2\cdot 7 = 28, ~~~2\cdot 5\cdot 7 = 70$.
Наконец, не забудем единицу и само разлагаемое число:
$1, ~140$.
Все найденные нами делители образуют множество делителей числа $140$, которое записывается с помощью фигурных скобок:
Множество делителей числа $140~=$
$\{1, ~2, ~4, ~5, ~7, ~10, ~14, ~20, ~28, ~35, ~70, ~140\}$.
Для удобства восприятия мы выписали здесь делители (элементы множества) в порядке возрастания, но, вообще говоря, это делать необязательно. Кроме того, введем сокращение записи. Вместо «Множество делителей числа $140$» будем писать «Д$(140)$» (читается «Дэ от $140$»). Таким образом,
Д$(140) = \{1, ~2, ~4, ~5, ~7, ~10, ~14, ~20, ~28, ~35, ~70, ~140\}$.
Точно так же можно найти множество делителей для любого другого натурального числа. Например, из разложения
$105 = 3 \cdot 5 \cdot 7$
мы получаем:
Д$(105) = \{1, ~3, ~5, ~7, ~15, ~21, ~35, ~105\}$.
От множества всех делителей следует отличать множество простых делителей, которые для чисел $140$ и $105$ равны соответственно:
ПД$(140) = \{2, ~5, ~7\}$.
ПД$(105) = \{3, ~5, ~7\}$.
Следует особо подчеркнуть, что в разложении числа $140$ на простые множители двойка присутствует два раза, в то время как во множестве ПД$(140)$ — только один. Множество ПД$(140)$ — это, по своей сути, все ответы на задачу: «Найти простой множитель числа $140$».
Сокращение дробей. Наибольший общий делитель
Рассмотрим дробь
$\dfrac{105}{140}$.
Мы знаем, что эту дробь можно сократить на такое число, которое одновременно является и делителем числителя ($105$) и делителем знаменателя ($140$). Взглянем на множества Д$(105)$ и Д$(140)$ и выпишем их общие элементы.
Д$(105) = \{1, ~3, ~5, ~7, ~15, ~21, ~35, ~105\}$;
Д$(140) = \{1, ~2, ~4, ~5, ~7, ~10, ~14, ~20, ~28, ~35, ~70, ~140\}$.
Общие элементы множеств Д$(105)$ и Д$(140)~=$
$\{1, ~5, ~7, ~35\}$.
Последнее равенство можно записать короче, а именно:
Д$(105)~\cap~$Д$(140)~=~\{1, ~5, ~7, ~35\}$.
Здесь специальный значок «$\cap$» («мешок отверстием вниз») как раз и указывает на то, что из двух множеств, записанных по разные стороны от него, надо выбрать только общие элементы. Запись «Д$(105)~\cap~$Д$(140)$» читается «пересечение множеств Дэ от $105$ и Дэ от $140$».
Замечание. Отметим по ходу дела, что с множествами можно производить разные бинарные операции, почти как с числами. Другой распространенной бинарной операцией является объединение, которое обозначается значком «$\cup$» («мешок отверстием вверх»). В объединение двух множеств входят все элементы как того, так и другого множества:
ПД$(105) = \{3, ~5, ~7\}$;
ПД$(140) = \{2, ~5, ~7\}$;
ПД$(105)~\cup~$ПД$(140) = \{2, ~3, ~5, ~7\}$.
Итак, мы выяснили, что дробь
$\dfrac{105}{140}$
можно сократить на любое из чисел, принадлежащих множеству
Д$(105)~\cap~$Д$(140) = \{1, ~5, ~7, ~35\}$
и нельзя сократить ни на какое другое натуральное число. Вот все возможные способы сокращения (за исключением неинтересного сокращения на единицу):
$\begin{align}
&\frac{105}{140} = \frac{105/5}{140/5} = \frac{21}{28},\\
&\frac{105}{140} = \frac{105/7}{140/7} = \frac{15}{20},\\
&\frac{105}{140} = \frac{105/35}{140/35} = \frac{\,3\,}{4}. \end{align}$
\end{align}$
Очевидно, что практичнее всего сокращать дробь на число, по возможности большее. В данном случае это число $35$, про которое говорят, что оно является наибольшим общим делителем (НОД) чисел $105$ и $140$. Это записывается как
НОД$(105, ~140) = 35$.
Впрочем, на практике, если нам даны два числа и требуется найти их наибольший общий делитель, мы вовсе не должны строить какие-либо множества. Достаточно просто разложить оба числа на простые множители и подчеркнуть те из этих множителей, которые являются общими для обоих разложений, например:
$105 = 3 \cdot \underline{\,5\,} \cdot \underline{\,7\,}$;
$140 = 2 \cdot 2 \cdot \underline{\,5\,} \cdot \underline{\,7\,}$.
Перемножая подчеркнутые числа (в любом из разложений), получаем:
НОД$(105, ~140) = 5 \cdot 7 = 35$.
Разумеется, возможен случай, когда подчеркнутых множителей окажется больше двух:
$168 = \underline{\,2\,} \cdot \underline{\,2\,} \cdot 2 \cdot \underline{\,3\,} \cdot 7$;
$396 = \underline{\,2\,} \cdot \underline{\,2\,} \cdot \underline{\,3\,} \cdot 3 \cdot 11$.
Отсюда видно, что
НОД$(168, ~396) = \underline{\,2\,} \cdot \underline{\,2\,} \cdot \underline{\,3\,} = 12$.
Особого упоминания заслуживает ситуация, когда общих множителей совсем нет и подчеркивать нечего, например:
$42 = 2 \cdot 3 \cdot 7$;
$55 = 5 \cdot 11$.
В этом случае,
НОД$(42, \,55) = 1$.
Два натуральных числа, для которых НОД равен единице, называются взаимно простыми. Если из таких чисел составить дробь, например,
$\dfrac{42}{55}$,
то такая дробь является несократимой.
Вообще говоря, правило сокращения дробей можно записать в таком виде:
$\dfrac{\,a\,}{b} = \dfrac{a/\text{НОД}(a, b)}{b/\text{НОД}(a, b)}\,$.
Здесь предполагается, что $a$ и $b$ — натуральные числа, а вся дробь положительна. Если мы теперь припишем знак «минус» к обоим частям этого равенства, то получим соответствующее правило для отрицательных дробей.
Сложение и вычитание дробей. Наименьшее общее кратное
Пусть требуется вычислить сумму двух дробей:
$\dfrac{1}{105} + \dfrac{1}{140}$. {1}}$
{1}}$
Нетрудно видеть, что оба исходных знаменателя (как $105$, так и $140$) являются делителями числа $420$, а число $420$, в свою очередь, кратно обоим знаменателям, — и не просто кратно, оно является
НОК$(105, ~140) = 420$.
Итак, чтобы получить НОК чисел $105$ и $140$, мы разложили их на простые множители, подчеркнули те множители, которые являются общими для обоих чисел, а далее написали:
НОК $=$ все множители первого числа $\times$ неподчеркнутые множители второго числа.
Отсюда следует, что
НОК$(105, 140) = 105 \cdot 140 /~$НОД$(105, 140)$.
Это можно также переписать в несколько более изящной, «симметричной» форме:
$105 \cdot 140~=~$НОК$(105, 140)~\cdot~$НОД$(105, 140)$.
Точно так же, для произвольных натуральных чисел $b$ и $d$:
$b \cdot d~=~$НОК$(b, d)~\cdot~$НОД$(b, d)$.
Теперь давайте доведем до конца суммирование наших дробей:
$\begin{align}
&\dfrac{1}{105} + \dfrac{1}{140} =\\[2mm]
&= \dfrac{1}{3 \cdot \underline{\,5\,} \cdot \underline{\,7\,}} + \frac{1}{2 \cdot 2 \cdot \underline{\,5\,} \cdot \underline{\,7\,}} =\\[2mm]
&= \dfrac{2 \cdot 2 }{2 \cdot 2 \cdot 3 \cdot \underline{\,5\,} \cdot \underline{\,7\,}}
+ \dfrac{3}{3 \cdot 2 \cdot 2 \cdot \underline{\,5\,} \cdot \underline{\,7\,}} =\\[2mm]
&= \dfrac{4 + 3}{2 \cdot 2 \cdot 3 \cdot \underline{\,5\,} \cdot \underline{\,7\,}}
= \dfrac{7}{2 \cdot 2 \cdot 3 \cdot \underline{\,5\,} \cdot \underline{\,7\,}}
= \dfrac{1}{2 \cdot 2 \cdot 3 \cdot \underline{\,5\,}} = \dfrac{1}{60}\,.
Подобным же образом можно посчитать разность:
$\dfrac{1}{105} — \dfrac{1}{140} = \dfrac{4}{4 \cdot 105} — \dfrac{3}{3 \cdot 140} = \dfrac{4}{420} — \dfrac{3}{420} = \dfrac{1}{420}$.
Для того чтобы получить общий знаменатель двух дробей $\frac{\,a\,}{b}$ и $\frac{\,c\,}{d}$, мы фактически проделываем ту же самую процедуру, что и при вычислении НОК$(b, d)$. Именно НОК$(b, d)$ и оказывается общим знаменателем. (Предполагается, что $a$, $b$, $c$ и $d$ — натуральные числа.)
Конспект
1. Правило сокращения дробей. Пусть $a$ и $b$ — натуральные числа (${b \ne 0}$). Тогда
$\dfrac{\,a\,}{b} = \dfrac{a/\text{НОД}(a, b)}{b/\text{НОД}(a, b)}$ ,
где НОД$(a, b)$ — наибольший общий делитель чисел $a$ и $b$. Чтобы найти НОД, надо разложить числа $a$ и $b$ на простые множители и подчеркнуть те множители, которые являются общими для обоих чисел. НОД равен произведению подчеркнутых множителей, взятых в любом из разложений.
2. Приведение дробей к общему знаменателю. Пусть $\,a$, $\,b$, $\,c$ и $\,d$ — натуральные числа (${b \ne 0}$, ${\,d \ne 0}$). В качестве общего знаменателя двух дробей $\frac{\,a\,}{b}$ и $\frac{\,c\,}{d}$ удобно брать НОК$(b, d)$ — наименьшее общее кратное знаменателей $b$ и $d$. Чтобы получить НОК$(b, d)$, мы раскладываем числа $b$ и $d$ на простые множители, причем общие множители подчеркиваем. Тогда
Пусть $\,a$, $\,b$, $\,c$ и $\,d$ — натуральные числа (${b \ne 0}$, ${\,d \ne 0}$). В качестве общего знаменателя двух дробей $\frac{\,a\,}{b}$ и $\frac{\,c\,}{d}$ удобно брать НОК$(b, d)$ — наименьшее общее кратное знаменателей $b$ и $d$. Чтобы получить НОК$(b, d)$, мы раскладываем числа $b$ и $d$ на простые множители, причем общие множители подчеркиваем. Тогда
НОК $=$ все множители числа $b~\times$ неподчеркнутые множители числа $d$.
3. НОК и НОД связаны соотношением
$b \cdot d = \text{НОК}(b, d) \cdot \text{НОД}(b, d)$.
Из «бесконечного» сборника типовых упражнений
Задачи, где требуется разлагать числа на простые множители
Примечание. Для решения некоторых задач требуется знать, что такое квадрат числа. Квадратом числа $a$ называется число $a$, помноженное само на себя, то есть $a \cdot a$. (Оно называется так, потому что равно площади квадрата со стороной $a$).
Примеры на тему нок и нод. Нод и нок двух чисел, алгоритм евклида
НОД — это наибольший общий делитель.
Чтобы найти наибольший общий делитель нескольких чисел необходимо:
- определить множители, общие для обоих чисел;
- найти произведение общих множителей.
Пример нахождения НОД:
Найдем НОД чисел 315 и 245.
315 = 5 * 3 * 3 * 7;
245 = 5 * 7 * 7.
2. Выпишем множители, общие для обоих чисел:
3. Найдем произведение общих множителей:
НОД(315; 245) = 5 * 7 = 35.
Ответ: НОД(315; 245) = 35.
Нахождение НОК
НОК — это наименьшее общее кратное.
Чтобы найти наименьшее общее кратное нескольких чисел необходимо:
- разложить числа на простые множители;
- выписать множители, входящие в разложение одного из чисел;
- допишем к ним недостающие множители из разложения второго числа;
- найти произведение получившихся множителей.
Пример нахождения НОК:
Найдем НОК чисел 236 и 328:
1. Разложим числа на простые множители:
236 = 2 * 2 * 59;
328 = 2 * 2 * 2 * 41.
2. Выпишем множители, входящие в разложение одного из чисел и допишем к ним недостающие множители из разложения второго числа:
2; 2; 59; 2; 41.
3. Найдем произведение получившихся множителей:
НОК(236; 328) = 2 * 2 * 59 * 2 * 41 = 19352.
Ответ: НОК(236; 328) = 19352.
Для нахождения НОД (наибольшего общего делителя) двух чисел необходимо:
2. Найти (подчеркнуть) все общие простые множители в полученных разложениях.
3. Найти произведение общих простых множителей.
Для нахождения НОК (наименьшего общего кратного) двух чисел необходимо:
1. Разложить данные числа на простые множители.
2. Разложение одного из них дополнить теми множителями разложения другого числа, которых нет в разложении первого.
3. Вычислить произведение полученных множителей.
Приступим к изучению наименьшего общего кратного двух и более чисел. В разделе мы дадим определение термина, рассмотрим теорему, которая устанавливает связь между наименьшим общим кратным и наибольшим общим делителем, приведем примеры решения задач.
Общие кратные – определение, примеры
В данной теме нас будет интересовать только общие кратные целых чисел, отличных от нуля.
Определение 1
Общее кратное целых чисел – это такое целое число, которое кратно всем данным числам. Фактически, это любое целое число, которое можно разделить на любое из данных чисел.
Определение общих кратных чисел относится к двум, трем и большему количеству целых чисел.
Пример 1
Согласно данному выше определению для числа 12 общими кратными числами будут 3 и 2 . Также число 12 будет общим кратным для чисел 2 , 3 и 4 . Числа 12 и — 12 являются общими кратными числами для чисел ± 1 , ± 2 , ± 3 , ± 4 , ± 6 , ± 12 .
В то же время общим кратным числом для чисел 2 и 3 будут числа 12 , 6 , − 24 , 72 , 468 , − 100 010 004 и целый ряд любых других.
Если мы возьмем числа, которые делятся на первое число из пары и не делятся на второе, то такие числа не будут общими кратными. Так, для чисел 2 и 3 числа 16 , − 27 , 5 009 , 27 001 не будут общими кратными.
0 является общим кратным для любого множества целых чисел, отличных от нуля.
Если вспомнить свойство делимости относительно противоположных чисел, то получается, что некоторое целое число k будет общим кратным данных чисел точно также, как и число – k . Это значит, что общие делители могут быть как положительными, так и отрицательными.
Для всех ли чисел можно найти НОК?
Общее кратное можно найти для любых целых чисел.
Пример 2
Предположим, что нам даны k целых чисел a 1 , a 2 , … , a k . Число, которое мы получим в ходе умножения чисел a 1 · a 2 · … · a k согласно свойству делимости будет делиться на каждый из множителей, который входил в изначальное произведение. Это значит, что произведение чисел a 1 , a 2 , … , a k является наименьшим общим кратным для этих чисел.
Сколько всего общих кратных могут иметь данные целые числа?
Группа целых чисел может иметь большое количество общих кратных. Фактически, их число бесконечно.
Пример 3
Предположим, что у нас есть некоторое число k . Тогда произведение чисел k · z , где z – это целое число, будет являться общим кратным чисел k и z . С учетом того, что количество чисел бесконечно, то и количество общих кратных бесконечно.
Наименьшее общее кратное (НОК) – определение, обозначение и примеры
Вспомним понятие наименьшего числа из данного множества чисел, которое мы рассматривали в разделе «Сравнение целых чисел». С учетом этого понятия сформулируем определение наименьшего общего кратного, которое имеет среди всех общих кратных наибольшее практическое значение.
Определение 2
Наименьшее общее кратное данных целых чисел – это наименьшее положительное общее кратное этих чисел.
Наименьшее общее кратное существует для любого количества данных чисел. Наиболее употребимой для обозначения понятия в справочной литературе является аббревиатура НОК. Краткая запись наименьшего общего кратного для чисел a 1 , a 2 , … , a k будет иметь вид НОК (a 1 , a 2 , … , a k) .
Пример 4
Наименьшее общее кратное чисел 6 и 7 – это 42 . Т.е. НОК (6 , 7) = 42 . Наименьшее общее кратное четырех чисел — 2 , 12 , 15 и 3 будет равно 60 . Краткая запись будет иметь вид НОК (- 2 , 12 , 15 , 3) = 60 .
Не для всех групп данных чисел наименьшее общее кратное очевидно. Часто его приходится вычислять.
Связь между НОК и НОД
Наименьшее общее кратное и наибольший общий делитель связаны между собой. Взаимосвязь между понятиями устанавливает теорема.
Теорема 1
Наименьшее общее кратное двух положительных целых чисел a и b равно произведению чисел a и b , деленному на наибольший общий делитель чисел a и b , то есть, НОК (a , b) = a · b: НОД (a , b) .
Доказательство 1
Предположим, что мы имеем некоторое число M , которое кратно числам a и b . Если число M делится на a , также существует некоторое целое число z , при котором справедливо равенство M = a · k . Согласно определению делимости, если M делится и на b , то тогда a · k делится на b .
Если мы введем новое обозначение для НОД (a , b) как d , то сможем использовать равенства a = a 1 · d и b = b 1 · d . При этом оба равенства будут взаимно простыми числами.
Мы уже установили выше, что a · k делится на b . Теперь это условие можно записать следующим образом:
a 1 · d · k делится на b 1 · d , что эквивалентно условию a 1 · k делится на b 1 согласно свойствам делимости.
Согласно свойству взаимно простых чисел, если a 1 и b 1 – взаимно простые числа, a 1 не делится на b 1 при том, что a 1 · k делится на b 1 , то b 1 должно делиться k .
В этом случае уместно будет предположить, что существует число t , для которого k = b 1 · t , а так как b 1 = b: d , то k = b: d · t .
Теперь вместо k подставим в равенство M = a · k выражение вида b: d · t . Это позволяет нам прийти к равенству M = a · b: d · t . При t = 1 мы можем получить наименьшее положительное общее кратное чисел a и b , равное a · b: d , при условии, что числа a и b положительные.
При t = 1 мы можем получить наименьшее положительное общее кратное чисел a и b , равное a · b: d , при условии, что числа a и b положительные.
Так мы доказали, что НОК (a , b) = a · b: НОД (a , b) .
Установление связи между НОК и НОД позволяет находить наименьшее общее кратное через наибольший общий делитель двух и более данных чисел.
Определение 3
Теорема имеет два важных следствия:
- кратные наименьшего общего кратного двух чисел совпадает с общими кратными этих двух чисел;
- наименьшее общее кратное взаимно простых положительных чисел a и b равно их произведению.
Обосновать эти два факта не составляет труда. Любое общее кратное M чисел a и b определяется равенством M = НОК (a , b) · t при некотором целом значении t . Так как a и b взаимно простые, то НОД (a , b) = 1 , следовательно, НОК (a , b) = a · b: НОД (a , b) = a · b: 1 = a · b .
Наименьшее общее кратное трех и большего количества чисел
Для того, чтобы найти наименьшее общее кратное нескольких чисел, необходимо последовательно найти НОК двух чисел.
Теорема 2
Предположим, что a 1 , a 2 , … , a k – это некоторые целые положительные числа. Для того, чтобы вычислить НОК m k этих чисел, нам необходимо последовательно вычислить m 2 = НОК (a 1 , a 2) , m 3 = НОК (m 2 , a 3) , … , m k = НОК (m k — 1 , a k) .
Доказательство 2
Доказать верность второй теоремы нам поможет первое следствие из первой теоремы, рассмотренной в данной теме. Рассуждения строятся по следующему алгоритму:
- общие кратные чисел a 1 и a 2 совпадают с кратными их НОК, фактически, они совпадают с кратными числа m 2 ;
- общие кратные чисел a 1 , a 2 и a 3 m 2 и a 3 m 3 ;
- общие кратные чисел a 1 , a 2 , … , a k совпадают с общими кратными чисел m k — 1 и a k , следовательно, совпадают с кратными числа m k ;
- в связи с тем, что наименьшим положительным кратным числа m k является само число m k , то наименьшим общим кратным чисел a 1 , a 2 , … , a k является m k .

Так мы доказали теорему.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Тема «Кратные числа» изучается в 5 классе общеобразовательной школы. Ее целью является совершенствование письменных и устных навыков математических вычислений. На этом уроке вводятся новые понятия — «кратные числа» и «делители», отрабатывается техника нахождения делителей и кратных натурального числа, умение находить НОК различными способами.
Эта тема является очень важной. Знания по ней можно применить при решении примеров с дробями. Для этого нужно найти общий знаменатель путем расчета наименьшего общего кратного (НОК).
Кратным А считается целое число, которое делится на А без остатка.
Каждое натуральное число имеет бесконечное количество кратных ему чисел. Наименьшим считается оно само. Кратное не может быть меньше самого числа.
Нужно доказать, что число 125 кратно числу 5. Для этого нужно первое число разделить на второе. Если 125 делится на 5 без остатка, то ответ положительный.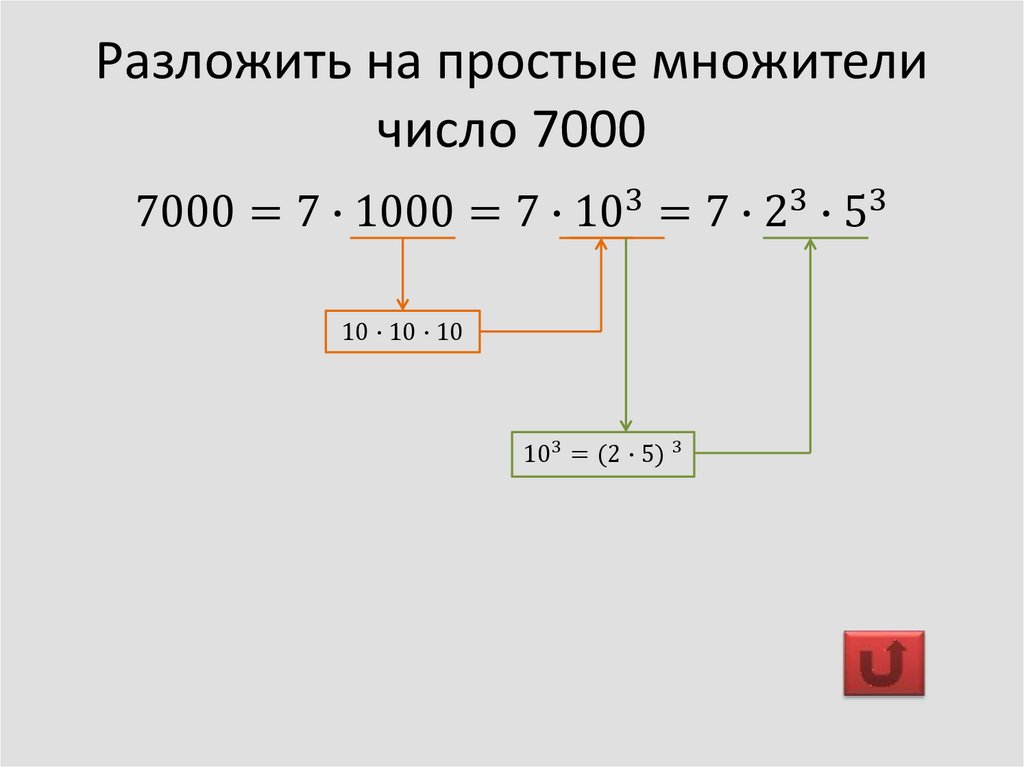
Данный способ применим для небольших чисел.
При расчёте НОК встречаются особые случаи.
1. Если необходимо найти общее кратное для 2-х чисел (например, 80 и 20), где одно из них (80) делится без остатка на другое (20), то это число (80) и есть наименьшее кратное этих двух чисел.
НОК (80, 20) = 80.
2. Если два не имеют общего делителя, то можно сказать, что их НОК — это произведение этих двух чисел.
НОК (6, 7) = 42.
Рассмотрим последний пример. 6 и 7 по отношению к 42 являются делителями. Они делят кратное число без остатка.
В этом примере 6 и 7 являются парными делителями. Их произведение равно самому кратному числу (42).
Число называется простым, если делится только само на себя или на 1 (3:1=3; 3:3=1). Остальные называются составными.
В другом примере нужно определить, является ли 9 делителем по отношению к 42.
42:9=4 (остаток 6)
Ответ: 9 не является делителем числа 42, потому что в ответе есть остаток.
Делитель отличается от кратного тем, что делитель — это то число, на которое делят натуральные числа, а кратное само делится на это число.
Наибольший общий делитель чисел a и b , умноженный на их наименьшее кратное, даст произведение самих чисел a и b .
А именно: НОД (а, b) х НОК (а, b) = а х b.
Общие кратные числа для более сложных чисел находят следующим способом.
Например, найти НОК для 168, 180, 3024.
Эти числа раскладываем на простые множители, записываем в виде произведения степеней:
168=2³х3¹х7¹
2⁴х3³х5¹х7¹=15120
НОК (168, 180, 3024) = 15120.
Множество делителей
Рассмотрим такую задачу: найти делитель числа 140. Очевидно, что у числа 140 не один делитель, а несколько. В таких случаях говорят, что задача имеет множество решений. Найдем их все. Прежде всего разложим данное число на простые множители:
140 = 2 ∙ 2 ∙ 5 ∙ 7.
Теперь мы без труда можем выписать все делители. Начнем с простых делителей, то есть тех, которые присутствуют в разложении, приведенном выше:
Затем выпишем те, которые получаются попарным умножением простых делителей:
2∙2 = 4, 2∙5 = 10, 2∙7 = 14, 5∙7 = 35.
Затем — те, которые содержат в себе три простых делителя:
2∙2∙5 = 20, 2∙2∙7 = 28, 2∙5∙7 = 70.
Наконец, не забудем единицу и само разлагаемое число:
Все найденные нами делители образуют множество делителей числа 140, которое записывается с помощью фигурных скобок:
Множество делителей числа 140 =
{1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, 140}.
Для удобства восприятия мы выписали здесь делители (элементы множества ) в порядке возрастания, но, вообще говоря, это делать необязательно. Кроме того, введем сокращение записи. Вместо «Множество делителей числа 140» будем писать «Д(140)». Таким образом,
Точно так же можно найти множество делителей для любого другого натурального числа. Например, из разложения
105 = 3 ∙ 5 ∙ 7
мы получаем:
Д(105) = {1, 3, 5, 7, 15, 21, 35, 105}.
От множества всех делителей следует отличать множество простых делителей, которые для чисел 140 и 105 равны соответственно:
ПД(140) = {2, 5, 7}.
ПД(105) = {3, 5, 7}.
Следует особо подчеркнуть, что в разложении числа 140 на простые множители двойка присутствует два раза, в то время как во множестве ПД(140) — только один. Множество ПД(140) — это, по своей сути, все ответы на задачу: «Найти простой множитель числа 140». Ясно, что один и тот же ответ не следует повторять больше одного раза.
Сокращение дробей. Наибольший общий делитель
Рассмотрим дробь
Мы знаем, что эту дробь можно сократить на такое число, которое одновременно является и делителем числителя (105) и делителем знаменателя (140). Взглянем на множества Д(105) и Д(140) и выпишем их общие элементы.
Д(105) = {1, 3, 5, 7, 15, 21, 35, 105};
Д(140) = {1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, 140}.
Общие элементы множеств Д(105) и Д(140) =
Последнее равенство можно записать короче, а именно:
Д(105) ∩ Д(140) = {1, 5, 7, 35}.
Здесь специальный значок «∩» («мешок отверстием вниз») как раз и указывает на то, что из двух множеств, записанных по разные стороны от него, надо выбрать только общие элементы. Запись «Д(105) ∩ Д(140)» читается «пересечение множеств Дэ от 105 и Дэ от 140».
Запись «Д(105) ∩ Д(140)» читается «пересечение множеств Дэ от 105 и Дэ от 140».
[Заметим по ходу дела, что с множествами можно производить разные бинарные операции, почти как с числами. Другой распространенной бинарной операцией является объединение , которое обозначается значком «∪» («мешок отверстием вверх»). В объединение двух множеств входят все элементы как того, так и другого множества:
ПД(105) = {3, 5, 7};
ПД(140) = {2, 5, 7};
ПД(105) ∪ ПД(140) = {2, 3, 5, 7}. ]
Итак, мы выяснили, что дробь
можно сократить на любое из чисел, принадлежащих множеству
Д(105) ∩ Д(140) = {1, 5, 7, 35}
и нельзя сократить ни на какое другое натуральное число. Вот все возможные способы сокращения (за исключением неинтересного сокращения на единицу):
Очевидно, что практичнее всего сокращать дробь на число, по возможности большее. В данном случае это число 35, про которое говорят, что оно является наибольшим общим делителем (НОД ) чисел 105 и 140. Это записывается как
Это записывается как
НОД(105, 140) = 35.
Впрочем, на практике, если нам даны два числа и требуется найти их наибольший общий делитель, мы вовсе не должны строить какие-либо множества. Достаточно просто разложить оба числа на простые множители и подчеркнуть те из этих множителей, которые являются общими для обоих разложений, например:
105 = 3 ∙ 5 ∙ 7 ;
140 = 2 ∙ 2 ∙ 5 ∙ 7 .
Перемножая подчеркнутые числа (в любом из разложений), получаем:
НОД(105, 140) = 5 ∙ 7 = 35.
Разумеется, возможен случай, когда подчеркнутых множителей окажется больше двух:
168 = 2 ∙ 2 ∙ 2 ∙ 3 ∙ 7;
396 = 2 ∙ 2 ∙ 3 ∙ 3 ∙ 11.
Отсюда видно, что
НОД(168, 396) = 2 ∙ 2 ∙ 3 = 12.
Особого упоминания заслуживает ситуация, когда общих множителей совсем нет и подчеркивать нечего, например:
42 = 2 ∙ 3 ∙ 7;
В этом случае,
НОД(42, 55) = 1.
Два натуральных числа, для которых НОД равен единице, называются взаимно простыми . Если из таких чисел составить дробь, например,
то такая дробь является несократимой .
Вообще говоря, правило сокращения дробей можно записать в таком виде:
a / НОД(a , b ) | |||
b / НОД(a , b ) |
Здесь предполагается, что a и b — натуральные числа, а вся дробь положительна. Если мы теперь припишем знак «минус» к обоим частям этого равенства, то получим соответствующее правило для отрицательных дробей.
Сложение и вычитание дробей. Наименьшее общее кратное
Пусть требуется вычислить сумму двух дробей:
Мы уже знаем, как раскладываются на простые множители знаменатели:
105 = 3 ∙ 5 ∙ 7 ;
140 = 2 ∙ 2 ∙ 5 ∙ 7 .
Из этого разложения сразу следует, что, для того чтобы привести дроби к общему знаменателю, достаточно числитель и знаменатель первой дроби умножить на 2 ∙ 2 (произведение неподчеркнутых простых множителей второго знаменателя), а числитель и знаменатель второй дроби — на 3 («произведение» неподчеркнутых простых множителей первого знаменателя). В результате знаменатели обеих дробей станут равны числу, которое можно представить так:
2 ∙ 2 ∙ 3 ∙ 5 ∙ 7 = 105 ∙ 2 ∙ 2 = 140 ∙ 3 = 420.
Нетрудно видеть, что оба исходных знаменателя (как 105, так и 140) являются делителями числа 420, а число 420, в свою очередь, кратно обоим знаменателям, — и не просто кратно, оно является наименьшим общим кратным (НОК ) чисел 105 и 140. Это записывается так:
НОК(105, 140) = 420.
Приглядевшись повнимательнее к разложению чисел 105 и 140, мы видим, что
105 ∙ 140 = НОК(105, 140) ∙ НОД(105, 140).
Точно так же, для произвольных натуральных чисел b и d :
b ∙ d = НОК(b , d ) ∙ НОД(b , d ).
Теперь давайте доведем до конца суммирование наших дробей:
3 ∙ 5 ∙ 7 | 2 ∙ 2 ∙ 5 ∙ 7 |
2 ∙ 2 ∙ 3 ∙ 5 ∙ 7 | 2 ∙ 2 ∙ 3 ∙ 5 ∙ 7 |
2 ∙ 2 ∙ 3 ∙ 5 ∙ 7 |
2 ∙ 2 ∙ 3 ∙ 5 ∙ 7 |
2 ∙ 2 ∙ 3 ∙ 5 |
Примечание. |
Наибольший общий делитель и наименьшее общее кратное — ключевые арифметические понятия, которые позволяют без усилий оперировать обыкновенными дробями. НОК и чаще всего используются для поиска общего знаменателя нескольких дробей.
Основные понятия
Делитель целого числа X — это другое целое число Y, на которое X разделяется без остатка. К примеру, делитель 4 — это 2, а 36 — 4, 6, 9. Кратное целого X — это такое число Y, которое делится на X без остатка. К примеру, 3 кратно 15, а 6 — 12.
Для любой пары чисел мы можем найти их общие делители и кратные. К примеру, для 6 и 9 общим кратным является 18, а общим делителем — 3. Очевидно, что делителей и кратных у пар может быть несколько, поэтому при расчетах используется наибольший делитель НОД и наименьшее кратное НОК.
Наименьший делитель не имеет смысла, так как для любого числа это всегда единица. Наибольшее кратное также бессмысленно, так как последовательность кратных устремляется в бесконечность.
Нахождение НОД
Для поиска наибольшего общего делителя существует множество методов, самые известные из которых:
- последовательный перебор делителей, выбор общих для пары и поиск наибольшего из них;
- разложение чисел на неделимые множители;
- алгоритм Евклида;
- бинарный алгоритм.
Сегодня в учебных заведениях наиболее популярными являются методы разложения на простые множители и алгоритм Евклида. Последний в свою очередь используется при решении диофантовых уравнений: поиск НОД требуется для проверки уравнения на возможность разрешения в целых числах.
Нахождение НОК
Наименьшее общее кратное точно также определяется последовательным перебором или разложением на неделимые множители. Кроме того, легко найти НОК, если уже определен наибольший делитель. Для чисел X и Y НОК и НОД связаны следующим соотношением:
Для чисел X и Y НОК и НОД связаны следующим соотношением:
НОК (X,Y) = X × Y / НОД(X,Y).
Например, если НОД(15,18) = 3, то НОК(15,18) = 15 × 18 / 3 = 90. Наиболее очевидный пример использования НОК — поиск общего знаменателя, который и является наименьшим общим кратным для заданных дробей.
Взаимно простые числа
Если у пары чисел нет общих делителей, то такая пара называется взаимно простой. НОД для таких пар всегда равен единице, а исходя из связи делителей и кратных, НОК для взаимно простых равен их произведению. К примеру, числа 25 и 28 взаимно просты, ведь у них нет общих делителей, а НОК(25, 28) = 700, что соответствует их произведению. Два любых неделимых числа всегда будут взаимно простыми.
Калькулятор общего делителя и кратного
При помощи нашего калькулятора вы можете вычислить НОД и НОК для произвольного количества чисел на выбор. Задания на вычисление общих делителей и кратных встречаются в арифметике 5, 6 класса, однако НОД и НОК — ключевые понятия математики и используются в теории чисел, планиметрии и коммуникативной алгебре.
Примеры из реальной жизни
Общий знаменатель дробей
Наименьшее общее кратное используется при поиске общего знаменателя нескольких дробей. Пусть в арифметической задаче требуется суммировать 5 дробей:
1/8 + 1/9 + 1/12 + 1/15 + 1/18.
Для сложения дробей выражение необходимо привести к общему знаменателю, что сводится к задаче нахождения НОК. Для этого выберите в калькуляторе 5 чисел и введите значения знаменателей в соответствующие ячейки. Программа вычислит НОК (8, 9, 12, 15, 18) = 360. Теперь необходимо вычислить дополнительные множители для каждой дроби, которые определяются как соотношение НОК к знаменателю. Таким образом, дополнительные множители будут выглядеть как:
- 360/8 = 45
- 360/9 = 40
- 360/12 = 30
- 360/15 = 24
- 360/18 = 20.
После этого умножаем все дроби на соответствующий дополнительный множитель и получаем:
45/360 + 40/360 + 30/360 + 24/360 + 20/360.
Такие дроби мы можем легко суммировать и получить результат в виде 159/360. Сокращаем дробь на 3 и видим окончательный ответ — 53/120.
Сокращаем дробь на 3 и видим окончательный ответ — 53/120.
Решение линейных диофантовых уравнений
Линейные диофантовы уравнения — это выражения вида ax + by = d. Если отношение d / НОД(a, b) есть целое число, то уравнение разрешимо в целых числах. Давайте проверим пару уравнений на возможность целочисленного решения. Сначала проверим уравнение 150x + 8y = 37. При помощи калькулятора находим НОД (150,8) = 2. Делим 37/2 = 18,5. Число не целое, следовательно, уравнение не имеет целочисленных корней.
Проверим уравнение 1320x + 1760y = 10120. Используем калькулятор для нахождения НОД(1320, 1760) = 440. Разделим 10120/440 = 23. В результате получаем целое число, следовательно, диофантово уравнение разрешимо в целых коэффициентах.
Заключение
НОД и НОК играют большую роль в теории чисел, а сами понятия широко используются в самых разных областях математики. Используйте наш калькулятор для расчета наибольших делителей и наименьших кратных любого количества чисел.
Действия с натуральными числами — Умскул Учебник
На этой странице вы узнаете:- Рассчитаться на раз-два-три! Какие числа мы используем при счете?
- Упрощаем: как разложить число на простые множители?
- Где могут пригодиться НОК и НОД?
Математика невозможна без чисел. Из них состоят примеры, задачи и модели. Чтобы случайно не наступить на математические грабли, нужно хорошо разбираться в действиях с натуральными числами, их свойствами и особенностями.
Действия с натуральными числамиСуществует несколько множеств чисел: натуральные, целые, рациональные и так далее. Но какие же числа мы можем отнести к натуральным? Может те, в которых нет ГМО, консервантов и красителей?
Натуральные числа – это числа, употребляемые при счете.
Натуральные числа начинаются с 1 и образуются путем сложения некоторого количества единиц. Примерами натуральных чисел могут служить 1, 2, 3, 10, 1320, 130024, 1248640 и т. д.
д.
| Рассчитаться на раз-два-три! Какие числа мы используем при счете? Натуральные числа – это числа, употребляемые при счете. Они начинаются с единицы. Например, 1, 2, 3, 4, 5, 11, 123, 15964 и так далее. |
Рассмотрим основные действия, которые проводятся с натуральными числами.
СложениеСложение – это арифметическая операция, в результате которой объединяются единицы двух чисел.
Например, 2 + 3 = 5.
2 состоит из двух единиц, 3 состоит из трех единиц, тогда (1 + 1) + (1 + 1 + 1) = 5.
Допустим, вместо наших единиц будут апельсины. У Саши будет 4 апельсина, а у Маши 3 апельсина. Если девочки сложат апельсины в один пакет, то получится 7 апельсинов. Это действие можно записать через сложение как 4 + 3 = 7.
| Сложение можно записать как m + n = p, где m и n — слагаемые, p – сумма. |
1 свойство. Переместительное свойство: a + b = b + a.
Переместительное свойство: a + b = b + a.
Иначе можно сказать, что от перемены слагаемых сумма не меняется.
Например, 1 + 3 = 4 и 3 + 1 = 4. Если бы у Маши оказалось 4 апельсина, а у Саши 3, то вместе у них также останется 7 апельсинов.
2 свойство. Сочетательное свойство: a + (b + c) = (a + b) + c.
При сложении чисел не имеет значения, какие из них складывать в первую очередь: сумма не изменится.
Например, 1 + (2 + 3) = 1 + 5 = 6 и (1 + 2) + 3 = 3 + 3 = 6.
ВычитаниеВычитание – это арифметическое действие, обратное сложению.
Если при сложении мы ищем сумму через слагаемые, то в вычитании можем найти слагаемое через сумму и другое слагаемое. Например, 6 — 2 = 4.
| Вычитание можно записать как p — n = m, p — уменьшаемое, n – вычитаемое, m — разность. |
1 свойство. а — (b + c) = a — b — c.
Если из числа нужно вычесть сумму других двух чисел, то можно вычесть эти числа последовательно.
Например, 10 — (2 + 5) = 10 — 2 — 5 = 3.
2 свойство. (a + b) — c = (a — c) + b.
Если из суммы чисел нужно вычесть другое число, то сначала можно вычесть число из любого слагаемого, а потом сложить получившийся результат и оставшееся число.
Например, (8 + 2) — 3 = (8 — 3) + 2 = 7.
УмножениеУмножение – это действие, в результате которого определенное слагаемое берется несколько раз.
Например, в записи 35 * 3, число 35 берется три раза: 35 + 35 + 35.
| Умножение можно записать как m * n = p, где m и n — множители, p – произведение. |
1 свойство. Переместительное. a * b = b * a.
От перестановки множителей произведение не изменяется.
Например, 3 * 4 = 4 * 3 = 12.
2 свойство. Сочетательное свойство умножения: a * (b * c) = (a * b) * c.
Сочетательное свойство умножения: a * (b * c) = (a * b) * c.
От изменения порядка умножения чисел произведение не меняется.
Например, 34 * (2 * 4) = (34 * 2) * 4 = 272.
3 свойство. Распределительное свойство умножения: a * (b + c) = a * b + a * c.
При умножении числа на сумму, можно умножить это число на каждое слагаемое, а после сложить результаты.
Например, 2 * (59 + 91) = 2 * 59 + 2 * 91 = 300.
ДелениеДеление – это действие, обратное умножению.
Например, 35 : 5 = 7.
| Деление можно записать как m : n = p, где m — делимое, n — делитель, p – частное. |
Следует запомнить, что делить на 0 натуральные числа нельзя.
Однако не всегда получается разделить число нацело, тогда при делении появляется остаток. Например, при делении 36 на 8 получается частное 4 и остаток 4. Иначе эту операцию можно записать так: 36 = 8 * 4 + 4.
| Деление с остатком можно записать как m = n * p + r, где m — делимое, n — делитель, p – частное и r – остаток. |
Существуют признаки делимости, которые помогают сразу определить, делится ли число нацело или нет. Вот некоторые из них:
- Число делится на 2, если последняя цифра его записи четная или ноль.
Например, 1946032 будет делиться на 2, поскольку последняя цифра четная. 1946032 : 2 = 973016.
- Число делится на 3, если сумма его цифр делится на 3.
Число 951 будет делиться на 3, поскольку 9 + 5 + 1 = 15, 15 : 3 = 5. Поэтому 951 : 3 = 317.
- Число делится на 4, если две его последние цифры кратны четырем или ноли.
45216 будет делиться на 4, поскольку 16 кратно 4, тогда 45216 : 4 = 11304. Так же 700 будет кратно 4, поскольку две последние цифры – ноли, тогда 700 : 4 = 175.
- Число делится на 5, если последняя его цифра 0 или 5.

Например, 63795 : 5 = 12759, 25570 : 5 = 5114.
- Число делится на 9, если сумма его цифр делится на 9.
Сумма цифр числа 927 равна 9 + 2 + 7 = 18, то есть кратна 9, поэтому 927 : 9 = 103.
- Число делится на 10, если последняя его цифра – ноль.
Например, 2561470 : 10 = 256147.
Заметим, что при сложении и умножении натуральных чисел всегда получаются натуральные числа, тогда как при вычитании и делении не всегда получаются натуральные числа (результат будет зависеть от конкретного примера). Например, 7 — 14 = -7, где -7 – не натуральное число, 21 : 4 = 5,25, где 5,25 – не натуральное число.
Возведение в степеньВозведение в степень очень похоже на умножение, но чтобы возвести число в степень нужно умножить его на само себя. Сколько раз число будет умножено на само себя, такая степень у него и будет.
Например, 405 = 40 * 40 * 40 * 40 * 40.
| Возведение в степень можно представить как mn = p, где m – основание степени, n – показатель степени. |
Извлечение корня – действие, обратное возведению в степень.
При извлечении корня мы узнаем, в какую степень нужно возвести число, чтобы получилось данное число.
| Извлечение корня можно записать как \(\sqrt[n]{m} = p\), где n – показатель корня, m – подкоренное выражение, p – корень. |
О том, как не запутаться в корнях, смотри статью “Понятие корня”
Подведем итог:
Натуральные числа можно складывать, вычитать, умножать, делить, возводить в степень и извлекать из них корень.
Для понимания дальнейших рассуждений необходимо ввести понятие простого числа.
Простое число – это число, которое делится только на себя и на единицу.
Например, у числа 2 делителями будут только 2 и 1, у числа 17 – 17 и 1, у числа 151 – 151 и 1.
Помимо простых чисел существуют и составные числа – это числа, у которых есть другие делители, кроме 1 и самого себя.
Любое составное число можно разложить на простые множители (причем только одним способом). Например, 6 = 2 * 3, где 2 и 3 – простые числа.
Разложение на простые множители – это действие, в результате которого мы можем представить любое составное число в виде произведения нескольких простых множителей.
Умение раскладывать числа на простые множители может пригодиться для анализа чисел и их свойств.
| Упрощаем: как разложить число на простые множители? Любое число состоит из нескольких простых множителей. Разложить число на простые множители значит представить это число в виде произведения нескольких его простых множителей. |
Чтобы разложить число на простые множители, необходимо последовательно делить его на простые множители, начиная с наименьшего возможного.
Для примера разложим число 123896.
Первый подходящий делитель будет равен 2: 123896 = 61948 * 2.
61948 не является простым числом, поэтому продолжаем раскладывать, следующий делитель также равен 2: 123896 = 30974 * 2 * 2.
Продолжаем раскладывать число до тех пор, пока справа не получится произведение только из простых чисел: 123896 = 2 * 2 * 2 * 17 * 911. Для удобства повторяющиеся числа можно записать в виде степеней: 123896 = 23 * 17*911.
Процесс разложения на простые множители можно записать в виде столбика, где слева будут получившиеся в результате деления числа, а справа множители. Для примера разложим число 156:
Разложение множителей удобно применять, если необходимо найти все делители числа. Например, в числе 156 мы можем выделить не только простые множители, но и составные: 2 * 2 * 3 = 12 (156 : 12 = 13) или 2 * 3 = 6 (156 : 6 = 26) и т. д.
д.
| Любой делитель числа равен произведению нескольких его простых множителей. |
У любых двух составных чисел можно найти общие делители, то есть такие числа, на которые будут нацело делиться данные числа.
Например, рассмотрим числа 150 и 315.
Разложим их на простые множители: 150 = 2 * 3 * 52, 315 = 32 * 5 * 7.
У числа 150 можно выделить следующие делители: 1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, 150.
У числа 315: 1, 3, 5, 7, 9, 15, 21, 35, 45, 63, 105, 315.
Из них совпадают: 3, 5, 15.
Совпадающие делители будут называться общими, а наибольший из них – наибольшим общим делителем (НОД). Он обозначается D(a,b).
Если НОД чисел a и b равен единице, то это взаимно простые числа. Взаимно простыми числами могут быть и составные, например, 15 и 16.
| Чтобы найти НОД чисел, необходимо: — Каждое из них разложить на простые множители; |
Найдем НОД чисел 45 и 105:
- 45 = 32 * 5
- 105 = 3 * 5 * 7.
Совпадающие простые множители: 3 и 5, тогда D(45, 105) = 3 * 5 = 15.
У любых составных чисел можно найти наименьшее общее кратное (НОК). Это такое число, которое нацело будет делиться на данные числа.
Например, рассмотрим числа 9 и 12. Числа, кратные 9: 9, 18, 27, 36, 45, 54, 63, 72 и т.д. Числа, кратные 12: 12, 24, 36, 48, 60, 72 и т.д. Среди этих чисел есть повторяющиеся 36 и 72, они будут общими кратными для чисел 9 и 12, а меньшее из них – это наименьшее общее кратное данных чисел (НОК). НОК обозначается как К(a, b).
| Чтобы найти НОК чисел, необходимо: — Разложить их на простые множители; |
Например, найдем НОК чисел 184 и 624.
- 184 = 23 * 23
- 624 = 24 * 3 * 13
Тогда К(184, 624) = 24 * 3 * 13 * 23 = 14352.
Наименьшее общее кратное двух взаимно простых чисел будет равно произведению этих чисел.
К(а, b) = a * b, где a, b – взаимно простые числа.
Между НОК и НОД существует следующая связь: произведение НОК и НОД некоторых чисел равно произведению этих чисел.
D(a, b) * K(a, b) = a * b
| Где могут пригодиться НОК и НОД? НОК и НОД активно используются в дробях. С помощью НОД можно сразу сократить дробь. Например, D(228, 1650) = 6, следовательно дробь с такими числами сразу можно сократить на 6: \(\frac{228}{1650} = \frac{38}{275}\) С помощью НОК можно привести дроби к общему знаменателю. Например, К(6, 22) = 66, тогда дроби \(\frac{1}{6}\) и \(\frac{1}{22}\) можно привести к общему знаменателю и получить \(\frac{11}{66}\) и \(\frac{3}{66}\). |
Рассмотренные операции являются основными для вычислений в задачах. Применение описанных свойств облегчает и ускоряет счет, что даст дополнительное время на экзамене и сократит количество вычислительных ошибок.
Фактчек- Натуральные числа – это числа, используемые при счете.
- Натуральные числа можно складывать, вычитать, умножать, делить, возводить в степень и извлекать корень,. При сложении и умножении натуральных чисел можно получить только натуральные числа, а при вычитании и делении – нет.
- Существуют простые и составные числа: простые числа делятся только на единицу и само себя; составные числа имеют еще и другие делители. Каждое составное число можно разложить на произведение простых множителей, причем только одним способом.
- У нескольких чисел можно найти наибольший общий делитель и наименьшее общее кратное. Если НОД двух чисел равен 1, то это взаимно простые числа. НОК двух взаимно простых чисел будет равен произведению этих чисел.

- Произведение НОК и НОД некоторых чисел равно произведению этих чисел.
Задание 1.
Какие числа называются натуральными?
- Числа, используемые при счете.
- Все числа, которые существуют.
- Все положительные и отрицательные целые числа.
- Все четные числа.
Задание 2.
Ответь, не вычисляя, какое число делится на 3?
- 113;
- 239;
- 158726;
- 26841.
Задание 3.
Ответь, не вычисляя, какое число делится на 4?
- 7673438;
- 2850;
- 526982;
- 264864.
Задание 4.
Какое число является составным?
- 26;
- 17;
- 3;
- 97.
Задание 5.
Какое число является простым?
- 39;
- 91;
- 59;
- 93.
Ответы: 1. — 1 2. — 4 3. — 4 4. — 1 5. — 3
— 4 4. — 1 5. — 3
Страница 23 №104-119 ГДЗ к учебнику «Математика» 6 класс Мерзляк, Полонский, Якир
Задание № 104
Среди чисел 1, 3, 6, 7, 12, 13, 21, 23, 24, 28, 29, 33, 45, 47 укажите:
1) простые;
2) составные.
Ответ 7 гуру
1) 3, 7, 13, 23, 29, 47 — простые
2) 6, 12, 21, 24, 28, 45, 46, 33- составные
Задание № 105
Запишите все делители числа, подчеркните те из них, которые являются простыми числами:
1) 21; 2) 30; 3) 48; 4) 54.
Ответ
1) Д(21) = {1 , 3 , 7 , 21}
2) Д(30) = {1 , 2 , 3 , 5 , 6 , 10 , 15 , 30}
3) Д(48) = {1 , 2 , 3 , 6 , 4 , 8 , 12 , 24 , 48}
4) Д(54) = {1 , 2 , 3 , 6 , 9 , 18 , 27 , 54}
Задание № 106
Разложите на простые множители число:
1) 12;
2) 42;
3) 216;
4) 450;
5) 920;
6) 2280;
7) 10850.
Решение
Задание № 107
Разложите на простые множители число:
1) 27;
2) 56;
3) 625;
4) 820;
5) 2772;
6) 702;
7) 1224.
Решение
Задание № 108
Запишите:
1) все простые числа, которые больше 10 и меньше 25;
2) все составные числа, которые больше 35 и меньше 49.
Ответ
1) 10 < x < 25 , х — простое
х = {11, 13, 17, 19, 23}2) 35 < а < 49 , а — составное
а = {36, 38, 39, 40, 42, 44, 45, 46, 48}
Задание № 109
Запишите:
1) все простые числа, которые больше 22 и меньше 38;
2) все составные числа, которые больше 60 и меньше 78.
Ответ
1) 22 < x < 38 , х — простое
х = {23, 29, 31, 37}2) 60 < а < 78 , а — составное
а = {62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77}
Задание № 110
Простым или составным числом является произведение:
1) 13 * 1;
2) 14 * 1;
3) 4 * 7;
4) 11 * 13;
5) 43 * 1;
6) 1 * 1.
Ответ
1) простым
2) составным
3) составным
4) составным
5) простым
6) простым
Задание № 111
Запишите все делители числа, равного произведению:
1) 2 * 2 * 5;
2) 3 * 5 * 7.
Ответ
1) 2 * 2 * 5 = 20
Д(20) = {1, 2, 4, 5, 10, 20}2) 3 * 5 * 7 = 105
Д(105) = {1, 3, 5, 7, 15, 21, 35, 105}
Задание № 112
Запишите все делители числа, равного произведению:
1) 2 * 5 * 13;
2) 3 * 3 * 3* 7.
Решение
1) 2 * 5 * 13 = 130
Д(130) = {1, 2, 5, 10, 13, 26, 65, 130}2) 3 * 3 * 3* 7 = 189
Д(189) = {1, 3, 9, 21, 27, 63, 189}
Задание № 113
Чему равно частное от деления числа a на число b, если:
1) a = 2 * 2 * 2 * 3 * 3 * 7, b = 2 * 2 * 3 * 7;
2) a = 3 * 5 * 5 * 13 * 17 * 19, b = 3 * 13 * 19.
Решение
1) a : b = (2 * 2 * 2 * 3 * 3 * 7) : (2 * 2 * 3 * 7) = (2 * 3) : 1 = 6
2) a : b = (3 * 5 * 5 * 13 * 17 * 19) : (3 * 13 * 19) = (5 * 5 * 17) : 1 = 425
Задание № 114
Чему равно частное от деления числа a на число b, если:
1) a = 2 * 3 * 5 * 5 * 7 * 11 * 13, b = 2 * 5 * 13;
2) a = 2 * 2 * 3 * 5 * 23 * 37, b = 2 * 3 * 37.
Решение
1) a : b = (2 * 3 * 5 * 5 * 7 * 11 * 13) : (2 * 5 * 13) = (3 * 5 * 7 * 11) : 1 = 1155
2) a : b = (2 * 2 * 3 * 5 * 23 * 37) : (2 * 3 * 37) = (2 * 5 * 23) : 1 = 230
Задание № 115
Запишите все двузначные числа, в разложении которых на простые множители один из множителей равен:
1) 7;
2) 17;
3) 23.
Решение
1) 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98.
2) 34, 51, 68, 85.
3) 46, 69, 92.
Задание № 116
Запишите все двузначные числа, разложение которых на простые множители состоит:
1) из двух одинаковых множителей;
2) из трех одинаковых множителей.
Ответ
1) 25, 49.
2) 27
Задание № 117
Сколько существует чисел, которые можно разложить на два двузначных простых множителя, один из которых на 2 больше другого?
Воспользуйтесь таблицей простых чисел.
Решение
Шесть простых чисел:
143 = 11 * 13;
323 = 17 * 19;
899 = 29 * 31;
1763 = 41 * 43;
3599 = 59 * 61;
5183 = 71 * 73.
Задание № 118
Найдите все числа, которые можно разложить на два двузначных простых множителя, разность которых равна 4. Воспользуйтесь таблицей простых чисел.
Решение
Шесть чисел:
13 * 17 = 221;
19 * 23 = 437;
37 * 41 = 1517;
43 * 47 = 2021;
67 * 71 = 4757;
79 * 83 = 6557.
Задание № 119
Задумали простое число. Известно, что следующее за ним натуральное число тоже простое. Какое число задумали?
Ответ
Число 2
Коэффициенты 105 — Найти простые факторизации/множители 105
Факторы 105 — это список целых чисел, которые можно без остатка разделить на 105. Всего существует 8 множителей 105, среди которых 105 — самый большой множитель, а 1, 3, 5 , 7, 15, 21, 35 и 105 — положительные факторы. Сумма всех множителей числа 105 равна 192, а его множители в парах равны (1, 105), (3, 35), (5, 21) и (7, 15).
Сумма всех множителей числа 105 равна 192, а его множители в парах равны (1, 105), (3, 35), (5, 21) и (7, 15).
- Факторы 105: 1, 3, 5, 7, 15, 21, 35 и 105
- Отрицательные Факторы 105: -1, -3, -5, -7, -15, -21, -35 и -105
- Простые множители числа 105: 3, 5, 7
- Факторизация числа 105: 3 × 5 × 7 = 3 × 5 × 7
- Сумма коэффициентов 105: 192
| 1. | Какие множители числа 105? |
| 2. | Как рассчитать коэффициенты числа 105? |
| 3. | Коэффициенты 105 с помощью простой факторизации |
| 4. | Коэффициенты 105 в парах |
| 5. | Часто задаваемые вопросы о факторах 105 |
Каковы делители числа 105?
Делители 105 — это числа, которые делят 105 без остатка.
Делители числа 105 равны 1, 3, 5, 7, 15, 21, 35 и 105.
Как рассчитать коэффициенты числа 105?
Чтобы вычислить коэффициенты 105, мы можем использовать метод деления. Начнем с 1.
105 ÷ 1 оставляет в остатке 0.
Поскольку 105 нечетное число, 2 не делит 105 полностью. Таким образом, он оставляет остаток.
105 ÷ 3 листья остальные 0,
105 ÷ 5 листьев оставшиеся 0,
105 ÷ 7 листьев оставшееся 0,
105 ÷ 15 листьев оставшиеся 0,
105 ÷ 21 листья. Остаток листьев 0,
105 ÷ 105 Остаток листьев 0,
Таким образом, коэффициенты 105, которые мы получили, равны 1, 3, 5, 7, 15, 21, 35 и 105,
Изучите множители с помощью иллюстраций и интерактивных примеров
- Факторы 75: множители 75 равны 1, 3, 5, 15, 25 и 75
- Множители 175: множители 15 равны 1, 3, 5 и 15.
- Множители 35: Множители 35 равны 1, 5, 7 и 35.
- Коэффициенты 70: Коэффициенты 70 равны 1, 2, 5, 7, 10, 14, 35 и 70.

- Множители 42: Множители 1, 2, 3, 6, 7, 14, 21 и 42.
Коэффициенты 105 с помощью простой факторизации
Разложение на простые множители означает выражение составного числа в виде произведения его простых множителей.
Разложение числа 105 на простые множители = 3 × 5 × 7. Другие составные множители числа 105 можно определить по его простым множителям. Мы можем видеть, что 35 — это множитель 105. Точно так же 15 и 21 также являются множителями 105.
Делители 105 в парах
Пара чисел, которые дают 105 при умножении, являются множителями 105 в парах. Посмотрите на радугу внизу. Мы начинаем с 1 и продвигаемся вперед, включая числа, которые дают нам 105 в качестве их произведения.
Получаем следующие комбинации: 1 × 105, 3 × 35, 5 × 21 и 7 × 15.
Советы и подсказки:
- Все числа имеют не менее двух делителей. 105 будет иметь первый множитель равный 1, а другой множитель равен 105.

- Факторы 105 — это все возможные числа, на которые делится 105. Это могут быть простые числа или составные числа.
- Коэффициенты всегда являются целыми числами. Они никогда не могут быть дробями или десятичными числами.
Коэффициенты 105 решенных примеров
Пример 1: 105 студентов должны быть разделены на группы так, чтобы в каждой группе было равное количество студентов. Сколькими способами их можно сгруппировать?
Решение:
Мы будем использовать концепцию факторного спаривания, чтобы разделить 105 учащихся на группы.
Мы знаем, что (35, 3), (5, 21) и (7, 15) — пары множителей числа 105.
Таким образом, учащихся можно сгруппировать тремя различными способами.
Пример 2: У Эмили есть коробка шоколадных конфет, в которой 105 конфет. Она раздала конфеты своим одноклассникам. Сможете ли вы найти общее количество учеников, если каждому из них она даст по 5 шоколадок?
Решение:
Дано общее количество шоколадок = 105
Конфет, розданных каждому ученику = 5
Таким образом, количество учеников в классе = 105 ÷ 5 = 21 ученик.

Здесь мы можем видеть используемые числа, то есть (5,21) – это парный коэффициент 105.
Пример 3: Есть ли шанс, что вы сможете разделить 105 геометрических фигур поровну между 50 детьми?
Решение: Очевидно, что ответ НЕТ! Поскольку 50 не является коэффициентом 105 и оставляет остаток, мы не можем поровну распределить 105 блоков геометрии среди 50 детей.
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Запишитесь на бесплатный пробный урок
Часто задаваемые вопросы о множителях 105
Что такое множители 105?
Коэффициенты числа 105 равны 1, 3, 5, 7, 15, 21, 35, 105, а его отрицательные множители равны -1, -3, -5, -7, -15, -21, -35, -105 .
Сколько множителей 105 также являются множителями 3?
Поскольку множители 105 равны 1, 3, 5, 7, 15, 21, 35, 105, а множители 3 равны 1, 3.
Следовательно, [1, 3] являются общими делителями чисел 105 и 3.
Чему равна сумма всех делителей числа 105?
Сумма всех множителей 105 = (3 1 + 1 — 1)/(3 — 1) × (5 1 + 1 — 1)/(5 — 1) × (7 1 + 1 — 1)/(7 — 1) = 192
Чему равен наибольший общий делитель чисел 105 и 97?
Делители числа 105 равны 1, 3, 5, 7, 15, 21, 35, 105, а делители числа 97 равны 1, 97. являются взаимно простыми.
Следовательно, наибольший общий делитель (НОД) чисел 105 и 97 равен 1.
Каковы парные делители числа 105?
Парные множители числа 105: (1, 105), (3, 35), (5, 21), (7, 15).
Факторизация простых чисел, методы, дерево и примеры
Факторы 105 в конечном счете делят его, давая нулевой остаток. 105 является нечетным составным числом, то есть имеет более двух делителей. В этом уроке будет подробно рассмотрено несколько методов расчета этих факторов.
Какие множители числа 105?
Делители числа 105 равны 1, 3, 5, 7, 15, 21, 35 и 105. Всего 105 имеет 8 делителей, что показывает, что это составное число, состоящее из нескольких делителей.
Всего 105 имеет 8 делителей, что показывает, что это составное число, состоящее из нескольких делителей.
Эти 8 факторов можно разделить на 4 пары факторов, и эти факторы вместе с парами факторов могут быть как положительными, так и отрицательными.
Как рассчитать коэффициенты числа 105?
Множитель 105 можно рассчитать с помощью нескольких методов, таких как деление и разложение на простые множители. Но сначала мы рассмотрим метод деления на , так как его проще понять и понять.
Деление
Метод деления основан на нахождении числа, которое дает нулевой остаток при делении на 105; это число будет множителем 105. Если это целое число, частное также будет множителем 105. Использование метода деления показано ниже:
\[ \frac{105}{ 2} = 52,5 \ (\text{Не коэффициент}) \]
\[ \frac{105}{ 3} = 35 \ (фактор) \]
\[ \frac{105}{ 5} = 21 \]
Так как 21 — целое число, то 5 является делителем 105 вместе с 21. Мы пропустим шесть и перейдем к 7.
\[\frac{105 }{ 7} = 15 \]
\[ \frac{105 }{ 105} = 1 \]
Они также полностью делят число; следовательно, 1 и 105 — это множители 105.
По методу деления множители 105 равны:
Коэффициенты 105 = 1, 3, 5, 7, 15, 21, 35 и 105.
Коэффициенты 105 с помощью простой факторизации он использует простые числа, чтобы узнать простые множители любого числа. Мы делим число на любое простое число, которое делит его полностью, и продолжаем, пока не получим единицу.
Этот метод основан исключительно на простых числах. Простые числа — это все числа, которые делятся только сами на себя или на универсальный делитель 1. Поскольку этот метод дает нам только простые числа, мы называем полученные множители простые множители .
Несмотря на то, что между методом деления и разложением на простые множители существует некоторое сходство, единственное различие между ними состоит в том, что при разложении на простые множители мы делим, используя простое число; частное затем действует как дивиденд для следующего шага.
Конечный результат, который мы ищем, это 1.
Нам дано число 105. Первое, на что нужно обратить внимание, это простое или составное число; мы понимаем, что 105 не является простым числом, поскольку оно имеет несколько делителей, отличных от 1 и 105. Чтобы понять простую факторизацию числа 105, оно показано ниже:
105 $\div$ 3 = 35
35 $\div$ 7 = 5 (Частное 35 действует как делимое для этого шага)
5 $\div$ 5 = 1 достигается результат, равный 1)
Эта простая факторизация была сделана в несколько шагов, но есть альтернативный метод ее записи: 105 приведен ниже:
Рисунок 1
Факторное дерево числа 105
Факторное дерево по сути является представлением простых множителей любого заданного числа в форме дерева. В то же время существует несколько методов нахождения факторов любого заданного числа. Этот инструмент развертывает визуальный элемент для понимания факторов любого числа.
Схема нарисована в виде дерева; исходный номер записывается в начале дерева, которое затем делится на две ветви при делении; хотя бы одна из ветвей должна иметь простое число. Другое в основном составное число, если исходное число было составным числом.
Другое в основном составное число, если исходное число было составным числом.
Если исходное число простое, то дерево будет иметь только две ветви, но в случае составного числа ветви идут дальше вниз, пока в корнях дерева не будут получены все простые числа. Как только они достигнуты, дальнейшее деление невозможно, поскольку простые числа не делятся дальше.
Хотя основное определение дерева факторов и того, как оно рисуется, достаточно ясно, чтобы лучше понять его, мы рассмотрим рисунок 2, на котором точно показано, как строится дерево факторов. Мы можем заметить, что 105 находится наверху и конкретизируется в 3 и 35, которые затем продолжаются дальше: 9Рисунок 2
Это также условие для того, чтобы любые два фактора образовывали пару факторов; если они дают заданное число при умножении, они составляют пару множителей; если нет, то это просто два любых случайных фактора.
Чтобы применить это определение, давайте посмотрим на множители 105:
Факторы 105 = 1, 3, 5, 7, 15, 21, 35 и 105
Среди этих факторов никакие два фактора не составляют факторную пару; например, возьмем 5 и 7:
5 x 7 = 35
Обратите внимание, что произведение 5 и 7 не равно 105. Следовательно, 5 и 7 не образуют пару множителей. Теперь давайте посмотрим на 5 и 21:
Следовательно, 5 и 7 не образуют пару множителей. Теперь давайте посмотрим на 5 и 21:
5 x 21 = 105
Произведение 5 и 21 дает 105. Следовательно, 5 и 21 являются парой множителей 105. При том же условии следующие множители пар 105:
Пары факторов 105 = (1, 105), (3, 35), (5, 21), (7, 15)
Пары факторов могут быть положительными и отрицательными; упомянутые выше пары положительны в соответствии с соглашением, согласно которому мы игнорируем положительный знак (+) при записи положительных целых чисел. Таким образом, положительные пары множителей числа 105:
Положительные пары множителей 105 = (1, 105), (3, 35), (5, 21), (7, 15)
Но пары множителей также отрицательны. , которые по существу являются положительными парами факторов, но с отрицательным знаком (-). Итак, это:
Пары отрицательных коэффициентов 105 = (-1, -105), (-3, -35), (-5, -21), (-7, -15)
Факторы 105 Решенные примеры
Теперь, когда мы тщательно изучили теоретическую математику, давайте применим наши знания к более практической стороне. Мы будем использовать примеры в этом разделе, чтобы продемонстрировать, как каждый метод может быть применен к математическим задачам множителей 105.
Мы будем использовать примеры в этом разделе, чтобы продемонстрировать, как каждый метод может быть применен к математическим задачам множителей 105.
Пример 1
Используйте метод деления, чтобы найти множители 105. и простые методы факторизации.
Решение
Метод деления зависит от простого деления заданного числа на другое число, которое в конечном итоге делит его. Если деление полное, то и делитель, и частное являются множителями.
Полное деление подразумевает нулевой остаток, полученный в результате этого деления. Метод деления для нахождения множителей 105 приведен ниже:
Начнем с деления 105 на два и продолжим соответственно:0003
52,5 не является целым числом; следовательно, 2 не является делителем 105. Попробуем следующее целое число в строке: 3
\[ \frac{105}{ 3} = 35 \]
35 — целое число; следовательно, и 3, и 35 являются множителями 105; давайте попробуем следующее число, 4.
\[ \frac{105 }{4} = 26,25\]
26,25 не является целым числом; следовательно, 4 не является делителем 105. Теперь мы посмотрим на следующее число в строке после четырех, которое равно 5. , поэтому 5 является коэффициентом 105 вместе с 21. Мы пропустим шесть и перейдем к 7.
Теперь мы посмотрим на следующее число в строке после четырех, которое равно 5. , поэтому 5 является коэффициентом 105 вместе с 21. Мы пропустим шесть и перейдем к 7.
\[ \frac{105}{ 7} = 15 \]
Так как 15 — целое число, и мы получили нулевые остатки, 7 является делителем 105 вместе с 15.
\[\frac{105} {105} = 1 \]
Они также полностью делят число; следовательно, и 1, и 105 являются множителями 105.
Из приведенных выше шагов мы можем сделать вывод, что множители 105 равны 1, 3, 5, 7, 15, 21, 35 и 105. Общее количество Факторы равны 9 из 105.
Всего факторов 105 по методу деления:
Множители 105 = 1, 3, 5, 7, 15, 21, 35 и 105.
Теперь, когда мы вычислили множители 105, мы рассмотрим другую часть вопроса. На этом примере можно понять разницу между методом деления и методом простой факторизации.
В методе деления мы делим число на составные и простые числа, а в методе простой факторизации мы делим только на простые числа. Во-вторых, при делении мы ищем нулевой остаток, тогда как при простой факторизации мы ищем окончательный ответ 1,9.0003
Во-вторых, при делении мы ищем нулевой остаток, тогда как при простой факторизации мы ищем окончательный ответ 1,9.0003
Пример 2
Перечислите делители числа 105, а также найдите среднее значение его делителей.
Решение
В приведенном выше примере мы нашли восемь различных множителей числа 105 с помощью метода деления; вот эти коэффициенты:
Коэффициенты 105 = 1, 3, 5, 7, 15, 21, 35 и 105. среднее значение 105. Среднее значение в основном представляет собой сумму всех факторов 105, деленную на общее количество факторов, равное 8.
Среднее = Сумма всех факторов 105 / Общее количество факторов
Среднее = (1 + 3 + 5 + 7 + 15 + 21 + 35 + 105) / 8 8
Среднее = 24
Это среднее всех делителей 105, а среднее равно 24.
Следовательно, среднее всех делителей 105 равно 24.
2 Все изображения/математические рисунки созданы с помощью GeoGebra.Факторы 104 | Список факторов | Множители числа 106
Найдите простую факторизацию числа 105 с использованием показателей степени
| Введите целое число, которое вы хотите получить, его простые делители: Пример: 2, 3, 4, 11, 10225 и т.  д. д. |
| Котировки |
Результат простой факторизации:Число 105 является составным числом, поэтому его можно разложить на множители. Другими словами, 105 можно разделить на 1, само по себе и по крайней мере на 3, 5 и 7. Составное число — это натуральное число, имеющее хотя бы один положительный делитель, отличный от единицы или самого числа. Другими словами, составное число — это любое целое число, большее единицы, которое не является простым числом. Разложение числа 105 на простые множители = 3•5•7. Простые делители числа 105 равны 3, 5 и 7. Факторное дерево или простое разложение для 105Поскольку 105 является составным числом, мы можем нарисовать его факторное дерево: |
Вот ответ на такие вопросы, как: Найдите разложение числа 105 на простые множители с использованием показателей степени или является ли 105 простым или составным числом?
Используйте приведенный выше инструмент факторизации простых чисел, чтобы определить, является ли данное число простым или составным, и в этом случае вычислите его простые множители. См. также на этой веб-странице диаграмму факторизации простых чисел со всеми простыми числами от 1 до 1000.
См. также на этой веб-странице диаграмму факторизации простых чисел со всеми простыми числами от 1 до 1000.
Что такое первичная факторизация?
Определение простой факторизации
Простой факторизации — это разложение составного числа на произведение простых множителей, которые при умножении воссоздают исходное число. Факторы по определению — это числа, которые умножаются, чтобы создать другое число. Простое число — это целое число больше единицы, которое делится только на единицу и само на себя. Например, единственные делители 7 — это 1 и 7, поэтому 7 — простое число, а число 72 имеет делители, полученные из 2·9.0216 3 •3 2 подобно 2, 3, 4, 6, 8, 12, 24 … и самому 72, что делает 72 не простым числом. Обратите внимание, что единственными «простыми» делителями числа 72 являются 2 и 3, которые являются простыми числами.
Пример 1 простой факторизации
Давайте найдем простую факторизацию числа 72.
Раствор 1
Начните с наименьшего простого числа, которое делится на 72, в данном случае 2. Мы можем записать 72 как:
Мы можем записать 72 как:
72 = 2 x 36
Теперь найдите наименьшее простое число, которое делится на 36. Снова мы можем использовать 2 и записать 36 как 2 х 18, чтобы дать.
72 = 2 x 2 x 18
18 также делится на 2 (18 = 2 x 9), поэтому мы имеем:
72 = 2 x 2 x 2 x 9
9 делится на 3 (9 = 3 x 3), поэтому у нас есть:
72 = 2 x 2 x 2 x 3 x 3
2, 2, 2, 3 и 3 — все простые числа, поэтому у нас есть ответ.
Короче говоря, решение можно записать так:
72 = 2 x 36
72 = 2 x 2 x 18
72 = 2 x 2 x 2 x 9
72 = 2 x 2 x 2 x 3 x 3
72 = 2 3 x 3 2 (экспоненциальная форма простой факторизации)
Раствор 2
Использование дерева факторов:
- Процедура:
- Найти 2 множителя числа;
- Посмотрите на 2 множителя и определите, не является ли хотя бы один из них простым;
- Если это не простой множитель это;
- Повторяйте этот процесс, пока все множители не станут простыми.

Посмотрите, как разложить число 72 на множители:
| 18 / \ 3 3 | 72 не простое —> разделить на 2 36 не простое —> разделить на 2 18 не простое —> разделить на 2 9 не простое —> разделить на 3 3 и 3 простые —> стоп |
Взяв левые числа и крайнее правое число последней строки (делители), умножив их, мы получим
72 = 2 x 2 x 2 x 3 x 3
72 = 2 3 x 3 2 (экспоненциальная форма простой факторизации)
Обратите внимание, что эти делители являются простыми множителями. Их также называют листьями факторного дерева.
Пример факторизации простых чисел 2
Посмотрите, как разложить число 588 на множители:
| 588 /\ 2 294 /\ 2 147 /\ 3 49 /\ 7 7 | 588 не простое —> разделить на 2 294 не простое —> разделить на 2 147 не простое —> разделить на 3 49 не простое —> разделить на 7 7 и 7 простые —> стоп |
Взяв левые числа и крайнее правое число последней строки (делители), умножив их, мы получим
588 = 2 x 2 x 3 x 7 x 7
588 = 2 2 x 3 x 7 2 (экспоненциальная форма простой факторизации)
Таблица факторизации простых чисел 1-1000
| n | Prime Factorization | ||
|---|---|---|---|
| 2 = | 2 | ||
| 3 = | 3 | ||
| 4 = | 2•2 | ||
| 5 = | 5 | ||
| 6 = | 2•3 | ||
| 7 = | 7 | ||
| 8 = | 2•2•2 | ||
| 9 = | 3•3 | ||
| 10 = | 2•5 | ||
| 11 = | 11 | ||
| 12 = | 2•2•3 | ||
| 13 = | 13 | ||
| 14 = | 2 •7 | ||
| 15 = | 3•5 | ||
| 16 = | 2•2•2•2 | ||
| 17 = | 17 | ||
| 18 = | 2•3•3 | ||
| 19 = | 19 | ||
| 20 = | 2•2•5 | ||
| 21 = | 3•7 | ||
| 22 = | 2•11 | ||
| 23 = | 23 | ||
| 24 = | 2•2•2•3 | ||
| 25 = | 5•5 | ||
| 26 = | 2•13 | ||
| 27 = | 3•3•3 | ||
| 28 = | 2•2•7 | ||
| 29 = | 29 | ||
| 30 = | 2•3•5 | ||
| 31 = | 31 | ||
| 32 = | 2•2•2•2•2 | ||
| 33 = | 3•11 | ||
| 34 = | 2•17 | ||
| 35 = | 5•7 | ||
| 36 = | 2•2•3•3 | ||
| 37 = | 37 | ||
| 38 = | 2•19 | ||
| 39 = | 3•13 | ||
| 40 = | 2•2•2•5 | ||
| 41 = | 41 | ||
| 42 = | 2•3•7 | ||
| 43 = | 43 | ||
| 44 = | 2•2•11 | ||
| 45 = | 3•3•5 | ||
| 46 = | 2•23 | ||
| 47 = | 47 | ||
| 48 = | 2•2 •2•2•3 | ||
| 49 = | 7•7 | ||
| 50 = | 2 • 5 • 5 | ||
| 51 = | 3 • 17 | ||
| 52 = | 2 • 2 • 13 | ||
| 53 = | 533 | 3339||
| 53 = | 53 | 33339||
| 53 = | 53 | 3339||
| 53 = | 5 | ||
| 53 = | |||
. | 2•3•3•3 | ||
| 55 = | 5•11 | ||
| 56 = | 2•2•2•7 | ||
| 57 = | 3•19 | ||
| 58 = | 2•29 | ||
| 59 = | 59 | ||
| 60 = | 2•2•3•5 | ||
| 61 = | 61 | ||
| 62 = | 2•31 | ||
| 63 = | 3•3•7 | ||
| 64 = | 2 • 2 • 2 • 2 • 2 • 2 | ||
| 65 = | 5 • 13 | ||
| 66 = | 2 • 3 • 11 | ||
| 67 = | 67 | ||
| 67 = | 67 | ||
| 67. | 68 = | 2•2•17 | |
| 69 = | 3•23 | ||
| 70 = | 2•5•7 | ||
| 71 = | 71 | ||
| 72 = | 2•2•2•3•3 | ||
| 73 = | 73 | ||
| 74 = | 2•37 | ||
| 75 = | 3•5•5 | ||
| 76 = | 2•2•19 | ||
| 77 = | 7•11 | ||
| 78 = | 2•3•13 | ||
| 79 = | 79 | ||
| 80 = | 2 • 2 • 2 • 2 • 5 | ||
| 81 = | 3 • 3 • 3 • 3 | ||
| 82 = | 2 • 41 | ||
| 83 = | 2 • 41 | ||
| 83 = | 33033333333033033030330303303030333 | 3 | 30333303033 | 303 | 303 | 303 | 39303 | = | 2. |
| 84 = | 2•2•3•7 | ||
| 85 = | 5•17 | ||
| 86 = | 2•43 | ||
| 87 = | 3•29 | ||
| 88 = | 2•2•2•11 | ||
| 89 = | 89 | ||
| 90 = | 2 • 3 • 3 • 5 | ||
| 91 = | 7 • 13 | ||
| 92 = | 2 • 2 • 23 | ||
| 9003 = | . | ||
| 94 = | 2•47 | ||
| 95 = | 5•19 | ||
| 96 = | 2•2•2•2•2•3 | ||
| 97 = | 97 | ||
| 98 = | 2•7•7 | ||
| 99 = | 3•3•11 | ||
| 100 = | 2•2•5•5 | ||
| 101 = | 101 | ||
| 102 = | 2•3•17 | ||
| 103 = | 103 | ||
| 104 = | 2 • 2 • 2 • 13 | ||
| 105 = | 3 • 5 • 7 | ||
| 106 = | 2 • 53 | ||
| 107 = | |||
| 107 = | |||
| 107 = | |||
107. | 2•2•3•3•3 | ||
| 109 = | 109 | ||
| 110 = | 2 • 5 • 11 | ||
| 111 = | 3 • 37 | ||
| 112 = | 2 • 2 • 2 • 7 | 2 • 2 • 2 • 7 | . | 113 |
| 114 = | 2•3•19 | ||
| 115 = | 5•23 | ||
| 116 = | 2•2•29 | ||
| 117 = | 3• 3•13 | ||
| 118 = | 2•59 | ||
| 119 = | 7 • 17 | ||
| . | |||
| 123 = | 3 • 41 | ||
| 124 = | 2 • 2 • 31 | ||
| 125 = | 5 • 5 • 5 | ||
| 126 = | 29 29 29 2,3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3. 3,3 • 3. 3,3 • 3. 3,3 • 3. 3,3 • 3. 3,3 • 3,3 • 3,3 • 3 | ||
| 127 = | 127 | ||
| 128 = | 2•2•2•2•2•2•2 | ||
| 129 = | 3•43 | ||
| 130 = | 2•5•13 | ||
| 131 = | 131 | ||
| 132 = | 2•2•3•11 | ||
| 133 = | 7 • 19 | ||
| 134 = | 2 • 67 | ||
| 135 = | 3 • 3 • 3 • 5 | ||
| 136 = | 9 29 29 29 29 29 29 29 2. • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 5 | ||
| 136 = | 29 29 29 29 29 2. • | ||
| 137 = | 137 | ||
| 138 = | 2•3•23 | ||
| 139 = | 139 | ||
| 140 = | 2•2•5•7 | ||
| 141 = | 3•47 | ||
| 142 = | 2 • 71 | ||
| 143 = | 11 • 13 | ||
| 144 = | 2 • 2 • 2 • 3 • 3 | ||
| 145 = | 5 • 2 | ||
| = | 5 • 2 | ||
| = | 5. | 2•73 | |
| 147 = | 3•7•7 | ||
| 148 = | 2•2•37 | ||
| 149 = | 149 | ||
| 150 = | 2•3•5•5 | ||
| 151 = | 151 | ||
| 152 = | 2 • 2 • 2 • 19 | ||
| 153 = | 3 • 3 • 17 | ||
| 154 = | 2 • 7 • 110030 | ||
| 155 = | 5 310030 | ||
| 155 = | 5 310030 | ||
| 155 = | 2•2•3•13 | ||
| 157 = | 157 | ||
| 158 = | 2•79 | ||
| 159 = | 3•53 | ||
| 160 = | 2•2•2•2•2•5 | ||
| 161 = | 7•23 | ||
| 162 = | 2•3•3•3•3 | ||
| 163 = | 163 | ||
| 164 = | 2•2•41 | ||
| 165 = | 3•5•11 | ||
| 166 = | 2•83 | ||
| 167 = | 167 | ||
| 168 = | 2•2•2•3•7 | ||
| 169 = | 13•13 | ||
| 170 = | 2•5•17 | ||
| 171 = | 3 • 3 • 19 | ||
| 172 = | 2 • 2 • 43 | ||
| 173 = | 173 | ||
| 174 = | |||
| 174 = | 2 • 3 2 | ||
| 174 = | 2 • 3 2 | ||
| 174 = | 2 • 3 2 | ||
| 174 = | 9003 = | 5•5•7 | |
| 176 = | 2•2•2•2•11 | ||
| 177 = | 3•59 | ||
| 178 = | 2•89 | ||
| 179 = | 179 | ||
| 180 = | 2•2•3•3•5 | ||
| 181 = | 181 | ||
| 182 = | 2•7•13 | ||
| 183 = | 3•61 | ||
| 184 = | 2•2•2•23 | ||
| 185 = | 5•37 | ||
| 186 = | 2•3•31 | ||
| 187 = | 11•17 | ||
| 188 = | 2•2•47 | ||
| 189 = | 3•3•3•7 | ||
| 190 = | 2•5•19 | ||
| 191 = | 191 | ||
| 192 = | 2•2•2•2•2•2•3 | ||
| 193 = | 193 | ||
| 194 = | 2•97 | ||
| 195 = | 3•5•13 | ||
| 196 = | 2•2•7•7 | ||
| 197 = | 197 | ||
| 198 = | 2•3•3•11 | ||
| 199 = | 199 | ||
| 200 = | 2 • 2 • 2 • 5 • 5 | ||
| 201 = | 3 • 67 | ||
| 202 = | 2 • 101 | ||
| 203 = | |||
| 203 = | |||
| 203 = | |||
| 203 = | |||
| 203 = | |||
| 203 = | |||
. | 204 = | 2•2•3•17 | |
| 205 = | 5 • 41 | ||
| 206 = | 2 • 103 | ||
| 207 = | 3 • 3 • 23 | ||
| 208 = | 2 • 2 • 2 • 2 • 13 | ||
| 2 • 2 • 2 • 13 | 208 = | 2 • 2 • 2 • 13 | 208 = | 2 • 2 • 2 • 13 |
| 208 = | 2 • 2 • 2 • 13 | ||
| 208 = 9003 = | 11•19 | ||
| 210 = | 2•3•5•7 | ||
| 211 = | 211 | ||
| 212 = | 2•2•53 | ||
| 213 = | 3•71 | ||
| 214 = | 2•107 | ||
| 215 = | 5 • 43 | ||
| 216 = | 2 • 2) | ||
| 219 = | 3 • 73 | ||
| 220 = | 2 • 2 • 5 • 11 | ||
| 221 = | 13 • 17 | ||
| 221 = | • 17 | ||
| 221 = | |||
| 221 = | . | ||
| 223 = | 223 | ||
| 224 = | 2•2•2•2•2•7 | ||
| 225 = | 3•3•5•5 | ||
| 226 = | 2•113 | ||
| 227 = | 227 | ||
| 228 = | 2•2•3•19 | ||
| 229 = | 229 | ||
| 230 = | 2 • 5 • 23 | ||
| 231 = | 3 • 7 • 110030 | ||
| 232 = | 3 • 7 • 2 | ||
| 232 = | 3 | . | |
| 233 = | 233 | ||
| 234 = | 2 • 3 • 3 • 13 | ||
| 235 = | 5 • 47 | ||
| 236 = | 2 • 2 • 59 | ||
| 237 = | 3 • 79 | 3 | |
| 237 = | 3 • 79 | 39 | |
| 3 • 79 | 333|||
| 237. | 2 • 7 • 17 | ||
| 239 = | 239 | ||
| 240 = | 2 • 2 • 2 • 3 • 5 | ||
| 241 = | 24130 | ||
| 241 = | 241330 | ||
| 241 = | 24130 | ||
241. | 2•11•11 | ||
| 243 = | 3•3•3•3•3 | ||
| 244 = | 2 • 2 • 61 | ||
| 245 = | 5 • 7 • 7 | ||
| 246 = | 2 • 3 • 41 | ||
| 2979 2479 2479 2479 2479 2479 2479 2479 2479 2479 2479 2479 2479 2479 2479 247. | |||
| 248 = | 2 • 2 • 2 • 31 | ||
| 249 = | 3 • 83 | ||
| 250 = | 2 • 5 • 5 |
| n | Простое число Факторизация | ||
|---|---|---|---|
| 251 = | 251 | ||
| 252 = | 2•2•3•3•7 | ||
| 253 = | 11•23 | ||
| 254 = | 2•127 | ||
| 255 = | 3 • 5 • 17 | ||
| 256 = | 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 | ||
| 257 = | 257 | ||
| 258 = | 2 • 3 • 43 | 3038 258 =2 • | |
| 259 = | 7•37 | ||
| 260 = | 2•2•5•13 | ||
| 261 = | 3 • 3 • 29 | ||
| 262 = | 2 • 131 | ||
| 263 = | 263 | ||
| 264 = | 263 | ||
| 264 = | 263 | ||
| 264 = | 263 | ||
| 264 = | 263 | ||
| 264 = | 263 | ||
| 264 = | 263 | .||
| 265 = | 5•53 | ||
| 266 = | 2•7•19 | ||
| 267 = | 3•89 | ||
| 268 = | 2•2•67 | ||
| 269 = | 269 | ||
| 270 = | 2 • 3 • 3 • 3 • 5 | ||
| 271 = | 271 | ||
| 272 = | 2 • 2 • 2 • 2 • 17 | ||
| 273 = | 3. | ||
| 274 = | 2•137 | ||
| 275 = | 5•5•11 | ||
| 276 = | 2•2•3•23 | ||
| 277 = | 277 | ||
| 278 = | 2•139 | ||
| 279 = | 3•3•31 | ||
| 280 = | 2•2•2•5•7 | ||
| 281 = | 281 | ||
| 282 = | 2•3•47 | ||
| 283 = | 283 | ||
| 284 = | 2 • 2 • 71 | ||
| 285 = | 3 • 5 • 19 | ||
| 286 = | 2 • 11 • 13 | ||
| 287 = | 7. 419333 419333 | ||
| 287 = | 7. 41333 | ||
| 287 = | 7. 419333 | ||
| 287 = | 7. 41333 | ||
| 287. 288 = | 2•2•2•2•2•3•3 | ||
| 289 = | 17•17 | ||
| 290 = | 2•5•29 | ||
| 291 = | 3•97 | ||
| 292 = | 2•2•73 | ||
| 293 = | 293 | ||
| 294 = | 2 • 3 • 7 • 7 | ||
| 295 = | 5 • 59 | ||
| 296 = | 2. •3•3•11 | ||
| 298 = | 2•149 | ||
| 299 = | 13•23 | ||
| 300 = | 2•2•3•5•5 | ||
| 301 = | 7•43 | ||
| 302 = | 2•151 | ||
| 303 = | 3•101 | ||
| 304 = | 2•2•2•2•19 | ||
| 305 = | 5•61 | ||
| 306 = | 2•3•3• 17 | ||
| 307 = | 307 | ||
| 308 = | 2•2•7•11 | ||
| 309 = | 3•103 | ||
| 310 = | 2•5•31 | ||
| 311 = | 311 | ||
| 312 = | 2•2•2•3•13 | ||
| 313 = | 313 | ||
| 314 = | 2•157 | ||
| 315 = | 3•3•5•7 | ||
| 316 = | 2•2•79 | ||
| 317 = | 317 | ||
| 318 = | 2 • 3 • 53 | ||
| 319 = | 11 • 29 | ||
| 320 = | 2 • 2 • 2 • 2 • 2 • 5 | ||
| 321 = | 39 39 3. 107 • 107 • 107 • 107 • 107 • 107 • 107 • 107 • 107. 107. 107. 107. 107. 100033 107 • 107 • 107 • 107 • 107 • 107 • 107 • 107 • 107. 107. 107. 107. 107. 100033 | ||
| 321 = | 39 39 39 3 | ||
| . | |||
| 322 = | 2•7•23 | ||
| 323 = | 17•19 | ||
| 324 = | 2•2•3•3•3•3 | ||
| 325 = | 5•5•13 | ||
| 326 = | 2•163 | ||
| 327 = | 3•109 | ||
| 328 = | 2•2•2•41 | ||
| 329 = | 7•47 | ||
| 330 = | 2•3•5•11 | ||
| 331 = | 331 | ||
| 332 = | 2•2•83 | ||
| 333 = | 3•3•37 | ||
| 334 = | 2•167 | ||
| 335 = | 5•67 | ||
| 336 = | 2•2•2•2•3•7 | ||
| 337 = | 337 | ||
| 338 = | 2•13•13 | ||
| 339 = | 3•113 | ||
| 340 = | 2•2•5•17 | ||
| 341 = | 11 • 31 | ||
| 342 = | 2 • 3 • 3 • 19 | ||
| 343 = | 7 • 7 • 7 | ||
| 344 = | 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 4333 | ||
| 344 = 9003 | |||
| 345 = | 3•5•23 | ||
| 346 = | 2•173 | ||
| 347 = | 347 | ||
| 348 = | 2•2•3•29 | ||
| 349 = | 349 | ||
| 350 = | 2•5•5• 7 | ||
| 351 = | 3•3•3•13 | ||
| 352 = | 2•2•2•2•2•11 | ||
| 353 = | 353 | ||
| 354 = | 2•3•59 | ||
| 355 = | 5•71 | ||
| 356 = | 2•2•89 | ||
| 357 = | 3•7•17 | ||
| 358 = | 2•179 | ||
| 359 = | 359 | ||
| 360 = | 2 • 2 • 2 • 3 • 3 • 5 | ||
| 361 = | 19 • 19 | ||
| 362 = | 2 • 181 | ||
| 363 = | 3 • 110030 | ||
| 363 = | 3 • 110030 | 363 = | 3 • 110030 |
| 363 = | 3 • 110030 | ||
| 363 = | 3 • | 364 = | 2•2•7•13 |
| 365 = | 5•73 | ||
| 366 = | 2•3•61 | ||
| 367 = | 367 | ||
| 368 = | 2•2•2•2•23 | ||
| 369 = | 3 • 3 • 41 | ||
| 370 = | 2 • 5 • 37 | ||
| 371 = | 7 • 53 | ||
| 372 = | 2 • 2 • 310030 | ||
. | 373 | ||
| 374 = | 2•11•17 | ||
| 375 = | 3 • 5 • 5 • 5 | ||
| 376 = | 2 • 2 • 2 • 47 | ||
| 377 = | 13 • 29 | ||
| 378 = | 3 | 3939 29 23 | 3 29 23 | 339 29 29 29 29 23 | 3333939 29 29 29. 333 29 29. 2
| 378 = | . 3•3•7 | ||
| 379 = | 379 | ||
| 380 = | 2•2•5•19 | ||
| 381 = | 3•127 | ||
| 382 = | 2• 191 | ||
| 383 = | 383 | ||
| 384 = | 2•2•2•2•2•2•2•3 | ||
| 385 = | 5•7•11 | ||
| 386 = | 2•193 | ||
| 387 = | 3•3•43 | ||
| 388 = | 2•2•97 | ||
| 389 = | 389 | ||
| 390 = | 2•3•5•13 | ||
| 391 = | 17•23 | ||
| 392 = | 2•2•2•7 •7 | ||
| 393 = | 3•131 | ||
| 394 = | 2•197 | ||
| 395 = | 5•79 | ||
| 396 = | 2•2•3•3•11 | ||
| 397 = | 397 | ||
| 398 = | 2 • 199 | ||
| 399 = | 3 • 7 • 19 | ||
| 400 = | 2 • 2 • 2 • 5 • 5 | ||
| 401 = | 4013030333 | ||
401. 402 = 402 = | 2•3•67 | ||
| 403 = | 13•31 | ||
| 404 = | 2•2•101 | ||
| 405 = | 3•3•3•3•5 | ||
| 406 = | 2•7•29 | ||
| 407 = | 11•37 | ||
| 408 = | 2•2•2•3•17 | ||
| 409 = | 409 | ||
| 410 = | 2•5•41 | ||
| 411 = | 3•137 | ||
| 412 = | 2•2•103 | ||
| 413 = | 7•59 | ||
| 414 = | 2•3•3•23 | ||
| 415 = | 5•83 | ||
| 416 = | 2•2•2•2• 2•13 | ||
| 417 = | 3•139 | ||
| 418 = | 2•11•19 | ||
| 419 = | 419 | ||
| 420 = | 2•2•3• 5•7 | ||
| 421 = | 421 | ||
| 422 = | 2•211 | ||
| 423 = | 3•3•47 | ||
| 424 = | 2•2•2•53 | ||
| 425 = | 5•5•17 | ||
| 426 = | 2•3•71 | ||
| 427 = | 7•61 | ||
| 428 = | 2•2•107 | ||
| 429 = | 3•11•13 | ||
| 430 = | 2•5•43 | ||
| 431 = | 431 | ||
| 432 = | 2•2•2•2•3•3•3 | ||
| 433 = | 433 | ||
| 434 = | 2•7•31 | ||
| 435 = | 3• 5•29 | ||
| 436 = | 2•2•109 | ||
| 437 = | 19•23 | ||
| 438 = | 2•3•73 | ||
| 439 = | 439 | ||
| 440 = | 2•2•2•5•11 | ||
| 441 = | 3•3•7•7 | ||
| 442 = | 2•13•17 | ||
| 443 = | 443 | ||
| 444 = | 2•2•3•37 | ||
| 445 = | 5 • 89 | ||
| 446 = | 2 • 223 | ||
| 447 = | 3 • 149 | ||
| 448 = | 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2. | ||
| 449 = | 449 | ||
| 450 = | 2•3•3•5•5 | ||
| 451 = | 11•41 | ||
| 452 = | 2•2•113 | ||
| 453 = | 3•151 | ||
| 454 = | 2•227 | ||
| 455 = | 5 • 7 • 13 | ||
| 456 = | 2 • 2 • 2 • 3 • 19 | ||
| 457 = | 457 | ||
| 458 = | 9 2. 229999999999999999999999999999999999999999999999999999999999 | ||
| 458. = | 3•3•3•17 | ||
| 460 = | 2•2•5•23 | ||
| 461 = | 461 | ||
| 462 = | 2•3•7•11 | ||
| 463 = | 463 | ||
| 464 = | 2•2•2•2•29 | ||
| 465 = | 3•5•31 | ||
| 466 = | 2•233 | ||
| 467 = | 467 | ||
| 468 = | 2•2•3•3•13 | ||
| 469 = | 7•67 | ||
| 470 = | 2•5•47 | ||
| 471 = | 3•157 | ||
| 472 = | 2•2•2•59 | ||
| 473 = | 11•43 | ||
| 474 = | 2•3•79 | ||
| 475 = | 5•5•19 | ||
| 476 = | 2•2•7•17 | ||
| 477 = | 3• 3•53 | ||
| 478 = | 2•239 | ||
| 479 = | 479 | ||
| 480 = | 2•2•2•2•2•3•5 | ||
| 481 = | 13•37 | ||
| 482 = | 2•241 | ||
| 483 = | 3•7•23 | ||
| 484 = | 2•2•11•11 | ||
| 485 = | 5•97 | ||
| 486 = | 2•3•3•3 •3•3 | ||
| 487 = | 487 | ||
| 488 = | 2•2•2•61 | ||
| 489 = | 3•163 | ||
| 490 = | 2•5•7•7 | ||
| 491 = | 491 | ||
| 492 = | 2•2•3•41 | ||
| 493 = | 17•29 | ||
| 494 = | 2•13•19 | ||
| 495 = | 3•3•5•11 | ||
| 496 = | 2•2 •2•2•31 | ||
| 497 = | 7•71 | ||
| 498 = | 2 • 3 • 83 | ||
| 499 = | 499 | ||
| 500 = | 2 • 2 • 5 • 5 • 5 |
| n | Prime Factorization | |
|---|---|---|
| 501 = | 3•167 | |
| 502 = | 2•251 | |
| 503 = | 503 | |
| 504 = | 2 •2•2•3•3•7 | |
| 505 = | 5•101 | |
| 506 = | 2•11•23 | |
| 507 = | 3•13•13 | |
| 508 = | 2•2•127 | |
| 509 = | 509 | |
| 510 = | 2 • 3 • 5 • 17 | |
| 511 = | 7 • 73 | |
| 512 = | 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 | |
| 513 = | 3•3•3•19 | |
| 514 = | 2•257 | |
| 515 = | 5•103 | |
| 516 = | 2•2•3•43 | |
| 517 = | 11•47 | |
| 518 = | 2•7•37 | |
| 519 = | 3 • 173 | |
| 520 = | 2 • 2 • 2 • 5 • 13 | |
| 521 = | 521 | |
| 522 = | ||
| 522 = | ||
| 522130 | ||
| 52 | ||
| = | ||
| = | ||
| . | ||
| 523 = | 523 | |
| 524 = | 2•2•131 | |
| 525 = | 3•5•5•7 | |
| 526 = | 2•263 | |
| 527 = | 17•31 | |
| 528 = | 2•2•2 •2•3•11 | |
| 529 = | 23•23 | |
| 530 = | 2•5•53 | |
| 531 = | 3•3•59 | |
| 532 = | 2•2•7•19 | |
| 533 = | 13•41 | |
| 534 = | 2•3•89 | |
| 535 = | 5•107 | |
| 536 = | 2•2•2•67 | |
| 537 = | 3•179 | |
| 538 = | 2•269 | |
| 539 = | 7•7•11 | |
| 540 = | 2•2•3•3•3•5 | |
| 541 = | 541 | |
| 542 = | 2•271 | |
| 543 = | 3•181 | |
| 544 = | 2•2•2•2•2•17 | |
| 545 = | 5•109 | |
| 546 = | 2•3•7•13 | |
| 547 = | 547 | |
| 548 = | 2•2•137 | |
| 549 = | 3•3•61 | |
| 550 = | 2•5•5•11 | |
| 551 = | 19•29 | |
| 552 = | 2•2•2•3•23 | |
| 553 = | 7•79 | |
| 554 = | 2•277 | |
| 555 = | 3•5•37 | |
| 556 = | 2•2•139 | |
| 557 = | 557 | |
| 558 = | 2•3•3•31 | |
| 559 = | 13•43 | |
| 560 = | 2•2•2•2•5•7 | |
| 561 = | 3•11•17 | |
| 562 = | 2•281 | |
| 563 = | 563 | |
| 564 = | 2•2•3•47 | |
| 565 = | 5•113 | |
| 566 = | 2•283 | |
| 567 = | 3•3•3•3•7 | |
| 568 = | 2•2•2•71 | |
| 569 = | 569 | |
| 570 = | 2 •3•5•19 | |
| 571 = | 571 | |
| 572 = | 2•2•11•13 | |
| 573 = | 3•191 | |
| 574 = | 2•7•41 | |
| 575 = | 5•5•23 | |
| 576 = | 2•2•2•2•2•2•3•3 | |
| 577 = | 577 | |
| 578 = | 2•17•17 | |
| 579 = | 3•193 | |
| 580 = | 2•2•5•29 | |
| 581 = | 7•83 | |
| 582 = | 2•3•97 | |
| 583 = | 11•53 | |
| 584 = | 2•2•2•73 | |
| 585 = | 3 • 3 • 5 • 13 | |
| 586 = | 2. 589 = 589 = | 19•31 |
| 590 = | 2•5•59 | |
| 591 = | 3•197 | |
| 592 = | 2•2•2•2•37 | |
| 593 = | 593 | |
| 594 = | 2•3•3• 3•11 | |
| 595 = | 5•7•17 | |
| 596 = | 2•2•149 | |
| 597 = | 3•199 | |
| 598 = | 2• 13•23 | |
| 599 = | 599 | |
| 600 = | 2 • 2 • 2 • 3 • 5 • 5 | |
| 601 = | 601 | |
| 602 = | 2 • 7 • 43 | |
| 603 = | 3 • 67 | |
| 603 = | 3 • 67 | 603 = | 3 • 3. 67 | 603 = | 3 • 3. 67 |
| . | ||
| 604 = | 2•2•151 | |
| 605 = | 5•11•11 | |
| 606 = | 2•3•101 | |
| 607 = | 607 | |
| 608 = | 2•2•2•2•2•19 | |
| 609 = | 3•7•29 | |
| 610 = | 2•5•61 | |
| 611 = | 13•47 | |
| 612 = | 2•2•3•3•17 | |
| 613 = | 613 | |
| 614 = | 2•307 | |
| 615 = | 3•5•41 | |
| 616 = | 2•2•2•7•11 | |
| 617 = | 617 | |
| 618 = | 2•3•103 | |
| 619 = | 619 | |
| 620 = | 2 • 2 • 5 • 31 | |
| 621 = | 3 • 3 • 3 • 23 | |
| 622 = 9 2100393 | 9 | |
| 622 = | ||
| 61212 | ||
. | 623 = | 7•89 |
| 624 = | 2•2•2•2•3•13 | |
| 625 = | 5•5•5•5 | |
| 626 = | 2•313 | |
| 627 = | 3•11•19 | |
| 628 = | 2 • 2 • 157 | |
| 629 = | 17 • 37 | |
| 630 = | 2 • 3 • 3 • 5 • 7 | |
| 631 = | 63130 | |
| 631 = | 3 | |
| 631 = | .2 • 2 • 2 • 79 | |
| 633 = | 3 • 211 | |
| 634 = | 2 • 317 | |
| 635 = | 5. • 127733 | |
| 635 = | ||
| 637 = | 7•7•13 | |
| 638 = | 2•11•29 | |
| 639 = | 3•3•71 | |
| 640 = | 2•2•2•2•2•2•2•5 | |
| 641 = | 641 | |
| 642 = | 2 • 3 • 107 | |
| 643 = | 643 | |
| 644 = | 2 | |
| 644 = | 2900 2 | |
644. | 3•5•43 | |
| 646 = | 2•17•19 | |
| 647 = | 647 | |
| 648 = | 2 • 2 • 2 • 3 • 3 • 3 • 3 | |
| 649 = | 11 • 59 | |
| 650 = | 29 2 • 5 • 5 • 5 • 5 • 5 • 5 • 5 • 5 • 5 • 5 • 5 • 5 • 5 • 5 • 5 • 5 • 5 • 5 • 5 • 5 • 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5. 5 | |
| 6503029 | ||
| 651 = | 3•7•31 | |
| 652 = | 2•2•163 | |
| 653 = | 653 | |
| 654 = | 2•3•109 | |
| 655 = | 5•131 | |
| 656 = | 2•2•2•2•41 | |
| 657 = | 3•3•73 | |
| 658 = | 2•7•47 | |
| 659 = | 659 | |
| 660 = | 2•2•3•5 •11 | |
| 661 = | 661 | |
| 662 = | 2•331 | |
| 663 = | 3•13•17 | |
| 664 = | 2•2•2•83 | |
| 665 = | 5•7•19 | |
| 666 = | 2•3•3•37 | |
| 667 = | 23•29 | |
| 668 = | 2•2•167 | |
| 669 = | 3•223 | |
| 670 = | 2•5•67 | |
| 671 = | 11•61 | |
| 672 = | 2•2•2•2•2•3•7 | |
| 673 = | 673 | |
| 674 = | 2•337 | |
| 675 = | 3•3•3•5•5 | |
| 676 = | 2•2•13•13 | |
| 677 = | 677 | |
| 678 = | 2•3•113 | |
| 679 = | 7•97 | |
| 680 = | 2•2•2•5•17 | |
| 681 = | 3•227 | |
| 682 = | 2•11•31 | |
| 683 = | 683 | |
| 684 = | 2•2•3•3•19 | |
| 685 = | 5 • 137 | |
| 686 = | 2 • 7 • 7 • 7 | |
| 687 = | 3 • 229 | |
| 688 = | ||
| . 43 | ||
| 689 = | 13•53 | |
| 690 = | 2•3•5•23 | |
| 691 = | 691 | |
| 692 = | 2•2•173 | |
| 693 = | 3•3•7•11 | |
| 694 = | 2•347 | |
| 695 = | 5•139 | |
| 696 = | 2•2•2•3•29 | |
| 697 = | 17•41 | |
| 698 = | 2•349 | |
| 699 = | 3•233 | |
| 700 = | 2•2•5•5•7 | |
| 701 = | 701 | |
| 702 = | 2• 3•3•3•13 | |
| 703 = | 19•37 | |
| 704 = | 2•2•2•2•2•2•11 | |
| 705 = | 3•5•47 | |
| 706 = | 2•353 | |
| 707 = | 7•101 | |
| 708 = | 2•2•3•59 | |
| 709 = | 709 | |
| 710 = | 2•5•71 | |
| 711 = | 3 •3•79 | |
| 712 = | 2•2•2•89 | |
| 713 = | 23 • 31 | |
| 714 = | 2 • 3 • 7 • 17 | |
| 715 = | 5 • 11 • 13 | |
| 716 = | 3•239 | |
| 718 = | 2•359 | |
| 719 = | 719 | |
| 720 = | 2•2•2•2•3•3•5 | |
| 721 = | 7•103 | |
| 722 = | 2•19•19 | |
| 723 = | 3•241 | |
| 724 = | 2•2•181 | |
| 725 = | 5•5•29 | |
| 726 = | 2•3•11 •11 | |
| 727 = | 727 | |
| 728 = | 2•2•2•7•13 | |
| 729 = | 3•3•3•3•3•3 | |
| 730 = | 2•5•73 | |
| 731 = | 17•43 | |
| 732 = | 2•2•3•61 | |
| 733 = | 733 | |
| 734 = | 2•367 | |
| 735 = | 3•5•7•7 | |
| 736 = | 2•2•2•2•2•23 | |
| 737 = | 11•67 | |
| 738 = | 2•3•3•41 | |
| 739 = | 739 | |
| 740 = | 2•2•5•37 | |
| 741 = | 3•13•19 | |
| 742 = | 2•7•53 | |
| 743 = | 743 | |
| 744 = | 2•2•2•3•31 | |
| 745 = | 5 • 149 | |
| 746 = | 2 • 373 | |
| 9003 = | 7•107 | |
| 750 = | 2•3•5•5•5 |
| n | Prime Factorization |
|---|---|
| 751 = | 751 |
| 752 = | 2•2•2•2•47 |
| 753 = | 3•251 |
| 754 = | 2 • 13 • 29 |
| 755 = | 5 • 151 |
| 756 = | 2 • 2 • 3 • 3 • 3 • |
| 757 = | |
| 757 = | 757 =3333 |
| 757 = | |
| 757 = | |
| 757 = | 757 =3339 | 757 =3333 | . |
| 758 = | 2•379 |
| 759 = | 3•11•23 |
| 760 = | 2•2•2•5•19 |
| 761 = | 761 |
| 762 = | 2•3•127 |
| 763 = | 7•109 |
| 764 = | 2•2•191 |
| 765 = | 3•3•5•17 |
| 766 = | 2•383 |
| 767 = | 13•59 |
| 768 = | 2•2•2•2•2•2•2•2•3 |
| 769 = | 769 |
| 770 = | 2•5•7•11 |
| 771 = | 3•257 |
| 772 = | 2•2•193 |
| 773 = | 773 |
| 774 = | 2•3•3•43 |
| 775 = | 5•5•31 |
| 776 = | 2•2•2•97 |
| 777 = | 3•7•37 |
| 778 = | 2•389 |
| 779 = | 19•41 |
| 780 = | 2•2•3•5•13 |
| 781 = | 11 • 71 |
| 782 = | 2 • 17 • 23 |
| 783 = | 3 • 3 • 3 • 29 |
| 784 = | 29 29 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2. •7•7 •7•7 |
| 785 = | 5•157 |
| 786 = | 2•3•131 |
| 787 = | 787 |
| 788 = | 2•2•197 |
| 789 = | 3•263 |
| 790 = | 2•5•79 |
| 791 = | 7•113 |
| 792 = | 2•2•2•3•3•11 |
| 793 = | 13•61 |
| 794 = | 2•397 |
| 795 = | 3•5•53 |
| 796 = | 2•2•199 |
| 797 = | 797 |
| 798 = | 2•3•7•19 |
| 799 = | 17•47 |
| 800 = | 2 • 2 • 2 • 2 • 2 • 5 • 5 |
| 801 = | 3 • 3 • 89 |
| 802 = | 2 • 401 |
| 803 = | 9 |
| 803 = | 99 |
. | |
| 804 = | 2•2•3•67 |
| 805 = | 5 • 7 • 23 |
| 806 = | 2 • 13 • 31 |
| 807 = | 3 • 269 |
| 808 = | 2 • 2 • 2 • 101 |
| 2 • 2 • 2 • 100039 | 9008 = | 2. | 809 |
| 810 = | 2•3•3•3•3•5 |
| 811 = | 811 |
| 812 = | 2•2•7•29 |
| 813 = | 3•271 |
| 814 = | 2•11•37 |
| 815 = | 5 • 163 |
| 816 = | 2 • 2 • 2 • 2 • 3 • 17 |
| 817 = | 19. • 43 |
| 818 818 = | . |
| 819 = | 3•3•7•13 |
| 820 = | 2•2•5•41 |
| 821 = | 821 |
| 822 = | 2•3 •137 |
| 823 = | 823 |
| 824 = | 2 • 2 • 2 • 103 |
| 825 = | 3 • 5 • 5 • 11 |
| 826 = | 2 • 7 • 59 |
| 827 = | 82777 |
| 827 = | 82777 |
827. = = | 2•2•3•3•23 |
| 829 = | 829 |
| 830 = | 2•5•83 |
| 831 = | 3•277 |
| 832 = | 2•2•2•2•2•2•13 |
| 833 = | 7•7•17 |
| 834 = | 2•3•139 |
| 835 = | 5•167 |
| 836 = | 2•2•11•19 |
| 837 = | 3•3• 3•31 |
| 838 = | 2•419 |
| 839 = | 839 |
| 840 = | 2•2•2•3•5•7 |
| 841 = | 29•29 |
| 842 = | 2•421 |
| 843 = | 3•281 |
| 844 = | 2•2•211 |
| 845 = | 5•13•13 |
| 846 = | 2•3•3•47 |
| 847 = | 7 • 11 • 11 |
| 848 = | 2 • 2 • 2 • 2 • 53 |
| 849 = | 3 • 283 |
| 850 = | 29 29 29 283 |
| 850 = | 29 29 29 2 |
| 850 = | 29 29 2 |
.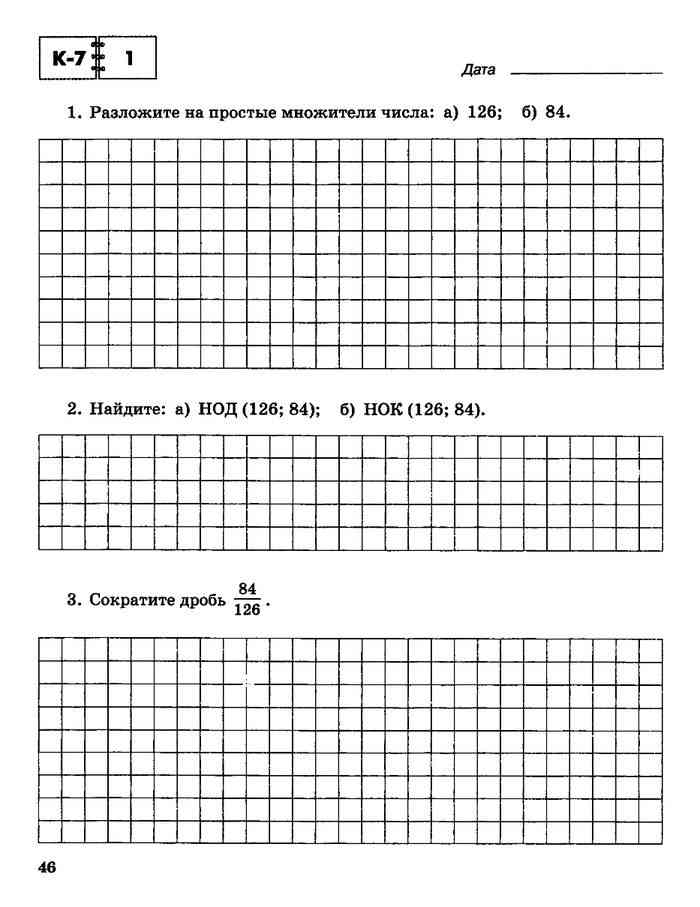 •17 •17 | |
| 851 = | 23•37 |
| 852 = | 2•2•3•71 |
| 853 = | 853 |
| 854 = | 2•7•61 |
| 855 = | 3•3•5•19 |
| 856 = | 2•2•2 •107 |
| 857 = | 857 |
| 858 = | 2•3•11•13 |
| 859 = | 859 |
| 860 = | 2•2•5•43 |
| 861 = | 3•7•41 |
| 862 = | 2•431 |
| 863 = | 863 |
| 864 = | 2•2•2•2•2•3•3•3 |
| 865 = | 5•173 |
| 866 = | 2•433 |
| 867 = | 3•17•17 |
| 868 = | 2•2•7•31 |
| 869 = | 11•79 |
| 870 = | 2•3•5•29 |
| 871 = | 13•67 |
| 872 = | 2•2•2•109 |
| 873 = | 3•3•97 |
| 874 = | 2•19•23 |
| 875 = | 5•5•5•7 |
| 876 = | 2•2•3•73 |
| 877 = | 877 |
| 878 = | 2•439 |
| 879 = | 3•293 |
| 880 = | 2•2•2•2•5•11 |
| 881 = | 881 |
| 882 = | 2•3•3•7•7 |
| 883 = | 883 |
| 884 = | 2•2•13•17 |
| 885 = | 3 • 5 • 59 |
| 886 = | 2 • 443 |
| 887 = | 887 |
| 888 = | 887 |
| 888 = | |
| 888 = | |
| 889 = | 7•127 |
| 890 = | 2•5•89 |
| 891 = | 3•3•3•3•11 |
| 892 = | 2•2•223 |
| 893 = | 19•47 |
| 894 = | 2 • 3 • 149 |
| 895 = | 5 • 179 |
| 896 = | 2 • 2 • 2 • 2 • 2 • 2 • 7 |
| 99797 297 897 297 297 297 297 297 297 297 297 297 297 297 297 297 297 297 297 297 297 297 297 29797. | 3•13•23 |
| 898 = | 2•449 |
| 899 = | 29•31 |
| 900 = | 2•2•3•3•5•5 |
| 901 = | 17•53 |
| 902 = | 2•11•41 |
| 903 = | 3•7•43 |
| 904 = | 2•2•2•113 |
| 905 = | 5•181 |
| 906 = | 2•3•151 |
| 907 = | 907 |
| 908 = | 2•2•227 |
| 909 = | 3•3•101 |
| 910 = | 2•5•7•13 |
| 911 = | 911 |
| 912 = | 2•2•2•2• 3•19 |
| 913 = | 11•83 |
| 914 = | 2•457 |
| 915 = | 3•5•61 |
| 916 = | 2•2• 229 |
| 917 = | 7•131 |
| 918 = | 2•3•3•3•17 |
| 919 = | 919 |
| 920 = | 2•2•2•5•23 |
| 921 = | 3•307 |
| 922 = | 2 • 461 |
| 923 = | 13 • 71 |
| 924 = | 2 • 2 • 3 • 7 • 11 |
| 925 = | |
| 925. | |
| 926 = | 2•463 |
| 927 = | 3•3•103 |
| 928 = | 2•2•2•2•2•29 |
| 929 = | 929 |
| 930 = | 2•3•5•31 |
| 931 = | 7 • 7 • 19 |
| 932 = | 2 • 2 • 233 |
| 933 = | 3 • 311 |
| 934 = | 2 • 467 | 934 = | 2. •17 |
| 936 = | 2•2•2•3•3•13 |
| 937 = | 937 |
| 938 = | 2•7•67 |
| 939 = | 3•313 |
| 940 = | 2•2•5•47 |
| 941 = | 941 |
| 942 = | 2 • 3 • 157 |
| 943 = | 23 • 41 |
| 944 = | 2 • 2 • 2 • 2 |
| 944 = | 3•3•3•5•7 |
| 946 = | 2•11•43 |
| 947 = | 947 |
| 948 = | 2 • 2 • 3 • 79 |
| 949 = | 13 • 73 |
. | |
| 951 = | 3•317 |
| 952 = | 2•2•2•7•17 |
| 953 = | 953 |
| 954 = | 2•3•3 •53 |
| 955 = | 5•191 |
| 956 = | 2•2•239 |
| 957 = | 3•11•29 |
| 958 = | 2•479 |
| 959 = | 7•137 |
| 960 = | 2 • 2 • 2 • 2 • 2 • 2 • 3 • 5 |
| 961 = | 31 • 31 |
| 962 = | 2 • 13 • 37 |
| 963 = | |
| 963 = | |
| 9003 = | |
| . •3•107 | |
| 964 = | 2•2•241 |
| 965 = | 5•193 |
| 966 = | 2•3•7•23 |
| 967 = | 967 |
| 968 = | 2•2•2•11•11 |
| 969 = | 3 • 17 • 19 |
| 970 = | 2 • 5 • 97 |
| 971 = | 971 |
| 972 = | 2 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3 • 3. 3 3 |
| 973 = | 7•139 |
| 974 = | 2•487 |
| 975 = | 3•5•5•13 |
| 976 = | 2•2•2•2•61 |
| 977 = | 977 |
| 978 = | 2• 3•163 |
| 979 = | 11•89 |
| 980 = | 2•2•5•7•7 |
| 981 = | 3•3•109 |
| 982 = | 2•491 |
| 983 = | 983 |
| 984 = | 2•2•2•3•41 |
| 985 = | 5•197 |
| 986 = | 2•17•29 |
| 987 = | 3•7•47 |
| 988 = | 2•2•13•19 |
| 989 = | 23•43 |
| 990 = | 2•3•3•5•11 |
| 991 = | 991 |
| 992 = | 2•2•2•2•2•31 |
| 993 = | 3•331 |
| 994 = | 2•7•71 |
| 995 = | 5•199 |
| 996 = | 2•2•3•83 |
| 997 = | 997 |
| 998 = | 2•499 |
| 999 = | 3•3•3•37 |
| 1000 = | 2•2•2•5•5•5 |
Калькулятор факторизации простых чисел
Пожалуйста, дайте ссылку на эту страницу! Просто щелкните правой кнопкой мыши на изображении выше, выберите «Скопировать адрес ссылки», а затем вставьте его в HTML-код.
Факторизация числа образцов.
- Prime factorization of 85
- Prime factorization of 11001
- Prime factorization of 1
- Prime factorization of 432
- Prime factorization of 27960
- Prime factorization of 8153
- Prime factorization of 2
- Prime факторизация числа 890
- Факторизация числа 701408733
| 9 | Оценить | квадратный корень из 12 | ||
| 10 | Оценить | квадратный корень из 20 | ||
| 11 | Оценить | квадратный корень из 50 | 94 | |
| 18 | Оценить | квадратный корень из 45 | ||
| 19 | Оценить | квадратный корень из 32 | ||
| 20 | Оценить | квадратный корень из 18 | 92 |
Добро пожаловать на курс математики 105 — Прикладная линейная алгебра
Начало работы: подготовка к первому учебному дню
Добро пожаловать на курс математики 105: Исчисление III в колледже Футхилл с Джеффом Андерсоном. Этот курс Math 105 является вторым в серии из двух четвертей по начальной и средней алгебре. Для получения дополнительной информации о математике 105 в колледже Футхилл посетите веб-сайт математического факультета Футхилла. Для студентов, пожалуйста, проверьте учетную запись электронной почты, которую вы указали на MyPortal.
Этот курс Math 105 является вторым в серии из двух четвертей по начальной и средней алгебре. Для получения дополнительной информации о математике 105 в колледже Футхилл посетите веб-сайт математического факультета Футхилла. Для студентов, пожалуйста, проверьте учетную запись электронной почты, которую вы указали на MyPortal.
В знак любезности по отношению к вам, мои ученики, я предоставляю вам электронные копии материалов нашего курса по курсу Jeff’s Math 105. в зимнем квартале 2020 года. К ним относятся: .0211 Календарь занятий: Зима 2022 г., математика 105: Календарь курсов Джеффа (.pdf) или (.docx)
Часто задаваемые вопросы на веб-странице курса: Зима 2022 г., математика 105: Часто задаваемые вопросы о веб-сайте курса
Часто задаваемые вопросы о посещении зимы 20207: 20007 105: Часто задаваемые вопросы о посещаемости
Часто задаваемые вопросы о перевернутом обучении: Зима 2022 г., математика 105: Часто задаваемые вопросы о перевернутом обучении
Часто задаваемые вопросы о командном обучении: Зима 2022 г. , математика 105: Часто задаваемые вопросы о групповом обучении
, математика 105: Часто задаваемые вопросы о групповом обучении
Часто задаваемые вопросы об оценивании: Зима 2022 г., Математика 105: Часто задаваемые вопросы об оценках
Математика Discord: Зима 2022 г., Математика 105 Канал Discord (спасибо, Ноэль)
Ресурсы для обучения Как учиться:
Сообщество Learning Code
The Sweet Spot: продуктивная борьба и глубокая практика
Безграничные ключи к обучению разуму
Покорение колледжа Учебные навыки Страница
Страница обучения навыкам математики
Математика 105, Алгебра среднего уровня: Ресурсы для урока
| МАТЕМАТИКА 105, ПРОМЕЖУТОЧНАЯ АЛГЕБРА | |
| НАЗВАНИЕ УРОКА | Плейлист для уроков |
|---|---|
УРОК 1: ВВЕДЕНИЕ В АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ
| УРОК 1 Плейлист |
УРОК 2: ОБЗОР ГРАФИКОВ
| УРОК 2 ПЛЕЙЛИСТ |
УРОК 3: ВВЕДЕНИЕ В ФАКТОРИНГ И СВОЙСТВО НУЛЕВОГО ПРОДУКТА (ZPP)
| УРОК 3 Плейлист |
УРОК 4: ФАКТОРИЗАЦИЯ ОБЩИХ КВАДРАТИЧНЫХ МНОГОЧЛЕНОВ
| ПЛЕЙЛИСТ ДЛЯ УРОКА 4 ДЖЕФФА ИЛИ ЖЕ M105 УРОК 4 ПЛЕЙЛИСТ |
УРОК 5: ФАКТОРИЗАЦИЯ СПЕЦИАЛЬНЫХ КВАДРАТИЧНЫХ МНОГОЧЛЕНОВ
| Плейлист для урока Джеффа 5 ИЛИ ЖЕ M105 УРОК 5 ПЛЕЙЛИСТ |
УРОК 6: РЕШЕНИЕ КВАДРАТИЧНЫХ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ ФАКТОРИНГА
| M105 УРОК 6 Плейлист |
УРОК 7: ВВЕДЕНИЕ В ФУНКЦИЮ АБСОЛЮТНОГО ЗНАЧЕНИЯ
| M105 УРОК 7 ПЛЕЙЛИСТ |
УРОК 8: РЕШЕНИЕ АБСОЛЮТНЫХ УРАВНЕНИЙ
| M105 УРОК 8 ПЛЕЙЛИСТ |
УРОК 9: ВВЕДЕНИЕ В РАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ
| М105 УРОК 9ПЛЕЙЛИСТ |
УРОК 10: УПРОЩЕНИЕ СУММЫ РАЦИОНАЛЬНЫХ УРАВНЕНИЙ
| M105 УРОК 10 Плейлист |
УРОК 11: РЕШЕНИЕ РАЦИОНАЛЬНЫХ УРАВНЕНИЙ
| M105 УРОК 11 ПЛЕЙЛИСТ |
УРОК 12: ВВЕДЕНИЕ В РАДИКАЛЬНЫЕ ВЫРАЖЕНИЯ
| M105 УРОК 12 Плейлист |
УРОК 13: ВВЕДЕНИЕ В ОБОЗНАЧЕНИЕ Дробной Степени
| M105 УРОК 13 Плейлист |
УРОК 14: Умножение и деление подкоренных выражений
| M105 УРОК 14 СПИСОК ВОСПРОИЗВЕДЕНИЯ |
УРОК 15: РЕШЕНИЕ РАДИКАЛЬНЫХ УРАВНЕНИЙ
| M105 УРОК 15 ПЛЕЙЛИСТ |
УРОК 16: РЕШАЙТЕ КВАДРАТНЫЕ УРАВНЕНИЯ, ЗАПОЛНЯЯ КВАДРАТ
| M105 УРОК 16 Плейлист |
УРОК 17: РЕШЕНИЕ КВАДРАТИЧНЫХ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ КВАДРАТИЧНОЙ ФОРМУЛЫ
| M105 УРОК 17 СПИСОК ВОСПРОИЗВЕДЕНИЯ |
УРОК 18: ИСПОЛЬЗУЙТЕ ДИСКРИМИНАНТ ДЛЯ КЛАССИФИКАЦИИ РЕШЕНИЙ КВАДРАТИЧНЫХ УРАВНЕНИЙ
| M105 УРОК 18 Плейлист |
Ресурсы для подготовки к тесту по математике 105
Ниже вы найдете ряд ресурсов, которые помогут вам подготовиться и успешно сдать экзамены в классе. Наслаждаться!
| МАТЕМАТИКА 105 РЕСУРСЫ ДЛЯ ВИКТОРИН НА НАВЫКИ | |
КОНТРОЛЬ НАВЫКОВ В КЛАССЕ 1: АКЦЕНТ НА УРОКАХ 1–2
| |
КОНТРОЛЬ НАВЫКОВ В КЛАССЕ 2: АКЦЕНТ НА УРОКАХ 3–4
| |
ТЕСТ ПО НАВЫКАМ В КЛАССЕ 3: АККУМУЛЯРНО НА УРОКАХ 4, 5, 6, 7 И 8
| |
КОНТРОЛЬ НАВЫКОВ В КЛАССЕ 4: АКЦЕНТ НА УРОКАХ 9, 10 и 11
| |
ТЕСТ ПО НАВЫКАМ В КЛАССЕ 5: АККУМУЛЯРНО НА УРОКАХ 11, 12, 13, 14 И 15
| |
Математика 105 Ресурсы для подготовки к экзаменам
Ниже вы найдете ряд ресурсов, которые помогут вам подготовиться и успешно сдать экзамены в классе. Наслаждаться!
| МАТЕМАТИКА 105 ЭКЗАМЕНАЦИОННЫЕ РЕСУРСЫ | |
ЭКЗАМЕН В КЛАССЕ 1
| |
ЗАКЛЮЧИТЕЛЬНЫЙ ЭКЗАМЕН В КЛАССЕ
| |
Математика 105 Контрольные и экзаменационные ресурсы
После вашей первой попытки сдать любую контрольную или экзамен в классе я призываю вас поразмышлять над своей успеваемостью. В частности, я предлагаю вам возможность заработать кредит за исправление ваших ошибок. Ниже приведен список документов, в которых даны подробные инструкции о том, как я ожидаю от вас форматирования ваших исправлений.
| МАТЕМАТИКА 105 ПОПРАВКИ К ВИКТОРАМ И ЭКЗАМЕНАМ | |
| |


 Для решения некоторых задач требуется знать, что такое квадрат числа. Квадратом числа a называется число a , помноженное само на себя, то есть a ∙a . (Как нетрудно видеть, оно равно площади квадрата со стороной a ).
Для решения некоторых задач требуется знать, что такое квадрат числа. Квадратом числа a называется число a , помноженное само на себя, то есть a ∙a . (Как нетрудно видеть, оно равно площади квадрата со стороной a ).
 Например, 18 = 2 * 3 * 3
Например, 18 = 2 * 3 * 3







 3
3
 3 3
3 3 2. 2, 2 2 229
2. 2, 2 2 229
 377. 377. 377. 3737.
377. 377. 377. 3737. pdf)
pdf) pdf)
pdf) pdf)
pdf) pdf)
pdf) pdf)
pdf) pdf)
pdf)