Каков главный корень числа √ 121? – Обзоры Вики
Квадратный корень из 121 равен 11 . Это положительное решение уравнения x 2 = 121. Число 121 представляет собой полный квадрат.
…
Корень квадратный из 121 в радикальной форме: √121.
| 1. | Что такое квадратный корень из 121? |
|---|---|
| 2. | Является ли квадратный корень из 121 рациональным или иррациональным? |
| 3. | Как найти квадратный корень из 121? |
Точно так же, каков главный корень из 25? Квадратные корни из 25 равны √25=5 и −√25 = −5, поскольку 52 = 25 и (−5) 2 = 25. Главный квадратный корень из 25 равен √25 = 5.
Чему равен главный корень числа 400? Мы знаем, что 20 × 20 = 400. Таким образом, длина сторон сарая равна 20 ярдам.
…
Квадратный корень 400.
| 1. | Что такое квадратный корень из 400? |
|---|---|
2. | Является ли квадратный корень из 400 рациональным или иррациональным? |
| 3. | Как найти квадратный корень из 400? |
| 4. | Часто задаваемые вопросы о квадратном корне из 400 |
Какой главный корень 225? Квадратный корень из 225 равен 15 . Это положительное решение уравнения x 2 = 225. Число 225 представляет собой полный квадрат.
…
Корень квадратный из 225 в радикальной форме: √225.
| 1. | Что такое квадратный корень из 225? |
|---|---|
| 2. | Является ли квадратный корень из 225 рациональным или иррациональным? |
| 3. | Как найти квадратный корень из 225? |
Во-вторых, каков главный корень числа 256? Это положительное решение уравнения x 2 = 256. Число 256 представляет собой полный квадрат.
…
Корень квадратный из 256 в радикальной форме: √256.
| 1. | Что такое квадратный корень из 256? |
|---|---|
| 2. | Является ли квадратный корень из 256 рациональным или иррациональным? |
| 3. | Как найти квадратный корень из 256? |
Каков главный корень √ 100?
Квадратный корень из 100 равен 10 . Это положительное решение уравнения x 2 = 100. Число 100 представляет собой полный квадрат.
…
Корень квадратный из 100 в радикальной форме: √100.
| 1. | Что такое квадратный корень из 100? |
|---|---|
| 2. | Является ли квадратный корень из 100 рациональным или иррациональным? |
| 3. | Как найти квадратный корень из 100? |
тогда каков главный корень из 64? 64 — это совершенное квадратное число, которое можно получить путем возведения в квадрат числа 8. Следовательно, квадратный корень из 64 — рациональное число.
…
Квадратный корень 64.
| 1. | Что такое квадратный корень из 64? |
|---|---|
| 3. | Как найти квадратный корень из 64? |
| 4. | Важные замечания |
| 5. | Мыслить нестандартно! |
| 6. | Часто задаваемые вопросы о квадратном корне из 64 |
Какой главный корень 144? Значение квадратного корня из 144 равно 12. В радикальной форме он обозначается как √144 = 12.
Каков главный корень √ 289?
Квадратный корень из 289 можно упростить до 17 либо используя простую факторизацию 289, либо выражая 289 как квадрат 17.
…
Корень квадратный из 289.
| 1. | Что такое квадратный корень из 289? |
|---|---|
| 2. | Является ли квадратный корень из 289 рациональным или иррациональным? |
| 3. | Как найти квадратный корень из 289? |
4. | Часто задаваемые вопросы о квадратном корне из 289 |
Какой главный корень 625? Квадратный корень из 625 равен 25 . Это положительное решение уравнения x 2 = 625. Число 625 представляет собой полный квадрат.
…
Корень квадратный из 625 в радикальной форме: √625.
| 1. | Что такое квадратный корень из 625? |
|---|---|
| 4. | Часто задаваемые вопросы о квадратном корне из 625 |
Какой главный корень числа 324?
Квадратный корень из 324 — это число, которое при умножении само на себя дает 324. Число 324 особенное, потому что это совершенный квадратный корень. Это указывает на то, что его квадратный корень является целым числом.
…
Корень квадратный из 324.
| 1. | Что такое квадратный корень из 324? |
|---|---|
| 3. | Как найти квадратный корень из 324? |
4. | Часто задаваемые вопросы о квадратном корне из 324 |
Какой главный корень числа 441? Число 441 — нечетное составное число. Квадратный корень из 441 — это число (целое число), которое при умножении само на себя дает 441, оно одновременно положительное и отрицательное.
…
Площадь 441: 194,481.
| 1. | Что такое квадратный корень из 441? |
|---|---|
| 2. | Является ли квадратный корень из 441 рациональным или иррациональным? |
| 3. | Как найти квадратный корень из 441? |
Каков главный квадратный корень из 289?
289 — это точное квадратное число, которое получается квадратом 17 . Следовательно, квадратный корень из 289 — рациональное число.
…
Корень квадратный из 289.
| 1. | Что такое квадратный корень из 289? |
|---|---|
| 3. | Как найти квадратный корень из 289? |
4. | Часто задаваемые вопросы о квадратном корне из 289 |
Каков главный квадратный корень из 169?
Таким образом, квадратный корень из 169 равен 13.
Каков главный корень числа √ 15? Квадратный корень из 15, округленный до 8 знаков после запятой, равен 3.87298335 . Это положительное решение уравнения x 2 = 15.
…
Корень квадратный из 15 в радикальной форме: √15.
| 1. | Что такое квадратный корень из 15? |
|---|---|
| 2. | Является ли квадратный корень из 15 рациональным или иррациональным? |
| 3. | Как найти квадратный корень из 15? |
Каковы корни ⁴√256? Кубический корень из 256 выражается как ∛256 или 4 ∛4 в радикальной форме и как (256) ⅓ или (256) . 33 в экспоненциальной форме. Кубический корень из 256.
…
IS 256 имеет совершенный 4-й корень?
1. | Что такое кубический корень из 256? |
|---|---|
| 4. | Часто задаваемые вопросы о Cube Root of 256 |
Декабрь 3, 2021
Чему равен главный квадратный корень из √ 625?
Квадратный корень из 625 равен 25 . Это положительное решение уравнения x 2 = 625. Число 625 представляет собой полный квадрат.
…
Корень квадратный из 625 в радикальной форме: √625.
| 1. | Что такое квадратный корень из 625? |
|---|---|
| 4. | Часто задаваемые вопросы о квадратном корне из 625 |
√ 16 — иррациональное число? √16 рационально потому что его значение равно 4, что можно выразить как отношение двух чисел, например 4/1 или 8/2.
Каков главный корень √ 169?
Каков квадратный корень из 169? Квадратный корень из 169 равен 13 – технически это главный квадратный корень из 169.
Какой главный корень числа 324? Квадратный корень из 324 равен √324 = 18. Следовательно, это идеальный квадратный корень.
Следовательно, это идеальный квадратный корень.
Чему равен главный корень квадратного корня из 169?
Главный квадратный корень из 169 равен 13 .
Что такое главный корень числа 361? Интерактивные вопросы
| Правда | |
|---|---|
| √361 рационально. | TrueTrue – √, 361 рационально. |
| Квадратный корень из 361 равен 19 . | TrueTrue — квадратный корень из 361 равен 19. |
| Квадратный корень из 361 — это целое число, так как это не полный квадрат. | TrueTrue — Квадратный корень из 361 — это целое число, поскольку оно не является полным квадратом. |
Как вычесть корень из числа
Содержание
- Правила сложения и вычитания квадратных корней
- Действия с корнями: основы
- Извлечение квадратного корня при помощи таблицы квадратов
- Разложение на простые множители
- Метод Герона
- Вычисление корня делением в столбик
- Поразрядное вычисление значения квадратного корня
Корень из числа проще всего вычесть с помощью калькулятора. Но, если у вас нет калькулятора, тогда надо знать алгоритм вычисления квадратного корня. Дело в том, что под корнем сидит число в квадрате. Например, 4 в квадрате — это 16. То есть корень квадратный из 16 будет равен четырем. Так же 5 в квадрате — это 25. Поэтому корень из 25 будет 5. И так далее.
Но, если у вас нет калькулятора, тогда надо знать алгоритм вычисления квадратного корня. Дело в том, что под корнем сидит число в квадрате. Например, 4 в квадрате — это 16. То есть корень квадратный из 16 будет равен четырем. Так же 5 в квадрате — это 25. Поэтому корень из 25 будет 5. И так далее.
Сейчас практически все калькуляторы, в том числе и на смартфонах умеют высчитывать квадратный корень из числа. НО если калькулятора у вас нет, то можно найти корень из числа несколькими простыми способами:
Разложение на простые множители
Разложите подкоренное число на множители, являющиеся квадратными числами. В зависимости от подкоренного числа, вы получите приблизительный или точный ответ. Квадратные числа – числа, из которых можно извлечь целый квадратный корень. Множители – числа, которые при перемножении дают исходное число.1 Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как √25 = 5, √36 = 6, √49 = 7. Квадратные множители – это множители, являющиеся квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители.
Квадратные множители – это множители, являющиеся квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители.
Например, вычислите квадратный корень из 400 (вручную). Сначала попытайтесь разложить 400 на квадратные множители. 400 кратно 100, то есть делится на 25 – это квадратное число. Разделив 400 на 25, вы получите 16, которое также является квадратным числом. Таким образом, 400 можно разложить на квадратные множители 25 и 16, то есть 25 х 16 = 400.
Запишите это как: √400 = √(25 х 16).
Квадратные корень из произведения некоторых членов равен произведению квадратных корней из каждого члена, то есть √(а х b) = √a x √b2. Воспользовавшись этим правилом, извлеките квадратный корень из каждого квадратного множителя и перемножьте полученные результаты, чтобы найти ответ.
В нашем примере извлеките корень из 25 и из 16.
Если подкоренное число не раскладывается на два квадратных множителя (а это происходит в большинстве случаев), вы не сможете найти точный ответ в виде целого числа. Но вы можете упростить задачу, разложив подкоренное число на квадратный множитель и обыкновенный множитель (число, из которого целый квадратный корень извлечь нельзя). Затем вы извлечете квадратный корень из квадратного множителя и будете извлекать корень из обыкновенного множителя.
Но вы можете упростить задачу, разложив подкоренное число на квадратный множитель и обыкновенный множитель (число, из которого целый квадратный корень извлечь нельзя). Затем вы извлечете квадратный корень из квадратного множителя и будете извлекать корень из обыкновенного множителя.
Например, вычислите квадратный корень из числа 147. Число 147 нельзя разложить на два квадратных множителя, но его можно разложить на следующие множители: 49 и 3. Решите задачу следующим образом:
Теперь вы можете оценить значение корня (найти приблизительное значение), сравнив его со значениями корней квадратных чисел, находящихся ближе всего (с обеих сторон на числовой прямой) к подкоренному числу. Вы получите значение корня в виде десятичной дроби, которую необходимо умножить на число, стоящее за знаком корня.
Вернемся к нашему примеру. Подкоренное число 3. Ближайшими к нему квадратными числами будут числа 1 (√1 = 1) и 4 (√4 = 2). Таким образом, значение √3 расположено между 1 и 2.
Этот метод также работает с большими числами. Например, рассмотрим √35. Подкоренное число 35. Ближайшими к нему квадратными числами будут числа 25 (√25 = 5) и 36 (√36 = 6). Таким образом, значение √35 расположено между 5 и 6. Та как значение √35 намного ближе к 6, чем к 5 (потому что 35 всего на 1 меньше 36), то можно заявить, что √35 немного меньше 6. Проверка на калькуляторе дает нам ответ 5,92 — мы были правы.
Еще один способ – разложите подкоренное число на простые множители. Простые множители – числа, которые делятся только на 1 и самих себя. Запишите простые множители в ряд и найдите пары одинаковых множителей. Такие множители можно вынести за знак корня.
Например, вычислите квадратный корень из 45. Раскладываем подкоренное число на простые множители: 45 = 9 х 5, а 9 = 3 х 3.
Рассмотрим другой пример: √88.
= √ (2 х 2 х 2 х 11). Вы получили три множителя 2; возьмите пару из них и вынесите за знак корня.
= 2√(2 х 11) = 2√2 х √11. Теперь можно оценить √2 и √11 и найти приблизительный ответ.
Может быть полезным будет еще это обучающее видео:
Извлечение квадрантного корня из числа не единственная операция, которую можно производить с этим математическим явлением. Так же как и обычные числа, квадратные корни складывают и вычитают.
Правила сложения и вычитания квадратных корней
Такие действия, как сложение и вычитание квадратного корня, возможны только при условии одинакового подкоренного выражения.
Можно сложить или вычесть выражения 2 3 и 6 3 , но не 5 6 и 9 4 . Если есть возможность упростить выражение и привести его к корням с одинаковым подкоренным числом, то упрощайте, а потом складывайте или вычитайте.
Действия с корнями: основы
6 50 — 2 8 + 5 12
- Упростить подкоренное выражение. Для этого необходимо разложить подкоренное выражение на 2 множителя, один из которых, — квадратное число (число, из которого извлекается целый квадратный корень, например, 25 или 9).
- Затем нужно извлечь корень из квадратного числа и записать полученное значение перед знаком корня. Обращаем ваше внимание, что второй множитель заносится под знак корня.
- После процесса упрощения необходимо подчеркнуть корни с одинаковыми подкоренными выражениями — только их можно складывать и вычитать.
- У корней с одинаковыми подкоренными выражениями необходимо сложить или вычесть множители, которые стоят перед знаком корня. Подкоренное выражение остается без изменений. Нельзя складывать или вычитать подкоренные числа!
Если у вас пример с большим количеством одинаковых подкоренных выражений, то подчеркивайте такие выражения одинарными, двойными и тройными линиями, чтобы облегчить процесс вычисления.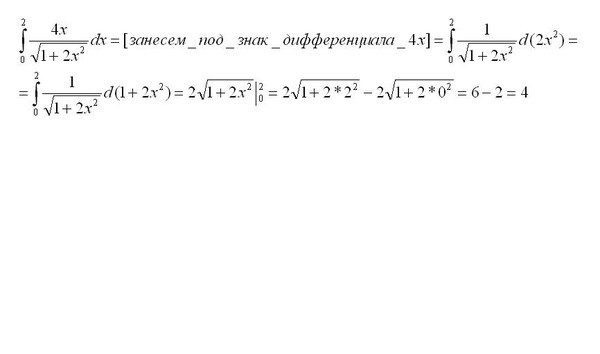
Давайте попробуем решить данный пример:
6 50 = 6 ( 25 × 2 ) = ( 6 × 5 ) 2 = 30 2 . Для начала необходимо разложить 50 на 2 множителя 25 и 2, затем извлечь корень из 25, который равен 5, а 5 вынести из-под корня. После этого нужно умножить 5 на 6 (множитель у корня) и получить 30 2 .
2 8 = 2 ( 4 × 2 ) = ( 2 × 2 ) 2 = 4 2 . Сперва необходимо разложить 8 на 2 множителя: 4 и 2. Затем из 4 извлечь корень, который равен 2, а 2 вынести из-под корня. После этого нужно умножить 2 на 2 (множитель у корня) и получить 4 2 .
5 12 = 5 ( 4 × 3 ) = ( 5 × 2 ) 3 = 10 3 . Сперва необходимо разложить 12 на 2 множителя: 4 и 3. Затем извлечь из 4 корень, который равен 2, и вынести его из-под корня. После этого нужно умножить 2 на 5 (множитель у корня) и получить 10 3 .
Результат упрощения: 30 2 — 4 2 + 10 3
30 2 — 4 2 + 10 3 = ( 30 — 4 ) 2 + 10 3 = 26 2 + 10 3 .
В итоге мы увидели, сколько одинаковых подкоренных выражений содержится в данном примере. А сейчас попрактикуемся на других примерах.
А сейчас попрактикуемся на других примерах.
- Упрощаем ( 45 ) . Раскладываем 45 на множители: ( 45 ) = ( 9 × 5 ) ;
- Выносим 3 из-под корня ( 9 = 3 ) : 45 = 3 5 ;
- Складываем множители у корней: 3 5 + 4 5 = 7 5 .
- Упрощаем 6 40 . Раскладываем 40 на множители: 6 40 = 6 ( 4 × 10 ) ;
- Выносим 2 из-под корня ( 4 = 2 ) : 6 40 = 6 ( 4 × 10 ) = ( 6 × 2 ) 10 ;
- Перемножаем множители, которые стоят перед корнем: 12 10 ;
- Записываем выражение в упрощенном виде: 12 10 — 3 10 + 5 ;
- Поскольку у первых двух членов одинаковые подкоренные числа, мы можем их вычесть: ( 12 — 3 ) 10 = 9 10 + 5 .
Как мы видим, упростить подкоренные числа не представляется возможным, поэтому ищем в примере члены с одинаковыми подкоренными числами, проводим математические действия (складываем, вычитаем и т.д.) и записываем результат:
( 9 — 4 ) 5 — 2 3 = 5 5 — 2 3 .
Советы:
- Перед тем, как складывать или вычитать, необходимо обязательно упростить (если это возможно) подкоренные выражения.

- Складывать и вычитать корни с разными подкоренными выражениями строго воспрещается.
- Не следует суммировать или вычитать целое число или корень: 3 + ( 2 x ) 1 / 2 .
- При выполнении действий с дробями, необходимо найти число, которое делится нацело на каждый знаменатель, потом привести дроби к общему знаменателю, затем сложить числители, а знаменатели оставить без изменений.
При решении различных задач из курса математики и физики ученики и студенты часто сталкиваются с необходимостью извлечения корней второй, третьей или n-ой степени. Конечно, в век информационных технологий не составит труда решить такую задачу при помощи калькулятора. Однако возникают ситуации, когда воспользоваться электронным помощником невозможно.
К примеру, на многие экзамены запрещено приносить электронику. Кроме того, калькулятора может не оказаться под рукой. В таких случаях полезно знать хотя бы некоторые методы вычисления радикалов вручную.
Извлечение квадратного корня при помощи таблицы квадратов
Один из простейших способов вычисления корней заключается в использовании специальной таблицы.
При помощи таблицы можно найти квадрат любого числа от 10 до 99. При этом в строках таблицы находятся значения десятков, в столбах — значения единиц. Ячейка на пересечении строки и столбца содержит в себе квадрат двузначного числа. Для того чтобы вычислить квадрат 63, нужно найти строку со значением 6 и столбец со значением 3. На пересечении обнаружим ячейку с числом 3969.
Поскольку извлечение корня — это операция, обратная возведению в квадрат, для выполнения этого действия необходимо поступить наоборот: вначале найти ячейку с числом, радикал которого нужно посчитать, затем по значениям столбика и строки определить ответ. В качестве примера рассмотрим вычисление квадратного корня 169.
Находим ячейку с этим числом в таблице, по горизонтали определяем десятки — 1, по вертикали находим единицы — 3. Ответ: √169 = 13.
Аналогично можно вычислять корни кубической и n-ой степени, используя соответствующие таблицы.
Преимуществом способа является его простота и отсутствие дополнительных вычислений. Недостатки же очевидны: метод можно использовать только для ограниченного диапазона чисел (число, для которого находится корень, должно быть в промежутке от 100 до 9801). Кроме того, он не подойдёт, если заданного числа нет в таблице.
Разложение на простые множители
Если таблица квадратов отсутствует под рукой или с её помощью оказалось невозможно найти корень, можно попробовать разложить число, находящееся под корнем, на простые множители. Простые множители — это такие, которые могут нацело (без остатка) делиться только на себя или на единицу. Примерами могут быть 2, 3, 5, 7, 11, 13 и т. д.
Рассмотрим вычисление корня на примере √576. Разложим его на простые множители. Получим следующий результат: √576 = √(2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 3 ∙ 3) = √(2 ∙ 2 ∙ 2)² ∙ √3². При помощи основного свойства корней √a² = a избавимся от корней и квадратов, после чего подсчитаем ответ: 2 ∙ 2 ∙ 2 ∙ 3 = 24.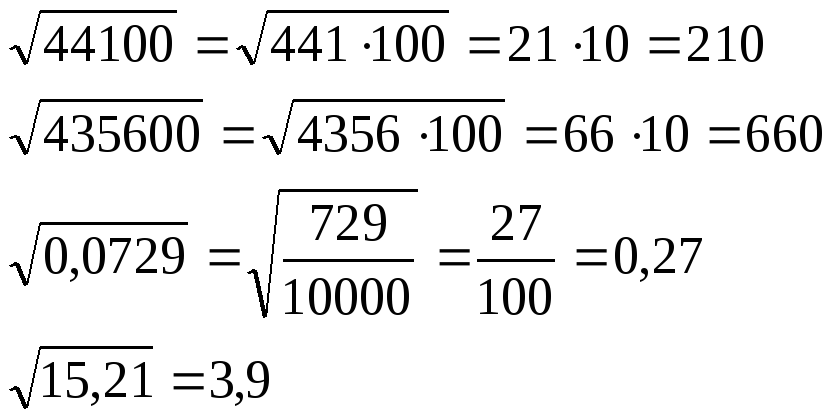
Что же делать, если у какого-либо из множителей нет своей пары? Для примера рассмотрим вычисление √54. После разложения на множители получаем результат в следующем виде: √54 = √(2 ∙ 3 ∙ 3 ∙ 3) = √3² ∙ √(2 ∙ 3) = 3√6. Неизвлекаемую часть можно оставить под корнем. Для большинства задач по геометрии и алгебре такой ответ будет засчитан в качестве окончательного. Но если есть необходимость вычислить приближённые значения, можно использовать методы, которые будут рассмотрены далее.
Метод Герона
Как поступить, когда необходимо хотя бы приблизительно знать, чему равен извлечённый корень (если невозможно получить целое значение)? Быстрый и довольно точный результат даёт применение метода Герона. Его суть заключается в использовании приближённой формулы:
где R — число, корень которого нужно вычислить, a — ближайшее число, значение корня которого известно.
Рассмотрим, как работает метод на практике, и оценим, насколько он точен.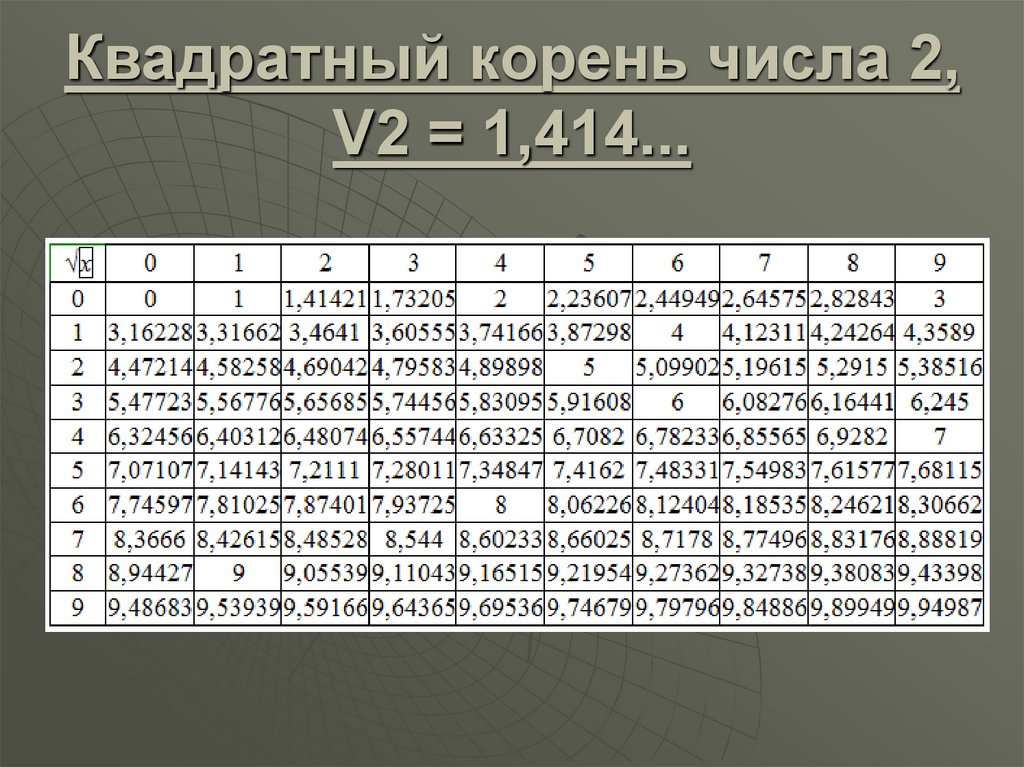 Рассчитаем, чему равен √111. Ближайшее к 111 число, корень которого известен — 121. Таким образом, R = 111, a = 121. Подставим значения в формулу:
Рассчитаем, чему равен √111. Ближайшее к 111 число, корень которого известен — 121. Таким образом, R = 111, a = 121. Подставим значения в формулу:
√111 = √121 + (111 — 121) / 2 ∙ √121 = 11 — 10 / 22 ≈ 10,55.
Теперь проверим точность метода:
Погрешность метода составила приблизительно 0,3. Если точность метода нужно повысить, можно повторить описанные ранее действия:
√111 = √111,3025 + (111 — 111,3025) / 2 ∙ √111,3025 = 10,55 — 0,3025 / 21,1 ≈ 10,536.
Проверим точность расчёта:
После повторного применения формулы погрешность стала совсем незначительной.
Вычисление корня делением в столбик
Этот способ нахождения значения квадратного корня является чуть более сложным, чем предыдущие. Однако он является наиболее точным среди остальных методов вычисления без калькулятора.
Допустим, что необходимо найти квадратный корень с точностью до 4 знаков после запятой.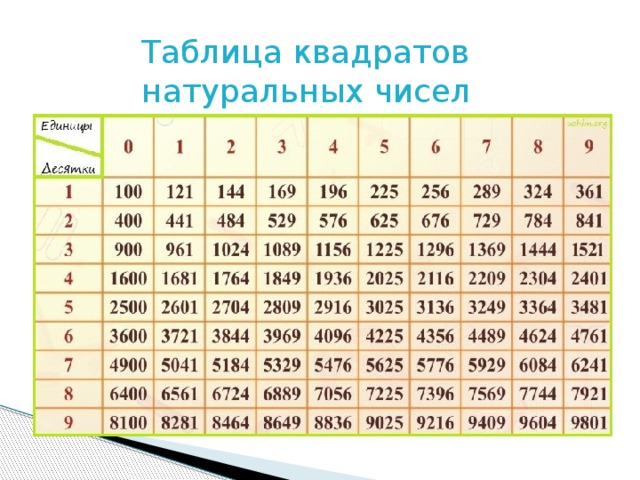 Разберём алгоритм вычислений на примере произвольного числа 1308,1912.
Разберём алгоритм вычислений на примере произвольного числа 1308,1912.
- Разделим лист бумаги на 2 части вертикальной чертой, а затем проведём от неё ещё одну черту справа, немного ниже верхнего края. Запишем число в левой части, разделив его на группы по 2 цифры, двигаясь в правую и левую сторону от запятой. Самая первая цифра слева может быть без пары. Если же знака не хватает в правой части числа, то следует дописать 0. В нашем случае получится 13 08,19 12.
- Подберём самое большое число, квадрат которого будет меньше или равен первой группе цифр. В нашем случае это 3. Запишем его справа сверху; 3 — первая цифра результата. Справа снизу укажем 3×3 = 9; это понадобится для последующих расчётов. Из 13 в столбик вычтем 9, получим остаток 4.
- Припишем следующую пару чисел к остатку 4; получим 408.
- Число, находящееся сверху справа, умножим на 2 и запишем справа снизу, добавив к нему _ x _ =. Получим 6_ x _ =.
- Вместо прочерков нужно подставить одно и то же число, меньшее или равное 408.
 Получим 66×6 = 396. Напишем 6 справа сверху, т. к. это вторая цифра результата. Отнимем 396 от 408, получим 12.
Получим 66×6 = 396. Напишем 6 справа сверху, т. к. это вторая цифра результата. Отнимем 396 от 408, получим 12. - Повторим шаги 3—6. Поскольку снесённые вниз цифры находятся в дробной части числа, необходимо поставить десятичную запятую справа сверху после 6. Запишем удвоенный результат с прочерками: 72_ x _ =. Подходящей цифрой будет 1: 721×1 = 721. Запишем её в ответ. Выполним вычитание 1219 — 721 = 498.
- Выполним приведённую в предыдущем пункте последовательность действий ещё три раза, чтобы получить необходимое количество знаков после запятой. Если не хватает знаков для дальнейших вычислений, у текущего слева числа нужно дописать два нуля.
В результате мы получим ответ: √1308,1912 ≈ 36,1689. Если проверить действие при помощи калькулятора, можно убедиться, что все знаки были определены верно.
Поразрядное вычисление значения квадратного корня
Метод обладает высокой точностью. Кроме того, он достаточно понятен и для него не требуется запоминать формулы или сложный алгоритм действий, поскольку суть способа заключается в подборе верного результата.
Извлечём корень из числа 781. Рассмотрим подробно последовательность действий.
121 — сто двадцать один. натуральное нечетное число. в ряду натуральных чисел находится между числами 120 и 122. Все о числе сто двадцать один.
- Главная
- О числе 121
121 — сто двадцать один. Натуральное нечетное число. В ряду натуральных чисел находится между числами 120 и 122.
Like если 121 твое любимое число!
Распространенные значения и факты
121 регион — Чувашская Республика
- Столица
- Чебоксары
- Автомобильный код
- 121
- Федеральный округ
- Приволжский
- Экономический район
- Волго-Вятский
- Дата образования
- 24 июня 1920 г. как автономная область21 апреля 1925 г. преобразована в республику
- Территория
- 18,3 тыс. кв. км 0,11 % от РФ 80 место в РФ
- Население
- Общая численность 1 313,9 тыс. чел. 0,91 % от РФ 40 место в РФ
Изображения числа 121
Склонение числа «121» по падежам
| Падеж | Вспомогательное слово | Характеризующий вопрос | Склонение числа 121 |
|---|---|---|---|
| Именительный | Есть | Кто? Что? | сто двадцать один |
| Родительный | Нет | Кого? Чего? | ста двадцати одного |
| Дательный | Дать | Кому? Чему? | ста двадцати одному |
| Винительный | Видеть | Кого? Что? | сто двадцать один |
| Творительный | Доволен | Кем? Чем? | ста двадцатью одним |
| Предложный | Думать | О ком? О чём? | ста двадцати одном |
Перевод «сто двадцать один» на другие языки
- Азербайджанский
- yüz iyirmi bir
- Албанский
- 121
- Английский
- one hundred twenty one
- Арабский
- 121
- Армянский
- հարյուր քսան մեկ
- Белорусский
- 121
- Болгарский
- сто двадесет и един
- Вьетнамский
- 121
- Голландский
- 121
- Греческий
- εκατόν είκοσι μία
- Грузинский
- ას ოცი ერთი
- Иврит
- 121
- Идиш
- 121
- Ирландский
- 121
- Исландский
- 121
- Испанский
- ciento veintiún
- Итальянский
- 121
- Китайский
- 121
- Корейский
- 백스물하나
- Латынь
- centum et viginti,
- Латышский
- 121
- Литовский
- 121
- Монгольский
- нэг зуун хорин нэгэн
- Немецкий
- 121
- Норвежский
- 121
- Персидский
- 121
- Польский
- sto dwadzieścia jeden
- Португальский
- 121
- Румынский
- 121
- Сербский
- сто двадесет један
- Словацкий
- sto dvadsať jedna
- Словенский
- 121
- Тайский
- 121
- Турецкий
- 121
- Украинский
- сто двадцять одна
- Финский
- satakaksikymmentäyksi
- Французский
- 121
- Хорватский
- 121
- Чешский
- sto dvacet jedna
- Шведский
- 121
- Эсперанто
- cent dudek unu
- Эстонский
- 121
- Японский
- 121
Перевод «121» на другие языки и системы
Римскими цифрами
- Римскими цифрами
- CXXI
Сервис перевода арабских чисел в римские
Арабско-индийскими цифрами
- Арабскими цифрами
- ١٢١
- Восточно-арабскими цифрами
- ۱۲۱
- Деванагари
- १२१
- Бенгальскими цифрами
- ১২১
- Гурмукхи
- ੧੨੧
- Гуджарати
- ૧૨૧
- Ория
- ୧୨୧
- Тамильскими цифрами
- ௧௨௧
- Телугу
- ౧౨౧
- Каннада
- ೧೨೧
- Малаялам
- ൧൨൧
- Тайскими цифрами
- ๑๒๑
- Лаосскими цифрами
- ໑໒໑
- Тибетскими цифрами
- ༡༢༡
- Бирманскими цифрами
- ၁၂၁
- Кхемерскими цифрами
- ១២១
- Монгольскими цифрами
- ᠑᠒᠑
В других системах счисления
- 121 в двоичной системе
- 1111001
- 121 в троичной системе
- 11111
- 121 в восьмеричной системе
- 171
- 121 в десятичной системе
- 121
- 121 в двенадцатеричной системе
- A1
- 121 в тринадцатеричной системе
- 94
- 121 в шестнадцатеричной системе
- 79
QR-код, MD5, SHA-1 числа 121
Адрес для вставки QR-кода числа 121, размер 500×500:
http://pro-chislo.ru/data/moduleImages/QRCodes/121/64d7e6be1f04987083c9bbbd636ca91e.png
- MD2 от 121
- f3a0e7af99a5523868c47b3dd1d918dc
- MD4 от 121
- 8fbaa1e96d5696ca413b4e89363d6572
- MD5 от 121
- 4c56ff4ce4aaf9573aa5dff913df997a
- SHA1 от 121
- 8bd7954c40c1e59a900f71ea3a266732609915b1
- SHA256 от 121
- 89aa1e580023722db67646e8149eb246c748e180e34a1cf679ab0b41a416d904
- SHA384 от 121
- ca87db07c098d292b5bb910d97c2d7df77c1687ac0639b6d9044b4218e10685769938881758ce261eddaad6b185cdb1c
- SHA512 от 121
- 363709c1bed1003ef69e586cbc9d7284f191673e339601d9009a3e193235fbcf2b7a14846c2839af418ab52e0a89d67cb7b08f9bc15f688a85b491b8ff09971f
- GOST от 121
- 2d2f43d454b6c3bf992e4df2ce93a2effc50d0120215e1762cd6137cc52370f6
- Base64 от 121
- MTIx
121й день в году
121й день в не високосном году — 1 мая
Праздник Весны и Труда
Первома́й — другие названия: День труда, День весны, Праздник весны и труда (в РФ), День международной солидарности трудящихся — отмечается в 142 странах и территориях мира 1 мая или в первый понедельник мая.
121й день в високосном году — 30 апреля
День Пожарной Охраны
Математические свойства числа 121
- Простые множители
- 11 * 11
- Делители
- 1, 11, 121
- Количество делителей
- 3
- Сумма делителей
- 133
- Простое число
- Нет
- Предыдущее простое
- 113
- Следующее простое
- 127
- 121е простое число
- 661
- Число Фибоначчи
- Нет
- Число Белла
- Нет
- Число Каталана
- Нет
- Факториал
- Нет
- Регулярное число (Число Хемминга)
- Нет
- Совершенное число
- Нет
- Полигональное число
- квадрат(11)
- Квадрат
- 14641
- Квадратный корень
- 11
- Натуральный логарифм (ln)
- 4.
 7957905455967
7957905455967 - Десятичный логарифм (lg)
- 2.0827853703165
- Синус (sin)
- 0.99881522472358
- Косинус (cos)
- -0.048663609200154
- Тангенс (tg)
- 0.524889977138
Комментарии о числе 121
← 120
122 →
- Распространенные значения и факты
- Изображения числа 121
- Склонение числа «121» по падежам
- Перевод «сто двадцать один» на другие языки
- Перевод «121» на другие языки и системы
- QR-код, MD5, SHA-1 числа 121
- 121й день в году
- Математические свойства числа 121
- Комментарии о числе 121
Как найти приблизительное значение корня. Вычисление квадратного корня вручную. Просмотр содержимого документа «Приближенные вычисления квадратного корня.»
Задача. Комната квадратной формы имеет площадь, равную 20 кв. м. Найти её длину и ширину.
Так как комната квадратная, то её длина х равна её ширине. По условию задачи мы должны иметь:
По условию задачи мы должны иметь:
и нам требуется найти арифметический корень из числа 20.
Очевидно, что х не может быть целым числом, так как , а между двумя соседними целыми числами 4 и 5 не содержится ни одного целого числа.
Наша задача имеет вполне определённый практический смысл, и её можно решить приближённо с требуемой точностью.
Покажем, как это можно сделать.
Мы указали два соседних целых числа 4 и 5 такие, что 42 меньше, а 52 больше, чем 20.
Число 4 называется приближённым квадратным корнем из 20 с точностью до 1 с недостатком, число 5 — приближённым корнем из 20 с точностью до 1 с избытком.
Рассмотрим теперь десятичные дроби, заключающиеся между 4 и 5 и имеющие целое число десятых долей:
Будем последовательно возводить эти дроби в квадрат, пока не получим числа, большего 20.
Итак, мы получили:
Числа 4,4 и 4,5 называются приближёнными значениями квадратного корня из 20 с точностью до 0,1 с недостатком и с избытком (соответственно).
Если нам недостаточна полученная точность, то поступим так: будем выписывать десятичные дроби, заключённые между 4,4 и 4,5 и содержащие целое число сотых долей, а затем будем последовательно возводить эти дроби в квадрат, пока не получим числа, большего 20.
Числа 4,47 и 4,48 называются приближёнными значениями квадратного корня из 20 с точностью до 0,01 с недостатком и с избытком.
Точно так же (если это нужно) можно получить приближённые значения с точностью до 0,001; это будут числа 4,472 и 4,473, так как , значит,
Итак, наша задача получила решение с точностью до трёх значащих цифр; такая точность вполне достаточна во многих практических измерениях. Можно считать, что
Дадим теперь общее определение приближённого корня.
Приближёнными значениями квадратного корня из данного числа с точностью до единицы называются два последовательных натуральных числа, из которых квадрат первого меньше, а квадрат второго больше данного числа.
Первое из этих чисел называется приближённым значением корня с недостатком, второе — приближённым значением корня с избытком.
Записывают приближённые значения корня так:
Вместо слов «приближённое значение квадратного корня» часто говорят просто «приближённый квадратный корень».
Чтобы найти приближённый корень с точностью до 1 с недостатком, надо найти наибольшее натуральное число, квадрат которого меньше подкоренного числа. Это можно сделать или путём испытаний, или пользуясь таблицами квадратов натуральных чисел.
Прибавив 1 к приближённому корню с недостатком, получим приближённый корень с избытком.
Определение. Приближёнными квадратными корнями с недостатком и с избытком из числа с точностью до 0,1 называются такие два числа, отличающиеся друг от друга на 0,1, из которых квадрат одного меньше, а квадрат другого больше данного числа.
ГУ « Средняя общеобразовательная школа №5 им. Бауыржана Момышулы»
отдела образования акимата г. Костаная
ПЛАН-КОСПЕКТ УРОКА
ФИО (полностью) Пластун Сергей Владимирович
Предмет алгебра
Класс 8А-8б-1
Дата 23. 09.17
09.17
Источники Алматы «Мектеп-2016»
Базовый учебник
Дополнительная литература
Нахождение приближенных значений квадратного корня.
1. Цель урока: познакомить учащихся с понятием « приближенное значение квадратного корня» и научить применять это понятие на практике.
Задачи:
Образовательные:
-научить находить приближенные значения квадратного корня;
-выработка умений рассуждать, четко формулировать правила, приводить примеры, применять свои знания и умения на практике.
корень, приводить и находить значения арифметического квадратного корня.
Развивающие:
-развивать у учащихся навык решения заданий на данную тему;
-развивать мыслительную деятельность учащихся.
Воспитательные:
— воспитывать внимательность, активность, ответственность.
2. Тип урока: комбинированный .
3. Формы работы с учащимися: фронтальная, индивидуальная.
4. Необходимое техническое оборудование.
5. Наглядные пособия, дидактические материалы, используемые на уроке.
6. Структура и ход урока.
СТРУКТУРА И ХОД УРОКА
Ход урока
1. Организационный момент .
Проверка готовности класса к уроку. Приветствие.
2. Проверка домашнего задания.
3. Повторение ранее изученного материала.
Начнем с повторения. Устная работа
Давайте вспомним, что такое квадратный корень (Квадратным корнем из неотрицательного числа а называется число, квадрат которого равен а).
(Арифметический квадратный корень) Арифметическим квадратным корнем из неотрицательного числа а называется такое неотрицательное число b , квадрат которого равен а.
Арифметический квадратный корень из числа а обозначается так:. Знак называется знаком арифметического квадратного корня, или радикалом, а –подкоренным выражением. Выражение читается так: «Арифметический квадратный корень из числа а».
Знак называется знаком арифметического квадратного корня, или радикалом, а –подкоренным выражением. Выражение читается так: «Арифметический квадратный корень из числа а».
По определению арифметического корня равенство
выполняется при условии, когда
.
4. Изучение нового материала.
1. Вычислите: 25 , 16, 9, 81,
Найдите значение выражения √2
— Что вам необходимо было сделать?
Что у вас получилось? (Учащиеся показывают свои варианты:)
В чём возникло затруднение?
Извлекается √2 нацело?
Как будем находить?
Какие знаем способы нахождения корней?
Ребята, видите, не всегда мы имеем дело с числами, легко представимыми в виде квадрата числа, которые извлекаются из- под корня нацело
1 МЕТОД вычислить √2 с точностью до двух знаков после запятой Будем рассуждать следующим образом.
Число √2 больше 1, так как 1 2
1
Теперь попытаемся отыскать цифру десятых.
Для этого будем дроби от единицы до двойки возводить в квадрат, пока не получим число большее двух.
Шаг деления возьмем 0,1, так как мы ищем число десятых.
Другими словами будем возводить в квадрат числа: 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9
1,1 2 =1,21; 1,2 2 =1,44; 1,3 2 =1,69; 1,4 2 =1,96; 1,5 2 =2,25.
Получили число превышающее двойку, остальные числа уже не надо возводить в квадрат. Число 1,4 2 меньше 2, а 1,5 2 уже больше двух, то число √2 должно принадлежать промежутку от 1,4 до 1,5 . Следовательно, десятичная запись числа √2 в разряде десятых должна содержать 4. √2=1,4… .
1,41 2 =1,9881, 1,42 2 =2,0164.
Уже при 1.42 получаем, что его квадрат больше двух, далее возводить в квадрат числа не имеет смысла.
Из этого получаем, что число √2 будет принадлежать промежутку от 1,41 до 1,42 (1,41
Так как нам необходимо записать √2 с точностью до двух знаков после запятой, то мы уже можем остановиться и не продолжать вычисления.
√2 ≈ 1,41. Это и будет ответом. Если бы необходимо было вычислить еще более точное значение, нужно было бы продолжать вычисления, повторяя снова и снова цепочку рассуждений.
Задание
Вычислите с точностью до двух знаков после запятой
√3 = , √5 = , √6 = , √7 =, √8 =
Вывод Данный прием позволяет извлекать корень с любой заданной наперед точностью.
2 МЕТОД Чтобы узнать целую часть квадратного корня числа, можно, вычитая из него все нечётные числа по порядку, пока остаток не станет меньше следующего вычитаемого числа или равен нулю, посчитать количество выполненных действий.
Например, найдем √16 так:
Выполнено 4 действия, значит, √16 = 4
Задание. Вычислите
√1 √6
При решении различных задач из курса математики и физики ученики и студенты часто сталкиваются с необходимостью извлечения корней второй, третьей или n-ой степени. Конечно, в век информационных технологий не составит труда решить такую задачу при помощи калькулятора. Однако возникают ситуации, когда воспользоваться электронным помощником невозможно.
К примеру, на многие экзамены запрещено приносить электронику. Кроме того, калькулятора может не оказаться под рукой. В таких случаях полезно знать хотя бы некоторые методы вычисления радикалов вручную.
Кроме того, калькулятора может не оказаться под рукой. В таких случаях полезно знать хотя бы некоторые методы вычисления радикалов вручную.
Один из простейших способов вычисления корней заключается в использовании специальной таблицы . Что же она собой представляет и как ей правильно воспользоваться?
При помощи таблицы можно найти квадрат любого числа от 10 до 99. При этом в строках таблицы находятся значения десятков, в столбах — значения единиц. Ячейка на пересечении строки и столбца содержит в себе квадрат двузначного числа. Для того чтобы вычислить квадрат 63, нужно найти строку со значением 6 и столбец со значением 3. На пересечении обнаружим ячейку с числом 3969.
Поскольку извлечение корня — это операция, обратная возведению в квадрат, для выполнения этого действия необходимо поступить наоборот: вначале найти ячейку с числом, радикал которого нужно посчитать, затем по значениям столбика и строки определить ответ. В качестве примера рассмотрим вычисление квадратного корня 169.
Находим ячейку с этим числом в таблице, по горизонтали определяем десятки — 1, по вертикали находим единицы — 3. Ответ: √169 = 13.
Аналогично можно вычислять корни кубической и n-ой степени, используя соответствующие таблицы.
Преимуществом способа является его простота и отсутствие дополнительных вычислений. Недостатки же очевидны: метод можно использовать только для ограниченного диапазона чисел (число, для которого находится корень, должно быть в промежутке от 100 до 9801). Кроме того, он не подойдёт, если заданного числа нет в таблице.
Разложение на простые множители
Если таблица квадратов отсутствует под рукой или с её помощью оказалось невозможно найти корень, можно попробовать разложить число, находящееся под корнем, на простые множители . Простые множители — это такие, которые могут нацело (без остатка) делиться только на себя или на единицу. Примерами могут быть 2, 3, 5, 7, 11, 13 и т. д.
Рассмотрим вычисление корня на примере √576. Разложим его на простые множители. Получим следующий результат: √576 = √(2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 3 ∙ 3) = √(2 ∙ 2 ∙ 2)² ∙ √3². При помощи основного свойства корней √a² = a избавимся от корней и квадратов, после чего подсчитаем ответ: 2 ∙ 2 ∙ 2 ∙ 3 = 24.
Разложим его на простые множители. Получим следующий результат: √576 = √(2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 3 ∙ 3) = √(2 ∙ 2 ∙ 2)² ∙ √3². При помощи основного свойства корней √a² = a избавимся от корней и квадратов, после чего подсчитаем ответ: 2 ∙ 2 ∙ 2 ∙ 3 = 24.
Что же делать, если у какого-либо из множителей нет своей пары? Для примера рассмотрим вычисление √54. После разложения на множители получаем результат в следующем виде: √54 = √(2 ∙ 3 ∙ 3 ∙ 3) = √3² ∙ √(2 ∙ 3) = 3√6. Неизвлекаемую часть можно оставить под корнем. Для большинства задач по геометрии и алгебре такой ответ будет засчитан в качестве окончательного. Но если есть необходимость вычислить приближённые значения, можно использовать методы, которые будут рассмотрены далее.
Метод Герона
Как поступить, когда необходимо хотя бы приблизительно знать, чему равен извлечённый корень (если невозможно получить целое значение)? Быстрый и довольно точный результат даёт применение метода Герона . Его суть заключается в использовании приближённой формулы:
√R = √a + (R — a) / 2√a,
где R — число, корень которого нужно вычислить, a — ближайшее число, значение корня которого известно.
Рассмотрим, как работает метод на практике, и оценим, насколько он точен. Рассчитаем, чему равен √111. Ближайшее к 111 число, корень которого известен — 121. Таким образом, R = 111, a = 121. Подставим значения в формулу:
√111 = √121 + (111 — 121) / 2 ∙ √121 = 11 — 10 / 22 ≈ 10,55.
Теперь проверим точность метода :
10,55² = 111,3025.
Погрешность метода составила приблизительно 0,3. Если точность метода нужно повысить, можно повторить описанные ранее действия:
√111 = √111,3025 + (111 — 111,3025) / 2 ∙ √111,3025 = 10,55 — 0,3025 / 21,1 ≈ 10,536.
Проверим точность расчёта:
10,536² = 111,0073.
После повторного применения формулы погрешность стала совсем незначительной.
Вычисление корня делением в столбик
Этот способ нахождения значения квадратного корня является чуть более сложным, чем предыдущие. Однако он является наиболее точным среди остальных методов вычисления без калькулятора .
Допустим, что необходимо найти квадратный корень с точностью до 4 знаков после запятой.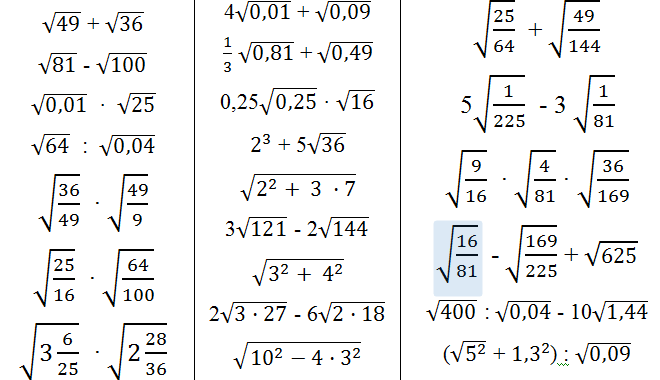 Разберём алгоритм вычислений на примере произвольного числа 1308,1912.
Разберём алгоритм вычислений на примере произвольного числа 1308,1912.
- Разделим лист бумаги на 2 части вертикальной чертой, а затем проведём от неё ещё одну черту справа, немного ниже верхнего края. Запишем число в левой части, разделив его на группы по 2 цифры, двигаясь в правую и левую сторону от запятой. Самая первая цифра слева может быть без пары. Если же знака не хватает в правой части числа, то следует дописать 0. В нашем случае получится 13 08,19 12.
- Подберём самое большое число, квадрат которого будет меньше или равен первой группе цифр. В нашем случае это 3. Запишем его справа сверху; 3 — первая цифра результата. Справа снизу укажем 3×3 = 9; это понадобится для последующих расчётов. Из 13 в столбик вычтем 9, получим остаток 4.
- Припишем следующую пару чисел к остатку 4; получим 408.
- Число, находящееся сверху справа, умножим на 2 и запишем справа снизу, добавив к нему _ x _ =. Получим 6_ x _ =.
- Вместо прочерков нужно подставить одно и то же число, меньшее или равное 408.
 Получим 66×6 = 396. Напишем 6 справа сверху, т. к. это вторая цифра результата. Отнимем 396 от 408, получим 12.
Получим 66×6 = 396. Напишем 6 справа сверху, т. к. это вторая цифра результата. Отнимем 396 от 408, получим 12. - Повторим шаги 3-6. Поскольку снесённые вниз цифры находятся в дробной части числа, необходимо поставить десятичную запятую справа сверху после 6. Запишем удвоенный результат с прочерками: 72_ x _ =. Подходящей цифрой будет 1: 721×1 = 721. Запишем её в ответ. Выполним вычитание 1219 — 721 = 498.
- Выполним приведённую в предыдущем пункте последовательность действий ещё три раза, чтобы получить необходимое количество знаков после запятой. Если не хватает знаков для дальнейших вычислений, у текущего слева числа нужно дописать два нуля.
В результате мы получим ответ: √1308,1912 ≈ 36,1689. Если проверить действие при помощи калькулятора, можно убедиться, что все знаки были определены верно.
Поразрядное вычисление значения квадратного корня
Метод обладает высокой точностью . Кроме того, он достаточно понятен и для него не требуется запоминать формулы или сложный алгоритм действий, поскольку суть способа заключается в подборе верного результата.
Извлечём корень из числа 781. Рассмотрим подробно последовательность действий.
- Выясним, какой разряд значения квадратного корня будет являться старшим. Для этого возведём в квадрат 0, 10, 100, 1000 и т. д. и выясним, между какими из них находится подкоренное число. Мы получим, что 10²
- Подберём значение десятков. Для этого будем по очереди возводить в степень 10, 20, …, 90, пока не получим число, превышающее 781. Для нашего случая получим 10² = 100, 20² = 400, 30² = 900. Значение результата n будет находиться в пределах 20
- Аналогично предыдущему шагу подбирается значение разряда единиц. Поочерёдно возведём в квадрат 21,22, …, 29: 21² = 441, 22² = 484, 23² = 529, 24² = 576, 25² = 625, 26² = 676, 27² = 729, 28² = 784. Получаем, что 27
- Каждый последующий разряд (десятые, сотые и т. д.) вычисляется так же, как было показано выше. Расчёты проводятся до тех пор, пока не будет достигнута необходимая точность.
Теперь такой вопрос: как возвести число в иррациональную степень? Например, нам хочется узнать, что такое 10 √2 Ответ в принципе очень прост. Возьмем вместо √2 его приближение в виде конечной десятичной дрдби — это- рациональное число. Возводить в рациональную степень мы умеем; дело сводится к возведению в целую степень и извлечению корня. Мы получим приближенное значение числа. Можно взять десятичную дробь подлиннее (это снова рациональное число). Тогда придется извлечь корень большей степени; ведь знаменатель рациональной дроби увеличится, но зато мы получим более точное приближение. Конечно, если взять приближенное значение √2 в виде очень длинной дроби, то возведение в степень будет делом очень трудным. Как справиться с этой задачей?
Возьмем вместо √2 его приближение в виде конечной десятичной дрдби — это- рациональное число. Возводить в рациональную степень мы умеем; дело сводится к возведению в целую степень и извлечению корня. Мы получим приближенное значение числа. Можно взять десятичную дробь подлиннее (это снова рациональное число). Тогда придется извлечь корень большей степени; ведь знаменатель рациональной дроби увеличится, но зато мы получим более точное приближение. Конечно, если взять приближенное значение √2 в виде очень длинной дроби, то возведение в степень будет делом очень трудным. Как справиться с этой задачей?
Вычисление квадратных корней, кубичных корней и других корней невысокой степени — вполне доступный нам арифметический процесс; вычисляя, мы последовательно, один за другим, пишем знаки десятичной дроби. Но для того, чтобы возвести в иррациональную степень или взять логарифм (решить обратную задачу), нужен такой труд, что применить прежнюю процедуру уже не просто. На помощь приходят таблицы. Их называют таблицами логарифмов или таблицами степеней, смотря по тому, для чего, они предназначены. Они экономят время: чтобы возвести число в иррациональную степень, мы не вычисляем, а только перелистываем страницы.
Их называют таблицами логарифмов или таблицами степеней, смотря по тому, для чего, они предназначены. Они экономят время: чтобы возвести число в иррациональную степень, мы не вычисляем, а только перелистываем страницы.
Хотя вычисление собранных в таблицы значений — процедура чисто техническая, а все же дело это интересное и имеет большую историю. Поэтому посмотрим, как это делается. Мы вычислим не только х = 10 √2 , но решим и другую задачу: 10 х = 2, или x = log 10 2. При решении этих задач мы не откроем новых чисел; это просто вычислительные задачи. Решением будут иррациональные числа, бесконечные десятичные дроби, а их как-то неудобно объявлять новым видом чисел.
Подумаем, как решить наши уравнения. Общая идея очень проста. Если вычислить 10 1 и 10 1/10 , и 10 1/100 , и 10 1/1000 , и т. д., а затем перемножить результаты, то мы получим 10 1,414… или l0 √2 Поступая так, мы решим любую задачу такого рода. Однако вместо 10 1/10 и т. д. мы будем вычислять 10 1/2 , и 10 1/4 и т. д. Прежде чем начинать вычисления, объясним еще, почему мы обращаемся к числу 10 чаще, чем к другим числам. Мы знаем, что значение таблиц логарифмов выходит далеко за рамки математической задачи вычисления корней, потому что
д. Прежде чем начинать вычисления, объясним еще, почему мы обращаемся к числу 10 чаще, чем к другим числам. Мы знаем, что значение таблиц логарифмов выходит далеко за рамки математической задачи вычисления корней, потому что
Это хорошо известно всем, кто пользовался таблицей логарифмов, чтобы перемножить числа. По какому же основанию b брать логарифмы? Это безразлично; ведь в основу таких вычислений положен только принцип, общее свойство логарифмической функции. Вычислив логарифмы один раз по какому-нибудь произвольному основанию, можно перейти к логарифмам по другому основанию при помощи умножения. Если умножить уравнение (22.3) на 61, то оно останется верным, поэтому если перемножить все числа в таблице логарифмов по основанию b на 61, то можно будет пользоваться и такой таблицей. Предположим, что нам известны логарифмы всех чисел по основанию b. Иначе говоря, можно решить уравнение b а = с для любого с; для этого существует таблица. Задача состоит в том, как найти логарифм этого же числа с по другому основанию, например x. Нам нужно решить уравнение х а’ = с. Это легко сделать, потому что х всегда можно представить так: х = b t . Найти t, зная х и b, просто: t = log b x. Подставим теперь х = b t в уравнение х а’ = с; оно перейдет в такое уравнение: (b t) а’ = b ta’ = c. Иными словами, произведение ta’ есть логарифм с по основанию b. Значит, а’ = a/t. Таким образом, логарифмы по основанию х равны произведениям логарифмов по основа нию b на постоянное число l/t. Следовательно, все таблицы логарифмов эквивалентны с точностью до умножения на число l/log b x. Это позволяет нам выбрать для составления таблиц любое основание, но мы решили, что удобнее всего взять за основание число 10. (Может возникнуть вопрос: не существует ли все-таки какого-нибудь естественного основания, при котором все выглядит как-то проще? Мы попытаемся ответить на этот вопрос позднее. Пока все логарифмы будут вычисляться по основанию 10.)
Нам нужно решить уравнение х а’ = с. Это легко сделать, потому что х всегда можно представить так: х = b t . Найти t, зная х и b, просто: t = log b x. Подставим теперь х = b t в уравнение х а’ = с; оно перейдет в такое уравнение: (b t) а’ = b ta’ = c. Иными словами, произведение ta’ есть логарифм с по основанию b. Значит, а’ = a/t. Таким образом, логарифмы по основанию х равны произведениям логарифмов по основа нию b на постоянное число l/t. Следовательно, все таблицы логарифмов эквивалентны с точностью до умножения на число l/log b x. Это позволяет нам выбрать для составления таблиц любое основание, но мы решили, что удобнее всего взять за основание число 10. (Может возникнуть вопрос: не существует ли все-таки какого-нибудь естественного основания, при котором все выглядит как-то проще? Мы попытаемся ответить на этот вопрос позднее. Пока все логарифмы будут вычисляться по основанию 10.)
Теперь посмотрим, как составляют таблицу логарифмов. Работа начинается с последовательных извлечений квадратного корня из 10. Результат можно увидеть в табл. 22.1. Показатели степеней записаны в ее первом столбце, а числа 10 s — в третьем. Ясно, что 10 1 = 10. Возвести 10 в половинную степень легко -это квадратный корень из 10, а как извлекать квадратный корень из любого числа, знает каждый. (Квадратный корень лучше всего извлекать не тем способом, которому обычно учат в школе, а немного иначе. Чтобы извлечь квадратный корень из числа N, выберем достаточно близкое к ответу число а, вычислим N/a и среднее а’ =1/2; это среднее будет новым числом а, новым приближением корня из N. Этот процесс очень быстро приводит к цели: число значащих цифр удваивается после каждого шага.) Итак, мы нашли первый квадратный корень; он равен 3,16228. Что это дает? Кое-что дает. Мы уже можем сказать, чему равно 10 0,5 , и знаем по крайней мере один логарифм.
Результат можно увидеть в табл. 22.1. Показатели степеней записаны в ее первом столбце, а числа 10 s — в третьем. Ясно, что 10 1 = 10. Возвести 10 в половинную степень легко -это квадратный корень из 10, а как извлекать квадратный корень из любого числа, знает каждый. (Квадратный корень лучше всего извлекать не тем способом, которому обычно учат в школе, а немного иначе. Чтобы извлечь квадратный корень из числа N, выберем достаточно близкое к ответу число а, вычислим N/a и среднее а’ =1/2; это среднее будет новым числом а, новым приближением корня из N. Этот процесс очень быстро приводит к цели: число значащих цифр удваивается после каждого шага.) Итак, мы нашли первый квадратный корень; он равен 3,16228. Что это дает? Кое-что дает. Мы уже можем сказать, чему равно 10 0,5 , и знаем по крайней мере один логарифм.
Логарифм числа 3,16228 очень близок к 0,50000. Однако нужно еще приложить небольшие усилия: нам нужна более подробная таблица. Извлечем еще один квадратный корень и найдем 10 1/4 , что равно 1,77828. Теперь мы знаем еще один логарифм: 1,250 -это логарифм числа 17,78; кроме того, мы можем сказать, чему равно 10 0,75: ведь это 10 (0,5+0,25) , т. е. произведение второго и третьего чисел из третьего столбца табл. 22.1. Если сделать первый столбец таблицы достаточно длинным, то таблица будет содержать почти все числа; перемножая числа из третьего столбца, мы получаем 10 почти в любой степени. Такова основная идея таблиц. В нашей таблице содержится десять последовательных корней из 10; основной труд по составлению таблицы вложен в вычисления этих корней.
Теперь мы знаем еще один логарифм: 1,250 -это логарифм числа 17,78; кроме того, мы можем сказать, чему равно 10 0,75: ведь это 10 (0,5+0,25) , т. е. произведение второго и третьего чисел из третьего столбца табл. 22.1. Если сделать первый столбец таблицы достаточно длинным, то таблица будет содержать почти все числа; перемножая числа из третьего столбца, мы получаем 10 почти в любой степени. Такова основная идея таблиц. В нашей таблице содержится десять последовательных корней из 10; основной труд по составлению таблицы вложен в вычисления этих корней.
Почему же мы не продолжаем повышать точность таблиц дальше? Потому что мы кое-что уже подметили. Возведя 10 в очень малую степень, мы получаем единицу с малой добавкой. Это, конечно, происходит потому, что если возвести, например, 10 1/1000 в 1000-ю степень, то мы снова получим 10; ясно, что 10 1/1000 не может быть большим числом: оно очень близко к единице. Более того, малые добавки к единице ведут себя так, будто их каждый раз делят на 2; поглядите-ка на таблицу повнимательнее: 1815 переходит в 903, потом в 450, 225 и т. д. Таким бразом, если вычислить еще один, одиннадцатый, квадратный корень, он с большой точностью будет равен 1,00112, и этот результат мы угадали еще до вычисления. Можно ли сказать, какова будет добавка к единице, если возвести 10 в степень ∆/1024, когда ∆ стремится к нулю? Можно. Добавка будет приблизительно равна 0,0022511∆. Конечно, не в точности 0,0022511∆; чтобы вычислить эту добавку поточнее, делают такой трюк: вычитают из 10 s единицу и делят разность на показатель степени s. Отклонения полученного таким образом частного от его точного значения одинаковы для любой степени s. Видно, что эти отношения (табл. 22.1) примерно равны. Сначала они сильно различаются, но потом все ближе подходят друг к другу, явно стремясь к какому-то числу. Что это за число? Проследим, как меняются числа четвертого столбца, если опускаться вниз по столбцу. Сначала разность двух соседних чисел равна 0,0211, потом 0,0104, потом 0,0053 и, наконец, 0,0026. Разность каждый раз убывает наполовину. Сделав еще один шаг, мы доведем ее до 0,0013, потом до 0,0007, 0,0003, 0,0002 и, наконец, примерно до 0,0001; надо последовательно делить 26 на 2.
д. Таким бразом, если вычислить еще один, одиннадцатый, квадратный корень, он с большой точностью будет равен 1,00112, и этот результат мы угадали еще до вычисления. Можно ли сказать, какова будет добавка к единице, если возвести 10 в степень ∆/1024, когда ∆ стремится к нулю? Можно. Добавка будет приблизительно равна 0,0022511∆. Конечно, не в точности 0,0022511∆; чтобы вычислить эту добавку поточнее, делают такой трюк: вычитают из 10 s единицу и делят разность на показатель степени s. Отклонения полученного таким образом частного от его точного значения одинаковы для любой степени s. Видно, что эти отношения (табл. 22.1) примерно равны. Сначала они сильно различаются, но потом все ближе подходят друг к другу, явно стремясь к какому-то числу. Что это за число? Проследим, как меняются числа четвертого столбца, если опускаться вниз по столбцу. Сначала разность двух соседних чисел равна 0,0211, потом 0,0104, потом 0,0053 и, наконец, 0,0026. Разность каждый раз убывает наполовину. Сделав еще один шаг, мы доведем ее до 0,0013, потом до 0,0007, 0,0003, 0,0002 и, наконец, примерно до 0,0001; надо последовательно делить 26 на 2. Таким образом, мы спустимся еще на 26 единиц и найдем для предела 2,3025. (Позднее мы увидим, что правильнее было бы взять 2,3026, но давайте возьмем то, что у нас получилось.) Пользуясь этой таблицей, можно возвести 10 в любую степень, если ее показатель каким угодно способом выражается через I/I024.
Таким образом, мы спустимся еще на 26 единиц и найдем для предела 2,3025. (Позднее мы увидим, что правильнее было бы взять 2,3026, но давайте возьмем то, что у нас получилось.) Пользуясь этой таблицей, можно возвести 10 в любую степень, если ее показатель каким угодно способом выражается через I/I024.
Теперь легко составить таблицу логарифмов, потому что все необходимое для этого мы уже припасли. Процедура этого изображена в табл. 22.2, а нужные числа берутся из второго и третьего столбцов табл. 22.1.
Предположим, что мы хотим знать логарифм 2. Это значит, что мы хотим знать, в какую степень надо возвести 10, чтобы получить 2. Может быть, возвести 10 в степень 1/2? Нет, получится слишком большое число. Глядя на табл.. 22.1, можно сказать, что нужное нам число лежит между 1/4 и 1/2. Поиск его начнем с 1/4; разделим 2 на 1,778…, получится 1,124…; при делении мы отняли от логарифма двух 0,250000, и теперь нас интересует логарифм 1,124…. Отыскав его, мы прибавим к результату 1/4 = 256/1024. Найдем в табл.22.1 число, которое бы при движении по третьему столбцу сверху вниз стояло сразу за 1,124… . Это 1,074607. Отношение 1,124… к 1,074607 равно 1,046598. В конце концов мы представим 2 в виде произведения чисел из табл. 22.1:
Найдем в табл.22.1 число, которое бы при движении по третьему столбцу сверху вниз стояло сразу за 1,124… . Это 1,074607. Отношение 1,124… к 1,074607 равно 1,046598. В конце концов мы представим 2 в виде произведения чисел из табл. 22.1:
2 = (1,77828) (1,074607) (1,036633). (1,0090350) (1,000573).
Для последнего множителя (1,000573) в нашей таблице места не нашлось; чтобы найти, его логарифм, надо представить это число в виде 10∆/1024 ≈ 1 + 2,3025∆/1024. Отсюда легко найти, что ∆ = 0,254. Таким образом, наше произведение можно представить в виде десятки, возведенной в степень 1/1024 (266 + 32+16 + 4 + 0,254). Складывая и деля, мы получаем нужный логарифм: log 10 2 = 0,30103; этот результат верен до пятого десятичного знака!
Мы вычисляли логарифмы точно так же, как это делал мистер Бриггс из Галифакса в 1620 г. Закончив работу, он сказал: «Я вычислил последовательно 54 квадратных корня из 10». На самом деле он вычислил только 27 первых корней, а потом сделал фокус с ∆. Вычислить 27 раз квадратный корень из 10, вообще-то говоря, немного сложнее, чем
10 раз, как это сделали мы. Однако мистер Бриггс сделал гораздо большее: он вычислял корни с точностью до шестнадцатого десятичного знака, а когда опубликовал свои таблицы, то оставил в них лишь 14 десятичных знаков, чтобы округлить ошибки. Составить таблицы логарифмов с точностью до четырнадцатого десятичного знака таким методом- дело очень трудное. Зато целых 300 лет спустя составители таблиц логарифмов занимались тем, что уменьшали таблицы мистера Бриггса, выкидывая из них каждый раз разное число десятичных знаков. Только в последнее время при помощи электронных вычислительных машин оказалось возможным составить таблицы логарифмов независимо от Мистера Бриггса. При этом использовался более эффективный метод вычислений, основанный на разложении логарифма в ряд.
Однако мистер Бриггс сделал гораздо большее: он вычислял корни с точностью до шестнадцатого десятичного знака, а когда опубликовал свои таблицы, то оставил в них лишь 14 десятичных знаков, чтобы округлить ошибки. Составить таблицы логарифмов с точностью до четырнадцатого десятичного знака таким методом- дело очень трудное. Зато целых 300 лет спустя составители таблиц логарифмов занимались тем, что уменьшали таблицы мистера Бриггса, выкидывая из них каждый раз разное число десятичных знаков. Только в последнее время при помощи электронных вычислительных машин оказалось возможным составить таблицы логарифмов независимо от Мистера Бриггса. При этом использовался более эффективный метод вычислений, основанный на разложении логарифма в ряд.
Составляя таблицы, мы натолкнулись на интересный факт; если показатель степени ε очень мал, то очень легко вычислить 10 ε ; это просто 1+2,3025ε. Это значит, что 10 n/2,3025 = 1 + n для очень малых n. Кроме того, мы говорили с самого начала, что вычисляем логарифмы по основанию 10 только потому, что у нас на руках 10 пальцев и по десяткам нам считать удобнее. Логарифмы по любому другому основанию получаются из логарифмов по основанию 10 простым умножением. Теперь настало время выяснить, не существует ли математически выделенного основания логарифмов, выделенного по причинам, не имеющим ничего общего с числом пальцев на руке. В этой естественной шкале формулы с логарифмами должны выглядеть проще. Составим новую таблицу логарифмов, умножив все логарифмы по основанию 10 на 2,3025…. Это соответствует переходу к новому основанию — натуральному, или основанию е. Заметим, что log e (l + n) ≈ n или е n ≈ 1 + n, когда n → 0.
Логарифмы по любому другому основанию получаются из логарифмов по основанию 10 простым умножением. Теперь настало время выяснить, не существует ли математически выделенного основания логарифмов, выделенного по причинам, не имеющим ничего общего с числом пальцев на руке. В этой естественной шкале формулы с логарифмами должны выглядеть проще. Составим новую таблицу логарифмов, умножив все логарифмы по основанию 10 на 2,3025…. Это соответствует переходу к новому основанию — натуральному, или основанию е. Заметим, что log e (l + n) ≈ n или е n ≈ 1 + n, когда n → 0.
Легко найти само число е; оно равно 101/ 2,3025 или 10 0,4342294… Это 10 в иррациональной степени. Для вычисления е можно воспользоваться таблицей корней из 10. Представим 0,434294… сначала в виде 444,73/1024, а числитель этой дроби в виде суммы 444,73 = 256 + 128 + 32 + 16 + 8 + 4 + 0,73. Число е поэтому равно произведению чисел
(1,77828) (1,33352) (1,074607) (1,036633) (1,018152) (1,009035) (1,001643) = 2,7184.
(Числа 0,73 нет в нашей таблице, но соответствующий ему результат можно представить в виде 1 + 2,3025∆/1024 и вы—числить при ∆ = 0,73. ) Перемножив все 7 сомножителей, мы получим 2,7184 (на самом деле должно быть 2,7183, но и этот результат хорош). Используя такие таблицы, можно возводить число в иррациональную степень и вычислять логарифмы иррациональных чисел. Вот как надо обращаться с иррациональностями!
) Перемножив все 7 сомножителей, мы получим 2,7184 (на самом деле должно быть 2,7183, но и этот результат хорош). Используя такие таблицы, можно возводить число в иррациональную степень и вычислять логарифмы иррациональных чисел. Вот как надо обращаться с иррациональностями!
Этап урока | Время мин | Формы организации учебной деятельности | Деятельность учителя | Деятельность обучающихся | Формирование УУД |
1.Орг. момент | 2-3 мин | фронтальная | Учитель приветствует учеников. Сегодня у нас урок необычный, к нам пришли гости, а девизом нашего урока станут слова китайской притчи: «Скажи мне и я забуду, Покажи мне и я запомню, Дай сделать и я пойму» (Слайд№1) | Приветствуют учителя | Личностные УУД: Развитие познавательных интересов, учебных мотивов, формирования мотивов достижения и социального признания, мотива, реализующего потребность в социально значимой и социально оцениваемой деятельности. |
2.Формулирование темы урока и постановка целей | 2 мин | фронтальная | Ребята, чтобы узнать тему отгадайте загадку: Он есть у дерева, цветка, он есть у уравнений. И знак особый радикал, с ним связан вне сомнений Заданий многих он итог, И с этим мы не спорим Надеемся, что каждый смог ответить: это…(корень) Какова тема нашего урока?(2 слайд) Какие цели и задачи мы поставим перед собой? (Слайд 3) Открываем тетради записываем дату и тему урока | Учащиеся называют тему и цели урока и записывают в тетради. Тема: «Арифметический квадратный корень» Цели: 1.Повторить, что такое арифметический квадратный корень? 2.Закрепить умения применять определение, свойства арифметического квадратного корня | Регулятивные УУД: целеполагание, планирование, саморегуляция. |
3 Устный счёт. | 5мин | фронтальная | (Слайд 4) -Что такое квадратный корень? -Что называется арифметическим квадратным корнем? -Как называется выражение, стоящее под знаком корня? -При каких значениях а имеет смысл выражение √а? -Объясните, почему верно или неверно равенство(5 слайд) √0,64=0,8 (равенство верно, т.к.0,80 и 0,82 = 0,64) √0,25= — 0,5 (равенство неверно, т.к. -0,5 — Вычислить арифметический квадратный корень из чисел: √400;√0,36; √25; √0,09, У вас на столах оценочные листы оцените свою работу за данный этап. | Учащиеся отвечают на вопросы. —Квадратным корнем из числа а называется число, квадрат которого равен а. —Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а. -Выражение, стоящее под знаком корня называется подкоренным выражением. -Выражение √а имеет смысл при а ≥0. 30; 0,6; 5;0,3;-8. Работают с оценочным листом | Коммуникативные УУД: умение с достаточной полнотой и точностью выражать свои мысли. Метапредметные результаты: Формирование умений воспринимать и перерабатывать информацию и представлять её в словесной форме, умение давать полные ответы. Оценивать себя |
4.Актуализация знаний учащихся. | 10-13мин | индивидуальная Работа в парах | Повторили материал, а теперь давайте применим при решении теста. Решите задания А1-В1.Тест раздается каждому ученику. Решение отображается на слайде. Выполните взаимопроверку. Оцените товарища. (Слайд 6) -Сможете ли вы, имея полученные знания об арифметическом квадратном корне, выполнить задание из КИМов ОГЭ? На столах задание. -Каждое из чисел√ 27,√13,√39 соотнесите с соответствующей ему точкой координатной прямой. Работа в парах. Оцените своего партнера. Ответ (слайд7) | Решают тест по вариантам. Взаимопроверка. Ответы на тест: 1 вариант А1-3,А2-1,А3-2,А4-3,В1-8. 2 вариант А1-4, А2-3, А3-1,А4-2,В1-5. Заполняют оценочный лист Выполняют задание из ОГЭ в парах и оценивают друг друга. Ответ:√27-P, √12-M, √39-Q. | Познавательные УУД: логические действия (анализ условия задания, установление причинно-следственных связей в получении результатов) Коммуникативные УУД: работа в паре, умение с достаточной полнотой и точностью выражать свои мысли. Метапредметные результаты: Формирование умений воспринимать и перерабатывать информацию и представлять её в словесной форме, овладение навыками планирования и оценки результатов своей деятельности |
5. | 2 мин | индивидуальная | На столах для каждого кроссворд. Разгадай кроссворд (радикал) | Работа в карточках. Оценивание себя. | |
6.Физминут-ка | 1мин | фронтальная | Я читаю вам равенство, если оно верно хлопаете в ладоши, если нет встаете. √ 144=12, √ 4/9=5/6, √ 6/8=не существует, √ -400=-20 | Учащиеся выполняют упражнения. | Коммуникативные УУД |
7. «Из истории математики» | 3мин | фронтальная | Итак, в кроссворде мы получили слово радикал. Какова же история возникновения знака корня? Историческая справка. | Один из учащихся представляет историческую справку. | Коммуникативные УУД: умение с достаточной полнотой и точностью выражать свои мысли. |
8.Самостоятельная работа (разноуровневые задания) | 12мин | индивидуальная | Объяснение правил выполнения самостоятельной работы. Оценивание по образцу. Взаимопроверка. (Слайд№8)Уровень 1 за каждый правильный ответ 1 балл Уровень 2 за каждый правильный ответ 2 балла Уровень 3 за каждый правильный ответ 3 балла | Ученики выбирают уровень сложности самостоятельной работы и самостоятельно выполняют задания. Взаимопроверка по образцу. | Предметные результаты: умение получать и применять полученные знания при решении задач. Умение работать в паре. |
9.Подведение итогов. Выставление оценок по результатам набранных баллов за урок. | 2 мин | индивидуальная | (слайд 9)Выставление оценок по результатам набранных баллов за урок (Слайд 10) -Итак, чем же мы с вами занимались сегодня на уроке? -Чему вы научились сегодня на уроке? -Где вам могут пригодиться эти знания? -Каким образом наш урок связан с китайской притчей? | Подсчёт баллов. Выставление оценок по результатам набранных баллов за урок. Отвечают на вопросы учителя. | Познавательные УУД: логические действия (анализ условия задания, установление причинно-следственных связей в получении результатов) Коммуникативные УУД: умение с достаточной полнотой и точностью выражать свои мысли. Метапредметные результаты: Формирование умений воспринимать и перерабатывать информацию и представлять её в словесной форме, овладение навыками планирования и оценки результатов своей деятельности |
10.Постановка домашнего задания | 1 мин | фронтальная | Запишем домашнее задание (дифференцированное) (Слайд 11) п.12 №302,303, №305(а ,д) Дополнительно №466 | Записывают домашнее задание | Формирование регулятивные УУД |
11 рефлексия | 1 мин | фронтальная | — Продолжите одну из фраз.
| Отвечают на вопрос учителя | Формирование умений воспринимать и перерабатывать информацию и представлять её в словесной форме |
Квадратный корень из 121 — Как найти квадратный корень из 121?
LearnPracticeDownload
Квадратный корень из 121 выражается как √121 в радикальной форме и как (121) ½ или (121) 0,5 в экспоненциальной форме. Квадратный корень из 121 равен 11. Это положительное решение уравнения x 2 = 121. Число 121 является полным квадратом.
- Квадратный корень из 121: 11
- Квадратный корень из 121 в экспоненциальной форме: (121) ½ или (121) 0,5
- Квадратный корень из 121 в подкоренной форме: √121
1. | Что такое квадратный корень из 121? |
| 2. | Квадратный корень из 121 рационален или иррационален? |
| 3. | Как найти квадратный корень из 121? |
| 4. | Часто задаваемые вопросы о квадратном корне из 121 |
Что такое квадратный корень из 121?
Мы знаем, что операция сложения обратна вычитанию, а операция умножения обратна делению. Точно так же нахождение квадратного корня является операцией, обратной возведению в квадрат. Квадратный корень из 121 — это число, которое умножается на само себя, чтобы получить число 121.
Является ли квадратный корень из 121 рациональным или иррациональным?
Рациональное число — это число, которое может быть выражено в виде p/q, где p и q — целые числа, а q не равно 0. Мы уже выяснили, что √ 121 = 11. Число 11 – рациональное число. Итак, квадратный корень из 121 – рациональное число.
Как найти квадратный корень из 121?
Мы обсудим два метода нахождения квадратного корня из 121
- Факторизация простых чисел
- Длинное деление
Квадратный корень из 121 с помощью факторизации простых чисел
Факторизация простых чисел — это способ представления числа как произведения его простых множителей. Простая факторизация числа 121 равна 121 = 11 × 11 = 11 9.0005 2 . Чтобы найти квадратный корень из 121, мы берем по одному числу из каждой пары одинаковых чисел и перемножаем их.
- 121 = 11 × 11
- √ 121 = 11
Квадратный корень из 121 методом деления в длину
Значение квадратного корня из 121 методом деления в длину состоит из следующих шагов:
- Шаг 1 : Начиная справа, мы соединим цифры поставив над ними полосу.
- Шаг 2 : Найдите число, которое при умножении на себя дает произведение, меньшее или равное 1.
 Итак, это число равно 1. Присвоив делителю 1, мы получим частное как 1, а остаток 0
Итак, это число равно 1. Присвоив делителю 1, мы получим частное как 1, а остаток 0 - Шаг 3 : Удвойте делитель и введите его с пробелом справа. Угадайте наибольшую возможную цифру, чтобы заполнить пробел, который также станет новой цифрой в частном, так что, когда новый делитель умножается на новое частное, произведение меньше или равно делимому. Разделите и запишите остаток.
Изучение квадратного корня с помощью иллюстраций и интерактивных примеров
- Квадратный корень из 64
- Квадратный корень из 144
- Квадратный корень из 1000
- Квадратный корень из 22
- Квадратный корень из 81
Важные примечания:
- Квадратный корень — это операция, обратная возведению в квадрат.
- Мы можем найти квадратный корень из 121, используя разложение на простые множители, многократное вычитание и метод длинного деления.
- Квадратный корень числа является как отрицательным, так и положительным для одного и того же числового значения, т.
 е. квадратный корень из 121 будет равен 11.
е. квадратный корень из 121 будет равен 11.
Аналитический центр:
- Мы знаем, что (-11) × (-11) = 121. Итак, можем ли мы сказать, что -11 – это квадратный корень из 121?
- Можете ли вы определить квадратное уравнение, корни которого равны 121 и -121?
Квадратный корень из 121 решенного примера
Пример 1 : учитель Тима попросил его найти квадратный корень из 121, используя метод простой факторизации. Вы можете помочь ему сделать это?
Решение
Разложение числа 121 = 11 × 11 на простые множители
Простые множители числа 11 в парах: (11 × 11)
. Квадратный корень из 121: √(11 × 11) = √(11 2 )
Следовательно, √121 = 11Пример 2 : Садовник купил 121 растение. Он хочет посадить их так, чтобы количество растений в каждом ряду и столбце было одинаковым. Сколько растений он посадит в каждом ряду?
Раствор
Если садовник сажает одинаковое количество растений в каждом ряду и столбце, то нам нужно найти число, квадрат которого равен 121
Мы знаем, что √121 = 11
Следовательно, садовник посадит 11 растений в каждом строка
Пример: если площадь круга равна 121π в 2 .
 Найдите радиус окружности.
Найдите радиус окружности. Решение:
Пусть ‘r’ будет радиусом окружности.
⇒ Площадь круга = πr 2 = 121π в 2
⇒ г = ±√121 в
Так как радиус не может быть отрицательным,
⇒ г = √121
Квадратный корень из 121 равен 11.
⇒ г = 11 в
перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Часто задаваемые вопросы о квадратном корне из 121
Каково значение квадратного корня из 121?
Квадратный корень из 121 равен 11.
Почему квадратный корень из 121 является рациональным числом?
При разложении на простые множители 121, т. е. 11 2 , мы обнаруживаем, что все простые множители имеют четную степень. Это означает, что квадратный корень из 121 является положительным целым числом. Следовательно, квадратный корень из 121 является рациональным.
Это означает, что квадратный корень из 121 является положительным целым числом. Следовательно, квадратный корень из 121 является рациональным.
Что такое квадратный корень из -121?
Квадратный корень из -121 является мнимым числом. Это можно записать как √-121 = √-1 × √121 = i √121 = 11i
где i = √-1 и называется мнимой единицей.
Вычислить 18 плюс квадратный корень из 6 121
Данное выражение равно 18 + 6 √121. Мы знаем, что квадратный корень из 121 равен 11. Следовательно, 18 + 6 √121 = 18 + 6 × 11 = 18 + 66 = 84
Чему равен квадрат квадратного корня из 121?
Квадрат квадратного корня из 121 равен самому числу 121, т. е. (√121) 2 = (121) 2/2 = 121.
Если квадратный корень из 121 равен 11. Найдите значение квадратный корень из 1,21.
Представим √1,21 в форме p/q, т.е. √(121/100) = 11/10 = 1,1. Следовательно, значение √1,21 = 1,1
Рабочие листы по математике и
наглядная программа
Квадратный корень из 121 (√121)
Здесь мы определим, проанализируем, упростим и вычислим квадратный корень из 121. Начнем с определением, а затем ответить на некоторые общие
вопросы о квадратном корне из 121. Затем мы покажем вам различные способы вычисления квадратного корня из 121 с и без
компьютер или калькулятор. У нас есть много информации, чтобы поделиться, так что давайте начнем!
Начнем с определением, а затем ответить на некоторые общие
вопросы о квадратном корне из 121. Затем мы покажем вам различные способы вычисления квадратного корня из 121 с и без
компьютер или калькулятор. У нас есть много информации, чтобы поделиться, так что давайте начнем!
Квадратный корень из 121 определение
Квадратный корень из 121 в математической форме записывается с таким знаком радикала √121. Мы называем это квадратным корнем из 121 в радикальной форме.
Квадратный корень из 121 — это величина (q), которая при умножении сама на себя будет равна 121.
√121 = q × q = q 2
Является ли число 121 полным квадратом?
121 является полным квадратом, если квадратный корень из 121 равен целому числу. Как мы рассчитали дальше
внизу на этой странице квадратный корень из 121 — это целое число.
121 — правильный квадрат.
Является ли квадратный корень из 121 рациональным или иррациональным?
Квадратный корень из 121 является рациональным числом, если 121 является полным квадратом. Это иррациональное число, если оно не является полным квадратом.
Поскольку 121 — полный квадрат, это рациональное число. Это означает, что ответ на вопрос «квадратный корень из 121?» не будет иметь десятичных знаков.
Это иррациональное число, если оно не является полным квадратом.
Поскольку 121 — полный квадрат, это рациональное число. Это означает, что ответ на вопрос «квадратный корень из 121?» не будет иметь десятичных знаков.
√121 — рациональное число
Можно ли упростить квадратный корень из 121?
Квадратный корень из полного квадрата можно упростить, потому что квадратный корень из полного квадрата будет равен целому числу:
√121 = 11
Как вычислить квадратный корень из 121 с помощью калькулятора
Самый простой и скучный способ вычислить квадратный корень из 121 — воспользоваться калькулятором!
Просто введите 121, а затем √x, чтобы получить ответ. Мы сделали это с помощью нашего калькулятора и получили следующий ответ:
√121 = 11
Как вычислить квадратный корень из 121 на компьютере
Если вы используете компьютер с Excel или Numbers, вы можете ввести SQRT(121) в ячейку, чтобы получить квадратный корень из 121. Ниже приведен результат, который мы получили:
Ниже приведен результат, который мы получили:
SQRT(121) = 11
Чему равен квадратный корень из 121, записанный с показателем степени?
Все квадратные корни можно преобразовать в число (основание) с дробным показателем степени. Квадратный корень из 121 не является исключением. Вот правило и ответ
на «квадратный корень из 121, преобразованный в основание с показателем степени?»:
√b = b ½
√121 = 121 ½
Как найти квадратный корень из 121 методом деления в длину 2
метод длинного деления. это потерянный
искусство того, как они вычисляли квадратный корень из 121 вручную до того, как были изобретены современные технологии.
Шаг 1)
Наберите 121 парами по две цифры справа налево:
Шаг 2)
Начнем с первого набора: самый большой совершенный квадрат, меньший или равный 1, равен 1, а квадратный корень из 1 равен 1. Поэтому поместите 1 сверху и 1 снизу следующим образом:
Поэтому поместите 1 сверху и 1 снизу следующим образом:
| 1 | ||||
| 01 | 21 | |||
| 1 | ||||
Step 3)
Calculate 1 minus 1 and put the difference below. Затем переместитесь вниз к следующему набору чисел.
| 1 | ||||
| 01 | 21 | |||
| 1 | ||||
| 0 | 21 | |||
Шаг 4)
Удвойте число, выделенное зеленым сверху: 1 × 2 = 2. Затем используйте 2 и нижнее число, чтобы решить эту задачу:
Затем используйте 2 и нижнее число, чтобы решить эту задачу:
2? × ? ≤ 21
Знаки вопроса «пробел» и такие же «пробел». Методом проб и ошибок мы нашли, что наибольшее число, которое может быть пустым, равно 1. Замените вопросительные знаки в задаче на 1, чтобы получить:
21 × 1 = 21.
Now, enter 1 on top, and 21 at the bottom:
| 1 | 1 | |||
| 01 | 21 | |||
| 1 | ||||
| 0 | 21 | |||
| 0 | 21 | |||
Разница между двумя нижними числами равна нулю, поэтому все готово! Ответ — зеленые цифры сверху. Еще раз, квадратный корень из
121 это 11.
Еще раз, квадратный корень из
121 это 11.
Квадратный корень из числа
Пожалуйста, введите другое число в поле ниже, чтобы получить квадратный корень из числа и другую подробную информацию, как вы получили для 121 на этой странице.
Примечания
Помните, что отрицательное значение, умноженное на отрицательное, равно положительному. Таким образом, квадратный корень из 121 имеет не только положительный ответ
что мы объяснили выше, но и отрицательный аналог.
На этой странице мы часто ссылаемся на совершенные квадратные корни. Вы можете использовать список идеальных квадратов для справки. 93-8
Квадратный корень из 121 | √121
| Пожалуйста, введите реальный номер: |
| Результат квадратного корня: |
Вот ответ на такие вопросы, как: Квадратный корень из 121 | √121 или чему равен квадратный корень из 121?
Используйте приведенный ниже калькулятор квадратного корня, чтобы найти квадратный корень любого мнимого или действительного числа. См. также на этой веб-странице таблицу квадратного корня от 1 до 100, а также вавилонский метод или метод Героя.
См. также на этой веб-странице таблицу квадратного корня от 1 до 100, а также вавилонский метод или метод Героя.
Вавилонский метод, также известный как метод Героя
Ниже показано, как шаг за шагом вычислить квадратный корень из 121 с помощью вавилонского метода , также известного как Метод Героя .
Что такое квадратный корень?
Определение квадратного корня
Квадратный корень из числа «а» — это число х, такое что х 2 = а, другими словами, число х, квадрат которого равен а. Например, 11 — это квадратный корень из 121, потому что 11 2 = 11•11 = 121, -11 — это квадратный корень из 121, потому что (-11) 2 = (-11)•(-11) = 121.
Таблица квадратных корней 1-100
Квадратные корни от 1 до 100, округленные до тысячных.
| нет | нет 2 | √ |
|---|---|---|
| 1 | 1 | 1. 000 000 |
| 2 | 4 | 1.414 |
| 3 | 9 | 1.732 |
| 4 | 16 | 2.000 |
| 5 | 25 | 2.236 |
| 6 | 36 | 2.449 |
| 7 | 49 | 2.646 |
| 8 | 64 | 2.828 |
| 9 | 81 | 3.000 |
| 10 | 100 | 3.162 |
| 11 | 121 | 3.317 |
| 12 | 144 | 3.464 |
| 13 | 169 | 3.606 |
| 14 | 196 | 3.742 |
| 15 | 225 | 3.873 |
| 16 | 256 | 4.000 |
| 17 | 289 | 4.123 |
| 18 | 324 | 4. 243 243 |
| 19 | 361 | 4.359 |
| 20 | 400 | 4.472 |
| 21 | 441 | 4.583 |
| 22 | 484 | 4.690 |
| 23 | 529 | 4.796 |
| 24 | 576 | 4.899 |
| 25 | 625 | 5.000 |
| нет | нет 2 | √ | |
|---|---|---|---|
| 26 | 676 | 5.099 | |
| 27 | 729 | 5.196 | |
| 28 | 784 | 5.292 | |
| 29 | 841 | 5.385 | |
| 30 | 900 | 5.477 | |
| 31 | 961 | 5.568 | |
| 32 | 1,024 | 5.657 | |
| 33 | 1,089 | 5. 745 745 | |
| 34 | 1,156 | 5.831 | |
| 35 | 1,225 | 5.916 | |
| 36 | 1,296 | 6.000 | |
| 37 | 1,369 | 6.083 | |
| 38 | 1,444 | 6.164 | |
| 39 | 1,521 | 6.245 | |
| 40 | 1,600 | 6.325 | |
| 41 | 1,681 | 6.403 | |
| 42 | 1,764 | 6.481 | |
| 43 | 1,849 | 6.557 | |
| 44 | 1,936 | 6.633 | |
| 45 | 2,025 | 6.708 | |
| 46 | 2,116 | 6.782 | |
| 47 | 2,209 | 6.856 | |
| 48 | 2,304 | 6.928 | |
| 49 | 2401 | 7. 000 000 | |
| 50 | 2500 | 7.071 |
| нет | нет 2 | √ |
|---|---|---|
| 51 | 2,601 | 7.141 |
| 52 | 2,704 | 7.211 |
| 53 | 2,809 | 7.280 |
| 54 | 2,916 | 7.348 |
| 55 | 3,025 | 7.416 |
| 56 | 3,136 | 7.483 |
| 57 | 3,249 | 7.550 |
| 58 | 3,364 | 7.616 |
| 59 | 3,481 | 7.681 |
| 60 | 3,600 | 7.746 |
| 61 | 3,721 | 7.810 |
| 62 | 3,844 | 7.874 |
| 63 | 3,969 | 7.937 |
| 64 | 4,096 | 8. 000 000 |
| 65 | 4,225 | 8.062 |
| 66 | 4,356 | 8.124 |
| 67 | 4,489 | 8.185 |
| 68 | 4,624 | 8.246 |
| 69 | 4,761 | 8.307 |
| 70 | 4,900 | 8.367 |
| 71 | 5,041 | 8.426 |
| 72 | 5,184 | 8.485 |
| 73 | 5,329 | 8.544 |
| 74 | 5476 | 8.602 |
| 75 | 5625 | 8.660 |
| нет | нет 2 | √ |
|---|---|---|
| 76 | 5,776 | 8.718 |
| 77 | 5,929 | 8.775 |
| 78 | 6,084 | 8.832 |
| 79 | 6,241 | 8. 888 888 |
| 80 | 6,400 | 8.944 |
| 81 | 6,561 | 9.000 |
| 82 | 6,724 | 9.055 |
| 83 | 6,889 | 9.110 |
| 84 | 7,056 | 9.165 |
| 85 | 7,225 | 9.220 |
| 86 | 7,396 | 9.274 |
| 87 | 7,569 | 9.327 |
| 88 | 7,744 | 9.381 |
| 89 | 7,921 | 9.434 |
| 90 | 8,100 | 9.487 |
| 91 | 8,281 | 9.539 |
| 92 | 8,464 | 9.592 |
| 93 | 8,649 | 9.644 |
| 94 | 8,836 | 9.695 |
| 95 | 9,025 | 9,747 |
| 96 | 9,216 | 9,798 |
| 97934 | 3444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444н. 0037 0037 | |
| 98 | 9,604 | 9.899 |
| 99 | 9,801 | 9.950 |
| 100 | 10,000 | 10.000 |
Что такое квадратный корень из 121?
В математике квадратный корень из числа, подобного 121, — это число, которое при умножении само на себя равно 121. Мы бы показали это в математической форме с помощью символа квадратного корня, который называется подкоренным символом: √
Любое число с подкоренным символом рядом с ним называется подкоренным членом или квадратным корнем из 121 в подкоренной форме.
Чтобы объяснить квадратный корень немного больше, квадратный корень из числа 121 — это величина (которую мы называем q), которая при умножении сама на себя равна 121:
√121 = q × q = q 2
Итак, что такое квадратный корень из 121 и как его вычислить? Хорошо, если у вас есть компьютер или калькулятор, вы можете легко вычислить квадратный корень. Если вам нужно сделать это вручную, то для этого потребуется старое доброе деление в длину с помощью карандаша и листа бумаги.
Если вам нужно сделать это вручную, то для этого потребуется старое доброе деление в длину с помощью карандаша и листа бумаги.
Для целей этой статьи мы вычислим его для вас (но позже в статье мы покажем вам, как вычислить его самостоятельно с помощью деления в большую сторону). Квадратный корень из 121 равен 11:
11 × 11 = 121
Является ли число 121 идеальным квадратом?
Когда квадратный корень данного числа является целым числом, это называется полным квадратом. Совершенные квадраты важны для многих математических функций и используются во всем, от плотницких работ до более сложных тем, таких как физика и астрономия.
Если мы посмотрим на число 121, то узнаем, что квадратный корень равен 11, а поскольку это целое число, мы также знаем, что 121 — это полный квадрат .
Если вы хотите узнать больше о числах с идеальным квадратом, у нас есть список идеальных квадратов, который охватывает первые 1000 чисел с идеальным квадратом.
121 — рациональное или иррациональное число?
Еще один распространенный вопрос, который может возникнуть при работе с корнями числа, например 121, заключается в том, является ли данное число рациональным или иррациональным. Рациональные числа можно записать в виде дроби, а иррациональные — нет.
Самый быстрый способ проверить, является ли число рациональным или иррациональным, — определить, является ли оно полным квадратом. Если да, то это рациональное число, а если не полный квадрат, то это иррациональное число.
Мы уже знаем, что 121 — рациональное число, потому что мы знаем, что это полный квадрат.
Вычисление квадратного корня из 121
Чтобы вычислить квадратный корень из 121 с помощью калькулятора, введите в калькулятор число 121 и нажмите клавишу √x:
√121 = 11,0000
Чтобы вычислить квадратный корень из 121 в Excel, Numbers of Google Sheets, вы можете использовать функцию SQRT() :
SQRT(121) = 11
Округление квадратного корня из 121
Иногда, когда вы работаете с квадратным корнем из 121, вам может понадобиться округлить ответ до определенного числа знаков после запятой:
10-й: √121 = 11,0
100-й: √121 = 11,00
1000-й: √121 = 11,000
Нахождение квадратного корня из 121 с помощью длинного деления
Если у вас нет калькулятора или компьютерной программы, вам придется использовать старое доброе деление в длину, чтобы извлечь квадратный корень из 121. Именно так математики вычисляли его задолго до того, как были изобретены калькуляторы и компьютеры.
Именно так математики вычисляли его задолго до того, как были изобретены калькуляторы и компьютеры.
Шаг 1
Установите 121 в виде пар двух цифр справа налево и присоедините один набор из 00, потому что нам нужен один десятичный знак:
Шаг 2
Начиная с первого набора: самый большой совершенный квадрат, меньший или равный 1, равен 1, а квадратный корень из 1 равен 1. Поэтому поставьте 1 сверху и 1 снизу вот так:
| 1 | |
1 | 21 |
1 |
Этап 3
Вычислите 1 минус 1 и поместите разницу ниже. Затем переместитесь вниз к следующему набору чисел.
| 1 | |
1 | 21 |
1 | |
21 |
Этап 4
Удвойте число, выделенное зеленым сверху: 1 × 2 = 2. Затем используйте 2 и нижнее число, чтобы решить эту задачу:
Затем используйте 2 и нижнее число, чтобы решить эту задачу:
2? × ? ≤ 21
Знаки вопроса «пробел» и такие же «пробел». Путем проб и ошибок мы обнаружили, что наибольшее число, которое может быть пустым, равно 1.
Теперь введите 1 сверху:
| 1 | 1 |
1 | 21 |
1 | |
21 |
Надеюсь, это дало вам представление о том, как извлечь квадратный корень с помощью деления в большую сторону, чтобы вы могли самостоятельно решать будущие задачи.
Практика извлечения квадратных корней на примерах
Если вы хотите продолжить изучение квадратных корней, взгляните на случайные вычисления на боковой панели справа от этой записи в блоге.
Мы перечислили несколько совершенно случайных чисел, которые вы можете щелкнуть и следовать информации о вычислении квадратного корня из этого числа, чтобы помочь вам понять числовые корни.
Вычислить другую задачу на квадратный корень
Введите число в поле А ниже и нажмите «Рассчитать», чтобы вычислить квадратный корень из заданного числа.
Пожалуйста, используйте инструмент ниже, чтобы вернуться на эту страницу или цитировать/ссылаться на нас во всем, для чего вы используете информацию. Ваша поддержка помогает нам продолжать предоставлять контент!
Квадратный корень из 121
Sqrt(121). Найдите квадратный корень из 121 или любого другого действительного числа, положительного или отрицательного. Вот ответы на такие вопросы, как: Квадратный корень из 121 или что такое квадратный корень из 121?
Что такое квадратный корень? Определение квадратного корня
Квадратный корень из числа ‘x’ – это число y такое, что y 2 = x, другими словами, число y, квадрат которого равен y. Например, 11 — это квадратный корень из 121, потому что 11 2 = 11•11 = 121, -11 — это квадратный корень из 121, потому что (-11) 2 = (-11)•(-11) = 121. При написании математических выражений люди часто используют sqrt(x) для обозначения квадратного корня из x. Подробнее о квадратном корне читайте здесь: Квадратный корень — Википедия и здесь: Квадратный корень — Wolfram
При написании математических выражений люди часто используют sqrt(x) для обозначения квадратного корня из x. Подробнее о квадратном корне читайте здесь: Квадратный корень — Википедия и здесь: Квадратный корень — Wolfram
Квадратный символ?
Вот символ квадратного корня. Он обозначается √, известным как радикальный знак или основание.
Таблица квадратного корня 1-100
Квадратные корни от 1 до 100 округляются до тысячных.
| номер | квадрат | квадрат корень |
|---|---|---|
| 1 | 1 | 1.000 |
| 2 | 4 | 1.414 |
| 3 | 9 | 1.732 |
| 4 | 16 | 2.000 |
| 5 | 25 | 2.236 |
| 6 | 36 | 2.449 |
| 7 | 49 | 2.646 |
| 8 | 64 | 2. 828 828 |
| 9 | 81 | 3.000 |
| 10 | 100 | 3.162 |
| 11 | 121 | 3.317 |
| 12 | 144 | 3.464 |
| 13 | 169 | 3.606 |
| 14 | 196 | 3.742 |
| 15 | 225 | 3.873 |
| 16 | 256 | 4.000 |
| 17 | 289 | 4.123 |
| 18 | 324 | 4.243 |
| 19 | 361 | 4.359 |
| 20 | 400 | 4.472 |
| 21 | 441 | 4.583 |
| 22 | 484 | 4.690 |
| 23 | 529 | 4.796 |
| 24 | 576 | 4.899 |
| 25 | 625 | 5. 000 000 |
| number | square | square root |
|---|---|---|
| 26 | 676 | 5.099 |
| 27 | 729 | 5.196 |
| 28 | 784 | 5.292 |
| 29 | 841 | 5.385 |
| 30 | 900 | 5.477 |
| 31 | 961 | 5.568 |
| 32 | 1,024 | 5.657 |
| 33 | 1,089 | 5.745 |
| 34 | 1,156 | 5.831 |
| 35 | 1,225 | 5.916 |
| 36 | 1,296 | 6.000 |
| 37 | 1,369 | 6.083 |
| 38 | 1,444 | 6.164 |
| 39 | 1,521 | 6.245 |
| 40 | 1,600 | 6. 325 325 |
| 41 | 1,681 | 6.403 |
| 42 | 1,764 | 6.481 |
| 43 | 1,849 | 6.557 |
| 44 | 1,936 | 6.633 |
| 45 | 2,025 | 6.708 |
| 46 | 2,116 | 6.782 |
| 47 | 2,209 | 6.856 |
| 48 | 2,304 | 6.928 |
| 49 | 2 401 | 7.000 |
| 50 | 2 500 | 7,071 |
| квадрат корень | ||
|---|---|---|
| 51 | 2,601 | 7. 141 141 |
| 52 | 2,704 | 7.211 |
| 53 | 2,809 | 7.280 |
| 54 | 2,916 | 7.348 |
| 55 | 3,025 | 7,416 |
| 56 | 3 136 | 7,483 |
| 57 | 7.550 | |
| 58 | 3,364 | 7.616 |
| 59 | 3,481 | 7.681 |
| 60 | 3,600 | 7.746 |
| 61 | 3,721 | 7.810 |
| 62 | 3,844 | 7.874 |
| 63 | 3,969 | 7.937 |
| 64 | 4,096 | 8.000 |
| 65 | 4,225 | 8.062 |
| 66 | 4,356 | 8.124 |
| 67 | 4,489 | 8. 185 185 |
| 68 | 4,624 | 8.246 |
| 69 | 4,761 | 8.307 |
| 70 | 4,900 | 8.367 |
| 71 | 5,041 | 8.426 |
| 72 | 5,184 | 8.485 |
| 73 | 5,329 | 8.544 |
| 74 | 5,476 | 8.602 |
| 75 | 5,625 | 8.660 |
| number | square | квадрат корень |
|---|---|---|
| 76 | 5 776 | 8,718 |
| 77 | 5 929 | 8,775 8 |
| 6,084 | 8.832 | |
| 79 | 6,241 | 8.888 |
| 80 | 6,400 | 8.944 |
| 81 | 6,561 | 9.000 |
| 82 | 6,724 | 9. 055 055 |
| 83 | 6,889 | 9.110 |
| 84 | 7,056 | 9.165 |
| 85 | 7,225 | 9.220 |
| 86 | 7,396 | 9.274 |
| 87 | 7,569 | 9.327 |
| 88 | 7,744 | 9.381 |
| 89 | 7,921 | 9.434 |
| 90 | 8,100 | 9.487 |
| 91 | 8,281 | 9.539 |
| 92 | 8,464 | 9.592 |
| 93 | 8,649 | 9.644 |
| 94 | 8,836 | 9.695 |
| 95 | 9,025 | 9.747 |
| 96 | 9,216 | 9.798 |
| 97 | 9,409 | 9.849 |
| 98 | 9,604 | 9. |

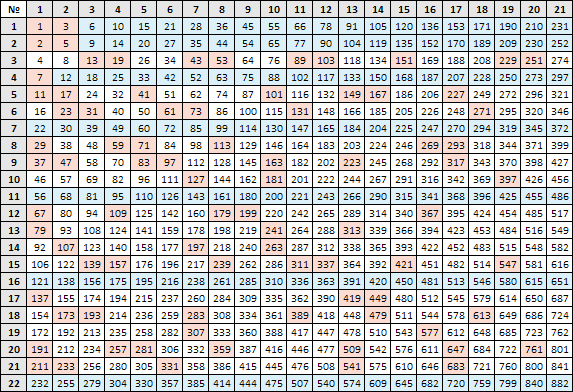
 Получим 66×6 = 396. Напишем 6 справа сверху, т. к. это вторая цифра результата. Отнимем 396 от 408, получим 12.
Получим 66×6 = 396. Напишем 6 справа сверху, т. к. это вторая цифра результата. Отнимем 396 от 408, получим 12. ru/data/moduleImages/QRCodes/121/64d7e6be1f04987083c9bbbd636ca91e.png
ru/data/moduleImages/QRCodes/121/64d7e6be1f04987083c9bbbd636ca91e.png 7957905455967
7957905455967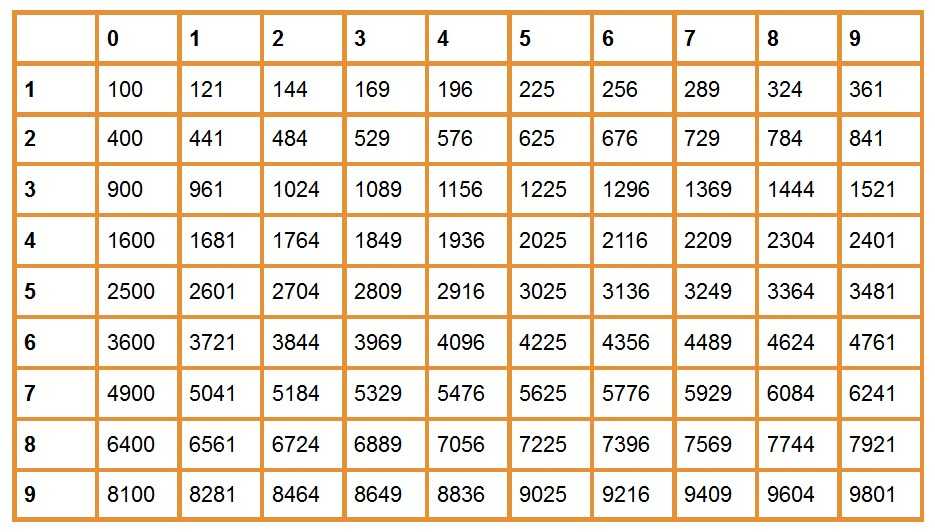 Получим 66×6 = 396. Напишем 6 справа сверху, т. к. это вторая цифра результата. Отнимем 396 от 408, получим 12.
Получим 66×6 = 396. Напишем 6 справа сверху, т. к. это вторая цифра результата. Отнимем 396 от 408, получим 12.