Пространство элементарных событий. Случайные события
События. Операции над событиями
Под событием в теории вероятностей понимается всякий факт, который в результате опыта может произойти или не произойти.
Примеры событий:
А – появился герб при бросании монеты;
В – появление трех гербов при трехкратном бросании монеты;
С – попадание в цель при выстреле;
D – появление туза при извлечении карты из колоды; и т.д.
Рассматривая вышеперечисленные события, мы видим, что каждое из них обладает какой-то степенью возможности: одни – большей, другие – меньшей. Причем, для некоторых событий мы сразу же можем решить, какое из них более, а какое менее возможно. Чтобы количественно сравнить между собой события по степени их возможности, очевидно нужно с каждым событием связать определенное число, которое тем больше, чем более возможно событие. Такое число мы называем вероятностью события.
Рассмотрим множество событий М, которые можно наблюдать в некотором эксперименте.
Для каждого события А из М введем противоположное событие А, которое состоит в том, что событие А не произошло.
Событие ∪, заключающееся в том, что из двух событий А и В происходит по крайней мере одно (либо А, либо В, либо А и В вместе), называется суммой (или объединением) событий А и В.
Событие ∩, заключающееся в том, что события А и В происходят одновременно, называется произведением (или пересечением) событий А и В.
Событие A \ B называется разностью событий А и В; оно заключается в том, что происходит А и не происходит В.
Операции над событиями обладают следующими свойствами:
- и — коммутативность сложения и умножения;
- и — ассоциативность сложения и умножения;
- — законы дистрибутивности.

Элементарные исходы
Предположим, что среди всех возможных событий A, которые в данном опыте по воле случая происходят или не происходят, можно выделить совокупность так называемых элементарных событий или элементарных исходов, обладающих следующими свойствами:
- во-первых, все они взаимоисключают друг друга, т.е. являются непересекающимися;
- во-вторых, в результате данного опыта обязательно происходит одно из этих элементарных событий;
- в-третьих, каково бы ни было событие A, по наступившему элементарному исходу всегда можно судить о том, происходит или не происходит это событие.
Элементарные исходы обычно обозначаются греческой буквой ω, а их совокупность Ω называется пространством элементарных событий.
Достоверное событие

Невозможное событие V, не наступающее ни при каком элементарном исходе ω, совпадает с пустым множеством и обозначается: V = Ø.
Два события А и В несовместимы (или несовместны), если А∩В = Ø (т.е. событие невозможно).
События — образуют полную группу событий, если они попарно несовместны и ∪∪∪…∪, т.е. из этих событий происходит одно и только одно.
ПРИМЕР 1. Победитель соревнования награждается: призом (событие А), денежной премией (событие В), медалью (событие С). Что представляют собой события: а) А + В; б) АВС; в) АС-В?
Решение:
а) Событие А + В состоит в том, что победитель награжден призом, или премией, или призом и премией одновременно.
б) Событие ABC состоит в том, что победитель награжден призом, премией и медалью одновременно.в) Событие АС-В состоит в награждении победителя призом и медалью одновременно, без выдачи премии.
Для наглядной иллюстрации алгебры событий воспользуемся диаграммами Эйлера – Венна.
Здесь каждой картинке (прямоугольнику) соответствует пространство элементарных событий Ω.
ПРИМЕР 9. Описать пространство элементарных событий следующего опыта. Брошены две игральные кости.
Решение. Очевидно, элементарным исходом данного опыта можно считать пару чисел ω = (a, b), где а — число очков на первой костиb – число очков на второй кости. Известно, что (1 ≤ a, b ≤ 6), причем количество очков на первой кости не зависит от того, сколько очков выпадет на второй кости и наоборот. Отсюда получим:
Ω =
На этом я заканчиваю, т.к. по данной теме мне дополнить уже нечего. Всем спасибо за внимание!
Уроки по теории вероятности
Множества Множество – это любая совокупность объектов, называемых элементами множества. К примеру, буквами N, Z, Q, R, C обозначаются множества: N (Naturalis) – натуральные числа; Z (Zahlen) – целые числа; Q (Quisque) – рациональные числа; R (Realis) – действительные числа; C (Complex) – комплексные числа. a ∈ A – объект «а» есть элемент множества
a ∈ A – объект «а» есть элемент множества
На прошлом занятии мы научились составлять дифференциальные уравнения кривых. О том, как вы усвоили данный материал мы узнаем в конце этого урока, когда проверим заданные вам задания, а сейчас новая тема. Уравнения с разделяющимися переменными На самом деле теории совсем чуть-чуть, по большей части мы все-таки займемся практической частью. Итак, уравнения с разделяющимися переменными могут
Составление уравнений семейства кривых Чтобы построить дифференциальное уравнение, которому удовлетворяют кривые семейства: φ (1) необходимо продифференцировать равенство (1) n раз, считая y функцией от x, а затем из полученных уравнений и уравнения (1) исключить произвольные постоянные C1 … Cn. Линии, пересекающие все кривые данного семейства под одним и тем же углом ϕ, называются изогональными
Первая тема, которую я бы хотел рассмотреть на уроках элементарной алгебры — это выражения. Числовые выражения Числовые выражения — это выражения, состоящие только из цифр и знаков арифметических действий. Число, которое получается в результате выполнения действий в числовом выражении, называют значением выражения. Пример №1 Найти значение выражения: 12 * 6 — 16 : 4 Значение
Число, которое получается в результате выполнения действий в числовом выражении, называют значением выражения. Пример №1 Найти значение выражения: 12 * 6 — 16 : 4 Значение
Курс данного предмета мы начнем непосредственно с матриц, потому что именно они составляют основу данной дисциплины. Определение матрицы Матрицей размерности называется прямоугольная таблица чисел, содержащая — строк и — столбцов, число расположенное в -ой строке и -столбце обозначается и называется элементом матрицы , т. е. Операции над матрицами Рассмотрим основные операции, проводимые над матрицами: сумма матриц;
Пространство элементарных событий — Журнальный зал
ЕВГЕНИЙ БУНИМОВИЧ
Пространство элементарных событий
стихи
Бунимович Евгений
Абрамович родился в
1954 году в Москве. Поэт, прозаик,
эссеист. Окончил механико-математический факультет
МГУ, более тридцати лет преподавал в школе, впоследствии был депутатом Московской
Думы трех созывов. С 2009 года — Уполномоченный по правам ребенка
в Москве. Автор полутора десятков книг стихов и прозы,
а также школьных учебников по математике.
Инициатор международного фестиваля «Биеннале поэтов в Москве» и профессиональной премии за лучшую
изданную в столице поэтическую книгу года «Московский счет». Лауреат многих литературных
премий. Живет в Москве.
С 2009 года — Уполномоченный по правам ребенка
в Москве. Автор полутора десятков книг стихов и прозы,
а также школьных учебников по математике.
Инициатор международного фестиваля «Биеннале поэтов в Москве» и профессиональной премии за лучшую
изданную в столице поэтическую книгу года «Московский счет». Лауреат многих литературных
премий. Живет в Москве.
* *
*
и что
открывать входящие
отправлять в нежелательные
в спам
регистрировать исходящие
удалять черновики
не выходя из подпрограммы
из народа
из себя
из гоголевской шинели
сообразовываться
соответствовать
подобать
приличествовать
оказываться впору
делать всё по уму
когда предутреннее относится к предсмертному
как два к одному
* *
*
потерянный ключ в замочной скважине
проворачивается не открывая
никаких ржавых чудес обретённого рая
как сундук не потащат за катафалком
так войдя не услышишь в ответ ю велкам
не позовут ни к больному ни к ужину
лишь немота победительней слова
брошенный дом материальней жилого
только отсутствие рядоположено
с существованием
с верой
с лихвою
иллюзия движения
инерция покоя
* *
*
пространство элементарных событий
система простых аксиом
равенство градусных мер
воздуха и стакана
что там за фудзияма на горизонте
никак сион
да и не всё ли едино
ежели нет стоп-крана
заволокло загустело
хоть пей
хоть ешь
хоть ножом его режь
хоть на хлеб намазывай
дым отечества
метасимвол
обратный слеш
и никак иначе
в такой евразии
жить надо долго и счастливо
счастливо это как
ну тогда долго
ввиду исчерпанности остальных вариантов
чего не скажешь про этот
как в каспийское
нефтедобывающее
газоснабжающее
высыхающее
впадает система водохранилищ и гидроузлов
но местами всё-таки волга
так и надобно жить
пусть это не довод
не выход
не повод
не диалектический метод
жить надо долго
искусство короче
молодцу плыть недалече
если корячится
если корячит
если не может быть речи
* *
*
если не это любовь а иное
скажи на кой мне такое ретро
чую затылком
ознобом
спиною
все твои перемещения
в радиусе полукилометра
* *
*
рукописи не горят
двоичное кодирование текстовой информации
инвариантно относительно огня
воды
земли
воздуха
и всех прочих стихий
включая медные трубы
я вас любил любовь ещё быть может
последовательностью нулей и единиц
110000101111101111010111001110101000001010111110111000010101110011
быть может алгебра и есть гармония
при декодировании
помехи и искажения
неизбежны
* *
*
в два часа ночи
на канале культура
обсуждают
кому сегодня нужны стихи
тому кто
вместо того чтобы
смотрит как
в два часа ночи
на канале культура
обсуждают
кому сегодня нужны стихи
* *
*
да нет и не думай
и кто ты вообще
истец одиноких прогулок
бледная овощ в московском борще
филолог
обмылок
придурок
ни к чёрту кочерга твоя
коптит ни богу свечка
процесс зазрения совести
как волос в казённом супе
жизнь ослепительна
покуда скоротечна
покуда швы трещат
на заячьем тулупе
* *
*
cамые невероятные
видения звуки слова мысли строки
приходят под утро
поймать
зафиксировать
явить
приготовить блокнот карандаш диктофон
инфракрасный видеорегистратор
с дальним оптическим прицелом
на ниоткуда приходящее
непреходящее
предрассветное
сокровенное
ну вот оно
вот
нет
не случилось
записывая просыпаешься
просыпаясь теряешь
нить интонацию воздух
видения звуки слова мысли строки
то что к утру обретает смысл
вообще не имеет смысла
-
Скопировать ссылку
Скопировано
Следующий материал
Тайна история Лизы Дьяконовой.
 Невымышленный роман
Невымышленный романГлава из книги
Пространство элементарных событий
22.02.2021
Пространство элементарных событий — множество Ω {displaystyle Omega } всех различных исходов случайного эксперимента.
Элемент этого множества ω ∈ Ω {displaystyle omega in Omega } называется элементарным событием или исходом. Пространство элементарных событий называется дискретным, если число его элементов конечно или счётно. Любое пространство элементарных событий, не являющееся дискретным, называется недискретным, и при этом, если наблюдаемыми результатами (не путать со случайными событиями) являются точки того или иного числового арифметического или координатного пространства, то пространство называется непрерывным (континуум). Пространство элементарных событий Ω {displaystyle Omega } вместе с алгеброй событий F {displaystyle {mathcal {F}}} и вероятностью P {displaystyle mathbf {P} } образует тройку ( Ω , F , P ) {displaystyle (Omega ,{mathcal {F}},mathbf {P} )} , которая называется вероятностным пространством.
Элементарное событие
В теории вероятностей элементарные события или события-атомы — это (элементарные) исходы случайного эксперимента, из которых в эксперименте происходит ровно один. Множество всех элементарных событий обычно обозначается Ω {displaystyle Omega } .
Всякое подмножество множества Ω {displaystyle Omega } элементарных событий называется случайным событием. Говорят, что в результате эксперимента произошло случайное событие A ⊂ Ω {displaystyle Asubset Omega } , если (элементарный) исход эксперимента является элементом A {displaystyle A} . Различие между понятиями «элементарное событие» и «случайное событие» заключается в том, что элементарные события — это элементы Ω {displaystyle Omega } (поэтому они называются событиями-атомами), а случайные события — это подмножества Ω {displaystyle Omega } , то есть случайное событие — это множество, элементами которого являются элементарные события.
В определении вероятностного пространства на множестве случайных событий вводится сигма-аддитивная конечная мера, называемая вероятностью.
Элементарные события могут иметь вероятности, которые строго положительны, нули, неопределенны, или любая комбинация из этих вариантов. Например, любое дискретное вероятностное распределение определяется вероятностями того, что может быть названо элементарными событиями. Напротив, все элементарные события имеют вероятность нуль для непрерывного распределения. Смешанные распределения, не будучи ни непрерывными, ни дискретными, могут содержать атомы, которые могут мыслиться как элементарные (то есть события-атомы) события с ненулевой вероятностью. В теории меры в определении вероятностного пространства вероятность произвольного элементарного события не могла быть определена до тех пор, пока математики не увидели различие между пространством исходов S и событиями, которые представляют интерес, и которые определяются как элементы σ-алгебры событий из S.
Формально говоря, элементарное событие — это подмножество пространства исходов случайного эксперимента, которое состоит только из одного элемента; то есть элементарное событие — это всё ещё множество, но не сам элемент. Однако элементарные события обычно записываются как элементы, а не как множества с целью упрощения, когда это не может вызвать недоразумения.
Примеры
Если бросается игральная кость, то в результате верхней гранью может оказаться одна из шести граней с количеством точек от одной до шести. Выпадение какой-либо грани в данном случае в теории вероятностей называется элементарным событием ω k {displaystyle omega _{k}} , то есть
- ω 1 {displaystyle omega _{1}} — грань с одной точкой;
- ω 2 {displaystyle omega _{2}} — грань с двумя точками;
- …
- ω 6 {displaystyle omega _{6}} — грань с шестью точками.

Множество всех граней { ω 1 , … , ω 6 } {displaystyle {,omega _{1},ldots ,omega _{6},}} образует пространство элементарных событий Ω {displaystyle Omega } , подмножества которого называются случайными событиями A {displaystyle A} . В случае однократного подбрасывания игровой кости примерами событий являются
- выпадение грани с нечётным количеством точек, то есть событие A {displaystyle A} — это выпадение грани с одной точкой или грани с тремя точками, или грани с пятью точками). Математически событие A {displaystyle A} записывается как множество, содержащее элементарные события: ω 1 {displaystyle omega _{1}} , ω 3 {displaystyle omega _{3}} и ω 5 {displaystyle omega _{5}} .
 Таким образом, A = { ω 1 , ω 3 , ω 5 } {displaystyle A={,omega _{1},omega _{3},omega _{5},}} ;
Таким образом, A = { ω 1 , ω 3 , ω 5 } {displaystyle A={,omega _{1},omega _{3},omega _{5},}} ; - выпадение грани с чётным количеством точек, то есть событие A {displaystyle A} — это выпадение грани с двумя точками или грани с четырьмя точками, или грани с шестью точками. Математически событие A {displaystyle A} записывается как множество, содержащее элементарные события: ω 2 {displaystyle omega _{2}} , ω 4 {displaystyle omega _{4}} и ω 6 {displaystyle omega _{6}} .
 Таким образом, A = { ω 2 , ω 4 , ω 6 } {displaystyle A={,omega _{2},omega _{4},omega _{6},}} ;
Таким образом, A = { ω 2 , ω 4 , ω 6 } {displaystyle A={,omega _{2},omega _{4},omega _{6},}} ;
Ещё несколько примеров пространств исходов эксперимента — Ω {displaystyle Omega } :
- Если число возможных исходов счётно, то элементарные события можно считать натуральными числами, пространство элементарных событий в этом случае будет множество натуральных чисел Ω = { 0 , 1 , 2 , 3 , . . . } {displaystyle Omega ={0,1,2,3,…}} .
- Если монета бросается дважды, Ω = { O O , O P , P O , P P } {displaystyle Omega ={OO,OP,PO,PP}} , O {displaystyle O} для орла, а P {displaystyle P} для решки, то элементарные события: O O {displaystyle OO} , O P {displaystyle OP} , P O {displaystyle PO} и P P {displaystyle PP} .

- Если X {displaystyle X} — это нормально распределенные случайные величины, то Ω = { − ∞ ; ∞ } {displaystyle Omega ={-infty ;infty }} , множество действительных чисел, а элементарные события — действительные числа. Этот пример показывает, что непрерывное вероятностное распределение не определяется вероятностями событий-атомов, поскольку здесь вероятности всех элементарных событий равны нулю.
- Биографический словарь деятелей естествознания и техники
- Манойлов, Иван Антонович
- Виндзорский договор (1386)
- Гнатенко, Марина Васильевна
- Скипетр (группа)
ТЕОРИЯ ВЕ РОЯТНОСТИ ЛЕКЦИЯ 1 ПРОСТРАНСТВО ЭЛЕМЕНТАРНЫХ СОБЫТИЙ
ТЕОРИЯ ВЕ РОЯТНОСТИ ЛЕКЦИЯ 1 ПРОСТРАНСТВО ЭЛЕМЕНТАРНЫХ СОБЫТИЙ Элементарными событиями ω называются события с взаимоисключающими исходами. Пространством элементарных событий Ω называется совокупность всех элементарных событий, возможных для данного опыта или явления. Понятия элементарные события и пространство элементарных событий являются фундаментальными, дальнейшему определению не подлежат и насыщаются конкретным содержанием при рассмотрении конкретных примеров. Теория вероятности – это раздел математики, описывающий случайные события и явления, происходящие в окружающем нас мире. При математическом описании окружающего мира всегда используется метод математического моделирования. Основная суть этого метода состоит в выделении главных для рассматриваемой задачи особенностей явления и пренебрежение малозначительными подробностями. Метод математического моделирования используется и в теории вероятности. 1
Пространством элементарных событий Ω называется совокупность всех элементарных событий, возможных для данного опыта или явления. Понятия элементарные события и пространство элементарных событий являются фундаментальными, дальнейшему определению не подлежат и насыщаются конкретным содержанием при рассмотрении конкретных примеров. Теория вероятности – это раздел математики, описывающий случайные события и явления, происходящие в окружающем нас мире. При математическом описании окружающего мира всегда используется метод математического моделирования. Основная суть этого метода состоит в выделении главных для рассматриваемой задачи особенностей явления и пренебрежение малозначительными подробностями. Метод математического моделирования используется и в теории вероятности. 1
ПРИМЕР 1. Подбрасывание монеты один раз. 2 Здесь возможными существенными элементарными событиями являются — выпадение герба, обозначим его Г; — выпадение числа (или решки), обозначим его Р. Тогда пространство элементарных событий ПРИМЕР 2. Подбрасывание игрального кубика один раз. Здесь возможны шесть элементарных событий , где i — соответствует числу на выпавшей гране ; Тогда пространство элементарных событий ПРИМЕР 3. Подбрасывание монеты n раз. Здесь элементарным событием является любая цепочка исходов при каждом отдельном подбрасывании длиной n
Подбрасывание игрального кубика один раз. Здесь возможны шесть элементарных событий , где i — соответствует числу на выпавшей гране ; Тогда пространство элементарных событий ПРИМЕР 3. Подбрасывание монеты n раз. Здесь элементарным событием является любая цепочка исходов при каждом отдельном подбрасывании длиной n
Пусть n = 3. Тогда 3 Число элементарных событий в данном примере равно 8, т. е. 23. При любом n число элементарных событий в Ω равно 2 n. Пример 4. Стрельба по мишени. Будем рассматривать не центрированную мишень, т. е. просто плоскость. Элементарным событием ω здесь является попадание в любую точку плоскости, а пространство элементарных событий Ω есть сама плоскость. Так каждой точке плоскости можно приписать пару действительных чисел, то пространство элементарных событий в данном Ω u ω примере есть множество пар действительных чисел v Таким образом, пространство элементарных событий может быть конечным дискретным множеством (примеры 1 -3) и бесконечным множеством (пример 4). Бесконечное множество называется счётным, если его элементы можно занумеровать, т. е. поставить им в соответствие цифры из натурального ряда чисел. Оно может быть конечным или бесконечным. Бесконечное множество называется несчётным, если его элементам нельзя поставить в соответствие числа натурального ряда, т. е нельзя пересчитать. Пространство элементарных событий примера 4 есть несчётное множество.
Бесконечное множество называется счётным, если его элементы можно занумеровать, т. е. поставить им в соответствие цифры из натурального ряда чисел. Оно может быть конечным или бесконечным. Бесконечное множество называется несчётным, если его элементам нельзя поставить в соответствие числа натурального ряда, т. е нельзя пересчитать. Пространство элементарных событий примера 4 есть несчётное множество.
СЛУЧАЙНЫЕ СОБЫТИЯ. ДЕЙСТВИЯ НАД СОБЫТИЯМИ. 4 Кроме событий с взаимоисключающими исходами можно указать много других случайных событий. Например, подбрасывая игральный кубик, мы можем интересоваться событием, при котором выпало чётное число. Это событие происходит только в том случае, когда произойдёт одно из трёх элементарных событий ω2, ω4 или ω6. Выпадению нечётного числа соответствуют элементарные события ω1 , ω3 , ω5. Случайным событием будем называть любое подмножество пространства элементарных событий, если оно конечно или счётно. Если оно несчётно, то в этом случае определение случайного события требует знания правил действий над событиями. Они совпадают с правилами действий над множествами. Суммой двух событий A и B называется событие, обозначаемое A+B или A U B, состоящее из всех элементарных событий, принадлежащих по крайней мере одному из событий A или B. Сумма событий, как событие, произошло, если произошло, по крайней мере, или событие A или событие B. Пусть события A и B являются попадания в круг A и B соответственно (пример 4).
Они совпадают с правилами действий над множествами. Суммой двух событий A и B называется событие, обозначаемое A+B или A U B, состоящее из всех элементарных событий, принадлежащих по крайней мере одному из событий A или B. Сумма событий, как событие, произошло, если произошло, по крайней мере, или событие A или событие B. Пусть события A и B являются попадания в круг A и B соответственно (пример 4).
A Сумме событий A и B отвечает вся площадь, ограниченная кругами A и B. 5 B Произведением событий A и B, называется событие, обозначаемое A AB или A B, состоящее из всех элементарных событий, принадлежащих одновременно и событию A и событию B. Произведение событий, как событие произошло, если одновременно произошло и событие A и событие B Произведению событий A и B отвечает площадь общая кругам A и B. B
Разностью событий A и B называется событие, обозначаемое AB, 6 состоящее из элементарных событий события A, не принадлежащих событию B. Событие AB произошло, если A произошло, а B не произошло. A Разности событий AB соответствует часть круга А , не принадлежащая кругу В. B Событие, состоящее из элементарных событий, не принадлежащих событию А, но принадлежащих рассматриваемому пространству элементарных событий Ω, называется событием противоположным событию А. Оно обозначается или Ω Α. Событие называется ещё дополнением события А. Событие произошло , если событие А не произошло. Ω ΩΑ А Событию отвечает часть пространства элементарных событий Ω, не принадлежащая кругу А.
A Разности событий AB соответствует часть круга А , не принадлежащая кругу В. B Событие, состоящее из элементарных событий, не принадлежащих событию А, но принадлежащих рассматриваемому пространству элементарных событий Ω, называется событием противоположным событию А. Оно обозначается или Ω Α. Событие называется ещё дополнением события А. Событие произошло , если событие А не произошло. Ω ΩΑ А Событию отвечает часть пространства элементарных событий Ω, не принадлежащая кругу А.
Если все элементарные события, входящие в событие В, входят одновременно 7 в событие А, то будем говорить, что событие В входит в событие А. Это можно записать так или. Это означает, что из наступления события В следует наступление события А. принадлежность элементарного события ω некоторому событию А обозначается так. Если события А и В могут осуществляться только вместе, то они называются эквивалентными. Для них справедливы соотношения Пространство элементарных событий Ω можно считать достоверным событием, так как в него входят все возможные элементарные события. Противоположностью достоверного события является невозможное событие или пустое множество. Оно обозначается. Невозможное событие не содержит ни одного элементарного события. События А и В называются несовместными, если .
Противоположностью достоверного события является невозможное событие или пустое множество. Оно обозначается. Невозможное событие не содержит ни одного элементарного события. События А и В называются несовместными, если .
8 СВОЙСТВА СУММЫ И ПРОИЗВЕДЕНИЯ СОБЫТИЙ 1) переместительное свойство 2) сочетательное свойство 3) распределительное свойство АЛГЕБРА СОБЫТИЙ Пусть Ω – произвольное пространство элементарных событий, а Ù – некоторый класс подмножества Ω. Класс подмножеств Ù называется алгеброй событий, если 1) Ù, 2) при любых Ùи Ù выполняются условия AB Ù , A+B Ù, AB Ù. 3) Ù. Если Ù система всех подмножества Ω, то Ù — алгебра событий. Если множество Ω состоит из N элементов, то число всех подмножеств = 2 N.
9 Алгебра событий Ù называется σ – алгеброй, если эта система событий содержит в себе все конечные и бесконечные суммы и произведения событий и их дополнения. Любое подмножество σ – алгебры событий называется случайным событием. Это есть общее определение случайного события. ЧАСТОТА ПОЯВЛЕНИЯ СОБЫТИЯ Предположим, что один и тот же опыт проводится в одинаковых условиях N раз, причём в части этих опытов появилось событие А. Обозначим NА число опытов, в которых появилось событие А. Рассмотрим отношение NА / N. Это отношение можно назвать частотой появления события А в серии опытов. Экспериментально было замечено, что отношение NА / N при увеличении числа опытов в серии стремиться к некоторому пределу Этот предел, число Р, интуитивно можно считать вероятностью события А.
ЧАСТОТА ПОЯВЛЕНИЯ СОБЫТИЯ Предположим, что один и тот же опыт проводится в одинаковых условиях N раз, причём в части этих опытов появилось событие А. Обозначим NА число опытов, в которых появилось событие А. Рассмотрим отношение NА / N. Это отношение можно назвать частотой появления события А в серии опытов. Экспериментально было замечено, что отношение NА / N при увеличении числа опытов в серии стремиться к некоторому пределу Этот предел, число Р, интуитивно можно считать вероятностью события А.
АКСИОМАТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ Числовая функция Р , определённая на классе событий Ù, называется вероятностью, если выполняются следующие условия Аксиома 1. Ù является алгеброй событий; Аксиома 2. для любого Ù; Аксиома 3. ; Аксиома 4 (аксиома конечной аддитивности). Если события А и В несовместны, то Тройку (Ω, Ù, Р ) , где Р удовлетворяет аксиомам А 1 – А 4, называют вероятностным пространством. Понятие вероятностного пространства содержит лишь самые общие требования к математической модели случайного явления, но не задаёт вероятность однозначно. Дальнейшее конкретизация определения проводиться применительно к рассматриваемой реальной задачи. 10
Дальнейшее конкретизация определения проводиться применительно к рассматриваемой реальной задачи. 10
Вернёмся к примеру 2, подбрасывания игрального кубика. Рассмотрим 11 событие А выпадение чётного числа. Оно включает в себя три элементарных события. Согласно аксиоме конечной аддитивности Чтобы вычислить Р(А) необходимо знать вероятности элементарных событий. Если кубик идеальный, то вероятности выпадения каждой грани одинаковы и равны 1/6. Тогда Р(А) = 12. Но если нам это заранее неизвестно, то вероятности элементарных событий надо устанавливать экспериментально. ФОРМУЛА ВЕРОЯТНОСТИ СУММЫ СОБЫТИЙ Из аксиом А 3 – А 4 и равенства. Полагая здесь А следует, что = Ω, получим Из аксиомы А 4 следует, что если два события несовместны, то вероятность суммы событий равны сумме вероятностей событий. Для любых событий (совместных и несовместных) имеет место формула Действительно, представим события А + В и В в виде
12 А В АВ События в правых частях этих равенств несовместны. Поэтому можно воспользоваться аксиомой конечной аддитивности. Исключая из правых частей этих равенств получим формулу вероятности суммы событий Из формулы вероятности суммы событий следует, что Равенство в последнем соотношении возникает, если А и В несовместны.
Поэтому можно воспользоваться аксиомой конечной аддитивности. Исключая из правых частей этих равенств получим формулу вероятности суммы событий Из формулы вероятности суммы событий следует, что Равенство в последнем соотношении возникает, если А и В несовместны.
Презентация на тему: «§2. Алгебра событий. Вероятность. Пусть — пространство элементарных событий. |
1
§2. Алгебра событий. Вероятность. Пусть — пространство элементарных событий. | | = n, n или n =. Каждое множество событий пространства называют классом. Класс событий обозначают: A = { A 1,A 2,…,A n }, где каждое A i — событие, A i, i = 1,…,n. Пример: бросание игральной кости. События А и В образуют класс событий. A = выпало четное число очков = { 2, 4, 6 } B = выпало нечетное число очков = { 1, 3, 5 } A = {A,В}
| | = n, n или n =. Каждое множество событий пространства называют классом. Класс событий обозначают: A = { A 1,A 2,…,A n }, где каждое A i — событие, A i, i = 1,…,n. Пример: бросание игральной кости. События А и В образуют класс событий. A = выпало четное число очков = { 2, 4, 6 } B = выпало нечетное число очков = { 1, 3, 5 } A = {A,В}
2
Определение 2.1. Класс событий A называют алгеброй событий, если он удовлетворяет условиям: 1. A и A ; 2. если A A и B A, то также A+B A и AB A ; 3. если A A, то A A. A замкнут относительно сложения, умножения и нахождения обратного события. Пример. A = {,, A, A} – алгебра событий, A.
если A A, то A A. A замкнут относительно сложения, умножения и нахождения обратного события. Пример. A = {,, A, A} – алгебра событий, A.
3 Пусть — пространство элементарных событий, A – класс событий – алгебра или — алгебра, тогда пару (, A ) – называют измеримым пространством или пространством событий. Аксиоматическое построение теории вероятностей В 1933 году русский математик Андрей Колмогоров ( ) обобщил результаты 300-летнего развития теории вероятностей в следующем аксиоматическом определении:
4
5
Определение 2. 4. Тройку (, A, P) называют вероятностным пространством. Конкретные методы вычисления вероятности (частные случаи общего аксиоматического определения) 1. Классическая вероятность. Формулу классической вероятности использовали уже в 17-ом веке французские математики P. Fermat ( ) и B.Pascal ( ).
4. Тройку (, A, P) называют вероятностным пространством. Конкретные методы вычисления вероятности (частные случаи общего аксиоматического определения) 1. Классическая вероятность. Формулу классической вероятности использовали уже в 17-ом веке французские математики P. Fermat ( ) и B.Pascal ( ).
6
1. Классическая вероятность. Пусть состоит из n равновозможных элементарных событий, | | = n = { 1, 2,…, n }. Исходя из предположения равновозможности, вероятность происхождения любого элементарного события i есть P( i ) = 1/n, где i = 1,. .., n. где n A = |A| — число элементарных событий, образующих событие A (благоприятствующих появлению события A ). Вероятность происхождения любого события A вычисляется по формуле классической вероятности:
.., n. где n A = |A| — число элементарных событий, образующих событие A (благоприятствующих появлению события A ). Вероятность происхождения любого события A вычисляется по формуле классической вероятности:
7
Пример. Из колоды карт (52 карты) выбирают 1 карту. Найти вероятность того, что выберут карту с картинкой (король, дама, валет). Решение. Т.к. в колоде 52 карты, то | | = n = 52. Событие А =выбор карты с картинкой. Карт с картинкой (король, дама, валет) в колоде n A = 4 * 3 = 12. Т.о. P( выбор карты с картинкой ) = 12/52 = 3/13.
Т.о. P( выбор карты с картинкой ) = 12/52 = 3/13.
8
2. Геометрическая вероятность. Рассмотрим эксперимент, результатом которого является выбор случайной точки на отрезке [a, b]. Требуется найти вероятность P(выбранная точка принадлежит подотрезку [a 1,b 1 ]). Предполагаем, что все точки отрезка [a, b] равновозможны. В этом случае = [a, b] и искомое событие A = [a 1,b 1 ]. Вероятность события A вычисляется по формуле геометрической вероятности: P(A) = l A / l, где l A = b 1 a 1 «размер» интересующего нас множества A, т. е. длина отрезка [ a 1,b 1 ] и l = b a «размер» всего множества, т.е. длина отрезка [ a,b ]. аba1a1 b1b1. Аналогичная формула действует в 2-мерном, 3-мерном и т.д. пространстве.
е. длина отрезка [ a 1,b 1 ] и l = b a «размер» всего множества, т.е. длина отрезка [ a,b ]. аba1a1 b1b1. Аналогичная формула действует в 2-мерном, 3-мерном и т.д. пространстве.
9
Пример. На мишени площадью S обозначена область площадью s. Найти вероятность поражения области s при выстреле по мишени, если поражение любой точки мишени является равновозможным. По определению геометрической вероятности событие с нулевой вероятностью является возможным, т.к. Возможно поражение одной конкретной точки мишени, площадь которой равна нулю. Решение. В этом случае элементарное событие: поражение любой точки мишени. S — «размер» пространства элементарных событий. Событие А : поражение любой точки заданной области s. s — «размер» события А. S s Геометрическая вероятность находится отношением благоприятной площади ко всей площади мишени:
Решение. В этом случае элементарное событие: поражение любой точки мишени. S — «размер» пространства элементарных событий. Событие А : поражение любой точки заданной области s. s — «размер» события А. S s Геометрическая вероятность находится отношением благоприятной площади ко всей площади мишени:
10
Пример. Выбирают одно случайное число из отрезка [-1;3]. Найти вероятность того, что это число: a)2.3; b)больше чем 0.5; Решение. Все варианты выбора = все числа отрезка [-1;3]. Т.о. «размер» всего множества = длина отрезка [-1;3] l = = 4. а) Интересующее нас событие A = выбрана точка 2.3 имеет «размер» l A = = 0. Вероятность события A вычисляется по формуле геометрической вероятности: P(A) = l A / l = 0/4 = b) Интересующее нас событие A = выбрана точка больше чем 0.5 имеет «размер» l A = = 2.5. Вероятность события A вычисляется по формуле геометрической вероятности: P(A) = l A / l = 2.5/4 =
Т.о. «размер» всего множества = длина отрезка [-1;3] l = = 4. а) Интересующее нас событие A = выбрана точка 2.3 имеет «размер» l A = = 0. Вероятность события A вычисляется по формуле геометрической вероятности: P(A) = l A / l = 0/4 = b) Интересующее нас событие A = выбрана точка больше чем 0.5 имеет «размер» l A = = 2.5. Вероятность события A вычисляется по формуле геометрической вероятности: P(A) = l A / l = 2.5/4 =
11
Пример. Найти вероятность того, что корни квадратного уравнения x 2 + 2kx + m = 0 являются действительными числами, если значения коэффициентов k и m равновозможны и удовлетворяют условиям : k 1, m 1. Решение. Корни квадратного уравнения ax 2 + bx + c = 0 являются действительными числами если дискриминант уравнения: D = b 2 — 4ac 0. По условию задачи все возможные значения коэффициентов k и m ограничены: k 1, m 1. Т.е. принадлежат квадрату со сторонами длинной 2 на km-плоскости: Дискриминант данного уравнения: D = 4k 2 – 4m 0 k 2 m или m k 2.
Решение. Корни квадратного уравнения ax 2 + bx + c = 0 являются действительными числами если дискриминант уравнения: D = b 2 — 4ac 0. По условию задачи все возможные значения коэффициентов k и m ограничены: k 1, m 1. Т.е. принадлежат квадрату со сторонами длинной 2 на km-плоскости: Дискриминант данного уравнения: D = 4k 2 – 4m 0 k 2 m или m k 2.
12
Элементарное событие: выбор любой пары значений k и m из заштрихованного квадрата. Площадь квадрата S = 2*2 = 4 — «размер» пространства элементарных событий. Событие А : выбор любой пары значений k и m, при которых корни уравнения являются действительными числами, т.е. m k 2, т.е. находятся ниже параболы m = k 2. s — «размер» события А- равен площади заштрихованного участка под параболой. Геометрическая вероятность:
Событие А : выбор любой пары значений k и m, при которых корни уравнения являются действительными числами, т.е. m k 2, т.е. находятся ниже параболы m = k 2. s — «размер» события А- равен площади заштрихованного участка под параболой. Геометрическая вероятность:
13
По «закону больших чисел» чем больше повторов эксперимента в серии, тем ближе статистическая вероятность к действительной вероятности события A. Статистическая вероятность не является однозначно определенной, т. к. зависит от результатов случайных экспериментов.
к. зависит от результатов случайных экспериментов.
14 Свойства вероятности Все следующие свойства следуют из определения вероятности:
15
1. Вероятность противоположного события P ( A ) = 1 — P (A). Доказательство: A A Ω Пространство элементарных событий является суммой двух несовместимых событий A и A, т.е. = A + А и A A =. Тогда по аксиоме аддитивности P4 из определения вероятности: Р ( ) = Р ( A + А ) = Р ( A ) + Р ( А ). С другой стороны по аксиоме P2 вероятность достоверного события: Р ( ) = 1. Т.о. Р ( A ) + Р ( А ) = 1 или P ( A ) = 1 — P (A).
Вероятность противоположного события P ( A ) = 1 — P (A). Доказательство: A A Ω Пространство элементарных событий является суммой двух несовместимых событий A и A, т.е. = A + А и A A =. Тогда по аксиоме аддитивности P4 из определения вероятности: Р ( ) = Р ( A + А ) = Р ( A ) + Р ( А ). С другой стороны по аксиоме P2 вероятность достоверного события: Р ( ) = 1. Т.о. Р ( A ) + Р ( А ) = 1 или P ( A ) = 1 — P (A).
16
2. Монотонность. Если B A, то P (B) P (A). Доказательство: В A Если B A, то А можно представить суммой двух несовместимых событий: А = В + A \ B и В A \ B =, где A \ B – «кольцо» вокруг В. Тогда по аксиоме аддитивности P4 из определения вероятности: Р (А) = Р ( В + A \ B ) = Р ( В ) + Р (A \ B). Т.к. Р (A \ B) 0, (аксиома неотрицательности Р1 ), то Р(А) Р( В ).
Тогда по аксиоме аддитивности P4 из определения вероятности: Р (А) = Р ( В + A \ B ) = Р ( В ) + Р (A \ B). Т.к. Р (A \ B) 0, (аксиома неотрицательности Р1 ), то Р(А) Р( В ).
17
3. Вероятность суммы событий A и B P (A B) = P (A) + P (B) — P (A B) Доказательство: Если А и В несовместимые события, то A B =, и действует аксиома аддитивности Р4 : P (A+B) = P (A) + P (B). Пусть события А и В совместимые: A B. A B A B Представим A B суммой несовместимых событий: A B = А + В\AB. Т.к. А В\AB =, то по Р 4: P (A+B) = P (A + В\AB) = P (A) + P (В\AB) А В\AB Ω В свою очередь В = A B + В\AB, где A B и В\AB несоместимые события. Т.о. по Р 4: P (B) = P (A B + В\AB) = P (A B ) + P (В\AB), Откуда P (В\AB)= P (B) — P (A B). Т.е. P (A+B)= P (A) + P (B) — P (A B).
Т.к. А В\AB =, то по Р 4: P (A+B) = P (A + В\AB) = P (A) + P (В\AB) А В\AB Ω В свою очередь В = A B + В\AB, где A B и В\AB несоместимые события. Т.о. по Р 4: P (B) = P (A B + В\AB) = P (A B ) + P (В\AB), Откуда P (В\AB)= P (B) — P (A B). Т.е. P (A+B)= P (A) + P (B) — P (A B).
18
P(A B) P(A) + P(B). 4. Следствие из свойства 3: Доказательство: Прямо следует из свойства 3: P(A B) = P(A) + P(B) — P(A B) И неотрицательности вероятности, по которой P(AB) 0. Т.о. P(A B) P(A) + P(B).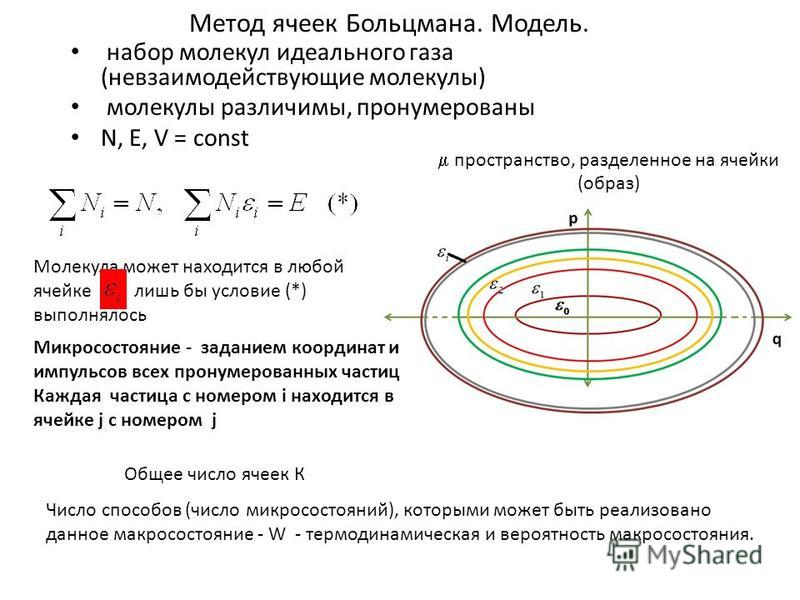
19 Замечание: доказывается методом математической индукции. Для n = 3 формула имеет вид: 6. Свойство 5 в более простом виде: Доказательство:для событияпротивоположное событие т.о. вероятность события
Случайные события, операции над событиями и отношения между ними. Пространство элементарных событий. Классическое определение вероятности. Теорема сложения вероятностей
Поделись
Теория вероятностей занимается изучением случайных событий и их вероятностей.
Будем говорить, что производится испытание (опыт, эксперимент, наблюдение), если осуществляется некоторая совокупность условий, в результате чего могут происходить какие-то события.
Примеры испытаний: 1)бросание одной или нескольких монет (или кубиков), 2) выбор наугад из заданной однородной группы предметов (урна с шарами, колода карт, партия деталей и т.п.) некоторого меньшего количества этих предметов, 3)стрельба по мишени.
Основным понятием в теории вероятностей является понятие случайного события. Событие называется случайным, если в результате испытания оно может произойти или не произойти (см. также с.5).
Все события можно разделить на три типа:
невозможное событие ( обозначим его — Æ) — это такое событие, которое в результате испытания не может произойти,
достоверное событие ( обозначим его W) — это событие, которое в результате испытания обязательно происходит. Наконец, основная масса событий – это
случайные события ( их обычно обозначают А, В, С. ..), т.е. такие, которые в результате испытания могут произойти, а могут и не произойти.
..), т.е. такие, которые в результате испытания могут произойти, а могут и не произойти.
Вероятность P(A) случайного события А — это число, отражающее меру возможности появления события А в данном испытании.
Отметим, что
0 Р(А) 1,
Р(Æ)= 0, Р( ) = 1.
Рассмотрим некоторое испытание и связанное с ним случайное событие А. Предположим, что это испытание произведено многократно при неизменных условиях. Пусть n — число всех проведенных испытаний, k — число испытаний, при которых событие А произошло.
Относительной частотой (частостью) события А в этой серии испытаний называется число
w = .
Длительные наблюдения показывают, что имеет место свойство устойчивости относительных частот:
1) при проведении нескольких серий из n испытаний относительные частоты каждой из этих серий будут примерно одинаковыми и
2) с увеличением числа испытаний n относительные частоты все меньше и меньше будут отклоняться друг от друга.
Если эти относительные частоты разумным образом округлить, то полученное таким образом число P(А) называют статистической вероятностью события А. Условно эту процедуру можно обозначить так:
P(A) = .
Статистическое определение вероятности используют в качестве оценки вероятности, но оно требует больших затрат времени. Однако в некоторых случаях статистическое определение является единственной пригодным.
Например, пусть испытанием является бросание заведомо несимметричного кубика или кубика, у которого центр тяжести смещен относительно геометрического центра (фальшивая игральная кость). В этом случае вероятности выпадения каждой из шести граней можно найти только статистически.
Проведение повторных испытаний может быть сопряжено с большими материальными затратами или невозможно. Поэтому важно уметь находить вероятность случайного события без проведения испытаний, а лишь используя знание о возможных результатах проведенного испытания.
Пространством элементарных исходов (событий) W некоторого испытания (опыта ) будем называть множество всех возможных результатов проведения этого испытания.
Примеры.
| № | Испытание | Случайные события | Пространство элементарных исходов W |
| Монету подбрасывают два раза | А — число орлов и решек будет поровну В — выпадет хотя бы один орел С — обе монеты выпадут орлом | ||
| Кубик (игральную кость) бросают два раза | А — выпадет хотя бы одна шестерка В — сумма выпавших очков будет меньше десяти С — выпадут две единицы | ||
| Из колоды в 36 карт достают наугад три карты | А — все три карты будут одной масти В — хотя бы одна из трех карт является тузом С — все три карты будут разного достоинства | ||
| Из урны, содержащей 4 белых и 6 черных шаров, достают по очереди наугад 3 шара | А — все шары будут одного цвета В — цвета шаров будут чередоваться С — среди вынутых шаров белых больше, чем черных | ||
| Производится один выстрел в тире | А — попадание в мишень | Стена в тире, на которой установлена мишень |
В случаях примеров испытаний 3),4) пространства W содержат большое число элементов, которое находят, применяя формулы комбинаторики (см. стр. 12).
стр. 12).
Понятие пространства элементарных исходов используется для определения понятия случайного события.
Случайным событием называется всякое подмножество А пространства элементарных исходов W некоторого испытания.
Случайное событие А происходит, если в результате испытания имеет место один из исходов события А. Поэтому исходы, входящие в событие А называются благоприятствующими событию А.
Случайное событие можно задать указанием характеристического свойства, как это было сделано в примерах 1) – 5) или в простых случаях, например, 1) и 2) перечислением исходов благоприятствующих случайному событию:
| № | Испытание | Случайные события |
| Монету подбрасывают два раза | А — число орлов и решек будет поровну А= В – выпадет хотя бы один орел В = С – обе монеты выпадут орлом С = | |
| Кубик (игральную кость) бросают два раза | А – выпадет хотя бы одна шестерка А= В – сумма выпавших очков будет меньше десяти В = С – выпадут две единицы, С = |
В теории вероятностей над случайными событиями производятся операции. Будет использоваться геометрическая интерпретация этих операций на примере испытания — неприцельной стрельбы в тире. Пусть W — ограниченная область на плоскости ( например, — стена в тире). Испытание состоит в том, что внутри области W наугад отмечается точка М (выстрел наудачу). Тогда каждому подмножеству А (мишень) в W соответствует (случайное) событие А, состоящее в том, что точка М попадет в А. Определим операции над случайными событиями:
Будет использоваться геометрическая интерпретация этих операций на примере испытания — неприцельной стрельбы в тире. Пусть W — ограниченная область на плоскости ( например, — стена в тире). Испытание состоит в том, что внутри области W наугад отмечается точка М (выстрел наудачу). Тогда каждому подмножеству А (мишень) в W соответствует (случайное) событие А, состоящее в том, что точка М попадет в А. Определим операции над случайными событиями:
1) суммой событий А и В называется событие A+B, состоящее в том, что в результате испытания произойдет хотя бы одно из событий А или В . Геометрически сумма событий соответствует объединению подмножеств А и В.
W
A B
A+B
Рис. 1
2) произведением событий А и В называется событие А×В, состоящее в том, что в результате испытания произойдут оба этих события А и В одновременно. Этой операции геометрически соответствует пересечение подмножеств А и В.
Этой операции геометрически соответствует пересечение подмножеств А и В.
W
A B
A×B
Рис. 2
Случайные события А и В называются несовместными (несовместимыми), если в результате испытания они не могут произойти одновременно, т.е. А×В=Æ. ( геометрически это означает, что подмножества А и В не пересекаются).
Если же А.В Æ, то события А и В называются совместными (Рис. 2). Так, например, в рассматриваемых выше примерах совместными являются следующие пары событий:
в 1-м испытании — А и В, В и С; во 2-м испытании — А и В, В и С;
несовместными являются следующие пары событий:
в 1-м испытании — А и С; в 4-м испытании — А и С;
3) разностью событий А и В называется событие А — В, состоящее в том, что в результате испытания произойдет событие А, а событие В не произойдет. Этой операции геометрически соответствует дополнению подмножества В в А..
Этой операции геометрически соответствует дополнению подмножества В в А..
АА
4) событием, противоположным к событию А, называется событие состоящее в том, что в результате испытания событие А не произойдет. Т.е. соответствует дополнению А в W или =W-А.
Событие удовлетворяет также следующим соотношениям: и Æ.
W
A
Множество всех случайных событий с введенными операциями называется алгеброй событий.
Элементарная вероятность, часть 4
Элементарная вероятность, часть 4Элементарная вероятность
Часть 4: Независимость
Предположим, А и B — события в демонстрационном пространстве. Знание того, что результат
находится в событии . может изменить вашу оценку вероятности того, что
результат в событии B . Например, предположим, что эксперимент
катится 2 игра в кости, событие A это: сумма игральных костей больше 10 и что событие B : По крайней мере, один из кубиков равен 5. Тогда, зная, что результат
находится в событии A, увеличивает вероятность того, что исход
находится в событии B . Как только мы узнаем, что результат находится в A ,
у нас есть новый эксперимент с пространством выборки: {(5,6), (6,5), (6,6)} .
Каждый из этих исходов равновероятен. Таким образом, вероятность того, что одна смерть
a 5 при условии, что сумма больше 10 равна 2/3 .
Знание того, что результат
находится в событии . может изменить вашу оценку вероятности того, что
результат в событии B . Например, предположим, что эксперимент
катится 2 игра в кости, событие A это: сумма игральных костей больше 10 и что событие B : По крайней мере, один из кубиков равен 5. Тогда, зная, что результат
находится в событии A, увеличивает вероятность того, что исход
находится в событии B . Как только мы узнаем, что результат находится в A ,
у нас есть новый эксперимент с пространством выборки: {(5,6), (6,5), (6,6)} .
Каждый из этих исходов равновероятен. Таким образом, вероятность того, что одна смерть
a 5 при условии, что сумма больше 10 равна 2/3 .
С другой стороны, если эксперимент подбрасывает честную монету
дважды, зная, что первый бросок — голова (событие A ), не меняется
вероятность того, что второй бросок окажется решкой (событие B ). Здесь новое пространство выборки равно {(H,H),(H,T)}. Опять же, оба исхода равновероятны, поэтому вероятность того, что второй бросок выпадет решкой, равна 1/2 — такую же вероятность мы бы присвоили, не зная о A .
Здесь новое пространство выборки равно {(H,H),(H,T)}. Опять же, оба исхода равновероятны, поэтому вероятность того, что второй бросок выпадет решкой, равна 1/2 — такую же вероятность мы бы присвоили, не зная о A .
Неформально два события A и B называются независимыми , если зная, что исход находится в событии A не изменяет вероятность что результат в событии B и наоборот.
- Предположим, вы одновременно подбрасываете монету и бросаете стандартный кубик. если ты известно, что выпал кубик 6 , какова вероятность того, что монета выпадет показывает головы? Что ваш ответ говорит вам о независимости события прокатки 6 и переворачивания головы?
- Предположим, что 50% жителей города имеют рост 5 футов 7 дюймов или выше и
что 50% жителей этого города мужчины.
 Если человек из г.
выбирается случайным образом, это события, когда человек выше 5 футов 7 дюймов.
а человек мужского пола скорее всего будет самостоятельным? Объяснять.
Если человек из г.
выбирается случайным образом, это события, когда человек выше 5 футов 7 дюймов.
а человек мужского пола скорее всего будет самостоятельным? Объяснять.
Вероятность того, что выбранное лицо случайным образом будут оба выше 5 футов 7 дюймов, и сначала может появиться мужчина быть 1/4 . Ведь половина населения выше 5 лет. футов 7 дюймов, и половина этой группы — мужчины, поэтому 1/2 из 1/2 1/4 . Но поскольку мужчины в среднем выше женщин, неверно предполагать, что 1/2 от 5 футов 7 дюймов и выше группа мужская. Знание того, является ли выбранный человек мужчиной, влияет на вероятность (вероятность), что его рост 5 футов 7 дюймов или выше.
Предположим, что для эксперимента
событие A имеет вероятность 1/4 и событие B имеет вероятность 1/3 . Если события A и В независимы, то в большом количестве экземпляров
этого эксперимента только 1/3 будет в событии A .
Из этих 1/3 только приблизительно 1/4 будут также
быть в событии B. Итак, вероятность события А и
B — это просто произведение двух вероятностей, 1/12 .
Если события A и В независимы, то в большом количестве экземпляров
этого эксперимента только 1/3 будет в событии A .
Из этих 1/3 только приблизительно 1/4 будут также
быть в событии B. Итак, вероятность события А и
B — это просто произведение двух вероятностей, 1/12 .
Это наблюдение принимается за определение независимости два события.
Определение: Предположим, мы рассматриваем результаты конкретного эксперимента. Если A и B являются событиями (подмножествами выборочного пространства результатов), мы говорим A и B являются независимыми если
Р(А и В) = Р(А) Р(В) .
- В вопросе 2 части 3 вы определили 8 членов выборки
место для подбрасывания правильной монеты 3 раз.
 Мы перечисляем элементы этого демонстрационного пространства здесь:
Мы перечисляем элементы этого демонстрационного пространства здесь:(H,H,H) (Ч,Ч,Т) (В, Т, В) (Н,Т,Т) (Т,Ч,Ч) (Т,Ч,Т) (Т, Т, Н) (Т,Т,Т) Пусть А будет событие, когда при первом подбрасывании выпадет решка, и пусть B будет событие, когда орел выпадает при третьем подбрасывании.
- Без расчета любые вероятности, объясните, почему события A и B должны быть независимым.
- Найти Р(А) .
- Найти P(B) .
- Найти P(A и B) .
- Покажите, что P(A и B) = P(A) P(B) , и, таким образом, события действительно независимы.
- Снова рассмотрим
выборочное пространство, полученное путем подбрасывания честной монеты 3 раз.
 Пусть A снова обозначает событие
что первый бросок — голова. Пусть C обозначают
случае, если не менее 2 3 флипов — решки.
Пусть A снова обозначает событие
что первый бросок — голова. Пусть C обозначают
случае, если не менее 2 3 флипов — решки.- Считаете ли вы, что события A и C , не вычисляя никаких вероятностей, являются независимый? Объяснять.
- Найти P(A) .
- Найти P(C) .
- Найти P(A и C) .
- Показать, что P(A и C) не равно П(А) П(С) , и, таким образом, события не являются независимыми. Это противоречит вашему объяснению? в)?
- Игральная кость окрашена так, что три стороны красные, две стороны синие и
одна сторона зеленая. Таким образом, бросок игральной кости имеет три возможных исхода R , B ,
и Г .
- Если раскрашенный кубик бросить один раз, какова вероятность того, что он прийти синий?
- Если раскрашенный кубик бросить дважды, мы можем обозначить девять возможных исходов.
 на RR , RB и т. д. Найдите вероятность каждого элемента в этом выборочном пространстве.
на RR , RB и т. д. Найдите вероятность каждого элемента в этом выборочном пространстве. - Рассмотрим следующие события в пространстве выборки, полученном путем двойного броска окрашенного игрального кубика.
- А: не менее один рулон будет красным.
- B: Двое рулоны будут иметь разные цвета.
- C: Оба рулона красные или оба синие.
- D: Либо оба рулона красные или один рулон синий
- E: Хотя бы один рулон красный или хотя бы один рулон синий.
- Предположим, что игральная кость подбрасывается дважды.
- Пусть A будет событием
что первый бросок больше или равен 2 . Пусть А быть событием, когда второй бросок больше или равен 4 .
Покажите, что A и B независимы.

- Пусть A будет событием, когда первый бросок больше или равен 2 . Пусть C будет событием, когда сумма бросков больше или равна 4 . Найдите P(A и C) и покажите, что A и C равны независимый.
- Пусть A будет событием
что первый бросок больше или равен 2 . Пусть А быть событием, когда второй бросок больше или равен 4 .
Покажите, что A и B независимы.
Независимость и Заблуждение игрока.
Недооценка концепции независимости лежит в основе сердце ошибочного убеждения что после пробежки неудачи, удача игрока должна измениться. Нажмите ниже для короткого обсуждение этого заблуждения:
Ошибка игрока
| модули на math.duke.edu | Copyright CCP и автор(ы), 2003 г. |
3.1: Выборочные пространства, события и их вероятности
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 530
Цели обучения
- Изучить понятие выборочного пространства, связанного со случайным экспериментом.

- Изучить понятие события, связанного со случайным экспериментом.
- Изучить понятие вероятности события.
Бросание обычного шестигранного игрального кубика является известным примером случайного эксперимента , действия, для которого можно перечислить все возможные результаты, но для которого фактический результат любого данного испытания эксперимента нельзя предсказать с уверенностью. В такой ситуации мы хотим присвоить каждому результату, например, выпадению двойки, число, называемое 9.0353 вероятность исхода, которая указывает, насколько вероятно, что исход произойдет. Точно так же мы хотели бы присвоить вероятность любому событию или набору результатов, например, выпадению четного числа, которое указывает, насколько вероятно, что событие произойдет, если эксперимент будет выполнен. Этот раздел обеспечивает основу для обсуждения вероятностных проблем с использованием только что упомянутых терминов.
Определение: случайный эксперимент
A случайный эксперимент — это механизм, который дает определенный результат, который невозможно предсказать с уверенностью. Выборочное пространство, связанное со случайным экспериментом, представляет собой набор всех возможных результатов. Событие — это подмножество выборочного пространства.
Выборочное пространство, связанное со случайным экспериментом, представляет собой набор всех возможных результатов. Событие — это подмножество выборочного пространства.
Определение: элемент и появление
Говорят, что событие \(E\) происходит в конкретном испытании эксперимента, если наблюдаемый результат является элементом множества \(E\).
Пример \(\PageIndex{1}\): Пример места для одной монеты
Создайте образец пространства для эксперимента, состоящего из подбрасывания одной монеты.
Решение
Исходы могут быть помечены \(h\) для голов и \(t\) для решек. Тогда образцом пространства является множество: \(S = \{h,t\}\)
Пример \(\PageIndex{2}\): Образец пространства для одного кубика
Создайте образец пространства для эксперимента, который состоит из броска одной кости. Найдите события, соответствующие фразам «выпало четное число» и «выпало число больше двух».
Решение :
Результаты могут быть помечены в соответствии с количеством точек на верхней грани игральной кости. Тогда выборочное пространство представляет собой набор \(S = \{1,2,3,4,5,6\}\)
Тогда выборочное пространство представляет собой набор \(S = \{1,2,3,4,5,6\}\)
. Четными являются результаты \(2, 4,\; \; \text{и }\; \; 6\), поэтому событием, соответствующим фразе «выпало четное число», является множество \(\{2,4,6\}\), которое естественно обозначить буквой \(Е\). Мы пишем \(E=\{2,4,6\}\).
Аналогично, событием, соответствующим фразе «выпало число больше двух», является множество \(T=\{3,4,5,6\}\), которое мы обозначили \(T\).
Графическое представление выборочного пространства и событий представляет собой диаграмму Венна , как показано на рисунке \(\PageIndex{1}\). В общем случае выборочное пространство \(S\) представлено прямоугольником, результаты — точками внутри прямоугольника, а события — овалами, заключающими в себе результаты, которые их составляют.
Рисунок \(\PageIndex{1}\): Диаграммы Венна для двух выборочных ячеекПример \(\PageIndex{3}\): Примерные ячейки для двух монет
Случайный эксперимент заключается в подбрасывании двух монет.
- Постройте примерную область для ситуации, когда монеты неразличимы, например, два новых пенни.
- Постройте пример пространства для ситуации, когда монеты различимы, например, одна копейка, а другая пятак.
Решение :
- После того, как монеты подброшены, можно увидеть либо две решки, которые можно пометить \(2h\), либо две решки, которые можно пометить \(2t\), либо разные монеты, которые могут быть помечено \(d\). Таким образом, выборочное пространство равно \(S=\{2h, 2t, d\}\).
- Поскольку мы можем отличить монеты друг от друга, теперь у них есть два способа различать монеты: пенни-орёл и пятицентовик решка или пенни-решка и пятицентовик решка. Мы можем обозначить каждый результат как пару букв, первая из которых указывает, как приземлился пенни, а вторая — как приземлился пятицентовик. Образцовое пространство тогда \(S’ = \{hh, ht, th, tt\}\).
Устройство, которое может быть полезно для определения всех возможных результатов случайного эксперимента, особенно такого, который можно рассматривать как протекающий поэтапно, называется древовидная диаграмма . Это описано в следующем примере.
Это описано в следующем примере.
Пример \(\PageIndex{4}\): Древовидная диаграмма
Постройте выборочное пространство, описывающее все семьи с тремя детьми в соответствии с полом детей в соответствии с порядком рождения.
Решение :
Два исхода — это «два мальчика, затем девочка», которые мы могли бы обозначить \(bbg\), и «девочка, затем два мальчика», которые мы могли бы обозначить \(gbb\).
Очевидно, что исходов много, и когда мы пытаемся перечислить их все, может быть трудно быть уверенным, что мы нашли их все, если мы не будем действовать систематически. Древовидная диаграмма, показанная на рисунке \(\PageIndex{2}\), дает систематический подход.
Рисунок \(\PageIndex{2}\) : Древовидная диаграмма для семей с тремя детьми Диаграмма была построена следующим образом. Есть две возможности для первого ребенка, мальчика или девочки, поэтому мы рисуем два отрезка, выходящие из начальной точки, один заканчивается на \(b\) для «мальчика», а другой заканчивается на \(g\) для «девушки». Для каждой из этих двух возможностей для первого ребенка есть две возможности для второго ребенка, «мальчика» или «девочки», поэтому из каждого из \(b\) и \(g\) мы проводим два отрезка, один отрезок, оканчивающийся на \(b\) и один на \(g\). Для каждой из четырех конечных точек теперь на диаграмме есть две возможности для третьего ребенка, поэтому мы повторяем процесс еще раз.
Для каждой из этих двух возможностей для первого ребенка есть две возможности для второго ребенка, «мальчика» или «девочки», поэтому из каждого из \(b\) и \(g\) мы проводим два отрезка, один отрезок, оканчивающийся на \(b\) и один на \(g\). Для каждой из четырех конечных точек теперь на диаграмме есть две возможности для третьего ребенка, поэтому мы повторяем процесс еще раз.
Отрезки называются ветвями дерева. Правая конечная точка каждой ветви называется узлом . Крайние правые узлы — это конечных узлов ; каждому соответствует исход, как показано на рисунке.
Из дерева легко прочитать восемь результатов эксперимента, поэтому пространство выборки, читая сверху вниз конечные узлы дерева,
\[S=\{bbb,\ ; ббг,\; бгб,\; бгг,\; гбб,\; гбг,\; гб,\; ггг\}\]
Определение: вероятность
Вероятность исхода \(e\) в выборочном пространстве \(S\) представляет собой число \(P\) между \(1\) и \(0\), которое измеряет вероятность что \(e\) произойдет в одном испытании соответствующего случайного эксперимента. Значение \(P=0\) соответствует исходу \(e\) невозможности, а значение \(P=1\) соответствует исходу \(e\) определенности.
Значение \(P=0\) соответствует исходу \(e\) невозможности, а значение \(P=1\) соответствует исходу \(e\) определенности.
Определение: вероятность события
вероятность события \(A\) представляет собой сумму вероятностей отдельных исходов, из которых оно состоит. Обозначается \(P(A)\).
Следующая формула выражает содержание определения вероятности события:
Если событие \(E\) равно \(E=\{e_1,e_2,…,e_k\}\), то
\[P(E)=P(e_1)+P(e_2)+…+P(e_k)\]
На следующем рисунке показано содержание определения вероятности события:
Рисунок \ (\PageIndex{3}\) : Выборочные пространства и вероятностьПоскольку все выборочное пространство \(S\) является событием, которое обязательно произойдет, сумма вероятностей всех результатов должна быть числом \( 1\).
На обычном языке вероятности часто выражаются в процентах. Например, мы бы сказали, что вероятность дождя завтра \(70\%\), что означает, что вероятность дождя равна \(0,70\). Мы будем использовать эту практику здесь, но во всех последующих расчетных формулах мы будем использовать форму \(0,70\), а не \(70\%\).
Мы будем использовать эту практику здесь, но во всех последующих расчетных формулах мы будем использовать форму \(0,70\), а не \(70\%\).
Пример \(\PageIndex{5}\)
Монета называется «уравновешенной» или «честной», если вероятность выпадения каждой стороны одинакова. Назначьте вероятность каждому результату в пространстве выборки для эксперимента, состоящего из подбрасывания одной честной монеты.
Решение :
С исходами, помеченными \(h\) для орла и \(t\) для решки, выборочное пространство представляет собой множество
\[S=\{h,t\}\]
Так как исходы имеют одинаковые вероятности, которые в сумме должны составлять \(1\), каждому исходу присваивается вероятность \(1/2\).
Пример \(\PageIndex{6}\)
Кость называется «сбалансированной» или «справедливой», если каждая грань с одинаковой вероятностью выпадет сверху. Назначьте вероятность каждому результату в пространстве выборки для эксперимента, состоящего в подбрасывании единственного игрального кубика. Найти вероятности событий \(E\): «выпало четное число» и \(T\): «выпало число больше двух».
Найти вероятности событий \(E\): «выпало четное число» и \(T\): «выпало число больше двух».
Решение :
С исходами, помеченными в соответствии с количеством точек на верхней грани игральной кости, пространство выборки равно множеству
\[S=\{1,2,3,4,5,6 \}\]
Поскольку существует шесть равновероятных исходов, которые в сумме должны давать \(1\), каждому присваивается вероятность \(1/6\).
Поскольку \(E = \{2,4,6\}\),
\[P(E) = \dfrac{1}{6} + \dfrac{1}{6} + \dfrac{1 }{6} = \dfrac{3}{6} = \dfrac{1}{2}\]
Так как \(T = \{3,4,5,6\}\),
\[P(T) = \dfrac{4}{6} = \dfrac{2}{3}\]
Пример \(\PageIndex{7}\)
Подбрасываются две правильные монеты. Найдите вероятность того, что монеты совпадут, т. е. обе решки или решки.
Решение :
В примере \(\PageIndex{3}\) мы построили выборочное пространство \(S=\{2h,2t,d\}\) для ситуации, когда монеты идентичны, а выборочное пространство \(S′=\{hh,ht,th,tt\}\) для ситуации, в которой две монеты можно отличить друг от друга.
Теория вероятностей не говорит нам, как присваивать вероятности исходам, а говорит только о том, что делать с ними после того, как они назначены. В частности, используя выборочное пространство \(S\), совпадающие монеты — это событие \(M=\{2h, 2t\}\), которое имеет вероятность \(P(2h)+P(2t)\). Используя выборочное пространство \(S’\), сопоставление монет — это событие \(M’=\{hh, tt\}\), которое имеет вероятность \(P(hh)+P(tt)\). В физическом мире не должно иметь значения, идентичны монеты или нет, поэтому мы хотели бы присвоить вероятности исходам так, чтобы числа \(P(M)\) и \(P(M’)\) одинаковы и лучше всего соответствуют тому, что мы наблюдаем, когда реальные физические эксперименты проводятся с монетами, которые кажутся честными. Фактический опыт показывает, что исходы в S’ равновероятны, поэтому мы присваиваем каждой вероятности \(\frac{1}{4}\), а затем…
\[P(M’) = P(hh) + P(tt) = \frac{1}{4} + \frac{1}{4} = \frac{1}{2}\]
Точно так же, исходя из опыта, подходящим выбором для результатов в \(S\) является:
\[P(2h) = \frac{1}{4}\]
\[P(2t) = \ frac{1}{4}\]
\[P(d) = \frac{1}{2}\]
Предыдущие три примера иллюстрируют, как вероятности могут быть вычислены простым подсчетом, когда выборочное пространство состоит из конечное число равновероятных исходов. В некоторых ситуациях отдельные результаты любого выборочного пространства, представляющего эксперимент, неизбежно неодинаково вероятны, и в этом случае вероятности не могут быть вычислены простым подсчетом, а должна использоваться вычислительная формула, данная в определении вероятности события.
В некоторых ситуациях отдельные результаты любого выборочного пространства, представляющего эксперимент, неизбежно неодинаково вероятны, и в этом случае вероятности не могут быть вычислены простым подсчетом, а должна использоваться вычислительная формула, данная в определении вероятности события.
Пример \(\PageIndex{8}\)
Распределение учащихся местной средней школы по расовому и этническому признаку: \(51\%\) белые, \(27\%\) черные, \ (11\%\) латиноамериканцев, \(6\%\) азиатов и \(5\%\) для всех остальных. Учащийся выбирается случайным образом из этой средней школы. (Выбор случайным образом означает, что все ученики имеют равные шансы быть выбранными.) Найдите вероятности следующих событий:
- \(B\): учащийся черный,
- \(M\): студент из меньшинства (то есть не белый),
- \(N\): студент не черный.
Решение :
Эксперимент представляет собой действие по случайному выбору учащегося из числа учащихся средней школы. Очевидным примерным пространством является \(S=\{w,b,h,a,o\}\). Поскольку \(51\%\) студентов белые, и все студенты имеют одинаковые шансы быть выбранными, \(P(w)=0,51\), и аналогично для других результатов. Эта информация сведена в следующую таблицу:
Очевидным примерным пространством является \(S=\{w,b,h,a,o\}\). Поскольку \(51\%\) студентов белые, и все студенты имеют одинаковые шансы быть выбранными, \(P(w)=0,51\), и аналогично для других результатов. Эта информация сведена в следующую таблицу:
\[\begin{array}{l|cccc}Результат & w & b & h & a & o \\ Вероятность & 0,51 & 0,27 & 0,11 & 0,06 & 0,05\end{ массив}\]
- Поскольку \(B=\{b\},\; \; P(B)=P(b)=0,27\)
- Поскольку \(M=\{b,h,a,o\},\; \; P(M)=P(b)+P(h)+P(a)+P(o)=0,27+0,11 +0,06+0,05=0,49\)
- Поскольку \(N=\{w,h,a,o\},\; \; P(N)=P(w)+P(h)+P(a)+P(o)=0,51+0,11 +0,06+0,05=0,73\)
Пример \(\PageIndex{9}\)
Контингент учащихся средней школы, рассмотренный в последнем примере, можно разбить на десять категорий следующим образом: \(25\%\) белые мужчины, \(26\ %\) белая женщина, \(12\%\) черный мужчина, \(15\%\) черная женщина, 6% латиноамериканец, \(5\%\) латиноамериканка, \(3\%\) азиат , \(3\%\) азиатки, \(1\%\) мужчины из других меньшинств вместе взятые и \(4\%\) женщины из других меньшинств вместе взятые. Учащийся выбирается случайным образом из этой средней школы. Найдите вероятности следующих событий:
Учащийся выбирается случайным образом из этой средней школы. Найдите вероятности следующих событий:
- \(B\): студент черный
- \(MF\): ученица небелая женщина
- \(FN\): студентка не черная
Решение :
Теперь выборочное пространство равно \(S=\{wm, bm, hm, am, om, wf, bf, hf, af, of\}\). Информацию, приведенную в примере, можно обобщить в следующей таблице, называемой двусторонней таблицей непредвиденных обстоятельств:
| Пол | Раса / Этническая принадлежность | ||||
|---|---|---|---|---|---|
| Белый | Черный | Латиноамериканец | Азиатка | Другие | |
| Мужской | 0,25 | 0,12 | 0,06 | 0,03 | 0,01 |
| Женский | 0,26 | 0,15 | 0,05 | 0,03 | 0,04 |
- Поскольку \(B=\{bm, bf\},\; \; P(B)=P(bm)+P(bf)=0,12+0,15=0,27\)
- Поскольку \(MF=\{bf, hf, af, of\},\; \; P(M)=P(bf)+P(hf)+P(af)+P(of)=0,15+0,05 +0,03+0,04=0,27\)
- Поскольку \(FN=\{wf, hf, af, of\},\; \; P(FN)=P(wf)+P(hf)+P(af)+P(of)=0,26+0,05 +0,03+0,04=0,38\)
- Выборочное пространство случайного эксперимента представляет собой совокупность всех возможных результатов.

- Событие, связанное со случайным экспериментом, является подмножеством выборочного пространства.
- Вероятность любого исхода — это число от \(0\) до \(1\). Вероятности всех исходов в сумме составляют \(1\).
- Вероятность любого события \(A\) равна сумме вероятностей исходов в \(A\).
Эта страница под названием 3.1: Примеры пространств, событий и их вероятностей распространяется по лицензии CC BY-NC-SA 3.0 и была создана, изменена и/или курирована посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами платформа LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Аноним
- Лицензия
- СС BY-NC-SA
- Версия лицензии
- 3,0
- Программа OER или Publisher
- Издатель, имя которого нельзя называть
- Показать оглавление
- нет
- Теги
- ЭЛЕМЕНТ
- ПРОИСШЕСТВИЕ
- случайный эксперимент
- пробное пространство
- источник@https://2012books.
 lardbucket.org/books/beginning-statistics
lardbucket.org/books/beginning-statistics - Древовидная диаграмма
- Диаграмма Венна
Образцовые пространства, события и их вероятности
Образцовые пространства и события
Бросание обычного шестигранного игрального кубика является знакомым примером случайного эксперимента , действия, для которого можно перечислить все возможные результаты, но для которого фактический результат любого конкретного испытания эксперимента нельзя предсказать с уверенностью. В такой ситуации мы хотим присвоить каждому результату, например, выпадению двойки, число, называемое 9.0353 вероятность исхода, которая указывает, насколько вероятно, что исход произойдет. Точно так же мы хотели бы присвоить вероятность любому событию или набору результатов, например, выпадению четного числа, которое указывает, насколько вероятно, что событие произойдет, если эксперимент будет выполнен. Этот раздел обеспечивает основу для обсуждения вероятностных проблем с использованием только что упомянутых терминов.
Этот раздел обеспечивает основу для обсуждения вероятностных проблем с использованием только что упомянутых терминов.
Определение
A Случайный эксперимент — это механизм, который дает определенный результат, который невозможно предсказать с уверенностью. Выборочное пространство Набор всех возможных исходов случайного эксперимента. Число 90 353, связанное со случайным экспериментом, представляет собой множество всех возможных исходов. Событие . Любой набор исходов. — это подмножество демонстрационного пространства.
Определение
Говорят, что событие E происходит в конкретном испытании эксперимента, если наблюдаемый результат является элементом набора Е .
Пример 1
Создайте образец пространства для эксперимента, состоящего в подбрасывании одной монеты.
Решение:
Результаты можно обозначить как h для орла и t для решки. Тогда образцом пространства является множество S={h,t}.
Тогда образцом пространства является множество S={h,t}.
Пример 2
Создайте пространство для эксперимента, состоящего из прокатки одного кубика. Найдите события, соответствующие фразам «выпало четное число» и «выпало число больше двух».
Решение:
Результаты могут быть помечены в соответствии с количеством точек на верхней грани игральной кости. Тогда образцом пространства является множество S={1,2,3,4,5,6}.
Четными исходами являются 2, 4 и 6, поэтому событием, соответствующим фразе «выпало четное число», является множество {2,4,6}, которое естественно обозначить буквой Е . Пишем E={2,4,6}.
Аналогично, событием, которое соответствует фразе «выпало число больше двух», является множество T={3,4,5,6}, которое мы обозначили Т .
Графическое представление выборочного пространства и событий представляет собой диаграмму Венна , как показано на рисунке 3.1 «Диаграммы Венна для двух выборочных пространств» для примечания 3. 6 «Пример 1» и примечания 3.7 «Пример 2». В общем случае выборочное пространство S представлено прямоугольником, исходы — точками внутри прямоугольника, а события — овалами, заключающими исходы, из которых они состоят.
6 «Пример 1» и примечания 3.7 «Пример 2». В общем случае выборочное пространство S представлено прямоугольником, исходы — точками внутри прямоугольника, а события — овалами, заключающими исходы, из которых они состоят.
Рисунок 3.1 Диаграммы Венна для двух пространств образцов
Пример 3
Случайный эксперимент заключается в подбрасывании двух монет.
- Постройте тестовое пространство для ситуации, когда монеты неразличимы, например, два новых пенни.
- Постройте пример пространства для ситуации, когда монеты различимы, например, одна копейка, а другая пятак.
Решение:
- После того, как монеты подброшены, вы видите либо две решки, которые можно обозначить как 2h, либо две решки, которые можно обозначить как 2t, либо разные монеты, которые можно обозначить как д . Таким образом, выборочное пространство равно S={2h,2t,d}.

- Поскольку мы можем отличить монеты друг от друга, теперь у них есть два способа различать монеты: пенни-орёл и пятицентовик решка или пенни-решка и пятицентовик решка. Мы можем обозначить каждый результат как пару букв, первая из которых указывает, как приземлился пенни, а вторая — как приземлился пятицентовик. Образцовое пространство тогда S′={hh,ht,th,tt}.
Устройство, которое может быть полезно для определения всех возможных результатов случайного эксперимента, особенно такого, который можно рассматривать как протекающий поэтапно, называется Древовидная диаграмма . Это описано в следующем примере.
Пример 4
Постройте выборочное пространство, описывающее все семьи с тремя детьми в соответствии с полом детей в соответствии с порядком рождения.
Решение:
Два исхода — «два мальчика, затем девочка», которые мы могли бы обозначить как bbg, и «девочка, затем два мальчика», которые мы могли бы обозначить как gbb. Очевидно, что исходов много, и когда мы пытаемся перечислить их все, может быть трудно быть уверенным, что мы нашли их все, если мы не будем действовать систематически. Древовидная диаграмма, показанная на рис. 3.2 «Древовидная диаграмма для семей с тремя детьми», дает систематический подход.
Очевидно, что исходов много, и когда мы пытаемся перечислить их все, может быть трудно быть уверенным, что мы нашли их все, если мы не будем действовать систематически. Древовидная диаграмма, показанная на рис. 3.2 «Древовидная диаграмма для семей с тремя детьми», дает систематический подход.
Рисунок 3.2 Древовидная диаграмма для трехдетных семей
Диаграмма была построена следующим образом. Есть две возможности для первого ребенка, мальчика или девочки, поэтому мы рисуем два отрезка, выходящих из начальной точки, один заканчивается на b для «мальчика», а другой заканчивается на g для «девочки». ” Для каждой из этих двух возможностей для первого ребенка есть две возможности для второго ребенка, «мальчик» или «девочка», поэтому из каждого из b и g мы рисуем два отрезка, один отрезок оканчивается на b , а другой на g . Для каждой из четырех конечных точек теперь на диаграмме есть две возможности для третьего ребенка, поэтому мы повторяем процесс еще раз.
Отрезки называются ветвями дерева. Правая конечная точка каждой ветви называется узлом . Крайние правые узлы — это конечных узлов ; каждому соответствует исход, как показано на рисунке.
Из дерева легко прочитать восемь результатов эксперимента, поэтому пространство выборки, читая сверху вниз конечные узлы дерева,
S={bbb,bbg,bgb, bgg,gbb,gbg,ggb,ggg}
Вероятность
Определение
Вероятность исхода Число, которое измеряет вероятность исхода. e в пространстве выборки S число p между 0 и 1, которое измеряет вероятность того, что e произойдет в одном испытании соответствующего случайного эксперимента. Значение p = 0 соответствует невозможности исхода e , а значение p = 1 соответствует достоверности исхода e .
Определение
Вероятность событияЧисло, которое измеряет вероятность события. A — это сумма вероятностей отдельных исходов, из которых она состоит. Обозначается П(А).
Следующая формула выражает содержание определения вероятности события:
Если событие E равно E={e1,e2,…,ek}, то
P(E)=P(e1 )+P(e2)+ · · · +P(ek)
Рисунок 3.3 «Выборочные пространства и вероятность» графически иллюстрирует определения.
Рис. 3.3 Пространства выборки и вероятность
Поскольку все пространство выборки S является событием, которое обязательно произойдет, сумма вероятностей всех исходов должна быть равна 1.
На обычном языке вероятности часто выражаются в процентах. Например, мы бы сказали, что вероятность дождя завтра составляет 70%, что означает, что вероятность дождя равна 0,70. Мы будем использовать эту практику здесь, но во всех последующих расчетных формулах мы будем использовать форму 0,70, а не 70%.
Пример 5
Монета называется «уравновешенной» или «честной», если вероятность выпадения каждой стороны одинакова. Назначьте вероятность каждому результату в пространстве выборки для эксперимента, состоящего из подбрасывания одной честной монеты.
Решение:
С исходами, помеченными h для орла и t для решки, выборочное пространство представляет собой множество S={h,t}. Поскольку исходы имеют одинаковые вероятности, которые в сумме должны составлять 1, каждому исходу присваивается вероятность 1/2.
Пример 6
Кость называется «сбалансированной» или «справедливой», если каждая грань с одинаковой вероятностью выпадет сверху. Назначьте вероятность каждому результату в пространстве выборки для эксперимента, состоящего в подбрасывании единственного игрального кубика. Найдите вероятности событий E : «выпало четное число» и T : «выпало число больше двух».
Решение:
С исходами, помеченными в соответствии с количеством точек на верхней грани игральной кости, выборочное пространство представляет собой множество S={1,2,3,4,5,6}. Поскольку существует шесть равновероятных исходов, сумма которых должна давать 1, каждому присваивается вероятность 1/6.
Поскольку существует шесть равновероятных исходов, сумма которых должна давать 1, каждому присваивается вероятность 1/6.
Поскольку E={2,4,6}, P(E)=1/6+1/6+1/6=3/6=1/2.
Поскольку T={3,4,5,6}, P(T)=4∕6=2∕3.
Пример 7
Подбрасываются две честные монеты. Найдите вероятность того, что монеты совпадут, т. е. обе решки или решки.
Решение:
В примечании 3.8 «Пример 3» мы построили выборочное пространство S={2h,2t,d} для ситуации, когда монеты идентичны, и выборочное пространство S′={hh,ht,th, tt} для ситуации, когда две монеты можно отличить друг от друга.
Теория вероятностей не говорит нам как присваивать вероятности исходам, а только что делать с ними после их присвоения. В частности, используя пространство выборки S , сопоставление монет — это событие M={2h,2t}, которое имеет вероятность P(2h)+P(2t). Используя выборочное пространство S ‘, сопоставление монет — это событие M ‘= {hh, tt}, которое имеет вероятность P (hh) + P (tt). В физическом мире не должно иметь значения, идентичны монеты или нет, и поэтому мы хотели бы присвоить вероятности исходам так, чтобы числа P(M) и P(M′) были одинаковыми и наилучшим образом соответствовали тому, что мы наблюдайте, когда настоящие физические эксперименты проводятся с монетами, которые кажутся честными. Фактический опыт показывает, что исходы в S’ равновероятны, поэтому мы присваиваем каждой вероятности 1/4, а затем
В физическом мире не должно иметь значения, идентичны монеты или нет, и поэтому мы хотели бы присвоить вероятности исходам так, чтобы числа P(M) и P(M′) были одинаковыми и наилучшим образом соответствовали тому, что мы наблюдайте, когда настоящие физические эксперименты проводятся с монетами, которые кажутся честными. Фактический опыт показывает, что исходы в S’ равновероятны, поэтому мы присваиваем каждой вероятности 1/4, а затем
P(M′)=P(hh)+P(tt)=14+14=12
Аналогичным образом, исходя из опыта, подходящим выбором для результатов в S являются:
P(2h)=14 P( 2t)=14 P(d)=12
, которые дают один и тот же окончательный ответ
P(M)=P(2h)+P(2t)=14+14=12
Предыдущие три примера иллюстрируют, как вероятности могут вычисляется простым подсчетом, когда выборочное пространство состоит из конечного числа равновероятных исходов. В некоторых ситуациях отдельные результаты любого выборочного пространства, представляющего эксперимент, неизбежно неодинаково вероятны, и в этом случае вероятности не могут быть вычислены простым подсчетом, а должна использоваться вычислительная формула, данная в определении вероятности события.
Пример 8
Распределение учащихся местной средней школы по расовому и этническому признаку: 51% белых, 27% черных, 11% латиноамериканцев, 6% азиатов и 5% всех остальных. Учащийся выбирается случайным образом из этой средней школы. (Выбор «случайным образом» означает, что каждый учащийся имеет равные шансы быть выбранным.) Найдите вероятности следующих событий:
- B : студент черный,
- M : студент из меньшинства (то есть не белый),
- N : студент не черный.
Решение:
Эксперимент заключается в случайном выборе учащегося из числа учащихся средней школы. Очевидным примерным пространством является S={w,b,h,a,o}. Поскольку 51% учащихся белые и все учащиеся имеют одинаковые шансы быть выбранными, P(w)=0,51, и аналогично для других результатов. Эта информация сведена в следующую таблицу:
OutcomewbhaoProbability0. 510.270.110.060.05
510.270.110.060.05
- Поскольку B={b}, P(B)=P(b)=0,27.
- Поскольку M={b,h,a,o}, P(M)=P(b)+P(h)+P(a)+P(o)=0,27+0,11+0,06+0,05=0,49
- Поскольку N={w,h,a,o}, P(N)=P(w)+P(h)+P(a)+P(o)=0,51+0,11+0,06+0,05=0,73
Пример 9
Контингент учащихся средней школы, рассмотренный в Примечании 3.18 «Пример 8», можно разбить на десять категорий следующим образом: 25% белых мужчин, 26% белых женщин, 12% черных мужчин, 15% черных женщин. , 6% латиноамериканских мужчин, 5% латиноамериканских женщин, 3% азиатских мужчин, 3% азиатских женщин, 1% мужчин из других меньшинств вместе взятых и 4% женщин из других меньшинств вместе взятых. Учащийся выбирается случайным образом из этой средней школы. Найдите вероятности следующих событий:
- B : студент черный,
- MF: студентка из меньшинства,
- ФН: студентка не черная.

Решение:
Теперь выборочное пространство равно S={wm,bm,hm,am,om,wf,bf,hf,af,of}. Информацию, приведенную в примере, можно обобщить в следующей таблице, называемой двусторонней таблицей непредвиденных обстоятельств :
| Пол | Раса/этническая принадлежность | ||||
|---|---|---|---|---|---|
| Белый | Черный | Латиноамериканец | Азиатка | Другие | |
| Мужской | 0,25 | 0,12 | 0,06 | 0,03 | 0,01 |
| Женский | 0,26 | 0,15 | 0,05 | 0,03 | 0,04 |
- Поскольку B={bm,bf}, P(B)=P(bm)+P(bf)=0,12+0,15=0,27.

- Поскольку MF={bf,hf,af,of}, P(M)=P(bf)+P(hf)+P(af)+P(of)=0,15+0,05+0,03+0,04=0,27
- Поскольку FN={wf,hf,af,of}, P(FN)=P(wf)+P(hf)+P(af)+P(of)=0,26+0,05+0,03+0,04=0,38
Ключевые выводы
- Выборочное пространство случайного эксперимента представляет собой совокупность всех возможных результатов.
- Событие, связанное со случайным экспериментом, является подмножеством выборочного пространства.
- Вероятность любого исхода — это число от 0 до 1. Вероятности всех исходов в сумме составляют 1.
- Вероятность любого события A равна сумме вероятностей исходов A .
Упражнения
В коробке 10 белых и 10 черных шариков. Создайте образец пространства для эксперимента по случайному извлечению с заменой двух шариков подряд и каждый раз отмечая цвет.
 (Вытягивание «с возвратом» означает, что первый шарик кладется на место до того, как будет извлечен второй шарик.)
(Вытягивание «с возвратом» означает, что первый шарик кладется на место до того, как будет извлечен второй шарик.)В коробке 16 белых и 16 черных шариков. Создайте образец пространства для эксперимента по случайному извлечению с заменой трех шариков подряд и каждый раз отмечая цвет. (Вытягивание «с замещением» означает, что каждый шарик возвращается до того, как будет вытащен следующий шарик.)
В коробке 8 красных, 8 желтых и 8 зеленых шариков. Создайте образец пространства для эксперимента по случайному извлечению с заменой двух шариков подряд и каждый раз отмечая цвет.
В коробке 6 красных, 6 желтых и 6 зеленых шариков. Создайте образец пространства для эксперимента по случайному извлечению с заменой трех шариков подряд и каждый раз отмечая цвет.
В ситуации упражнения 1 перечислите исходы, включающие каждое из следующих событий.

- Извлечено хотя бы по одному шарику каждого цвета.
- Белый шарик не нарисован.
В ситуации упражнения 2 перечислите исходы, включающие каждое из следующих событий.
- Извлечено хотя бы по одному шарику каждого цвета.
- Белый шарик не нарисован.
- Черных шариков больше, чем белых.
В ситуации упражнения 3 перечислите исходы, включающие каждое из следующих событий.
- Желтый шарик не нарисован.
- Два вытащенных шарика одного цвета.
- Извлечено хотя бы по одному шарику каждого цвета.
В ситуации упражнения 4 перечислите исходы, которые включают каждое из следующих событий.

- Желтый шарик не нарисован.
- Три вытащенных шарика одного цвета.
- Извлечено хотя бы по одному шарику каждого цвета.
Предполагая, что все исходы равновероятны, найдите вероятность каждого события в упражнении 5.
Предполагая, что все исходы равновероятны, найдите вероятность каждого события в упражнении 6.
Предполагая, что все исходы равновероятны, найдите вероятность каждого события в упражнении 7.
Предполагая, что все исходы равновероятны, найдите вероятность каждого события в упражнении 8.
Пример пространства S={a,b,c,d,e}.
 Определите два события как U={a,b,d} и V={b,c,d}. Предположим, что P(a) и P(b) равны 0,2, а P(c) и P(d) равны 0,1.
Определите два события как U={a,b,d} и V={b,c,d}. Предположим, что P(a) и P(b) равны 0,2, а P(c) и P(d) равны 0,1.- Определите, каким должен быть P(e).
- Найти P(U).
- Найти P(V).
Пример пространства: S={u,v,w,x}. Определите два события как A={v,w} и B={u,w,x}. Предположим, что P(u)=0,22, P(w)=0,36 и P(x)=0,27.
- Определите, каким должно быть P(v).
- Найти П(А).
- Найти P(B).
Пример пространства S={m,n,q,r,s}. Определите два события как U={m,q,s} и V={n,q,r}. Вероятности некоторых исходов приведены в следующей таблице:
OutcomemnqrsProbablity0.
 180.160.240.21
180.160.240.21- Определите, каким должно быть P(q).
- Найти P(U).
- Найти P(V).
Пример пространства S={d,e,f,g,h}. Определите два события как M={e,f,g,h} и N={d,g}. Вероятности некоторых исходов приведены в следующей таблице:
OutcomedefghProbablity0.220.130.270.19
- Определите, каким должно быть P(g).
- Найти P(M).
- Найти P(N).
Базовый
В примечании 3.9 «Пример 4» построено выборочное пространство, описывающее все трехдетные семьи в соответствии с полом детей в порядке их рождения.
 Определите результаты, которые включают каждое из следующих событий в эксперименте случайного выбора семьи из трех детей.
Определите результаты, которые включают каждое из следующих событий в эксперименте случайного выбора семьи из трех детей.- По крайней мере, один ребенок — девочка.
- Не более одного ребенка — девочка.
- Все дети девочки.
- Ровно двое детей — девочки.
- Первенец — девочка.
Пример пространства, описывающего три подбрасывания монеты, такой же, как и в примечании 3.9.«Пример 4» с заменой «мальчика» на «орел» и «девочку» на «решку». Определите исходы каждого из следующих событий в эксперименте по подбрасыванию монеты три раза.
- Монета чаще выпадает орлом, чем решкой.
- Монета выпадает орлом столько же раз, сколько и решкой.
- Монета выпадает как минимум дважды.

- Монета выпадает орлом при последнем подбрасывании.
Предполагая, что исходы равновероятны, найдите вероятность каждого события в упражнении 17.
Предполагая, что исходы равновероятны, найдите вероятность каждого события в упражнении 18.
Приложения
Следующая двусторонняя таблица непредвиденных обстоятельств дает разбивку населения в конкретном регионе по возрасту и употреблению табака:
Возраст Употребление табака Коптильня Для некурящих До 30 лет 0,05 0,20 Старше 30 лет 0,20 0,55 Человек выбирается случайным образом.
 Найдите вероятность каждого из следующих событий.
Найдите вероятность каждого из следующих событий.- Курильщик.
- Человек моложе 30 лет.
- Курильщик моложе 30 лет.
Следующая двусторонняя таблица непредвиденных обстоятельств дает разбивку населения в конкретном регионе в соответствии с партийной принадлежностью ( A , B , C или None ) и мнением о выпуске облигаций:
Принадлежность Мнение Сувениры Противостоит Затрудняюсь ответить А 0,12 0,09 0,07 Б 0,16 0,12 0,14 С 0,04 0,03 0,06 Нет 0,08 0,06 0,03 Человек выбирается случайным образом.
 Найдите вероятность каждого из следующих событий.
Найдите вероятность каждого из следующих событий.- Лицо связано с партией B .
- Лицо связано с какой-то партией.
- Лицо выступает за выпуск облигаций.
- Лицо не имеет партийной принадлежности и не определилось с выпуском облигаций.
Следующая двусторонняя таблица непредвиденных обстоятельств дает разбивку населения замужних или ранее состоявших в браке женщин старше детородного возраста в определенной местности в зависимости от возраста вступления в первый брак и количества детей:
Возраст Количество детей 0 1 или 2 3 или больше До 20 лет 0,02 0,14 0,08 20–29 0,07 0,37 0,11 30 лет и старше 0,10 0,10 0,01 Женщина выбирается случайным образом.
 Найдите вероятность каждого из следующих событий.
Найдите вероятность каждого из следующих событий.- Женщине было за двадцать, когда она вышла замуж в первый раз.
- В первый брак женщине было 20 лет и больше.
- У женщины не было детей.
- Женщине было около двадцати лет, когда она вышла замуж в первый раз, и у нее было как минимум трое детей.
Следующая двусторонняя таблица непредвиденных обстоятельств дает разбивку взрослого населения в определенной местности в зависимости от самого высокого уровня образования и от того, регулярно ли человек принимает пищевые добавки:
Образование Использование добавок Берет Не берет Без диплома об окончании средней школы 0,04 0,06 Диплом средней школы 0,06 0,44 Степень бакалавра 0,09 0,28 Высшее образование 0,01 0,02 Взрослый выбирается случайным образом.
 Найдите вероятность каждого из следующих событий.
Найдите вероятность каждого из следующих событий.- Лицо имеет диплом средней школы и регулярно принимает пищевые добавки.
- Человек имеет высшее образование и регулярно принимает пищевые добавки.
- Человек регулярно принимает пищевые добавки.
- Человек не принимает БАД регулярно.
Дополнительные упражнения
Большие наборы данных 4 и 4А записывают результаты 500 подбрасываний монеты. Найдите относительную частоту каждого исхода 1, 2, 3, 4, 5 и 6. Является ли монета «сбалансированной» или «честной»?
Большие наборы данных 6, 6A и 6B содержат результаты случайного опроса 200 избирателей в каждом из двух регионов, в ходе которых их просили выразить, предпочитают ли они кандидата A на место в Сенате США или какого-либо другого кандидата.

- Найдите вероятность того, что случайно выбранный избиратель из этих 400 отдаст предпочтение кандидату A .
- Найдите вероятность того, что случайно выбранный избиратель из 200 жителей округа 1 отдаст предпочтение кандидату 9.0353 A (отдельно записано в большом наборе данных 6A).
- Найдите вероятность того, что случайно выбранный избиратель из 200 жителей района 2 предпочтет кандидата A (отдельно записанного в большом наборе данных 6B).
Упражнения с большими наборами данных
Примечание. Эти наборы данных отсутствуют, но вопросы приведены здесь для справки.
Ответы
S={бб,чб,вб,вв}
S={rr,ry,rg,yr,yy,yg,gr,gy,gg}
- {чб, бб}
- {бб}
- {рр,рг,гр,гг}
- {рр, гг, гг}
- ∅
- 2/4
- 1/4
- 4/9
- 3/9
- 0
- 0,4
- 0,5
- 0,4
- 0,21
- 0,6
- 0,61
- {bbg, bgb, bgg, gbb, gbg, ggb, ggg}
- {ббб,ббг,бгб,гбб}
- {гггг}
- {бгг, гбг, ггг}
- {гбб, гбг, ггб, ггг}
- 7/8
- 4/8
- 1/8
- 3/8
- 4/8
- 0,25
- 0,25
- 0,05
- 0,55
- 0,76
- 0,19
- 0,11
Относительные частоты от 1 до 6: 0,16, 0,194, 0,162, 0,164, 0,154 и 0,166.
 Создается впечатление, что матрица не сбалансирована.
Создается впечатление, что матрица не сбалансирована.
Элементарное событие: концепция, примеры решения
Начнем с вопроса. Что такое вероятность? Вероятность , говоря простым языком, означает, насколько вероятно, что что-то произойдет. Итак, какова вероятность того, что машина полетит? Может ли машина летать? Вероятность того, что машина сможет летать, равна нулю. Какова вероятность того, что на броске игральной кости выпадет число? Как бы мы ни бросали кубик, мы получим число. Значит, вероятность одна. Вероятность 0 указывает, что это невозможное событие, а вероятность 1 указывает на стопроцентную вероятность того, что событие произойдет. Это доказывает, что вероятность любого события будет лежать между 0 и 1.
Примем P за вероятность. Вероятность наступления события — это количество способов, которыми событие может произойти, из общего числа возможных событий.
P = количество способов, которыми событие может происходить / большее количество событий
Читать также: События по вероятности
СТАЛЕЙ
|
Event and outcome
A possible result of an experiment is the outcome . Хорошее заявление о результатах должно быть измеримым, конкретным и реалистичным. Например, выпадение 1, 2, 3, 4, 5 и 6 на кубике — все это исходы.
Событие — это совокупность всех возможных исходов. Теоретически совокупность всех возможных исходов случайного эксперимента называется выборочным пространством.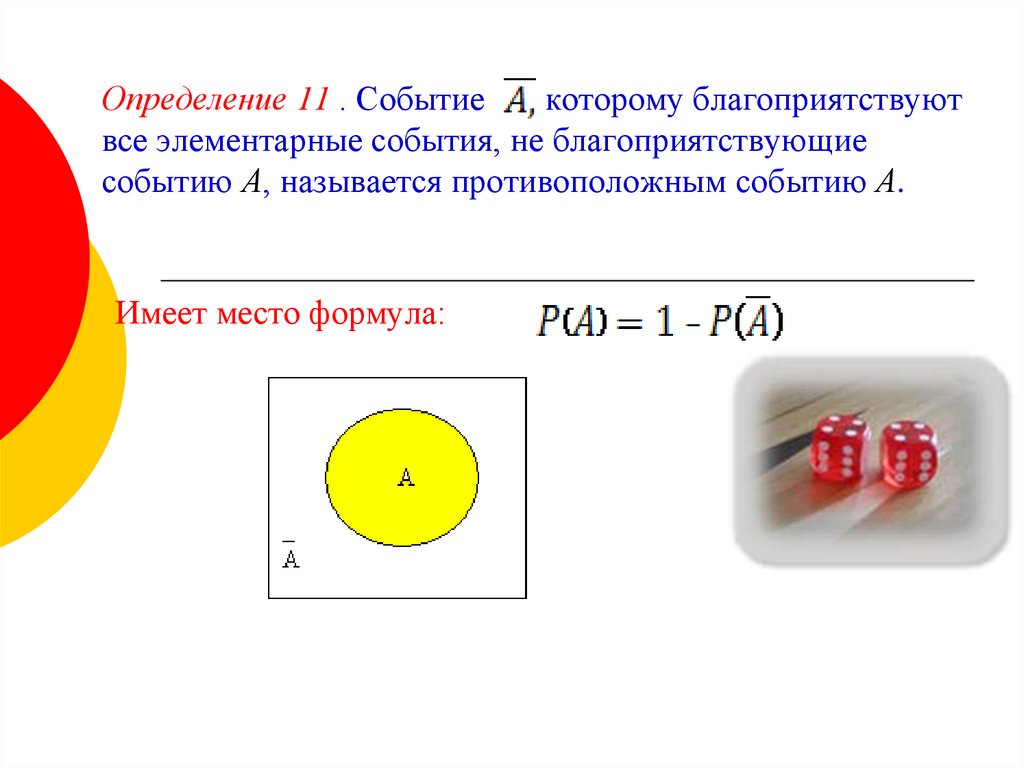 Итак, событие — это любое подмножество выборочного пространства.
Итак, событие — это любое подмножество выборочного пространства.
Совокупность всех возможных результатов случайного эксперимента называется пространством выборки или пространством описания выборки или пространством возможностей . Обычно его обозначают S. Любое подмножество E выборочного пространства S называется событием.
Например, , подбросьте игральную кость. Демонстрационное пространство S = {1, 2, 3, 4, 5, 6}. E = {2, 4, 6} — событие,
, которое можно описать словами как «число четное», а E = {1, 3, 5} — событие, которое можно описать словами как «число четное». число нечетное».
Читайте также:
Элементарное событие
Когда эксперимент состоит из одного результата в пространстве выборки, это называется элементарным событием. Его также называют атомарным событием или простым событием. Другими словами, если в множестве, представляющем событие, имеется только один элемент выборочного пространства, то это событие называется простым или элементарным событием.
Например, , если мы подбрасываем монету, то выборочное пространство S = {Орел, Решка}. Теперь событие «Голова», выпавшее на кубике, простое и задается как E = {Голова}.
Важные термины и формулы называется экспериментом.
Равновероятные события – События считаются равновероятными, если ни одно из них не ожидается в большей степени, чем другие.
Вероятность возникновения события P(E) = Количество исходов, благоприятных для E / Общее количество возможных исходов
Дополнительное событие: быть событием, которое происходит только тогда, когда «Е» не происходит.
Событие (не E) называется дополнительным событием E.
Тогда P(E) + P (не E) = 1
P(E) = 1 – P (не E) → 0 ≤ P(E) ≤ 1
Сумма вероятностей всех элементарных событий опыта всегда равна единице, т. е. равна 1. получает 1,2,3,4,5 и 6. Выборочное пространство S = {1, 2, 3, 4, 5, 6}.
е. равна 1. получает 1,2,3,4,5 и 6. Выборочное пространство S = {1, 2, 3, 4, 5, 6}.
Е = {1}, Е = {2}, Е = {3}, Е = {4}, Е = {5}, Е = {6}.
Сумма вероятностей всех элементарных событий = 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 6/6 = 1.
Некоторые выборочные пространства S = n(S) = 6 2 S = {HH, HT, TH, TT}; n(S) = 4 = 2 2 S = {HHH, HHT, HTH, THH, TTT, TTH, THT, HTT}; n(S) = 8 = 2 3 Читайте также: Вопросы. Найдите вероятность того, что при одном бросании игральной кости выпадет число меньше 4. Решение: Возможный результат = {1, 2, 3} ∴ P (получение числа < 4) = 3/6 = 1/2 Вопросы. Если P(E) = 0,05, какова вероятность «не E»? Решение \(\потому что \) P(E) + P (не E) = 1 ∴ 0,05 + P (не E) = 1 ⇒ P (не E) = 1 – 0,05 = 0,95 Таким образом, вероятность «не E» = 0,95. Вопросы. В мешке 3 красных и 5 черных шаров. Наугад извлекается мячик из мешка. Какова вероятность того, что вынутый шар равен 9?0009 Решение Общее количество шаров = 3 + 5 = 8 ∴ Количество всех возможных исходов = 8 Что следует помнить

Примеры вопросов

9000 .
∴ Количество благоприятных исходов = 3
∴P Красный = Количество благоприятных исходов / Количество всех возможных исходов = 3/8
- Для не красных шаров:
Probability of the ball drawn which is not red
= 1- 3 8 = 8-3 8 = 5 8
Check out Important Links для:
Вопрос. В коробке 5 красных, 8 белых и 4 зеленых шарика. Из коробки наугад достают один шарик. Какова вероятность того, что вынутый шарик будет красного цвета
Какова вероятность того, что вынутый шарик будет красного цвета
- ? и
- белый?
- не зеленый?
Раствор.
Общее количество шариков = 5 + 8 + 4 = 17
- Для красных шариков:
\(\потому что \)Количество красных шариков = 5
∴ Количество благоприятных исходов = 5
∴ Вероятность 900 красных шариков, P(red) = 517- Для белых шаров:
\(\потому что\)Количество белых шаров = 8
∴ Вероятность белых шаров,
P(Белый) = 817
- Для не зеленых шаров:
\(\потому что \)Количество белых шаров = 4
∴ Количество «не зеленых» шаров = 17 – 90 = 40
т. е. благоприятные исходы = 13
∴ Вероятность того, что мяч «не зеленый»
P(белый) = 1317
Подробнее: Класс 12 Вероятность
7 Ques.
 Азартная игра состоит из вращения стрелки, которая останавливается и указывает на одно из чисел 1, 2, 3, 4, 5, 6, 7, 8 (см. рисунок), и это равновероятные исходы. Какова вероятность того, что он укажет на:
Азартная игра состоит из вращения стрелки, которая останавливается и указывает на одно из чисел 1, 2, 3, 4, 5, 6, 7, 8 (см. рисунок), и это равновероятные исходы. Какова вероятность того, что он укажет на: - 8?
- нечетное число?
- число больше 2?
Раствор.
Всего отмеченных чисел = 8
- Когда указатель указывает на 8:
Общее количество исходов = 8
Количество благоприятных исходов = 1
∴ P (8) Количество благоприятных исходов = Количество благоприятных исходов всех возможных результатов = 18
- Когда указатель указывает на нечетное число:
Количество нечетных чисел от 1 до 8 = 4 [\(\потому что \) нечетные числа равны 1,3,5 и 7]
Количество благоприятных исходов = 4
∴ P (нечетное) = Число благоприятного исхода / Число всех возможных исходов = 48 = 12
- Когда указатель указывает на число больше 2:
Количество чисел больше 2 = 6 [\(\потому что \) числа равны 2 ,3,4,5,6,7 и 8]
Количество благоприятных исходов = 6
∴ P (больше 2) = Количество благоприятных исходов / Количество всех возможных исходов = 68 = 34
Ссылки по теме:
Вся элементарная математика
События
Мероприятие. Элементарное мероприятие. Пространство
элементарные события.
Элементарное мероприятие. Пространство
элементарные события.
Определенное событие. Невозможное событие. Идентичные события.
Сумма, произведение, разница События. Дополнительные события.
Взаимоисключающие события. Равновероятные события.
Событие в теории вероятностей любое факт, который может возникнуть в результате эксперимента со случайным исходом или может нет. Простейший результат такого эксперимента называется элементарное событие ( например, появление голов или решка при подбрасывании монеты, стрельбе по мячу, внешний вид туза при получении карты вне пачки, случайное появление числа в бросание игральной кости и др.).
А
установлен
всех элементарных
События Е является
называется пространство
элементарный События . Так,
это
пространство состоит из шести элементарных событий при бросании игральной кости и 52
элементарные события при извлечении карты
пачки.
Событие может состоять из одного
или же
несколько
элементарный
события, например, появление
двух тузов друг за другом при извлечении карты из колоды, или появление
одного и того же числа при трехкратном бросании игральной кости. Тогда можно определить событие как произвольное подмножество пространства элементарных событий.
Так,
это
пространство состоит из шести элементарных событий при бросании игральной кости и 52
элементарные события при извлечении карты
пачки.
Событие может состоять из одного
или же
несколько
элементарный
события, например, появление
двух тузов друг за другом при извлечении карты из колоды, или появление
одного и того же числа при трехкратном бросании игральной кости. Тогда можно определить событие как произвольное подмножество пространства элементарных событий.
А
определенное событие является
все пространство
элементарного
События.
Таким образом, определенное событие это событие,
что должно произойти
в качестве
а
результат
экспериментировать обязательно. Такое событие при метании
die — это падение игральной кости на одну из ее граней.
Такое событие при метании
die — это падение игральной кости на одну из ее граней.
невозможное событие ( ) называется пустым подмножеством пространства элементарных событий. То есть, невозможное событие не может произойти в результате эксперимента. Итак, такое событие при бросании игральной кости это падение кубика на ребро.
События А а также Б находятся
называется идентичные события ( А знак равно Б ), если событие А происходит тогда и только тогда, когда
мероприятие Б имеет место. Событие А включает в себя
событие Б ( А Â ), если условие «событие Б произошло » следует из условия »
произошло событие А » .
Событие С называется сумма событий А а также Б ( С знак равно А Â ), если событие С происходит тогда и только тогда, когда либо событие А происходит или происходит событие B.
Событие С называется продукт событий А а также Б ( С знак равно А Â ),
если событие С происходит тогда и только тогда, когда оба
мероприятие А и произойдет событие B.
Событие С называется а разница событий А а также Б ( С знак равно А – Â ), если событие С происходит тогда и только тогда, когда мероприятие А происходит, а событие B — нет.
Событие А’ является а дополнительное событие к событию А , если событие А не происходит. Таким образом, попадание в цель и промах являются дополнительными событиями.
События А а также Б находятся
называется взаимоисключающий ( А Â знак равно
), если
их одновременное появление
невозможно. За
пример,
ан
возникновение как орла, так и решки
при подбрасывании монеты.
За
пример,
ан
возникновение как орла, так и решки
при подбрасывании монеты.
Если несколько событий могут произойти как результат эксперимента, и каждый из них не более возможно чем другие по объективным условиям, то такие события называются равновероятные события . Примеры равновероятных событий: выпадение двойки, туза и валета. при извлечении карты из колоды появление любого числа от 1 до 6 на бросание игральной кости и др.
Назад
элементарное событие | Примеры предложений
Словарь > Примеров elementary event
elementary event еще нет в Cambridge Dictionary. Ты можешь помочь!
Добавить определение
Событие, содержащее ровно один исход, называется элементарным событием .
Из
Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Используя терминологию теории множеств, элементарное событие является одноэлементным.
From
Wikipedia
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
В дискретном распределении вероятностей с конечным пространством выборки каждое элементарному событию присваивается особая вероятность.
From
Wikipedia
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
При теоретико-мерном определении вероятностного пространства вероятность элементарного события даже не требуется определять.
From
Wikipedia
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Элементарные процессы складывания происходят намного быстрее, чем можно изучить с помощью традиционной кинетики остановленного потока.
Из Кембриджского корпуса английского языка
Готовим с кальцием: рецепты составления глобальных сигналов из элементарных событий.
Из Кембриджского корпуса английского языка
Подмножества выборочного пространства, содержащие только один элемент, называются элементарными событиями.
From
Wikipedia
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Элементарные события и соответствующие им исходы часто для простоты записываются взаимозаменяемо, поскольку такое событие соответствует ровно одному исходу.
From
Wikipedia
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Позвольте быть образцом пространства с элементарными событиями.
From
Wikipedia
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Эти элементарные события (которые он назвал случаями) отчасти ментальны.
From
Wikipedia
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.
Эти примеры взяты из корпусов и из источников в Интернете. Любые мнения в примерах не отражают мнение редакторов Кембриджского словаря, издательства Кембриджского университета или его лицензиаров.
БЕТА
Добавить определение
elementary event еще нет в Cambridge Dictionary. Ты можешь помочь!
Часть речи
Выберите существительное, глагол и т. д. прилагательноенаречиевосклицательноесуществительноечислопрефикссуффиксглагол
Определение
Отменить
элемент
элементаль
элементарно
элементарный
элементарное событие БЕТА
элементарная частица
Начальная школа
элементы
слон
БЕТА
Помогите нам улучшить Кембриджский словарь
У элементарного события еще нет определения.



 Таким образом, A = { ω 1 , ω 3 , ω 5 } {displaystyle A={,omega _{1},omega _{3},omega _{5},}} ;
Таким образом, A = { ω 1 , ω 3 , ω 5 } {displaystyle A={,omega _{1},omega _{3},omega _{5},}} ; Таким образом, A = { ω 2 , ω 4 , ω 6 } {displaystyle A={,omega _{2},omega _{4},omega _{6},}} ;
Таким образом, A = { ω 2 , ω 4 , ω 6 } {displaystyle A={,omega _{2},omega _{4},omega _{6},}} ;
 Если человек из г.
выбирается случайным образом, это события, когда человек выше 5 футов 7 дюймов.
а человек мужского пола скорее всего будет самостоятельным? Объяснять.
Если человек из г.
выбирается случайным образом, это события, когда человек выше 5 футов 7 дюймов.
а человек мужского пола скорее всего будет самостоятельным? Объяснять. Мы перечисляем элементы этого демонстрационного пространства здесь:
Мы перечисляем элементы этого демонстрационного пространства здесь: Пусть A снова обозначает событие
что первый бросок — голова. Пусть C обозначают
случае, если не менее 2 3 флипов — решки.
Пусть A снова обозначает событие
что первый бросок — голова. Пусть C обозначают
случае, если не менее 2 3 флипов — решки. на RR , RB и т. д. Найдите вероятность каждого элемента в этом выборочном пространстве.
на RR , RB и т. д. Найдите вероятность каждого элемента в этом выборочном пространстве.
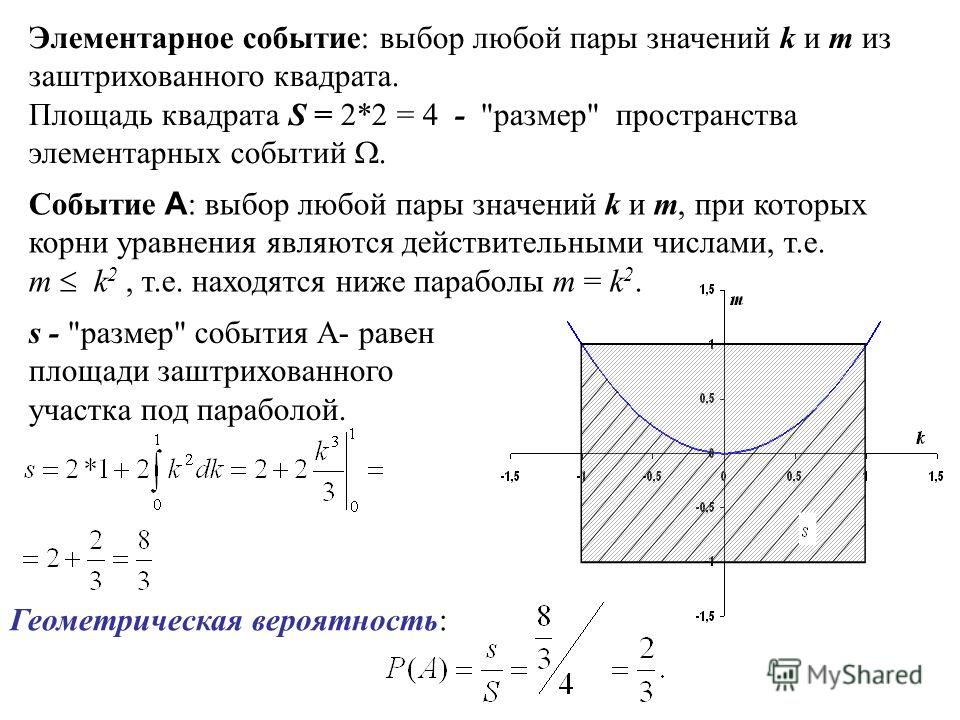

 lardbucket.org/books/beginning-statistics
lardbucket.org/books/beginning-statistics


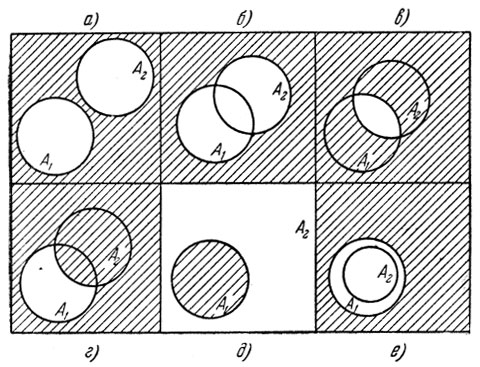 (Вытягивание «с возвратом» означает, что первый шарик кладется на место до того, как будет извлечен второй шарик.)
(Вытягивание «с возвратом» означает, что первый шарик кладется на место до того, как будет извлечен второй шарик.)

 Определите два события как U={a,b,d} и V={b,c,d}. Предположим, что P(a) и P(b) равны 0,2, а P(c) и P(d) равны 0,1.
Определите два события как U={a,b,d} и V={b,c,d}. Предположим, что P(a) и P(b) равны 0,2, а P(c) и P(d) равны 0,1. 180.160.240.21
180.160.240.21 Определите результаты, которые включают каждое из следующих событий в эксперименте случайного выбора семьи из трех детей.
Определите результаты, которые включают каждое из следующих событий в эксперименте случайного выбора семьи из трех детей.
 Найдите вероятность каждого из следующих событий.
Найдите вероятность каждого из следующих событий. Найдите вероятность каждого из следующих событий.
Найдите вероятность каждого из следующих событий. Найдите вероятность каждого из следующих событий.
Найдите вероятность каждого из следующих событий. Найдите вероятность каждого из следующих событий.
Найдите вероятность каждого из следующих событий.
 Создается впечатление, что матрица не сбалансирована.
Создается впечатление, что матрица не сбалансирована.