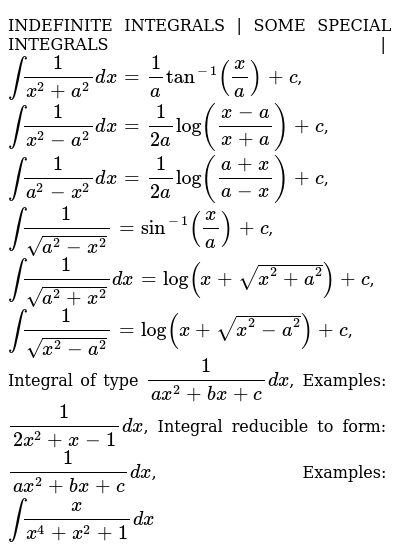2 интеграл dx: ∫ Найти интеграл от y = f(x) = dx/2 (дэ икс делить на 2)

… — Учеба и наука

Лучший ответ по мнению автора

29. 03.17 Лучший ответ по мнению автора Ответ понравился автору вопроса

Михаил Александров Читать ответы

Андрей Андреевич Читать ответы

Eleonora Gabrielyan Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

задача для 5 класса. После строительства дома осталось некоторое количество плиток. Их можно использовать для выкладывания прямоугольной площадки на

Решено

в зоопарке живут крокодилы и страусы. В сумме у них 40 голов и 94 ноги. Сколько там крокодилов и страусов?

В океане расположено три острова AA, BB и CC, причем расстояния от AA до BB и от BB до CC — по 45 км, а от AA до CC — 65 км. Одновременно из AA в

Решено

В лесу на разных кустах висят 100 шнурков. Сова утверж-дает, что в среднем три шнурка из четырёх, которые мож-но найти в лесу, ей не подходят,

Решено

Вдоль дороги в стране Дураков растут 40 кустов, на каждом кусте по 9 монет. Прохожие должны срывать с каждого куста 22, 33 или 44 монеты, но при этом

Пользуйтесь нашим приложением

Неопределенный интеграл dx/(x^2-x-2).

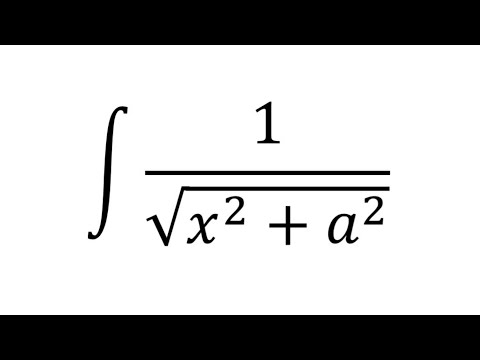2* sinx/x* dx…

Начерти окружность данного диаметра.Проведи радиус и запишите, каково его длина.а.4см,б.6см.в.9см,г.10см…

Сравните:
а)-52n(2n-это степень) и (-5)2n(2n-это степень).
б)-74n+1(4n+1-это степень) и (-7)4n+1(4n+1-это степень)
в)234n+2(4n+2-это степень) и (-23)4n+2(4n+2-это степень)
г)-154n(4n-это степень) и (-15)4n(4n-это степень).
РЕШИТЕ ПОЖАЛУЙСТА….

*Запишите наименьшее пятизначное число, делящееся на 18…

Выполните действия 5 2/5 : 1 1/2
Можете просто ответ))…

Математика

Литература

Алгебра

Русский язык

Геометрия

Английский язык

Химия

Физика

Биология

Другие предметы

История

Обществознание

Окружающий мир

География

Українська мова

Українська література

Қазақ тiлi

Беларуская мова

Информатика

Экономика

Музыка

Право

Французский язык

Немецкий язык

МХК

ОБЖ

Психология

Что такое dx в интегралах

Здравствуйте, дорогие студенты вуза Аргемоны!

Мы с вами закончили подкурс, посвящённый непосредственно функциям, а теперь переходим к интегралам. И оставшиеся два модуля будут посвящены именно им.
Для начала нам, конечно, необходимо будет ознакомиться с самим заклинанием «Интеграл». Постараюсь вам рассказать про него как можно проще. Мы не будем вдаваться глубоко в механизм действия этого заклинания. Нам достаточно научиться им пользоваться в не самых сложных случаях.

Это заклинание по действию обратно заклинанию «производная», однако есть небольшие ньюансы. При действии заклинания «интеграл» получается не одна функция, а целое семейство (они ещё называются первообразными), которые отличаются друг от друга лишь наличием константы, обеспечивающей параллельный перенос функции по вертикали.

Если мы применим ко всему семейству таких функций F(x)+C (где C=const) заклинание «производная», то результатом будет функция f(x), потому что производная от константы равна 0 (C’=0).

Давайте рассмотрим более пристально заклинание «интеграл». Оно состоит из трёх частей:
– значка интеграла (∫),
– подынтегральной функции (f(x))
– и так называемого дифференциала dx, который нам будет очень хорошо помогать при выполнении заклинания.

Действие дифференциала чем-то похоже на действие заклинание «производная», потому что

Ну и, соответственно, чтобы занести какую-то функцию под дифференциал, надо вычислить её первоообразную

g(x)*dx=d(G(x)), где G(x) – одна из первоообразных функции g(x).

Понятно, что dx=d(x+2)=d(x-7), то есть добавлять константу в качестве слагаемого под дифференциал (если это нужно) можно безболезненно.

d(k*f(x))=k*d(f(x)), где k=const, то есть из-под дифференциала можно выносить множитель-константу. Или заносить, если это надо.

Не пугайтесь, если на данный момент вы смутно поняли объяснение. Дальше мы разберём всё подробнее, а пока представляю вам табличку интегралов основных элементарных функций (ТИОЭФ)

и основные правила вычисления интегралов (ОПВИ)

А теперь давайте на примерах изучим, как пользоваться этим заклинанием.

Видно, что интеграл подходит под формулу 6 ТИОЭФ, но, к сожалению, степень 2 и то, что под дифференциалом, не совпадает, а совпадать должно в обязательном порядке. Только тогда заклинание придёт в действие. Значит, нам сейчас надо сделать некие преобразования, чтобы достичь такого равновесия.

1-й способ. Пригоден для более опытных в таких преобразованиях магов.
Ставим под дифференциал 3х-1, но чтобы уравновесить всю конструкцию, нам надо всё поделить на 3

Если мы выполним заклинание «дифференциал», то получим наше исходное выражение

Значит, преобразование сделано верно.

Если не видно сразу, на что надо поделить или умножить, то просто делаем замену переменных. Вместо х введём другую переменную

Подставляем всё, применяем 1-е правило ОПВИ и получаем табличный интеграл. Вычислив его, необходимо сделать обратную замену

Замену полезно делать, чтобы избавиться от сложных выражений. Например, вот тут

В 7-ю степень возводить очень хлопотливо (чтобы всё привести к многочлену), поэтому делаем вот такую замену

Таким образом, степень 7 оказалась около простой переменной.

Очень интересный метод интегрирования по частям. x, а какая-либо тригонометрическая функция совместно со степенным выражением.

Иногда в результате применения такого заклинания мы возвращаемся вроде как к началу, но с некоторым довеском. Например,

При работе с тригонометрическими функциями полезно применять небольшие заклинания, позволяющие понизить степень:

А также не забывать об основном тригонометрическом тождестве, которое позволяет при необходимости выразить одну функцию через другую

Ну, думаю, нам этих сведений вполне хватит для того, чтобы применять заклинание «интеграл» к несложным функциям.

А теперь домашнее задание.
Выберите, на свой вкус, 10 функций из предложенных и примените к ним заклинание «интеграл».

Отправляйте работы через ЛИЧНЫЙ КАБИНЕТ
Свои вопросы смело можете передать с Персефоной

Таблица интегралов представляет собой набор интегралов от различных функций, таких как:

Эти интегралы в основном от элементарных функций и эта таблица приведена ниже:

В колонках этой таблицы:

• В этой таблице в первой колонке приведен интеграл и чему он равен
• Во второй колонке таблицы находится описание этого интеграла в словах
• В третье колонке приведены примеры, как же пользоваться калькулятором интегралов

Получается, что ваша задача здесь научиться не только пользоваться таблицей интегралов, но и научиться вычислять интегралы с помощью калькулятора онлайн на этом сайте kontrolnaya-rabota. ru. Сам калькулятор интегралов находится по ссылке решение интегралов онлайн. Самое интересное, он умеет выдавать не только ответ, но и подробное решение бесплатно!

Пожалуйста, пишите, что вам не понятно будет на почту [email protected] о недостатках данной таблицы, чтобы вы хотели видеть еще здесь.

Видео примеры по использованию таблицы

Определение. Функция F(x) называется первообразной от функции f(x) на отрезке [a;b] , если во всех точках этого отрезка выполняется равенство F`(x) = f(x) .

(1 – cos x)` = sin x

Функция f(x) непрерывная функция на отрезке [a;b] .

Теорема . Если функция F 1 (x) b F 2 (x) – две первообразные от функции f(x) на отрезке [a;b] , то разность между ними равна постоянному числу.

F 2 `(x) = f(x) , то F 1 `(x) – F 2 `(x) = Const .

φ ` ( x ) = F 1 ` – F 2 ` = 0

F 1 (x) – F 2 (x) = φ( x ) (2)

Тогда на основании равенств (1) будет:

F 1 `(x) – F 2 ` ( x ) = f(x) – f(x) = 0 или φ ` ( x ) = [F 1 (x) – F 2 (x)]` = 0 при любом значении x на отрезке [a;b] . Но из равенства φ ` ( x ) = 0 следует, что φ( x ) есть постоянная.

Действительно , применим теорему Лагранжа к функции φ( x ), которая, очевидно, непрерывна и дифференцируема на отрезке [a;b] . Какова ни была точка x на отрезке [a;b] , мы имеем в силу теоремы Лагранжа.

φ ( x ) – φ ( a ) = φ ` ( x ) (x-a) , где a x x .

Так как φ ` ( x ) = 0, то φ ( x ) – φ ( a ) = 0 или φ ( x ) = φ ( a ) (3)

Таким образом, функция φ( x ) в любой точке x отрезка [a;b] сохраняет значения φ( a ) , а это значит, что функция φ( x ) является постоянной на отрезке [a;b] . Обозначая постоянную φ( a ) через С, из равенств (2) , (3) полу ч аем :

Определение. Если функция F (x) является первообразной для f (x) , то выражение F (x) + С называется неопределённым интегралом от функции f (x) и обозначается символом ∫ f (x) dx. Таким образом, по определению,

∫ f (x) dx = F (x) + С, если F (x) = f (x) .

При этом функцию f (x) называют подынтегральной функцией, f (x) dx – подынтегральным выражением, знак ∫ – знаком интеграла.

Из этого определения следуют свойства:
1. Производная от неопределённого интеграла равна подынтегральной функции, т.е. если F`(x) = f (x) , то и

( ∫ f (x) dx )` = (F (x) + C)` = f (x) (4)

Последнее равенство нужно принимать в том смысле, что производная от любой первообразной равна подынтегральной функции.

2. Дифференциал от неопределённого интеграла равен подынтегральному выражению

d ( ∫ f (x) dx ) = f (x) dx (5)

Это получается на основании формулы (4)

3. Неопределённый интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная

Справедливость последнего равенства легко проверить дифференцированием (дифференциала от обоих частей равенства равны dFx) )

Таблица неопределённых интегралов.

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

Интегрирование – есть линейная операция.

1. ∫ [f 1 (x) + f 2 (x)] dx = ∫ f 1 (x) dx + ∫ f 2 (x) dx

∫ a f (x) dx = a ∫ f (x) dx

2. ∫ f (x+c) dx = F (x+c) + C

3. Подстановка. 1-ый способ вычисления неопределённых интегралов.

x = φ (t), тогда ∫ f ( φ (t)) φ ` (t) dt = F (x) + C = ∫ f (x) dx

x = φ (t) dx dt = φ `

Интегрирование по частям.

Пусть u и v – две дифференцируемые функции от x . Тогда, как известно, дифференциал произведения uv вычисляется по следующей формуле:

Отсюда, интегрируя, получаем:

Последняя формула называется формулой интегрирования по частям. Эта формула чаще всего применяется к интегрированию выражений, которые можно так представить в виде произведения двух сомножителей u и dv , чтобы отыскание функции v по её дифференциалу dv и вычисление интеграла ∫ v du составляли в совокупности задачу более простую, чем непосредственное вычисление интеграла ∫ u dv .

Пример. ∫ x sin x dx = ∫ – x cos x + ∫ cos x dx = -x cos x + sin x + C

определенный интеграл в 2 ч. Часть 1 — Образовательная платформа «Юрайт». Для вузов и ссузов.

• Скопировать в буфер библиографическое описание

  Садовничая, И. В.  Математический анализ: определенный интеграл в 2 ч. Часть 1 : учебное пособие для вузов / И. В. Садовничая, Е. В. Хорошилова. — 2-е изд., перераб. и доп. — Москва : Издательство Юрайт, 2020. — 242 с. — (Высшее образование). — ISBN 978-5-534-05714-0. — Текст : электронный // Образовательная платформа Юрайт [сайт]. — URL: https://urait.ru/bcode/454274 (дата обращения: 30.09.2022).

• Добавить в избранное

2-е изд. , пер. и доп. Учебное пособие для вузов

• Нравится
• Посмотреть кому понравилось
• Поделиться

• Описание
• Программа курса
• Выбор редакции
• Нет в мобильном приложении
Ознакомиться
• Аннотация
• Программа курса
• Комплекты 7

Настоящее издание является первой частью пособия, посвященного теоретическим и практическим аспектам вычисления определенных интегралов, а также методам их оценок, свойствам и приложениям к решению различных геометрических и физических задач. Цель данного пособия — помочь студенту во время прохождения темы «Определенный интеграл» на лекциях и практических занятиях по курсу математического анализа. Данная книга содержит разделы, посвященные определению, свойствам и методам вычисления собственных интегралов, свойствам несобственных интегралов. Изложение теоретического материала подкреплено большим количеством разобранных примеров вычисления, оценок и исследования свойств определенных интегралов. В конце каждой главы приводятся задачи для самостоятельного решения, подавляющее большинство из них с решениями.

2 $
• исчисление
• интегрирование
• производные
• обозначения

$\endgroup$

10

$\begingroup$

$dx$ не является важной частью фактического расчета, нет. Если вам нравится мнение, что интегральная запись означает «интегрировать все, что находится между $\int$ и $dx$», вы можете это сделать. Однако это затруднит запоминание и правильное выполнение чего-либо более сложного, чем простая антидифференциация.

Исторически $dx$ происходит от преобразования, лежащего в основе определения интегралов $$ \sum_i f(x_i)\Delta x \to \int f(x)dx $$ и его можно рассматривать просто как пережиток от того, если хотите.

Тем не менее, $dx$ можно придать действительное значение, имея в виду, что более сложные вещи, такие как теоретические рассуждения и подстановка, будут выполняться намного проще.

На самом деле, есть несколько возможных значений, в зависимости от вашего вкуса. Я думаю, что проще всего объяснить интуитивно можно из теории меры: здесь $f(x)dx$ можно рассматривать как плотность , и вы интегрируете плотность вдоль части числовой прямой, чтобы найти общую массу. Это сделало бы $dx$ стандартной единичной плотностью числовой прямой, в то время как $f(x)$ говорит вам фактическую плотность в любой точке в единицах $dx$.

$\endgroup$

$\begingroup$

В начале 1970-х годов (я хочу сказать, что в 1973 году, но я не уверен на 100 %) этот вопрос обсуждался в колонке писем в нескольких выпусках American Math Monthly. Насколько я помню, было три школы мысли.

1. Это просто знак препинания, который просто говорит вам, где подынтегральная функция заканчивается.
2. Это фиктивная переменная.
3. Это неотъемлемая часть обозначения; мы интегрируем дифференциальные формы, а не функции.

Никаких выводов сделано не было, и в итоге редакция отказалась публиковать письма на эту тему.

Меня не устраивает ни один из этих ответов, но мне нечего предложить вместо них.

$\endgroup$

2

$\begingroup$

Нижеследующее изначально было моим комментарием, но я хочу поместить его в ответ, потому что был достигнут вывод , что противоречит ответу выше.

---

Перейдите сюда $\longrightarrow$ https://m.youtube.com/watch?v=U_q7R5JJvb4, чтобы узнать значение $\text{d}x$ в общем интеграле. В Интеграле Римана определение $\text{d}x$ немного отличается от , так как оно получено из Сумма Римана . Для этого предлагаю перейти сюда $\longrightarrow$ https://m.youtube.com/watch?v=Stbc1E5t5E4.

Были такие определения, как , рассматривающие $\text{d}x$ как точку , но это только для облегчения записи интеграла в символах. Это не определение $\text{d}x$.

---

Я также нашел еще одну ссылку на видео на YouTube, которое является частью серии под названием Essence of Calculus . В этом видео конкретно рассказывается об интегралах $\longrightarrow$ https://m.youtube.com/watch?v=rfG8ce4nNh0, однако это видео довольно сложное и, возможно, поначалу его трудно понять, потому что может быть многое, что нужно не отставать. с. 9{*}$ — точка в $[x_{i}, x_{i+1}]$. Если вы помните из исчисления, эта сумма представляет собой сумму площадей прямоугольников, которые вместе дают нам приближение к площади под кривой $f(x)$. В каком смысле эти суммы Римана являются аппроксимацией площади? В том смысле, что по мере того, как основания прямоугольников становятся все меньше и меньше (так что прямоугольники становятся все тоньше и тоньше), вы получаете все более и более точное приближение. {*})(x_{i+1}-x_{i})$ интуитивно становится $\int f(x)\,dx$, где символ $\int$ означает, что мы «складываем» теперь бесконечно много прямоугольников, а $f(x)\,dx$ интуитивно представляет собой площадь каждого прямоугольника. Итак, для меня, исходя из этого понимания предела, я всегда интерпретирую интеграл в своем уме как означающий $\underbrace{\int}_{\text{добавление}} \underbrace{f(x)\,dx}_{\ подстек {\ ​​текст {площадь прямоугольника} \\ \ текст {ш / высота} f (x) \ текст {и основание} dx}} $. Конечно, это всего лишь интуиция, потому что $\int f(x)\,dx$ — это просто обозначение предела. $dx$ сам по себе ничего не значит, по крайней мере, на уровне исчисления, хотя, как заметил кто-то другой, есть способ сделать эту интуитивную интерпретацию строгой. Он включает в себя определение бесконечно малых величин (поищите тему нестандартного анализа, если вам это интересно).

$\endgroup$

$\begingroup$

Здесь есть несколько возможных глубин понимания. n f(x)\Delta x$, где $||P||\to 0$ при $n \to \infty$ и $P=\{a=x_0

$\endgroup$

исчисление — Что означает dx в интеграле?

Спросил 7 лет, 3 месяца назад

Изменено 7 лет, 3 месяца назад

Просмотрено 44k раз

$\begingroup$

Я знаю, что dy/dx, например, означает «производное y по отношению к x «, но меня смущает другой контекст. Обычно вы просто видите dx термин, стоящий в конце интегрального уравнения, и я просто не знаю точно, что он означает и почему он здесь.

Например, если я введу в Wolfram Alpha «интеграл от 2x», он выпишет:

Этот dx там! Я предполагаю, что он говорит «интеграл 2x по отношению к x»? Но зачем это вообще нужно? Разве это не подразумевается? Это раздражает, потому что это похоже на умножение, как будто это означает «2 * x * dx», и это просто вводящая в заблуждение запись. 92 ? $$ Является ли $s$ переменной или $t$ переменной? Конечно, иногда «очевидно», что это за переменная, но это не всегда так.

Если вы хотите узнать, что на самом деле означает $dx$, этот вопрос задавался здесь много раз. См., например, Что означает $dx$?

$\endgroup$

1

$\begingroup$

Это потому, что интеграл означает, что вы суммируете множество очень тонких прямоугольников под кривой. Высота прямоугольника равна f(x), а ширина называется $\delta x$ (эти два символа следует читать как один символ, это не означает $\delta \times x$). Таким образом, вы бы написали это так:

$\sum f(x) \delta x$

Знак $\Sigma$ означает сигму и означает «сумма». В интеграле вы берете предел, когда $\delta x$ стремится к нулю. Поэтому мы заменяем сигму другим типом s: $\int$. И $\delta$ меняется на d. Итак, теперь написано:

$\int f(x) dx $

и это «интеграл от f(x) по x». Но dx сам по себе ничего не значит.

$\endgroup$

$\begingroup$

Мне лично нравится думать о знаке $\int$ и «d» в $dx$ как о левой и правой скобках: они ограничивают размер подынтегральной функции. «x» в $dx$ указывает вам переменную интегрирования.

Существует также интуитивное понятие, заключающееся в том, что вы суммируете значения подынтегральной функции при изменении $x$ и умножаете каждое значение на маленькую «ширину», чтобы получить площадь прямоугольника, а суммируя эти площади, получаете интеграл . .. если вы берете предел, поскольку «крошечная ширина $\Delta x$ становится все меньше и меньше». «$dx$» позволяет людям неформально думать, что вы умножаете высоту $f(x)$ на «бесконечно малую ширину» $dx$, а затем получаете бесконечную сумму.

$\endgroup$

9n f(x_k)\Delta x_k$$

Что имеет смысл, если вы знакомы с аппроксимацией площади под кривой фигурой, похожей на прямоугольник (суммы Римана). Вы находите сумму площадей прямоугольников, длина которых уменьшается. Когда вы берете предел, когда количество прямоугольников увеличивается до бесконечности, вы получаете площадь под кривой. Вот полезная анимация, показывающая процесс перехода $\Delta x_k$ к 0,

. $\endgroup$

$\begingroup$

9{k-1}$», «$2x$» означает то же, что и «$\left(2\frac{i}{k}\right)$», а $dx$ означает то же, что и «$\ left(\frac{i+1}{k}-\frac{i}{k}\right)$».

Этот ход мыслей, конечно, не совсем верен, поскольку $\lim\limits_{k\rightarrow\ infty}\left(\frac{i+1}{k}-\frac{i}{k}\right)=0$, но передает идею о том, что $dx$ просто относится к произвольно малому изменению $x $

$\endgroup$

$\begingroup$

Предположим, что $x$ является константой, тогда

9{n-1}}}$$

$\endgroup$

2

Твой ответ

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Мэтуэй | Популярные проблемы

92) 9(3x) по отношению к x 92+1

1	Найдите производную — d/dx	натуральное бревно х
2	Оценить интеграл	интеграл натурального логарифма x относительно x
3	Найдите производную — d/dx
21	Оценить интеграл	интеграл от 0 до 1 кубического корня из 1+7x относительно x
22	Найдите производную — d/dx	грех(2x)
23	Найдите производную — d/dx
41	Оценить интеграл	интеграл от cos(2x) по x
42	Найдите производную — d/dx	1/(корень квадратный из х)
43	Оценить интеграл 9бесконечность
45	Найдите производную — d/dx	х/2
46	Найдите производную — d/dx	-cos(x)
47	Найдите производную — d/dx	грех(3x)
68	Оценить интеграл	интеграл от sin(x) по x
69	Найдите производную — d/dx	угловой синус(х)
70	Оценить предел	ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х
85	Найдите производную — d/dx	лог х
86	Найдите производную — d/dx	арктан(х)
87	Найдите производную — d/dx	бревно натуральное 5х92

Интегрирование 2x — формула, доказательство, примеры

LearnPracticeDownload

Интегрирование 2x — это процесс нахождения интеграла 2x относительно x. Используя правила интегрирования, такие как интеграл от скалярного кратного функции и степенное правило интегрирования, мы можем определить интеграцию 2x. Как мы знаем, интегрирование — это процесс, обратный дифференцированию, и, следовательно, мы можем сказать, что интеграл от 2x является первообразной 2x. Математически интегрирование 2x записывается как ∫2x dx = x ² + C, где C — постоянная интегрирования.

В этой статье мы узнаем интеграл от 2x и его формулу. Мы также определим определенную интеграцию 2x, используя ее формулу вместе с некоторыми примерами для лучшего понимания концепции.

1.	Что такое интеграция 2x?
2.	Интеграция 2х формул
3.	Интеграл 2x Proof
4.	Интеграция 2x dx От 10 до 13
5.	Часто задаваемые вопросы по интеграции 2x

Что такое интеграция 2x?

Интегрирование 2x в исчислении равно квадрату x плюс постоянная интегрирования, которая символически записывается как ∫2x dx = x ² + C, где ∫ — символ интеграла, dx показывает, что интегрирование 2x по переменной x и C постоянная интегрирования. Мы можем найти формулу интеграла от 2x, используя различные правила интегрирования. Давайте рассмотрим формулу интегрирования 2x в следующем разделе.

Интеграция 2х формул

Формула для интегрирования 2x определяется как ∫2x dx = x ² + C, где C является константой интегрирования. Мы можем вычислить интеграл от 2x, используя правила первообразных, а именно правило первообразных для скалярного умножения функции и правило степеней первообразных. На изображении ниже показана формула для интегрирования 2x:

Интеграл 2x Proof

В этом разделе мы выведем интегрирование 2x, используя правила первообразной. Мы будем использовать следующие правила интегрирования для вычисления интеграла от 2x:

• ∫x ⁿ dx = x ⁿ⁺¹ /(n + 1), где n ≠ -1 → Это правило называется степенным правилом. интеграции
• ∫kf(x) dx = k ∫f(x) dx, где k — действительное число. → Это правило называется правилом первообразной для скалярного кратного функции
.

Используя приведенные выше правила интегрирования, мы имеем

∫2x dx = 2 ∫x dx

= 2 ∫x ¹ dx

= 2 [x ¹⁺¹ /(1 + 1)] + C

2 / 4 4

= 2 + C

= x ² + C (Вычеркнув двойки в числителе и знаменателе)

Таким образом, мы доказали, что интегрирование 2x равно x ² + C, где C – постоянная интегрирования .

Интеграция 2x dx От 10 до 13

Определенное интегрирование — это значение, полученное путем взятия разности первообразной функции на верхнем и нижнем пределах. Теперь, когда мы знаем формулу интегрирования 2x, которая дается как x 92+C)\\&=169-100\\&=69 \end{align}\)

Следовательно, интеграл от 2x с пределами от 10 до 13 равен 69.

Важные замечания по интегрированию of 2x

• Интегрирование 2x записывается как ∫2x dx = x ² + C, где C — постоянная интегрирования.
• Используя правила интегрирования — Интеграл от скалярного кратного функции и степенное правило интегрирования, мы можем определить интегрирование 2х.
• Интегрирование 2x с пределами от a до b определяется как [(b ² + С)-(а ² + С)]. Следовательно, интеграл от 2x в пределах от 10 до 13 равен 69.

☛ Статьи по теме:

• Формулы интегрирования
• Приложения интегралов
• Формулы интегрирования

 

Интеграция двух примеров

1. Пример 1: Оценка интегрирования 2x dx limit от 1 до 12.

   +C)\\&=144-1\\&=143 \end{align}\)

   Ответ: Следовательно, интеграл от 2x в пределах от 1 до 12 равен 143.

2. Пример 2: Вычислить значение интегрирования 2x по формуле (1 + x ² ).

   Решение: Чтобы найти интеграл от 2x / (1 + x ² ), воспользуемся методом подстановки.

   Предположим, что 1 + x ² = u ⇒ 2x dx = du, поэтому имеем

   ∫[2x / (1 + x ² )] dx = ∫du/u

   = ln |u| + C

   = ln |1 + x ² | + C

   Ответ: Следовательно, интегрирование 2x по (1 + x ² ) равно ln |1 + x ² | + С.

перейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Забронировать бесплатный пробный урок

Интеграция 2 вопросов

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы по интеграции 2x

Что такое интегрирование 2x в исчислении?

Интегрирование 2x — это процесс нахождения интеграла от 2x по x. Математически интегрирование 2x записывается как ∫2x dx = x ² + C, где C — постоянная интегрирования.

Что такое формула интегрирования 2x?

Формула для интегрирования 2x определяется следующим образом: ∫2x dx = x ² + C, где C — константа интегрирования.

Как решить интеграл от 2x?

Используя правила интегрирования, такие как интеграл от скалярного кратного функции и степенное правило интегрирования, мы можем определить интегрирование 2x.

Что такое определенная интеграция 2x с ограничениями от 10 до 13?

Интеграл от 2x в пределах от 10 до 13 равен 69. Это можно рассчитать по формуле ∫2x dx = x ² + C.

Как найти интегрирование 2x + 3?

Интегрирование 2x + 3 можно определить как ∫(2x + 3)dx = 2 ∫x dx + 3 ∫dx = x ² + 3x + C, где C — постоянная интегрирования. Правила интегрирования, используемые для нахождения этого интеграла от 2x + 3, представляют собой правило произведения, интеграл от константы и правило интегрирования скалярного кратного функции.

Скачать БЕСПЛАТНЫЕ учебные материалы

Интеграция 2x Worksheet

Рабочие листы по математике и
наглядный учебный план

Калькулятор неявного дифференцирования с шагами

Введение в калькулятор неявного дифференцирования?

Калькулятор неявного дифференцирования — это онлайн-инструмент, с помощью которого можно вычислить любую производную функцию через x и y. Калькулятор неявной производной с шагами позволяет крупным производителям быстро освоить это, выполняя вычисления во время выполнения. Пошаговые результаты калькулятора неявной производной заставят вас выполнить конкретную задачу в рамках менуэта.

Интегрирование и дифференцирование обратны друг другу. Вы можете найти полезные калькуляторы интеграции на этом веб-сайте, а также полезные блоги.

Что такое неявное дифференцирование?

В исчислении слово неявный используется для функций, которые могут быть выражены как через x, так и через y. Неявное дифференцирование — это процесс, в котором мы находим производную зависимой переменной. Это делается с помощью

Раздельного дифференцирования каждого члена

Выражения производной зависимой переменной в виде символа 92 \right) = \frac{d}{dx} (1) $$

Этот веб-сайт предлагает другие полезные инструменты дифференцирования, например, вы можете использовать калькулятор дифференцирования на главной странице или калькулятор частных производных, чтобы получить мгновенное решение. вашей проблемы.

Преимущества использования калькулятора неявных функций

Всегда лучше использовать онлайн-инструмент, чем ручной метод. Вот некоторые из основных преимуществ калькулятора dy/dx с шагами:

1. Он экономит ваше время, которое вы тратите на ручные вычисления.
2. Неявный калькулятор прост и удобен в использовании.
3. Обеспечивает точные и пошаговые результаты.
4. Вы можете увидеть график и возможные промежуточные шаги неявного дифференцирования.
5. Калькулятор неявной производной с шагами поможет вам попрактиковаться в Интернете, чтобы закрепить свои концепции.

Помимо этого калькулятора неявного дифференциала, вы также можете использовать калькулятор аппроксимации касательной для нахождения производной наклона или кривой.

Преимущества использования калькулятора dy dx

Всегда полезно и разумно использовать калькулятор второй неявной производной с шагами для обучения и практики. Вот некоторые из основных преимуществ этого решателя неявного дифференцирования:

1. Он экономит ваше время, затрачиваемое на ручные вычисления.
2. Этот неявный калькулятор с шагами прост и удобен в использовании.
3. Вы можете попрактиковаться, чтобы закрепить свои концепции неявной дифференциации.
4. Предоставляет пошаговые точные результаты.
5. Вы можете найти график и возможные промежуточные шаги неявного дифференцирования.
6. Вам не нужна плата или подписка, чтобы использовать калькулятор производной неявной функции.

Связанный: Также найдите сопутствующие инструменты, такие как калькулятор частных производных, и бесплатно найдите производные с помощью калькулятора правил произведения.

Как пользоваться калькулятором неявной дифференциации?

Наш калькулятор неявного дифференцирования с шагами очень прост в использовании. Просто выполните следующие действия, чтобы получить точные результаты. Эти шаги:

1. Введите функцию в основной ввод или загрузите пример.

2. Выберите переменную, относительно которой вы хотите оценить.

3. Подтвердите в предварительном просмотре правильность функции или переменной.

4. Нажмите кнопку «РАССЧИТАТЬ», чтобы получить пошаговый ответ.

Надеемся, вам понравился наш калькулятор неявных функций. На этом веб-сайте есть и другие полезные онлайн-инструменты, которые вы можете использовать, такие как калькулятор третьей производной или калькулятор цепного правила с шагами. Такие инструменты могут сэкономить ваше время, которое вы тратите на ручные вычисления.

Часто задаваемые вопросы

Является ли неявное дифференцирование тем же, что и частичное дифференцирование?

При неявном дифференцировании функция дифференцируется по одной переменной, но в конце другая переменная исчезает. В то время как при частичном дифференцировании функция дифференцируется одновременно по двум переменным. Используйте калькулятор неявных частных производных, чтобы получить точные результаты онлайн.

Что такое производная неявной функции?

Неявное дифференцирование, функция дифференцируется по одной переменной, рассматривая другую как функцию первой переменной.

No related posts.