Каково значение 2 корня 2? – Обзоры Вики
Значение 2√2 равно 2.828.
Точно так же, как вы добавляете корень 3 в корень 3?
- 2√3.
- Добавление √3 + √3.
- = 2√3.
- √3 + √3.
- = 2 раза по √3.
- = 2×√3.
- = 2√3.
- √3 + √3 = 2√3.
Как найти квадратный корень из 2? Квадратный корень из 2, округленный до 10 знаков после запятой, равен 1.4142135624. Это положительное решение уравнения x 2 = 2 .
…
Корень квадратный из 2 в радикальной форме: √2.
| 1. | Что такое квадратный корень из 2? |
|---|---|
| 2. | Является ли квадратный корень из 2 рациональным или иррациональным? |
| 3. | Важные примечания относительно квадратного корня из 2 |
Где корень из 3? Квадратный корень из 3 равен 1.732.
Во-вторых Что такое квадрат 4761? Если это не вопрос с подвохом, квадратный корень из 4,761 равен 69.
Какое значение имеет 2 Root 5?
Значение 2 корня 5 равно 4.47. Пошаговое объяснение: Значение 2 корень 5 решается как, Значение корня 5 составляет 2.2360679775.
тогда что является сопряженным корня 5 корня 3? Ответ: сопряжение 5+√3 равно 5 − √3 .
Каков ответ корня 2 корня 3? Чтобы определить значение √2×√3, мы должны умножить значение квадратного корня из 2, равного 1.41, на квадратный корень из 3, равный 1.732. Таким образом, значение ✓2×✓3 равно 2.44.
Почему √ 2 — иррациональное число?
В частности, греки обнаружили, что диагональ квадрата, длина сторон которого равна 1 единице, имеет диагональ, длина которой не может быть рациональной. По теореме Пифагора длина диагонали равна квадратному корню из 2. Итак, квадратный корень из 2 иррационален!
Как найти корень 5? Как найти квадратный корень из 5?
- √5 = √5.

- √5 = 2.23.
Является ли корень 2 рациональным или иррациональным?
Доказательство: √2 иррационально.
Как решить корень 8? Квадратный корень из 8 в радикальной форме представлен как √8, что также равно 2√2, а в виде дроби он равен 2.828 примерно.
…
Таблица квадратного корня от 1 до 15.
| Число | Площади | Квадратный корень (до 3 десятичных знаков) |
|---|---|---|
| 6 | 6 2 = 36 | √6 = 2.449 |
| 7 | 7 2 = 49 | √7 = 2.646 |
| 8 | 8 2 = 64 | √8 = 2.828 |
| 9 | 9 2 = 81 | √9 = 3.000 |
Что такое квадратный корень из 4?
Квадратный корень от 1 до 25
| Число | Квадратный корень |
|---|---|
| 4 | 2 |
| 5 | 2.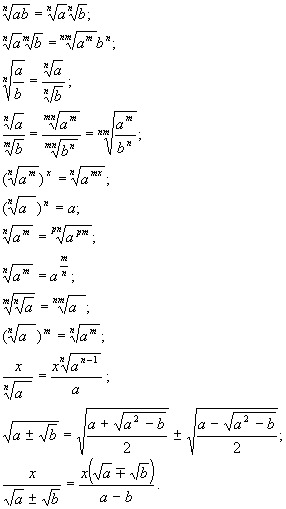 236 236 |
| 6 | 2.449 |
| 7 | 2.646 |
Как найти рут 5?
Как найти квадратный корень из 5?
- √5 = √5.
- √5 = 2.23.
Является ли 4761a идеальным квадратом? Следовательно, следующая цифра в делителе равна 9. Теперь остаток равен 0. Следовательно, квадратный корень из 4761 равен 69 .
…
Найдите квадратный корень из 4761. А. 69. Б. 59. В. 49. Г. 48.
| 3 | 4761 |
|---|---|
| 23 | 23 |
| 1 |
Что такое квадратный корень 200 упрощенный? Квадратный корень из 200 можно упростить как 10√2.
Чему равен квадратный корень из двойного корня?
Квадратный корень из 2 или корень 2 представляется с помощью символа квадратного корня √ и записывается как √2, значение которого равно 1.414 . Это значение широко используется в математике.
…
Похожие темы:
| Таблица квадратного корня | Квадратный корень от 1 до 25 |
|---|---|
| Квадратный корень из 3 | Поиск квадратного корня |
| Уловки с квадратным корнем | Квадратный корень и кубический корень |
Чему равен квадрат корня из 2 из 5? Ответ: Значение корня 2 из 5 определяется как Значение корня 5 равно 2.2360679775.
Каковы 2 квадратных корня из 10?
Чему равен корень числа 6? √6 = 2.449
Таким образом, мы нашли значение корня 6.
Чему равно квадратный корень из 5 плюс квадратный корень из 3?
Следовательно, сопряжение $5+sqrt{3}$ есть 5 долл. США{3}$ . Итак, правильный ответ: «Вариант А».
Какая сопряженная пара 2 корень 5 корень 3? Ответ проверен экспертом
( 2 √ 5 + √ 3 ) равно ( 2√5–√3 ).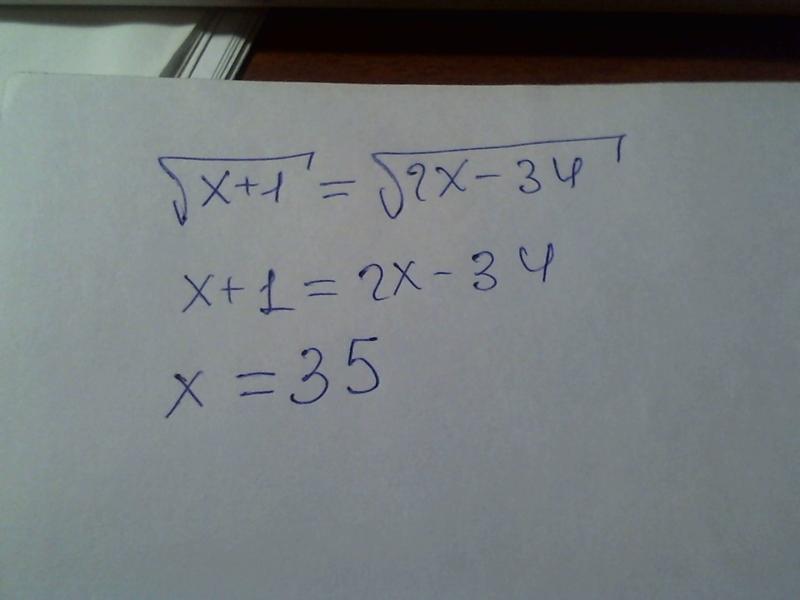 Вариант (С) правильный.
Вариант (С) правильный.
Что является сопряженным 2 3?
Если a = √3 и b= 1, то знаменатель равен (ab), если мы умножим (a+b) или √3+1, получится a2-b2, а √3 будет возведено в квадрат. = 2(кв.{3}+1) . В приведенном выше примере √3+1 используется в качестве рационализирующего множителя, который является сопряженным с √3-1.
Урок 41. извлечение корня из комплексного числа — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №41. Извлечение корня из комплексного числа.
Перечень вопросов, рассматриваемых в теме
1) понятие корня из комплексного числа;
2) алгоритмы извлечения корня из комплексного числа;
3) пример извлечения корня из комплексного числа в тригонометрической форме.
Глоссарий по теме
Определение. Корнем n-ой степени из комплексного числа ω называется комплексное число z такое, что zn=ω. Множество всех корней n-ой степени из ω обозначается через .
Теорема. Уравнение zn=ω, где ω- комплексное число, n- натуральное, имеет ровно n различных комплексных корней.
Все n корней zk лежат на оркужности радиусом с центом в начале кооринат; они делят окружность на n дуг величиной каждая и являются вершинами вписанного в нее правильного n-угольника.
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Определение. Корнем n-ой степени из комплексного числа ω называется комплексное число z такое, что zn=ω. Множество всех корней n-ой степени из ω обозначается через .
Теорема. Уравнение zn=ω, где ω- комплексное число, n- натуральное, имеет ровно n различных комплексных корней.
Доказательство. Пусть ω=|ω|∙(cosφ+isinφ), число z будем искать в виде
z=|z|∙(cosα+isinα).
Преобразуем уравнение zn=ω, используя формулу Муавра:
|z|n(cosnζ+isinnζ)=|ω|∙(cosθ+isinθ).
Отсюда вытекают равенства:
|z|n=|ω|, nζ= θ+2πk, k- целое,
Из которых для модуля искомого корня получается определенное значение , тогда как его аргумент , k- целое, может принимать различные значения при разных k. При этом значениям k= 0, 1, 2, …, n-1 соответствуют различные значения корня, а при k= n значение корня совпадает с его значением при k=0. При k=n+1 получим значение корня, что и при k=1, и т.д.
Таким образом, число различных значений корня равно n- это
, где k=0, 1, 2,…, n-1 что и требовалось доказать.
Все n корней zk лежат на оркужности радиусом с центом в начале кооринат; они делят окружность на n дуг величиной каждая и являются вершинами вписанного в нее правильного n-угольника.
Пример 1. Найдите все корни n-ой степени из действительного числа x>0.
Решение. Если х- положительное действительное число, то |x|=x, θ=arg x=0. Формула корней в этом случае дает ответ:
, где k=0, 1, 2,…, n-1.
При k=0 получим – это арифметический корень. При четном n=2m имеется еще один дейсвтиельный корень., получающийся при k=m. (ζ= arg zm=π):
Корни n-ой степени из 1 часто обозначают через εk, k= 0, 1, 2, …, n-1. Согласно предыдущему примеру:
Пример 2. Вычислите корни третьей степени из комплексного числа 2+2i.
Решение: Найдем тригонометрическую форму данного числа:
По формуле корней из комплексного числа имеем:
, где k пробегает значения 0, 1, 2. Запишем полученные корни:
Используя формулы для косинуса и синуса разности углов, получаем:
Ответ: ; -1+i; .
Немного иначе извлекаются корни из комплексных чисел, аргумент которых не приводится к виду , где m, n – целые числа.
Пример 3. Найдите
Решение. Пусть ω=3+4i. Положим φ=arg ω.
, тогда ω=5(cosφ+isinφ), где , .
Следовательно, , где k=0, 1.
Запишем подробнее:
Найдем и , используя формулу двойного угла:
, откуда , ; тогда , Угол φ лежит в первой четверти, а следовательно, и угол тоже, поэтому Тогда
Ответ:
Пример 4. Выполнить операцию извлечения корня z3 для заданных комплексных чисел в алгебраической форме представления: .
Решение: Тригонометрическая форма записи некоторого комплексного числа имеет вид z=r(cosφ+i⋅sinφ). По условию . Вычислим модуль исходного комплексного числа:
Вычислим аргумент исходного комплексного числа, используя формулу (*):. Подставим полученные значения и получим:
Для k=0 получаем:
Для k=1 получим:
Для k=2 получим:
Разбор решения заданий тренировочного модуля
№1. Тип задания: множественный выбор
Найдите
Выберите верные ответы из предложенных:
- 2+i
- -2+i
- -2-i
- 2-i
Решение. Пусть ω=3-4i. Положим φ=arg ω.
Пусть ω=3-4i. Положим φ=arg ω.
, тогда ω=5(cosφ+isinφ), где , .
Следовательно, , где k=0, 1.
Запишем подробнее:
Найдем и , используя формулу двойного угла:
, откуда , ; тогда , Угол φ лежит в первой четверти, а следовательно, и угол тоже, поэтому Тогда
Ответ: 2+i; -2-i
Верные ответы: 1, 3
№2. Тип задания: ввод с клавиатуры пропущенных элементов в тексте.
Чему будет равно произведение: (5 + 3i)∙(1 — 2i)=______
Решение:
((5 + 3i) · (1 — 2i) = 5·1 — 5·2i + 3·1i — 3·2i2 = 5 — 10i + 3i + 6 =11 — 7i
Ответ: 11-7i
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Решено
В прямоугольном треугольнике АВС угол С равен 90 градусов, AB = 4, tg А=0. 75 . Найдите АС.
75 . Найдите АС.
Решено
На полке было 12 книг. Несколько книг взяли с полки. После этого осталось на 4 книги больше, чем взяли. Сколько книг взяли с полки?
Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его … 1,3,5,7,9,11,13,15 нужно взять 3 числа и только сложением получить 30.
Имеется два сосуда, содержащие 30 кг и 20 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 81%
Решено
какой цифрой оканчивается значение 2017 в степени 2016
Пользуйтесь нашим приложением
| Метод дихотомии | ||||
| Найти корни уравнения (arccos(0.008*(x*x*x))=0), используя Метод дихотомии | Метод дихотомии | |||
| Найти корни уравнения (2*exp(x)-5*x+2 =0), используя Метод Ньютона | Метод Ньютона | |||
| Найти корни уравнения (2*exp(x)-5*x+2 =0), используя Метод Ньютона | Метод Ньютона | |||
| Найти корни уравнения (2*exp(x)-5*x+2 =0), используя Метод дихотомии | Метод дихотомии | |||
| Найти корни уравнения (2*exp(x)-5*x+2 =0), используя Метод хорд | Метод хорд | |||
| Найти корни уравнения (2*exp(x)-5*x+2 =0), используя Метод итераций | Метод итераций | |||
| Найти корни уравнения (2*exp(x)-5*x+2=0), используя Метод дихотомии | Метод дихотомии | |||
| Найти корни уравнения (2*exp(x)-5*x+2=0), используя Метод золотого сечения | Метод золотого сечения | |||
| Найти корни уравнения (2*exp(x)-5*x+2=0), используя Метод хорд | Метод хорд | |||
| Найти корни уравнения (2*exp(x)-5*x+2=0), используя Комбинированный метод | Комбинированный метод | |||
| Найти корни уравнения (2*exp(x)-5*x+2=0), используя Метод Ньютона | Метод Ньютона | |||
Найти корни уравнения (x^2-tan(0. {-i\frac{\pi}{2}}.$ {-i\frac{\pi}{2}}.$
3-8 | ||||
| 9 | Оценить | квадратный корень из 12 | ||
| 10 | Оценить | квадратный корень из 20 | ||
| 11 | Оценить | квадратный корень из 50 | 94 | |
| 18 | Оценить | квадратный корень из 45 | ||
| 19 | Оценить | квадратный корень из 32 | ||
| 20 | Оценить | квадратный корень из 18 | 93-8 | |
| 9 | Оценить | квадратный корень из 12 | ||
| 10 | Оценить | квадратный корень из 20 | ||
| 11 | Оценить | квадратный корень из 50 | 94 | |
| 18 | Оценить | квадратный корень из 45 | ||
| 19 | Оценить | квадратный корень из 32 | ||
| 20 | Оценить | квадратный корень из 18 | 92 |
Корни квадратного уравнения — формула, как найти, примеры
Для заданного квадратного уравнения ax 2 + bx + c = 0 значения x, которые удовлетворяют уравнению, известны как его корни. т. е. они являются значениями переменной (x), которая удовлетворяет уравнению. Корни квадратичной функции — это x-координаты x-перехватов функции. Поскольку степень квадратного уравнения равна 2, оно может иметь максимум 2 корня. Мы можем найти корни квадратных уравнений, используя различные методы.
т. е. они являются значениями переменной (x), которая удовлетворяет уравнению. Корни квадратичной функции — это x-координаты x-перехватов функции. Поскольку степень квадратного уравнения равна 2, оно может иметь максимум 2 корня. Мы можем найти корни квадратных уравнений, используя различные методы.
- Факторинг (по возможности)
- Квадратичная формула
- Завершение квадрата
- Графики (используется для поиска только действительных корней)
Давайте узнаем больше о корнях квадратного уравнения, а также о дискриминанте, природе корней, сумме корней, произведении корней и многом другом вместе с некоторыми примерами.
| 1. | Корни квадратного уравнения |
| 2. | Как найти корни квадратного уравнения? |
| 3. | Природа корней квадратного уравнения |
| 4. | Сумма и произведение корней квадратного уравнения |
5. | Часто задаваемые вопросы о корнях квадратного уравнения |
Корни квадратного уравнения
корней квадратного уравнения — значения переменной, удовлетворяющие уравнению. Они также известны как «решения» или «нули» квадратного уравнения. Например, корнями квадратного уравнения x 2 — 7x + 10 = 0 являются x = 2 и x = 5, поскольку они удовлетворяют уравнению. т. е. при подстановке каждого из них в данное уравнение получаем 0,
- при x = 2, 2 2 — 7(2) + 10 = 4 — 14 + 10 = 0,
- при x = 5, 5 2 — 7(5) + 10 = 25 — 35 + 10 = 0, г.
Но как найти корни общего квадратного уравнения ax 2 + bx + c = 0? Попробуем решить его относительно x, заполнив квадрат.
ax 2 + bx = — c
Разделив обе части на ‘a’,
x 2 + (b/a) x = — c/a
Здесь коэффициент при x равен b/ а. Половина его равна b/(2a). Его площадь равна b 2 /4a 2 . Добавление b 2 /4a 2 с обеих сторон,
Половина его равна b/(2a). Его площадь равна b 2 /4a 2 . Добавление b 2 /4a 2 с обеих сторон,
x 2 92 формула)
Извлечение квадратного корня с обеих сторон,
x + (b/2a) = ±√ [(b 2 — 4ac) / 4a 2 ]
x + (b/2a) = ± √ (b 2 — 4ac) / 2a
Вычитание b/2a с обеих сторон,
x = — (b/2a) ±√ (b 2 — 4ac) / 2a
x = (- b ± √ (b 2 — 4ac))/2a
Это известно как квадратичная формула , и ее можно использовать для нахождения любого типа корней квадратного уравнения.
Как найти корни квадратного уравнения?
Процесс нахождения корней квадратных уравнений известен как «решение квадратных уравнений». В предыдущем разделе мы видели, что корни квадратного уравнения можно найти с помощью квадратной формулы. Наряду с этим методом у нас есть несколько других методов нахождения корней квадратного уравнения. Чтобы узнать об этих методах подробно, нажмите здесь. Обсудим здесь каждый из этих методов, решив пример нахождения корней квадратного уравнения x 2 — 7x + 10 = 0 (о чем говорилось в предыдущем разделе) в каждом случае. Обратите внимание, что в каждом из этих методов уравнение должно быть в стандартной форме ax 2 + bx + c = 0.
Чтобы узнать об этих методах подробно, нажмите здесь. Обсудим здесь каждый из этих методов, решив пример нахождения корней квадратного уравнения x 2 — 7x + 10 = 0 (о чем говорилось в предыдущем разделе) в каждом случае. Обратите внимание, что в каждом из этих методов уравнение должно быть в стандартной форме ax 2 + bx + c = 0.
Нахождение корней квадратного уравнения с помощью факторизации
- Фактор левой части.
(х — 2) (х — 5) = 0 - Установите каждый из этих коэффициентов равным нулю и решите.
х — 2 = 0, х — 5 = 0
х = 2, х = 5.
Нахождение корней квадратного уравнения по квадратичной формуле
- Найдите значения a, b и c, сравнив данное уравнение с ax 2 + bx + c = 0,
Тогда a = 1, b = -7 и c = 10 - Подставляем их в квадратную формулу и упрощаем.
х = [-(-7) ± √((-7) 2 — 4(1)(10))] / (2(1))
= [ 7 ± √ (49 — 40) ] / 2
= [ 7 ± √ (9) ] / 2
= [ 7 ± 3 ] / 2
= (7 + 3) / 2, (7 — 3) / 2
= 10/2, 4/2
= 5, 2
Следовательно, х = 2, х = 5.
Нахождение корней квадратного уравнения путем заполнения квадрата
- Заполните квадрат с левой стороны.
(х — (7/2) ) 2 = 9/4 - Решите, извлекая квадратный корень из обеих сторон.
х — 7/2 = ± 3/2
х — 7/2 = 3/2, х — 7/2 = -3/2
х = 10/2, х = 4/2
х = 5, х = 2
Нахождение корней квадратного уравнения с помощью графика
- Постройте график левой части (квадратичной функции) либо вручную, либо с помощью калькулятора графического дисплея (GDC).
График показан ниже. - Найдите точки пересечения, которые являются не чем иным, как корнями квадратного уравнения.
Следовательно, корни квадратного уравнения равны x = 2 и x = 5 .
Мы можем заметить, что корни квадратного уравнения x 2 — 7x + 10 = 0 равны x = 2 и x = 5 в каждом из методов. Обратите внимание, что метод факторинга работает только тогда, когда квадратное уравнение факторизуемо; и мы не можем найти комплексные корни квадратного уравнения с помощью графического метода. Таким образом, лучшие методы, которые всегда работают для нахождения корней, — это квадратичная формула и методы завершения квадрата.
Таким образом, лучшие методы, которые всегда работают для нахождения корней, — это квадратичная формула и методы завершения квадрата.
Природа корней квадратного уравнения
Природа корней квадратного уравнения говорит о том, «сколько корней имеет уравнение?» и «какой тип корней имеет уравнение?». Квадратное уравнение может иметь:
- два действительных и разных корня
- два сложных корня
- два действительных и равных корня (это означает только один действительный корень)
Например, в приведенном выше примере корни квадратного уравнения x 2 — 7x + 10 = 0 — это x = 2 и x = 5, где 2 и 5 — два разных действительных числа. и поэтому мы можем сказать, что уравнение имеет два действительных и различных корня. Но чтобы найти природу корней, нам на самом деле не нужно решать уравнение. Мы можем определить природу корней, используя дискриминант

Квадратичная формула x = (-b ± √ (b 2 — 4ас) )/2а. Таким образом, это можно записать как x = (-b ± √ D )/2a. Поскольку дискриминант D находится в квадратном корне, мы можем определить природу корней в зависимости от того, является ли D положительным, отрицательным или нулевым.
Природа корней при D > 0
Тогда приведенная выше формула принимает вид
x = (-b ± √ положительное число)/2a
и это дает нам два действительных и разных корня. Таким образом, квадратное уравнение имеет два действительных и различных корня, когда b 2 — 4ac > 0,
Природа корней при D
< 0Тогда приведенная выше формула принимает вид
x = (-b ± √ отрицательное число)/2a
и это дает нам два комплексных корня (которые различны), поскольку квадратный корень из отрицательного числа является комплексным числом. Таким образом, квадратное уравнение имеет два комплексных корня, когда b 2 — 4ac < 0.
Примечание. Квадратное уравнение никогда не может иметь один комплексный корень. Комплексные корни всегда встречаются парами. т. е. если a + bi — корень, то a — bi тоже корень.
Квадратное уравнение никогда не может иметь один комплексный корень. Комплексные корни всегда встречаются парами. т. е. если a + bi — корень, то a — bi тоже корень.
Природа корней Когда D = 0
Тогда приведенная выше формула принимает вид
х = (-b ± √ 0)/2a = -b/2a
и, следовательно, уравнение имеет только один действительный корень. Таким образом, квадратное уравнение имеет только один действительный корень (или два равных корня -b/2a и -b/2a), когда b 2 — 4ac = 0,
Сумма и произведение корней квадратного уравнения
Мы видели, что корнями квадратного уравнения x 2 — 7x + 10 = 0 являются x = 2 и x = 5. Таким образом, сумма его корней = 2 + 5 = 7, а произведение его корней = 2 × 5 = 10. Но сумма и произведение корней квадратного уравнения ах
Мы знаем, что корнями квадратного уравнения ax 2 + bx + c = 0 по квадратичной формуле являются (-b + √ (b 2 — 4ac))/2a и (-b — √ (b 2 — 4ач) )/2а. Представим их как x 1 и x 2 соответственно.
Представим их как x 1 и x 2 соответственно.
Сумма корней квадратного уравнения
Сумма корней = x 1 + x 2
= (-b + √ (b 2 — 4ac))/2a + (-b — √ (b 2 — 4ac))/2a
= -b/2a — b/2a
= -2b/2a
= -b/a
Следовательно, сумма корней квадратного уравнения ax 2 + bx + c = 0 равна -b/a.
Для уравнения x 2 — 7x + 10 = 0, сумма корней = -(-7)/1 = 7 (что было суммой фактических корней 2 и 5).
Произведение корней квадратного уравнения
Произведение корней = x 1 · x 2
= (-b + √ (b² — 4ac))/2a · (-b — √ (b² — 4ac))/2a
= (-b/2a) 2 — ( √ (b 2 — 4ac)/ 2a) 2 ( по формуле a² — b²)
= b 2 / 4a 2 — b 91 2 — 4AC) / 4A 2
= B 2 / 4A 2 — B 2 / 4A 2 + 4AC / 4A 2 2 + 4A 4A 2 18
+ 4A 4A 2 18 + 4A 9AC / 4A 2 9AC / 4A 2 9AC / 4A . 1811 2
1811 2
= c/a
Следовательно, произведение корней квадратного уравнения ax 2 + bx + c = 0 равно c/a.
Для уравнения x 2 — 7x + 10 = 0, произведение корней = 10/1 = 10 (которое было произведением фактических корней 2 и 5).
Важные формулы, относящиеся к корням квадратных уравнений:
Для квадратного уравнения ax 2 + bx + c = 0,
- Корни вычисляются по формуле x = (-b ± √ (b 2 — 4ас) )/2а.
- Дискриминант есть, D = b 2 — 4ас.
Если D > 0, то уравнение имеет два действительных и различных корня.
Если D < 0, уравнение имеет два комплексных корня.
Если D = 0, уравнение имеет только один действительный корень. - Сумма корней = -b/a
- Произведение корней = c/a
☛ Похожие темы:
- Калькулятор корней квадратного уравнения
- Корни квадратного уравнения с помощью калькулятора квадратных формул
- Корни квадратного уравнения путем заполнения квадратного калькулятора
Часто задаваемые вопросы о корнях квадратного уравнения
Что такое корни квадратного уравнения?
корней квадратного уравнения x 2 + bx + c = 0 — это значения переменной (x), которые удовлетворяют уравнению. Например, корни уравнения x 2 + 5x + 6 = 0 равны -2 и -3.
Например, корни уравнения x 2 + 5x + 6 = 0 равны -2 и -3.
Как найти корни квадратного уравнения?
Корни квадратного уравнения ax 2 + bx + c = 0 можно найти с помощью квадратной формулы, которая гласит: x = (-b ± √ (b 2 — 4ac))/2a. В качестве альтернативы, если квадратное выражение можно разложить на множители, мы можем разложить его на множители и установить множители равными нулю, чтобы найти корни.
Какие три типа корней корней квадратного уравнения?
Квадратное уравнение ax 2 + bx + c = 0 может иметь:
- два действительных и различных корня, когда b 2 — 4ac > 0.
- два комплексных корня, когда b 2 — 4ac < 0,
- два действительных и равных корня, когда b 2 — 4ac = 0.
Как найти корни квадратного уравнения, заполнив квадрат?
Чтобы найти корни квадратного уравнения ax 2 + bx + c = 0, заполнив квадрат, сначала заполните квадрат в левой части. Затем найдите x, извлекая квадратный корень из обеих сторон.
Затем найдите x, извлекая квадратный корень из обеих сторон.
Как определить природу корней квадратного уравнения?
Характер корней квадратного уравнения ax 2 + bx + c = 0 определяется его дискриминантом D = b 2 — 4ac.
- Если D > 0, уравнение имеет два действительных и различных корня.
- Если D < 0, уравнение имеет два комплексных корня.
- Если D = 0, уравнение имеет два равных действительных корня.
Как найти корни квадратного уравнения, используя квадратную формулу?
Квадратная формула говорит, что корни квадратного уравнения ax 2 + bx + c = 0 равны x = (-b ± √ (b 2 — 4ac))/2a. Чтобы решить любое квадратное уравнение, приведите его к стандартной форме ax 2 + bx + c = 0, найдите значения a, b и c, подставьте их в квадратную формулу и упростите.
Как найти сумму и произведение корней квадратного уравнения?
Для любого квадратного уравнения ax 2 + bx + c = 0,
- сумма корней, α + β = -b/a
- произведение корней, α × β = c/a
Могут ли оба корня квадратного уравнения быть нулями?
Да, оба корня квадратного уравнения могут быть нулями. Например, два корня квадратного уравнения x 2 = 0 равны 0 и 0.
Например, два корня квадратного уравнения x 2 = 0 равны 0 и 0.
Как найти корни квадратного уравнения с помощью факторинга?
Чтобы найти корни квадратного уравнения ax 2 + bx + c = 0 с помощью факторизации, разложите его левую часть на множители, приравняйте каждый из множителей к нулю и решите. 92/5-(9)=0
Пошаговое решение:
Шаг 1:
(x - 9) 2
Упростить ————————
5
Уравнение в конце шага 1 :
(x - 9) 2
———————— - 9 = 0
5
Шаг 2 :
Преобразование целого в виде эквивалентной дроби:
2.1 Вычитание целого из дроби
Преобразование целого в виде дроби с использованием 5 в качестве знаменателя:
9 9 • 5
9 = — = —————
1 5
Эквивалентная дробь: полученная таким образом дробь выглядит иначе, но имеет то же значение, что и целое
Общий знаменатель: эквивалентная дробь и другая дробь, участвующая в вычислении, имеют один и тот же знаменатель
Сложение дробей, имеющих общий знаменатель:
2. 2 Сложение двух эквивалентных дробей
2 Сложение двух эквивалентных дробей
Сложение двух эквивалентных дробей, которые теперь имеют общий знаменатель
Соедините числители, поднесите сумму или разность к общему знаменателю, затем приведите к наименьшему числу, если возможно:
(x-9) 2 - (9 • 5) x 2 - 18x + 36
знак равно
5 5
Попытка разложить на множители путем разделения среднего члена
2.3 Разложение на множители x 2 — 18x + 36
Первый член равен x 2 , его коэффициент равен 1 .
Средний член равен -18x, его коэффициент равен -18.
Последний член, «константа», равен +36
. Шаг 1: умножьте коэффициент первого члена на константу 1 • 36 = 36
. среднего члена, что составляет -18 .
| -36 | + | -1 | = | -37 | ||||||||||||||||||||||
| -18 | + | -2 | -18 | + | 9000 40004—18 | +9005 9000 40004 | —18 | +9005 | —18 | +9005 9000. | —18 | |||||||||||||||
| -20 | ||||||||||||||||||||||||||
| -12 | + | -3 | = | -15 | ||||||||||||||||||||||
| -9 | + | -9 | + | -9 | + | -9 | + | + | 9+ | 119 | + | . | ||||||||||||||
| -6 | + | -6 | = | -12 | ||||||||||||||||||||||
| + | -9 | = | -13 |
Для аккуратности печать 12 строк, в которой не удалось найти два таких фактора, была исключена.
Вывод: Трехчлен нельзя разложить на множители
Уравнение в конце шага 2 :
x 2 - 18x + 36
————————————— = 0
5
Шаг 3 :
Когда дробь равна нулю:
3.1 Когда дробь равна нулю...
Если дробь равна нулю, ее числитель, часть над чертой дроби, должен быть равен нулю.
Теперь, чтобы избавиться от знаменателя, Тигр умножает обе части уравнения на знаменатель.
Вот как:
x 2 -18x+36
————————— • 5 = 0 • 5
5
Теперь в левой части 5 уравновешивает знаменатель, а в правой части ноль, умноженный на что-либо, по-прежнему равен нулю.
Теперь уравнение принимает вид :
x 2 -18x+36 = 0
Парабола, нахождение вершины :
3.2 Найдите вершину y = x 2 -18x+36
Параболы имеют самую низкую точку или вершину, называемую анизшей точкой аболы. Наша парабола раскрывается и, соответственно, имеет низшую точку (абсолютный минимум). Мы знаем это еще до того, как начертили «у», потому что коэффициент первого члена, 1 , положителен (больше нуля). Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину. Из-за этой симметрии линия симметрии, например, будет проходить через середину двух точек пересечения x (корней или решений) параболы. То есть, если парабола действительно имеет два действительных решения.
Из-за этой симметрии линия симметрии, например, будет проходить через середину двух точек пересечения x (корней или решений) параболы. То есть, если парабола действительно имеет два действительных решения.
Параболы могут моделировать многие реальные жизненные ситуации, такие как высота над землей объекта, брошенного вверх через некоторый период времени. Вершина параболы может предоставить нам такую информацию, как максимальная высота, на которую может подняться объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины.
Для любой параболы, Ax 2 +Bx+C, x-координата вершины определяется как -B/(2A) . В нашем случае координата x равна 9,0000
Подключение к формуле Параболы 9.0000 Для x Мы можем рассчитать Y -координату:
Y = 1,0 * 9,00 * 9,00 -18,0 * 9,00 + 36,0
или y = -45,000
Парабола, график вершины и X -intercepts:
4.Корневой график для: y = x 2 -18x+36
Ось симметрии (штриховая) {x}={ 9,00}
Вершина в {x,y} = {9,00,-45,00}
x -Перехваты (корни ) :
Корень 1 в точке {x,y} = {2,29, 0,00}
Корень 2 в точке {x,y} = {15,71, 0,00}Решить квадратное уравнение, заполнив квадрат
3.
3 Решение x 2 -18x+36 = 0, заполнив квадрат .
Вычтите 36 из обеих частей уравнения:
x 2 -18x = -36Теперь немного хитрости: возьмите коэффициент x, равный 18, разделите на два, получите 9, и, наконец, возведите его в квадрат, получив 81
Добавьте 81 к обеим частям уравнения:
В правой части имеем:
-36 + 81 или (-36/1)+(81/1)
Общий знаменатель двух дробей равен 1. Сложение (-36/1)+(81/1) дает 45/1
Таким образом, складывая обе части, мы окончательно получаем:
x 2 -18x+81 = 45Добавление 81 завершило левую часть в полный квадрат:
x 2 -18x+81 =
(x-9) • (x-9) =
(x-9) 2
Вещи, которые равны к одному и тому же и равны друг другу. Так как
x 2 -18x+81 = 45 и
x 2 -18x+81 = (x-9) 2
тогда, согласно закону транзитивности,
(x-9) 2 = 45#3.
3.1
Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны.
Обратите внимание, что квадратный корень из
(x-9) 2 равен
(x-9) 2/2 =
(x-9) 1 =
18x-91, применяя Принцип квадратного корня в уравнении #3.3.1 получаем:
x-9 = √ 45Добавьте 9 к обеим частям, чтобы получить:
x = 9 + √ 45Так как квадратный корень имеет два значения, одно положительное, а другое отрицательное
x 2 - 18x + 36 = 0
имеет два решения:
x = 9 + √ 45
или
x = 9 - √ 45Решение квадратичного уравнения с использованием квадратичной формулы
3.4 Решение X 2 -18x + 36 = 0 по квадратичной форме.
Согласно квадратичной формуле, x , решение для Ax 2 +bx +c = 0, где A, B и C являются числами, часто называемыми коэффициентами, определяется:
-B ± √ B 2 -4AC
x = ————————————————————————————————————————————— ——
2AВ нашем случае A = 1
B = -18
C = 36Соответственно, B 2 -4AC =
324-144 =
180Применяя формулу квадрата:
18 ± √ 180
x = ——————
2можно упростить 8 1?
Да! Разложение числа 180 на простые множители равно
2•2•3•3•5
Чтобы иметь возможность удалить что-то из-под корня, должно быть 2 этих экземпляра (потому что мы берем квадрат, то есть корень второй степени).√ 180 = √ 2•2•3•3•5 =2•3•√ 5 =
± 6 • √ 5√ 5 , округленное до 4 десятичных знаков 1, 2 равно 3 десятичным цифрам 2.1973 Итак, теперь мы рассматриваем:
x = ( 18 ± 6 • 2,236 ) / 2Два действительных решения:
x = (18+√180)/2=9+3√ 5 или 15,703: 918 103: 918 103
x =(18-√180)/2=9-3√ 5 = 2,292
Было найдено два решения:
- x =(18-√180)/2=9-3√ 5 = 2,292 x =(18+√180)/2=9+3√ 5 = 15,708
Формула суммы и произведения корней квадратного уравнения
Рабочий лист на эту тему - Сумма и произведение корней Рабочий лист (бесплатно 25 вопросов в формате pdf с ответами)
Калькулятор квадратичных формул
Квадратичная формула Главная
Формулы
сумма корней : $ \frac{ -b}{a} $
произведение корней 92 + 5x + 6 $$.
Как видите, сумма корней действительно равна $$\color{Red}{\frac{-b}{a}}$$, а произведение корней равно $$ \color{Red}{\frac{c {а}}$$.
Пример 2
В приведенном ниже примере показано, как эта формула применяется к квадратному уравнению x 2 - 2x - 8. Опять же, обе формулы - для суммы и произведения сводятся к -b/a и c/a соответственно.
г. Практика ПроблемыПроблема 1
Не решая, найдите сумму и произведение корней уравнения: 2х 2 - 3х -2 = 0.
Определите коэффициенты:
а = 2
б = -3
с = -2.Теперь подставьте эти значения в формулы.
Сумма корней:
$$ \color{Red}{\frac{-b}{a} } = \frac{-(-3)}{2} = \frac{3}{2} $$
Продукт корней:
$$ \color{Red}{ \frac{c}{a} } = \frac{-2}{2} = -1 $$
г.Проблема 2
Не решая, найдите сумму и произведение корней следующего уравнения: -9x 2 - 8x = 15.
Сначала вычтите 15 с обеих сторон, чтобы ваше уравнение имело вид 0 = ax 2 + bx + c, переписанное уравнение: -9x 2 - 8x - 15 = 0.
Определите коэффициенты:
a = -9
b = -8
c = -15.Теперь подставьте эти значения в формулы.
Сумма корней:
$$ \color{Red}{\frac{-b}{a} } = \frac{-(-8)}{-9} = \frac{-8}{9} $$
Продукт корней:
$$ \color{Red}{\frac{c}{a} } = \frac{-15}{9} = \frac{-5}{3} $$
Проблема 3
Напишите квадратное уравнение, зная следующие корни: 4 и 2.
Есть несколько способов решить такую задачу: вы можете создать два бинома (x-4) и (x-2) и умножить их.
Однако, поскольку на этой странице используются наши формулы, давайте воспользуемся ими, чтобы ответить на это уравнение.
Сумма корней = 4 + 2 = 6.
Произведение корней = 4 * 2 = 8.Мы можем использовать наши формулы, чтобы составить следующие два уравнения.
Сумма корней:
$$ \frac{-b}{a} = 6 = \frac{6}{1} $$
Продукт корней:
$$ \frac{c}{a} = 8 = \frac{8}{1} $$
Теперь мы знаем значения всех трех коэффициентов:
a = 1
b = -6
c = 8
.Итак, наше окончательное квадратное уравнение: y = 1x 2 - 6x + 8.
Вы можете перепроверить свою работу, изменив биномы (x - 4)(x - 2), чтобы получить то же уравнение.
г.Проблема 4
Если один корень уравнения ниже равен 3, чему равен другой корень? х 2 - 5х + к = 0.
Запишите, что вы знаете:
a = 1
b = -5
r 1 = 3.Теперь подставьте эти значения в сумму формулы корней.
Сумма корней:
г 1 + г 2 = -б/а 3 + г 2 = -(-5)/1 3 + г 2 = 5 г 2 = 2
Следовательно, недостающий корень равен 2.
Мы можем проверить нашу работу, сорвав биномы.
(х - 3)(х - 2) = х 2 - 5х + 6
Рабочий лист на эту тему - Сумма и произведение корней Рабочий лист (бесплатно 25 вопросов в формате pdf с ключом ответа)
Калькулятор квадратичных формул
Квадратичная формула Главная
г.Квадраты: многочлены второй степени
Темы в
ПРЕДВАРИТЕЛЬНАЯ РАБОТА
Содержание | Главная
10
Решение квадратного уравнения с помощью факторизации
Двойной корень
Квадратное неравенство
Сумма и произведение корней
г.КВАДРАТ — ДРУГОЕ НАЗВАНИЕ многочлена 2-й степени. 2 является наивысшим показателем.
1. Какой вид имеет полиномиальная функция 2-й степени?
у = ах 2 + бх + с
2.
Какой вид имеет квадратное уравнение?
ах 2 + бх + с = 0
3. Что мы понимаем под корнем квадратного?
г.Решение квадратного уравнения.
4. Сколько корней всегда имеет квадратное число?
Двойка, действительная или комплексная.
5. Графом квадратичного уравнения всегда является форма, называемая -- ?
Парабола.
6. Какие три метода решения квадратного уравнения,
6. то есть для нахождения корней?1. Факторинг. 2. Завершение квадрата.
г.3. Квадратичная формула.
Начнем с метода факторинга. В следующей теме мы представим как «Заполнение квадрата», так и «Квадратную формулу».
7. Если произведение множителей равно 0 -- если ab = 0 -- то что вы можете
7. сделать вывод о множителях a , b ?Либо a = 0, либо b = 0.
Пример 1.
г.Решение факторингом.
f ( х ) = х 2 -2 х -3. Найдите корни f ( x ) и нарисуйте график y = f ( x ).
Решение . х 2 -2 х -3 = ( х + 1)( х - 3).
91 810 Следовательно, корни равны −1 и 3. (См. Урок 37 Алгебры.) Это х - перехваты графика.Точка пересечения y представляет собой постоянный член, −3.
В каждом многочлене точка пересечения y является постоянным членом, потому что постоянный член является значением y , когда x = 0,
Пример 2. Двойной корень
f ( x ) = x 2 −10 x + 25. Найдите корни числа 9.1973 f ( x ) и нарисуйте график y = f ( x ).
Решение . x 2 -10 x + 25 =
( x - 5)( x - 5) = ( x - 5) 2 .Два корня равны, они равны 5, 5. Число 5 называется двойным корнем. (См. урок 37 по алгебре, вопрос 4.)
При двойном корне график не пересекает x -ось. Это просто касается его.
Двойной корень возникает, когда квадратное число является полным трехчленом: то есть, когда квадрат является квадратом бинома: ( x ± a ) 2 .
Пример 3. Сколько действительных корней, т. е. корней, являющихся действительными числами, имеет квадратичная функция каждого графика?
Ответ . График а) имеет два действительных корня. Он имеет два x -intercepts.
График б) не имеет действительных корней. У него нет перехватов x . Оба корня сложные.
График в) имеет два действительных корня. Но они являются двойным корнем.
Пример 4. Квадратное неравенство.
Решите это неравенство:
х 2 − 4 х − 5
Для этого просмотрите граф
y = х 2 - 4 х - 5.
Решение . Для каких значений x этот квадрат будет отрицательным? То есть где график ниже оси х ?
График отрицателен между корнями, равными −1 и 5. Решением неравенства является −1 x Мы также можем заметить, что квадратное выражение будет иметь положительные значения — график будет выше x -оси -- слева и справа от корней:
х х > 5.
В то время как квадратичный будет иметь значение 0 в корнях.
Теперь мы рассмотрели три возможности:
Это квадратичное число равно 0 в двух корнях.
Это меньше, чем 0 между двумя корнями.
Это больше, чем 0 слева и справа от двух корней.
г.Эти три возможности, которые верны для любого действительного числа, имеют причудливое название закона трихотомии. Любое число должно быть равно, меньше или больше 0.
Закон трихотомии также принимает следующую форму:
Для любых действительных чисел a, b , либо a = b , a b, либо a > b .
Однако мы должны знать, какая из этих возможностей верна. Для любых двух чисел мы должны знать их относительный порядок. Это заложено в значении «числа».
г.Задача 1. Нарисуйте график y = x 2 − 2 x −8. То есть покажите точки пересечения x и и .
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите "Обновить" ("Reload").х 2 -2 х - 8 = ( х + 2)( х - 4). Таким образом, корни равны −2, 4. y - точка пересечения — постоянный член, −8.
Задача 2. Нарисуйте граф числа 91 813.
y = x 2 + 4 x + 4.
х 2 + 4 х + 4 = ( х + 2) 2 . В -2 есть двойной корень. Отрезок y - постоянный член, 4.
Задача 3.
г.а) Чтобы решить это квадратное неравенство—
x 2 + 2 x − 3 > 0
— просмотрите граф
.y = х 2 + 2 х - 3,
Квадратичный будет положительным -- выше оси x -- для значений x слева и справа от корней. Решение
х х > 1.б) Решите это квадратное неравенство:
х 2 + 2 х - 3
−3 х
Квадратичный будет отрицательным между корнями.
Проблема 4. Квадратное уравнение имеет следующие корни. Запишите каждое квадратичное число как произведение линейных множителей.
а) 3, 4 ( х - 3)( х - 4)
б) −3, −4 ( х + 3)( х + 4)
в) − г , с ( x + r )( x − с )
г) 3 + , 3 – ( х - 3 - )( х -3 + )
Сумма и произведение корней
Теорема.
В квадратном со старшим коэффициентом 1:
Сумма корней минус коэффициента x ;
произведение корней является постоянным членом.
То есть если
х 2 + бх + с = 0,
и корни r и s , затем
| р + с | = | − б , |
| руб. | = | с . |
Если корни r и s , то квадратичный равен
| ( x − r )( x − с ) | = | х 2 − rx − sx + rs |
| = | x 2 − ( r + s ) x + rs . | |
Коэффициент x равен −( r + s ), что является минусом суммы корней. Постоянный член равен рупий , что является их произведением.
г.Пример 5. Постройте квадратное число, корни которого равны 2 и 3.
Решение . Сумма корней равна 5, их произведение равно 6, поэтому квадратное число равно x 2 − 5 x + 6,
.Сумма корней минус коэффициента x . Произведение корней - постоянный член.
Пример 6. Построить квадратное число, корни которого равны 2 + , 2 − .
г.Решение . Сумма корней равна 4. Их произведение равно разности двух квадратов:
Квадратное число равно x 2 − 4 x + 1,
.Пример 7. Постройте квадратное число, корни которого равны 2 + 3 i , 2 − 3 i , где i — комплексная единица.
Решение . Сумма корней равна 4. Произведение снова равно разности двух квадратов: 4 − 9 i 2 = 4 + 9 = 13,
Сумма корней равна 4. Произведение снова равно разности двух квадратов: 4 − 9 i 2 = 4 + 9 = 13,
Квадратное число с этими корнями равно
.x 2 − 4 x + 13.
Задача 5. Построить квадратное число, корни которого равны −3, 4.
Сумма корней равна 1. Их произведение равно −12. Следовательно, квадратичный равен х 2 − х − 12,
Задача 6. Построить квадратное число, корни которого равны 3 + , 3 − .
Сумма корней равна 6. Их произведение равно 9 − 3 = 6,
. Следовательно, квадратное число равно x 2 − 6 x + 6,
Задача 7. Построить квадратное число, корни которого равны 2 + i , 2 − i .
Сумма корней равна 4. Их произведение равно 4 − ( i ) 2 = 4 + 5 = 9,
Следовательно, квадратное число равно
*
В более общем случае для любого коэффициента x 2 , то есть, если квадратичный равен
топор 2 + бх + в ,
и корни r и s , затем
| р + с | = | − | б а | , |
руб. |


 02.17
02.17 2*log(x+11)-1=0), используя Метод дихотомии
2*log(x+11)-1=0), используя Метод дихотомии