| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | сфера (4) | | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | ||
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | 3/9 | ||
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0. 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
Умножение дробей онлайн с решением.
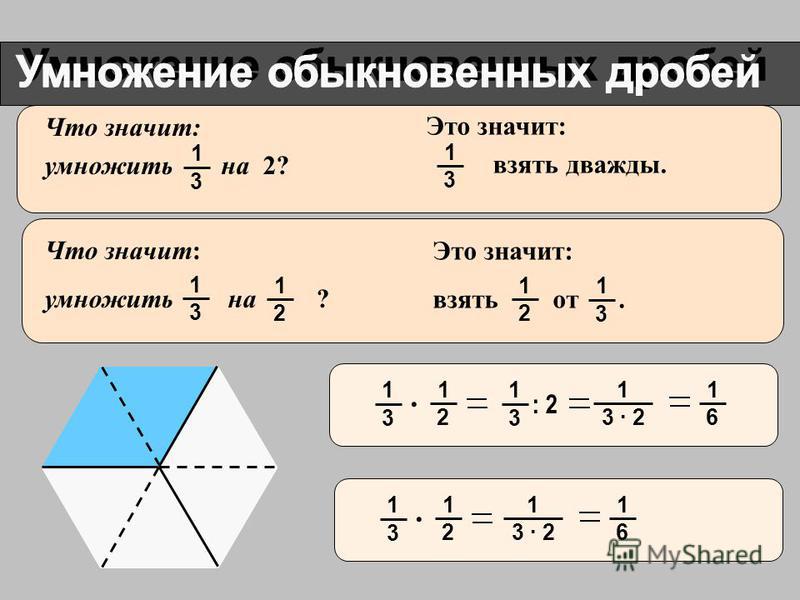
Калькулятор умножения дробей.Чтобы умножить дробь на дробь нужно перемножить их числители и знаменатели, первое произведение записать числителем, а второе знаменателем.
Правила умножения дробей
Произведение двух дробей равно дроби. В числителе которой произведение числителей, а в знаменателе произведение знаменателей.
×
=
a × c
b × d
Как умножать обыкновенные дроби
Для умножения обыкновенных дробей нужно найти произведение числителей и произведение знаменателей. Первое произведение записать числителей а второе знаменателем.
Разберём пример: умножим дроби 1/4 × 1/3. Для этого перемножим числители 1 × 1 = 1 и знаменатели 4 × 3 = 12 в итоге у нас получится дробь 1/12
×
=
1 × 1
4 × 3
=
Как умножать натуральное число на дробь
Чтобы умножить дробь на натуральное число нужно числитель умножить на это число а знаменитель оставить без изменения.
×
=
a × b
c
Как умножать 3 и более дробей
При умножении 3 и более дробей мы пользумеся теми же правилами что и при умножении двух дробей.
Разберём пример: умножим правильную дробь 1/4 на натуральное число 5 и на смешанную дробь 3 целые 1/8.
Перед умножением нужно смешанную дробь перевести в неправильную 3 целые 1/8 = 25/8. Затем перемножить числители 1*5*25 = 125 и знаменатели 4*8 = 32. Полученное записать в виде дроби 125/32. При необходимости сократить и перевести в смешанную дробь.
×
×
=
×
×
=
1 × 5 × 25
4 × 8
=
=
Как умножить смешанную дробь на целое число
Чтобы умножить смешанную дробь на целое число нужно смешанную дробь перевести в неправильную. Затем числитель неправильной дроби умножить на целое число. Знаменатель оставить без изменения.
Разберём пример: умножим смешанную дробь 2 целые 1/4 на целое число 6.
Перед умножением нужно смешанную дробь перевести в неправильную 2 целые 1/4 = 9/4. Затем умножить числитель неправильной дроби на целое число 9*6 = 54 а знаменатель останется без изменения 4. При необходимости сократить и перевести в смешанную дробь.
×
=
×
=
9 × 6
4
=
=
=
Как перемножить смешанные дроби
Чтобы перемножить смешанные дроби, нужно их перевести в неправильные. Затем перемножить числители и знаменатели.
Разберём пример: умножим смешанную дробь 1 целая 2/5 на смешанную дробь 2 целые 1/3.
Переведём смешанные дроби в нерпавильные 1 целая 2/5 = 7/5 и 2 целые 1/3 = 7/3. Затем перемножим числители 7*7 = 49 и знаменатели 5*3 = 15. Получится дробь 49/15. При необходимости сократить и перевести в смешанную дробь.
×
=
×
=
7 × 7
5 × 3
=
=
Умножить дробь 1/3 на дробь 10/12
Умножить дробь 1/25 на дробь 12/10
Умножить дробь 22/10 на дробь 14/10
Умножить дробь 13/1 на дробь 11/21
Умножить дробь 12/23 на дробь 5/16
Умножить дробь 3/7 на дробь 7/10
Похожие калькуляторы
Перевести бесконечную периодическую дробь в обыкновенную дробь
Перевести десятичную дробь в обыкновенную
Привести дробь к новому знаменателю
Деление дробей
Преобразовать смешанную дробь в неправильную дробь
Преобразовать неправильная дробь в смешанную дробь
Сравнение дробей
Сложение дробей
Вычитание дробей
Приведение дробей к наименьшему общему знаменателю
Сократить дробь
Калькулятор дробей
Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражения с дробями:
Дроби — используйте косую черту для деления числителя на знаменатель, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной строки и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.
е. 1,45 .
Math Symbols
| Symbol | Symbol name | Symbol Meaning | Example | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| + | plus sign | addition | 1/2 + 1/3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| — | знак минус | вычитание | 1 1/2 — 2/3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| * | asterisk | multiplication | 2/3 * 3/4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| × | times sign | multiplication | 2 /3 × 5/6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| : | division sign | division | 1/2 : 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| / | division slash | division | 1/3 / 5 1/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
more math problems »
Калькулятор умножения дробейGENERATE WORK сообщите об этом объявлении GENERATE WORK Умножение дробей — работа с шагами `b,c,d\ne0`, и вычисляет частное для `a/b`, деленное на `c/d`. Это онлайн-инструмент для нахождения частного в простейшей форме двух правильных или неправильных дробей. Необходимо выполнить следующие шаги:
Ввод: Две дроби Дроби Правило умножения: Произведение двух дробей `a/b` и `c/d` определяется по следующей формуле $$\frac{a}{b}\times\frac{c}{d}=\frac{ a\times c}{b\times d},\quad \mbox{for}\;b,d\ne0$$ Как умножать дроби? Умножение дробей (или любых других чисел или переменных) может обозначаться знаком умножения × между двумя дробями, точкой между двумя дробями или круглыми скобками вокруг одной или обеих дробей. $$\frac{8}{3}\times \frac{7}{2},\quad\frac{8}{3}\cdot\frac{7}{2},\quad\Big(\frac {8}{3}\Big) \frac{7}{2}, \quad\frac{8}{3}\Big( \frac{7}{2}\Big),\quad \Big(\frac {8}{3}\Big) \Big(\frac{7}{2}\Big)$$ Результатом умножения является произведение. Когда мы имеем дело с умножением дробей, есть три типа умножения Умножение дроби на дробь $$\frac{a}{b}\times\frac{c}{d}=\frac{a\times c}{b\times d},\quad b,d\ne0$$ Следовательно, чтобы умножить две или более дроби, необходимо выполнить три шага:
Например, перемножим дроби 8/3 и 7/2. Реальные задачи на умножение дробей Умножение дробей полезно при анализе размерностей. Размерный анализ — это процесс включения единиц измерения в умножение. Метки единиц считаются общими факторами при умножении дробей. Например, поскольку расстояние равно скорости, умноженной на время, мы получаем $$d= \mbox{миль в час}\times\mbox{час}=\frac{\mbox{миль}}{\mbox{ час}}\times \frac{\mbox{час}}{1}=\mbox{миль}$$ При нахождении площади мы обычно рассматриваем умножение дробей. Практические задачи 2: Калькулятор умножения дробей, формулы, пошаговые расчеты, задачи из реальной жизни и практические задачи будут очень полезны для учащихся начальных классов (образование K-12), чтобы понять умножение двух или более чисел, представленных в виде дробей. Используя эту концепцию, они могут решать сложные алгебраические задачи и уравнения в реальном мире.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Наиболее распространенные мнемоники для запоминания этого порядка операций: 
Какую часть населения составляют младенцы?
Сократите обе дроби до их основной формы.
Например, 
Используя формулу умножения, получаем 
Длина и ширина прямоугольника представляют собой факторы, а площадь прямоугольника представляет собой их произведение. Например, давайте найдем произведение «1/3» и «1/2». Разделите прямоугольник пополам по вертикали и заштрихуйте левую `1/2` внутренней части прямоугольника. Разделите прямоугольник на трети по горизонтали и используйте другое затенение, чтобы заштриховать нижнюю `1/3` внутренней части. Части, которые были заштрихованы дважды, являются произведением этих дробей, то есть `1/2\times1/3 = 1/6` . Это иллюстрируется следующей картинкой: 92/9` и запишите результат в простейшей форме.
6/5/5/5/5/5/5/5/5/5/5/5/5/5/5/5/5/5/56/5/5/5/5/5/56/5 66/5 6/56/5 6.6/56/5 6.6/56/5 6.6/5/5 6.6/5 6.6/5 6.6/5 6.6/5 6.6/56/5 6/5 6.6/5 6.6/56/5 6.6/56/5 6.6/5 6.6/5 6.6/5 6/5.
