Является ли 25 целым числом?
Система счисления включает в себя различные типы чисел, например, простые числа, нечетные числа, четные числа, рациональные числа, целые числа и т. д. Эти числа могут быть выражены в виде цифр или слов соответственно. Например, такие числа, как 40 и 65, выраженные в виде цифр, также могут быть записаны как сорок и шестьдесят пять.
A Система счисления или Система счисления определяется как элементарная система для выражения чисел и цифр. Это уникальный способ представления чисел в арифметической и алгебраической структуре.
Числа используются в различных арифметических значениях, применимых для выполнения различных арифметических операций, таких как сложение, вычитание, умножение и т. д., которые применяются в повседневной жизни для целей вычислений. Значение числа определяется цифрой, ее разрядностью в числе и основанием системы счисления.
Числа, также известные как цифры, представляют собой математические значения, используемые для подсчета, измерения, маркировки и измерения основных величин.
Числа — это математические значения или цифры, используемые для измерения или вычисления величин. Он представлен цифрами как 2, 4, 7 и т. д. Примерами чисел являются целые числа, целые числа, натуральные числа, рациональные и иррациональные числа и т. д. задается системой счисления. Типы описаны ниже:
- Натуральные числа : Натуральные числа — это положительные числа, которые считаются от 1 до бесконечности. Множество натуральных чисел обозначается буквой «N». Это числа, которые мы обычно используем для счета. Набор натуральных чисел можно представить как N=1,2,3,4,5,6,7,……………
- Целые числа: Целые числа — положительные числа, включая ноль, который считается от 0 до бесконечность. Целые числа не включают дроби или десятичные дроби. Множество целых чисел обозначается буквой «W». Множество можно представить в виде W=0,1,2,3,4,5,………………
- Целые числа : Целые числа представляют собой набор чисел, включающий все положительные числа, нуль, а также все отрицательные числа, которые считаются от отрицательной бесконечности до положительной бесконечности.
В наборе нет дробей и десятичных знаков. Множество целых чисел обозначается Z. Набор целых чисел можно представить в виде Z=………..,-5.-4,-3,-2,-1,0,1,2,3,4,5,………….
- Десятичные числа : Любое числовое значение, состоящее из десятичной точки, является десятичным числом. Его можно выразить как 2,5, 0,567 и т. д.
- Вещественное число: Вещественные числа — это заданные числа, не содержащие мнимых значений. Он включает в себя все положительные целые числа, отрицательные целые числа, дроби и десятичные значения. Обычно обозначается буквой «R».
- Комплексный номер: Комплексные числа — это набор чисел, включающий мнимые числа. Его можно выразить как a+bi, где «a» и «b» — действительные числа. Обозначается буквой «С».
- Рациональные числа : Рациональные числа — это числа, которые могут быть выражены как отношение двух целых чисел. Он включает в себя все целые числа и может быть выражен в виде дробей или десятичных знаков.
- Иррациональные числа : Иррациональные числа — это числа, которые не могут быть выражены в дробях или отношениях целых чисел. Он может быть записан десятичными знаками и иметь бесконечные неповторяющиеся цифры после запятой. Обозначается буквой «П».
Определение целых чисел
Подмножество чисел, состоящих из нуля и всех положительных целых чисел, является целыми числами. Целое число считается от нуля до бесконечности. Эти числа используются для повседневных расчетов, в основном для измерения фундаментальных величин.
Целые числа являются единственным составным элементом натуральных чисел, включая ноль. Подмножество задается {0,1,2, 3,4, 5,……….}, набор не включает дробные, десятичные и отрицательные целые числа.
Примеры целых чисел
Положительные целые числа также известны как счетные числа, включая ноль, являющийся частью целых чисел, таких как 0,1, 2, 3, 4, 5 и т. д.
10, 11, 22,100,1000 и т. д. — все это примеры целых чисел.
Теперь давайте перейдем к вопросу
Является ли 25 целым числом?
Ответ:
Поскольку целые числа представляют собой набор действительных чисел, который включает ноль и все положительные счетные числа, такие как 0,1,2,3,4 и т. д. Принимая во внимание, что исключаются дроби, отрицательные целые числа, дроби и десятичные дроби.
Следовательно, 25, будучи частью действительного числа, является целым числом.
Аналогичные вопросы
Вопрос 1: Каковы примеры целых чисел?
Ответ:
Действительные числа, такие как 55, 60, 100 и 110, являются примерами целых чисел.
Вопрос 2: Является ли 2/3 целым числом?
Ответ:
Нет, 2/3 — дробное число, а множество целых чисел не включает дроби.
Вопрос 3: Является ли 0 целым числом?
Ответ:
Поскольку целые числа представляют собой множество действительных чисел, включающее ноль и все положительные счетные числа, 0 также является целым числом.
Вопрос 4. Является ли 3,55 целым числом?
Ответ:
Целые числа представляют собой набор действительных чисел, включающий ноль и все положительные счетные числа. Принимая во внимание, что исключаются дроби, отрицательные целые числа, дроби и десятичные числа. Следовательно, 3,55, являющееся десятичным значением, не является целым числом.
Какое максимальное четное число нельзя представить в виде суммы двух составных нечетных чисел?
спросил
Изменено 5 лет, 7 месяцев назад
Просмотрено 3к раз
$\begingroup$
Вопрос: Какое максимальное четное число НЕ может быть представлено в виде суммы двух составных нечетных чисел?
Например, $14=7+7=5+9=3+11=1+13$ — одно из таких четных чисел, но, вероятно, не максимальное.
Я понятия не имею, как с этим справиться. Спасибо.
- теория чисел
$\endgroup$
0 $\begingroup$
Рассмотрим три нечетные комбинации $9,25,35$. Это, соответственно, $0,1,2\pmod 3$. Таким образом, если $n$ — четное число, то одно из $n-9,n-25,n-35$ является нечетным составным числом, делящимся на $3$ (ну, допустим, хотя бы $>3$). Таким образом, $35+3=\fbox {38}$ является наибольшим четным числом, которое может быть примером… проверка показывает, что это действительно пример, следовательно, максимальный пример.
$\endgroup$
2
$\begingroup$
Подсказка : Если $x\geq 18$ делится на $6$, то мы можем записать $x$ как $(6n+3)+9$ для некоторого натурального числа $n$, где оба $6n+3 $ и $9$ составные.
В наборе нет дробей и десятичных знаков. Множество целых чисел обозначается Z. Набор целых чисел можно представить в виде Z=………..,-5.-4,-3,-2,-1,0,1,2,3,4,5,………….
Обозначается буквой Q.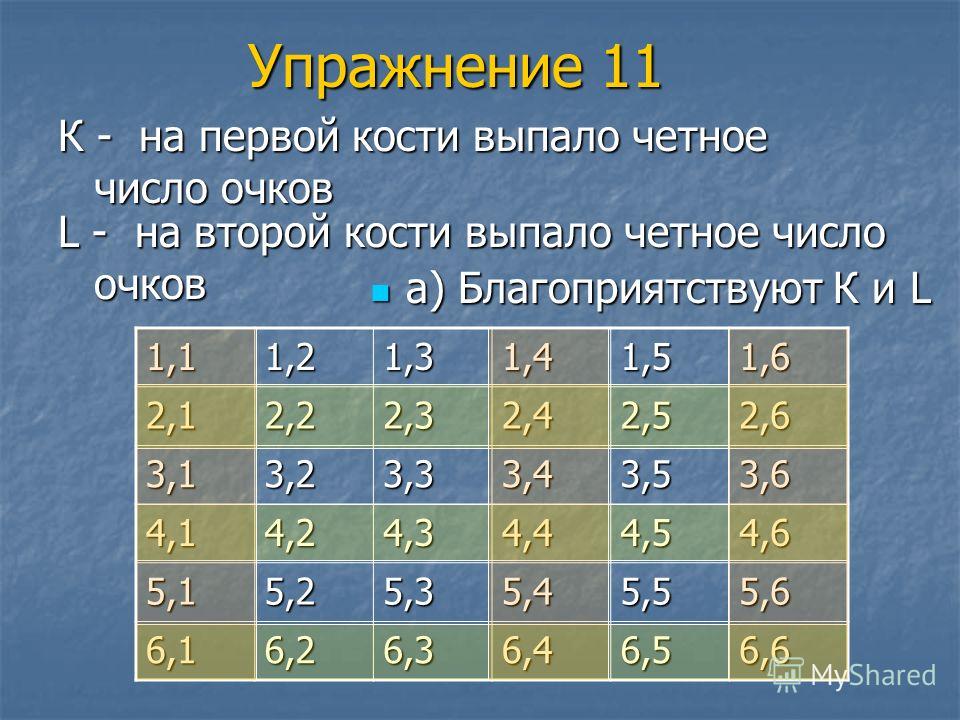
, исключая отрицательные целые числа, дроби и десятичные дроби.
24 доллара = 9+15=3\times3+3\times5$ не является одним из таких чисел.