Четные и нечетные числа в математике
Стремление человека делить и половинить сопровождает его всю жизнь. Нас хлебом не корми, дай поделить на два.
Прежде чем разобраться, зачем и почему мы это делаем, давайте познакомимся с определениями.
Четное число — это число, которое делится нацело на 2.
4 : 2 = 2
Это значит, что 4 — четное число.
Нечетное число — это число, которое не делится на 2 без остатка.
5 не делится на 2 без остатка — значит, 5 это нечетное число.
Если число оканчивается на 0, 2, 4, 6, 8, то это число четное. Если число оканчивается на 1, 3, 5, 7, 9, то это число нечетное. Если двузначное число круглое, то это число четное. Например, 20, 30, 40, 50 и т. д. — четные числа. |
Свойства четных и нечетных чисел
- Если сложить два четных числа, получится четное число:
8 + 8 = 16
16 : 2 = 8 - Если сложить два нечетных числа, получится четное число:
6 : 2 = 3 - Если сложить четное число с нечетным, получится нечетное число:
4 + 5 = 9
9 : 2 = 4 (остаток 1) - Если четное число умножить на четное число, получится четное число:
2 × 2 = 4
4 : 2 = 2 - Если четное число умножить на нечетное число, получится четное число:
4 × 3 = 12
12 : 2 = 6 - Если нечетное число умножить на нечетное, получится нечетное:
3 × 3 = 9
Четные и нечетные числа чередуются друг с другом
1 — нечетное,
2 — четное,
3 — нечетное,
4 — четное,
5 — нечетное,
6 — четное,
7 — нечетное,
8 — четное,
9 — нечетное.
Внимательно рассмотрите таблицу четных и нечетных чисел. На ней хорошо видно, как они чередуются между собой.
| 1 | 11 | 21 | 31 | 41 | 51 | 61 | 71 | 81 | 91 |
| 2 | 12 | 22 | 32 | 42 | 52 | 62 | 72 | 82 | 92 |
| 3 | 13 | 23 | 33 | 43 | 53 | 63 | 73 | 83 | 93 |
| 4 | 14 | 24 | 44 | 54 | 64 | 74 | 84 | 94 | |
| 5 | 15 | 25 | 35 | 45 | 55 | 65 | 75 | 85 | 95 |
| 6 | 16 | 26 | 36 | 46 | 56 | 66 | 76 | 86 | 96 |
| 7 | 17 | 27 | 37 | 47 | 57 | 67 | 77 | 87 | 97 |
| 8 | 18 | 28 | 38 | 48 | 58 | 68 | 78 | 88 | 98 |
| 9 | 19 | 29 | 39 | 49 | 59 | 69 | 79 | 89 | 99 |
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Умение быстро определять четность и нечетность поможет в решении примеров, особенно, когда нужно посчитать в уме. Вот шпаргалка — держите ее под рукой, чтобы быстро ориентироваться в цифрах и числах.
Вот шпаргалка — держите ее под рукой, чтобы быстро ориентироваться в цифрах и числах.
|
Онлайн-курсы по математике для детей помогут быстрее освоить новую тему при поддержке опытного преподавателя.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Задачи для практики
Давайте проверим, как хорошо вы научились определять четность и нечетность. Выполним несколько несложных заданий.
Выполним несколько несложных заданий.
Задачка 1. Назовите числа, которые спрятаны за ♥. Назовите их по порядку. Какие из них — четные, а какие — нечетные?
| 1 | ♥ | 17 |
| 2 | 10 | ♥ |
| ♥ | 19 | |
| 4 | ♥ | 20 |
| 5 | 13 | ♥ |
| ♥ | 14 | 22 |
| 7 | 15 | 23 |
| 8 | ♥ | ♥ |
Ответ: 3 — нечетное, 6 — четное, 9 — нечетное, 12 — четное, 16 — четное, 18 — четное, 21 — нечетное, 24 — четное.
Задачка 2. Вставьте в таблицу пропущенные числа. Определите, четное или нечетное получилось число.
| X | 2 | 4 | 6 | 8 | 10 |
| X × 2 | |||||
| X : 2 |
| X | 2 | 4 | 6 | 8 | 10 |
| X × 2 | 4 | 8 | 12 | 16 | 20 |
| X : 2 | 1 | 2 | 3 | 4 | 5 |
Как решаем:
2 × 2 = 4 — четное
2 : 2 = 1 — нечетное
4 × 2 = 8 — четное
4 : 2 = 2 — четное
6 × 2 = 12 — четное
6 : 2 = 3 — нечетное
8 × 2 = 16 — четное
8 : 2 = 4 — нечетное
10 × 2 = 20 — четное
Задачка 3. В коробке 44 конфеты: 15 шоколадных и 12 — с карамелью. А все остальные с воздушным рисом. Сколько в коробке конфет с воздушным рисом? Получившееся значение — четное или нечетное?
В коробке 44 конфеты: 15 шоколадных и 12 — с карамелью. А все остальные с воздушным рисом. Сколько в коробке конфет с воздушным рисом? Получившееся значение — четное или нечетное?
Как решаем:
Посчитаем, сколько в сумме конфет шоколадных и с карамелью:
15 + 12 = 27 (к)Отнимем от общего количества конфет получившееся число:
44 — 27 = 17 (к)
Ответ: в коробке 17 конфет с воздушным рисом. 17 — нечетное число.
Задачка 4. В инстаграме у Маши четное количество фотографий. Она добавила еще пять фотографий. Теперь фотографий 51. Сколько у Маши изначально было фотографий?
Как решаем:
51 — 5 = 46 (ф)
46 — четное число.
Ответ: изначально у Маши в инстаграме было 46 фотографий.
Задачка 5. Назовите числа, закрытые ☆. Распределите их по четности и нечетности. Сложите их и назовите получившееся значение.
| 1 | ☆ | 3 | ☆ | 5 |
| 6 | ☆ | ☆ | 9 | 10 |
| ☆ | 12 | 13 | ☆ | 15 |
| 16 | ☆ | ☆ | 19 | 20 |
| ☆ | 22 | 23 | ☆ | 25 |
Ответ:
2 — четное, 4 — четное, 7 — нечетное, 8 — четное, 11 — нечетное, 14 — четное, 17 — нечетное, 18 — четное, 21 — нечетное, 24 — четное.
Как решаем:
Складываем сначала четные: 2 + 4 + 8 + 14 + 18 + 24 = 70
Затем складываем нечетные: 7 + 11 + 17 + 21 = 56
70 + 56 = 126
Число 126 оканчивается на четную цифру 6. Значит, число 126 — четное.
Ответ: 126 — четное.
Четные числа как научить ребенка. Конспект нод по фэмп «клуб юных знатоков». Четные и нечетные числа
Наркас Кудабаева
Конспект занятия «Четные и нечетные числа»
Тема : Четные и нечетные числа
Цели : 1). Дать понятие четные и нечетные числа .
2). Совершенствовать вычислительные навыки и умения решать
текстовые задачи.
3). Развивать математическую смекалку и творческое мышление.
Оборудование : карточка, счетная палочка .
План урока
I. Организационный момент.
III. Минута чистописания.
IV. Устный счет.
V. Работа над новой темой.
VI. Физкультминутка.
Ход урока
I. Организационный момент.
Ребята, сегодня к нам пришел гость. Я сейчас вам прочитаю о нем, а вы должны угадать его.
…Он похож на плывущего лебедя. Голову склонив незнает, что делать от стыда. (Появляется) . Частый гость в тетрадях у грязнуль, нерях. О нем много сочиняют стихи, рассказы. Его никто не любит, а вот его друга «пятерку» все любят. (Цифра 2) . Показ карточки.
II.Сообщение темы и целей урока.
У цифры «два» есть свой секрет
Она гордится этим.
А мы раскроем твой секрет
И всем расскажем детям.
Сегодня нам нужно раскрыть секрет цифры «два» . Кто хорошо будет участвовать на уроке цифра «два» приготовила подарок.
III. Минута чистописания.
Откройте тетради. Напишите число .
Прописываем число . Какое число будем прописывать ? (Трехзначное число 232 ) .
IV. Устный счет.
1. Огорчился старый кот :
«Мне сегодня не везет :
Пара мышек скрылась в нору,
Три запрятались стремглав,
Под тяжелый старый шкаф.
Пара юркнула с испугу,
В короб, где хранился уголь,
Трое – в угол за панель,
А одна забилась щель».
Сколько всего мышей сумели спрятаться от кота?
2. Как в комнате расставить 7 стульев, чтобы у каждой стены стояло 2 стула?
Ответ :
V. Работа над новой темой.
1. Работа со счетными палочками .
Возьмите 9 счетных палочек и разложите их по парам.
Что значит по парам? (По две) .
Сколько пар получили? (4 и еще одна осталась) . Хорошо! Тогда возьмите 10 палочек и разложите по две.
Сколько пар получили? (5 пар) .
А сейчас работаем по рядам. Каждый ряд получает числа и соответственно раскладывает палочки парами : 1 ряд – 7,8; 2 ряд – числа 9 ,12; 3 ряд – числа 10 ,5.
Что у вас получилось? Вам удалось разложить по две? (Не совсем, в работе с числом 7 одна палочка осталась без пары. Также с 9 и 5).
То есть названные вами числа на 2 не делятся .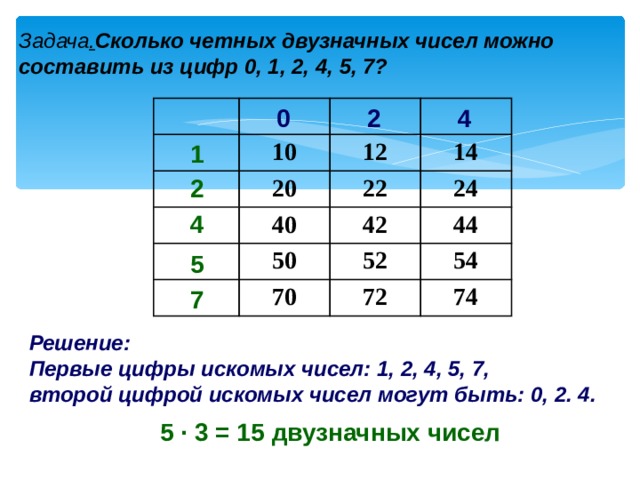 Запись чисел на доске :
Запись чисел на доске :
1 2 3 4 5 6 7 8 9 11 12
А как они расположены в числовом ряду ? (5 не делится, а 6 делится, 7 не делится, а 8 делится, 9 не делится, а 10 делится, 11 не делится)
Посмотрите числа чередуются . Давайте дополним числовой ряд справа (запись дополняется) . Мы с вами открыли секрет числа два . Оказывается, что взятые в кружочки числа называют четными .
Что их объединяет? (Эти числа делятся на «два» ). А остальные нечетные .
Вы смогли их разделить на «два» ? (Нет) .
Скажите, а с какого числа начинается натуральный ряд? (с 1) .
Какое это число ? (Нечетное ) . Числовой ряд будет продолжаться дальше.
Как вы определите в нем четные числа ? (Если число делится на 2 , то оно четное , а если не делится на два — нечетное ).
Молодцы!
2. А сейчас применим правило на практике.
Запишите в тетради по порядку числа от 10 до 19 , обведите в кружок четные числа . (Ученик работает у доски) .
Назовите нечетные числа (11, 13, 15, 17, 19) .
3. Найдите № 3, с. 34. (Выполняем вместе, на доске) .
Какие получили числа ? (Четные ) .
Какие получили числа ? (Четные ) .
Умножив нечетное число , получили четное число . Видите, каким секретом обладает числа 2 .
VI. Физкультминутка.
Игра на внимание. Показ рисунка.
Приседаем столько раз,
Сколько ягодок у нас.
Сколько видите кружков,
Столько делаем прыжков.
Наклонились столько раз,
Сколько бабочек у нас.
VII.Работа над пройденным материалом.
Найдите задачу № 4. Прочитайте. Решаем самостоятельно.
От мотка проволки отрезали 8м, и в нем осталось 7м. Сколько?
8 = 7 (м.)
15 – 8 = 7 Ответ : 15м было в мотке.
Решаем задачу № 5. Ответы только записываем в тетрадях.
Множитель 2 9 8 7 2 5
Множитель 9 2 2 2 6 2
Произведение 18 18 16 14 12 10
(18, 18, 8, 2, 2, 2)
В ответе какие числа получили ? (Четные ) .
а). Внимательно послушайте логическую задачу.
На дереве сидели 3 галки и 2 вороны. Две птицы улетели. Сколько и какие птицы могли остаться? (Все возможные ответы : 1) 3 галки; 2) 1 ворона и 2 галки; 3) 2 вороны и одна галка) .
б). Дополнительно.
Заполните пропуски математическими знаками и числами .
15*2+9=39 12+4*2=20
VIII. Итог урока. и домашнее задание.
Мы сегодня открыли секрет цифры «два» . Какой же секрет? (Числа , которые делятся на 2 называются четными , а числа которые на 2 не делятся — нечетными ).
Цифра «два» приготовила подарки для тех учеников, кто активно участвовал на уроке. Сами скажите мне, кто хорошо сидел и активно участвовал? (Ляйсан, Альберт, Малик) . Этим ребятам дарим вот такой рисунок.
Этим ребятам дарим вот такой рисунок.
Домашнее задание № 6. Вам нужно решить примеры.
Публикации по теме:
Конспект занятия «Путешествие в мир цифр. Цифра 10 и состав числа 10» Тема: «ПУТЕШЕСТВИЕ В МИР ЦИФР. ЗНАКОМСТВО С ЦИФРОЙ 10 И СОСТАВОМ ЧИСЛА 10». Возрастная группа: 5-6 лет. Форма совместной деятельности:.
Муниципальное бюджетное дошкольное образовательное учреждение «Детский сад общеразвивающего вида с приоритетным осуществлением деятельности.
Конспект интегрированного занятия по математике и конструированию «Состав числа 7» Конспект интегрированного занятия по математике и конструированию Тема: «Состав числа 7» Цель: Познакомить детей с образованием числа 7.
Конспект занятия «Цифра и состав числа 8» в старшей группе. Задачи: 1. Закрепить знание геометрических фигур. 2. Закрепить знание дней недели, их последовательности. 3. Развивать умение ориентироваться.
Конспект занятия по английскому языку «Числа»
Цели: Практическая: закрепление представлений о единственное число и множественное число существительных. Образовательная: введение нового.
Образовательная: введение нового.
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 1 класса
Электронное учебное пособие к учебнику Моро М.И.
Электронное учебное пособие к учебнику Петерсон Л.Г.
Определение четных и нечетных чисел от 1 до 10 с картинками.
1. Сколько собачек на картинке? Это число четное или не четное?
2. Сколько клоунов на картинке? Это число четное или не четное?
3. Сколько стульев на картинке? Это число четное или не четное?
4. Сколько ламп на картинке? Это число четное или не четное?
5. Сколько мужчин на картинке? Это число четное или не четное?
6. Сколько морковок на картинке? Это число четное или не четное?
7. Сколько девочек на картинке? Это число четное или не четное?
Четные и нечетные числа до 10
1. Обведите все нечетные числа.
Обведите все нечетные числа.
10, 8, 7, 9, 5, 6, 4, 1, 3
2. Обведи все четные числа.
9, 7, 3, 4, 8, 5, 2, 1, 10,
3. Выбери наибольшее четное число из числового ряда.
2, 3, 6, 5, 1
4. Выбери наименьшее четное число из числового ряда.
1, 7, 9, 6, 5
5. Выбери наибольшее нечетное число из числового ряда.
5, 4, 2, 6, 7
6. Выбери наименьшее нечетное число из числового ряда.
4, 10, 6, 6, 1
8, 4, 1, 8, 6
Сложи или вычти числа от 1 до 10. Определи, является ли результат четным или нечетным. Подчеркни правильный ответ.
2 + 2 = _____ четное/нечетное 4 + 5 = _____ четное/нечетное 3 + 5 = _____ четное/нечетное 4 + 2 = _____ четное/нечетное 3 + 1 = _____ четное/нечетное 8 + 2 = _____ четное/нечетное 7 + 3 = _____ четное/нечетное 8 + 2 = _____ четное/нечетное 3 + 3 = _____ четное/нечетное 8 + 1 = _____ четное/нечетное 7 + 2 = _____ четное/нечетное 1 + 3 = _____ четное/нечетное 6 + 4 = _____ четное/нечетное 4 + 2 = _____ четное/нечетное 4 + 4 = _____ четное/нечетное 3 + 6 = _____ четное/нечетное 1 + 4 = _____ четное/нечетное 2 + 1 = _____ четное/нечетное 9 + 1 = _____ четное/нечетное 2 + 1 = _____ четное/нечетное 3 — 3 = _____ четное/нечетное 8 — 1 = _____ четное/нечетное 7 — 2 = _____ четное/нечетное 1 — 3 = _____ четное/нечетное 6 — 3 = _____ четное/нечетное 4 — 2 = _____ четное/нечетное 4 — 4 = _____ четное/нечетное 3 + 6 = _____ четное/нечетное 1 + 4 = _____ четное/нечетное 2 — 1 = _____ четное/нечетное 9 — 1 = _____ четное/нечетное 2 — 1 = _____ четное/нечетное 4 — 4 = _____ четное/нечетное 3 + 6 = _____ четное/нечетное 1 + 4 = _____ четное/нечетное 2 — 1 = _____ четное/нечетное 9 — 1 = _____ четное/нечетное 2 — 1 = _____ четное/нечетное
Определение четных и нечетных чисел о 1 до 20 с картинками.

1. Количество головок чеснока четное или нечетное? _______
2. Количество очков четное или нечетное? _______
3. Количество зонтов четное или нечетное? _______
4. Количество туфель четное или нечетное? _______
5. Количество мальчиков четное или нечетное? _______
Четные и нечетные числа до 20
1. Обведи все нечетные числа.
7, 10, 11, 14, 1, 1, 2, 12, 11, 10
2. Обведи все четные числа.
12, 4, 8, 7, 14, 7, 20, 17, 15, 8
3. Обведи все нечетные числа.
15, 19, 14, 4, 15, 11, 1, 10, 15, 9
4. Обведи все четные числа.
15, 9, 1, 7, 5, 9, 14, 8, 3, 15
5. Подчеркни все нечетные числа.
9, 18, 20, 13, 12, 10, 6, 20, 10, 2
6. Подчеркни все четные числа.
7, 17, 3, 3, 15, 10, 8, 14, 17, 1
7. Выбери наибольшее четное число из заданной числовой последовательности.
5, 5, 15, 7, 15, 4, 17, 19, 17, 11
8. Выбери наименьшее четное число из заданной числовой последовательности.
11, 16, 8, 8, 19, 10, 15, 15, 15, 9
3, 9, 6, 7, 13, 11, 11, 13, 6, 3
10. Выбери наименьшее нечетное число из заданной числовой последовательности.
20, 20, 8, 12, 8, 1, 18, 2, 2, 17
11. Выбери наибольшее четное число из заданной числовой последовательности.
8, 7, 15, 15, 8, 2, 5, 19, 15, 5
12. Выбери наибольшее нечетное число из заданной числовой последовательности.
20, 11, 2, 13, 3, 1, 14, 5, 19, 2
13. Выбери наименьшее четное число из заданной числовой последовательности.
4, 11, 20, 9, 15, 14, 16, 9, 17, 13
14. Выбери наименьшее нечетное число из заданной числовой последовательности.
15, 20, 8, 18, 16, 17, 9, 5, 12, 8
Сложи или вычти числа от 1 до 20. Определи, является ли результат четным или нечетным. Подчеркни правильный ответ.
2 + 4 = _____ четное/нечетное 16 — 5 = _____ четное/нечетное 5 + 13 = _____ четное/нечетное 14 + 4 = _____ четное/нечетное 7 + 9 = _____ четное/нечетное 16 — 16 = _____ четное/нечетное 7 + 10 = _____ четное/нечетное 2 + 18 = _____ четное/нечетное 18 — 6 = _____ четное/нечетное 9 — 6 = _____ четное/нечетное 3 + 7 = _____ четное/нечетное 5 + 11 = _____ четное/нечетное 15 — 2 = _____ четное/нечетное 18 — 6 = _____ четное/нечетное 20 — 18 = _____ четное/нечетное 2 + 5 = _____ четное/нечетное 19 — 5 = _____ четное/нечетное 4 + 9 = _____ четное/нечетное 1 + 3 = _____ четное/нечетное 14 — 11 = _____ четное/нечетное 3 + 7 = _____ четное/нечетное 5 + 8 = _____ четное/нечетное 15 + 2 = _____ четное/нечетное 18 — 6 = _____ четное/нечетное 20 — 18 = _____ четное/нечетное 2 + 5 = _____ четное/нечетное 19 — 5 = _____ четное/нечетное 4 + 9 = _____ четное/нечетное 1 + 3 = _____ четное/нечетное 14 — 11 = _____ четное/нечетное
Четные и нечетные числа до 50
1. Обведи все нечетные числа.
Обведи все нечетные числа.
6, 36, 22, 25, 19, 24, 10, 39, 48, 37, 26, 50, 8, 35, 7, 3, 40, 47, 11, 9, 38, 28, 43, 41, 18, 23, 21, 1, 46, 30
2. Обведи все нечетные числа.
18, 31, 12, 28, 29, 35, 10, 4, 40, 39, 20, 6, 45, 30, 14, 36, 16, 48, 25, 24, 47, 37, 34, 11, 46, 32, 42, 2, 27, 41
3. Обведи все нечетные числа.
28, 35, 32, 47, 37, 43, 22, 14, 45, 24, 39, 29, 21, 42, 8, 41, 17, 36, 20, 9, 38, 46, 1, 23, 15, 27, 4, 12, 34, 26
4. Обведи все четные числа.
17, 36, 48, 12, 29, 49, 20, 9, 47, 27, 28, 6, 37, 4, 16, 25, 7, 34, 41, 18, 42, 32, 5, 23, 40, 2, 39, 45, 26, 14
5. Обведи все четные числа.
13, 47, 18, 50, 6, 5, 34, 48, 45, 33, 15, 3, 42, 26, 17, 22, 39, 25, 2, 30, 29, 4, 38, 8, 16, 35, 40, 31, 20, 23
30, 39, 46, 40, 2, 17, 50, 16, 19, 31, 50, 9, 20, 2, 12
7. Выбери наибольшее четное число из заданной числовой последовательности.
15, 37, 38, 45, 46, 26, 49, 25, 35, 22, 33, 42, 13, 8, 31
39, 28, 50, 14, 32, 11, 8, 40, 18, 34, 6, 45, 21, 37, 43
9. Выбери наибольшее нечетное число из заданной числовой последовательности.
Выбери наибольшее нечетное число из заданной числовой последовательности.
24, 41, 49, 35, 21, 37, 20, 10, 1, 36, 8, 25, 4, 12, 40
2, 21, 10, 45, 36, 48, 40, 14, 38, 13, 25, 28, 30, 42, 8
39, 6, 26, 11, 50, 17, 7, 30, 10, 24, 19, 33, 1, 25, 31
28, 42, 21, 36, 39, 10, 2, 37, 13, 20, 38, 11, 17, 18, 40
Сложи или вычти числа от 1 до 50. Определи, является ли результат четным или нечетным. Подчеркни правильный ответ.
21 + 18 = _____ четное/нечетное 42 + 3 = _____ четное/нечетное 10 + 40 = _____ четное/нечетное 12 + 14 = _____ четное/нечетное 7 + 29 = _____ четное/нечетное 15 — 3 = _____ четное/нечетное 5 + 12 = _____ четное/нечетное 47 — 1 = _____ четное/нечетное 46 — 46 = _____ четное/нечетное 47 — 26 = _____ четное/нечетное 38 — 41 = _____ четное/нечетное 23 + 25 = _____ четное/нечетное 24 + 13 = _____ четное/нечетное 7 + 40 = _____ четное/нечетное 19 + 2 = _____ четное/нечетное 26 + 8 = _____ четное/нечетное 8 + 36 = _____ четное/нечетное 19 + 28 = _____ четное/нечетное 40 + 9 = _____ четное/нечетное 25 + 15 = _____ четное/нечетное 22 + 14 = _____ четное/нечетное 19 + 24 = _____ четное/нечетное 46 — 48 = _____ четное/нечетное 13 + 23 = _____ четное/нечетное 21 + 21 = _____ четное/нечетное 36 + 2 = _____ четное/нечетное 20 — 19 = _____ четное/нечетное 14 + 13 = _____ четное/нечетное 35 — 23 = _____ четное/нечетное 39 — 34 = _____ четное/нечетное 43 + 4 = _____ четное/нечетное 6 + 10 = _____ четное/нечетное 20 + 26 = _____ четное/нечетное 2 + 43 = _____ четное/нечетное 17 + 23 = _____ четное/нечетное 37 + 5 = _____ четное/нечетное 16 + 15 = _____ четное/нечетное 22 + 15 = _____ четное/нечетное 33 + 6 = _____ четное/нечетное
Четные и нечетные числа до 100.

1. Обведи все нечетные числа.
25, 72, 53, 47, 14, 92, 91, 45, 73, 27, 31, 7, 19, 28, 26, 82, 66, 65, 32, 69, 90, 13, 40, 77, 88, 86, 12, 16, 38, 59
2. Обведи все нечетные числа.
8, 16, 42, 62, 36, 64, 45, 35, 51, 98, 99, 81, 83, 65, 77, 82, 43, 4, 10, 33, 68, 27, 13, 34, 48, 21, 49, 90, 11, 25
3. Обведи все нечетные числа.
83, 42, 13, 99, 27, 37, 73, 67, 38, 95, 66, 63, 6, 92, 12, 89, 5, 77, 74, 21, 39, 59, 78, 15, 35, 20, 54, 32, 75, 81
4. Обведи все четные числа.
49, 74, 2, 1, 100, 32, 54, 7, 51, 82, 33, 47, 96, 46, 78, 65, 36, 69, 75, 19, 31, 77, 35, 64, 97, 84, 37, 98, 85, 30
5. Обведи все четные числа.
22, 77, 90, 33, 10, 41, 23, 49, 53, 40, 84, 32, 13, 8, 60, 85, 89, 31, 30, 42, 96, 28, 62, 27, 45, 65, 66, 26, 55, 56
6. Выбери наибольшее четное число из заданной числовой последовательности.
9, 20, 55, 7, 100, 37, 52, 65, 19, 28, 47, 61, 32, 57, 93
7. Выбери наибольшее четное число из заданной числовой последовательности.
62, 90, 12, 34, 74, 37, 75, 91, 97, 53, 33, 60, 45, 16, 61
8. Выбери наибольшее нечетное число из заданной числовой последовательности.
81, 12, 49, 3, 52, 33, 34, 64, 41, 94, 93, 83, 80, 23, 24
9. Выбери наибольшее нечетное число из заданной числовой последовательности.
56, 4, 67, 34, 60, 88, 76, 85, 99, 33, 17, 79, 61, 7, 10
10. Выбери наименьшее четное число из заданной числовой последовательности.
94, 95, 25, 80, 71, 32, 99, 24, 8, 44, 69, 93, 38, 4, 68
11. Выбери наименьшее нечетное число из заданной числовой последовательности.
20, 12, 5, 68, 32, 54, 57, 13, 64, 82, 35, 38, 52, 92, 46
12. Выбери наименьшее четное число из заданной числовой последовательности.
2, 70, 82, 87, 27, 38, 55, 73, 84, 37, 60, 23, 63, 4, 86
Сложи или вычти числа от 1 до 100. Определи, является ли результат четным или нечетным. Подчеркни правильный ответ.
9 + 18 = _____ четное/нечетное 46 + 28 = _____ четное/нечетное 43 + 52 = _____ четное/нечетное 76 — 43 = _____ четное/нечетное 84 — 42 = _____ четное/нечетное 12 + 84 = _____ четное/нечетное 95 — 87 = _____ четное/нечетное 38 + 6 = _____ четное/нечетное 84 — 48 = _____ четное/нечетное 94 — 53 = _____ четное/нечетное 69 — 48 = _____ четное/нечетное 96 — 39 = _____ четное/нечетное 27 + 62 = _____ четное/нечетное 48 — 26 = _____ четное/нечетное 44 + 32 = _____ четное/нечетное 26 + 52 = _____ четное/нечетное 37 + 48 = _____ четное/нечетное 97 — 43 = _____ четное/нечетное 74 — 36 = _____ четное/нечетное 30 + 3 = _____ четное/нечетное 69 + 2 = _____ четное/нечетное 37 + 44 = _____ четное/нечетное 34 + 55 = _____ четное/нечетное 44 + 38 = _____ четное/нечетное 25 + 26 = _____ четное/нечетное 55 + 43 = _____ четное/нечетное 33 + 92 = _____ четное/нечетное 44 + 35 = _____ четное/нечетное 64 + 34 = _____ четное/нечетное 5 + 46 = _____ четное/нечетное 67 + 2 = _____ четное/нечетное 73 + 42 = _____ четное/нечетное 51 — 33 = _____ четное/нечетное 9 + 23 = _____ четное/нечетное 48 — 34 = _____ четное/нечетное 34 + 35 = _____ четное/нечетное 21 — 6 = _____ четное/нечетное 42 — 20 = _____ четное/нечетное 71 — 50 = _____ четное/нечетное 4 + 94 = _____ четное/нечетное 36 + 53 = _____ четное/нечетное 39 + 48 = _____ четное/нечетное 99 — 33 = _____ четное/нечетное 83 — 34 = _____ четное/нечетное 87 — 83 = _____ четное/нечетное 42 + 4 = _____ четное/нечетное 8 + 15 = _____ четное/нечетное 24 + 50 = _____ четное/нечетное 39 + 46 = _____ четное/нечетное 81 — 30 = _____ четное/нечетное
В этом материале дети узнают, что такое четные и нечетные числа от 1 до 20 и научатся различать их, выполняя различные задания в картинках. Дети дошкольного возраста еще не умеют делить числа, поэтому основное правило четных чисел (т.е. четное — это число, которое делится на 2) им будет очень сложно понять. Чтобы решить эту проблему, воспользуйтесь нашими рекомендациями и заданиями, которые предназначены для первого ознакомления с этим математическим понятием.
Дети дошкольного возраста еще не умеют делить числа, поэтому основное правило четных чисел (т.е. четное — это число, которое делится на 2) им будет очень сложно понять. Чтобы решить эту проблему, воспользуйтесь нашими рекомендациями и заданиями, которые предназначены для первого ознакомления с этим математическим понятием.
Четные и нечетные числа от 1 до 20 для дошкольников
Прежде чем выполнять задания, ребенок должен понять, что такое четные и нечетные числа от 1 до 20. Для этого можете распечатать и показать ему самое первое правило, которое он должен запомнить (можно прикрепить его к стене на время обучения). Объясните ребенку, что все числа, заканчивающиеся на 0, 2, 4, 6 и 8 — четные. Руководствуясь этим правилом, пусть ребенок ответит, на какие цифры должны заканчиваться нечетные числа (т.е. на 1, 3, 5, 7, 9).
Затем объясните ребенку, что все четные числа делятся на 2, а нечетные — не делятся на 2. Распечатайте второе правило:
Распечатайте Лист задания №1 и предложите ребенку обвести все четные числа, затем все нечетные числа.
Лист задание №1
Можете пояснить ребенку, что деление числа на 2 означает, что число делится пополам. Попросите его поделить пополам некоторые числа. Если ребенок затрудняется с ответами, то делить поровну нужно не числа, а предметы. Разложите перед ним несколько конфет, карандашей или других мелких предметов. Попросите его, например, поделить поровну 6 карандашей. Когда ребенок разделит карандаши, скажите ему, что он только что разделил число 6 на 2. Значит, 6 — это четное число. Попросите поделить поровну 5 карандашей. Когда ребенок поймет, что 5 невозможно поделить на одинаковое количество — скажите, что это и есть НЕчетное число, его невозможно разделить на 2.
Соедини числа по правилу — четное, нечетное
После того, как ребенок разобрался с понятием четных и нечетных чисел, предложите ему выполнить наши веселые задания в картинках. В первом задании обаятельного волка из всеми известного мультика «Ну погоди!» нужно привести к зайцу. Волк в этом задании настроен очень дружелюбно и совершенно не хочет конфликтовать с зайцем, поэтому идет к нему с цветами. Чтобы волк смог дойти, ему нужно проложить путь с помощью кружочков с числами. Но соединять эти числа между собой нужно определенным образом. Пусть ребенок возьмет цветной карандаш и, начиная с самой маленькой цифры, начнет проводить путь только через кружки с четными числами, и самое главное — по порядку счета! Второе задание выполняется аналогично — только теперь путь прокладывается через кружки с нечетными числами.
Чтобы волк смог дойти, ему нужно проложить путь с помощью кружочков с числами. Но соединять эти числа между собой нужно определенным образом. Пусть ребенок возьмет цветной карандаш и, начиная с самой маленькой цифры, начнет проводить путь только через кружки с четными числами, и самое главное — по порядку счета! Второе задание выполняется аналогично — только теперь путь прокладывается через кружки с нечетными числами.
Скачать задание «Соедини четные и нечетные числа» вы можете внизу страницы.
Посчитай и найди четные или нечетные числа
Еще одна проверка знаний четных и нечетных чисел для детей представлена в следующем упражнении. В первом задании ребенок должен сказать, какие продукты зайчики поделили поровну между собой. Чтобы узнать это, ребенку необходимо посчитать количество продуктов в каждой группе и сказать, четное оно или нечетное. Если четное — продукты поделятся поровну, если нечетное — то нет. Во втором задании нужно посчитать, сколько на картинке: солнечных лучиков, тучек, яблок, грибов, птичек, зверят, деревьев, цветов. А затем ответить, чего или кого получилось четное количество?
А затем ответить, чего или кого получилось четное количество?
Скачать задания по нахождению четных и нечетных чисел вы можете во вложениях внизу страницы.
Вам могут быть полезны и другие материалы по обучению счету для распечатки:
Здесь вы можете состав числа до 20 распечатать в виде числовой таблицы и дать ребенку для заполнения. Такое занятие прекрасно тренирует навыки счета дошкольников, а также приучает решать примеры до 20.
В этих занимательных задачках мы учимся считать до 20 вместе с героями мультиков и сказок. Дети дошкольного возраста совершенно не любят однообразие и скуку.
Здесь мы считаем до 20, используя карточки с числами. На каждом листе-карточке расположено число от 1 до 20 и различные предметы, количество которых равняется данному числу.
Здесь мы подготовили для вас устный счет в пределах 10 в виде математических заданий в картинках.
Чтобы дети могли быстро и с интересом освоить счет в пределах 10, мы подготовили для вас веселые раскраски с заданиями.
Здесь вы можете скачать прописи цифры, распечатать их на принтере и использовать в домашнем обучении для подготовки детей к школе
А также потренируйтесь в математических играх от лисенка Бибуши:
Поочередный счет. Когда малыш хорошо выучит названия чисел, поиграйте с ним в поочередный счет: вы говорите 1, он говорит 2, вы говорите 3, он говорит 4 и т.д. Вначале он захочет называть ваши числа; объясните ему, что это запрещено правилами игры. В следующий раз начинать должен он: он говорит 1, вы говорите 2 и т.д. Когда ребенок будет легко справляться с подобным заданием, привлеките к игре кого-нибудь еще (скажем, другого ребенка, ему это тоже понравится!) и поиграйте втроем, потом вчетвером, и т.д. Теперь, когда он быстро разберется, что к чему, продолжайте играть только в том случае, если он проявляет интерес.
Четные и нечетные числа. Чтобы объяснить ребенку это понятие, возьмите две тарелки и горсть фасолин:
Это твоя тарелка, а это — моя. Вот две фасолины. Можешь ли ты положить столько же фасолин в мою тарелку, сколько и в свою? Да, конечно! Ты можешь положить одну фасолину в свою тарелку и одну — в мою. Теперь вот тебе три фасолины, посмотри, можно ли сделать с ними то же самое?.. Нет! В одной тарелке оказывается две фасолины, а в другой — одна. Видишь, оказывается, число 2 можно разделить на две равные части (такое число называется четным), а число 3 нельзя разделить на две равные части (его называют нечетным). Посмотрим теперь, как ведет себя 4…
Вот две фасолины. Можешь ли ты положить столько же фасолин в мою тарелку, сколько и в свою? Да, конечно! Ты можешь положить одну фасолину в свою тарелку и одну — в мою. Теперь вот тебе три фасолины, посмотри, можно ли сделать с ними то же самое?.. Нет! В одной тарелке оказывается две фасолины, а в другой — одна. Видишь, оказывается, число 2 можно разделить на две равные части (такое число называется четным), а число 3 нельзя разделить на две равные части (его называют нечетным). Посмотрим теперь, как ведет себя 4…
Когда малыш поймет разницу между четным и нечетным числом, поиграйте с ним в поочередный счет, при этом один из вас будет называть нечетные числа, а второй — четные.
Цифры в их графической форме. Прежде чем показать ребенку абстрактные символы, обозначающие числа, нужно, чтобы он научился хорошо считать. В противном случае он уподобится большинству из нас (а это нежелательно!): счет будет означать для него лишь игру абстрактными символами. Представьте себе человека, для которого слова «банан», «стул», «ботинок» ассоциируются исключительно с их письменной формой, а не с конкретными предметами. Такой человек в действительности ничего не знал бы об окружающем его мире, и его знакомство с языком было бы поверхностным и бесполезным. Как он напоминает всех тех, кто в ужасе замирает при слове «математика». Такие люди знают символы, но не поняли по-настоящему, зачем они нужны и что символизируют!
Такой человек в действительности ничего не знал бы об окружающем его мире, и его знакомство с языком было бы поверхностным и бесполезным. Как он напоминает всех тех, кто в ужасе замирает при слове «математика». Такие люди знают символы, но не поняли по-настоящему, зачем они нужны и что символизируют!
Как и в случае с алфавитом, есть дети, которых очень увлекает процедура придания имени абстрактному символу. Они моментально выучивают цифры, достаточно их несколько раз им показать. Но есть и другие дети, которые, умея хорошо считать, не могут запомнить, какая цифра соответствует какому числу. Потому что это им неинтересно! Вот игра, которая должна им понравиться.
Сначала покажите малышу рисунок с тремя первыми цифрами. Когда он их выучит, вознаградите его, включив в игру четвертый персонаж. По-прежнему используйте только вопросительную форму. Только в этом случае число будет называть он, а не вы. Когда ребенок выучит цифры с маленькими рисунками, покажите ему те же. цифры, но без рисунков. Напомните малышу текст, если он его забудет. Таким способом даже самый упрямый ребенок быстро выучит цифры. НО ПЕРЕХОДИТЕ К ЦИФРАМ ТОЛЬКО ТОГДА, КОГДА ОН НАУЧИТСЯ НАЗЫВАТЬ ЧИСЛА И СЧИТАТЬ!
Напомните малышу текст, если он его забудет. Таким способом даже самый упрямый ребенок быстро выучит цифры. НО ПЕРЕХОДИТЕ К ЦИФРАМ ТОЛЬКО ТОГДА, КОГДА ОН НАУЧИТСЯ НАЗЫВАТЬ ЧИСЛА И СЧИТАТЬ!
С. Лупан. Поверь в свое дитя. «Дельта»,Спб. — 494 с
Цифры и числа. Их существует великое множество. Для маленького школьника это бесконечны крючки, загогулины и кружочки. Только-только начиная их осваивать, он узнает, что, оказывается, кроме просто чисел еще есть «четные» и «нечетные». Что это такое и как же все запомнить? Без помощи мамы и папы тут не обойтись. Наша статья даст вам полезные советы, как можно быстро в форме игры объяснить ребенку, что есть что.
Как легко и просто объяснить ребенку четные и нечетные числа
Итак, что следует предпринять заботливым родителям, желающим научить малыша отличать один вид чисел от других:
 Правила просты: скажите ребенку, что вы назовете самую первую цифру – 1. А его задачей является назвать следующую. Затем опять идет ваша очередь, потом его. И так, чередуясь, вы последовательно назовете числовой ряд. Затем поменяйтесь местами. Пусть ребенок начинает называть. Как показывает практика, во время игры процесс запоминания происходит быстрее и эффективнее.
Правила просты: скажите ребенку, что вы назовете самую первую цифру – 1. А его задачей является назвать следующую. Затем опять идет ваша очередь, потом его. И так, чередуясь, вы последовательно назовете числовой ряд. Затем поменяйтесь местами. Пусть ребенок начинает называть. Как показывает практика, во время игры процесс запоминания происходит быстрее и эффективнее. Обычно дети хорошо понимают то, что смогли увидеть собственными глазами.
Обычно дети хорошо понимают то, что смогли увидеть собственными глазами.Когда ребенок хорошо запомнит последовательность, название чисел и их графическое выражение, используйте эти знания везде, где находитесь. Например, можете называть вслух номера домов и спрашивать, четное это число или нечетное. В игре можно использовать ценники в магазинах, количество собак у тети Клавы, количество конфет, которые мама достала к чаю. Простор для фантазии в данном случае безграничен.
Объяснять школьнику понятия, которые для него являются новыми и неизвестными, задача не самая простая. Но важно проявить терпение и сделать процесс обучения интересным, чтобы не отбить у ребенка стремление к знаниям.
Какие знаки отличаются хорошей совместимостью в дружбе?
С днем ангела св николая
Натуральные числа /qualihelpy
Натуральными числами называют числа, с помощью которых определяется количество предметов того или иного множества. Ряд натуральных чисел бесконечен: , , , , , , , , , , , , … Множество всех натуральных чисел обозначают .
Ряд натуральных чисел бесконечен: , , , , , , , , , , , , … Множество всех натуральных чисел обозначают .
Любое натуральное число можно записать с помощью десяти цифр: , , , , , , , , , . Цифры , , , , называют четными, а цифры , , , , – нечетными.
Числа, запись которых оканчивается четной цифрой, называют четными числами.
Числа, запись которых оканчивается нечетной цифрой, называют нечетными числами.
Например, натуральные числа , , , , , , , , , , … – четные, а натуральные числа , , , , , , , , , , … – нечетные.
Четные числа записывают в виде , где – любое натуральное число. Нечетные числа записывают в виде , если – любое натуральное число, или в виде , если – любое натуральное число и число .
Над натуральными числами можно производить арифметические действия:
1) сложение: , где и – слагаемые, – сумма;
2) вычитание: , где – уменьшаемое, – вычитаемое, – разность;
3) умножение: , где и – множители, – произведение;
4) деление: , где – делимое, – делитель, – частное.
Чтобы найти неизвестное слагаемое, необходимо из суммы вычесть известное слагаемое.
Чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое.
Чтобы найти неизвестное вычитаемое, необходимо из уменьшаемого вычесть разность.
Чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель.
Чтобы найти неизвестное делимое, необходимо частное умножить на делитель.
Чтобы найти неизвестный делитель, необходимо делимое разделить на частное.
Законы сложения:
1) переместительный: от перестановки слагаемых значение суммы не изменится, т. е. ,
например, ;
2) сочетательный: чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего, т. е. ,
например, .
Законы умножения:
1) переместительный: от перестановки множителей значение произведения не изменится, т. е. ;
2) сочетательный: чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего, т. е. ;
3) распределительный закон умножения относительно сложения: чтобы умножить сумму на число, можно каждое слагаемое умножить на это число и полученные произведения сложить, т. е. ;
4) распределительный закон умножения относительно вычитания: чтобы умножить разность на число, можно уменьшаемое и вычитаемое умножить на это число и из первого произведения вычесть второе, т. е. .
Например:1) ;
2) ;
3) ;
4) .
Делимость натуральных чисел
Если натуральное число делится без остатка на натуральное число , то число называют кратным числа , а число – делителем числа . Например, . Говорят, что число кратно числу , а число является делителем числа .
Если число кратно числу , то записывают: .
Признаки делимости натуральных чисел на , , , , , , , и .
1. Число делится на , если его запись оканчивается четной цифрой. Например, числа , и делятся на .
2. Число делится на , если сумма цифр числа делится на . Например, делится на , так как сумма цифр этого числа и число делится на .
3. Число делится на , если его запись оканчивается цифрой или цифрой Например, числа и делятся на .
4. Число делится на , если сумма цифр числа делится на . Например, число делится на , так как сумма цифр этого числа и число делится на .
5. Число делится на , если его запись оканчивается цифрой . Например, число делится на .
6. Число делится на , если две последние цифры его записи образуют число, которое делится на . Например, число делится на , так как число делится на .
7. Число делится на , если три последние цифры его записи образуют число, которое делится на . Например, число делится на , так как число делится на .
8. Число делится на , если разность сумм цифр, стоящих на четных и нечетных местах, делится на . Например, число делится на , так как и число делится на .
9. Число делится на , если две последние цифры его записи образуют число, которое делится на . Например, числа , , и делятся на .
Например, числа , , и делятся на .
Деление с остатком
Разделить натуральное число на натуральное число с остатком – значит представить число в виде , где – неполное частное, а – остаток от деления на и меньше .
Если же остаток равен нулю, то говорят, что число делится нацело на число .
Например, при делении натуральных чисел на , будем получать один из остатков: или , или , или , или .
Простые и составные числа
Числа, которые имеют только два различных делителя (делятся только сами на себя и на число 1), называют простыми.
Например, простыми являются числа , , , , , , , , , …. .
Числа, которые имеют более двух различных делителей, называют составными. Составные числа можно представить в виде произведения двух и более простых множителей.
Например, число составное, так как .
Натуральные числа называются взаимно простыми, если они не имеют общих делителей, за исключением числа .
Например, числа и взаимно простые;
Наибольший общий делитель и наименьшее общее кратное
Общим делителем нескольких чисел называют число, которое является делителем каждого из этих чисел. Среди всех общих делителей всегда имеется наибольший. Это число называется наибольшим общим делителем (НОД).
Например, числа , , и являются общими делителями чисел и , а число – их наибольший общий делитель;
Общим кратным нескольких чисел называют число, которое является кратным каждого из этих чисел. Среди всех общих кратных всегда есть наименьшее. Это число называется наименьшим общим кратным (НOК).
Например, числа и кратны числам , , , и , а число – наименьшее общее кратное чисел и .
Чтобы найти НОД нескольких чисел, необходимо разложить их на простые множители и найти произведение только тех множителей, которые имеются в разложениях всех чисел.
Чтобы найти НOК нескольких чисел, необходимо разложить их на простые множители, найти произведение всех множителей, входящих в разложение одного из чисел и недостающих множителей из разложений оставшихся чисел.
Пример 1. Найдите наибольший общий делитель и наименьшее общее кратное чисел , и .
Решение. Разложим эти числа на простые множители:
Найдем наибольший общий делитель чисел , и :
НОД .
Найдем наименьшее общее кратное чисел , и :
НОК .
Ответ: и .
Пример 2. При делении пятизначного числа на в остатке получается . Найдите это число, если известно, что оно делится на .
Найдите это число, если известно, что оно делится на .
Решение. Согласно условию задачи число делится на , следовательно, оно делится и на и на .
Если искомое число делится на , то число делится на . Тогда может принимать одно из значений: или , или , или . Поскольку при делении числа на в остатке получается , то .
Если же число делится на , то сумма цифр этого числа делится на , то есть . Тогда при условии, что число будет делиться на .
Запишем искомое число: .
Ответ: .
1. Число не является ни простым и ни составным.
2. В результате сложения и умножения натуральных чисел всегда будем получать натуральное число.
3. В результате вычитания натуральных чисел получим натуральное число только в том случае, если уменьшаемое больше вычитаемого.
4. Деление одного натурального числа на другое не всегда выполнимо. В этом случае имеет место деление с остатком.
5. Множество делителей числа конечно, а множество чисел, кратных числу, бесконечно. Например, число имеет делителя: ; ; ; ; ; . Числу кратны числа: , , и т. д.
6. Числа, кратные числу , записывают в виде , где – любое натуральное число. Например, все числа, кратные числу , можно записать так: где – натуральное число.
7. Рассмотрим буквенную запись чисел в десятичной позиционной системе счисления. Так, например, если – цифра десятков, – цифра единиц некоторого двузначного числа, то запишем: . Аналогично запишем трехзначное число, у которого – цифра сотен, – цифра десятков, – цифра единиц: .
24 — двадцать четыре. натуральное четное число. факториал 4!, регулярное число (число хемминга). в ряду натуральных чисел находится между числами 23 и 25.
 Все о числе двадцать четыре. 24 — двадцать четыре. натуральное четное число. факториал 4!, регулярное число (число хемминга). в ряду натуральных чисел находится между числами 23 и 25. Все о числе двадцать четыре.
Все о числе двадцать четыре. 24 — двадцать четыре. натуральное четное число. факториал 4!, регулярное число (число хемминга). в ряду натуральных чисел находится между числами 23 и 25. Все о числе двадцать четыре.- Главная
- О числе 24
24 — двадцать четыре. Натуральное четное число. Факториал 4!, Регулярное число (Число Хемминга). В ряду натуральных чисел находится между числами 23 и 25.
Like если 24 твое любимое число!
Распространенные значения и факты
24 регион — Красноярский край
- Столица
- Красноярск
- Автомобильный код
- 24, 84, 88, 124
- Федеральный округ
- Сибирский
- Экономический район
- Восточно-Сибирский
- Дата образования
- 7 декабря 1934 г.
- Территория
- 710 тыс. кв. км 4,16 % от РФ 8 место в РФ
- Население
- Общая численность 2 908,7 тыс. чел. 2 % от РФ 12 место в РФ
Изображения числа 24
Склонение числа «24» по падежам
| Падеж | Вспомогательное слово | Характеризующий вопрос | Склонение числа 24 |
|---|---|---|---|
| Именительный | Есть | Кто? Что? | двадцать четыре |
| Родительный | Нет | Кого? Чего? | двадцати четырёх |
| Дательный | Дать | Кому? Чему? | двадцати четырём |
| Винительный | Видеть | Кого? Что? | двадцать четыре |
| Творительный | Доволен | Кем? Чем? | двадцатью четырьмя |
| Предложный | Думать | О ком? О чём? | двадцати четырёх |
Перевод «двадцать четыре» на другие языки
- Азербайджанский
- iyirmi dörd
- Албанский
- njëzet e katër
- Английский
- twenty-four
- Арабский
- أربع وعشرين
- Армянский
- քսանչորս
- Белорусский
- дваццаць чатыры
- Болгарский
- двадесет и четири
- Вьетнамский
- hai mươi bốn
- Голландский
- vierentwintig
- Греческий
- είκοσι τέσσερις
- Грузинский
- ოცი ოთხი
- Иврит
- עשרים וארבעה
- Идиш
- פיר און צוואנציק
- Ирландский
- ceithre cinn is fiche
- Исландский
- tuttugu og fjórir
- Испанский
- veinticuatro
- Итальянский
- ventiquattro
- Китайский
- 24
- Корейский
- 스물 네
- Латынь
- XXIIII
- Латышский
- divdesmit četri
- Литовский
- dvidešimt keturi
- Монгольский
- хорин дөрвөн
- Немецкий
- vierundzwanzig
- Норвежский
- tjuefire
- Персидский
- بیست و چهار
- Польский
- dwadzieścia cztery
- Португальский
- vinte e quatro
- Румынский
- douăzeci și patru
- Сербский
- двадесет четири
- Словацкий
- dvadsať štyri
- Словенский
- štiriindvajset
- Тайский
- ยี่สิบสี่
- Турецкий
- Yirmi dört
- Украинский
- двадцять чотири
- Финский
- kaksikymmentäneljä
- Французский
- vingt-quatre
- Хорватский
- dvadeset četiri
- Чешский
- dvacet čtyři
- Шведский
- tjugofyra
- Эсперанто
- dudek kvar
- Эстонский
- kakskümmend neli
- Японский
- 24
Перевод «24» на другие языки и системы
Римскими цифрами
- Римскими цифрами
- XXIV
Сервис перевода арабских чисел в римские
Арабско-индийскими цифрами
- Арабскими цифрами
- ٢٤
- Восточно-арабскими цифрами
- ۲۴
- Деванагари
- २४
- Бенгальскими цифрами
- ২৪
- Гурмукхи
- ੨੪
- Гуджарати
- ૨૪
- Ория
- ୨୪
- Тамильскими цифрами
- ௨௪
- Телугу
- ౨౪
- Каннада
- ೨೪
- Малаялам
- ൨൪
- Тайскими цифрами
- ๒๔
- Лаосскими цифрами
- ໒໔
- Тибетскими цифрами
- ༢༤
- Бирманскими цифрами
- ၂၄
- Кхемерскими цифрами
- ២៤
- Монгольскими цифрами
- ᠒᠔
В других системах счисления
- 24 в двоичной системе
- 11000
- 24 в троичной системе
- 220
- 24 в восьмеричной системе
- 30
- 24 в десятичной системе
- 24
- 24 в двенадцатеричной системе
- 20
- 24 в тринадцатеричной системе
- 1B
- 24 в шестнадцатеричной системе
- 18
Известные люди умершие в 24 года
- Шолин, Игорь Николаевич Украинский футболист, полузащитник; остановка сердца
16 декабря Дисней, Рой Эдвард (79) племянник Уолта Диснея, бывший вице-председатель совета директоров и председатель департамента анимации The Walt Disney Company; рак желудка
17 декабря аль-Хафез, Амин (88) бывший председатель Национального Совета Революционного Командования, председатель Президентского Совета Сирии (19631966)
17 декабря Дженнифер Джонс (90) американская актриса, лауреат премии «Оскар», а также первая актриса, награждённая премией «Золотой глобус»
17 декабря О`Бэннон, Дэн (63) американский режиссёр и сценарист
17 декабря Юрий Овсянников (72) Приднестровский государственный деятель, министр внутренних дел ПМР, министр юстиции ПМР.
 Смерть наступила в 2009 году в 24 года.
Смерть наступила в 2009 году в 24 года. - Френч, Кэти Ирландская модель, писательница и филантроп; повреждение головного мозга. Смерть наступила в 2007 году в 24 года.
- Сиосэй Кода Японский турист; обезглавливание. Смерть наступила в 2004 году в 24 года.
- Миклош Фехер Венгерский футболист; гипертрофическая кардиомиопатия. Смерть наступила в 2004 году в 24 года.
- Ляшенко, Роман Юрьевич Профессиональный российский хоккеист, центральный нападающий. Смерть наступила в 2003 году в 24 года.
- Космачева, Юлия Александровна Советская и белорусская актриса театра и кино. Смерть наступила в 2000 году в 24 года.
- Боченков, Михаил Владиславович Герой Российской Федерации. Смерть наступила в 2000 году в 24 года.
- Мур, Грег Канадский автогонщик; автокатастрофа. Смерть наступила в 1999 году в 24 года.

- Big L Рэп-исполнитель. Смерть наступила в 1999 году в 24 года.
- Симмонс, Кадамба Английская киноактриса; убийство. Смерть наступила в 1998 году в 24 года.
- Notorious B.I.G. Известный американский рэпер; убийство. Смерть наступила в 1997 году в 24 года.
- Алиев, Амираслан Рза оглы Азербайджанский офицер, национальный герой Азербайджана. Смерть наступила в 1995 году в 24 года.
- Наджафов, Фахраддин Вилаяддин оглы Азербайджанский офицер, Национальный герой Азербайджана. Смерть наступила в 1992 году в 24 года.
- Дягилева, Яна Станиславовна Советская рок-певица, поэтесса, автор песен, участница групп «Гражданская оборона», «Великие Октябри» и др. Смерть наступила в 1991 году в 24 года.
- Гоборов, Валерий Григорьевич Советский баскетболист. Смерть наступила в 1989 году в 24 года.

- Бёртон, Клиффорд Ли Американский музыкант, бас-гитарист группы Metallica. Смерть наступила в 1986 году в 24 года.
- Жиров, Александр Васильевич Советский горнолыжник, мастер спорта СССР международного класса. Смерть наступила в 1983 году в 24 года.
- Жданько, Станислав Алексеевич Советский актёр 13 апреля Иван Костыря (46) украинский и советский писатель. Смерть наступила в 1978 году в 24 года.
- Освальд, Ли Харви Единственный официальный подозреваемый в убийстве американского президента Кеннеди; убит. Смерть наступила в 1963 году в 24 года.
- Довекар, Альбер Сержант Французского Иностранного Легиона, член ОАС, участник покушения на комиссара Алжира Роже Гавури. Смерть наступила в 1962 году в 24 года.
Все люди умершие в 24 года (99)
QR-код, MD5, SHA-1 числа 24
Адрес для вставки QR-кода числа 24, размер 500×500:
http://pro-chislo.ru/data/moduleImages/QRCodes/24/f116f0a91cf1145fcab17c4a254a71ef.png
- MD2 от 24
- 6b29cdfe49153f5a51def96d46e34bee
- MD4 от 24
- 69d283f316e994b0ae1dac25be100255
- MD5 от 24
- 1ff1de774005f8da13f42943881c655f
- SHA1 от 24
- 4d134bc072212ace2df385dae143139da74ec0ef
- SHA256 от 24
- c2356069e9d1e79ca924378153cfbbfb4d4416b1f99d41a2940bfdb66c5319db
- SHA384 от 24
- ac379cd723f549e2410050ae58541ca19f0cafbff2e83b2cbf07b5a4e20d1aa3f8060bf3c6d62980380323ba46a0a8fe
- SHA512 от 24
- c0033b5f5a4815a172984d64037dd49a8663fb8b3a71e47f11ecd332c8c3819c57e1631fdf46d66c6ff0e58763a61529fefcfa2a6675e186ee901e5452fedd94
- GOST от 24
- d66c7b83f5c75645297568fd536953232112a62fdffc5c47607ad187a9fdfab4
- Base64 от 24
- MjQ=
Математические свойства числа 24
- Простые множители
- 2 * 2 * 2 * 3
- Делители
- 1, 2, 3, 4, 6, 8, 12, 24
- Количество делителей
- 8
- Сумма делителей
- 60
- Простое число
- Нет
- Предыдущее простое
- 23
- Следующее простое
- 29
- 24е простое число
- 89
- Число Фибоначчи
- Нет
- Число Белла
- Нет
- Число Каталана
- Нет
- Факториал
- Да 4!
- Регулярное число (Число Хемминга)
- Да
- Совершенное число
- Нет
- Полигональное число
- девятиугольник(3)
- Квадрат
- 576
- Квадратный корень
- 4.
 8989794855664
8989794855664 - Натуральный логарифм (ln)
- 3.1780538303479
- Десятичный логарифм (lg)
- 1.3802112417116
- Синус (sin)
- -0.90557836200662
- Косинус (cos)
- 0.424179007337
- Тангенс (tg)
- 2.1348966977217
Фильмы про 24
24 кадра ужаса (24 cuadros de terror), 2008 год
Серийный убийца, называющий себя «Леди Киллер», заманивает жертв под предлогом съемки фильма. В процессе «работы» он их убивает, что и…
24 меры (24 mesures), 2007 год
Хелли, Дидье, Мэри и Крис — четверо молодых людей… Бессонная ночь двадцать четвертого декабря навсегда полностью изменит их судьбы. Хелли,…
24 часа (Trapped), 2002 год
Преступление, оставшееся для всех неизвестным, можно назвать идеальным. Супруги Черил и Джо Хики вместе с кузеном Джоем Марвином – трое…
Все фильмы о числе 24 (5)
Комментарии о числе 24
← 23
25 →
- Распространенные значения и факты
- Изображения числа 24
- Склонение числа «24» по падежам
- Перевод «двадцать четыре» на другие языки
- Перевод «24» на другие языки и системы
- Известные люди умершие в 24 года
- QR-код, MD5, SHA-1 числа 24
- Математические свойства числа 24
- Фильмы про 24
- Комментарии о числе 24
Математика — Центр дополнительного образования
Четность
Все знают, что числа бывают четные и нечетные. Четные числа — это те, которые делятся на 2 без остатка (например, 2, 4, 6 и т. п.). Каждое такое число можно записать в виде 2k, подобрав подходящее целое k (например, 4 = 2 × 2, 6 = 2 × 3, и т. д.). Нечетные числа — это те, которые при делении на 2 дают в остатке 1 (например, 1, 3, 5 и т. п.). Каждое такое число можно записать в виде 2k + 1, подобрав целое подходящее k (например, 3 = 2 × 1 + 1, 5 = 2 × 2 + 1, и т. д.).
Четные и нечетные числа обладают замечательными свойствами:
а) сумма двух четных чисел четна;
б) сумма двух нечетных чисел четна;
в) сумма четного и нечетного чисел — нечетное число.
Задачи
1.1. Докажите приведенные выше свойства а) — в).
1.2. Какой (четной или нечетной) будет сумма нескольких
а) четных чисел;
б) нечетных чисел?
1.3. Докажите, что
а) произведение двух четных чисел четно;
б) произведение двух нечетных нечетно;
в) произведение четного и нечетного чисел — четное число.
1.4. Каким (четным или нечетным) будет произведение нескольких
а) четных чисел;
б) нечетных чисел?
1.5. Придумайте четыре целых числа, сумма и произведение которых являются нечетными числами.
1.6. Гости на дне рождения великого русского художника Валентина Серова сидели за круглым столом и ели персики. Когда персики закончились, гости посчитали персиковые косточки, и оказалось, что у каждой пары сидящих рядом гостей количество косточек отличалось на 1. Могло ли за столом сидеть а) 3; б) 4; в) 98; г) 99 гостей? |
1.7. В карманных часах Наполеона было 7 шестеренок, соединенных по цепочке (см. рис.). Кутузов, посмотрев на это, сказал, что они не могут вращаться одновременно. Прав ли великий русский полководец? |
1. |
1.9. В дружине Дядьки Черномора 100 богатырей, и каждый вечер трое из них идут за пивом. Может ли через некоторое время оказаться так, что каждый с каждым ходил за пивом ровно один раз?
1.10. 25 гусар и 25 воспитанниц пансиона благородных девиц сидят за круглым столом. Докажите, что у кого-то из сидящих за столом оба соседа — гусары. |
1.11. Улитка ползет по плоскости с постоянной скоростью, каждые 15 минут поворачивая под прямым углом. Докажите, что вернуться в исходную точку она сможет лишь через целое число часов.
1. |
1.13. В ряд выписаны числа от 1 до 10. Можно ли расставить между ними знаки «+» и «-» так, чтобы значение полученного выражения было равно нулю?
1.14. Дан осесимметричный выпуклый 101-угольник. Докажите, что ось симметрий проходит через одну из его вершин. Что можно сказать в случае 10-угольника?
1.15. В парламенте страны Зям-Лям две палаты, имеющие равное число депулямов. В голосовании по важному вопросу приняли участие все депулямы, причем воздержавшихся не было. Когда председатель сообщил, что решение принято с преимуществом в 23 голоса, лидер оппозиции заявил, что результаты голосования сфальсифицированы. Как он это понял? |
1. 16. На доске написаны числа 0, 1, 0, 0. За один шаг разрешается прибавить 1 к любым двум из них. Можно ли, повторяя эту операцию, добиться, чтобы все числа стали равными?
16. На доске написаны числа 0, 1, 0, 0. За один шаг разрешается прибавить 1 к любым двум из них. Можно ли, повторяя эту операцию, добиться, чтобы все числа стали равными?
Графы
Мы определим граф как набор точек (вершин), некоторые из которых соединены между собой линиями (ребрами). Количество ребер, выходящих из данной вершины, мы будем называть ее степенью. Вершина графа, имеющая нечетную степень, называется нечетной, а имеющая четную степень — четной.
Теорема. Число нечетных вершин любого графа — четно.
Задачи
2.1. Между 9 планетами Солнечной системы введено космическое сообщение. Ракеты летают по следующим маршрутам: Земля — Меркурий, Плутон — Венера, Земля — Плутон, Плутон — Меркурий, Меркурий — Венера, Уран — Нептун, Нептун — Сатурн, Сатурн — Юпитер, Юпитер — Марс и Марс — Уран. Можно ли добраться с Земли до Марса?
2. |
2.3. Доска имеет форму креста, который получается, если из квадратной доски 4 × 4 выкинуть угловые клетки. Можно ли обойти ее ходом шахматного коня и вернуться на исходное поле, побывав на всех полях ровно по одному разу?
2.4. В городе Маленьком 15 телефонов. Можно ли их соединить проводами так, чтобы каждый телефон был соединен ровно с пятью другими?
2.5. В классе 30 человек. Может ли быть так, что 9 из них имеют по 3 друга (в этом классе), 11 — по 4 друга, а 10 — по 5 друзей?
2.6. В городе Маленьком все еще 15 телефонов. Можно ли их соединить проводами так, чтобы было 4 телефона, каждый из которых соединен с тремя другими, 8 телефонов, каждый из которых соединен с шестью, и 3 телефона, каждый из которых соединен с пятью другими? |
2. 7. У короля 19 баронов-вассалов. Может ли оказаться так, что у каждого вассального баронства 1, 5 или 9 соседних баронств?
7. У короля 19 баронов-вассалов. Может ли оказаться так, что у каждого вассального баронства 1, 5 или 9 соседних баронств?
2.8. Может ли в государстве, в котором из каждого города выходит 3 дороги, быть ровно 100 дорог?
2.9. Джон, приехав из Диснейленда, рассказывал, что там на заколдованном озере имеются 7 островов, с каждого из которых ведет 1, 3 или 5 мостов. Верно ли, что хотя бы один из этих мостов выходит на берег озера?
2.10. Докажите, что число людей, когда-либо живших на Земле и сделавших нечетное число рукопожатий, четно. |
2.11. Можно ли на плоскости нарисовать 9 отрезков так, чтобы каждый пересекался ровно с тремя другими?
Четные числа определение: Что такое четное число? Ответ на webmath.ru — ЭкоДом: Дом своими руками
Содержание
Четные и Нечетные числа в Математике
Четные и нечетные числа: что, как, зачем, почему
Стремление человека делить и половинить сопровождает его всю жизнь. Нас хлебом не корми, дай поделить на два.
Нас хлебом не корми, дай поделить на два.
Прежде чем разобраться, зачем и почему мы это делаем, давайте познакомимся с определениями.
Четное число — это целое число, которое делится на 2.
Целые числа — это натуральные числа, нуль, а также числа, противоположные натуральным.
4 : 2 = 2
Это значит, что 4 — четное число.
Нечетное число — это целое число, которое не делится на 2.
5 : 2 = 2,5
Это значит, что 5 — нечетное число, так как в результате деления не получается целое число.
Если число оканчивается на 0, 2, 4, 6, 8, то это число четное. Если число оканчивается на 1, 3, 5, 7, 9, то это число нечетное. Если двузначное число круглое, то это число четное. Например, 20, 30, 40, 50 и т. д. — четные числа. |
Свойства четных и нечетных чисел
- если сложить два четных числа, получится четное число
8 + 8 = 16
16 : 2 = 8 - если сложить два нечетных числа, получится четное число
3 + 3 = 6
6 : 2 = 3 - если сложить четное число с нечетным, получится нечетное число
4 + 5 = 9
9 : 2 = 4,5 - если четное число умножить на четное число, получится четное число
2 * 2 = 4
4 : 2 = 2 - если четное число умножить на нечетное число, получится четное число
4 * 3 = 12
12 : 6 = 2 - если нечетное число умножить на нечетное, получится нечетное.

3 * 3 = 9
Четные и нечетные числа чередуются друг с другом
1 — нечетное
2 — четное
3 — нечетное
4 — четное
5 — нечетное
6 — четное
7 — нечетное
8 — четное
9 — нечетное
Внимательно рассмотрите таблицу четных и нечетных чисел. На ней хорошо видно, как они чередуются между собой.
| 1 | 11 | 21 | 31 | 41 | 51 | 61 | 71 | 81 | 91 |
| 2 | 12 | 22 | 32 | 42 | 52 | 62 | 72 | 82 | 92 |
| 3 | 13 | 23 | 33 | 43 | 53 | 63 | 73 | 83 | 93 |
| 4 | 14 | 24 | 34 | 44 | 54 | 64 | 74 | 84 | 94 |
| 5 | 15 | 25 | 35 | 45 | 55 | 65 | 75 | 85 | 95 |
| 6 | 16 | 26 | 36 | 46 | 56 | 66 | 76 | 86 | 96 |
| 7 | 17 | 27 | 37 | 47 | 57 | 67 | 77 | 87 | 97 |
| 8 | 18 | 28 | 38 | 48 | 58 | 68 | 78 | 88 | 98 |
| 9 | 19 | 29 | 39 | 49 | 59 | 69 | 79 | 89 | 99 |
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Чтобы быстро разобраться в теме, послушайте песню-считалочку про четность и нечетность.
Умение быстро определять четность и нечетность поможет в решении примеров, особенно, когда нужно посчитать в уме. Вот шпаргалка — держите ее под рукой, чтобы быстро ориентироваться в цифрах.
|
Давайте проверим, как хорошо вы научились определять четные и нечетность. Выполним несколько несложных заданий.
Задачка 1. Назовите числа, которые спрятаны за ♥. Назовите их по порядку. Какие из них — четные, а какие — нечетные?
Какие из них — четные, а какие — нечетные?
| 1 | ♥ | 17 |
| 2 | 10 | ♥ |
| ♥ | 11 | 19 |
| 4 | ♥ | 20 |
| 5 | 13 | ♥ |
| ♥ | 14 | 22 |
| 7 | 15 | 23 |
| 8 | ♥ | ♥ |
Ответ: 3 — нечетное, 6 — четное, 9 — нечетное, 12 — четное, 16 — четное, 18 — четное, 21 — нечетное, 24 — четное.
Задачка 2. Вставьте в таблицу пропущенные числа.
| X | 2 | 4 | 6 | 8 | 10 |
| X * 2 | |||||
| X : 2 |
| X | 2 | 4 | 6 | 8 | 10 |
| X * 2 | 4 | 8 | 12 | 16 | 20 |
| X : 2 | 1 | 2 | 3 | 4 | 5 |
Как решаем:
2 * 2 = 4 — четное
2 : 2 = 1 — нечетное
4 * 2 = 8 — четное
4 : 2 = 2 — четное
6 * 2 = 12 — четное
6 : 2 = 3 — нечетное
8 * 2 = 16 — четное
8 : 2 = 4 — нечетное
10 * 2 = 20 — четное
10 : 2 = 5 — нечетное
Задачка 3. В коробке 44 конфеты: 15 шоколадных и 12 — с карамелью. А все остальные с воздушным рисом. Сколько в коробке конфет с воздушным рисом? Получившееся значение — четное или нечетное?
В коробке 44 конфеты: 15 шоколадных и 12 — с карамелью. А все остальные с воздушным рисом. Сколько в коробке конфет с воздушным рисом? Получившееся значение — четное или нечетное?
Как решаем:
всего 44 конфеты — 15 — 12 = 17 (конфет).
17 — нечетное.
Ответ: в коробке 17 конфет с воздушным рисом.
Задачка 4. В инстаграме у Маши четное количество фотографий. Она добавила еще пять фотографий. Теперь фотографий 51. Сколько у маши изначально было фотографий?
Как решаем:
Всего 51 фотография — 5 = 46.
46 — четное.
Ответ: изначально у Маши в инстаграме было 46 фотографий.
Задачка 5. Назовите числа, закрытые ☆. Распределите их по четности и нечетности. Сложите их и назовите получившееся значение.
| 1 | ☆ | 3 | ☆ | 5 |
| 6 | ☆ | ☆ | 9 | 10 |
| 11 | 12 | 13 | ☆ | 15 |
| 16 | ☆ | ☆ | 19 | 20 |
| ☆ | 22 | 23 | ☆ | 25 |
Ответ:
2 — четное, 4 — четное, 7 — нечетное, 8 — четное, 11 — нечетное, 14 — четное, 17 — нечетное, 18 — четное, 21 — нечетное, 24 — четное.
Как решаем:
Складываем сначала четные: 2 + 4 + 8 + 14 + 18 + 24 = 70
Затем складываем нечетные: 7 + 11 + 17 + 21 = 56
70 + 56 = 126
126 : 2 = 63
Ответ: 126 — четное.
Тебе стоит повторить тему — знаки больше, меньше или равно!
Научиться быстро считать ребенку помогут в детской онлайн-школе Skysmart. Наши преподаватели просто и весело объяснят любую тему по математике, а красочный интерактивный учебник и онлайн-доска не дадут ребенку заскучать.
Записывайтесь на бесплатный вводный урок математики и развивайте математическое мышление вместе со Skysmart.
Урок 6. чётные и нечётные числа. таблица умножения и деления с числом 2 — Математика — 3 класс
Математика, 3 класс
Урок №6. Чётные и нечётные числа. Таблица умножения и деления с числом 2
Перечень вопросов, рассматриваемых в теме:
- По какому правилу составлена таблица умножения с числом 2.
- Какие числа называются чётными, какие – нечётными.

Глоссарий по теме:
В основе таблицы умножения с числом 2 лежит то, что произведение увеличивается на 2.
Чётные числа – числа, которые делятся на 2.
Нечётные числа – числа, которые не делятся на 2.
Обязательная и дополнительная литература к уроку:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 20.
2. Моро М. И., Волкова С. И. Математика. Рабочая тетрадь 3 класс. Часть 1. М.; Просвещение, 2016. – с. 9-11.
Теоретический материал для самостоятельного изучения.
Вспомним, что такое умножение?
Про это математическое действие есть стихотворение.
Это умное сложение.
Ведь умней – умножить раз.
Чем слагать всё целый час.
Умножения таблица
Всем нам в жизни пригодится
И недаром названа
УМНО жением она!
Умножение – сложение одинаковых чисел.
Попробуем:
— прибавлять по 2 пока не получится 20.
2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 = 20
— убавлять по 2 от 18, пока не получится 2
18 — 2 — 2 — 2 — 2 — 2 — 2 — 2 — 2 = 2
— за 1 минуту решить примеры: 2 ∙ 7; 6 ∙ 9; 8 ∙ 8
За такое короткое время трудно решить эти примеры. Как быть?
Нам поможет таблица умножения, именно таблица умножения поможет быстро решить примеры.
Выучить всю таблицу умножения непросто. Учить её надо постепенно.
Начнём с числа 2.
Найдём значение следующего выражения:
2 ∙ 2
Число 2 нужно взять 2 раза: 2 + 2 = 4. Значить 2 ∙ 2 = 4
Рассмотрим другие примеры из таблицы умножения на 2.
2 ∙ 3 = 6
2 ∙ 4 = 8
2 ∙ 5 = 10
2 ∙ 6 = 12
2 ∙ 7 = 14
2 ∙ 8 = 16
2 ∙ 9 = 18
Первый множитель не меняется, второй множитель увеличивается на 1. Произведение увеличивается на 2, потому что число 2 в каждом следующем примере прибавляется на один раз больше.
Зная правило: «Если произведение разделить на один множитель, то получим другой множитель» – можем составить примеры на деление.
2 ∙ 2 = 4;
4 : 2 = 2;
2 ∙ 3 = 6;
6 : 2 = 3;
6 : 3 = 2;
2 ∙ 4 = 8;
8 : 2 = 4;
8 : 4 = 2;
2 ∙ 5 = 10;
10 : 2 = 5;
10 : 5 = 2;
2 ∙ 6 = 12;
12 : 2 = 6;
12 : 6 = 2;
2 ∙ 8 = 16;
16 : 2 = 8;
16 : 8 = 2;
2 ∙ 9 = 18;
18 : 2 = 9;
18 : 9 = 2.
Выпишем числа из второго столбика, которые разделили на 2:
4, 6, 8, 10, 12, 14, 16, 18.
Числа, которые делятся на 2, называются чётными.
Числа, которые не делятся на 2, называются нечётными. Например, такие числа: 3, 5, 7, 9,11, 13, 15, 17, 19.
При делении на 2 мы получаем половину числа (вторую часть).
Рассмотрим четырёхугольник и посчитаем разными способами, на сколько квадратов он разделён.
3 + 3 = 6; 3 ∙ 2 = 6.
2 + 2 + 2 = 6; 2 ∙ 3 = 6.
Посмотрим на примеры второго столбика:
Множители поменяли местами, но значение произведения не изменилось.
Можно сделать вывод: от перестановки множителей произведение не изменяется.
Выполним тренировочные упражнения.
1. Выберите выражения к рисунку.
2 ∙ 5;
5 + 2;
5 + 5;
2 + 2 + 2 + 2 + 2;
10 : 2.
Правильный ответ:
2 ∙ 5;
10 : 2;
5 + 5;
2 + 2 + 2 + 2 + 2.
2. Вставьте в таблицу пропущенные числа.
Правильный ответ:
В таблицу нужно вставить числа:
Вывод: чтобы выполнить эти задания, необходимо знать таблицу умножения с числом 2.
Четные числа — это… Что такое Четные числа?
Чётность в теории чисел — характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет — нечётным (примеры: 1, 3, 75, −19). Нуль считается чётным числом. [1]
Чётное число — целое число, которое делится без остатка на 2: …−4, −2, 0, 2, 4, 6, 8…
Нечётное число — целое число, которое не делится без остатка на 2: …−3, −1, 1, 3, 5, 7, 9…
Иными словами, чётные и нечётные числа — это элементы соответственно классов вычетов [0] и [1] по модулю 2.
Признак чётности
Если в десятичной форме записи числа последняя цифра является чётным числом (0, 2, 4, 6 или 8), то всё число так же является чётным, в противном случае — нечётным.
42, 104, 11110, 9115817342 — чётные числа.
31, 703, 78527, 2356895125 — нечётные числа.
Арифметика
- Сложение и вычитание:
- Чётное ± Чётное = Чётное
- Чётное ± Нечётное = Нечётное
- Нечётное ± Чётное = Нечётное
- Нечётное ± Нечётное = Чётное
- Умножение:
- Чётное × Чётное = Чётное
- Чётное × Нечётное = Чётное
- Нечётное × Нечётное = Нечётное
- Деление:
- Чётное / Чётное — однозначно судить о чётности результата невозможно (если результат целое число, то оно может быть как чётным, так и нечётным)
- Чётное / Нечётное = если результат целое число, то оно Чётное
- Нечётное / Чётное — результат не может быть целым числом, а соответственно обладать атрибутами чётности
- Нечётное / Нечётное = если результат целое число, то оно Нечётное
История и культура
Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение. Так, в древнекитайской мифологии нечётные числа соответствовали Инь, а чётные — Ян.
Так, в древнекитайской мифологии нечётные числа соответствовали Инь, а чётные — Ян.
В разных странах существуют связанные с количеством даримых цветов традиции, например в США, Европе и некоторых восточных странах считается что чётное количество даримых цветов приносит счастье. В России чётное количество цветов принято приносить лишь на похороны умершим; в случаях когда в букете много цветов, чётность или нечётность их количества уже не играет такой роли.
Примечания
- ↑ «Чётные числа» в БСЭ.
Wikimedia Foundation.
2010.
Определить чётное или нечётное число онлайн
Чтобы определить, является ли число чётным или нечётным, воспользуйтесь нашим очень удобным онлайн определителем:
Просто введите целое число и получите ответ.
Сколько чётных и нечётных чисел между…
Теория
Чётное ли число
Чётным является целое число, которое делится на 2 без остатка (нацело).
Все многозначные числа, оканчивающиеся на 0,2,4,6 или 8, являются чётными числами:
10 , 12, 134, 2786, 6389246858 и др.
Примеры
Чётное ли число 10?
10 ÷ 2 = 5
Десять разделилось на два без остатка, следовательно 10 является чётным числом.
Чётное ли число 1?
1 ÷ 2 = 0.5
После деления единицы на два мы получаем нецелое число, следовательно 1 не является чётным числом.
Чётность нуля
Чётное ли число 0?
Ноль (0) является чётным числом.
Ноль чётное число, так как оно делится на два без остатка: 0 ÷ 2 = 0
В числовом ряду с обоих сторон от чётного числа стоят нечётные числа, и ноль тут не исключение, так как -1 это нечётное число:
-5 -4 -3 -2 -1 0 1 2 3 4 5
Нечётные числа
Нечетным является целое число, которое не делится на 2 без остатка.
Все многозначные числа, оканчивающиеся на 1,3,5,7 или 9, являются нечётными числами:
11 , 113, 1245, 43547, 63563469 и др.
Пример
Для примера рассмотрим число 67. Так как оно заканчивается цифрой 7 (нечётной), уже можно утверждать, что оно нечётное. Для пущей уверенности разделим 67 на два:
67 ÷ 2 = 33.5, то есть 33 и остаток 1 (67 = 33 ⋅ 2 + 1)
Окончательно делаем вывод, что число 67 является нечётным числом.
Сколько чётных и нечётных чисел в ряду
Сколько чётных и нечётных чисел находится в ряду между n и m?
Если n и m разные по чётности
Если n и m разные по чётности числа, то есть одно из них четное, а второе нечётное, то количество чётных и нечётных чисел в ряду одинаковое:
Кол чёт/нечёт = (m — n +1) ÷ 2, m > n
Пример
Возьмём ряд чисел между n = 22 и m = 31:
22, 23, 24, 25, 26, 27, 28, 29, 30, 31
Определим количество чётных и нечётных чисел в этом ряду.
Так как 22 и 31 являются числами разной чётности делаем вывод, что чётных и нечётных чисел в данном ряду поровну:
Кол чёт/нечёт = (31 — 22 + 1) / 2 = 10 / 2 = 5
5 чётных и 5 нечётных
| 22 | 24 | 26 | 28 | 30 | |||||
| 23 | 25 | 27 | 29 | 31 |
Если n и m чётные
Если n и m чётные числа, то чётных чисел в ряду будет на одно больше, чем нечётных:
Кол чёт = (m — n) ÷ 2 + 1 , m > n
Кол нечёт = (m — n) ÷ 2 , m > n
Пример
Возьмём ряд чисел между n = 10 и m = 20:
10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20
Определим количество чётных и нечётных чисел в этом ряду.
Кол чёт = (20 — 10) ÷ 2 + 1 = 6
Кол нечёт = (20 — 10) ÷ 2 = 5
6 чётных и 5 нечётных
| 10 | 12 | 14 | 16 | 18 | 20 | |||||
| 11 | 13 | 15 | 17 | 19 |
Если n и m нечётные
Если n и m нечётные числа, то чётных чисел в ряду будет на одно меньше, чем нечётных:
Кол чёт = (m — n) ÷ 2 , m > n
Кол нечёт = (m — n) ÷ 2 + 1 , m > n
Пример
Возьмём ряд чисел между n = 11 и m = 19:
11, 12, 13, 14, 15, 16, 17, 18, 19
Определим количество чётных и нечётных чисел в этом ряду.
Кол чёт = (19 — 11) ÷ 2 = 4
Кол нечёт = (19 — 11) ÷ 2 + 1 = 5
4 чётных и 5 нечётных
| 12 | 14 | 16 | 18 | |||||
| 11 | 13 | 15 | 17 | 19 |
Натуральные числа /qualihelpy
Числа, запись которых оканчивается четной цифрой, называют четными числами.
Числа, запись которых оканчивается нечетной цифрой, называют нечетными числами.
Над натуральными числами можно производить арифметические действия:
Чтобы найти неизвестное слагаемое, необходимо из суммы вычесть известное слагаемое.
Чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое.
Чтобы найти неизвестное вычитаемое, необходимо из уменьшаемого вычесть разность.
Чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель.
Чтобы найти неизвестное делимое, необходимо частное умножить на делитель.
Чтобы найти неизвестный делитель, необходимо делимое разделить на частное.
Если число кратно числу , то записывают: .5. Число делится на , если его запись оканчивается цифрой . Например, число делится на .
Деление с остатком
Если же остаток равен нулю, то говорят, что число делится нацело на число .
Простые и составные числа
Числа, которые имеют только два различных делителя (делятся только сами на себя и на число 1), называют простыми.
Например, простыми являются числа , , , , , , , , , …. .
Числа, которые имеют более двух различных делителей, называют составными. Составные числа можно представить в виде произведения двух и более простых множителей.
Например, число составное, так как . Натуральные числа называются взаимно простыми, если они не имеют общих делителей, за исключением числа . Например, числа и взаимно простые;
Наибольший общий делитель и наименьшее общее кратное
Общим делителем нескольких чисел называют число, которое является делителем каждого из этих чисел. Среди всех общих делителей всегда имеется наибольший. Это число называется наибольшим общим делителем (НОД).
Общим кратным нескольких чисел называют число, которое является кратным каждого из этих чисел. Среди всех общих кратных всегда есть наименьшее. Это число называется наименьшим общим кратным (НOК).
Среди всех общих кратных всегда есть наименьшее. Это число называется наименьшим общим кратным (НOК).
Чтобы найти НОД нескольких чисел, необходимо разложить их на простые множители и найти произведение только тех множителей, которые имеются в разложениях всех чисел.
Чтобы найти НOК нескольких чисел, необходимо разложить их на простые множители, найти произведение всех множителей, входящих в разложение одного из чисел и недостающих множителей из разложений оставшихся чисел.
Как определить, является ли число нечетным или четным без мод-или-побитовых операций? [закрыто]
питон
Поскольку я не совсем уверен, каковы критерии оценки, вот несколько решений, которые я предложил для развлечения. Большинство из них используют abs(n)для поддержки отрицательных чисел. Большинство из них, если не все, никогда не должны использоваться для реальных расчетов.
Этот скучный
from __future__ import division
def parity(n):
"""An even number is divisible by 2 without remainder. """
return "Even" if n/2 == int(n/2) else "Odd"
"""
return "Even" if n/2 == int(n/2) else "Odd"
def parity(n):
"""In base-10, an odd number's last digit is one of 1, 3, 5, 7, 9."""
return "Odd" if str(n)[-1] in ('1', '3', '5', '7', '9') else "Even"
def parity(n):
"""An even number can be expressed as the sum of an integer with itself.
Grossly, even absurdly inefficient.
"""
n = abs(n)
for i in range(n):
if i + i == n:
return "Even"
return "Odd"
def parity(n):
"""An even number can be split into two equal groups. "
g1 = []
g2 = []
for i in range(abs(n)):
g1.append(None) if len(g1) == len(g2) else g2.append(None)
return "Even" if len(g1) == len(g2) else "Odd"
import ent # Download from: http://wstein.org/ent/ent_py
def parity(n):
"""An even number has 2 as a factor."""
# This also uses modulo indirectly
return "Even" if ent.factor(n)[0][0] == 2 else "Odd"
И это мой фаворит, хотя, к сожалению, он не работает (как указывает март Хо ниже: только то, что все четные числа являются суммой двух простых чисел, не означает, что все нечетные числа не являются).
import itertools
import ent # Download from: http://wstein.org/ent/ent_py
def parity(n)
"""Assume Goldbach's Conjecture: all even numbers greater than 2 can
be expressed as the sum of two primes.
Not guaranteed to be efficient, or even succeed, for large n.
"""
# A few quick checks
if n in (-2, 0, 2): return "Even"
elif n in (-1, 1): return "Odd"
if n < 0: n = -n # a bit faster than abs(n)
# The primes generator uses the Sieve of Eratosthenes
# and thus modulo, so this is a little bit cheating
primes_to_n = ent. primes(n)
# Still one more easy way out
if primes_to_n[-1] == n: return "Odd"
# Brutish!
elif n in (p1+p2 for (p1, p2) in itertools.product(primes_to_n, primes_to_n)):
return "Even"
else:
return "Odd"
Функция ЕЧЁТН — Служба поддержки Office
В этой статье описаны синтаксис формулы и использование функции Е. В.ВОВ
В.ВОВ
в Microsoft Excel.
Описание
Возвращает значение ИСТИНА, если число четное, и значение ЛОЖЬ, если число нечетное.
Синтаксис
ЕЧЁТН(число)
Аргументы функции ЕЧЁТН описаны ниже.
Замечания
Если число не является числом, то ЕСЕН возвращает #VALUE! значение ошибки #ЗНАЧ!.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
|
|
|---|---|---|
|
=ЕЧЁТН(-1) |
Проверяет, является ли число -1 четным |
ЛОЖЬ |
|
=ЕЧЁТН(2,5) |
Проверяет, является ли число 2,5 четным. Дробная часть (0,5) усекается, поэтому проверяется число 2. |
ИСТИНА |
|
=ЕЧЁТН(5) |
Проверяет, является ли число 5 четным. |
ЛОЖЬ |
|
=ЕЧЁТН(0) |
Нуль (0) считается четным. |
ИСТИНА |
|
23.12.2011 |
Проверяет дату в ячейке A6. Десятичное представление даты 23.12.2011 — 40900. |
ИСТИНА |
Что такое четные и нечетные числа?
Четные и нечетные числа
Число, которое делится на 2 и дает остаток от 0, называется четным числом. Нечетное число — это число, которое не делится на 2. Остаток в случае нечетного числа всегда равен «1».
Свойство, по которому мы классифицируем целое число в математике как четное или нечетное, также известно как четность.
Идентификационное четное или нечетное число
1. Понимая число на месте «единиц»
В этом подходе мы анализируем число в разряде «единиц» целого числа, чтобы проверить, является ли число четным или нечетным.
Все числа, заканчивающиеся на 1,3,5,7 и 9, являются нечетными. Например, такие числа, как 11, 23, 35, 47 и т. Д., Являются нечетными числами.
Д., Являются нечетными числами.
Все числа, оканчивающиеся на 0,2,4,6 и 8, являются четными числами. Например, такие числа, как 14, 26, 32, 40 и 88, являются четными числами.
| 25, 32, 38, 87, 95, 64, 76, 53 | |
| Четный | Нечетный |
| 32, 38, 64, 76 | 25, 87, 95, 53 |
2. По группировке
Если мы разделим число на две группы с равным количеством элементов в каждой, то это будет четное число. В случае нечетных чисел при группировке мы получаем остаток 1.
- Группами по два в каждой
Для числа, если оно образует несколько групп по два без остатка, это четное число. В случае остатка число является нечетным числом.
Данная таблица объясняет результат, когда мы применяем разные операции к набору двух чисел.
Заявка
Элементарные навыки распознавания чисел полезны в старших классах для изучения математики, естественных наук и систем коммуникации. Мы применяем эту концепцию при проектировании схем с использованием логических вентилей и двоичных кодов. В древней математике изучение геометрических фигур началось с разделения фигур на четные и нечетные по количеству сторон.
Мы применяем эту концепцию при проектировании схем с использованием логических вентилей и двоичных кодов. В древней математике изучение геометрических фигур началось с разделения фигур на четные и нечетные по количеству сторон.
Интересные факты
|
Четные числа — ChiliMath
Четное число — это целое число, которое можно точно или равномерно разделить на \ color {red} 2. Если число точно делится на \ color {red} 2, это означает, что у рассматриваемого числа есть остаток \ color {blue} 0 после деления \ color {red} 2.
Проведя в уме математические вычисления, становится очевидным, что приведенные ниже числа, включая отрицательные числа, равны, потому что все они делятся на 2 .
Кроме того, я хочу отметить, что многие студенты думают, что ноль не является ни четным, ни нечетным.
Поверьте, ноль считается четным числом по той же простой причине, что он также является целым числом, которое делится на 2, поэтому при делении на 2 не остается остатка. То есть 0 \ div 2 = 0.
Наблюдение: Из приведенных выше примеров мы можем легко обобщить, что четные числа всегда заканчиваются цифрой 0, 2, 4, 6 или 8.
Однако есть способ лучше определить четное число, поскольку он более точен с математической точки зрения. Вот!
Общая форма четного числа
ОПРЕДЕЛЕНИЕ: Число \ large {n} является четным числом, если мы можем выразить его как \ large {2k}, где \ large {k} — это просто еще одно целое число. Это означает, что \ large {n} даже если \ large {n = 2k} такое, что \ large {k} является целым числом.
Это означает, что \ large {n} даже если \ large {n = 2k} такое, что \ large {k} является целым числом.
Примеры четных чисел, представленных в общей форме
Давайте проверим общую форму четного числа.Какую бы математическую концепцию нам ни представили, очень важно ее проверить. Прежде чем включать его в наш «набор математических инструментов», он должен иметь для нас какой-то смысл.
Ниже приведены несколько примеров, демонстрирующих концепцию четного числа как n = 2 \, k, где k — целое число.
\ color {красный} \ LARGE {n = 2k}
- 0 \ to 0 = 2 \ left (0 \ right)
- 14 \ to 14 = 2 \ left (7 \ right)
- — 32 \ to — 32 = 2 \ left ({- 16 } \ right)
- 50 \ to 50 = 2 \ left ({25} \ right)
- — 78 \ to — 78 = 2 \ left ({- 39} \ right)
Константа Появление 2 как одного из множителей четного числа предполагает, что любые четные числа действительно являются кратными 2 .
Возможно, вас заинтересует:
Что такое нечетное число?
Список четных чисел
Список нечетных чисел
четных и нечетных чисел | Блестящая вики по математике и науке
Четное число имеет четность 000, потому что остаток при делении на 222 равен 000, а нечетное число имеет четность 111, потому что остаток при делении на 222 равен 111. Например, 0,2,4,10, −60,2, 4,10, -60,2,4,10, −6 — все четные числа, потому что они оставляют остаток 0 при делении на 222.Целые числа 1,3,5,11, −71,3,5,11, -71,3,5,11, −7 — все нечетные числа, потому что они оставляют остаток 1 при делении на 222.
Каждое целое число может быть четным или нечетным, и ни одно целое число не может быть четным или нечетным. Это включает 0, что является четным.
Выясните, является ли 1729 четным или нечетным числом.
Поскольку остаток, полученный при делении 1729 на 2, равен 1, 1729 является нечетным числом.
ИЛИ \ text {ИЛИ} ИЛИ
Число 1729 оканчивается цифрой «9».
»Таким образом, это нечетное число. □ _ \ square □
Выясните, является ли 1000 четным или нечетным числом.
Поскольку остаток, полученный при делении 1000 на 2, равен 0, 1000 — четное число.
ИЛИ \ text {ИЛИ} ИЛИ
Число 1000 заканчивается цифрой «0». Таким образом, это четное число. □ _ \ квадрат □
а)
(б)
(c)
Ни один из вышеперечисленных
Какое из утверждений относительно числа −163? -163? −163 верно?
(а) Это нечетное число.
(b) Это четное число.
(c) Это не четное и нечетное число.
Отправьте свой ответ
Сколько из следующих 10 чисел являются четными целыми числами?
0,1, −2,3, −1,5.0, −2,4,2 × 2, −2 × 3,5,22 \ begin {array} {rrrrr} 0, && 1, && — 2, && 3, && — 1, \\ 5.0, && — 2.4, && 2 \ times 2 , && — 2 \ times 3.5, && \ frac {2} {2} \ end {array} 0,5.0, 1, −2.4, −2,2 × 2, 3, −2 × 3. 5 , −1,22
5 , −1,22
Число 2222452122 четное или нечетное?
Последняя цифра — 2, а 2 — четное число. Итак, 2222452122 — четное число. □ _ \ квадрат □
Четных и нечетных чисел
Четные и нечетные числа — простые понятия.Я начну легко, но я постараюсь немного оспорить эту тему.
Что такое четные числа?
Четное число — это любое число, которое дает остаток от нуля при делении на 2. Например, 12 дает остаток от 0 при делении на 2, поэтому 12 является четным.
Мы видели в правилах делимости
что число делится на 2 или дает остаток от нуля, если его последняя цифра 0,2,4,6 или 8.
Следовательно, любое число, последняя цифра которого равна 0, 2, 4, 6 или 8, является четное число.
Другие примеры четных чисел: 58, 44884, 998632, 98, 48 и 10000000.
Формальное определение четного числа:
Число n даже если существует число k, такое что n = 2k, где k — целое число.
Это формальный способ сказать, что если n делится на 2, мы всегда получаем частное k без остатка. Отсутствие остатка означает, что фактически n можно разделить на 2.
Отсутствие остатка означает, что фактически n можно разделить на 2.
Что такое нечетные числа?
Нечетное число — это любое число, которое дает остаток 1 при делении на 2. Например, 25 дает остаток 1 при делении на 2, поэтому 25 является нечетным.
Опять же, мы видели в правилах делимости
что число делится на 2 или дает остаток от нуля, если его последняя цифра 0,2,4,6 или 8.
Следовательно, любое число, последняя цифра которого равна , а не 0, 2, 4, 6 или 8 — нечетное число.
Другие примеры нечетных чисел: 53, 881, 238637, 99, 45 и 100000023
Формальное определение нечетного числа:
Число n является нечетным, если существует число k, такое, что n = 2k + 1, где k — целое число.
Это формальный способ сказать, что если n делится на 2, мы всегда получаем частное k с остатком 1. Наличие остатка 1 означает, что на самом деле n не может делиться на 2.
Основные операции с четными и нечетными числами
Сложение
четное + четное = четное
4 + 2 = 6
четное + нечетное = нечетное
6 + 3 = 9
нечетное + нечетное = четное
13 + 13 = 26
Умножение
четное × четное = четное
2 × 6 = 12
четное × нечетное = четное
8 × 3 = 24
нечетное × нечетное = нечетное
3 × 5 = 15
Вычитание
четное — четное = четное
8 — 4 = 4
четное — нечетное = нечетное
6 — 3 = 3
нечетное — нечетное = четное
13 — 3 = 10
Если у вас есть какие-либо вопросы об этом четном и нечетном урок чисел, просто свяжитесь со мной.
Графики количественных данных
18 мая, 21 06:54
Графики количественных данных, также называемые сгруппированными данными, могут отображаться с помощью гистограммы или многоугольника. Узнайте, как строить гистограммы, используя необработанные данные
Подробнее
Любое целое число, которое можно точно разделить на 2 , известно как четных чисел , тогда как целое число, которое точно не делится на 2 , известно как нечетных чисел .Примером четных чисел является 2, 4, 6, 8, 10, и т. Д. В этой статье мы обсудим четные числа, способы их проверки и их свойства. Что такое четное число? Любое целое число, полностью разделенное на 2 , называется четным числом . Четные числа всегда заканчиваются последней цифрой 0, 2, 4, 6 и 8 . Как проверить, четное или нечетное число?Чтобы проверить, является ли данное целое число нечетным или четным числом, мы должны проверить последнюю цифру числа. Последняя цифра числа говорит о том, что число четное или нечетное. Нижеследующие пункты объясняют это более ясно:
Свойства четных чиселЧетные числа в основном имеют три следующих свойства:
Свойства дополнения1. Если сложить четное число с нечетным числом , получится всегда нечетное число . Пример: 14 + 7 = 21 2. Если сложить четное число с другим четным числом , получится всегда четное число . Пример: 22 + 8 = 30 3.Если сложить нечетное число с другим нечетным числом , получится всегда четное число . Пример: 17 + 7 = 24 Свойства вычитания1. Вычитая четное число из нечетного числа , полученное число всегда будет нечетным числом . Пример: 18-5 = 13 2. Вычитая четное число из другого четного числа , в результате всегда получается четное число . Пример: 28 — 12 = 16 3. Вычитая нечетное число из другого нечетного числа , полученное число всегда будет четным числом . Пример: 19-15 = 4 Свойства умноженияУмножение четного числа на другое четное число , в результате всегда получается четное число . Пример: 4 * 8 = 32 Умножение четного числа на нечетное число , в результате всегда получается четное число . Пример: 12 * 5 = 60 Умножение нечетного числа на другое нечетное число , в результате всегда получается нечетное число . Пример: 13 * 3 = 39 Список четных чисел (от 1 до 100)В таблице ниже показан список четных чисел от 1 до 100:
| |||||||||
Что такое четные и нечетные числа? — Определение и примеры — Видео и стенограмма урока
Даже Стивен
Класс работает так, потому что 4 — четное число. Четное число представляет группу элементов, которые могут быть равномерно объединены в пары, не пропуская ни одного элемента. Другими словами, четные числа делятся на 2 без остатка.
Четное число представляет группу элементов, которые могут быть равномерно объединены в пары, не пропуская ни одного элемента. Другими словами, четные числа делятся на 2 без остатка.
В предыдущем примере, например, 4 ученика в группе репетиторства г-на Домингеса могут быть разделены на пары поровну, без исключения ни одного ученика. Но что, если директор добавит в группу еще одного ученика? Этот студент будет исключен:
Нам пришлось бы добавить еще одного студента в группу, чтобы снова получить четное число:
Итак, чтобы класс оставался равномерным, нам нужно было добавлять студентов по два за раз.Таким образом, у поступающих студентов всегда будет с кем поработать. Итак, чтобы сгенерировать четные числа, нам нужно добавить 2 к уже четному числу. Поскольку мы только что определили, что 6 — четное число, мы должны добавить 2, чтобы найти следующее четное число. 6 + 2 = 8, поэтому 8 — следующее четное число после 6.
Пока что у нас есть четные числа 4, 6 и 8. Но 2 также является четным числом, потому что если бы у нас было 2 ученика, они бы образовали пара. Очевидно, что мы могли бы добавлять 2 бесконечно, поэтому существует бесконечное количество четных чисел, начиная с 2: 2, 4, 6, 8, 10, 12, 14, 16 и т. Д.Вы уловили идею.
Но 2 также является четным числом, потому что если бы у нас было 2 ученика, они бы образовали пара. Очевидно, что мы могли бы добавлять 2 бесконечно, поэтому существует бесконечное количество четных чисел, начиная с 2: 2, 4, 6, 8, 10, 12, 14, 16 и т. Д.Вы уловили идею.
Odd One Out
Давайте вернемся к трем первоначальным студентам-репетиторам. В этом классе был исключен один ученик, поэтому 3 — нечетное число. Нечетное число представляет собой группу парных элементов, одна из которых не указана. Другими словами, нечетные числа не делятся на 2 без остатка.
Когда мы добавили в класс еще одного ученика, мы получили четное количество учеников. Но добавьте еще один, и мы вернемся к одному пропущенному студенту:
Итак, как и четные числа, мы можем сгенерировать нечетные числа, добавив 2 к уже нечетному числу.Мы просто добавили 2 к нечетному числу 3. Это дало нам нечетное число 5. Мы могли добавить еще два, и мы получили бы 7, следующее нечетное число после 5.
Хотя мы начали с 3, 1 — первое нечетное число, потому что, если бы у мистера Домингеса был только один ученик, этому ученику не с кем было бы объединиться. Пока что у нас есть нечетные числа 1, 3, 5 и 7. Но, как и в случае с четными числами, существует бесконечное количество нечетных чисел, потому что мы можем добавлять 2 бесконечно.
Переменные числа
Давайте поместим наши нечетные и четные числа рядом друг с другом, чтобы увидеть взаимосвязь между ними:
Как видно из этой диаграммы, четные и нечетные числа чередуются.1 — нечетное, 2 — четное, 3 — нечетное, 4 — четное и т. Д. Этот шаблон, как и сами нечетные и четные числа, существует бесконечно.
Странный ноль
Четный 0 или нет, зависит от того, кого вы спрашиваете. На этот вопрос есть разные ответы. Мы могли бы сказать, что 0 является четным, потому что он предшествует 1 (нечетное число), а четные числа всегда идут до и после нечетного числа, потому что они чередуются.
Мы могли бы также сказать, что 0 является четным, потому что 0 + 2 = 2 (четное число), и мы добавляем 2 к уже четным числам, чтобы определить следующее четное число. Но мы могли бы сказать, что 0 не является даже потому, что он не представляет пару элементов. На самом деле ноль означает полное отсутствие каких-либо предметов, поэтому некоторые могут сказать, что это ни чётно, ни чётно.
Но мы могли бы сказать, что 0 не является даже потому, что он не представляет пару элементов. На самом деле ноль означает полное отсутствие каких-либо предметов, поэтому некоторые могут сказать, что это ни чётно, ни чётно.
Однако нет аргументов в пользу того, что утверждение 0 является нечетным числом, поэтому вы обнаружите, что некоторые говорят, что 0 является четным, в то время как другие говорят, что 0 не является ни нечетным, ни четным. Однако мы все можем согласиться с тем, что 0 не является нечетным числом.
Важные окончания
Простой способ определить, является ли большое число четным или нечетным, — это посмотреть на его последнюю цифру.Если число заканчивается нечетной цифрой (1, 3, 5, 7 или 9), то оно нечетное. С другой стороны, если число заканчивается четной цифрой или 0 (0, 2, 4, 6 или 8), то оно четное.
Чтобы определить, является ли 35 258 364 578 нечетным или четным, нам не нужно считать до него, чередуя четные и нечетные на этом пути. Поскольку число заканчивается четным числом (8), оно четное.
Аналогично, поскольку 73 789 246 233 оканчиваются нечетной цифрой (3), это нечетное число. Не имеет значения, насколько велико число и четны или нечетны другие его цифры.Последняя цифра числа определяет его нечетность или четность.
Давайте еще раз проверим мистера Домингеса. Его группа дополнительного обучения была настолько успешной, что в конечном итоге она выросла до 20 учеников. Поскольку 20 заканчивается на 0, это четное число. Итак, у каждого ученика в группе был еще один ученик, с которым можно было сотрудничать, что значительно облегчило жизнь мистеру Домингесу.
Краткое содержание урока
Вот несколько важных моментов, которые следует запомнить:
- Нечетное число представляет собой количество элементов, которые нельзя разделить поровну, потому что один из них отсутствует.Оно не делится на 2 без остатка. Например, из группы из трех учеников мы можем составить одну пару, исключив одного ученика, поэтому 3 — нечетное число.
- Четное число представляет собой количество элементов, которые могут быть равномерно объединены в пары.
 Оно делится на 2 без остатка. Например, из группы из четырех учеников мы можем составить две пары, и ни один ученик не останется один, поэтому 4 — четное число.
Оно делится на 2 без остатка. Например, из группы из четырех учеников мы можем составить две пары, и ни один ученик не останется один, поэтому 4 — четное число. - Чтобы создать нечетные числа, мы просто добавляем 2 к существующему нечетному числу.
- Чтобы создать четные числа, мы просто добавляем 2 к существующему четному числу.
- Чередуются нечетные и четные числа.
- Существует бесконечное количество как нечетных, так и четных чисел.
- Четные числа заканчиваются либо 0, либо четной цифрой, а нечетные числа — нечетной цифрой.
Результаты обучения
Когда вы закончите, вы сможете:
- Объяснять, что такое четные и нечетные числа
- Определить четные и нечетные числа
- Создать четные и нечетные числа
Является ли ноль четным числом?
Прежде чем ответить на этот вопрос, мне кажется удобным уточнить понимание четного числа.На самом деле определение четного числа может применяться только к целым числам. Таким образом, число есть даже тогда, когда оно делится на число два, и в результате получается целое число. Если мы предпочитаем использовать математический язык, лучше сказать, что «четное число означает число, которое может быть записано как« 2n », где« n »принадлежит набору целых чисел.
Таким образом, число есть даже тогда, когда оно делится на число два, и в результате получается целое число. Если мы предпочитаем использовать математический язык, лучше сказать, что «четное число означает число, которое может быть записано как« 2n », где« n »принадлежит набору целых чисел.
Но в конце концов, является ли ноль четным числом?
После выяснения, что такое четное число, на этот вопрос будет легче ответить.И ответ — «да, это так». Нулевое число равно , поскольку если мы разделим ноль на два, результатом будет целое число, это «0: 2 = 0». Кроме того, если мы имеем в виду предыдущее определение того, что такое четное число, мы можем записать нулевое число как «2n», поскольку «2 xx 0 = 0».
Ну, я не уверен. Не могли бы вы дать мне другое объяснение?
На самом деле, возможна и другая мысль: внутри множества, состоящего из всех целых чисел, перед нечетным числом мы всегда находим четное.
Программа Python для подсчета четных и нечетных чисел в списке
Имея список чисел, напишите программу Python для подсчета четных и нечетных чисел в списке. Пример:
Пример:
Ввод: список1 = [2, 7, 5, 64, 14] Выход: четное = 3, нечетное = 2 Ввод: список2 = [12, 14, 95, 3] Вывод: четное = 2, нечетное = 2
Пример 1: подсчет четных и нечетных чисел из заданного списка с использованием цикла for Перебрать каждый элемент в списке с помощью цикла for и проверить, если num % 2 == 0, условие для проверки четных чисел . Если условие удовлетворяет, то увеличьте четное количество, иначе увеличьте нечетное количество.
Python3
|
Вывод:
Четные числа в списке: 3 Нечетные числа в списке: 4
Пример 2. Использование цикла while
Использование цикла while
Python3
|
Вывод:
Четные числа в списке: 3 Odd numbers in the list: 4
Example 3 : Using Python Lambda Expressions
Python3
|
Output:
Четные числа в списке: 3 Odd numbers in the list: 4
Example 4 : Using List Comprehension
Python3
|
Output:
Even numbers in the list: 3 Odd numbers in the list: 4
Example 5: Using Recursion
Python3
|
Вывод
Четные числа в списке: 3 Нечетные числа в списке: 4
Пример 6: Использование побитового оператора XOR
Идея состоит в том, чтобы проверить, установлен ли последний бит числа или нет. Если последний бит установлен, то число нечетное, иначе четное. Как мы знаем, побитовая операция XOR числа на 1 увеличивает значение числа на 1, если число четное, в противном случае оно уменьшает значение числа на 1, если значение нечетное.
Если последний бит установлен, то число нечетное, иначе четное. Как мы знаем, побитовая операция XOR числа на 1 увеличивает значение числа на 1, если число четное, в противном случае оно уменьшает значение числа на 1, если значение нечетное.
ПРОВЕРИТЬ ЧЕТНОЕ ИЛИ НЕЧЕТНОЕ ЧИСЛО, ИСПОЛЬЗУЯ ОПЕРАТОР XOR0017 = [ 10 , 21 , 4 , 45 , 66 , 93 , 1 ]
even_count, odd_count = 0 , 0
for num in list1:
1 = = num + 1 : even_count + = 1
else :
ODD_COUNT + = 1
Печать (
. 0018
0018 "ровные числа в списке:" , evel_count)
Печать ( "Нечетные номера в списке:" , ODD_COUNT)
, ODD_COUNT) 9015 , ODD_COUNT) 9015 , ODD_COUNT) 9015 , ODD_COUNT) 9015 . Четные числа в списке: 3
Нечетные числа в списке: 4 Пример 7: Использование побитового оператора И
Идея состоит в том, чтобы проверить, установлен ли последний бит числа или нет. Если последний бит установлен, то число нечетное, иначе четное.
Как мы знаем, побитовое И Операция Числа на 1 будет равна 1, если оно нечетное, потому что последний бит уже будет установлен. В противном случае на выходе будет 0.
Python3
list1 = [ 10 , 21 , 4 , 45 , 66 , 93 , 1 ]
even_count, odd_count = 0 , 0
for num in list1:
если не число & 1 :
четное_счет + 8
else :
odd_count + = 1
print ( "Even numbers in the list : " , четное_счетчик)
print ( "Нечетные числа в списке:" , нечетное_счетчик)
Выход
Четные числа в списке: 3
Нечетные числа в списке: 4
Пример 8 : Использование оператора побитового ИЛИ
Идея состоит в том, чтобы проверить, установлен ли последний бит числа или нет. Если последний бит установлен, то число нечетное, иначе четное. Как мы знаем, побитовая операция ИЛИ числа на 1 увеличивает значение числа на 1, если число четное, иначе оно останется неизменным. Итак, если после операции ИЛИ над числом с 1 результат будет больше числа, то оно четное и мы вернем true, иначе нечетное и вернем false.
Если последний бит установлен, то число нечетное, иначе четное. Как мы знаем, побитовая операция ИЛИ числа на 1 увеличивает значение числа на 1, если число четное, иначе оно останется неизменным. Итак, если после операции ИЛИ над числом с 1 результат будет больше числа, то оно четное и мы вернем true, иначе нечетное и вернем false.
Python3
list1 = [ 10 , 21 , 4 , 45 , 66 , 93 , 1 ]
even_count, odd_count = 0 , 0
for Num в List1:
IF NUM | 1 > num:
even_count + = 1
else :
odd_count + = 1
Печать ( "ровные числа в списке:" , ровная_Коунт)
(vest_count)
(vest_count)
(vest_count)
.
, нечетное_счетчик)
Вывод
Четные числа в списке: 3
Нечетные числа в списке: 4
Метод: использование функции перечисления
Python3
lst = [ 12 , 14 , 95 , 3 ];c = 0 ;c1 = 0
for i,a in enumerate (lst):
if a % 2 = = 0 :
c + = 1
else :
c1 + = 1
Печать ( "ровное количество чисел" , C, "Нечетное количество чисел" , C1)
, C1) 9 99 9 , C1) 4 9 9 , C1) 9003
4 9 9 , C1) " , C1) " , C1) " , C1) "0165
Вывод
подсчет четных чисел 2 подсчет нечетных чисел 2
Дополнительный пробел: O(1)
Четные и нечетные числа | Brilliant Math & Science Wiki
Содержание
- Определение
- Четные и нечетные (четные) свойства
- Решение проблем
- Смотрите также
Четное число имеет четность 000, потому что остаток при делении на 222 равен 000, а нечетное число имеет четность 111, потому что остаток при делении на 222 равен 111. Например, 0,2,4,10,−60,2 ,4,10,-60,2,4,10,−6 — все четные числа, потому что при делении на 222 они оставляют остаток 0. Целые числа 1,3,5,11,−71,3,5,11 ,-71,3,5,11,−7 — все нечетные числа, потому что они оставляют остаток 1 при делении на 222.
Например, 0,2,4,10,−60,2 ,4,10,-60,2,4,10,−6 — все четные числа, потому что при делении на 222 они оставляют остаток 0. Целые числа 1,3,5,11,−71,3,5,11 ,-71,3,5,11,−7 — все нечетные числа, потому что они оставляют остаток 1 при делении на 222.
Каждое целое число либо четное, либо нечетное, и ни одно целое число не является одновременно четным и нечетным. Сюда входит 0, что является четным.
Выясните, является ли 1729 нечетным или четным числом.
Поскольку остаток от деления 1729 на 2 равен 1, 1729 — нечетное число.
ИЛИ\text{ИЛИ}ИЛИ
Число 1729 заканчивается цифрой «9». Таким образом, это нечетное число. □_\квадрат□
Выясните, является ли 1000 нечетным или четным числом.
Поскольку остаток от деления 1000 на 2 равен 0, 1000 — четное число.
ИЛИ\text{ИЛИ}ИЛИ
Число 1000 заканчивается цифрой "0". Таким образом, это четное число. □_\квадрат□
(а)
(б)
(с)
Ничего из вышеперечисленного
Что из следующего верно относительно числа -163?-163?-163?
(а) Это нечетное число.
(b) Это четное число.
(c) Это ни нечетное, ни четное число.
Сколько из следующих 10 чисел являются четными целыми числами?
0,1,−2,3,−1,5,0,−2,4,2×2,−2×3,5,22 \begin{массив} {rrrrr} 0, && 1, &&-2, &&3, &&- 1, \\ 5.0, &&-2.4, &&2 \times 2, &&-2 \times 3.5, &&\frac{2}{2} \end{массив} 0,5.0,1,−2.4,− 2,2×2,3,−2×3,5,−1,22
Число 2222452122 четное или нечетное?
Последняя цифра — 2, а 2 — четное число. Итак, 2222452122 — четное число. □_\квадрат□
Ниже приведены свойства четности четных и нечетных чисел:
- четный ± \pm± четный = четный
- нечетное ± \pm± нечетное=четное
- четный ± \pm± нечетный= нечетный
- четный × \times× четный= четный
- четный ×\times× нечетный= четный
- нечетное × \times× нечетное= нечетное
Эти свойства часто полезны для проверки того, является ли равенство ложным, с помощью арифметических правил четности, чтобы увидеть, имеют ли обе стороны одинаковую четность. Применение этих правил становится понятным из следующих примеров и задач:
Применение этих правил становится понятным из следующих примеров и задач:
Если nnn — целое число, какова четность 2n+2?2n+2?2n+2?
Поскольку nnn — целое число, n+1n+1n+1 также является целым числом. Тогда 2n+2=2(n+1)+02n+2 = 2(n+1) + 02n+2=2(n+1)+0 показывает, что четность 2n+22n+22n+2 равна 0 ,0,0, что означает, что 2n+22n+22n+2 всегда четное число. □_\квадрат□
Число (47630750675+453407032)×5453\влево(47630750675+453407032\вправо) \умножить на 5453(47630750675+453407032)×5453 четное или нечетное?
Чтобы ответить на этот вопрос, было бы неразумно умножать эти числа. Вместо этого мы можем применить свойства четных и нечетных чисел.
Поскольку число 476307506754763075067547630750675 оканчивается на 5, оно нечетное. С другой стороны, поскольку 453407032453407032453407032 оканчивается на 2, оно четное. По свойству 3 четное ± \pm± нечетное = нечетное, поэтому 47630750675+45340703247630750675+45340703247630750675+453407032 нечетно. Поскольку эта сумма умножается на 5453,5453,5453, что является нечетным, все число является нечетным, поскольку свойство 6 дает нечетное × \times× нечетное = нечетное. □_\квадрат□
Поскольку эта сумма умножается на 5453,5453,5453, что является нечетным, все число является нечетным, поскольку свойство 6 дает нечетное × \times× нечетное = нечетное. □_\квадрат□
Вот несколько задач, которые стоит попробовать.
б-аб-аб-а
а+ба+ба+б
абабаб
−ab-ab−ab
Если aaa — отрицательное нечетное число, а bbb — положительное четное число, то какое из следующих чисел должно быть положительным четным числом?
всегда нечетный
всегда даже
четные или нечетные, в зависимости от значений aaa и bbb 92+a+7) \times (2b+1) (a2+a+7)×(2b+1)
равно __________.\text{\_\_\_\_\_\_\_\_ \_\_}.__________.
Даже
это странно
Это даже если xxx даже
Это даже если yyy даже
Даже если xyxyxy отрицательное
Пусть xxx и yyy будут целыми числами. {2}+xy?(x+y)2+xy?
{2}+xy?(x+y)2+xy?
Вот примеры и задачи, мотивированные для улучшения навыков решения задач на четность нечетных и четных чисел. Пройдите их, чтобы достичь целей этого раздела.
Если aaa и bbb целые числа, какова четность a×b?a \times b?a×b?
Мы знаем, что нечетное число, умноженное на нечетное число, остается нечетным, четное число, умноженное на нечетное число, будет четным, а четное число, умноженное на четное число, будет четным. Это можно обобщить как
(четность a) × (четность b) = (четность ab). □ ( \mbox{Четность } a ) \times ( \mbox{Четность } b ) = (\mbox{Четность } ab). \ _\square(Четность a)×(Четность b)=(Четность ab). □
Пусть P P P будет произведением первых 100 простых чисел. Какова четность P? П?П?
Мы видим, что первое простое число — 2, то есть четное. Остальные 99 простых чисел нечетные. Произведение этих 99 простых чисел будет целым числом, скажем, k k k. Умножение четного числа на другое целое всегда дает четное число; поэтому мы можем записать P P P как 2k 2 k 2k. Деление P P P на 2 не дает остатка, поэтому P P P четно. □_\квадрат □
92 + k = k (k+1),k2+k=k(k+1), где k kk и (k+1) (k+1)(k+1) имеют разную четность. Тогда по арифметическим правилам четности четность k(k+1) k(k+1)k(k+1) равна 0 00. □_\square□
Деление P P P на 2 не дает остатка, поэтому P P P четно. □_\квадрат □
92 + k = k (k+1),k2+k=k(k+1), где k kk и (k+1) (k+1)(k+1) имеют разную четность. Тогда по арифметическим правилам четности четность k(k+1) k(k+1)k(k+1) равна 0 00. □_\square□
Да
№
Может ли четное число, поделенное на другое четное число, умножить на другое четное число, получить нечетное число?
Если «да», то найдите три подходящих числа.
Если «нет», то почему? 92 + nn2+n на 2,2,2, мы получим целое число. □_\квадрат □
Попробуйте решить следующие задачи:
Нечетное для всех значений aaa и bbb
Даже для всех значений aaa и bbb
Даже ровно для 1 значения aaa и 1 значения bbb
Нечетное ровно для 1 значения aaa и 2 значений bbb
Учитывая, что aaa и bbb — целые числа, какой вывод мы можем сделать о выражении 9{ 2 }+a+2011 \big) ( 2b+1 ) ? (а2+а+2011)(2б+1)?
Произведение цифр числа 38 четно, потому что 3×8=24,3\умножить на 8 = 24,3×8=24. Точно так же
произведение цифр числа 57 нечетно, потому что 5×7=35,5 х 7 = 35,5×7=35.
Точно так же
произведение цифр числа 57 нечетно, потому что 5×7=35,5 х 7 = 35,5×7=35.
Сколько двузначных чисел имеют нечетное произведение?
Поскольку nnn охватывает все действительные значения в интервале [0,100] [0, 100] [0,100], сколько существует таких значений nnn, что 4n+1 4n+ 1 4n+1 является нечетным целым числом?
Дополнительные сведения о применении четности в комбинаторике см. в разделе «Промежуточная четность».
Простые числа
Правила делимости (2, 3, 5, 7, 11, 13, 17, 19,…)
Остаток
Факторизация простых чисел
Цитировать как: Четные и нечетные числа. Brilliant.org .
Извлекаются из
https://brilliant.org/wiki/even-and-odd-numbers/
Список составных чисел от 1 до 100
Положительное целое число, которое можно получить путем умножения двух меньших положительных целых чисел, является составным числом. Все составные числа можно записать в виде произведения двух или более простых чисел. Например, целое число 21 является составным числом, поскольку оно является произведением двух меньших целых чисел 3 и 7.
Все составные числа можно записать в виде произведения двух или более простых чисел. Например, целое число 21 является составным числом, поскольку оно является произведением двух меньших целых чисел 3 и 7.
Список составных чисел от 1 до 100
Ниже перечислены составные числа до 100.
4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100.
Есть 74 числа от 1 до 100 составных чисел.
Нечетные и четные составные числа
Нечетные составные числа — это все нечетные целые числа, не являющиеся простыми.
9, 15, 21, 25, 27 и т. д. являются примерами составных нечетных чисел.
Наименьшее нечетное составное число — 9.
Четные составные числа — все четные числа, а не простые.
4, 6, 8, 10, 12, 14, 16 и т. д. являются примерами четных составных чисел.
Наименьшее четное составное число равно 4.
Решенные задачи на составные числа
1: Сколько составных чисел находится в диапазоне от 1 до 50?
Ответ: Существует 34 составных числа от 1 до 50, а именно:
4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50.
2. Из чего состоят составные числа 1 к 100? Представьте их на таблице составных чисел.
Ответ: Есть 74 составных числа до 100, которые представлены в таблице составных чисел следующим образом:
1
11
21
31
41
51
61
71
81
91
2
12
12
. 0164
0164
32
42
52
62
72
82
92
3
13
23
33
43
53
63
73
83
93
4
14
24
34
44
54
64
74
84
94
5
15
25
35
45
55
65
75
85
95
6
16
26
36
46
56
66
76
86
96
7
17
27
37
47
57
67
77
87
97
8
18
28
38
48
58
68
78
88
98
9
19
29
39
49
59
69
79
89
99
10
20
30
40
50
60
70
80
90
100
Here the numbers in red color are composite numbers up to 100.
3. Запишите наименьшее нечетное составное число?
Ответ: Наименьшее нечетное составное число равно 9.
4. Перечислите первые пять нечетных составных чисел.
Ответ: Первые пять нечетных составных чисел следующие: 9, 15, 21, 25, 27.
Согласно основам математики, составные числа — это числа, имеющие более двух делителей. Составные числа или то, что также обычно называют составными, являются противоположностью простых чисел, которые состоят только из двух множителей и не более того. Когда мы говорим два множителя, будет присутствовать 1 и другое число. Все те числа, которые не являются простыми числами, будут классифицированы как составные числа. Чтобы вы лучше понимали составные числа и то, как они находятся, вот список составных чисел от 1 до 100 через Веданту, к которому вы можете получить доступ и узнать больше. Это поможет вам понять составные числа и их назначение в различных математических уравнениях.
Свойства составных чисел, отличающие их от других чисел:
Составными числами являются только те числа, которые имеют более двух делителей.
Составные числа также считаются делящимися без остатка на множество множителей.
Видно, что каждое из составных чисел является самостоятельным делителем, кроме 1, являющегося общим делителем.
Самое маленькое из всех составных чисел — 4, так как оно делится на 1, 2 и 4.
Каждое из составных чисел будет состоять как минимум из двух простых чисел, которые действуют как его делители. Например, если вы проверите составное число 10, оно будет состоять из 2 и 5 в качестве простых чисел, произведение которых даст 10.
Как взять половину любого числа. Как найти четверть или 25%. Как найти 15%. — Полный курс арифметики
Навыки
дюймов
А Р И Т М Е Т И К
Содержание | Главная | Введение
Урок 16 Раздел 2
Назад к разделу 1
7. Какие натуральные числа называются четными числами? Числа, которые можно разделить на две равные части.
8 — четное число, потому что мы можем разделить его «равномерно» на две 4.
4 это половина из 8.
9 не четное число. Есть «нечет» 1:
Поэтому мы называем 9 нечетным числом. Мы не можем взять половину натурального числа, которое является нечетным. Мы не можем взять половину из 9 человек.
Мы не можем взять половину натурального числа, которое является нечетным. Мы не можем взять половину из 9 человек.
Таким образом, четные числа — это числа, которые делятся на 2: 2, 4, 6, 8 и так далее. Нечетные числа 1, 3, 5, 7 и так далее.
Если вы не знаете половину какого-то четного числа, вы можете найти его, мысленно разложив его на два четных числа, половину которых вы знаете. Мы видели, как это сделать, в Разделе 1, Примере 8.
Пример 1. Сколько будет половина от 54?
Ответ . Половина из 54 = Половина из 50 + Половина из 4 = 25 + 2 = 27.
Что касается нечетных чисел, обратите внимание, что каждое нечетное число равно четному числу плюс 1.
3 = 2 + 1.
5 = 4 + 1.
7 = 6 + 1.
9 = 8 + 1.
И так далее.
Опять же, если натуральное число нечетное, мы не можем взять его половину. Поэтому теперь мы предположим, что мы не обязательно имеем дело с натуральными числами, и что 1 теперь является непрерывной единицей — единицей, которую мы используем для измерения, — и у которой есть половина: 1 минута, 1 сантиметр, 1 фунт и скоро. (Урок 20.)
8. Какое число составляет половину от 1? ½ («Половина»)
½ должно быть половиной чего-то. Это половина 1.
Половина 1 доллара, конечно же, составляет долларов. 50.
9.
Как мы можем взять половину нечетного числа? Половина 7 Возьмите половину его четной части и добавьте половину 1.
Пример 2. Сколько будет половина от 7?
Ответить . 7 = 6 + 1. Половина 6 равна 3; половина 1 равна ½; поэтому половина 7
равна 3½.
Половина 7 долларов . 00 составляет 3 долларов США. 50.
Пример 3. Шарф, который обычно стоит 17 долларов, продается за полцены. Что вы платите?
Ответ . 17 = 16 + 1. Половина от 16 – это 8. Следовательно, половина от 17 долларов – это 8 долларов. 50.
Пример 4. Сколько будет половина от 25%?
Ответить . 12½%.
12½%.
25 = 24 + 1. Половина 24 равна 12. Половина 1 равна ½.
Итак, если вы знали, что 25% означают четверть, то теперь вы знаете, что 12½% означают восьмую часть.
(см. урок 27, пример 7)
Пример 5 Сколько будет половина от 27 долларов . 40?
Ответить . Мы возьмем половину от 27 долларов и добавим к ней половину от 92 297 долларов. 40.
Так как 27 = 26 + 1, то
Половина от 27 долларов составляет 13 долларов . 50.
Половина от $. 40 стоит долларов. 20.
Таким образом, половина от 27,40 долл. США составляет 13 долл. США. 70.
Пример 6. Сколько будет половина от 90?
Ответить . 90 = 80 + 10. Половина 80 равна 40; половина 10 равна 5; поэтому половина 90 равна 45.
См. задачу 21.
Пример 7. Сколько будет половина от 9 долларов США 92 297 . 70?
Ответить . Половина от $9 . 00 (8 + 1) составляет 4 долларов США. 50. Половина
$ . 70 стоит долларов. 35. Таким образом, половина от 9,70 доллара – это 4 доллара. 85.
Половина от $9 . 00 (8 + 1) составляет 4 долларов США. 50. Половина
$ . 70 стоит долларов. 35. Таким образом, половина от 9,70 доллара – это 4 доллара. 85.
Пример 8. Знаменитое число π («пи») приблизительно равно 3·9.2297 . 14. Как
многое составляет половину π; то есть №
2 ?
Ответ. Игнорировать десятичную точку в числе 3 . 14. Тогда половина от 300 равна 150; половина 14 равна 7; поэтому половина от 314 равна 157. При замене десятичной точки
№
2 1 . 57.
10. Как мы можем взять четвертый или 25% числа? Возьмите половину половины.
Разделить число пополам означает разделить его на две равные части. Разделить его на Кварты, или четверти, значит разделить его на четыре равные части. И мы можем сделать это, взяв половину каждой половины.
Четверть — это половина половины. Сравните урок 15.
Пример 9. Сколько стоит четверть или четверть от 60?
Ответить . Половина от 60 — это 30. Половина от 30 — это 15.
Пример 10. Сколько будет 25% от 180?
Ответить . 25% означает четверть. (Урок 15.) Половина от 180 равна 90. Половина от 90 равна 45.
Пример 11. Сколько будет 25% от 112?
Ответить . Половина от 112 = половина от 100 + половина от 12 = 56.
Ответить . Половина от 56 = половина от 50 + половина от 6 = 25 + 3 = 28.
Пример 12. Сколько будет 25% от 9,60 доллара?
Ответ . Половина от 9,60 доллара = 4,50 доллара + 0,30 доллара = 4,80 доллара. Половина от 4,80 доллара = 2 долларов. 40
Половина от 9,60 доллара = 4,50 доллара + 0,30 доллара = 4,80 доллара. Половина от 4,80 доллара = 2 долларов. 40
11. Как мы можем умножить на 5? 5 × 123 Возьмите половину от умножения на 10.
Поскольку 5 составляет половину от 10, то число, умноженное на 5, будет равно половине числа, умноженного на 10.
Пример 13. 5 × 123 = половина 10 × 123
Пример 13 5 × 123 = половина от 1230 (Урок 4, вопрос 1.)
Пример 13. 5 × 123 = 615.
Пример 14. 5 × 1 долларов США. 50 = половина от 15 долларов
Пример 14. 5 × 1 долларов США. 50 = 7 долларов США. 50.
5 × 1 долларов США. 50 = 7 долларов США. 50.
Пример 15. 5 × 46 долларов США. 80 = половина от 468 долларов
Пример 15. 5 × 46 долл. США . 80 = 234 доллара.
12. Как мы можем взять 5% числа? Возьмите половину 10%.
Пример 16. Сколько будет 5 % от 162 долларов?
Ответ. 10 % – это 16 долларов США. 20. (Урок 4, вопрос 7.) Поэтому 5% составляют 8 долларов. 10.
Написать 0,05 и умножить — письменный метод для тех, кто не понимает процентов.
Пример 17. Сколько будет 5 % от 475 долларов?
Ответить . 10% это 47 $. 50. Таким образом, 5 % – это 23 долларов США. 50 + $. 25 = 23 долларов . 75.
50. Таким образом, 5 % – это 23 долларов США. 50 + $. 25 = 23 долларов . 75.
13. Как мы можем умножить на 15? 15 × 8 Умножьте на 10 и прибавьте половину.
Ибо, 15 = 10 + половина 10.
Пример 18. 15 × 8 = 80 + половина 80
Пример 18. 15 × 8 = 80 + 40
Пример 18. 15 × 8 = 120.
Пример 19. 15 × 42 = 420 + 210.
Пример 19. 15 × 42 = 630.
14. Как мы можем взять 15% числа? Возьмите 10% и прибавьте половину.
Пример 20. Сколько будет 15% от 70 долларов??
Ответ . 15% = 10% + половина 10% = $7 . 00 + $3 . 50 = 10 долларов . 50.
Пример 21. Если вы даете чаевые в размере 15%, а счет составляет 40 долларов США, сколько вы оставляете?
Ответ . 15% = 10% + половина 10% = 4 долларов . 00 + 2 долларов . 00
00 = $6 . 00.
В этот момент, пожалуйста, «переверните» страницу и выполните несколько Задач.
или
Перейти к следующему уроку.
Предыдущий раздел
1-й урок о частях натуральных чисел
Введение | Главная | Содержание
Copyright © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: [email protected]
Q2 Укажите, верны или нет следующие утверждения i Сумма трех нечетных чисел четна i…
Перейти к
- Упражнение 3.1
- Упражнение 3.2
- Упражнение 3.
 3
3 - Упражнение 3.4
- Упражнение 3.5
- Упражнение 3.6
- Упражнение 3.7
- Зная наши цифры
- Целые числа
- Игра с числами
- Основные геометрические идеи
- Понимание элементарных форм
- Целые числа
- Фракции
- Десятичные
- Обработка данных
- Измерение
- Алгебра
- Соотношение и пропорция
- Симметрия
- Практическая геометрия
Главная >
Решения НЦЭРТ
Класс 6
Математика
>
Глава 3. Игра с числами
>
Упражнение 3.2
>
Вопрос 2
Игра с числами
>
Упражнение 3.2
>
Вопрос 2
Вопрос 2 Упражнение 3.2
В2) Укажите, верны или неверны следующие утверждения:
(i) Сумма трех нечетных чисел четна.
(ii) Сумма двух нечетных чисел и одного четного числа является четной.
(iii) Произведение трех нечетных чисел нечетно.
(iv) Если четное число разделить на 2, то частное всегда будет нечетным.
(v) Все простые числа нечетные.
(vi) Простые числа не имеют делителей.
(vii) Сумма двух простых чисел всегда четна.
(viii) 2 — единственное четное простое число.
(ix) Все четные числа являются составными числами.
(x) Произведение двух четных чисел всегда четно.
Ответ:
решение:
(i) неверно
(ii) верно
(iii) верно
(iv) неверно
(v) неверно
(vi) неверно
(vii) неверно
3 верно
(ix) неверно
(x) неверно
Связанные вопросы
Q1) Какова сумма любых двух (i) нечетных чисел? (ii) Четные числа?
Q5) Какое самое большое простое число между 1 и 10?
Q3) Числа 13 и 31 являются простыми числами. Оба эти числа имеют одинаковые цифры 1 и 3. Найдите s…
Оба эти числа имеют одинаковые цифры 1 и 3. Найдите s…
Q11) Запишите пять пар простых чисел меньше 20, сумма которых делится на 5.
Q6) Выразите следующее в виде суммы двух нечетных простых чисел. (i) 44 (ii) 36 (iii) 24 (iv) 18
Q7) Назовите три пары простых чисел, разность которых равна 2. [Примечание: два простых числа, разность которых…
Фейсбук
WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Упражнение 3. 1
1
Упражнение 3.2
Упражнение 3.3
Упражнение 3.4
Упражнение 3.5
Упражнение 3.6
Упражнение 3.7
Главы
Знание наших чисел
ВСЕГО НОМЕР
Играть с номерами
. Геометрические идеи
Понимание элементарных фигур
Целые числа
Дроби
Десятичные числа
Обработка данных
Измерение
Алгебра
Отношение и пропорция
Симметрия
Практическая геометрия
Курсы
Быстрые ссылки
Условия и политика
Условия и политика
2022 © Quality Tutorials Pvt Ltd Все права защищены
Основы четных и нечетных чисел
: любое целое число, которое делится на 2. Примеры: 2, 4, 14.
Odd : любое целое число, которое не делится на 2, т.е. дает остаток 1 при делении на 2. Примеры: 1, 3, 5, 7, 9
Пока все хорошо. Рассмотрим это потенциальное заблуждение:
0 четный или нечетный?
При делении 0 на 2 получается 0 ÷ 2 = 0. Другими словами, 0 делится на 2. Следовательно, ноль соответствует критериям, установленным для четных целых чисел. Следовательно, ноль четный.
Другими словами, 0 делится на 2. Следовательно, ноль соответствует критериям, установленным для четных целых чисел. Следовательно, ноль четный.
Ноль нейтрален, когда речь идет о положительных и отрицательных числах, т.е. ноль не является ни положительным, ни отрицательным — он нейтрален. Не путайте это с четным и нечетным.
Но ноль делится на 3, 5 и 7…. также?
Тот факт, что ноль делится и на другие нечетные целые числа (и да, ноль делится на 3, 5, 7 или любое другое целое число, кроме самого себя), не имеет значения.
Определение четного или нечетного числа имеет отношение только к делимости на 2. Например, 6 является четным числом, потому что оно делится на 2. 6 также делится на 3, но это не имеет значения.
Запомните этот факт: Ноль четен.
Нечетные и четные целые числа также могут быть отрицательными; например, ?7 нечетно, а ?18 четно.
Четные числа: {…. , -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10, ….}
, -10, -8, -6, -4, -2, 0, 2, 4, 6, 8, 10, ….}
Нечетные числа: {…., -9 , -7, -5, -3, -1, 1, 3, 5, 7, 9, ….}
Какое из следующих чисел НЕ является четным?
- -117
- -4.222
- -2
- 0
- 2,2
- 100.002
- 498
- 117 — нечетное число, поскольку оно не делится на 2.
- -4,222 — десятичное число. Десятичные значения не являются ни четными, ни нечетными.
- -2 — четное число, так как оно делится на 2.
- 0 — четное число, поскольку оно делится на 2.
- -2,2 — десятичное число. Десятичные значения не являются ни четными, ни нечетными.
- 100,002 — десятичное число. Десятичные значения не являются ни четными, ни нечетными.
- 498 — четное число, так как оно делится на 2.
Как и у большинства людей, сдающих GRE, ваши знания по математике могут быть немного заржаветыми. Хорошей новостью является то, что GRE проверяет вас только по математике, которую вы уже выучили в старшей школе. Если вы беспокоитесь, что забыли большую часть того, что выучили в старшей школе, вам придется…
Хорошей новостью является то, что GRE проверяет вас только по математике, которую вы уже выучили в старшей школе. Если вы беспокоитесь, что забыли большую часть того, что выучили в старшей школе, вам придется…
читать дальше
Стандартное отклонение – важный статистический термин, проверенный на GRE. Это дает вам представление об отклонении или разбросе набора чисел от его среднего значения; следовательно, низкое стандартное отклонение означает, что числа очень близки к среднему, и наоборот…
подробнее
Каждое целое число больше 1 является либо простым, либо составным числом. Все составные числа можно представить в виде произведения простых чисел. Например, 6 можно выразить как 2 × 3. Простые делители 6 — это 2 и 3. Тогда как выражение 2 × 3 называется…
читать далее
Давайте посмотрим, как мы используем диаграмму, чтобы ответить на этот вопрос: сколько положительных факторов имеет 100? Настройте диаграмму: 100 Левая колонка Правая колонка 1 100 2 50 4 25 5 20 10 10 Помните правило: как только факторы повторяются (например, 10 и 10), остановитесь. С…
С…
подробнее
Вы уже видели прекрасную таблицу множителей — простой способ найти все множители целого числа. Давайте посмотрим, как мы используем диаграмму, чтобы ответить на этот вопрос: сколько положительных факторов имеет число 140? Вопрос касается факторов, поэтому таблица факторов…
читать дальше
Некоторые целочисленные вопросы могут потребовать от вас найти множители целого числа. Таблица множителей — это основной метод нахождения всех множителей любого целого числа. Этот метод также может быть полезен для вопросов о том, сколько множителей имеет конкретное целое число. Техника…
подробнее
Простые числа играют центральную роль в целочисленных вопросах. Излишняя самоуверенность здесь опасна: в то время как почти каждый может без труда назвать определение простого числа, поле на самом деле изобилует неправильными представлениями.
