25 на 6 умножить на: Mathway | Популярные задачи

Содержание

ГДЗ по математике 4 класс учебник Моро, Бантова 1 часть

Тип: ГДЗ, Решебник.
Автор: Моро М. И., Волкова С. И., Бантова М. А.
Год: 2020.
Серия: Школа России (ФГОС).
Издательство: Просвещение.

❤️️Ответ к странице 77. Математика 4 класс учебник 1 часть. Авторы: М.И. Моро, М.А. Бантова.

Решебник — страница 77Готовое домашнее задание

Учимся выполнять умножение многозначного числа на однозначное.
Письменное умножение любого многозначного числа на однозначное выполняется так же, как умножение трёхзначного числа на однозначное: сначала умножают единицы, потом десятки, сотни и т. д.
Объясни, как выполнено умножение.

Ответ:

Умножаем единицы: 3 умножить на 2, получится 6. Записываем под единицами. Умножаем на десятки: 3 умножить на 3, получится 9.

Записываем под десятками. Умножаем сотни: 3 умножить на 4, получится 12. 2 пишем, 1 десяток запоминаем. Умножаем единицы тысяч: 3 умножить на 5, получится 15, прибавляем 1, получается 16. Читаем ответ: 16296.

Номер 333.

Выполни умножение, используя, когда это удобно, перестановку множителей.

Ответ:

2 км 425 м ∙ 8 = 19 км 400 м 2 км 425 м = 2425 м 19400 м = 19 км 400 м

18 ц 02 кг ∙ 4 = 72 ц 08 кг 18 ц 02 кг = 1802 кг 7208 кг = 72 ц 08 кг

230 см² ∙ 4 = 920 см²

Номер 334.

В куске 40 м полотна. От него отрезали полотна на 6 детских простыней, по 1 м 80 см на каждую, и на наволочки 10 м 20 см. Сколько метров полотна осталось?

Ответ:

Было – 40 м Отрезали – 6 шт. по 1 м 80 см Отрезали – 10 м 20 см Осталось – ? м 1) 1 м 80 см ∙ 6 = 10 м 80 см – ушло полотно на простыни.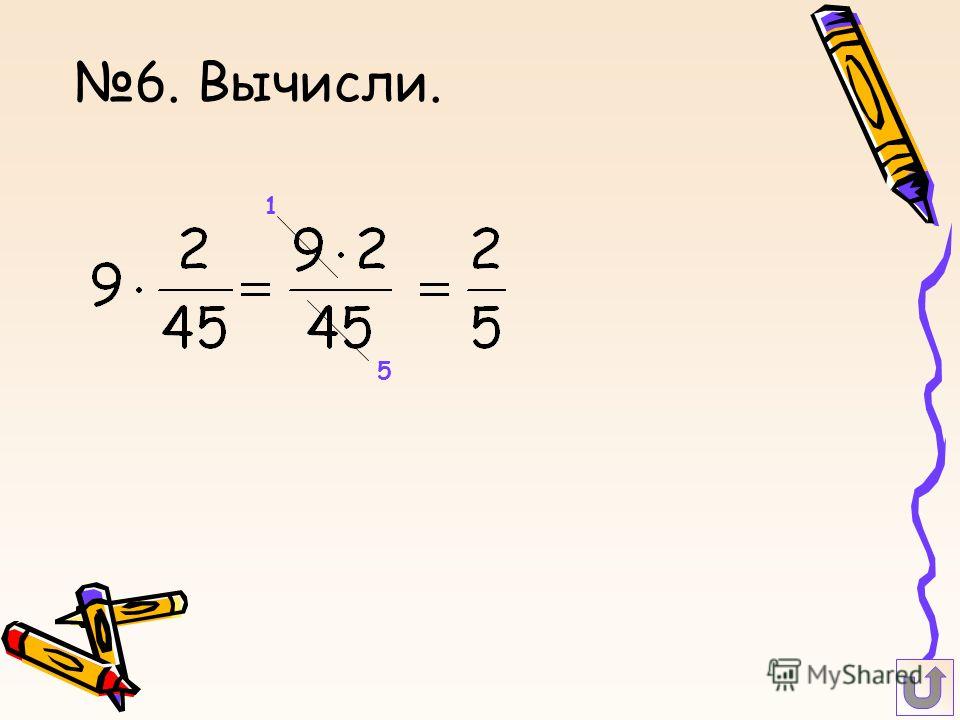

2) 10 м 80 см + 10 м 20 см = 21 м – ушло полотна на простыни и наволочки. 3) 40 м − 21 м = 19 (м) Ответ: 19 метров полотна осталось.

Номер 335.

В мастерской сшили 6 простыней, расходуя на каждую по 2 м 20 см полотна, и 8 наволочек, расходуя на каждую по 1 м 25 см полотна. Поставь вопрос и реши задачу.

Ответ:

Сколько метров полотна израсходовали?

1) 2 м 20 см ∙ 6 = 1320 (см) – ушло на простыни.

2) 1 м 25 см ∙ 8 = 1000 (см) – ушло на наволочки.

3) 1320 см + 1000 см = 2320 (см) 4) 2320 см = 23 м 20 (см) Ответ: 23 м 20 см полотна израсходовали.

Номер 336.

Папа прошёл 500 м за 5 мин. Сколько километров он пройдёт за 1 ч, если считать, что за каждую минуту он проходит одинаковое количество метров?

Ответ:

Можно оформить так:
5 мин – 500 м 1 ч – ? м 1) 500 : 5 = 100 (м) – за 1 мин. 2) 1 ч = 60 мин 3) 100 ∙ 60 = 6000 (м) 4) 6000 м = 6 км Ответ: 6 км за 1 час.

Номер 337.

Ответ:

Номер 338.

1) Сравни площади прямоугольников ABCD и KMOP.
2) Сравни площади квадрата ATFD и треугольника KOP.

Ответ:

1) Sᴀʙᴄᴅ = 6 ∙ 3 = 18 см² Sᴋᴍᴏᴘ = 6 ∙ 3 = 18 см² Sᴀʙᴄᴅ = Sᴋᴍᴏᴘ
2) Sᴀᴛғᴅ = 3 ∙ 3 = 9 см² Sᴋᴏᴘ = (6 ∙ 3) : 2 = 9 см² Sᴀᴛғᴅ = Sᴋᴏᴘ

Номер 339.

В первой корзине было 25 кг слив, а во второй – на 7 кг меньше. Из первой корзины переложили во вторую 4 кг слив. Догадайся, в какой корзине слив стало больше и на сколько килограммов. Проверь себя вычислением.

Ответ:

1) 25 − 7 = 18 (кг) – слив во второй корзине. 2) 25 − 4 = 21 (кг) – слив в первой корзине. 3) 18 + 4 = 22 (кг) – слив стало во второй корзине. 4) 22 − 21 = 1 (кг) Ответ: на 1 кг слив больше во 2-ой корзине.

Задание внизу страницы

Ответ:

26 м 85 см ∙ 7 = 187 м 95 см 26 м 85 см = 2685 см 18795 см = 187 м 95 см

1 т 250 кг ∙ 8 = 10 т 1 т 250 кг = 1250 кг 10000 кг = 10 т

190 мм² ∙ 5 = 950 мм²

Рейтинг

Выберите другую страницу

1 часть

Учебник Моро	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111

2 часть

4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45	46	47	48	49	50	51	52	53	54	55	56	57	58	59	60	61	62	63	64	65	66	67	68	69	70	71	72	73	74	75	76	77	78	79	80	81	82	83	84	85	86	87	88	89	90	91	92	93	94	95	96	97	98	99	100	101	102	103	104	105	106	107	108	109	110	111	112	113	114	115	116	117	118	119	120	121	122	123	124	125	126	127

Ваше сообщение отправлено!

Калькулятор дробей

Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.

Правила выражения с дробями:

Дроби — используйте косую черту для деления числителя на знаменатель, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.

Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной строки и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т. е. 1,45 .

Math Symbols

Symbol

Symbol name

Symbol Meaning

Example

plus sign

addition

1/2 + 1/3

—

знак минус

вычитание

1 1/2 — 2/3

asterisk

multiplication

2/3 * 3/4 

times sign

multiplication

2 /3 × 5/6

division sign

division

1/2 : 3

division slash

division

1/3 / 5 1/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целых чисел и дробей: 5 ÷ 1/2
• сложные дроби: 5/8 : 2 2/3
• десятичная дробь: 0,625
• Преобразование дроби в десятичную: 1/4
• Преобразование дроби в процент: 1/8 %
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4
• квадратный корень дроби: sqrt(1/16)
• уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение со скобками: 1/3 * (1/2 — 3 3/8)
• составная дробь: 3/4 от 5/7
• кратные дроби: 2/3 от 3/5
• разделить, чтобы найти частное: 3/5 ÷ 2/3

Калькулятор следует известным правилам для порядка операций . Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — Скобки, Экспоненты, Умножение, Деление, Сложение, Вычитание.
BEDMAS — Скобки, Экспоненты, Деление, Умножение, Сложение, Вычитание
BODMAS — Скобки, Порядок, Деление, Умножение, Сложение, Вычитание.
GEMDAS — Символы группировки — скобки (){}, возведения в степень, умножение, деление, сложение, вычитание.
MDAS — Умножение и деление имеют тот же приоритет, что и сложение и вычитание. Правило MDAS является частью порядка операций правила PEMDAS.
Будьте осторожны; всегда выполняйте умножение и деление перед сложением и вычитанием . Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны оцениваться слева направо.

Использование денег
Из 550 000,00, переданных школе, было использовано 325 000,00. Какая часть от общей суммы была использована?
Дети 9
В комнате 11 детей. Шесть детей — девочки. Какую часть детей составляют девочки?
Упрощение 12
Упрощение {1/3 + 1/12} ÷ {2/3 — 5/8}
Одна суббота
В один из субботних вечеров в кинотеатре 40 девушек, 25 юношей, 18 женщин и 17 мужчин. Какую часть составляют девочки?
Что такое 22
Что такое 7/21 в простейшей форме?
Дробями
Муравей поднимается на 2/5 шеста за первый час и на 1/4 шеста за следующий час. Какую часть шеста преодолевает муравей за два часа?
У Макса 2
У Макса 13 пар носков. Отсюда шесть пар синих, три пары коричневых, две черных и две белых. Какая часть носков Макса коричневого или черного цвета?
Дроби 80134
В школе 420 учеников. Двести пятьдесят два ученика переходят на 1-й уровень. Напишите в виде дроби, какая часть учеников идет в 1-й класс, а какая во 2-й класс. Сократите обе дроби до их основной формы.
Дети
Двое взрослых, двое детей и четверо младенцев находятся в автобусе. Какую часть населения составляют младенцы?
Женитьба
Женитьба имела 1 1/2 дюжины яиц в холодильнике. Использовала 1/3 яйца. Какая часть яиц использовалась?
Вычислить выражение
Вычислить значение выражения z/3 — 2 z/9 + 1/6, для z = 2

другие математические задачи »

десятичные числа
дроби 60209 Δ089 треугольник 2ABC
Permille ‰
Prime Factors
Комплексные номера
LCM
GCD
LCD
Comminatorics
Уравнения

… Уравнения. Таблица 2, 3,4,5,6,7 и преимущества

Что такое умножение?

Процесс нахождения произведения двух или более чисел называется умножением. Полученный таким образом результат называется продукт . Предположим, вы купили 6 ручек в один день и 6 ручек на следующий день. Всего ручек, которые вы купили, теперь 2 умножить на 6 или 6 + 6 = 12.

Это также можно записать как 2 x 6 = 12

Обратите внимание на символ, используемый для умножения. Символ (x) обычно используется для обозначения умножения. Другими распространенными символами, которые используются для умножения, являются звездочка (*) и точка (.)

Что подразумевается под умножением как сравнением?

Умножение путем сравнения означает, что вы сравниваете две величины таким образом, что при умножении одной величины на определенное число получается другая величина. Возьмем пример. Рассмотрим предложение «Гарри в два раза выше Питера». Это означает, что если возраст Питера равен «p», то возраст Гарри будет в два раза больше, чем у Питера, т. е. 2p.

Возьмем другой пример.

Пример

Длина скамейки 30 м. это в три раза больше длины стула. Какова длина табурета?

Решение

Нам дано, что длина скамьи 30 м. это в три раза больше длины стула. Теперь пусть длина табурета будет « s ». Следовательно, имеем

3 s = 30

⇒ s = 10 м

Следовательно, длина табурета 30 м

Представление таблицы умножения в виде умножения путем сравнения

Давайте теперь разберемся, как читать некоторые таблицы умножения в форме умножения путем сравнения

Умножение как сравнение для таблицы 2 4 Умножение Таблица

Умножение как сравнение
2 × 1 = 2	2 в один раз больше, чем в 2, и в 2 раза больше, чем один
2 × 2 = 4	4 в два раза больше 2
2 × 4 = 8	8 в четыре раза больше 2 и в два раза больше четырех умножить на пять
2 × 6 = 12	12 в шесть раз больше 2 и в 2 раза больше шести
2 × 7 = 14 2 × 8 = 16	16 в восемь раз больше 2 и в два раза больше восьми
2 × 9 = 18 как девять
2 × 10 = 20	20 в десять раз больше 2 и в 2 раза больше десяти
2 x 11 = 22	22 в одиннадцать раз больше 2 и в 2 раза больше одиннадцати 2 x 12 = 24	24 в двенадцать раз больше 2 и в два раза больше двенадцати
тринадцать
2 x 14 = 28	28 в четырнадцать раз больше 2 и в два раза больше четырнадцати
2 x 15 = 30 2 x 16 = 32	32 в шестнадцать раз больше 2 и в 2 раза больше шестнадцати
2 x 17 = 34 семнадцать
2 x 18 = 36	36 в восемнадцать раз больше 2 и в два раза больше восемнадцати
2 x 19 = 38 as nineteen
2 x 20 = 40	40 is twenty times as many as 2 and 2 times as many as twenty

Multiplication as Comparison for Table of 3 в четыре раза больше 3 и в 3 раза больше четырех 3 × десять раз больше

Таблица умножения	Умножение по сравнению с сравнением
3 × 1 = 3	3 — это одно время 3 и 3 раза до одного
3 3 × 2 = 2
3 и 3 раза. в два раза больше 3 и в три раза больше двух
3 × 3 = 9	3 в три раза больше 3
3 × 4 = 12	12
3 × 5 = 15	15 в пять раз больше 3 и в 3 раза больше пяти
3 × 6 = 18 В 3 раза больше, чем шесть
3 × 7 = 21	21 в семь раз больше, чем в 3, и в 3 раза больше, чем семь
3 × 8 = 24 9046 восемь в 3 раза больше, чем в 3 раза, и в 3 раза больше, чем в восемь раз
3 × 9 = 27	27 в девять раз больше 3 и в три раза больше девяти
3 × 10 = 30
3 x 11 = 33	33 в одиннадцать раз больше 3 и в 3 раза больше одиннадцати целых 3 и 3 раза больше двенадцати
3 x 13 = 39	39 — в тринадцать раз до 3 и 3 раза до тринадцати
3 x 14 = 42	42 42 года. четырнадцать раз
3 x 15 = 45	45 в пятнадцать раз больше, чем в 3, и в три раза больше, чем пятнадцать целых 3 и 3 раза больше шестнадцати
3 x 17 = 51	51 в семнадцати раз в 3 и 3 раза больше семнадцати
3 x 18 = 54	54 54 раза. Времена до восемнадцати
3 x 19 = 57	57 в девятнадцать раз до 3 и 3 раза до девятнадцати
3 x 20 = 60	6045 60276 3 x 20 = 60 70046	6045 60276 целых 3 и 3 раза больше двадцати

Умножение в качестве сравнения для таблицы 4 469695 4 × 5 = 20 70046 4004666469695 4 × 5 = 200027 70046

СПАСИВАНИЕ	. В 4 и 4 раза больше, чем один
4 × 2 = 8	8 в два раза больше, чем в 4 и в 4 раза больше, чем два
4 × 3 = 7 9 46	12 в три раза до 4 и 4 раза до трех
4 × 4 = 16	16 — четыре раза до 4
4 × 5 = 20
4 × 5 = 200046
4	20 в пять раз больше 4 и в 4 раза больше пяти
4 × 6 = 24	24 в шесть раз больше 4 и в 4 раза больше шести × 7 = 28	28 в семь раз больше 4 и в 4 раза больше семи
4 × 8 = 32	32 в восемь раз больше 4 и в 4 раза больше восьми
4 × 9 = 36 В 4 раза больше девяти
4 × 10 = 40	40 в десять раз больше в 4 и в 4 раза больше десяти
4 × 11 = 47 904 = 47 904 раз больше и в 4 раза больше одиннадцати
4 x 12 = 48	48 в двенадцать раз больше, чем в 4, и в четыре раза больше, чем двенадцать
4 x 13 = 52 Время в тринадцать
4 x 14 = 56	56 в четырнадцать раз до 4 и 4 раза до четырнадцати
4 x 15 = 60 7	6045 6045 6045 6045 6045 6045 6045 6045 6045 6045 6045 6045 6045 6045 40276 целых 4 и 4 раза больше пятнадцати
4 x 16 = 64	64 в шестнадцать раз до 4 и 4 раза до шестнадцати
4 x 17 = 68	68 6. 4 раза больше семнадцати
4 x 18 = 72	72 в восемнадцать раз до 4 и 4 раза до восемнадцати
4 x 19 = 76 77796	76 76 76 76 76 76 6 раза 19 = 76 77777796	76 76 76 76 76 76 76 6 целых 4 и 4 раза больше девятнадцати
4 x 20 = 80	80 — в двадцать раз до 4 и 4 раза до двадцати

Умножение по сравнению с сравнением

5 × 1 = 5

5 — это одно время 5 и 5 раз, до одного

5 5 × 2 = 100046

576.0277

10 вдвое больше 5 и в 5 раз больше двух

5 × 3 = 15

15 в три раза больше 5 и в 5 раз больше трех 5 × 4 = 20

20 в четыре раза до 5 и 5 раз до четырех

5 × 5 = 25

25 — пять раз 5

76 — это пять раз до 5

76. 5 × 6 = 30

30 в шесть раз больше, чем 5, и в 5 раз больше, чем шесть

5 × 7 = 35

35 в семь раз больше и в 5 раз больше, чем семь

5 × 8 = 40 0 в восемь раз больше, чем

5 × 9 = 45

45 в девять раз больше 5 и в 5 раз больше девяти

5 × 10 = 90 9047 раз десять целых 5 и 5 раз больше десяти

5 x 11 = 55

55 в одиннадцать раз больше 5 и в пять раз больше одиннадцати

5 x 12 = 60 Время до двенадцати

5 x 13 = 65

65 — в тринадцать раз до 5 и 5 раз больше, чем тринадцать

5 x 14 = 7027777 70046

7045 7045 7045 7045 7045 7045 7045 7045 7045 7045 7045 7045 7045 7045 7045 7045

целых 5 и 5 раз больше четырнадцати

5 x 15 = 75

75 в пятнадцать раз больше, чем в 5, и в пять раз больше, чем пятнадцать 5 раз шестнадцать

5 x 17 = 85

85 — в семнадцать раз до 5 и 5 раз больше семнадцати

5 x 18 = 90 7

5 x 18 = 90 77

5 x 18 = 90 777

5 x 18 = 90

5 X целых 5 и 5 раз больше восемнадцати

5 x 19 = 95

95 в девятнадцати раз до 5 и 5 раз до девятнадцати

5 x 20 = 100

1005 5 x 20 = 100

100 100 — это двадние времена.

5 раз двадцать

Умножение в качестве сравнения для таблицы 6 9004 6 и 6 раз больше четырех

Таблица

.0276 6 × 1 = 6

6 в 1 раз больше, чем в 6 и в 6 раз больше, чем один

6 × 2 = 12 как два

6 × 3 = 18

18 в три раза больше 6 и в 6 раз больше трех

6 × 4 = четыре раза больше 24

6 × 5 = 30

60 в пять раз до 6 и 6 раз до пяти

6 × 6 = 36

36 — это шесть раз 6

6 × 70277777777777

6 42 77777777777777777777

6 × 7027777777777777777779

6 × 7027777777777

42 в семь раз больше и в 6 раз больше семи × 9 = 54

54 в девять раз больше 6 и в 6 раз больше девяти

6 × 10 = 60

60 в десять раз больше 6 и в 6 раз больше десяти В 6 раз до одиннадцати

6 × 12 = 72

72 в двенадцать раз до 6 раз до двенадцати

6 × 13 = 78 70046

6 × 13 = 78 7 70046

6 × раз больше 6 и в 6 раз больше тринадцати

6 × 14 = 84

84 в четырнадцать раз больше 6 и в шесть раз больше четырнадцати 6 раза до пятнадцати

6 × 16 = 96

96 в шестнадцать раз до 6 и 6 раз до шестинадцати

6 × 17 = 102 779646

6 × 17 = 102 7 70046

6 6 × 17 = 1027777 70046

раз больше 6 и в 6 раз больше семнадцати

6 × 18 = 108

108 в восемнадцать раз в 6 и 6 раз до восемнадцати

6 × 19 = 114

114 — это многие. В 6 раз больше девятнадцати

6 × 20 = 120

120 — в двадцать раз больше, чем в 6 раза до двадцати

Multiplication As Compecore Table at Table of 7 7777777 70039

. Multiplication Table Multiplication as Comparison 7 × 1 = 7 7 is one time as many as 7 and 7 times as many as one 7 × 2 = 14 14 вдвое больше 7 и в 7 раз больше двух 7 × 3 = 21 21 в три раза больше 7 и в 7 раз больше трех 7 × 4 = 28 28 в четыре раза больше, чем 7, и в 7 раз больше, чем четыре пять 7 × 6 = 42 42 в шесть раз больше 7 и в 7 раз больше шести 7 7 × 8 = 56 56 в восемь раз больше, чем 7, и в 7 раз больше, чем восемь 7 × 9 = 63 63 в девять раз больше 7 и в 7 раз больше девяти 7 × 10 = 70 7 раз больше десяти 7 х 11 = 77 77 в одиннадцать раз больше 7 и в 7 раз больше одиннадцати 6 х 902 двенадцать = 84 904 раз больше 7 и в 7 раз больше двенадцати 7 x 13 = 91 91 в тринадцать раз до 7 и 7 раз больше, чем тринадцать 7 x 14 = 98 98 7. В 7 раз четырнадцать 7 x 15 = 105 105 — в пятнадцать раз до 7 и 7 раз больше пятнадцати 7 x 16 = 11277777 70046. раз больше 7 и в 7 раз больше шестнадцати 7 x 17 = 119 119 в семнадцать раз до 7 и 7 раз больше семнадцати 7 x 18 = 126 126 — это восемь. Времена до восемнадцати 7 x 19 = 133 133 в девятнадцать раз до 7 и 7 раз больше девятнадцати 7 x 20 = 140 70046 7 x 20 = 140 7 70046 7 x 20 = 140. целых 7 и 7 раз больше двадцати
Преимущества обучения умножению в сравнении
Ниже приведены преимущества обучения умножению в сравнении –
Понимание умножения путем сравнения величин позволяет учащимся понять понятия, поскольку они повышают уровень сложности умножения.
Легче связать, как числа умножаются друг на друга, когда они проецируются как сравнительные величины.
Ключевые факты и резюме
Процесс нахождения произведения двух или более чисел называется умножением. Полученный таким образом результат называется произведением.
Символ (x) обычно используется для обозначения умножения. Другими распространенными символами, которые используются для умножения, являются звездочка (*) и точка (.)
Умножение в сравнении означает, что вы сравниваете две величины таким образом, что при умножении одной величины на определенное число получается другая величина. произведено.
Понимание умножения путем сравнения величин позволяет учащимся понять понятия, поскольку они повышают уровень сложности умножения.
Легче связать, как числа умножаются друг на друга, когда они проецируются как сравнительные величины.
Мультипликативные сравнения и уравнения Рабочие листы по математике для 4-го класса
Свойство умножения (на тему Дня святого Валентина) Рабочие листы по математике
Таблицы умножения (на тему Дня святого Патрика) Рабочие листы по математике
Ссылка/ссылка на нас
Мы тратим много времени на изучение и сбор информации на этом сайте.

No related posts.