9 класс. Алгебра. Рациональные неравенства и их системы. — Линейное неравенство с модулем.
Комментарии преподавателяОпределение модуля и его геометрический смысл.
Модулем числа t называется само число t, если оно больше либо равно 0. Либо противоположное ему число t, если оно меньше 0
Иногда определение дают иначе. Модуль t равен t для положительных чисел и для нуля. И модуль t равен -t, когда под модулем стоит отрицательное число либо 0.
Пример.
Модулем называется само число, если оно не отрицательное, и противоположное число, если оно отрицательное.
Рис. 3. Модуль числа 3
Геометрически (рис. 3)
– это расстояние от точки с координатой 3 до 0.
– это расстояние от точки с координатой -3 до 0.
– это расстояние от точки с координатой х до 0.
– это расстояние от точки с координатой х -3 до 0, т.
е. это расстояние от точки х до 3.
– это расстояние от точки х до -3
1 способ. Применим общий приём освобождения от модуля на основе его определения.
Чтобы освободиться от модуля, нужно рассмотреть два случая.
Случай 2
Если под модулем стоит неотрицательное число, то модуль можно просто отбросить.
Рис. 4. Иллюстрация к примеру
[2;5) (рис. 4)
Случай 2
Если под модулем стоит число отрицательное, то нужно отбросить модуль, поставить знак минус перед всем подмодульным выражением.
Рис. 5. Иллюстрация к примеру
(-1;2) (рис. 5)
Решение первой системы и решение второй системы нужно объединить.
Рис. 6. Иллюстрация к примеру
-1 < х <-5
(-1; 5) (рис. 6)
2 способ. Используем геометрический смысл модуля.
Что такое модуль х-2? Это расстояние между точками с координатами х и 2.
Согласно условию неравенства, это расстояние не должно превышать 3 (рис. 7).
Рис. 7. Иллюстрация к примеру
Поставим на числовой оси точку 2. Отступим от нее на 3 вправо и влево по оси. Справа получим точку 2 + 3 = 5; слева точку 2 — 3 = -1
Итак, геометрический смысл неравенства: найти те значения х, которые отстоят от 2 не больше, чем на 3. То есть, можно записать
-3+2 < х <3+2
-1 < х < 5
Решим двойное неравенство. Перенесем «-2» с противоположным знаком вправо и влево.
Решим противоположную задачу.
Что такое модуль х-2? Это расстояние между точками с координатами х и 2. Согласно условию неравенства, это расстояние должно превышать 3 или быть равно 3.
Рис. 8. Иллюстрация к примеру
Поставим на числовой оси точку 2. Отложим 3 в одну сторону и 3 в другую сторону. Где же те значения х, которые отстоят от 2 на расстояние 3 или далее?
На расстоянии 3 находятся точки -1 и 5.
На большем расстоянии находятся точки левее -1 и правее 5 (рис. 8).
Итак, ответ: .
Источник конспекта: http://interneturok.ru/ru/school/algebra/9-klass/itogovoe-povtorenie-kursa-algebry-9go-klassa/lineynye-neravenstva-i-ih-sistemy-modul?konspekt&chapter_id=41
Источник видео: http://www.youtube.com/watch?v=DNG-BwsJmvk
ФайлыНет дополнительных материалов для этого занятия.
Иррациональные неравенства. Неравенства с модулем
Дата публикации: .
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Скачать:Иррациональные неравенства. Неравенства с модулем (PPTX)
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 11 класса
Интерактивное пособие для 9–11 классов «Тригонометрия»
Интерактивное пособие для 10–11 классов «Логарифмы»
Ребята, на данном уроке мы рассмотрим способы решений двух видов неравенств.
Они могут пригодиться при подготовке к единому государственному экзамену, если вы будете решать задачи из второй части экзамена.
Такие неравенства называются иррациональными. В нашем выражении присутствует корень квадратный, который накладывает свои ограничения на область допустимых значений.
Первое, что мы должны иметь в виду, корень квадратный извлекается только из положительных чисел, поэтому $f(x)≥0$.
Второе, вспомните график функции корня квадратного. Значения, которые он принимает не меньше нуля. Тогда для выполнения условий неравенства, требуется условие $g(x)>0$, равенство нулю не возможно, так как наше исходное неравенство строгое и равенство значений не возможно.
Третье, обе части неравенства не отрицательные. Тогда, используя теорему 5, урока о равносильности неравенств, мы можем обе части нашего неравенства возвести квадрат, то есть получить неравенство: $f(x)
Итак, при решении иррациональных неравенств можно переходить к следующей системе неравенств:
$\sqrt{f(x)}<g(x)\begin {cases} f(x)≥0, \\ g(x)>0, \\ f(x)<{(g(x))}^{2} \end {cases}$.
Решим систему: $\begin {cases} (x-5)(x+6)≥0, \\ x>0, \\ x
Воспользуемся методом интервалов.
Решения всех трех неравенств системы пересекаются на отрезке $[5;30)$, который и есть решение исходного неравенства.
б) Нам нужно решить совокупность двух систем:
Решения каждой системы очевидны, даже не применяя метод интервалов:
Ответ: а) $хϵ[5;30)$: б) $хϵ(-∞;6]U(30;+∞)$.
Неравенства с модулями
Неравенства, которые содержат переменную под знаком модуля, могут решаться разными методами. Мы рассмотрим три способа решения. Советую применять третий способ. Он может занимать немного больше времени, но зато гораздо больше шансов на правильное решение неравенства.
Пример.
Решить неравенство: $|3x-6|>6$.
Решение.
Первый способ.
$|3(x-2)|>6$; $|(x-2)|>2$.
Как мы помним, геометрически смысл модуля есть ни что иное, как расстояние между точка х и 2. Согласно нашему неравенству оно должно превышать 2. Тогда решением будет $(-∞;0)U(4;+∞)$.
2$.
Integrated Math 1
Mr. Math Blog
Interior and Exterior Angles — Module 22.1
Isosceles and Equilateral Triangles — Module 22.2
Triangle Inequalities — Module 22.3
Creating Linear Systems — Module 12.1 (Part 1)
Создание линейных систем из графов — Модуль 12.1 (Часть 2)
Графовые системы линейных неравенств — Модуль 12.2
Моделирование линейных систем — Модуль 12.3
Блок 5 Обзор испытаний
Практический тест на блоке 5
Первый семестр 1-12
. Теорема о конгруэнтности — Модуль 20.2
SAS Теорема о конгруэнтности треугольников — Модуль 20.3
SSS Теорема о конгруэнтности треугольников — Модуль 20.4
Второй семестр Модули 14-22
Измерение центра и разброса — модуль 9.
1 (часть 1)
Измерение стандартного отклонения — модуль 9.1 (часть 2)
Распределение данных с точечной диаграммой и выбросами — модуль 9.2
9000 9.3 (Часть 1)
Построение коробчатых диаграмм — Модуль 9.3 (Часть 2)
Нормальное распределение — Модуль 9.4
Понимание геометрических последовательностей — Модуль 14.1
Построение геометрических фигур0003
Подробнее Построение геометрии. Seq.s — Модуль 14.2 (Часть 2)
Построение экспоненциальных функций — Модуль 14.3 (Часть 1)
Построение экспоненциальных функций из описаний — Модуль 14.3 (Часть 2)
Графики экспоненциальных функций — Модуль 9004 14.4
Преобразование экспоненциальных функций — модуль 14.5 (часть 1)
Преобразование экспоненциальных функций — модуль 14.5 (часть 2)
Повторение теста по модулю 14
Свойства параллелограмма — Модуль 24.
1
Условия для параллелограммы — Модуль 24.2
Свойства прямоугольников ромбов и квадратов — Мод 24.3
Прямоязы Свойства и условия воздушных змеев и трапеций — Мод. 24.5
Практический тест по Модулю 24 — Свойства четырехугольников
Моделирование линейных отношений — Урок 7.1
Решите одну переменную уравнения — Урок 7.2 (Часть 1)
Решить одну переменную уравнения — Урок 7.2 (часть 2)
Линейные неравенства в двух переменных — Урок 7.3
Практический тест для блока 3
110003
Невязки — модуль 10.2
Периметр и площадь на координатной плоскости — модуль 25.5
Ваше небольшое пожертвование помогает мне поддерживать вас. Благодарю вас! 🙂
Биссектрисы треугольников — Модуль 23.1
Биссектрисы углов треугольников — Модуль 23.2
Медианы треугольника — Модуль 23.
3 (Часть 1)
90 Высоты 2 Треугольников
Средние сегменты треугольников — Модуль 23.4
Практический тест
Пожалуйста, сделайте пожертвование, если вы постоянный клиент!
Ссылка для пожертвований находится ниже. Спасибо большое!!
Форма перехвата наклона — Урок 6.1
Форма точка -наклона — Урок 6.2
Стандартная форма — Урок 6.3
Блок 7 Практический тест Обзор
Понимание линейных функций — Урок 5.1 (Часть 1)
Моделирование с помощью линейных функций — Урок 5.1 (Часть 2)
Использование перехватов — Урок 5.2
Интерпретация скорости изменения и наклона — Урок 5.3
Спасибо, что старались! 🙂
Длина отрезка и его середины — Модуль 16.1 (Часть 1)
Длина отрезка и его середины — Модуль 16.1 (Часть 2)
Измерения углов и биссектрисы углов — Модуль 16.
2 (Часть 1) и биссектрисы угла — Модуль 16.2 (Часть 2)
Представление и описание преобразований — Модуль 16.3
Рассуждение и доказательство — модуль 16.4
Обзор для модуля 16 Викторина
Переводы — Модуль 17.1
Размышления — Модуль 17.2
Ротации — Модуль 17.3
.
Идентификация и графическое отображение последовательностей — Урок 4.1 (Часть 1)
Графическое построение последовательностей — Урок 4.1 (Часть 2)
Построение арифметических последовательностей — Урок 4.2 (Часть 1)
Конструирование и написание арифметических последовательностей — Урок 4.2 (часть 2)
Моделирование с арифметическими последовательностями — Урок 4.3 (часть 1)
больше моделирования с арифметической последовательности — Урок 4.3 (Часть 2)
. 2 Тестовый обзор модулей 3 и 4
Отношения и интерпретация графиков — Урок 3.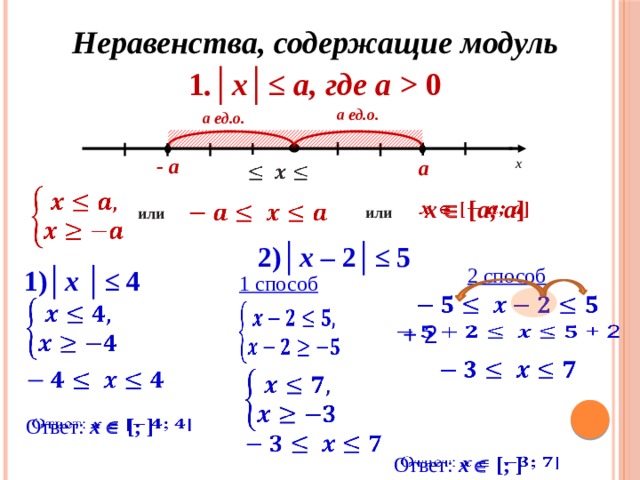
1 (Часть 1)
Наброски графиков для ситуаций — Урок 3.1 (Часть 2)
Понимание отношений и функций 3. 20003
Моделирование с помощью функций — Урок 3.3 (Часть 1)
Моделирование функций с областью определения и диапазоном — Урок 3.3 (Часть 2)
Графические функции — Урок 3.4 (Часть 1)
Задание на производительность — Проверка для теста — Модуль 3
Моделирование с помощью выражений — Урок 2.1 (Часть 1)
Сравнение и моделирование алгебраических выражений — Урок 2.1 (Часть 2)0003
Создание и решение уравнений – Урок 2.2 (Часть 1)
Переменные с обеих сторон – Урок 2.2 (Часть 2)
Решение переменных в буквенных уравнениях – Урок 2.3
4 9 2.4. Часть 1 )
Блок 1 Практическая викторина Обзор
Проверка задачи выполнения для теста — Блок 1 Модуль 2
Решение уравнения — Урок 1.
Уравнения определения единицы — Урок 1.1 (Часть 1)
Часть 2)
Использование соотношений и пропорций для решения задач — Урок 1.2 (Часть 1)
Преобразование мер и графических пропорций — Урок 1.2 (Часть 2)
Точность и точность отчетов — Урок 1.3 (Часть 1)
с использованием значительных цифр — Урок 1.3 (Часть 2)
Производительная задача 1 Модуль 1
Интегрированный
Математика 1
Уравнения раствования с экспонентами — Модуль 15.1
Экспрессионный рост. Затухание – Модуль 15.2
Обзор для Блока 6 Тест экспоненциальных функций
Двухсторонняя таблица частот – Модуль 8.1
Относительная частота – Модуль 8.2 (Часть 1)
Условная относительная частота — модуль 8.2 (часть 2)
У углы, образованные последовавшими линиями — модуль 19.1
Походные и параллельные линии — Модуль 19.
2
. Модуль 19.4
Уравнения параллельных и перпендикулярных прямых — Модификация 19.5
Модуль 19 Повторение прямых и углов
Практический тест по Модулю 19
Обзор для окончательного рабочего листа в 1 -м семестре № 1
Обзор для окончательного рабочего листа 1 -го семестра № 2
Обзор для окончательного рабочего листа 1 -й семестра # 3
Обзор для окончательного рабочего листа 1 -го семестра № 4
Модуль 21.1
Конгруэнтность треугольников AAS — Модуль 21.2
HL Конгруэнтность треугольников — Модуль 21.3
Часть 8 Практический тест по модам 19, 20, 21
Математический онлайн-класс
Решение линейных систем с помощью графика — Модуль 11.1
Решение систем с помощью подстановки — Модуль 11.2 (Часть 1) Метод — Модуль 11.3
Решение систем путем умножения первого — Модуль 11.
4
Обзор модуля 11 — Решение систем линейных уравнений
Обзор MOD 11 от г -жи Денни
Обзор мод 11 от г -жи Ромо -Диаз
Последовательности преобразований — Модуль 18.1
СРЕДИ СРЕДИ Конгруэнтные фигуры — Модуль 18.3
Модуль 2.5 Линейные неравенства — ПЛАН: I. Алгебраическое решение неравенств с одной переменной II.
OUTLINE:
I. Алгебраическое решение неравенств с одной переменной
II. Составные неравенства
III. Неравенства абсолютного значения
Свойство трихотомии порядка утверждает, что любая точка a или b на действительном числовая прямая лежит левее другой, иначе они являются одной и той же точкой. То есть, если и b — действительные числа, верно только одно из следующих трех утверждений:
a < б б < a a = b
Свойство транзитивности порядка утверждает, что если a, b и c являются действительными числами и если
a < б и б < с, затем < в.
Область определения переменной в неравенстве — это множество действительных чисел, для которых определены члены неравенства. Любой номер в домене, для которого неравенство является решением неравенства, а множество всех решений называется набор решений.
I. Алгебраическое решение неравенств с одной переменной
Для решения неравенств используются следующие свойства:
- Свойство сложения: Если 푎 < 푏, затем 푎 + 푐 < 푏 + 푐.
- Свойство вычитания: если 푎 < 푏, затем 푎 − 푐 < 푏 − 푐.
- Свойство умножения: если 푎 < 푏 и 푐 > 0, затем 푎푐 < 푏푐.
- Свойство умножения: если 푎 < 푏 и 푐 < 0, затем 푎푐 > 푏푐.
Пример 1: Решите следующие неравенства а) 푥 — 15 < 4 б) 6 ≥ 푥 — 1 в) 푥 + 7 > 9 Решение: а) 푥 — 15 < 4 푥 — 15 + 15 < 4 + 15 푥 < 19 Обозначение построителя сетов: {푥|푥 < 19}. Обозначение интервала: (−∞, 19).
б) 6 ≥ 푥 − 1 6 + 1 ≥ 푥 — 1 + 1 7 ≥ 푥 Обозначение конструктора наборов: {푥|푥 ≤ 7} Обозначение интервала: (−∞,7]
c) 푥 + 7 > 9 푥 + 7 — 7 > 9 − 7 푥 > 2 Обозначение конструктора наборов: {푥|푥 > 2} Обозначение интервала: (2,∞)
II.
Составные неравенстваСоставное неравенство включает в себя два неравенства в одном выражении. Заявление такое как 4 < 푥 ≤ 6 означает 4 < 푥 и 푥 ≤ 6. Есть два способа решения сложных неравенства: разделить их на два отдельных неравенства или оставить составным неравенство без изменений и выполнение операций над всеми тремя частями одновременно.
Пример 4. Решение составного неравенства 3 ≤ 2푥 + 2 < 6 Решение: Первый метод: запишите в виде двух отдельных неравенств. 3 ≤ 2 푥 + 2 2 푥 + 2 < 6 3 − 2 ≤ 2 푥 2 푥 < 6 — 2 1 ≤ 2 2 2 < 4 1 2
≤ 푥 푥 < 2
Тогда мы можем записать решение в виде составного неравенства 1 2 ≤ 푥 < 2 Второй метод: оставьте составное неравенство без изменений и выполните операции на трех частях одновременно. 3 ≤ 2푥 + 2 < 6 3 — 2 ≤ 2+ 2 — 2 < 6 — 2 1 ≤ 2 푥 < 4 1 2
≤ 2푥
2
< 4
2
1
2
≤ 푥 < 2
Таким образом, набор решений Обозначение конструктора наборов: {푥| 12 ≤ 푥 < 2}
Обозначение интервала: [ 12 ,2).