01Математика — 9 класс. Алгебра — Построение графика корня \(\small y=k\sqrt{x}, k>0\)
Заполним таблицу значений функции \(\displaystyle y=2\sqrt{x}{\small :}\)
| \(\displaystyle x\) | \(\displaystyle 0\) | \(\displaystyle 1\) | \(\displaystyle 2\) | \(\displaystyle 3\) | \(\displaystyle 4\) | \(\displaystyle 5\) | \(\displaystyle 6\) |
| \(\displaystyle y=2\sqrt{x}\) | \(\displaystyle 2\sqrt{0}\) | \(\displaystyle 2\sqrt{1}\) | \(\displaystyle 2\sqrt{2}\) | \(\displaystyle 2\sqrt{3}\) | \(\displaystyle 2\sqrt{4}\) | \(\displaystyle 2\sqrt{5}\) | \(\displaystyle 2\sqrt{6}\) |
Вычислим значения \(\displaystyle y{\small .} \)
Поскольку \(\displaystyle 2\sqrt{0}=0{ \small ,}\,2\sqrt{1}=2\) и \(\displaystyle 2\sqrt{4}=4{ \small ,} \) то нужно лишь приближенно вычислить значения
\(\displaystyle 2\sqrt{2}{ \small ,}\, 2\sqrt{3}{ \small ,}\,2\sqrt{5} \) и \(\displaystyle 2\sqrt{6}{\small . 2+\color{blue}{ 1}} \approx \color{green}{ 1}+\frac{\color{blue}{ 1}}{2\cdot \color{green}{ 1}}=1{,}5{\small .}\)
2+\color{blue}{ 1}} \approx \color{green}{ 1}+\frac{\color{blue}{ 1}}{2\cdot \color{green}{ 1}}=1{,}5{\small .}\)
Значит,
\(\displaystyle 2\sqrt{ 2}\approx 2\cdot 1{,}5=3{\small .}\)
Таким образом, \(\displaystyle 2\sqrt{2}\approx 3{\small .} \)
\(\displaystyle 2\sqrt{3} \) равно примерно \(\displaystyle 3{,}5\)
\(\displaystyle 2\sqrt{5} \) равно примерно \(\displaystyle 4{,}5\)
\(\displaystyle 2\sqrt{6} \) равно примерно \(\displaystyle 5\)
Заполним таблицу значений функции:
| \(\displaystyle x\) | \(\displaystyle 0\) | \(\displaystyle 1\) | \(\displaystyle 2\) | \(\displaystyle 3\) | \(\displaystyle 4\) | \(\displaystyle 5\) | \(\displaystyle 6\) |
| \(\displaystyle y=2\sqrt{x}\) | \(\displaystyle 0\) | \(\displaystyle 2\) | \(\displaystyle 3\) | \(\displaystyle 3{,}5\) | \(\displaystyle 4\) | \(\displaystyle 4{,}5\) | \(\displaystyle 5\) |
Построим точки на плоскости:
Построим примерный график функции \(\displaystyle y=2\sqrt{x}\) по полученным точкам, добавляя еще точки, если это необходимо:
График функции корень из.
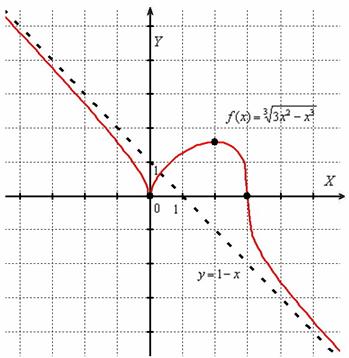 Степенная функция и корни
Степенная функция и корниОсновные цели:
1) сформировать представление о целесообразности обобщённого исследования зависимостей реальных величин на примере величин, связанных отношением у=
2) формировать способность к построению графика у= и его свойства;
3) повторить и закрепить приёмы устных и письменных вычислений, возведение в квадрат, извлечение квадратного корня.
Оборудование, демонстрационный материал: раздаточный материал.
1. Алгоритм:
2. Образец для выполнения задания в группах:
3. Образец для самопроверки самостоятельной работы:
4. Карточка для этапа рефлексии:
1) Я понял, как построить график функции у=.
2) Я могу по графику перечислить его свойства.
3) Я не допустил ошибок в самостоятельной работе.
4) Я допустил ошибки в самостоятельной работе (перечислить эти ошибки и указать их причину).
Ход урока
1. Самоопределение к учебной деятельности
Цель этапа:
1) включить учащихся в учебную деятельность;
2) определить содержательные рамки урока:
продолжаем работать с действительными числами.
Организация учебного процесса на этапе 1:
– Что мы изучали на прошлом уроке? (Мы изучали множество действительных чисел, действия с ними, построили алгоритм для описания свойств функции, повторяли функции изученные в 7 классе).
– Сегодня мы продолжим работать с множеством действительных чисел, функцией.
2. Актуализация знаний и фиксация затруднений в деятельности
Цель этапа:
1) актуализировать учебное содержание, необходимое и достаточное для восприятия нового материала: функция, независимая переменная, зависимая переменна, графики
y = kx + m, y = kx, y =c, y =x 2 , y = — x 2 ,
2) актуализировать мыслительные операции, необходимые и достаточные для восприятия нового материала: сравнение, анализ, обобщение;
3) зафиксировать все повторяемые понятия и алгоритмы в виде схем и символов;
4) зафиксировать индивидуальное затруднение в
деятельности, демонстрирующее на личностно
значимом уровне недостаточность имеющихся
знаний.
Организация учебного процесса на этапе 2:
1. Давайте вспомним как можно задать зависимости между величинами? (С помощью текста, формулы, таблицы, графика)
2. Что называется функцией? (Зависимость между двумя величинами, где каждому значению одной переменной соответствует единственное значение другой переменной y = f(x)).
Как называется х? (Независимая переменная — аргумент)
Как называется у? (Зависимая переменная).
3. В 7- м классе мы изучили функции? (y = kx + m, y = kx, y =c, y =x 2 , y = — x 2 , ).
Индивидуальное задание:
Что является графиком функций y = kx + m, y =x 2 , y = ?
3. Выявление причин затруднений и постановка цели деятельности
Цель этапа:
1) организовать коммуникативное взаимодействие, в ходе которого выявляется и фиксируется отличительное свойство задания, вызвавшего затруднение в учебной деятельности;
2) согласовать цель и тему урока.
Организация учебного процесса на этапе 3:
– Что особенного в этом задании? (Зависимость
задана формулой y = с которой мы еще не встречались).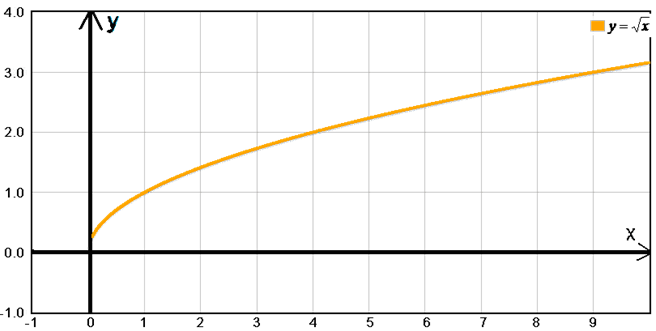
– Какая цель урока? (Познакомиться с функцией y = , ее свойствами и графиком. Функцией в таблице определять вид зависимости, строить формулу и график.)
– Можно сформулировать тему урока? (Функция у=, ее свойства и график).
– Запишите тему в тетради.
4. Построение проекта выхода из затруднения
Цель этапа:
1) организовать коммуникативное взаимодействие для построения нового способа действия, устраняющего причину выявленного затруднения;
2) зафиксировать новый способ действия в знаковой, вербальной форме и с помощью эталона.
Организация учебного процесса на этапе 4:
Работу на этапе можно организовать по группам, предложив группам построить график y = , затем проанализировать получившиеся результаты. Также группам можно предложить по алгоритму описать свойства данной функции.
5. Первичное закрепление во внешней речи
Цель этапа: зафиксировать изученное учебное содержание во внешней речи.
Организация учебного процесса на этапе 5:
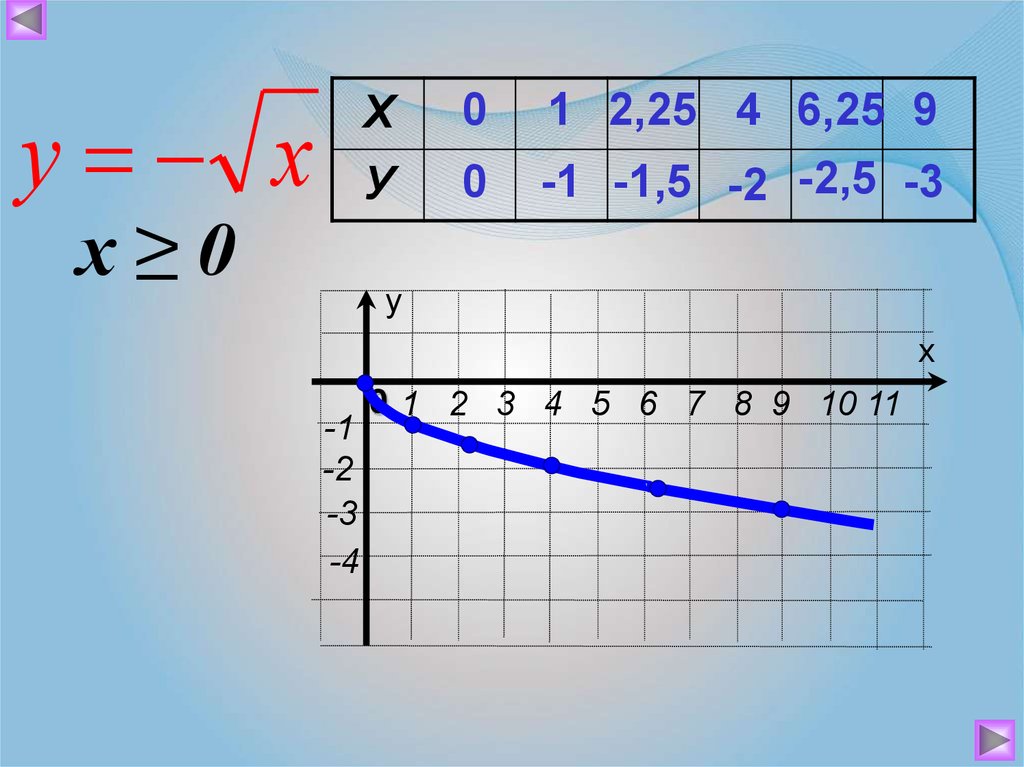
Постройте график у= — и опишите его свойства.
Свойства у= — .
1.Область определения функции.
2.Область значений функции.
3. y = 0, y> 0, y
y =0, если x = 0.
y
4.Возрастания, убывания функции.
Функция убывает при х .
Построим график у=.
Выделим его часть на отрезке . Заметим, что у наим. = 1 при х = 1, а у наиб. =3 при х = 9.
Ответ: у наим. = 1, у наиб. =3
6. Самостоятельная работа с самопроверкой по эталону
Цель этапа: проверить своё умение применять новое учебное содержание в типовых условиях на основе сопоставления своего решения с эталоном для самопроверки.
Организация учебного процесса на этапе 6:
Учащиеся выполняют задание самостоятельно, проводят самопроверку по эталону, анализируют, исправляют ошибки.
Построим график у=.
С помощью графика найдите наименьшее и наибольшее значения функции на отрезке .
7. Включение в систему знаний и повторение
Цель этапа: тренировать навыки
использования нового содержания совместно с
ранее изученным: 2) повторить учебное содержание,
которое потребуется на следующих уроках.
Организация учебного процесса на этапе 7:
Решите графически уравнение: = х – 6.
Один ученик у доски остальные в тетрадях.
8. Рефлексия деятельности
Цель этапа:
1) зафиксировать новое содержание, изученное на уроке;
2) оценить собственную деятельность на уроке;
3) поблагодарить одноклассников, которые помогли получить результат урока;
4) зафиксировать неразрешённые затруднения как направления будущей учебной деятельности;
5) обсудить и записать домашнее задание.
Организация учебного процесса на этапе 8:
– Ребята, какая цель стояла сегодня перед нами? (Изучить функцию у=, ее свойства и график).
– Какие знания нам помогли в достижении цели? (Умение искать закономерности, умение читать графики.)
– Проанализируйте свою деятельность на уроке. (Карточки с рефлексией)
Домашнее задание
п. 13 (до примера 2)
Решите графически уравнение.
Квадратный корень как элементарная функция.
Квадратный корень — это элементарная функция и частный случай степенной функции при . Арифметический квадратный корень является гладким при , а нуле он непрерывен справа, но не дифференцируется.
Как функция комплексный переменный корень — двузначная функция, у которой листы сходятся в нуле.
Построение графика функции квадратного корня.
- Заполняем таблицу данных:
2. Наносим точки, которые мы получили на координатную плоскость.
3. Соединяем эти точки и получаем график функции квадратного корня:
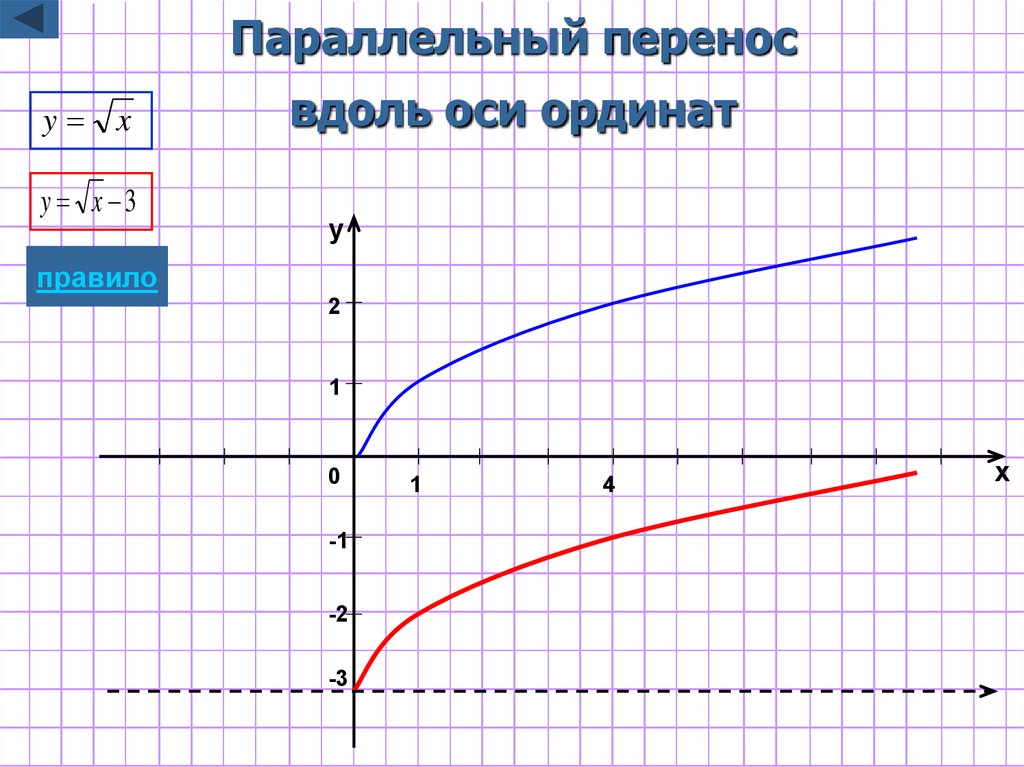
Преобразования графика функции квадратного корня.
Определим, какие преобразования функции необходимо сделать для того, чтобы построить графики функций. Определим виды преобразований.
Вид преобразования | Преобразование | |
Перенос функции по оси OY на 4 ед. | ||
внутреннее | Перенос функции по оси OX на 1 ед. вправо. | |
внутреннее | График приближается к оси OY в 3 раза и сжимается по оси OХ . | |
График отдаляется от оси OX OY . | ||
внутреннее | График отдаляется от оси OY в 2 раза и растягивается по оси OХ . |
Зачастую преобразования функций оказываются комбинированными.
Например , нужно построить график функции . Это график квадратного корня , который нужно перенести на одну единицу вниз по оси OY и на единицу вправо по оси ОХ и одновременно растянув в 3 раза его по оси
Бывает непосредственно перед построением графика функции, нужны предварительные тождественные преобразования либо упрощения функций.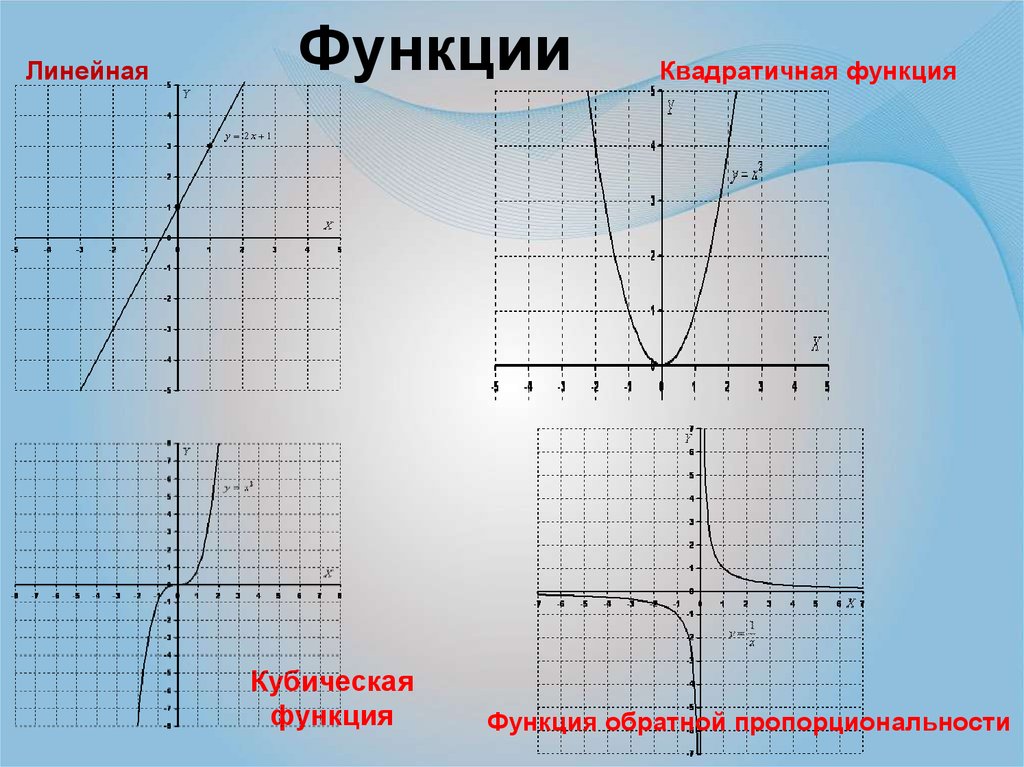
Вы искали x корень из x равно? . Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и x корень из y, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «x корень из x равно».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как x корень из x равно,x корень из y,корень из x,корень из х равен х,корень из х равно х,корень х равен х,функция y корень из минус x,функция y минус корень из x,х корень y,х корень из х равно.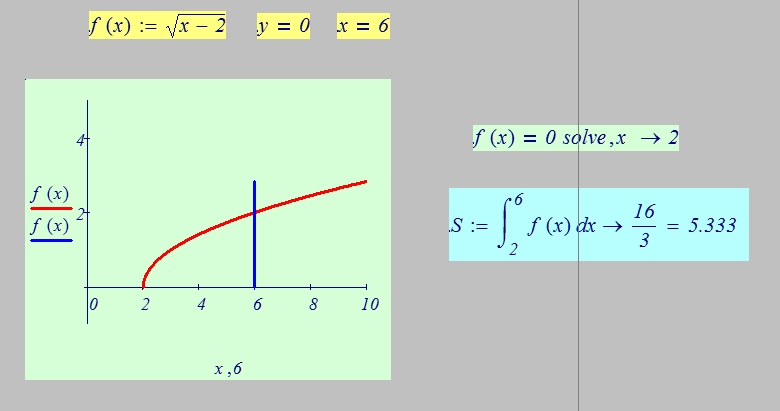
Где можно решить любую задачу по математике, а так же x корень из x равно Онлайн?
Решить задачу x корень из x равно вы можете на нашем сайте . Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Основные цели:
1) сформировать представление о целесообразности обобщённого исследования зависимостей реальных величин на примере величин, связанных отношением у=
2) формировать способность к построению графика у= и его свойства;
3) повторить и закрепить приёмы устных и
письменных вычислений, возведение в квадрат,
извлечение квадратного корня.
Оборудование, демонстрационный материал: раздаточный материал.
1. Алгоритм:
2. Образец для выполнения задания в группах:
3. Образец для самопроверки самостоятельной работы:
4. Карточка для этапа рефлексии:
1) Я понял, как построить график функции у=.
2) Я могу по графику перечислить его свойства.
3) Я не допустил ошибок в самостоятельной работе.
4) Я допустил ошибки в самостоятельной работе (перечислить эти ошибки и указать их причину).
Ход урока
1. Самоопределение к учебной деятельности
Цель этапа:
1) включить учащихся в учебную деятельность;
2) определить содержательные рамки урока: продолжаем работать с действительными числами.
Организация учебного процесса на этапе 1:
– Что мы изучали на прошлом уроке? (Мы изучали множество действительных чисел, действия с ними, построили алгоритм для описания свойств функции, повторяли функции изученные в 7 классе).
– Сегодня мы продолжим работать с множеством
действительных чисел, функцией.
2. Актуализация знаний и фиксация затруднений в деятельности
Цель этапа:
1) актуализировать учебное содержание, необходимое и достаточное для восприятия нового материала: функция, независимая переменная, зависимая переменна, графики
y = kx + m, y = kx, y =c, y =x 2 , y = — x 2 ,
2) актуализировать мыслительные операции, необходимые и достаточные для восприятия нового материала: сравнение, анализ, обобщение;
3) зафиксировать все повторяемые понятия и алгоритмы в виде схем и символов;
4) зафиксировать индивидуальное затруднение в деятельности, демонстрирующее на личностно значимом уровне недостаточность имеющихся знаний.
Организация учебного процесса на этапе 2:
1. Давайте вспомним как можно задать зависимости между величинами? (С помощью текста, формулы, таблицы, графика)
2. Что называется функцией? (Зависимость между
двумя величинами, где каждому значению одной
переменной соответствует единственное значение
другой переменной y = f(x)).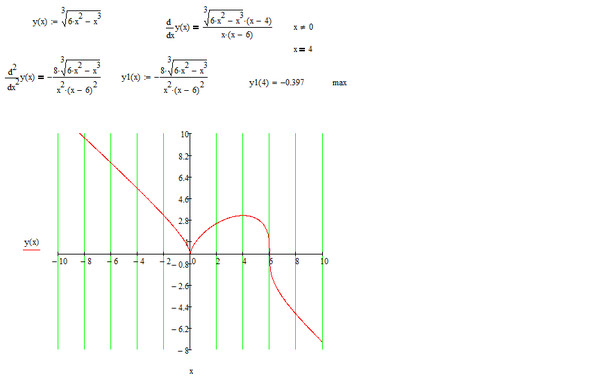
Как называется х? (Независимая переменная — аргумент)
Как называется у? (Зависимая переменная).
3. В 7- м классе мы изучили функции? (y = kx + m, y = kx, y =c, y =x 2 , y = — x 2 , ).
Индивидуальное задание:
Что является графиком функций y = kx + m, y =x 2 , y = ?
3. Выявление причин затруднений и постановка цели деятельности
Цель этапа:
1) организовать коммуникативное взаимодействие, в ходе которого выявляется и фиксируется отличительное свойство задания, вызвавшего затруднение в учебной деятельности;
2) согласовать цель и тему урока.
Организация учебного процесса на этапе 3:
– Что особенного в этом задании? (Зависимость задана формулой y = с которой мы еще не встречались).
– Какая цель урока? (Познакомиться с функцией y = , ее свойствами и графиком. Функцией в таблице определять вид зависимости, строить формулу и график.)
– Можно сформулировать тему урока? (Функция у=, ее свойства и
график).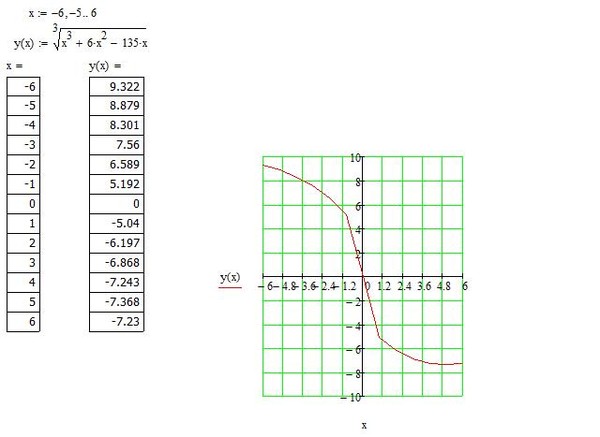
– Запишите тему в тетради.
4. Построение проекта выхода из затруднения
Цель этапа:
1) организовать коммуникативное взаимодействие для построения нового способа действия, устраняющего причину выявленного затруднения;
2) зафиксировать новый способ действия в знаковой, вербальной форме и с помощью эталона.
Организация учебного процесса на этапе 4:
Работу на этапе можно организовать по группам, предложив группам построить график y = , затем проанализировать получившиеся результаты. Также группам можно предложить по алгоритму описать свойства данной функции.
5. Первичное закрепление во внешней речи
Цель этапа: зафиксировать изученное учебное содержание во внешней речи.
Организация учебного процесса на этапе 5:
Постройте график у= — и опишите его свойства.
Свойства у= — .
1.Область определения функции.
2.Область значений функции.
3. y = 0, y> 0, y
y =0, если x = 0.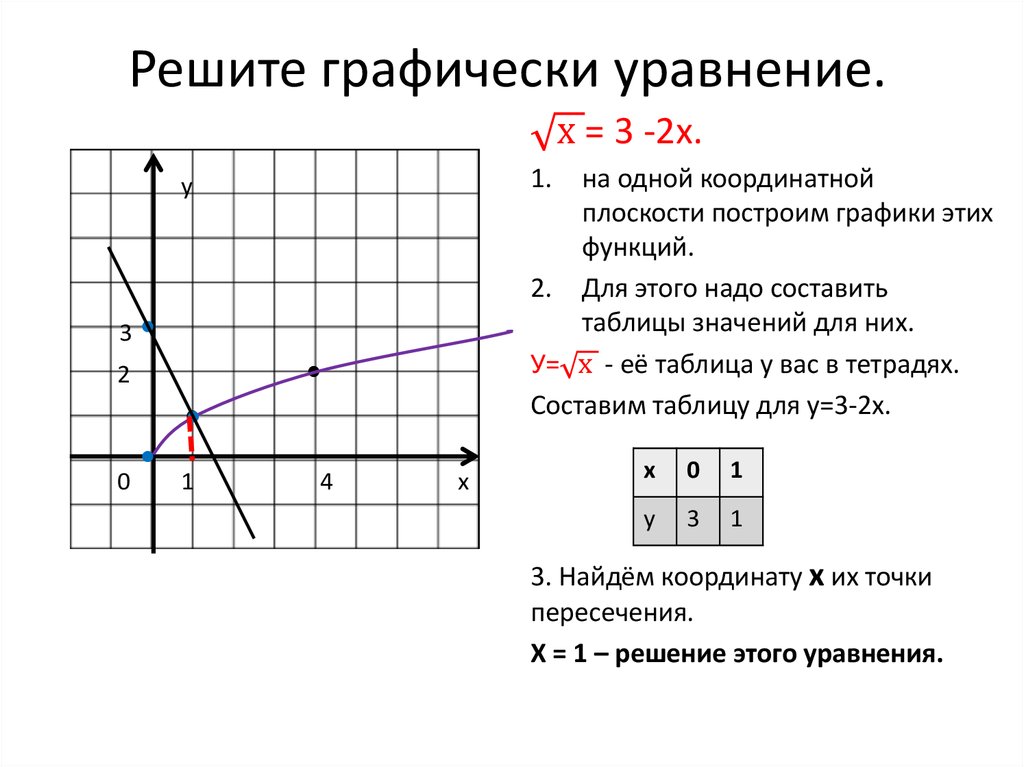
y
4.Возрастания, убывания функции.
Функция убывает при х .
Построим график у=.
Выделим его часть на отрезке . Заметим, что у наим. = 1 при х = 1, а у наиб. =3 при х = 9.
Ответ: у наим. = 1, у наиб. =3
6. Самостоятельная работа с самопроверкой по эталону
Цель этапа: проверить своё умение применять новое учебное содержание в типовых условиях на основе сопоставления своего решения с эталоном для самопроверки.
Организация учебного процесса на этапе 6:
Учащиеся выполняют задание самостоятельно, проводят самопроверку по эталону, анализируют, исправляют ошибки.
Построим график у=.
С помощью графика найдите наименьшее и наибольшее значения функции на отрезке .
7. Включение в систему знаний и повторение
Цель этапа: тренировать навыки использования нового содержания совместно с ранее изученным: 2) повторить учебное содержание, которое потребуется на следующих уроках.
Организация учебного процесса на этапе 7:
Решите графически уравнение: = х – 6.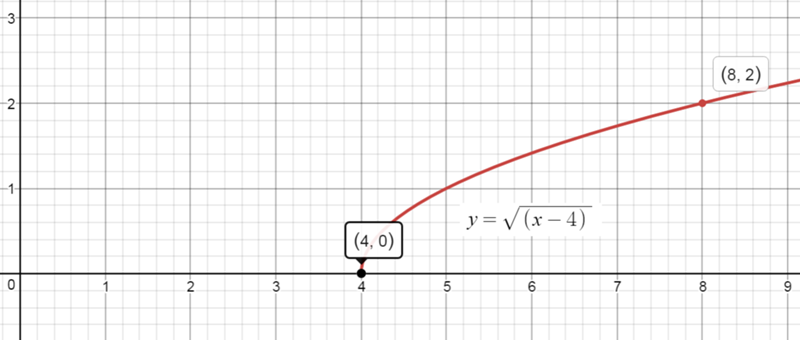
Один ученик у доски остальные в тетрадях.
8. Рефлексия деятельности
Цель этапа:
1) зафиксировать новое содержание, изученное на уроке;
2) оценить собственную деятельность на уроке;
3) поблагодарить одноклассников, которые помогли получить результат урока;
4) зафиксировать неразрешённые затруднения как направления будущей учебной деятельности;
5) обсудить и записать домашнее задание.
Организация учебного процесса на этапе 8:
– Ребята, какая цель стояла сегодня перед нами? (Изучить функцию у=, ее свойства и график).
– Какие знания нам помогли в достижении цели? (Умение искать закономерности, умение читать графики.)
– Проанализируйте свою деятельность на уроке. (Карточки с рефлексией)
Домашнее задание
п. 13 (до примера 2) № 13.3, 13.4
Решите графически уравнение.
Рассмотрим функцию y=√x. График этой функции показан на рисунке ниже.
График функции y=√x
Как видите, график напоминает повернутую параболу, точнее одну из её ветвей.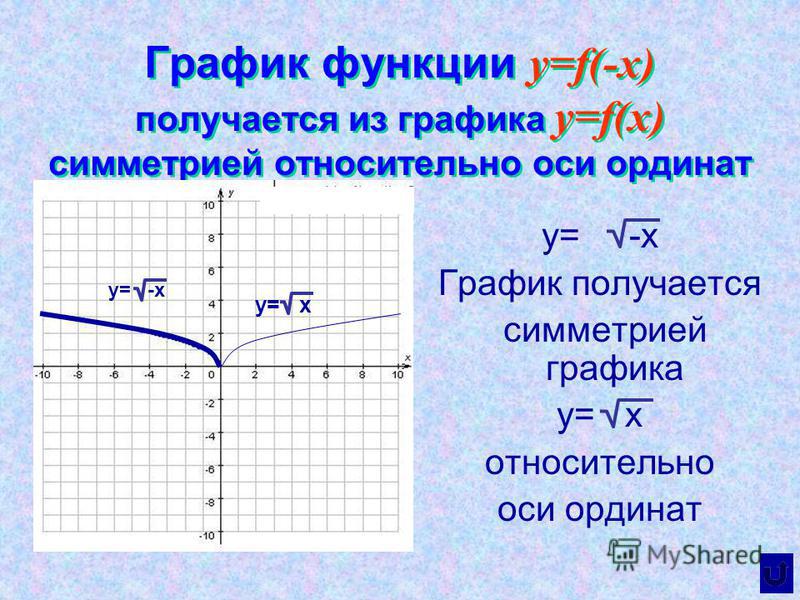 2. Из рисунка видно, что график лишь один раз касается оси Оу, в точке с координатами (0;0).
2. Из рисунка видно, что график лишь один раз касается оси Оу, в точке с координатами (0;0).
Теперь стоит отметить основные свойства этой функции.
Свойства функции y=√x
1. Область определения функции явяется луч }
Полное руководство по построению графиков кубических функций и кубических корней — Mashup Math
Следующее пошаговое руководство покажет вам, как строить графики кубических функций и кубических корней с помощью таблиц или уравнений (алгебра)Добро пожаловать в это бесплатное руководство, сопровождающее это учебное пособие по построению графиков корневых функций куба, где вы узнаете ответы на следующие ключевые вопросы и информацию:
Как построить график кубической функции?
Как построить график функции кубического корня?
Как нарисовать уравнение кубической функции?
Как построить график функции в ограниченной области?
Полное руководство по построению графиков кубических функций включает несколько примеров, пошаговое руководство и анимированное видеоруководство.
*Это руководство к уроку прилагается к нашему анимированному объяснению графических кубических функций! видео.
Хотите больше бесплатных уроков математики и видео? Подпишитесь на наш канал бесплатно!
В этом примере вы будете строить график функции в ограниченной области, но используемый нами метод будет работать для построения графика любой кубической функции.
Пример:
Поскольку вы строите график этой функции в ограниченной области, вас интересует только график поведения функции в диапазоне от -6 до 10.
Начните с создания таблицы, которую вы можете использовать, чтобы помочь себе найти значение координаты y для всех значений x от -6 до 10 следующим образом:
Теперь вы готовы начать поиск точек на графике. Начнем с поиска значения y при x=-6 (первая точка в таблице).
Начнем с поиска значения y при x=-6 (первая точка в таблице).
Подставьте каждое значение x в функцию и найдите y!
Чтобы найти значение y при x=-6, просто подставьте -6 вместо x в исходную функцию и решите следующим образом:
Кубический корень из -8 равен -2.
Поскольку кубический корень из -8 равен -2, вы можете сделать вывод, что когда x=-6, y=-2, и вы знаете, что точка (-6,-2) находится на графике этой кубической функции!
(-6,-2) — одна из точек, через которые проходит эта функция!
Остальные значения y можно найти в таблице с помощью:
A. ) Повторяя вышеуказанный процесс для каждого значения x
) Повторяя вышеуказанный процесс для каждого значения x
или
B.) Используя графический калькулятор чтобы ввести функцию в y= и сгенерировать таблицу следующим образом:
После того, как вы заполните таблицу, вы заметите, что некоторые координаты являются целыми числами, а другие — десятичными:
Чтобы построить график функции, вы будете отображать только точки, которые являются целыми числами (таким образом, вам не придется оценивать, где на графике лежат десятичные точки)
Теперь вы можете продолжить и построить график следующие точки на графике:
(-6,-2), (1,-1), (2,0), (3,1), (10,2)
Последний шаг — соединить точки изогнутой линией следующим образом:
Это график кубической функции в ограниченной области!
Вы также можете использовать свой графический калькулятор, чтобы проверить правильность вашего графика.
Вот и все!
Посмотрите этот анимационный видеоурок по построению графиков кубических функций!
Ознакомьтесь со следующими бесплатными корневыми ресурсами куба:Free Cube Root Справочное руководство
Есть мысли? Поделитесь своими мыслями в разделе комментариев ниже!
(Никогда не пропустите блог Mashup Math — нажмите здесь, чтобы получать нашу еженедельную рассылку!)
Автор: Энтони Персико Вы часто можете увидеть, как я с радостью разрабатываю анимированные уроки математики, которыми я делюсь на своих Канал YouTube . Или проводить слишком много времени в тренажерном зале или играть на своем телефоне.
Комментарий
Как построить график квадратного корня (график квадратного корня без калькулятора) – JDM Educational
Функции квадратного корня используются в алгебре, предварительном исчислении, исчислении и других предметах.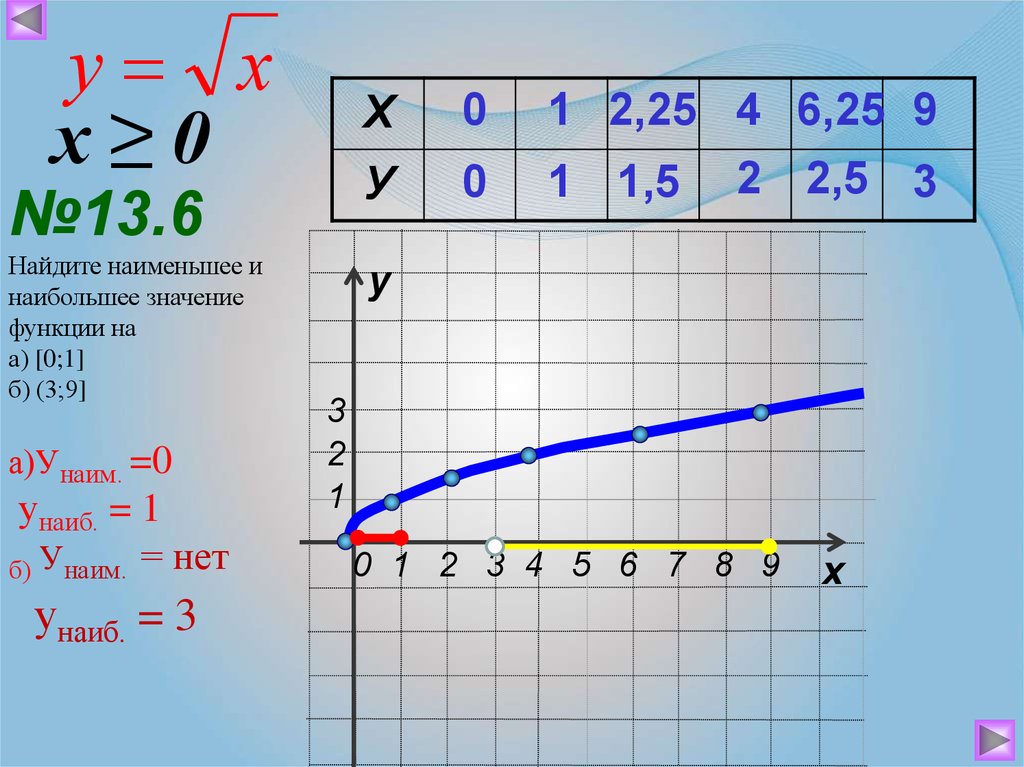 Полезно знать, как выводить квадратные корни и другие радикалы (либо рисовать их вручную, либо проверять, что показывает калькулятор).
Полезно знать, как выводить квадратные корни и другие радикалы (либо рисовать их вручную, либо проверять, что показывает калькулятор).
Итак, как построить график функции квадратного корня? Сначала найдите домен – подкоренное число не может быть отрицательным. Затем нанесите на график несколько точек, в том числе точку в конце домена. Затем обратите внимание на отрицательные знаки, которые могут «перевернуть» график через линию. Наконец, соедините точки, нарисовав форму функции квадратного корня.
Конечно, таблица значений может помочь вам в графическом отображении первых нескольких точек. Кроме того, вам необходимо знать общий вид функции квадратного корня и то, как она меняется при изменении знака.
В этой статье мы поговорим о том, как построить график любой функции квадратного корня. Мы также рассмотрим несколько примеров, показывающих шаги по ходу дела.
Начнем.
Как построить график функции квадратного корня
Чтобы построить график функции квадратного корня, мы можем выполнить 4 шага, чтобы разбить процесс:
- 1.
 Найдите область — это говорит нам, где график будет определена функция квадратного корня. Помните, что квадратный корень из отрицательного числа является мнимым, поэтому мы не можем изобразить его в двумерной действительной системе счисления. Это означает, что мы должны решить неравенство, которое делает подкоренное число больше или равным нулю.
Найдите область — это говорит нам, где график будет определена функция квадратного корня. Помните, что квадратный корень из отрицательного числа является мнимым, поэтому мы не можем изобразить его в двумерной действительной системе счисления. Это означает, что мы должны решить неравенство, которое делает подкоренное число больше или равным нулю. - 2. Нанесите несколько точек – это поможет нам узнать, где на следующем шаге нарисовать кривую квадратного корня. Отображение конечной точки области говорит нам, где начинается график, а отображение еще нескольких точек помогает нам увидеть приблизительную форму кривой до того, как мы ее нарисуем.
- 3. Обратите внимание на отрицательные значения – обратите особое внимание на любые отрицательные знаки в функции извлечения квадратного корня. Отрицательное значение перед x может отразить функцию по вертикальной оси (например, по оси Y), а отрицательное значение перед целым квадратным корнем может отразить функцию по горизонтальной оси (например, по оси x).

- 4. Нарисуйте кривую – используйте общую форму функции извлечения квадратного корня, чтобы соединить все точки из шага 3 при построении кривой. Начальная точка говорит вам, с чего начать, а другие точки дают представление о том, куда должна идти кривая.
Прежде чем мы рассмотрим несколько примеров, давайте освежим в памяти то, как выглядят функции квадратного корня. Мы также рассмотрим, как негативные знаки влияют на их внешний вид.
Вот график самой простой функции квадратного корня, f(x) = √x:
Сумма и число
Пожалуйста, включите JavaScript
Сумма и число
Функция f(x) = √x неограниченно растет с увеличением x. Обратите внимание, что функция не определена для любого x < 0, так как квадратный корень из отрицательного числа является мнимым. Также обратите внимание, что мы берем только главный (положительный) квадратный корень для любого положительного значения x (например, квадратный корень из 4 принимается равным 2, а не -2 — если бы мы взяли оба, у нас не было бы функции).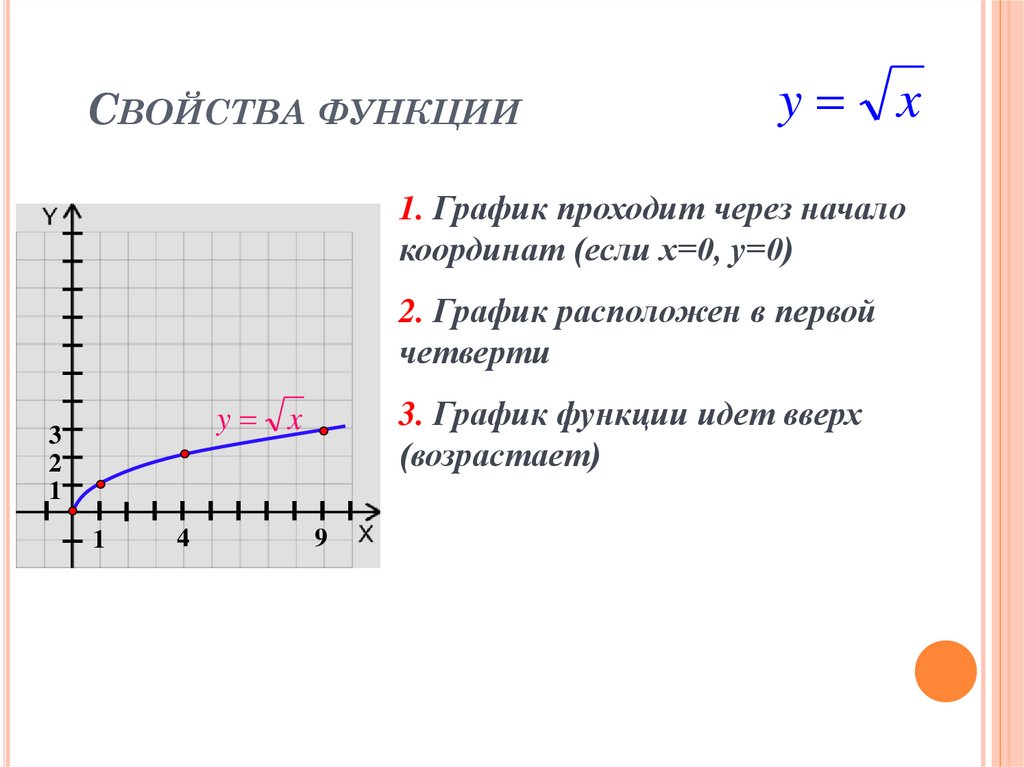
Если мы поставим знак минус перед x, мы перевернем кривую по оси x, чтобы получить g(x) = √-x:
Функция f(x) = √-x неограниченно растет с уменьшением x. Это зеркальное отображение функции f(x) = √x, отраженное поперек оси y.Это «зеркальное отражение» f(x) = √x, отраженное поперек оси x. Обратите внимание, что функция не определена ни для какого x > 0, поскольку квадратный корень из отрицательного числа является мнимым (если x положительное, то –x отрицательное).
Если мы поставим перед квадратным корнем отрицательный знак, мы перевернем кривую по оси y, чтобы получить h(x) = -√x:
Функция f(x) = -√x становится более отрицательной без ограничивается по мере увеличения x. Это зеркальное отображение функции f(x) = √x, отраженное поперек оси x.Это «зеркальное отражение» f(x) = √x, отраженное поперек оси y. Обратите внимание, что функция не определена для любого x < 0, поскольку квадратный корень из отрицательного значения является мнимым.
Наконец, если мы поставим знак минус перед x и перед квадратным корнем, мы перевернем кривую по оси x, а затем по оси y, чтобы получить j(x) = -√-x:
Функция f(x) = -√-x неограниченно возрастает с уменьшением x.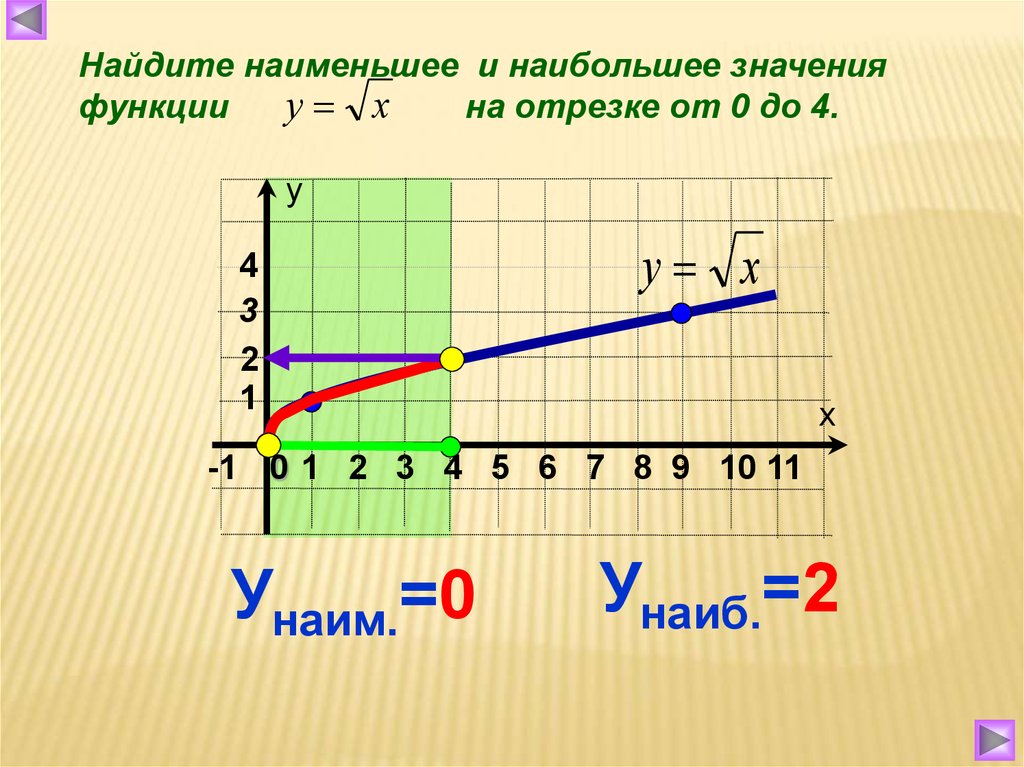 Это зеркальное отображение функции f(x) = √x, отраженное по оси x, а затем по оси y (отражение относительно начала координат).
Это зеркальное отображение функции f(x) = √x, отраженное по оси x, а затем по оси y (отражение относительно начала координат).Это еще одно «зеркальное отображение» f(x) = √x, отраженное по оси x, а затем по оси y. Обратите внимание, что функция не определена ни для какого x > 0, поскольку квадратный корень из отрицательного числа является мнимым (если x положительное, то –x отрицательное).
Теперь, когда у нас есть представление о том, как выглядят функции извлечения квадратного корня (их основная форма), мы можем попробовать несколько примеров.
Пример 1. Как построить график функции квадратного корня
Давайте построим график функции квадратного корня f(x) = 2√x.
Сначала находим домен. Это означает поиск неотрицательного подкоренного числа или x >= 0 (что означает конечную точку x = 0).
Далее наносим несколько точек. A table will help, starting with the endpoint x = 0:
| x | f(x) |
|---|---|
| 0 | 0 |
| 1 | 2 |
| 2 | 2 √2 |
| 3 | 2√3 |
для f(x) = 2√x.
Теперь нанесем эти несколько точек на график:
Здесь мы нанесли четыре точки из таблицы выше.Затем ищем отрицательные знаки в функции (здесь их нет).
Наконец, мы рисуем кривую квадратного корня, соединяющую наши точки, начиная с конечной точки x = 0.
График f(x) = 2√x.Обратите внимание, что 2 перед квадратным корнем «удваивает» высоту базовой функции квадратного корня в каждой точке. Таким образом, f(x) = 2√x имеет ту же основную форму, что и √x, но с удвоенной высотой (значением y) в каждой точке.
Пример 2. Как построить график функции квадратного корня
Давайте построим график функции квадратного корня f(x) = –√(x – 3).
Сначала находим домен. Это означает поиск неотрицательного подкоренного числа, или x – 3 >= 0. Это дает нам область определения x >= 3 (что означает, что конечная точка x = 3).
Далее наносим несколько точек. Поможет таблица, начиная с конечной точки x = 3:
| x | f(x) |
|---|---|
| 3 | 0 |
| 4 | -1 |
| 5 | -√2 |
| 6 | -√3 |
for f(x) = –√(x – 3).

Теперь нанесем эти несколько точек на график:
Здесь мы нанесли четыре точки из таблицы выше.Затем ищем отрицательные знаки в функции. Здесь перед квадратным корнем стоит минус, который «перевернет» кривую по оси x.
Наконец, мы рисуем кривую квадратного корня, чтобы соединить наши точки, начиная с конечной точки x = 3.
График f(x) = -√(x – 3).Обратите внимание, что x – 3 под радикалом сдвигает базовую кривую √x на 3 единицы вправо. Кроме того, кривая находится ниже оси x, поскольку отрицательный знак перед квадратным корнем «переворачивает» базовую функцию квадратного корня по оси x.
Пример 3. Как построить график функции квадратного корня
Давайте построим график функции квадратного корня f(x) = 3√-x.
Сначала находим домен. Это означает поиск неотрицательного подкоренного числа, или –x >= 0. Это дает нам область значений x <= 0 (что означает, что конечная точка равна x = 0).
Далее наносим несколько точек. A table will help, starting with the endpoint x = 0:
| x | f(x) |
|---|---|
| 0 | 0 |
| -1 | 3 |
| -2 | 3√2 |
| -3 | 3√3 |
для f(x) = 3√-x.

Теперь нанесем эти несколько точек на график:
Здесь мы нанесли четыре точки из таблицы выше.Затем ищем отрицательные знаки в функции. Здесь перед x стоит минус, который «перевернет» кривую по оси y.
Наконец, мы рисуем кривую квадратного корня, соединяющую наши точки, начиная с конечной точки x = 0.
График f(x) = 3√-x.Обратите внимание, что кривая находится полностью слева от оси y, поскольку отрицательный знак перед x «переворачивает» базовую функцию квадратного корня по оси y. Также обратите внимание, что 3 перед радикалом делают кривую в 3 раза выше базовой функции √x во всех местах.
Пример 4. Как построить график функции квадратного корня
Давайте построим график функции квадратного корня f(x) = -4√(-x + 2).
Сначала находим домен. Это означает поиск неотрицательного подкоренного числа, или –x + 2 >= 0. Это дает нам область определения x <= 2 (что означает, что конечная точка x = 2).
Далее наносим несколько точек.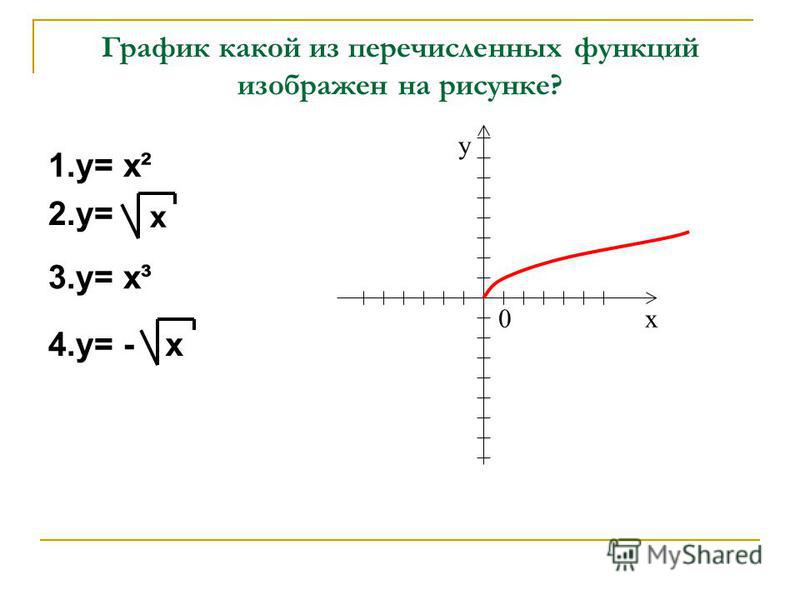 Поможет таблица, начиная с конечной точки x = 2:
Поможет таблица, начиная с конечной точки x = 2:
| x | f(x) |
|---|---|
| 2 | 0 |
| 1 | -4 |
| 0 | -4√2 |
| -1 | -4√3 |
for f(x) = -4√ (-х + 2).
Теперь нанесем эти несколько точек на график:
Здесь мы нанесли четыре точки из таблицы выше.Затем ищем отрицательные знаки в функции. Здесь перед x стоит минус, который «перевернет» кривую по оси y.
Наконец, мы рисуем кривую квадратного корня, чтобы соединить наши точки, начиная с конечной точки x = 2.
График f(x) = -4√(-x + 2). Обратите внимание, что кривая находится полностью слева от вертикальной линии x = 2, так как отрицательное значение перед x «переворачивает» базовую функцию квадратного корня через вертикальную линию x = 2.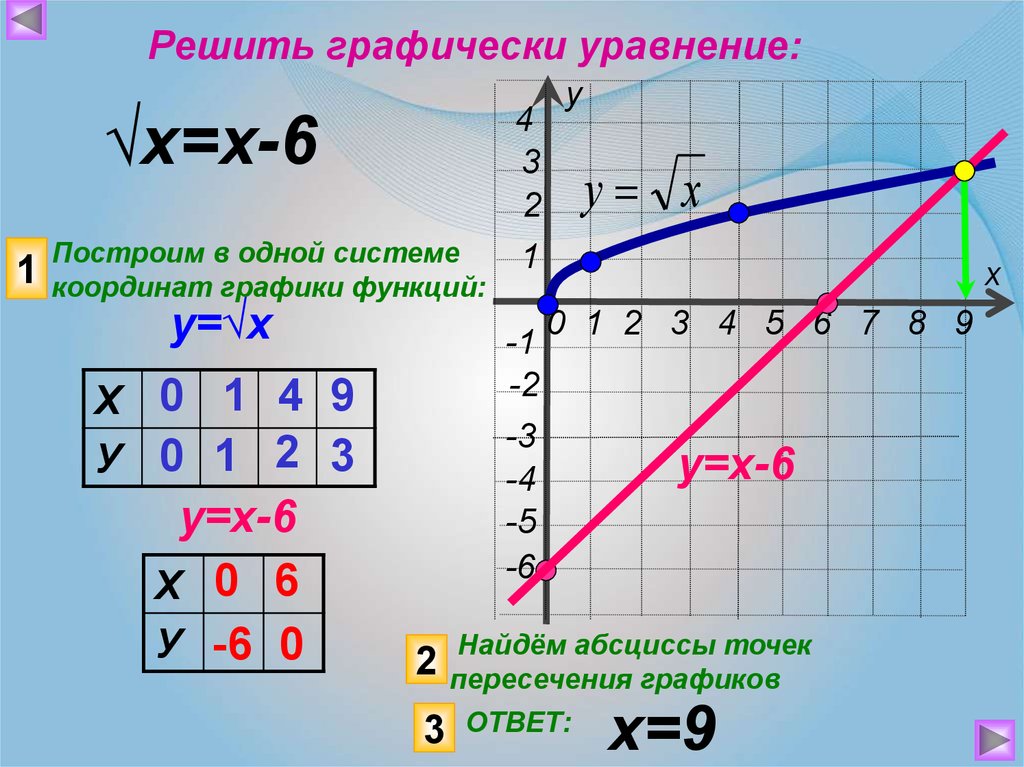
Также обратите внимание, что 4 перед радикалом сделайте кривую в 3 раза выше базовой функции √x во всех местах.
Наконец, минус перед 4 «переворачивает» функцию по оси x.
Пример 5. Как построить график функции квадратного корня
Построим график функции квадратного корня f(x) = -√(x – 3) + 2.
Сначала найдем домен. Это означает поиск неотрицательного подкоренного числа, или x – 3 >= 0. Это дает нам область значений x >= 3 (что означает, что конечная точка равна x = 3).
Далее наносим несколько точек. Таблица поможет, начиная с конечной точки x = 3:
| x | F (x) |
|---|---|
| 3 | 2 | 2 | 424692 | 42462 | 7777777777777777777777777777777777777777777777797779н.
| 5 | -√2 + 2 |
| 6 | -√3 + 2 |
Затем ищем отрицательные знаки в функции. Здесь перед квадратным корнем стоит минус, который «перевернет» кривую по оси x.
Наконец, мы рисуем кривую квадратного корня, чтобы соединить наши точки, начиная с конечной точки x = 3.
График f(x) = -√(x – 3) + 2.Обратите внимание, что кривая находится полностью справа от вертикальной линии x = 3.
Также обратите внимание, что x – 3 в радикале сдвигает функцию на 3 единицы вправо. Точно так же +2 сдвигает кривую на две единицы вверх.
Наконец, минус перед квадратным корнем «переворачивает» функцию по вертикальной линии x = 3.
Заключение
Теперь вы знаете, как построить квадратный корень без калькулятора. Вы также знаете, как отрицательные знаки могут влиять на эти графики, «переворачивая» кривую по оси.

 Найдите область — это говорит нам, где график будет определена функция квадратного корня. Помните, что квадратный корень из отрицательного числа является мнимым, поэтому мы не можем изобразить его в двумерной действительной системе счисления. Это означает, что мы должны решить неравенство, которое делает подкоренное число больше или равным нулю.
Найдите область — это говорит нам, где график будет определена функция квадратного корня. Помните, что квадратный корень из отрицательного числа является мнимым, поэтому мы не можем изобразить его в двумерной действительной системе счисления. Это означает, что мы должны решить неравенство, которое делает подкоренное число больше или равным нулю.
 0242
0242