| 1 | Найти число возможных исходов | 7 выбор 3 | |
| 2 | Найти число возможных исходов | 8 выбор 3 | |
| 3 | Найти число возможных исходов | 5 выбор 2 | |
| 4 | Найти число возможных исходов | 4 выбор 2 | |
| 5 | Найти число возможных исходов | 8 выбор 4 | |
| 6 | Найти число возможных исходов | 10 выбор 3 | |
| 7 | Найти число возможных исходов | 7 выбор 4 | |
| 8 | Найти число возможных исходов | 6 выбор 3 | |
| 9 | Найти число возможных исходов | 9 выбор 3 | |
| 10 | Найти число возможных исходов | 3 выбор 2 | |
| 11 | Найти число возможных исходов | 6 выбор 4 | |
| 12 | Найти число возможных исходов | 5 выбор 4 | |
| 13 | Найти число возможных исходов | 7 перестановка 3 | |
| 14 | Найти число возможных исходов | 7 выбор 2 | |
| 15 | Найти число возможных исходов | 10 выбор 5 | |
| 16 | Найти число возможных исходов | 10 выбор 6 | |
| 17 | Найти число возможных исходов | 13 выбор 5 | |
| 18 | Найти число возможных исходов | 3 выбор 3 | |
| 19 | Найти число возможных исходов | 4 выбор 1 | |
| 20 | Найти число возможных исходов | 4 выбор 4 | |
| 21 | 5 выбор 1 | ||
| 22 | Найти число возможных исходов | 6 перестановка 3 | |
| 23 | Найти число возможных исходов | 8 выбор 5 | |
| 24 | Найти число возможных исходов | 9 перестановка 4 | |
| 25 | Найти число возможных исходов | 13 выбор 3 | |
| 26 | Найти число возможных исходов | 12 выбор 2 | |
| 27 | Найти число возможных исходов | 12 выбор 4 | |
| 28 | Найти число возможных исходов | 12 выбор 3 | |
| 29 | Найти число возможных исходов | 9 выбор 5 | |
| 30 | Найти число возможных исходов | 9 выбор 2 | |
| 31 | Найти число возможных исходов | 7 выбор 5 | |
| 32 | Найти число возможных исходов | 6 перестановка 6 | |
| 33 | Найти число возможных исходов | 8 перестановка 5 | |
| 34 | Найти число возможных исходов | 8 перестановка 3 | |
| 35 | Найти число возможных исходов | 7 перестановка 5 | |
| 36 | Найти число возможных исходов | 52 выбор 5 | |
| 37 | Найти число возможных исходов | 5 перестановка 3 | |
| 38 | Найти число возможных исходов | 12 выбор 5 | |
| 39 | Найти число возможных исходов | 3 выбор 1 | |
| 40 | Найти число возможных исходов | 11 выбор 5 | |
| 41 | Найти число возможных исходов | 10 выбор 2 | |
| 42 | Найти число возможных исходов | 15 выбор 3 | |
| 43 | Найти число возможных исходов | 52 выбор 4 | |
| 44 | Найти число возможных исходов | 9 выбор 4 | |
| 45 | Найти число возможных исходов | 9 перестановка 3 | |
| 46 | Найти число возможных исходов | 7 перестановка 4 | |
| 47 | Найти число возможных исходов | 7 перестановка 2 | |
| 48 | 11 выбор 4 | ||
| 49 | Найти число возможных исходов | 11 выбор 2 | |
| 50 | Найти число возможных исходов | 11 выбор 3 | |
| 51 | Найти число возможных исходов | 10 перестановка 5 | |
| 52 | Найти число возможных исходов | 5 выбор 5 | |
| 53 | Найти число возможных исходов | 6 выбор 1 | |
| 54 | Найти число возможных исходов | 8 перестановка 4 | |
| 55 | Найти число возможных исходов | 8 выбор 6 | |
| 56 | Найти число возможных исходов | 13 выбор 4 | |
| 57 | Вычислить | e | |
| 58 | Найти уравнение, перпендикулярное прямой | -7x-5y=7 | |
| 59 | Найти число возможных исходов | 13 выбор 2 | |
| 60 | Найти число возможных исходов | 10 перестановка 2 | |
| 61 | Найти число возможных исходов | 10 перестановка 3 | |
| 62 | Найти число возможных исходов | 10 выбор 7 | |
| 63 | Найти число возможных исходов | 20 выбор 4 | |
| 64 | Найти число возможных исходов | 6 перестановка 4 | |
| 65 | Найти число возможных исходов | 5 перестановка 4 | |
| 66 | Найти число возможных исходов | 6 выбор 5 | |
| 67 | Найти число возможных исходов | 52 выбор 3 | |
| 68 | Найти число возможных исходов | 4 выбор 0 | |
| 69 | Найти число возможных исходов | 9 перестановка 7 | |
| 70 | Найти число возможных исходов | 6 выбор 2 | |
| 71 | Найти число возможных исходов | 5 перестановка 5 | |
| 72 | Найти число возможных исходов | 5 перестановка 2 | |
| 73 | Найти число возможных исходов | 6 выбор 6 | |
| 74 | Найти число возможных исходов | 7 выбор 6 | |
| 75 | Найти число возможных исходов | 8 перестановка 6 | |
| 76 | Найти число возможных исходов | 7 перестановка 7 | |
| 77 | Найти число возможных исходов | 9 перестановка 5 | |
| 78 | Найти число возможных исходов | 2 перестановка 2 | |
| 79 | Найти число возможных исходов | 10 выбор 8 | |
| 80 | Найти число возможных исходов | 12 выбор 7 | |
| 81 | Найти число возможных исходов | 15 выбор 5 | |
| 82 | Найти обратный элемент | [[1,0,1],[2,-2,-1],[3,0,0]] | |
| 83 | Определить область значений | 1/4x-7 | |
| 84 | Найти число возможных исходов | 10 перестановка 7 | |
| 85 | Найти число возможных исходов | 12 выбор 6 | |
| 86 | Найти число возможных исходов | 2 выбор 1 | |
| 87 | Найти число возможных исходов | 30 выбор 3 | |
| 88 | Найти число возможных исходов | 9 выбор 6 | |
| 89 | Найти число возможных исходов | 8 перестановка 2 | |
| 90 | Найти число возможных исходов | 7 выбор 1 | |
| 91 | Найти число возможных исходов | 6 перестановка 2 | |
| 92 | Найти число возможных исходов | 4 перестановка 2 | |
| 93 | Найти число возможных исходов | 4 перестановка 3 | |
| 94 | Найти число возможных исходов | 3 перестановка 3 | |
| 95 | Найти число возможных исходов | 46 выбор 6 | |
| 96 | Найти число возможных исходов | 5 перестановка 1 | |
| 97 | Найти число возможных исходов | 52 выбор 7 | |
| 98 | Найти число возможных исходов | 52 перестановка 5 | |
| 99 | Найти число возможных исходов | 9 выбор 1 | |
| 100 | Найти число возможных исходов | 9 перестановка 6 |
Простые числа.
 Примеры — МАТВОКС Простые числа. Примеры — МАТВОКС
Примеры — МАТВОКС Простые числа. Примеры — МАТВОКС
Перейти к содержанию
ПОИСК
Страница Вконтакте открывается в новом окне
Вы здесь:
Как определить, является число простым или составным
Является ли число простым можно узнать при помощи таблицы простых чисел.
Но не всегда таблица бывает под рукой.
Для таких случаев, чтобы определить, является ли число простым, можно использовать следующую теорему.
Теорема о делителе составного числа
Наименьший положительный и отличный от 1 делитель составного числа a не превосходит √a, где √a – арифметический квадратный корень из a.
Где:
b — наименьший положительный и отличный от 1 делитель составного числа a
Доказательство теоремы
Обозначим буквой b наименьший и отличный от 1 делитель составного числа a (число b – простое). Тогда существует такое целое число q, что:
Тогда существует такое целое число q, что:
q будет положительным числом, исходя из правил умножения целых чисел, причем:
Если b>q, то нарушится условие того, что b – наименьший делитель числа a, так как q также является делителем числа a, исходя из равенства для a.
Умножим обе части неравенства на положительное и большее 1 целое число b. получим:
Так как:
Тогда:
Извлечем квадратный корень:
ПримерыПример 1Не пользуясь таблицей простых чисел, определите, является число 479 составным или простым.
Решение
Число будет простым, если оно будет делиться только на 1 и на само себя. Значит, чтобы узнать, является ли число простым, нужно убедиться, что у него нет других делителей кроме 1 и 479.
Чтобы упростить задачу «перебора возможных делителей» воспользуемся теоремой, согласно которой, если число – составное, то его наименьший положительный и отличный от 1 делитель — это арифметический квадратный корень из этого числа.
Итак, рассмотрим число 479. Если оно составное, то его наименьший положительный делитель (обозначим его буквой b):
Причем этот делитель должен быть простым числом.
Из 479 квадратный корень не извлекается, значит, определим его приблизительное значение. Ближайшее к 479 число, из которого квадратный корень извлекается, это 484:
Тогда:
Значит,
Таким образом, если 479 – составное число, то его наименьший делитель будет одним из простых чисел, меньших 22.
Выпишем ряд простых чисел, меньших 22:
2, 3, 5, 7, 11, 13, 17, 19
По признакам делимости, очевидно, что 479 не будет без остатка делиться на 2, 3 и 5.
Проверим оставшиеся возможные делители.
479:7
479:11
479:13
479:17
479:19
Число 479 нацело не разделилось ни на одно простое число меньшее 22. Следовательно, 479 – простое число.
Ответ: 479 – простое число
Пример 2Определить, является число 143 простым или составным.
Решение
Число будет простым, если оно будет делиться только на 1 и на само себя. Значит, чтобы узнать, является ли число простым, нужно убедиться, что у него нет других делителей кроме 1 и 143.
Чтобы упростить задачу «перебора возможных делителей» воспользуемся теоремой, согласно которой, если число – составное, то его наименьший положительный и отличный от 1 делитель — это арифметический квадратный корень из этого числа.
Итак, рассмотрим число 143. Если оно составное, то его наименьший положительный делитель (обозначим его буквой b) будет меньше или равен арифметическому квадратному корню из 143:
Причем этот делитель должен быть простым числом.
Из 143 квадратный корень не извлекается, значит, определим его приблизительное значение. Ближайшее к 143 число, из которого квадратный корень извлекается, это 144:
Тогда:
Значит,
Таким образом, если 143 – составное число, то его наименьший делитель будет одним из простых чисел, меньших 12.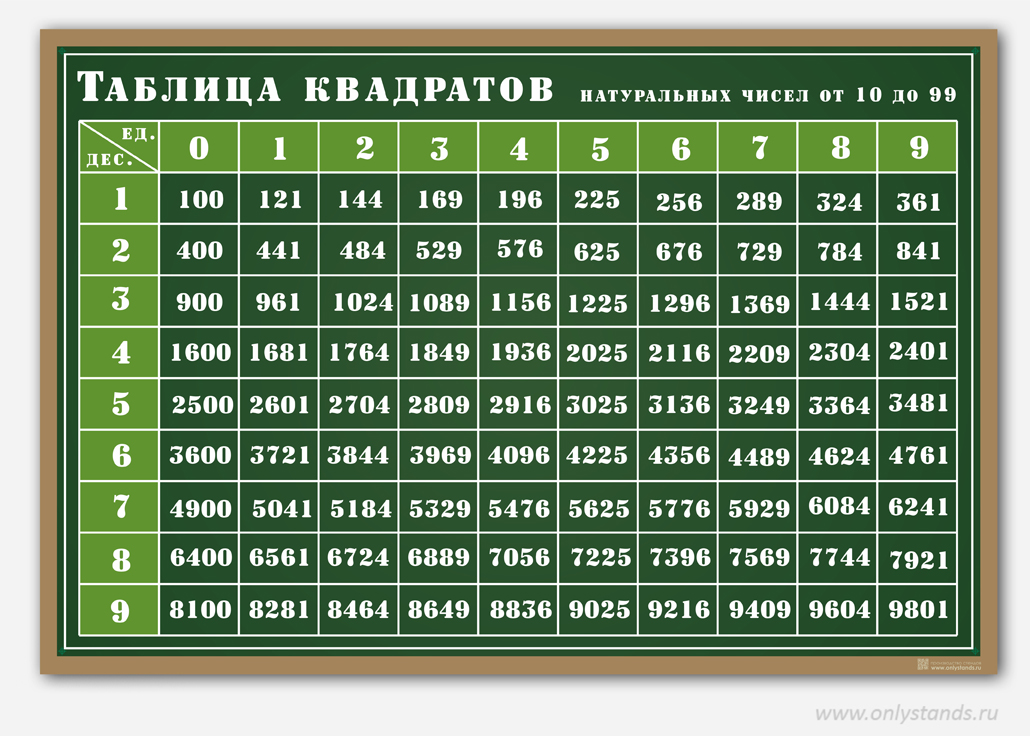
Выпишем ряд простых чисел, меньших 12:
2, 3, 5, 7, 11
По признакам делимости, очевидно, что 143 не будет без остатка делиться на 2, 3 и 5.
Проверим оставшиеся возможные делители.
143:7
143:11
Так как число 143 делится на 11 без остатка, то число 143 – составное.
Ответ: 143 – составное
Пример 3Не пользуясь таблицей простых чисел, определить, является число 97 составным или простым.
Решение
Число будет простым, если оно будет делиться только на 1 и на само себя. Значит, чтобы узнать, является ли число простым, нужно убедиться, что у него нет других делителей кроме 1 и 97.
Чтобы упростить задачу «перебора возможных делителей» воспользуемся теоремой, согласно которой, если число – составное, то его наименьший положительный и отличный от 1 делитель — это арифметический квадратный корень из этого числа.
Итак, рассмотрим число 97. Если оно составное, то его наименьший положительный делитель (обозначим его буквой b) должен быть:
Причем этот делитель должен быть простым числом.
Из 97 квадратный корень не извлекается, значит, определим его приблизительное значение. Ближайшее к 97 число, из которого квадратный корень извлекается, это 100:
Тогда:
Значит,
Таким образом, если 97 – составное число, то его наименьший делитель будет одним из простых чисел, меньших 9.
Выпишем ряд простых чисел, меньших 9:
2, 3, 5, 7
По признакам делимости, очевидно, что 97 не будет без остатка делиться на 2, 3 и 5.
Проверим, делится ли 97 на 7 без остатка.
97:7=13 ост 6
Следовательно, 97 – простое число.
Ответ: 97 – простое число
Пример 4Определить, является число 247 простым или составным.
Решение
Число будет простым, если оно будет делиться только на 1 и на само себя. Значит, чтобы узнать, является ли число простым, нужно убедиться, что у него нет других делителей кроме 1 и 247.
Чтобы упростить задачу «перебора возможных делителей» воспользуемся теоремой, согласно которой, если число – составное, то его наименьший положительный и отличный от 1 делитель — это арифметический квадратный корень из этого числа.
Итак, рассмотрим число 247. Если оно составное, то его наименьший положительный делитель (обозначим его буквой b) будет меньше или равен арифметическому квадратному корню из 247:
Причем этот делитель должен быть простым числом.
Из 247 квадратный корень не извлекается, значит, определим его приблизительное значение. Ближайшее к 247 число, из которого квадратный корень извлекается, это 256:
Тогда:
Значит,
Таким образом, если 247 – составное число, то его наименьший делитель будет одним из простых чисел, меньших 16.
Выпишем ряд простых чисел, меньших 16:
2, 3, 5, 7, 11, 13
По признакам делимости, очевидно, что 247 не будет без остатка делиться на 2, 3 и 5.
Проверим оставшиеся возможные делители.
247:7
247:11
247:13
Так как число 247 делится на 13 без остатка, то число 247 – составное.
Ответ: 247 – составное
9E09BEAE0A118E93DED3D74128EA2C147A65428915829EB11235F7758F7B38C3
MATHVOX
Вверх
Этот сайт использует файлы cookies для более комфортной работы пользователя. Продолжая просмотр страниц сайта, вы соглашаетесь с использованием файлов cookies. Если вам нужна дополнительная информация , пожалуйста, посетите страницу Политика Конфиденциальности Принять
Продолжая просмотр страниц сайта, вы соглашаетесь с использованием файлов cookies. Если вам нужна дополнительная информация , пожалуйста, посетите страницу Политика Конфиденциальности Принять
Privacy & Cookies Policy
Don`t copy text!
Квадратный корень из 100 равен. Что такое квадратный корень? Внесение под знак корня
Сегодня мы с вами разберемся на этой странице нашего сайта сайт о том, квадратный корень из 100 сколько будет. Давайте вместе с вами разберемся сколько будет квадратный корень из 100, так как над этой темой многие десятилетия ломали свои умы 1000 научных сотрудников и многие пришли без поворотному выводу по расчётам, что такого корня вообще не существует и его просто невозможно вычислить. Также очень важно в данном случае задать именно правильный вопрос по выявлению квадратного корня из 100. Если быть точным, то мы будем высчитывать арифметический корень квадрата из 100 так как в обычном квадратном корне из 100 в результате у нас будет получаться два числа: 10 и -10.
Сумму нужных нам этих чисел мы можем посчитать простым арифметическим приемом с помощью вертикальной, привычной чертой, цифры и корни которые прописываются справа внизу. Там мы будем находить нужный нам квадрат единиц корня, затем умножать десятки и находить удвоенное а не утроенное произведение десятка любого корня на единицы. Некоторые цифры нам придётся возводить в квадрат, чтобы в сумме получилось двузначное число, если в итоге у нас получилась число 10, значит мы всё сделали с вами верно. Главное изначально перед началом расчетов хотя бы немного подружиться с математикой и с математической прогрессией составление квадратного корня.
Запомните одно единственное и основное правило: чтобы нам извлечь нужный корень квадратный из любого целого числа, в первую очередь извлекаем любой нужный нам корень из числа его сумм и сотен. Если число равняется или больше 100, тогда мы начинаем искать корень из сотен фактических чисел этих данных сотен, потом из десятков тысяч фактического числа, тем более если данное число намного больше чем 100, затем уже в обязательном порядке извлекаем корень числа из сотен десятков тысяч или если быть точнее: из миллиона данного числа. На эту тему есть много правил и различных научных рекомендаций, школьных программ по извлечению квадратного корня из числа 100 будет всегда неизменным.
На эту тему есть много правил и различных научных рекомендаций, школьных программ по извлечению квадратного корня из числа 100 будет всегда неизменным.
Если рассматривать прогресс нахождения корня из числа 100, нам надо обратить внимание что в корне находится столько же цифр, сколько и под конечным числом граней, при этом левая грань может состоять всего лишь из одной цифры. Исходя из всего этого, самым точным на планете земля квадратным корнем из любого числа, будет называться такая сумма чисел, квадрат которого в точности при подсчетах равняется данному числу. Именно на этом мы можем окончить свой краткий курс по вычислению квадратного корня из 100 который будет равняться (10) десяти.
Константинова Вера
Как найти корень числа
Задача нахождения корня в математике является обратной задачей возведения числа в степень. Корни бывают различные: корни второй степени, корни третьей степени, корни четвертой степени и так далее. Это зависит от того, в какую степень изначально было возведено число. Корень обознается символом: √ – это квадратный корень, то есть корень из второй степени, если у корня степень больше, чем вторая, то над знаком корня приписывается соответствующая степень. Число, которое находится под знаком корня – это подкоренное выражение. При нахождении корня существует несколько правил, которые помогут не ошибиться в нахождении корня:
Корень обознается символом: √ – это квадратный корень, то есть корень из второй степени, если у корня степень больше, чем вторая, то над знаком корня приписывается соответствующая степень. Число, которое находится под знаком корня – это подкоренное выражение. При нахождении корня существует несколько правил, которые помогут не ошибиться в нахождении корня:
- Корень четной степени (если степень равна 2, 4, 6, 8 и так далее) из отрицательного числа НЕ существует. Если подкоренное выражение отрицательно, но ищется корень нечетной степени (3, 5, 7 и так далее), то результат будет отрицательным.
- Корень любой степени от единицы всегда единица: √1 = 1.
- Корень нуля есть нуль: √0 = 0.
Как найти корень из числа 100
Если в задаче не написано, корень какой степени необходимо найти, то обычно подразумевается, что необходимо найти корень второй степени (квадратный).
Найдем √100 = ? Нам необходимо найти такое число, при возведении которого во вторую степень, получится число 100. Очевидно, что таким числом является число 10, так как: 10 2 = 100. Следовательно, √100 = 10: квадратный корень из 100 равен 10.
Очевидно, что таким числом является число 10, так как: 10 2 = 100. Следовательно, √100 = 10: квадратный корень из 100 равен 10.
При решении различных задач из курса математики и физики ученики и студенты часто сталкиваются с необходимостью извлечения корней второй, третьей или n-ой степени. Конечно, в век информационных технологий не составит труда решить такую задачу при помощи калькулятора. Однако возникают ситуации, когда воспользоваться электронным помощником невозможно.
К примеру, на многие экзамены запрещено приносить электронику. Кроме того, калькулятора может не оказаться под рукой. В таких случаях полезно знать хотя бы некоторые методы вычисления радикалов вручную.
Извлечение квадратного корня при помощи таблицы квадратов
Один из простейших способов вычисления корней заключается в использовании специальной таблицы . Что же она собой представляет и как ей правильно воспользоваться?
При помощи таблицы можно найти квадрат любого числа от 10 до 99. При этом в строках таблицы находятся значения десятков, в столбах — значения единиц. Ячейка на пересечении строки и столбца содержит в себе квадрат двузначного числа. Для того чтобы вычислить квадрат 63, нужно найти строку со значением 6 и столбец со значением 3. На пересечении обнаружим ячейку с числом 3969.
При этом в строках таблицы находятся значения десятков, в столбах — значения единиц. Ячейка на пересечении строки и столбца содержит в себе квадрат двузначного числа. Для того чтобы вычислить квадрат 63, нужно найти строку со значением 6 и столбец со значением 3. На пересечении обнаружим ячейку с числом 3969.
Поскольку извлечение корня — это операция, обратная возведению в квадрат, для выполнения этого действия необходимо поступить наоборот: вначале найти ячейку с числом, радикал которого нужно посчитать, затем по значениям столбика и строки определить ответ. В качестве примера рассмотрим вычисление квадратного корня 169.
Находим ячейку с этим числом в таблице, по горизонтали определяем десятки — 1, по вертикали находим единицы — 3. Ответ: √169 = 13.
Аналогично можно вычислять корни кубической и n-ой степени, используя соответствующие таблицы.
Преимуществом способа является его простота и отсутствие дополнительных вычислений. Недостатки же очевидны: метод можно использовать только для ограниченного диапазона чисел (число, для которого находится корень, должно быть в промежутке от 100 до 9801). Кроме того, он не подойдёт, если заданного числа нет в таблице.
Кроме того, он не подойдёт, если заданного числа нет в таблице.
Разложение на простые множители
Если таблица квадратов отсутствует под рукой или с её помощью оказалось невозможно найти корень, можно попробовать разложить число, находящееся под корнем, на простые множители . Простые множители — это такие, которые могут нацело (без остатка) делиться только на себя или на единицу. Примерами могут быть 2, 3, 5, 7, 11, 13 и т. д.
Рассмотрим вычисление корня на примере √576. Разложим его на простые множители. Получим следующий результат: √576 = √(2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 3 ∙ 3) = √(2 ∙ 2 ∙ 2)² ∙ √3². При помощи основного свойства корней √a² = a избавимся от корней и квадратов, после чего подсчитаем ответ: 2 ∙ 2 ∙ 2 ∙ 3 = 24.
Что же делать, если у какого-либо из множителей нет своей пары? Для примера рассмотрим вычисление √54. После разложения на множители получаем результат в следующем виде: √54 = √(2 ∙ 3 ∙ 3 ∙ 3) = √3² ∙ √(2 ∙ 3) = 3√6. Неизвлекаемую часть можно оставить под корнем. Для большинства задач по геометрии и алгебре такой ответ будет засчитан в качестве окончательного. Но если есть необходимость вычислить приближённые значения, можно использовать методы, которые будут рассмотрены далее.
Для большинства задач по геометрии и алгебре такой ответ будет засчитан в качестве окончательного. Но если есть необходимость вычислить приближённые значения, можно использовать методы, которые будут рассмотрены далее.
Метод Герона
Как поступить, когда необходимо хотя бы приблизительно знать, чему равен извлечённый корень (если невозможно получить целое значение)? Быстрый и довольно точный результат даёт применение метода Герона . Его суть заключается в использовании приближённой формулы:
√R = √a + (R — a) / 2√a,
где R — число, корень которого нужно вычислить, a — ближайшее число, значение корня которого известно.
Рассмотрим, как работает метод на практике, и оценим, насколько он точен. Рассчитаем, чему равен √111. Ближайшее к 111 число, корень которого известен — 121. Таким образом, R = 111, a = 121. Подставим значения в формулу:
√111 = √121 + (111 — 121) / 2 ∙ √121 = 11 — 10 / 22 ≈ 10,55.
Теперь проверим точность метода :
10,55² = 111,3025.
Погрешность метода составила приблизительно 0,3. Если точность метода нужно повысить, можно повторить описанные ранее действия:
√111 = √111,3025 + (111 — 111,3025) / 2 ∙ √111,3025 = 10,55 — 0,3025 / 21,1 ≈ 10,536.
Проверим точность расчёта:
10,536² = 111,0073.
После повторного применения формулы погрешность стала совсем незначительной.
Вычисление корня делением в столбик
Этот способ нахождения значения квадратного корня является чуть более сложным, чем предыдущие. Однако он является наиболее точным среди остальных методов вычисления без калькулятора .
Допустим, что необходимо найти квадратный корень с точностью до 4 знаков после запятой. Разберём алгоритм вычислений на примере произвольного числа 1308,1912.
- Разделим лист бумаги на 2 части вертикальной чертой, а затем проведём от неё ещё одну черту справа, немного ниже верхнего края. Запишем число в левой части, разделив его на группы по 2 цифры, двигаясь в правую и левую сторону от запятой.
 Самая первая цифра слева может быть без пары. Если же знака не хватает в правой части числа, то следует дописать 0. В нашем случае получится 13 08,19 12.
Самая первая цифра слева может быть без пары. Если же знака не хватает в правой части числа, то следует дописать 0. В нашем случае получится 13 08,19 12. - Подберём самое большое число, квадрат которого будет меньше или равен первой группе цифр. В нашем случае это 3. Запишем его справа сверху; 3 — первая цифра результата. Справа снизу укажем 3×3 = 9; это понадобится для последующих расчётов. Из 13 в столбик вычтем 9, получим остаток 4.
- Припишем следующую пару чисел к остатку 4; получим 408.
- Число, находящееся сверху справа, умножим на 2 и запишем справа снизу, добавив к нему _ x _ =. Получим 6_ x _ =.
- Вместо прочерков нужно подставить одно и то же число, меньшее или равное 408. Получим 66×6 = 396. Напишем 6 справа сверху, т. к. это вторая цифра результата. Отнимем 396 от 408, получим 12.
- Повторим шаги 3-6. Поскольку снесённые вниз цифры находятся в дробной части числа, необходимо поставить десятичную запятую справа сверху после 6. Запишем удвоенный результат с прочерками: 72_ x _ =.
 Подходящей цифрой будет 1: 721×1 = 721. Запишем её в ответ. Выполним вычитание 1219 — 721 = 498.
Подходящей цифрой будет 1: 721×1 = 721. Запишем её в ответ. Выполним вычитание 1219 — 721 = 498. - Выполним приведённую в предыдущем пункте последовательность действий ещё три раза, чтобы получить необходимое количество знаков после запятой. Если не хватает знаков для дальнейших вычислений, у текущего слева числа нужно дописать два нуля.
В результате мы получим ответ: √1308,1912 ≈ 36,1689. Если проверить действие при помощи калькулятора, можно убедиться, что все знаки были определены верно.
Поразрядное вычисление значения квадратного корня
Метод обладает высокой точностью . Кроме того, он достаточно понятен и для него не требуется запоминать формулы или сложный алгоритм действий, поскольку суть способа заключается в подборе верного результата.
Извлечём корень из числа 781. Рассмотрим подробно последовательность действий.
- Выясним, какой разряд значения квадратного корня будет являться старшим. Для этого возведём в квадрат 0, 10, 100, 1000 и т.
 д. и выясним, между какими из них находится подкоренное число. Мы получим, что 10²
д. и выясним, между какими из них находится подкоренное число. Мы получим, что 10² - Подберём значение десятков. Для этого будем по очереди возводить в степень 10, 20, …, 90, пока не получим число, превышающее 781. Для нашего случая получим 10² = 100, 20² = 400, 30² = 900. Значение результата n будет находиться в пределах 20
- Аналогично предыдущему шагу подбирается значение разряда единиц. Поочерёдно возведём в квадрат 21,22, …, 29: 21² = 441, 22² = 484, 23² = 529, 24² = 576, 25² = 625, 26² = 676, 27² = 729, 28² = 784. Получаем, что 27
- Каждый последующий разряд (десятые, сотые и т. д.) вычисляется так же, как было показано выше. Расчёты проводятся до тех пор, пока не будет достигнута необходимая точность.
Видео
Из видео вы узнаете, как извлекать квадратные корни без использования калькулятора.
Среди множества знаний, которые являются признаком грамотности, на первом месте стоит азбука. Следующим, таким же «знаковым» элементом, являются навыки сложения-умножения и, примыкающие к ним, но обратные по смыслу, арифметические операции вычитания-деления. Усвоенные в далеком школьном детстве навыки, служат верой и правдой денно и нощно: ТВ, газета, СМС, И везде читаем, пишем, считаем, складываем, вычитаем, умножаем. А, скажите, часто ли вам приходилось по жизни, извлекать корни, кроме, как на даче? Например, такая занимательная задачка, типа, корень квадратный из числа 12345… Есть еще порох в пороховницах? Осилим? Да нет ничего проще! Где тут мой калькулятор… А без него, врукопашную, слабо?
Усвоенные в далеком школьном детстве навыки, служат верой и правдой денно и нощно: ТВ, газета, СМС, И везде читаем, пишем, считаем, складываем, вычитаем, умножаем. А, скажите, часто ли вам приходилось по жизни, извлекать корни, кроме, как на даче? Например, такая занимательная задачка, типа, корень квадратный из числа 12345… Есть еще порох в пороховницах? Осилим? Да нет ничего проще! Где тут мой калькулятор… А без него, врукопашную, слабо?
Сначала уточним, что же это такое — квадратный корень числа. Вообще говоря, «извлечь корень из числа» означает выполнить арифметическое действие противоположное возведению в степень — вот вам и единство противоположностей в жизненном приложении. допустим, квадрат, это умножение числа на самое себя, т.е., как учили в школе, Х * Х = А или в другой записи Х2 = А, а словами — «Х в квадрате равняется А». Тогда обратная задача звучит так: квадратный корень числа А, представляет собой число Х, которое будучи возведено в квадрат равно А.
Извлекаем квадратный корень
Из школьного курса арифметики известны способы вычислений «в столбик», которые помогают выполнить любые подсчеты с применением первых четырех арифметических действий.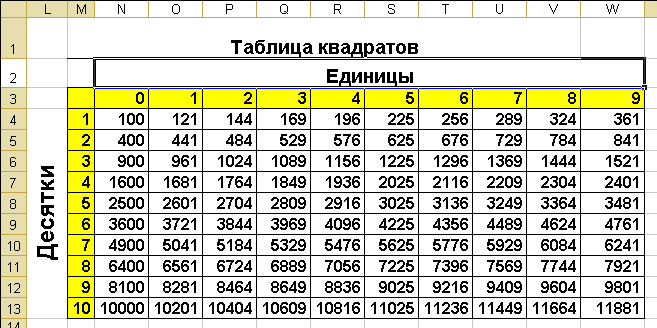 Увы… Для квадратных, и не только квадратных, корней таких алгоритмов не существует. А в таком случае, как извлечь квадратный корень без калькулятора? Исходя из определения квадратного корня вывод один — необходимо подбирать значение результата последовательным перебором чисел, квадрат которых приближается к значению подкоренного выражения. Только и всего! Не успеет пройти час-другой, как можно посчитать, используя хорошо известный прием умножения в «столбик», любой квадратный корень. При наличии навыков для этого достаточно пары минут. Даже не совсем продвинутый пользователь калькулятора или ПК делает это одним махом — прогресс.
Увы… Для квадратных, и не только квадратных, корней таких алгоритмов не существует. А в таком случае, как извлечь квадратный корень без калькулятора? Исходя из определения квадратного корня вывод один — необходимо подбирать значение результата последовательным перебором чисел, квадрат которых приближается к значению подкоренного выражения. Только и всего! Не успеет пройти час-другой, как можно посчитать, используя хорошо известный прием умножения в «столбик», любой квадратный корень. При наличии навыков для этого достаточно пары минут. Даже не совсем продвинутый пользователь калькулятора или ПК делает это одним махом — прогресс.
А если серьезно, то вычисление квадратного корня часто выполняют, используя прием «артиллерийской вилки»: сначала берут число, квадрат которого, примерно, соответствует подкоренному выражению. Лучше, если «наш квадрат» чуть меньше этого выражения. Затем корректируют число по собственному умению-разумению, например, умножают на два, и… вновь возводят в квадрат. Если результат больше числа под корнем, последовательно корректируя исходное число, постепенно приближаются к его «коллеге» под корнем. Как видите — никакого калькулятора, только умение считать «в столбик». Конечно же, есть множество научно-аргументированных и оптимизированных алгоритмов вычислений квадратного корня, но для «домашнего применения» указанный выше прием дает 100% уверенность в результате.
Если результат больше числа под корнем, последовательно корректируя исходное число, постепенно приближаются к его «коллеге» под корнем. Как видите — никакого калькулятора, только умение считать «в столбик». Конечно же, есть множество научно-аргументированных и оптимизированных алгоритмов вычислений квадратного корня, но для «домашнего применения» указанный выше прием дает 100% уверенность в результате.
Да, чуть не забыл, чтобы подтвердить свою возросшую грамотность, вычислим квадратный корень ранее указанного числа 12345. Делаем пошагово:
1. Возьмем, чисто интуитивно, Х=100. Подсчитаем: Х * Х = 10000. Интуиция на высоте — результат меньше 12345.
2. Попробуем, тоже чисто интуитивно, Х = 120. Тогда: Х * Х = 14400.И опять с интуицией порядок — результат больше 12345.
3. Выше получена «вилка» 100 и 120. Выберем новые числа — 110 и 115. Получаем, соответственно, 12100 и 13225 — вилка сужается.
4. Пробуем на «авось» Х=111. Получаем Х * Х = 12321. Это число уже достаточно близко к 12345. В соответствии с требуемой точностью «подгонку» можно продолжить или остановиться на полученном результате. Вот и все. Как и было обещано — все очень просто и без калькулятора.
В соответствии с требуемой точностью «подгонку» можно продолжить или остановиться на полученном результате. Вот и все. Как и было обещано — все очень просто и без калькулятора.
Совсем немного истории…
Додумались до использования квадратных корней еще пифагорейцы, ученики школы и последователи Пифагора, за 800 лет до н.э. и тут же, «нарвались» на новые открытия в области чисел. И откуда что взялось?
1. Решение задачи с извлечением корня, дает результат в виде чисел нового класса. Их назвали иррациональными, иначе говоря, «неразумными», т.к. они не записываются законченным числом. Самый классический пример такого рода — квадратный корень из 2. Этот случай соответствует вычислению диагонали квадрата со стороной равной 1 — вот оно, влияние школы Пифагора. Оказалось, что у треугольника с вполне конкретным единичным размером сторон, гипотенуза имеет размер, который выражается числом, у которого «нет конца». Так в математике появились
2. Известно, что Оказалось, что эта математическая операция содержит еще один подвох — извлекая корень, мы не знаем, квадратом какого числа, положительного или отрицательного, является подкоренное выражение. Эта неопределенность, двойной результат от одной операции, так и записывается.
Эта неопределенность, двойной результат от одной операции, так и записывается.
Изучение связанных с этим явлением проблем стало направлением в математике под названием теория комплексной переменной, имеющим большое практическое значение в математической физике.
Любопытно, что обозначение корня — радикал — применил в своей «Универсальной арифметике» все тот же вездесущий И. Ньютон, а в точности современный вид записи корня известен с 1690 года из книги француза Ролля «Руководство алгебры».
«Торговая» революция
Комков Сергей 26.12.2012
На фоне только что состоявшегося вступления России в ВТО уничтожение РГТЭУ — ведущего российского вуза в системе торговых (и, в первую очередь, внешнеторговых) отношений, а также увольнение его ректора, известного политика Сергея Бабурина выглядят не просто как глупость. Все это весьма похоже на заранее спланированную провокацию.
Похоже, Всемирная Торговая Организация и, главным образом, США, играющие в ней ключевую роль, оказались не на шутку озабочены возможными последствиями вступления в данную организацию России.
Но тут они вовремя вспомнили о том, что в России уже давно и успешно действует выращенная и вскормленная ими организация – Высшая Школа Экономики. Именно она была создана в 1992-м году на деньги Всемирного Банка с целью уничтожения в нашей стране всего интеллектуального потенциала нации. Именно под её руководством сегодня действует главный коллективный «агент влияния» в этой сфере – Министерство образования и науки России.
Можно много и до бесконечности говорить о глупости и некомпетентности новоявленного министра – господина Ливанова, который с трудом различает виды и направления образования. Но сам по себе господин Ливанов – абсолютный ноль без палочки. Из уст которого при каждом их открывании непременно выскакивает какая-нибудь очередная чушь. За его спиной маячат более колоритные фигуры. Например, главного «идеолога» всех экономических преобразований в нашей стране гражданина США Евгения Ясина и его подручного – ректора «Вышки» Ярослава Кузьминова.
Именно они с подачи американских советников из Всемирного Банка, активно работающих на базе ВШЭ, состряпали критерии так называемого «мониторинга» российских вузов.
И уже ни для кого не секрет, что, в соответствии с данными «критериями», в разряд «неэффективных» попали наиболее значимые российские высшие учебные заведения. Вузы с богатой историей и традициями, обладающие огромным творческим потенциалом. Например, МАРХИ, РГГУ, Литературный институт.
Попал в эту категорию и Российский Государственный Торгово-Экономический университет – РГТЭУ. Хотя по многим своим показателям этот вуз может дать сто очков форы той самой «Плешке», к которой его так скоропостижно решили присоединить. И, в первую очередь, в вопросах подготовки специалистов для системы внешней торговли.
РГТЭУ не просто имеет огромные международные связи. В нем досконально изучаются особенности торгового развития зарубежных стран. В стенах этого вуза постоянно выступают ведущие экономические и политические деятели мира, послы иностранных государств. Почетными докторами данного вуза являются ведущие мировые лидеры. Например, Фидель Кастро и Уго Чавес.
А это, как известно, «заклятые друзья» Америки. Вот и пошли в ход инструменты по уничтожению столь опасного учебного заведения. Дабы Россия, не дай Бог, не свернула с «истинного пути» и не предала интересы американских заказчиков.
Вот и пошли в ход инструменты по уничтожению столь опасного учебного заведения. Дабы Россия, не дай Бог, не свернула с «истинного пути» и не предала интересы американских заказчиков.
Да и личность самого ректора – известного в России и далеко за её пределами политика и ученого – встала у наших американских дядюшек как кость в горле.
Сергей Бабурин был не просто одним из лидеров парламентской оппозиции, занимая в предыдущем составе Государственной Думы России место вице-спикера. Он был активным сторонником новой политики России на всем постсоветском пространстве. Именно он в 2006-м году активнейшим образом помогал народу Абхазии выйти из глубочайшего политического кризиса. В который, кстати говоря, его вогнали опять все те же тупые и послушные воле американских советников чиновники правительства и администрации президента России.
Благодаря усилиям Сергея Бабурина верх в Абхазии тогда взяли прогрессивные силы во главе с Сергеем Багапшем. И с 2008-го года Абхазия стала главным стратегическим партнером России на Северном Кавказе.
Подобная позиция является выражением здравого, взвешенного патриотизма. Поэтому на протяжении ряда лет Бабурин возглавляет Российский Общенародный Союз и является организатором ежегодных традиционных Русских Маршей. Не тех, что со свастикой и фашистскими лозунгами «Россия только для русских!» А вполне понятных для всего населения страны выступлений с требованиями соблюдать российские национальные интересы в вопросах внешней политики и выполнять социальные обещания, данные своему собственному народу.
Но именно это не нравится американским приспешникам, окопавшимся в кабинетах российского правительства. Потому что для них требование соблюдения наших национальных интересов как нож по сердцу.
Вот и пришло кому-то на ум одним ударом убить сразу двух зайцев: и вуз, готовящий специалистов для успешной внешней торговли России, и её патриотически настроенного ректора.
Обычно для подобного рода действий больше всего подходят дураки. Ибо, им, как известно, не ведомо, что они на самом деле творят. Но в данном конкретном случае может получиться весьма серьезная промашка, чреватая тяжелейшими социальными последствиями для всей страны.
Но в данном конкретном случае может получиться весьма серьезная промашка, чреватая тяжелейшими социальными последствиями для всей страны.
Наши чиновники, зажравшиеся на казенных харчах и считающие себя полностью правыми в любом неправедном деле, забыли простейшую истину: они не властны над юношескими душами и юношескими порывами.
Именно подобного рода порывы смели в конце 60-х годов прошлого века правительство генерала Де Голля во Франции. Там тоже начиналось все с, казалось бы, внешне безобидных вещей. А закончилось всеобщим хаосом, беспорядками, горящими автомобилями и офисами.
Молодежь (особенно организованная студенческая молодежь) – это не кучка обанкротившихся политиков-оппозиционеров, побывавших во власти и, по сему, на неё весьма обиженных. Студенческая молодежь всегда и во все времена была одной из главных движущих сил революции. И сегодняшняя молодежь не является исключением из правил. Скорее наоборот. Именно сегодняшняя молодежь, особенно остро воспринимающая возникшую в обществе социальную несправедливость и неравенство, способна на самые крутые и самые радикальные шаги. И, если власть попытается применить силу, это будет для неё убийственно. Потому что молодежь никогда ей этого не простит.
И, если власть попытается применить силу, это будет для неё убийственно. Потому что молодежь никогда ей этого не простит.
Когда господин Ливанов и Ко объявили о своем намерении силовым методом начать решение проблемы высшего образования, закрывая и сливая вузы, они фактически подписали себе приговор. Они даже не удосужились задуматься над тем, какие глубинные силы они поднимают. И это кончится трагически не только для тех, кто сегодня оказался на руководящих постах в Министерстве образования и науки, но и для всего российского руководства в целом. Ибо, даже подавленный локально молодежный бунт не уходит в небытие. Он зреет с новой силой. Но где и когда он грянет, уже не сможет предсказать никто.
Так что события в РГТЭУ только на первый взгляд выглядят как некая «торговая революция». На самом деле они предвестники другой – более жесткой и более кровавой социальной войны, победителей в которой не будет.
Проигравший же известен заранее. Это наша Родина. Страна, которую мы пока еще иногда с некоторой гордостью называем Россией.
Поэтому сегодняшние действия руководства Минобрнауки в отношении отдельно взятого учебного заведения и в отношении отдельно взятого ректора можно расценивать как разжигание социальной войны во имя и во благо другого государства.
А это называется: Национальная Измена.
Задача нахождения корня в математике является обратной задачей возведения числа в степень. Корни бывают различные: корни второй степени, корни третьей степени, корни четвертой степени и так далее. Это зависит от того, в какую степень изначально было возведено число. Корень обознается символом: √ — это квадратный корень, то есть корень из второй степени, если у корня степень больше, чем вторая, то над знаком корня приписывается соответствующая степень. Число, которое находится под знаком корня — это подкоренное выражение. При нахождении корня существует несколько правил, которые помогут не ошибиться в нахождении корня:
- Корень четной степени (если степень равна 2, 4, 6, 8 и так далее) из отрицательного числа НЕ существует.
 Если подкоренное выражение отрицательно, но ищется корень нечетной степени (3, 5, 7 и так далее), то результат будет отрицательным.
Если подкоренное выражение отрицательно, но ищется корень нечетной степени (3, 5, 7 и так далее), то результат будет отрицательным. - Корень любой степени от единицы всегда единица: √1 = 1.
- Корень нуля есть нуль: √0 = 0.
Как найти корень из числа 100
Если в задаче не написано, корень какой степени необходимо найти, то обычно подразумевается, что необходимо найти корень второй степени (квадратный).
Найдем √100 = ? Нам необходимо найти такое число, при возведении которого во вторую степень, получится число 100. Очевидно, что таким числом является число 10, так как: 10 2 = 100. Следовательно, √100 = 10: квадратный корень из 100 равен 10.
Извлечение корней: определение, методы извлечения, примеры
Из этой статьи вы узнаете:
- что такое «извлечение корня»;
- в каких случаях он извлекается;
- принципы нахождения значения корня;
- основные способы извлечения корня из натуральных и дробных чисел.
Что такое «извлечение корня»
Для начала введем определение «извлечение корня».
Извлечение корня — процесс нахождения значения корня.
При извлечении корня n-ной степени из числа a, мы находим число b, n-ная степень которого равняется a. Если мы нашли такое число b, можно утверждать, что корень извлечен.
Замечание 1Выражения «извлечение корня» и «нахождение значения корня» равнозначны.
В каких случаях извлекается корень?
Определение 2Корень n-ной степени можно извлечь из числа a точно в случае, если a можно представить в виде n-ной степени некоторого числа b.
Пример 14=2×2, следовательно, из числа 4 можно точно извлечь квадратный корень, который равен 2
Определение 3Когда корень n-ной степени из числа a невозможно представить в виде n-ной степени числа b, то такой корень не извлекается, либо извлекается только приближенное значение корня с точностью до любого десятичного разряда.
Пример 22≈1,4142.
Принципы нахождения значения корня и способы их извлечения
- Использование таблицы квадратов, таблицы кубов и т.
 д.
д. - Разложение подкоренного выражения (числа) на простые множители
- Извлечение корней из дробных чисел
- Извлечение корня из отрицательного числа
- Поразрядное нахождение значения корня
Необходимо понять, по каким принципам находится значение корней, и каким образом они извлекаются.
Определение 4Главный принцип нахождения значения корней — основываться на свойствах корней, в том числе на равенстве: bnn=b, которое является справедливым для любого неотрицательного числа b.
Начать следует с наиболее простого и очевидного способа: таблицы квадратов, кубов и т.д.
Когда таблицы под руками нет, вам поможет способ разложения подкоренного числа на простые множители (способ незатейливый).
Стоит уделить внимание извлечению корня из отрицательного числа, что является возможным для корней с нечетными показателями.
Изучим, как извлекать корни из дробных чисел, в том числе из смешанных чисел, обыкновенных и десятичных дробей.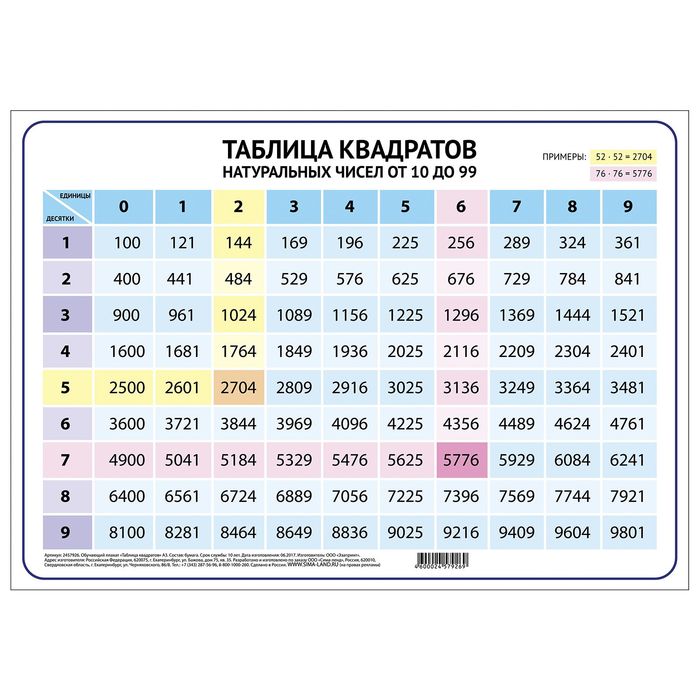
И потихоньку рассмотрим способ поразрядного нахождения значения корня — наиболее сложного и многоступенчатого.
Использование таблицы квадратов, кубов и т.д.
Таблица квадратов включает в себя все числа от 0 до 99 и состоит из 2 зон: в первой зоне можно составить любое число до 99 с помощью вертикального столбца с десятками и горизонтальной строки с единицами, во второй зоне содержатся все квадраты образуемых чисел.
Таблица квадратов
| Таблица квадратов | единицы | ||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| десятки | 0 | 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 |
| 1 | 100 | 121 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 361 | |
| 2 | 400 | 441 | 484 | 529 | 576 | 625 | 676 | 729 | 784 | 841 | |
| 3 | 900 | 961 | 1024 | 1089 | 1156 | 1225 | 1296 | 1369 | 1444 | 1521 | |
| 4 | 1600 | 1681 | 1764 | 1849 | 1936 | 2025 | 2116 | 2209 | 2304 | 2041 | |
| 5 | 2500 | 2601 | 2704 | 2809 | 2916 | 3025 | 3136 | 3249 | 3364 | 3481 | |
| 6 | 3600 | 3721 | 3844 | 3969 | 4096 | 4225 | 4356 | 4489 | 4624 | 4761 | |
| 7 | 4900 | 5041 | 5184 | 5329 | 5476 | 5625 | 5776 | 5929 | 6084 | 6241 | |
| 8 | 6400 | 6561 | 6724 | 6889 | 7056 | 7225 | 7396 | 7569 | 7744 | 7921 | |
| 9 | 8100 | 8281 | 8464 | 8649 | 8836 | 9025 | 9216 | 9409 | 9604 | 9801 | |
Существуют также таблицы кубов, четвертой степени и т. д., которые созданы по принципу, аналогичному таблице квадратов.
д., которые созданы по принципу, аналогичному таблице квадратов.
Таблица кубов
| Таблица кубов | единицы | ||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| десятки | 0 | 0 | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 |
| 1 | 1000 | 1 331 | 1 728 | 2 197 | 2 744 | 3 375 | 4 096 | 4 913 | 5 832 | 6 859 | |
| 2 | 8000 | 9 261 | 10 648 | 12 167 | 13 824 | 15 625 | 17 576 | 19 683 | 21 952 | 24 389 | |
| 3 | 27000 | 29 791 | 32 768 | 35 937 | 39 304 | 42 875 | 46 656 | 50 653 | 54 872 | 59 319 | |
| 4 | 64000 | 68 921 | 74 088 | 79 507 | 85 184 | 91 125 | 97 336 | 103 823 | 110 592 | 117 649 | |
| 5 | 125000 | 132 651 | 140 608 | 148 877 | 157 464 | 166 375 | 175 616 | 185 193 | 195 112 | 205 379 | |
| 6 | 216000 | 226 981 | 238 328 | 250 047 | 262 144 | 274 625 | 287 496 | 300 763 | 314 432 | 328 509 | |
| 7 | 343000 | 357 911 | 373 248 | 389 017 | 405 224 | 421 875 | 438 976 | 456 533 | 474 552 | 493 039 | |
| 8 | 512000 | 531 441 | 551 368 | 571 787 | 592 704 | 614 125 | 636 056 | 658 503 | 681 472 | 704 969 | |
| 729000 | 753 571 | 778 688 | 804 357 | 830 584 | 857 375 | 884 736 | 912 673 | 941 192 | 970 299 | ||
Принцип функционирования таких таблиц прост, однако их часто нет под рукой, что значительно усложняет процесс извлечение корня, поэтому необходимо владеть минимум несколькими способами извлечения корней.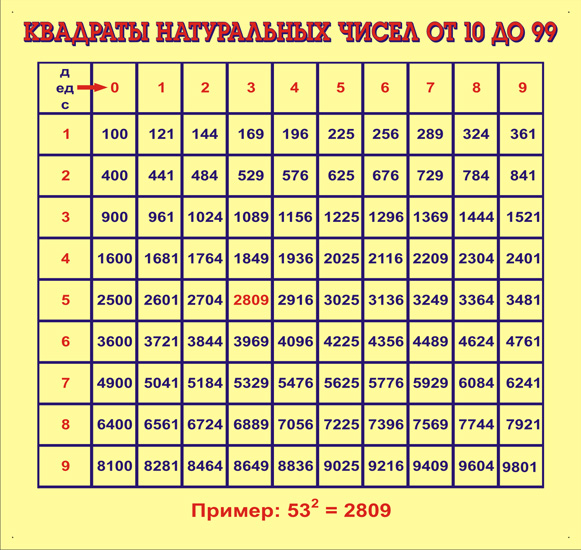
Разложение подкоренного числа на простые множители
Наиболее удобный способ нахождения значения корня после таблицы квадратов и кубов.
Определение 5Способ разложения подкоренного числа на простые множители подразумевает под собой представление числа в виде степени с необходимым показателем, что дает нам возможность получить значение корня.
Пример 3Извлечем квадратный корень из 144.
Разложим 144 на простые множители:
Таким образом: 144=2×2×2×2×3×3=(2×2)2×32=(2×2×3)2=122. Следовательно, 144=122=12.
Также при использовании свойств степени и корней можно записать преобразование немного по-другому:
144=2×2×2×2×3×3=24×32=24×32=22×3=12
144=12 — окончательный ответ.
Извлечение корней из дробных чисел
Запоминаем: любое дробное число должно быть записано в виде обыкновенной дроби.
Определение 6Следуя свойству корня из частного, справедливым является следующее равенство:
pqn=pnqn. Исходя из этого равенства, необходимо воспользоваться правилом извлечения корня из дроби: корень из дроби равен от деления корня числителя на корень знаменателя.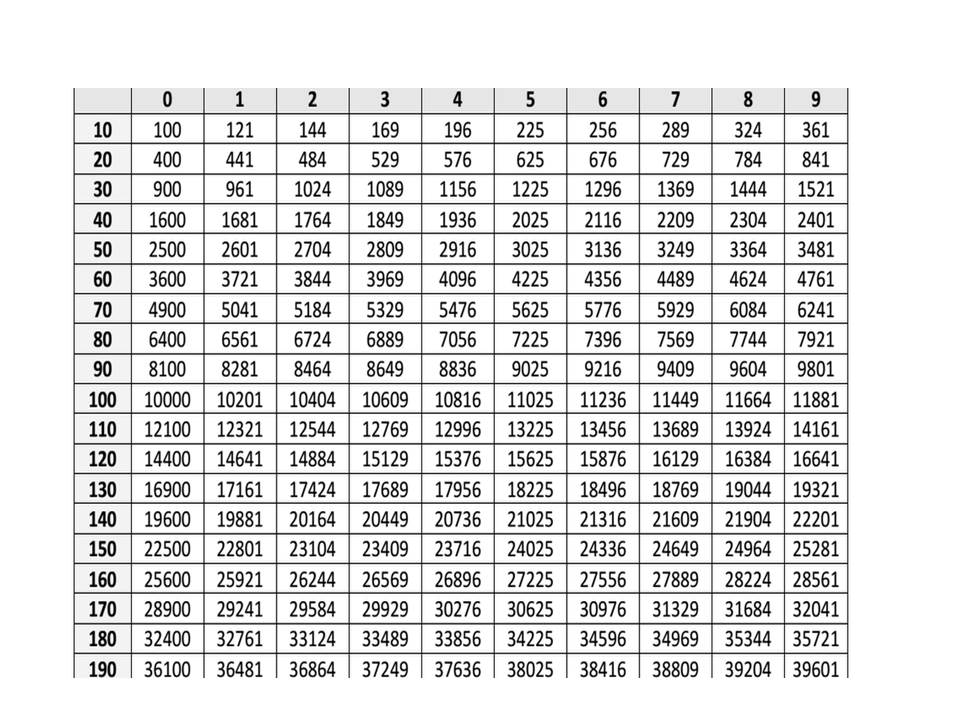
Рассмотрим пример извлечения корня из десятичной дроби, поскольку извлечь корень из обыкновенной дроби можно с помощью таблицы.
Необходимо извлечь кубический корень из 474,552. Первым делом, представим десятичную дробь в виде обыкновенной: 474,552 = 474552/1000. Из этого следует: 47455210003=474552310003. Затем можно приступить к процессу извлечения кубических корней в числителе и знаменателе:
474552=2×2×2×3×3×3×13×13×13=(2×3×13)3=783 и 1000=103, то
4745523=7833=78 и 10003=1033=10.
Завершаем вычисления: 474552310003=7810=7,8.
Извлечение корня из отрицательных чисел
Если знаменатель является нечетным числом, то число под знаком корня может оказаться отрицательным. Из этого следует: для отрицательного числа -a и нечетного показателя корня 2n-1 справедливо равенство:
-a2×n-1=-a2×n-1
Определение 7Правило извлечения нечетной степени из отрицательных чисел: чтобы извлечь корень из отрицательного числа необходимо извлечь корень из противоположного ему положительного числа и поставить перед ним знак минус.
-122092435. Для начала необходимо преобразовать выражение, чтобы под знаком корня оказалось положительно число:
-122092435=12209243-5
Затем следует заменить смешанное число обыкновенной дробью:
12209243-5=3125243-5
Пользуясь правилом извлечения корней из обыкновенной дроби, извлекаем:
3125243-5=-312552435
Вычисляем корни в числителе и знаменателе:
-312552435=-555355=-53=-123
Краткая запись решения:
-122092435=12209243-5=3125243-5=-312552435=-555355=-53=-123.
Ответ: -122092435=-123.
Поразрядное нахождение значения корня
Бывают случаи, когда под корнем находится число, которое не получается представить в виде n-ной степени некоторого числа. Но необходимо знать значение корня с точностью до некоторого знака.
В таком случае необходимо воспользоваться алгоритмом поразрядного нахождения значения корня, с помощью которого можно получить достаточное количество значений искомого числа.
Пример 6Как это происходит, разберем на примере извлечения квадратного корня из 5.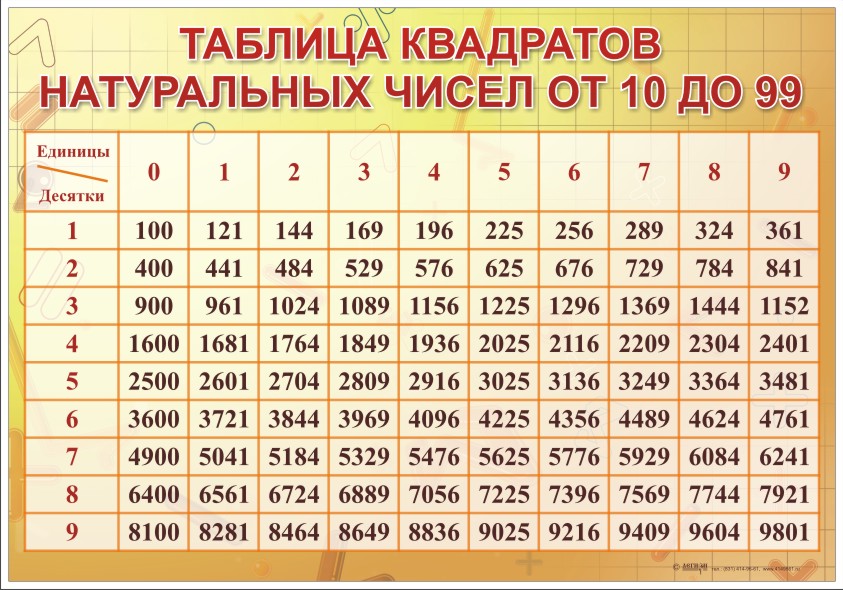
Сперва необходимо найти значение разряда единиц. Для этого начнем перебирать значения 0,1,2,…,9, вычисляя при этом 02, 12, …, 92 до необходимого значения, которое больше, чем подкоренное число 5. Все это удобно представить в виде таблицы:
| Возможное значение корня | 0 | 1 | 2 | 3 |
| Это значение в степени | 0 | 1 | 4 | 9 |
Значение ряда единиц равняется 2 (так как 22<5, а 23>5). Переходим в разряду десятых — будем возводить в квадрат числа 2,0, 2,1, 2,2,…,2,9, , сравнивая полученные значения с числом 5.
| Возможное значение корня | 2,0 | 2,1 | 2,2 | 2,3 |
| Это значение в степени | 4 | 4,41 | 4,84 | 5,29 |
Поскольку 2,22<5, а 2,32>5, то значение десятых равняется 2. Переходим к нахождению значения сотых:
Переходим к нахождению значения сотых:
| Возможное значение корня | 2.20 | 2,21 | 2,22 | 2,23 | 2,24 |
| Это значение в степени | 4,84 | 4,8841 | 4,8294 | 4,9729 | 5,0176 |
Таким образом, найдено значение корня из пяти — 2,23. Можно находить значения корня дальше:
2,236, 2,2360, 2, 23606, 2,236067,…
Итак, мы изучили несколько наиболее распространенных способов нахождения значения корня, воспользоваться которыми можно в любой ситуации.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р. Реферат
от 1 дня / от 700 р.
Реферат
от 1 дня / от 700 р.
Что такое квадратный корень. Таблица квадратных корней
В данной статье разберем понятие «квадратный корень» и приведем таблицу квадратных корней от 1 до 10000.
Чтобы возвести в квадрат число нужно умножить число на само себя. Кратко запись числа в квадрате выглядит следующим образом:
3 · 3 = 32 = 9
Но как быть, если нам нужно получить обратный результат? Например, узнать, какое число при возведении в квадрат дало бы число «9»?
Нужно запомнить, что:
- Нахождение исходного числа, которое в квадрате дало бы требуемое, называется извлечением квадратного корня.

- Извлечение квадратного корня — это действие, обратное возведению в квадрат.
У квадратного корня есть специальный знак. Исходя из вычислений выше, нетрудно догадаться, что число, которое в квадрате дает «9», это число «3». Запись извлечения квадратного корня из числа «9» выглядит так:
√9 = 3
Читаем запись: «Арифметический квадратный корень из девяти». Можно опустить слово «арифметический». Словосочетания «арифметический квадратный корень» и «квадратный корень» полностью равнозначны.
Квадратный корень из нуля равен нулю: √0 = 0
В таблице приведены квадратные корни натуральных чисел от 1 до 100.
| √1 = 1 √4 = 2 √9 = 3 √16 = 4 √25 = 5 √36 = 6 √49 = 7 √64 = 8 √81 = 9 √100 = 10 | √121 = 11 √144 = 12 √169 = 13 √196 = 14 √225 = 15 √256 = 16 √289 = 17 √324 = 18 √361 = 19 √400 = 20 | √441 = 21 √484 = 22 √529 = 23 √576 = 24 √625 = 25 √676 = 26 √729 = 27 √784 = 28 √841 = 29 √900 = 30 | √961 = 31 √1024 = 32 √1089 = 33 √1156 = 34 √1225 = 35 √1296 = 36 √1369 = 37 √1444 = 38 √1521 = 39 √1600 = 40 | √1681 = 41 √1764 = 42 √1849 = 43 √1936 = 44 √2025 = 45 √2116 = 46 √2209 = 47 √2304 = 48 √2401 = 49 √2500 = 50 |
| √2601 = 51 √2704 = 52 √2809 = 53 √2916 = 54 √3025 = 55 √3136 = 56 √3249 = 57 √3364 = 58 √3481 = 59 √3600 = 60 | √3721 = 61 √3844 = 62 √3969 = 63 √4096 = 64 √4225 = 65 √4356 = 66 √4489 = 67 √4624 = 68 √4761 = 69 √4900 = 70 | √5041 = 71 √5184 = 72 √5329 = 73 √5476 = 74 √5625 = 75 √5776 = 76 √5929 = 77 √6084 = 78 √6241 = 79 √6400 = 80 | √6561 = 81 √6724 = 82 √6889 = 83 √7056 = 84 √7225 = 85 √7396 = 86 √7569 = 87 √7744 = 88 √7921 = 89 √8100 = 90 | √8281 = 91 √8464 = 92 √8649 = 93 √8836 = 94 √9025 = 95 √9216 = 96 √9409 = 97 √9604 = 98 √9801 = 99 √10000 = 100 |
Последние материалы
-
Какой лучший стиль эмоционального воспитания
-
Родители, дети, эмоции… В вашей семье это похоже на «Бермудский треугольник»?
-
Їжа для «мозку» дитини і не тільки дитини…
Рубрики
- Айкидо для детей
- Английский язык
- Важливі звички, які обов’язково потрібно розвинути у дитини
- Дети и родители
- Информатика, основы программирования
- Йога для детей
- Логопедия
- Математика, логика, мышление
- Музыка для детей
- Оборудование для занятий в клубе
- Обучение без стресса
- Обучение ребенка
- Онлайн обучение (e-learning)
- Подготовка ребенка к школе
- Развитие ребенка 1-3 лет
- Развитие ребенка 3-7 лет
- Развитие ребенка 7-17 лет
- Развитие ребенка до 1 года
- Рисование, лепка, оригами
- Театральная студия
- Учебные программы
- Фитнес для детей
- Чтение, письмо
- Що робити, якщо…
- Эмоциональный интеллект ребенка
Добро пожаловать в детский клуб Kokoro
Мечтаете об успешном будущем для Вашего ребенка? Хотите дать детям навыки, которые обязательно пригодятся им в будущем? Хотите, чтобы Ваш ребенок всесторонне развивался на увлекательных занятиях? Тогда детский клуб Kokoro — это то, что Вам нужно!
Запишитесь на бесплатное пробное занятие уже сегодня по тел. 095-65-38-165, 097-497-28-68
095-65-38-165, 097-497-28-68
Читать далее
Наш Facebook
Квадратный корень из 484 — Как найти квадратный корень из 484?
LearnPracticeDownload
Квадрат 22 дает 484. Следовательно, 484 – число в совершенном квадрате. Квадратный корень из 484 – рациональное число. В этом мини-уроке мы научимся находить квадратный корень из 484 вместе с решенными примерами. Теперь найдем квадратный корень из 484.
- Квадратный корень из 484 : √ 484 = 22
- Квадрат 484: 484 2 = 2,34,256
| 1. | Что такое квадратный корень из 484? |
| 2. | Является ли квадратный корень из 484 рациональным или иррациональным? |
3. | Как найти квадратный корень из 484? |
| 4. | Часто задаваемые вопросы о квадратном корне из 484 |
Что такое квадратный корень из 484?
При возведении 22 в квадрат получается 484. Следовательно, квадратный корень из 484 равен 22. Записывается как √ 484 = 22. Следовательно, 484 – полный квадрат.
Является ли квадратный корень из 484 рациональным или иррациональным?
Поскольку √ 484 = 22, можно легко выразить √ 484 в форме p/q. Следовательно, √ 484 — рациональное число.
Как найти квадратный корень из 484?
Существуют разные методы определения квадратного корня из любого числа. Нажмите здесь, чтобы узнать больше об этом. Квадратный корень из 484 можно найти двумя способами: 9.0003
- Квадратный корень из 484 путем длинного деления
- Квадратный корень из 484 с помощью простой факторизации
Квадратный корень из 484 путем деления в длину
Квадратный корень из 484 можно найти с помощью деления в длину, используя следующие шаги:
- Шаг 1 : Сначала мы соединим цифры заданного числа, начиная с место юнита.
 Поместите горизонтальную черту, чтобы обозначить сопряжение.
Поместите горизонтальную черту, чтобы обозначить сопряжение. - Шаг 2 : Мы найдем число, которое при умножении на себя дает произведение, меньшее или равное 4. Мы знаем, что 2 × 2 = 4. Следовательно, разность равна 0, а частное равно 2.
- Шаг 3 : Теперь нам нужно уменьшить 84 и умножить частное на 2. Это даст нам 4. Следовательно, 4 – начальная цифра нового делителя.
- Шаг 4 : 2 ставится на место единицы нового делителя, потому что при умножении 42 на 2 получается 84. Полученный ответ равен 0,
- Шаг 5 : Следовательно, квадратный корень из 484 равен 22.
Квадратный корень из 484 с помощью простой факторизации
484 также может быть выражен как (2 × 2 × 11 × 11). В квадратном корне повторяются числа 2 и 11. Следовательно, квадратный корень из 484 равен 2 × 11 = 22,9.0003
Таким образом, квадратный корень из 484 равен 22.
Изучите квадратный корень с помощью иллюстраций и интерактивных примеров
- Квадратный корень из 169
- Квадратный корень из 196
- Квадратный корень из 225
- Квадратный корень из 289
- Квадратный корень из 400
Важные примечания:
- 484 — это число с полным квадратом, поскольку значение, полученное после извлечения из него квадратного корня, является целым числом.

- Квадратный корень из 484 упрощается до 22 либо путем разложения числа 484 на простые множители, либо путем выражения 484 в виде квадрата 22.
Аналитический центр:
- Может ли значение квадратного корня из 484 быть выражено в виде десятичной дроби?
- Являются ли — √ 484 и √ -484 одинаковыми?
Пример 1 : Какова разница в длине квадратных коробок площадью 484 квадратных дюйма и 400 квадратных дюймов?
Решение
Площадь квадратного прямоугольника можно рассчитать по формуле = длина × длина
Длина квадратной коробки площадью 484 квадратных дюйма равна √ 484 = 22 дюйма 90 173. Точно так же длина квадратной коробки площадью 400 квадратных дюймов равна √ 400 = 20 дюймов
. Разница в длине двух коробок составляет (22–20) дюймов = 2 дюйма 90 173. Таким образом, разница в длине квадратных коробок площадью 484 квадратных дюйма и 400 квадратных дюймов составляет 2 дюйма.
Пример 2 : Радиус круга площадью 484π квадратных дюймов меньше 25 дюймов или больше 25 дюймов?
Решение
Радиус можно найти по формуле площади круга, то есть πr 2 . Из предоставленной информации
πr 2 = 484π
r 2 = 484Извлекая квадратный корень из обеих частей, мы получаем √ r 2 = √ 484. Мы знаем, что квадратный корень из r 2 р. Квадратный корень из 484 равен 22 дюймам. Следовательно, радиус круга площадью 484π квадратных дюймов меньше 25 дюймов.
перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о квадратном корне из 484
Чему равны два квадратных корня из 484?
Два квадратных корня из 484 равны -22 и +22.
Является ли 484 идеальным квадратом?
Да, 484 — правильный квадрат.
Имеет ли число 484 квадратный корень?
Да, 484 имеет квадратный корень. √ 484 равно 22.
Можно ли упростить квадратный корень из 484?
484 разбивается как произведение 2 × 2 × 11 × 11. Квадратный корень из 484 дает 22.
Является ли квадратный корень из 484 рациональным или иррациональным?
Квадратный корень из 484 является рациональным.
Является ли квадратный корень из 484 действительным числом?
Да, квадратный корень из 484 — действительное число.
Рабочие листы по математике и визуальный учебный план
Квадратный корень из 484 (√484)
Здесь мы определим, проанализируем, упростим и вычислим квадратный корень из 484. Мы начнем с определения, а затем ответим на некоторые общие вопросы.
вопросы о квадратном корне из 484. Затем мы покажем вам различные способы вычисления квадратного корня из 484 с и без
компьютер или калькулятор. У нас есть много информации, чтобы поделиться, так что давайте начнем!
У нас есть много информации, чтобы поделиться, так что давайте начнем!
Квадратный корень из 484 определение
Квадратный корень из 484 в математической форме записывается с таким знаком радикала √484. Мы называем это квадратным корнем из 484 в радикальной форме.
Квадратный корень из 484 — это величина (q), которая при умножении сама на себя будет равна 484.
√484 = q × q = q 2
Является ли 484 полным квадратом?
484 является полным квадратом, если квадратный корень из 484 равен целому числу. Как мы рассчитали дальше
внизу на этой странице квадратный корень из 484 — это целое число.
484 — правильный квадрат.
Является ли квадратный корень из 484 рациональным или иррациональным?
Квадратный корень из 484 является рациональным числом, если 484 является полным квадратом. Это иррациональное число, если оно не является полным квадратом.
Поскольку 484 — совершенный квадрат, это рациональное число. Это означает, что ответ на вопрос «квадратный корень из 484?» не будет иметь десятичных знаков.
Это иррациональное число, если оно не является полным квадратом.
Поскольку 484 — совершенный квадрат, это рациональное число. Это означает, что ответ на вопрос «квадратный корень из 484?» не будет иметь десятичных знаков.
√484 — рациональное число
Можно ли упростить квадратный корень из 484?
Квадратный корень из полного квадрата можно упростить, потому что квадратный корень из полного квадрата будет равен целому числу:
√484 = 22
Как вычислить квадратный корень из 484 с помощью калькулятора
Самый простой и скучный способ вычислить квадратный корень из 484 — воспользоваться калькулятором!
Просто введите 484, а затем √x, чтобы получить ответ. Мы сделали это с помощью нашего калькулятора и получили следующий ответ:
√484 = 22
Как вычислить квадратный корень из 484 на компьютере
Если вы используете компьютер с Excel или Numbers, вы можете ввести SQRT(484) в ячейку, чтобы получить квадратный корень из 484. Ниже приведен результат, который мы получили:
Ниже приведен результат, который мы получили:
SQRT(484) = 22
Чему равен квадратный корень из 484, записанный с показателем степени?
Все квадратные корни можно преобразовать в число (основание) с дробным показателем степени. Квадратный корень из 484 не является исключением. Вот правило и ответ
на «квадратный корень из 484, преобразованный в основание с показателем степени?»:
√b = b ½
√484 = 484 ½
Как найти квадратный корень из 484 методом деления в длину метод длинного деления. это потерянный искусство того, как они вычисляли квадратный корень из 484 вручную до того, как были изобретены современные технологии.
Шаг 1)
Наберите 484 парами по две цифры справа налево:
Шаг 2)
Начиная с первого набора: самый большой совершенный квадрат, меньше или равный 4, равен 4, а квадратный корень из 4 равен 2. Следовательно, поместите 2 сверху и 4 снизу следующим образом:
Следовательно, поместите 2 сверху и 4 снизу следующим образом:
| 2 | ||||
| 04 | 84 | |||
| 4 | ||||
Step 3)
Calculate 4 minus 4 and put the difference below. Затем переместитесь вниз к следующему набору чисел.
| 2 | ||||
| 04 | 84 | |||
| 4 | ||||
| 0 | 84 | |||
Шаг 4)
Удвойте число, выделенное зеленым сверху: 2 × 2 = 4. Затем используйте 4 и нижнее число, чтобы решить эту задачу:
Затем используйте 4 и нижнее число, чтобы решить эту задачу:
4? × ? ≤ 84
Знаки вопроса «пробел» и такие же «пробел». Методом проб и ошибок мы нашли, что наибольшее число «пустых» может быть равно 2. Замените вопросительные знаки в задаче на 2, чтобы получить:
42 × 2 = 84.
Now, enter 2 on top, and 84 at the bottom:
| 2 | 2 | |||
| 04 | 84 | |||
| 4 | ||||
| 0 | 84 | |||
| 0 | 84 | |||
Разница между двумя нижними числами равна нулю, поэтому все готово! Ответ — зеленые цифры сверху. Еще раз, квадратный корень из
484 это 22.
Еще раз, квадратный корень из
484 это 22.
Квадратный корень из числа
Пожалуйста, введите другое число в поле ниже, чтобы получить квадратный корень из числа и другую подробную информацию, как вы получили для 484 на этой странице.
Примечания
Помните, что отрицательное значение, умноженное на отрицательное, равно положительному. Таким образом, квадратный корень из 484 имеет не только положительный ответ
что мы объяснили выше, но и отрицательный аналог.
На этой странице мы часто ссылаемся на совершенные квадратные корни. Вы можете использовать список идеальных квадратов для справки.
Квадратный корень из 485
Вот следующее число в нашем списке, о котором у нас есть такая же подробная информация о квадратном корне.
Авторское право | Политика конфиденциальности | Отказ от ответственности | Контакт
Квадратный корень из 484
Sqrt(484). Найдите квадратный корень из 484 или любого другого действительного числа, положительного или отрицательного. Вот ответы на такие вопросы, как: Квадратный корень из 484 или что такое квадратный корень из 484?
Найдите квадратный корень из 484 или любого другого действительного числа, положительного или отрицательного. Вот ответы на такие вопросы, как: Квадратный корень из 484 или что такое квадратный корень из 484?
Что такое квадратный корень? Определение квадратного корня
Квадратный корень числа ‘x’ — это число y такое, что y 2 = x, другими словами, число y, квадрат которого равен y. Например, 22 — это квадратный корень из 484, потому что 22 2 = 22•22 = 484, —22 — это квадратный корень из 484, потому что (-22) 2 = (—22)•(—22) = 484. При написании математических выражений люди часто используют sqrt(x) для обозначения квадратного корня из x. Подробнее о квадратном корне читайте здесь: Квадратный корень — Википедия и здесь: Квадратный корень — Wolfram
Квадратный символ?
Вот символ квадратного корня. Он обозначается √, известным как радикальный знак или основание.
Таблица квадратного корня 1-100
Квадратные корни от 1 до 100 округляются до тысячных.
| номер | квадрат | квадрат корень | ||
|---|---|---|---|---|
| 1 | 1 | 1.000 | ||
| 2 | 4 | 1.414 | ||
| 3 | 9 | 1.732 | ||
| 4 | 16 | 2.000 | ||
| 5 | 25 | 2.236 | ||
| 6 | 36 | 2.449 | ||
| 7 | 49 | 2.646 | ||
| 8 | 64 | 2.828 | ||
| 9 | 81 | 3.000 | ||
| 10 | 100 | 3.162 | ||
| 11 | 121 | 3.317 | ||
| 12 | 144 | 3.464 | ||
| 13 | 169 | 3.606 | ||
| 14 | 196 | 3.742 | ||
| 15 | 225 | 3.873 | ||
| 16 | 256 | 4. 000 000 | ||
| 17 | 289 | 4.123 | ||
| 18 | 324 | 4.243 | ||
| 19 | 361 | 4,359 | ||
| 20 | 40024497397777777777777777777777777777777977777777474747.0022 | 21 | 441 | 4.583 |
| 22 | 484 | 4.690 | ||
| 23 | 529 | 4.796 | ||
| 24 | 576 | 4.899 | ||
| 25 | 625 | 5.000 |
| номер | квадрат | квадрат корень |
|---|---|---|
| 26 | 676 | 5,099 |
| 27 | 729 | 5.196 |
| 28 | 784 | 5.292 |
| 29 | 841 | 5.385 |
| 30 | 900 | 5.477 |
| 31 | 961 | 5. 568 568 |
| 32 | 1,024 | 5.657 |
| 33 | 1,089 | 5.745 |
| 34 | 1,156 | 5.831 |
| 35 | 1,225 | 5.916 |
| 36 | 1,296 | 6.000 |
| 37 | 1,369 | 6.083 |
| 38 | 1,444 | 6.164 |
| 39 | 1,521 | 6.245 |
| 40 | 1,600 | 6.325 |
| 41 | 1,681 | 6.403 |
| 42 | 1,764 | 6.481 |
| 43 | 1,849 | 6.557 |
| 44 | 1,936 | 6.633 |
| 45 | 2,025 | 6.708 |
| 46 | 2,116 | 6.782 |
| 47 | 2,209 | 6. 856 856 |
| 48 | 2,304 | 6.928 |
| 49 | 2,401 | 7.000 |
| 50 | 2,500 | 7.071 |
| number | square | square root |
|---|---|---|
| 51 | 2,601 | 7.141 |
| 52 | 2,704 | 7.211 |
| 53 | 2,809 | 7.280 |
| 54 | 2,916 | 7.348 |
| 55 | 3,025 | 7.416 |
| 56 | 3,136 | 7.483 |
| 57 | 3,249 | 7.550 |
| 58 | 3,364 | 7.616 |
| 59 | 3,481 | 7.681 |
| 60 | 3,600 | 7.746 |
| 61 | 3,721 | 7. 810 810 |
| 62 | 3,844 | 7.874 |
| 63 | 3,969 | 7.937 |
| 64 | 4,096 | 8.000 |
| 65 | 4,225 | 8.062 |
| 66 | 4,356 | 8.124 |
| 67 | 4,489 | 8.185 |
| 68 | 4,624 | 8.246 |
| 69 | 4,761 | 8.307 |
| 70 | 4,900 | 8.367 |
| 71 | 5,041 | 8.426 |
| 72 | 5,184 | 8.485 |
| 73 | 5,329 | 8.544 |
| 74 | 5,476 | 8.602 |
| 75 | 5,625 | 8.660 |
| number | square | square корень |
|---|---|---|
| 76 | 5,776 | 8. 718 718 |
| 77 | 5,929 | 8.775 |
| 78 | 6,084 | 8.832 |
| 79 | 6,241 | 8.888 |
| 80 | 6,400 | 8.944 |
| 81 | 6,561 | 9.000 |
| 82 | 6,724 | 9.055 |
| 83 | 6,889 | 9.110 |
| 84 | 7,056 | 9.165 |
| 85 | 7,225 | 9.220 |
| 86 | 7,396 | 9.274 |
| 87 | 7,569 | 9.327 |
| 88 | 7,744 | 9.381 |
| 89 | 7,921 | 9.434 |
| 90 | 8,100 | 9.487 |
| 91 | 8,281 | 9.539 |
| 92 | 8,464 | 9. 592 592 |
| 93 | 8,649 | 9.644 |
| 94 | 8,836 | 9.695 |
| 95 | 9,025 | 9.747 |
| 96 | 9,216 | 9.798 |
| 97 | 9,409 | 9.849 |
| 98 | 9,604 | 9.899 |
| 99 | 9,801 | 9.950 |
| 100 | 10,000 | 10.000 |
Square root of values around 484
| Number | Sqrt | |||
|---|---|---|---|---|
| 480 | 21.909 | |||
| 481 | 21.932 | |||
| 482 | 21.954 | |||
| 9 | Оценить | квадратный корень из 12 | ||
| 10 | Оценить | квадратный корень из 20 | ||
| 11 | Оценить | квадратный корень из 50 | 94 | |
| 18 | Оценить | квадратный корень из 45 | ||
| 19 | Оценить | квадратный корень из 32 | ||
| 20 | Оценить | квадратный корень из 18 | 92 |
Квадратный корень из 484 пошаговое решение
| Пожалуйста, введите реальное число: |
| Результат квадратного корня: |
Вот ответ на такие вопросы, как: Квадратный корень из 484 пошаговое решение | √484 или чему равен квадратный корень из 484?
Используйте приведенный ниже калькулятор квадратного корня, чтобы найти квадратный корень любого мнимого или действительного числа. См. также на этой веб-странице таблицу квадратного корня от 1 до 100, а также вавилонский метод или метод Героя.
См. также на этой веб-странице таблицу квадратного корня от 1 до 100, а также вавилонский метод или метод Героя.
Вавилонский метод, также известный как метод Героя.
Что такое квадратный корень?
Определение квадратного корня
Квадратный корень из числа «а» — это число х, такое что х 2 = а, другими словами, число х, квадрат которого равен а. Например, 22 — это квадратный корень из 484, потому что 22 2 = 22•22 = 484, а -22 — это квадратный корень из 484, потому что (-22) 2 = (-22)•(-22) = 484.
Таблица квадратных корней 1-100
Квадратные корни от 1 до 100, округленные до ближайшей тысячной.
| нет | нет 2 | √ |
|---|---|---|
| 1 | 1 | 1.000 |
| 2 | 4 | 1.414 |
| 3 | 9 | 1.732 |
| 4 | 16 | 2. 000 000 |
| 5 | 25 | 2.236 |
| 6 | 36 | 2.449 |
| 7 | 49 | 2.646 |
| 8 | 64 | 2.828 |
| 9 | 81 | 3.000 |
| 10 | 100 | 3.162 |
| 11 | 121 | 3.317 |
| 12 | 144 | 3.464 |
| 13 | 169 | 3.606 |
| 14 | 196 | 3.742 |
| 15 | 225 | 3.873 |
| 16 | 256 | 4.000 |
| 17 | 289 | 4.123 |
| 18 | 324 | 4.243 |
| 19 | 361 | 4.359 |
| 20 | 400 | 4.472 |
| 21 | 441 | 4. 583 583 |
| 22 | 484 | 4.690 |
| 23 | 529 | 4.796 |
| 24 | 576 | 4.899 |
| 25 | 625 | 5.000 |
| нет | нет 2 | √ |
|---|---|---|
| 26 | 676 | 5.099 |
| 27 | 729 | 5.196 |
| 28 | 784 | 5.292 |
| 29 | 841 | 5.385 |
| 30 | 900 | 5.477 |
| 31 | 961 | 5.568 |
| 32 | 1,024 | 5.657 |
| 33 | 1,089 | 5.745 |
| 34 | 1,156 | 5.831 |
| 35 | 1,225 | 5.916 |
| 36 | 1,296 | 6. 000 000 |
| 37 | 1,369 | 6.083 |
| 38 | 1,444 | 6.164 |
| 39 | 1,521 | 6.245 |
| 40 | 1,600 | 6.325 |
| 41244 | 333333333333333333333333333333333333333333333333333.68 | |
| 41244 | 333333333333333333333333333333333333333333333333333333.68||
| 42 | 1,764 | 6.481 |
| 43 | 1,849 | 6.557 |
| 44 | 1,936 | 6.633 |
| 45 | 2,025 | 6.708 |
| 46 | 2,116 | 6.782 |
| 47 | 2,209 | 6.856 |
| 48 | 2,304 | 6.928 |
| 49 | 2 401 | 7.000 |
| 50 | 2 500 | 7.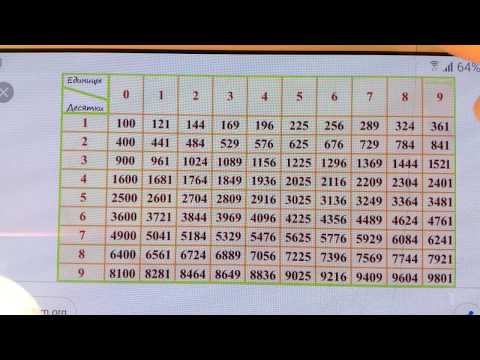 071 071 |
| нет | нет 2 | √ |
|---|---|---|
| 51 | 2,601 | 7.141 |
| 52 | 2,704 | 7.211 |
| 53 | 2,809 | 7.280 |
| 54 | 2,916 | 7.348 |
| 55 | 3,025 | 7.416 |
| 56 | 3,136 | 7.483 |
| 57 | 3,249 | 7.550 |
| 58 | 3,364 | 7.616 |
| 59 | 3,481 | 7.681 |
| 60 | 3,600 | 7.746 |
| 61 | 3,721 | 7.810 |
| 62 | 3,844 | 7.874 |
| 63 | 3,969 | 7.937 |
| 64 | 4,096 | 8.000 |
| 65 | 4,225 | 8. 062 062 |
| 66 | 4,356 | 8.124 |
| 67 | 4,489 | 8.185 |
| 68 | 4,624 | 8.246 |
| 69 | 4,761 | 8.307 |
| 70 | 4,900 | 8.367 |
| 71 | 5,041 | 8.426 |
| 72 | 5,184 | 8.485 |
| 73 | 5,329 | 8.544 |
| 74 | 5 476 | 8.602 |
| 75 | 5 625 | 8.660 |
| нет | нет 2 | √ |
|---|---|---|
| 76 | 5,776 | 8.718 |
| 77 | 5,929 | 8.775 |
| 78 | 6,084 | 8.832 |
| 79 | 6,241 | 8.888 |
| 80 | 6,400 | 8. 944 944 |
| 81 | 6,561 | 9.000 |
| 82 | 6,724 | 9.055 |
| 83 | 6,889 | 9.110 |
| 84 | 7,056 | 9.165 |
| 85 | 7,225 | 9.220 |
| 86 | 7,396 | 9.274 |
| 87 | 7,569 | 9.327 |
| 88 | 7,744 | 9.381 |
| 89 | 7,921 | 9.434 |
| 90 | 8,100 | 9.487 |
| 91 | 8,281 | 9.539 |
| 92 | 8,464 | 9.592 |
| 93 | 8,649 | 9.644 |
| 94 | 8,836 | 9.695 |
| 95 | 9,025 | 9.747 |
| 96 | 9,216 | 9. 798 798 |
| 97 | 9,409 | 9.849 |
| 98 | 9,604 | 9.899 |
| 99 | 9,801 | 9.950 |
| 100 | 10,000 | 10.000 |
Квадратный корень из 484 | Как найти квадратный корень из 484
Все виды уравнений, решаемых онлайн
Как найти квадратный корень из 484Квадрат 484:
В математике найти квадрат любого числа в основном легко, потому что, когда мы умножаем одно и то же число на себя, мы получаем квадрат это число.
Например:
- Предположим, нам нужно найти квадрат любого числа, скажем, X , затем мы умножаем X само на себя, то есть X , и мы получим его квадрат как Y . Это можно записать как (X) 2 = X*X= Y
- Аналогичным образом находим квадрат числа 22 .
- Чтобы найти квадрат 22, мы умножаем 22 на само число, то есть на 22, и запишем это следующим образом.
- (484) 2 = 22*22= 484

Квадратный корень из 484:
- Теперь в обратном порядке, если нам нужно найти квадратный корень из Y . Квадратный корень из Y — это единственное значение, которое при умножении само на себя дает значение Y .
- Это означает, что √ Y = √(X*X) = X
Где √ — символ, названный радикалом.
Например:
- Квадратный корень из 22 можно записать как
√484 = √ (22*22) = 22
Где √ – это символ, который называется подкоренным знаком.
- Короче говоря, мы помним квадрат из 22 и квадратный корень из 484 как .
Примечание:
- Каждое положительное действительное число имеет два корня.

- Квадрат любого отрицательного числа всегда является положительным числом.
Например:
- 484 — положительный совершенный квадрат, который также имеет два корня +22 и -22.
- Но в основном берется положительное значение квадратного корня, которое называется главным квадратным корнем или неотрицательным квадратным корнем.
- Следовательно, √484 = √(-22)*(-22) = -22 и √484 = √(22)*(22) = 22
Аналогично
- (-22)*(-22) = (-22) 2 = +484 и (+22)*(+22) = (+22)1 6 =5 2 . 484
Существует много методов нахождения квадратного корня из полных квадратов, из которых мы подробно рассмотрим следующий метод.
- Метод повторного вычитания
- Метод простой факторизации
Метод многократного вычитания:
- В методе многократного вычитания мы должны вычесть последовательные нечетные числа, начиная с 1, из совершенного квадратного числа, квадратный корень которого мы должны найти.

- эл. чтобы найти квадратный корень из 484, сначала мы вычитаем из него 1. 484 – 1 = 483
- Тогда следующее нечетное число равно 3, поэтому мы должны вычесть его из 483 483–3 = 480
- Таким образом, мы вычитаем последовательные нечетные числа из соответствующих значений, полученных после непрерывного вычитания, пока не получим окончательное значение 0.
- И значение количества нечетных чисел, необходимых для получения 0, является искомым квадратным корнем.
Например:
- Находим квадратный корень из 484 методом многократного вычитания следующим образом:
484−1=483
483−3=480
480−5=475
468−9=459
459−11=448
448−13=435
435−15=420
420–17 = 403
403–19 = 384
384–21 = 363
363–23 = 340
340–25 = 315
315-27 = 288
288-29 = 259
315-27 = 288
288-29 = 259
315-27 = 288
288-29 = 259
315-27 = 288
288-29 = 259
315-27 = 288
288-29 = 259
315-27 259−31=228
228−33=195
195−35=160
160−37=123
123−39=84
84−41=43
43−43=0
Таким образом, здесь используются нечетные числа 1, 3, 5, 7, 9, 11. , 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41 и 43, которые равны 22 числам.
, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41 и 43, которые равны 22 числам.
Следовательно, квадратный корень из 484 методом многократного вычитания равен 22.
Метод простой факторизации:
- В методе простой факторизации мы должны разделить совершенное квадратное число, квадратный корень которого мы должны найти, на простое число, начиная с 2, 3, 5… и так далее, пока остаток не будет равен 1.
- Сначала мы должны разделить на простое число 2, если это число не делится на 2, тогда мы должны взять следующее простое число, то есть 3, и процесс будет продолжаться до тех пор, пока мы не получим остаток как 1.
- Наконец, мы должны составить пары простых чисел, взятых в форме умножения, а затем мы должны извлечь из них квадратный корень.
Например:
- Ниже описан процесс нахождения квадратного корня из 484 методом простой факторизации.
- Поскольку 484 четное число, оно должно делиться на два простых числа 2 и 11 92
И 484= (2*2*11*11)
- Взяв квадратный корень с обеих сторон, мы получим
√484 = √(2*2)√(11*11) = (2*11)
√484= 22
- Таким образом, мы нашли квадратный корень из 484 как 22, используя простое число факторизации
1) 484-это квадрат ———
A) 23
B) 21
C) +22 и 22
D).


 Самая первая цифра слева может быть без пары. Если же знака не хватает в правой части числа, то следует дописать 0. В нашем случае получится 13 08,19 12.
Самая первая цифра слева может быть без пары. Если же знака не хватает в правой части числа, то следует дописать 0. В нашем случае получится 13 08,19 12. Подходящей цифрой будет 1: 721×1 = 721. Запишем её в ответ. Выполним вычитание 1219 — 721 = 498.
Подходящей цифрой будет 1: 721×1 = 721. Запишем её в ответ. Выполним вычитание 1219 — 721 = 498. д. и выясним, между какими из них находится подкоренное число. Мы получим, что 10²
д. и выясним, между какими из них находится подкоренное число. Мы получим, что 10² Если подкоренное выражение отрицательно, но ищется корень нечетной степени (3, 5, 7 и так далее), то результат будет отрицательным.
Если подкоренное выражение отрицательно, но ищется корень нечетной степени (3, 5, 7 и так далее), то результат будет отрицательным. д.
д.
 Поместите горизонтальную черту, чтобы обозначить сопряжение.
Поместите горизонтальную черту, чтобы обозначить сопряжение.
