Примечание: у меня не было большой практики в тригонометрии, поэтому, пожалуйста, не отвечайте какими-то сложными вещами с рядом Тейлора (я слышал об этом, но не совсем понимаю). Еще раз спасибо
- тригонометрия
$\endgroup$
5
$\begingroup$
Нет, размещение постоянного множителя внутри функции синуса, как в sin(a*x), изменяет частоту функции; если |а| больше единицы, она «сжимает» функцию синуса по горизонтали , заставляя ее колебаться «быстрее», а если |a| меньше единицы, функция «растягивается» по горизонтали , заставляя ее колебаться «медленнее».
Лучший способ наблюдать за этим — посмотреть на график и посмотреть, что он делает: http://www.wolframalpha.com/input/?i=plot+sin+x%2C+sin+3x%2C+ 3*sin+x
Я предлагаю поиграть с другими значениями на графиках, чтобы посмотреть, что они делают.
$\endgroup$
$\begingroup$
Я попытаюсь объяснить разницу между ними с помощью рисунка: (Извините, это грубый набросок, сделанный в Microsoft Paint.)
Здесь у нас есть окружность (предположим, радиусом 1) с центром в точке (0,0) с линией (назовем ее $l$), проведенной от центра к краю окружности (заканчивающейся в точке $ П$). $A$ — это угол, который линия образует с осью $x$.
Чтобы получить $5\sin(A)$, мы увеличиваем линию и окружность в 5 раз по сравнению с их первоначальным размером.
Чтобы получить $\sin(5A)$, на этот раз мы не увеличиваем круг и линию. Вместо этого мы вращаем линию вокруг центра круга, так что угол, который она образует с осью $x$ , в 5 раз больше. Теперь $y$-координата точки пересечения $l$ с краем окружности равна $\sin(5A)$.
Попробуйте на примере или двух; вы сами увидите разницу.
$\endgroup$
2
$\begingroup$
1) Вы могли бы просто построить графики функций, например, в wolfram alpha и посмотреть сами.
2) при $t=\frac{\pi}{2}$ имеем $\sin (t)=1$, а так как $|\sin (x)|\le 1$, то ясно, что $\ sin (5\cdot t)\ne 5\cdot \sin(t)$.
$\endgroup$
$\begingroup$
Что-то вроде $a\cdot f(x)= f(a\cdot x)$ истинно тогда и только тогда, когда $f(x)$ линейно.
Поскольку в разложении Тейлора тригонометрической функции всегда есть нелинейные члены, это не может быть верно ни для одного из них. 9\circ) = 0$. Это правда?
$\endgroup$
1
$\begingroup$
Тригонометрические функции являются функциями и поэтому обычно представляются с использованием обозначения функций. Напомним, что обозначение функции $f(x)$ означает, что функция $f$ принимает $x$ на вход. , а не означает, что $f$ и $x$ перемножаются. Таким образом, обозначение $\sin(5x)$ означает, что синусоидальная функция принимает $5x$ на вход. Обозначение $5\sin(x)$ означает, что 5 умножается на выход синусоидальной функции, когда ее вход равен $x$. Теперь все ясно?
$\endgroup$
1
$\begingroup$
Оба равенства, которые вы написали выше, НЕ верны.
Один из способов взглянуть на это может состоять в том, чтобы использовать их расширение ряда Тейлора. $\sin (5x)$ означает синус $5$, умноженный на угловую меру $x$. Это означает, что в прямоугольном треугольнике, гипотенуза которого имеет длину $1$, перпендикуляр, соответствующий острому углу $5x$, имеет длину $\sin (5x)$.
Тогда как для $5 \sin x$ нужно рассмотреть прямоугольный треугольник с гипотенузой длины один и перпендикуляром, соответствующим острому углу $x$, а затем взять $5$ длины этого перпендикуляра.
Вы можете нарисовать несколько таких прямоугольных треугольников, чтобы проверить результат самостоятельно.
$\endgroup$
2
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почтаТребуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙПримечание: Если вы хотите ознакомиться с обзором тригонометрии, нажмите на тригонометрия.
Пример 4: Найдите x в следующем уравнении.
Существует бесконечное множество решений этой проблемы.
Выделите синусоидальный член. Для этого перепишем левую часть уравнения в эквивалентная факторизованная форма.
Произведение двух множителей равно нулю, если хотя бы один из множителей равняется нулям. Это означает, что если или же
Мы просто превратили сложную проблему в две проблемы. Чтобы найти решения исходного уравнения, , находим решения уравнений а также
а также
Как выделить x в уравнении? Мы могли бы взять
арксинус обеих сторон.
Однако функция синуса не является взаимно однозначной.
функция.
Ограничим область определения так, чтобы функция была взаимно однозначной на ограниченный домен с сохранением исходного диапазона. Синусоидальная функция один к одному на интервале Если мы ограничим область определения функции синуса этим интервалом, мы можем взять арксинус обеих частей каждого уравнения.
Мы знаем это Следовательно, если , тогда
С периода
равно ,
эти решения будут повторяться
каждый
единицы. Точные решения
где n — целое число.
Приближенные значения этих решений равны
где n — целое число.
Каждое решение можно проверить алгебраически, подставив каждое решение в исходное уравнение. Если после подстановки левая часть исходное уравнение равно правой части исходного уравнения, решение в силе.
Можно также проверить решения графически, построив график функции, образованной левой частью исходного уравнения, и график функции, образованной правой частью исходного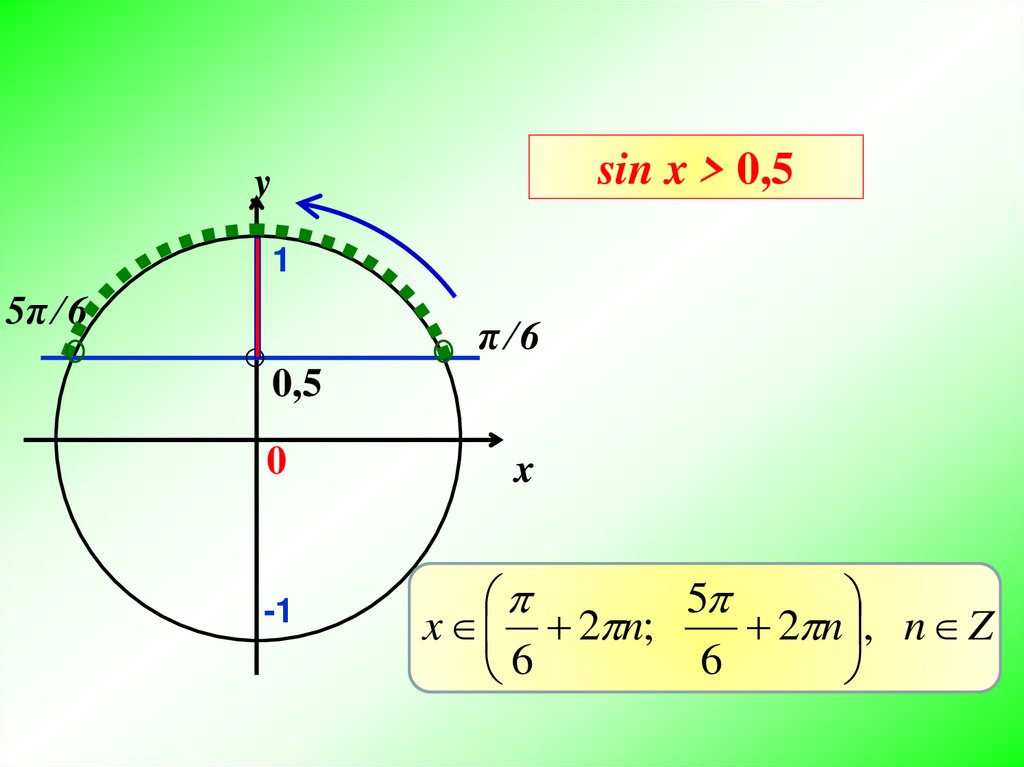 уравнения.
Координаты x точек пересечения являются решениями. Правая часть уравнения равна 0, а f ( x )=0 — это ось x. Так что на самом деле то, что вы ищете, это
x-пересекает функцию, образованную левой частью уравнения.
Алгебраическая проверка:
Проверить решение
Левая сторона:
Правая сторона: 0
Так как левая часть исходного уравнения равна правой части исходное уравнение при замене -1,5707963 для х, тогда -1,5707963 — это решение.
Проверить решение
Левая сторона:
Правая сторона: 0
Так как левая часть исходного уравнения равна правой части исходное уравнение при замене 4.71238898 вместо х, тогда 4.71238898 — это решение.
Мы только что убедились, что а также являются точными решениями, и эти решения повторяются каждые единицы. Приближенные значения этих решений равны а также и эти решения повторяются каждые единицы.
Графическая проверка: Нарисуйте уравнение Обратите внимание, что график пересекает ось x много раз, что указывает на множество решений.
График пересекает ось x в точке -1,5707963. Так как период , вы можете убедиться, что график также пересекает ось x снова в -1,5707963+6,2831853=4,71238898 и в , и т.п.
Примечание. Если задача состоит в том, чтобы найти решения в интервале , затем вы выбираете эти решения из множества бесконечных решения, принадлежащие множеству
Если вы хотите проверить себя, решив некоторые задачи, подобные этой например, щелкните Проблема.
Если вы хотите перейти к следующему разделу, нажмите далее.
Если вы хотите вернуться к предыдущему разделу, нажмите на предыдущий .
Если вы хотите вернуться к оглавлению уравнения, нажмите на Содержание.
Домашняя страница S.