6 умножить на 9: Таблица умножения на 9

2

Умножение на 9 | Таблица умножения

    На этой странице представлены примеры, описывающие умножение на 9 и умножение числа 9, деление, некоторые способы произношения и записи, таблица умножения на 9 без ответов, в конце статьи — картинки для скачивания, с помощью которых можно распечатать часть таблицы.

Умножение на 9:
1 x 9 = 9
2 x 9 = 18
3 x 9 = 27
4 x 9 = 36
5 x 9 = 45
6 x 9 = 54
7 x 9 = 63
8 x 9 = 72
9 x 9 = 81
10 x 9 = 90

Первый вариант произношения:
1 x 9 = 9 (1 умножить на 9, равно 9)
2 x 9 = 18 (2 умножить на 9, равно 18)
3 x 9 = 27 (3 умножить на 9, равно 27)
4 x 9 = 36 (4 умножить на 9, равно 36)
5 x 9 = 45 (5 умножить на 9, равно 45)
6 x 9 = 54 (6 умножить на 9, равно 54)
7 x 9 = 63 (7 умножить на 9, равно 63)
8 x 9 = 72 (8 умножить на 9, равно 72)
9 x 9 = 81 (9 умножить на 9, равно 81)
10 x 9 = 90 (10 умножить на 9, равно 90)

Второй вариант произношения:
1 x 9 = 9 ( по 1 взять 9 раз, получится 9)
2 x 9 = 18 ( по 2 взять 9 раз, получится 18)
3 x 9 = 27 ( по 3 взять 9 раз, получится 27)
4 x 9 = 36 ( по 4 взять 9 раз, получится 36)
5 x 9 = 45 ( по 5 взять 9 раз, получится 45)
6 x 9 = 54 ( по 6 взять 9 раз, получится 54)
7 x 9 = 63 ( по 7 взять 9 раз, получится 63)
8 x 9 = 72 ( по 8 взять 9 раз, получится 72)
9 x 9 = 81 ( по 9 взять 9 раз, получится 81)
10 x 9 = 90 ( по 10 взять 9 раз, получится 90)

От перемены мест множителей значение произведения не меняется, поэтому, зная результаты умножения на 9, можно легко найти результаты умножения числа 9. В качестве знака умножения в разных источниках используют разные символы. Выше был показан пример со знаком « x », в этот раз сделаем запись с помощью приподнятой точки ( ∙ ).

Умножение числа 9:

9 ∙ 1 = 9
9 ∙ 2 = 18
9 ∙ 3 = 27
9 ∙ 4 = 36
9 ∙ 5 = 45

9 ∙ 6 = 54
9 ∙ 7 = 63
9 ∙ 8 = 72
9 ∙ 9 = 81
9 ∙ 10 = 90

Варианты произношения:
9 ∙ 1 = 9 (по 9 взять 1 раз, получится 9)
9 ∙ 2 = 18 (по 9 взять 2 раза, получится 18)
9 ∙ 3 = 27 (по 9 взять 3 раза, получится 27)
9 ∙ 4 = 36 (по 9 взять 4 раза, получится 36)
9 ∙ 5 = 45 (по 9 взять 5 раз, получится 45)
9 ∙ 6 = 54 (по 9 взять 6 раз, получится 54)
9 ∙ 7 = 63 (по 9 взять 7 раз, получится 63)
9 ∙ 8 = 72 (по 9 взять 8 раз, получится 72)
9 ∙ 9 = 81 (по 9 взять 9 раз, получится 81)
9 ∙ 10 = 90 (по 9 взять 10 раз, получится 90)

9 ∙ 1 = 9 (9 умножить на 1, равно 9)
9 ∙ 2 = 18 (9 умножить на 2, равно 18)
9 ∙ 3 = 27 (9 умножить на 3, равно 27)
9 ∙ 4 = 36 (9 умножить на 4, равно 36)
9 ∙ 5 = 45 (9 умножить на 5, равно 45)
9 ∙ 6 = 54 (9 умножить на 6, равно 54)
9 ∙ 7 = 63 (9 умножить на 7, равно 63)
9 ∙ 8 = 72 (9 умножить на 8, равно 72)
9 ∙ 9 = 81 (9 умножить на 9, равно 81)
9 ∙ 10 = 90 (9 умножить на 10, равно 90)

Деление на 9:

9 ÷ 9 = 1 (9 разделить на 9, равно 1)
18 ÷ 9 = 2 (18 разделить на 9, равно 2)
27 ÷ 9 = 3 (27 разделить на 9, равно 3)
36 ÷ 9 = 4 (36 разделить на 9, равно 4)
45 ÷ 9 = 5 (45 разделить на 9, равно 5)
54 ÷ 9 = 6 (54 разделить на 9, равно 6)
63 ÷ 9 = 7 (63 разделить на 9, равно 7)
72 ÷ 9 = 8 (72 разделить на 9, равно 8)
81 ÷ 9 = 9 (81 разделить на 9, равно 9)
90 ÷ 9 = 10 (90 разделить на 9, равно 10)

9 ÷ 9 = 1 (9 разделить на 9, равно 1)
18 ÷ 9 = 2 (18 разделить на 9, равно 2)
27 ÷ 9 = 3 (27 разделить на 9, равно 3)
36 ÷ 9 = 4 (36 разделить на 9, равно 4)
45 ÷ 9 = 5 (45 разделить на 9, равно 5)
54 ÷ 9 = 6 (54 разделить на 9, равно 6)
63 ÷ 9 = 7 (63 разделить на 9, равно 7)
72 ÷ 9 = 8 (72 разделить на 9, равно 8)
81 ÷ 9 = 9 (81 разделить на 9, равно 9)
90 ÷ 9 = 10 (90 разделить на 9, равно 10)

Картинка: 

Деление.

Картинка: 

Таблица умножения и деления на 9 без ответов (по порядку и вразброс):

1 ∙ 9 =	10 ∙ 9 =	9 ÷ 9 =	63 ÷ 9 =
2 ∙ 9 =	6 ∙ 9 =	18 ÷ 9 =	27 ÷ 9 =
3 ∙ 9 =	1 ∙ 9 =	27 ÷ 9 =	18 ÷ 9 =
4 ∙ 9 =	4 ∙ 9 =	36 ÷ 9 =	9 ÷ 9 =
5 ∙ 9 =	2 ∙ 9 =	45 ÷ 9 =	36 ÷ 9 =
6 ∙ 9 =	7 ∙ 9 =	54 ÷ 9 =	54 ÷ 9 =
7 ∙ 9 =	3 ∙ 9 =	63 ÷ 9 =	72 ÷ 9 =
8 ∙ 9 =	5 ∙ 9 =	72 ÷ 9 =	90 ÷ 9 =
9 ∙ 9 =	9 ∙ 9 =	81 ÷ 9 =	45 ÷ 9 =
10 ∙ 9 =	8 ∙ 9 =	90 ÷ 9 =	81 ÷ 9 =

Способы записи таблицы умножения на 9:

x	Приподнятая точка	*	Знак не указан
1 x 9 = 9	1 ∙ 9 = 9	1 * 9 = 9	1 __ 9 = 9
2 x 9 = 18	2 ∙ 9 = 18	2 * 9 = 18	2 __ 9 = 18
3 x 9 = 27	3 ∙ 9 = 27	3 * 9 = 27	3 __ 9 = 27
4 x 9 = 36	4 ∙ 9 = 36	4 * 9 = 36	4 __ 9 = 36
5 x 9 = 45	5 ∙ 9 = 45	5 * 9 = 45	5 __ 9 = 45
6 x 9 = 54	6 ∙ 9 = 54	6 * 9 = 54	6 __ 9 = 54
7 x 9 = 63	7 ∙ 9 = 63	7 * 9 = 63	7 __ 9 = 63
8 x 9 = 72	8 ∙ 9 = 72	8 * 9 = 72	8 __ 9 = 72
9 x 9 = 81	9 ∙ 9 = 81	9 * 9 = 81	9 __ 9 = 81
10 x 9 = 90	10 ∙ 9 = 90	10 * 9 = 90	10 __ 9 = 90

Способы записи таблицы деления на 9:

/	:	÷	Знак не указан
9 / 9 = 1	9 : 9 = 1	9 ÷ 9 = 1	9 __ 9 = 1
18 / 9 = 2	18 : 9 = 2	18 ÷ 9 = 2	18 __ 9 = 2
27 / 9 = 3	27 : 9 = 3	27 ÷ 9 = 3	27 __ 9 = 3
36 / 9 = 4	36 : 9 = 4	36 ÷ 9 = 4	36 __ 9 = 4
45 / 9 = 5	45 : 9 = 5	45 ÷ 9 = 5	45 __ 9 = 5
54 / 9 = 6	54 : 9 = 6	54 ÷ 9 = 6	54 __ 9 = 6
63 / 9 = 7	63 : 9 = 7	63 ÷ 9 = 7	63 __ 9 = 7
72 / 9 = 8	72 : 9 = 8	72 ÷ 9 = 8	72 __ 9 = 8
81 / 9 = 9	81 : 9 = 9	81 ÷ 9 = 9	81 __ 9 = 9
90 / 9 = 10	90 : 9 = 10	90 ÷ 9 = 10	90 __ 9 = 10

Умножение на:

‹ Умножение на 8 Вверх

[ 6 x 9 = 42 ] Как шесть раз девять равно сорок два, и почему это самая мощная формула во вселенной!

Шесть раз девять равно сорок два.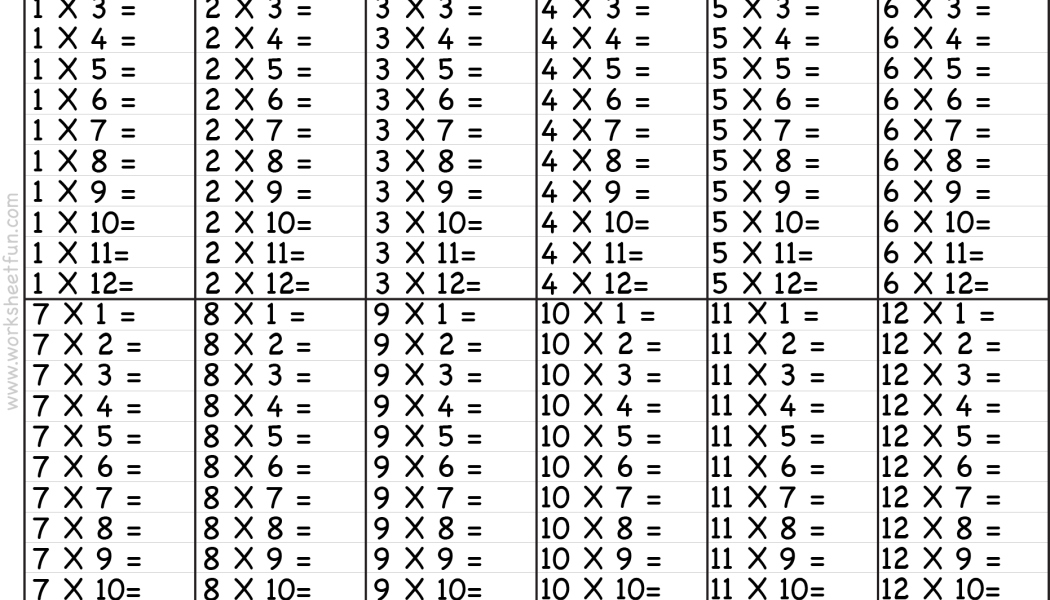 Это культурная и математическая определенность.

Но это не… не так ли? Да!

Понимание того, как работает это очевидное отклонение от математики, может раскрыть секреты жизни, работы, отношений, бизнеса и всего.

Так что без паники! Возьмите чашку чая, найдите свое полотенце и приготовьтесь разрушить свою вселенную.

Почему сорок два?

Сорок два — очень важное число.

На самом деле это не просто число. Это ответ. Окончательный ответ. Ответ на жизнь, вселенную и все такое.

Об этом знают многие. Если вы спросите у сорока двух человек, в чем смысл жизни, один из них обязательно ответит «сорок два». Я предлагаю вам попробовать это и сообщить мне о результатах через clinkedin.

То, что сорок два — это смысл жизни, Вселенной и всего остального, установлено Дугласом Адамсом в эпической трилогии из пяти книг «Автостопом по Галактике».

В этой фантастически смешной истории суперкомпьютер под названием Deep Thought создан для «Ответить на главный вопрос жизни, Вселенной и всего остального».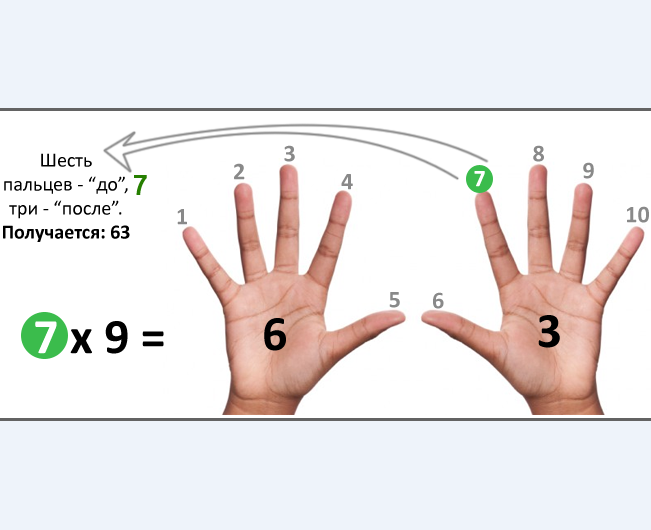

После нескольких миллионов лет анализа Deep Thought раскрывает очень разочарованной публике ответ: «сорок два» .

«Я проверил это очень тщательно, — сказал компьютер, — и это определенно и есть ответ. Я думаю, что проблема, если быть с вами откровенной, в том, что вы никогда не знали, в чем вопрос».

Совершенно очевидно, что очень важно понимать и задавать правильные вопросы.

И так вопрос ищется.

После ряда странных обстоятельств, связанных; главный герой рассказа Артур Дент; Конец света; какие-то пещерные люди и мешок с письмами… кандидат на пропущенный вопрос идентифицируется как;

«Что получится, если шесть умножить на девять?».

 

Дуглас Адамс никогда не упоминает о том, как шесть раз девять равняется сорока двум, ни в одной из своих книг, но здесь все становится интереснее, так что оставайтесь со мной.

Что получится, если шесть умножить на девять?

Шесть раз девять пятьдесят четыре, не так ли? Так как же шесть раз девять будет сорок два?

Математически проницательным поклонникам Дугласа Адамса не потребовалось много времени, чтобы подсчитать и отметить (с большой гордостью), что 6 * 9 на самом деле равно 42 при использовании системы счета с основанием 13.

А что теперь?

Возьми полотенце. Я объясню.

Люди в большинстве стран мира считают блоками по 10.  Мы считаем до 10, увеличиваем единицу десятков, считаем до 10 еще девять раз, добавляем приращение сотен и так далее. Это называется «системой счета с основанием 10» или, чаще, «десятичной».

Антропологи считают, что система счета с основанием 10 развилась из-за того, что люди имели 10 пальцев и использовали их для счета. Если бы у нас было 12 пальцев, мы бы, вероятно, считали по основанию 12.

Система счета по основанию 10 – не единственная система счета. Есть гораздо больше, и они используются повсюду вокруг нас. Вот некоторые из наиболее распространенных из них;

Десятичный (основание 10)  – система счета, которую мы обычно используем сегодня.

Считаются как: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17 … 99, 100, 101, 102 и т. д.

Математически по основанию десять: 6 * 9 = 54 2) – до десятичной системы эта система использовалась в Соединенном Королевстве и его империи для подсчета денег, мер длины и мер веса. Некоторые математики утверждают, что он функционально превосходит десятичный.

В Соединенном Королевстве даже существует общество под названием «Общество дюжины», которое выступает за переход от десятичной к двенадцатеричной системе счета. Хотя я не думаю, что у них есть план дать нам дополнительные пальцы.

Считаются как: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 1A , 1B, 20, 21 и т. д.

Математически по основанию двенадцать: 6 * 9 = 46

Восьмеричное (основание 8) — используется в некоторых коренных американских языках. Несколько раз предлагалась в качестве системы счета в Европе за последние несколько сотен лет. Это система счета На’ви из фильма Аватар.

Считаются как: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11, 12, 13, 14, 15, 16, 17, 20, 21, 22 и т. д.

Математически в восьмеричной системе счисления: 6 * 9 = ОШИБКА  так как в восьмеричной системе нет 9.

Двоичный (основание 2) — основная система счета современных компьютеров.

Считаются как: 0, 1, 10, 11, 100, 101, 111, 1000, 1001 и т. д. Однако десятичное число 42 представлено как 101 010 в двоичном формате.

Шестнадцатеричный (основание 16) — популярная система счета, используемая в вычислениях. Также традиционная китайская система подсчета веса.

Подсчитывается как: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 10, 11, 12, 13, 14, 15, 16 , 17, 18, 19, 1A, 1B, 1C, 1D, 1E, 1F, 20, 21, и т.д. 66 — наверное, больше всего известна своей системой счета, в которой шесть умножить на девять на самом деле равно сорок двум.

Подсчитывается как: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19 1А, 1Б, 1С, 20, 21 и т. д.

Математически по основанию тринадцать: 6 * 9 = 42

Предположение, восприятие, реальность!

Если мы предположим, что выражение 6×9=42 находится в базе 10 либо по выбору, либо по незнанию о существования других систем счета, то это будет выглядеть неправильно и запутанно. Мы можем отклонить это как ошибку.

Даже зная, что существуют другие системы счета, мы можем увидеть, как это выражение может быть на самом деле правильным.

Иногда, когда что-то кажется неправильным или сложным, на самом деле это не так. Мы просто не знаем, что у нас нет всей информации.

Разгадка тайн Вселенной

Когда-то астрономы считали Землю центром Вселенной. Основываясь на этом предположении, хотя, возможно, подтвержденном наблюдении того времени, Клавдий Птолемей разработал сложную геоцентрическую модель Солнечной системы около 150 г. н.э.

В модели Птолемея Солнце вращается вокруг Земли, а планеты движутся по кругу эпициклы, которые сами следуют по определенной орбите вокруг Земли.

В результате получается несколько замысловатый набор межпланетных спиралей, не поддающихся гравитации.

Птолемеевская (геоцентрическая) модель  

Несмотря на то, что модель Птолемея совершенно неверна в отношении фактического движения планет, модель Птолемея довольно точно предсказывает наблюдаемые положения планет. Настолько аккуратной, что она оставалась излюбленной моделью движения планет на протяжении более тринадцати столетий.

Так было до тех пор, пока Николай Коперник серьезно не бросил вызов гелиоцентрической идее о том, что на самом деле все намного проще. А возможно, Земля и другие планеты действительно вращались вокруг Солнца!

Коперниканская (гелиоцентрическая) модель

 

Потрясающее видео

В этом видео показана крутая анимация того, как работают обе модели.

Хотя геоцентрическая (Птолемеевская) модель очаровательна, и видео выше показывает, насколько она очаровательна, я думаю, мы все знаем, какая модель является предпочтительной среди современного научного сообщества.

Сорок два?

Так почему же 6 * 9 = 42 самая мощная формула во вселенной?

Потому что он напоминает нам о том, что наше восприятие реальности формируется фильтрами и ограничениями нашего опыта и знаний.

Помня об этом, мы открываем свой разум для большего количества возможностей и решений.

Ответы, объяснения, возможности, любовь, счастье, богатство… все, что мы ищем… можно легко найти в областях, о существовании которых мы даже не подозреваем.

Я полагаю, что это верно для всего; от простой математики до небесного движения, до смысла жизни, вселенной и всего остального.

И… 42 — это просто очень-очень обычное смешное число.

———

Приложение

Что Дуглас Адамс говорит обо всем этом?

У него был какой-то глубокий скрытый смысл за всем этим?

Видимо нет. Сорок два было обычным, произвольным, забавным числом.

Когда его спросили о шести умноженных на девять, что на самом деле равняется сорока двум с основанием тринадцать, он, как сообщается, ответил;

«Может, я и прискорбен, но я не пишу шутки с основанием тринадцать».

«Двоичные представления, основание тринадцать, тибетские монахи — полная ерунда. Я сел за свой стол, посмотрел в сад и подумал: «Сойдет и 42». Я напечатал это. Конец истории.»

Ссылки

1-∞: Почему в этой статье нет ссылок или примечаний?

Я все это выдумал? Я не уважаю свои источники? Что за академическое богохульство?

Недавно я прочитал потрясающую книгу Джона Тейлора Гатто. Это называется Оружие массового обучения: Путешествие школьного учителя через темный мир обязательного школьного образования.

Это отличная книга, и я очень рекомендую ее. После «Автостопом по Галактике», конечно.

Было бы преуменьшением сказать, что Гатто является активным сторонником критического мышления.

Из-за того, что мне врезали в него в универе, одна вещь, которая выделяется в книге Гато, — это полное отсутствие ссылок на источники. Сначала я находил это тревожным. Если бы книга была представлена ​​академически как статья, я бы, вероятно, поставил ей большую жирную пятерку за отсутствие ссылки на источники изложенных фактов.

Однако это заставило меня задуматься. В чем, наверное, был смысл.

В наш информационный век невероятно легко и просто проверить идеи самостоятельно. Поэтому я собираюсь последовать примеру Гатто и предоставить вам возможность критически исследовать любые факты и идеи, представленные в этой статье.

Если вы хотите прокомментировать или обсудить любой материал здесь, вы можете найти меня на clinkedin.

Больше информации из интернета

 

Довольно милое видео о числах и системах счета – TranslatorsCafe.com

Еще одно потрясающее видео о геоцентрической модели — Youtube.com

Оружие Массы Инструкция: (Книга в формате PDF для скачивания) — wordpress.com

 

Что такое общие кратные? Определение, примеры, факты

Что такое общие кратные в математике?

Общие кратные — это кратные, которые являются общими для данного набора чисел.

Умножение числа путем подсчета чисел дает нам его кратность. В математике значение кратного — это произведение или результат одного числа, умноженного на другое число.

Все мы знаем таблицу умножения, потому что всегда используем ее для решения математических задач. Когда мы используем эти таблицы, мы также используем , кратные . Видите ли, когда мы умножаем два числа, ответ будет их кратным .

Взгляните на таблицы умножения чисел от 1 до 10. Здесь мы получили умножения этих чисел путем умножения их на натуральные числа.

Alt Tag: Факты умножения от 1 до 10

Итак, что такое общие кратные? Давайте попробуем понять на примере. Это довольно просто. Найдем общие кратные 6 и 7. 

Во-первых, мы можем вывести числа, кратные 6 и 7, умножив их на числа 1, 2, 3, … и так далее.

Кратно 6: 6, 12, 18, 24, 30, 36, 42 , 48, 54, 60, 66, 72, 79, 84 , …

9 0002 Кратность 7 составляют: 7, 14, 21, 28, 35, 42 , 49, 56, 63, 70, 77, 84 , …

Итак, какие числа вы найдете общими в числах, кратных 6 и 7?

Общие кратные 6 и 7: 42, 84, …

Связанные игры

Общие кратные Определение

Обычное кратное определяется как целое число, которое является общим кратным данного набора чисел.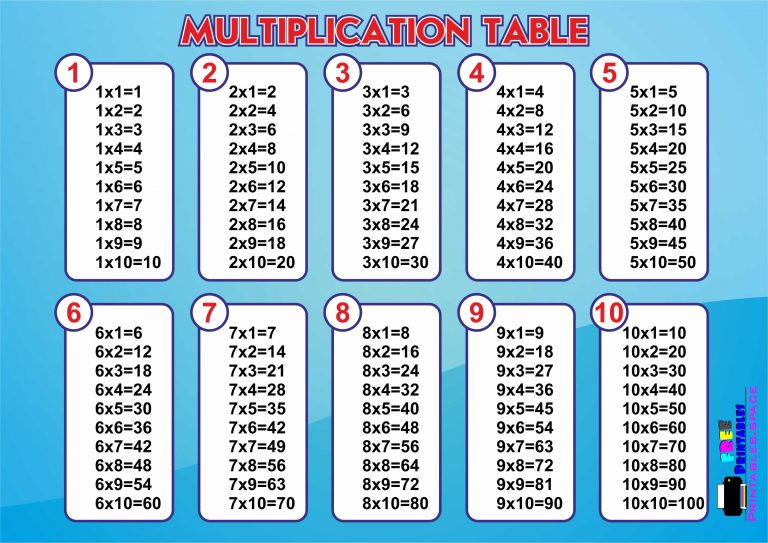 Общие кратные двух или более чисел называются общими кратными этих чисел.

Связанные рабочие листы

Как найти общие кратные

Мы можем найти общие кратные двух или более чисел, перечислив кратные каждого числа.

Рассмотрим предыдущий пример. Чтобы найти общие кратные 6 и 7, отметим кратные 6 и 7 на сетке сотен. Мы будем отмечать числа, кратные 6, кружком, а числа, кратные 7, — крестиком.

Обведенные и зачеркнутые числа являются общими кратными 6 и 7.

Итак, общие кратные 6 и 7 равны 42 и 84.

Посмотрите еще один пример.

Пример: найти общие кратные 4 и 12. , …

Кратно 12 = 12 , 24 , 36 , 48, 60, 72, …

Общие кратные 4 и 12 = 12, 24, …

Что такое наименьшее общее кратное?

Наименьшее общее кратное двух или более чисел называется Наименьшим Общим кратным (НОК) .

Например, чтобы найти общие кратные чисел 3 и 4, мы перечисляем их кратные, а затем находим их общие кратные.

Кратность 3: 3, 6, 9, 12 , 15, 18, 21, 24 , 27, 30, 33, 36 , …

Кратность 4 есть: 4, 8 , 12 , 16, 20, 24 , 28, 32, 36 , 40, …

Общие кратные 3 и 4: 12, 24, 36, ….

Наименьшее общее кратное равно 12. Таким образом, НОК 3 и 4 равно 12.

Свойства общих кратных

• Число может иметь бесконечное число кратных. Следовательно, любые два числа или набор чисел могут иметь бесконечное число общих кратных.

• Для любых двух чисел a и b произведение $a \times b$ всегда является общим кратным чисел a и b.

Пример: $6 \times 8 = 48$ является общим кратным 6 и 8.

• Если два числа a и b взаимно просты, то их общие кратные кратны $(a \times b)$ .

Пример: 2 и 3 взаимно простые числа.

$2 \times 3 = 6$

Общие кратные 2 и $3 = 6,\; 12,\; 18,\; 24,\; 30$, …

• НОК двух взаимно простых чисел равен произведению этих двух чисел.

• Если b кратно a, то LCM a и b равно b.

Пример: НОК $(5,\; 10) = 10$

Решенные примеры на общих кратных

1. Чему кратно число 9?

Решение:

Мы знаем, что можем получить кратное число, умножив его на 1, 2, 3, … и так далее.

Итак, числа кратные 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, …

2. Найдите два общих кратных числа 2 и 10.

Решение:

Мы знаем, что общие кратные двух или более чисел называются общими кратными этих чисел.

Теперь числа кратны 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20 , … 9 0003

и числа, кратные 10: 10 , 20 , 30, 40, 50, 60, 70, 80, 90, 100, …

Итак, два общих кратных 2 и 10 равны 10 и 20.

3. Найдите НОК чисел 3 и 5.

Решение:

Наименьшее общее кратное двух или более чисел называется наименьшим общим кратным (НОК).

Кратные 3: 3, 6, 9, 12, 15 , 18, 21, 24, 27, 30 , …

 Кратные 5: 5, 10, 15, 20, 25, 30 , 35, 40, 45, 50, …

Общие кратные 3 и 5: 15, 30, …

Наименьшее из них равно 15. Таким образом, НОК 3 и 5 15,

Практические задачи на кратные

1

Какое из следующих чисел не кратно 8?

16

28

64

88

Правильный ответ: 28
Число кратно 8: 8, 16, 24, 32, 40, …
Итак, 28 не кратно 8.

2

Какое из следующих чисел является общим кратным 16 и 20?

16

20

40

80

Правильный ответ: 80
Теперь число, кратное 16, равно $\colon$16, 32, 48, 64, $\underline{80 }$, 96, 112, 128,144, $\underline{160}\dots$
, а число, кратное 20, равно $\colon$20, 40, $\underline{60}$, 80, 100, 120, 140, $\underline{160. }$, 180, 200$\dots$
Итак, общие кратные чисел 16 и 20 равны $\colon$80 и 160, из которых 80 — это вариант d.

3

Какое из следующих чисел не является общим кратным 12 и 15?

30

60

120

180

Правильный ответ: 30
30 кратно 15, но не 12. Значит, 30 не является общим кратным 12 и 1. 5.

4

Что из нижеперечисленного является LCM 9 и 18?

19

18

27

36

Правильный ответ: 18
18 — наименьшее общее кратное 9 и 18. Итак, 18 — НОК 9 и 18. 900 03

Часто задаваемые вопросы о многоквартирных домах

Чему кратно число ноль?

Число, кратное нулю, равно нулю. Каждое другое целое число имеет бесконечно много кратных.

Например: 25 × 0 = 0 ; 1,0836 × 0 = 0; -9/87 × 0 = 0.

Чему кратно число один?

Все натуральные числа кратны 1.

No related posts.