Перевод в двоичную систему счисления
Пример №1. Перевести число 87,4510 в двоичное представление.Используем калькулятор
Перевод чисел.
| Целая часть от деления | Остаток от деления |
| 87 div 2 = 43 | 87 mod 2 = 1 | 43 div 2 = 21 | 43 mod 2 = 1 | 21 div 2 = 10 | 21 mod 2 = 1 | 10 div 2 = 5 | 10 mod 2 = 0 | 5 div 2 = 2 | 5 mod 2 = 1 | 2 div 2 = 1 | 2 mod 2 = 0 | 1 div 2 = 0 | 1 mod 2 = 1 |
Остаток от деления записываем в обратном порядке. Получаем число в 2-ой системе счисления: 1010111
87 = 10101112
Для перевода дробной части числа последовательно умножаем дробную часть на основание 2. В результате каждый раз записываем целую часть произведения.
0.45*2 = 0.9 (целая часть 0)
0.9*2 = 1.8 (целая часть 1)
0.8*2 = 1.6 (целая часть 1)
0.
Получаем число в 2-ой системе счисления: 0111
0.45 = 01112
Таким образом, число 87,45 в двоичной системе счисления записывается как 1010111,0111.
Пример №2. Перевести число 321,18 в двоичное представление.
Переводим целую часть числа. Заменяем каждый разряд на код из таблицы.
| Двоичная СС | Восьмеричная СС |
| 000 | 0 |
| 001 | 1 |
| 010 | 2 |
| 011 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
Переводим дробную часть числа.
Получаем число: 1 8 = 0012
Таким образом, число 321,18 в двоичной системе счисления записывается как 011010001,001.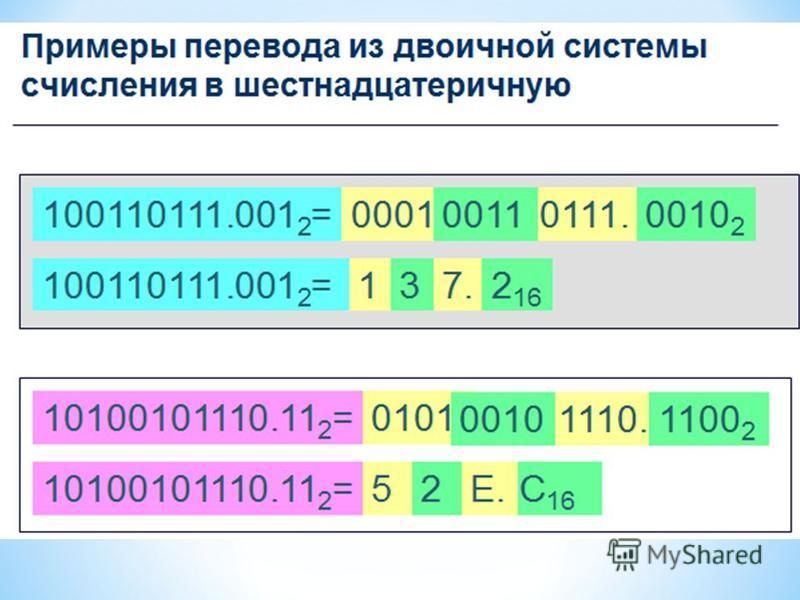
Пример №3. Перевести число AD,6716 в двоичное представление.
Переводим целую часть числа. Заменяем каждый разряд на код из таблицы.
| Двоичная СС | Шестнадцатеричная СС |
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
Переводим дробную часть числа.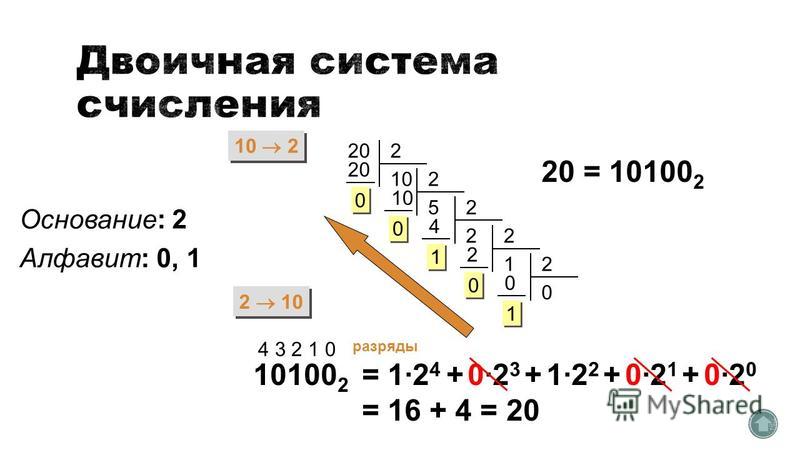
Получаем число: 6716 = 011001112
Таким образом, число AD,6716 в двоичной системе счисления записывается как 10101101,01100111.
Перейти к онлайн решению своей задачи
Пример №2. Перевести числа 581,10610, 115,7078, D21,E616 в двоичную систему.
Решение
Для проверки решения используем автоматический перевод чисел в двоичную систему счисления.
а) 581,10610;
| Целая часть от деления | Остаток от деления |
| 581 div 2 = 290 | 581 mod 2 = 1 | 290 div 2 = 145 | 290 mod 2 = 0 | 145 div 2 = 72 | 145 mod 2 = 1 | 72 div 2 = 36 | 72 mod 2 = 0 | 36 div 2 = 18 | 36 mod 2 = 0 | 18 div 2 = 9 | 18 mod 2 = 0 | 9 div 2 = 4 | 9 mod 2 = 1 | 4 div 2 = 2 | 4 mod 2 = 0 | 2 div 2 = 1 | 2 mod 2 = 0 | 1 div 2 = 0 | 1 mod 2 = 1 |
Остаток от деления записываем в обратном порядке.
Получаем число в 2-ой системе счисления: 1001000101
581 = 10010001012
Для перевода дробной части числа последовательно умножаем дробную часть на основание 2. В результате каждый раз записываем целую часть произведения.
0.106*2 = 0.212 (целая часть 0)
0.212*2 = 0.424 (целая часть
0.424*2 = 0.848 (целая часть 0)
0.848*2 = 1.696 (целая часть 1)
Получаем число в 2-ой системе счисления: 0001
0.106 = 00012
б) 115,7078;
Переводим целую часть числа. Заменяем каждый разряд на код из таблицы.
| Двоичная система счисления | Восьмеричная система счисления |
| 000 | 0 |
| 001 | 1 |
| 010 | 2 |
| 011 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
Переводим дробную часть числа.
Получаем число: 7078 = 1110001112
в) D21,E616.
Переводим целую часть числа. Заменяем каждый разряд на код из таблицы.
| Двоичная система счисления | шестнадцатеричная система счисления |
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| F |
Переводим дробную часть числа.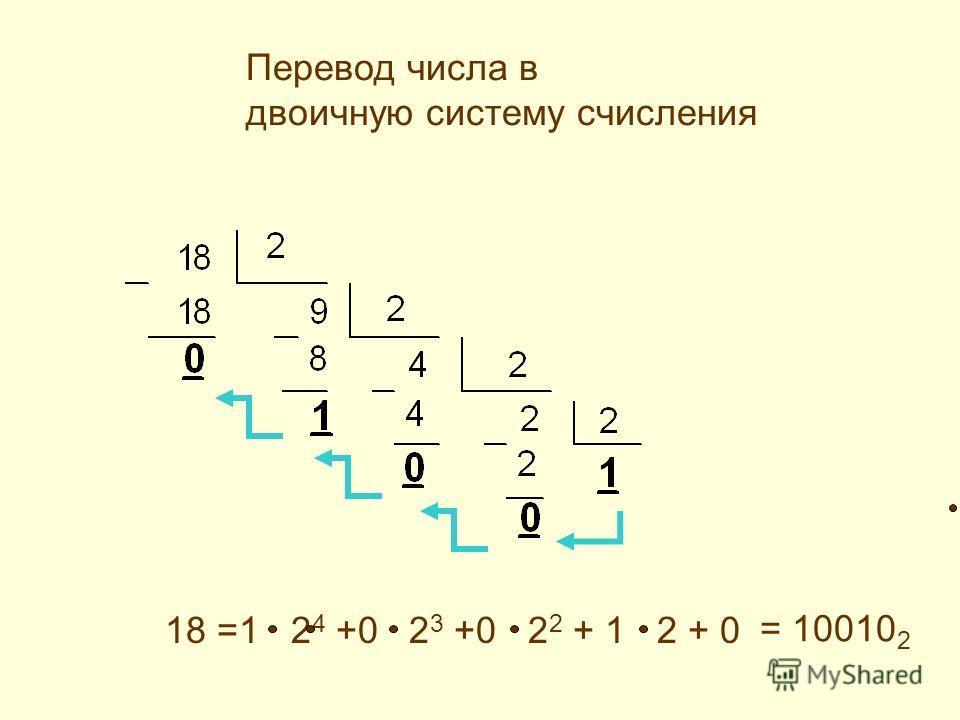
Получаем число: E616 = 111001102
Перейти к онлайн решению своей задачи
6.Двоичная система счисления. Двоичные таблицы сложения и умножения.
Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления, числа записываются с помощью двух символов (0 и 1).
Таблица сложения
+ | 0 | 1 |
0 | 0 | 1 |
1 | 1 | 10 |
Пример сложения «столбиком»:
1 | ↖ | ||||
+ | 1 | 1 | 1 | 0 | |
1 | 0 | 1 | |||
1 | 0 | 0 | 1 | 1 | |
Таблица умножения
× | 0 | 1 |
0 | 0 | 0 |
1 | 0 | 1 |
7.
Перевод числа (целого и дробного) из десятичной системы в двоичную систему. Преобразование десятичных чисел в двоичныеДопустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой :
19 /2 = 9 с остатком 1
9 /2 = 4 c остатком 1
4 /2 = 2 без остатка 0
2 /2 = 1 без остатка 0
1 /2 = 0 с остатком 1
Итак, мы делим каждое частное на 2 и записываем остаток в конец двоичной записи. Продолжаем деление до тех пор, пока в частном не будет 0. Результат записываем справо налево. Т.е. нижнее число будет самым левым и.т.д. В результате получаем число 19 в двоичной записи: 10011.
Преобразование дробных десятичных чисел в двоичные
Перевод дробного числа из десятичной системы счисления в двоичную осуществляется по следующему алгоритму:
Вначале переводится целая часть десятичной дроби в двоичную систему счисления;
Затем дробная часть десятичной дроби умножается на основание двоичной системы счисления;
В полученном произведении выделяется целая часть, которая принимается в качестве значения первого после запятой разряда числа в двоичной системе счисления;
Алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений.
В противном случае вычисления
продолжаются с предыдущего шага.
В противном случае вычисления
продолжаются с предыдущего шага.Пример: Требуется перевести дробное десятичное число 206,116 в дробное двоичное число.
Перевод
целой части дает 20610=110011102 по ранее описанным алгоритмам; дробную
часть умножаем на основание 2, занося
целые части произведения в разряды
после запятой искомого дробного двоичного
числа:
.116 • 2 = 0.232
.232 • 2 =
0.464
.464 • 2 = 0.928
.928 • 2 = 1.856
.856 • 2
= 1.712
.712 • 2 = 1.424
.424 • 2 = 0.848
.848 •
2 = 1.696
.696 • 2 = 1.392
.392 • 2 =
0.784
и т. д.
Получим:
206,116
8. Восьмеричная и шестнадцатеричная системы счисления.
Шестнадцатеричная система счисления — это позиционная система счисления с основанием 16. Для записи чисел в шестнадцатеричной системе используется 10 цифр от нуля до девяти (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) и латинские буквы A, B, C, D, E, F, обозначающие числа от 10 до 15.
Таким образом, все символы шестнадцатеричной системы:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Применение:
шестнадцатеричная система используется
в цифровой электронике и компьютерной
технике, в частности в низкоуровневом
программировании на языке ассемблера
для различных ЭВМ.
Восьмеричная система счисления — это позиционная система счисления с основанием 8. Для записи чисел в восьмеричной системе используется 8 цифр от нуля до семи (0,1,2,3,4,5,6,7). Применение: восьмеричная система наряду с двоичной и шестнадцатеричной используется в цифровой электронике и компьютерной технике, однако в настоящее время применяется редко (ранее использовалась в низкоуровневом программировании, вытеснена шестнадцатеричной).
6 в двоичном формате — Как преобразовать 6 из десятичного в двоичный?
6 в двоичном формате равно 110. В отличие от десятичной системы счисления, где мы используем цифры от 0 до 9 для представления числа, в двоичной системе мы используем только 2 цифры, которые равны 0 и 1 (биты). Мы использовали 3 бита для представления 6 в двоичном формате. В этой статье давайте узнаем, как преобразовать десятичное число 6 в двоичное.
Как преобразовать 6 в двоичном формате?
Шаг 1: Разделите 6 на 2.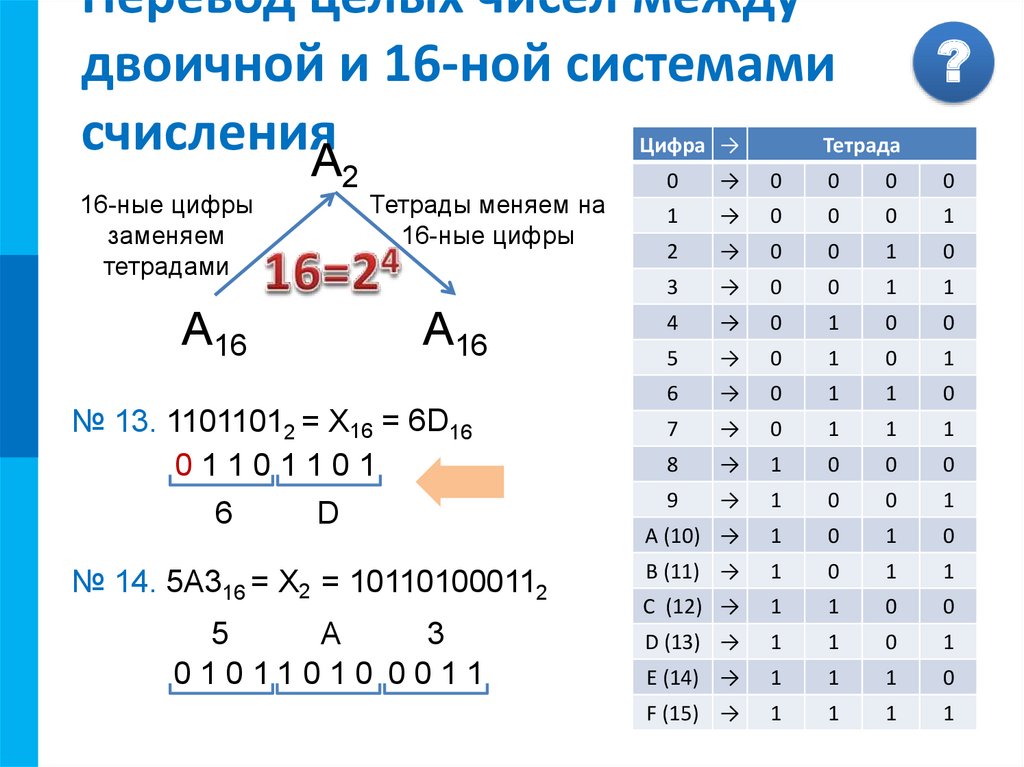
Используйте целое частное, полученное на этом шаге, в качестве делимого для следующего шага. Повторяйте процесс, пока частное не станет равным 0,9.0005
| Дивиденд | Остаток |
|---|---|
| 6/2 = 3 | 0 |
| 3/2 = 1 | 1 |
| 1/2 = 0 | 1 |
Шаг 2: Запишите остаток снизу вверх, т.е. в обратном хронологическом порядке. Это даст двоичный эквивалент 6.
Следовательно, двоичный эквивалент десятичного числа 6 равен 110.
☛ Калькулятор преобразования десятичного числа в двоичный
Давайте посмотрим на значение десятичного числа 6 в различных системах счисления.
- 6 в двоичном виде: 6₁₀ = 110₂
- 6 в восьмеричной системе: 6₁₀ = 6₈
- 6 в шестнадцатеричном формате: 6₁₀ = 6₁₆
- 110₂ в десятичном формате: 6₁₀
Описание проблемы:
Часто задаваемые вопросы о 6 в двоичном формате
Что такое 6 в двоичном формате?
6 в двоичном формате равно 110.
Чтобы найти десятичный эквивалент в двоичном, разделите 6 последовательно на 2, пока частное не станет равным 0. Двоичный эквивалент можно получить, записывая остаток на каждом шаге деления снизу вверх.
☛ Двоичный код в десятичный
Какой двоичный эквивалент 6 + 61?
6 в двоичной системе счисления равно 110, а 61 равно 111101. Мы можем сложить двоичный эквивалент 6 и 61, используя правила двоичного сложения [0 + 0 = 0, 0 + 1 = 1, 1 + 1 = 10, обратите внимание, что 1 равно перенос на следующий бит]. Следовательно, (110)₂ + (111101)₂ = (1000011)₂, что есть не что иное, как 67,9.0005
☛ Двоично-десятичный калькулятор
Как преобразовать 6 в двоичный эквивалент?
Мы можем разделить 6 на 2 и продолжать деление, пока не получим 0. Записывайте остаток на каждом шаге.
- 6 mod 2 = 0 — LSB (младший значащий бит)
- 3 мод 2 = 1
- 1 mod 2 = 1 — MSB (старший бит)
Записать остатки от MSB до LSB. Следовательно, десятичное число 6 в двоичном виде можно представить как 110.
Сколько бит имеет 6 в двоичном формате?
Мы можем подсчитать количество нулей и единиц, чтобы увидеть, сколько битов используется для представления 6 в двоичном формате, т. е. 110. Таким образом, мы использовали 3 бита для представления 6 в двоичном формате.
Найдите значение 9 × 6 в двоичной форме.
Мы знаем, что 6 в двоичном формате равно 110, а 9 равно 1001. Используя правила двоичного умножения (0 × 0 = 0; 0 × 1 = 0, 1 × 0 = 0 и 1 × 1 = 1), мы можем умножить 110 × 1001 = 110110, что равно 54 в десятичной системе счисления. [6 × 9= 54]
☛ Также проверьте:
- 7 в двоичном формате — 111
- 45 в двоичном формате — 101101
- 83 в двоичном формате — 1010011
- 29 в двоичном формате — 11101
- 43 в двоичном формате — 101011
- 199 в двоичном формате — 11000111
- 99 в двоичном формате — 1100011
Рабочие листы по математике и визуальный учебный план
Преобразователь десятичных чисел в двоичные
Преобразователь десятичных чисел в двоичныеГлавная›Преобразование›Преобразование чисел›Десятичное число в двоичное
От BinaryDecimalOctalHexadecimalText
Кому BinaryDecimalOctalHexadecimalText
Введите десятичное число
Двоичный номер
Дополнение до 2 с двоичной подписью
Шестнадцатеричный номер
Группировка цифр
Little endian
| Адрес |
| Данные |
Big endian
| Адрес |
| Данные |
Шаги преобразования десятичных чисел в двоичные
Разделите на 2, чтобы получить цифры из остатков:
| Деление на 2 | Частное | Остаток (цифра) | Бит # |
|---|
Двоичное преобразование в десятичное ►
Как преобразовать десятичное число в двоичное
Шаги преобразования:
- Разделите число на 2.
- Получить целое частное для следующей итерации.
- Получить остаток двоичной цифры.
- Повторяйте шаги, пока частное не станет равным 0.
Пример #1
Преобразование 13 10 в двоичное число:
| Разделение на 2 | Частное | Остаток | Бит # | |||
|---|---|---|---|---|---|---|
| 13/2 | 6 | 1 | 0 | |||
| 6/2 | 3 | 0 | 1 | |||
| 3/2 | 1 | 1 | 2 | |||
| 1/2 | 0 | 1 | 3 | Пример №2Частное | Остаток | Бит # |
| 174/2 | 87 | 0 | 0 | |||
| 87/2 | 43 | 1 | 1 | |||
| 43/2 | 21 | 1 | 2 | |||
| 21/2 | 10 | 1 | 3 | |||
| 10/2 | 5 | 0 | 4 | |||
| 5/2 | 2 | 1 | 5 | |||
| 2/2 | 1 | 0 | 6 | |||
| 1/2 | 0 | 1 | 7 |
So 174 10 = 10101110 2
Таблица преобразования десятичных чисел в двоичные
| Десятичное число Число | Двоичный Число | Шестигранник Число |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 10 | 2 |
| 3 | 11 | 3 |
| 4 | 100 | 4 |
| 5 | 101 | 5 |
| 6 | 110 | 6 |
| 7 | 111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | А |
| 11 | 1011 | Б |
| 12 | 1100 | С |
| 13 | 1101 | Д |
| 14 | 1110 | Е |
| 15 | 1111 | Ф |
| 16 | 10000 | 10 |
| 17 | 10001 | 11 |
| 18 | 10010 | 12 |
| 19 | 10011 | 13 |
| 20 | 10100 | 14 |
| 21 | 10101 | 15 |
| 22 | 10110 | 16 |
| 23 | 10111 | 17 |
| 24 | 11000 | 18 |
| 25 | 11001 | 19 |
| 26 | 11010 | 1А |
| 27 | 11011 | 1Б |
| 28 | 11100 | 1С |
| 29 | 11101 | 1Д |
| 30 | 11110 | 1Э |
| 31 | 11111 | 1F |
| 32 | 100000 | 20 |
| 64 | 1000000 | 40 |
| 128 | 10000000 | 80 |
| 256 | 100000000 | 100 |
См.
