Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||
Другие ответы
| ||||||||||||
09.14
| ||||||||||||
09.14
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Решено
В 480 гр.
2=20-xy
Ответы
lsllalap 11.11.2020 13:15
1.x + 3*y = 10x*y = 3×1 = 1y1 = 3
2.x — 2*y = -7x*y = -6×1 = -4 y1 = 3/2 = 1.5×2 = -3 y2 = 2
3.x*y = 12
x1 = -4y1 = -3 x2 = -3y2 = -4
вот 3) 4-е без понятия))
ПОКАЗАТЬ ОТВЕТЫ
yakov228 11.11.2020 13:1512
Объяснение:
12 ответ
ПОКАЗАТЬ ОТВЕТЫ
artem222529ozd6op 11.11.2020 13:15
x^2-y^2=-40
x^2-2xy+y^2=16
(x-y)(x+y)=-40
(x-y)^2=16
a) x-y=4
x+y=-10
x=-3, y=-7
b) x-y=-4
x+y=10
x=3 y=7
(-3.
2=-15
ПОКАЗАТЬ ОТВЕТЫ
nastiarabadj 11.11.2020 13:15
В 1 ответы 4 и 5
в 2 ответы 9 и 4
в 3 ответы 4 и 3
решение на фото быстро делал обащайся
ПОКАЗАТЬ ОТВЕТЫ
p0m41k 11.11.2020 13:15
Вычтем из второго у-я первое x²-y²=(x-y)(x+y)=28+12=30
сложим оба уравнения x²+y²-2xy=(x-y)²=16
1/ x-y=4 y=x-4
(x-y)(x+y)30 ⇒x+y=30/4=7,5 x+x-4=7,5 2x=11,5 x= 5,75
y=5,75-4=1,75
2/ x-y=-4 y=x+4 x+y=-30/4=-7,5 x+x+4=-7,5 2x=-11,5 x=-5,75
y=-5,75+4=-1,75
ПОКАЗАТЬ ОТВЕТЫ
ernarsailaubek
11.
2-2у-15=0
D=4-4*(-15)=64
y1=8+2/2=5
y2=8-2/2=3
x1=2-5=-3
x2=2-3=-1
Все остальные примеры можно сделать по аналогии, удачи)
ПОКАЗАТЬ ОТВЕТЫ
dkdjdhhs 11.11.2020 13:15
Посмотри во вложениях. Там обрати внимание на обозначение * — это выражение х через у, или у через х
ПОКАЗАТЬ ОТВЕТЫ
vehera087 11.11.2020 13:15
Я надеюсь, тут все понятно.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
katehell11
28.
05.2019 02:40
Найдите первый отрицательный член арифметической прогрессии 12,5; 11, 2) сколько положительных членов в арифметической прогресии 94,6; 91,…
lihach221 22.10.2020 13:08
Вычислите рациональным…
Аккаунт удален 04.06.2019 21:20
Турист км, что составляет 4/5 всего пути. найти длину пути….
kkkddd90 04.06.2019 21:20
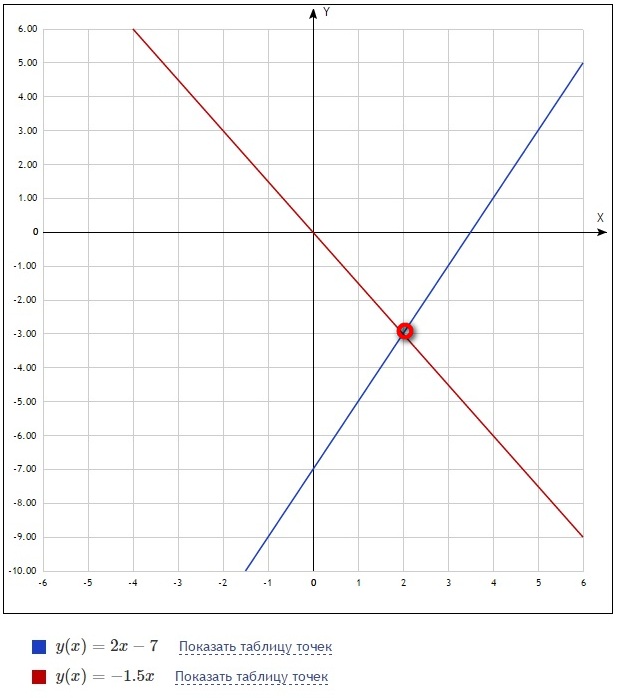
Найдите координаты точек пересечениянайдите координаты точек пересечения графиков функций y=x в квадрате и y=7х-12.
2 = 9 задана точка м(1; 0; 2). вектор (a, b, c) – вектор нормали к поверхности s в точке м. известна одна из координат нормали…
toroshinaalena 06.09.2021 16:37
5 : 5/6 + 1 2/7 * 5 5/6 — 4 3/4…
lizka12343 06.09.2021 16:38
(-32,64:0,8+4,324:(-46))*1,5+28,16…
rzaevibragim 19.10.2021 10:23
Какими тремя цифрами оканчивается произведение 1*2*3…16*17 а)0,1 и 2б)0,6 и 7в)0,0 и 0г)2,2 и 2д)0,0 и 2…
Древность5
24.
05.2019 19:38
Найти первообразные функций 8sin x + 4/x…
3-8Вычесть 6xy из 12xy.
..Перейти к
- Упражнение 12.1
- Упражнение 12.2
- Упражнение 12.3
- Упражнение 12.4
- Целые числа
- Дроби и десятичные дроби
- Обработка данных
- Простые уравнения
- Линии и углы
- Треугольник и его свойства.
- Конгруэнтность треугольников
- Сравнение количеств
- Рациональное число
- Практическая геометрия
- Алгебраические выражения
- Показатели и силы
- Симметрия
- Визуализация твердых фигур
Главная >
Решения НЦЭРТ
Класс 7
Математика
>
Глава 12.
Вопрос 28 Упражнение 12.2
Вычесть:
6xy из –12xy
Ответ:
ОТВЕТ:
Когда термины имеют одинаковые алгебраические множители, они подобны терминам.
Тогда мы должны вычесть подобные члены
= -12xy – 6xy
= — 18xy
Стенограмма видео
привет всем, добро пожаловать на канал обучения лидера, меня зовут Рахна, два выражения, чтобы вычесть эти выражения из минус 12xy мы можем ясно сказать, что эти два термина похожи, потому что они имеют одни и те же переменные, поэтому я пишу выражение как, потому что мы должны вычесть из минус 12 x y, поэтому давайте напишем это сначала поставить знак минус, а затем 6 x y теперь минус 12 x y минус 6 x y, поэтому, когда у нас должен быть один и тот же знак, мы должны добавить переменные, мы должны добавить константы, поэтому 12 плюс 6 равно 18, но переменные будут такими же, как знак минус, потому что здесь они имеют одинаковый знак, поэтому всякий раз, когда у нас есть знак в обоих терминах, которые станут окончательным ответом, так что это окончательное решение вопроса, я надеюсь, вы понимаете метод, увидимся в моем следующем видео, не забудьте поставить лайк и подписаться на канал, спасибодля просмотра
Связанные вопросы
Q2) Добавить:i) ii) iii) iv) v) vi) vii) viii) ix) x)
Q3) Вычитание) ii) iii) iv) v) vi) vii) viii)
Q4) (a) Что нужно добавить, чтобы получить? (b) Что нужно вычесть, чтобы получить
Q5) Что нужно отнять, чтобы получить?
Q6) (a) Из суммы и вычесть .
(b) Из суммы и вычесть сумму и .
Q1) Упрощение объединения одинаковых терминов:i) ii) iii) iv) v) vi)
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Exercises
Exercise 12.1
Exercise 12.2
Exercise 12.3
Exercise 12.4
Chapters
Integers
Fractions and Decimals
Data Handling
Simple Equations
Lines and Angles
The Triangle and its properties
Конгруэнтность треугольников
Сравнение величин
Рациональные числа
Практическая геометрия
Периметр и площадь
Алгебраические выражения
Экспоненты и степени
Симметрия
9 ВизуализацияКурсы
Быстрые ссылки
Условия и политика
Условия и политика
2022 © Quality Tutorials Pvt Ltd Все права защищены
Rd Sharma for Class 8 Math Chapter 8
- Решения для учебников
- Класс 8
- Математика
- деление алгебраических выражений
Rd Sharma Решения для 8-го класса по математике Глава 8 Раздел алгебраических выражений представлены здесь с простыми пошаговыми объяснениями.
Эти решения для раздела алгебраических выражений чрезвычайно популярны среди учащихся 8 класса. Решения по математическому разделу алгебраических выражений пригодятся для быстрого выполнения домашних заданий и подготовки к экзаменам. Все вопросы и ответы из книги Rd Sharma по математике для 8-го класса, глава 8, предоставляются здесь для вас бесплатно. Вам также понравится возможность без рекламы на Meritnation’s Rd Sharma Solutions. Все решения Rd Sharma для класса 8 по математике подготовлены экспертами и на 100% точны.
Страница № 8.11:
Вопрос 1:
Разделить 5 x 3 − 15 x 2 + 25 x 9107 2 17 9 10 9 9 10 9 9 10 9 9 10 9 9 9 9
Ответ:
Страница № 8.11:
Вопрос 2:
Разделитель 4 Z 3 + 6 Z 2 — + 6 Z 2 — + 6 Z 2 — Z .
Ответ:
Номер страницы 8.
11:Вопрос 3:
Разделить 9 x 2 y − 6 xy + 12 xy 2 на −32 xy .
Answer:
Page No 8.11:
Question 4:
Divide 3 x 3 y 2 + 2 x 2 y + 15 xy by 3 ху .
Ответ:
Номер страницы 8.11:
Вопрос 5:
Divide x 2 + 7 x + 12 на x + 4.
Ответ:
Страница № 8.11:
ВОПРОС 6:
6. + 3 y + 12 by 2 y + 1.
Answer:
Page No 8.11:
Question 7:
Divide 3 x 3 + 4 x 2 + 5 х + 18 на х + 2.
Answer:
Page No 8.11:
Question 8:
Divide 14 x 2 − 53 x + 45 by 7 x − 9.
Answer:
Страница № 8.11:
Вопрос 9:
Разделить -21 + 71 x — 31 x 2 — 24 x 3 9171 8 x 9 10,7 1071 8
Ответ:
Номер страницы 8.11:
Вопрос 10:
Divide 3 Y 4 — 3Y 3 — 4 Y 2 — 4 Y на Y 2 — 2 Y .
Answer:
Page No 8.11:
Question 11:
Divide 2 y 5 + 10 y 4 + 6 y 3 + y 2 + 5 у + 3 на 2 у 3 + 1.
Ответ:
Страница № 8.11:
Вопрос 12:
Разделитель x 4 — 2 x 3 + 2 x 2 3 + 2 x 2 3 + 2 x 2 2 3 + 2 x 2 2 3 + 2 .
2 + x + 1.
Answer:
Page No 8.11:
Question 13:
Divide m 3 − 14 m 2 + 37 m − 26 на м 2 − 12 м +13.
Answer:
Page No 8.11:
Question 14:
Divide x 4 + x 2 + 1 by x 2 + x + 1.
Answer:
Page No 8.11:
Question 15:
Divide x 5 + x 4 + x 3 + x 2 + x + 1 по x 3 + 1.
Ответ:
Страница № 8.11:
Вопрос 16:
Разделение 14 x 3 7
. +9 x — 1 на 2 x — 1 и найдите коэффициент и остаток
Ответ:
COTITION = 7×2+X+5REMAINDE 6 х 3 − x 2 — 10 x — 3 на 2 x — 3 и найдите частное и остаток.
Answer:
Quotient = 3×2+ 4x + 1 Remainder = 0
Page No 8.11:
Question 18:
Divide 6 x 3 + 11 x 2 − 39 x − 65 на 3 x 2 + 13 x + 13 и найдите частное и остаток.
Ответ:
Частное = 2x-5Остаток =0
Page No 8.12:
Question 19:
Divide 30 x 4 + 11 x 3 − 82 x 2 − 12 x + 48 by 3 x 2 + 2 x — 4 и найдите частное и остаток.
Ответ:
Коэффициент = 10×2-3x-12Remainder = 0
Страница № 8,12:
Вопрос 20:
Разделите x 4 -4 x 4 -4 x 4 -4 x 4 -4 .1074 + 4 на 3 x 2 − 4 x + 2 и найдите частное и остаток.
Ответ:
∴ Частное = 3x 2 + 4x + 2 andостаток = 0 .
Страница № 8.12:
Вопрос 21:
Проверьте алгоритм деления, т. е. делимое = делитель × частное + остаток, в каждом из следующих случаев. Также запишите частное и остаток.
| Дивиденд | Делитель | |
| (и) | 14 x 2 + 13x − 15 | 7 х − 4 |
| (ii) | 15 z 3 − 20 z 2 + 13 z − 12 | 3 z − 6 |
| (iii) | 6 г 5 − 28 г 3 + 3 года 2 + 30 г − 9 | 2 г 2 − 6 |
| (iv) | 34 x — 22 x 3 — 12 x 4 — 10 x 2 — 75 | 3 x + 7 |
| (в) | 15 г 4 − 16 г 3 + 9 г 2 − 103 г + 6 | 3 г − 2 |
| (vi) | 4 г 3 + 8 г + 8 г 2 + 7 | 2 г 2 — у + 1 |
| (vii) | 6 Y 5 + 4 Y 4 + 4 Y 3 + 7 Y 2 + 27 Y + 6 | 5.2 г 3 + 1 |
Ответ:
(i)
Частное = 2 x + 3
Remainder = -3
Divisor = 7 x — 4
Divisor × Quotient + Remainder = (7 x — 4) (2 x + 3) — 3
= 14 x 2 + 21 x -8 x -12 -3
= 14 x 2 + 13 x -15 = Dividend -15
= Dividend -15
= Dividend -15
Делитель × Частное + Остаток = Делимое
Следовательно, проверено.
(II)
Коэффициент = 5Z2+103Z+11Remainder = 54Divisor = 3Z-6Divisor × COWIENT+остаток = (3Z-6) 5Z2+103Z+11+54 = 15Z3+10Z2+33Z-30Z2-20Z-66+. 54 = 15Z3-20Z2+13Z-12 = DividendThus, Divisor × Coverity+остаток = дивиденд
Таким образом проверено.
(iii)
Частное = 3y3-5y+32
Остаток = 0
Делитель = 2y 2 — 6
Делитель × =6y5-10y3+3y2-18y3+30y-9=6y5-28 y3+3y2+30y-9
= Делимое
Таким образом, Делитель × Частное + Остаток = Делимое
Следовательно, проверено.
(iv)
Частное = — 4 x 3 + 2 x 2 — 8 x + 30
Remainder = — 285
Divisor = 3 x + 7
Divisor × Quotient + Remainder = (3 x + 7) (- 4 x 3 + 2 x 2 — 8 x + 30) — 285
= — 12 x 4 + 6 x 3 — 24 x 2 + 90 x — 28 x 3 + 14 x 2 — 56 x + 210 — 285
= — 12 x 4 — 22 x 3 — 10 x 2 + 34 x — 75
= Делимое
Таким образом,
Делитель × Частное + Остаток = Делимое
Следовательно, проверено.
(v)
Частное = 5y3-2y2+53y
Остаток = 6
Divisor = 3y -2
Divisor × Covertient+остаток = (3y -2) (5y 3 -2y 2 +53y)+6
= 15y4-6y3+5y2-10y3+4y2-103y2-103y2-103y2-103y2-103y2-103y2-103y2-103y2-103y2-103y2-103y2-103y2-103y2-103y2-103y2-103y2-103y2-103y2-103y2-103y2-103y2-103y2-103y2. +6
= 15y4-16y3+9y2-103y+6
= дивиденд
Таким образом,
Divisor × Covertite+остаток = дивиденд
Следовательно, подтверждено.
(vi)
Частное = 2 y + 5
Remainder = 11 y + 2
Divisor = 2 y 2 — y + 1
Divisor × Quotient + Remainder = (2 y 2 — y + 1) (2 y + 5) + 11 y + 2
= 4 y 3 +10 y 2 — 2 y 2 — 5 y + 2 y + 5 + 11 y + 2
= 4 y 3 + 8 y 2 + 8 y + 7
= Дивидимное
Таким образом,
Делитель × Частное + Остаток = Делимое
Следовательно, проверено.
(vii)
Частное = 3 y 2 + 2 Y + 2
Остаток = 4 Y 2 + 25 Y + 4
Divisor = 2 y 3 + 1
1 Diviser × 2 3 + 1
111111111411914 гг. y 3 + 1) (3 y 2 + 2 y + 2) + 4 y 2 + 25 y + 4
= 6 y 5 + 4 y 4 + 4 y 3 + 3 y 2 + 2 y + 2 + 4 y 2 + 25 y + 4
= 6 y 5 + 4 y 4 + 4 Y 3 + 7 Y 2 + 27 Y + 6
= Dividend
Таким образом,
Divisor × × × hoatient + Dividend
.
Page No 8.12:
Question 22:
Divide 15 y 4 + 16 y 3 + 103 y − 9 y 2 − 6 by 3 y − 2. Запишите коэффициенты при членах в частном.
Ответ:
∴ Covertient = 5 Y 3 + (26/3) y 2 + (25/9) Y + (80/27)
= (-2) Y + (80/27)
= (-2. /27)
Коэффициент y 3 = 5
Коэффициент y 2 = (26/3)
Коэффициент y = (2841/9)
Страница № 8.12:
Вопрос 23:
Используя деление многочленов, укажите, является ли
(i) x + 6 является коэффициентом x 2 — x — 42
(ii) 4 x — 1 является коэффициентом 4 x 2 9174 — 13 9107 ) 2 y − 5 is a factor of 4 y 4 − 10 y 3 − 10 y 2 + 30 y − 15
(iv) 3 y 2 + 5 является делителем 6 y 5 + 15 y 4 + 16 y 3 + 4 Y 2 + 10 Y — 35
(V) Z 2 + 3 является фактором Z 5 – Z 5 ‘.
Z 5 ‘ 1 V . ) 2 x 2 − x + 3 is a factor of 6 x 5 − x 4 + 4 x 3 − 5 x 2 − x − 15
Ответ:
(i)
Остаток равен нулю. Отсюда ( x +6) является коэффициентом x 2 — x -42
(ii)
Поскольку остаток не равен нулю . Следовательно (4 x -1) не является фактором 4 x 2 -13 x -12
(III)
∵ Остаток не является Zero,
2
∵ Остаток не является Zero,
2
∵. — 5 не является коэффициентом 4y4-10y3-10y2+30y-15.
(iv)
Остаток равен нулю. Таким образом, 3 y 2 + 5 является коэффициентом 6y5+15y4+16y3+4y2+10y-35.
(v)
Остаток равен нулю; поэтому z 2 + 3 является коэффициентом z5 -9z.
(vi)
Остаток равен нулю; следовательно, 2 x 2-x+3 является коэффициентом 6 x5-x4 +4×3-5×2-x-15.
Страница № 8.12:
Вопрос 24:
Найти значение A , если x + 2 является фактором 4 x 4 + 2 x 3 4 + 2 x 3 4 + 2 x 3 4 3 + 2 x 3 4 + 2 x 3 4 . 2 + 8 х + 5 и .
Ответ:
Нам нужно найти значение a, если (x+2) является множителем (4×4+2×3-3×2+8x+5a). Подставив x=-2 в 4×4+2×3-3×2+8x+ 5а, получаем:4(-2)4+2(-2)3-3(-2)2+8(-2)+5a=0или, 64-16-12-16+5а=0или, 5а= -20или, a=-4∴ Если (x+2) является фактором (4×4+2×3-3×2+8x+5a), a=-4.
Page No 8.12:
Question 25:
What must be added to x 4 + 2 x 3 − 2 x 2 + x − 1 , so that the полученный многочлен точно делится на х 2 + 2х — 3?
Ответ:
Таким образом, ( x — 2) нужно добавить к (x4+2×3-2×2+x-1), чтобы получившийся многочлен точно делился на (x2+2x-3).
Страница № 8.15:
Вопрос 1:
Разделите первый многочлен на второй в каждом из следующих случаев. Также запишите частное и остаток:
(i) 3 x 2 + 4 x + 5, x − 2
(ii) 10 x 2 — 7 x + 8, 5 x — 3
(III) 5 Y 3 — 6 Y 2 + 6 Y — 1, 5 — — 1 Y — 1, 5 — — 1 Y — 1, 5 — — 1 Y — 1, 5 — — 1 Y — 1, 5 — 1 + 6 Y — 1, 5 .
(iv) x 4 − x 3 + 5 x , x − 1
(v) y 4 + y 2 , y 2 − 2
Ответ:
(i) 3×2+4x+5x-2=3x(x-2)+10(x-2)+25(x-2)=(x-2)( 3x+10)+25(x-2)=(3x+10)+25(x-2) Следовательно, частное=3x+10 и остаток=25. (ii) 10×2-7x+85x-3=2x(5x -3)-15(5x-3)+475(5x-3)=(5x-3)(2x-15)+475(5x-3)=(2x-15)+4755x-3Следовательно, частное=2x- 15 и остаток = 475.
(iii) 5y3-6y2+6y-15y-1=y2(5y-1)-y(5y-1)+1(5y-1)(5y-1)=(5y-1) (y2-y+1)(5y-1)=(y2-y+1)Следовательно, частное = y2-y+1 и остаток = 0
(iv) x4-x3+5xx-1=x3(x-1)+5(x-1)+5x-1=(x-1)(x3+5)+5x-1=(x3+5) )+5x-1 Следовательно, частное = x3+5 и остаток = 5.
(v) y4+y2y2-2=y2(y2-2)+3(y2-2)+6y2-2=(y2-2)( y2+3)+6y2-2=(y2+3)+6y2-2. Следовательно, частное = y2+3 и остаток = 6. второй.
(i) x + 1, 2 x 2 + 5 x + 4
(ii) y − 2, 3 y 3 + 5 y 2 + 5 y + 2
(iii) 4 x 2 − 5, 4 x 4 + 7 x 2 + 15
(iv) 4 − z , 3 z 2 − 13 z + 4
(v) 2 a − 3, 10 a 2 − 9 a − 5
( vi) 4 y + 1, 8 y 2 − 2 y + 1
Ответ:
(i) 2×2+5x+4x+1=2x(x+1)+3(x +1)+1x+1=(x+1)(2x+3)+1(x+1)=(2x+3)+1x+1∵ Остаток=1.
2х2+5х+4
(ii) 3y3+5y2+5y+2y-2=3y2(y-2)+11y(y-2)+27(y-2)+56y-2=(y-2)(3y2+11y+ 27)+56y-2=(3y2+11y+27)+56y-2∵ Остаток = 56∴(y-2) не является множителем 3y3+5y2+5y+2.
(iii) 4×4+2+154×2-5= x2(4×2-5)+3(4×2-5)+304×2-5= (4×2-5)(x2+3)+304×2-5=(x2+ 3)+304×2-5∵ Остаток = 30 Следовательно, (4×2-5) не является множителем 4×4+7×2+15
(iv) 3z2-13z+44-z=3z2-12z-z+44-z=3z (z-4)-1(z-4)4-z=(z-4)(3z-1)4-z=(4-z)(1-3z)4-z=1-3z∵ Остаток = 0∴ (4-z) является коэффициентом 3z2-13z+4.
(В) 10а2-9a-52a-3=5a(2a-3)+3(2a-3)+42a-3=(2a-3)(5a+3)+42a-3=(5a+3)+42a-3∵ Остаток = 4∴ ( 2a-3) не является множителем 10a2-9a-5.
(vi) 8y2-2y+14y+1=2y(4y+1)-1(4y+1)+24y+1=(4y+1)(2y-1)+24y+1=(2y-1 )+24y+1∵ Остаток = 2∴ (4y+1) не является множителем 8y2-2y+1.
Стр. № 8.17:
Вопрос 1:
Разделитель:
x 2 -5 x + 6 по x -3
6. =x2-3x-2x+6x-3=x(x-3)-2(x-3)(x-3)=(x-3)(x-2)(x-3)= x-2
Стр.
№ 8.17:Вопрос 2:
Разделитель:
AX 2 — AY 2 на AX + AY 9072 2 на AX + AY
Номер страницы 8.17:
Вопрос 3:
Разделить:
x Ответ:
x4-y4x2-y2=(x2)2-(y2)2(x2-y2)=(x2+y2)(x2-y2)(x2-y2)= x2+y2
Номер страницы 8.17:
Question 4:
Divide:
acx 2 + ( bc + ad ) x + bd by ( ax + b )
Answer:
acx2+(bc+ad)x +bd(ax+b)=acx2+bcx+adx+bd(ax+b)=cx(ax+b)+d(ax+b)(ax+b)=(ax+b)(cx+d) (ax+b)= cx+d
Страница № 8.17:
Вопрос 5:
Разделить:
( a 2 + 2 AB + B 2 ) — ( A 2 + 2 AC + C 2 ) на 2 A + 2 ) на 2 A + 2 ) на 2 A + 2 ).
Ответ:
(a2+2ab+b2)-(a2+2ac+c2)(2a+b+c)=(a+b)2-(a+c)2(2a+b+c) =(a+b+a+c)(a+b-a-c)(2a+b+c)=(2a+b+c)(b-c)(2a+b+c)=b-c
Страница № 8.17:
Вопрос 6:
Разделить:
14×2-12x-12 на 12x-4
Ответ:
14×2-12x-1212x-4=12x(12x-4)+3(12x-4)12x-4=(12x-4)(12x+3)(12x-4)=12x+3
Страница № 8.2 :
Вопрос 1:
Напишите степень каждого из следующих многочленов.
(i) 2 x 2 + 5 x 2 — 7
(II) 5 x 2 — 3 x + 2
(III) 2 x x + 2
(III) 2 x + + + + + + + + + + + + + + + + + + + + + 2
) 2 − 8
(iv) 12y7-12y6+48y5-10
(v) 3 x 3 + 1
(vi) 5
(vii) 20 x 3 + 12 x 2 Y 2 -10 Y 2 + 20
Ответ:
(I) Коррекция: это 2×3 + 5x.
2х2+5х2-7. Степень многочлена 2×3+5×2-7 равна 3. (ii) Степень многочлена 5×2-35x+2 равна 2. (iii) Степень многочлена 2x+x2-8 равна 2. (iv) Степень многочлена 12y7-12y6+48y5-10 равно 7. (v) Степень многочлена 3×3+1 равна 3. (vi) 5 — постоянный многочлен, и его степень равна 0. (vii) Степень многочлена 20×3 +12x2y2-10y2+20 равно 4,
Страница № 8.2:
Вопрос 2:
Какие из следующих выражений не являются полиномами?
(I) x 2 + 2 x −2
(II) AX + x2-x3
(III) 3 Y 3 -5Y +
(IV) -5Y +
(IV) 3 -5Y +
(IV) 3 -5Y +
(IV) 3 -5y +
(IV) 3 -5y +
(iv. 1/2 + a x + 9 x 2 + 4
(v) 3 x −2 + 2 x −1 + 4 x +5
Ответ:
(i) x2+2x-2 не является многочленом, потому что -2 – степень переменной x, не является неотрицательным целым числом.
не является неотрицательным целым числом. (iii) 3y3-5y+9 является полиномом, поскольку степени переменной y являются неотрицательными целыми числами. (iv) ax12+ax+9×2+4 не является многочленом, поскольку 12 является степенью переменной x не является неотрицательным целым числом. (v) 3x-2+2x-1+4x+5 не является полиномом, потому что -2 и -1 являются степенями переменной x и не являются неотрицательными целыми числами.
Страница № 8.2:
Вопрос 3:
Запишите каждый из следующих многочленов в стандартной форме. Кроме того, напишите их степень. 74 + 11) (i) Стандартная форма данного многочлена может быть выражена как: (5×4+x2+6x+ 3) или (3+6x+x2+5×4) Степень полинома равна 4. Разделить 6 x 3 y 2 z 2 на 3 x 2 yz 6x3y2z23x2yz=6×x×x×x×y×y×z×z3×x×x×y×z = 2x(3-2)y(2-1)z(2-1) = 2xyz Разделитель 15 M 2 N 3 на 5 M 2 1 N . 15m2n35m2n2=15×m×m×n×n×n5×m×m×n×n=3m(2-2)n(3-2)=3m0n1=3n Разделите 24 a 3 b 3 на −8ab. 24a3b3-8ab= 24×a×a×a×b×b×b-8×a×b=-3a(3-1)b(3-1)=-3a2b2 Разделить −21 abc 2 на 7 abc . -21abc27abc= -21×a×b×c×c7×a×b×c=-3a(1-1)b(1-1)c(2-1)=-3c Разделить 72 xyz 2 на -9 xz . 72xyz2-9xz=72×x×y×z×z-9×x×z=-8x(1-1)yz(2-1)=-8yz Divide −72 a 4 b 5 c 8 by −9 a 2 b 2 c 3 . -72a4b5c8-9a2b2c3=-72×a×a×a×a×b×b×b×b×b×c×c×c×c×c×c×c×c-9×a×a×b×b×c×c×c=8a(4-2)b(5-2)c(8-3)=8a2b3c5 Упрощение: 16m3y24m2y=16×m×m×m×y×y4×m×m×y=4m(3-2)y(2-1)=4my Упрощение: 32m2n3p24mnp=32×m×m×n×n×n×p×p4×m×n×p=8m(2-1)n(3-1) )p(2-1)=8mn2p Разделить x + 2 x 2 + 3 x 4 − x 5 на 2 x . x+2×2+3×4-x52x = x2x+2x22x+3x42x-x52x = 12+x+32×3-12×4 Divide y4-12y 3y 3y 3y 3y 3y 3y 3y 3y 3y 3y3y 3y 3y 3y 3. . y4-3y3+12y23y=y43y-3y33y+12y23y=13y(4-1)-y(3-1)+16y(2-1)=13y3-y2+16y Разделить −4 a 3 + 4 a 2 + a на 2 a .
(i) x 2 + 3 + 6 x + 5 x 4
(ii) a 2 + 4 + 5 a 6
(iii ) ( x 3 − 1)( x 3 − 4)
(iv) ( y 3 − 2)( 3 2 y
(v) a3-38a3+1617
(vi) a+34a+43 Ответ:
(ii) Стандартная форма данного полинома может быть выражена как: (5a6+a2+4) или (4+a2+5a6) степень многочлена равна 6. (iii) (x3-1)(x3-4)=x6-5×3+4Стандартная форма данного многочлена может быть выражена как: (x6-5×3+4) или (4-5×3+x6 ) Степень многочлена 6. (iv) (y3-2)(y3+11)=y6+9y3-22Стандартная форма данного многочлена может быть выражена как: (y6+9y3-22) или (-22+9y3+y6) Степень многочлена равна 6.(v) (a3-38)(a3+1617) =a6+77136a3-617Стандартная форма данного полинома может быть выражена как: (a6+77136a3-617) или (-617+77136a3+a6)Степень полинома – 6.(vi) (a+34)(a +43)=a2+2512a+1Стандартная форма данного многочлена может быть выражена как: (a2+2512a+1) или (1+2512a+a2) Степень многочлена равна 2. Страница № 8.4:
Вопрос 1:
Ответ:
Стр.
№ 8,4: Вопрос 2:
Ответ:
Страница № 8.4:
Вопрос 3:
Ответ:
Номер страницы 8.4:
Вопрос 4:
Ответ:
Страница № 8.4:
Вопрос 5:
Ответ:
Страница № 8.4:
Question 6:
Ответ:
Номер страницы 8.4:
Вопрос 7:
16m3y24m2y Ответ:
Страница № 8.4:
Вопрос 8:
32m2n3p24mnp Ответ:
Страница № 8.6:
Вопрос 1:
Ответ:
Page № 8.6:
Вопрос 2:
Ответ:
Страница № 8.6:
Вопрос 3:
