70 человек знают хотя бы один из трех языков причем 10 человек: 70 человек знают хотя бы один из трех языков, при чем 10 человек знают только…

UML_4822 дм практикум — Стр 3

3)A = {1, 2, 3, 4}, B = {3, 4, 5, 6, 7, 8, 9}, C = { };

4)A = , B = {1, 3, 4, 5, 6, 7, 0}, C = {7, 9, 0};

5)A = {1, c, 3, d}, B = {3, a, 5, d, 7, 0, 9}, C = {a, 9, d};

6)A = {a, 2, b, 4}, B = , C = {e, 9, 2}.

Решение. Поскольку задания 1) – 6) аналогичны, то приведем реше-

ние 1) Р(А) = {{1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}, {1, 2, 3}, {1, 2, 4}, {1, 3, 4}, {2, 3, 4}, {1, 2, 3, 4}, },

А\В = {1, 2}; А С = {1, 2, 3, 4, 7, 9, 10}, СВС = {3, 4, 5, 6, 8}.

При решении 2) – 6) следует понимать разницу между и { }, первое из которых – пустое множество, а второе одноэлементное множество.

1.4.Тождества и основные свойства операций над множествами

Спомощью операций объединения, пересечения и дополнения из множеств можно составить алгебраические различные выражения.

Обозначим через Q(A, B, C) некоторое алгебраическое выражение, составленное из множеств A, B, C и представляющее некоторое множество.

Пусть N(A, B, C) — другое алгебраическое выражение, составленное из тех же множеств. Если оба выражения представляют одно и то же множество, то их можно приравнять друг другу, получая алгебраическое тождество вида

Q(A, B, C) = N(A, B, C).

Далее приведем основные свойства операций над множествами.

а) A	B B A;				б) A	B B A;				(1.9)
а) A	B	C A	B	C ;	б) A	B	C A	B	C ;	(1.10)
а) A	B	C A	B	A	C ; б) A	B	C A	B	A	C . (1.11)

Тождества (1.9, а – 1.11, а) выражают соответственно коммутативный, ассоциативный и дистрибутивный законы для объединения множества, а тождества (1.9, б – 1.11, б) – те же законы для пересечения мно-

жеств.

а) A

A;

б) A

U A;

(1.12)

а) A

б) A

(1. 13)

A

U ;

A

;

а) A

U U ;

б) A

;

(1.14)

а)

U ;

б) U

.

(1.15)

Соотношения (1.12, а – 1.15, а) определяют свойства пустого множества и универсума U относительно объединения, а соотношения (1.12, б

– 1.15, б) – относительно пересечения. Из симметрии этих формул относительно А и A следует не только то, что A является дополнением А, но и что А является дополнением A .

С помощью операции дополнения можно в удобном виде представить разность множеств

72-76.

Задачи на нахождение элементов множеств

72-76. Задачи на нахождение элементов множеств

Это надо знать

Круги Эйлера – это геометрическая схема, которая помогает находить и делать более наглядными логические связи. А также помогает изобразить отношения между каким-либо множеством и его частью.

Автор метода — ученый Леонард Эйлер (1707-1783). Он говорил о названных его именем схемах: «круги подходят для того, чтобы облегчить наши размышления». 

Задача про любимые мультфильмы

Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах. Оказалось, что большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок», шестерым — «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма.

У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка Боб Квадратные Штаны».

Решение:

Всего в классе — 38 учеников — большой круг. Так как по условиям задачи у нас даны три множества, чертим три круга. А так как по ответам ребят выходит, что множества пересекаются друг с другом, чертеж будет выглядеть так:

Укажем на чертеже все числа, которые даны по условию, причем, мультфильмы «Волк и теленок» и «Губка  Боб Квадратные Штаны» любят: 5 — 3 = 2 ученика (пятеро из которых назвали в анкете два мультфильма).

1) 13 — (2 + 3 + 1) = 7 (уч.) — любят только мультфильм «Волк и теленок»

2) 21 — (6 + 3 + 1) = 11 (уч.) — любят только мультфильм «Белоснежка и семь гномов»

3) 38 — (7  +11 + 3 + 1 + 2 + 6) = 8 (уч.) — любят только мультфильм «Губка Боб Квадратные Штаны»

4) 8 + 2 + 1 + 6 = 17 (уч.) — любят мультфильм «Губка Боб Квадратные Штаны».

Ответ: 17 учеников.

Зимние каникулы

В классе 24 ученика. Все они хорошо провели зимние каникулы.10 человек катались на лыжах, 16 ездили на каток, а 12 — лепили снеговиков. Сколько учеников смогли покататься и на лыжах, и на коньках, и слепить снеговика?

Решение:

Пусть х — количество учеников, которые  смогли покататься и на лыжах, и на коньках, и слепить снеговика.

Составим и решим уравнение:

(12 — х) + (16 — х) + (10 — х) + х = 24;

38 — 2х = 24;

2х = 38 — 24;

2х = 14;

х = 14 : 2;

х = 7 (уч.)

Ответ: 7 учеников.

---

Принцип Дирихле

При решении многих задач используется принцип Дирихле. Принцип назван по имени его автора немецкого математика Петера Густава Дирихле. Принцип устанавливает связь между объектами («кроликами») и контейнерами («клетками»).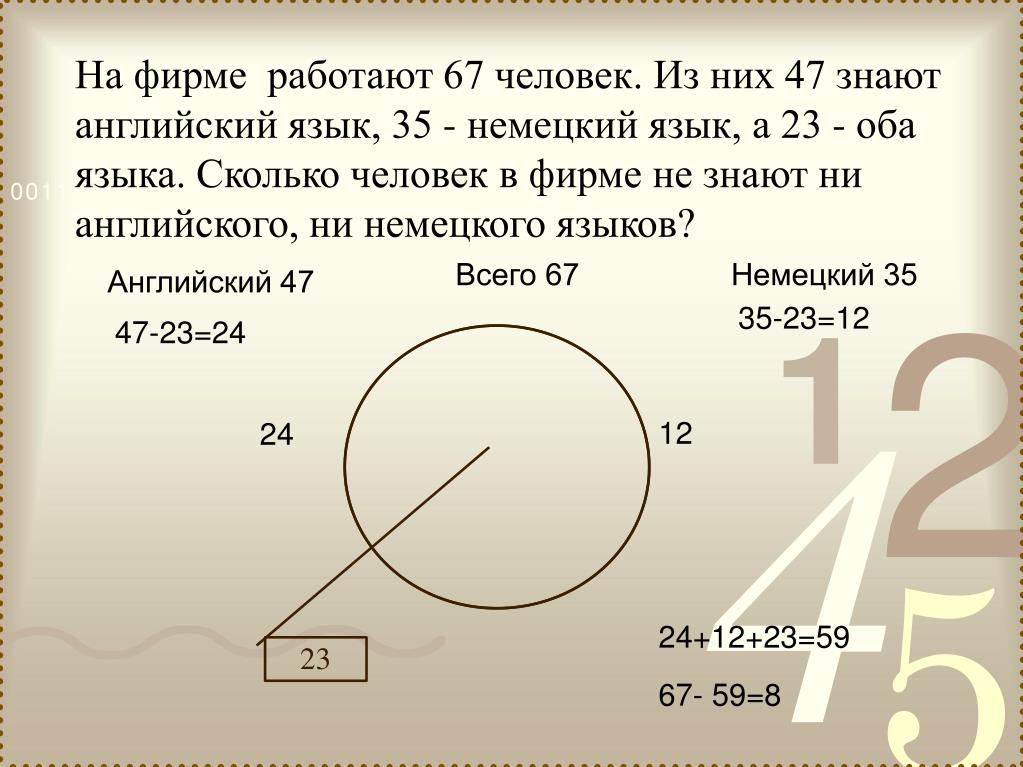

Принцип Дирихле — это положение, утверждающее, что если по N ящикам разложить предметы, число которых больше N, то найдется ящик, в котором находится больше одного предмета.

Слова «ящик» и «предметы» следует понимать в обобщенном смысле.

Пример:

Имеется 4 кролика и 3 клетки. Найдется хотя бы одна клетка, в которой будет не менее одного кролика.

Доказательство:
Допустим, что не существует клеток, где более одного кролика. Тогда в 3-х клетках окажется не более трех кроликов, а их — 4. Получили противоречие.

Обобщенный принцип Дирихле — это положение, утверждающее, что если по N ящикам разложить предметы, число которых больше N * k (k — натуральное число), то найдется ящик, в котором находится больше k предметов.

Пример:

Имеется 10 кроликов и 3 клетки. Найдется хотя бы одна клетка, в которой будет не менее 4 кроликов.

Доказательство:
Допустим, что не существует клеток, где более 3 кроликов.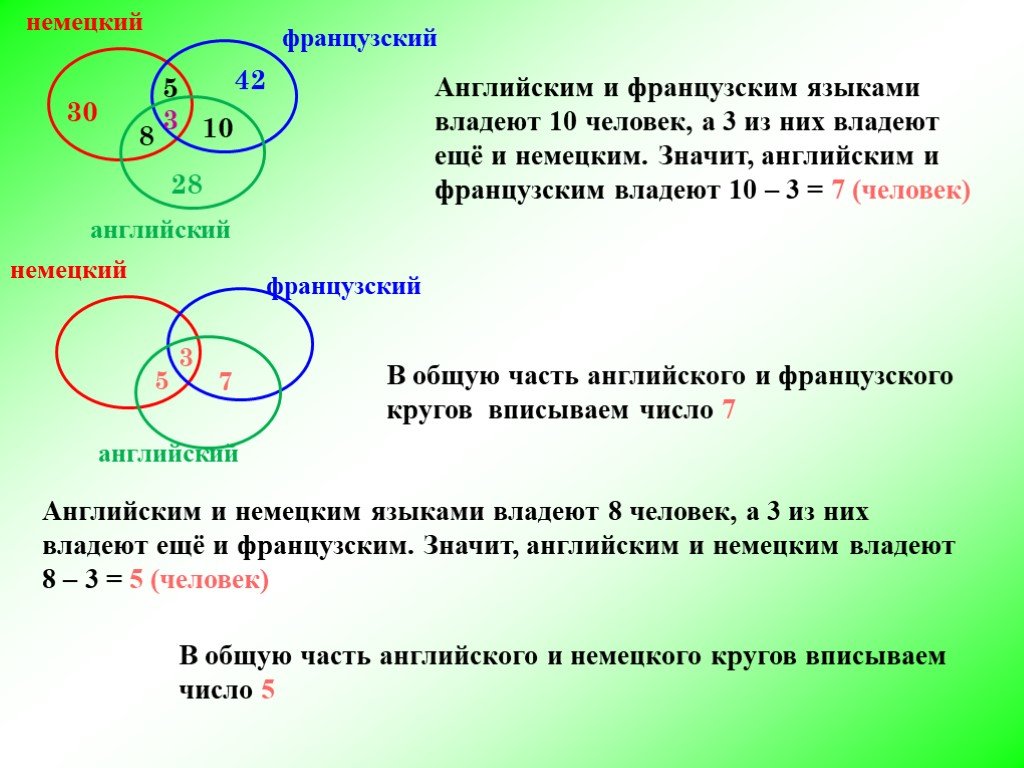 Тогда в 3-х клетках окажется не более 3*3 = 9  кроликов, а их — 10. Получили противоречие.

Пример:

В школе 30 классов и 1000 учащихся. Доказать, что есть класс, в котором не менее 34 учеников.

Доказательство:
Допустим, в каждом классе учится не более 33  учащихся, тогда 33 * 30= 990 учащийся учились бы в школе. Противоречие, т.к. учащихся 1000, следовательно есть классы в которых может быть не менее 34 учащихся.

---

Табличный метод решения логических задач

В финале турнира по шахматам встретились представители шести воинских званий: майор, капитан, лейтенант, старшина, сержант и ефрейтор, причем разных специальностей: летчик, танкист, артиллерист, минометчик, сапер и связист. Определите специальность и звание каждого из шахматистов по следующим данным:

1) в первом туре лейтенант выиграл у летчика, майор — у танкиста, а сержант — у минометчика;

2) во втором туре капитан выиграл у танкиста;

3) в третьем и четвертом турах минометчик из-за болезни не участвовал в турнире, поэтому свободными от игры оказались капитан и ефрейтор;

4) в четвертом туре майор выиграл у связиста;

5) победителями турнира оказались лейтенант и майор, а хуже всех выступил сапер.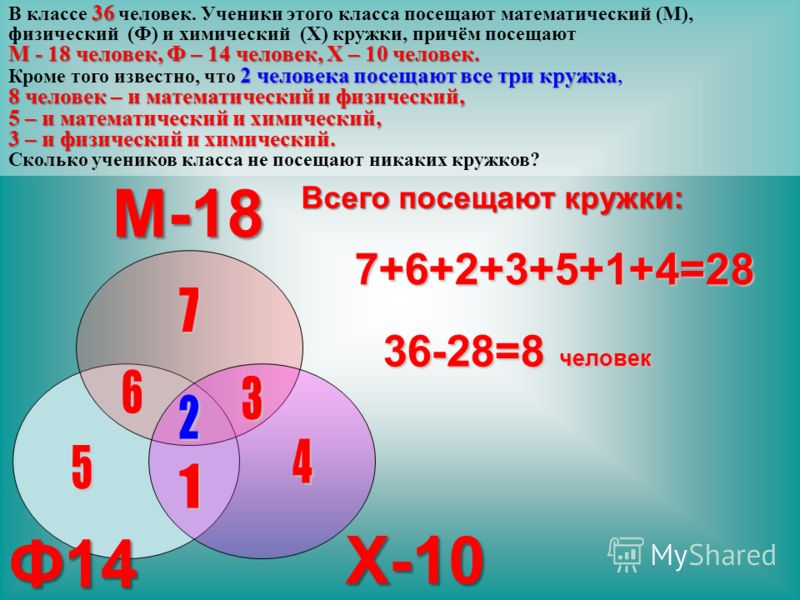

Для удобства решения составим прямоугольную таблицу, в которой по вертикали запишем воинские звания шахматистов, а по горизонтали – их специальности.

Ставим «+», если есть соответствие, если  признака нет, то ставим «-«. По смыслу задачи в каждой строке и в каждом столбце должен быть плюс и только один, так как  каждую специальность имеет только один из шахматистов, и каждое воинское звание имеет только один из шахматистов, так как всего шесть различных воинских званий и шесть разных специальностей.  

	Летчик	Танкист	Артиллерист	Минометчик		Связист
Капитан
Лейтенант
Старшина
Сержант
Ефрейтор

Ответ: летчик – капитан, сапер – сержант, связист – лейтенант, майор – артиллерист.

Видеоурок

Домашнее задание

К уроку 72 (на 20.12)

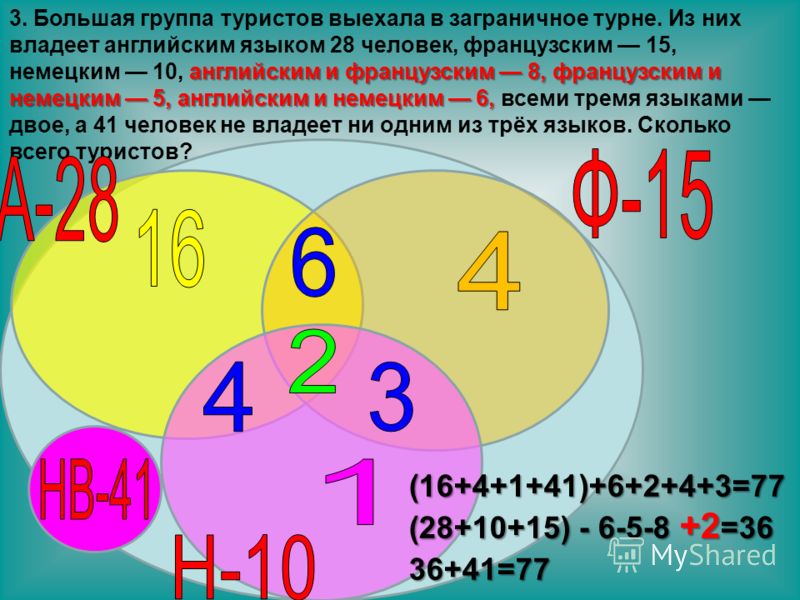
1. В школе с углубленным изучением иностранных языков провели опрос среди 100 учащихся. Ученикам задали вопрос: «Какие иностранные языки вы изучаете?». Выяснилось, что 48 учеников изучают английский, 26 — французский, 28 — немецкий. 8 школьников изучают английский и немецкий, 8 — английский и французский, 13 — французский и немецкий. 24 школьника не изучают ни английский, ни французский, ни немецкий. Сколько школьников, прошедших опрос, изучают одновременно три языка: английский, французский и немецкий?

2. Ребята посещают три кружка: математики, физики и химии. Решено было организовать кружок юных техников и пригласить тех ребят, которые не занимаются ни в одном из трех перечисленных. Сколько таких ребят, если всего в классе 36 человек, занимаются математикой- 18, физикой – 14, химией – 10.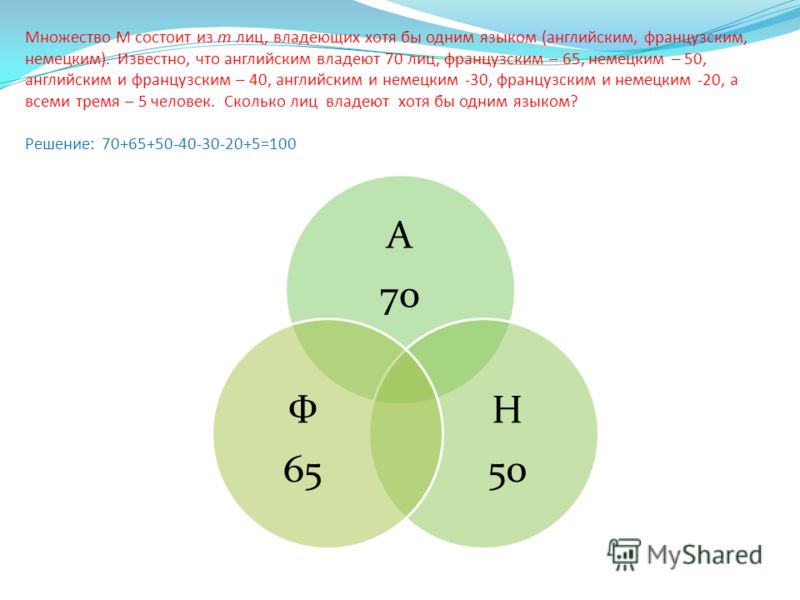 2 посещают все три кружка, 8 – математику и физику, 5 – математику и химию, 3 – химию и физику.

---

К уроку 73 (на 21.12)

1. Часть жителей нашего дома выписывают только газету «Комсомольская правда», часть – только газету «Известия», а часть – и ту, и другую газету. Сколько процентов жителей дома выписывают обе газеты, если на газету «Комсомольская правда» из них подписаны 85%, а на «Известия» – 75%?

2. В классе 30 человек. 20 из них каждый день пользуются метро, 15 – автобусом, 23 – троллейбусом, 10 – и метро, и троллейбусом, 12 – и метро, и автобусом, 9 – и троллейбусом, и автобусом. Сколько человек ежедневно пользуется всеми тремя видами транспорта?

---

К уроку 74 (на 22.12)

1. В ящике лежат носки 4 цветов. Какое наименьшее количество носков надо вытащить, чтобы из них можно было составить одну пару?

2. В классе 34 ученика. Докажите, что среди них обязательно найдутся по меньшей мере двое, у которых фамилии начинаются с одной и той же буквы.

3. 15 мальчиков собрали 100 орехов. Докажите, что какие-то два из них собрали одинаковое число орехов.

4. В классе 37 человек. Найдется ли такой месяц в году, в котором отмечают свой день рождения не менее, чем 4 ученика этого класса?

---

К уроку 75 (на 23.12)

1. Три друга после школы едут домой на различном транспорте: автобусе, троллейбусе, трамвае. Однажды после уроков Алеша пошел проводить своего друга до остановки автобуса. Когда мимо них проходил троллейбус, третий друг крикнул из окна: «Боря, ты забыл в школе тетрадку». Кто на чем ездит домой?

2. Клоуны Бам, Бим, Бом вышли на арену в красной, синей и зеленой рубашках. Их туфли тоже были этих трех цветов. Туфли и рубашка Бима были одного цвета. На Боме не было ничего красного. Туфли Бама были синие, а рубашка нет. Каких цветов были туфли и рубашка у Бома и Бима?

Шаблоны для решения

---

   

Подписаться на: Сообщения (Atom)

включение исключение — Вероятность того, что учащийся говорит на заданном языке

$\begingroup$

Вопрос

---

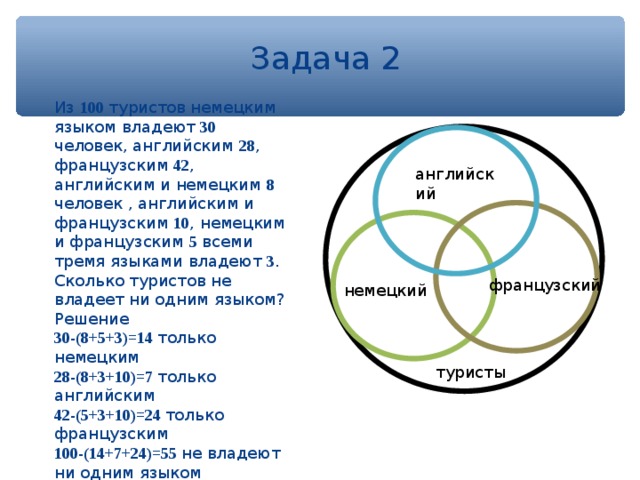
Каждый ученик в классе говорит хотя бы на одном из три языка. Для каждого языка вероятность того, что случайный учащийся говорит на этом конкретном языке, равна $\frac{3}{4}$, а для каждой пары языков вероятность того, что случайный учащийся говорит на этой паре, равна $\frac{1}{2 }$. Какова вероятность того, что студент говорит на всех трех языках?

Моя попытка решения:

Пусть $A$ будет событием, когда учащийся говорит на одном языке.

Пусть $B$ будет событием, когда учащийся говорит на двух языках.

Пусть $C$ будет событием, когда учащийся говорит на трех языках.

Тогда $A \subseteq B \subseteq C$.

Мы можем найти количество студентов, говорящих только на одном языке:

Большое спасибо пользователю @N. Ф. Тауссиг

Теперь мы видим, что by в принципе включения-исключения

$$\mathbb{P}(A\cup B \cup C)=\mathbb{P}(A)+\mathbb{P}(B)+\mathbb{P}(C)-\mathbb{P }(A \cap B)-\mathbb{P}(A \cap C)-\mathbb{P}(B \cap C)+\mathbb{P}(A \cap B \cap C) $$

$$1=3*(\frac{3}{4}-\frac{1}{4})+\mathbb{P}(A \cap B \cap C) $$ $$\implies \mathbb{P}(A\cap B \cap C)=\frac{1}{4}. $$

Спасибо за ваше время.

• вероятность
• включение-исключение

$\endgroup$

$\begingroup$

Давайте по-другому определим наши события.

Пусть это будут языки $L_1$, $L_2$ и $L_3$. Пусть $\Pr(L_k)$ — вероятность того, что студент говорит на языке $k$, $1 \leq k \leq 3$. Нам дана следующая информация:

1. Каждый ученик говорит хотя бы на одном языке, поэтому $\Pr(L_1 \cup L_2 \cup L_3) = 1$.
2. Для каждого языка вероятность того, что учащийся говорит на этом языке, равна $3/4$, поэтому $\Pr(L_1) = \Pr(L_2) = \Pr(L_3) = 3/4$.
3. Для каждой пары языков вероятность того, что учащийся говорит на этой паре языков, равна $1/2$, поэтому $\Pr(L_1 \cap L_2) = \Pr(L_1 \cap L_3) = \Pr(L_2 \cap L_3) = 1/2$.

По принципу включения-исключения, $$\Pr(L_1 \чашка L_2 \чашка L_3) = \Pr(L_1) + \Pr(L_2) + \Pr(L_3) — \Pr(L_1 \cap L_2) — \Pr(L_1 \cap L_3) — \Pr(L_2 \cap L_3) + \Pr(L_1 \cap L_2 \cap L_3)$$ Подставьте указанные выше значения для $\Pr(L_1 \cup L_2 \cup L_3)$, $Pr(L_1)$, $\Pr(L_2)$, $\Pr(L_3)$, $\Pr(L_1 \cap L_2)$, $\Pr(L_1 \cap L_3)$ и $\Pr(L_2 \cap L_3)$, чтобы определить $\Pr(L_1 \cap L_2 \cap L_3)$, вероятность того, что учащийся говорит на всех трех языках. языки.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

комбинаторика — комбинаторная задача по изучению языков

спросил 4 года 5 месяцев назад

Изменено 4 года, 5 месяцев назад

Просмотрено 44 раза

$\begingroup$

Проблема:

1. $95$% студентов изучают иностранные языки: английский, немецкий и французский
2. $75$% изучение английского языка
3. $70$% Французский или немецкий
4. $3$% студентов одновременно изучают три языка
5. $36$% студентов изучают английский и немецкий языки
6. $10$% процентов студентов изучают французский и немецкий языки
7. Никто не изучает только немецкий

Сколько человек в процентах изучают не менее двух языков?

Мне нужно решить эту задачу с помощью теории множеств. но я больше про общую логику, переход к теории множеств не должен быть сложным.

Итак, о чем я подумал:

$36+10 = 46$% эти люди изучают как минимум два языка, согласно описанию задачи нам нужно два или более.

$36+10+3 = 49$ % — два и более языка.

$75 — 49 = 26$% только на английском языке $70 — 49 = 21$% либо французский, либо немецкий

Но я не уверен, что моя логика вообще верна, а также не знаю, как здесь поступить с немецким языком.

• комбинаторика
• дискретная математика

$\endgroup$

$\begingroup$

Вам может помочь диаграмма Венна. Предположим, что всего имеется 100$ студентов. Установить переменные $7$:

• $a_1$ люди изучают только английский

• $a_2$ человек изучают только немецкий язык (при $a_2=0$)

• $a_3$ люди изучают только французский язык

• $a_4$ люди изучают только английский и немецкий

• $a_5$ люди изучают только немецкий и французский

• $a_6$ люди изучают только французский и английский

• $a_7$ человек изучают их все (учитывая $a_7=3$)

Задача требовала найти $a_4+a_5+a_6+a_7$ (то есть два или более языков).

Сначала я скажу кое-что о вашей логике. Вы сказали, что «по крайней мере два языка» — это $36\%+10\%=46\%$, это неверно, потому что на диаграмме выше этот метод эквивалентен $(a_4+a_7)+(a_5+a_7)$ , так как $a_7$ считается дважды, а не $a_6$.

$36\%+10\%+3\%=49\%$ еще более неправильно, потому что теперь $a_7$ считается трижды.

Вы также сказали, что «только английский» составляет $75\%-49\%=26\%$, я бы сказал, что это эквивалентно $(a_1+a_4+a_6+a_7)-(a_4+a_7+a_5+a_7+ a_7)\ne a_1$, это тоже не может быть правдой.

Для $7$ вещей, перечисленных в задании соответственно, имеем

${\begin{cases}a_1+a_2+a_3+a_4+a_5+a_6+a_7=95\\a_1+a_4+a_6+a_7=75\ \a_2+a_3+a_4+a_5+a_6+a_7=70\\a_7=3\\a_4+a_7=36\\a_5+a_7=10\\a_2=0\end{case}}$

Из первого и третьего уравнений получаем $a_1=25$.

Из четвертого, пятого, шестого уравнений имеем $a_4=33$; $a_5=7$.

От $a_1=25$; $a_4=33$; второе и четвертое уравнения, имеем $a_6=14$.

Из $a_1=25;a_2=0;a_4=33;a_5=7;a_6=14;a_7=13$ и первого и третьего уравнений получаем $a_3=3$.