Число \(n\) при этом называют показателем корня.
Если \(n=2\), то перед вами корень 2-й степени или обычный квадратный корень.
Если \(n=3\), то корень 3-й степени и т.д.
Операция извлечения корня n-й степени является обратной к операции возведения в n-ю степень.
Пример 1 $$ \sqrt[3]{27}=3 $$
Кубический корень из числа 27 равняется 3. Действительно, если число 3 возвести в 3-ю степень, то мы получим 27.
Пример 2 $$ \sqrt[4]{16}=2 $$
Корень 4-й степени из 16-и равен 2. Двойка в 4-й степени равна 16.
Пример 3 $$ \sqrt[3]{0}=0 $$
Если извлечь корень n-й степени из 0, всегда будет 0.
Пример 4 $$ \sqrt[3]{19}= ? $$
Мы не можем в уме подобрать такое число, которое при возведении в 3-ю степень даст 19. Если посчитать на калькуляторе, то получим \(2,668…\) – иррациональное число с бесконечным количеством знаков после запятой.
Обычно, в математике, когда у вас получается иррациональное число, корень не считают и оставляют так как есть \(\sqrt[3]{19}\).
Что же делать, если под рукой нет калькулятора, а нужно оценить, чему равен такой корень. В этом случае нужно подобрать справа и слева такие ближайшие числа, корень из которых посчитать можно:
$$ \sqrt[3]{8} \le \sqrt[3]{19} \le \sqrt[3]{27} $$ $$ 2 \le \sqrt[3]{19} \le 3 $$Получается, что наш корень лежит между числами 2 и 3.
Корень четной и нечетной степени
Надо четко различать правила работы четными и нечетными степенями. Дело в том, что корень четной степени можно взять только из положительного числа. Из отрицательных чисел корень четной степени не существует.
Корень нечетной степени можно посчитать из любых действительных чисел. Иногда в школьной программе встречаются задания, в которых требуется определить имеет ли смысл выражение:
Пример 5 $$ \sqrt[3]{-27}=-3 $$
Данное выражение имеет смысл, так как корень нечетной степени можно посчитать из любого числа, даже отрицательного.
Пример 6 $$ \sqrt[4]{-27} $$
Так как корень четной степени, а под корнем стоит отрицательное число, то выражение не имеет смысла.
k} $$
цена лечения 3-х канального зуба от 9 000 ₽ в Smile-Estet
Воспаление пульпы — мягкой соединительной ткани зуба, где расположены нервы и сосуды, достаточно болезненно, а несвоевременное лечение пульпита часто приводит к потере зуба. Поэтому при малейшем дискомфорте необходимо обратиться в стоматологическую клинику и не заниматься самолечением.
Что такое пульпа и почему она воспаляется
Под твердой оболочкой зуба расположена мягкая ткань — пульпа, через которую происходит его кровоснабжение. Пульпа содержит элементы, отвечающие за регенерацию зубных тканей, насыщение их полезными веществами.
Чтобы этого не допустить, нужно своевременно проводить лечение пульпита, цена затягивания с походом в стоматологию слишком высока — это потеря зуба.
Как распознать пульпит
Патология характерна для жевательных зубов. На первой стадии зуб остро реагирует на холодное/горячее. На втором этапе возникают приступы острой боли, часто без всякой причины. Неприятные ощущения могут затрагивать всю челюсть с одной стороны, поэтому иногда трудно понять, какой именно зуб болит. Визуально можно отличить его по темной кариозной полости, кровоточащей десне, посеревшей эмали.
Преимущества лечения зубов в стоматологии Smile EstetНаши врачи-стоматологи сделают ваше пребывание в стоматологическом кресле комфортным
- Высококвалифицированные специалисты
- Современное оборудование
- Семейная система
скидок - Рассрочка на лечение зубов
Записаться на консультацию
Или позвоните по телефону
+7 (495) 177-86-32Врачи, оказывающие данную услугу
Как проводится лечение пульпита и сколько стоит услуга
Различают острую и хроническую формы заболевания и 12 его видов (фиброзный, гангренозный, очаговый, гнойный, трехканальный и др.). В зависимости от данных диагностики врачи выбирает оптимальный протокол лечения.
В большинстве случаев необходимо:
- очистить зубы от твердых отложений (камня) и бактериального налета;
- удалить кариозные поражения;
- вскрыть пульпу;
- очистить корневые каналы от инфицированных тканей;
- провести тщательную антибактериальную обработку каналов;
- герметизировать их стоматологической гуттаперчей;
- восстановить зуб пломбой из современных светоотверждаемых материалов.
Наши врачи при лечении пульпита используют мощную увеличительную технику, позволяющую с высокой точностью удалить все зараженные ткани и максимально качественно очистить корневые каналы. На цену лечения это не влияет. Для каждого пациента индивидуально подбирается местная анестезия, поэтому манипуляции проходят комфортно и без боли.
ВАЖНО! Лечение пульпита проводится по приемлемой цене даже в тех случаях, когда в других клиниках Москвы принимают решение об удалении зуба.
Сколько стоит лечение пульпита?
В стандартных случаях в стоимость лечения пульпита зуба в клинике Smile Estet входят все указанные выше манипуляции. Однако клинический случай может быть осложнен воспалением десны, кистой в области верхушки корня. Могут понадобиться услуги хирурга, что несколько увеличит цену лечения пульпита. Запишитесь на прием и уточните, сколько стоит восстановление зуба в вашем случае.
| Услуга | Цена |
|---|---|
| Лечение периодонтита | |
| Лечение периодонтита 1 канального зуба | 9 500 Р |
| Лечение периодонтита 2 канального зуба | 12 000 Р |
| Лечение пульпита | |
| Лечение пульпита 1 канального зуба | от 6 000 Р Акция до 31 июля |
| Лечение пульпита 2 канального зуба | Акция до 31 июля |
| Лечение пульпита 3 и более каналов | 10 000 Р Акция до 31 июля |
| Лечение кариеса | |
| Лечение кариеса начальная стадия | от 3 000 Р |
| Лечение кариеса средней и высокой сложности | от 4500 Р |
| Клиновидный дефект лечение пришеечного кариеса | от 5 000 Р |
| Лечение зубов без сверления | от 5 000 Р |
| Лечение зубов под седацией (за 1 час) | 15 000 Р |
| Консультация | |
| Прием и осмотр врача стоматолога-терапевта | 1 000 Р |
| Прием врача стоматолога-хирурга | 1 000 Р |
| Прием врача стоматолога-ортопеда | 1 000 Р |
Интересует точная стоимость лечение пульпита?
Оставьте заявку и мы перезвоним!
Интересные материалы
Ответы на часто задаваемые вопросы
Несколько дней болит 6 зуб коренной.
Все дни на обезболивающих. Может ли это быть причиной отечности глаза ведь это шестерка снизу
Артём (20 лет)
25.04.2019
Отвечает: ,
Здравствуйте! При острой боли необходимо показаться врачу стоматологу. К сожалению, далеко не все принимают правильное решение о том, что им следует делать при появлении зубной боли: кто-то ждет до последнего и терпит, кто-то глотает таблетки в надежде, что все само собой пройдет. Действительно, зубная боль иногда может отдавать в голову, провоцируя тем самым сильную мигрень.Обычно такие боли носят кратковременный «стреляющий» характер. Но вряд ли это может быть связано с отеком глаза. Необходимо срочно провести осмотр и диагностику и выяснить причину боли и отека и метод устранения.
Задайте свой вопрос
Как ввести символы квадратного корня, кубического корня и четвертого корня? »WebNots
Легко сказать, что квадратный корень из 9 равен 3. Однако набрать это в удобочитаемом формате непросто. Вы можете использовать редактор формул в Microsoft Office или специальные приложения, такие как LaTex. К сожалению, использование редактора формул в Word или Excel — сложная задача, так как содержимое не будет совпадать с другим текстовым содержимым вашего документа. Кроме того, для использования несколько раз вам не понадобится редактор формул. Если вы хотите ввести символы квадратного корня, кубического корня и четвертого корня в свои документы, тогда простой способ — использовать сочетания клавиш alt-кода.
Сочетание клавиш Alt-кода для символа квадратного корня
Символ квадратного корня или главного квадратного корня √ не имеет двойки в корне.
Когда2 =B, тогда A — квадратный корень из B, обозначенный как √B = A. Например, √4 = 2. Вот ярлыки для квадратного корня на компьютерах Windows и Mac.
| Название символа | Квадратный корень |
| категория | Математический символ |
| Альтернативный код (Windows) | Альт 8730 |
| Alt + X (слово) | 221A Альтернативный X |
| Код опции (Mac) | Вариант 221А |
| Имя объекта HTML | & Радич; |
| HTML Entity Decimal | & # 8730; |
| HTML-объект шестнадцатеричный | & # X221A; |
| Значение CSS | 221А; |
| JS Value | u221A |
| Десятичный | 8730 |
| шестнадцатеричный | 221А |
| Точка Юникода | U + 221А |
Сочетание клавиш Alt-кода для символа корня куба
Когда3 = B, то A — кубический корень B, обозначенный как ∛B = A.
Например, ∛9 = 3.
| Название символа | Кубический корень |
| категория | Математический символ |
| Альтернативный код (Windows) | Альт 8731 |
| Alt + X (слово) | 221B Alt X |
| Код опции (Mac) | Вариант 221B |
| HTML Entity Decimal | & # 8731; |
| HTML-объект шестнадцатеричный | & # X221B; |
| Значение CSS | 22; |
| JS Value | u221B |
| Десятичный | 8731 |
| шестнадцатеричный | 221В |
| Точка Юникода | U + 221B |
Ярлыки альтернативного кода для четвертого корневого символа
Когда4 = B, то A — корень четвертой степени из B, обозначенный как B = A. Например, ∜16 = 4.
| Название символа | Четвертый корень |
| категория | Математический символ |
| Альтернативный код (Windows) | Альт 8732 |
| Alt + X (слово) | 221C Alt X |
| Код опции (Mac) | Вариант 221C |
| HTML Entity Decimal | & # 8732; |
| HTML-объект шестнадцатеричный | & # X221C; |
| Значение CSS | 221с; |
| JS Value | u221C |
| Десятичный | 8732 |
| шестнадцатеричный | 221C |
| Точка Юникода | U + 221C |
Ввод квадратного корня, кубического корня и четвертого корня в Windows
Используйте один из методов в документах на базе Windows, таких как Word, PowerPoint, Excel и Outlook.
- Нажмите клавишу alt и введите 8730 с цифровой клавиатуры, чтобы получить символ квадратного корня √.
- Только в документах Microsoft Word введите 221B и нажмите клавиши alt и x, чтобы сделать символ корня куба ∛.
- Нажмите «Win +;» клавиши, чтобы открыть клавиатуру эмодзи Windows. Щелкните значок «Символы», а затем — «Математические» символы. Найдите и вставьте квадратный корень и другие символы корня высокого порядка.
- Когда вы находитесь в приложении Office, таком как Word, выберите «Вставить> Символы» и вставьте корневые символы.
- Включите функцию автозамены математическими символами для ввода с помощью сочетаний клавиш, как показано ниже:
| SQRT | √ | Квадратный корень |
| cbrt | ∛ | кубический корень |
| qdrt | ∜ | Четвертый корень |
Вставка в документы Mac
- На MacBook измените раскладку клавиатуры на Unicode Hex Input. Удерживая клавишу option или alt, введите 221C, чтобы получить символ корня четвертой степени ∜.
- Откройте средство просмотра символов, нажав «Control + Command + Space». Либо перейдите в «Математические символы», либо найдите «корень» с помощью поля поиска. Найдите символы квадрата, куба или корня четвертой степени для вставки на Pages, Keynote и Numbers.
Удерживая клавишу option или alt, введите 221C, чтобы получить символ корня четвертой степени ∜.Отображение символов
Как видите, у корневых символов не будет верхней горизонтальной линии при наборе с помощью ярлыков. Однако на Mac вы можете выбрать варианты шрифта из средства просмотра символов, которое включает верхнюю панель в корневых символах.
Другие имена для корневых символов
В математике квадратный корень и другие символы корня имеют следующие имена.
- Радикальный символ
- Радикальный знак
- Корневой символ
- основание системы счисления
- Глухой
Арабский куб и символы четвертого корня
В системе Unicode есть еще два корневых символа на арабском языке, перечисленные ниже.
| Условное обозначение | ؆ | ؇ |
| название | Арабско-индийский кубический корень | Арабско-индийский корень четвертой степени |
| Windows | Alt + 1542 | Alt + 1543 |
| макинтош | Option + 0606 | Option + 0607 |
Просмотры: 29
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Wella Koleston Rich Natural 9/3 Очень светлый блонд золотистый Кленовый сироп 60 мл.
Wella Koleston Perfect Rich Natural 9/3 Очень светлый блонд золотистый Кленовый сироп 60 мл.Название оттенка 9/3 в палитре с прядями (Имиджевое): Кленовый сироп
Название оттенка 9/3 на тюбике (Техническое): Очень светлый блонд золотистый
Холодные оттенки Wella Koleston Perfect Rich Natural: 10/1, 9/1, 8/1, 7/1, 6/1, 5/1, 10/16, 9/16, 9/17, 7/17, 7/18, 6/2, 5/2, 10/38, 9/38, 8/38, 7/38, 10/8, 9/8, 2/8. 9/81, 10/86, 10/95, 10/96, 9/96 , 8/96, 10/97, 9/97, 8/97, и 6/97
Теплые оттенки Wella Koleston Perfect Rich Natural: 10/3, 9/3, 8/3, 7/3, 6/3, 10/31, 9/31, 7/31, 7/37 и 5/37
Изысканный, элегантный и утонченный цвет волос. Переливающиеся оттенки с теплыми / холодными акцентами. Получите изысканный, элегантный и естественный цвет волос для создания потрясающего образа с профессиональной краской для волос Koleston Perfect Rich Naturals (Насыщенные Натуральные оттенки.)
В значительной степени уменьшает повреждение волос, окрашивание за окрашиванием* (нейтрализует частицы металлов, что снижает образование свободных радикалов, обеспечивая контроль за формированием цвета)
* — По сравнению с предыдущей версией Koleston Perfect.
Данная информация действительна для нового Koleston Perfect с технологией Pure Balance
Откройте для себя широкий спектр гармоничных оттенков как с теплыми, так и холодными акцентами, разработанными Wella Professionals. Благодаря особой комбинации компонентов, эта перманентная крем-краска для волос обеспечивает чувственный и притягательный стойкий цвет, полностью закрашивая обесцвеченные волосы или седину.
Осветление на 3 уровня или выше и закрашивание седых волос на 100%
Koleston Perfect стойкая краска с технологией ME+ , которую выбирают в более чем 100 000 салонах красоты по всему миру.
Равномерный чистый цвет с естественной глубиной и блеском.
Благодаря технологии МE+ вероятность возникновения аллергии на краску для волос снизилась до 60 раз*
*Для людей без аллергии на краску. Хотя риск возникновения аллергии снижается, остается риск возникновения аллергической реакции, которая может иметь тяжелые последствия. Всегда выполняйте тест на аллергию за 48 часов до любого окрашивания.
Следуйте инструкции. Не окрашивайте волосы, если у вашего клиента когда-либо уже наблюдалась аллергическая реакция на краску. ME+ представлена в оттенках следующих групп Koleston Perfect: Чистые Натуральные, Насыщенные Натуральные, Яркие Красные, Special Blondes и Глубокие Коричневые.
Для идеального результата мы рекомендуем сочетать Насыщенные Натуральные оттенки Koleston Perfect с Welloxon Perfect. Простая пропорция смешивания 1:1. Быстро нанесите красящую смесь, двигаясь от корней к концам волос.
Koleston Perfect всегда используется с Welloxon Perfect для получения идеального результата. Использование продукции со сбалансированным уровнем pH позволит дольше сохранять цвет и придаст волосам здоровый вид после окрашивания. После истечения времени выдержки сэмульгируйте краску теплой водой и вымойте волосы шампунем INVIGO Сolor Brilliance для окрашенных волос. Для стабилизации цвета используйте стабилизатор окраски INVIGO Color Post Treatment.
Только для профессионального использования.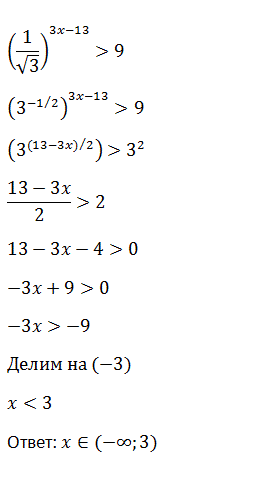
Этот косметический продукт безопасен для потребителей и других пользователей при условии правильного использования. Дополнительная информация о составе предоставляется поставщиком по запросу.
Глаза: избегайте попадания в глаза, при попадании немедленно промойте их водой. Попадание в глаза продукта может вызывать покраснение и жжение. Кожа: может вызывать раздражение на коже при склонности к аллергии.
Дыхание: может вызвать легкое временное раздражение дыхательных путей. Не вдыхать продукт и стараться избегать длительного контакта при его испарении. Проглатывание: продукт, используемый по назначению, не вызывает раздражения желудочно-кишечного тракта. Случайное проглатывание продукта может вызвать легкое раздражение желудочно-кишечного тракта, тошноту, рвоту и диарею.
Краску Wella Koleston Rich Natural 9/3 Очень светлый блонд золотистый Кленовый сироп 60 мл. могут искать различными вариантами написания
значений Уровня глубины тона и Направления тона.
Вот некоторые из возможных написаний:
- Краска Wella Koleston 9/3
- Краска Wella Koleston 9\3
- Краска Wella Koleston 9:3
- Краска Wella Koleston 9-3
- Краска Wella Koleston 9_3
- Краска Wella Koleston 9+3
- Краска Wella Koleston 9=3
- Краска Wella Koleston 9.3
- Краска Wella Koleston 9,3
- Краска Wella Koleston 9 и 3
Обзор формул — Excel
Если вы еще не Excel в Интернете, скоро вы увидите, что это не просто сетка для ввода чисел в столбцах или строках. Да, с помощью Excel в Интернете можно найти итоги для столбца или строки чисел, но вы также можете вычислять платежи по ипотеке, решать математические или инженерные задачи или находить лучшие сценарии в зависимости от переменных чисел, которые вы подключали.
Excel в Интернете делает это с помощью формул в ячейках. Формула выполняет вычисления или другие действия с данными на листе. Формула всегда начинается со знака равенства (=), за которым могут следовать числа, математические операторы (например, знак «плюс» или «минус») и функции, которые значительно расширяют возможности формулы.
Ниже приведен пример формулы, умножающей 2 на 3 и прибавляющей к результату 5, чтобы получить 11.
=2*3+5
Следующая формула использует функцию ПЛТ для вычисления платежа по ипотеке (1 073,64 долларов США) с 5% ставкой (5% разделить на 12 месяцев равняется ежемесячному проценту) на период в 30 лет (360 месяцев) с займом на сумму 200 000 долларов:
=ПЛТ(0,05/12;360;200000)
Ниже приведены примеры формул, которые можно использовать на листах.
-
=A1+A2+A3 Вычисляет сумму значений в ячейках A1, A2 и A3.
-
=КОРЕНЬ(A1) Использует функцию КОРЕНЬ для возврата значения квадратного корня числа в ячейке A1.
-
=СЕГОДНЯ() Возвращает текущую дату.
-
=ПРОПИСН(«привет») Преобразует текст «привет» в «ПРИВЕТ» с помощью функции ПРОПИСН.
-
=ЕСЛИ(A1>0) Анализирует ячейку A1 и проверяет, превышает ли значение в ней нуль.
Элементы формулы
Формула также может содержать один или несколько из таких элементов: функции, ссылки, операторы и константы.
(«крышка») применяется для возведения числа в степень, а оператор * («звездочка») — для умножения.
Использование констант в формулах
Константа представляет собой готовое (не вычисляемое) значение, которое всегда остается неизменным. Например, дата 09.10.2008, число 210 и текст «Прибыль за квартал» являются константами. выражение или его значение константами не являются. Если формула в ячейке содержит константы, но не ссылки на другие ячейки (например, имеет вид =30+70+110), значение в такой ячейке изменяется только после изменения формулы.
Использование операторов в формулах
Операторы определяют операции, которые необходимо выполнить над элементами формулы.
Вычисления выполняются в стандартном порядке (соответствующем основным правилам арифметики), однако его можно изменить с помощью скобок.
Типы операторов
Приложение Microsoft Excel поддерживает четыре типа операторов: арифметические, текстовые, операторы сравнения и операторы ссылок.
Арифметические операторы
Арифметические операторы служат для выполнения базовых арифметических операций, таких как сложение, вычитание, умножение, деление или объединение чисел. Результатом операций являются числа. Арифметические операторы приведены ниже.
Арифметический оператор | Значение | Пример |
|---|---|---|
|
+ (знак «плюс») |
Сложение |
3+3 |
|
– (знак «минус») |
Вычитание |
3–1 |
|
* (звездочка) |
Умножение |
3*3 |
|
/ (косая черта) |
Деление |
3/3 |
|
% (знак процента) |
Доля |
20% |
|
^ (крышка) |
Возведение в степень |
3^2 |
Операторы сравнения
Операторы сравнения используются для сравнения двух значений.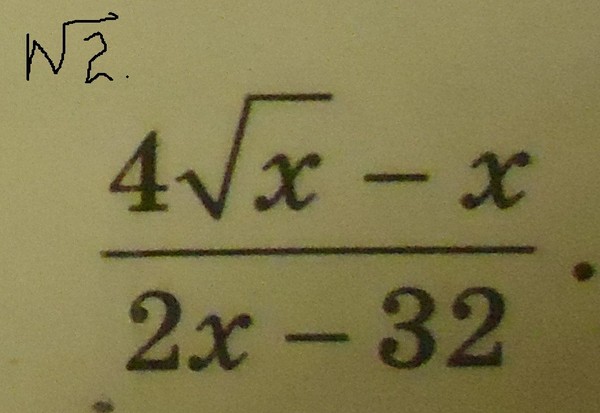
Результатом сравнения является логическое значение: ИСТИНА либо ЛОЖЬ.
Оператор сравнения | Значение | Пример |
|---|---|---|
|
= (знак равенства) |
Равно |
A1=B1 |
|
> (знак «больше») |
Больше |
A1>B1 |
|
< (знак «меньше») |
Меньше |
A1<B1 |
|
>= (знак «больше или равно») |
Больше или равно |
A1>=B1 |
|
<= (знак «меньше или равно») |
Меньше или равно |
A1<=B1 |
|
<> (знак «не равно») |
Не равно |
A1<>B1 |
Текстовый оператор конкатенации
Амперсанд (&) используется для объединения (соединения) одной или нескольких текстовых строк в одну.
Текстовый оператор | Значение | Пример |
|---|---|---|
|
& (амперсанд) |
Соединение или объединение последовательностей знаков в одну последовательность |
Выражение «Северный»&«ветер» дает результат «Северный ветер». |
Операторы ссылок
Для определения ссылок на диапазоны ячеек можно использовать операторы, указанные ниже.
Оператор ссылки | Значение | Пример |
|---|---|---|
|
: (двоеточие) |
Оператор диапазона, который образует одну ссылку на все ячейки, находящиеся между первой и последней ячейками диапазона, включая эти ячейки. |
B5:B15 |
|
; (точка с запятой) |
Оператор объединения. Объединяет несколько ссылок в одну ссылку. |
СУММ(B5:B15,D5:D15) |
|
(пробел) |
Оператор пересечения множеств, используется для ссылки на общие ячейки двух диапазонов. |
B7:D7 C6:C8 |
Порядок выполнения Excel в Интернете формулах
В некоторых случаях порядок вычисления может повлиять на возвращаемое формулой значение, поэтому для получения нужных результатов важно понимать стандартный порядок вычислений и знать, как можно его изменить.
Порядок вычислений
Формулы вычисляют значения в определенном порядке.
Формула всегда начинается со знака равно(=).Excel в Интернете интерпретирует знаки после знака равно как формулу. После знака равно вычисляются элементы (операнды), такие как константы или ссылки на ячейки. Они разделены операторами вычислений. Excel в Интернете вычисляет формулу слева направо в соответствии с определенным порядком для каждого оператора в формуле.
Приоритет операторов
Если в одной формуле несколько операторов, Excel в Интернете выполняет операции в том порядке, который показан в таблице ниже. Если формула содержит операторы с одинаковым приоритетом, например операторы деления и умножения, Excel в Интернете эти операторы оцениваются слева направо.
Оператор | Описание |
|---|---|
|
: (двоеточие) (один пробел) , (запятая) |
Операторы ссылок |
|
– |
Знак «минус» |
|
% |
Процент |
|
^ |
Возведение в степень |
|
* и / |
Умножение и деление |
|
+ и — |
Сложение и вычитание |
|
& |
Объединение двух текстовых строк в одну |
|
= |
Сравнение |
Использование круглых скобок
Чтобы изменить порядок вычисления формулы, заключите ее часть, которая должна быть выполнена первой, в скобки.
Например, следующая формула дает результат 11, так как Excel в Интернете умножение выполняется перед с добавлением. В этой формуле число 2 умножается на 3, а затем к результату прибавляется число 5.
=5+2*3
Если же изменить синтаксис с помощью скобок, Excel в Интернете сбавляет 5 и 2, а затем умножает результат на 3, чтобы получить 21.
=(5+2)*3
В следующем примере скобки, в которые заключена первая часть формулы, принудительно Excel в Интернете сначала вычислить ячейки B4+25, а затем разделить результат на сумму значений в ячейках D5, E5 и F5.
=(B4+25)/СУММ(D5:F5)
Использование функций и вложенных функций в формулах
Функции — это заранее определенные формулы, которые выполняют вычисления по заданным величинам, называемым аргументами, и в указанном порядке. Эти функции позволяют выполнять как простые, так и сложные вычисления.
Синтаксис функций
Приведенный ниже пример функции ОКРУГЛ, округляющей число в ячейке A10, демонстрирует синтаксис функции.
1.
Структура. Структура функции начинается со знака равно (=), за которым следуют имя функции, открывая скобка, аргументы функции, разделенные запятой, и закрывая скобка.
2. Имя функции. Чтобы отобразить список доступных функций, щелкните любую ячейку и нажмите клавиши SHIFT+F3.
3. Аргументы. Существуют различные типы аргументов: числа, текст, логические значения (ИСТИНА и ЛОЖЬ), массивы, значения ошибок (например #Н/Д) или ссылки на ячейки. Используемый аргумент должен возвращать значение, допустимое для данного аргумента. В качестве аргументов также используются константы, формулы и другие функции.
4.
Всплывающая подсказка аргумента. При вводе функции появляется всплывающая подсказка с синтаксисом и аргументами. Например, всплывающая подсказка появляется после ввода выражения =ОКРУГЛ(. Всплывающие подсказки отображаются только для встроенных функций.
Ввод функций
Диалоговое окно Вставить функцию упрощает ввод функций при создании формул, в которых они содержатся. При вводе функции в формулу в диалоговом окне Вставить функцию отображаются имя функции, все ее аргументы, описание функции и каждого из аргументов, текущий результат функции и всей формулы.
Чтобы упростить создание и редактирование формул и свести к минимуму количество опечаток и синтаксических ошибок, пользуйтесь автозавершением формул.
После того как вы введите знак «= » (знак равно) и начинательные буквы или триггер отображения Excel в Интернете под ячейкой будет отображаться динамический список действительных функций, аргументов и имен, которые соответствуют этим буквам или триггеру. После этого элемент из раскрывающегося списка можно вставить в формулу.
Вложенные функции
В некоторых случаях может потребоваться использовать функцию в качестве одного из аргументов другой функции. Например, в приведенной ниже формуле для сравнения результата со значением 50 используется вложенная функция СРЗНАЧ.
1.
Функции СРЗНАЧ и СУММ вложены в функцию ЕСЛИ.
Допустимые типы вычисляемых значений Вложенная функция, используемая в качестве аргумента, должна возвращать соответствующий ему тип данных. Например, если аргумент должен быть логическим, т. е. Если эта функция не работает, Excel в Интернете отобразит #VALUE! В противном случае TE102825393 выдаст ошибку «#ЗНАЧ!».
<c0>Предельное количество уровней вложенности функций</c0>. В формулах можно использовать до семи уровней вложенных функций. Если функция Б является аргументом функции А, функция Б находится на втором уровне вложенности. Например, в приведенном выше примере функции СРЗНАЧ и СУММ являются функциями второго уровня, поскольку обе они являются аргументами функции ЕСЛИ.
Функция, вложенная в качестве аргумента в функцию СРЗНАЧ, будет функцией третьего уровня, и т. д.
Использование ссылок в формулах
Ссылка указывает на ячейку или диапазон ячеек на сайте и сообщает Excel в Интернете, где искать значения или данные, которые вы хотите использовать в формуле. С помощью ссылок в одной формуле можно использовать данные, которые находятся в разных частях листа, а также значение одной ячейки в нескольких формулах. Вы также можете задавать ссылки на ячейки разных листов одной книги либо на ячейки из других книг. Ссылки на ячейки других книг называются связями или внешними ссылками.
Стиль ссылок A1
Стиль ссылок по умолчанию По умолчанию в Excel в Интернете используется стиль ссылок A1, который ссылается на столбцы буквами (от A до XFD, всего 16 384 столбца) и ссылается на строки с числами (от 1 до 1 048 576).
Эти буквы и номера называются заголовками строк и столбцов. Для ссылки на ячейку введите букву столбца, и затем — номер строки. Например, ссылка B2 указывает на ячейку, расположенную на пересечении столбца B и строки 2.
Ячейка или диапазон | Использование |
|---|---|
|
Ячейка на пересечении столбца A и строки 10 |
A10 |
|
Диапазон ячеек: столбец А, строки 10-20. |
A10:A20 |
|
Диапазон ячеек: строка 15, столбцы B-E |
B15:E15 |
|
Все ячейки в строке 5 |
5:5 |
|
Все ячейки в строках с 5 по 10 |
5:10 |
|
Все ячейки в столбце H |
H:H |
|
Все ячейки в столбцах с H по J |
H:J |
|
Диапазон ячеек: столбцы А-E, строки 10-20 |
A10:E20 |
<c0>Ссылка на другой лист</c0>.
В приведенном ниже примере функция СРЗНАЧ используется для расчета среднего значения диапазона B1:B10 на листе «Маркетинг» той же книги.
1. Ссылка на лист «Маркетинг».
2. Ссылка на диапазон ячеек с B1 по B10 включительно.
3. Ссылка на лист, отделенная от ссылки на диапазон значений.
Различия между абсолютными, относительными и смешанными ссылками
<c0>Относительные ссылки</c0>.
Относительная ссылка в формуле, например A1, основана на относительной позиции ячейки, содержащей формулу, и ячейки, на которую указывает ссылка. При изменении позиции ячейки, содержащей формулу, изменяется и ссылка. При копировании или заполнении формулы вдоль строк и вдоль столбцов ссылка автоматически корректируется. По умолчанию в новых формулах используются относительные ссылки. Например, при копировании или заполнении относительной ссылки из ячейки B2 в ячейку B3 она автоматически изменяется с =A1 на =A2.
<c0>Абсолютные ссылки</c0>. Абсолютная ссылка на ячейку в формуле, например $A$1, всегда ссылается на ячейку, расположенную в определенном месте. При изменении позиции ячейки, содержащей формулу, абсолютная ссылка не изменяется. При копировании или заполнении формулы по строкам и столбцам абсолютная ссылка не корректируется.
По умолчанию в новых формулах используются относительные ссылки, а для использования абсолютных ссылок надо активировать соответствующий параметр. Например, при копировании или заполнении абсолютной ссылки из ячейки B2 в ячейку B3 она остается прежней в обеих ячейках: =$A$1.
Смешанные ссылки Смешанная ссылка имеет абсолютный столбец и относительную строку либо абсолютную строку и относительный столбец. Абсолютная ссылка на столбец принимает форму $A 1, $B 1 и так далее. Абсолютная ссылка на строку имеет форму A$1, B$1 и так далее. При изменении позиции ячейки, содержаной формулу, изменяется относительная ссылка, а абсолютная ссылка не изменяется. При копировании или заполнении формулы по строкам или вниз по столбцам относительная ссылка автоматически корректируется, а абсолютная ссылка не корректируется. Например, при копировании или заполнении смешанной ссылки из ячейки A2 в B3 она будет меняться с =A$1 на =B$1.
Стиль трехмерных ссылок
Удобный способ для ссылки на несколько листов Трехмерные ссылки используются для анализа данных из одной и той же ячейки или диапазона ячеек на нескольких листах одной книги. Трехмерная ссылка содержит ссылку на ячейку или диапазон, перед которой указываются имена листов. Excel в Интернете использует все таблицы, которые хранятся между начальным и конечним именами ссылки. Например, формула =СУММ(Лист2:Лист13!B5) суммирует все значения, содержащиеся в ячейке B5 на всех листах в диапазоне от листа 2 до листа 13 включительно.
-
При помощи трехмерных ссылок можно создавать ссылки на ячейки на других листах, определять имена и создавать формулы с использованием следующих функций: СУММ, СРЗНАЧ, СРЗНАЧА, СЧЁТ, СЧЁТЗ, МАКС, МАКСА, МИН, МИНА, ПРОИЗВЕД, СТАНДОТКЛОН.
Г, СТАНДОТКЛОН.В, СТАНДОТКЛОНА, СТАНДОТКЛОНПА, ДИСПР, ДИСП.В, ДИСПА и ДИСППА. -
Трехмерные ссылки нельзя использовать в формулах массива.
-
Трехмерные ссылки нельзя использовать вместе с оператор пересечения (один пробел), а также в формулах с неявное пересечение.
Г, СТАНДОТКЛОН.В, СТАНДОТКЛОНА, СТАНДОТКЛОНПА, ДИСПР, ДИСП.В, ДИСПА и ДИСППА.<c0>Что происходит при перемещении, копировании, вставке или удалении листов</c0>. Нижеследующие примеры поясняют, какие изменения происходят в трехмерных ссылках при перемещении, копировании, вставке и удалении листов, на которые такие ссылки указывают. В примерах используется формула =СУММ(Лист2:Лист6!A2:A5) для суммирования значений в ячейках с A2 по A5 на листах со второго по шестой.
-
Вставка или копирование Если вставить листы между листами 2 и 6, Excel в Интернете будет включать в расчет все значения из ячеек с A2 по A5 на добавленных листах.
-
Удалить Если удалить листы между листами 2 и 6, Excel в Интернете вы вычислите их значения.
-
Переместить Если переместить листы между листами 2 и 6 в место за пределами диапазона, на который имеется ссылка, Excel в Интернете удалит их значения из вычислений.
-
Перемещение конечного листа Если переместить лист 2 или 6 в другое место книги, Excel в Интернете скорректирует сумму с учетом изменения диапазона листов.
-
Удаление конечного листа Если удалить лист 2 или 6, Excel в Интернете скорректирует сумму с учетом изменения диапазона листов между ними.
Стиль ссылок R1C1
Можно использовать такой стиль ссылок, при котором нумеруются и строки, и столбцы.
Стиль ссылок R1C1 удобен для вычисления положения столбцов и строк в макросах. В стиле R1C1 Excel в Интернете указывает на расположение ячейки с помощью R, за которым следует номер строки, и C, за которым следует номер столбца.
Ссылка | Значение |
|---|---|
|
R[-2]C |
относительная ссылка на ячейку, расположенную на две строки выше в том же столбце |
|
R[2]C[2] |
Относительная ссылка на ячейку, расположенную на две строки ниже и на два столбца правее |
|
R2C2 |
Абсолютная ссылка на ячейку, расположенную во второй строке второго столбца |
|
R[-1] |
Относительная ссылка на строку, расположенную выше текущей ячейки |
|
R |
Абсолютная ссылка на текущую строку |
При записи макроса Excel в Интернете некоторые команды с помощью стиля ссылок R1C1.
Например, если записать команду (например, нажать кнопку «Автоумма»), чтобы вставить формулу, в которую добавляется диапазон ячеек, Excel в Интернете записи формулы со ссылками с помощью стиля R1C1, а не A1.
Использование имен в формулах
Можно создавать определенные имена для представления ячеек, диапазонов ячеек, формул, констант и Excel в Интернете таблиц. Имя — это значимое краткое обозначение, поясняющее предназначение ссылки на ячейку, константы, формулы или таблицы, так как понять их суть с первого взгляда бывает непросто. Ниже приведены примеры имен и показано, как их использование упрощает понимание формул.
Тип примера | Пример использования диапазонов вместо имен | Пример с использованием имен |
|---|---|---|
|
Ссылка |
=СУММ(A16:A20) |
=СУММ(Продажи) |
|
Константа |
=ПРОИЗВЕД(A12,9. |
=ПРОИЗВЕД(Цена,НСП) |
|
Формула |
=ТЕКСТ(ВПР(MAX(A16,A20),A16:B20,2,FALSE),»дд.мм.гггг») |
=ТЕКСТ(ВПР(МАКС(Продажи),ИнформацияОПродажах,2,ЛОЖЬ),»дд.мм.гггг») |
|
Таблица |
A22:B25 |
=ПРОИЗВЕД(Price,Table1[@Tax Rate]) |
5%)Типы имен
Существует несколько типов имен, которые можно создавать и использовать.
Определенное имя Имя, используемое для представления ячейки, диапазона ячеек, формулы или константы.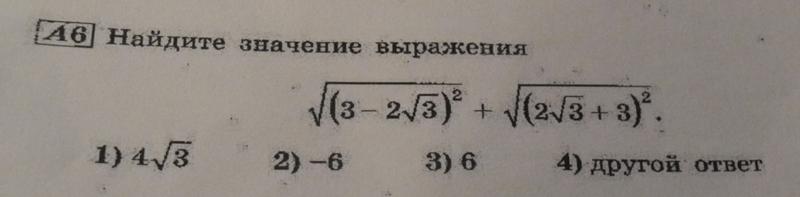
Вы можете создавать собственные определенные имена. Кроме Excel в Интернете иногда задайте определенное имя, например при создании области печати.
Имя таблицы Имя таблицы Excel в Интернете, которая является набором данных по определенной теме, которые хранятся в записях (строках) и полях (столбцах). Excel в Интернете создает таблицу Excel в Интернете имя таблицы «Таблица1», «Таблица2» и так далее, каждый раз при вставке таблицы Excel в Интернете, но эти имена можно изменить, чтобы сделать их более осмысленными.
Создание и ввод имен
Имя создается с помощью «Создать имя из выделения». Можно удобно создавать имена из существующих имен строк и столбцов с помощью фрагмента, выделенного на листе.
Примечание: По умолчанию в именах используются абсолютные ссылки на ячейки.
Имя можно ввести указанными ниже способами.
-
Ввод с клавиатуры Введите имя, например, в качестве аргумента формулы.
-
<c0>Автозавершение формул</c0>. Используйте раскрывающийся список автозавершения формул, в котором автоматически выводятся допустимые имена.
Использование формул массива и констант массива
Excel в Интернете не поддерживает создание формул массива.
Вы можете просматривать результаты формул массива, созданных в классическом приложении Excel, но не сможете изменить или пересчитать их. Если на вашем компьютере установлено классическое приложение Excel, нажмите кнопку Открыть в Excel, чтобы перейти к работе с массивами.
В примере формулы массива ниже вычисляется итоговое значение цен на акции; строки ячеек не используются при вычислении и отображении отдельных значений для каждой акции.
При вводе формулы «={СУММ(B2:D2*B3:D3)}» в качестве формулы массива сначала вычисляется значение «Акции» и «Цена» для каждой биржи, а затем — сумма всех результатов.
<c0>Вычисление нескольких значений</c0>.
Некоторые функции возвращают массивы значений или требуют массив значений в качестве аргумента. Для вычисления нескольких значений с помощью формулы массива необходимо ввести массив в диапазон ячеек, состоящий из того же числа строк или столбцов, что и аргументы массива.
Например, по заданному ряду из трех значений продаж (в столбце B) для трех месяцев (в столбце A) функция ТЕНДЕНЦИЯ определяет продолжение линейного ряда объемов продаж. Чтобы можно было отобразить все результаты формулы, она вводится в три ячейки столбца C (C1:C3).
Формула «=ТЕНДЕНЦИЯ(B1:B3;A1:A3)», введенная как формула массива, возвращает три значения (22 196, 17 079 и 11 962), вычисленные по трем объемам продаж за три месяца.
Использование констант массива
В обычную формулу можно ввести ссылку на ячейку со значением или на само значение, также называемое константой. Подобным образом в формулу массива можно ввести ссылку на массив либо массив значений, содержащихся в ячейках (его иногда называют константой массива). Формулы массива принимают константы так же, как и другие формулы, однако константы массива необходимо вводить в определенном формате.
Константы массива могут содержать числа, текст, логические значения, например ИСТИНА или ЛОЖЬ, либо значения ошибок, такие как «#Н/Д». В одной константе массива могут присутствовать значения различных типов, например {1,3,4;ИСТИНА,ЛОЖЬ,ИСТИНА}. Числа в константах массива могут быть целыми, десятичными или иметь экспоненциальный формат.
Текст должен быть заключен в двойные кавычки, например «Вторник».
Константы массива не могут содержать ссылки на ячейку, столбцы или строки разной длины, формулы и специальные знаки: $ (знак доллара), круглые скобки или % (знак процента).
При форматировании констант массива убедитесь, что выполняются указанные ниже требования.
-
Константы заключены в фигурные скобки ( { } ).
-
Столбцы разделены запятыми (,). Например, чтобы представить значения 10, 20, 30 и 40, введите {10,20,30,40}.
Эта константа массива является матрицей размерности 1 на 4 и соответствует ссылке на одну строку и четыре столбца. -
Значения ячеек из разных строк разделены точками с запятой (;). Например, чтобы представить значения 10, 20, 30, 40 и 50, 60, 70, 80, находящиеся в расположенных друг под другом ячейках, можно создать константу массива с размерностью 2 на 4: {10,20,30,40;50,60,70,80}.
Эта константа массива является матрицей размерности 1 на 4 и соответствует ссылке на одну строку и четыре столбца.Лечение зубов при беременности – можно ли лечить зубы в 1, 2, 3 триместре
Лечить зубы при беременности можно и даже необходимо. Терпеть зубную боль не стоит, это стресс для будущей мамы и малыша. К тому же санация полости рта показана и из других соображений: чтобы убрать очаги хронических инфекций и снизить риски осложнений. Визит к врачу откладывать не нужно, да и осмотр у стоматолога при беременности входит в план обследования.
Посетить стоматолога при хорошем состоянии здоровья полости рта необходимо дважды — в первом триместре при постановке на учет и непосредственно перед родами.
При выявлении заболеваний, требующих лечения, врач расскажет о дальнейших действиях.
Особенности лечения зубов при беременности
Беременность не противопоказание к проведению стоматологических процедур. Однако важно учитывать как срок беременности, так и особенности ее протекания, а также общее состояние здоровья женщины. Есть несколько особенностей лечения:
Срочному лечению подлежат кариес, пульпит, периодонтит, воспалительные заболевания десен и мягких тканей: стоматиты, гингивит, пародонтит, глоссит, хейлит. Также срочная помощь показана при травмах, таких как перелом корня зуба, сколы, трещины, и необходимости хирургического вмешательства при абсцессах, периостите и пр. В некоторых случаях отложить можно ортодонтическое, ортопедическое лечение, а также отбеливание. Например, установку брекетов или одного имплантата зуба можно перенести на более благоприятное время, после рождения малыша. При отсутствии большого количества зубов можно прибегнуть к съемным протезам, они не предусматривают подготовки в виде препарирования зубов и других сложностей.
При пломбировании врач может использовать любые материалы по показаниям. Лампы, которые используются для отверждения, не вредны для плода.
Лечение зубов при беременности может сопровождаться качественным обезболиванием. Терпеть неприятные ощущения будущей маме не стоит, есть препараты, разрешенные к применению. Единственным ограничением выступает наркоз.
Противопоказания и ограничения
Противопоказанием к проведению любых стоматологических вмешательств может выступать угроза прерывания беременности или преждевременных родов. Безусловно, если женщина находится в стационаре и проходит лечение для сохранения беременности, проблемы с полостью рта могут отступать на второй план. Но если состояние позволяет посетить стоматолога, лучше сделать это и обсудить целесообразность лечения.
Отложить до окончания беременности придется некоторые процедуры:
Имплантация: хирургический этап может быть противопоказан ввиду применения лекарственных средств в период восстановления, необходимости выполнения нескольких рентгеновских снимков.
Однако в некоторых случаях, например, при установке постоянного протеза на уже приживленные имплантаты, допускается проведение процедуры по согласованию с гинекологом, ведущим беременность.
Однако в некоторых случаях, например, при установке постоянного протеза на уже приживленные имплантаты, допускается проведение процедуры по согласованию с гинекологом, ведущим беременность.Имплантация требует серьезной подготовки. Во время беременности все силы организма направлены на развитие малыша. Меняется работа иммунных сил, особенности кровоснабжения органов и тканей, обменные процессы. Это может привести к непредсказуемым результатам приживления искусственного корня. Кроме того, восстановительный период после установки может включать прием лекарственных средств, которые противопоказаны при вынашивании ребенка.
Профессиональное отбеливание: беременность является противопоказанием к отбеливанию, поскольку эмаль зубов может быть ослаблена в связи беременностью и результат предсказать сложнее.
Установка несъемных протезов: при отсутствии большого количества зубов лучше предпочесть съемное протезирование, оно предусматривает меньший объем вмешательств.
Во всех случаях, когда удаление зуба можно отложить, необходимо это сделать. Речь идет об удалении ретинированных, дистопированных зубов, не вызывающих сильной боли и не несущих в себе риска серьезных последствий в ближайшее время. Если же зуб не подлежит восстановлению и вызывает сильную боль, является потенциально опасным очагом инфекции, удаление рекомендовано.
Антибактериальная терапия, а также рентгенография нежелательны в период беременности, но их может назначить врач при наличии строгих показаний. При выполнении рентгеновского снимка важно защитить область живота свинцовым фартуком. Антибиотики специалист подбирает с учетом срока беременности, тщательно взвешивая потенциальную опасность при отсутствии лечения и возможный вред для плода. Есть антибактериальные средства, разрешенные при беременности и не обладающие тератогенным действием.
Лечение в разных триместрах беременности
Особенности лечения могут зависеть от конкретного срока беременности.
Первый триместр — это период до 12-й недели. В это время происходит закладка органов ребенка, а несформированная плацента еще не обеспечивает надежную защиту плода от негативных факторов. К тому же до 8−9-й недели вероятность самопроизвольного прерывания выше. Также важно помнить, что у многих женщин в первом триместре наблюдается токсикоз, характеризующийся тошнотой, рвотой, повышенным слюноотделением, головокружением. Поэтому вмешательства в этом периоде стараются избегать, и если можно отложить лечение, врач порекомендует сделать это. Реминерализирующая терапия, профессиональная чистка зубов без ультразвукового воздействия разрешены.
Лечение зубов во 2 триместре беременности — с 13-й по 24-ю неделю — наиболее безопасно. Сформировавшаяся плацента выступает надежной защитой для ребенка. Периоды высоких рисков прерывания позади, а самочувствие мамы позволяет провести достаточно много времени в стоматологическом кресле. Все плановые процедуры рекомендовано проводить именно в это время. К ним относят профессиональную чистку, лечение заболеваний, которые могут обостриться со временем.
Лечение зубов при беременности в 3 триместре — с 25-й недели и до конца срока — также имеет несколько ограничений. Организм женщины может быть ослаблен к концу вынашивания. Могут наблюдаться одышка, тахикардия, низкое артериальное давление. К тому же в положении полулежа симптомы могут усиливаться из-за сдавливания нижней полой вены маткой. Допускается положение немного на левом боку, чтобы уменьшить нагрузку на аорту и нижнюю полую вену.
Матка становится более чувствительной к неблагоприятным факторам, в том числе медикаментам. Сама женщина может становиться более тревожной, быстрее уставать. Поэтому лечение проводится только по строгим показаниям, если ждать родоразрешения нельзя и состояние женщины может резко ухудшиться.
Особенности диагностики
Точная диагностика определяет результаты лечения, поэтому пренебрегать ею не стоит. Прицельный рентгеновский снимок зуба может быть противопоказан, особенно в первом триместре беременности, когда клетки восприимчивы к радиации. Но если другие методы диагностики недоступны, а без снимка нельзя правильно разработать схему лечения, прибегнуть к нему можно. Наиболее безопасным методом является цифровая радиовизиография. В сравнении с пленочным снимком нагрузка в несколько раз меньше, поэтому можно прибегнуть к такой диагностике. При обследовании соблюдается радиологическая защита.
Безопасное обезболивание
Лечение зубов во время беременности предусматривает качественное обезболивание. Для этого используются местные анестетики последнего поколения, которые не преодолевают плацентарный барьер. Многие составы включают в себя сосудосуживающий компонент, что повышает эффективность анестетика. В препаратах для беременных концентрация такого компонента несколько ниже. Он не влияет на кровоток в плаценте и матке.
Есть несколько разрешенных к применению у беременных местных анестетиков:
Они не оказывают системного действия и безвредны для малыша и беременной женщины.
Особенности проведения процедур
Удаление зуба представляет собой хирургическое вмешательство. Оно сопровождается небольшой кровопотерей, а также стрессом. Повышенная психоэмоциональная нагрузка нежелательна при беременности, поэтому к удалению зуба должны быть строгие показания. К крайним случаям, когда без вмешательства не обойтись, относят следующие:
перелом коронки, корня;
кариес корня,
пульпит третьих моляров, выступающие причиной острого гнойного воспаления,
периодонтит с образованием кист;
разрушение зуба, сопровождающееся острой болью.
Плановое удаление зубов мудрости не проводится. Это связано с высокими рисками альвеолита и другими возможными осложнениями, при которых потребуется повторное вмешательство и мощная антибактериальная терапия.
Как лечить зубы при беременности, подробно расскажет врач. Если терапия поверхностного и среднего кариеса в этот период практически не отличается от стандартной процедуры, то лечение пульпита потребует особого подхода. Врач подберет средство без мышьяка для девитализации пульпы. Есть необходимость проведения минимум двух рентгенографических снимков — до процедуры для определения структуры, количества и размеров каналов корней и после нее для контроля эффективности лечения. Поэтому применяется метод цифровой радиовизиографии.
Лечение пародонтологических заболеваний проводится обязательно. К тому же беременность существенно повышает риск их развития. Например, гингивит беременных встречается сравнительно часто. Врач выберет тактику лечения с учетом индивидуальных особенностей, пропишет медикаментозную терапию, разрешенную к применению.
Лечением зубов при беременности успешно занимаются врачи клиник «СТОМА». У нас есть все необходимое для оказания срочной помощи и проведения плановых мероприятий. В клиниках сети вы можете проходить регулярный осмотр стоматолога или обратиться для лечения кариеса, гингивита беременных, пародонтита, пульпита и др. Гарантируем использование только разрешенных анестетиков и качественного оборудования, безопасную диагностику. Записаться на прием вы можете по указанному телефону или через специальную форму на сайте.
квадратный корень из 9 — Как найти квадратный корень из 9?
Квадратный корень из 9 выражается как √9 в радикальной форме и как (9) ½ или (9) 0,5 в экспоненциальной форме. Квадратный корень из 9 равен 3. Это положительное решение уравнения x 2 = 9. Число 9 представляет собой полный квадрат.
- Квадратный корень 9: 3
- Квадратный корень из 9 в экспоненциальной форме: (9) ½ или (9) 0,5
- Квадратный корень из 9 в радикальной форме: √9
Что такое квадратный корень из 9?
Квадратный корень из 9 равен 3, т.е.Например, умножение 3 на 3 дает 9. 3 2 = 3 × 3 = 9. Здесь 3 называется квадратным корнем из 9, а 9 — точным квадратом.
Является ли квадратный корень из 9 рациональным или иррациональным числом?
Если число можно выразить в форме p / q, то это рациональное число. √9 = ± 3 можно записать в виде дроби 3/1. Это доказывает, что √9 — рациональное число.
Как найти квадратный корень из 9?
Квадратный корень можно вычислить с помощью различных методов.Давайте найдем квадратный корень из 9, используя разложение на простые множители. Мы можем выразить 9 как произведение его простого множителя, то есть 3. 3 × 3 = 9 — это точное квадратное число.
Квадратный корень из 9 методом длинного деления
Чтобы найти квадратный корень из 9 методом деления в длину, нам нужно выполнить шаги, указанные ниже.
- Шаг 1: Составьте пару цифр данного числа, начиная с цифры на месте единицы. Поставьте планку на каждую пару.
- Шаг 2: Теперь нам нужно умножить число на само себя так, чтобы получилось 9.Здесь 3 × 3 = 9
Исследуйте квадратные корни с помощью иллюстраций и интерактивных примеров
- Квадратный корень 9 равен 3 и -3.
- 9 — точное квадратное число.
- Квадратный корень из полного квадратного числа легко найти с помощью разложения на простые множители.
Квадратный корень из 9 решенных примеров
Пример 1 Вычислить квадратный корень из 4/9, используя разложение на простые множители.
Решение
Разложение на простые множители из 4 = 2 × 2
Разложение на простые множители 9 = 3 × 3
Следовательно, квадратный корень из 4/9 = √4 / √9 = √2 × √2 / √3 × √3 = 2/3.Пример 2 Можете ли вы помочь Джо найти квадратный корень из 9/49?
Решение
Разложение на простые множители из 49 = 7 × 7
Разложение на простые множители 9 = 3 × 3
Следовательно, квадратный корень из 9/49 = √9 / √49 = √3 × √3 / √7 × √7 = 3/7Пример 3 Найдите сумму квадрата 9 и квадратного корня из 9.
Решение
.
Квадрат 9 = 81
Квадратный корень из 9 = 3
Следовательно, сумма квадрата 9 и квадратного корня из 9 = 81 + 3 = 84
перейти к слайду перейти к слайду
Разбивайте сложные концепции с помощью простых визуальных элементов.
Математика больше не будет сложным предметом, особенно если вы понимаете концепции посредством визуализации.
Забронируйте бесплатную пробную версию Класс
Часто задаваемые вопросы о квадратном корне из 9
Что такое квадратный корень из 9?
Квадратный корень из 9 равен 3.
Почему квадратный корень из 9 является рациональным числом?
После разложения на простые множители 9, т. Е. 3 2 , мы обнаруживаем, что все простые множители имеют четную степень. Это означает, что квадратный корень из 9 является положительным целым числом.Следовательно, квадратный корень из 9 является рациональным.
Что такое квадрат квадратного корня из 9?
Квадрат квадратного корня из 9 — это само число 9, т. {2} = a \ cdot a = \ left (-a \ right) \ cdot \ left (-a \ right) $$
Квадратный корень записывается с помощью символа корня √, а число или выражение внутри символа корня, обозначенное ниже a, называется подкоренным выражением.
$$ \ sqrt {a} $$
Чтобы указать, что нам нужен как положительный, так и отрицательный квадратный корень из подкоренной части, мы помещаем символ ± (читается как плюс минус) перед корнем.
$$ \ pm \ sqrt {9} = \ pm 3 $$
У нуля один квадратный корень, равный 0.
$$ \ sqrt {0} = 0 $$
Отрицательные числа не имеют действительных квадратных корней, поскольку квадрат либо положительный, либо 0.
Если квадратный корень целого числа является другим целым числом, квадрат называется полным квадратом.Например, 25 — это идеальный квадрат, так как
$$ \ pm \ sqrt {25} = \ pm 5 $$
Если подкоренное выражение не является точным квадратом, то есть квадратный корень не является целым числом, вам нужно приблизительно вычислить квадратный корень
$$ \ pm \ sqrt {3} = \ pm 1.73205 … \ приблизительно \ pm 1,7 $$
Квадратные корни из чисел, не являющихся полным квадратом, являются членами иррациональных чисел. Это означает, что они не могут быть записаны как частное двух целых чисел. Десятичная форма иррационального числа не прерывается и не повторяется.Иррациональные числа вместе с рациональными числами составляют действительные числа.
Пример
$$ иррационально \: number \ Rightarrow \ sqrt {19} \ приблизительно 4,35889 … $$
$$ рациональное \: число \ Rightarrow 0.5 = \ frac {1} {2} $$
Видеоуроки
Решить
Определите, являются ли эти числа рациональными или иррациональными
Калькулятор квадратного корня
Калькулятор квадратного корня
О калькуляторе квадратного корня
Калькулятор квадратного корня используется для нахождения квадратного корня из введенного числа.
Квадратный корень
В математике квадратный корень из числа x — это такое число r, что r 2 = x.
Например:
1. Квадратный корень из 25 равен 5, потому что 5 2 = 25.
3. Квадратный корень из 2 приблизительно равен 1,41421356237.
3. Квадратный корень числа пи (π) приблизительно равен 1,77245385102.
Таблица квадратного корня
Ниже приводится таблица квадратного корня от 1 до 1000 с округлением до 5 цифр:
| x | √x | ||
|---|---|---|---|
| 1 | 1 | ||
| 2 | 1.41421 | ||
| 3 | 1,73205 | ||
| 4 | 2 | ||
| 5 | 2,23607 | ||
| 6 | |||
| 9 | 3 | ||
| 10 | 3,16228 | ||
| 11 | 3,31662 | ||
| 12 | 3,4662 | ||
| 360555 | |||
| 14 | 3,74166 | ||
| 15 | 3,87298 | ||
| 16 | 4 | ||
| 17 | 4,12311 | 902 9022 | 4,12311 | 902
| 20 | 4.47214 | ||
| 21 | 4.58258 | ||
| 22 | 4.69042 | ||
| 23 | 4.79583 | ||
| 24 | 4,89898 | ||
| 25 | 5 | ||
| 26 | 5,09902 | ||
| 27 | 5,19615 | ||
| 30 | 5,47723 | ||
| 31 | 5,56776 | ||
| 32 | 5,65685 | ||
| 33 | 5.74456 | ||
| 34 | 5,83095 | ||
| 35 | 5, | ||
| 36 | 6 | ||
| 37 | 6.08276 | ||
| 40 | 6.32456 | ||
| 41 | 6.40312 | ||
| 42 | 6.48074 | ||
| 43 | 6.55744 | ||
| 44 | 6.63325 | ||
| 45 | 6.7082 | ||
| 46 | 6.78233 | 2 | 2 |
| 50 | 7.07107 | ||
| 51 | 7.14143 | ||
| 52 | 7.2111 | ||
| 53 | 7.28011 | ||
| 54 | 7,34847 | ||
| 55 | 7,4162 | ||
| 56 | 7,48331 | ||
| 57 | 57 | 7,54983||
| 57 | |||
| 60 | 7.74597 | ||
| 61 | 7.81025 | ||
| 62 | 7.87401 | ||
| 63 | 7. | ||
| 64 | 8 | ||
| 65 | 8.06226 | ||
| 66 | 8.12404 | ||
| 67 | 8.18535 | 902 9028,18535 | 902 902|
| 70 | 8.3666 | ||
| 71 | 8.42615 | ||
| 72 | 8.48528 | ||
| 73 | 8.544 | ||
| 74 | 8,60233 | ||
| 75 | 8,66025 | ||
| 76 | 8,7178 | ||
| 77 | 2 9066 | 902 902 902 902 902 902 902||
| 80 | 8. | ||
| 81 | 9 | ||
| 82 | 9.05539 | ||
| 83 | 9.11043 | ||
| 84 | 9.16515 | ||
| 85 | 9.21954 | ||
| 86 | 9.27362 | ||
| 87 | 2 | 9.32738 9.32722 | 9.3272 902|
| 90 | 9,48683 | ||
| 91 | 9,53939 | ||
| 92 | 9,59166 | ||
| 93 | 9.64365 | ||
| 94 | 9.69536 | ||
| 95 | 9.74679 | ||
| 96 | 9.79796 | ||
| 97 | 9.84886|||
| 100 | 10 | ||
| 101 | 10,04988 | ||
| 102 | 10,0995 | ||
| 103 | 10.14889 | ||
| 104 | 10.19804 | ||
| 105 | 10.24695 | ||
| 106 | 10.29563 | ||
| 107 | 1092 902 902 902 902 902 | 1092 902 902 902||
| 110 | 10.48809 | ||
| 111 | 10.53565 | ||
| 112 | 10.58301 | ||
| 113 | 10.63015 | ||
| 114 | 10,67708 | ||
| 115 | 10,72381 | ||
| 116 | 10,77033 | 117 | 902 902 902 902 902|
| 120 | 10. | ||
| 121 | 11 | ||
| 122 | 11.04536 | ||
| 123 | 11.09054 | ||
| 124 | 11.13553 | ||
| 125 | 11.18034 | ||
| 126 | 11.22497 | ||
| 127 | 129252|||
| 130 | 11.40175 | ||
| 131 | 11.44552 | ||
| 132 | 11.48913 | ||
| 133 | 11.53256 | ||
| 134 | 11,57584 | ||
| 135 | 11,61895 | ||
| 136 | 11,6619 | 137 | 1382 902 902 13702 902|
| 140 | 11.83216 | ||
| 141 | 11.87434 | ||
| 142 | 11. | ||
| 143 | 11. | ||
| 144 | 12 | ||
| 145 | 12.04159 | ||
| 146 | 12.08305 | ||
| 147 | 12.12436 902147 | 12.12436 902 | |
| 150 | 12.24745 | ||
| 151 | 12.28821 | ||
| 152 | 12.32883 | ||
| 153 | 12.36932 | ||
| 154 | 12,40967 | ||
| 155 | 12,4499 | ||
| 156 | 12,49 | ||
| 157 | 12,52996 | ||
| 158 | 12,56981 | ||
| 159 | 12,60952 | ||
| 160 | 12.64911 | ||
| 161 | 12.68858 | ||
| 162 | 12.72792 | ||
| 163 | 12.76715 | ||
| 164 | 12,80625 | ||
| 165 | 12,84523 | ||
| 166 | 12,8841 | ||
| 167 | 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902|||
| 170 | 13.0384 | ||
| 171 | 13.0767 | ||
| 172 | 13.11488 | ||
| 173 | 13.15295 | ||
| 174 | 13,19091 | ||
| 175 | 13,22876 | ||
| 176 | 13,2665 | ||
| 177 | 13,30413 | ||
| 178 | 13,34166 | ||
| 179 | 13,37909 | ||
| 180 | 13.41641 | ||
| 181 | 13.45362 | ||
| 182 | 13.49074 | ||
| 183 | 13.52775 | ||
| 184 | 13,56466 | ||
| 185 | 13,60147 | ||
| 186 | 13,63818 | ||
| 187 | 13,67479 | ||
| 188 | 13,71131 | ||
| 189 | 13,74773 | ||
| 190 | 13.78405 | ||
| 191 | 13.82027 | ||
| 192 | 13.85641 | ||
| 193 | 13.89244 | ||
| 194 | 13. | ||
| 195 | 13. | ||
| 196 | 14 | ||
| 197 | 197 | 902 902 902||
| 200 | 14.14214 | ||
| 201 | 14.17745 | ||
| 202 | 14.21267 | ||
| 203 | 14.24781 | ||
| 204 | 14,28286 | ||
| 205 | 14,31782 | ||
| 206 | 14,3527 | ||
| 207 | 14,38749 | ||
| 208 | 14,42221 | ||
| 209 | 14,45683 | ||
| 210 | 14.49138 | ||
| 211 | 14.52584 | ||
| 212 | 14.56022 | ||
| 213 | 14.59452 | ||
| 214 | 14,62874 | ||
| 215 | 14,66288 | ||
| 216 | 14,69694 | ||
| 217 | 14,73092 | ||
| 218 | 14,76482 | ||
| 219 | 14,79865 | ||
| 220 | 14.8324 | ||
| 221 | 14.86607 | ||
| 222 | 14.89966 | ||
| 223 | 14. | ||
| 224 | 14. | ||
| 225 | 15 | ||
| 226 | 15.0333 | ||
| 227 | 152652 | ||
| 227 | 152652 | ||
| 2 | |||
| 230 | 15.16575 | ||
| 231 | 15.19868 | ||
| 232 | 15.23155 | ||
| 233 | 15.26434 | ||
| 234 | 15,29706 | ||
| 235 | 15,32971 | ||
| 236 | 15,36229 | ||
| 237 | 15,3948 | ||
| 238 | 15,42725 | ||
| 239 | 15,45962 | ||
| 240 | 15,49193 | ||
| 241 | 15,52417 | ||
| 242 | 15,55635 | ||
| 243 | 15.58846 | ||
| 244 | 15,6205 | ||
| 245 | 15,65248 | ||
| 246 | 15,68439 | ||
| 247 | 15,71623 | ||
| 248 | 15,74802 | ||
| 249 | 15,77973 | ||
| 250 | 15.81139 | ||
| 251 | 15.84298 | ||
| 252 | 15.87451 | ||
| 253 | 15. | ||
| 254 | 15, | ||
| 255 | 15. | ||
| 256 | 16 | ||
| 257 | |||
| 257 | 162122|||
| 257 | 162122|||
| 257 | |||
| 257 | 162122 902 902 | ||
| 260 | 16.12452 | ||
| 261 | 16.15549 | ||
| 262 | 16.18641 | ||
| 263 | 16.21727 | ||
| 264 | 16,24808 | ||
| 265 | 16,27882 | ||
| 266 | 16,30951 | ||
| 267 | 16,34013 | ||
| 268 | 16,37071 | ||
| 269 | 16,40122 | ||
| 270 | 16.43168 | ||
| 271 | 16.46208 | ||
| 272 | 16.49242 | ||
| 273 | 16.52271 | ||
| 274 | 16,55295 | ||
| 275 | 16,58312 | ||
| 276 | 16,61325 | ||
| 277 | 16,64332 | ||
| 278 | 16,67333 | ||
| 279 | 16,70329 | ||
| 280 | 16.7332 | ||
| 281 | 16.76305 | ||
| 282 | 16.79286 | ||
| 283 | 16.8226 | ||
| 284 | 16,8523 | ||
| 285 | 16,88194 | ||
| 286 | 16, | ||
| 287 | 16, | ||
| 288 | 16, | ||
| 289 | 17 | ||
| 290 | 17.02939 | ||
| 291 | 17.05872 | ||
| 292 | 17.08801 | ||
| 293 | 17.11724 | ||
| 294 | 17,14643 | ||
| 295 | 17,17556 | ||
| 296 | 17,20465 | ||
| 297 | 17,23369 | ||
| 298 | 17,26268 | ||
| 299 | 17,29162 | ||
| 300 | 17.32051 | ||
| 301 | 17.34935 | ||
| 302 | 17.37815 | ||
| 303 | 17.4069 | ||
| 304 | 17,4356 | ||
| 305 | 17,46425 | ||
| 306 | 17,49286 | ||
| 307 | 17,52142 | ||
| 308 | 17,54993 | ||
| 309 | 17,5784 | ||
| 310 | 17.60682 | ||
| 311 | 17.63519 | ||
| 312 | 17.66352 | ||
| 313 | 17.69181 | ||
| 314 | 17,72005 | ||
| 315 | 17,74824 | ||
| 316 | 17,77639 | ||
| 317 | 17,80449 | ||
| 318 | 17,83255 | ||
| 319 | 17,86057 | ||
| 320 | 17.88854 | ||
| 321 | 17. | ||
| 322 | 17. | ||
| 323 | 17.9722 | ||
| 324 | 18 | ||
| 325 | 18.02776 | ||
| 326 | 18.05547 | ||
| 327 | |||
| 330 | 18.1659 | ||
| 331 | 18.19341 | ||
| 332 | 18.22087 | ||
| 333 | 18.24829 | ||
| 334 | 18,27567 | ||
| 335 | 18,30301 | ||
| 336 | 18,3303 | ||
| 337 | 18,35756 | ||
| 338 | 18,38478 | ||
| 339 | 18,41195 | ||
| 340 | 18.43909 | ||
| 341 | 18.46619 | ||
| 342 | 18.49324 | ||
| 343 | 18.52 026 | ||
| 344 | 18,54724 | ||
| 345 | 18,57418 | ||
| 346 | 18,60108 | ||
| 347 | 18,62794 | ||
| 348 | 18,65476 | ||
| 349 | 18,68154 | ||
| 350 | 18.70829 | ||
| 351 | 18.73499 | ||
| 352 | 18.76166 | ||
| 353 | 18.78829 | ||
| 354 | 18,81489 | ||
| 355 | 18,84144 | ||
| 356 | 18,86796 | ||
| 357 | 18,89444 | ||
| 358 | 18, | ||
| 359 | 18,9473 | ||
| 360 | 18. | ||
| 361 | 19 | ||
| 362 | 19.0263 | ||
| 363 | 19.05256 | ||
| по ремонту 364 | 19,07878 | ||
| 365 | 19,10497 | ||
| 366 | 19,13113 | ||
| 367 | 19,15724 | ||
| 368 | 19,18333 | ||
| 369 | 19,20937 | ||
| 370 | 19.23538 | ||
| 371 | 19.26136 | ||
| 372 | 19.2873 | ||
| 373 | 19.31321 | ||
| 374 | 19,33908 | ||
| 375 | 19,36492 | ||
| 376 | 19,39072 | ||
| 377 | 19,41649 | ||
| 378 | 19,44222 | ||
| 379 | 19,46792 | ||
| 380 | 19.49359 | ||
| 381 | 19.51922 | ||
| 382 | 19.54482 | ||
| 383 | 19.57039 | ||
| 384 | 19,59592 | ||
| 385 | 19,62142 | ||
| 386 | 19,64688 | ||
| 387 | 19,67232 | ||
| 388 | 19,69772 | ||
| 389 | 19,72308 | ||
| 390 | 19.74842 | ||
| 391 | 19.77372 | ||
| 392 | 19.79899 | ||
| 393 | 19.82423 | ||
| 394 | 19,84943 | ||
| 395 | 19,87461 | ||
| 396 | 19,89975 | ||
| 397 | 19, | ||
| 398 | 19, | ||
| 399 | 19, | ||
| 400 | 20 | ||
| 401 | 20.02498 | ||
| 402 | 20.04994 | ||
| 403 | 20.07486 | ||
| 404 | 20,09975 | ||
| 405 | 20,12461 | ||
| 406 | 20,14944 | ||
| 407 | 20,17424 | ||
| 408 | 20,19901 | ||
| 409 | 20,22375 | ||
| 410 | 20.24846 | ||
| 411 | 20.27313 | ||
| 412 | 20.29778 | ||
| 413 | 20.3224 | ||
| 414 | 20,34699 | ||
| 415 | 20,37155 | ||
| 416 | 20,39608 | ||
| 417 | 20,42058 | ||
| 418 | 20,44505 | ||
| 419 | 20,46949 | ||
| 420 | 20.4939 | ||
| 421 | 20.51828 | ||
| 422 | 20.54264 | ||
| 423 | 20.56696 | ||
| 424 | 20,59126 | ||
| 425 | 20,61553 | ||
| 426 | 20,63977 | ||
| 427 | 20,66398 | ||
| 428 | 20,68816 | ||
| 429 | 20,71232 | ||
| 430 | 20.73644 | ||
| 431 | 20.76054 | ||
| 432 | 20.78461 | ||
| 433 | 20.80 865 | ||
| 434 | 20,83267 | ||
| 435 | 20,85665 | ||
| 436 | 20,88061 | ||
| 437 | 20, | ||
| 438 | 20, | ||
| 439 | 20, | ||
| 440 | 20. | ||
| 441 | 21 | ||
| 442 | 21.0238 | ||
| 443 | 21.04 757 | ||
| 444 | 21,07131 | ||
| 445 | 21,09502 | ||
| 446 | 21,11871 | ||
| 447 | 21,14237 | ||
| 448 | 21,16601 | ||
| 449 | 21,18962 | ||
| 450 | 21.2132 | ||
| 451 | 21.23676 | ||
| 452 | 21.26029 | ||
| 453 | 21.2838 | ||
| 454 | 21,30728 | ||
| 455 | 21,33073 | ||
| 456 | 21,35416 | ||
| 457 | 21,37756 | ||
| 458 | 21,40093 | ||
| 459 | 21,42429 | ||
| 460 | 21.44761 | ||
| 461 | 21.47091 | ||
| 462 | 21.49419 | ||
| 463 | 21.51743 | ||
| 464 | 21,54066 | ||
| 465 | 21,56386 | ||
| 466 | 21,58703 | ||
| 467 | 21,61018 | ||
| 468 | 21,63331 | ||
| 469 | 21,65641 | ||
| 470 | 21.67948 | ||
| 471 | 21.70253 | ||
| 472 | 21.72556 | ||
| 473 | 21.74856 | ||
| 474 | 21,77154 | ||
| 475 | 21,79449 | ||
| 476 | 21,81742 | ||
| 477 | 21,84033 | ||
| 478 | 21,86321 | ||
| 479 | 21,88607 | ||
| 480 | 21.9089 | ||
| 481 | 21. | ||
| 482 | 21.9545 | ||
| 483 | 21. | ||
| 484 | 22 | ||
| 485 | 22,02272 | ||
| 486 | 22,04541 | ||
| 487 | |||
| 487 | |||
| 487 | 2 | ||
| 487 | 2 902 | ||
| 490 | 22.13594 | ||
| 491 | 22.15852 | ||
| 492 | 22.18107 | ||
| 493 | 22.2036 | ||
| 494 | 22,22611 | ||
| 495 | 22,2486 | ||
| 496 | 22,27106 | ||
| 497 | 22,2935 | ||
| 498 | 22,31591 | ||
| 499 | 22,33831 | ||
| 500 | 22.36068 | ||
| 501 | 22.38303 | ||
| 502 | 22.40536 | ||
| 503 | 22.+42766 | ||
| 504 | 22,44994 | ||
| 505 | 22,47221 | ||
| 506 | 22,49444 | ||
| 507 | 22,51666 | ||
| 508 | 22,53886 | ||
| 509 | 22,56103 | ||
| 510 | 22.58318 | ||
| 511 | 22.60531 | ||
| 512 | 22.62742 | ||
| 513 | 22.6495 | ||
| 514 | 22,67157 | ||
| 515 | 22,69361 | ||
| 516 | 22,71563 | ||
| 517 | 22,73763 | ||
| 518 | 22,75961 | ||
| 519 | 22,78157 | ||
| 520 | 22.80351 | ||
| 521 | 22.82542 | ||
| 522 | 22.84732 | ||
| 523 | 22.86919 | ||
| 524 | 22.89105 | ||
| 525 | 22. | ||
| 526 | 22. | ||
| 527 | 2|||
| 527 | |||
| 527 | |||
| 530 | 23.02173 | ||
| 531 | 23.04344 | ||
| 532 | 23.06513 | ||
| 533 | 23.+08679 | ||
| 534 | 23,10844 | ||
| 535 | 23,13007 | ||
| 536 | 23,15167 | ||
| 537 | 23,17326 | ||
| 538 | 23,19483 | ||
| 539 | 23,21637 | ||
| 540 | 23.2379 | ||
| 541 | 23.25941 | ||
| 542 | 23.28089 | ||
| 543 | 23.30236 | ||
| 544 | 23,32381 | ||
| 545 | 23,34524 | ||
| 546 | 23,36664 | ||
| 547 | 23,38803 | ||
| 548 | 23,4094 | ||
| 549 | 23,43075 | ||
| 550 | 23.45208 | ||
| 551 | 23.47339 | ||
| 552 | 23.49468 | ||
| 553 | 23.51595 | ||
| 554 | 23,5372 | ||
| 555 | 23,55844 | ||
| 556 | 23,57965 | ||
| 557 | 23,60085 | ||
| 558 | 23,62202 | ||
| 559 | 23,64318 | ||
| 560 | 23.66432 | ||
| 561 | 23.68544 | ||
| 562 | 23.70654 | ||
| 563 | 23.72762 | ||
| 564 | 23,74868 | ||
| 565 | 23,76973 | ||
| 566 | 23,79075 | ||
| 567 | 23,81176 | ||
| 568 | 23,83275 | ||
| 569 | 23,85372 | ||
| 570 | 23.87467 | ||
| 571 | 23.89561 | ||
| 572 | 23. | ||
| 573 | 23. | ||
| 574 | 23,9583 | ||
| 575 | 23. | ||
| 576 | 24 | ||
| 577 | |||
| 577 | |||
| 577 | 24,0202 | 2 | |
| 580 | 24.08319 | ||
| 581 | 24.10394 | ||
| 582 | 24.12468 | ||
| 583 | 24.14539 | ||
| 584 | 24,16609 | ||
| 585 | 24,18677 | ||
| 586 | 24,20744 | ||
| 587 | 24,22808 | ||
| 588 | 24,24871 | ||
| 589 | 24,26932 | ||
| 590 | 24.28992 | ||
| 591 | 24.31049 | ||
| 592 | 24.33105 | ||
| 593 | 24.35159 | ||
| 594 | 24,37212 | ||
| 595 | 24,39262 | ||
| 596 | 24,41311 | ||
| 597 | 24,43358 | ||
| 598 | 24,45404 | ||
| 599 | 24,47448 | ||
| 600 | 24,4949 | ||
| 601 | 24,5153 | ||
| 602 | 24,53569 | ||
| 603 | 24.55606 | ||
| 604 | 24,57641 | ||
| 605 | 24,59675 | ||
| 606 | 24,61707 | ||
| 607 | 24,63737 | ||
| 608 | 24,65766 | ||
| 609 | 24,67793 | ||
| 610 | 24.69818 | ||
| 611 | 24.71841 | ||
| 612 | 24.73863 | ||
| 613 | 24.75884 | ||
| 614 | 24,77902 | ||
| 615 | 24,79919 | ||
| 616 | 24,81935 | ||
| 617 | 24,83948 | ||
| 618 | 24,85961 | ||
| 619 | 24,87971 | ||
| 620 | 24,8998 | ||
| 621 | 24, | ||
| 622 | 24, | ||
| 623 | 24. | ||
| 624 | 24. | ||
| 625 | 25 | ||
| 626 | 25,01999 | ||
| 627 | |||
| 627 | |||
| 627 | 25,03 | ||
| 630 | 25,0998 | ||
| 631 | 25,11971 | ||
| 632 | 25,13961 | ||
| 633 | 25.15949 | ||
| 634 | 25,17936 | ||
| 635 | 25,19921 | ||
| 636 | 25,21904 | ||
| 637 | 25,23886 | ||
| 638 | 25,25866 | ||
| 639 | 25,27845 | ||
| 640 | 25.29822 | ||
| 641 | 25.31798 | ||
| 642 | 25.33772 | ||
| 643 | 25.35744 | ||
| 644 | 25,37716 | ||
| 645 | 25,39685 | ||
| 646 | 25,41653 | ||
| 647 | 25,43619 | ||
| 648 | 25,45584 | ||
| 649 | 25,47548 | ||
| 650 | 25,4951 | ||
| 651 | 25,5147 | ||
| 652 | 25,53429 | ||
| 653 | 25.55386 | ||
| 654 | 25,57342 | ||
| 655 | 25,59297 | ||
| 656 | 25,6125 | ||
| 657 | 25,63201 | ||
| 658 | 25,65151 | ||
| 659 | 25,671 | ||
| 660 | 25.69047 | ||
| 661 | 25.70992 | ||
| 662 | 25.72936 | ||
| 663 | 25.74879 | ||
| 664 | 25,7682 | ||
| 665 | 25,78759 | ||
| 666 | 25,80698 | ||
| 667 | 25,82634 | ||
| 668 | 25,8457 | ||
| 669 | 25,86503 | ||
| 670 | 25.88436 | ||
| 671 | 25. | ||
| 672 | 25. | ||
| 673 | 25. | ||
| 674 | 25. | ||
| 675 | 25. | ||
| 676 | 26 | 26 | |
| 677 | 26.0192 | ||
| 680 | 26.07681 | ||
| 681 | 26.09598 | ||
| 682 | 26.11513 | ||
| 683 | 26.13427 | ||
| 684 | 26,15339 | ||
| 685 | 26,1725 | ||
| 686 | 26,1916 | ||
| 687 | |||
| 687 | 26,21068 | 26,21068||
| 690 | 26.26785 | ||
| 691 | 26.28688 | ||
| 692 | 26.30589 | ||
| 693 | 26.32489 | ||
| 694 | 26,34388 | ||
| 695 | 26,36285 | ||
| 696 | 26,38181 | ||
| 697 | 26,40076 | ||
| 698 | 26,41969 | ||
| 699 | 26,43861 | ||
| 700 | 26.45751 | ||
| 701 | 26.4764 | ||
| 702 | 26.49528 | ||
| 703 | 26.51415 | ||
| 704 | 26,533 | ||
| 705 | 26,55184 | ||
| 706 | 26,57066 | ||
| 707 | 26,58947 | ||
| 708 | 26,60827 | ||
| 709 | 26,62705 | ||
| 710 | 26.64583 | ||
| 711 | 26.66458 | ||
| 712 | 26.68333 | ||
| 713 | 26.70206 | ||
| 714 | 26,72078 | ||
| 715 | 26,73948 | ||
| 716 | 26,75818 | ||
| 717 | 26,77686 | ||
| 718 | 26,79552 | ||
| 719 | 26,81418 | ||
| 720 | 26.83282 | ||
| 721 | 26.85144 | ||
| 722 | 26.87006 | ||
| 723 | 26.88866 | ||
| 724 | 26, | ||
| 725 | 26, | ||
| 726 | 26, | ||
| 727 | 26, | ||
| 728 | 26, | ||
| 729 | 27 | ||
| 730 | 27.01851 | ||
| 731 | 27.03701 | ||
| 732 | 27.0555 | ||
| 733 | 27.07 397 | ||
| 734 | 27,09243 | ||
| 735 | 27,11088 | ||
| 736 | 27,12932 | ||
| 737 | 27,14774 | ||
| 738 | 27,16616 | ||
| 739 | 27,18455 | ||
| 740 | 27.20294 | ||
| 741 | 27.22132 | ||
| 742 | 27.23968 | ||
| 743 | 27.25803 | ||
| 744 | 27,27636 | ||
| 745 | 27,29469 | ||
| 746 | 27,313 | ||
| 747 | 27,3313 | ||
| 748 | 27,34959 | ||
| 749 | 27,36786 | ||
| 750 | 27.38613 | ||
| 751 | 27.40438 | ||
| 752 | 27.42262 | ||
| 753 | 27.44085 | ||
| 754 с | 27,45906 | ||
| 755 | 27,47726 | ||
| 756 | 27,49545 | ||
| 757 | 27,51363 | ||
| 758 | 27,5318 | ||
| 759 | 27,54995 | ||
| 760 | 27,5681 | ||
| 761 | 27,58623 | ||
| 762 | 27.60435 | ||
| 763 | 27.62245 | ||
| 764 | 27,64055 | ||
| 765 | 27,65863 | ||
| 766 | 27,67671 | ||
| 767 | 27,69476 | ||
| 768 | 27,71281 | ||
| 769 | 27,73085 | ||
| 770 | 27,74887 | ||
| 771 | 27,76689 | ||
| 772 | 27,78489 | ||
| 773 | 27.80288 | ||
| 774 | 27,82086 | ||
| 775 | 27,83882 | ||
| 776 | 27,85678 | ||
| 777 | 27,87472 | ||
| 778 | 27,89265 | ||
| 779 | 27, | ||
| 780 | 27. | ||
| 781 | 27. | ||
| 782 | 27. | ||
| 783 | 27. | ||
| 784 | 28 | ||
| 785 | 28,01785 | ||
| 786 | 28,03569 | ||
| 787 | 2|||
| 787 | 2|||
| 787 | 2|||
| 790 | 28.10694 | ||
| 791 | 28.12472 | ||
| 792 | 28.14249 | ||
| 793 | 28.16026 | ||
| 794 | 28,17801 | ||
| 795 | 28,19574 | ||
| 796 | 28,21347 | ||
| 797 | 28,23119 | ||
| 798 | 28,24889 | ||
| 799 | 28,26659 | ||
| 800 | 28.28427 | ||
| 801 | 28.30194 | ||
| 802 | 28.3196 | ||
| 803 | 28.33725 | ||
| 804 | 28,35489 | ||
| 805 | 28,37252 | ||
| 806 | 28,39014 | ||
| 807 | 28,40775 | ||
| 808 | 28,42534 | ||
| 809 | 28,44293 | ||
| 810 | 28.4605 | ||
| 811 | 28.47806 | ||
| 812 | 28.49561 | ||
| 813 | 28.51315 | ||
| 814 | 28,53069 | ||
| 815 | 28,5482 | ||
| 816 | 28,56571 | ||
| 817 | 28,58321 | ||
| 818 | 28,6007 | ||
| 819 | 28,61818 | ||
| 820 | 28.63564 | ||
| 821 | 28.6531 | ||
| 822 | 28.67054 | ||
| 823 | 28.68 798 | ||
| 824 | 28,7054 | ||
| 825 | 28,72281 | ||
| 826 | 28,74022 | ||
| 827 | 28,75761 | ||
| 828 | 28,77499 | ||
| 829 | 28,79236 | ||
| 830 | 28.80972 | ||
| 831 | 28.82707 | ||
| 832 | 28.84441 | ||
| 833 | 28.86174 | ||
| 834 | 28,87906 | ||
| 835 | 28,89637 | ||
| 836 | 28, | ||
| 837 | 28, | ||
| 838 | 28, | ||
| 839 | 28,9655 | ||
| 840 | 28. | ||
| 841 | 29 | ||
| 842 | 29.01724 | ||
| 843 | 29.03446 | ||
| 844 | 29,05168 | ||
| 845 | 29,06888 | ||
| 846 | 29,08608 | ||
| 847 | 29,10326 | ||
| 848 | 29,12044 | ||
| 849 | 29,1376 | ||
| 850 | 29.15476 | ||
| 851 | 29.1719 | ||
| 852 | 29.18904 | ||
| 853 | 29.20616 | ||
| 854 | 29,22328 | ||
| 855 | 29,24038 | ||
| 856 | 29,25748 | ||
| 857 | 29,27456 | ||
| 858 | 29,29164 | ||
| 859 | 29,3087 | ||
| 860 | 29.32576 | ||
| 861 | 29.3428 | ||
| 862 | 29.35984 | ||
| 863 | 29.37686 | ||
| 864 | 29,39388 | ||
| 865 | 29,41088 | ||
| 866 | 29,42788 | ||
| 867 | 29,44486 | ||
| 868 | 29,46184 | ||
| 869 | 29,47881 | ||
| 870 | 29.49576 | ||
| 871 | 29.51271 | ||
| 872 | 29.52965 | ||
| 873 | 29.54657 | ||
| 874 | 29,56349 | ||
| 875 | 29,5804 | ||
| 876 | 29,5973 | ||
| 877 | 29,61419 | ||
| 878 | 29,63106 | ||
| 879 | 29,64793 | ||
| 880 | 29,66479 | ||
| 881 | 29,68164 | ||
| 882 | 29,69848 | ||
| 883 | 29.71532 | ||
| 884 | 29,73214 | ||
| 885 | 29,74895 | ||
| 886 | 29,76575 | ||
| 887 | 29,78255 | ||
| 888 | 29,79933 | ||
| 889 | 29,8161 | ||
| 890 | 29.83287 | ||
| 891 | 29.84962 | ||
| 892 | 29.86637 | ||
| 893 | 29.88311 | ||
| 894 | 29,89983 | ||
| 895 | 29, | ||
| 896 | 29, | ||
| 897 | 29, | ||
| 898 | 29, | ||
| 899 | 29, | ||
| 900 | 30 | ||
| 901 | 30.01666 | ||
| 902 | 30.03331 | ||
| 903 | 30.04996 | ||
| 904 | 30,06659 | ||
| 905 | 30,08322 | ||
| 906 | 30,09983 | ||
| 907 | 30,11644 | ||
| 908 | 30,13304 | ||
| 909 | 30,14963 | ||
| 910 | 30.16621 | ||
| 911 | 30.18278 | ||
| 912 | 30.19934 | ||
| 913 | 30.21589 | ||
| 914 | 30,23243 | ||
| 915 | 30,24897 | ||
| 916 | 30,26549 | ||
| 917 | 30,28201 | ||
| 918 | 30,29851 | ||
| 919 | 30,31501 | ||
| 920 | 30.3315 | ||
| 921 | 30.34798 | ||
| 922 | 30.36445 | ||
| 923 | 30.38092 | ||
| 924 | 30,39737 | ||
| 925 | 30,41381 | ||
| 926 | 30,43025 | ||
| 927 | 30,44667 | ||
| 928 | 30,46309 | ||
| 929 | 30,4795 | ||
| 930 | 30,4959 | ||
| 931 | 30,51229 | ||
| 932 | 30,52868 | ||
| 933 | 30.54505 | ||
| 934 | 30,56141 | ||
| 935 | 30,57777 | ||
| 936 | 30,59412 | ||
| 937 | 30,61046 | ||
| 938 | 30,62679 | ||
| 939 | 30,64311 | ||
| 940 | 30.65942 | ||
| 941 | 30.67572 | ||
| 942 | 30.69202 | ||
| 943 | 30.70831 | ||
| 944 | 30,72458 | ||
| 945 | 30,74085 | ||
| 946 | 30,75711 | ||
| 947 | 30,77337 | ||
| 948 | 30,78961 | ||
| 949 | 30,80584 | ||
| 950 | 30,82207 | ||
| 951 | 30,83829 | ||
| 952 | 30,8545 | ||
| 953 | 30.8707 | ||
| 954 | 30,88689 | ||
| 955 | 30, | ||
| 956 | 30, | ||
| 957 | 30, | ||
| 958 | 30, | ||
| 959 | 30, | ||
| 960 | 30. | ||
| 961 | 31 | ||
| 962 | 31.01612 | ||
| 963 | 31.03 224 | ||
| 964 | 31,04835 | ||
| 965 | 31,06445 | ||
| 966 | 31,08054 | ||
| 967 | 31,09662 | ||
| 968 | 31,1127 | ||
| 969 | 31,12876 | ||
| 970 | 31.14482 | ||
| 971 | 31.16087 | ||
| 972 | 31.17691 | ||
| 973 | 31.19295 | ||
| 974 | 31.20897 | ||
| 975 | 31.22499 | ||
| 976 | 31.241 | 31.241 | |
| 977 | |||
| 977 | |||
| 980 | 31.30495 | ||
| 981 | 31.32092 | ||
| 982 | 31.33688 | ||
| 983 | 31.35283 | ||
| 984 | 31,36877 | ||
| 985 | 31,38471 | ||
| 986 | 31,40064 | ||
| 987 | 31,41656 | ||
| 988 | 31,43247 | ||
| 989 | 31,44837 | ||
| 990 | 31.46427 | ||
| 991 | 31.48015 | ||
| 992 | 31.49603 | ||
| 993 | 31.5119 | ||
| 994 | 31,52777 | ||
| 995 | 31,54362 | ||
| 996 | 31,55947 | ||
| 997 | 31,57531 | ||
| 998 | 31,59114 | ||
| 999 | 31,60696 | ||
| 1000 | 31.62278 |
Связанные
Часто используемые инструменты Miniwebtools:
Все минивеб-инструменты (отсортировано по названию):
PWA (прогрессивное веб-приложение) Инструменты (17) Финансовые калькуляторы (121) Здоровье и фитнес (31) Математика (161) Случайность (17) Спорт (8) Текстовые инструменты (30) Время и Дата (27) Инструменты для веб-мастеров (10) Хеш и контрольная сумма (8) Разное (108)Квадрат, куб, квадратный корень и кубический корень
Калькулятор квадрата, куба, квадратного корня и кубического корня
Квадрат, куб, квадратный корень и кубический корень для чисел с диапазоном 0-100
| Число x | Квадрат x 2 | Куб x 3 | Квадратный корень x 1/2 | Кубический корень x 1/3 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 902 1.000 | 1.000 | ||||||
| 2 | 4 | 8 | 1.414 | 1.260 | ||||||
| 3 | 9 | 27 | 1.732 | 4442672,000 | 1,587 | |||||
| 5 | 25 | 125 | 2,236 | 1,710 | ||||||
| 6 | 36 | 216 | 2.449 | 1,817 | ||||||
| 7 | 49 | 343 | 2,646 | 1,913 | ||||||
| 8 | 64 | 512 | 2,828 | 902 902512 | 2,828 | 902 902 9022,828 | 902 902 9023.000 | 2.080 | ||
| 10 | 100 | 1000 | 3.162 | 2.154 | ||||||
| 11 | 121 | 1331 | 3.317 | 2,224 | ||||||
| 12 | 144 | 1728 | 3,464 | 2,289 | ||||||
| 13 | 169 | 2197 | 3,602 902 902 902 | 902 902 902 902 902 902 902 902 902 9023,742 | 2,410 | |||||
| 15 | 225 | 3375 | 3,873 | 2,466 | ||||||
| 16 | 256 | 4096 | 4.000 | 2,520 | ||||||
| 17 | 289 | 4913 | 4,123 | 2,571 | ||||||
| 18 | 324 | 5832 | 4,243 19267 902 902 | 4,359 | 2,668 | |||||
| 20 | 400 | 8000 | 4,472 | 2,714 | ||||||
| 21 | 441 | 9261 | 4.583 | 2,759 | ||||||
| 22 | 484 | 10648 | 4,690 | 2,802 | ||||||
| 23 | 529 | 12167 | 902 902 902 902 | 12167 | 902 902 902 902 902 | 4,796 902 | 12167 | 902 902 902 902 902 | 4,899 | 2,884 |
| 25 | 625 | 15625 | 5.000 | 2,924 | ||||||
| 26 | 676 | 17576 | 17576 | 099 | 2,962 | |||||
| 27 | 729 | 19683 | 5,196 | 3,000 | ||||||
| 28 | 784 | 21952 | 902 902 902 902 | 21952 | 902 902 902 902 | 5,385 | 3,072 | |||
| 30 | 900 | 27000 | 5,477 | 3,107 | ||||||
| 31 | 961 | 29791 | 5.568 | 3,141 | ||||||
| 32 | 1024 | 32768 | 5,657 | 3,175 | ||||||
| 33 | 1089 | 35937 | 902 902 902 | 35937 | 902 902 902 902 902 902 9025,831 | 3,240 | ||||
| 35 | 1225 | 42875 | 5,916 | 3,271 | ||||||
| 36 | 1296 | 46656 | 000 | 3,302 | ||||||
| 37 | 1369 | 50653 | 6,083 | 3,332 | ||||||
| 38 | 1444 | 3,366 54872902 902 902 902 | 902 902 902 | 902 902 902 | 6,245 | 3,391 | ||||
| 40 | 1600 | 64000 | 6,325 | 3,420 | ||||||
| 41 | 1681 | 68921 | 6.403 | 3,448 | ||||||
| 42 | 1764 | 74088 | 6,481 | 3,476 | ||||||
| 43 | 1849 | 79507 | 902 902 902 | 79507 | 902 902 902 | 79507 | 902 902 902 | 6,633 | 3,530 | |
| 45 | 2025 | 6,708 | 3,557 | |||||||
| 46 | 2116 | 782 | 3,583 | |||||||
| 47 | 2209 | 103823 | 6,856 | 3,609 | ||||||
| 48 | 2304 | 110592 | 2302 | 110592 | 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 9027.000 | 3.659 | ||||
| 50 | 2500 | 125000 | 7.071 | 3.684 | ||||||
| 51 | 2601 | 132651 | 7141 | 3.708 | ||||||
| 52 | 2704 | 140608 | 7.211 | 3,733 | ||||||
| 53 | 2809 | 148877 | 2802 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 902 | 7,348 | 3,780 | |||||
| 55 | 3025 | 166375 | 7,416 | 3,803 | ||||||
| 56 | 3136 | 175616 | 483 | 3,826 | ||||||
| 57 | 3249 | 185193 | 7,550 | 3,849 | ||||||
| 58 | 3364 | 1 | 3364 | 1 | 902 902 902 902 902 | 902 902 902 902 902 902 9027,681 | 3,893 | |||
| 60 | 3600 | 216000 | 7,746 | 3,915 | ||||||
| 61 | 3721 | 226981 7 | 8103,936 | |||||||
| 62 | 3844 | 238328 | 7,874 | 3,958 | ||||||
| 63 | 3969 | 250047 | 250047 | 250047 | 7 | 8.000 | 4.000 | |||
| 65 | 4225 | 274625 | 8.062 | 4.021 | ||||||
| 66 | 4356 | 287496 | 124 | 4,041 | ||||||
| 67 | 4489 | 300763 | 8,185 | 4,062 | ||||||
| 68 | 4624 | 314432 | 8,246 902 902 | 314432 | 8,246 902 902 | 8,307 | 4,102 | |||
| 70 | 4900 | 343000 | 8,367 | 4,121 | ||||||
| 71 | 5041 | 356611 | 426 | 4,141 | ||||||
| 72 | 5184 | 373248 | 8,485 | 4,160 | ||||||
| 73 | 5329 | 389017 | 902 902 902 | 389017 | 902 902 902 | 389017 | 902 902 902 902 902 | 8,602 | 4,198 | |
| 75 | 5625 | 421875 | 8,660 | 4,217 | ||||||
| 76 | 5776 | 4389766 8,267 | 7184,236 | |||||||
| 77 | 5929 | 456533 | 8,775 | 4,254 | ||||||
| 78 | 6084 | 474552 | 902 902 902 902 902 902 902 902 902902 902 902 | 902 902 902 902 902 9028,888 | 4,291 | |||||
| 80 | 6400 | 512000 | 8,944 | 4,309 | ||||||
| 81 | 6561 | 531441 | 000 | 4,327 | ||||||
| 82 | 6724 | 551368 | 9,055 | 4,344 | ||||||
| 83 | 6889 | 571787 | 902 902 902 | 84252 902 902 902 84252 902 902 902 84252 902 9029,165 | 4,380 | |||||
| 85 | 7225 | 614125 | 9,220 | 4,397 | ||||||
| 86 | 7396 | 636056 | .2744,414 | |||||||
| 87 | 7569 | 658503 | 9,327 | 4,431 | ||||||
| 88 | 7744 | 681472 | 902 902 | 681472 | 902 902 9022 | 9,434 | 4,465 | |||
| 90 | 8100 | 729000 | 9,487 | 4,481 | ||||||
| 91 | 8281 | 75356671 | 5394,498 | |||||||
| 92 | 8464 | 778688 | 9,592 | 4,514 | ||||||
| 93 | 8649 | 804357 | 9,695 | 4,547 | ||||||
| 95 | 9025 | 857375 | 9,747 | 4,563 | ||||||
| 96 | 9216 | 884736 | 798 | 4,579 | ||||||
| 97 | 9409 | |||||||||
| 9,849 | 4,595 | |||||||||
| 98 | 9604 | 2 | 9604 | 2 | 9602 | 2 | 9.950 | 4.626 | ||
| 100 | 10000 | 1000000 | 10.000 | 4,642 |
Загрузите и распечатайте квадрат, куб, квадратный корень 900 и кубический корень
. 3D-модельИспользуйте расширение Engineering ToolBox Sketchup — чтобы добавить кубические линии в модели Sketchup.
Извлечение квадратного корня
Извлечение квадратного корня
Напомним, что квадратное уравнение имеет стандартную форму Любое квадратное уравнение имеет вид ax2 + bx + c = 0, где a , b и c — действительные числа и a 0. если он равен 0:
, где a , b и c — действительные числа и ≠ 0. Решение такого уравнения называется корневым решением квадратного уравнения в стандартной форме.. Квадратные уравнения могут иметь два действительных решения, одно действительное решение или не иметь реального решения. Если квадратное выражение слева множители, то мы можем решить его путем факторизации. Обзор шагов, используемых для решения с помощью факторинга, следующий:
Шаг 1: Выразите квадратное уравнение в стандартной форме.
Шаг 2: Разложите квадратное выражение на множители.
Шаг 3: Примените свойство нулевого произведения и установите каждый переменный коэффициент равным 0.
Шаг 4: Решите полученные линейные уравнения.
Например, мы можем решить x2−4 = 0, разложив на множители следующим образом:
Двумя решениями являются −2 и 2. Цель этого раздела — разработать альтернативный метод, который можно использовать для простого решения уравнений, где b = 0, что дает форму
Уравнение x2−4 = 0 находится в этой форме и может быть решено путем выделения x2 вначале.
Если извлечь квадратный корень из обеих частей этого уравнения, мы получим следующее:
Здесь мы видим, что x = −2 и x = 2 являются решениями полученного уравнения. В общем, это описывает свойство квадратного корня для любого действительного числа k , если x2 = k, то x = ± k .; для любого действительного числа к ,
Обозначение «±» читается как «плюс или минус» и используется как компактное обозначение, обозначающее два решения.Следовательно, утверждение x = ± k указывает, что x = −k или x = k. Применение свойства квадратного корня как средства решения квадратного уравнения называется извлечением корней Применение свойства квадратного корня как средства решения квадратного уравнения.
Пример 1: Решить: x2−25 = 0.
Решение: Начните с выделения квадрата.
Затем примените свойство квадратного корня.
Ответ: Решения — 5 и 5.Чек предоставляется читателю.
Конечно, предыдущий пример можно было бы так же легко решить с помощью факторинга. Тем не менее, он демонстрирует метод, который можно использовать для решения уравнений в этой форме, которые не учитывают факторы.
Пример 2: Решить: x2−5 = 0.
Решение: Обратите внимание, что квадратное выражение слева не учитывается. Мы можем извлечь корни, если сначала выделим главный член x2.
Примените свойство квадратного корня.
Для полноты проверьте, что эти два действительных решения решают исходное квадратное уравнение. Как правило, проверка не является обязательной.
Ответ: Решения — 5 и 5.
Пример 3: Решить: 4×2−45 = 0.
Решение: Начните с изоляции x2.
Примените свойство квадратного корня, а затем упростите.
Ответ: Решения — 352 и 352.
Иногда квадратные уравнения не имеют реального решения.
Пример 4: Решить: x2 + 9 = 0.
Решение: Начните с изоляции x2.
После применения свойства квадратного корня у нас остается квадратный корень из отрицательного числа. Следовательно, у этого уравнения нет реального решения.
Ответ: Реального решения нет
Обратитесь к этому процессу, чтобы найти уравнения с заданными решениями вида ± k .
Пример 5: Найдите уравнение с решениями −23 и 23.
Решение: Начните с возведения в квадрат обеих частей следующего уравнения:
Наконец, вычтите 12 из обеих частей и представьте уравнение в стандартной форме.
Ответ: x2−12 = 0
Попробуй! Решить: 9×2−8 = 0.
Ответ: x = −223 или x = 223
Рассмотрите возможность решения следующего уравнения:
Чтобы решить это уравнение путем факторизации, сначала возведите в квадрат x + 2, а затем представьте его в стандартной форме, равной нулю, путем вычитания 25 из обеих частей.
Коэффициент, а затем применить свойство нулевого продукта.
Два решения: −7 и 3.
Когда уравнение имеет такую форму, мы можем получить решения за меньшее количество шагов, извлекая корни.
Пример 6: Решить: (x + 2) 2 = 25.
Решение: Решить, извлекая корни.
На этом этапе разделите «плюс или минус» на два уравнения и упростите каждое по отдельности.
Ответ: Решения -7 и 3.
В дополнение к меньшему количеству шагов этот метод позволяет нам решать уравнения, не учитывающие множители.
Пример 7: Решите: (3x + 3) 2−27 = 0.
Решение: Начните с выделения квадрата.
Затем извлеките корни и упростите.
Решите относительно x .
Ответ: Решения: −1−3 и −1 + 3.
Пример 8: Решить: 9 (2x − 1) 2−8 = 0.
Решение: Начните с выделения квадратного множителя.
Примените свойство квадратного корня и решите.
Ответ: Решения 3−226 и 3 + 226.
Попробуй! Решите: 3 (x − 5) 2−2 = 0.
Ответ: 15 ± 63
Пример 9: Длина прямоугольника вдвое больше его ширины. Если диагональ составляет 2 фута, найдите размеры прямоугольника.
Решение:
Диагональ любого прямоугольника образует два прямоугольных треугольника. Таким образом, применима теорема Пифагора. Сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы:
Решить.
Здесь мы получаем два решения, w = −25 и w = 25. Поскольку в задаче требовалась длина прямоугольника, мы игнорируем отрицательный ответ. Кроме того, мы рационализируем знаменатель и представим наши решения без каких-либо радикалов в знаменателе.
Обратно подставьте, чтобы найти длину.
Ответ: Длина прямоугольника составляет 455 футов, а ширина — 255 футов.
Основные выводы
- Решите уравнения вида ax2 + c = 0, извлекая корни.
- Извлечение корней включает выделение квадрата и последующее применение свойства квадратного корня. После применения свойства квадратного корня у вас есть два линейных уравнения, каждое из которых можно решить. Обязательно упростите все радикальные выражения и при необходимости рационализируйте знаменатель.
Тематические упражнения
Часть A: извлечение квадратного корня
Решите, разложив на множители, а затем вычислив корни.Проверить ответы.
1. x2−36 = 0
2. x2−81 = 0
3. 4y2−9 = 0
4. 9y2−25 = 0
5. (x − 2) 2−1 = 0
6. (x + 1) 2−4 = 0
7. 4 (y − 2) 2−9 = 0
8. 9 (y + 1) 2−4 = 0
9. −3 (t − 1) 2 + 12 = 0
10. −2 (t + 1) 2 + 8 = 0
11. (x − 5) 2−25 = 0
12. (x + 2) 2−4 = 0
Решите, извлекая корни.
13. x2 = 16
14. x2 = 1
15. y2 = 9
16. y2 = 64
17. x2 = 14
18. x2 = 19
19. y2 = 0,25
20. y2 = 0,04
21. x2 = 12
22. x2 = 18
23. 16×2 = 9
24. 4×2 = 25
25. 2t2 = 1
26.3t2 = 2
27. x2−100 = 0
28. x2−121 = 0
29. y2 + 4 = 0
30. y2 + 1 = 0
31. x2−49 = 0
32. x2−925 = 0
33. y2−0.09 = 0
34. y2−0,81 = 0
35. x2−7 = 0
36. x2−2 = 0
37. x2−8 = 0
38. t2−18 = 0
39. x2 + 8 = 0
40.х2 + 125 = 0
41. 16×2−27 = 0
42. 9×2-8 = 0
43. 2y2−3 = 0
44. 5y2−2 = 0
45. 3×2−1 = 0
46. 6×2−3 = 0
47. (x + 7) 2−4 = 0
48. (x + 9) 2−36 = 0
49. (2y − 3) 2−81 = 0
50. (2у + 1) 2−25 = 0
51. (x − 5) 2−20 = 0
52. (x + 1) 2−28 = 0
53.(3t + 2) 2−6 = 0
54. (3т − 5) 2−10 = 0
55,4 (y + 2) 2−3 = 0
56. 9 (y − 7) 2−5 = 0
57,4 (3x + 1) 2−27 = 0
58. 9 (2x − 3) 2−8 = 0
59. 2 (3x − 1) 2 + 3 = 0
60,5 (2x − 1) 2−3 = 0
61,3 (y − 23) 2−32 = 0
62. 2 (3y − 13) 2−52 = 0
Найдите квадратное уравнение стандартной формы со следующими решениями.
63. ± 7
64. ± 13
65. ± 7
66. ± 3
67. ± 35
68. ± 52
69. 1 ± 2
70,2 ± 3
Решите и округлите решения до ближайшей сотой.
71. 9x (x + 2) = 18x + 1
72. x2 = 10 (x2−2) −5
73. (x + 3) (x − 7) = 11−4x
74.(x − 4) (x − 3) = 66−7x
75. (x − 2) 2 = 67−4x
76. (x + 3) 2 = 6x + 59
77. (2x + 1) (x + 3) — (x + 7) = (x + 3) 2
78. (3x − 1) (x + 4) = 2x (x + 6) — (x − 3)
Составьте алгебраическое уравнение и используйте его для решения следующих задач.
79. Если 9 вычесть из четырех квадратов числа, то результат будет 3. Найдите число.
80. Если из квадрата числа вычесть 20, то получится 4.Найдите номер.
81. Если 1 прибавить к троекратному квадрату числа, то получится 2. Найдите число.
82. Если 3 прибавить к двукратному квадрату числа, получится 12. Найдите число.
83. Если квадрат имеет площадь 8 квадратных сантиметров, найдите длину каждой стороны.
84. Если круг имеет площадь 32π квадратных сантиметра, найдите длину радиуса.
85.Объем правого кругового конуса составляет 36π кубических сантиметров при высоте 6 сантиметров. Найдите радиус конуса. (Объем правого кругового конуса равен V = 13πr2h.)
86. Площадь поверхности сферы составляет 75π квадратных сантиметров. Найдите радиус сферы. (Площадь поверхности сферы определяется как SA = 4πr2.)
87. Длина прямоугольника в 6 раз больше его ширины. Если площадь составляет 96 квадратных дюймов, найдите размеры прямоугольника.
88. Основание треугольника вдвое больше его высоты. Если площадь составляет 16 квадратных сантиметров, то найдите длину его основания.
89. Квадрат имеет площадь 36 квадратных единиц. На какую равную величину необходимо увеличить стороны, чтобы получить квадрат с удвоенной заданной площадью?
90. Круг имеет площадь 25π квадратных единиц. На какую величину нужно увеличить радиус, чтобы создать круг с удвоенной заданной площадью?
91.Если стороны квадрата равны 1 единице, то найдите длину диагонали.
92. Если стороны квадрата равны 2 единицам, найдите длину диагонали.
93. Диагональ квадрата составляет 5 дюймов. Найдите длину каждой стороны.
94. Диагональ квадрата составляет 3 дюйма. Найдите длину каждой стороны.
95. Длина прямоугольника вдвое больше его ширины. Если диагональ составляет 10 футов, найдите размеры прямоугольника.
96. Длина прямоугольника вдвое больше его ширины. Если диагональ составляет 8 футов, найдите размеры прямоугольника.
97. Длина прямоугольника в 3 раза больше его ширины. Если диагональ 5 метров, то найдите размеры прямоугольника.
98. Длина прямоугольника в 3 раза больше его ширины. Если диагональ составляет 2 фута, найдите размеры прямоугольника.
99. Высота в футах объекта, падающего с 9-футовой лестницы, определяется выражением h (t) = — 16t2 + 9, где t представляет время в секундах после того, как объект был сброшен.Сколько времени нужно, чтобы объект упал на землю? (Подсказка: когда объект ударяется о землю, высота равна 0.)
100. Высота в футах объекта, сброшенного с 20-футовой платформы, определяется выражением h (t) = — 16t2 + 20, где t представляет время в секундах после падения объекта. Сколько времени нужно, чтобы объект упал на землю?
101. Высота в футах объекта, падающего с вершины 144-футового здания, определяется выражением h (t) = — 16t2 + 144, где t измеряется в секундах.
а. Сколько времени потребуется, чтобы достичь половины расстояния до земли, 72 фута?
г. Сколько времени потребуется, чтобы добраться до земли?
Округлите до сотых долей секунды.
102. Высота в футах объекта, сброшенного с самолета на высоте 1600 футов, определяется как h (t) = — 16t2 + 1,600, где t — в секундах.
а. Сколько времени потребуется, чтобы добраться до земли на половину расстояния?
г.Сколько времени потребуется, чтобы добраться до земли?
Округлить до сотых долей секунды .
Часть B: Обсуждение
103. Создайте собственное уравнение, которое можно решить, извлекая корень. Поделитесь им и решением на доске обсуждений.
104. Объясните, почему метод извлечения корней значительно расширяет наши возможности решать квадратные уравнения.
105. Объясните своими словами, как решить, извлекая корни.
106. Выведите формулу диагонали квадрата через его стороны.
ответов
1: −6, 6
3: −3/2, 3/2
5: 1, 3
7: 1/2, 7/2
9: -1, 3
11: 0, 10
13: ± 4
15: ± 3
17: ± 1/2
19: ± 0.5
21: ± 23
23: ± 3/4
25: ± 22
27: ± 10
29: Реального решения нет
31: ± 2/3
33: ± 0,3
35: ± 7
37: ± 22
39: Реального решения нет
41: ± 334
43: ± 62
45: ± 33
47: −9, −5
49: −3, 6
51: 5 ± 25
53: −2 ± 63
55: −4 ± 32
57: -2 ± 336
59: Реального решения нет
61: 4 ± 326
63: x2−49 = 0
65: x2−7 = 0
67: x2-45 = 0
69: x2−2x − 1 = 0
71: ± 0.33
73: ± 5,66
75: ± 7,94
77: ± 3.61
79: −3 или 3
81: −33 или 33
83:22 сантиметра
85:32 сантиметра
87: Длина: 24 дюйма; ширина: 4 дюйма
89: −6 + 62≈2,49 ед.
91: 2 шт.
93: 522 дюйма
95: Длина: 45 футов; ширина: 25 футов
97: Длина: 3102 метра; ширина: 102 метра
99: 3/4 секунды
101: а.2,12 секунды; б. 0,88 секунды
Wolfram | Примеры альфа: арифметика
Сложение и вычитание
Выполните сложение и вычитание.
Совместите сложение и вычитание:
Создайте таблицу сложения:
Другие примеры
Умножение и деление
Выполните умножение и деление.
Создайте таблицу умножения:
Другие примеры
Силы и корни
Вычислить степени и корни числа.
Другие примеры
Множественные операции
Выполните комбинацию арифметических операций.
Совместите несколько арифметических операций:
Другие примеры
Решение кубических уравнений — методы и примеры
Решение полиномиальных уравнений высшего порядка — важный навык для любого, кто изучает естественные науки и математику.Однако понять, как решать такие уравнения, довольно сложно.
В этой статье будет обсуждаться, как решать кубические уравнения, используя различные методы, такие как метод деления, теорема о множителях и разложение на множители по группировке.
Но прежде чем перейти к этой теме, давайте обсудим , что такое полиномиальное и кубическое уравнение.
Многочлен — это алгебраическое выражение с одним или несколькими членами, в которых знак сложения или вычитания разделяет константу и переменную.
Общая форма многочлена: ax n + bx n-1 + cx n-2 +…. + kx + l, где каждая переменная сопровождается константой в качестве коэффициента. Различные типы полиномов включают в себя; двучлены, трехчлены и четырехчлены. Примеры полиномов: 3x + 1, x 2 + 5xy — ax — 2ay, 6x 2 + 3x + 2x + 1 и т. Д.
Кубическое уравнение — это алгебраическое уравнение третьей степени.
Общий вид кубической функции: f (x) = ax 3 + bx 2 + cx 1 + d.Кубическое уравнение имеет вид ax 3 + bx 2 + cx + d = 0, где a, b и c — коэффициенты, а d — постоянная.
Как решать кубические уравнения?
Традиционный способ решения кубического уравнения — свести его к квадратному уравнению, а затем решить его либо факторизацией, либо квадратной формулой.
Подобно тому, как квадратное уравнение имеет два действительных корня , кубическое уравнение может иметь три действительных корня. Но в отличие от квадратного уравнения, которое может не иметь реального решения, кубическое уравнение имеет по крайней мере один действительный корень.
Два других корня могут быть действительными или мнимыми.
Всякий раз, когда вам задают кубическое уравнение или какое-либо уравнение, вы всегда должны сначала преобразовать его в стандартную форму.
Например, если вам дано что-то вроде этого, 3x 2 + x — 3 = 2 / x, вы перегруппируете его в стандартную форму и напишете это как, 3x 3 + x 2 — 3x — 2 = 0. Тогда вы можете решить это любым подходящим методом.
Давайте рассмотрим несколько примеров ниже для лучшего понимания:
Пример 1
Определите корни кубического уравнения 2x 3 + 3x 2 — 11x — 6 = 0
Решение
Так как d = 6, то возможными множителями являются 1, 2, 3 и 6.
Теперь примените теорему о факторах, чтобы проверить возможные значения методом проб и ошибок.
f (1) = 2 + 3 — 11 — 6 ≠ 0
f (–1) = –2 + 3 + 11 — 6 ≠ 0
f (2) = 16 + 12 — 22 — 6 = 0
Следовательно, x = 2 — первый корень.
Мы можем получить другие корни уравнения, используя метод синтетического деления.
= (x — 2) (ax 2 + bx + c)
= (x — 2) (2x 2 + bx + 3)
= (x — 2) (2x 2 + 7x + 3 )
= (x — 2) (2x + 1) (x +3)
Следовательно, решения следующие: x = 2, x = -1/2 и x = -3.
Пример 2
Найдите корни кубического уравнения x 3 — 6x 2 + 11x — 6 = 0
Решение
x 3 — 6x 2 + 11x — 6
(x — 1) — один из факторов.
Разделив x 3 — 6x 2 + 11x — 6 на (x — 1),
⟹ (x — 1) (x 2 — 5x + 6) = 0
⟹ (x — 1) (x — 2) (x — 3) = 0
Это решение кубического уравнения: x = 1, x = 2 и x = 3.
Пример 3
Решить x 3 — 2x 2 — x + 2
Решение
Факторизуйте уравнение.
x 3 — 2x 2 — x + 2 = x 2 (x — 2) — (x — 2)
= (x 2 — 1) (x — 2)
= (x + 1) (x — 1) (x — 2)
x = 1, -1 и 2.
Пример 4
Решите кубическое уравнение x 3 — 23x 2 + 142x — 120
Решение
Сначала разложите полином на множители.
x 3 — 23x 2 + 142x — 120 = (x — 1) (x 2 — 22x + 120)
Но x 2 — 22x + 120 = x 2 — 12x — 10x + 120
= x (x — 12) — 10 (x — 12)
= (x — 12) (x — 10)
Следовательно, x 3 — 23x 2 + 142x — 120 = ( x — 1) (x — 10) (x — 12)
Приравняйте каждый множитель к нулю.
x — 1 = 0
x = 1
x — 10 = 10
x — 12 = 0
x = 12
Корни уравнения — x = 1, 10 и 12.
Пример 5
Решите кубическое уравнение x 3 — 6 x 2 + 11x — 6 = 0.
Решение
Чтобы решить эту задачу методом деления, возьмите любой множитель постоянная 6;
let x = 2
Разделите многочлен на x-2 до
(x 2 — 4x + 3) = 0.
Теперь решите квадратное уравнение (x 2 — 4x + 3) = 0 чтобы получить x = 1 или x = 3
Следовательно, решения следующие: x = 2, x = 1 и x = 3.
Пример 6
Решите кубическое уравнение x 3 — 7x 2 + 4x + 12 = 0
Решение
Пусть f (x) = x 3 — 7x 2 + 4x + 12
Поскольку d = 12, возможные значения — 1, 2, 3, 4, 6 и 12.
Методом проб и ошибок мы находим, что f (–1) = –1 — 7 — 4 + 12 = 0
Итак, (x + 1) является множителем функции.
x 3 — 7x 2 + 4x + 12
= (x + 1) (x 2 — 8x + 12)
= (x + 1) (x — 2) (x — 6)
Следовательно, x = –1, 2, 6
Пример 7
Решите следующее кубическое уравнение:
x 3 + 3x 2 + x + 3 = 0.
Решение
x 3 + 3x 2 + x + 3
= (x 3 + 3x 2 ) + (x + 3)
= x 2 (x + 3) + 1 (x + 3)
= (x + 3) (x 2 + 1)
Следовательно, x = -1, 1-3.
Пример 8
Решить x 3 — 6x 2 + 11x — 6 = 0
Решение
Разложить на множители
x 3 — 6x 2 — 6000 0 ⟹ (x — 1) (x — 2) (x — 3) = 0
Приравнивание каждого множителя к нулю дает;
x = 1, x = 2 и x = 3
Пример 9
Решить x 3 — 4x 2 — 9x + 36 = 0
Решение
Разложить каждый набор два срока.
x 2 (x — 4) — 9 (x — 4) = 0
Извлеките общий множитель (x — 4), чтобы получить
(x 2 — 9) (x — 4) = 0
Теперь разложите разность двух квадратов на множители
(x + 3) (x — 3) (x — 4) = 0
Приравнивая каждый множитель к нулю, мы получаем;
x = −3, 3 или 4
Пример 10
Решите уравнение 3x 3 −16x 2 + 23x — 6 = 0
Решение
Divide 3x 3 3 −16x 2 + 23x — 6 на x -2, чтобы получить 3x 2 — 1x — 9x + 3
= x (3x — 1) — 3 (3x — 1)
= (x — 3) ( 3x — 1)
Следовательно, 3x 3 −16x 2 + 23x — 6 = (x- 2) (x — 3) (3x — 1)
Приравняем каждый множитель к нулю, чтобы получить,
x = 2, 3 и 1/3
Пример 11
Найдите корни 3x 3 — 3x 2 — 90x = 0
Решение
множитель 3x
3x 3 — 3x 2 — 90x ⟹3x (x 2 — x — 30)
Найдите пару множителей, произведение которых равно −30, а сумма равна −1.
⟹- 6 * 5 = -30
⟹ −6 + 5 = -1
Перепишите уравнение, заменив член «bx» на выбранные множители.
⟹ 3x [(x 2 — 6x) + (5x — 30)]
Разложите уравнение на множители;
⟹ 3x [(x (x — 6) + 5 (x — 6)]
= 3x (x — 6) (x + 5)
Приравнивая каждый множитель к нулю, получаем:
x = 0, 6, -5
Решение кубических уравнений с использованием графического метода
Если вы не можете решить кубическое уравнение ни одним из вышеперечисленных методов, вы можете решить его графическим способом.Для этого вам необходимо иметь точный набросок данного кубического уравнения.
Точка (точки), где его график пересекает ось x, является решением уравнения. Количество реальных решений кубических уравнений равно количеству пересечений его графиком оси абсцисс.
Пример 12
Найдите корни x 3 + 5x 2 + 2x — 8 = 0 графически.
Решение
Просто нарисуйте график следующей функции, подставив случайные значения x:
f (x) = x 3 + 5x 2 + 2x — 8
Вы можете увидеть График отсекает ось абсцисс в 3 точках, следовательно, существует 3 реальных решения.
На графике решения следующие:
x = 1, x = -2 & x = -4.
Практические вопросыРешите следующие кубические уравнения:
- x 3 — 4x 2 — 6x + 5 = 0
- 2x 3 — 3x 2 — 4x — 35 = 0
- x 3 — 3x 2 — x + 1 = 0
- x 3 + 3x 2 — 6x — 8 = 0
- x 3 + 4x 2 + 7x + 6 = 0
- 2x 3 + 9x 2 + 3x — 4 = 0
- x 3 + 9x 2 + 26x + 24 = 0
- x 3 — 6x 2 — 6x — 7 = 0
- x 3 — 7x — 6 = 0
- x 3 — 5x 2 — 2x + 24 = 0
- 2x 3 + 3x 2 + 8x + 12 = 0
- 5x 3 — 2x 2 + 5x — 2 = 0
- 4x 3 + x 2 — 4x — 1 = 0
- 5x 3 — 2x 2 + 5x — 2 = 0
- 4x 3 900 04 — 3x 2 + 20x — 15 = 0
- 3x 3 + 2x 2 — 12x — 8 = 0
- x 3 + 8 = 0
- 2x 3 — x 2 + 2x — 1 = 0
- 3x 3 — 6x 2 + 2x — 4 = 0
- 3x 3 + 5x 2 — 3x — 5 = 0