Алгебра окружность: Числовая окружность, макеты числовой окружности — урок. Алгебра, 10 класс.

Содержание

Числовая окружность в 10 классе по алгебре, урок и презентация

Дата публикации: 09 апреля 2017.

Урок и презентация на тему: «Числовая окружность: определение, общий вид, длина. Единичная окружность»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.

Скачать:Числовая окружность (PPTX )

Что будем изучать:
1. Числовая окружность в жизни.
2. Определение числовой окружности.
3. Общий вид и длина числовой окружности.
4. Местонахождение основных точек окружности.

Числовая окружность и жизнь

В реальной жизни часто встречается движение по окружности. Например, соревнования велосипедистов, которые проезжают определенный круг на время или соревнования гоночных автомобилей, которым надо проехать наибольшее количество кругов за отведенное время.

Рассмотрим конкретный пример…

Бегун бежит по кругу длиной 400 метров. Спортсмен стартует в точке А (рис. 1) и движется против часовой стрелки. Где он будет находится через 200 м, 800 м, 1500 м? А где провести финишную черту, если бегуну необходимо пробежать 4195 м?
Решение:
Через 200 м бегун будет находиться в точке С. Так как он пробежит ровно половину дистанции.

Пробежав 800 м, бегун сделает ровно два круга и окажется в точке А.

1500м – это 3 круга по 400 м (1200 м) и еще 300 м , то есть $\frac{3}{4}$ от беговой дорожки, финиш этой дистанции в точке D.

Где будет находиться наш бегун пробежав 4195 м? 10 кругов – это 4000 м, останется пробежать 195 м, это на 5 м меньше, чем половина дистанции. Значит финиш будет в точки K, расположенной около точки С.

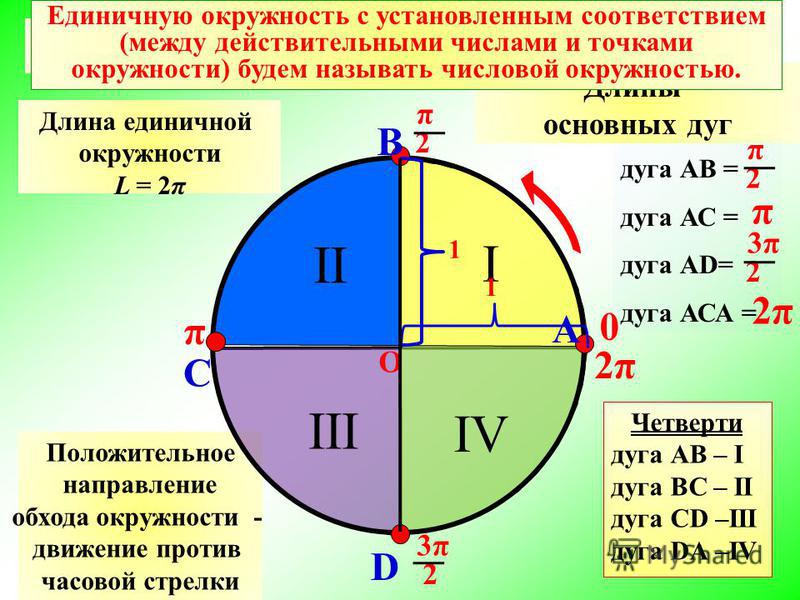
Определение числовой окружности

Запомните!
Числовая окружность – это единичная окружность, точки которой соответствуют определенным действительным числам.

Единичной окружностью называют окружность радиуса 1.

Общий вид числовой окружности

1) Радиус окружности принимается за единицу измерения.
2) Горизонтальный диаметр обозначают AC, причем А – это крайняя правая точка.
Вертикальный диаметр обозначают BD, причем B – это крайняя верхняя точка.

Диаметры АС и BD делят окружность на четыре четверти:
первая четверть – это дуга AB.
вторая четверть – дуга BC.
третья четверть – дуга CD.
четвертая четверть – дуга DA.

3) Начальная точка числовой окружности – точка А.
Отсчет от точки А против часовой стрелки называется положительным направлением. Отсчет от точки А по часовой стрелке называется отрицательным направлением.

Длина числовой окружности

Длина числовой окружности вычисляется по формуле:
$L = 2 π * R = 2 π * 1 = 2 π$.
Так как это единичная окружность, то $R = 1$.
Если взять $π ≈ 3,14$, то длина окружности L может быть выражена числом:
$2 π ≈ 2 * 3,14 = 6,28$.

Длина каждой четверти равна: $\frac{1}{4}*2π=\frac{π}{2}$.

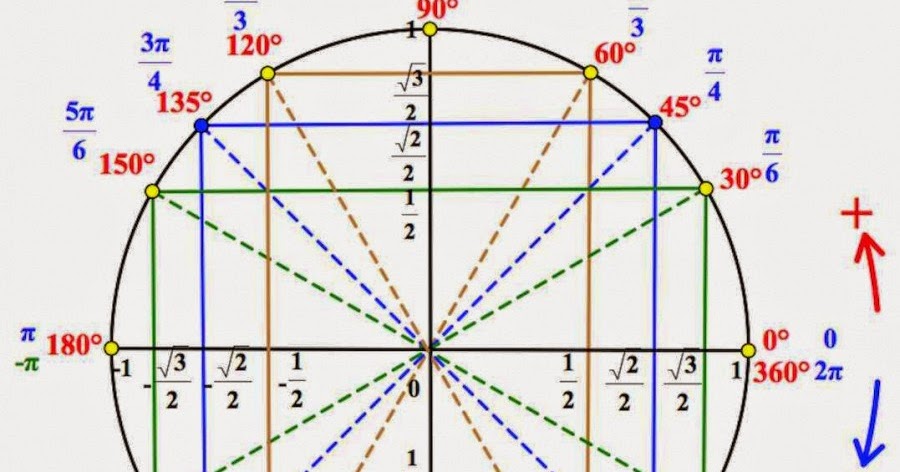
Местонахождение основных точек окружности

Основные точки на окружности и их названия представлены на рисунке:

Каждая из четырёх четвертей числовой окружности разделена на три равные части. Около каждой из полученных двенадцати точек записано число, которому она соответствует.

Для числовой окружности верно следующее утверждение:

Если точка $М$ числовой окружности соответствует числу $t$ , то она соответствует и числу вида $t+2π *k$, где $k$ – целое число. $М(t) = M(t+2π*k)$.

Рассмотрим пример.
В единичной окружности дуга АВ разделена точкой М на две равные части, а точками К и Р — на три равные части. Чему равна длина дуги: AM, МВ, АК, КР, РB, АР, КМ?

Длина дуги $АВ =\frac{π}{2}$. Разделив ее на две равные части точкой М, получим две дуги, длиной $\frac{π}{4}$ каждая. Значит, $AM =МВ=\frac{π}{4}$.

Дуга АВ разбита на три равные части точками К и Р. Длина каждой полученной части равна $\frac{1}{3}* \frac{π}{2}$, т. е. $\frac{π}{6}$. Значит, $АК = КР = РВ =\frac{π}{6}$.

Дуга АР состоит из двух дуг АК и КР длиной — $\frac{π}{6}$. Значит, $АР = 2 *\frac{π}{6} =\frac{π}{3}$.

Осталось вычислить длину дуги КМ. Эта дуга получается из дуги AM исключением дуги АК. Таким образом, $КМ = AM – АК =\frac{π}{4} — \frac{π}{6} = \frac{π}{12}$.

Задача:

Найти на числовой окружности точку, которая соответствует заданному числу:
$2π$, $\frac{7π}{2}$, $\frac{π}{4}$, $-\frac{3π}{2}$.

Решение:

Числу $2π$ соответствует точка А, т.к. пройдя по окружности путь длиной $2π$, т.е. ровно одну окружность, мы опять попадем в точку А.

Числу $\frac{7π}{2}$ соответствует точка D, т.к. $\frac{7π}{2}=2π+\frac{3π}{2}$, т.е. двигаясь в положительном направлении, нужно пройти целую окружность и дополнительно путь длиной $\frac{3π}{2}$, который закончится в точке D.

Числу $\frac{π}{4}$ соответствует точка М, т.к. двигаясь в положительном направлении, нужно пройти путь в половину дуги АВ длиной $\frac{π}{2}$, который закончится в точке M.

Числу $-\frac{3π}{2}$ соответствует точка В, т.к. двигаясь в отрицательном направлении из точки А, нужно пройти путь длиной $\frac{3π}{2}$, который закончится в точке В.

Пример.

Найти на числовой окружности точки:
а) $21\frac{π}{4}$;
б) $-37\frac{π}{6}$.

Решение:
Воспользуемся формулой: $М(t) = M(t+2π*k)$ (8 слайд) получим:

а) $\frac{21π}{4} = (4+\frac{5}{4})*π = 4π +\frac{5π}{4} = 2*2π +\frac{5π}{4}$, значит числу $\frac{21π}{4}$ соответствует такое же число, что и числу $\frac{5}{4π}$ – середина третьей четверти.

б) $-\frac{37π}{6}=-(6+\frac{1}{6})*π =-(6π +\frac{π}{6}) = -3*2π — \frac{π }{6}$. Значит, числу $-\frac{37π}{6}$ соответствует такое же число, что и числу $-\frac{1}{6π}$. Тоже самое, что и $\frac{11π}{6}$.

Пример.

Найти все числа t, которым на числовой окружности соответствуют точки, принадлежащие заданной дуге:
а) ВА;
б) МK.

Решение:

а) Дуга ВА – это дуга с началом в точке В и концом в точке А, при движении по окружности против часовой стрелки.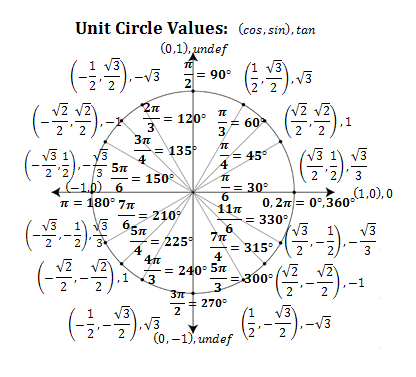 Точка В соответственно равна $\frac{π}{2}$, а точка А равна $2π$. Значит, для точек t имеем: $\frac{π}{2} ≤ t ≤ 2π$. Но согласно формуле на слайде 8, числам $\frac{π}{2}$ и $2π$ соответствуют числа вида $\frac{π}{2}+2π*k$ и $2π+2π*k$ соответственно.
Тогда наше число t принимает значения:

$\frac{π}{2} +2π*k ≤ t ≤ 2π +2π*k$, где $к$ – целое число.

б) Дуга МK – это дуга с началом в точке М и концом в точке К. Точка М соответственно равна $-\frac{3π}{4}$, а точка К равна $\frac{π}{4}$.
Значит для точек t имеем:
$\frac{-3π}{4} ≤ t ≤\frac{π}{4}$.
Согласно формуле на слайде 8 числам $-\frac{3π}{4}$ и $\frac{π}{4}$ соответствуют числа вида: $-\frac{3π}{4}+2π*k$ и $\frac{π}{4}+2π*k$ соответственно.
Тогда наше число t принимает значения:
$-\frac{3π}{4}+2π*k ≤ t ≤ \frac{π}{4} +2π*k$, где $к$ – целое число.

Задачи для самостоятельного решения

1) На единичной окружности дуга ВС разделена точкой Т на две равные части, а точками К и Р на три равные части. 2} = 36.\)

Задача 3. В одной системе координат постройте прямую $y = x$ и окружность с центром в начале координат и радиусом 3. Определите координаты их точек пересечения.

Ответ

ОТВЕТ: $\left( {\frac{3}{{\sqrt 2 }};\frac{3}{{\sqrt 2 }}} \right),\;\;\left( { — \frac{3}{{\sqrt 2 }}; — \frac{3}{{\sqrt 2 }}} \right).$

Задача 4. В одной системе координат постройте прямую $y = — x$ и окружность с центром в начале координат и радиусом 3. Определите координаты их точек пересечения.

Ответ

ОТВЕТ: $\left( { — \frac{3}{{\sqrt 2 }};\frac{3}{{\sqrt 2 }}} \right),\;\;\left( {\frac{3}{{\sqrt 2 }}; — \frac{3}{{\sqrt 2 }}} \right).$

Задача 5. Окружность с центром в начале координат проходит через точку $A\left( { — 1;3} \right).$ Проходит ли эта окружность через точку $B\left( {\sqrt 2 ; — 2\sqrt 2 } \right)?$

Ответ

ОТВЕТ: Проходит.

Задача 6. 2} = a,} \\   {x + y = 1\,\,\,\,\,\,\,} \end{array}} \right.\) имеет ровно два различных решения?
Ответ
ОТВЕТ: $\left( {0,5;\, + \infty } \right).$
Задача 28. Найдите радиус окружности R на плоскости, которая одновременно касается осей абсцисс и ординат и проходит через точку с координатами $\left( {\,1;\,1} \right)$.
Ответ
ОТВЕТ: $2 \pm \sqrt 2 .$
Реклама
Поддержать нас
OpenAlgebra.com: Круги
Окружность — это множество точек, равноудаленных от фиксированной точки, называемой центром. Расстояние от центра до любой точки называется радиусом. Вспомните следующие формулы из геометрии:

Окружность можно рассматривать как периметр круга. В этом разделе нас будут интересовать уравнения, описывающие окружности.

Из уравнения окружности в стандартной форме видно, что окружность полностью определяется своим центром и радиусом.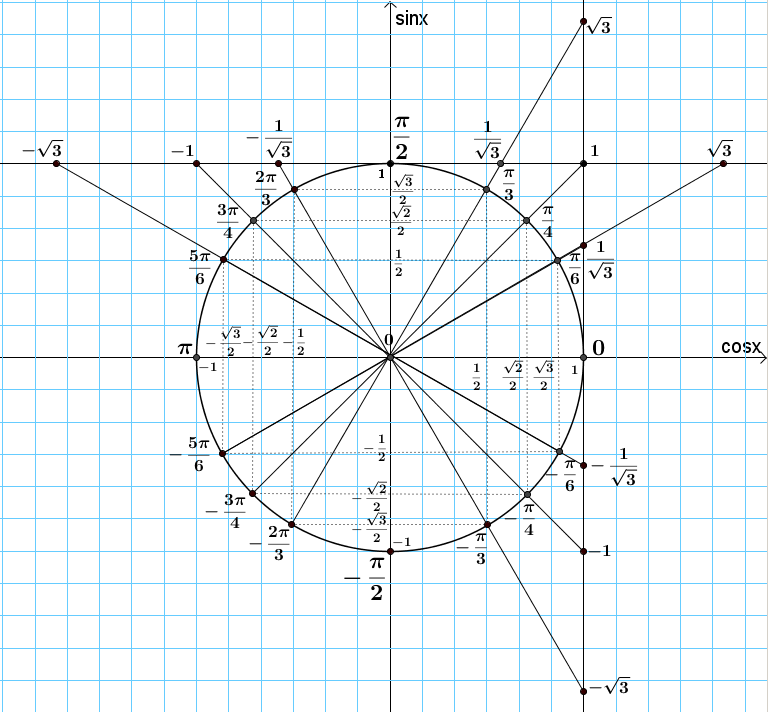
Кроме того, обратите внимание, что это не функция, потому что она не прошла тест вертикальной линии.
[ Interactive : Circles ]
Имея уравнение окружности в стандартной форме, вы можете построить его график, выполнив следующие действия:
Нанесите центр ( h , k ).
Используйте радиус r для построения четырех точек вверх, вниз, влево и вправо от центра.
Соедините точки и пометьте их.

Несмотря на то, что окружность не является функцией, это отношение, и мы все же можем найти домен и диапазон. Кроме того, нас попросят найти
x — и y — перехваты. В этом конкретном примере их нет, но метод их поиска тот же, что и в этом учебном пособии.
Чтобы найти y , задайте x = 0 и найдите y .
Чтобы найти x -перехваты, установите y = 0 и найдите x .
Нарисуйте круги и обозначьте точки пересечения x и y .



Для построения кругов в стандартной форме достаточно определить центр и радиус. Сложность возникает, когда круг не задан в стандартной форме. В этом случае, когда задана общая форма, мы заполним квадрат дважды, как показано ниже.
Сгруппировать все термины с переменной x и сгруппировать все термины с переменной y .
Заполните квадрат для каждой группы. 92 к обеим частям уравнения.
<noscript><img loading='lazy' src='/800/600/http/images.myshared.ru/4/305899/slide_9.jpg' /></noscript> youtube.com/embed/Ms8NESnqs6s»>
Перепишите круги в стандартной форме и определите центр.

Найдите площади следующих кругов.

Постройте график и найдите точки пересечения x и y , площадь и окружность.

Зная центр и радиус, найдите уравнение окружности.

Видео на YouTube:
Окружность
Окружность — это множество точек на плоскости, равноудаленных от одной точки. Эта точка называется центром окружности, а расстояние от нее до любой точки окружности называется радиусом окружности. Стандартная форма уравнения окружности с центром в точке (0, 0) и радиусом r представлена уравнением
х ² + y ² = r ²
Example 1
Graph x ² + y ² = 16.
Recognize that x ² + y ² = 16 представляет собой уравнение окружности с центром в точке (0, 0) с r ² = 16. Таким образом, r = 4, как показано на рисунке 1.
Рисунок 1. Окружность в стандартная позиция.
Пример 2
Найдите стандартную форму уравнения окружности с центром (0, 0) и радиусом .
Стандартная форма для окружности с центром в точке (0, 0) и радиусом r
x ² + Y ² = R ²
R с, уравнение становится
, R с, уравнение становится
, R , уравнение становится
, R . — стандартная форма уравнения окружности с центром в точке (0, 0) и радиусом .
The standard form for a circle centered at ( h, k ) with a radius of r is
( x – h ) ² + ( y – k ) ² = r ²
Обратите внимание, что если ( h, k ) = (0, 0), это приведет к
уравнению для окружности с центром в начале координат.
Пример 3
Нарисуйте уравнение ( x – 3) ² + ( y + 2) ² = 25.
Это уравнение представляет окружность с центром в точке (3, –2) и радиусом , как показано на рисунке 2.
Рисунок 2. Смещение окружности вниз и вправо.
Пример 4
Найдите стандартную форму уравнения окружности с центром в точке (–6, 2) и радиусом .
Стандартная форма уравнения окружности с центром в точке ( h, k ) и радиусом r :
( x – H ) ² + ( y — K ) ² = R ²
H с –6
. уравнение принимает вид
Следовательно, ( x + 6) ² + ( y – 2) ² = 18, что является стандартной формой уравнения окружности с центром в точке (–6, 2) с радиус .
Пример 5
Из приведенного уравнения найдите центр и радиус следующей окружности.
No related posts.