15. Введение первообразной и неопределенного интеграла
В дифференциальном исчислении мы решали следующую основную задачу: по данной функции найти ее производную. Многочисленные вопросы науки и техники приводят к постановке обратной задачи: для функции , определенной на сегменте (или интервале), найти такую функцию , производная которой равнялась бы заданной функции , т. е.
(1)
Назовем произведение F (X)Dx — дифференциальным выражением. Тогда только что поставленную задачу можно сформулировать в следующей, равносильной ей форме: для данного дифференциального выражения F(X)Dx найти такую функцию , дифференциал которой равнялся бы заданному дифференциальному выражению, т. е.
(2)
Функция F(X), связанная с функцией F(x) соотношением (1) или (2), называется ее Первообразной.
Таким образом,
Первообразной от данной функции f(x) называется функция, производная которой равна данной функции, или, что то же самое, дифференциал которой равен дифференциальному выражению f (х) dx.
Так, например, первообразной от функции будет функция , так как , или, что то же самое, .
Отыскание по данной функции ее первообразной составляет одну из основных задач интегрального исчисления. Действие — отыскание первообразной — называется интегрированием функции. При этом, естественно, возникает следующий вопрос: для всякой ли функции существует первообразная?
Утвердительный ответ на этот вопрос для достаточно широкого класса функций дает следующая теорема, принимаемая нами без доказательства.
Теорема 1. Любая непрерывная на сегменте функция имеет на этом сегменте первообразную.
На протяжении всего нашего изложения функции, для которых ищутся первообразные, мы будем считать непрерывными.
Если же функция, для которой мы ищем первообразную, имеет точки разрыва, то мы будем ее рассматривать только в интервалах непрерывности.
Задача отыскания по данной функции ее первообразной решается неоднозначно. В самом деле, если, например, , то первообразной для нее является не только функция (-cos Х), но также и , и , и вообще , где С — Произвольное число.
Как мы сейчас докажем, функция Не имеет других первообразных, кроме тех, которые могут быть представлены в виде: — . Это будет вытекать из следующей общей теоремы.
Теорема 2. Если функция есть первообразная для функции на сегменте [А; B], то всякая другая первообразная для отличается от на постоянное слагаемое, т. е. может быть представлена в виде: где С — постоянное число.
ПреДВарительно сформулируем без доказательства лемму, из которой непосредственно следует теорема 2.
Лемма. Функция, производная которой во всех точках сегмента [а;
Перейдем теперь к доказательству теоремы 2.
Доказательство теоремы 2. Пусть — какая-либо первообразная функция от , а Ф(Х) — Любая другая первообразная от той же функции; таким образом, на [А; B].
Производная разности равна нулю всюду на сегменте [А; B], так как
Но функция, производная которой всюду на сегменте [А; B] равна нулю, в силу леммы, постоянна на этом сегменте, т. е. , где С — постоянное число. Таким образом,
Теорема 2 показывает, что выражение где — Некоторая первообразная для функции , а С — произвольная постоянная, охватывает совокупность всех первообразных от данной функции .
Введем теперь основное понятие — понятие Неопределенного интеграла .
Если — одна из первообразных для функции , то выражение где С — произвольная постоянная, называется неопределенным интегралом от этой функции.
Неопределенный интеграл от функции обозначается символом (читается: «неопределенный интеграл на Dx»).
Следовательно,
При этом называется Подынтегральной функцией, — Подынтегральным выражением, х — Переменной интегрирования, А символ ∫ — Знаком неопределенного интеграла.
Под знаком интеграла мы пишем не производную искомой функции, а ее дифференциал.
Полагая, например, , имеем
Из самого определения первообразной следует, что дифференциал этой первообразной равен подынтегральному выражению. Так как это утверждение имеет место для любой первообразной от данной функции, его кратко можно выразить следующим образом:
1. Дифференциал от неопределенного интеграла равен подынтегральному выражению, Т. е.
(3)
Отметим, наконец, еще одно свойство, которое, как и свойство 1, устанавливает связь между операциями дифференцирования и интегрирования.
2. Неопределенный интеграл от дифференциала некоторой функции равен самой ЭТой функции плюс произвольная постоянная.
В самом деле, пусть — Дифференцируемая функция, для которой
Следовательно,
Но . Поэтому
Например:
Свойства 1 и 2 означают, что дифференцирование и интегрирование являются взаимно обратными действиями.
Рассмотрим некоторые задачи, приводящие к неопределенному интегралу.
Задача 1. Требуется найти кривую, у которой тангенс угла наклона касательной в каждой ее точке есть заданная функция абсциссы этой точки.
Пусть — уравнение искомой кривой. Согласно геометрическому смыслу производной, тангенс угла наклона касательной к кривой В точке с абсциссой Х равен значению производной в этой точке. Значит, нам нужно найти такую функцию , для которой
. (4)
Соотношение (4) показывает, что искомая функция Является первообразной для . Следовательно, наша задача свелась к основной задаче интегрального исчисления — к нахождению первообразной от данной функции. Поэтому уравнение искомой кривой имеет вид
Мы видим, что условию задачи удовлетворяет не одна кривая, а семейство кривых. Если есть одна из таких кривых, то всякая другая может быть получена из нее параллельным переносом вдоль оси Оу (рис.
Назовем график первообразной функции от — Интегральной кривой.
Неопределенный интеграл геометрически представляет совокупность всех интегральных кривых.
Все кривые из этой совокупности могут быть получены из одной интегральной кривой параллельным сдвигом в
Направлении оси Оу.
Для того чтобы из данного семейства кривых выделить одну определенную кривую, нужно к условию задачи присоединить дополнительное условие, например, потребовать, чтобы кривая проходила через данную точку . Такое условие называется Начальным. Задание начального условия, вообще говоря, позволяет выделить из семейства всех интегральных кривых вполне определенную кривую, а именно ту кривую, которая проходит через точку . Координаты этой точки должны удовлетворять уравнению искомой кривой , т. е. . Из этого условия однозначно определяем С: . Следовательно, уравнение искомой интегральной кривой имеет вид:
Рассмотрим конкретный пример.
Через точку (1; 2) провести кривую, у которой угловой коэффициент касательной в каждой точке с абсциссой Х равен 3Х2.
Имеем У’=3Х2. Легко сообразить, что одной из первообразных для 3Х2 будет Х3. Следовательно,
Итак, кривые, для которых в точках с абсциссой Х тангенс угла наклона касательной равен 3Х2, образуют семейство кубических парабол (рис.2). Из этого семейства кривых нам нужно выбрать ту кривую, которая проходит через точку (1; 2) (начальное условие). Поэтому откуда С = 1. Таким образом, уравнение искомой кривой будет:
Задача 2. Теперь рассмотрим задачу из совершенно другой области.
Материальная точка массы Т движется по вертикальной прямой под действием силы тяжести. Определить путь, Пройденный Точкой за время
Пройденный точкой путь Х будет некоторой функцией времени: . Наша задача заключается в том, чтобы определить вид этой функции, т.Е. зависимость пройденного пути от времени T.Из физики известно, что скорость падающего тела за каждую секунду возрастает на величину G). Поэтому, если при T=0 скорость материальной точки равна нулю, то к моменту времени T скорость точки V возрастает до значения Gt. Таким образом,
(5)
С другой стороны, мы знаем, что скорость есть производная пути по времени: . Следовательно, приравняв два найденных выражения для скОРости, найдем
(6)
Соотношение (6) показывает, что искомая функция Является первообразной для функции Gt. Поэтому
).
Постоянную С находим из начального условия: при , . Следовательно, т. е. С=0.
Таким образом, путь Х, пройденный точкой к моменту времени T, выразится следующей формулой, хорошо известной из курса физики
Уже эти элементарные примеры показывают, что поставленная нами задача об отыскании для данной функции ее первообраЗНой имеет не только формально математический интерес, как операция, обратная дифференцированию, но что к этой задаче мы непосредственно приходим при решении целого ряда вопросов естествознания и техники.
| < Предыдущая | Следующая > |
|---|
Решение высшей математики онлайн
‹— Назад
Пусть функция задана на некотором интервале . Если найдётся такая функция , что при всех имеет место равенство
то функция называется первообразной для функции .
Пример 1.1 Рассмотрим функцию на всей числовой оси — на интервале . Тогда функция — это первообразная для на .
Для доказательства найдём производную от :
Поскольку равенство верно при всех , то — первообразная для на .
Аналогичное определение дадим и для случая, когда функция задана не на одном интервале, а на объединении нескольких непересекающихся интервалов:
Назовём функцию первообразной для , если при всех выполнено равенство .
Пример 1.2 Рассмотрим функцию на объединении двух интервалов . Тогда функция — это первообразная для на .
Действительно, при
и
при
и
Итак, — первообразная для , если — производная от . Например, — первообразная для , поскольку ; — первообразная для , поскольку , и т. п. Тем самым, нахождение первообразной определяется как операция, обратная к операции вычисления производной. Найти первообразную по данной функции означает восстановить функцию по её производной.
Заметим теперь, что однозначно восстановить функцию по её производной невозможно даже в таком простом случае, когда . Действительно, вычисление производной любой постоянной даёт , так что различить, какое значение имела постоянная , по невозможно.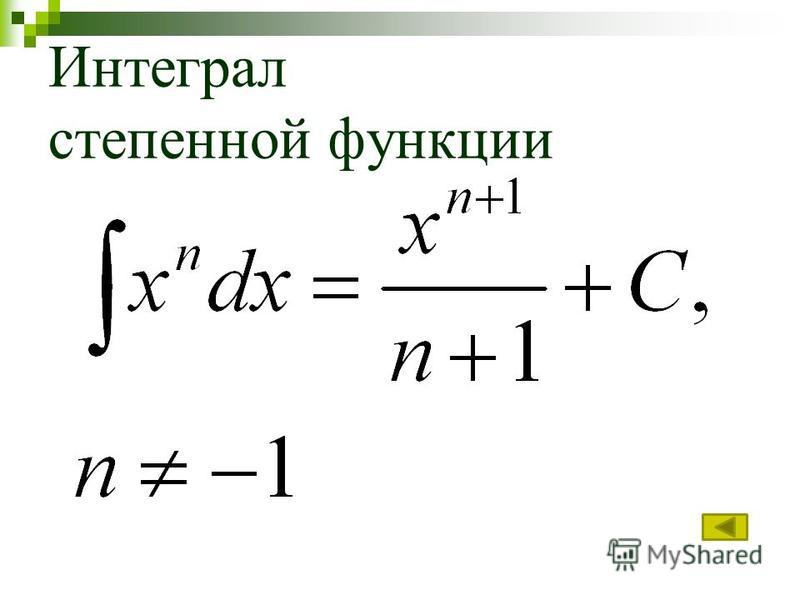
Следовательно, для любая постоянная служит первообразной: , где — произвольное число.
Ещё один такой пример:
Пример 1.3 Поскольку и при , то и , и служат первообразными для одной и той же функции на интервале . Заметим, что при , так что .
Точно так же, любая функция вида , где — произвольная постоянная, служит первообразной для ; любая функция вида , где — постоянная, — это первообразная для и т. д. Очевидно, что имеет место такое общее утверждение.
Теорема 1.1 Пусть — некоторая первообразная для на интервале и — произвольная постоянная. Тогда функция также является первообразной для на .
Доказательство. Покажем, что производная от даёт :
при всех . Таким образом, — первообразная для .
Итак, если — первообразная для на , то множество всех первообразных для , во всяком случае, содержит все функции вида . Покажем, что никаких других функций множество всех первообразных не содержит, то есть что все первообразные для фиксированной функции отличаются от лишь постоянным на слагаемым .
Теорема 1.2 Пусть — первообразная для на и — некоторая другая первообразная. Тогда
при некоторой постоянной .
Доказательство. Рассмотрим разность . Поскольку и , то . Покажем, что функция , такая что при всех , — это постоянная. Для этого рассмотрим две произвольные точки и , принадлежащие , и к отрезку между и (пусть это ) применим формулу конечных приращений
где .
(Напомним, что эта формула — следствие из теоремы Лагранжа, которую мы рассматривали в первом семестре). Поскольку во всех точках , в том числе и , то . Следовательно, в произвольной точке функция принимает то же значение, что в точке , то есть .
Для первообразной это означает, что при любом , то есть
что и требовалось доказать.
Замечание 1.1 Заметим, что если равенства и выполнены для функций и не на одном интервале , а на двух или больше непересекающихся интервалах , , то мы можем лишь утверждать, что, согласно доказанной теореме, , где постоянные могут быть разными для разных интервалов . С другой стороны, очевидно, что при любых функция даёт ту же производную, что и , в любой точке объединения интервалов.
Например, поскольку при всех , где (то есть функция — это первообразная для функции на каждом из непересекающихся интервалов области определения тангенса ), то при любых постоянных функция , заданная на объединении всех этих интервалов равенством
при
будет давать .
Эту функцию можно назвать первообразной для с тем же правом, что и функцию . Заметим, что мы не можем утверждать, что в этом случае: — это не постоянная, а кусочно постоянная на интервалах области определения тангенса функция. Итак, утверждение, что первообразная для имеет вид , нужно правильно понимать: либо имеется в виду, что при этом изменяется лишь в пределах только одного из интервалов непрерывности тангенса, либо что — кусочно постоянная на объединении этих интервалов функция.
Аналогично обстоит дело и в случае других функций, имеющих в качестве области определения объединение непересекающихся интервалов. Например, поскольку при всех имеет место равенство
то на объединении двух интервалов первообразной для будет служить любая функция , где а и — произвольные постоянные.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
б \ эквив с \ текст { (мод } п) \end{уравнение*}, где \(a\) или \(b\) может быть переменной, а \(n\) может быть простым числом или степенью простого числа.
j\) для некоторого \(i,j\in\mathbb{Z}\text{.}\) Тогда наша конгруэнтность станет равной 9j\text{(mod}n)
\end{уравнение*}
и думать о нем как о решении в показателях \(ib\) и \(j\) будет продуктивно.
Подраздел 10.5.1 Нахождение более высокого корня
¶В качестве введения давайте рассмотрим один из способов решения первого сравнения, используя эту идею.
Во-первых, найдите примитивный корень по модулю \(17\text{.}\). Очевидно, мы могли бы просто попросить Sage и его встроенную команду примитивный_корень или использовать Лемму 10.2.3 методом проб и ошибок. В недалеком прошлом в конце каждого текста по теории чисел была таблица первообразных корней! 9{5}\Стрелка вправо 3i=5 \Стрелка вправо i=5/3\текст{.}
\end{уравнение*}
Здесь мы попробуем сделать что-то очень похожее.
Что очень важно, так это то, что эта конгруэнтность в каком-то смысле больше не является конгруэнтностью в \(\mathbb{Z}_{17}\text{.}\). (U_{17}\text{,}\) циклическая группа порядка \(\phi(17)=16\text{.
}\) Но циклическая группа порядка \(16\) будет такой же, как мышление по модулю шестнадцать! Таким образом, мы можем убрать показатели, как в предварительном исчислении, но сделать что-то (mod \(16\)): 9{10}\text{ (мод. }19)
\end{уравнение*}
дает
\begin{уравнение*} 16x\equiv 10\text{ (mod }18)\text{.} \end{уравнение*}
Поскольку каждое из чисел в этом последнем сравнении четно, мы можем свести его к \(8x\equiv 5\) (mod \(9\)), что далее сводится к легко решаемому \(-x\ эквивалент 5\) (mod \(9\)).
Взяв \(x\equiv -5\equiv 4\text{,}\) и приняв во внимание исходный модуль \(18\text{,}\), который предполагает, что мы могли бы положить \(x\equiv 4, 13\) при решении исходного сравнения. И действительно 9{5}\text{ (мод. }19) \end{уравнение*}
, что дает
\begin{уравнение*} 4x\equiv 5\text{ (mod }18)\text{.} \end{уравнение*}
Однако, поскольку \(\gcd(4,18)=2\nmid 5\text{,}\) по предложению 5.1.1 это последнее сравнение не имеет решений, то и исходное сравнение не имеет решений.
(Оказывается, \(16\) имеет только порядок \(9\) как элемент \(U_{19}\text{,}\) и, очевидно, \(13\) не является одним из элементов в подгруппа, сгенерированная \(16\text{.}\))
Развлечение с теорией чисел: примитивные корни | Рассел Лим
Нежное введение, использующее только умножение и остаток
Вопросы по теории чисел, подобные приведенному ниже, часто появляются на олимпиадах по математике в средней школе и на тестах способностей:
Найдите последнюю цифру 2²⁰²².
Если вы никогда раньше не сталкивались с чем-то подобным, это кажется компьютерным кошмаром. Пока вы не погрузитесь в изучение, начните исследовать первые несколько степеней числа 2, и появится закономерность:
Все изображения автора Последние цифры повторяются в циклах длиной 4: {2, 4, 8, 6, …}.
Таким образом, последняя цифра 2²⁰²² будет такой же, как последняя цифра 2².
Проблема решена!
Если вы находите этот циклический паттерн странным образом удовлетворительным, то вас тронула магия ✨ теории чисел.
Дальнейшее изучение циклов приведет нас к понятию в теории чисел, называемому «примитивными корнями». Держитесь, это не займет много времени… 🧚♀️
Тот факт, что последние цифры повторяются циклами, не относится к основному числу 2. Любое основание вообще может давать повторяющийся узор, хотя длина цикла может быть короче или длиннее 4,
Чтобы понять, почему мы должны получать повторяющийся цикл, достаточно двух следующих наблюдений:
- существует только конечное число возможных последних цифр (от 0 до 9)
- с умножением могут повлиять только последние цифры последняя цифра произведения (и помните, что степени получаются повторным умножением)
Таким образом, как только повторяется одна единственная цифра, весь цикл повторяется.
Кроме того, давайте выйдем за пределы нашей системы счисления с основанием 10. «Последняя цифра» — это просто остаток после деления на 10. Но мы могли бы также рассмотреть остаток после деления на любое целое число 9.
0011 n . В теории чисел это называется взятием числа «по модулю n ».
напр. 16 (mod 7) ≡ 2
, потому что 16 имеет остаток от 2 после деления на 7
Давайте посмотрим на степени 2 (mod 7):
Степени 2 по модулю 7 повторяются в циклах длины 3: {2 , 4, 1, …}.
Какой самый длинный возможный цикл по модулю 7?
Ваше первое предположение может быть 7 из-за 7 возможных остатков {0, 1, 2, 3, 4, 5, 6}. Но как 0 мог появиться в цикле? Умножение на 0 может дать только 0 (даже в модульной арифметике), поэтому цикл с одним 0 может содержать только 9.0178 только 0.
Ну как насчет 6? Существует ли число, степени которого повторяются в циклах длины 6?
Да! Нам не нужно далеко ходить, чтобы обнаружить, что их два: и 3, и 5 имеют степени, которые повторяются в циклах длины 6.
Из-за этого мы говорим, что 3 и 5 являются первообразными корнями по модулю 7.
3 является первообразным корнем по модулю 7. Для простого числа p первообразным корнем по модулю p является тот, степени которого дают все классы конгруэнтности (т.
е. остатки) в множестве {1, 2, 3, … ( р − 1)}.
Как показано выше, и 3, и 5 являются примитивными корнями по модулю 7, потому что существуют степени 3 и 5, конгруэнтные каждому из {1, 2, 3, 4, 5, 6}.
Когда у нас есть определение первообразного корня, возникают естественные вопросы:
- Все ли простые числа имеют первообразный корень?
- если да, то как их найти?
Ответ на первый вопрос — да! Доказательство следует из двух известных теорем теории чисел: 9( P — 1) ≡ 1 (MOD P )
LAGRANGE’SPHEREM
для Prime P и Polynomial F ( x ) с степенью n , но не все, что не так, не все. делится на p:
f ( x ) = 0 (mod p ) имеет не более n решений
Маленькая теорема Ферма, по-видимому, называется «маленькой», чтобы отличить ее от «большой» последней теоремы Ферма. Но не заблуждайтесь, маленькая теорема Ферма по-прежнему важна! Внизу есть ссылка на статью Йоргена Вейсдала, которая дает больше информации о теореме, а также несколько доказательств.
Понятно, что малая теорема Ферма тесно связана с первообразными корнями. Это причина того, что нижняя строка таблицы выше содержит только 1. 1 всегда появляется в конце цикла и начинает новый цикл, потому что 1 × a ≡ a (mod p ).
Доказательство того, что все простые числа имеют первообразный корень
Пусть n — наименьшее натуральное число такое, что все ненулевые значения a являются решениями aⁿ ≡ 1 (mod 9( p − 1) ≡ 1 (mod p ) для всех ненулевых a , что уже гарантирует, что n ≤ p − 03. , поскольку решение уравнения aⁿ ≡ 1 (mod p ) эквивалентно нахождению корней многочлена f ( x ) = xⁿ − 1 (т. ( x ) ≡ 0 mod p).
Теорема Лагранжа говорит нам, что этот многочлен может иметь максимум n различных корней. Таким образом, для любого n < p − 1 будет по крайней мере одно ненулевое значение a , при котором не удовлетворяет aⁿ ≡ 1 (mod p ).
Таким образом, наименьшее положительное целое число n , которое мы ищем, максимальная длина цикла, должно быть n = p − 1.
Таким образом, все простые числа должны иметь хотя бы один примитивный корень. 👨🌾
Вопрос «Как же нам найти первообразные корни?» не решен. Как и многие другие вопросы, связанные с простыми числами, здесь нам все еще нужно «получить большой старый компьютер и много раз угадывать и проверять»!
Мало того, что все простые числа имеют примитивный корень, они кратны. На самом деле известно, что число первообразных корней равно ϕ ( p − 1), где ϕ — функция Эйлера, число положительных целых чисел меньше 9.0011 n взаимно просты с n.
Это потрясающе? Я нахожу это удивительным. 🤯
Доказательство не привожу, но поясню теорему на другом примере (потому что я так катаюсь 🕵).
Сначала давайте определим понятие «заказ». Порядок a в основном представляет собой длину цикла степеней a (mod p ) или наименьшее значение k такое, что aᵏ ≡ 1 (mod p ) .
В приведенном выше примере мы говорим, что порядок числа 2 (mod 7) равен 3, поскольку степени следуют циклу {2, 4, 1}.
Вот степени всех ненулевых значений x по модулю 11.
Мы видим, что 11 имеет 4 первообразных корня: 2, 6, 7 и 8.
Тот факт, что существует 4 первообразных корня, определяется как ϕ ( p — 1) = ϕ (10)
(существуют 4 целых числа меньше 10, которые взаимно просты с 10, а именно 1, 3, 7, 9).
Порядок остальных целых чисел:
- 1 имеет порядок 1 (это неудивительно)
- 10 имеет порядок 2 (тоже не удивительно, потому что 10 ≡ − 1 mod 11 и ( − 1)² = 1)
- 3, 4, 5 и 9 имеют порядок 5
Существующие порядки {1, 2, 5, 10} в точности являются множителями 10.
В общем случае порядки являются множителями ( p − 1 ).
Опять же, количество целых чисел с каждым порядком k равно ϕ ( k ).
Например, имеется 4 целых числа порядка 5, потому что ϕ (5) = 4.
Все страньше и страньше! 🦄
Понятие первообразных корней не ограничивается простыми числами. Но не все целые числа имеют первообразные корни.
Для любого целого числа n, первообразный корень по модулю n — это корень, степени которого дают все классы конгруэнтности, взаимно простые с n.
Например, 2 является примитивным корнем по модулю 9, потому что классы конгруэнтности взаимно просты с 9равны {2, 4, 5, 7, 8}, которые задаются как {2¹, 2², 2⁵, 2⁴, 2³} соответственно.
Но 15 не имеет первообразного корня, потому что нет значения a , степени которого дают все классы конгруэнтности в {2, 4, 7, 8, 11, 13, 14}.
Известно, что целые числа с первообразными корнями равны 1, 2, 4 и любым pᵏ или 2 pᵏ , где p — нечетное простое число.
Теорема Вильсона утверждает, что
( p − 1)! ≡ − 1 по модулю p
Теорему можно доказать, используя первообразные корни:
Сначала докажите теорему для p = 2, используя подстановку, чтобы убедиться, что
(2 − 1)! ≡ − 1 mod 2
Тогда для p > 2 мы используем тот факт, что p должно иметь первообразный корень, и называем этот первообразный корень x.
Мы знаем, что степени x должны давать все классы конгруэнтности в {1, 2, 3, … ( p − 1)} в некотором порядке, поэтому факториал ( p − 1)! должно быть конгруэнтно произведению степеней x :
Теперь мы можем использовать некоторые индексные законы и арифметический ряд, чтобы упростить показатель степени:
Теперь другой индексный закон, мы можем переписать это выражение как степень степени :
Выражение в скобках представляет собой целую степень x , первообразный корень. Поскольку x — это примитивный корень, он должен удовлетворять 9 k ≢ 1 (mod p ) для всех k < p − 1. Другими словами, квадрат выражения в скобках должен быть конгруэнтен 1 (mod p ) , но само выражение не может быть конгруэнтно 1 (mod p ). Следовательно, единственный класс соответствия, который он может принять, должен быть − 1 (mod p ).