Линейные неравенства, примеры, решения
После получения начальных сведений о неравенствах с переменными, переходим к вопросу их решения. Разберем решение линейных неравенств с одной переменной и все методы для их разрешения с алгоритмами и примерами. Будут рассмотрены только линейные уравнения с одной переменной.
Что такое линейное неравенство?
В начале необходимо определить линейное уравнение и выяснить его стандартный вид и чем оно будет отличаться от других. Из школьного курса имеем, что у неравенств нет принципиального различия, поэтому необходимо использовать несколько определений.
Определение 1Линейное неравенство с одной переменной x – это неравенство вида a·x+b>0, когда вместо > используется любой знак неравенства <, ≤, ≥, а и b являются действительными числами, где a≠0.
Определение 2Неравенства a·x<c или a·x>c, с x являющимся переменной, а a и c некоторыми числами, называют линейными неравенствами с одной переменной.
Так как ничего не сказано за то, может ли коэффициент быть равным 0, тогда строгое неравенство вида 0·x>c и 0·x<c может быть записано в виде нестрогого, а именно, a·x≤c, a·x≥c. Такое уравнение считается линейным.
Их различия заключаются в:
- форме записи a·x+b>0 в первом, и a·x>c – во втором;
- допустимости равенства нулю коэффициента a, a≠0 — в первом, и a=0 — во втором.
Считается, что неравенства a·x+b>0 и a·x>c равносильные, потому как получены переносом слагаемого из одной части в другую. Решение неравенства 0·x+5>0 приведет к тому, что его необходимо будет решить, причем случай а=0 не подойдет.
Определение 3Считается, что линейными неравенствами в одной переменной x считаются неравенства вида a·x+b<0, a·x+b>0, a·x+b≤0 и a·x+b≥0, где a и b являются действительными числами. Вместо x может быть обычное число.
Исходя из правила, имеем, что 4·x−1>0, 0·z+2,3≤0, -23·x-2<0 являются примерами линейных неравенств. А неравенства такого плана, как 5·x>7, −0,5·y≤−1,2 называют сводящимися к линейному.
А неравенства такого плана, как 5·x>7, −0,5·y≤−1,2 называют сводящимися к линейному.
Как решить линейное неравенство
Основным способом решения таких неравенств сводится к равносильным преобразованиям для того, чтобы найти элементарные неравенства x<p (≤, >, ≥), p являющееся некоторым числом, при a≠0, а вида a<p (≤, >, ≥) при а=0.
Для решения неравенства с одной переменной, можно применять метода интервалов или изображать графически. Любой из них можно применять обособленно.
Используя равносильные преобразования
Чтобы решить линейное неравенство вида a·x+b<0 (≤, >, ≥), необходимо применить равносильные преобразования неравенства. Коэффициент может быть равен или не равен нулю. Рассмотрим оба случая. Для выяснения необходимо придерживаться схемы, состоящей из 3 пунктов: суть процесса, алгоритм, само решение.
Определение 4Алгоритм решение линейного неравенства a·x+b<0 (≤, >, ≥) при a≠0
- число b будет перенесено в правую часть неравенства с противоположным знаком, что позволит прийти к равносильному a·x<−b (≤, >, ≥);
- будет производиться деление обеих частей неравенства на число не равное 0.
 Причем , когда a является положительным, то знак остается, когда a – отрицательное, меняется на противоположный.
Причем , когда a является положительным, то знак остается, когда a – отрицательное, меняется на противоположный.
Рассмотрим применение данного алгоритма на решении примеров.
Пример 1Решить неравенство вида 3·x+12≤0.
Решение
Данное линейное неравенство имеет a=3 и b=12. Значит, коэффициент a при x не равен нулю. Применим выше сказанные алгоритмы, решим.
Необходимо перенести слагаемое 12 в другую часть неравенства с изменением знака перед ним. Тогда получаем неравенство вида 3·x≤−12. Необходимо произвести деление обеих частей на 3. Знак не поменяется, так как 3 является положительным числом. Получаем, что (3·x):3≤(−12):3, что даст результат x≤−4.
Неравенство вида x≤−4 является равносильным. То есть решение для 3·x+12≤0 – это любое действительное число, которое меньше или равно 4. Ответ записывается в виде неравенства x≤−4, или числового промежутка вида (−∞, −4].
Весь выше прописанный алгоритм записывается так:
3·x+12≤0; 3·x≤−12; x≤−4.
Ответ: x≤−4 или (−∞, −4].
Пример 2Указать все имеющиеся решения неравенства −2,7·z>0.
Решение
Из условия видим, что коэффициент a при z равняется -2,7, а b в явном виде отсутствует или равняется нулю. Первый шаг алгоритма можно не использовать, а сразу переходить ко второму.
Производим деление обеих частей уравнения на число -2,7. Так как число отрицательное, необходимо поменять знак неравенства на противоположный. То есть получаем, что (−2,7·z):(−2,7)<0:(−2,7), и дальше z<0.
Весь алгоритм запишем в краткой форме:
−2,7·z>0; z<0.
Ответ: z<0 или (−∞, 0).
Пример 3Решить неравенство -5·x-1522≤0.
Решение
По условию видим, что необходимо решить неравенство с коэффициентом a при переменной x, которое равняется -5, с коэффициентом b, которому соответствует дробь -1522. Решать неравенство необходимо, следуя алгоритму, то есть: перенести -1522 в другую часть с противоположным знаком, разделить обе части на -5, изменить знак неравенства:
-5·x≤1522;-5·x:-5≥1522:-5x≥-322
При последнем переходе для правой части используется правило деления числе с разными знаками 1522:-5=-1522:5, после чего выполняем деление обыкновенной дроби на натурально число -1522:5=-1522·15=-15·122·5=-322.
Ответ: x≥-322 и [-322+∞).
Рассмотрим случай, когда а=0. Линейное выражение вида a·x+b<0 является неравенством 0·x+b<0, где на рассмотрение берется неравенство вида b<0, после чего выясняется, оно верное или нет.
Все основывается на определении решения неравенства. При любом значении x получаем числовое неравенство вида b<0, потому что при подстановке любого t вместо переменной x, тогда получаем 0·t+b<0, где b<0. В случае, если оно верно, то для его решения подходит любое значение. Когда b<0 неверно, тогда линейное уравнение не имеет решений, потому как не имеется ни одного значения переменной, которое привело бы верному числовому равенству.
Все суждения рассмотрим в виде алгоритма решения линейных неравенств 0·x+b<0 (≤, >, ≥):
Определение 5Числовое неравенство вида b<0 (≤, >, ≥) верно, тогда исходное неравенство имеет решение при любом значении, а неверно тогда, когда исходное неравенство не имеет решений.
Пример 4Решить неравенство 0·x+7>0.
Решение
Данное линейное неравенство 0·x+7>0 может принимать любое значение x. Тогда получим неравенство вида 7>0. Последнее неравенство считается верным, значит любое число может быть его решением.
Ответ: промежуток (−∞, +∞).
Пример 5Найти решение неравенства 0·x−12,7≥0.
Решение
При подстановке переменной x любого числа получим, что неравенство получит вид −12,7≥0. Оно является неверным. То есть 0·x−12,7≥0 не имеет решений.
Ответ: решений нет.
Рассмотрим решение линейных неравенств , где оба коэффициента равняется нулю.
Пример 6Определить не имеющее решение неравенство из 0·x+0>0 и 0·x+0≥0.
Решение
При подстановке любого числа вместо x получим два неравенства вида 0>0 и 0≥0. Первое является неверным. Значит, 0·x+0>0 не имеет решений, а 0·x+0≥0 имеет бесконечное количество решений, то есть любое число.
Ответ: неравенство 0·x+0>0 не имеет решений, а 0·x+0≥0 имеет решения.
Методом интервалов
Данный метод рассматривается в школьном курсе математики. Метод интервалов способен разрешать различные виды неравенств, также и линейные.
Метод интервалов применяется для линейных неравенств при значении коэффициента x не равному 0. Иначе придется вычислять при помощи другого метода.
Определение 6Метод интервалов – это:
- введение функции y=a·x+b;
- поиск нулей для разбивания области определения на промежутки;
- определение знаков для понятия их на промежутках.
Соберем алгоритм для решения линейных уравнений a·x+b<0 (≤, >, ≥) при a≠0 с помощью метода интервалов:
- нахождение нулей функции y=a·x+b, чтобы решить уравнение вида a·x+b=0. Если a≠0, тогда решением будет единственный корень, который примет обозначение х0;
- построение координатной прямой с изображением точки с координатой х0, при строгом неравенстве точка обозначается выколотой, при нестрогом – закрашенной;
- определение знаков функции y=a·x+b на промежутках, для этого необходимо находить значения функции в точках на промежутке;
- решение неравенства со знаками > или ≥ на координатной прямой добавляется штриховка над положительным промежутком, < или ≤ над отрицательным промежутком.

Рассмотрим несколько примеров решения линейного неравенства при помощи метода интервалов.
Решить неравенство −3·x+12>0.
Решение
Из алгоритма следует, что для начала нужно найти корень уравнения −3·x+12=0. Получаем, что −3·x=−12, x=4. Необходимо изобразить координатную прямую, где отмечаем точку 4. Она будет выколотой, так как неравенство является строгим. Рассмотрим чертеж, приведенный ниже.
Нужно определить знаки на промежутках. Чтобы определить его на промежутке (−∞, 4), необходимо произвести вычисление функции y=−3·x+12 при х=3. Отсюда получим, что −3·3+12=3>0. Знак на промежутке является положительным.
Определяем знак из промежутка (4, +∞), тогда подставляем значение х=5. Имеем, что −3·5+12=−3<0. Знак на промежутке является отрицательным. Изобразим на числовой прямой, приведенной ниже.
Мы выполняем решение неравенства со знаком >, причем штриховка выполняется над положительным промежутком.
Из чертежа видно, что искомое решение имеет вид (−∞, 4) или x<4.
Ответ: (−∞, 4) или x<4.
Графическим способом
Чтобы понять, как изображать графически, необходимо рассмотреть на примере 4 линейных неравенства: 0,5·x−1<0, 0,5·x−1≤0, 0,5·x−1>0 и 0,5·x−1≥0. Их решениями будут значения x<2, x≤2, x>2 и x≥2. Для этого изобразим график линейной функции y=0,5·x−1, приведенный ниже.
Видно, что
Определение 7- решением неравенства 0,5·x−1<0 считается промежуток, где график функции y=0,5·x−1 располагается ниже Ох;
- решением 0,5·x−1≤0 считается промежуток, где функция y=0,5·x−1 ниже Ох или совпадает;
- решением 0,5·x−1>0 считается промежуток, гре функция располагается выше Ох;
- решением 0,5·x−1≥0 считается промежуток, где график выше Ох или совпадает.
Смысл графического решения неравенств заключается в нахождении промежутков, которое необходимо изображать на графике.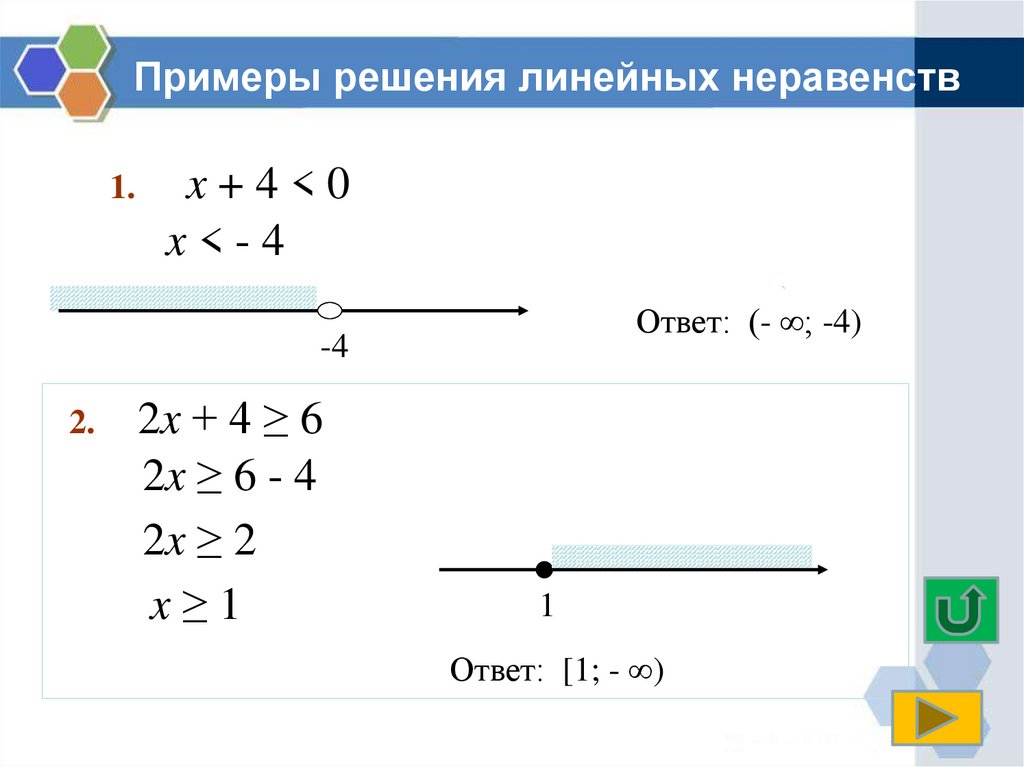
Алгоритм решения линейных неравенств графическим способом.
Определение 8Построение графика функции y=a·x+b производится:
- во время решения неравенства a·x+b<0 определяется промежуток, где график изображен ниже Ох;
- во время решения неравенства a·x+b≤0 определяется промежуток, где график изображается ниже оси Ох или совпадает;
- во время решения неравенства a·x+b>0 производится определение промежутка, где график изображается выше Ох;
- во время решения неравенства a·x+b≥0 производится определение промежутка, где график находится выше Ох или совпадает.
Решить неравенство -5·x-3>0 при помощи графика.
Решение
Необходимо построить график линейной функции -5·x-3>0. Данная прямая является убывающей, потому как коэффициент при x является отрицательным. Для определения координат точки его пересечения с Ох-5·x-3>0 получим значение -35. Изобразим графически.
Изобразим графически.
Решение неравенства со знаком >, тогда необходимо обратить внимание на промежуток выше Ох. Выделим красным цветом необходимую часть плоскости и получим, что
Необходимый промежуток является частью Ох красного цвета. Значит, открытый числовой луч -∞, -35 будет решением неравенства. Если бы по условию имели нестрогое неравенство, тогда значение точки -35 также являлось бы решением неравенства. И совпадало бы с Ох.
Ответ: -∞, -35 или x<-35.
Графический способ решения используется, когда левая часть будет отвечать функции y=0·x+b, то есть y=b. Тогда прямая будет параллельна Ох или совпадающей при b=0. Эти случаю показывают, что неравенство может не иметь решений, либо решением может быть любое число.
Пример 8Определить из неравенств 0·x+7<=0, 0·x+0≥0 то, которое имеет хотя бы одно решение.
Решение
Представление y=0·x+7 является y=7, тогда будет задана координатная плоскость с прямой, параллельной Ох и находящейся выше Ох. Значит, 0·x+7<=0 решений не имеет, потому как нет промежутков.
Значит, 0·x+7<=0 решений не имеет, потому как нет промежутков.
График функции y=0·x+0, считается y=0, то есть прямая совпадает с Ох. Значит, неравенство 0·x+0≥0 имеет множество решений.
Ответ: второе неравенство имеет решение при любом значении x.
Неравенства, сводящиеся к линейным
Решение неравенств можно свести к решению линейного уравнения, которые называют неравенствами, сводящимися к линейным.
Данные неравенства были рассмотрены в школьном курсе, так как они являлись частным случаем решения неравенств, что приводило к раскрытию скобок и приведению подобных слагаемых. Для примера рассмотрим, что 5−2·x>0, 7·(x−1)+3≤4·x−2+x, x-35-2·x+1>27·x.
Неравенства, приведенные выше, всегда приводятся к виду линейного уравнения. После чего раскрываются скобки и приводятся подобные слагаемые, переносятся из разных частей, меняя знак на противоположный.
При сведении неравенства 5−2·x>0 к линейному, представляем его таким образом, чтобы оно имело вид −2·x+5>0, а для приведения второго получаем, что 7·(x−1)+3≤4·x−2+x. Необходимо раскрыть скобки, привести подобные слагаемые, перенести все слагаемые в левую часть и привести подобные слагаемые. Это выглядит таким образом:
Необходимо раскрыть скобки, привести подобные слагаемые, перенести все слагаемые в левую часть и привести подобные слагаемые. Это выглядит таким образом:
7·x−7+3≤4·x−2+x 7·x−4≤5·x−2 7·x−4−5·x+2≤0 2·x−2≤0
Это приводит решение к линейному неравенству.
Эти неравенства рассматриваются как линейные, так как имеют такой же принцип решения, после чего возможно приведение их к элементарным неравенствам.
Для решения такого вида неравенства такого вида необходимо свести его к линейному. Это следует делать таким образом:
Определение 9- раскрыть скобки;
- слева собрать переменные, а справа числа;
- привести подобные слагаемые;
- разделить обе части на коэффициент при x.
Решить неравенство 5·(x+3)+x≤6·(x−3)+1.
Решение
Производим раскрытие скобок, тогда получим неравенство вида 5·x+15+x≤6·x−18+1. После приведения подобных слагаемых имеем, что 6·x+15≤6·x−17. После перенесения слагаемых с левой в правую, получим, что 6·x+15−6·x+17≤0. Отсюда имеет неравенство вида 32≤0 из полученного при вычислении 0·x+32≤0. Видно, что неравенство неверное, значит, неравенство, данное по условию, не имеет решений.
Отсюда имеет неравенство вида 32≤0 из полученного при вычислении 0·x+32≤0. Видно, что неравенство неверное, значит, неравенство, данное по условию, не имеет решений.
Ответ: нет решений.
Стоит отметить, что имеется множество неравенств другого вида, которые могут сводится к линейному или неравенству вида, показанного выше. Например, 52·x−1≥1 является показательным уравнением, которое сводится к решению линейного вида 2·x−1≥0. Эти случаи будут рассмотрены при решении неравенств данного вида.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р. Реферат
от 1 дня / от 700 р.
Реферат
от 1 дня / от 700 р.
Линейные неравенства, примеры, решения
После получения начальных сведений о неравенствах с переменными, переходим к вопросу их решения. Разберем решение линейных неравенств с одной переменной и все методы для их разрешения с алгоритмами и примерами. Будут рассмотрены только линейные уравнения с одной переменной.
Что такое линейное неравенство?
В начале необходимо определить линейное уравнение и выяснить его стандартный вид и чем оно будет отличаться от других. Из школьного курса имеем, что у неравенств нет принципиального различия, поэтому необходимо использовать несколько определений.
Из школьного курса имеем, что у неравенств нет принципиального различия, поэтому необходимо использовать несколько определений.
Линейное неравенство с одной переменной x – это неравенство вида a·x+b>0, когда вместо > используется любой знак неравенства <, ≤, ≥, а и b являются действительными числами, где a≠0.
Определение 2Неравенства a·x<c или a·x>c, с x являющимся переменной, а a и c некоторыми числами, называют линейными неравенствами с одной переменной.
Так как ничего не сказано за то, может ли коэффициент быть равным 0, тогда строгое неравенство вида 0·x>c и 0·x<c может быть записано в виде нестрогого, а именно, a·x≤c, a·x≥c. Такое уравнение считается линейным.
Их различия заключаются в:
- форме записи a·x+b>0 в первом, и a·x>c – во втором;
- допустимости равенства нулю коэффициента a, a≠0 — в первом, и a=0 — во втором.
Считается, что неравенства a·x+b>0 и a·x>c равносильные, потому как получены переносом слагаемого из одной части в другую. Решение неравенства 0·x+5>0 приведет к тому, что его необходимо будет решить, причем случай а=0 не подойдет.
Решение неравенства 0·x+5>0 приведет к тому, что его необходимо будет решить, причем случай а=0 не подойдет.
Считается, что линейными неравенствами в одной переменной x считаются неравенства вида a·x+b<0, a·x+b>0, a·x+b≤0 и a·x+b≥0, где a и b являются действительными числами. Вместо x может быть обычное число.
Исходя из правила, имеем, что 4·x−1>0, 0·z+2,3≤0, -23·x-2<0 являются примерами линейных неравенств. А неравенства такого плана, как 5·x>7, −0,5·y≤−1,2 называют сводящимися к линейному.
Как решить линейное неравенство
Основным способом решения таких неравенств сводится к равносильным преобразованиям для того, чтобы найти элементарные неравенства x<p (≤, >, ≥), p являющееся некоторым числом, при a≠0, а вида a<p (≤, >, ≥) при а=0.
Для решения неравенства с одной переменной, можно применять метода интервалов или изображать графически. Любой из них можно применять обособленно.
Используя равносильные преобразования
Чтобы решить линейное неравенство вида a·x+b<0 (≤, >, ≥), необходимо применить равносильные преобразования неравенства. Коэффициент может быть равен или не равен нулю. Рассмотрим оба случая. Для выяснения необходимо придерживаться схемы, состоящей из 3 пунктов: суть процесса, алгоритм, само решение.
Коэффициент может быть равен или не равен нулю. Рассмотрим оба случая. Для выяснения необходимо придерживаться схемы, состоящей из 3 пунктов: суть процесса, алгоритм, само решение.
Алгоритм решение линейного неравенства a·x+b<0 (≤, >, ≥) при a≠0
- число b будет перенесено в правую часть неравенства с противоположным знаком, что позволит прийти к равносильному a·x<−b (≤, >, ≥);
- будет производиться деление обеих частей неравенства на число не равное 0. Причем , когда a является положительным, то знак остается, когда a – отрицательное, меняется на противоположный.
Рассмотрим применение данного алгоритма на решении примеров.
Пример 1Решить неравенство вида 3·x+12≤0.
Решение
Данное линейное неравенство имеет a=3 и b=12. Значит, коэффициент a при x не равен нулю. Применим выше сказанные алгоритмы, решим.
Необходимо перенести слагаемое 12 в другую часть неравенства с изменением знака перед ним.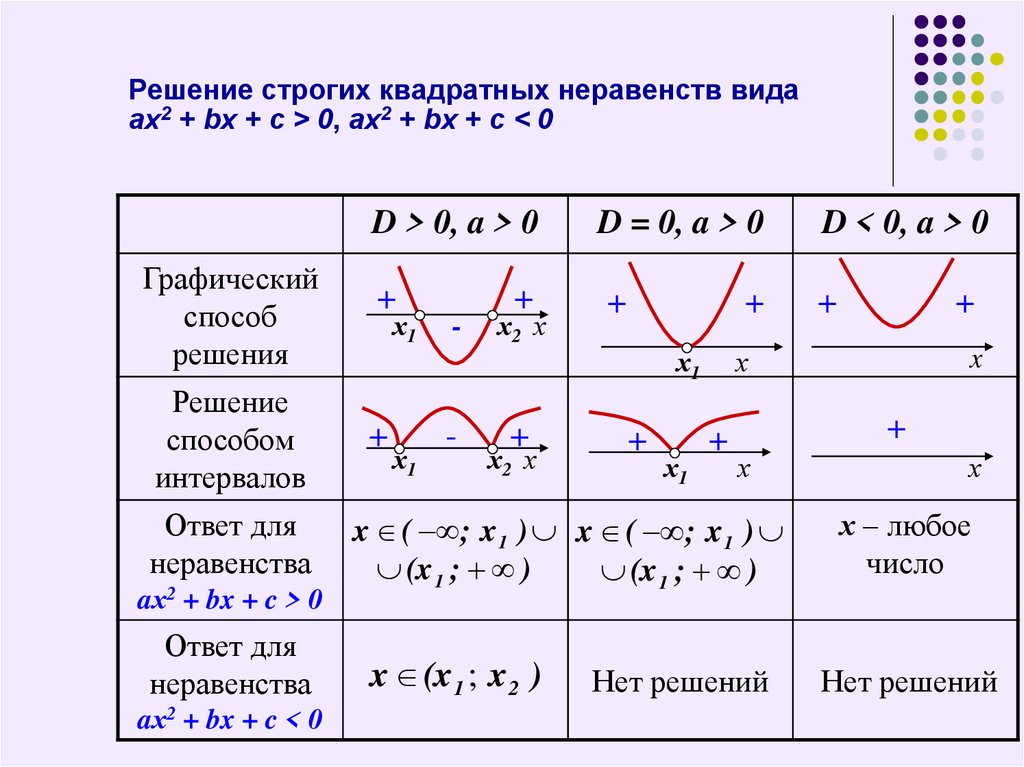 Тогда получаем неравенство вида 3·x≤−12. Необходимо произвести деление обеих частей на 3. Знак не поменяется, так как 3 является положительным числом. Получаем, что (3·x):3≤(−12):3, что даст результат x≤−4.
Тогда получаем неравенство вида 3·x≤−12. Необходимо произвести деление обеих частей на 3. Знак не поменяется, так как 3 является положительным числом. Получаем, что (3·x):3≤(−12):3, что даст результат x≤−4.
Неравенство вида x≤−4 является равносильным. То есть решение для 3·x+12≤0 – это любое действительное число, которое меньше или равно 4. Ответ записывается в виде неравенства x≤−4, или числового промежутка вида (−∞, −4].
Весь выше прописанный алгоритм записывается так:
3·x+12≤0; 3·x≤−12; x≤−4.
Ответ: x≤−4 или (−∞, −4].
Пример 2Указать все имеющиеся решения неравенства −2,7·z>0.
Решение
Из условия видим, что коэффициент a при z равняется -2,7, а b в явном виде отсутствует или равняется нулю. Первый шаг алгоритма можно не использовать, а сразу переходить ко второму.
Производим деление обеих частей уравнения на число -2,7. Так как число отрицательное, необходимо поменять знак неравенства на противоположный. То есть получаем, что (−2,7·z):(−2,7)<0:(−2,7), и дальше z<0.
Весь алгоритм запишем в краткой форме:
−2,7·z>0; z<0.
Ответ: z<0 или (−∞, 0).
Пример 3Решить неравенство -5·x-1522≤0.
Решение
По условию видим, что необходимо решить неравенство с коэффициентом a при переменной x, которое равняется -5, с коэффициентом b, которому соответствует дробь -1522. Решать неравенство необходимо, следуя алгоритму, то есть: перенести -1522 в другую часть с противоположным знаком, разделить обе части на -5, изменить знак неравенства:
-5·x≤1522;-5·x:-5≥1522:-5x≥-322
При последнем переходе для правой части используется правило деления числе с разными знаками 1522:-5=-1522:5, после чего выполняем деление обыкновенной дроби на натурально число -1522:5=-1522·15=-15·122·5=-322.
Ответ: x≥-322 и [-322+∞).
Рассмотрим случай, когда а=0. Линейное выражение вида a·x+b<0 является неравенством 0·x+b<0, где на рассмотрение берется неравенство вида b<0, после чего выясняется, оно верное или нет.
Все основывается на определении решения неравенства. При любом значении x получаем числовое неравенство вида b<0, потому что при подстановке любого t вместо переменной x, тогда получаем 0·t+b<0, где b<0. В случае, если оно верно, то для его решения подходит любое значение. Когда b<0 неверно, тогда линейное уравнение не имеет решений, потому как не имеется ни одного значения переменной, которое привело бы верному числовому равенству.
Все суждения рассмотрим в виде алгоритма решения линейных неравенств 0·x+b<0 (≤, >, ≥):
Определение 5Числовое неравенство вида b<0 (≤, >, ≥) верно, тогда исходное неравенство имеет решение при любом значении, а неверно тогда, когда исходное неравенство не имеет решений.
Пример 4Решить неравенство 0·x+7>0.
Решение
Данное линейное неравенство 0·x+7>0 может принимать любое значение x. Тогда получим неравенство вида 7>0. Последнее неравенство считается верным, значит любое число может быть его решением.
Ответ: промежуток (−∞, +∞).
Пример 5Найти решение неравенства 0·x−12,7≥0.
Решение
При подстановке переменной x любого числа получим, что неравенство получит вид −12,7≥0. Оно является неверным. То есть 0·x−12,7≥0 не имеет решений.
Ответ: решений нет.
Рассмотрим решение линейных неравенств , где оба коэффициента равняется нулю.
Пример 6Определить не имеющее решение неравенство из 0·x+0>0 и 0·x+0≥0.
Решение
При подстановке любого числа вместо x получим два неравенства вида 0>0 и 0≥0. Первое является неверным. Значит, 0·x+0>0 не имеет решений, а 0·x+0≥0 имеет бесконечное количество решений, то есть любое число.
Ответ: неравенство 0·x+0>0 не имеет решений, а 0·x+0≥0 имеет решения.
Методом интервалов
Данный метод рассматривается в школьном курсе математики. Метод интервалов способен разрешать различные виды неравенств, также и линейные.
Метод интервалов применяется для линейных неравенств при значении коэффициента x не равному 0.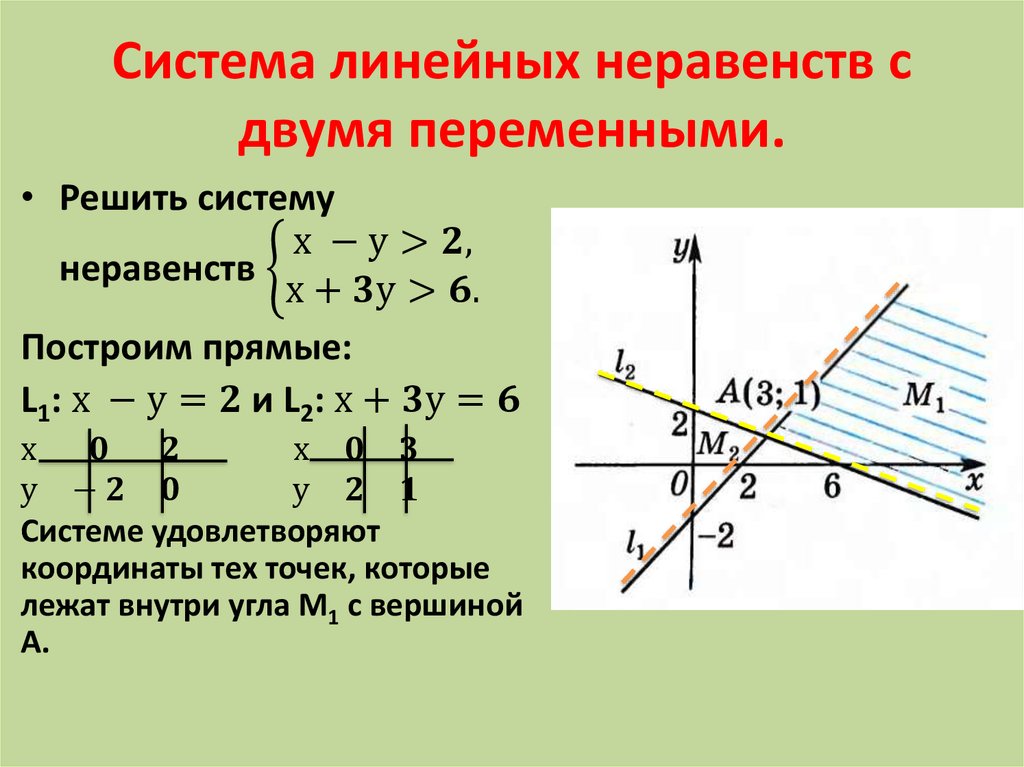 Иначе придется вычислять при помощи другого метода.
Иначе придется вычислять при помощи другого метода.
Метод интервалов – это:
- введение функции y=a·x+b;
- поиск нулей для разбивания области определения на промежутки;
- определение знаков для понятия их на промежутках.
Соберем алгоритм для решения линейных уравнений a·x+b<0 (≤, >, ≥) при a≠0 с помощью метода интервалов:
- нахождение нулей функции y=a·x+b, чтобы решить уравнение вида a·x+b=0. Если a≠0, тогда решением будет единственный корень, который примет обозначение х0;
- построение координатной прямой с изображением точки с координатой х0, при строгом неравенстве точка обозначается выколотой, при нестрогом – закрашенной;
- определение знаков функции y=a·x+b на промежутках, для этого необходимо находить значения функции в точках на промежутке;
- решение неравенства со знаками > или ≥ на координатной прямой добавляется штриховка над положительным промежутком, < или ≤ над отрицательным промежутком.

Рассмотрим несколько примеров решения линейного неравенства при помощи метода интервалов.
Пример 6Решить неравенство −3·x+12>0.
Решение
Из алгоритма следует, что для начала нужно найти корень уравнения −3·x+12=0. Получаем, что −3·x=−12, x=4. Необходимо изобразить координатную прямую, где отмечаем точку 4. Она будет выколотой, так как неравенство является строгим. Рассмотрим чертеж, приведенный ниже.
Нужно определить знаки на промежутках. Чтобы определить его на промежутке (−∞, 4), необходимо произвести вычисление функции y=−3·x+12 при х=3. Отсюда получим, что −3·3+12=3>0. Знак на промежутке является положительным.
Определяем знак из промежутка (4, +∞), тогда подставляем значение х=5. Имеем, что −3·5+12=−3<0. Знак на промежутке является отрицательным. Изобразим на числовой прямой, приведенной ниже.
Мы выполняем решение неравенства со знаком >, причем штриховка выполняется над положительным промежутком.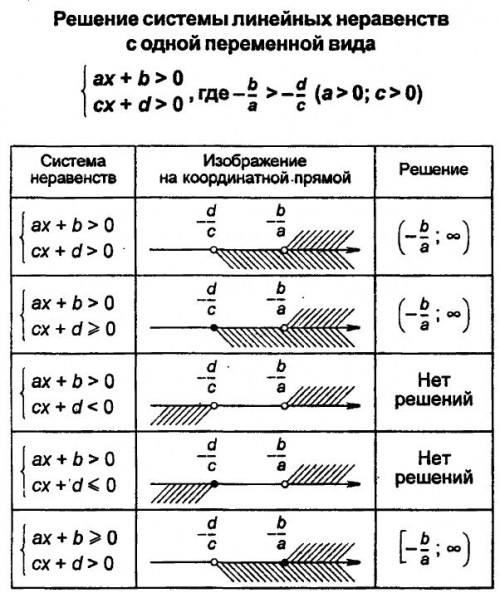 Рассмотрим чертеж, приведенный ниже.
Рассмотрим чертеж, приведенный ниже.
Из чертежа видно, что искомое решение имеет вид (−∞, 4) или x<4.
Ответ: (−∞, 4) или x<4.
Графическим способом
Чтобы понять, как изображать графически, необходимо рассмотреть на примере 4 линейных неравенства: 0,5·x−1<0, 0,5·x−1≤0, 0,5·x−1>0 и 0,5·x−1≥0. Их решениями будут значения x<2, x≤2, x>2 и x≥2. Для этого изобразим график линейной функции y=0,5·x−1, приведенный ниже.
Видно, что
Определение 7- решением неравенства 0,5·x−1<0 считается промежуток, где график функции y=0,5·x−1 располагается ниже Ох;
- решением 0,5·x−1≤0 считается промежуток, где функция y=0,5·x−1 ниже Ох или совпадает;
- решением 0,5·x−1>0 считается промежуток, гре функция располагается выше Ох;
- решением 0,5·x−1≥0 считается промежуток, где график выше Ох или совпадает.
Смысл графического решения неравенств заключается в нахождении промежутков, которое необходимо изображать на графике. В данном случае получаем, что левая часть имеет y=a·x+b, а правая – y=0, причем совпадает с Ох.
В данном случае получаем, что левая часть имеет y=a·x+b, а правая – y=0, причем совпадает с Ох.
Алгоритм решения линейных неравенств графическим способом.
Определение 8Построение графика функции y=a·x+b производится:
- во время решения неравенства a·x+b<0 определяется промежуток, где график изображен ниже Ох;
- во время решения неравенства a·x+b≤0 определяется промежуток, где график изображается ниже оси Ох или совпадает;
- во время решения неравенства a·x+b>0 производится определение промежутка, где график изображается выше Ох;
- во время решения неравенства a·x+b≥0 производится определение промежутка, где график находится выше Ох или совпадает.
Решить неравенство -5·x-3>0 при помощи графика.
Решение
Необходимо построить график линейной функции -5·x-3>0. Данная прямая является убывающей, потому как коэффициент при x является отрицательным. Для определения координат точки его пересечения с Ох-5·x-3>0 получим значение -35. Изобразим графически.
Изобразим графически.
Решение неравенства со знаком >, тогда необходимо обратить внимание на промежуток выше Ох. Выделим красным цветом необходимую часть плоскости и получим, что
Необходимый промежуток является частью Ох красного цвета. Значит, открытый числовой луч -∞, -35 будет решением неравенства. Если бы по условию имели нестрогое неравенство, тогда значение точки -35 также являлось бы решением неравенства. И совпадало бы с Ох.
Ответ: -∞, -35 или x<-35.
Графический способ решения используется, когда левая часть будет отвечать функции y=0·x+b, то есть y=b. Тогда прямая будет параллельна Ох или совпадающей при b=0. Эти случаю показывают, что неравенство может не иметь решений, либо решением может быть любое число.
Пример 8Определить из неравенств 0·x+7<=0, 0·x+0≥0 то, которое имеет хотя бы одно решение.
Решение
Представление y=0·x+7 является y=7, тогда будет задана координатная плоскость с прямой, параллельной Ох и находящейся выше Ох.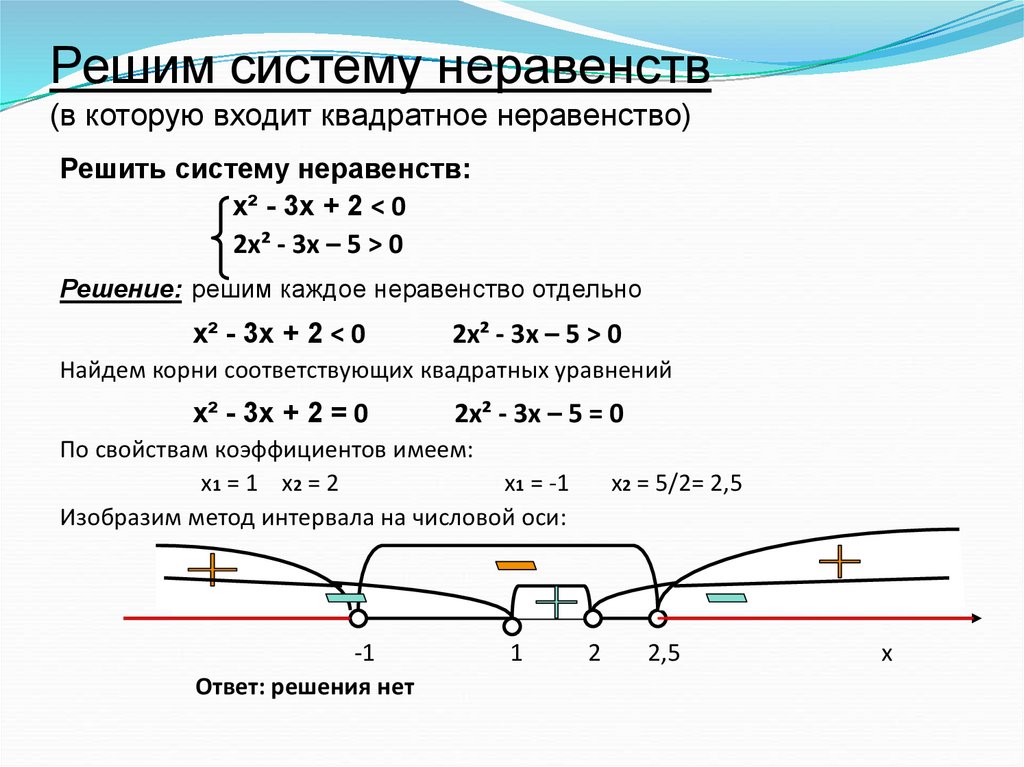 Значит, 0·x+7<=0 решений не имеет, потому как нет промежутков.
Значит, 0·x+7<=0 решений не имеет, потому как нет промежутков.
График функции y=0·x+0, считается y=0, то есть прямая совпадает с Ох. Значит, неравенство 0·x+0≥0 имеет множество решений.
Ответ: второе неравенство имеет решение при любом значении x.
Неравенства, сводящиеся к линейным
Решение неравенств можно свести к решению линейного уравнения, которые называют неравенствами, сводящимися к линейным.
Данные неравенства были рассмотрены в школьном курсе, так как они являлись частным случаем решения неравенств, что приводило к раскрытию скобок и приведению подобных слагаемых. Для примера рассмотрим, что 5−2·x>0, 7·(x−1)+3≤4·x−2+x, x-35-2·x+1>27·x.
Неравенства, приведенные выше, всегда приводятся к виду линейного уравнения. После чего раскрываются скобки и приводятся подобные слагаемые, переносятся из разных частей, меняя знак на противоположный.
При сведении неравенства 5−2·x>0 к линейному, представляем его таким образом, чтобы оно имело вид −2·x+5>0, а для приведения второго получаем, что 7·(x−1)+3≤4·x−2+x. Необходимо раскрыть скобки, привести подобные слагаемые, перенести все слагаемые в левую часть и привести подобные слагаемые. Это выглядит таким образом:
Необходимо раскрыть скобки, привести подобные слагаемые, перенести все слагаемые в левую часть и привести подобные слагаемые. Это выглядит таким образом:
7·x−7+3≤4·x−2+x 7·x−4≤5·x−2 7·x−4−5·x+2≤0 2·x−2≤0
Это приводит решение к линейному неравенству.
Эти неравенства рассматриваются как линейные, так как имеют такой же принцип решения, после чего возможно приведение их к элементарным неравенствам.
Для решения такого вида неравенства такого вида необходимо свести его к линейному. Это следует делать таким образом:
Определение 9- раскрыть скобки;
- слева собрать переменные, а справа числа;
- привести подобные слагаемые;
- разделить обе части на коэффициент при x.
Решить неравенство 5·(x+3)+x≤6·(x−3)+1.
Решение
Производим раскрытие скобок, тогда получим неравенство вида 5·x+15+x≤6·x−18+1. После приведения подобных слагаемых имеем, что 6·x+15≤6·x−17. После перенесения слагаемых с левой в правую, получим, что 6·x+15−6·x+17≤0. Отсюда имеет неравенство вида 32≤0 из полученного при вычислении 0·x+32≤0. Видно, что неравенство неверное, значит, неравенство, данное по условию, не имеет решений.
Отсюда имеет неравенство вида 32≤0 из полученного при вычислении 0·x+32≤0. Видно, что неравенство неверное, значит, неравенство, данное по условию, не имеет решений.
Ответ: нет решений.
Стоит отметить, что имеется множество неравенств другого вида, которые могут сводится к линейному или неравенству вида, показанного выше. Например, 52·x−1≥1 является показательным уравнением, которое сводится к решению линейного вида 2·x−1≥0. Эти случаи будут рассмотрены при решении неравенств данного вида.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р. Реферат
от 1 дня / от 700 р.
Реферат
от 1 дня / от 700 р.
Линейные неравенства, примеры, решения
После получения начальных сведений о неравенствах с переменными, переходим к вопросу их решения. Разберем решение линейных неравенств с одной переменной и все методы для их разрешения с алгоритмами и примерами. Будут рассмотрены только линейные уравнения с одной переменной.
Что такое линейное неравенство?
В начале необходимо определить линейное уравнение и выяснить его стандартный вид и чем оно будет отличаться от других. Из школьного курса имеем, что у неравенств нет принципиального различия, поэтому необходимо использовать несколько определений.
Из школьного курса имеем, что у неравенств нет принципиального различия, поэтому необходимо использовать несколько определений.
Линейное неравенство с одной переменной x – это неравенство вида a·x+b>0, когда вместо > используется любой знак неравенства <, ≤, ≥, а и b являются действительными числами, где a≠0.
Определение 2Неравенства a·x<c или a·x>c, с x являющимся переменной, а a и c некоторыми числами, называют линейными неравенствами с одной переменной.
Так как ничего не сказано за то, может ли коэффициент быть равным 0, тогда строгое неравенство вида 0·x>c и 0·x<c может быть записано в виде нестрогого, а именно, a·x≤c, a·x≥c. Такое уравнение считается линейным.
Их различия заключаются в:
- форме записи a·x+b>0 в первом, и a·x>c – во втором;
- допустимости равенства нулю коэффициента a, a≠0 — в первом, и a=0 — во втором.
Считается, что неравенства a·x+b>0 и a·x>c равносильные, потому как получены переносом слагаемого из одной части в другую. Решение неравенства 0·x+5>0 приведет к тому, что его необходимо будет решить, причем случай а=0 не подойдет.
Решение неравенства 0·x+5>0 приведет к тому, что его необходимо будет решить, причем случай а=0 не подойдет.
Считается, что линейными неравенствами в одной переменной x считаются неравенства вида a·x+b<0, a·x+b>0, a·x+b≤0 и a·x+b≥0, где a и b являются действительными числами. Вместо x может быть обычное число.
Исходя из правила, имеем, что 4·x−1>0, 0·z+2,3≤0, -23·x-2<0 являются примерами линейных неравенств. А неравенства такого плана, как 5·x>7, −0,5·y≤−1,2 называют сводящимися к линейному.
Как решить линейное неравенство
Основным способом решения таких неравенств сводится к равносильным преобразованиям для того, чтобы найти элементарные неравенства x<p (≤, >, ≥), p являющееся некоторым числом, при a≠0, а вида a<p (≤, >, ≥) при а=0.
Для решения неравенства с одной переменной, можно применять метода интервалов или изображать графически. Любой из них можно применять обособленно.
Используя равносильные преобразования
Чтобы решить линейное неравенство вида a·x+b<0 (≤, >, ≥), необходимо применить равносильные преобразования неравенства. Коэффициент может быть равен или не равен нулю. Рассмотрим оба случая. Для выяснения необходимо придерживаться схемы, состоящей из 3 пунктов: суть процесса, алгоритм, само решение.
Коэффициент может быть равен или не равен нулю. Рассмотрим оба случая. Для выяснения необходимо придерживаться схемы, состоящей из 3 пунктов: суть процесса, алгоритм, само решение.
Алгоритм решение линейного неравенства a·x+b<0 (≤, >, ≥) при a≠0
- число b будет перенесено в правую часть неравенства с противоположным знаком, что позволит прийти к равносильному a·x<−b (≤, >, ≥);
- будет производиться деление обеих частей неравенства на число не равное 0. Причем , когда a является положительным, то знак остается, когда a – отрицательное, меняется на противоположный.
Рассмотрим применение данного алгоритма на решении примеров.
Пример 1Решить неравенство вида 3·x+12≤0.
Решение
Данное линейное неравенство имеет a=3 и b=12. Значит, коэффициент a при x не равен нулю. Применим выше сказанные алгоритмы, решим.
Необходимо перенести слагаемое 12 в другую часть неравенства с изменением знака перед ним. Тогда получаем неравенство вида 3·x≤−12. Необходимо произвести деление обеих частей на 3. Знак не поменяется, так как 3 является положительным числом. Получаем, что (3·x):3≤(−12):3, что даст результат x≤−4.
Тогда получаем неравенство вида 3·x≤−12. Необходимо произвести деление обеих частей на 3. Знак не поменяется, так как 3 является положительным числом. Получаем, что (3·x):3≤(−12):3, что даст результат x≤−4.
Неравенство вида x≤−4 является равносильным. То есть решение для 3·x+12≤0 – это любое действительное число, которое меньше или равно 4. Ответ записывается в виде неравенства x≤−4, или числового промежутка вида (−∞, −4].
Весь выше прописанный алгоритм записывается так:
3·x+12≤0; 3·x≤−12; x≤−4.
Ответ: x≤−4 или (−∞, −4].
Пример 2Указать все имеющиеся решения неравенства −2,7·z>0.
Решение
Из условия видим, что коэффициент a при z равняется -2,7, а b в явном виде отсутствует или равняется нулю. Первый шаг алгоритма можно не использовать, а сразу переходить ко второму.
Производим деление обеих частей уравнения на число -2,7. Так как число отрицательное, необходимо поменять знак неравенства на противоположный. То есть получаем, что (−2,7·z):(−2,7)<0:(−2,7), и дальше z<0.
Весь алгоритм запишем в краткой форме:
−2,7·z>0; z<0.
Ответ: z<0 или (−∞, 0).
Пример 3Решить неравенство -5·x-1522≤0.
Решение
По условию видим, что необходимо решить неравенство с коэффициентом a при переменной x, которое равняется -5, с коэффициентом b, которому соответствует дробь -1522. Решать неравенство необходимо, следуя алгоритму, то есть: перенести -1522 в другую часть с противоположным знаком, разделить обе части на -5, изменить знак неравенства:
-5·x≤1522;-5·x:-5≥1522:-5x≥-322
При последнем переходе для правой части используется правило деления числе с разными знаками 1522:-5=-1522:5, после чего выполняем деление обыкновенной дроби на натурально число -1522:5=-1522·15=-15·122·5=-322.
Ответ: x≥-322 и [-322+∞).
Рассмотрим случай, когда а=0. Линейное выражение вида a·x+b<0 является неравенством 0·x+b<0, где на рассмотрение берется неравенство вида b<0, после чего выясняется, оно верное или нет.
Все основывается на определении решения неравенства. При любом значении x получаем числовое неравенство вида b<0, потому что при подстановке любого t вместо переменной x, тогда получаем 0·t+b<0, где b<0. В случае, если оно верно, то для его решения подходит любое значение. Когда b<0 неверно, тогда линейное уравнение не имеет решений, потому как не имеется ни одного значения переменной, которое привело бы верному числовому равенству.
Все суждения рассмотрим в виде алгоритма решения линейных неравенств 0·x+b<0 (≤, >, ≥):
Определение 5Числовое неравенство вида b<0 (≤, >, ≥) верно, тогда исходное неравенство имеет решение при любом значении, а неверно тогда, когда исходное неравенство не имеет решений.
Пример 4Решить неравенство 0·x+7>0.
Решение
Данное линейное неравенство 0·x+7>0 может принимать любое значение x. Тогда получим неравенство вида 7>0. Последнее неравенство считается верным, значит любое число может быть его решением.
Ответ: промежуток (−∞, +∞).
Пример 5Найти решение неравенства 0·x−12,7≥0.
Решение
При подстановке переменной x любого числа получим, что неравенство получит вид −12,7≥0. Оно является неверным. То есть 0·x−12,7≥0 не имеет решений.
Ответ: решений нет.
Рассмотрим решение линейных неравенств , где оба коэффициента равняется нулю.
Пример 6Определить не имеющее решение неравенство из 0·x+0>0 и 0·x+0≥0.
Решение
При подстановке любого числа вместо x получим два неравенства вида 0>0 и 0≥0. Первое является неверным. Значит, 0·x+0>0 не имеет решений, а 0·x+0≥0 имеет бесконечное количество решений, то есть любое число.
Ответ: неравенство 0·x+0>0 не имеет решений, а 0·x+0≥0 имеет решения.
Методом интервалов
Данный метод рассматривается в школьном курсе математики. Метод интервалов способен разрешать различные виды неравенств, также и линейные.
Метод интервалов применяется для линейных неравенств при значении коэффициента x не равному 0. Иначе придется вычислять при помощи другого метода.
Иначе придется вычислять при помощи другого метода.
Метод интервалов – это:
- введение функции y=a·x+b;
- поиск нулей для разбивания области определения на промежутки;
- определение знаков для понятия их на промежутках.
Соберем алгоритм для решения линейных уравнений a·x+b<0 (≤, >, ≥) при a≠0 с помощью метода интервалов:
- нахождение нулей функции y=a·x+b, чтобы решить уравнение вида a·x+b=0. Если a≠0, тогда решением будет единственный корень, который примет обозначение х0;
- построение координатной прямой с изображением точки с координатой х0, при строгом неравенстве точка обозначается выколотой, при нестрогом – закрашенной;
- определение знаков функции y=a·x+b на промежутках, для этого необходимо находить значения функции в точках на промежутке;
- решение неравенства со знаками > или ≥ на координатной прямой добавляется штриховка над положительным промежутком, < или ≤ над отрицательным промежутком.

Рассмотрим несколько примеров решения линейного неравенства при помощи метода интервалов.
Пример 6Решить неравенство −3·x+12>0.
Решение
Из алгоритма следует, что для начала нужно найти корень уравнения −3·x+12=0. Получаем, что −3·x=−12, x=4. Необходимо изобразить координатную прямую, где отмечаем точку 4. Она будет выколотой, так как неравенство является строгим. Рассмотрим чертеж, приведенный ниже.
Нужно определить знаки на промежутках. Чтобы определить его на промежутке (−∞, 4), необходимо произвести вычисление функции y=−3·x+12 при х=3. Отсюда получим, что −3·3+12=3>0. Знак на промежутке является положительным.
Определяем знак из промежутка (4, +∞), тогда подставляем значение х=5. Имеем, что −3·5+12=−3<0. Знак на промежутке является отрицательным. Изобразим на числовой прямой, приведенной ниже.
Мы выполняем решение неравенства со знаком >, причем штриховка выполняется над положительным промежутком. Рассмотрим чертеж, приведенный ниже.
Рассмотрим чертеж, приведенный ниже.
Из чертежа видно, что искомое решение имеет вид (−∞, 4) или x<4.
Ответ: (−∞, 4) или x<4.
Графическим способом
Чтобы понять, как изображать графически, необходимо рассмотреть на примере 4 линейных неравенства: 0,5·x−1<0, 0,5·x−1≤0, 0,5·x−1>0 и 0,5·x−1≥0. Их решениями будут значения x<2, x≤2, x>2 и x≥2. Для этого изобразим график линейной функции y=0,5·x−1, приведенный ниже.
Видно, что
Определение 7- решением неравенства 0,5·x−1<0 считается промежуток, где график функции y=0,5·x−1 располагается ниже Ох;
- решением 0,5·x−1≤0 считается промежуток, где функция y=0,5·x−1 ниже Ох или совпадает;
- решением 0,5·x−1>0 считается промежуток, гре функция располагается выше Ох;
- решением 0,5·x−1≥0 считается промежуток, где график выше Ох или совпадает.
Смысл графического решения неравенств заключается в нахождении промежутков, которое необходимо изображать на графике. В данном случае получаем, что левая часть имеет y=a·x+b, а правая – y=0, причем совпадает с Ох.
В данном случае получаем, что левая часть имеет y=a·x+b, а правая – y=0, причем совпадает с Ох.
Алгоритм решения линейных неравенств графическим способом.
Определение 8Построение графика функции y=a·x+b производится:
- во время решения неравенства a·x+b<0 определяется промежуток, где график изображен ниже Ох;
- во время решения неравенства a·x+b≤0 определяется промежуток, где график изображается ниже оси Ох или совпадает;
- во время решения неравенства a·x+b>0 производится определение промежутка, где график изображается выше Ох;
- во время решения неравенства a·x+b≥0 производится определение промежутка, где график находится выше Ох или совпадает.
Решить неравенство -5·x-3>0 при помощи графика.
Решение
Необходимо построить график линейной функции -5·x-3>0. Данная прямая является убывающей, потому как коэффициент при x является отрицательным. Для определения координат точки его пересечения с Ох-5·x-3>0 получим значение -35. Изобразим графически.
Изобразим графически.
Решение неравенства со знаком >, тогда необходимо обратить внимание на промежуток выше Ох. Выделим красным цветом необходимую часть плоскости и получим, что
Необходимый промежуток является частью Ох красного цвета. Значит, открытый числовой луч -∞, -35 будет решением неравенства. Если бы по условию имели нестрогое неравенство, тогда значение точки -35 также являлось бы решением неравенства. И совпадало бы с Ох.
Ответ: -∞, -35 или x<-35.
Графический способ решения используется, когда левая часть будет отвечать функции y=0·x+b, то есть y=b. Тогда прямая будет параллельна Ох или совпадающей при b=0. Эти случаю показывают, что неравенство может не иметь решений, либо решением может быть любое число.
Пример 8Определить из неравенств 0·x+7<=0, 0·x+0≥0 то, которое имеет хотя бы одно решение.
Решение
Представление y=0·x+7 является y=7, тогда будет задана координатная плоскость с прямой, параллельной Ох и находящейся выше Ох. Значит, 0·x+7<=0 решений не имеет, потому как нет промежутков.
Значит, 0·x+7<=0 решений не имеет, потому как нет промежутков.
График функции y=0·x+0, считается y=0, то есть прямая совпадает с Ох. Значит, неравенство 0·x+0≥0 имеет множество решений.
Ответ: второе неравенство имеет решение при любом значении x.
Неравенства, сводящиеся к линейным
Решение неравенств можно свести к решению линейного уравнения, которые называют неравенствами, сводящимися к линейным.
Данные неравенства были рассмотрены в школьном курсе, так как они являлись частным случаем решения неравенств, что приводило к раскрытию скобок и приведению подобных слагаемых. Для примера рассмотрим, что 5−2·x>0, 7·(x−1)+3≤4·x−2+x, x-35-2·x+1>27·x.
Неравенства, приведенные выше, всегда приводятся к виду линейного уравнения. После чего раскрываются скобки и приводятся подобные слагаемые, переносятся из разных частей, меняя знак на противоположный.
При сведении неравенства 5−2·x>0 к линейному, представляем его таким образом, чтобы оно имело вид −2·x+5>0, а для приведения второго получаем, что 7·(x−1)+3≤4·x−2+x. Необходимо раскрыть скобки, привести подобные слагаемые, перенести все слагаемые в левую часть и привести подобные слагаемые. Это выглядит таким образом:
Необходимо раскрыть скобки, привести подобные слагаемые, перенести все слагаемые в левую часть и привести подобные слагаемые. Это выглядит таким образом:
7·x−7+3≤4·x−2+x 7·x−4≤5·x−2 7·x−4−5·x+2≤0 2·x−2≤0
Это приводит решение к линейному неравенству.
Эти неравенства рассматриваются как линейные, так как имеют такой же принцип решения, после чего возможно приведение их к элементарным неравенствам.
Для решения такого вида неравенства такого вида необходимо свести его к линейному. Это следует делать таким образом:
Определение 9- раскрыть скобки;
- слева собрать переменные, а справа числа;
- привести подобные слагаемые;
- разделить обе части на коэффициент при x.
Решить неравенство 5·(x+3)+x≤6·(x−3)+1.
Решение
Производим раскрытие скобок, тогда получим неравенство вида 5·x+15+x≤6·x−18+1. После приведения подобных слагаемых имеем, что 6·x+15≤6·x−17. После перенесения слагаемых с левой в правую, получим, что 6·x+15−6·x+17≤0. Отсюда имеет неравенство вида 32≤0 из полученного при вычислении 0·x+32≤0. Видно, что неравенство неверное, значит, неравенство, данное по условию, не имеет решений.
Отсюда имеет неравенство вида 32≤0 из полученного при вычислении 0·x+32≤0. Видно, что неравенство неверное, значит, неравенство, данное по условию, не имеет решений.
Ответ: нет решений.
Стоит отметить, что имеется множество неравенств другого вида, которые могут сводится к линейному или неравенству вида, показанного выше. Например, 52·x−1≥1 является показательным уравнением, которое сводится к решению линейного вида 2·x−1≥0. Эти случаи будут рассмотрены при решении неравенств данного вида.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р. Реферат
от 1 дня / от 700 р.
Реферат
от 1 дня / от 700 р.
Гибридный алгоритм решения линейных неравенств по методу наименьших квадратов
Беннет К.П., Мангасарян О.Л.: Надежное различение двух линейно неразделимых множеств с помощью линейного программирования. Оптимиз. Программное обеспечение Методы. 1 , 23–34 (1992)
Статья Google ученый
Бьорк, А.: Численные методы решения задач наименьших квадратов. СИАМ, Филадельфия (1996)
Google ученый
Бойд С., Ванденберг Л.: Выпуклая оптимизация. Издательство Кембриджского университета (2004)
Брэмли, Р., Винника, Б.: Решение линейных неравенств методом наименьших квадратов. SIAM J. Sci. вычисл. 17 , 275–286 (1996)
МАТЕМАТИКА Статья MathSciNet Google ученый
Цензор Ю., Альтшулер М.Д., Паулис В.Д.: Вычислительное решение обратной задачи планирования лучевой терапии. заявл. Мат. вычисл. 25 , 57–87 (1988)
МАТЕМАТИКА Статья MathSciNet Google ученый
Цензор Ю., Бен-Исраэль А., Сяо Ю., Галвин Дж. М.: О линейной невозможности, возникающей при обратном планировании лучевой терапии с модулированной интенсивностью. Приложение линейной алгебры. 428 , 1406–1420 (2008)
МАТЕМАТИКА Статья MathSciNet Google ученый
Цензор Ю., Эльфвинг Т.: Новые методы линейных неравенств. Приложение линейной алгебры. 42 , 199–211 (1982)
МАТЕМАТИКА Статья MathSciNet Google ученый
Цензор Ю., Зениос С.А.: Параллельная оптимизация, теоретические алгоритмы и приложения. Издательство Оксфордского университета, Оксфорд (1997)
МАТЕМАТИКА Google ученый
Чиннек, Дж. В.: Поиск полезного подмножества ограничений для анализа в невозможной линейной программе. ИНФОРМ J. Comput. 9 , 164–174 (1997)
МАТЕМАТИКА Статья MathSciNet Google ученый
Чиннек, Дж. В. Л.: Возможность и невозможность оптимизации: алгоритмы и вычислительные методы. В: Международная серия исследований операций и управленческих наук, том. 118. Springer-Verlag (2007)
Чиннек, Дж. В., Дравниекс, Э. В.: Поиск минимальных невыполнимых наборов ограничений в линейных программах. ОРСА Дж. Вычисл. 3 , 157–168 (1991)
МАТЕМАТИКА Google ученый
Кларк, Д.И., Осборн, М.Р.: О линейных ограниченных и интервальных задачах наименьших квадратов. IMA J. Нумер. Анальный. 8 , 23–36 (1988)
МАТЕМАТИКА Статья MathSciNet Google ученый
Коулман Т., Халберт Л.: Глобально и суперлинейно сходящийся алгоритм квадратичного программирования с простыми оценками. СИАМ Дж. Оптим. 3 , 298–321 (1993)
МАТЕМАТИКА Статья MathSciNet Google ученый
Дакс, А.: Сходимость линейных стационарных итерационных процессов для решения сингулярных неструктурированных систем линейных уравнений. SIAM Rev. 32 , 611–635 (1990)
SIAM Rev. 32 , 611–635 (1990)
МАТЕМАТИКА Статья MathSciNet Google ученый
Дакс, А.: Метод релаксации ряда для больших ℓ 1 проблемы. Приложение линейной алгебры. 156 , 793–818 (1991)
Статья MathSciNet Google ученый
Дакс, А.: О вычислительных аспектах ограниченных линейных задач наименьших квадратов. АКМ транс. Мат. ПО 17 , 64–73 (1991)
МАТЕМАТИКА Статья MathSciNet Google ученый
Дакс, А.: Наименьшая коррекция противоречивой системы линейных неравенств. Оптимиз. англ. 2 , 349–359 (2001)
МАТЕМАТИКА Статья Google ученый
Дакс А.: Приключения простого алгоритма. Приложение линейной алгебры. 361 , 41–61 (2003)
361 , 41–61 (2003)
МАТЕМАТИКА Статья MathSciNet Google ученый
Дакс, А.: Открытый вопрос о циклической релаксации. БИТ Номер. Мат. 43 , 929–943 (2003)
МАТЕМАТИКА Статья MathSciNet Google ученый
Дакс, А.: ℓ 1 решение линейных неравенств. вычисл. Статист. Анализ данных. 50 , 40–60 (2006)
МАТЕМАТИКА Статья MathSciNet Google ученый
Дакс, А.: Расстояние между двумя выпуклыми множествами. Приложение линейной алгебры. 416 , 184–213 (2006)
МАТЕМАТИКА Статья MathSciNet Google ученый
Де Леоне, Р., Мангасарян, О.Л.: Последовательное и параллельное решение крупномасштабных линейных программ с помощью расширенной лагранжевой последовательной сверхрелаксации. В: Куржански А., Нойвманн К., Паллашке Д. (ред.) Оптимизация, параллельная обработка и приложения. Конспект лекций по экономике и математическим системам, том. 304, стр. 103–124. Спрингер, Берлин (1988)
В: Куржански А., Нойвманн К., Паллашке Д. (ред.) Оптимизация, параллельная обработка и приложения. Конспект лекций по экономике и математическим системам, том. 304, стр. 103–124. Спрингер, Берлин (1988)
Google ученый
Деннис, Дж. Э., Шнабель, Р. Б.: Численные методы безусловной оптимизации и нелинейных уравнений. СИАМ, Филадельфия (1996)
МАТЕМАТИКА Google ученый
Де Пьерро, А.Р., Иусем, А.Н.: Метод одновременной проекции для линейных неравенств. Приложение линейной алгебры. 64 , 243–253 (1985)
МАТЕМАТИКА Статья MathSciNet Google ученый
Элден, Л.: Алгоритмы регуляризации плохо обусловленных задач наименьших квадратов. БИТ 17 , 134–145 (1977)
МАТЕМАТИКА Статья Google ученый
Флетчер Р.: Практические методы оптимизации. Wiley (1980)
Флетчер Р., Джексон М.П.: Минимизация квадратичной функции многих переменных с учетом только нижних и верхних границ. Дж. Инст. Мат. заявл. 14 , 159–174 (1974)
МАТЕМАТИКА Статья MathSciNet Google ученый
Гилл, П.Е., Мюррей, В., Райт, М.Х.: Практическая оптимизация. Academic Press, Лондон (1981)
МАТЕМАТИКА Google ученый
Гилл, П.Е., Мюррей, В., Райт, М.Х.: Численная линейная алгебра и оптимизация. Аддисон-Уэсли (1991)
Голуб, Г.Х., Ван Лоан, К.Ф.: Матричные вычисления. Johns Hopkins University Press (1983)
Хан, С.П.: Решение линейных неравенств методом наименьших квадратов. Технический отчет 2141, Матем. Рез. Центр, Университет Висконсин-Мэдисон (1980)
Хансен, П.К.: Дефектные по рангу и дискретные некорректные задачи. СИАМ, Филадельфия (1998)
Google ученый
Хэнсон, Р. Дж.: Линейный метод наименьших квадратов с границами и линейными ограничениями. SIAM J. Sci. Статист. вычисл. 7 , 826–834 (1986)
МАТЕМАТИКА Статья MathSciNet Google ученый
Герман, Г.Т.: Метод релаксации для реконструкции объектов по зашумленным рентгеновским лучам. Мат. прогр. 8 , 1–19 (1975)
МАТЕМАТИКА Статья MathSciNet Google ученый
Герман, Г.Т.: Реконструкция изображения по проекциям: основы компьютерной томографии. Academic Press, Нью-Йорк, США (1982)
Google ученый
Герман, Г.Т., Лент, А. : Семейство итерационных алгоритмов квадратичной оптимизации для пар неравенств с приложениями в диагностической радиологии. Мат. прогр. Этюд 9 , 15–29 (1978)
: Семейство итерационных алгоритмов квадратичной оптимизации для пар неравенств с приложениями в диагностической радиологии. Мат. прогр. Этюд 9 , 15–29 (1978)
MathSciNet Google ученый
Юсем А.Н., Де Пьерро А.Р.: Одновременный итерационный метод вычисления проекций на многогранники. SIAM J. Control 25 , 231–243 (1987)
МАТЕМАТИКА Статья Google ученый
Лент А., Цензор Ю.: Расширения метода строк Хилдрета для квадратичного программирования. СИАМ Дж. Контроль Оптим. 18 , 444–454 (1980)
МАТЕМАТИКА Статья MathSciNet Google ученый
Мэдсен, К., Нильсен, Х.Б., Пинар, М.К.: Связанное квадратичное программирование с ограничениями с помощью кусочно-квадратичных функций. Мат. прог. 85 , 135–156 (1999)
МАТЕМАТИКА Статья MathSciNet Google ученый
Мэдсен, К., Нильсен, Х.Б., Пинар, М.К.: Алгоритм конечного продолжения для квадратичного программирования со связанными ограничениями. СИАМ Дж. Оптим. 9 , 62–83 (1999)
Статья MathSciNet Google ученый
Мангасарян О.Л. Линейное и нелинейное разделение шаблонов с помощью линейного программирования. Опер. Рез. 13 , 444–452 (1965)
МАТЕМАТИКА Статья MathSciNet Google ученый
Мангасарян О.Л. Итеративное решение линейных программ. СИАМ Дж. Нумер. Анальный. 18 , 606–614 (1981)
МАТЕМАТИКА Статья MathSciNet Google ученый
Мангасарян О.Л. Математическое программирование в машинном обучении. В: Ди Пилло, Г., Джаннези, Ф. (ред.) Нелинейная оптимизация и приложения. Пленум Пресс, Нью-Йорк (1996)
Google ученый
Мангасарян О.Л.: Разделяющая плоскость произвольной нормы. Опер. Рез. лат. 24 , 15–23 (1999)
МАТЕМАТИКА Статья MathSciNet Google ученый
Мангасарян, О.Л., Де Леоне, Р.: Параллельная проекция градиента, последовательная сверхрелаксация для симметричных линейных задач дополнительности и линейных программ. Анна. Опер. Рез. 14 , 41–59 (1988)
МАТЕМАТИКА Статья MathSciNet Google ученый
Мангасарян О.Л., Сетионо Р., Вольберг В.Х.: Распознавание образов с помощью линейного программирования: теория и применение в медицинской диагностике. В: Коулман, Т.Ф., Ли, Ю. (ред.) Крупномасштабные численные оптимизации, стр. 22–31. СИАМ, Филадельфия (1990)
Google ученый
Море, Дж. Дж., Торальдо, Г.: Алгоритмы для задач квадратичного программирования со связанными ограничениями. Число. Мат. 55 , 377–400 (1989)
Число. Мат. 55 , 377–400 (1989)
МАТЕМАТИКА Статья MathSciNet Google ученый
Пинар, М.К.: Метод Ньютона для систем линейного неравенства. Евро. Дж. Опер. Рез. 107 , 710–719 (1998)
МАТЕМАТИКА Статья Google ученый
Стюарт, Г.В.: Матричные алгоритмы, Том 1: Основные разложения. СИАМ, Филадельфия (1998)
Google ученый
Уотсон, Г.А.: Выбор норм для подбора данных и аппроксимации функций. Акта. Число. 7 , 337–377 (1998)
Статья Google ученый
[PDF] Двухфазный метод абс для решения над определенными системами линейных неравенств
- DOI: 10.1007/BF02896404
- Идентификатор корпуса: 35434078
@article{Guo2006AnTP,
title={Двухфазный абс-метод решения над определенными системами линейных неравенств},
автор={Цян Го и Цзянго Лю},
journal={Журнал прикладной математики и вычислений},
год = {2006},
объем = {21},
страницы = {259-267}
} - Q.
 Guo, Jianguo Liu
Guo, Jianguo Liu - Опубликовано 1 мая 2006 г.
- Mathematics
- Journal of Applied Mathematics and Computing
Представлен метод, называемый многоступенчатым алгоритмом АБС, для решения системы переопределенных линейных неравенств и системы, объединенной с переопределенными линейными неравенствами и уравнениями. Этот метод характеризуется преобразованием системы неравенств в систему уравнений с резервными переменными. Явное решение с резервными переменными системы уравнений задается неявным алгоритмом LU, тогда резервные переменные могут быть заданы алгоритмом ABS. Наконец…
View on Springer
basilo.kaist.ac.kr
Новый метод BFGS для задачи безусловной оптимизации на основе модифицированного линейного поиска Армиджо
- Чжун Ван, К. Тео, Сяньлунматик Шен, Чаомин Ху
- 2014
В статье рассматривается класс невыпуклых задач безусловной оптимизации. Поскольку линейный поиск Armijo менее затратен при поиске длины шага, новый линейный поиск типа Armijo (называемый WALS)…
Свойства глобальной сходимости двух модифицированных методов типа BFGS
- Q.
 Guo, Jianguo Liu
Guo, Jianguo Liu Математика
- 2007
Модифицированный метод BFGS основан на новом квазиньютоновском уравнении Bk+1sk=yk…
Новый осторожный алгоритм BFGS на основе модифицированного поиска линии типа Армиджо
- Zhong Wan, Shuai Huang, Xiaodong Zheng
Информатика
- 2012
В этой статье представлено новое правило неточного поиска строки, которое является модифицированной версией классического правила поиска строки Armijo. С более низкой стоимостью вычислений, большей величиной спуска…
ПОКАЗЫВАЕТСЯ 1-10 ИЗ 11 ССЫЛОК
СОРТИРОВАТЬ ПОРелевантностиБольше всего влияющих статейНедавность
ЯВНОЕ АБС-РЕШЕНИЕ КЛАССА СИСТЕМ ЛИНЕЙНОГО НЕРАВЕНСТВА И ЛП-ЗАДАЧ 9037e. Амири, Э. Спедикато
Математика
Методы АБС, разработанные с 1981 г. в более чем 400 статьях, в последнее время применялись для решения линейных диофантовых уравнений, обеспечивая наиболее общее решение 10-й проблемы Гильберта в линейной…
An Алгоритм ABS для решения сингулярных нелинейных систем с дефектами ранга
- Rendong Ge, Z.
 Xia
Xia Математика
- 2002
Модифицированный алгоритм ABS для решения класса сингулярных нелинейных систем, F(x)=0, F∈Rn, построенный путем объединения дискретного алгоритма ABS и метода Хоя и Шветлика (1990), представлен.…
Алгоритм ABS для решения сингулярных нелинейных систем с дефектом первого ранга
- Rendong Ge, Z. Xia
Информатика
- 2002
Модифицированный алгоритм ABS для решения дискретизационного алгоритма Представлен класс сингулярных нелинейных систем, F(x) = 0, где x, F ∈ Rn, построенный путем объединения алгоритма ABS дискретизации и метода…
АЛГОРИТМЫ ABS ДЛЯ РЕШЕНИЯ ЛИНЕЙНЫХ НЕРАВЕНСТВ
- 赵金熙
Математика
- 1994
Рассматривается класс алгоритмов типа АБС для решения системы линейных неравенств, в которых число неравенств не превышает числа переменных.
Класс прямых методов для линейных систем. представлены и теоретически проанализированы неполноценные ранговые линейные системы.
 Класс можно рассматривать как…
Класс можно рассматривать как…Алгоритмы проекции ABS: математические методы для линейных и нелинейных уравнений
- J. Abaffy, E. Spedicato
Matematic Алгоритм АБС Хуанга и стратегия Гольдфарба-Иднани, QDMSIA
- 1995
Метод поиска допустимой точки неравенств
Труды первой международной конференции по алгоритмам АБС,
- 1991
An ABS Algorithm for Generating nonnegative solutions of linear systems
Proceedings of the First International Conference on ABS Algorithms, Luoyang, China,
- 1991
A Class of Direct Methods for Solving Linear Неравенства
Графическое решение линейных неравенств с двумя переменными
Мы умеем составлять уравнения разной степени, и это очень много используется в реальной жизни, но возникает вопрос, всегда ли можно преобразовать ситуацию в уравнение? Иногда мы получаем заявления о том, что число случаев Covid в день в Дели достигло более 10 000.
 Это фразы «Меньше чем», «Больше чем», «меньше или равно» и т.д. Такие фразы сложно перевести в уравнения. Для таких случаев нам нужно научиться составлять уравнения с неравенствами в них. Давайте посмотрим на это подробно.
Это фразы «Меньше чем», «Больше чем», «меньше или равно» и т.д. Такие фразы сложно перевести в уравнения. Для таких случаев нам нужно научиться составлять уравнения с неравенствами в них. Давайте посмотрим на это подробно.Что такое неравенство?
Давайте рассмотрим пример. Анил хочет купить прохладительных напитков. Каждый холодный напиток стоит 20 рупий, а всего у него с собой 190 рупий. Предположим, он покупает x холодных напитков. Каким может быть максимальное значение x? Его можно представить в виде уравнения, приведенного ниже,
20x < 190
Два действительных выражения или действительные числа, связанные символами «<», «>», «≤» или «≥», называются неравенствами. Приведенное выше утверждение является неравенством. Существует два типа неравенства:
- Числовые неравенства: 3 < 5 или 7 > 5.
- Буквенные неравенства: x > 5 и y < 7.
Некоторые общие примеры неравенств:
ax + by + c > 0 ….
 (1)
(1)ax + by + c < 0 ….(2)
ax + by + c ≥ 0 ….(3)
ax + by + c ≤ 0 ….(4)
Из приведенного выше уравнений, уравнения (1) и (2) называются строгими неравенствами, а (3) и (4) – слабыми неравенствами.
Решения неравенств
Любое решение неравенства — это значение той переменной, которая делает неравенство истинным утверждением. Например, предположим, что у нас есть неравенство x < 5. В таком случае все значения x, которые меньше 5, делают это неравенство истинным неравенством. При решении неравенств необходимо помнить о некоторых правилах:
- К обеим частям неравенства можно прибавлять или вычитать одинаковые числа.
- Обе части неравенства можно умножить (или разделить) на одно и то же положительное число. Но когда обе части умножаются или делятся на отрицательное число, то знак неравенства меняется на противоположный.
Эти операции не влияют на неравенство и могут быть использованы для упрощения неравенства для нас.

Вопрос: Решите неравенство 20x < 80 и покажите его решения на графике.
Решение:
Нам дано,
20x < 80
Мы знаем, что деление неравенства на положительное число ничего не меняет. Разделим неравенство на 20.
x < 4.
Теперь все значения меньше 10 являются решениями этого неравенства. На рисунке ниже это решение представлено на графике.
Графическое представление неравенства с двумя переменными
Мы видели график линейного неравенства с одной переменной. Линейное уравнение с двумя переменными представляет собой линию, которая делит плоскость на две части. Назовем каждую часть полуплоскостью. Если линия вертикальна, то она разделит плоскость на левую полуплоскость и правую полуплоскость, а невертикальная линия разделит плоскость на верхнюю левую полуплоскость и нижнюю полуплоскость.
Любая точка декартовой плоскости будет лежать либо на прямой, либо на любой из полуплоскостей I и II.

Допустим, у нас есть линия,
ax + by = c
Здесь a ≠ 0 и b ≠ 0.
Теперь, когда мы помещаем любую точку (x, y) в уравнение, есть три возможные случаи:
- ax + by > c
- ax + by < c
- ax + by = c
Рассмотрим все случаи
Случай (i): ax + by > c
Допустим, b > 0. Рассмотрим точку (h, k), которая удовлетворяет уравнению. Затем
ah + bk = c
Возьмем другую произвольную точку (h, l). На рисунке ниже представлены две точки вместе с линией. Мы знаем, что
l > k
bl > bk
ah + bl > ah +bk
ah + bl > c
Таким образом, точки (h, l) удовлетворяют свойству ax + by > c. Таким образом, все точки, лежащие в полуплоскости II, удовлетворяют этому неравенству. Аналогично можно доказать и для b < 0.

Случай (ii): ax + by = c
Все точки, удовлетворяющие прямой, лежащей на прямой, удовлетворяют этому уравнению.
Случай (iii): ax + by < c
Все остальные точки, то есть точки, лежащие в полуплоскости, удовлетворяют этому неравенству.
Давайте рассмотрим некоторые проблемы с этими концепциями.
Примеры задач
Вопрос 1. Решите уравнение 5x + 3y > 6 графически.
Решение:
Сначала нам нужно нарисовать график для 5x + 3y = 6. Это можно сделать, приведя уравнение в форме пересечения наклона или в форме пересечения.
Теперь произвольно выберите точку для проверки. Возьмем (0,0).
Подставив эту точку (0,0) в уравнение,
5(0) + 3(0) = 0 < 6.
Таким образом, точки в нижней половине будут удовлетворять 5x + 3y < 6. Таким образом, все точки, удовлетворяющие данному уравнению, будут лежать на верхней полуплоскости.

Вопрос 2: Решите уравнение 6x + 2y > 3 графически.
Решение:
Сначала нам нужно нарисовать график для 6x + 2y = 3. Это можно сделать, представив уравнение в форме пересечения наклона или в форме пересечения.
Подставляя (0,0) в уравнение,
6(0) + 2(0) = 0 < 3. Таким образом, точки верхней полуплоскости удовлетворяют данному уравнению.
6x + 2y > 3
Вопрос 3: Решите уравнение x + y < 2 графически.
Решение:
Приведенное уравнение: x + y < 2.
Подставив (0, 0) в уравнение,
0 < 2.
Эта точка удовлетворяет заданному уравнению. Таким образом, график будет таким:
Вопрос 4: Решите уравнение 3x – 5y < 20 графически.
Решение:
Как обычно, мы возьмем (0, 0) в качестве точки, которую мы хотим протестировать.


 Причем , когда a является положительным, то знак остается, когда a – отрицательное, меняется на противоположный.
Причем , когда a является положительным, то знак остается, когда a – отрицательное, меняется на противоположный.

 Guo, Jianguo Liu
Guo, Jianguo Liu Guo, Jianguo Liu
Guo, Jianguo Liu Xia
Xia Это фразы «Меньше чем», «Больше чем», «меньше или равно» и т.д. Такие фразы сложно перевести в уравнения. Для таких случаев нам нужно научиться составлять уравнения с неравенствами в них. Давайте посмотрим на это подробно.
Это фразы «Меньше чем», «Больше чем», «меньше или равно» и т.д. Такие фразы сложно перевести в уравнения. Для таких случаев нам нужно научиться составлять уравнения с неравенствами в них. Давайте посмотрим на это подробно. (1)
(1)



