Арифметическая и геометрическая прогрессии: Арифметическая и геометрическая прогрессии — урок. Основной государственный экзамен (9 класс), Математика.

Последовательности, арифметическая и геометрическая прогрессии (формат-2020). Задания 14 ОГЭ по математике

1	В геометрической прогрессии (b_n) b_5=-36,b_7=-1296. Найдите знаменатель прогрессии,если известно,что он отрицательный.	Смотреть видеоразбор >>
2	(b_n) — геометрическая прогрессия, знаменатель прогрессии равен \frac{1}{5},b_1=375.Найдите сумму первых 5 её членов.	Смотреть видеоразбор >>
3	Геометрическая прогрессия задана условиями b_1=-3, b_{n+1}=-2b_n. Найдите b_6.	Смотреть видеоразбор >>
4	Последовательность задана формулой a_n=\frac{40}{n+1}. Сколько членов этой последовательности больше 2?	Смотреть видеоразбор >>
5	Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 8 квадратов больше, чем в предыдущей. Сколько квадратов в 16 – й строке?	Смотреть видеоразбор >>
6	Последовательность задана условиями c_1=-1, c_{n+1}=c_n-1. Найдите c_7.	Смотреть видеоразбор >>
7	Выписано несколько последовательных членов геометрической прогрессии: …; 1,75; x; 28; -112;… Найдите член прогрессии, обозначенный буквой x.	Смотреть видеоразбор >>
8	Выписаны первые несколько членов геометрической прогрессии: 3,5;7; 14;… Найдите сумму первых 7 её членов.	Смотреть видеоразбор >>
9	Дана арифметическая прогрессия: 87; 69; 51;… Найдите первый отрицательный член этой прогрессии.	Смотреть видеоразбор >>
10	В арифметической прогрессии (a_n)a_{10}=19, a_{15}=44. Найдите разность прогрессии.	Смотреть видеоразбор >>
11	Дана геометрическая прогрессия (b_n), знаменатель которой равен 5, b_1=\frac{2}{5}.Найдите сумму первых 6 её членов.	Смотреть видеоразбор >>
12	Выписаны первые несколько членов арифметической прогрессии: 2,6;3,3;4;… Найдите сумму первых 21 её членов.	Смотреть видеоразбор >>
13	Дана арифметическая прогрессия 11,18,25,… Какое число стоит в этой последовательности на 6 – м месте?	Смотреть видеоразбор >>
14	Последовательность задана условиями b_1=-5, b_{n+1}=-2 \cdot \frac{1}{b_n}. Найдите b_3.	Смотреть видеоразбор >>
15	В геометрической прогрессии (b_n) b_5=-14, b_6=28. Найдите знаменатель прогрессии.	Смотреть видеоразбор >>
16	Дана геометрическая прогрессия (b_n), знаменатель которой равен 2, b_1=16. Найдите b_4.	Смотреть видеоразбор >>
17	Выписано несколько последовательных членов арифметической прогрессии: …; 1; x; -5; -8;… Найдите член прогрессии,обозначенный буквой x.	Смотреть видеоразбор >>
18	Дана арифметическая прогрессия (a_n), разность которой равна -8,5, a_1=-6,8. Найдите a_{11}.	Смотреть видеоразбор >>
19	Арифметическая прогрессия задана условием a_n=0,9-0,7n. Найдите сумму первых 6 её членов.	Смотреть видеоразбор >>
20	В геометрической прогрессии (b_n) b_5=-15,b_8=-405.Найдите знаменатель прогрессии.	Смотреть видеоразбор >>
21	Выписаны первые несколько членов геометрической прогрессии: 17;68;272;… Найдите её четвёртый член.	Смотреть видеоразбор >>
22	Арифметическая прогрессия (c_n) задана условиями: c_1=4,c_{n+1}=c_n+2. Найдите c_{12}.	Смотреть видеоразбор >>
23	Дана арифметическая прогрессия 11,18,25,… Какое число стоит в этой последовательности на 21 – м месте?	Смотреть видеоразбор >>
24	Геометрическая прогрессия задана условиями b_1=-7,b_{n+1}=3b_n. Найдите сумму первых 5 её членов.	Смотреть видеоразбор >>
25	Арифметическая прогрессия задана условием a_n=3,8-5,7n. n.Найдите сумму первых её 4 членов.	Смотреть видеоразбор >>
29	В первом ряду кинозала 24 места, а в каждом следующем на 2 больше, чем в предыдущем. Сколько мест в седьмом ряду?	Смотреть видеоразбор >>
30	Дана арифметическая прогрессия (a_n), разность которой равна -8,4, a_1=-4,7. Найдите сумму первых 12 её членов.	Смотреть видеоразбор >>

Задание 12 ОГЭ по математике. Арифметическая и геометрическая прогрессии.

Задание 12 ОГЭ по математике – это задача на арифметическую и геометрическую прогрессии. Надо знать определение и все необходимые формулы.

Арифметическая прогрессия — это последовательность чисел  (членов прогрессии), в которой каждое число, начиная со второго, получается из предыдущего прибавлением к нему постоянного числа d (разности прогрессии), т.е.

или .

Любой (n-й) член арифметической прогрессии может быть вычислен по формуле общего члена:

Сумма первых членов арифметической прогрессии может быть найдена по одной из двух формул:

, если известно значение ,

, если неизвестно значение .

Замечание. Практически в любой задаче для успешного её решения необходимо знать два числа: первый член прогрессии и разность .

Приступим к решению задач.

Пример 1. Дана арифметическая прогрессия: −75; −40; −5; … Найдите её девятый член.

Решение.

Определимся с тем, что нам дали в условии задачи. Итак, −75 — это первый член прогрессии, т.е. . Далее необходимо узнать, чему равна разность прогрессии . Можно её найти, например, так: или

Для нахождения используем формулу общего члена .

Отсюда получаем, .

Ответ: 205.

Пример 2. Дана арифметическая прогрессия (), разность которой равна 1,1,=−7. Найдите сумму первых 8 её членов.

Решение. Для нахождения суммы имеются две формулы. Какую из них удобнее использовать в данной задаче? Конечно, вторую, т.к. неизвестно.

Итак,

Ответ:

Пример 3. Найдите сумму всех положительных членов арифметической прогрессии 11,2; 10,8; ….

Решение. По условию . Тогда разность

Найдём последний положительный член арифметической прогрессии и его номер:

Т.к. , то решим неравенство . Отсюда а значит,

Тогда .

Осталось вычислить сумму. Используем формулу для известного значения .

Ответ: .

Геометрическая прогрессия — это последовательность чисел (членов прогрессии), в которой каждое число, начиная со второго, получается как результат умножения предыдущего на постоянное число (знаменатель прогрессии), т.е.

или .

Любой (n-й) член геометрической прогрессии может быть вычислен по формуле общего члена:

Сумма первых членов геометрической прогрессии может быть найдена по формуле:

, если .

Замечание. Практически в любой задаче для успешного её решения необходимо знать два числа: первый член прогрессии и знаменатель .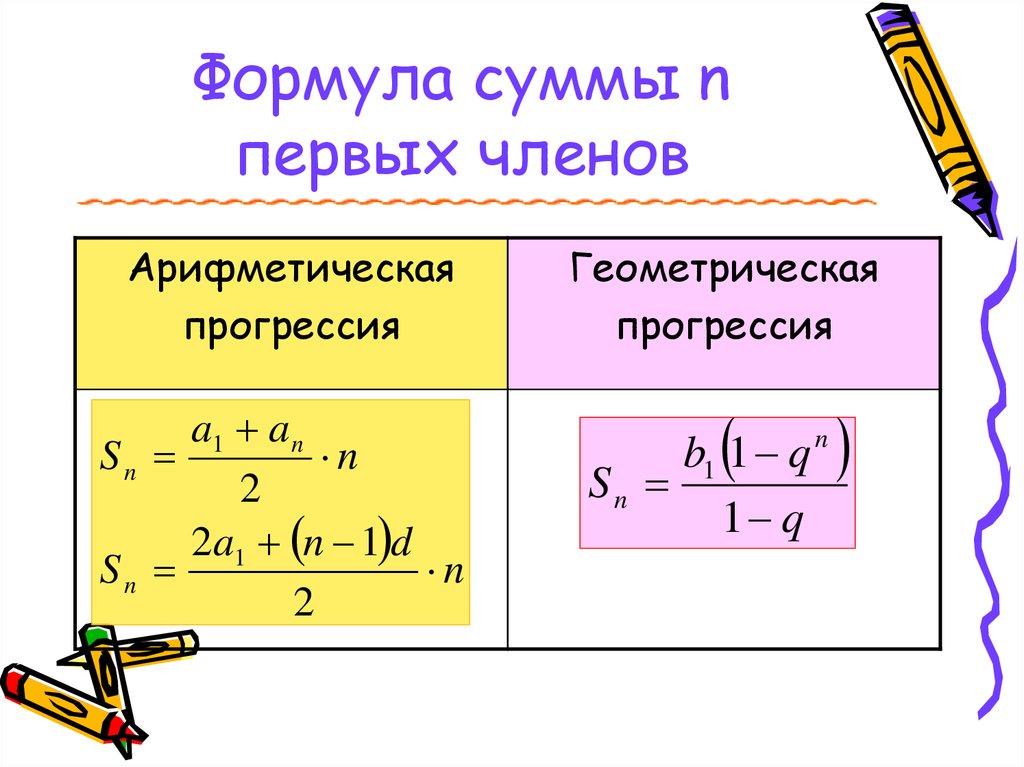

Приступим к решению задач.

Пример 4. Выписано несколько последовательных членов геометрической прогрессии:

…; 3; X; 75; −375; …

Найдите X.

Решение. В условии этой задачи нет конкретного значения , но при этом можно найти знаменатель прогрессии: . Теперь можно найти Х:

Ответ: −15.

Пример 5. Выписаны первые несколько членов геометрической прогрессии: −196; 392; −784; … Найдите её пятый член.

Решение. Здесь , а .

Тогда найдём пятый член геометрической прогрессии, используя формулу общего члена:

Ответ: 3136.

Пример 6. Дана геометрическая прогрессия (), знаменатель которой равен 5, а . Найдите сумму первых шести её членов.

Решение. Используем формулу . Подставим все известные значения:

Ответ: .

Решим задачу посложнее.

Пример 7. В геометрической прогрессии сумма первого и второго членов равна 150, а сумма второго и третьего членов равна 75. Найдите первые три члена этой прогрессии. В ответе запишите первый, второй и третий члены прогрессии без пробелов.

Решение. Запишем условие задачи в виде системы уравнений и решим её, применяя формулу общего члена:

Итак, , , .

Не забудем требование задачи: в ответе запишите первый, второй и третий члены прогрессии без пробелов.

Ответ: 1005025

Больше объяснений и задач:

Арифметическая прогрессия на ОГЭ по математике https://ege-study.ru/arifmeticheskaya-progressiya-v-zadachax-oge-po-matematike/

Геометрическая прогрессия на ОГЭ по математике https://ege-study.ru/geometricheskaya-progressiya-v-zadachax-oge-po-matematike/

Арифметическая прогрессия и геометрическая прогрессия

Слово «последовательность» в английском языке означает набор некоторых чисел или объектов таким образом, что он имеет первый член, второй член и так далее. Например, последовательности могут быть любыми. — Январь Февраль, …. это последовательность месяцев в году. Последовательности используются в реальных реальных жизнях людей каждый день. Дни недели также можно рассматривать как последовательность. Таким образом, становится необходимым изучать последовательности и находить в них закономерности, чтобы мы могли предсказывать следующие члены последовательности и извлекать из них информацию.

Последовательности

Рассмотрим последовательность: 2,4,6,8 и так далее. Различные числа, встречающиеся в нем, называются его членами. Они обозначаются ₁ , ₂ , ₃ … _n. Нижние индексы обозначают n-й термин. N-й член последовательности также называется общим членом последовательности, потому что мы можем вывести из него любой другой член, подставляя различные значения n. В этом случае

a ₁ = 2, a ₂ = 4, a ₃ = 6 и так далее…

Последовательность с конечным числом членов называется конечной последовательностью, и аналогично последовательность с бесконечным числом членов называется бесконечной последовательностью.

Последовательность можно рассматривать как функцию, областью определения которой является множество натуральных чисел или некоторое его подмножество. Иногда мы используем функциональное обозначение a(n) для a _n .

Серия

Для данной последовательности a ₁ , a ₂ , a ₃ … а _n . Приведенное ниже выражение называется рядом. Ряд может быть бесконечным или конечным в зависимости от количества членов в его последовательности. ∑ — общепринятое обозначение, используемое для обозначения серии. Это указывает на вовлеченное суммирование.

= a ₁ + a ₂ + a ₃ +… a _n 

Эти понятия порождают последовательности, известные как арифметическая прогрессия и геометрическая прогрессия.

Арифметическая прогрессия (А.П)

Рассмотрим последовательность 1, 3, 5, 7, ….. Обратите внимание, что в этой последовательности разница между последовательными элементами постоянна. Это означает, что на каждом шаге к каждому члену этой последовательности добавляется постоянное значение. Последовательность a ₁ , a ₂ , a ₃ … a _n можно назвать арифметической прогрессией, если _{n + 1} = a _n + d, где n — любое натуральное число. В таком ряду a ₁ называется первым членом, а постоянный член d называется общей разностью AP. Таким образом, AP выглядит как

а, а + г, а + 2д, а + 3д ….. и так далее.

Число n для AP можно определить как

a _n = a ₁ + (n-1)d

Сумма n членов AP определяется как,

S

7 n 3

7

или

S _n =  

Геометрическая прогрессия (Г.П)

Рассмотрим следующую последовательность: 2, 4, 8, 16 ….. Здесь ясно, что каждый член в этой последовательность. Такие последовательности, в которых последовательные члены умножаются на постоянное число, называются геометрическими прогрессиями. В более общем смысле последовательность a ₁ , a ₂ , a ₃ … a _n можно назвать геометрической прогрессией, если _n+1 = a _n . r, где n — любое натуральное число. В таком ряду a ₁ называется первым членом, а постоянный член r называется обыкновенным отношением Г.П. Итак, GP выглядит так:

a, ar, ar ² , ar ⁿ ….. и так далее.

Число n для GP может быть определено как

a _n = a ₁ r ^n-1

В общем, ВП может быть конечным и бесконечным, но в случае бесконечного ВП общее отношение должно быть между 0 и 1, иначе значения ВП доходят до бесконечности. Сумма GP состоит из двух случаев:

Обозначим S _n a + ar + ar ² + ….. ar ⁿ

Случай 1: Если r = 1, ряд схлопывается до

а, а, а, а… и так далее.

S _n = na

Случай 2: Если r≠1, ряд остается прежним,

a + ar + ar ² + …. . ar ⁿ

S _n =

Давайте рассмотрим некоторые задачи со словами, связанные с этими понятиями начинался с 5 долларов. После этого каждый день он повышается на 2 доллара. Найдите цену акции в конце 16-го дня.

Ответ: 

В приведенном выше вопросе каждый раз, когда к предыдущему термину добавляется постоянное число, получается новый термин. Это АП.

5, 7, 9, … и так далее.

Используя формулу для n-го члена AP.

a _n = a ₁ + (n-1)d

Здесь a ₁ обозначает первый член, а d обозначает общую разность. В этом случае

а ₁ = 5, d = 2 и n = 16

а ₁₀ = а ₁ + (16-1)d

⇒ 5 + а 15 _{80 )2}

⇒ а ₁₀ = 5 + 30

⇒ а ₁₀ = 35 

Таким образом, цена акций составляет 35 долларов.

Вопрос 2: Человек посадил 3 дерева при рождении сына. После этого в последующие дни рождения он каждый год сажал еще по 5 деревьев. Найдите количество деревьев на его заднем дворе, когда его сыну исполнится 10 лет.

Ответ: 

В приведенном выше вопросе каждый раз, когда к предыдущему термину добавляется постоянное число, получается новый термин. Это АП.

3, 8, 13, … и так далее.

Используя формулу для n-го члена AP.

a _n = a ₁ + (n-1)d

Здесь a ₁ обозначает первый член, а d обозначает общую разность. В этом случае

а ₁ = 3, d = 5 и n = 10

а ₁₀ = а 1 + (10-1)d

⇒ а 90 90 _{8 10 + (9)d}

⇒ a ₁₀ = 3 + 9(5)

⇒ a ₁₀ = 3 + 45 

⇒ a ₁₀ = 38 9000 деревьев на заднем дворе. в настоящее время.

Вопрос 3. Английская рок-группа the1975 летом выпустила новый альбом, и за один день было продано 100 000 копий. Сейчас альбом возглавляет чарты, и каждый день продается на 20 000 копий больше, чем в предыдущий день. Найдите общий объем продаж альбомов за неделю.

Ответ: 

В приведенном выше вопросе каждый раз, когда к предыдущему термину добавляется постоянное число, получается новый термин. Это АП.

100 000; 120 000; 140 000; … и так далее.

Цель состоит в том, чтобы вычислить сумму последовательности в конце 10-го дня.

Используя формулу для суммы до n-го члена AP.

S _n = 

Здесь _{обозначает первый член, а d обозначает общую разность. В этом случае}

A = 100 000, D = 20 000 и n = 7

S _N =

⇒S ₇ =

⇒ ₇ =

⇒ ₇ =

⇒ С ₇ =

⇒ С ₇ =

⇒S ₇ = 770000

Таким образом, общий объем продаж альбомов составляет 770 000 экземпляров.

Вопрос 4: Популяция оленей в Национальном парке Корбетт увеличивается. В 2015 году он был 1000, с тех пор он увеличивается, и каждый год становится в 2 раза. Найдите население в 2021 году. 

Решение.

Здесь каждый год население становится в 2 раза больше. Постоянное число умножается на предыдущий член, чтобы получить новый термин. Это геометрическая прогрессия.

1000, 2000… и так далее.

Здесь a = 1000 и r = 2

Используя формулу для n-го члена ГП

a _n = a ₁ r ^n-1

2, вставка n Значения в формуле

A _N = A ₁ R ^N-1

⇒A _N = (1000) (2) ^(7-1)

⇒ _N = = (1000)(2) ⁶

⇒a _n = (1000)(64)

⇒ a _n = 64000 

Сейчас в Национальном парке Корбетт должно быть 64 000 оленей.

Вопрос 5: У человека 2 родителя, 4 дедушки и бабушки, 8 прабабушек и дедушек и так далее. Найдите количество предков в последних 10 поколениях этой семьи.

Раствор.

 Здесь каждый год количество увеличивается в 2 раза. Постоянное число умножается на предыдущий член, чтобы получить новый термин. Это геометрическая прогрессия.

2,4 … и так далее.

Здесь a = 2 и r = 2

Используя формулу для n-го члена ГП

a _n = a ₁ r ^n-1

= nging in 20211, Значения в формуле

A _N = A ₁ R ^N-1

⇒A _N = (2) (2) ^(10-1)

⇒ _N = = (2)(2) ⁹

⇒a _n = (2) ¹⁰

⇒a _n = 64000 

Сейчас в Национальном парке Корбетт должно быть 64 000 оленей.

Вопрос 6: Вставьте два числа от 4 до 256 так, чтобы полученная последовательность стала GP.

Ответ:

Допустим, эти два числа равны x и y. Результирующая последовательность примет следующий вид:

4, x, y, 256

Эта последовательность состоит из четырех членов и является GP. Здесь

a = 4 и r = ?

Формула для n-го члена ГП равна  

A _N = A ₁ R ^N-1

4-й срок-256,

256 = 4R ^(4-1)

64 = R ³

Это означает, что R = 4

Таким образом,

x = AR

⇒ x = (4) (4)

⇒ x = 16

y = AR ²

⇒ y = 4 (4) ²

⇒ y = 4 (4) ²

⇒ y = 64

Итак, нужно вставить два числа: 16 и 64

Вопрос 7: Количество бактерий в чашке равно 100, и каждый час они увеличиваются вдвое по сравнению с предыдущим значением. Найдите количество бактерий в чашке через 6 часов.

Ответ:

Здесь каждый год количество увеличивается в 2 раза. Постоянное число умножается на предыдущий член, чтобы получить новый термин. Это геометрическая прогрессия.

100,200, 400… и так далее.

Здесь a = 100 и r= 2

Используя формулу для суммы до n-го члена ГП

S _n =

n = 6. Подставив значения в формулу =

2 n 8

70

⇒ С _N =

⇒ S ₆ =

⇒ S ₆ =

⇒ S ₆ =

⇒ S ₆ = 6300

Должно быть 63,00 бактерии в блюде. .

Разница между арифметической и геометрической последовательностями (со сравнительной таблицей)

Последовательность описывается как систематический набор чисел или событий, называемых терминами, которые расположены в определенном порядке. Арифметические и геометрические последовательности — это два типа последовательностей, которые следуют шаблону, описывая, как вещи следуют друг за другом. Когда существует постоянная разница между последовательными терминами, говорят, что последовательность представляет собой арифметическая последовательность ,

С другой стороны, если последовательные члены находятся в постоянном соотношении, последовательность геометрическая . В арифметической последовательности члены могут быть получены путем прибавления или вычитания константы к предыдущему члену, при этом в случае геометрической прогрессии каждый член получается путем умножения или деления константы на предыдущий член.

Здесь, в этой статье, мы собираемся обсудить существенные различия между арифметической и геометрической последовательностями.

Содержание: арифметическая последовательность и геометрическая последовательность

1. Сравнительная таблица
2. Определение
3. Ключевые отличия
4. Заключение

Сравнительная таблица

Основание для сравнения	Арифметическая последовательность	Геометрическая последовательность
Значение	Арифметика Последовательность описывается как список чисел, в котором каждый новый член отличается от предыдущего на постоянную величину.	Геометрическая последовательность — это набор чисел, в котором каждый элемент после первого получается путем умножения предыдущего числа на постоянный коэффициент.
Идентификация	Общий Разница между последовательными сроками.	Обыкновенное отношение между последовательными сроками.
Расширенный по	Сложение или вычитание	Умножение или деление
Вариация терминов	Линейная	Экспоненциальный
Бесконечные последовательности	Расходящиеся	Расходящиеся или сходящиеся

Определение арифметической последовательности

Арифметическая последовательность относится к списку чисел, в котором разница между последовательными элементами постоянна. Проще говоря, в арифметической прогрессии мы прибавляем или вычитаем фиксированное, отличное от нуля число, каждый раз бесконечно. Если a является первым членом последовательности, то это можно записать как:

a, a+d, a+2d, a+3d, a+4d..

где, a = первый член
d = общая разница между терминами

Пример : 1, 3, 5 , 7, 9…
5, 8, 11, 14, 17…

Определение геометрической последовательности

В математике геометрическая последовательность представляет собой набор чисел, в котором каждый член прогрессии постоянно кратен предыдущему члену . Говоря более точно, последовательность, в которой мы умножаем или делим фиксированное, отличное от нуля число, каждый раз до бесконечности, называется геометрической прогрессией. Далее, если a является первым элементом последовательности, тогда он может быть выражен как:

a, ar, ar ² , ar ³ , ar ⁴ …

где, 5 = первый член d = общая разница между терминами

Пример : 3, 9, 27, 81…
4, 16, 64, 256..

Ключевые различия между арифметической и геометрической последовательностями

Следующие пункты заслуживают внимания, поскольку разница между арифметической и геометрической последовательностями:

1. Список чисел, в котором каждый новый член отличается от предыдущего на постоянную величину, представляет собой арифметическую последовательность. Набор чисел, в котором каждый элемент после первого получается путем умножения предыдущего числа на постоянный коэффициент, известен как геометрическая последовательность.

   No related posts.