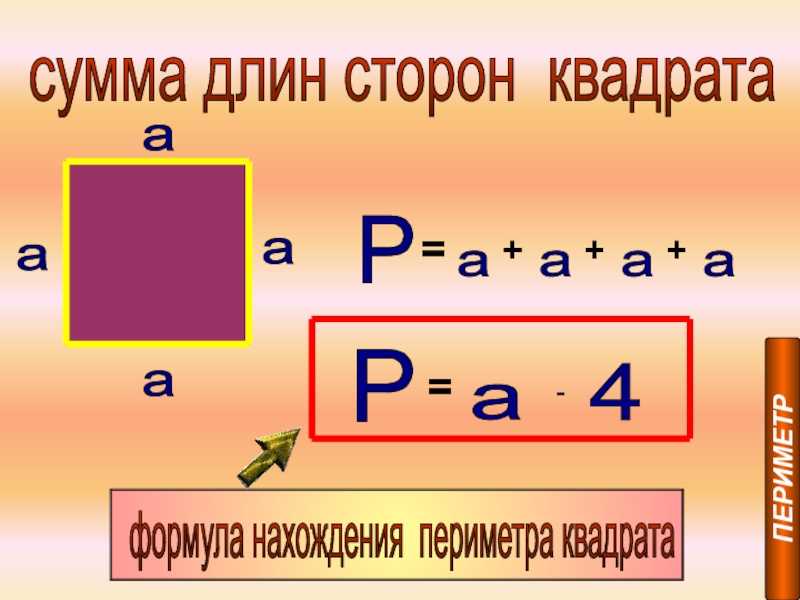
Что токое периметр. Что такое периметр
Урок и презентация на тему: «Периметр и площадь прямоугольника»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 3 класса
Тренажер для 3 класса «Правила и упражнения по математике»
Электронное учебное пособие для 3 класса «Математика за 10 минут»
Что такое прямоугольник и квадрат
Прямоугольник – это четырёхугольник, у которого все углы прямые. Значит, противоположные стороны равны друг другу.
Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.
Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D . ..
..
Пример.
Читается так: четырёхугольник ABCD; квадрат EFGH.
Что такое периметр прямоугольника? Формула расчета периметра
Периметр обозначается латинской буквой P . Так как периметр — это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.
Например, периметр прямоугольника АВСD обозначается как P ABCD , где А, В, С, D — это вершины прямоугольника.
Запишем формулу периметра четырехугольника ABCD:
P ABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)
Пример.
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см.
Определим P ABCD .
Решение:
1. Нарисуем прямоугольник ABCD с исходными данными.
2. Напишем формулу для расчета периметра данного прямоугольника:
P ABCD = 2 * (AB + BС)
P ABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см
Ответ: P ABCD = 16 см.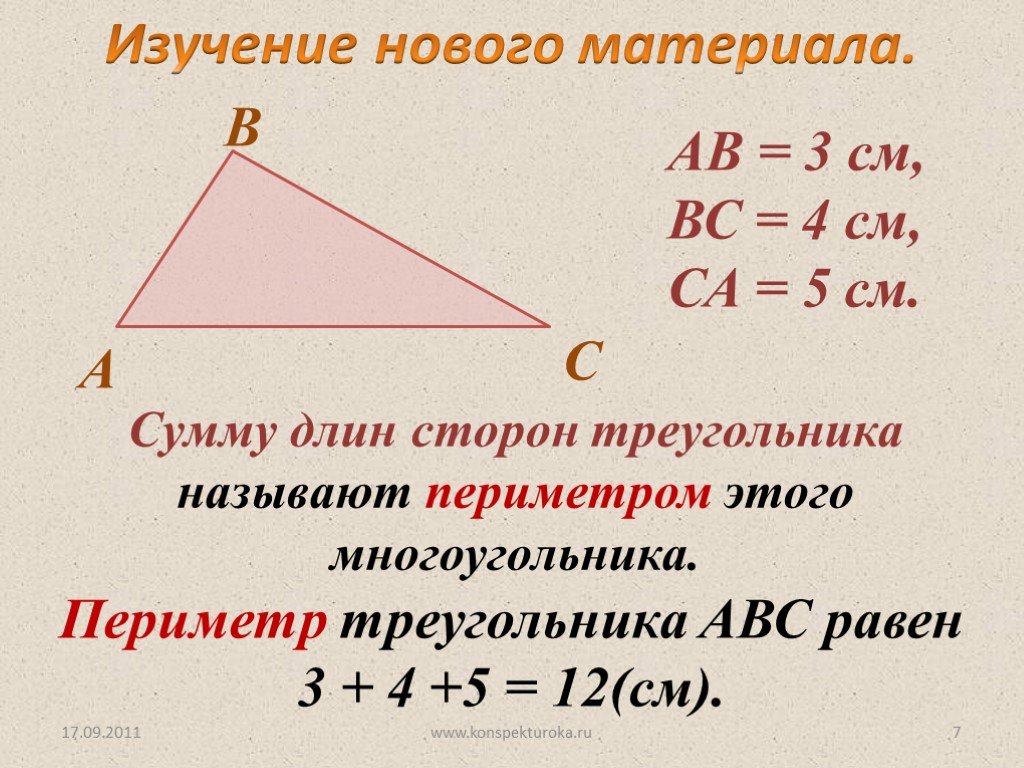
Формула расчета периметра квадрата
У нас есть формула для определения периметра прямоугольника.
P ABCD = 2 * (AB + BC)
Применим её для определения периметра квадрата. Учитывая, что все стороны квадрата равны, получаем:
P ABCD = 4 * AB
Пример.
Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата.
Решение.
1. Нарисуем квадрат ABCD с исходными данными.
2. Вспомним формулу расчета периметра квадрата:
P ABCD = 4 * AB
3. Подставим в формулу наши данные:
P ABCD = 4 * 6 см = 24 см
Ответ: P ABCD = 24 см.
Задачи на нахождение периметра прямоугольника
1. Измерь ширину и длину прямоугольников. Определи их периметр.
2. Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника.
3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.
Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.
Где используется расчет периметра прямоугольника?
1. Задан участок земли, его нужно обнести забором. Какой длины будет забор?
В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора.
2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев.
Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.
Что такое площадь прямоугольника?
Площадь – это числовая характеристика фигуры.
Площадь измеряется квадратными единицами длины: см 2 , м 2 , дм 2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.)
В вычислениях обозначается латинской буквой S .
Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Площадь прямоугольника вычисляется умножением длины АК на ширину КМ. Запишем это в виде формулы.
S AKMO = AK * KM
Пример.Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?
S AKMO = AK * KM = 7 см * 2 см = 14 см 2 .
Ответ: 14 см 2 .
Формула вычисления площади квадрата
Площадь квадрата можно определить, умножив сторону саму на себя.
Пример.
В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.
S AВСО = AB * BC = AB * AB
Пример.
Определи площадь квадрата AKMO со стороной 8 см.
S AKMО = AK * KM = 8 см * 8 см = 64 см 2
Ответ: 64 см 2 .
Задачи на нахождение площади прямоугольника и квадрата
1.Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.
Вычисли его площадь. Запиши ответ в квадратных сантиметрах.
2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.
Подписаться на сайт
Ребята, мы вкладываем душу в сайт. Cпасибо за то,
что открываете эту красоту. Спасибо за вдохновение и мурашки.
Присоединяйтесь к нам в Facebook и ВКонтакте
Периметр – это геометрический термин, который часто встречается в задачах. Чтобы понять, что такое периметр, следует нарисовать произвольный многоугольник и вооружиться линейкой. В переводе с греческого языка этот термин обозначает «измеряю вокруг».
Как вычислить периметр
Периметр обозначается латинской буквой P . Его можно измерить в сантиметрах, миллиметрах, метрах или дециметрах. Чтобы узнать периметр, следует измерить длину всех сторон многоугольника. Полученные значения нужно сложить. Итоговая сумма и станет ответом на вопрос: «Чему равен периметр многоугольника».
Периметр – это длина линий, которые ограничивают замкнутую фигуру (квадрат, прямоугольник, треугольник и др.).
Например, перед вами многоугольник со сторонами 10, 12, 13 и 11 см. Складываем вышеназванные числа (10+12+13+11) и получаем сумму 46. Это и есть периметр многоугольника.
Для удобства вычисления периметра в геометрии существует ряд формул. Каждая формула соответствует определенной фигуре.
Периметр и площадь квадрата
Это сумма его четырех сторон. Как мы знаем, все стороны квадрата имеют равный размер. Поэтому мы можем узнать периметр квадрата, умножив длину его стороны на четыре:
P= a+a+a+a
Например, перед нами квадрат со стороной 10 см.
Ответ: 40 см
P = 10+10+10+10
P =40
Ответ: 40 см
Чтобы разобраться, что такое периметр и площадь, следует уяснить, что периметр вычисляет длину контура фигуры, а площадь – размер всей ее поверхности.
Чтобы узнать площадь квадрата, необходимо воспользоваться простой формулой:
S – это площадь, а – сторона квадрата.
Например, в задаче указано, что длина стороны квадрата составляет 10см.
S= 100 см 2
Ответ: 10 0 см 2
Периметр и площадь прямоугольника
Стороны прямоугольника, находящиеся друг напротив друга и имеющие одинаковую длину, называются противолежащими. Это длина и ширина, они условно обозначаются латинскими буквами a и b. Формула для вычисления периметра прямоугольника выглядит так:
P= (a+b)*2
Используя эту формулу, мы сначала находим сумму ширины и длины, а затем умножаем ее на два.
Например, перед нами прямоугольник, имеющий длину 6 см и ширину 2 см.
P = (6+2) * 2
P = 16
Ответ: 16 см
Чтобы узнать площадь прямоугольника, следует длину умножить на ширину. Формула выглядит так:
Например, в условиях задачи сказано, что прямоугольник имеет длину 5 см и ширину 2см. Меняем буквы a и b на указанные числа.
S = 5*2
S =10см 2
Ответ: 10 см 2
Периметр круга (длина окружности)
Каждый круг имеет центр. Расстояние от центра круга до любой точки, расположенной на окружности, имеет название радиус круга. Часто ученики путают понятия «круг» и «окружность» и пытаются определить площадь окружности. Это серьезная ошибка. Следует разделить в голове понятия «круг» и «окружность». У окружности нет и не может быть площади, у нее есть только длина.
Расстояние от центра круга до любой точки, расположенной на окружности, имеет название радиус круга. Часто ученики путают понятия «круг» и «окружность» и пытаются определить площадь окружности. Это серьезная ошибка. Следует разделить в голове понятия «круг» и «окружность». У окружности нет и не может быть площади, у нее есть только длина.
Чтобы найти периметр круга, следует вычислить длину его окружности. Существует формула для нахождения длины окружности:
L = 2πr
L – длина окружности
π – это число «пи», математическая константа. Она равна отношению длины окружности к длине ее диаметра. Древнее название числа «пи» – лудольфово число. Это число иррационально, его десятичное представление после точки никогда не заканчивается.
π = 3.141 592 653 589 793 238 462 643 383 279 502
Для удобства вычислений обычно используют значение 3.14
R – это радиус окружности
D – Диаметр окружности
Итак, чтобы определить периметр круга, надо найти произведение радиуса и 2π. Если в задаче указан диаметр, то
Если в задаче указан диаметр, то
Например, перед нами круг с радиусом 3 см. Найдем его периметр.
L = 2*3,14*3
L =6 π
L=6*3.14
L = 18.84 см
P к = 18,84 см
Ответ: 18.84 см
Отличие периметра от площади
Площадь – это размер поверхности фигуры, а периметр – это сумма ее границ.
Площадь всегда измеряется в квадратных единицах (см 2 , м 2 , мм 2). Периметр измеряется в единицах длины – в сантиметрах, миллиметрах, метрах, дециметрах.
Инструкция
Источники:
- как найти периметр abcd
Периметр – это сумма длин сторон какой-либо геометрической фигуры. Иными словами, если взять нить и выложить с ее помощью на столе, например, квадрат, а потом измерить длину этой нити, то полученная цифра и будет периметром данного квадрата. Все знают, что такое периметр, но не каждый может сразу сообразить, как его рассчитать.
Для измерения периметра разных фигур существуют различные способы.
Инструкция
Квадрат. Общеизвестно, что у квадрата есть 4 стороны и они . Поэтому для вычисления его периметра так:
где а – это длина одной стороны данной фигуры.
Проще говоря, измерьте одну из сторон квадрата и умножьте эту цифру на количество сторон, то есть на 4. В нашем случае равен 16 см (4*4).
Прямоугольник и ромб. У этих двух фигур только параллельные друг другу стороны равны, соответственно периметр определяется следующим образом:
где а и b – соприкасающиеся стороны. Таким образом, на нашем примере периметр прямоугольника равен 24 см (2*(8+4)).
Треугольник. Поскольку треугольники бывают совершенно разными – равнобедренными, неправильными, с углами, то единственным верным способом периметр такой фигуры является формула:
То есть для вычисления периметра треугольника просто измерьте длины всех трех сторон и сложите полученные цифры. В нашем случае периметр треугольника равен 10,7 см (2+5+3,7).
Периметр называют длиной окружности, которая вычисляется по особой формуле:
где d – это окружности, а 3,14 – это число «пи», которое специально выведено учеными для определения периметра данной геометрической фигуры. Наш круг (см.) имеет 3 см, то есть периметр окружности равен 9,42см (3*3,14).
Источники:
- как находить длину окружности
Ом в общем случае называют длину линии, которая ограничивает замкнутую фигуру. Для многоугольников периметром является сумма всех длин сторон. Эту величину можно измерить, а для многих фигур и просто рассчитать, если известны длины соответствующих элементов.
Вам понадобится
- — линейка или рулетка;
- — прочная нить;
- — роликовый дальномер.
Инструкция
Чтобы измерить произвольного многоугольника, измерьте при линейки или другим измерительным прибором все его стороны, а затем найдите их сумму. Если дан четырехугольник со сторонами 5, 3, 7 и 4 см, которые измерены линейкой, найдите периметр, сложив их вместе Р=5+3+7+4=19 см.
Если же фигура произвольная и включает в себя не только прямые линии, то измерьте ее периметр обычной веревкой или ниткой. Для этого расположите ее так, она точно повторяла все линии, ограничивающие фигуру, и сделайте на ней отметку, если можно, просто обрежьте ее чтобы избежать путаницы. Затем при помощи рулетки или линейки, измерьте длину нитки, она и будет равна периметру данной фигуры. Обязательно следите за тем, чтобы нить максимально точно повторяла линию для большей точности результата.
Периметр сложной геометрической фигуры измеряйте роликовым дальномером (курвиметром). Для этого не линии намечается точка, в которую устанавливается ролик дальномера и прокатывается по ней, до возвращения в исходную точку. Дистанция, измеренная роликовым дальномером, и будет равна периметру фигуры.
Периметр некоторых геометрических фигур вычисляйте. Например, чтобы найти периметр любого правильного многоугольника (выпуклого многоугольника, стороны которого ), длину стороны умножьте на количество углов или сторон (они равны). Чтобы найти периметр правильного треугольника со стороной 4 см умножьте это на 3 (Р=4∙3=12 см).
Чтобы найти периметр правильного треугольника со стороной 4 см умножьте это на 3 (Р=4∙3=12 см).
Чтобы найти периметр , сложите длины всех его сторон. Если не даны все стороны, а есть углы ними, найдите их по теореме синуса или косинуса. Если известны две стороны прямоугольного треугольника, третью найдите по теореме Пифагора и найдите их сумму. Например, если известно, что катеты прямоугольного треугольника равны 3 и 4 см, то гипотенуза будет равна √(3²+4²)=5 см. Тогда периметр Р=3+4+5=12 см.
Источники:
- периметру
Для решения этой задачи методами векторной алгебры, вам необходимо знать следующие понятия: геометрическая векторная сумма и скалярное произведение векторов, а также следует помнить свойство суммы внутренних углов четырехугольника.
Вам понадобится
- — бумага;
- — ручка;
- — линейка.
Инструкция
Вектор – это направленный отрезок, то есть величина, считающаяся заданной полностью, если задана его длина и направление (угол) к заданной оси. 2))=1/(sqrt2sqrt5), ф3=arcos(-1/sqrt(10))=п-ф1.
2))=1/(sqrt2sqrt5), ф3=arcos(-1/sqrt(10))=п-ф1.
В соответствии с замечанием 2 — ф4=2п- ф1 — ф2- ф3=п/4.
Видео по теме
Обратите внимание
Замечание 1. В определении скалярного произведения используется угол между векторами. Здесь, например, ф2 — это угол между АВ и ВС, а между a и b этот угол п-ф2. сos(п- ф2)=- сosф2. Аналогично для ф3.
Замечание 2. Известно, что сумма углов четырехугольника равна 2п. Поэтому ф4=2п- ф1 — ф2- ф3.
Любая выпуклая и плоская геометрическая фигура имеет ограничивающую ее внутреннее пространство линию — периметр. У многоугольников он состоит из отдельных отрезков (сторон), сумма длин которых определяет протяженность периметра. Участок плоскости, ограниченный этим периметром, тоже может быть выражен через длины сторон и углы в вершинах фигуры. Ниже приведены соответствующие формулы для одного из видов многоугольников — параллелограмма.
Инструкция
Если в задачи даны длины двух смежных сторон параллелограмма (a и b) и величина угла между ними (γ), то этого будет достаточно для вычисления обоих параметров. Для расчета периметра (P) четырехугольника сложите длины сторон и вдвое увеличьте полученное значение: P = 2*(a+b). Вычислять (S) фигуры придется с помощью тригонометрической функции — синуса. Перемножьте длины сторон, а результат умножьте на известного угла: S = a*b*sin(γ).
Для расчета периметра (P) четырехугольника сложите длины сторон и вдвое увеличьте полученное значение: P = 2*(a+b). Вычислять (S) фигуры придется с помощью тригонометрической функции — синуса. Перемножьте длины сторон, а результат умножьте на известного угла: S = a*b*sin(γ).
Если известна длина лишь одной из сторон (a) параллелограмма, но есть данные о (h) и величине угла (α) в любой из вершин , то это позволит и периметр (P) (S). Сумма всех углов в любом равна 360°, а в параллелограмме те из них, что лежат в противоположных вершинах, одинаковы. Поэтому для нахождения величины оставшегося неизвестным угла отнимите от 180° величину известного. После этого рассмотрите треугольник, составленный из высоты и лежащего напротив него угла, величины которых известны, а также неизвестной пока стороны. Примените к нему теорему синусов, и выясните, что длина стороны будет равна отношению высоты к синусу угла, лежащего напротив нее: h/sin(α).
После проведения предварительных расчетов предыдущего шага составьте нужные . Подставьте полученное выражение в формулу из первого шага и получите равенство: P = 2*(a+h/sin(α)). В том случае, если высота соединяет две противоположные стороны параллелограмма, длина которых дана в исходных условиях, для нахождения площади просто перемножьте эти два значения: S=a*h. Если же это условие не соблюдено, то подставьте в формулу выражение для другой стороны, полученное в предыдущем шаге: S=a*h/sin(α).
Подставьте полученное выражение в формулу из первого шага и получите равенство: P = 2*(a+h/sin(α)). В том случае, если высота соединяет две противоположные стороны параллелограмма, длина которых дана в исходных условиях, для нахождения площади просто перемножьте эти два значения: S=a*h. Если же это условие не соблюдено, то подставьте в формулу выражение для другой стороны, полученное в предыдущем шаге: S=a*h/sin(α).
Видео по теме
Среди основных задач аналитической геометрии на первом месте стоит представление геометрических неравенством, уравнением или системой тех или других. Это возможно благодаря применению координат. Опытный математик, только взглянув на уравнение, без труда скажет, какую геометрическую фигуру можно начертить.
Инструкция
Уравнением F (x, y) можно задать кривую или прямую линию при выполнении двух условий: если координаты точки, которая не принадлежит заданной линии, не удовлетворяют уравнению; если каждая точка искомой линии со координатами удовлетворяет этому уравнению.
Уравнение вида x+√(y(2r-y))=r arccos (r-y)/r задает в декартовых координатах циклоиду – траекторию, которая описывается точкой на окружности c радиусом r. При этом окружность не по оси абсцисс, а катится. Какая при этом получается фигура, смотрите на рисунке 1.
Фигура, координаты точек которой задаются следующими уравнениями:
x=(R+r) cosφ — rcos (R+r)/r φ
y=(R+r) sinφ — rsin (R-r)/r φ,
называется эпициклоидой. Она траекторию, которую описывает точка на окружности с радиусом r. Эта окружность катится по другой окружности, имеющей радиус R, с внешней стороны. То, эпициклоида, смотрите на рисунке 2.
Периметр — один из математических, а точнее — геометрических терминов, применяется в основном для вычисления сторон фигуры.
Из нашей статьи вы узнаете, что такое периметр и как он измеряется на примере основных геометрических фигур.
Определение периметра
Периметром называют общую длину всех сторон или окружности той или иной фигуры. Обозначается периметр большой буквой «Р», а измерять его можно в различных единицах длины, таких как миллиметры (мм), сантиметры (см), метры (м) и т. д. Для различных фигур существуют различные формулы для нахождения периметра. Ниже мы приведем несколько примеров, как узнать периметр у прямоугольника и некоторых других фигур.
Обозначается периметр большой буквой «Р», а измерять его можно в различных единицах длины, таких как миллиметры (мм), сантиметры (см), метры (м) и т. д. Для различных фигур существуют различные формулы для нахождения периметра. Ниже мы приведем несколько примеров, как узнать периметр у прямоугольника и некоторых других фигур.
Измеряем периметр
Если вам необходимо узнать периметр у сложной фигуры (к таким фигурам можно отнести фигуры с неровными линиями), то для этого вам понадобится веревка или нитка. При помощи этих вещей необходимо описать точный контур фигуры, а чтобы не запутаться, вы можете на веревке сделать отметки карандашом. Или же можно просто ее обрезать, а после приложить все части к линейке. Таким образом, вы узнаете, чему равен периметр практически у любой сложной фигуры.
Существует еще одно приспособление для вычисления периметра у сложных фигур: его называют курвиметр (роликовый дальномер). С его помощью вам нужно установить ролик в любую точку фигуры и описать роликом контур фигуры. Полученное число и будет равно периметру. О нахождении периметра у других геометрических фигур вы сможете узнать из нашей статьи . Ну а мы расскажем ещё о нескольких способах изменения периметра для разных фигур.
Полученное число и будет равно периметру. О нахождении периметра у других геометрических фигур вы сможете узнать из нашей статьи . Ну а мы расскажем ещё о нескольких способах изменения периметра для разных фигур.
Круг, квадрат, равносторонний треугольник
Давайте также рассмотрим, как узнать периметр круга. Это довольно-таки просто: достаточно лишь определить длину окружности, а сделать это можно, умножив радиус «r» на число π≈3,14 и затем на 2 (P=L=2∙π∙r).
Научитесь вычислять периметр квадрата.
Глядя вокруг себя, мы наблюдаем множество правильных и неправильных геометрических фигур. От основных принципов евклидовой геометрии (точка, прямая, плоскость и т. д.) и до наших дней мы можем наблюдать великие преобразования, которые произошли в геометрии объектов, домов, искусства, появляются новые и смелые архитектуры, бросающие вызов всем. формы классической геометрии. Периметр плоской геометрической фигуры широко применяется математикой во многих случаях. Среди этих фигур квадрат имеет большое значение и постоянно появляется в гражданском строительстве, машиностроении, искусстве и других приложениях. В связи с этим сегодня мы поговорим о фигуре квадрата и научим вас, как найти периметр этой геометрической фигуры. Еще больше информации можно узнать на https://skysmart.ru/courses/matematika.
В связи с этим сегодня мы поговорим о фигуре квадрата и научим вас, как найти периметр этой геометрической фигуры. Еще больше информации можно узнать на https://skysmart.ru/courses/matematika.
Площадь и периметр
Площадь и периметр — величины, имеющие большое значение для изучения плоских фигур в планиметрии. Существуют специальные формулы для расчета площади и периметра.
Площадь и периметр являются важными расчетами при изучении плоских фигур. Мы знаем площадь как меру поверхности фигуры, периметр — это длина контура фигуры, и его значение находится при вычислении суммы всех сторон фигуры. При изучении многоугольников, являющихся частными случаями плоских фигур, для нахождения их периметра достаточно выполнить сумму длин всех сторон, при этом площадь вычисляется по конкретным формулам для каждого многоугольника.
Площадь и периметр фигуры очень полезны в гражданском строительстве, на плантациях, а также для того, чтобы иметь представление о размерах поверхностей в быту, с несколькими приложениями этих понятий.
Что такое площадь?
Площадь является важной величиной геометрии. Для данной геометрической фигуры площадь является измерением поверхности этой фигуры. Для вычисления площади плоских фигур используем специфические формулы для каждой из них, при необходимости делим плоскую фигуру на известные плоские фигуры и складываем площади. Вот основные плоские фигуры и формула для расчета площади каждой из них.
Что такое периметр?
Периметр плоской фигуры равен сумме длин всех сторон фигуры. Таким образом, хотя и существует формула для некоторых плоских фигур, просто помните, что сумма их сторон дает их периметр.
Как рассчитать периметр?
Периметр всегда равен сумме всех сторон плоской фигуры, поэтому для некоторых плоских фигур можно использовать соответствующую формулу. Посмотрим на периметр основных плоских фигур.
Определение квадрата
Квадрат – это плоская геометрическая фигура, имеющая четыре стороны одинаковой длины, называемая правильным квадратом. Углы, образуемые этими сторонами квадрата, равны 90° (прямой угол). Также квадрат можно разделить по диагонали, соединив две диагонально противоположные вершины. То есть мы можем провести линию, которая соединит его углы (вершины) по диагонали.
Углы, образуемые этими сторонами квадрата, равны 90° (прямой угол). Также квадрат можно разделить по диагонали, соединив две диагонально противоположные вершины. То есть мы можем провести линию, которая соединит его углы (вершины) по диагонали.
Вычисление периметра квадрата
Вычислить периметр квадрата несложно и можно сделать в уме. Ввиду того, что все его стороны имеют одинаковую меру, то мы можем определить периметр квадрата, только зная меру одной из сторон. Самое большое определение периметра – это измерение контура двумерной геометрической фигуры.
Итак, исходя из этой концепции, мы можем определить периметр квадрата, сложив каждую сторону этого квадрата. Формула выглядит следующим образом:
P = L + L + L + L или P = L x 4
Где «L» — сторона квадрата.
Пример:
Собственник участка выделил участок площадью 25 м под огороженное место с экраном. Он намерен посадить листья и немного овощей на этом небольшом пространстве. Однако он хочет использовать в этой ручке как можно меньше экрана. Какая плоская геометрическая фигура будет использовать как можно меньший экран, чтобы окружить эту область?
Какая плоская геометрическая фигура будет использовать как можно меньший экран, чтобы окружить эту область?
Решение:
В этом случае это было бы возможно только с фигурой четырехугольника.
Начнем с прямоугольника:
Возможные измерения для прямоугольника площадью 25 м будут иметь ширину 4 метра и длину 6,25 метра, откуда мы можем получить периметр:
Р = 4 + 4 + 6,25 + 6,25 = 20,5
Итак, мы знаем, что периметр прямоугольника площадью 25 м эквивалентен 20,5 метрам в длину. В этом случае это будет размер экрана, используемый в данной конфигурации.
Теперь вычислим периметр этой самой площади в 25 м, используя фигуру квадрата.
Единственная возможная мерка для площади 25 м от обычного квадрата – по 5 метров с каждой стороны.
Р = 5 х 4
Р = 20
Итак, мы знаем, что используя угольник, длина периметра забора составит 20 метров. В этом случае владелец участка будет использовать меньше холста с конфигурацией квадрата в своем ограждении.
Эта важная особенность квадрата может остаться незамеченной при проектировании комнаты или любой другой среды. Квадрат всегда будет иметь меньший периметр той же площади по сравнению с другими четырехугольниками.
Brilliant Math & Science Wiki
Мэй Ли, Ариэль Гершон, Ашиш Менон, а также
способствовал
Содержимое
- Периметр правильных многоугольников
- Периметр неправильных многоугольников
- Периметр других фигур (круги, фракталы и т. д.)
- Периметр с использованием полярных координат
- Решение проблем
- Реальные приложения
Чему равен периметр квадрата со стороной 6?
Поскольку у квадрата четыре стороны одинаковой длины, а периметр квадрата равен сумме длин его сторон, периметр квадрата равен
6+6+6+6=24.
□ 6 + 6 + 6 + 6 = 24. \ _\квадрат 6+6+6+6=24. □
Вы также можете сделать 6×46 \× 46×4, считая, что это квадрат.
Чему равен периметр правильного пятиугольника, все стороны которого равны 6?
Поскольку у правильного пятиугольника пять сторон, а длины всех его сторон равны 666, периметр пятиугольника равен
6+6+6+6+6=5⋅6=30. □ 6 + 6 + 6 + 6 + 6= 5 \cdot 6 = 30 . \ _\квадрат 6+6+6+6+6=5⋅6=30. □
Найдите минимальный периметр треугольника, площадь которого равна 34 \frac{\sqrt{3}}{4} 43.
Чему равен периметр прямоугольника шириной 444 и высотой 7×7×7?
Поскольку у прямоугольника две стороны одинаковой ширины и две стороны одинаковой высоты, а периметр прямоугольника равен сумме длин его сторон, периметр прямоугольника равен 9{2} \ подразумевает AC=5.AC2=AB2+BC2=32+42⟹AC=5.
Затем добавьте AB,BC,CAAB,BC,CAAB,BC,CA, чтобы получить периметр, который равен
.3+4+5=12 (см). □3+4+5 =12\текст{ (см)}.\ _\квадрат3+4+5=12 (см). □
Предположим, муравей идет по границе треугольника с длинами сторон 4, 6, 4, 6, 4, 6 и 777. Если муравей начнет с одной вершины треугольника и совершит 333 полных обхода границы треугольника, чтобы вернуться в его отправная точка, каково общее расстояние, пройденное муравьем?
Поскольку периметр равен сумме длин ребер, периметр треугольника равен 4+6+7=174 + 6+7 = 174+6+7=17. Поскольку муравей совершает 333 полных обхода границы треугольника, общее расстояние, пройденное муравьем, равно
.17×3=51. □ 17\умножить на 3 = 51. \ _\квадрат 17×3=51. □
Найдите периметр данной фигуры.У нас есть
Периметр=Сумма длин сторон=9+8+7+3+4+5=36. □\begin{выровнено} \text{Периметр} & = \text{Сумма длин сторон}\\ & = 9+ 8 + 7 + 3 + 4 + 5\\ & = 36.\ _\квадрат \end{aligned}Периметр=Сумма длин сторон=9+8+7+3+4+5=36.
□
Пусть на декартовой плоскости нарисован треугольник с координатами вершин (−3,0),(1,−3),(4,1).(-3,0), (1,-3), (4,1).(−3,0),(1, −3),(4,1). Найдите периметр этого треугольника с точностью до целого числа.
Периметр круга с радиусом rrr равен 2πr2\pi r2πr. Периметр дуги окружности, опирающейся на угол θ\thetaθ (в градусах) в центре, равен 2πr×θ3602\pi r \times \frac {\theta}{360}2πr×360θ.
Чему равен периметр (длина окружности) круга диаметром 14 см?14\text{ см}?14 см?
У нас есть
Радиус=Диаметр2=142=7 (см) Окружность=2×π×r=2×227×7=44 (см). □\begin{выровнено} \text{Радиус} & = \dfrac{\text{Диаметр}}{2}\\ & = \dfrac{14}{2}\\ & = 7\текст{ (см)}\\ \\ \text{Окружность} & = 2× \pi × r\\ & = 2 × \dfrac{22}{7} × 7\\ & = 44\text{ (см)}.\ _\квадрат \end{align}RadiusCircumference=2Diameter=214=7 (см)=2×π×r=2×722×7=44 (см). □
Найдите периметр полукруга радиусом 212121 см.
У нас есть
Периметр полукруга=(12×2×π×r)+2r=(12×2×227×21)+2×21=66+42=106 (см). □\begin{выровнено} \text{Периметр полукруга} & = \left( \dfrac{1}{2} × 2 × \pi × r \right) + 2r\\ & = \left( \dfrac{1}{2} × 2× \dfrac{22}{7} × 21\right) + 2×21\\ & = 66 + 42\\ & = 106\text{ (см)}.\ _\квадрат \end{align}Периметр полукруга=(21×2×π×r)+2r=(21×2×722×21)+2×21=66+42=106 (см). □
На рисунке справа вокруг правильного шестиугольника описана окружность, и такая же окружность вписана в другой правильный шестиугольник.
Пусть P1P_1P1 будет периметром большего шестиугольника, пусть P2P_2P2 будет периметром меньшего шестиугольника, и пусть CCC будет окружностью круга.
Длину окружности можно приблизительно определить, найдя среднее значение двух периметров:
C≈P1+P22.C\приблизительно \frac{P_1+P_2}{2}.C≈2P1+P2.
Если π\piπ аппроксимируется с использованием приведенной выше аппроксимации длины окружности, то π≈ab+c\pi\приблизительно\frac{a}{b}+\sqrt{c}π≈ba+c, где b,ca, b, ca,b,c — положительные целые числа, aaa и bbb взаимно просты, а ccc не содержит квадратов.
Найти a+b+ca+b+ca+b+c.
Периметр замкнутой фигуры можно вычислить, если ее график на декартовой плоскости является функцией в полярных координатах. В частности, предположим, что фигура имеет уравнение r=f(θ)r = f(\theta)r=f(θ), такое что fff — непрерывная неотрицательная функция для θ∈[0,2π]\theta \in [0 , 2\pi]θ∈[0,2π] и f(0)=f(2π)f(0) = f(2\pi)f(0)=f(2π). Тогда его периметр определяется по следующей формуле: 9на 24 см2 больше, чем у прямоугольника.
Если все стороны обоих четырехугольников имеют длины в виде простых чисел (((в см),\текст{см}),см), то каков периметр квадрата?
Если высота и периметр трапеции равны 333 и A+B2+C3,A+B \sqrt{2}+C \sqrt{3},A+B2+C3 соответственно, найти A+B+CA+ Б+КА+Б+В.
Найдите периметр этой фигуры в см.\си{\см}.см. 92A=630 м2 и его длина l=42 м,l = 42\text{ м},l=42 м, мы знаем, что
A=l×b ⟹ b=Al=63042=15 (m). A = l \times b \ подразумевает b = \dfrac{A}{l} = \dfrac{630}{42} = 15\ (\ text{m}).A=l×b⟹b=lA=42630=15 (m).
A = l \times b \ подразумевает b = \dfrac{A}{l} = \dfrac{630}{42} = 15\ (\ text{m}).A=l×b⟹b=lA=42630=15 (m).
Теперь найдем периметр: P=2(l+b)=2(42+15)=114 (m).P = 2(l + b) = 2(42 + 15) = 114\ (\text{ м}).P=2(l+b)=2(42+15)=114 (м).
Поскольку стоимость ограждения за метр составляет 3 доллара, общая стоимость ограждения всего поля составляет 3×P=3×114=342 3 \times P = 3 \times 114 = 3423×P=3×114=342 доллара. □_\квадрат□
Цитировать как: Периметр. Brilliant.org . Извлекаются из https://brilliant.org/wiki/perimeter/
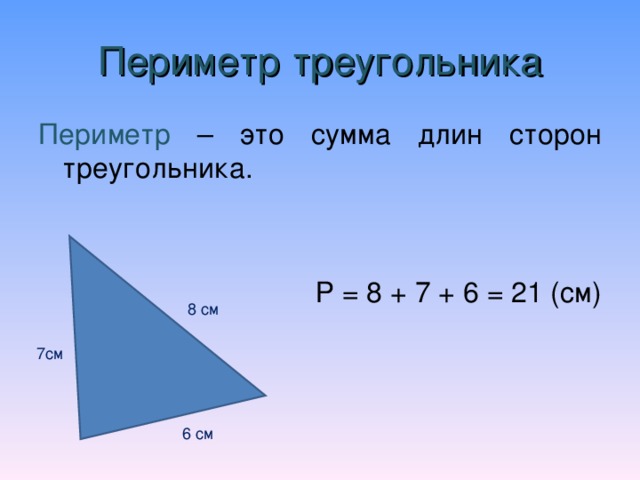
Периметр треугольника: определение и пример
Все мы знаем, что треугольник — это фигура, имеющая три стороны и три вершины, которые, соединяясь, образуют замкнутую фигуру. Различные свойства определяют характеристики треугольника, некоторые связаны с его углами, а другие — со сторонами. Одним из таких свойств является периметр треугольника.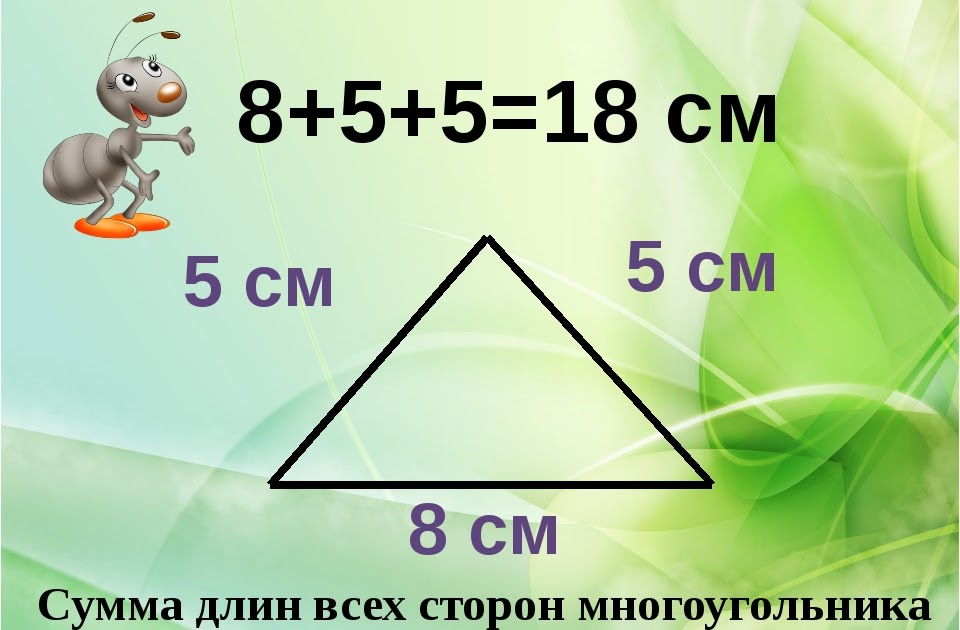 периметр треугольника — это свойство, основанное исключительно на сторонах треугольника. Давайте посмотрим, что это такое на самом деле и как мы можем вычислить периметр любого треугольника.
периметр треугольника — это свойство, основанное исключительно на сторонах треугольника. Давайте посмотрим, что это такое на самом деле и как мы можем вычислить периметр любого треугольника.
В этой статье мы увидим определение периметра треугольника, его формулу и как решить периметр треугольника, когда даны точки или задано изображение, или когда стороны отсутствуют.
Определение периметра треугольника
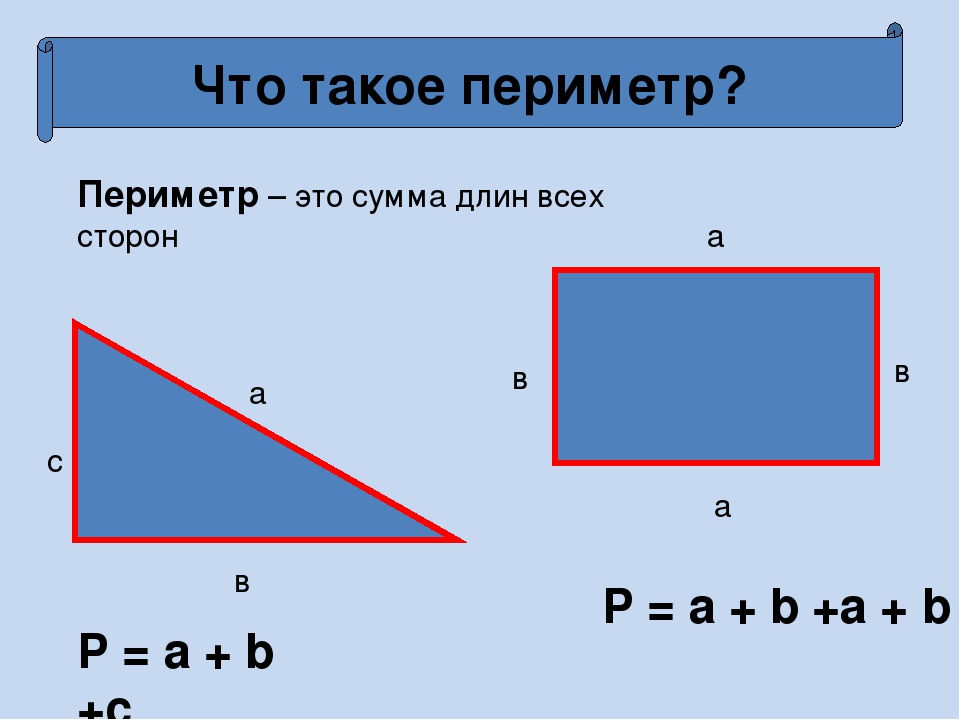
Периметр треугольника представляет собой сумму всех трех его сторон.
Определение периметра любого другого многоугольника то же самое: сумма всех сторон. Периметр явно зависит от сторон треугольника и не зависит от сторон. Итак, если задана мера всех сторон треугольника, периметр — это просто сумма всех этих сторон. Далее его можно разделить на три типа: периметр разностороннего, равнобедренного и равностороннего треугольника.
Формула периметра разностороннего треугольника
Напомним, что разносторонний треугольник — это треугольник, все стороны которого различны по длине.
Пусть a, b и c будут длинами всех сторон разностороннего треугольника, тогда по определению периметр равен:
,
, где P обозначает периметр.
Периметр разностороннего треугольника, StudySmarter Original
Найдите периметр треугольника, длина сторон которого равна a = 4, b = 5 и c = 7 единицам.
Решение:
Периметр определяется следующим образом:
Формула периметра равнобедренного треугольника
Равнобедренный треугольник – это треугольник, в котором длины двух сторон одинаковы, а длина третьей другой.
Пусть a будет длиной каждой из равных сторон, а длина третьей стороны будет b , тогда периметр треугольника будет:
.
Периметр равнобедренного треугольника, StudySmarter Original
Это всего лишь частный случай разностороннего треугольника для a = c .
Найдите периметр равнобедренного треугольника, две стороны которого имеют длину 4 единицы каждая, а третья сторона равна 5 единицам.
Решение:
Периметр равнобедренного треугольника равен:
.
где a = 4 и b = 5 даны:
Следовательно, периметр этого треугольника равен 13 единицам.
Формула периметра равностороннего треугольника
Равносторонний треугольник — это треугольник, все стороны которого имеют одинаковую длину.
Пусть a — длина каждой из сторон, тогда периметр определяется как:
Следовательно, периметр равностороннего треугольника в три раза больше длины каждой из его сторон. Опять же, равносторонний треугольник — это всего лишь частный случай разностороннего треугольника.
Периметр равностороннего треугольника, StudySmarter Original
Найдите периметр равностороннего треугольника, длина каждой стороны которого равна 3 единицам.
Решение:
Мы можем использовать формулу, чтобы найти периметр равностороннего треугольника:
Следовательно, периметр треугольника равен 9 единицам.
Периметр, когда заданы точки
Предположим, что нам не заданы длины сторон треугольника напрямую, а заданы координаты его вершин. Это особенно верно, когда треугольник вписан в декартову плоскость . Координаты помогают найти треугольник.
Чтобы найти периметр, когда известны координаты его вершин, нам нужно каким-то образом найти длину отдельных сторон. Для этого мы можем рассчитать расстояние между вершинами, используя формулу расстояния , а отрезки, образованные при соединении вершин, являются сторонами самого треугольника.
Следовательно, длина отрезков, соединяющих вершины, будет равна длине сторон образовавшегося треугольника.
Треугольник с декартовыми координатами, StudySmarter Originals
Пусть A, B и C — вершины треугольника, а координаты — точки, в которых все точки различны. Стороны треугольника ABC будут равны AB, BC и AC.
Используя формулу расстояния:
Итак, теперь, когда у нас есть длины сторон треугольника через координаты вершин, мы можем использовать формулу периметра:
Таким образом, мы нашли формула вычисления периметра треугольника, вершины которого заданы.
Найдите периметр треугольника, вершины которого расположены в точках A(–3, 1), B(2, 1) и C(2, –1).
Решение:
Чтобы найти длину периметра, нам нужно найти длины соответствующих сторон, и мы можем сделать это, используя формулу расстояния для всех трех вершин.
Для первой стороны AB:
Для второй стороны, BC:
И для третьей стороны, AC:
И теперь периметр можно вычислить, сложив все эти стороны:
Следовательно, периметр треугольника с вершинами A(–3, 1), B(2, 1) и C(2, –1) равен единицам.
Периметр треугольника с отсутствующими сторонами
Иногда указываются не все стороны. В большинстве случаев дана длина двух сторон и угол между ними. Используя только эту информацию, мы должны найти периметр треугольника.
Опять же, используя данную информацию, нам нужно найти длину недостающей стороны. Если задан угол между двумя известными сторонами, для определения длины недостающей стороны используется закон косинуса.
Пусть A, B и C — три угла треугольника, а противоположные им стороны имеют длину соответственно.
Предположим, что нам дана длина двух сторон как a, b, , а угол между ними задан как C. найдите третью сторону c , используя данную информацию, здесь мы используем закон косинуса, чтобы определить недостающую сторону. Напомним, что закон косинуса задается следующим образом:
где единственным неизвестным является c и поэтому мы можем довольно легко вычислить его. Очень специфическим случаем будет прямоугольный треугольник, где член cosC будет равен нулю, поскольку C = π/2, а закон косинуса просто приведет к теореме Пифагора.
Теперь, используя формулу для периметра треугольника, получаем:
Подставляя вместо c , получаем:
Найдите периметр треугольника, две стороны которого имеют длину 4 и 5 единиц, а угол между этими сторонами равен радианам.
Решение:
Обозначим две стороны как a и b соответственно, так что a = 4 и b = 5 , а угол равен C , длину оставшейся стороны, чтобы найти периметр.
Используя закон косинуса здесь:
Следовательно, периметр определяется как:
Таким образом, периметр данного треугольника равен единицам.
Периметр треугольника на графике
Предположим, что нам известны не длины сторон треугольника, а координаты его вершин. Это особенно верно, когда треугольник вписан в декартову плоскость . Координаты помогают найти треугольник.
Чтобы найти периметр, когда известны координаты его вершин, нам нужно каким-то образом найти длину отдельных сторон. Для этого мы можем рассчитать расстояние между вершинами, используя формулу расстояния , а отрезки, образованные при соединении вершин, являются сторонами самого треугольника.
Следовательно, длина отрезков, соединяющих вершины, будет равна длине сторон образовавшегося треугольника.
Пусть A, B и C — вершины треугольника, а координаты — точки, в которых все точки различны. Стороны треугольника ABC будут равны AB, BC и AC.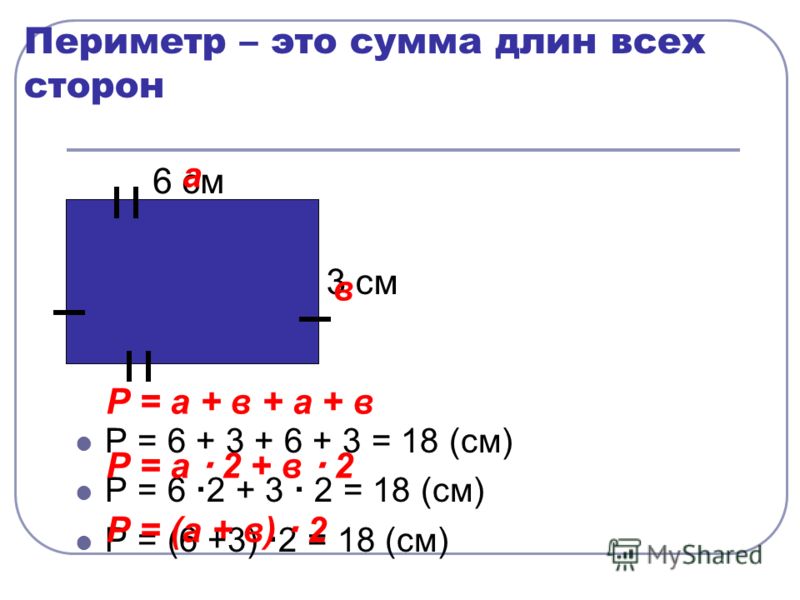

 □ 6 + 6 + 6 + 6 = 24. \ _\квадрат 6+6+6+6=24. □
□ 6 + 6 + 6 + 6 = 24. \ _\квадрат 6+6+6+6=24. □
 □
□