Матрица (математика)
В математике матрица (множественное число: матрицы) — это прямоугольник чисел, расположенных в строках и столбцах. Строки — это каждая слева направо (горизонтальная) линия, а столбцы идут сверху вниз (вертикальная). Левая верхняя ячейка находится в строке 1, столбец 1 (см. диаграмму справа).
Существуют правила сложения, вычитания и «умножения» матриц вместе, но эти правила отличаются от правил для чисел. Например, A ⋅ B {\displaystyle A\cdot B} не всегда дает тот же результат, что и B ⋅ A {\displaystyle B\cdot A}. что и происходит при умножении обычных чисел. Матрица может иметь более 2-х измерений, например, 3D-матрица. Кроме того, матрица может быть одномерной, в виде одной строки или столбца.
Многие естественные науки довольно часто используют матрицы. Во многих университетах курсы по матрицам (обычно называемые линейной алгеброй) преподаются очень рано, иногда даже на первом курсе. Матрицы также очень распространены в компьютерных науках.
На конкретные записи матрицы часто ссылаются, используя пары подписок, для номеров в каждой строке и столбце.
См. также
- Линейная алгебра
- числовая линейная алгебра
административный контроль |
|
Детерминанты
Детерминант берет квадратную матрицу и вычисляет простое число — скаляр. Чтобы понять, что означает это число, возьмите каждый столбец матрицы и нарисуйте его как вектор. Параллелограмма, построенная по этим векторам, имеет область, которая является детерминантой. Для всех матриц 2х2 формула очень проста: det ( [ a b c d ] ) = a d — b c {\displaystyle \det \left({\begin{bmatrix}a&b\c&d\end{bmatrix}}\right)=ad-bc}.
Для матриц 3х3 формула сложнее: det ( [ a 1 b 1 c 1 a 2 b 2 c 2 a 3 b 3 c 3 ] ) = a 1 ( b 2 c 3 — c 2 b 3 ) — a 2 ( b 1 c 3 — c 1 b 3 ) + a 3 ( b 1 c 2 — c 1 b 2 ) {\displaystyle \det \left({\begin{bmatrix}a_{1}&b_{1}&c_{1}\a_{2}&b_{2}&c_{2}\a_{3}&b_{3}&c_{3}\end{bmatrix}}\right)=a_{1}(b_{2}c_{3}-c_{2}b_{3})-a_{2}(b_{1}c_{3}-c_{1}b_{3})+a_{3}(b_{1}c_{2}-c_{1}b_{2})}
Простых формул для определения детерминант больших матриц не существует, и многие компьютерные программисты изучают, как заставить компьютеры быстро находить большие детерминанты.
Свойства детерминантов
Есть три правила, которым следуют все детерминанты. Вот эти:
- Детерминант матрицы идентичности — 1
- Если происходит обмен двумя строками или двумя столбцами матрицы, то детерминант умножается на -1. Математики называют это чередованием.
- Если все числа в одной строке или столбце умножить на другое число n, то определитель умножается на n. Также, если в матрице M есть столбец v — это сумма матриц из двух столбцов v 1 {\displaystyle v_{1}} и v 2 {\displaystyle v_{2}}. тогда детерминантом M является сумма детерминантов M с v 1 {\displaystyle v_{1}} вместо v и M с v 2 {\displaystyle v_{2}} вместо v. Эти два условия называются мультилинейностью.
Специальные матрицы
Есть специальные матрицы.
Квадратная матрица
Квадратная матрица имеет такое же количество строк, что и столбцы, поэтому m=n.
Примером квадратной матрицы является
[ 5 — 2 4 0 9 1 — 7 6 8 ] {\displaystyle {\begin{bmatrix}5&-2&4_COPY11&9&1-7&6&8\end{bmatrix}}}
Эта матрица имеет 3 строки и 3 столбца: m=n=3.
Идентификация
Каждый квадратный размерный набор матрицы имеет специальный аналог, называемый «матрицей идентичности». Матрица тождественности не имеет ничего, кроме нулей, кроме главной диагонали, где все они есть. Например:
[ 1 0 0 0 0 1 ] {\displaystyle {\begin{bmatrix}1&0&0_COPY11&1&0_COPY11&0&1\end{bmatrix}}}
это матрица личности. Для каждого набора квадратных размеров существует ровно одна матрица идентичности. Матрица идентичности особенная, потому что при умножении любой матрицы на матрицу идентичности, результатом всегда является исходная матрица без изменений.
обратная матрица
Обратная матрица — это матрица, которая при умножении на другую матрицу равна матрице идентичности. Например:
[ 7 8 6 7 ] ⋅ [ 7 — 8 — 6 7 ] = [ 1 0 0 1 ] {\displaystyle {\begin{bmatrix}7&8\6&7\end{bmatrix}}\cdot {\begin{bmatrix}7&-8-6&7\end{bmatrix}}={\begin{bmatrix}1&0_COPY11&1\end{bmatrix}}}
[ 7 — 8 — 6 7 ] {\displaystyle {\begin{bmatrix}7&-8-6&7\end{bmatrix}}} является обратной величиной [ 7 8 6 7 ] {\displaystyle {\begin{bmatrix}7&8\6&7\end{bmatrix}}}} .
Формула обратной матрицы 2х2, [ x y z v ] {\displaystyle {\begin{bmatrix}x&y\z&v\end{bmatrix}}} есть:
(1 d e t) [ v — y — z x ] {\displaystyle \left({\frac {1}{det}}\right){\begin{bmatrix}v&-y-z&x\end{bmatrix}}}
Где d e t {\displaystyle det} — детерминант матрицы. В матрице 2х2 детерминант равен:
x v — y z {\displaystyle {xv-yz}}
Матрица из одной колонки
Матрица, в которой много строк, но только один столбец, называется вектором столбца.
Определения и обозначения
Горизонтальные линии в матрице называются строками, а вертикальные — столбцами. Матрица с m строками и n столбцами называется m-by-n матрицей (или m×n матрицей) и m и n называются ее размерами.
Места в матрице, где номера называются записями. Запись матрицы A, которая лежит в строке с номером i и номером столбца j, называется записью i,j A. Это записывается как A[i,j] или ai,j.
Пишем A := ( a i j ) m × n {\displaystyle A:=(a_{ij})_{m\times n}} для определения m × n матрицы A, при этом каждая запись в матрице называется ai,j для всех 1 ≤ i ≤ m и 1 ≤ j ≤ n.
Пример
Матрица
[ 1 2 3 1 2 7 4 9 2 6 1 5 ] {\displaystyle {\begin{bmatrix}1&2&3\1&2&7\4&9&2\6&1&5\end{bmatrix}}}
это матрица 4×3. Эта матрица имеет m=4 строки, а n=3 столбца.
Элемент A[2,3] или a2,3 равен 7.
Операции
Добавление
Сумма двух матриц — это матрица, которая (i,j)-четвертая запись равна сумме (i,j)-четвертых записей двух матриц:
[ 1 3 2 1 0 0 1 2 ] + [ 0 5 7 5 0 2 1 ] = [ 1 + 0 3 + 0 2 + 5 1 + 7 0 + 5 0 + 0 1 + 2 2 + 1 2 + 1 ] = [ 1 3 7 8 5 0 3 3 ] {\displaystyle {\begin{bmatrix}1&3&2\1&0&0\1&2&2\end{bmatrix}}+{\begin{bmatrix}0&0&5\7&5&0\2&1&1\end{bmatrix}}={\begin{bmatrix}1+0&3+0&2+5\1+7&0+5&0+0\1+2&2+1&2+1\end{bmatrix}}={\begin{bmatrix}1&3&7\8&5&0\3&3&3\end{bmatrix}}}
Две матрицы имеют одинаковые размеры.
Здесь A + B = B + A {\displaystyle A+B=B+A} истинно.
Умножение двух матриц
Умножение двух матриц немного сложнее:
[ a 1 a 2 a 3 a 4 ] ⋅ [ b 1 b 2 b 3 b 4 ] = [ ( a 1 a ⋅ b 1 + a 2 a ⋅ b 3 ) ( a 1 a ⋅ b 2 + a 2 a 2 ⋅ b 4 ) ( a 3 a ⋅ b 1 + a 4 a ⋅ b 3 ) ( a 3 a ⋅ b 2 + a 4 a ⋅ b 4 ) ] ] {\displaystyle {\begin{bmatrix}a1&a2\a3&a4\end{bmatrix}}\cdot {\begin{bmatrix}b1&b2\b3&b4\end{bmatrix}}={\begin{bmatrix}(a1\cdot b1+a2\cdot b3)&(a1\cdot b2+a2\cdot b4)(a3\cdot b1+a4\cdot b3)&(a3\cdot b2+a4\cdot b4)\end{bmatrix}}}
Итак, с Numbers:
[ 3 5 1 4 ] ⋅ [ 2 3 5 0 ] = [ ( 3 ⋅ 2 + 5 ⋅ 5 ) ( 3 ⋅ 3 + 5 ⋅ 0 ) ( 1 ⋅ 2 + 4 ⋅ 5 ) ( 1 ⋅ 3 + 4 ⋅ 0 ) ] = [ 31 9 22 3 ] {\displaystyle {\begin{bmatrix}3&5\1&4\end{bmatrix}}\cdot {\begin{bmatrix}2&3\5&0\end{bmatrix}}={\begin{bmatrix}(3\cdot 2+5\cdot 5)&(3\cdot 3+5\cdot 0)(1\cdot 2+4\cdot 5)&(1\cdot 3+4\cdot 0)\end{bmatrix}}={\begin{bmatrix}31&9\22&3\end{bmatrix}}}
- две матрицы можно умножать друг с другом, даже если они имеют разные размеры, при условии, что количество столбцов в первой матрице равно количеству строк во второй.
- Результатом умножения, называемого продуктом, является другая матрица с тем же количеством строк, что и первая матрица, и тем же количеством столбцов, что и вторая матрица.
- умножение матриц не является коммутативным, что в целом означает, что A ⋅ B ≠ B ⋅ A {\displaystyle A\cdot B\neq B\cdot A}.
- умножение матриц является ассоциативным, что означает, что ( A ⋅ B ) ⋅ C = A ⋅ ( B ⋅ C ) {\displaystyle (A\cdot B)\cdot C=A\cdot (B\cdot C)}
Автор
Alegsaonline.com — Матрица (математика) — Leandro Alegsa — 18/11/2020 — url: https://ru.alegsaonline.com/art/62849С помощью матрицы алгебраических дополнений
— транспонированная матрица алгебраических дополнений;
Полученная матрица A−1 и будет обратной. Сложность алгоритма зависит от сложности алгоритма расчета определителя Odet и равна O(n²)·Odet.
Иначе
говоря, обратная матрица равна единице,
делённой на определитель исходной
матрицы и умноженной натранспонированную
матрицу алгебраических
дополнений элементов
исходной матрицы.
Матричное уравнение для обратной матрицы можно рассматривать как совокупность систем вида . Обозначим -ый столбец матрицы через ; тогда , ,поскольку -м столбцом матрицы является единичный вектор . другими словами, нахождение обратной матрицы сводится к решению n уравнений с одной матрицей и разными правыми частями. После выполнения LUP-разложения (время O(n³)) на решение каждого из n уравнений нужно время O(n²), так что и эта часть работы требует времени O(n³) [1].
Если
матрица A невырождена, то для неё можно
рассчитать LUP-разложение
.
Пусть
,
.
Тогда из свойств обратной матрицы можно
записать:
.
Если умножить это равенство на U и L то
можно получить два равенства вида
и
.
Первое из этих равенств представляет
собой систему из n² линейных уравнений
для
из
которых известны правые части (из свойств
треугольных матриц). Второе представляет
также систему из n² линейных уравнений
для
из
которых известны правые части (также
из свойств треугольных матриц).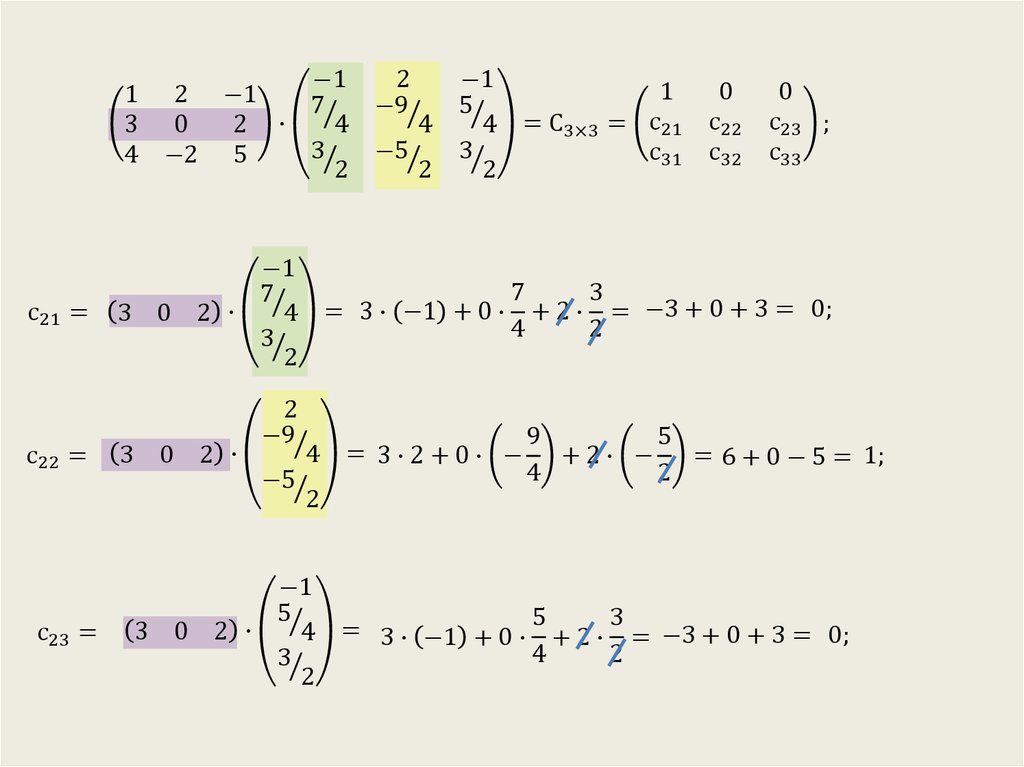
Вместе
они представляют собой систему из n²
равенств. С помощью этих равенств можно
реккурентно определить все n² элементов
матрицы D. Тогда из равенства (PA)−1 =
A−1P−1
В случае использования LU-разложения не требуется перестановки столбцов матрицы D но решение может разойтись даже если матрица A невырождена.
Сложность алгоритма — O(n³).
Итерационные методы
Методы Шульца
Оценка погрешности
Выбор начального приближения
Проблема
выбора начального приближения
в
рассматриваемых здесь процессах
итерационного обращения матриц не
позволяет относиться к ним как к
самостоятельным универсальным методам,
конкурирующими с прямыми методами
обращения, основанными, например, на
LU-разложении матриц. Имеются некоторые
рекомендации по выбору
,
обеспечивающие выполнение
условия
(спектральный
радиус матрицы меньше единицы), являющегося
необходимым и достаточным для сходимости
процесса.
Однако при этом, во-первых,
требуется знать сверху оценку спектра
обращаемой матрицы A либо матрицы
(а
именно, если A — симметричная
положительно определённая матрица и
,
то можно взять
,
где
;
если же A — произвольная невырожденная
матрица и
,
то полагают
,
где также
;
можно конечно упростить ситуацию и,
воспользовавшись тем, что
,
положить
).
Во-вторых, при таком задании начальной
матрицы нет гарантии, что
будет
малой (возможно, даже окажется
),
и высокий порядок скорости сходимости
обнаружится далеко не сразу.
Примеры
Матрица 2х2
Обращение матрицы 2х2 возможно только при условии, что .
Транспонирование.
Транспонированная матрица — матрица , полученная из исходной матрицы заменой строк на столбцы.
Пример:
и
Системы линейных уравнений
Решение
систем линейных уравнений методом
Крамера. Пусть
нам требуется решить систему линейных
алгебраических уравнений
в
которой число уравнений равно числу
неизвестных переменных и определитель
основной матрицы системы отличен от
нуля, то есть,
.
Основным
недостатком метода Крамера (если это
можно назвать недостатком) является
трудоемкость вычисления определителей,
когда число уравнений системы больше
трех.Решение систем линейных алгебраических уравнений матричным методом (с помощью обратной матрицы). Пусть система линейных алгебраических уравнений задана в матричной форме , где матрицаA имеет размерность
Основная
проблема при нахождении решения систем
линейных алгебраических уравнений
матричным методом заключается в
трудоемкости нахождения обратной
матрицы, особенно для квадратных матриц
порядка выше третьего.Решение систем линейных уравнений методом Гаусса. Пусть нам требуется найти решение системы из n линейных уравнений с n неизвестными переменными определитель основной матрицы которой отличен от нуля. Суть метода Гаусса состоит в последовательном исключении неизвестных переменных: сначала исключается x1 из всех уравнений системы, начиная со второго, далее исключается x2 из всех уравнений, начиная с третьего, и так далее, пока в последнем уравнении останется только неизвестная переменная
Процесс вычисления неизвестных переменных
при движении от последнего уравнения
системы к первому называется обратным
ходом метода Гаусса.
Кратко
опишем алгоритм исключения неизвестных
переменных.
Будем считать, что
,
так как мы всегда можем этого добиться
перестановкой местами уравнений системы.
Исключим неизвестную переменную x1 из
всех уравнений системы, начиная со
второго. Для этого ко второму уравнению
системы прибавим первое, умноженное
на
,
к третьему уравнению прибавим первое,
умноженное на
,
и так далее, к n-ому уравнению
прибавим первое, умноженное на
.
Система уравнений после таких
преобразований примет вид
где
,
а
.
К
такому же результату мы бы пришли, если
бы выразили x1 через
другие неизвестные переменные в первом
уравнении системы и полученное выражение
подставили во все остальные уравнения.
Таким образом, переменная x1 исключена
из всех уравнений, начиная со второго.
Далее
действуем аналогично, но лишь с частью
полученной системы, которая отмечена
на рисунке
Будем
считать, что
(в
противном случае мы переставим местами
вторую строку с k-ой,
где
).
Приступаем к исключению неизвестной
переменной x2 из
всех уравнений, начиная с третьего.
Для
этого к третьему уравнению системы
прибавим второе, умноженное на
,
к четвертому уравнению прибавим второе,
умноженное на
,
и так далее, к n-ому уравнению
прибавим второе, умноженное на
.
Система уравнений после таких
преобразований примет вид
где
,
а
.
Таким образом, переменная x2 исключена
из всех уравнений, начиная с третьего.
Далее
приступаем к исключению неизвестной x3,
при этом действуем аналогично с отмеченной
на рисунке частью системы
Так
продолжаем прямой ход метода Гаусса
пока система не примет вид
С
этого момента начинаем обратный ход
метода Гаусса: вычисляем xn из
последнего уравнения как
,
с помощью полученного значения xn находим xn-1 из
предпоследнего уравнения, и так далее,
находим x1 из
первого уравнения.
Пример. Решите
систему линейных уравнений
методом
Гаусса. Решение. Исключим
неизвестную переменную x1 из
второго и третьего уравнения системы.
Для этого к обеим частям второго и
третьего уравнений прибавим соответствующие
части первого уравнения, умноженные
на
и
на
соответственно:
Теперь
из третьего уравнения исключим x2,
прибавив к его левой и правой частям
левую и правую части второго уравнения,
умноженные на
:
На
этом прямой ход метода Гаусса закончен,
начинаем обратный ход.
Из последнего
уравнения полученной системы уравнений
находим x3:
Из
второго уравнения получаем
.
Из
первого уравнения находим оставшуюся
неизвестную переменную и этим завершаем
обратный ход метода Гаусса
. Ответ: x1 =
4, x2 =
0, x3 =
-1. Решение
систем линейных алгебраических уравнений
общего вида.
В
общем случае число уравнений системы p не
совпадает с числом неизвестных
переменных n:
Такие
СЛАУ могут не иметь решений, иметь
единственное решение или иметь бесконечно
много решений. Это утверждение относится
также к системам уравнений, основная
матрица которых квадратная и
вырожденная.
Далее
нам потребуется понятие минора матрицы
и ранга матрицы, которые даны в статье ранг
матрицы: определение, методы нахождения,
примеры, решения.
Прежде
чем находить решение системы линейных
уравнений необходимо установить ее
совместность. Ответ на вопрос когда
СЛАУ совместна, а когда несовместна,
дает теорема
Кронекера – Капелли:
для
того, чтобы система из p уравнений
с n неизвестными
(p может
быть равно n)
была совместна необходимо и достаточно,
чтобы ранг основной матрицы системы
был равен рангу расширенной матрицы,
то есть, Rank(A)
= Rank(T).
Рассмотрим
на примере применение теоремы Кронекера
– Капелли для определения совместности
системы линейных уравнений.
Пример. Выясните,
имеет ли система линейных
уравнений
решения. Решение. Найдем
ранг основной матрицы системы
.
Воспользуемся методом окаймляющих
миноров. Минор второго порядка
отличен
от нуля. Переберем окаймляющие его
миноры третьего порядка:
Так
как все окаймляющие миноры третьего
порядка равны нулю, то ранг основной
матрицы равен двум.
В свою очередь
ранг расширенной матрицы
равен
трем, так как минор третьего
порядка
отличен
от нуля.
Таким образом, Rang(A)
< Rang(T),
следовательно, по теореме Кронекера –
Капелли можно сделать вывод, что исходная
система линейных уравнений
несовместна. Ответ:
система решений не имеет.
Обратная матрица 2х2 онлайн: калькулятор, примеры и формула
Вам нужен калькулятор обратной матрицы 2х2 онлайн , чтобы сэкономить время? Воспользуйтесь нашим калькулятором, и вы сможете получить обратную матрицу автоматически за считанные секунды, шаг за шагом.
Чтобы сделать это, вы должны записать каждый из элементов, составляющих матричную обратную 2×2 и пульсар эль ботон де исчисления cuando lo hayas hecho.
Tras eso, conocerás el resultado y los pasos previos que conlleva a este cálculo como son el determinante 2×2 y la matriz adjunta.
Статьи Разделы
- Fórmula Para Calcular Matriz Inversa 2×2
- Пример обратной матрицы
- Hallar Matriz Inversa 2×2 Con Excel
Fórmul
или размером nxn методом вложений можно воспользоваться формулой, возглавляющей этот теоретический пункт.Как упоминалось выше, для того, чтобы вычислить матрицу обратного 2×2 вам нужно знать:
- Расчетный определитель 2×2 де ла матриз
- Вычислите сопряженную матрицу, а затем нарисуйте ее транспонированную.
Por último, la matriz inversa 2×2 será el resultado de dividir cada elemento de la transpuesta de la matriz adjunta entre el valor del determinante.
Помните, что первое, что вы должны сделать, это вычислить определитель, потому что в случае, если он окажется равным нулю, матрица не будет иметь обратного , и задача будет решена.
Пример обратной матрицы
Давайте посмотрим как вычислить обратную матрицу примера a partir de la teoría que acabamos de contarte. En este caso, la matriz es de orden 3 pero si lo que quieres es hallar la inversa de una matriz 2×2, el procedimiento es calculatemente el mismo o incluso más fácil, ya que es más pequeña y tiene menos elementos.
1 — Определяющие вычисления
Чтобы узнать, есть ли обратная матрица или нет, первое, что нужно сделать, это решить его определитель . Если результат не равен нулю, как в этом случае, мы перейдем к следующему пункту, чтобы решить обратную матрицу.
Если вы не знаете, cómo se resuelve el determinante de una matriz 2×2Мы рекомендуем вам нажать на ссылку, которую мы оставили для вас и в которой мы подробно объясним, как это делается.
2 — Sacar matriz adjunta
Следующий шаг для вычисления обратной матрицы примера состоит из рисования прикрепленной матрицы.
Здесь нам нужно выбрать один за другим все элементы матрицы таким образом, чтобы мы сократили ее столбец и строку, чтобы сформировать определитель, который нужно решить и поместить на его место.
Кроме того, должно соблюдаться правило знаков , которое вы представили на следующем рисунке и которое диктует места, где мы должны будем разместить знак плюс или минус в соответствии с положением каждого элемента матрицы.
Применяя все вышесказанное к нашему примеру, у нас остаются следующие вычислений для каждого из элементов смежной матрицы :
Наконец, мы группируем все результаты, и у нас остается следующее прикрепленная матрица, которую мы будем использовать для следующего шага:
3 — Transpuesta de la matriz adjunta
После того, как прикрепленная матрица будет рассчитана на предыдущем шаге, ее транспонирование займет всего несколько секунд. Для этого нам нужно поменять местами строки на столбцы , как показано ниже:
4 — Aplicar la fórmula para Hallar la Matriz inversa
Теперь мы вернемся назад и скопируем формулу, которую мы видели в первом разделе этого статья для рисуем обратную матрицу .
Подставляем, решаем операции и у нас будет примерно так:
В случае, если вам нужно вычислить матрицу в обратном порядке 2×2, процедура точно соответствует , чем в этом примере, но намного проще, поскольку у нас меньше элементов и, следовательно, меньше операций для выполнения.
Обратная матрица 2×2 с Excel
Excel позволяет вычислять обратную матрицу 2×2 Системой очень легко пользоваться, так как она включает в себя специальную функцию для этой цели.
Просто следуйте инструкциям ниже, и вы сможете вычислить любую обратную матрицу nxn с помощью Excel :
- Вписать матрицу 2×2 в один из вычислений Excel вместо
- Busca un rango de celdas 2×2 vacío, selecciónalo y enscribe la siguiente formula, además, recuerda que entre los paréntesis irá el rango de celdas en el que has escrito la matriz para la cual quieres hallar su inversa.
=MINVERSE()
- Нажмите клавиши CTRL + Shift на клавиатуре и, не отпуская их, нажмите ENTER, чтобы подтвердить свой выбор. Формула Excel для расчета обратной матрицы .
Формула Excel для расчета обратной матрицы .Если процесс был выполнен правильно, вы сразу увидите результат.
Nacho
Ingeniero de Telecomunicaciones dedicado al mundo de Internet. En Esta веб-те Ayudo hacer cálculos у преобразования sencillas дие кон-эль-Пасо-де-лос-Años се-нос-ха olvidado Cómo себе Hace. Si tienes dudas, déjame un commentario y te ayudaré. Si quieres mejorar tu proyecto online o necesitas asesoramiento, напишите мне сообщение.
- Определитель матрицы 2×2 онлайн
- Определитель матрицы 3×3 онлайн
- Определитель матрицы 4×4 онлайн
- Обратная матрица 2×2 онлайн
- Обратная матрица 3×3 онлайн
- Обратная матрица 4× 4 онлайн
- Транспонированная матрица
- Умножение матрицы 2×2
- Вычисление умножения матрицы 3×3
Калькулятор лимитов — Примеры, Калькулятор лимитов онлайн
Калькулятор лимитов вычисляет лимит данной функции в определенной точке.
Предел определяется как значение, которого достигает функция, когда входные данные приближаются к указанному числу. Пределы используются для анализа поведения данной функции.
Что такое калькулятор лимитов?
Калькулятор пределов — это онлайн-инструмент, который помогает рассчитать значение функции по мере приближения входных данных к заданной точке. Когда мы хотим сделать приближение при выполнении вычислений, мы используем ограничения. Они помогают определить значение величины как можно ближе к ее фактическому значению. Чтобы использовать этот калькулятор пределов , введите значения в данные поля ввода.
Калькулятор лимитов
Как пользоваться калькулятором лимитов?
Чтобы найти предел функции с помощью онлайн-калькулятора лимитов, выполните следующие шаги:
- Шаг 1: Перейдите к онлайн-калькулятору лимитов Cuemath.
- Шаг 2: Введите функцию и предельное значение в соответствующие поля ввода калькулятора пределов.
- Шаг 3: Нажмите кнопку «Рассчитать» , чтобы найти предел функции.
- Шаг 4: Нажмите на «Сброс» кнопка для очистки полей и ввода новых значений.
Как работает калькулятор лимитов?
Допустим, у нас есть функция y = f(x). Предположим, что f(x) принимает неопределенный вид при x = a. Мы рассматриваем значения функции, близкие к а. Если эти значения стремятся к некоторому уникальному числу, когда x приближается к a, то мы можем сказать, что это уникальное число является пределом функции f(x) при x = a. Формула пределов может быть представлена следующим образом:
\(\lim_{x\rightarrow a}f(x) = A\)
Существует множество различных методов оценки пределов. Некоторые из них приведены ниже.
- Прямая подстановка — Мы можем получить предел непрерывной функции прямой подстановкой. Этим методом можно определить большинство пределов полиномиальной функции.
