Период пружинного маятника формула: Формула периода колебаний пружинного маятника в физике

Формула периода колебаний пружинного маятника в физике

Формула периода колебаний пружинного маятника в физике

Определение

Период — это минимальное время, за которое совершается одно полное колебательное движение.

Обозначают период буквой $T$.

\[T=\frac{\Delta t}{N}\left(1\right),\]

где $\Delta t$ — время колебаний; $N$ — число полных колебаний.

Уравнение колебаний пружинного маятника

Рассмотрим простейшую колебательную систему, в которой можно реализовать механические колебания. Это груз массы $m$, подвешенный на пружине, коэффициент упругости которой равен $k\ $(рис.1). Рассмотри вертикальное движение груза, которое обусловлено действием силы тяжести и силы упругости пружины. В состоянии равновесия такой системы, сила упругости равна по величине силе тяжести. Колебания пружинного маятника возникают, когда систему выводят из состояния равновесия, например, слегка дополнительно растянув пружину, после этого маятник предоставляют самому себе.

2_0=\frac{k}{m}$ — циклическая частота колебаний пружинного маятника. Решением уравнения (7) (это проверяется непосредственной подстановкой) является функция:

\[x=A{\cos \left({\omega }_0t+\varphi \right)=A{\sin \left({\omega }_0t+{\varphi }_1\right)\ }\ }\left(8\right),\]

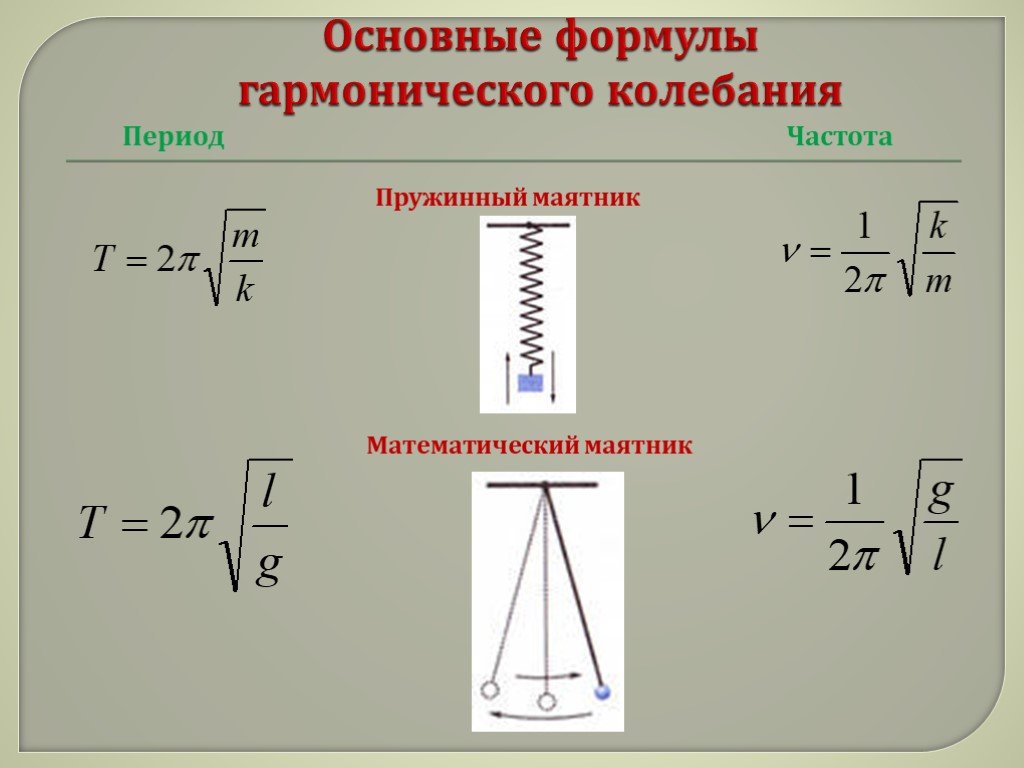
где ${\omega }_0=\sqrt{\frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ — амплитуда колебаний; ${(\omega }_0t+\varphi )$ — фаза колебаний; $\varphi $ и ${\varphi }_1$ — начальные фазы колебаний.

Формулы периода колебаний пружинного маятника

Мы получили, что колебания пружинного маятника описывается функцией косинус или синус. Это периодические функции, значит, смещение $x$ будет принимать равные значения через определенные одинаковые промежутки времени, которые называют периодом колебаний. Обозначают период буквой T.

Еще одной величиной, характеризующей колебания является величина обратная периоду колебаний, ее называют частотой ($\nu $):

\[T=\frac{1}{\nu }\left(9\right). \]

Период связан с циклической частотой колебаний как:

\[T=\frac{2\pi }{{\omega }_0}\left(10\right).\]

Выше мы получали для пружинного маятника ${\omega }_0=\sqrt{\frac{k}{m}}$, следовательно, период колебаний пружинного маятника равен:

\[T=2\pi \sqrt{\frac{m}{k}}\ \left(11\right).\]

Формула периода колебаний пружинного маятника (11) показывает, что $T$ зависит от массы груза, прикрепленного к пружине и коэффициента упругости пружины, но не зависит от амплитуды колебаний (A). Данное свойство колебаний называют изохронностью. Изохронность выполняется до тех пор, пока справедлив закон Гука. При больших растяжениях пружины закон Гука нарушается, появляется зависимость колебаний от амплитуды. Подчеркнем, что формула (11) для вычисления периода колебаний пружинного маятника справедлива при малых колебаниях.

Примеры задач на период колебаний

Пример 1

Задание.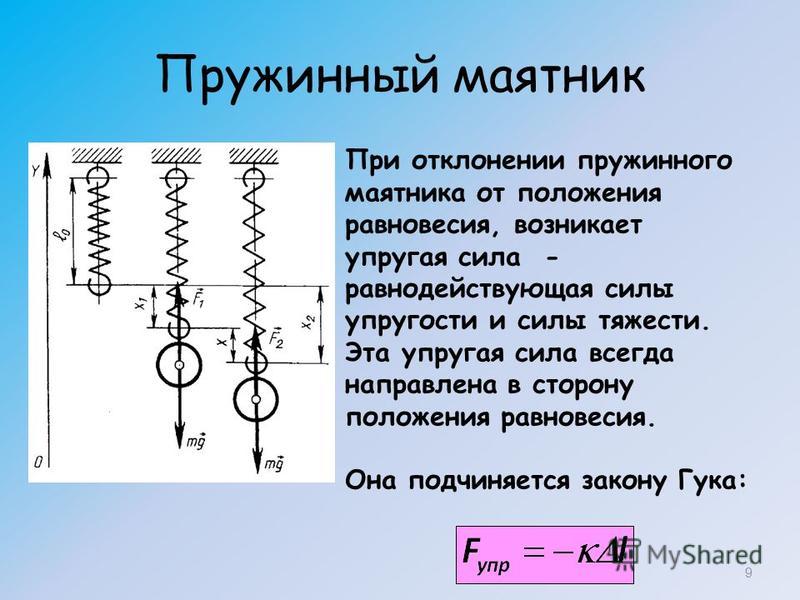 Пружинный маятник совершил 50 полных колебаний за время равное 10 с . Каков период колебаний маятника? Чему равна частота этих колебаний?

Решение. Так как период — это минимальное время необходимое маятнику для совершения одного полного колебания, то найдем его как:

\[T=\frac{\Delta t}{N}\left(1.1\right).\]

Вычислим период:

\[T=\frac{10}{50}=0,2\ \left(с\right).\]

Частота — величина обратная периоду, следовательно:

\[\nu =\frac{1}{T}\left(1.2\right).\]

Вычислим частоту колебаний:

\[\nu =\frac{1}{0,2}=5\ \left(Гц\right).\]

Ответ. $1)\ T=0,2$ с; 2) 5Гц

Пример 2

Задание.Две пружины, имеющие коэффициенты упругости $k_1$ и $k_2$ соединены параллельно (рис.2), к системе присоединен груз массы $M$. Каков период колебаний полученного пружинного маятника, если массами пружин можно пренебречь, сила упругости, действующая на груз, подчиняется закону Гука?

Решение. Воспользуемся формулой для вычисления периода колебаний пружинного маятника:

\[T=2\pi \sqrt{\frac{M}{k}}\ \left(2.1\right).\]

При параллельном соединении пружин результирующая жесткость системы находится как:

\[k=k_1{+k}_2\left(2.2\right).\]

Это означают, что вместо $k$ в формулу для вычисления периода пружинного маятника подставим правую часть выражения (2.2), имеем:

\[T=2\pi \sqrt{\frac{M}{k_1{+k}_2}}.\]

Ответ. $T=2\pi \sqrt{\frac{M}{k_1{+k}_2}}$

Читать дальше: формула плеча силы.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Период колебания пружинного маятника, теория и онлайн калькуляторы

Период колебания пружинного маятника, теория и онлайн калькуляторы

Рассмотрим простейшую систему, в которой возможна реализация механических колебаний.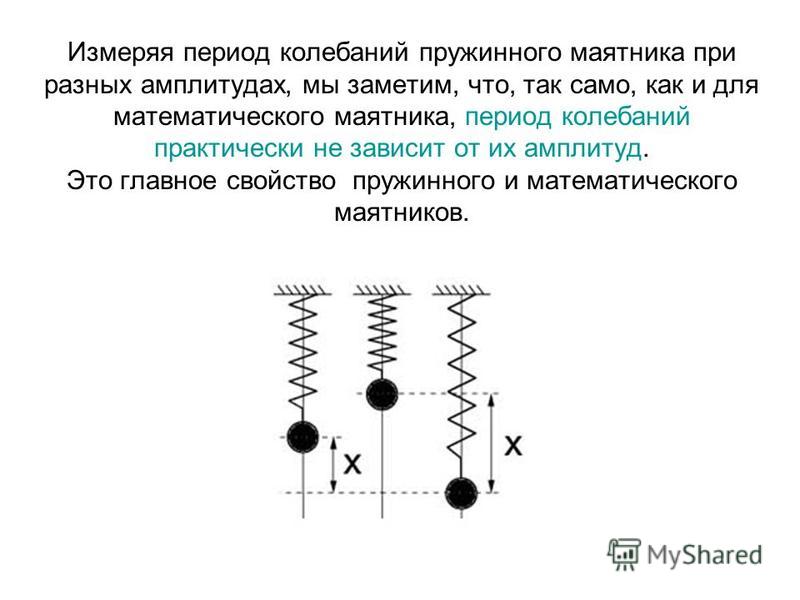 2_0=\frac{k}{m}$ — циклическая частота колебаний пружинного маятника. Решением уравнения (1) является функция:

\[x=A{\cos \left({\omega }_0t+\varphi \right)=B{\sin \left({\omega }_0t+{\varphi }_1\right)\ }\ }\left(2\right),\]

где ${\omega }_0=\sqrt{\frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ и $B$ — амплитуда колебаний; ${(\omega }_0t+\varphi )$ — фаза колебаний; $\varphi $ и ${\varphi }_1$ — начальные фазы колебаний.

Частота и период колебаний пружинного маятника

Косинус (синус) — периодическая функция, смещение $x$ будет принимать одинаковые значения через определенные одинаковые промежутки времени, которые называют периодом колебаний. Обозначают период буквой T.

Еще одной величиной, характеризующей колебания является величина обратная периоду колебаний, ее называют частотой ($\nu $):

\[T=\frac{1}{\nu }\left(3\right).\]

Период связан с циклической частотой колебаний как:

\[T=\frac{2\pi }{{\omega }_0}\left(4\right). \]

Зная, что для пружинного маятника ${\omega }_0=\sqrt{\frac{k}{m}}$, период колебаний его определим как:

\[T=2\pi \sqrt{\frac{m}{k}}\ \left(5\right).\]

Из выражения (5) мы видим, что период колебаний пружинного маятника зависит от массы груза, находящегося на пружине и коэффициента упругости пружины, но не зависит от амплитуды колебаний (A). Такое свойство колебаний называют изохронностью. Изохронность выполняется до тех пор, пока справедлив закон Гука. При больших растяжениях пружины закон Гука нарушается, при этом возникает зависимость колебаний от амплитуды. Отметим, что формула (5) для вычисления периода колебаний пружинного маятника справедлива при малых колебаниях.

Единицей измерения периода являются единицы времени, в Международной системе единиц это секунды:

\[\left[T\right]=с.\]

Примеры задач на период колебания пружинного маятника

Пример 1

Задание. К упругой пружине прикрепили небольшой груз, при этом пружина растянулась на $\Delta x$=0,09 м. Каким будет период колебаний данного пружинного маятника, если его вывести из равновесия?

Решение. Сделаем рисунок.

Рассмотрим состояние равновесия пружинного маятника. Груз прикрепили, после этого пружина растянулась на величину $\Delta x$, маятник находится в состоянии равновесия. На груз действуют две силы: сила тяжести и сила упругости. Запишем второй закон Ньютона для состояния равновесия груза:

\[m\overline{g}+{\overline{F}}_u=0\ \left(1.1\right).\]

Запишем проекцию уравнения (1.1) на ось Y:

\[mg=F_u\left(1.2\right).\]

Так как груз по условию задачи небольшой, пружина растянулась не сильно, следовательно выполняется закон Гука, величину силы упругости найдем как:

\[F_u=k\Delta x\ \left(1.3\right).\]

Используя выражения (1. 2}$:

\[T=2\pi \sqrt{\frac{0,09\ \ }{9,8}\ \approx 0,6\ (с)}\]

Ответ. $T$=0,6 с

   

Пример 2

Задание. Две пружины с жесткостями $k_1$ и $k_2$ соединены последовательно (рис.2), к концу второй пружины присоединен груз массы $m$, Каков период колебаний данного пружинного маятника, если массами пружин можно пренебречь, сила упругости, действующая на груз, подчиняется закону Гука.

Решение.Период колебаний пружинного маятника равен:

\[T=2\pi \sqrt{\frac{m}{k}}\ \left(2.1\right).\]

Если две пружины соединены последовательно, то их результирующая жесткость ($k$) находится как:

\[\frac{1}{k}=\frac{1}{k_1}+\frac{1}{k_2}\to k=\frac{k_1k_2}{k_1{+k}_2}\left(2.2\right).\]

Вместо $k$ в формулу для вычисления периода пружинного маятника подставим правую часть выражения (2.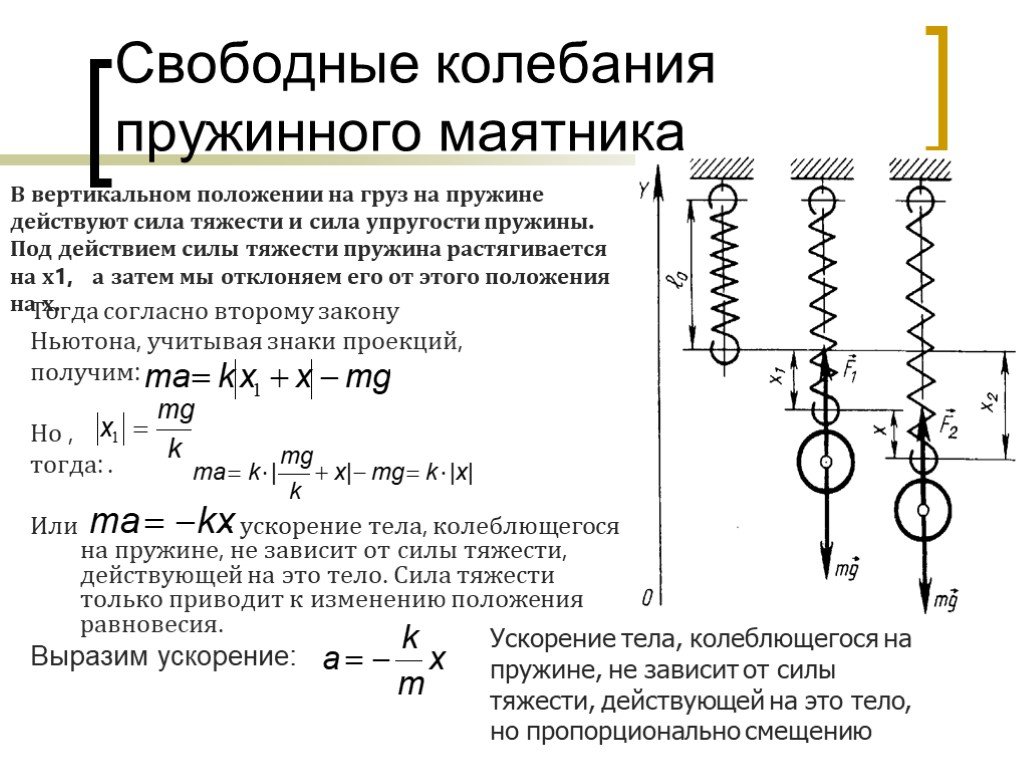

2), имеем:

\[T=2\pi \sqrt{\frac{m(k_1{+k}_2)}{k_1k_2}}.\]

Ответ. $T=2\pi \sqrt{\frac{m(k_1{+k}_2)}{k_1k_2}}$

   

Читать дальше: плечо силы.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Физика — простое гармоническое движение

Колебания происходят повсюду вокруг нас, от биения человеческого сердца до вибрирующих атомов, из которых состоит все. Простое гармоническое движение является очень важным типом периодических колебаний, где ускорение ( α ) пропорционально смещению ( x ) от положения равновесия в направлении положения равновесия.

Перейти к:

Введение

Видео

В фокусе

Подкаст

Заключение

Следующие шаги

Что такое частота и период?

Поскольку простое гармоническое движение представляет собой периодическое колебание, мы можем измерить его период (время, необходимое для одного колебания) и, следовательно, определить его частоту (количество колебаний в единицу времени или обратную величину периода).

Два наиболее распространенных эксперимента, демонстрирующих это:

1. Маятник. Масса m , прикрепленная к концу маятника длиной l , будет колебаться с периодом ( T ). Описывается формулой: T = 2π√(l/g) , где g — ускорение свободного падения.

2. Масса на пружине. Если масса m , прикрепленная к пружине с жесткостью пружины k , будет колебаться с периодом ( T ). Описывается: T = 2π√(m/k) .

Измерив продолжительность одного полного колебания, мы можем определить период и, следовательно, частоту. Обратите внимание, что в случае маятника период не зависит от массы, а в случае массы на пружине период не зависит от длины пружины. Период простого гармонического осциллятора также не зависит от его амплитуды.

По определению, ускорение a объекта в простом гармоническом движении пропорционально его смещению, х :

, где ω — угловая частота, которую можно определить, зная период ( ω = 2π/T ) или частоту ( ω = 2πf ). Вспоминая, что скорость ( v ) является производной расстояния по времени, а ускорение является производной скорости по времени, можно показать, что, начиная с амплитуды ( A ), решение следует синусоидальной функции формы x = А cos(ωt)

Смещение во времени будет выглядеть примерно так: 

С графиками скорости и ускорения, заданными производными по времени. Эти осцилляторы также демонстрируют передачу кинетической и потенциальной энергии. При максимальном смещении вся энергия в системе находится в форме потенциальной энергии, а скорость равна нулю, но вся эта энергия преобразуется в кинетическую энергию, как только масса достигает положения равновесия, при котором она имеет максимальную скорость.

 Как мы измеряем колебания?

 

Простые гармонические колебания

 Насколько точны наши измерения?

Описанные здесь эксперименты демонстрируют использование комбинации аналоговых и цифровых приборов для измерения величин, включая массу, длину и время. В этом эксперименте одним из основных источников ошибки является время реакции человека при измерении периода. Чтобы повысить точность периода, синхронизация может быть получена по нескольким колебаниям и путем усреднения по нескольким измерениям периода. Чтобы получить более точные измерения жесткости пружины и ускорения свободного падения, следует проводить повторные измерения с использованием маятника различной длины и массы.

Кроме того, измерение периода на более длительном временном интервале (и, следовательно, на нескольких колебаниях) повысит точность, поскольку человеческая ошибка будет составлять меньшую часть записанного времени. Также может быть полезно использовать булавку или бирку в качестве фидуциарного маркера, показывающего положение равновесия. Предполагая простое гармоническое движение, периодическая природа этих систем означает, что не должно быть никаких оправданий, когда дело доходит до проведения нескольких измерений!

Labor Confessions

В подкасте Labor Confessions исследователи рассказывают о своем лабораторном опыте в контексте практических оценок уровня A.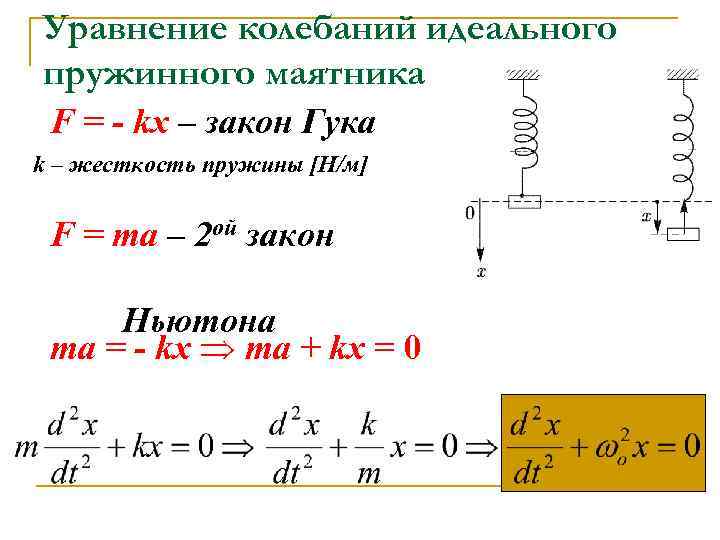 В этом выпуске мы рассмотрим генерацию и измерение волн и использование соответствующих цифровых инструментов.

Что означают ваши измерения?

Вибрации и колебания, окружающие нас в повседневной жизни, как правило, намного сложнее, чем те, с которыми мы сталкиваемся в простом гармоническом движении. Это означает, что такие эффекты, как демпфирование, уменьшающее амплитуду за счет удаления энергии из системы, являются хорошим примером того, как простое гармоническое движение способствует улучшению нашей повседневной жизни. Хотя простое гармоническое движение является упрощением, оно все же является очень хорошим приближением.

Простое гармоническое движение играет важную роль в исследованиях по моделированию колебаний, например, в ветряных турбинах и вибраций в автомобильных подвесках. В Университете Бирмингема один из исследовательских проектов, в котором мы участвовали, — обнаружение гравитационных волн в обсерватории лазерных интерферометров гравитационных волн (LIGO). Там детекторы настолько чувствительны, что решающее значение имеет тщательное моделирование и минимизация окружающих вибраций и шума. Еще одним заметным исследовательским проектом является работа Бирмингемской сети солнечных колебаний (BiSON), которая занимается измерением колебаний Солнца (гелиосейсмология) и близлежащих звезд (астросейсмология), чтобы узнать об их внутреннем строении.

Следующие шаги

 

Эти ссылки предоставляются для удобства и только в информационных целях; они не являются подтверждением или одобрением Бирмингемским университетом какой-либо информации, содержащейся на внешнем веб-сайте. Университет Бирмингема не несет ответственности за точность, законность или содержание внешнего сайта или последующих ссылок. Пожалуйста, свяжитесь с внешним сайтом для получения ответов на вопросы, касающиеся его содержания.

ньютоновская механика — Пружинный маятник — почему можно использовать это уравнение?

спросил 6 лет, 6 месяцев назад

Изменено 6 лет, 6 месяцев назад

Просмотрено 2к раз

$\begingroup$

Известно, что при описании пружинного маятника мы обязаны пользоваться формулой $T = 2\pi \sqrt{m/k}$, однако можно пойти дальше и положить
$\omega = \frac{2\pi}{T}$
Я размышляю, почему эта замена законна, ведь в этом маятнике нет углового движения!

• ньютоновская механика
• гармонический осциллятор
• частота
• пружина

$\endgroup$

2

$\begingroup$

В этом уравнении $\omega$ относится не к скорости углового движения, а к частоте колебаний, измеренной в угловых единицах (обычно в радианах/сек, но может быть и в градусах/сек). Частота обычно измеряется в циклах в секунду (Герцах), но иногда ее удобнее измерять в угловых единицах, когда ее называют угловой частотой.

Угол, который здесь измеряется, является фазовым углом, который описывает, как далеко за цикл прошло колебание, как если бы колебание двигалось по кругу с постоянной угловой скоростью $\omega$.

Вы можете быть сбиты с толку, потому что не видите никакого углового движения в «пружинном» маятнике. Но это еще более запутанно, когда имеешь дело со «струнным» маятником, потому что здесь смещение измеряется углом $\theta$, но этот угол не совпадает с фазовым углом (который обычно называют $\phi$, т.е. греческое фи для фазы). Угловая скорость равна $\large{\frac{d\theta}{dt}}$, что обычно называют $\omega$, но это $\omega=\large{\frac{d\theta}{dt}} $ не совпадает с угловой частотой $\omega=\large{\frac{d\phi}{dt}=\frac{2\pi}{T}}$. Угловая скорость во время колебаний изменяется от $0$ в крайних точках до максимальной при прохождении через вертикаль. Но угловая частота при колебании не меняется, она является постоянной величиной для идеальных струнных или пружинных маятников, зависящей от $\large{\frac Lg}$ или $\large{\frac km}$.

$\endgroup$

$\begingroup$

Представьте себе точку $P$, движущуюся по окружности радиуса $R$ с угловой скоростью $\omega$.

Проекция $P$ на ось $y$:

$$y=R\sin \theta=R\sin \omega t$$

Точка $P’$ находится в простых гармонических колебаниях (ШО).

Для системы пружинных масс так получилось, что:

$$x=A\sin \omega t$$ куда: $$\omega=\sqrt{\frac{k}{m}}$$

Итак, хотя в пружинной массе SHO нет углового движения, по аналогии с SHO точки $P’$ мы все же называем ее угловой скоростью.

$\endgroup$

$\begingroup$

Уравнение для периода $T$ получено путем использования второго закона Ньютона $F=ma$ для получения уравнения движения системы пружина-масса

$$-kx =ma \Rightarrow a=-\frac k m$ $

где $x$ — смещение от фиксированной точки, а $a$ — ускорение.