Mathway | Популярные задачи
Mathway | Популярные задачиПопулярные задачи
Элементарная математика Основы алгебры Алгебра Тригонометрия Основы мат. анализа Математический анализ Конечная математика Линейная алгебра ХимияЭтот веб-сайт использует cookie файлы, чтобы сделать использование нашего ресурса максимально удобным для вас.
Убедитесь, что ваш пароль содержит не менее 8 символов и как минимум один из следующих символов:- число
- буква
- специальный символ: @$#!%*?&
| 1 | Trovare la Derivata — d/dx | квадратный корень x | |
| 2 | Trovare la Derivata — d/dx | натуральный логарифм x | |
| 3 | Вычислим интеграл | интеграл натурального логарифма x по x | |
| 4 | Trovare la Derivata — d/dx | e^x | |
| 5 | Вычислим интеграл | интеграл e^(2x) относительно x | |
| 6 | Trovare la Derivata — d/dx | 1/x | |
| 7 | Trovare la Derivata — d/dx | x^2 | |
| 8 | Вычислим интеграл | интеграл e^(-x) относительно x | |
| 9 | Trovare la Derivata — d/dx | 1/(x^2) | |
| 10 | Trovare la Derivata — d/dx | sin(x)^2 | |
| 11 | Trovare la Derivata — d/dx | sec(x) | |
| 12 | Вычислим интеграл | интеграл e^x относительно x | |
| 13 | Вычислим интеграл | интеграл x^2 относительно x | |
| 14 | Вычислим интеграл | интеграл квадратного корня x по x | |
| 15 | Вычислить | натуральный логарифм 1 | |
| 16 | Вычислить | e^0 | |
| 17 | Вычислить | sin(0) | |
| 18 | Trovare la Derivata — d/dx | cos(x)^2 | |
| 19 | Вычислим интеграл | интеграл 1/x относительно x | |
| 20 | Вычислить | cos(0) | |
| 21 | Вычислим интеграл | интеграл sin(x)^2 относительно x | |
| 22 | Trovare la Derivata — d/dx | x^3 | |
| 23 | Trovare la Derivata — d/dx | sec(x)^2 | |
| 24 | Trovare la Derivata — d/dx | 1/(x^2) | |
| 25 | Вычислим интеграл | интеграл arcsin(x) относительно x | |
| 26 | Вычислим интеграл | интеграл cos(x)^2 относительно x | |
| 27 | Вычислим интеграл | интеграл sec(x)^2 относительно x | |
| 28 | Trovare la Derivata — d/dx | e^(x^2) | |
| 29 | Вычислим интеграл | интеграл в пределах от 0 до 1 кубического корня 1+7x по x | |
| 30 | Trovare la Derivata — d/dx | sin(2x) | |
| 31 | Вычислим интеграл | интеграл натурального логарифма x по x | |
| 32 | Trovare la Derivata — d/dx | tan(x)^2 | |
| 33 | Вычислим интеграл | интеграл e^(2x) относительно x | |
| 34 | Вычислим интеграл | интеграл 1/(x^2) относительно x | |
| 35 | Trovare la Derivata — d/dx | 2^x | |
| 36 | График | натуральный логарифм a | |
| 37 | Вычислить | e^1 | |
| 38 | Вычислим интеграл | интеграл 1/(x^2) относительно x | |
| 39 | Вычислить | натуральный логарифм 0 | |
| 40 | Trovare la Derivata — d/dx | cos(2x) | |
| 41 | Trovare la Derivata — d/dx | xe^x | |
| 42 | Вычислим интеграл | интеграл 1/x относительно x | |
| 43 | Вычислим интеграл | интеграл 2x относительно x | |
| 44 | Trovare la Derivata — d/dx | ( натуральный логарифм x)^2 | |
| 45 | Trovare la Derivata — d/dx | натуральный логарифм (x)^2 | |
| 46 | Trovare la Derivata — d/dx | 3x^2 | |
| 47 | Вычислить | натуральный логарифм 2 | |
| 48 | Вычислим интеграл | интеграл xe^(2x) относительно x | |
| 49 | Trovare la Derivata — d/dx | 2e^x | |
| 50 | Trovare la Derivata — d/dx | натуральный логарифм 2x | |
| 51 | Trovare la Derivata — d/dx | -sin(x) | |
| 52 | Вычислить | tan(0) | |
| 53 | Trovare la Derivata — d/dx | 4x^2-x+5 | |
| 54 | Trovare la Derivata — d/dx | y=16 корень четвертой степени 4x^4+4 | |
| 55 | Trovare la Derivata — d/dx | 2x^2 | |
| 56 | Вычислим интеграл | интеграл e^(3x) относительно x | |
| 57 | Вычислим интеграл | интеграл cos(2x) относительно x | |
| 58 | Вычислим интеграл | интеграл cos(x)^2 относительно x | |
| 59 | Trovare la Derivata — d/dx | 1/( квадратный корень x) | |
| 60 | Вычислим интеграл | интеграл e^(x^2) относительно x | |
| 61 | Вычислить | sec(0) | |
| 62 | Вычислить | e^infinity | |
| 63 | Вычислить | 2^4 | |
| 64 | Trovare la Derivata — d/dx | x/2 | |
| 65 | Вычислить | 4^3 | |
| 66 | Trovare la Derivata — d/dx | -cos(x) | |
| 67 | Trovare la Derivata — d/dx | sin(3x) | |
| 68 | Вычислить | натуральный логарифм 1/e | |
| 69 | Вычислим интеграл | интеграл x^2 относительно x | |
| 70 | Упростить | 1/( кубический корень от x^4) | |
| 71 | Trovare la Derivata — d/dx | 1/(x^3) | |
| 72 | Вычислим интеграл | интеграл e^x относительно x | |
| 73 | Вычислим интеграл | интеграл tan(x)^2 относительно x | |
| 74 | Вычислим интеграл | интеграл 1 относительно x | |
| 75 | Trovare la Derivata — d/dx | x^x | |
| 76 | Trovare la Derivata — d/dx | x натуральный логарифм x | |
| 77 | Вычислим интеграл | интеграл sin(x)^2 относительно x | |
| 78 | Trovare la Derivata — d/dx | x^4 | |
| 79 | Оценить предел | предел (3x-5)/(x-3), если x стремится к 3 | |
| 80 | Вычислим интеграл | интеграл от x^2 натуральный логарифм x по x | |
| 81 | Trovare la Derivata — d/dx | f(x) = square root of x | |
| 82 | Trovare la Derivata — d/dx | x^2sin(x) | |
| 83 | Вычислим интеграл | интеграл sin(2x) относительно x | |
| 84 | Trovare la Derivata — d/dx | 3e^x | |
| 85 | Вычислим интеграл | интеграл xe^x относительно x | |
| 86 | Trovare la Derivata — d/dx | y=x^2 | |
| 87 | Trovare la Derivata — d/dx | квадратный корень x^2+1 | |
| 88 | Trovare la Derivata — d/dx | sin(x^2) | |
| 89 | Вычислим интеграл | интеграл e^(-2x) относительно x | |
| 90 | Вычислим интеграл | интеграл натурального логарифма квадратного корня x по x | |
| 91 | Вычислить | 2^5 | |
| 92 | Trovare la Derivata — d/dx | e^2 | |
| 93 | Trovare la Derivata — d/dx | x^2+1 | |
| 94 | Вычислим интеграл | интеграл sin(x) относительно x | |
| 95 | Вычислить | 2^3 | |
| 96 | Trovare la Derivata — d/dx | arcsin(x) | |
| 97 | Оценить предел | предел (sin(x))/x, если x стремится к 0 | |
| 98 | Вычислить | e^2 | |
| 99 | Вычислим интеграл | интеграл e^(-x) относительно x | |
| 100 | Вычислим интеграл | интеграл 1/x относительно x |
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(60) | |
| 4 | Найти точное значение | sin(30 град. ) | |
| 5 | Найти точное значение | sin(60 град. ) | |
| 6 | Найти точное значение | tan(30 град. ) | |
| 7 | Найти точное значение | arcsin(-1) | |
| 8 | Найти точное значение | sin(pi/6) | |
| 9 | Найти точное значение | cos(pi/4) | |
| 10 | Найти точное значение | sin(45 град. ) | |
| 11 | Найти точное значение | sin(pi/3) | |
| 12 | Найти точное значение | arctan(-1) | |
| 13 | Найти точное значение | cos(45 град. ) | |
| 14 | Найти точное значение | cos(30 град. ) | |
| 15 | Найти точное значение | tan(60) | |
| 16 | Найти точное значение | csc(45 град. ) | |
| 17 | Найти точное значение | tan(60 град. ) | |
| 18 | Найти точное значение | sec(30 град. ) | |
| 19 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 20 | График | y=sin(x) | |
| 21 | Преобразовать из радианов в градусы | pi/6 | |
| 22 | Найти точное значение | cos(60 град. ) | |
| 23 | Найти точное значение | cos(150) | |
| 24 | Найти точное значение | tan(45) | |
| 25 | Найти точное значение | sin(30) | |
| 26 | Найти точное значение | sin(60) | |
| 27 | Найти точное значение | cos(pi/2) | |
| 28 | Найти точное значение | tan(45 град. ) | |
| 29 | График | y=sin(x) | |
| 30 | Найти точное значение | arctan(- квадратный корень 3) | |
| 31 | Найти точное значение | csc(60 град. ) | |
| 32 | Найти точное значение | sec(45 град. ) | |
| 33 | Найти точное значение | csc(30 град. ) | |
| 34 | Найти точное значение | sin(0) | |
| 35 | Найти точное значение | sin(120) | |
| 36 | Найти точное значение | cos(90) | |
| 37 | Преобразовать из радианов в градусы | pi/3 | |
| 38 | Найти точное значение | sin(45) | |
| 39 | Найти точное значение | tan(30) | |
| 40 | Преобразовать из градусов в радианы | 45 | |
| 41 | Найти точное значение | tan(60) | |
| 42 | Упростить | квадратный корень x^2 | |
| 43 | Найти точное значение | cos(45) | |
| 44 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 45 | Преобразовать из радианов в градусы | pi/6 | |
| 46 | Найти точное значение | cot(30 град. ) | |
| 47 | Найти точное значение | arccos(-1) | |
| 48 | Найти точное значение | arctan(0) | |
| 49 | График | y=cos(x) | |
| 50 | Найти точное значение | cot(60 град. ) | |
| 51 | Преобразовать из градусов в радианы | 30 | |
| 52 | Упростить | ( квадратный корень x+ квадратный корень 2)^2 | |
| 53 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 54 | Найти точное значение | sin((5pi)/3) | |
| 55 | Упростить | 1/( кубический корень от x^4) | |
| 56 | Найти точное значение | sin((3pi)/4) | |
| 57 | Найти точное значение | tan(pi/2) | |
| 58 | Найти угол А | tri{}{90}{}{}{}{} | |
| 59 | Найти точное значение | sin(300) | |
| 60 | Найти точное значение | cos(30) | |
| 61 | Найти точное значение | cos(60) | |
| 62 | Найти точное значение | cos(0) | |
| 63 | Найти точное значение | arctan( квадратный корень 3) | |
| 64 | Найти точное значение | cos(135) | |
| 65 | Найти точное значение | cos((5pi)/3) | |
| 66 | Найти точное значение | cos(210) | |
| 67 | Найти точное значение | sec(60 град. ) | |
| 68 | Найти точное значение | sin(300 град. ) | |
| 69 | Преобразовать из градусов в радианы | 135 | |
| 70 | Преобразовать из градусов в радианы | 150 | |
| 71 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 72 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 73 | Преобразовать из градусов в радианы | 89 град. | |
| 74 | Преобразовать из градусов в радианы | 60 | |
| 75 | Найти точное значение | sin(135 град. ) | |
| 76 | Найти точное значение | sin(150) | |
| 77 | Найти точное значение | sin(240 град. ) | |
| 78 | Найти точное значение | cot(45 град. ) | |
| 79 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 80 | Упростить | 1/( кубический корень от x^8) | |
| 81 | Найти точное значение | sin(225) | |
| 82 | Найти точное значение | sin(240) | |
| 83 | Найти точное значение | cos(150 град. ) | |
| 84 | Найти точное значение | tan(45) | |
| 85 | Вычислить | sin(30 град. ) | |
| 86 | Найти точное значение | sec(0) | |
| 87 | Упростить | arcsin(-( квадратный корень 2)/2) | |
| 88 | Найти точное значение | cos((5pi)/6) | |
| 89 | Найти точное значение | csc(30) | |
| 90 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 91 | Найти точное значение | tan((5pi)/3) | |
| 92 | Найти точное значение | tan(0) | |
| 93 | Вычислить | sin(60 град. ) | |
| 94 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 95 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 96 | Вычислить | arcsin(-1) | |
| 97 | Найти точное значение | sin((7pi)/4) | |
| 98 | Найти точное значение | arcsin(-1/2) | |
| 99 | Найти точное значение | sin((4pi)/3) | |
| 100 | Найти точное значение | csc(45) |
| 1 | Trovare la Derivata — d/dx | квадратный корень x | |
| 2 | Trovare la Derivata — d/dx | натуральный логарифм x | |
| 3 | Вычислим интеграл | интеграл натурального логарифма x по x | |
| 4 | Trovare la Derivata — d/dx | e^x | |
| 5 | Вычислим интеграл | интеграл e^(2x) относительно x | |
| 6 | Trovare la Derivata — d/dx | 1/x | |
| 7 | Trovare la Derivata — d/dx | x^2 | |
| 8 | Вычислим интеграл | интеграл e^(-x) относительно x | |
| 9 | Trovare la Derivata — d/dx | 1/(x^2) | |
| 10 | Trovare la Derivata — d/dx | sin(x)^2 | |
| 11 | Trovare la Derivata — d/dx | sec(x) | |
| 12 | Вычислим интеграл | интеграл e^x относительно x | |
| 13 | Вычислим интеграл | интеграл x^2 относительно x | |
| 14 | Вычислим интеграл | интеграл квадратного корня x по x | |
| 15 | Вычислить | натуральный логарифм 1 | |
| 16 | Вычислить | e^0 | |
| 17 | Вычислить | sin(0) | |
| 18 | Trovare la Derivata — d/dx | cos(x)^2 | |
| 19 | Вычислим интеграл | интеграл 1/x относительно x | |
| 20 | Вычислить | cos(0) | |
| 21 | Вычислим интеграл | интеграл sin(x)^2 относительно x | |
| 22 | Trovare la Derivata — d/dx | x^3 | |
| 23 | Trovare la Derivata — d/dx | sec(x)^2 | |
| 24 | Trovare la Derivata — d/dx | 1/(x^2) | |
| 25 | Вычислим интеграл | интеграл arcsin(x) относительно x | |
| 26 | Вычислим интеграл | интеграл cos(x)^2 относительно x | |
| 27 | Вычислим интеграл | интеграл sec(x)^2 относительно x | |
| 28 | Trovare la Derivata — d/dx | e^(x^2) | |
| 29 | Вычислим интеграл | интеграл в пределах от 0 до 1 кубического корня 1+7x по x | |
| 30 | Trovare la Derivata — d/dx | sin(2x) | |
| 31 | Вычислим интеграл | интеграл натурального логарифма x по x | |
| 32 | Trovare la Derivata — d/dx | tan(x)^2 | |
| 33 | Вычислим интеграл | интеграл e^(2x) относительно x | |
| 34 | Вычислим интеграл | интеграл 1/(x^2) относительно x | |
| 35 | Trovare la Derivata — d/dx | 2^x | |
| 36 | График | натуральный логарифм a | |
| 37 | Вычислить | e^1 | |
| 38 | Вычислим интеграл | интеграл 1/(x^2) относительно x | |
| 39 | Вычислить | натуральный логарифм 0 | |
| 40 | Trovare la Derivata — d/dx | cos(2x) | |
| 41 | Trovare la Derivata — d/dx | xe^x | |
| 42 | Вычислим интеграл | интеграл 1/x относительно x | |
| 43 | Вычислим интеграл | интеграл 2x относительно x | |
| 44 | Trovare la Derivata — d/dx | ( натуральный логарифм x)^2 | |
| 45 | Trovare la Derivata — d/dx | натуральный логарифм (x)^2 | |
| 46 | Trovare la Derivata — d/dx | 3x^2 | |
| 47 | Вычислить | натуральный логарифм 2 | |
| 48 | Вычислим интеграл | интеграл xe^(2x) относительно x | |
| 49 | Trovare la Derivata — d/dx | 2e^x | |
| 50 | Trovare la Derivata — d/dx | натуральный логарифм 2x | |
| 51 | Trovare la Derivata — d/dx | -sin(x) | |
| 52 | Вычислить | tan(0) | |
| 53 | Trovare la Derivata — d/dx | 4x^2-x+5 | |
| 54 | Trovare la Derivata — d/dx | y=16 корень четвертой степени 4x^4+4 | |
| 55 | Trovare la Derivata — d/dx | 2x^2 | |
| 56 | Вычислим интеграл | интеграл e^(3x) относительно x | |
| 57 | Вычислим интеграл | интеграл cos(2x) относительно x | |
| 58 | Вычислим интеграл | интеграл cos(x)^2 относительно x | |
| 59 | Trovare la Derivata — d/dx | 1/( квадратный корень x) | |
| 60 | Вычислим интеграл | интеграл e^(x^2) относительно x | |
| 61 | Вычислить | sec(0) | |
| 62 | Вычислить | e^infinity | |
| 63 | Вычислить | 2^4 | |
| 64 | Trovare la Derivata — d/dx | x/2 | |
| 65 | Вычислить | 4^3 | |
| 66 | Trovare la Derivata — d/dx | -cos(x) | |
| 67 | Trovare la Derivata — d/dx | sin(3x) | |
| 68 | Вычислить | натуральный логарифм 1/e | |
| 69 | Вычислим интеграл | интеграл x^2 относительно x | |
| 70 | Упростить | 1/( кубический корень от x^4) | |
| 71 | Trovare la Derivata — d/dx | 1/(x^3) | |
| 72 | Вычислим интеграл | интеграл e^x относительно x | |
| 73 | Вычислим интеграл | интеграл tan(x)^2 относительно x | |
| 74 | Вычислим интеграл | интеграл 1 относительно x | |
| 75 | Trovare la Derivata — d/dx | x^x | |
| 76 | Trovare la Derivata — d/dx | x натуральный логарифм x | |
| 77 | Вычислим интеграл | интеграл sin(x)^2 относительно x | |
| 78 | Trovare la Derivata — d/dx | x^4 | |
| 79 | Оценить предел | предел (3x-5)/(x-3), если x стремится к 3 | |
| 80 | Вычислим интеграл | интеграл от x^2 натуральный логарифм x по x | |
| 81 | Trovare la Derivata — d/dx | f(x) = square root of x | |
| 82 | Trovare la Derivata — d/dx | x^2sin(x) | |
| 83 | Вычислим интеграл | интеграл sin(2x) относительно x | |
| 84 | Trovare la Derivata — d/dx | 3e^x | |
| 85 | Вычислим интеграл | интеграл xe^x относительно x | |
| 86 | Trovare la Derivata — d/dx | y=x^2 | |
| 87 | Trovare la Derivata — d/dx | квадратный корень x^2+1 | |
| 88 | Trovare la Derivata — d/dx | sin(x^2) | |
| 89 | Вычислим интеграл | интеграл e^(-2x) относительно x | |
| 90 | Вычислим интеграл | интеграл натурального логарифма квадратного корня x по x | |
| 91 | Вычислить | 2^5 | |
| 92 | Trovare la Derivata — d/dx | e^2 | |
| 93 | Trovare la Derivata — d/dx | x^2+1 | |
| 94 | Вычислим интеграл | интеграл sin(x) относительно x | |
| 95 | Вычислить | 2^3 | |
| 96 | Trovare la Derivata — d/dx | arcsin(x) | |
| 97 | Оценить предел | предел (sin(x))/x, если x стремится к 0 | |
| 98 | Вычислить | e^2 | |
| 99 | Вычислим интеграл | интеграл e^(-x) относительно x | |
| 100 | Вычислим интеграл | интеграл 1/x относительно x |
Как найти асимптоты функции — 11 Февраля 2014 — Примеры решений задач
График функции может иметь вертикальную, горизонтальную или наклонную асимптоты.
Как найти вертикальную асимптоту:
♦ Если имеются точки разрыва функции, то в этих точках проверяем правый и левый пределы функции, если хотя бы один стремится к бесконечности, то в данной точке имеем вертикальную асимптоту.
Пример 1. Найти вертикальную асимптоту
В точке x0 = 1 функция имеет разрыв (знаменатель обращается в ноль), следовательно в данной точке функция может иметь вертикальную асимптоту, проверяем:
левый предел
правый предел
Левый и правый пределы в точке x = 1 стремятся к бесконечности, следовательно в данной точке функция имеет вертикальную асимптоту.
Для наглядности построим график функции.
Как найти горизонтальную асимптоту:
♦ Находим пределы
если хотя бы один предел конечный, то функция имеет горизонтальную асимптоту.
Пример 2. Найти горизонтальную асимптоту функции
Решение.
Находим пределы
— следовательно y = 2 — горизонтальная асимптота.
Для наглядности построим график — вставляем в калькулятор 8/(x-1)+2.
Как найти наклонную асимптоту:
Если функция имеет наклонные асимптоты, то их уравнение имеет вид
где
Пример 3. Найти наклонную асимптоту функции
Решение. Находим пределы
Следовательно наклонная асимптота
Для наглядности построим график — вставляем в калькулятор 3x^2/(x+1)+2.
P.S. Как видим задача нахождения асимптот сводится к вычислению пределов.
Вычислить пределы (также левые и правые) можно с помощью калькулятора вычисления пределов
Асимптота
Асимптота в переводе с греческого языка обозначает — не совпадающая. То есть это несколько продолженная линия, которая в приближении к кривой или какой-либо её части, делает так, что бы расстояние у них было меньше чем у всех данных величин. Другими словами D соприкасается с кривой, на не кончающемся участке оси координат. И любая линия которая параллельна D, дублирующая её, не сможет быть с тем же названием, потому что по произволению расстояние между ней и кривой не может идти в меньшую сторону. Из чего следует что D имеет ограниченные рамки относительно кривой. Когда в Греции ученые математики изучали какими свойствами обладает кривая линия в конусе по пересечению его плоскости, они вывели если ветви гиперболы несколько удлиненны, то обязательно приблизятся к прямым идущим от центра фигуры при этом равно наклонены к оси фигуры. Данные прямые и есть D. Ньютон доказал что кривые алгебраические D, идут они от последнего третьего порядка. Следовательно, есть как прямые (Асимп.) так и кривые (Асимптотическая кривая) D линии.
Отталкиваясь от всего выше сказанного, найдем уравнение D. y=f(х) — уравнение кривой, координаты х,у — касательная в точке = Y — y =dy/dx(X-x) либо У =(dy/dx) X+y-x(dy/dx).
Для перехода к D нужно любое из предположений:
— х и у = + или — бесконечность.
— х = + или — бесконечность, у = крайнему числу.
— у = + бесконечность, х = крайнему числу.
Потому как данные предложения показывают что расстояние из начала координат до точки касания, бесконечно.
Если Вам нужен проект на газоснабжение. Перейдите по ссылке http://proekt-gaz.ru/forum/ , где вы сможете заказать готовый проект.
Асимптота бывает нескольких видов — вертикальная, горизонтальная и наклонная.
Вертикальная — это прямая линия типа х=а и с условием что существует придел lim(х от а) f(x) = ?. находить нужно два односторонних предела, для того что бы знать поведение функции с двух сторон.
Горизонтальная — так же прямая линия типа y=a с условием что существует предел lim (x от + или — ?) f(x) =a
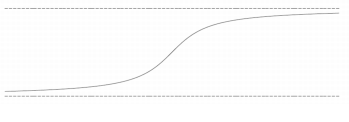
Наклонная — тип у=kх + b с пределами: lim(x от +,- ?) f(x) / x = k, и lim (x от +,- ?) (f(x) — kx) = b. В данной функции не больше двух наклонных асимптот.
Существует связь наклонной и горизонтальной асимптот, она заключается в вычислении предела lim (x +,- ?) f(x)/x =0, значит они совпадают.
Частный случай горизонтальной асимптоты является
lim (x +,- ?)f(x)/x =0, следовательно,
— функция имеет только горизонтальную асимптоту когда х зависит от + бесконечности, так же и при х зависящем от — бесконечности. Асимптот может и не быть.
— существующие асимптоты зависят от существования пределов.
Рассмотрим на примере:
найти асимптоту с помощью выделения целой части
f(X) = 2x3+5x2+1/x2+1
поделив данное равенство получаем
f(X) = 2x + 5 +(-2x-4 / x2+1) = 2x + 5 + (-2) (x+2/x2+1)
x от ?, х+2/х2+1 от 0. или
Ответ: lim (x от +, — ?) f(x) = lim (x от +,- ?) (2x+5) = +,- ?. и у= 2х + 5.

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Асимптоты графика функций: их виды, примеры решений
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Если предварительно построить асимптоты кривой, то многих случаях построение графика функции облегчается.
Судьба асимптоты полна трагизма. Представьте себе, каково это: всю жизнь двигаться по прямой к заветной цели, подойти к ней максимально близко, но так и не достигнуть её. Например, стремиться соединить свой жизненный путь с путём желанного человека, в какой-то момент приблизиться к нему почти вплотную, но даже не коснуться его. Или стремиться заработать миллиард, но до достижения этой цели и записи в книгу рекордов Гиннеса для своего случая не достаёт сотых долей цента. И тому подобное. Так и с асимптотой: она постоянно стремится достигнуть кривой графика функции, приближается к нему на минимальное возможное расстояние, но так и не касается его.
Определение 1. Асимптотами называются такие прямые, к которым сколь угодно близко приближается график функции, когда переменная стремится к плюс бесконечности или к минус бесконечности.
Определение 2. Прямая называется асимптотой графика функции, если расстояние от переменной точки М графика функции до этой прямой стремится к нулю при неограниченном удалении точки М от начала координат по какой-либо ветви графика функции.
Различают три вида асимптот: вертикальные, горизонтальные и наклонные.
Первое, что нужно узнать о вертикальных асимптотах: они параллельны оси Oy.
Определение. Прямая x = a является вертикальной асимптотой графика функции, если точка x = a является точкой разрыва второго рода для этой функции.
Из определения следует, что прямая x = a является вертикальной асимптотой графика функции f(x), если выполняется хотя бы одно из условий:
 (предел функции при значении аргумента, стремящимся к некоторому значению a слева, равен плюс или минус бесконечности)
(предел функции при значении аргумента, стремящимся к некоторому значению a слева, равен плюс или минус бесконечности) (предел функции при значении аргумента, стремящимся к некоторому значению a справа, равен плюс или минус бесконечности).
(предел функции при значении аргумента, стремящимся к некоторому значению a справа, равен плюс или минус бесконечности).
При этом функция f(x) может быть вообще не определена соответственно при x ≥ a и x ≤ a.
Замечание:
- символом
 обозначается стремление x к a справа, причём x остаётся
больше a;
обозначается стремление x к a справа, причём x остаётся
больше a; - символом
 обозначается стремление x к a слева, причём x остаётся меньше a.
обозначается стремление x к a слева, причём x остаётся меньше a.
Пример 1. График функции y=lnx имеет вертикальную асимптоту x = 0 (т.е. совпадающую с осью Oy) на границе области определения, так как предел функции при стремлении икса к нулю справа равен минус бесконечности:
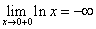
(рис. сверху).
Найти асимптоты графика функции самостоятельно, а затем посмотреть решения
Пример 2. Найти асимптоты графика функции 
Пример 3. Найти асимптоты графика функции 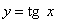
Первое, что нужно узнать о горизонтальных асимптотах: они параллельны оси Ox.
Если
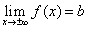 (предел функции при стремлении аргумента к плюс или минус бесконечности равен некоторому значению b),
то y = b – горизонтальная асимптота кривой y = f(x)
(правая при иксе, стремящимся к плюс бесконечности, левая при иксе, стремящимся к минус бесконечности,
и двусторонняя, если пределы при стремлении икса к плюс или минус бесконечности равны).
(предел функции при стремлении аргумента к плюс или минус бесконечности равен некоторому значению b),
то y = b – горизонтальная асимптота кривой y = f(x)
(правая при иксе, стремящимся к плюс бесконечности, левая при иксе, стремящимся к минус бесконечности,
и двусторонняя, если пределы при стремлении икса к плюс или минус бесконечности равны).

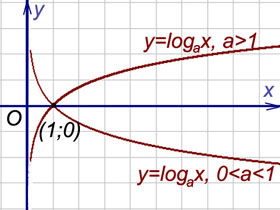
Пример 5. График функции
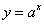
при a > 1 имеет левую горизонтальную асимпототу y = 0 (т.е. совпадающую с осью Ox), так как предел функции при стремлении «икса» к минус бесконечности равен нулю:

Правой горизонтальной асимптоты у кривой нет, поскольку предел функции при стремлении «икса» к плюс бесконечности равен бесконечности:

Вертикальные и горизонтальные асимптоты, которые мы рассмотрели выше, параллельны осям координат, поэтому для их построения нам требовалось лишь определённое число — точка на оси абсцисс или ординат, через которую проходит асимптота. Для наклонной асимптоты необходимо больше — угловой коэффициент k, который показывает угол наклона прямой, и свободный член b, который показывает, насколько прямая находится выше или ниже начала координат. Не успевшие забыть аналитическую геометрию, а из неё — уравнения прямой, заметят, что для наклонной асимптоты находят уравнение прямой с угловым коэффициентом. Существование наклонной асимптоты определяется следующей теоремой, на основании которой и находят названные только что коэффициенты.
Теорема. Для того, чтобы кривая y = f(x) имела асимптоту y = kx + b, необходимо и достаточно, чтобы существовали конечные пределы k и b рассматриваемой функции при стремлении переменной x к плюс бесконечности и минус бесконечности:
 (1)
(1)и
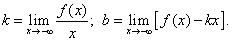 (2)
(2)
Найденные таким образом числа k и b и являются коэффициентами наклонной асимптоты.
В первом случае (при стремлении икса к плюс бесконечности) получается правая наклонная асимптота, во втором (при стремлении икса к минус бесконечности) – левая. Правая наклонная асимптота изображена на рис. снизу.
При нахождении уравнения наклонной асимптоты необходимо учитывать стремление икса и к плюс бесконечности, и к минус бесконечности. У некоторых функций, например, у дробно-рациональных, эти пределы совпадают, однако у многих функций эти пределы различны а также может существовать только один из них.
При совпадении пределов при иксе, стремящемся к плюс бесконечности и к минус бесконечности прямая y = kx + b является двусторонней асимптотой кривой.
Если хотя бы один из пределов, определяющих асимптоту y = kx + b, не существует, то график функции не имеет наклонной асимптоты (но может иметь вертикальную).
Нетрудно видеть, что горизонтальная асимптота y = b является частным случаем наклонной y = kx + b при k = 0.
Поэтому если в каком-либо направлении кривая имеет горизонтальную асимптоту, то в этом направлении нет наклонной, и наоборот.
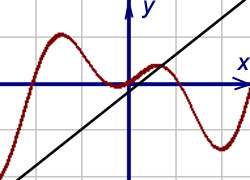
Пример 6. Найти асимптоты графика функции

Решение. Функция определена на всей числовой прямой, кроме x = 0, т.е.
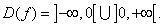
Поэтому в точке разрыва x = 0 кривая может иметь вертикальную асимптоту. Действительно, предел функции при стремлении икса к нулю слева равен плюс бесконечности:
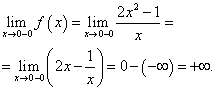

Следовательно, x = 0 – вертикальная асимптота графика данной функции.
Горизонтальной асимптоты график данной функции не имеет, так как предел функции при стремлении икса к плюс бесконечности равен плюс бесконечности:
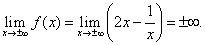
Выясним наличие наклонной асимптоты:
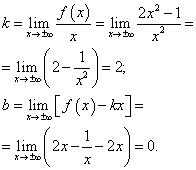
Получили конечные пределы k = 2 и b = 0. Прямая y = 2x является двусторонней наклонной асимптотой графика данной функции (рис. внутри примера).
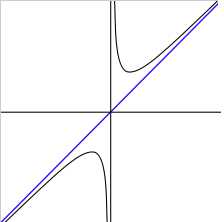
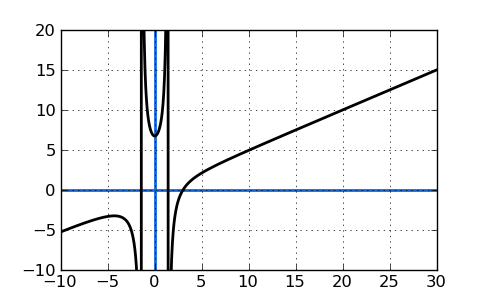
Пример 7. Найти асимптоты графика функции
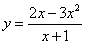
Решение. Функция имеет одну точку разрыва x = −1. Вычислим односторонние пределы и определим вид разрыва:
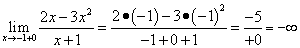 ,
,
 .
.
Заключение: x = −1 — точка разрыва второго рода, поэтому прямая x = −1 является вертикальной асимптотой графика данной функции.
Ищем наклонные асимптоты. Так как данная функция — дробно-рациональная, пределы при
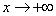 и при
и при
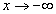 будут совпадать. Таким
образом, находим коэффициенты для подстановки в уравнение прямой — наклонной асимптоты:
будут совпадать. Таким
образом, находим коэффициенты для подстановки в уравнение прямой — наклонной асимптоты:


Подставляя найденные коэффициенты в уравнение прямой с угловым коэффициентом, получаем уравнение наклонной асимптоты:
y = −3x + 5.
На рисунке график функции обозначен бордовым цветом, а асимптоты — чёрным.
Пример 8. Найти асимптоты графика функции
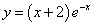 .
.
Решение. Так как данная функция непрерывна, её график не имеет вертикальных асимптот. Ищем наклонные асимптоты:
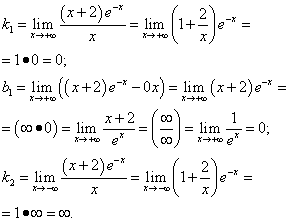 .
.
Таким образом, график данной функции имеет асимптоту y = 0 при
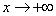 и не имеет асиптоты при
и не имеет асиптоты при
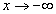 .
.
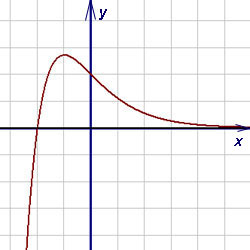
Пример 10. Найти асимптоты графика функции
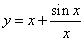
Решение. Функция имеет область определения 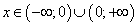 .
Так как вертикальная асимптота графика этой функции может быть только на границе области определения,
найдём односторонние пределы функции при
.
Так как вертикальная асимптота графика этой функции может быть только на границе области определения,
найдём односторонние пределы функции при  :
:
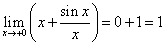 ,
,
 .
.
Оба предела нашли, используя первый замечательный предел. Заключение: x = 0 — точка устранимого разрыва, поэтому у графика функции нет вертикальных асимптот.
Ищем наклонные асимптоты:

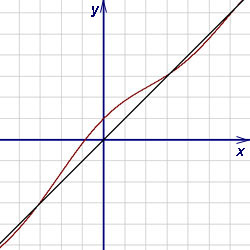
Таким образом, при  наклонной асимптотой графика данной функции является прямая y = x.
Но при
наклонной асимптотой графика данной функции является прямая y = x.
Но при  найденные пределы
не изменяются. Поэтому при
найденные пределы
не изменяются. Поэтому при 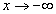 наклонной асимптотой графика данной функции также является y = x.
наклонной асимптотой графика данной функции также является y = x.
Пример 11. Найти асимптоты графика функции
 .
.
Решение. Сначала найдём вертикальные асимптоты. Для этого найдём точки разрыва функции
и их виды. Знаменатель не может быть равным нулю, поэтому должно соблюдаться условие
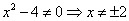 .
Функция имеет две точки разрыва:
.
Функция имеет две точки разрыва:  ,
,
 . Чтобы установить вид
разрыва, найдём односторонние пределы:
. Чтобы установить вид
разрыва, найдём односторонние пределы:

Так как все пределы равны бесконечности, обе точки разрыва — второго рода. Поэтому график данной функции имеет две вертикальные асимптоты: x = 2 и x = −2.
Ищем наклонные асимптоты. Так как данная функция является дробно-рациональной,
пределы при 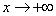 и при
и при
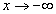 совпадают. Поэтому,
определяя коэффициенты прямой, ищем просто пределы:
совпадают. Поэтому,
определяя коэффициенты прямой, ищем просто пределы:
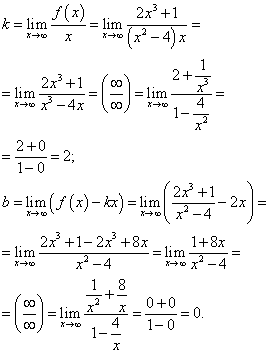
Подставляем найденные коэффициенты в уравнение прямой с угловым коэффициентом, получаем уравнение наклонной асимптоты y = 2x. Таким образом, график данной функции имеет три асимптоты: x = 2, x = −2 и y = 2x.
Найти асимптоты графика функции самостоятельно, а затем посмотреть решения

Поделиться с друзьями
Весь блок «Производная»
Асимптоты калькулятора функций

Поиск инструмента
Асимптота функции
Инструмент для нахождения уравнений асимптот (горизонтальных, вертикальных, наклонных) функции. Асимптоты — это линии, которые стремятся (подобно касательной) функционировать к бесконечности.
Результаты
Асимптота функции — dCode
Тег (и): Функции
Поделиться

dCode и вы
dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !
Асимптоты вычислителя функций
Инструмент для поиска уравнений асимптот (горизонтальных, вертикальных, наклонных) функции.Асимптоты — это линии, которые стремятся (подобно касательной) функционировать к бесконечности.
Ответы на вопросы
Как найти горизонтальную асимптоту?
Функция $ f (x) $ имеет горизонтальную асимптоту $ y = a $ if
$$ \ lim \ limits_ {x \ rightarrow + \ infty} f (x) = a \ mbox {or} \ lim \ limits_ {x \ rightarrow — \ infty} f (x) = a \ mbox {(или оба)} $$
Чтобы найти горизонтальную асимптоту , вычисление этого предела является достаточным условием.
Пример: $ 1 / x $ имеет для асимптоты $ y = 0 $, потому что $ \ lim \ limits_ {x \ rightarrow \ infty} 1 / x = 0 $
Не может быть более 2 горизонтальных асимптот .
Как найти вертикальную асимптоту?
Функция $ f (x) $ имеет вертикальную асимптоту $ x = a $, если она допускает бесконечный предел в $ a $ ($ f $ стремится к бесконечности).
$$ \ lim \ limits_ {x \ rightarrow \ pm a} f (x) = \ pm \ infty $$
Чтобы найти горизонтальную асимптоту , вычисление этого предела является достаточным условием.
Пример: $ 1 / x $ имеет для asymtote $ x = 0 $, потому что $ \ lim \ limits_ {x \ rightarrow 0} 1 / x = \ infty $
Обычно функция не определена в $ a $, необходимо проанализировать область определения функции, чтобы найти потенциальные асимптоты .
Может существовать бесконечное количество вертикальных асимптот .
Как найти наклонную / наклонную асимптоту?
Функция $ f (x) $ имеет наклонную асимптоту $ g (x) = ax + b $, когда
$$ \ lim \ limits_ {x \ rightarrow \ pm \ infty} \ left (f (x) -g (x) = 0 \ right) $$
Вычисление наклонной асимптоты можно упростить, вычислив этот предел:
$$ \ lim \ limits_ {x \ rightarrow \ pm \ infty} \ left (\ frac {f (x)} {g (x)} = 1 \ right) $$
Как найти нелинейную асимптоту?
Функция $ f (x) $ имеет нелинейную асимптоту $ g (x) $, когда
$$ \ lim \ limits_ {x \ rightarrow \ pm \ infty} \ left (f (x) -g (x) = 0 \ right) $$
Метод тот же, что и при вычислении наклонной асимптоты .
Задайте новый вопросИсходный код
dCode сохраняет за собой право собственности на исходный код онлайн-инструмента «Асимптота функции». За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / free), любой алгоритм, апплет или фрагмент (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любая функция (преобразование, решение, дешифрование / encrypt, decipher / cipher, decode / encode, translate), написанные на любом информатическом языке (PHP, Java, C #, Python, Javascript, Matlab и т. д.)) доступ к данным, скриптам или API не будет бесплатным, то же самое касается загрузки Asymptote of a Function для автономного использования на ПК, планшете, iPhone или Android!
Нужна помощь?
Пожалуйста, заходите в наше сообщество в Discord для получения помощи!
Вопросы / комментарии
Сводка
Инструменты аналогичные
Поддержка
Форум / Справка

Рекламные объявления
Ключевые слова
асимптота, функция, бесконечность, вертикальная, горизонтальная, наклонная, наклонная
Ссылки
Источник: https: // www.dcode.fr/asymptote-function
© 2020 dCode — Лучший «инструментарий» для решения любых игр / загадок / геокэшинга / CTF. .Поиск асимптот — Бесплатная справка по математике
Определение асимптоты:
Прямая линия на графике, представляющая предел для заданной функции. Представьте себе кривую, которая приближается к линии, но не пересекает ее.
Пример:
Функция \ (y = \ frac {1} {x} \) — очень простая асимптотическая функция. Когда x приближается к положительной бесконечности, y становится , на самом деле близко к 0.2-9} $$
Если вы разложите на множитель числитель и знаменатель в приведенной выше функции, вы измените функцию из стандартной формы на факторизованную. В разложенной форме приведенная выше функция обнаружит две интересные вещи:
1) Расположение любых вертикальных асимптот.
2) Местоположение любых точек пересечения по оси абсцисс.
Вот как выглядит приведенная выше функция в факторизованном виде:
$$ y = \ frac {x + 2} {x + 3} $$После того, как исходная функция была разложена на множители, корни знаменателя будут равны нашим вертикальным асимптотам , а корни числителя будут равны нашим пересечениям по оси x.Это означает, что , когда знаменатель равен нулю , мы нашли вертикальную асимптоту.
Итак, при каких значениях x знаменатель функции будет равен нулю? Ответ: \ (x = -3 \). Вот что происходит: когда x приближается к -3, знаменатель начинает становиться очень маленьким и приближается к нулю. Правильно? Что ж, когда знаменатель приближается к нулю, вся функция начинает стремительно приближаться к бесконечности. Попробуйте это с чем-то вроде \ (x = -2,999 \) для доказательства.
Когда мы построим график функции, мы увидим, что кривая приближается к воображаемой вертикальной линии при x = -3.
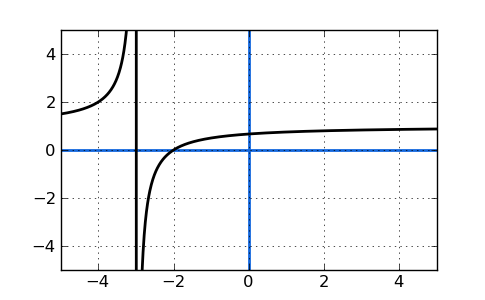
Хотя кажется, что есть сплошная линия на x = -3, на самом деле она не существует и вызвана программой построения графиков (к сожалению, большинство из них так и поступают), соединяющей две точки данных по обе стороны от x = -3. Эта вертикальная линия является вертикальной асимптотой x = -3.
Надеюсь, вы видите, что асимптоту часто можно найти, разложив функцию на множители для создания простого выражения в знаменателе. Этот знаменатель откроет ваши асимптоты. Прочтите следующий урок, чтобы найти горизонтальные асимптоты.
Бесплатная математическая помощь и мистер Фелиз
.Поиск горизонтальных асимптот — Бесплатная справка по математике
Что такое горизонтальная асимптота?
Горизонтальная асимптота — это значение y на графике, к которому функция приближается, но фактически не достигает. Вот простой графический пример, в котором изображенная на графике функция приближается, но никогда не достигает, \ (y = 0 \). Фактически, как бы сильно вы ни уменьшили масштаб на этом графике, он все равно не достигнет нуля. Однако я должен отметить, что горизонтальные асимптоты могут появляться только в одном направлении и могут пересекаться при малых значениях x.3-8x + 3} \). Они возникают, когда график функции становится все ближе и ближе к определенному значению, даже не достигнув этого значения, поскольку x становится очень положительным или очень отрицательным.
Чтобы найти горизонтальные асимптоты:
1) Представьте уравнение или функцию в форме y =.
2) Умножьте (разверните) любые разложенные на множители полиномы в числителе или знаменателе.
3) Удалите все, кроме членов с наибольшим показателем x, найденных в числителе и знаменателе.3-9} $$
Помните, что горизонтальные асимптоты появляются, когда x расширяется до положительной или отрицательной бесконечности, поэтому нам нужно выяснить, к чему приближается эта доля, когда x становится огромным. Для этого мы выберем «доминирующие» члены в числителе и знаменателе. Доминирующими являются термины с наибольшими показателями. Поскольку x стремится к бесконечности, другие члены слишком малы, чтобы иметь большое значение.
Наибольшие показатели в этом случае совпадают в числителе и знаменателе (3). Доминирующие члены в каждом имеют показатель степени 3.3} $$
В данном случае 2/3 — это горизонтальная асимптота указанной выше функции. Фактически вы должны выразить это как \ (y = \ frac {2} {3} \). Это значение является асимптотой, потому что, когда мы приближаемся к \ (x = \ infty \), «доминирующие» члены будут затмевать остальные, и функция всегда будет приближаться к \ (y = \ frac {2} {3} \ ). Вот график этой функции в качестве последней иллюстрации, что это правильно:
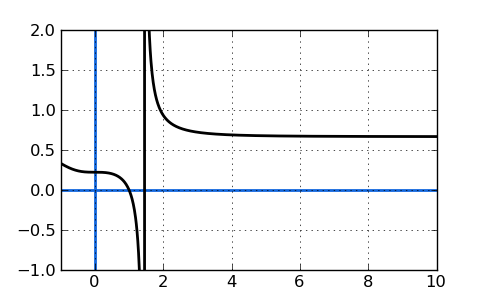
(Обратите внимание, что в этой функции также присутствует вертикальная асимптота.)
Если показатель степени в знаменателе функции больше показателя степени в числителе, горизонтальная асимптота будет иметь вид y = 0, который является осью x.2-4} $$
Горизонтальных асимптот НЕ БУДЕТ, потому что в числителе БОЛЬШЕ показателя степени, который равен 3. Видите? Это заставит функцию постоянно увеличиваться, а не приближаться к асимптоте. График этой функции ниже. Обратите внимание, что на графике снова присутствуют вертикальные асимптоты.
Образец B:
Найдите горизонтальные асимптоты: \ (\ frac {(2x-1) (x + 3)} {x (x-2)} \)
В этом примере функция представлена в факторизованной форме.2 \) в числителе и знаменателе, и у нас останется 2. Наша горизонтальная асимптота для образца B — это горизонтальная линия \ (y = 2 \).
Ссылки на похожие уроки с других сайтов:
Горизонтальные асимптоты (Purplemath.com)
Калькулятор асимптоты
Просто введите свою функцию и выберите «Найти асимптоты» в раскрывающемся списке. Щелкните ответ, чтобы увидеть все асимптоты (совершенно бесплатно), или подпишитесь на бесплатную пробную версию, чтобы увидеть полные пошаговые сведения о решении.
.Асимптота
Асимптота — это линия , к которой приближается кривая, когда она направляется к бесконечности:
Типы
Есть три типа: горизонтальный, вертикальный и наклонный:
Направление также может быть отрицательным:
Кривая может приближаться с любой стороны (например, сверху или снизу для горизонтальной асимптоты),
или может действительно пересекаться (возможно, много раз), и даже уйти и снова вернуться.
Важным моментом является то, что:
Расстояние между кривой и асимптотой стремится к нулю , когда они устремляются к бесконечности (или — бесконечности)
Горизонтальные асимптоты
Это горизонтальная асимптота, когда: , когда x стремится к бесконечности (или — бесконечности), кривая приближается к некоторому постоянному значению b |
Вертикальные асимптоты
Это вертикальная асимптота, когда: , когда x приближается к некоторому постоянному значению c (слева или справа), кривая уходит в сторону бесконечности (или −infinity). |
Косые асимптоты
Это наклонная асимптота, когда: , когда x стремится к бесконечности (или −infinity), кривая направляется к прямой y = mx + b (примечание: m не равно нулю, поскольку это горизонтальная асимптота). |
Пример: (x 2 −3x) / (2x − 2)
График (x 2 -3x) / (2x-2) имеет:
- Вертикальная асимптота при x = 1
- Наклонная асимптота: y = x / 2 — 1
Эти вопросы будут иметь смысл, только если вы знаете Rational Expressions:
.
 (предел функции при значении аргумента, стремящимся к некоторому значению a слева, равен плюс или минус бесконечности)
(предел функции при значении аргумента, стремящимся к некоторому значению a слева, равен плюс или минус бесконечности)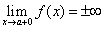 (предел функции при значении аргумента, стремящимся к некоторому значению a справа, равен плюс или минус бесконечности).
(предел функции при значении аргумента, стремящимся к некоторому значению a справа, равен плюс или минус бесконечности). обозначается стремление x к a справа, причём x остаётся
больше a;
обозначается стремление x к a справа, причём x остаётся
больше a; обозначается стремление x к a слева, причём x остаётся меньше a.
обозначается стремление x к a слева, причём x остаётся меньше a.