3 Приложения двойных интегралов
3 Приложения двойных интегралов
3.1 Теоретическое введение
Рассмотрим приложения двойного интеграла к решению ряда геометрических задач и задач механики.
3.1.1 Вычисление площади и массы плоской пластины
Рассмотрим тонкую материальную пластину D, расположенную в плоскости Оху. Площадь S этой пластины может быть найдена с помощью двойного интеграла по формуле:
| (1) |
Пусть в каждой точке пластины задана ее поверхностная плотность γ = γ (x, y) ≥ 0. Будем считать, что функция γ = γ (x, y) непрерывна в области D. Тогда масса m этой пластины равна двойному интегралу от функции плотности
| (2) |
3.1.2 Статические моменты. Центр масс плоской пластины
Статическим моментом Mx относительно оси Ox материальной точки P(x;y), лежащей в плоскости Oxy и имеющей массу m, называется произведение массы точки на ее ординату, т.е. Mx= my. Аналогично определяется статический момент My относительно оси Oy: My = mx. Статические моменты плоской пластины с поверхностной плотностью γ = γ (x, y) вычисляются по формулам:
| (3) |
| (4) |
Как известно из механики, координаты xc , yc центра масс плоской материальной системы определяются равенствами:
| (5) |
где m – масса системы, а Mx и My – статические моменты системы. Масса плоской пластины m определяется формулой (1), статические моменты плоской пластины можно вычислить по формулам (3) и (4). Тогда, согласно формулам (5), получаем выражение для координат центра масс плоской пластины:
| (6) |
3.2 Содержание типового расчета
Типовой расчет содержит две задачи. В каждой задаче задана плоская пластина D, ограниченная линиями, указанными в условии задачи. Г(x,y) – поверхностная плотность пластины D. Для этой пластины найти: 1. S – площадь; 2. m – массу; 3. My , Mx – статические моменты относительно осей Оy и Ох соответственно; 4. ,– координаты центра масс.
3.3 Порядок выполнения типового расчета
При решении каждой задачи необходимо: 1. Выполнить чертеж заданной области. Выбрать систему координат, в которой будут вычисляться двойные интегралы. 2. Записать область в виде системы неравенств в выбранной системе координат. 3. Вычислить площадь S и массу m пластины по формулам (1) и (2). 4. Вычислить статические моменты My , Mx по формулам (3) и (4). 5. Вычислить координаты центра масс ,по формулам (6). Нанести центр масс на чертеж. При этом возникает визуальный (качественный) контроль полученных результатов. Численные ответы должны быть получены с тремя значащими цифрами.
3.4 Примеры выполнения типового расчета
Задача 1. Пластина D ограничена линиями: y = 4 – x2; х = 0; y = 0 (x ≥ 0; y ≥ 0) Поверхностная плотность γ0 = 3. Решение. Область, заданная в задаче, ограничена параболой y = 4 – x2, осями координат и лежит в первой четверти (рис. 1). Задачу будем решать в декартовой системе координат. Эта область может быть описана системой неравенств:
 Рис.
1
Рис.
1
Площадь S пластины равна (1): Так как пластина однородная, ее массаm = γ0S = 3·= 16. По формулам (3), (4) найдем статические моменты пластины:Координаты центра масс находятся по формуле (6):
Задача 2. Пластина D ограничена линиями: х2 + у2 = 4; х = 0, у = х ( х ≥ 0, у ≥ 0). Поверхностная плотность γ(x,y) = у. Решение. Пластина ограничена окружностью и прямыми, проходящими через начало координат (рис. 2). Поэтому для решения задачи удобно использовать полярную систему координат. Полярный угол φ меняется от π/4 до π/2. Луч, проведенный из полюса через пластину, «входит» в неё при ρ = 0 и «выходит» на окружность, уравнение которой: х2 + у2 = 4 <=> ρ = 2.
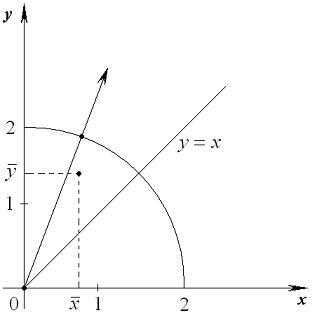 Рис.
2
Рис.
2
Следовательно, заданную область можно записать системой неравенств: Площадь пластины найдем по формуле (1):Массу пластины найдем по формуле (2), подставив γ(x,y) = у = ρ sinφ: Для вычисления статических моментов пластины используем формулы (3) и (4):Координаты центра масс получим по формулам (6):Ответ: S ≈ 1,57; m ≈ 1,886; Mx = 2,57; My = 1; = 0,53;= 1,36.
3.5 Оформление отчета
В отчете должны быть представлены все выполненные расчеты, аккуратно выполненные чертежи. Численные ответы должны быть получены с тремя значащими цифрами.
studfiles.net
Механические приложения двойного интеграла / Двойной интеграл / 3dstroyproekt.ru
Будем считать, что $\mathbf { \textit { D } } $ — неоднородная плоская пластина с поверхностной плотностью материала в точке $P$ равной $\mu (P)$. В механике $\mu (P)$ определяется так. Точка $P$ окружается малой областью $\mathbf { \textit { S } } $, находится масса $\mathbf { \textit { m } } (\mathbf { \textit { S } } )$ и площадь этой области { площадь тоже будем обозначать буквой $\mathbf { \textit { S } } $ } и $\mu (P)=\mathop { \lim } \limits_ { diam(S)\to 0 } \frac { m(S) } { S } $.
Для нахождения массы по заданной плотности мы решим обратную задачу. Разобьём $\mathbf { \textit { D } } $ на малые подобласти $\mathbf { \textit { D } } _ { 1 } $, $\mathbf { \textit { D } } _ { 2 } $,$\mathbf { \textit { D } } _ { 3 } , { \ldots } , \mathbf { \textit { D } } _ { n } $, в каждой из подобластей $\mathbf { \textit { D } } _ { i } $ выберем произвольную точку $\mathbf { \textit { P } } _ { i } $, и, считая что в пределах $\mathbf { \textit { D } } _ { i } $ плотность постоянна и равна $\mu (P_i )$, получим, что масса $\mathbf { \textit { D } } _ { i } $ приближённо есть $\mu (P_i )\cdot s(D_i )$, а масса всей пластины $\sum\limits_ { i=1 } ^n { \mu (P_i )\cdot s(D_i ) } $.
Это интегральная сумма, при уменьшении $d=\mathop { \max } \limits_ { i=1,2,\ldots ,n } diam(D_i )$ точность приближения увеличивается, и в пределе $m(D)=\mathop { \lim } \limits_ { \begin{array} { l } d\to 0 \\ (n\to \infty ) \\ \end{array} } \sum\limits_ { i=1 } ^n { \mu (P_i )\cdot \Delta s(D_i ) } =\iint\limits_D { \mu (P)ds } $.
Аналогично находятся другие параметры пластины:
Координаты центра тяжести
$x_c =\frac { 1 } { m(D) } \iint\limits_D { x\cdot \mu (P)ds } $, $y_c =\frac { 1 } { m(D) } \iint\limits_D { y\cdot \mu (P)ds } $;
Моменты инерции пластины
- $I_x =\iint\limits_D { y^2\cdot \mu (P)ds } $ { относительно оси $\mathbf { \textit { Ox } } $ } ,
- $I_y =\iint\limits_D { x^2\cdot \mu (P)ds } $ { относительно оси $\mathbf { \textit { Oy } } $ } ,
- $I_O =\iint\limits_D { (x^2+y^2)\cdot \mu (P)ds } =I_x +I_y $ { относительно начала координат } .
Пластина расположена в области (R) и ее плотность в точке ( { \left( { x,y }\right) } ) равна ( { \rho \left( { x,y }\right) } ).
Масса пластины
(m = \large\iint\limits_R\normalsize { \rho \left( { x,y }\right)dA } )
Статические моменты пластины
Момент пластины относительно оси (Ox) определяется формулой
( { M_x } = \large\iint\limits_R\normalsize { y\rho \left( { x,y }\right)dA } )
Аналогично, момент пластины относительно оси (Oy) выражается в виде
( { M_y } = \large\iint\limits_R\normalsize { x\rho \left( { x,y }\right)dA } )
Координаты центра масс пластины
- (\bar x = \large\frac { { { M_y } } } { m } \normalsize = \large\frac { 1 } { m } \normalsize \large\iint\limits_R\normalsize { x\rho \left( { x,y }\right)dA } = \large\frac { { \iint\limits_R { x\rho \left( { x,y }\right)dA } } } { { \iint\limits_R { \rho \left( { x,y }\right)dA } } } \normalsize,\;)
- (\bar y = \large\frac { { { M_x } } } { m } \normalsize = \large\frac { 1 } { m } \normalsize \large\iint\limits_R\normalsize { y\rho \left( { x,y }\right)dA } = \large\frac { { \iint\limits_R { y\rho \left( { x,y }\right)dA } } } { { \iint\limits_R { \rho \left( { x,y }\right)dA } } } \normalsize ).
Заряд пластины
(Q = \large\iint\limits_R\normalsize { \sigma \left( { x,y }\right)dA } ),
где электрический заряд распределен по области (R) и его плотность в точке ( { \left( { x,y }\right) } ) равна ( { \sigma \left( { x,y }\right) } ).
Среднее значение функции
(\mu = \large\frac { 1 } { S } \iint\limits_R\normalsize { f\left( { x,y }\right)dA } ,\;) где (S = \large\iint\limits_R\normalsize { dA } ).
Пример 1
Найти параметры неоднородной плоской пластины, ограниченной кривыми
$D:\left[{ \begin{array} { l } y=x^2, \\ y=4; \\ \end{array} }\right.$ если плотность $\mu (x,y)=y+1$.
Решение:
$m(D)=\iint\limits_D { (y+1)dxdy } =2\int\limits_0^2 { dx } \int\limits_ { x^2 } ^4 { (y+1)dy } =2\int\limits_0^2 { \left. { \left( { y^2/2+y }\right) }\right|_ { x^2 } ^4 dx } =$ $ =2\int\limits_0^2 { \left( { 12-x^4/2-x^2 }\right)dx } =2\left. { \left( { 12x-x^5/10-x^3/3 }\right) }\right|_0^2 =2\left( { 24-\frac { 16 } { 5 } -\frac { 8 } { 3 } }\right)=\frac { 544 } { 15 } . $ $ x_c =\frac { 1 } { m(D) } \iint\limits_D { x(y+1)dx } dy=\frac { 15 } { 544 } \int\limits_ { -2 } ^2 { dx } \int\limits_ { x^2 } ^4 { x(y+1)dy } =\frac { 15 } { 544 } \int\limits_ { -2 } ^2 { x\left. { \left( { y^2/2+y }\right) }\right|_ { x^2 } ^4 dx } = $ $=\frac { 15 } { 544 } \int\limits_ { -2 } ^2 { \left( { 12x-x^5/2-x^3 }\right)dx } = \quad =\frac { 1 } { 544 } \left. { \left( { 6x^2-x^6/10-x^4/4 }\right) }\right|_ { -2 } ^2 =0$ { что и следовало ожидать, так как область и плотность симметричны относительно оси Оу). $ \begin{array} { l } y_c =\frac { 1 } { m(D) } \iint\limits_D { y(y+1)dx } dy=\frac { 15 } { 544 } \int\limits_ { -2 } ^2 { dx } \int\limits_ { x^2 } ^4 { y(y+1)dy } =\frac { 15 } { 272 } \int\limits_0^2 { \left. { \left( { y^3/3+y^2/2 }\right) }\right|_ { x^2 } ^4 dx } = \\ =\frac { 15 } { 272 } \int\limits_0^2 { \left( { 64/3+8-x^6/3-x^4/2 }\right)dx } =\frac { 15 } { 272 } \left. { \left( { 88x/3-x^7/21-x^5/10 }\right) }\right|_0^2 =\frac { 15 } { 272 } \left( { \frac { 176 } { 3 } -\frac { 128 } { 21 } -\frac { 16 } { 5 } }\right)=\frac { 15 } { 272 } \cdot \frac { 1728 } { 35 } \approx 2,72. \\ \end{array} $ $ I_x =\iint\limits_D { y^2(y+1)dx } dy=2\int\limits_0^2 { dx } \int\limits_ { x^2 } ^4 { y^2(y+1)dy } =2\int\limits_0^2 { \left. { \left( { y^4/4+y^3/3 }\right) }\right|_ { x^2 } ^4 dx } =2\int\limits_0^2 { \left( { \frac { 256 } { 3 } -\frac { x^8 } { 4 } -\frac { x^6 } { 3 } }\right)dx } = $ $ =2\left. { \left( { \frac { 256 } { 3 } x-\frac { x^9 } { 36 } -\frac { x^7 } { 21 } }\right) }\right|_0^2 \approx 300,7. $ $ I_y =\iint\limits_D { x^2(y+1)dx } dy=2\int\limits_0^2 { x^2dx } \int\limits_ { x^2 } ^4 { (y+1)dy } =2\int\limits_0^2 { x^2\left. { \left( { y^2/2+y }\right) }\right|_ { x^2 } ^4 dx } =2\int\limits_0^2 { x^2\left( { 12-\frac { x^4 } { 2 } -x^2 }\right)dx } = $ $ =2\left. { \left( { 4x^3-\frac { x^7 } { 14 } -\frac { x^5 } { 5 } }\right) }\right|_0^2 \approx 32,9. \quad I_O =\iint\limits_D { \left( { x^2+y^2 }\right)(y+1)dx } dy=I_x +I_y \approx 333,6. $
Пример 2
Вычислить моменты инерции треугольника, ограниченного прямыми (x + y = 1,) (x = 0,) (y = 0) и имеющего плотность $\rho \left( { x,y }\right) = xy.$
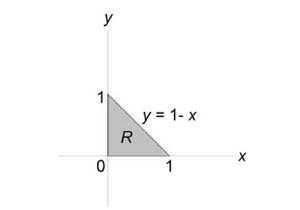
Решение:
Найдем момент инерции пластины относительно оси (Ox:) $ { { I_x } = \iint\limits_R { { y^2 } \rho \left( { x,y }\right)dxdy } } = { \int\limits_0^1 { \left[ { \int\limits_0^ { 1 — x } { { y^2 } xydy } }\right]dx } } = { \int\limits_0^1 { \left[ { \int\limits_0^ { 1 — x } { { y^3 } dy } }\right]xdx } } = { \int\limits_0^1 { \left[ { \left. { \left( { \frac { { { y^4 } } } { 4 } }\right) }\right|_0^ { 1 — x } }\right]xdx } } = \\ = { \frac { 1 } { 4 } \int\limits_0^1 { { { \left( { 1 — x }\right) } ^4 } xdx } } = { \frac { 1 } { 4 } \int\limits_0^1 { \left( { 1 — 4x + 6 { x^2 } — 4 { x^3 } + { x^4 } }\right)xdx } } = \\ = { \frac { 1 } { 4 } \int\limits_0^1 { \left( { x — 4 { x^2 } + 6 { x^3 } — 4 { x^4 } + { x^5 } }\right)dx } } = { \frac { 1 } { 4 } \left. { \left( { \frac { { { x^2 } } } { 2 } — \frac { { 4 { x^3 } } } { 3 } + \frac { { 6 { x^4 } } } { 4 } — \frac { { 4 { x^5 } } } { 5 } + \frac { { { x^6 } } } { 6 } }\right) }\right|_0^1 } = { \frac { 1 } { 4 } \left( { \frac { 1 } { 2 } — \frac { 4 } { 3 } + \frac { 3 } { 2 } — \frac { 4 } { 5 } + \frac { 1 } { 6 } }\right) } = { \frac { { 49 } } { { 120 } } . } $
Аналогично вычислим момент инерции относительно оси (Oy:) $ { { I_y } = \iint\limits_R { { x^2 } \rho \left( { x,y }\right)dxdy } } = { \int\limits_0^1 { \left[ { \int\limits_0^ { 1 — x } { { x^2 } xydy } }\right]dx } } = { \int\limits_0^1 { \left[ { \int\limits_0^ { 1 — x } { ydy } }\right] { x^3 } dx } } = { \int\limits_0^1 { \left[ { \left. { \left( { \frac { { { y^2 } } } { 2 } }\right) }\right|_0^ { 1 — x } }\right] { x^3 } dx } } = { \frac { 1 } { 2 } \int\limits_0^1 { { { \left( { 1 — x }\right) } ^2 } { x^3 } dx } } = \\ = { \frac { 1 } { 2 } \int\limits_0^1 { \left( { 1 — 2x + { x^2 } }\right) { x^3 } dx } } = { \frac { 1 } { 2 } \int\limits_0^1 { \left( { { x^3 } — 2 { x^4 } + { x^5 } }\right)dx } } = { \frac { 1 } { 2 } \left. { \left( { \frac { { { x^4 } } } { 4 } — \frac { { 2 { x^5 } } } { 5 } + \frac { { { x^6 } } } { 6 } }\right) }\right|_0^1 } = { \frac { 1 } { 2 } \left( { \frac { 1 } { 4 } — \frac { 2 } { 5 } + \frac { 1 } { 6 } }\right) } = { \frac { 1 } { { 120 } } . } $
Пример 3
Электрический заряд распределен по площади диска ( { x^2 } + { y^2 } = 1) таким образом, что его поверхностная плотность равна $\sigma \left( { x,y }\right) = 1 + { x^2 } + { y^2 } \;\left( { \text { Кл/м } ^2 }\right)$ Вычислить полный заряд диска.
Решение:
В полярных координатах область, занятая диском, описывается множеством (\left[{ \left( { r,\theta }\right)|\;0 \le r \le 1,0 \le \theta \le 2\pi }\right].)
Полный заряд будет равен $ { Q = \iint\limits_R { \sigma \left( { x,y }\right)dxdy } } = { \int\limits_0^ { 2\pi } { \left[ { \int\limits_0^1 { \left( { 1 + { r^2 } { { \cos } ^2 } \theta + { r^2 } { \sin^2 } \theta }\right)rdr } }\right]d\theta } } = { \int\limits_0^ { 2\pi } { d\theta } \int\limits_0^1 { \left( { 1 + { r^2 } }\right)rdr } } = { 2\pi \int\limits_0^1 { \left( { r + { r^3 } }\right)dr } } = \\ = { 2\pi \left. { \left( { \frac { { { r^2 } } } { 2 } + \frac { { { r^4 } } } { 4 } }\right) }\right|_0^1 } = { 2\pi \left( { \frac { 1 } { 2 } + \frac { 1 } { 4 } }\right) } = { \frac { { 3\pi } } { 2 } \;\left( { \text { Кл } }\right). } $
3dstroyproekt.ru
Физические приложения двойного интеграла.
Пусть D – плоская пластина, лежащая в плоскости Оху с поверхностной плотностью ρ(х,у). Тогда:
1. массу m пластинки находят по формуле
(10)
(11)
3.кординаты центра тяжести и пластинки – по формулам
(12)
4. Моменты инерции , и пластинки соответственно относительно координатных осей Ох и Оу и начала координат находят по формулам
(13)
(14)
Для однородных пластинок поверхностная плотность . В некоторых задачах для простоты полагают .
Пример 1. Найти массу круглой пластины D с поверхностной плотностью ρ(х,у)=3-х—у.
Решение: Массу пластины вычисляем по формуле (10):
Поскольку пластина является круглой, вначале в двойном интеграле переходим к полярным координатам, а затем при вычислении внутреннего интеграла учитываем тот факт, что интеграл по периоду от тригонометрических функций равен нулю.
Пример 2. Найти статический момент однородного прямоугольника со сторонами а и b относительно стороны а, считая, что прямоугольник лежит в плоскости Оху.Решение: Поместим начало координат в одну из вершин прямоугольника так, чтобы ось Ох совпадала со стороной а, а ось Оу – со стороной b. Статический
момент прямоугольника относительно стороны а будет равен статическому моменту относительно оси Ох. По первой из формул (11) получаем:
Пример 3. Найти координаты центра тяжести однородной пластины плотности , ограниченной параболой и прямой х+у=2.
Решение: Чертеж области приведен на рис.27. Найдем абсциссы точек пересечения графиков. Из системы получаем и . Тогда масса пластины вычисляется по формуле:
Рис.27.
Вычислим статические моменты пластины относительно координатных осей
Теперь вычисляем по формулам (12) координаты центра тяжести пластины:
Пример 4. Вычислить моменты инерции однородного треугольника со сторонами х+у=1, х+2у=2 , у=0, относительно координатных осей.
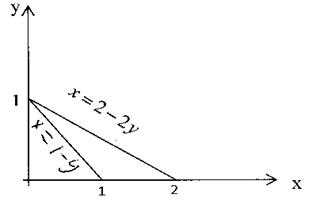
Решение: Треугольник приведен на рис 28. Моменты инерции относительно осей вычисляем по формулам (13):
Рис.28
Пример 5. Найти момент инерции однородной области, ограниченной лемнискатой относительно начала координат.
Решение: Полярный момент инерции вычисляем по формуле (14), при этом в двойном интеграле перейдем к полярным координатам. В результате уравнение лемнискаты в полярных координатах принимает вид , а координата (рис. 29). Тогда получаем:
Рис.29.
1.7. Задачи для самостоятельного решения:
Вычислить двойной интеграл:
1. , где D – прямоугольник .
2. , где D — ограниченна параболой и прямой у=х.
3. , D ограничена линиями , х=0, 2у=3х.
Двойной интеграл представить в виде повторного двумя способами:
4. D – треугольник с вершинами А(-1,-1), В(1,3), С(2,-4).
5. D – параллелограмм с вершинами А(-3,1), В(2,1), С(6,4), D(1,4).
6. D ограничена линиями , .
7. D ограничена линиями .
8. 9.
10. 11.
12. 13.
14. 15.
Выбирая подходящие замены переменных, вычислить двойные интегралы:
16. , где D ограничена линиями , у=х+1, у=х-3.
17. , где D – параллелограмм со сторонами у=х, у=х+3, у=-2х+1, у=-2х+5.
18. , D ограничена кривыми , ху=p, ху=q (0<a<b, 0<p<q).
В двойном интеграле перейти к полярным координатам r и φ (х=rcosφ, y=rsinφ) и расставить пределы интегрирования:
19. D – круг .
20. D – область, ограниченная окружностями и прямыми у=х и у=2х.
21. D –область, ограниченная прямыми у=х, у=-х и у=1.
22. D – общая часть кругов и .
Вычислить двойной интеграл, переходя к полярным координатам:
23. .
24. , D ограничена лемнискатой .
25. , где D – круг .
26. , где D – четверть круга .
Вычислить площади фигур, ограниченных кривыми:
27. , у=х. 28. , .
29., ху=4, х+у-5=0. 30. , х+у=а
31. , у=х, у=0. 32. , у=-1, у=-х.
33. . 34. .
Вычислить объем тела, ограниченного поверхностями:
35. . 36. .
37. .
38.
39. Найти площадь части плоскости , лежащей в первом октанте.
40. Найти площадь части поверхности параболоида , отсекаемой цилиндром и плоскостью х=3а.
41. Найти массу пластинки, ограниченной кривыми , если ее плотность равна ρ(х,у)=х+2у.
42. Вычислить координаты центра тяжести фигуры, ограниченной кардиоидой .
43. Найти координаты центра тяжести однородной пластики, ограниченной параболой и прямой у=2 (а>0).
44. Найти координаты центра тяжести однородной пластинки, ограниченной окружностью и двумя радиусами у=0 и у=хtgα .
45. Найти статический момент однородного полукруга радиуса R, лежащего в плоскости Оху, относительно диаметра.
46. Найти статические моменты относительно осей Ох и Оу однородной пластины, ограниченной кардиоидой и полярной осью.
47. Найти статические моменты однородной пластины, ограниченной кривой y=sinx и прямой ОА, проходящей через начало координат и точку ( ,относительно осей Ох и Оу.
48. Найти моменты инерции прямоугольника ОАСВ со сторонами ОА=а и ОВ=b относительно вершины О и сторон ОА и ОВ, если его плотность равна расстоянию до стороны ОВ, считая, что прямоугольник лежит в плоскости Оуz.
49. Найти моменты инерции однородной пластины, ограниченной эллипсом , относительно осей Ох, Оу и относительно начала координат.
50. Найти полярный момент инерции однородной фигуры, ограниченной кардиоидой .
Глава 2. ТРОЙНЫЕ ИНТЕГРАЛЫ.
infopedia.su
3.Приложения двойных интегралов к задачам
механики.
а) Масса плоской пластинки переменной плотности.
Рассмотрим тонкую пластинку, расположенную на плоскости Оху и занимающую область D. Толщину этой пластинки считаем настолько малой, что изменением плотности по толщине ее можно пренебречь.
Поверхностной плотностью такой пластинки в данной точке называется предел отношения массы площадки к ее площади при условии, что площадка стягивается к данной точке.
Определенная таким образом поверхностная плотность будет зависеть только от положения данной точки, т. е. являться функцией ее координат:
Если бы плотность была постоянной (), то масса всей пластинки равнялась бы, гдеS — площадь пластинки. Найдем теперь массу неоднородной пластинки, считая, что ее плотность является заданной функцией . Для этого разобьем область, занимаемую пластинкой, на частичные области с площадями (рис. 16). Выбирая в каждой частичной области произвольную точку, будем считать, что плотность во всех точках частичной области постоянна и равна плотностив выбранной точке. Составим приближенное выражение для массы пластинки в виде интегральной суммы
(*)
Для точного выражения массы следует найти предел суммы (*) при условии и каждая частичная область стягивается к точке. Тогда
б) Статические моменты и центр тяжести пластинки.
Перейдём теперь к вычислению статических моментов рассматриваемой пластинки относительно осей координат. Для этого сосредоточим в точках массы соответствующих частичных областей и найдем статические моменты полученной системы материальных точек :
Переходя к пределу при обычных условиях и заменяя интегральные суммы интегралами, получим
Находим координаты центра тяжести :
Если пластинка однородна, т.е. то формулы упрощаются :
где S — площадь пластинки.
в) Моменты инерции пластинки.
Моментом инерции материальной точки Р с массой m относительно какой-либо оси называется произведение массы на квадрат расстояния точки Р от этой оси.
Метод составления выражений для моментов инерции пластинки относительно осей координат совершенно такой же, какой мы применяли для вычисления статических моментов. Приведем поэтому только окончательные результаты, считая, что :
Отметим еще, что интеграл называется центробежным моментом инерции; он обозначается .
В механике часто рассматривают полярный момент инерции точки, равный произведению массы точки на квадрат ее расстояния до данной точки — полюса. Полярный момент инерции пластинки относительно начала координат будет равен
4. Вычисление площадей и объёмов с помощью двойных интегралов.
а) Объём.
Как мы знаем, объем V тела, ограниченного поверхностью , где — неотрицательная функция, плоскостьюи цилиндрической поверхностью, направляющей для которой служит граница областиD, а образующие параллельны оси Oz, равен двойному интегралу от функции по областиD :
Пример 1. Вычислить объем тела, ограниченного поверхностями x=0, у=0, х+у+z=1, z=0 (рис. 17).
Рис.17 Рис.18
Решение. D — заштрихованная на рис. 17 треугольная область в плоскости Оху, ограниченная прямыми x=0, у=0, x+y=1. Расставляя пределы в двойном интеграле, вычислим объем:
Итак, куб. единиц.
Замечание 1. Если тело, объем которого ищется, ограничено сверху поверхностью а снизу—поверхностью, причем проекцией обеих поверхностей на плоскостьОху является область D, то объем V этого тела равен разности объемов двух “цилиндрических” тел; первое из этих цилиндрических тел имеет нижним основанием область D, а верхним — поверхность второе тело имеет нижним основанием также областьD, а верхним — поверхность (рис.18).
Поэтому объём V равен разности двух двойных интегралов :
или
(1)
Легко, далее, доказать, что формула (1) верна не только в том случае, когда инеотрицательны, но и тогда, когдаи- любые непрерывные функции, удовлетворяющие соотношению
Замечание 2. Если в области D функция меняет знак, то разбиваем область на две части: 1) областьD1 где 2) область D2 ,где . Предположим, что областиD1 и D2 таковы, что двойные интегралы по этим областям существуют. Тогда интеграл по области D1 будет положителен и будет равен объему тела, лежащего выше плоскости Оху. Интеграл по D2 будет отрицателен и по абсолютной величине равен объему тела, лежащего ниже плоскости Оху, Следовательно, интеграл по D будет выражать разность соответствующих объемов.
б) Вычисление площади плоской области.
Если мы составим интегральную сумму для функции по областиD, то эта сумма будет равна площади S,
при любом способе разбиения. Переходя к пределу в правой части равенства, получим
Если область D правильная , то площадь выразится двукратным интегралом
Производя интегрирование в скобках, имеем, очевидно,
Пример 2. Вычислить площадь области, ограниченной кривыми
Рис.19
Решение. Определим точки пересечения данных кривых (Рис.19). В точке пересечения ординаты равны, т.е. , отсюдаМы получили две точки пересечения
Следовательно, искомая площадь
studfiles.net
Приложения двойного интеграла.
Площадь плоской фигуры
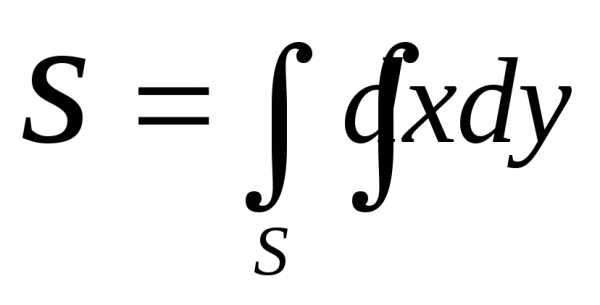 (6)
(6)
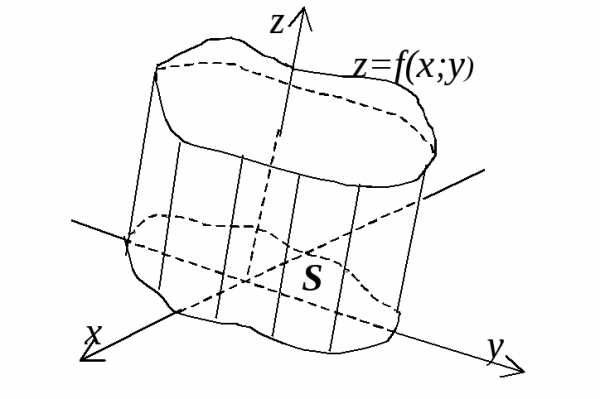
 Объем
цилиндрического тела, снизу ограниченного
частью S плоскости (ху),
сверху – поверхностью z=f(x;y),
а с боков цилиндрической поверхностью,
образующие которой параллельны оси Oz:
Объем
цилиндрического тела, снизу ограниченного
частью S плоскости (ху),
сверху – поверхностью z=f(x;y),
а с боков цилиндрической поверхностью,
образующие которой параллельны оси Oz:
(7)
Масса плоской пластинки, занимающей область S и плотность которой задается функцией ху
(8)
Координаты центра тяжести плоской пластины С(хс;ус)
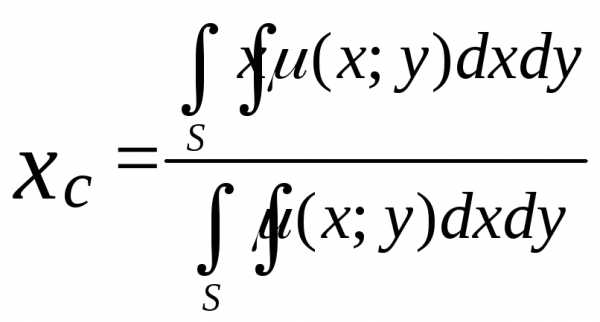 ;
; 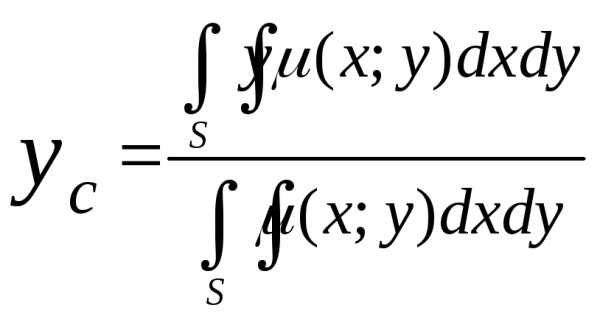 (9)
(9)
Момент инерции плоской пластины относительно координатных осей
; (10)
Пример. Вычислить площадь плоской фигуры, ограниченной линиями: х=0, у=5, у=х2+1.
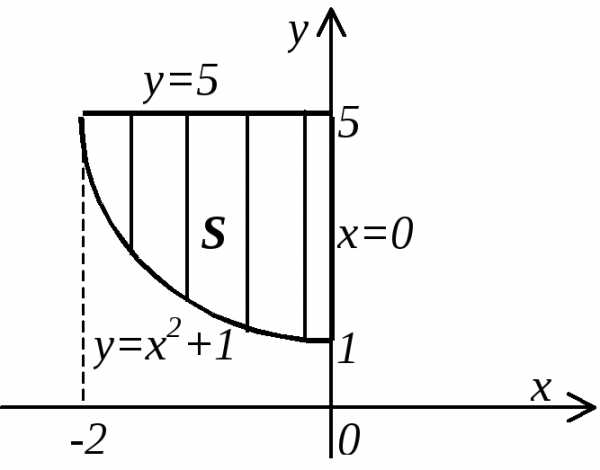
;
Пример. Вычислить массу плоской пластины ограниченной линиями x=0, y=0, y=1-x2, если ее плотность в каждой точке равна абсциссе этой точки, =х;
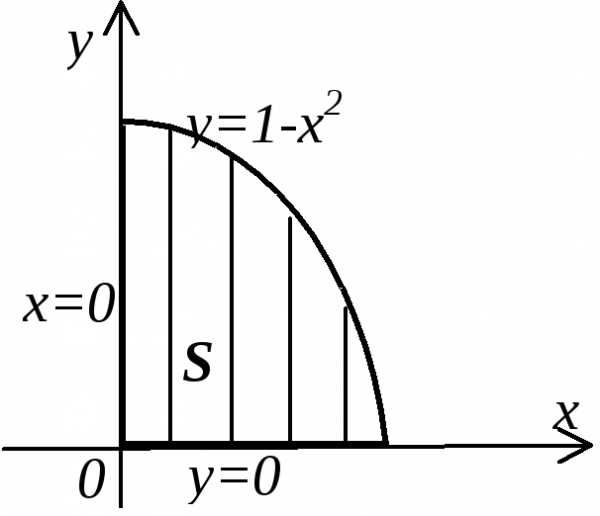
;
Пример. Вычислить координаты центра тяжести однородной пластинки, ограниченной линиями x=0, y=0, y=1-x2,=const.
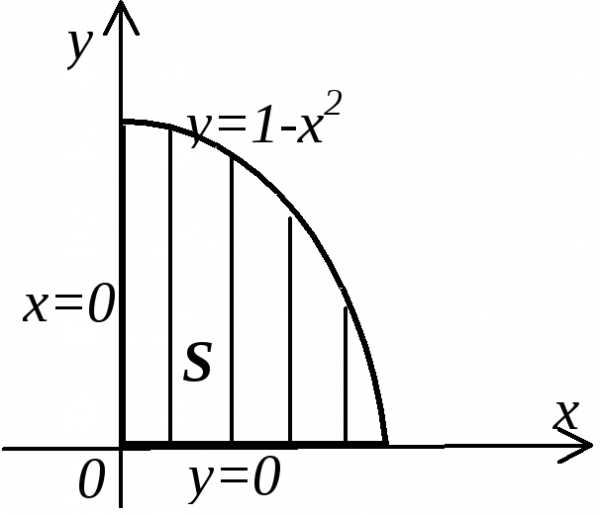 ;
;
;
;
 ;
; 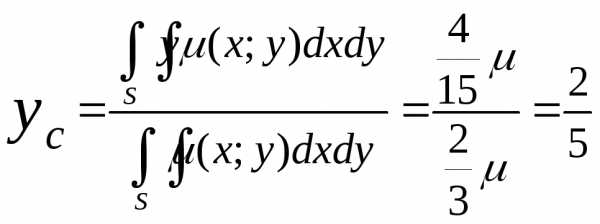 ;
;
C .
.
ТРОЙНОЙ ИНТЕРГРАЛ
Пусть в ограниченной замкнутой пространственной области V задана непрерывная функция f(x;y;z). Тогда тройной интеграл от этой функции определяется как
(11)
Пусть область V снизу ограниченна поверхностью z1(x;y), а сверху – поверхностью z2(x;y), причем 1(x;y)2(x;y). Проекция Vxy области V на плоскость хОу ограничена линиями: x=a, x=b, y=1(x), y=2(x), где аb 1х2х хa, b.
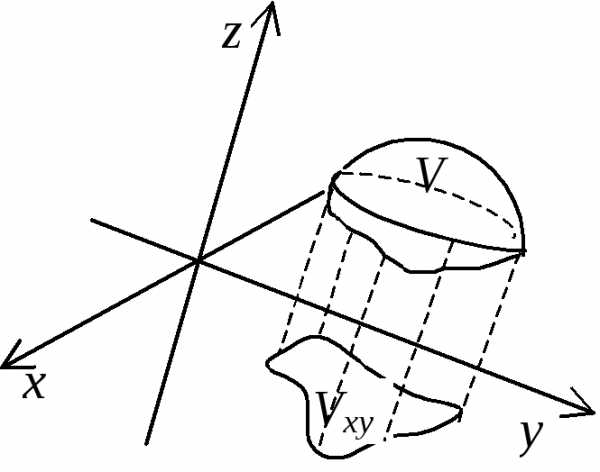
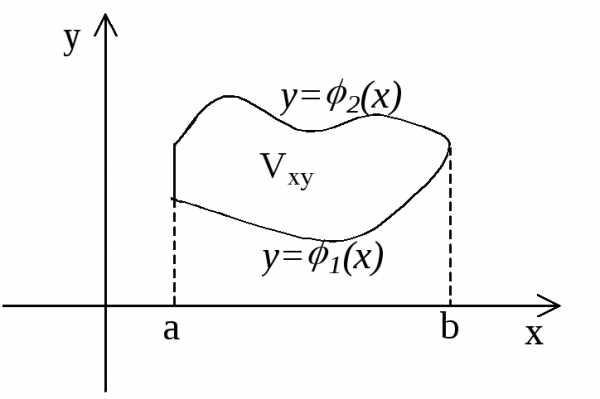
Тогда тройной интеграл вычисляется по формуле
(12)
Элемент объема dV в декартовой системе координат равен произведению дифференциалов декартовых координат dV=dxdydz. Формула (12) обычно записывается в виде
(13)
При вычислении интеграла по одной из переменных все другие считаются постоянными
Пример.
Вычислить 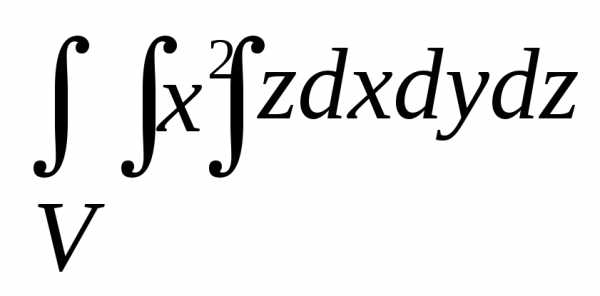 ,
гдеV ограничена поверхностями: x=0, y=0, y=3x, z=0, z=xy.
,
гдеV ограничена поверхностями: x=0, y=0, y=3x, z=0, z=xy.
Первые четыре уравнения в пространстве задают плоскости, пятое – гиперболический параболоид.
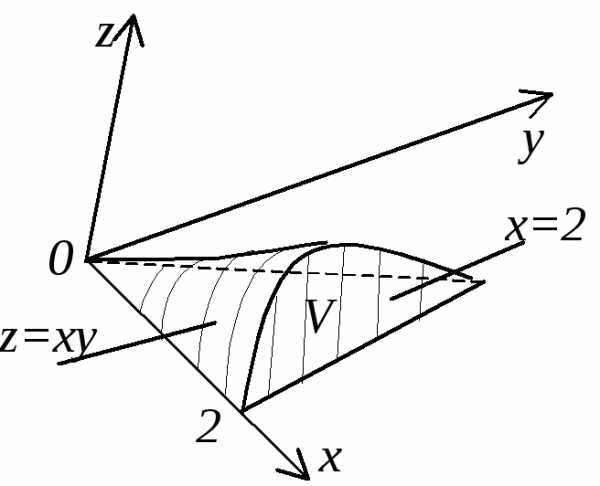
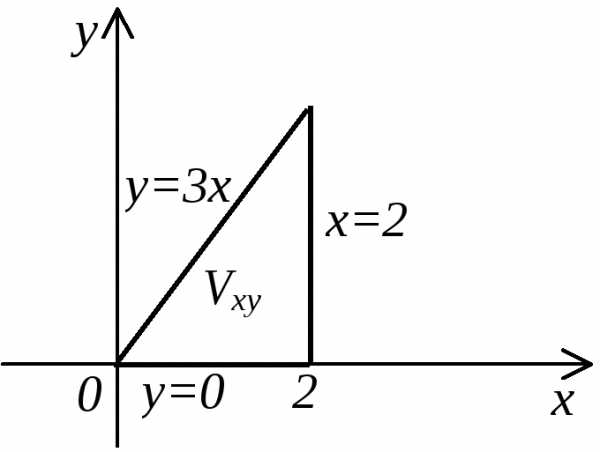
По формуле (13) расставляем пределы интегрирования:
Последовательно вычисляем три определенных интеграла:
;
;
; Таким образом:
.
Часто бывает удобным при вычислении тройного интеграла применять другой порядок интегрирования. Так, если V ограничена поверхностями x1(y;z) и x2(y;z), а ее проекция Vyz на координатную плоскость yOz ограничена линиями: y=a, y=b, z=1(y), z=2(y), то вычисление тройного интеграла удобнее проводить по формуле:
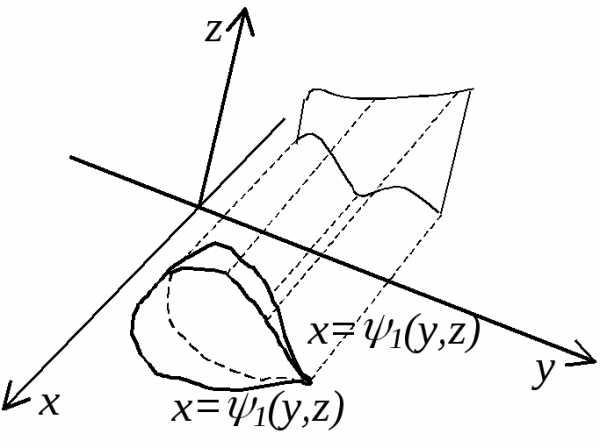
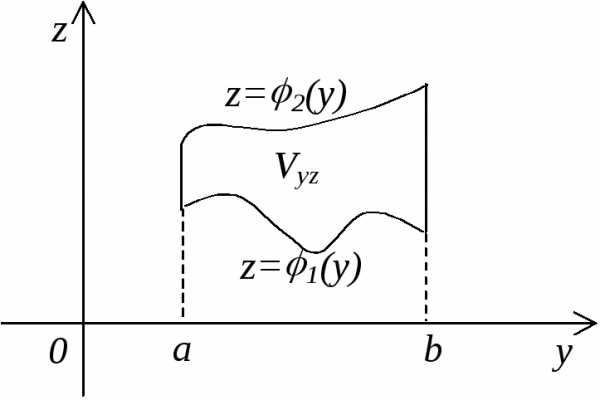
(14)
Приложения тройного интеграла
Объем тела, занимающего пространственную область V:
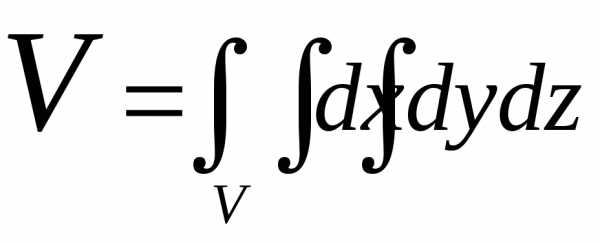 (15)
(15)
Масса тела плотностью (x;y;z):
(16)
Статические моменты тела с плотностью (x;y;z) относительно координатных плоскостей:
; ;(17)
Координаты центра тяжести объемного тела C(xc; yc; zc):
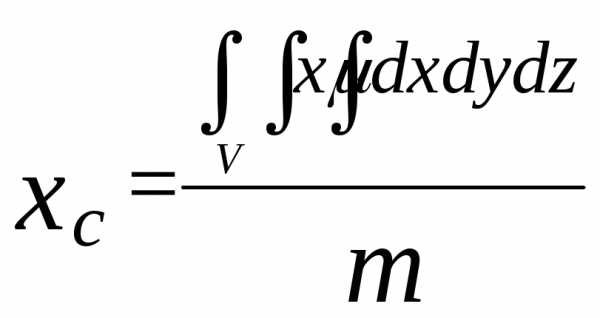 ;
; 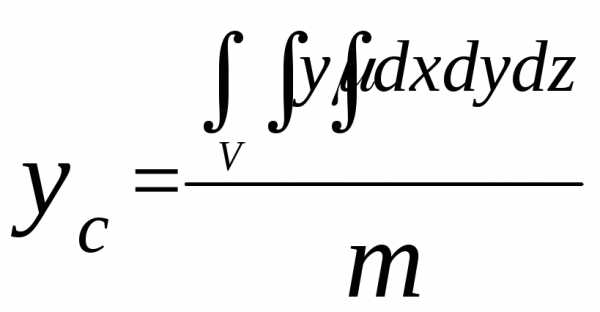 ;
;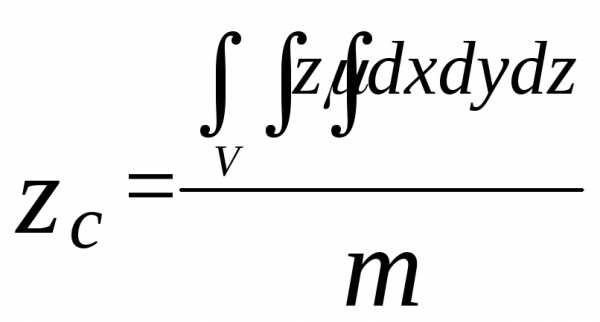 (18)
(18)
Часто для вычисления тройного интеграла удобнее перейти к другой системе координат.
studfiles.net
1.4 Приложения двойного интеграла
Объём тела
Объём цилиндрического тела находится по формуле
,
где — уравнение поверхности, ограничивающей тело сверху.
Площадь плоской фигуры
Если в вышеуказанной формуле положить , то цилиндрическое тело превратится в прямой цилиндр с высотойh=1. Объём такого цилиндра численно равен площадиS основанияD. Получаем формулу для вычисления площади областиD
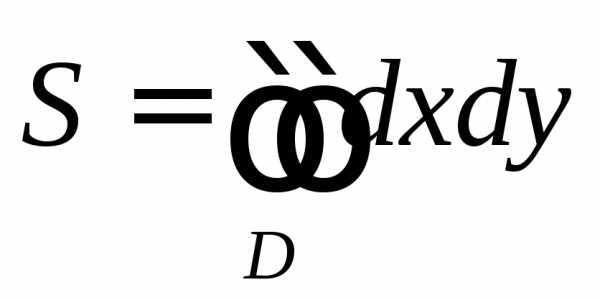
В полярных координатах
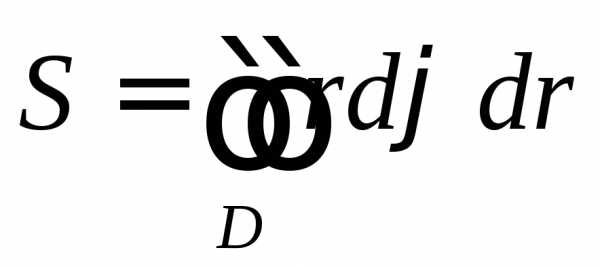
Масса плоской пластины(физ. смысл двойного интеграла).
Если плоская пластина Dимеет плотность, определённую функцией, то масса пластины находится по формуле
Статические моменты и координаты центра тяжести плоской фигуры.
Пусть на плоскости Oxyзадана система материальных точексоответственно с массами.
Определение. Статическим моментом Sxсистемы материальных точек относительно осиOxназывается сумма произведений масс этих точек на их ординаты (т.е. на расстояние этих точек от осиOx).
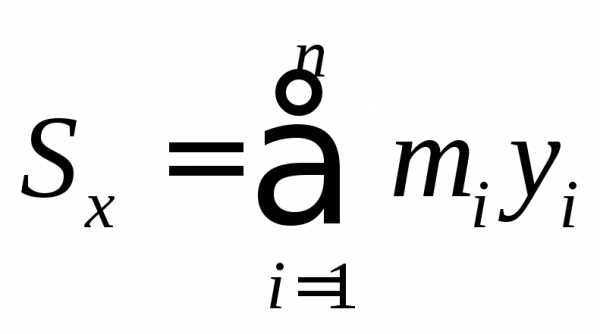
Аналогично определяется статический момент Syэтой системы относительно осиOy
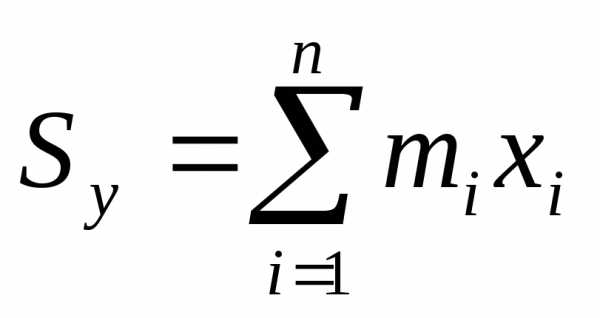
Статические моменты плоской фигуры D с переменной плотностьюотносительно осейOx иOyмогут быть вычислены по формулам
,
а координаты центра масс по формулам
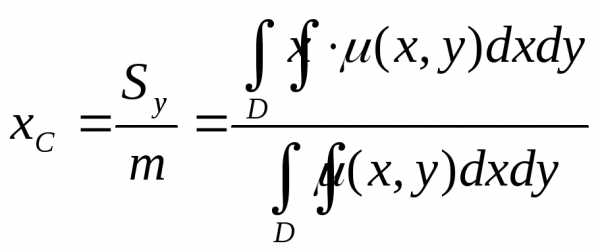
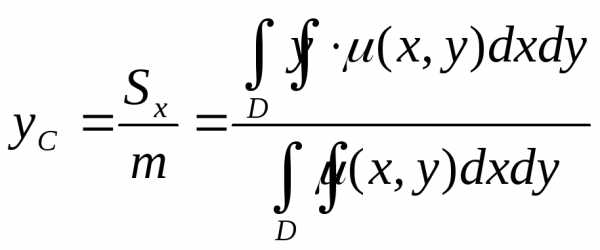
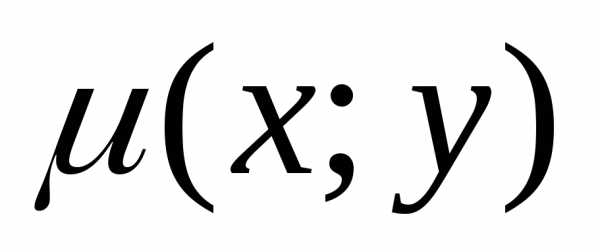 — плотность.
— плотность.
Если пластина Dоднородная, то в формуле, т.е.
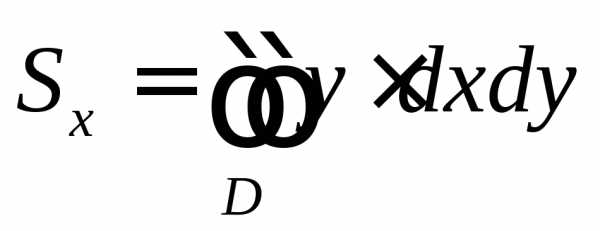
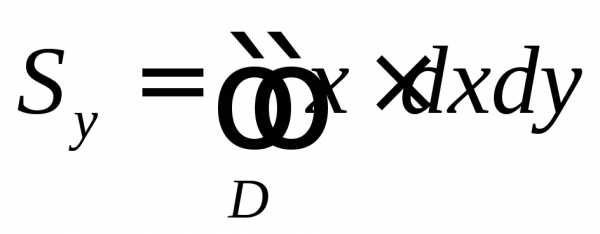
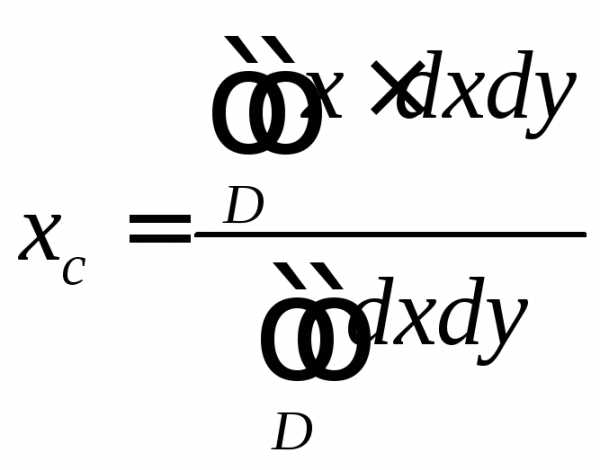
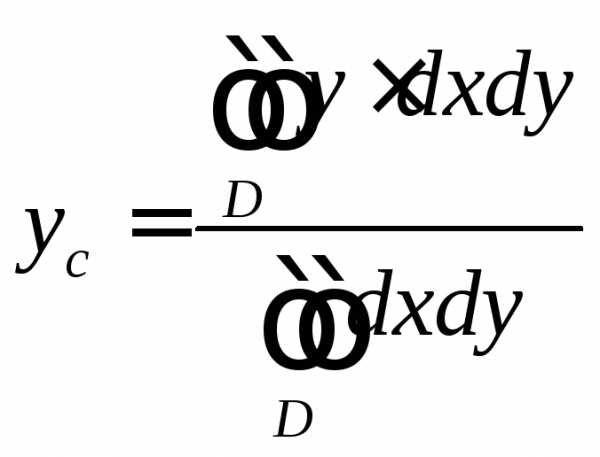
Момент инерции плоской фигуры
Определение.
Моментом инерции материальной точки
массы mотносительно
оси lназывается
произведение массы на квадрат расстоянияdточки до оси, т.е.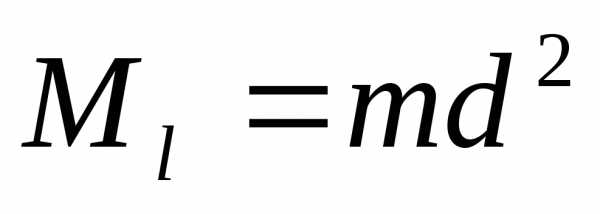 .
.
Момент инерции плоской фигуры относительно осей OxиOy могут быть вычисленные по формулам
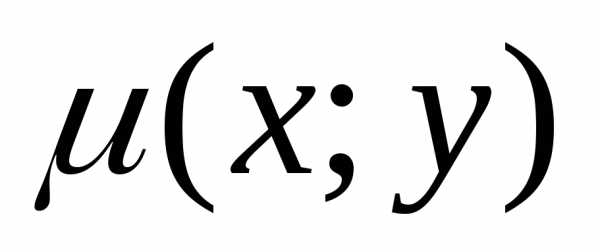 — функция плотности.
— функция плотности.
Момент инерции фигуры относительно начала координат определяется по формуле.
Пример: Найти массу пластины ограниченной областью (рис. 11)
, ,.
Плотность пластинки 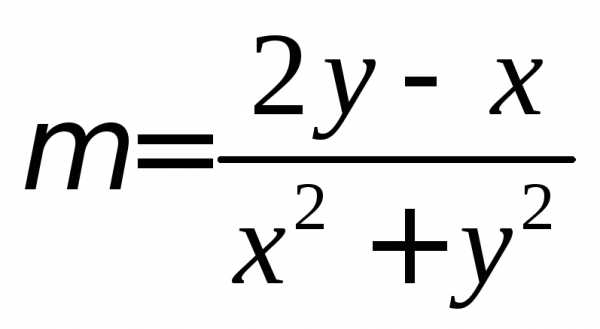 .
.
Р
Рис. 11
ешение:Массу вычисляем по формуле .
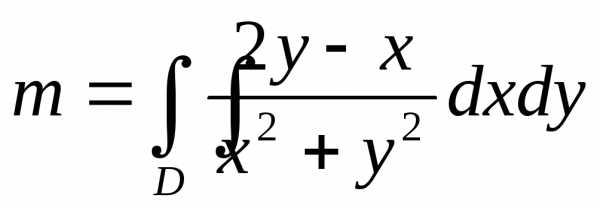 .
Так как пластинка часть кольца,
целесообразно перейти в полярную
систему координат. Формулы перехода:
.
.
Так как пластинка часть кольца,
целесообразно перейти в полярную
систему координат. Формулы перехода:
.
— функция плотности в полярной системе координат. r=3, r=5–уравнения окружностей в полярной системе координат. Составляем интеграл:
1.5 Тройной интеграл
Обобщением определенного интеграла на случай функции трех переменных является так называемый «тройной интеграл». Теория тройного интеграла аналогична теории двойного.
Понятие тройного
интеграла связано с задачей о массе
неоднородного тела. Если тело однородно,
т.е. в каждой точке плотность одна и та
же, то масса М тела находится по формуле  .
Определим массу неоднородного тела V,
с переменной плотностью ρ=f(x,y,z).
.
Определим массу неоднородного тела V,
с переменной плотностью ρ=f(x,y,z).
Р
Рис. 12
азобьем областьV сеткой поверхностей на n частей . Рассмотрим элементарную область (рис.
12). Так как
(рис.
12). Так как 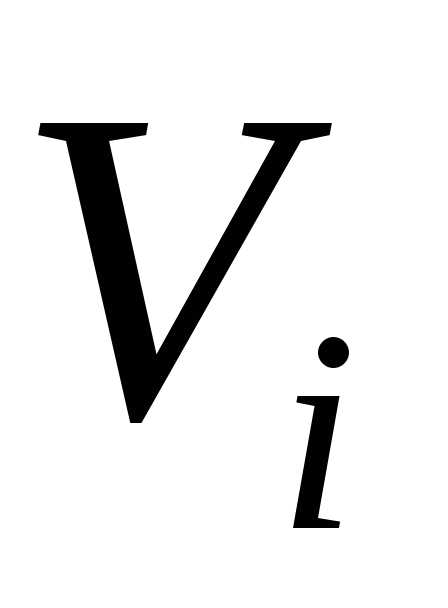 можно считать параллелепипедом со
сторонами
,
то объем элементарной области будет
равен
.
можно считать параллелепипедом со
сторонами
,
то объем элементарной области будет
равен
.Выберем произвольную точку в каждой элементарной области. В силу того, что область очень мала, считаем плотность постоянной и равной значению функции ρ=f(x,y,z) в точке , т.е. . Тогда масса элементарной области находится по формуле . Масса всего тела будет складываться из масс элементарных областей, т.е. .
Будем неограниченно увеличивать n (), получим .
Если этот предел существует, то он называется тройным интегралом и обозначается
(-элемент объема).
Теорема. Если функция f(x,y,z) непрерывна в ограниченной замкнутой области V , то предел интегральной суммы существует и не зависит ни от способа разбиения области V на части, ни от выбора точек в них.
Физический смысл тройного интеграла:
Если функция f(x,y,z) непрерывна и показывает плотность распределения вещества в замкнутой области V, то масса всего вещества, заключенного в области, вычисляется с помощью тройного интеграла
.
studfiles.net
Вычислить массу неоднородной пластины D, ограниченной линиями:
x=0, y=0, x+y=2, если поверхностная плотность в каждой ее точке \(\mu =x^2+y^2\)
Решение:
Для вычисления массы m плоской пластины поданной поверхностной плотностью \(\mu\) воспользуемся физическим содержанием двойного интеграла и формулой:
\(\mu=\int \int_{D}{(x^2+y^2)}dxdy\),
где область интегрирования D показана на рисунке 1.1
Рисунок 1.1
\(m=\int \int_{D}^{}{}\left(x^{2} +y^{2}\right)dxdy=\int_{0}^{2}{dx}\int_{0}^{2-x}{\left(x^{2} +y^{2}\right)}dy=\int_{0}^{2}{\left(x^{2}y+\frac{y^{3}}{3} \right)}\mid_{0}^{2-x}dx=\)
\(=\int_{0}^{2}{\left(x^{2} \left(2-x \right)+\frac{\left(2-x \right)^{3}}{3}\right)}dx=\int_{0}^{2}{\left(2x^{2}-x^{3}+\frac{\left(2-x \right)^{3}}{3} \right)}dx=\)
\(=\int_{0}^{2}{2x^{2}}dx-\int_{0}^{2}{x^{3}dx}+\int_{0}^{2}{\left(\frac{\left(2-x^{3}
\right)}{3}
\right)}dx=\frac{2x^{3}}{3}\mid_{0}^{2}-\frac{x^{4}}{4}\mid_{0}^{2}+\frac{\left(2-x
\right)^{4}}{12}\mid_{0}^{2}=\)
\(=\frac{16}{3}-\frac{16}{4}+\frac{16}{12}=\frac{\left(4-3+1 \right).16}{12}=\frac{32}{12}=\frac{8}{3}\)
2012-12-25 • Просмотров [ 18465 ]
primat.org

 Объем
цилиндрического тела, снизу ограниченного
частью S плоскости (ху),
сверху – поверхностью z=f(x;y),
а с боков цилиндрической поверхностью,
образующие которой параллельны оси Oz:
Объем
цилиндрического тела, снизу ограниченного
частью S плоскости (ху),
сверху – поверхностью z=f(x;y),
а с боков цилиндрической поверхностью,
образующие которой параллельны оси Oz: