Урок 13. производные элементарных функций — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №13. Производные элементарных функций.
Перечень вопросов, рассматриваемых в теме
1) определение элементарной функции;
2) производная показательной функции;
2) производные тригонометрических функций;
3) производная логарифмической функции.
Глоссарий по теме
Элементарными функциями называют степенную, показательную, логарифмическую и тригонометрические функции, а также их различные комбинации.
- (ex) ‘= ex
- (ekx+b) ‘=kekx+b
- (ax) ‘=axlna
- (sin x) ‘=cosx
- (cos x) ‘= -sinx
Основная литература:
Колягин Ю.
Дополнительная литература:
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Элементарными функциями называют степенную, показательную, логарифмическую и тригонометрические функции, а также их различные комбинации. При решении многих практических задач часто приходится находить производные таких функций.
1.Производная показательной функции.
Показательная функция f(x)=ax, где а>0, a ≠1, определена на всей числовой прямой и имеет производную в каждой ее точке. Любую показательную функцию можно выразить через показательную функцию с основанием у по формуле:
ax=exln a (1)
так как exln a= (eln a)х= ах.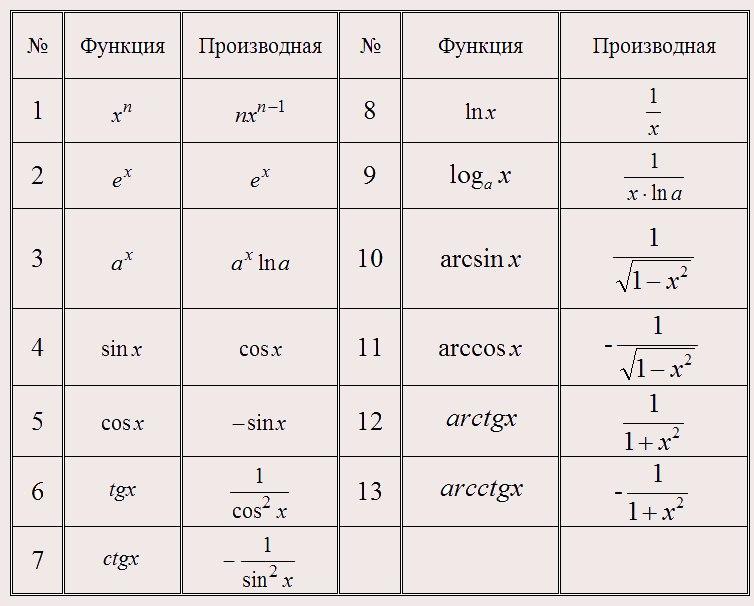
Стоит отметить свойств о функции ех: производная данной функции равна ей самой
(ex) ‘= ex. (2)
Применяя правило дифференцирования сложной функции, получим:
(ekx+b) ‘ = kekx+b. (3)
Производная для ax:
(ax) ‘ = axlna. (4)
2.Производная логарифмической функции.
Логарифмическую функцию с любым основанием а > 0, а≠ 1 можно выразить через логарифмическую функцию с основанием е с помощью формулы перехода
(5)
Производная функции lnх выражается формулой
(6)
Применяя правило дифференцирования сложной функции, получаем
(7)
(8)
3.Производные тригонометрических функций.
Для тригонометрических функций справедливы следующие равенства:
(sin x)’=cosx (9)
(cos x)’= -sinx (10)
Примеры и разбор решения заданий тренировочного модуля
Найти производную:
- f(x) = 3lnx
Решение:
Ответ:
- f(x) = 3·e2x
Решение: (3e2x) ‘ = 3·2· e2x = 6 ·e2x
Ответ: 6 ·e2x
- f(x) = 2x
Решение: (2x) ‘ = 2xln2
Ответ: 2xln2
Решение:
Ответ:
- f(x) = sin (2x+1) — 3cos(1-x)
Решение: (sin (2x+1) — 3cos(1-x)) ‘ = 2cos(2x+1) — 3sin(1-x)
Ответ: 2cos(2x+1) — 3sin(1-x)
Функции с числом е
Функции с числом е. Друзья! На сайте «Математический тандем» проходит конкурс «Лучший комментатор декабря 2012 года», так что добро пожаловать, будут призы. В данной статье мы с вами рассмотрим задачи, входящие в сотав типовых заданий экзамена по математике, связанные с исследованием функций (где присутствует число е).
Друзья! На сайте «Математический тандем» проходит конкурс «Лучший комментатор декабря 2012 года», так что добро пожаловать, будут призы. В данной статье мы с вами рассмотрим задачи, входящие в сотав типовых заданий экзамена по математике, связанные с исследованием функций (где присутствует число е).
Рекомендую вам ещё раз внимательно прочитать статью «Исследование функций. Это нужно знать!» и освежить в памяти изложенную информацию. Не устану повторять, что для того чтобы решать задачи на нахождение наибольшего или наименьшего значения, задачи на нахождение экстремумов, важно понимать свойства производной для исследования функций, знать таблицу производных и правила дифференцирования.
После решения каждой задачи есть разъяснения другого подхода к решению (я обещал вам «хитрости» — они здесь). Рекомендую посмотреть, выглядит график показательной функции.
Рассмотрим задачи:
Найдите наименьшее значение функции у = (х–17)ех–16
на отрезке [15;17].
Мы знаем, что для того, чтобы найти наибольшее или наименьшее значение функции на отрезке, необходимо вычислить её значение на границах заданного интервала и в точках, где производная равна нулю. Действуем по алгоритму:
1. Найдём производную заданной функции:
2. Найдем нули производной на заданном отрезке, то есть приравниваем производную к нулю и вычислим корни уравнения:
*Выражение ех-16 не равно нулю ни при каких х, так как известно, что показательная функция имеет положительные значения на всей области определения.
3. Определяем принадлежит ли найденная точка интервалу.
Точка х = 16 принадлежит интервалу [15;17]. Значит значение функции будем вычислять в точках 15, 16 и 17:
*Учтите, что число е ≈ 2,71. Это нецелое число и неконечная десятичная дробь, поэтому любое выражение с этим числом в подобных задачах на ЕГЭ не является верным ответом, но вы всё равно его проанализируйте. В данной задаче, если мы –2 разделим на число 2,71 то результат будет лежать в пределах от –1 до 0 (можно посчитать столбиком для проверки).
4. Делаем вывод.
Таким образом, наименьшее значение функции равно –1.
Ответ: –1
В этой статье я обещал вам какие-то там «хитрости», которые можно использовать при решении. Если вы поняли теорию производной и знаете, как находить максимальные и минимальные значения, то тогда читайте дальше — представленный приём будет хорошим дополнительным «инструментом» и позволит решать подобные задания мгновенно.
Итак! Мы знаем, что ответом в задачах на ЕГЭ в части В должно быть целое число, либо конечная десятичная дробь.
Посмотрите на данную функцию. Сразу можно сказать, что значение функции будет являться целым числом только при х = 16 или при х = 17, и ни при каких других значениях х. Поэтому достаточно вычислить:
и далее записать ответ.
Ещё один путь решения (без нахождения производной). Сразу подставляем в функцию все целые значения из интервала (их всего три 15, 16 и 17), вычисляем и выбираем наименьшее значение:
Решите самостоятельно:
Посмотреть решение
Найдите точку минимума функции у = (х + 18)ех-18
1. Найдём производную заданной функции:
Найдём производную заданной функции:
2. Найдем нули производной:
Получаем, что х = –19.
*Выражение ех-18 не равно нулю ни при каких х, так как известно, что показательная функция имеет положительные значения на всей области определения.
3. Определим знаки производной функции на интервалах (подставляем любые произвольные значения в производную) и изобразим на рисунке поведение функции:
В точке х = –19 функция меняет знак с отрицательного на положительный, значит это искомая точка минимума.
Ответ: –19
Как решать быстрее данный тип задач?
Когда мы получили производную и приравняли её к нулю:
(х + 19)ех–18 = 0
Далее получили, что х=–19. Данное решение и будет являться ответом задачи.
*То есть, в при решении данного типа задач, можно обойтись без определения знаков производной на интервалах. Но будьте осторожны! В других заданиях на нахождение максимума (минимума), где получите несколько нулей производной, её знаки на интервалах нужно определять обязательно.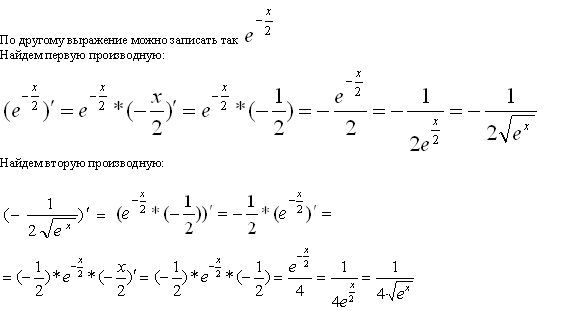
Решите самостоятельно:
Посмотреть решение
Найдите точку максимума функции у = (3х2 – 15х + 15)е7–х
Найдём производную заданной функции:
Найдем нули производной:
Число е7-х не может быть равно нулю, так как степень положительного числа всегда даст в результате число положительное.
Решаем – 3 (х–5)(х–2) = 0. Получим х1 = 5 и х2 = 2 .
Определим знаки производной функции (подставляя любые значения из интервалов в найденную производную) и изобразим на рисунке поведение функции:
В точке х = 5 функция меняет знак с положительного на отрицательный, значит это искомая точка максимума.
Ответ: 5
Решите самостоятельно:
Посмотреть решение
Найдите наибольшее значение функции у = (22 – х)ех–21
на отрезке [16;25].
Найдём производную заданной функции:
Найдем нули производной:
Число ех-21 не может быть равно нулю, так как степень положительного числа всегда даст в результате число положительное, значит х = 21.
Полученное значение принадлежит интервалу [16;25].
Вычислим значения данной в условии функции в точках 16, 21 и 25:
*То есть на границах интервала и в точке, где производная обращается в нуль.
Первый результат меньше единицы (это понятно и без вычислений).
Третий результат так же меньше единицы (отрицательное число).
Значит наибольшее значение функции на заданном интервале равно 1.
*Помните, что ответы с числом е (по требованиеям ЕГЭ) не являются верными.
Ответ: 1
Если у вас всё-таки неразрешимые проблемы с нахождением производной, то подставляйте в исходную функцию все целые значения из интервала и выбирайте наибольшее полученное значение.
*Кроме того, по данной функции сразу видно, что её значение будет целым числом только при х = 21 или при х = 22.
Можете подставить только их в функцию, далее произвести вычисления и выбрать наибольшее значение.
Решите самостоятельно:
Посмотреть решение
Найдите наибольшее значение функции у = (2х2 – 10х + 10)е х
на отрезке [–4; 3].
Необходимо определить значения на границах интервала, и в точках, где производная обращается в нуль.
Найдём производную заданной функции:
Найдем нули производной:
Произведение множителей равно нулю, когда какой либо из этих множителей равен нулю.
Число ех не может быть равно нулю, так как степень положительного числа всегда даст в результате число положительное.
Значит решением являются корни: х1=0 и х2=3
Обе точки принадлежат интервалу [–4;3], х=3 совпадает с границей интервала.
Вычисляем значения функции в точках: – 4, 0 и 3:
Значит наибольшее значение функции равно 10.
Ответ: 10
*Как вы уже поняли, можно в заданную функцию можно подставить все целые значения х из интервала, и таким образом найти наибольшее значение функции. Но в данном случае придётся перебрать 8 чисел (–4;–3;–2;–1;0;1;2;3).
Решите самостоятельно:
Посмотреть решение
Найдите наименьшее значение функции у = (х + 44)2е–44–х
на отрезке [– 46; –43]
Найдём производную заданной функции:
Обратите внимание, что результат мы представили сразу в виде множителей, это будет удобно при вычислении нулей производной.
Найдем нули производной:
Решением являются корни: х1= – 44 и х2= – 42.
Заданному интервалу [– 46;–43] принадлежит только точка х = – 44.
Вычисляем значения функции в точках – 46, – 44 и – 43, то есть на границах интервала и в точке, где производная равна нулю:
Наименьшее значение функции равно 0.
Ответ: 0
*Как это задание решить быстро?
Учитывая, что ответом должно быть целое число, видно что значение данной функции будет целым только при х= – 44 и х= 44.
указанному в условии интервалу принадлежит х= – 44, вычисляем:
Решите самостоятельно:
Посмотреть решение
В данной рубрике продолжим рассматривать задачи, не пропустите!
На этом закончим. Всем удачи!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Число е | Материалы для подготовки к ЕГЭ по математике ЕГЭ-Студия
С замечательным числом e мы впервые встречаемся, начиная изучать показательную функцию, логарифмы и производные. Поэтому для лучшего понимания мы рекомендуем вам прочитать наши статьи «Показательная функция» и «Геометрический смысл производной».
В статье «Показательная функция» мы говорили о важнейшем свойстве функции — при эта функция очень быстро растет. И не просто «быстро растет» — чем больше x, тем больше скорость ее роста, тем круче идет график. Можно сказать, что с увеличением x растут и значения показательной функции, и ее производная. А если аргументом показательной функции является время, то при такая функция является математическим выражением стремительно развивающегося процесса.
И не просто «быстро растет» — чем больше x, тем больше скорость ее роста, тем круче идет график. Можно сказать, что с увеличением x растут и значения показательной функции, и ее производная. А если аргументом показательной функции является время, то при такая функция является математическим выражением стремительно развивающегося процесса.
Среди показательных функций есть особенная. Называется она экспонента, ее формула . Особенность ее в том, что в каждой точке скорость роста этой функции равна значению самой функции в этой точке. Другими словами, , то есть производная функции равна ей самой.
Нарисуем несколько графиков функции при , а также при . Среди этих графиков есть такой, что касательная к нему, проведенная в точке , идет ровно под углом к положительному направлению оси OX.
Это и есть график функции . Само число e — иррациональное, то есть выражается бесконечной непериодической десятичной дробью. Приблизительно оно равно 2,718.
Логарифм по основанию e называется натуральным и обозначается . Если в уравнении или неравенстве вам встретились такие логарифмы, вы работаете с ними так же, как и с любыми другими, у которых основание больше 1.
Функция также обладает интересным свойством:
Это значит, что с ростом x график логарифмической функции идет более и более полого, скорость роста его уменьшается, что мы и видим.
Число e, как и число , является одной из мировых констант. Так называют числа, которые можно встретить в математических формулах, выражающих фундаментальные законы природы, — в физике, статистике, биологии или экономике.
Число известно людям с глубокой древности. Оно равно отношению длины окружности к ее диаметру. А вот с числом e (названным так в честь великого математика Леонарда Эйлера) человечество познакомилось намного позже. Впервые его вычислил математик Якоб Бернулли в начале XVIII века, причем сделал это, решая чисто практическую задачу о начислении процентов на банковский вклад.
В заданиях вариантов ЕГЭ вам встречались задачи, где вклад величиной x помещен в банк под p % годовых. Найти нужно было, например, каким станет вклад через два года. Рассказывая о решении таких задач, мы вывели удобные формулы:
если величину x дважды увеличить на p процентов, получим Именно таким станет вклад через два года;
если вклад пролежит в банке n лет, его величина станет равной
Итак, если вклад поместить банк под 10% годовых, он вырастет за год в 1,1 раз, за два года — в 1,21 раза, за десять — примерно в 2,6 раза. Значит, рост вклада зависит от того, сколько он пролежит в банке, то есть сколько раз начисляются проценты. А что будет через сто лет? А если найти такой банк, где процент начисляется не раз в год, а раз в день? И пусть даже каждый день начисляется совсем небольшой процент, но ведь дней-то много! Верно ли, что можно положить в такой банк один доллар под одну сотую процента в день, а через пару десятков лет забрать из банка миллион?
Давайте так и сформулируем задачу.
? И к чему будет стремиться величина , если n стремится к бесконечности?
Вот такую задачу и решал Бернулли. Если n будет очень большим, или, как говорят математики, бесконечно большим, будет стремиться к бесконечности (то есть больше миллиона, больше миллиарда, больше двух миллиардов. . . ) — то величина будет, наоборот, очень малой. Можно сказать, что будет стремиться к нулю.
Оказывается, что в этом случае величина будет стремиться к числу e. Если банк каждый год начисляет по 1%, через 100 лет вклад увеличится примерно в e раз (напомним, что e ≈ 2,718). Еще большая точность будет достигнута, если каждый день банк начисляет по 0,01 процента. Через 10000 дней вклад увеличится примерно в e раз. Итак, если 
Этот неожиданный факт называется вторым замечательным пределом. Вы встретитесь с ним в курсе математического анализа.
Производная и первообразная показательной функции: число е и примеры
График показательной функции представляет собой кривую плавную линию без изломов, к которой в каждой точке, через которую она проходит, можно провести касательную. Логично предположить, что если можно провести касательную, значит функция будет дифференцируема в каждой точке своей области определения.
Отобразим в одних координатных осях несколько графиков функции y = xa, Для а = 2; a = 2,3; a = 3; a = 3,4.
В точке с координатами (0;1). Углы наклона этих касательных будут равны приблизительно 35, 40, 48 и 51 градусов соответственно. Логично предположить, что на интервале от 2 до 3 существует число, при котором угол наклона касательной будет равен 45 градусов.
Дадим точную формулировку этого утверждения: существует такое число большее 2 и меньшее 3, обозначаемое буквой е, что показательная функция y = ex в точке 0, имеет производную равную 1. То есть: (e∆x-1) / ∆x стремится к 1 при стремлении ∆х к нулю.
То есть: (e∆x-1) / ∆x стремится к 1 при стремлении ∆х к нулю.
Данное число e является иррациональным и записывается в виде бесконечной непериодической десятичной дробью:
e = 2,7182818284…
Так как число е положительно и отлично от нуля, то существует логарифм по основанию e. Данный логарифм называется натуральным логарифмом. Обозначается ln(x) = loge(x).
Производная показательной функции
Теорема: Функция ex дифференцируема в каждой точке своей области определения, и (ex)’ = ex.
Показательная функция ax дифференцируема в каждой точке своей области определения, и причем (ax)’ = (ax)*ln(a).
Следствием из этой теоремы является тот факт, что показательная функция непрерывна в любой точке своей области определения.
Пример: найти производную функции y = 2x.
По формуле производной показательной функции получаем:
(2x)’ = (2x)*ln(2).
Ответ: (2x)*ln(2).
Первообразная показательной функции
Для показательной функции ax заданной на множестве вещественных чисел первообразной будет являться функция (ax)/(ln(a)).
ln(a) – некоторая постоянная, тогда (ax / ln(a))’= (1 / ln(a)) * (ax) * ln(a) = ax для любого х. Мы доказали эту теорему.
Рассмотрим пример на нахождение первообразной показательной функции.
Пример: найти первообразную к функции f(x) = 5x. Воспользуемся формулой приведенной выше и правилами нахождения первообразных. Получим: F(x) = (5x) / (ln(5)) +C.
Ответ: (5x) / (ln(5)) + C.
Нужна помощь в учебе?
Предыдущая тема: Понятие об обратной функции: график функции и теорема
Следующая тема:   Производная и первообразная логарифмической функции: примеры и алгоритм
Задание 14 (№ 3773) — smartrepetitor.
 ru
ruНайдите точку максимума функции y = (х + 16) · е х — 16
Решение
- Данная задача решается по следующему алгоритму:
1)Находим производную от данной функции;
2)Находим стационарные точки, то есть точки, в которых производная равна нулю, эти точки являются экстремумами (экстремумы – это точки, в которых функция принимает наибольшее или наименьшее значение на выбранном отрезке).
3)Выбираем из всех найденных точек те, которые попадают в исследуемый отрезок.
4)Находим значение данной функции в выбранных точках.
5)Выбираем среди них наименьшее (минимум) или наибольшее (максимум), это зависит от условия задачи.
- Теперь по этим пунктам начинаем решать нашу задачу.
- В первую очередь найдем производную функции. Для этого нам необходимо уметь находить производную от произведения, суммы, сложной функции, математических функций:
-Производная от произведения двух множителей: (f · g)‘ = f ‘ · g + g ‘ ·f
-Производная суммы (разницы) двух любых выражений: (f ± g)‘ = f ‘ ± g ‘
-Производная сложной функции: (f(g(x))) ‘ = f ‘ (g(x)) · g ‘ (x)
-Производная от простых математических функций: (ex) ‘ = ex ; С‘ = 0; x‘ = 0; (С · х)‘ = С · х‘ , где С – постоянное число.
- С помощью данных формул находим производную исходной функции y = (х + 16)eх – 16:
y‘ = ((х + 16)eх – 16)‘ = (х + 16)‘ · eх – 16 + (х + 16) · (eх – 16)‘ = (х‘+ 16‘) · eх – 16 + (х + 16) · (eх – 16)‘ · (х – 16)‘ = (1 + 0) · eх – 16 + (х + 16) · eх – 16 · (х‘ — 16‘) = eх – 16 + (х + 16) · eх – 16 · (1 – 0) = eх – 16(1 + х + 16) = eх – 16(х + 17)
- Производная от функции найдена. Приравняем данную производную к нулю, тем самым найдет стационарные точки, по-другому экстремумы функции (в точках экстремумах производная функции равна 0):
eх – 16(х + 17) = 0
Получили произведение, которое равно 0. Первый множитель равен нулю быть не может, поэтому
х + 17 = 0
х = -17
- Получили одну стационарную точку, то есть одну точку экстремума, которая и является точкой максимума.
 x = \ exp (x) $.2}}} \ ln 4.} \]
x = \ exp (x) $.2}}} \ ln 4.} \]Производные экспоненциальной и логарифмической функций
14
Производная ln x
Производная от e с функциональным показателем
Производная ln u ( x )
Общее правило власти
СИСТЕМА ЕСТЕСТВЕННЫХ ЛОГАРИФМОВ имеет в основе число, называемое e; это система, которую мы используем во всех теоретических работах.(В следующем уроке мы увидим, что e приблизительно равно 2 . 718.) Система натуральных логарифмов отличается от системы десятичных логарифмов, которая имеет основу 10 и используется в большинстве практических работ.
Обозначим логарифмическую функцию с основанием e как «ln x ».
ln x = лог e x .
y = ln x подразумевает e y = x .
Другими словами, это функция логарифма —
y = ln x
— имеет в качестве обратной экспоненциальной функции,
y = e x .

Вот обратные отношения:
ln e x = x и e ln x = x .
А логарифм самого основания всегда 1:
(Тема 20 Precalculus.)
Функция y = ln x является непрерывной и определена для всех положительных значений x . Он будет подчиняться обычным законам логарифмов:
1 . ln ab = ln a + ln b .
2 . пер. a
b= ln a — ln b . 3 . ln a n = n ln a .
(Тема 20 Precalculus.)
Как и все правила алгебры, они подчиняются правилу симметрии.
Например,n ln a = ln a n .
Производная ln x
Теперь применим определение производной, чтобы доказать:
d
dxдюйм x = 1
xВ ходе доказательства это сильно упростит, если мы определим основание системы натуральных логарифмов, число, которое мы называем e, как следующий предел:
Предел в доказательстве будет иметь такой же вид.

Позже мы будем называть переменную x , а не v . И в следующем уроке, после изменения переменной с v на, следует знакомое определение.
Вот коэффициент разницы:
= при умножении на x / x ; = согласно 3-му закону. Теперь возьмем предел, равный ч приближается к 0.
= Ограничение не распространяется на 1
x, потому что h — это переменная Теперь мы определяем этот предел как основание натуральных логарифмов, число, которое мы назовем e.(Этот предел равен указанному выше: v =; когда 0, 0.)
Следовательно,
= = = Это то, что мы хотели доказать.

Чтобы увидеть, что этот лимит —
— то есть е существует, когда x приближается к 0, вот график
y имеет определенное значение, поскольку x приближается к 0. И в следующем уроке мы увидим, что это примерно 2,718.
Производная от e x
Теперь докажем:
«Производная e x по x
равно e x .«
Поскольку y = e x является обратной величиной y = ln x , мы можем получить его производную следующим образом:
y = e x подразумевает пер y = перемычка x = х . 
Следовательно, взяв производную от обеих сторон относительно x и применив правило цепочки к ln y :
= 1. y ‘ = y . То есть = e x . e x является собственной производной.
Что это означает? Это подразумевает экспоненциальный рост. Ведь мы говорим, что количество растет «экспоненциально», когда оно растет со скоростью , что пропорционально его размеру. Чем он больше в любой момент времени, тем быстрее он растет в это время. Типичный пример — население. Чем больше будет особей, тем больше будет рождений, и, следовательно, тем больше будет скорость изменения населения — количества рождений за каждый год.

Все экспоненциальные функции имеют вид a x , где a — основание. Следовательно, сказать, что скорость роста пропорциональна его размеру, означает сказать, что производная от a x пропорциональна a x .
d
dxa x = ка x , где k — константа пропорциональности.(Урок 39 алгебры.) Когда мы вычислим эту производную ниже, мы увидим, что эта константа принимает вид ln a .
d
dxa x = ln a · a x . В системе натуральных логарифмов, в которой e является основанием, у нас есть простейшая из возможных постоянных, а именно 1.

d
dxe x = e x . Производная от e с функциональным показателем
Если y = e u ( x ) , то согласно цепному правилу:
То есть
«Производная от e с функциональным показателем
равно e с этим показателем, умноженным на
производной этого показателя.«Пример 1. Вычислить производную e 2 x + 3 .
Решение . Задача 1. Вычислить производную e x 2 .
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!e x 2 · 2 x = 2 x e x 2
Задача 2. Вычислить производную от следующего.
a) e sin x . e sin x cos x
б) д −x . e — x (−1) = −e — x
c) x 2 e x . x 2 e x + 2 x e x
Согласно правилу продукта.
Производная ln u ( x )
Когда y = ln u ( x ), то согласно цепному правилу:
То есть
Пример 2. Пример 3. d
dxлин.  Sin x
Sin x = 1
sin x· cos x = cos x
sin x= детская кроватка x . Пример 4. Найти производную ln x 2 .
Решение . Мы можем применять законы логарифмов:
d
dxдюйм x 2 = d
dx2 пер. x , 3-й закон, = 2 d
dxдюйм x = 2
x. 
Пример 5. Найти производную ln .x
3 x — 4. Решение . Согласно 2-му Закону:
d
dxпер. x
3 x — 4= d
dx[ln x — ln (3 x — 4)] = = = Проблема 3.Различают следующее.
a) ln x 3 . d
dxдюйм x 3 = d
dx3 дюйма x = 3
xb) (лин x ) 3 . 
3 (внутренний x ) 2 · 1
x= 3 (лин x ) 2
xc) ln (3 x 2 — 4 x ). 1
3 x 2 — 4 x· (6 x -4) = 6 x — 4
3 x 2 — 4 xd) ln (3 x — 4) 2 . 1
(3 x -4) 2· 2 (3 x — 4) · 3 = 6 (3 x — 4)
(3 x — 4) 2= 6
3 x -4e) ln cos x . 1
cos x(−sin x ) = – sin x
cos x= −тан x Проблема 4.  Вычислить производную ln
Вычислить производную ln2
x. d
dxпер. 2
x= d
dx(ln 2 — ln x ) = 0 — 1
x= — 1
xПроблема 5.Производная журнала a x .
Согласно правилу перехода с базы e на другую базу a :
Тема 20 Precalculus.
Вычислить предел этой производной
a) когда x больше 1 и становится больше.
Эта производная приближается к 0, то есть становится меньше.
б) когда x меньше 1 и становится меньше.
Эта производная становится больше.

Общее правило власти
Теперь мы можем доказать, что производная f ( x ) = x n , где n — любой рациональный показатель степени, имеет следующий вид:
d
dxx n = n x n −1 Пусть
y = x n . Затем пер y = n ln x (3-й закон). Следовательно, при взятии производной по отношению к x : = n
xтак что г = n
x· y = n
x· x n = n x n −1 . 
Это то, что мы хотели доказать.
(Если n равно 0, тогда x 0 = 1, постоянная; его производная равна 0. Если n иррационально, потребуется рациональное приближение.)
Задача 6. Вычислить производную от .Производная от a x
Докажем:
d
dxa x = ln a · a x «Производная экспоненты с основанием a
равно натуральному логарифму основания
.раз экспоненциальной функции.«
Пусть
Это то, что мы хотели доказать.
Пример 6. d
dx2 x = ln 2 · 2 x . 
Задача 7. Вычислить производную от y = 10 5 x .
По цепному правилу:
Следующий урок: оценка e
Содержание | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: themathpage @ яндекс.com
Расчет производных от экспоненциальных функций
Показательная функция — одна из самых важных функций в исчислении. На этой странице мы выведем выражение для производной e x и применим его для вычисления производной других экспоненциальных функций.Наш первый контакт с числом e и экспоненциальной функцией был на странице о непрерывных сложных процентах и числе e. На этой странице мы дали интуитивное определение числа e, а также интуитивное определение экспоненциальной функции.

Мы также вывели альтернативное выражение для экспоненциальной функции. Новым выражением для экспоненциальной функции стал ряд, то есть бесконечная сумма .
Вы можете спросить, определение предела намного компактнее и проще, чем эта уродливая бесконечная сумма, зачем беспокоиться?
Оказывается, самый простой способ вывести правило взятия производной от e x — использовать это представление бесконечной серии. Это почему? Выражение ряда для e x выглядит как полином.Мы можем обобщить идею полинома, допустив бесконечное количество членов, как в выражении для экспоненциальной функции. Бесконечный многочлен называется степенным рядом .
Хорошая особенность степенного ряда заключается в том, что для вычисления его производной вы действуете так же, как и с многочленом. То есть вы берете производную по срокам. Давайте сделаем это с помощью экспоненциальной функции.
Производная от e
xРассмотрим выражение ряда для экспоненциальной функции
Мы можем вычислить производную левой части, применив правило для производной суммы.
Рассчитываем производную член по члену То есть производная суммы равна сумме производных каждого члена
То есть производная суммы равна сумме производных каждого членаНам известны производные от каждого из этих терминов
Мы применяем правило мощности для вычисления производной каждого членаЯ добавил дополнительный термин, чтобы прояснить схему. Теперь есть числа, которые отменяют
. Мы сокращаем некоторые числа и получаем удивительный результатМы получили удивительный результат. Выражение для производной такое же, как и для исходной функции.То есть
Производная от e x равна e x . Производная от e x равна e x . Это одно из свойств, которое делает экспоненциальную функцию действительно важной.Теперь вы можете на время забыть о выражении ряда для экспоненты. Здесь он нам понадобился только для доказательства приведенного выше результата. Теперь мы можем применить это для вычисления производной других функций, включающих экспоненту.
Пример 1: f (x) = e axВычислим производную функции
На первый взгляд это может показаться неочевидным, но это сложная функция.
. Производная внешней функции равна исходной функции Это означает, что нам нужно применить цепное правило. Внешняя функция — экспонента. Его производная равна itslef. Внутренняя функция — ax:
Это означает, что нам нужно применить цепное правило. Внешняя функция — экспонента. Его производная равна itslef. Внутренняя функция — ax:Это было просто. Может потребоваться еще несколько примеров, чтобы привыкнуть к тому факту, что производная экспоненты — это та же самая экспонента.
Пример 2: f (x) = e x 2Рассмотрим теперь еще одну составную функцию
Чтобы вычислить его производную, мы снова применяем цепное правило.Поскольку внешняя функция является экспонентой, ее производная равна
. Пример 3: f (x) = e x (1-x 2 )Теперь этот выглядит сложнее
Здесь у нас есть продукт, поэтому мы должны использовать правило продукта. Для этого мы определяем два фактора
И мы применяем правило продукта
А теперь множим e x , чтобы получить окончательный ответ. Пример 4: f (x) = e cos (x) sin (x)Рассмотрим следующую функцию
Это требует большего внимания, потому что нам нужно применить и правило продукта, и правило цепочки.
. Посмотрим, что я имею в виду. Сначала мы применяем правило продукта
Посмотрим, что я имею в виду. Сначала мы применяем правило продуктаТеперь, чтобы вычислить u ‘, нам нужно применить цепное правило
Мы подключаем это к правилу продукта
Пример 5: Экспонента с другим основанием, f (x) = a xТеперь давайте рассмотрим экспоненту с основанием, отличным от e.
Как вычислить производную этой функции? Мы используем прием, который регулярно используется при работе с логарифмами. Мы можем записать эту функцию как
Вы можете проверить, что это равенство истинно, используя определение логарифма.Теперь мы воспользуемся свойством логарифмов, которое позволяет нам извлекать экспоненты из логарифмического знака
.Теперь это экспоненциальная функция с основанием e, производную которой мы умеем вычислять.
Но используя уравнение несколькими строками выше, мы можем записать это как
Это показывает одну из причин, почему естественным выбором в качестве основания экспоненциальной функции является число e.
Пример 6: f (x) = a x 2 Для любой другой базы вы получите ln (a), засоряющую выражение ее производной.
Для любой другой базы вы получите ln (a), засоряющую выражение ее производной.Рассмотрим
Здесь нам нужно применить правило цепочки.Внешняя функция — экспонента, поэтому мы знаем, как вычислить ее производную из предыдущего примера
.Вот так. Следующим шагом может быть изучение производной ln (x). Если у вас есть сомнения или вы хотите обсудить собственную проблему, просто оставьте мне комментарий ниже.
Математическая сцена — Функции 2 — Урок 5
Математическая сцена — Функции 2 — Урок 5 — Вторая производная2009 Rasmus ehf и Джанн Сак Функции 2
Урок 5
Вторая производная
Если мы дифференцируем функцию, а затем дифференцируя производную, мы получаем то, что называется второй производной.
 Если исходная функция называется f (x), мы находим f (x)
а затем дифференцируем f (x). Результат записывается как f (x).
Если исходная функция называется f (x), мы находим f (x)
а затем дифференцируем f (x). Результат записывается как f (x).Пример 1
Найти вторую производную из следующих функций:
а) f (x) = x 3 + x 2 + х + 1
f (x) = 3x 2 + 2x + 1
f (x) = 6x + 2
б) f (x) = x 4 + x 3 + x 1 + 1
f (x) = 4x 3 + 3x 2 x 2
f (x) = 12x 2 + 6x + 2x 3
в) е (х) = грех х
f (x) = cos x
f (x) = грех x
г) f (x) = cos x
f (x) = грех x
f (x) = cos x
е) f (x) = e x
f (x) = e x
f (x) = e x
е) f (x) = ln x
f (x) = 1 / x = x 1
f (x) = x 2
Если мы определим функцию f (t) как положение объект в момент времени t мы получаем следующие определения в физике.

f (t) — позиция объект по прошествии времени t.
f (t) дает нам скорость объекта в момент времени t.
f (t) дает ускорение объекта в момент времени t.
Скорость — это мера изменение положения в единицу времени. Ускорение — это мера изменения по скорости в единицу времени.
Если f (t) измеряется в метров и t в секундах, тогда f (t) измеряется в м / с и f (t) в м / с 2 .
Пример 2
Когда стрела летит вертикально в воздух, мы можно найти функцию h (t), которая дает высоту стрелки над землей в время t. Эта функция зависит от различных факторов, таких как сила стрелок и тип лука и стрел.
Следующая функция дает высоту h кончика стрелки в метров через t секунд после выстрела из лука.h (t) = 4,9 т 2 + 24,5 т + 2,4.
а) Найти время, необходимое для того, чтобы стрела упала на землю.
Представьте себе систему координат с высотой h на по вертикальной оси (y) и время t по горизонтальной оси (x).  Представьте, что стрелок стоит у истока системы и наконечника
Стрела выходит из лука на высоте 2,4 м.
Представьте, что стрелок стоит у истока системы и наконечника
Стрела выходит из лука на высоте 2,4 м.
Стрелка идет вверх, а затем снова опускается, достигая земли. когда высота h равна 0.Для решения проблемы нам нужно определить, когда функция h (t) = 0. Это можно сделать с помощью калькулятора или квадратичная формула.Значение t ≈ 0 не совсем точное, поскольку мы начинаем измерять время, когда стрелка находится на высоте 2,4 м.
Другое значение t говорит нам, что стрелка ударяется о землю через 5 секунд.б) Теперь посчитаем высоту, которую достигает стрелка.
Стрелка замедляется по мере того, как поднимается и достигает максимальной высоты, когда скорость равна нулю. h (t) дает скорость в момент времени t. Итак, мы нужно найти h (t) и решить уравнение h (t) = 0.
ч (т) = 9,8 т + 24,5 = 0
9,8 т = 24,5
t = 24,5 / 9.
 8 = 2,5 с
8 = 2,5 с ср сделайте вывод, что стрелка достигает максимальной высоты через 2,5 секунды. Сейчас мы можно использовать формулу для h (t), чтобы найти максимальную высоту.
ч (2,5) = 4,92,5 2 + 24,52,5 + 2,4 = 33,025 мСтрела достигает высоты 33 м .
в) Теперь мы снова находим ускорение, дифференцируя.
ч (т) = 9.8т + 24,5
h (t) = 9,8 м / с 2
Это очень важный результат, значение, которое дает ускорение из-за гравитационного поля Земля. Отрицательное значение означает, что стрелка замедляется.
Давайте разберемся, что информацию о графике функции дает вторая производная. В первая производная говорит нам о наклоне графика.Если производная равна положительный — наклон увеличивается, если отрицательный — наклон уменьшается.
Вторая производная говорит нам, как меняется наклон. Если вторая производная положительный, это означает, что наклон графика увеличивается, если отрицательный наклон уменьшается.
Когда знак второй производной меняется с положительного на отрицательный, означает, что градиент перестает увеличиваться и начинает уменьшаться. Другими словами график меняется с выпуклого (изгиб вверх) на вогнутый (изгиб вниз).Обратное происходит, когда вторая производная изменяется с отрицательной на положительный. Точка, в которой изменяется изгиб кривой, называется точкой перегиб. Когда непрерывная функция меняется с положительной на положительную отрицательный, он должен пройти через ноль, поэтому в точке перегиба второй производная равна нулю. Если вы попытаетесь провести касательную в точке перегиба, вы обнаружит, что он разрезает график.Обобщение:
Когда вторая производная положительный градиент графика увеличивается, а кривая изгибается вверх, выпуклый..
Когда вторая производная отрицательна, градиент графика уменьшается. а кривая изгибается вниз, имеет вогнутую форму.Производная от функция f (x) = e x это f (x) = e x а вторая производная f (x) = e x .
 Вторая производная всегда положительна, поэтому график всегда
выпуклый. См. Диаграмму ниже.
Вторая производная всегда положительна, поэтому график всегда
выпуклый. См. Диаграмму ниже.Функция g (x) = ln x определена только для x больше нуля.Производная равна g (x) = 1 / x = x 1 а вторая производная g (x) = x 2 = 1 / х 2 . Второй производная всегда отрицательна, поэтому график изгибается вниз или является вогнутым по мере того, как диаграмма показывает.
f (x) = e x выпуклый.
f (x) положительно
(+).г (х) = ln x вогнутая.
г (х) отрицательно
().Пример 3
Найдите первое и второе производные функций f (x) = x 2 + 4x + 3 и g (x) = x 2 + 4x 3.

f (x) = x 2 + 4x + 3 г (x) = х 2 + 4 х 3
ф (х) = 2х + 4 г (х) = 2х + 4
f (х) = 2 г (х) = 2
f (x) положительно, поэтому график функции f (x) выпуклый.g (x) отрицательно, поэтому график g (x) вогнутый.
Используйте производную для найти вершину каждой функции. Вершина возникает, когда градиент тангенс равен нулю, поэтому:
ф (х) = 2х + 4 = 0 г (х) = 2x + 4 = 0
2x = 4 2x = 4
х = 2 Икс = 2
f (2) = (2) 2 + 4 (2) + 3 = 1 г (2) = 2 2 + 42 3 = 1
График f (x) выпуклая и поэтому имеет точку минимума (2, 1).
График g (x) вогнутый и поэтому имеет точку максимума (2, 1). Графики представлены ниже.
Пример 4
Найдите первое и второе производные функции f (x) = x 3 3x 2 + 4, максимальная и минимальная точки и точка перегиб (если они есть). Затем найдите уравнение касательной в точке перегиба.

f (x) = x 3 3x 2 + 4
f (x) = 3x 2 6x
f (x) = 3x 2 6х = 3х (х 2) = 0
x = 0 или 2
Теперь посмотрим, как знаки изменения производной вокруг нулей:
ф (1) = 3 (1) 2 6 (1) = 3 + 6 = 9 (+)
ф (1) = 31 2 61 = 3 ()
ф (3) = 33 2 63 = 9 (+)
Мы сделайте то же самое для второй производной:
f (x) = 6x 6 = 0
6x = 6
х = 1
ж (0) = 60 6 = 6 ()
ф (2) = 62 6 = 6 (+)
Собрав всю эту информацию вместе, мы можем сделать следующая таблица:
График вогнутый, когда x меньше 1, что показано кривой, изгибающейся вниз.График выпуклый, когда x больше 1 показано кривой, изгибающейся вверх. Мы видим что там является максимумом при x = 0, минимумом при x = 2 и точкой перегиба когда х = 1.
Теперь мы можем рассчитать координаты этих точек.

f (0) = 0 3 30 2 + 4 = 4 Максимальная точка = (0, 4)
f (2) = 2 3 32 2 + 4 = 0 Минимальная точка = (2, 0)
f (1) = 1 3 31 2 + 4 = 2 Точка перегиба = (1, 2)
Теперь, чтобы найти уравнение касательная в точке перегиба.
Общее уравнение касательная к функции f (x) в точке (a, b) имеет вид y = е (а) (х а) + б. В этом случае (a, b) — точка перегиба, (1, 2).
Мы уже обнаружили, что f (1) = 3, поэтому нам просто нужно положить это информацию в уравнение касательной.у = 3 (х 1) + 2
= 3х + 3 + 2
= 3x + 5
Уравнение касательной в точке перегиба y = 3х + 5.
Мы можем проверить работу по построение графика f (x) и касательной на графическом калькуляторе. Обратите внимание, как касательная разрезает график в точке перегиба.
Попрактикуйтесь в этих методах, затем попробуйте Тест 5 по функциям 2.

Не забудьте использовать контрольный список, чтобы отслеживать свою работу.Исчисление I — Производные от экспоненциальных и логарифмических функций
Показать мобильное уведомление Показать все заметки Скрыть все заметкиПохоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
 {\ ln x}}}} = \ frac {1} {Икс}\]
{\ ln x}}}} = \ frac {1} {Икс}\]Последний шаг просто использует тот факт, что две функции инвертируют друг друга.
Если сложить все вместе, получится
\ [\ frac {d} {{dx}} \ left ({\ ln x} \ right) = \ frac {1} {x} \ hspace {0,5 дюйма} x> 0 \]Обратите внимание, что нам нужно потребовать, чтобы \ (x> 0 \), поскольку это требуется для логарифма и, следовательно, необходимо также для его производной. Также можно показать, что
\ [\ frac {d} {{dx}} \ left ({\ ln \ left | x \ right |} \ right) = \ frac {1} {x} \ hspace {0,5 дюйма} x \ ne 0 \]Все, что нам нужно избежать, это \ (x = 0 \).
В этом случае, в отличие от случая экспоненциальной функции, мы действительно можем найти производную функции общего логарифма.Все, что нам нужно, это производная от натурального логарифма, который мы только что нашли, и замена основной формулы. Используя замену основной формулы, мы можем записать общий логарифм как,
\ [{\ log _a} x = \ frac {{\ ln x}} {{\ ln a}} \]Тогда дифференцировать довольно просто.
\ [\ begin {align *} \ frac {d} {{dx}} \ left ({{{\ log} _a} x} \ right) & = \ frac {d} {{dx}} \ left ({ \ frac {{\ ln x}} {{\ ln a}}} \ right) \\ & = \ frac {1} {{\ ln a}} \ frac {d} {{dx}} \ left ({ \ ln x} \ right) \\ & = \ frac {1} {{x \ ln a}} \ end {align *} \]
Мы воспользовались тем фактом, что \ (a \) было константой, поэтому \ (\ ln a \) также является константой и может быть вычленен из производной.2}}} \ end {выровнять *} \]
На данном этапе действительно не так уж сложно различать натуральные логарифмы и натуральные экспоненциальные функции, если вы помните формулы. В следующих разделах, по мере того, как мы получим больше формул, они будут усложняться.
Затем нам нужно решить нашу обязательную задачу по применению / интерпретации, чтобы не забыть о них.
Пример 2 Предположим, что положение объекта задается формулой \ [s \ left (t \ right) = t {{\ bf {e}} ^ t} \]Объект когда-нибудь перестает двигаться?
Показать решениеСначала нам понадобится производная.
 t} = 0 \]
t} = 0 \]Теперь мы знаем, что экспоненциальные функции никогда не равны нулю и поэтому они будут равны нулю только при \ (t = — 1 \). Итак, если мы собираемся разрешить отрицательные значения \ (t \), то объект перестанет двигаться один раз в \ (t = — 1 \). Если мы не допустим отрицательные значения \ (t \), то объект никогда не перестанет двигаться.
Прежде чем перейти к следующему разделу, нам нужно вернуться к паре производных, чтобы убедиться, что мы не перепутали их.x} \ ln a & \ hspace {0.5in} {\ mbox {Производная экспоненциальной функции}} \ end {array} \]
Важно отметить, что с правилом мощности показатель степени ДОЛЖЕН быть константой, а основание ДОЛЖНО быть переменной, в то время как для производной экспоненциальной функции нам нужно прямо противоположное. Для экспоненциальной функции показатель ДОЛЖЕН быть переменной, а основание ДОЛЖНО быть константой.
Легко привязаться к одной из этих формул и просто использовать ее для обеих.
 Мы также даже не обсуждали, что делать, если и показатель степени, и основание включают переменные. Мы увидим эту ситуацию в следующем разделе.
Мы также даже не обсуждали, что делать, если и показатель степени, и основание включают переменные. Мы увидим эту ситуацию в следующем разделе.DerivSource — Руководители бывших банков запускают Derivative Path, Inc.
Руководители бывшего банка запускают Derivative Path, Inc. и предлагают новый подход к управлению внебиржевыми операциями с производными финансовыми инструментами с процентной ставкой
Группа экспертов по продажам, трейдингу, управлению рисками и технологиям, ранее работавшая в Wells Fargo, запустила Derivative Path, Inc. — компания, предоставляющая финансовые услуги, которая приближается к внебиржевым рынкам производных финансовых инструментов со свежими, технологически ориентированными предложениями услуг. Derivative Path предоставит технологическое решение для оказания помощи финансовым учреждениям и коммерческим конечным пользователям в выполнении и управлении их внебиржевыми сделками с производными процентными деривативами.

Отдел продаж и торговли руководил продажами и исполнением деривативов для нескольких крупных банков, работал с соответствующими группами рынков капитала и кредитования, а также с многочисленными финансовыми учреждениями над созданием программ взаимного хеджирования деривативов.
«В условиях усложняющейся нормативно-правовой базы финансовые учреждения и их коммерческие конечные пользователи считают более обременительным выполнение простых, снижающих риски процентных свопов и других производных финансовых инструментов», — говорит Стив Хок , соучредитель и со-генеральный директор компании Производный путь. «Мы предлагаем рентабельное внешнее решение, чтобы помочь этим учреждениям продолжать предлагать такие продукты и соответствовать возросшим нормативным требованиям, предъявляемым к отрасли.”
«Мы полностью привержены применению нашего коллективного опыта в управлении успешным производным бизнесом и доступе к другим отраслевым экспертам и ресурсам по мере необходимости, чтобы гарантировать нашим клиентам достижение желаемых целей программы управления финансовыми рисками».
 говорит Прадип Бхатия , соучредитель и со-генеральный директор.
говорит Прадип Бхатия , соучредитель и со-генеральный директор.Derivative Path будет предлагать полный набор услуг по структурированию хеджирования, заключению сделок, обязательной нормативной отчетности Dodd-Frank и хранению записей, а также управление рисками, операционную, юридическую и бухгалтерскую поддержку.Команда также будет предлагать клиентам помощь в настройке хеджирования, кредитной и других связанных банковских политик, а также в обучении банкиров.
«В ближайшие месяцы компания планирует запустить безопасную технологическую платформу, способную помочь своим клиентам финансового учреждения в отслеживании процесса хеджирования клиентов от предложения до исполнения и текущего обслуживания жизненного цикла торговли. «Наша технологическая команда имеет многолетний опыт создания и управления крупномасштабными системами торговли производными финансовыми инструментами.Мы используем этот опыт для создания доступной для клиентов современной технологической платформы, которая значительно расширит возможности производных рабочих процессов для наших клиентов », — говорит Джон Флеминг , технический директор Derivative Path.


 x = \ exp (x) $.2}}} \ ln 4.} \]
x = \ exp (x) $.2}}} \ ln 4.} \]






 Sin x
Sin x 

 Вычислить производную ln
Вычислить производную ln



 То есть производная суммы равна сумме производных каждого члена
То есть производная суммы равна сумме производных каждого члена Это означает, что нам нужно применить цепное правило. Внешняя функция — экспонента. Его производная равна itslef. Внутренняя функция — ax:
Это означает, что нам нужно применить цепное правило. Внешняя функция — экспонента. Его производная равна itslef. Внутренняя функция — ax: Посмотрим, что я имею в виду. Сначала мы применяем правило продукта
Посмотрим, что я имею в виду. Сначала мы применяем правило продукта Для любой другой базы вы получите ln (a), засоряющую выражение ее производной.
Для любой другой базы вы получите ln (a), засоряющую выражение ее производной. Если исходная функция называется f (x), мы находим f (x)
а затем дифференцируем f (x). Результат записывается как f (x).
Если исходная функция называется f (x), мы находим f (x)
а затем дифференцируем f (x). Результат записывается как f (x).
 Представьте, что стрелок стоит у истока системы и наконечника
Стрела выходит из лука на высоте 2,4 м.
Представьте, что стрелок стоит у истока системы и наконечника
Стрела выходит из лука на высоте 2,4 м.  8 = 2,5 с
8 = 2,5 с 
 Вторая производная всегда положительна, поэтому график всегда
выпуклый. См. Диаграмму ниже.
Вторая производная всегда положительна, поэтому график всегда
выпуклый. См. Диаграмму ниже.


 {\ ln x}}}} = \ frac {1} {Икс}\]
{\ ln x}}}} = \ frac {1} {Икс}\]
 t} = 0 \]
t} = 0 \] Мы также даже не обсуждали, что делать, если и показатель степени, и основание включают переменные. Мы увидим эту ситуацию в следующем разделе.
Мы также даже не обсуждали, что делать, если и показатель степени, и основание включают переменные. Мы увидим эту ситуацию в следующем разделе.
 говорит Прадип Бхатия , соучредитель и со-генеральный директор.
говорит Прадип Бхатия , соучредитель и со-генеральный директор.