Сообщение на тему тригонометрия. История развития тригонометрии. Средневековье: исследования индийских ученых
тригонометрия
Важнейший период истории тригонометрии связан с деятельностью учёных Ближнего и Среднего Востока. Начало его можно датировать VIII в., когда в столице арабского халифата Багдаде началась активная работа по изучению индийского и греческого научного наследия. Среди успешно развивавшихся научных дисциплин были те направления астрономии и математики, в рамках которых формировалась плоская и сферическая тригонометрия.
Астрономия — одна из древнейших наук — на протяжении всего средневековья развивалась в неразрывной связи с другими дисциплинами. Необходимое в разных областях практической деятельности людей, например, при точном определении времени, составлении календаря, ориентировки на местности, измерении расстояний и т.д., она, в свою очередь, нуждалась в совершенном математическом аппарате. Именно потребности астрономии явились в тот период важнейшим стимулом быстрого прогресса математики и, в частности, разработки новых вычислительных приёмов.
Большое внимание в это время привлекала гномоника — теория солнечных часов, широко применявшихся в практике. При решении астрономических задач использовались древние графические приёмы, основанные на ортогональном проектировании сферы на плоскость. Всё большее значение приобретало учение о линиях в тригонометрическом круге.
Обобщив результаты, полученные предшественниками, учёные ближнего и Среднего востока развили тригонометрические методы и уже в XII в. фактически превратили тригонометрию в самостоятельную науку.
Прежде чем перейти к обзору тригонометрии на средневековом ближнем и Среднем востоке, следует назвать некоторых учёных, чьи труды сыграли особенно важную роль в ее истории.
Вначале необходимо упомянуть выдающихся переводчиков античной научной литературы с греческого и сирийского языка. Это работавшие в Багдаде в конце VIII — начале IX вв. Хаджжадж ибн Йусуф ибн Матар (жил между 786 и 833 гг.), математик, физик и медик Исхак ибн Хунайн 9830 — 910). Большой вклад в развитие тригонометрии внесли уроженцы Средней Азии Муххамад ибн Мусса ал-Хорезми (ок.
Особое место в истории тригонометрии занимает выдающийся астроном средневекового Востока Мухаммад ибн Джабир ал-Баттани (ок. 850 — 929). Следует упомянуть также крупнейшего философа, основоположника восточного аристотелизма Абу Насра Мухаммада ал — Фараби (ок. 870 — 950 гг.).
К концу XI в. общими усилиями учёных Ближнего и Среднего Востока были заложены основы тригонометрии как самостоятельной науки. Оформлялась она и в трудах западноарабских математиков, среди которых должны быть названы Мухаммад ибн Йусуф ибн Ахмад ибн My»аз ал-Джаййани (989 — ок. 1080 гг.) и Абу Мухаммад джабир ибн Афлах (XII в.).
Оформлялась она и в трудах западноарабских математиков, среди которых должны быть названы Мухаммад ибн Йусуф ибн Ахмад ибн My»аз ал-Джаййани (989 — ок. 1080 гг.) и Абу Мухаммад джабир ибн Афлах (XII в.).
В XIII в. важный шаг в развитии тригонометрии сделали представители марагинской научной школы — прежде всего ее руководитель, учёный Насир ад-Дин ат-Туси (1201 — 1274 гг.) и его ученики Мухьи ад-Дин ал-Магриби и кутб ад-Дин аш-Ширази.
Средневековые учёные стран ислама продолжали в своих сочинениях традиции предшественников, наследниками которых в области точных наук они явились. Поэтому в астрономо- математической литературе этого периода, имеющей отношение к тригонометрии, четко выделяются, во-первых. Комментарии к греческим трудам (прежде всего к «Альмагесту» Птолемея и к сочинениям о сферике) и их обработки, и, во-вторых, сочинения, в которых развиваются индийские методы. Третью группу составляют труды, в которых эти методы сочетаются с греческими.
Индийское влияние сказалось в арабской тригонометрической терминологии. Линия синуса была названа джайб. Это арабизированный индийский термин джива, обозначающий хорду или тетиву лука. Косинус обозначался термином «синус дополнения». Обращённый синус называли вслед за индийцами «стрелой».
Линия синуса была названа джайб. Это арабизированный индийский термин джива, обозначающий хорду или тетиву лука. Косинус обозначался термином «синус дополнения». Обращённый синус называли вслед за индийцами «стрелой».
Вплоть до X — XI вв. зиджи и близкие им по характеру астрономические сочинения включались сводки основных сведений по тригонометрии и тригонометрические таблицы. Среди авторов трудов, внёсших значительный вклад в развитие науки и увеличение этого материала, были такие учёные как Абу Насар Мансур ибн Ирак и его великий ученик Абу Райхан Беруни. А работа Насир ад-Дина ат-Туси оставила важный след в истории тригонометрии.
Плоская тригонометрия излагалась, как правило, в специальных разделах астрономических сочинениях, прежде всего зиджей. Здесь приводились определения тригонометрических функций и устанавливались соотношения между ними, предлагались правила решения треугольников. Наибольшее внимание, естественно, уделялось вопросу, важному для практики, — составлению тригонометрических таблиц.
Понятие синуса и обращённого синуса встречаются — по-видимому, впервые арабоязычной литературе — в зидже ал-Хорезми. Он приводит таблицу синусов (до секунд включительно) и правило пользования ею, разъясняет, как с помощью этой таблицы найти синус и обращённый синус по данной дуге и как по данному синусу найти дугу. В качестве угловой единицы у ал-Харезми служит «знак зодиака», равный окружности круга, т.е. 30°. Значение синусов даются в частях радиуса, который принят равный 60, и выражаются в шестидесятеричных дробях.
Рис.6 рис.7
Правило определения обращённого синуса, словесно сформулированное ал-Харезми, с помощью современной математической символике можно записать так: если обозначить линию обращённого синуса дуги б через sinvers б, то
sinvers а = 60° — sin (90° — а), при б
sinvers а = 60° + sin (90° — а), при б > 90°.
Если радиус круга, как принято сейчас, взять равным 1, то это правило примет вид sinvers б = 1 — cos б, где соответственно cos б > 0 и cos
Тангенс, котангенс, а также секанс и косеканс, введённые и табулированные тогда же, рассматривались вначале, как линии, фигурировавшие в науке о солнечных часах — гномонике.
Правило, по которому находился котангенс угла б, в современных обозначениях имеет вид
множитель 12 появляется здесь в связи с тем, что гномон подразделяется на 12 частей. Аналогично правило приводится дня тангенса, которая выражается в долях единицы
Однако уже ал-Фараби при изложении труда Птолемея не только отказался от понятия хорды, но и рассматривал линии тангенса и котангенса как линии, связанные с кругом. Тем самым он нарушил традиционную связь этих тригонометрических функций с гномоникой.
Приведём для иллюстрации цитату из его «Книги приложений к Альмагесту», содержащую определение тангенса и котангенса в связи с задачей нахождения высоты солнца: «Пусть ABCD (рис.7) — круг высоты, его центр Е, a DI — пересечение плоскостей круга, высоты и круга горизонта; DE — гномон, стоящий под прямым углом к плоскости горизонта в точке D, СК — пересечение плоскости круга высоты и плоскости, стоящий под прямым углом к горизонту в точке С, а СЕ — гномон, стоящий на этой плоскости.
При этом ал-Фараби особо отмечает, что тангенс «изменяется и увеличивается с увеличением высоты солнца», а котангенс «уменьшается с увеличением этой высоты».
Но если в приведённом рассуждении связь с гномоникой ещё сильна, то далее, при нахождении величины линий тангенса и котангенса, ал-Фараби рассматривает их только как линии в круге — наряду с линией синуса и косинуса.
Где r-радиус круга.
Существенно также, что ал-Фараби выражает тангенс и котангенс (также, как синус и косинус) в далях радиуса, подразделённого на 60 частей, а не в седьмых и двенадцатых долях гномона, как было принято раньше.
Тригонометрическая функция косинус в трудах восточных математиков рассматривалась только как синус дополнения угла до 90.
Таким образом, к концу ІХ века учёные средневекового Востока знали все шесть тригонометрических функций. Соотношение между ними, которые были выведены из геометрических соображений, формулировались словесно. С помощью математической символики эти соотношения приведенные, например, ал-Баттани, будут иметь вид:
Чрезвычайно важный шаг для развития тригонометрии сделал Абу- л-Вафа ал-Бузджанни, положив г = 1 вместо б= 60. Он стал рассматривать тригонометрические функции в единичном круге и тем самым существенно облегчил вычисления. Ему же принадлежит более изящное, чем у Птолемея, доказательство соотношения, которое сейчас мы выражаем формулой
А у Ибн Йуниса встречается другое, сыгравшее существенную роль в истории тригонометрии:
Далее следуют уже известные из «Альмагеста» теоремы о хорде дополнительной дуги, хорде удвоенной дуги, хорде суммы и разности двух данных дуг, равносильные теоремам о синусе удвоенного и половинного углов, о синусе суммы и разности двух углов.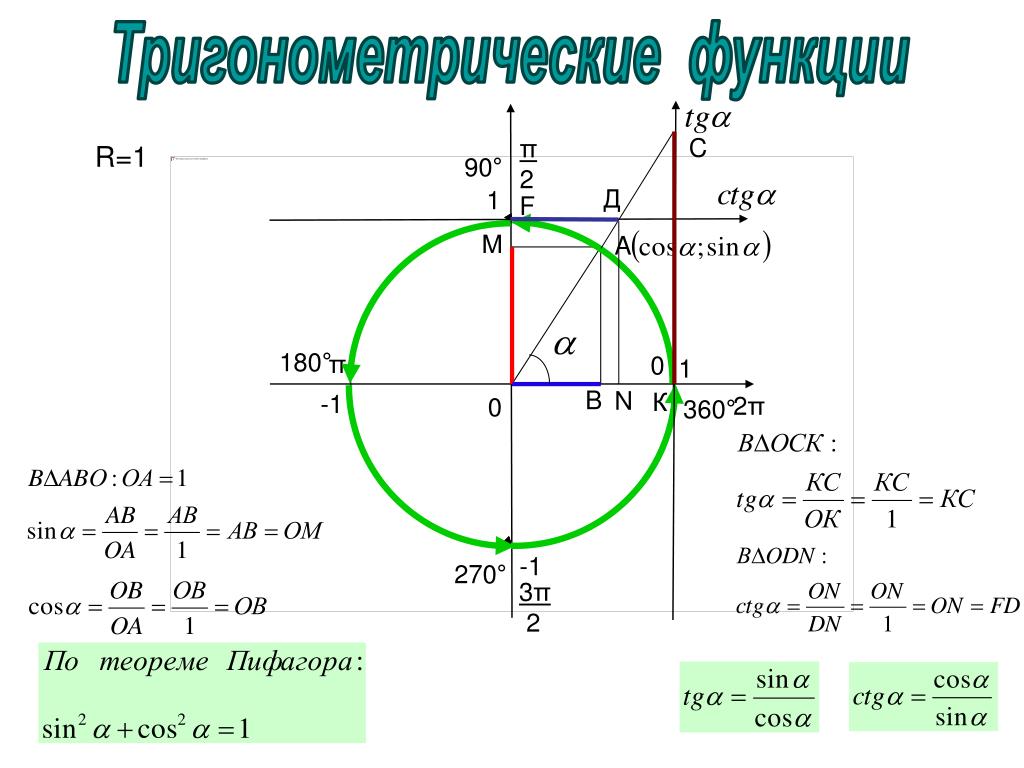
Значительно облегчила решение треугольников доказанная в X в. теорема синусов, устанавливающая пропорциональность сторон и противолежащих углов.
Теорема косинусов а 2 = b 2 + с 2 — 2 bc cos А, где а, b, с — стороны треугольника, А — его угол, в общем виде сформулирована не была.
Мини — проектная работа по теме «История развития тригонометрии»
обучающегося 11 «а» класса МБОУ «Килемарская СОШ» Килемарского муниципального района Республики Марий Эл Иванцова Василия
Учитель: И.П.Конюшкова
Цели и задачи:
- Найти сведения о развитии тригонометрии
- Изучить литературу по данной теме
План:
6. Развитие тригонометрии современности
В своей работе я рассматриваю историю развития тригонометрии.
1.Возникновение тригонометрии как науки
Тригонометрия возникла и развивалась в древности как один из разделов астрономии, как её вычислительный аппарат. Некоторые тригонометрические сведения были известны древним вавилонянам и египтянам, но основы этой науки заложены в Древней Греции.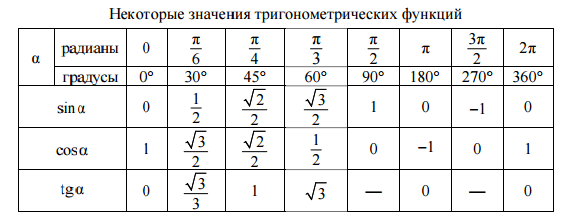 Древнегреческие астрономы успешно решали отдельные вопросы из тригонометрии, связанные с астрономией. Однако они рассматривали не линии синуса, косинуса и др., а хорды. Первые тригонометрические таблицы были составлены Гиппархом Никейским (180-125 лет до н. э.). Гиппарх был первым, кто свёл в таблицы соответствующие величины дуг и хорд для серии углов.
Древнегреческие астрономы успешно решали отдельные вопросы из тригонометрии, связанные с астрономией. Однако они рассматривали не линии синуса, косинуса и др., а хорды. Первые тригонометрические таблицы были составлены Гиппархом Никейским (180-125 лет до н. э.). Гиппарх был первым, кто свёл в таблицы соответствующие величины дуг и хорд для серии углов.
Более полные сведения по тригонометрии содержаться в «Альмагесте» Птолемея. Птолемей делил окружность на 360 градусов, а диаметр на 120 частей. Радиус он считал за 60 частей и пользовался шестидесятеричной системой счисления. Для прямоугольного треугольника с гипотенузой, равной диаметру круга, он записывал на основании теоремы Пифагора: (хорда α)²+(хорда /180-α /)² = (диаметру)², что соответствует современной формуле sin²α+cos²α=1. Таблица Птолемея, сохранившаяся до нашего времени, равнозначна таблице синусов с пятью верными десятичными знаками.
2.Развитие тригонометрии в Индии
В IV веке центр развития математики переместился в Индию. Индийские математики были хорошо знакомы с трудами греческих астрономов и геометров. Их вклад в прикладную астрономию и расчётные аспекты тригонометрии очень значителен. В первую очередь индийцы изменили некоторые концепции тригонометрии, приблизив их к современным. В Индии было положено начало тригонометрии как общему учению о соотношениях в треугольнике, хотя, в отличие от греческих хорд, индийский подход ограничивался только функциями острого угла. Синус индийцы определяли несколько иначе, чем в современной математике, но первыми ввели в использование косинус.
Индийские математики были хорошо знакомы с трудами греческих астрономов и геометров. Их вклад в прикладную астрономию и расчётные аспекты тригонометрии очень значителен. В первую очередь индийцы изменили некоторые концепции тригонометрии, приблизив их к современным. В Индии было положено начало тригонометрии как общему учению о соотношениях в треугольнике, хотя, в отличие от греческих хорд, индийский подход ограничивался только функциями острого угла. Синус индийцы определяли несколько иначе, чем в современной математике, но первыми ввели в использование косинус.
3. Дальнейшее развитие тригонометрии в странах Среднего и Ближнего Востока
Дальнейшее развитие тригонометрия получила в IX-XV вв. в странах Среднего и Ближнего Востока. Самые ранние из сохранившихся трудов принадлежат ал-Хорезми и ал-Марвази (IX век), которые рассмотрели, наряду с известными ещё индийцам синусом и косинусом, новые тригонометрические функции: тангенс, котангенс, секанс и косеканс. Хорезми (аль-Хорезми) Мухаммед бен Муса составил таблицы синусов и котангенсов. Он является автором ряда астрономических сочинений: работ о солнечных часах, астролябии; составил ряд математических и астрономических таблиц. Сохранилась также его рукопись «Изображение земли» (опубликована в 1878), посвященная географии. Однако известность ученому принесли прежде всего его работы в области математики. Больших результатов в развитии тригонометрии добился Абу-л-Вафа во второй половине X века, который впервые использовал для определения тригонометрических функций круг единичного радиуса, как это делается в современной математике.
Он является автором ряда астрономических сочинений: работ о солнечных часах, астролябии; составил ряд математических и астрономических таблиц. Сохранилась также его рукопись «Изображение земли» (опубликована в 1878), посвященная географии. Однако известность ученому принесли прежде всего его работы в области математики. Больших результатов в развитии тригонометрии добился Абу-л-Вафа во второй половине X века, который впервые использовал для определения тригонометрических функций круг единичного радиуса, как это делается в современной математике.
Одной из важнейших задач науки того времени являлось составление тригонометрических таблиц с как можно меньшим шагом. В IX веке ал-Хорезми составил таблицы синусов с шагом 1°, его современник ал-Марвази добавил к ним первые таблицы тангенсов, котангенсов и косекансов с тем же шагом. В начале X века ал-Баттани опубликовал таблицы с шагом 30″, в конце того же столетия Ибн Юнис составил таблицы с шагом 1″. При составлении таблиц ключевым было вычисление значения
. Искусные методы для вычисления этой величины изобрел наряду с Ибн Юнис и Абу-л-Вафа также ал-Бируни. Первым специализированным трактатом по тригонометрии было его сочинение «Книга ключей науки астрономии» (995-996 годы). Наибольшего успеха добился в XV веке ал- Каши, в одной из своих работ он подсчитал, что
(все знаки верны). Его тригонометрические таблицы с шагом 1′ на протяжении 250 лет были непревзойденными. Ат-Туси, Насир ад-Дин (1201-1274) в «Трактате о полном четырехстороннике» впервые изложил тригонометрические сведения как самостоятельный отдел математики, а не придаток к астрономии.
Искусные методы для вычисления этой величины изобрел наряду с Ибн Юнис и Абу-л-Вафа также ал-Бируни. Первым специализированным трактатом по тригонометрии было его сочинение «Книга ключей науки астрономии» (995-996 годы). Наибольшего успеха добился в XV веке ал- Каши, в одной из своих работ он подсчитал, что
(все знаки верны). Его тригонометрические таблицы с шагом 1′ на протяжении 250 лет были непревзойденными. Ат-Туси, Насир ад-Дин (1201-1274) в «Трактате о полном четырехстороннике» впервые изложил тригонометрические сведения как самостоятельный отдел математики, а не придаток к астрономии.
4. Продолжение развития тригонометрии в Европе
После того как арабские трактаты были в XII-XIII веках переведены на латынь, многие идеи индийских и персидских математиков стали достоянием европейской науки. В Европе продолжилось развитие тригонометрии. Первоначально сведения о тригонометрии приводились в сочинениях по астрономии, однако в сочинении Фибоначи «Практика геометрии», написанном около 1220 года, тригонометрия излагается как часть геометрии. Первым европейским сочинением, целиком посвященным тригонометрии, часто называют «Четыре трактата о прямых и обращенных хордах» английского астронома Ричарда Уоллингфордского (около 1320 г.).
Первым европейским сочинением, целиком посвященным тригонометрии, часто называют «Четыре трактата о прямых и обращенных хордах» английского астронома Ричарда Уоллингфордского (около 1320 г.).
Самым же видным европейским представителем этой эпохи был Региомонтан. Его работы изложенные в математическом труде «Пять книг о треугольниках всех видов» имели большое значение в дальнейшем развитии тригонометрии в XVI-XVII вв.
На пороге XVII в. в развитии тригонометрии намечается новое направление — аналитическое. Если до этого главной целью тригонометрии считалось решение треугольников, вычисление элементов геометрических фигур и учение о тригонометрических функциях строилось на геометрической основе, то в XVII-XIX вв. тригонометрия постепенно становится одной из глав математического анализа. Она находит широкое применение в механике, физике и технике, особенно при изучении колебательных движений и других периодических процессов. О свойстве периодичности тригонометрических функций знал еще Виет, первые математические исследования которого относились к тригонометрии. Швейцарский математик Иоганн Бернулли (1642-1727) уже применял символы тригонометрических функций. Расширение представления о тригонометрических функциях привело к обоснованию их на новой, аналитической базе: тригонометрические функции определяются независимо от геометрии при помощи степенных рядов и других понятий математического анализа.
Швейцарский математик Иоганн Бернулли (1642-1727) уже применял символы тригонометрических функций. Расширение представления о тригонометрических функциях привело к обоснованию их на новой, аналитической базе: тригонометрические функции определяются независимо от геометрии при помощи степенных рядов и других понятий математического анализа.
Развитию аналитической теории тригонометрических функций содействовали И. Ньютон и Л. Эйлер. Леонард Эйлер ввел и само понятие функции и принятую в наши дни символику. Он придал всей тригонометрии ее современный вид. В трактате «Введение в анализ бесконечных» (1748) Эйлер дал определение тригонометрических функций, эквивалентное современному, и определил обратные функции. Подход Эйлера с этих пор стал общепризнанным и вошёл в учебники.
5. Развитие тригонометрии в России
В России первые сведения о тригонометрии были опубликованы в сборнике «Таблицы логарифмов, синусов и тангенсов к изучению мудролюбивых тщателей», опубликованном при участии Л. Ф.Магницкого в 1703 году. В 1714 году появилось содержательное руководство «Геометрия практика», первый русский учебник по тригонометрии, ориентированный на прикладные задачи артиллерии, навигации и геодезии. Завершением периода освоения тригонометрических знаний в России можно считать фундаментальный учебник академика М. Е. Головина (ученика Эйлера) «Плоская и сферическая тригонометрия с алгебраическими доказательствами» (1789).
Ф.Магницкого в 1703 году. В 1714 году появилось содержательное руководство «Геометрия практика», первый русский учебник по тригонометрии, ориентированный на прикладные задачи артиллерии, навигации и геодезии. Завершением периода освоения тригонометрических знаний в России можно считать фундаментальный учебник академика М. Е. Головина (ученика Эйлера) «Плоская и сферическая тригонометрия с алгебраическими доказательствами» (1789).
В конце XVIII века в Петербурге возникла авторитетная тригонометрическая школа, которая внесла большой вклад в плоскую и сферическую тригонометрию.
Дальнейшее развитие теории тригонометрии было продолжено в XIX в Н. И. Лобачевским и другими учеными.
В начале XIX века Н. И. Лобачевский добавил к плоской и сферической тригонометрии третий раздел — гиперболическую. В XIX-XX веках бурное развитие получили теория тригонометрических рядов и связанные с ней области математики: например, кодирование аудио и видеоинформации и другие.
В наше время важнейшая часть тригонометрии – учение о тригонометрических функциях рассматривается в математическом анализе, а -решение треугольников является частью геометрии
Работая над данной темой, я изучил ряд источников и нашел сведения о развитии тригонометрии.
Литература: 1.Глейзер Г.И. История математики в школе: IX-X кл. Пособие для учителей.- М.: Просвещение, 1983г.
2. Ресурсы сети Интернет
История тригонометрии как науки
Тригонометрия, как и любая другая научная дисциплина, возникла из потребностей практической деятельности человека. Различные задачи астрономии, мореплавания, землемерия, архитектуры привели к необходимости разработки способа вычисления элементов геометрических фигур по известным значениям других их элементов, найденных путем непосредственных измерений. Само название «тригонометрия» греческого происхождения, обозначающее «измерение треугольников»: (тригонон) — треугольник, (метрейн) — измерение.
Зарождение тригонометрии относится к глубокой древности. Еще задолго до новой эры вавилонские ученые умели предсказывать солнечные и лунные затмения. Это позволяет сделать вывод о том, что им были известны некоторые простейшие сведения из тригонометрии. Постепенно в геометрии и астрономии установились понятия синуса, косинуса и тангенса угла. По существу, ими оперировали еще древние математики, рассматривая отношение отрезков в треугольниках и окружностях.
По существу, ими оперировали еще древние математики, рассматривая отношение отрезков в треугольниках и окружностях.
Накопившийся материал астрономических наблюдений потребовал математической обработки. Одним из основоположников тригонометрии считается древнегреческий астроном Гиппарх, живший во II в. до н.э. Гиппарх является автором первых тригонометрических таблиц. Эти таблицы до нас не дошли, но они вошли (в усовершенствованном виде) в сочинение «Великое построение» (Альмагест) знаменитого александрийского астронома Клавдия Птолемея, жившего во второй половине II в. н.э. В этих таблицах, в течение многих веков служивших средством для решения треугольников, давались значения хорд окружности для различных значений соответствующего центрального угла. Единицей измерения хорд служила часть радиуса.
Эти таблицы, говоря современным языком, являются таблицами значений удвоенного синуса половины соответствующего центрального угла. В них были даны значения хорд для всех углов (через каждые полградуса) от 00 до 1800. Однако надо иметь в виду, что в древней Греции тригонометрия не выделялась в самостоятельную науку, а считалась частью астрономии.
Однако надо иметь в виду, что в древней Греции тригонометрия не выделялась в самостоятельную науку, а считалась частью астрономии.
Важный вклад в развитие тригонометрии был внесен индийской математикой в период V — XII вв. н.э. Индийские математики стали вычислять не полную хорду, как это делали греки, а ее половину (то есть «линию синусов»). Линия синусов именовалась ими «архаджива», что буквально означало «половина тетивы лука». Индийцы составилди таблицу синусов, в которой были даны значения полухорд, измеренных частями (минутами) окружности для всех углов от 00 до 900 (через каждые). Эти таблицы были точнее таблиц Птолемея. Об их высокой точности говорит тот факт, что для синуса и косинуса были вычислены значения и, отличающиеся от истинных менее чем на.
Индийским математикам были известны соотношения, которые в современных обозначениях пишутся так:
В XI — XIII вв. в трудах математиков Средней Азии, Закавказья, Ближнего Востока и Индии началось формирование тригонометрии как отдельной науки. И в дальнейшем потребности географии, геодезии, военного дела способствовали развитию тригонометрии как науки. Особенно усиленно тригонометрия развивалась в средние века, в первую очередь на юго-востоке: в Индии (Ариабхата, Брамагупта, Бхаскара), в Узбекистане, Азербайджане и Таджикистане (Насирад-Дин ат-Туси, ал-Каши, ал-Бируни), в Арабии (Ахмад, ибн-Абдаллах, ал-Баттани). Большая заслуга в формировании тригонометрии как отдельной науки принадлежит азербайджанскому ученому Насирад-Дину Муххамаду ат-Туси (1201 — 1274), написавшему «Трактат о полном четырехугольнике». Работы ученых этого периода привели к выделению тригонометрии как нового самостоятельного раздела математики. Однако в их трудах еще не было необходимой символики, и поэтому развитие тригонометрии происходило медленно.
И в дальнейшем потребности географии, геодезии, военного дела способствовали развитию тригонометрии как науки. Особенно усиленно тригонометрия развивалась в средние века, в первую очередь на юго-востоке: в Индии (Ариабхата, Брамагупта, Бхаскара), в Узбекистане, Азербайджане и Таджикистане (Насирад-Дин ат-Туси, ал-Каши, ал-Бируни), в Арабии (Ахмад, ибн-Абдаллах, ал-Баттани). Большая заслуга в формировании тригонометрии как отдельной науки принадлежит азербайджанскому ученому Насирад-Дину Муххамаду ат-Туси (1201 — 1274), написавшему «Трактат о полном четырехугольнике». Работы ученых этого периода привели к выделению тригонометрии как нового самостоятельного раздела математики. Однако в их трудах еще не было необходимой символики, и поэтому развитие тригонометрии происходило медленно.
С XV в. и в Европе появляются работы, посвященные вопросам тригонометрии. Немецкий ученый Иоганн Мюллер (1436 — 1476), известный в науке под именем Региомонтан, издал труд «Пять книг о треугольниках всех видов», сыгравший важную роль в развитии тригонометрии. В нем дано систематическое изложение тригонометрии как самостоятельной научной дисциплины. Региомонтан составил таблицы синусов с точностью уже до. В его таблицах радиус круга принимался за вместо числа кратного 60, то есть по сути был совершен переход от шестидесятиричной системы измерения к десятичной. В 1595 г. появился труд Варфоломея Питискуса «Тригонометрия, или Краткий обзорный трактат о решении треугольников».
В нем дано систематическое изложение тригонометрии как самостоятельной научной дисциплины. Региомонтан составил таблицы синусов с точностью уже до. В его таблицах радиус круга принимался за вместо числа кратного 60, то есть по сути был совершен переход от шестидесятиричной системы измерения к десятичной. В 1595 г. появился труд Варфоломея Питискуса «Тригонометрия, или Краткий обзорный трактат о решении треугольников».
В XV — XVII в. в Европе было составлено и издано несколько тригонометрических таблиц. Над их составлением работали крупнейшие ученые: Н. Коперник (1473 — 1543), и. Кеплер (1571 — 1630), Ф. Виет (1540 — 1603) и др. В России первые тригонометрические таблицы были изданы в 1703 г. при участии Л.Ф. Магницкого.
Таким образом, тригонометрия возникла на геометрической основе, имела геометрический язык и применялась к решению геометрических задач. Развитие алгебраической символики позволило записывать тригонометрические соотношения в виде формул; применение отрицательных чисел позволило рассматривать направленные углы и дуги и распространить понятие тригонометрических линий (определенных отрезков в круге) для любых углов. В этот период создалась база для изучения тригонометрических функций как функций числового аргумента, основа аналитической теории тригонометрических (круговых) функций. Аналитический аппарат, позволяющий вычислять значения тригонометрических функций с любой степенью точности, был разработан Ньютоном.
В этот период создалась база для изучения тригонометрических функций как функций числового аргумента, основа аналитической теории тригонометрических (круговых) функций. Аналитический аппарат, позволяющий вычислять значения тригонометрических функций с любой степенью точности, был разработан Ньютоном.
Современный вид тригонометрия получила в трудах великого ученого, члена Российской академии наук Л. Эйлера (1707 — 1783). Эйлер стал рассматривать значения тригонометрических функций как числа — величины тригонометрических линий в круге, радиус которого принят за единицу («тригонометрический круг» или «единичная окружность»). Эйлер дал окончательное решение о знаках тригонометрических функций в разных четвертях, вывел все тригонометрические формулы из нескольких основных, установил несколько неизвестных до него формул, ввел единообразные обозначения. Именно в его трудах впервые встречаются записи. Он также открыл связь между тригонометрическими и показательной функциями от комплексного аргумента. На основании работ Л. Эйлера были составлены учебники тригонометрии, излагавшие ее в строгой научной последовательности.
На основании работ Л. Эйлера были составлены учебники тригонометрии, излагавшие ее в строгой научной последовательности.
Аналитическое (не зависящее от геометрии) построение теории тригонометрических функций, начатое Эйлером, получило завершение в трудах великого русского ученого Н.И. Лобачевского.
Современная точка зрения на тригонометрические функции как на функции числового аргумента во многом обусловлена развитием физики, механики, техники. Эти функции легли в основу математического аппарата, при помощи которого изучаются различные периодические процессы: колебательные движения, распространение волн, движения механизмов, колебание переменного электрического тока. Как показал Ж. Фурье (1768 — 1830), всякое периодическое движение с любой степенью точности можно представить в виде суммы простейших синусоидальных (гармонических) колебаний. Если в начале развития тригонометрии соотношение
лишь выражало зависимость между площадями квадратов, построенных на сторонах переменного прямоугольного треугольника с гипотенузой равной 1, то в последующем это отношение стало отражать также сложение двух колебательных движений с происходящей при этом интерференцией.
Таким образом, на первоначальных стадиях своего развития тригонометрия служила средством решения вычислительных геометрических задач. Ее содержанием считалось вычисление элементов простейших геометрических фигур, то есть треугольников. Но в современной тригонометрии самостоятельное и столь же важное значение имеет изучение свойств тригонометрических функций. Этот период развития тригонометрии был подготовлен всем ходом развития механики колебательных движений, физики звуковых, световых и электромагнитных волн.
В этот период даны обобщения многим терминам тригонометрии и, в частности, выведены соотношения для, где n — натуральное число, и др. Функции и рассматриваются теперь как суммы степенных рядов:
Одновременно развивается учение о тригонометрических функциях комплексного переменного.
Тригонометрия как учебный предмет
История изучения тригонометрии в школе чрезвычайно поучительна для специалистов в области обучения математике. Это история одного из разделов математической науки, только во второй половине XVIII в. обретшего достаточно стройный и завершенный вид.
обретшего достаточно стройный и завершенный вид.
Современному учителю уже достаточно сложно найти материалы, раскрывающие идеи и структуру прежних программ обучения математике. В то же время в современной школе, в условиях определенной академической свободы учителя, эти сведения могут быть полезны для обоснования планирования изучения тригонометрии, поскольку они иллюстрируют иные подходы к изучению этого курса, отличающие от предлагаемых сегодня во многих учебниках.
Напомним, что в связи с открытием Н.И. Лобачевским новой геометрии выяснилось, что тригонометрия состоит из двух различных частей:
- а) первой (ее обычно называют гониометрией) — части математического анализа, где независимо от геометрических соображений аналитически раскрывается учение о трансцендентных тригонометрических функциях с их свойствами;
- б) второй — собственно тригонометрии, где соединяются математический анализ и геометрия того или иного пространства.
Гониометрия не зависит от аксиомы параллельных, а тригонометрия в собственном смысле зависит от этой аксиомы. Соотношение характеризует в общем случае операции с соответствующими рядами и только в евклидовом пространстве выражает соотношение между площадями квадратов, построенных на сторонах прямоугольного треугольника с гипотенузой равной 1.
Соотношение характеризует в общем случае операции с соответствующими рядами и только в евклидовом пространстве выражает соотношение между площадями квадратов, построенных на сторонах прямоугольного треугольника с гипотенузой равной 1.
Известное соотношение между сторонами и углами треугольника
Тригонометрические неравенства
Пример 1. Решим неравенство
Решение. Обозначив, перепишем неравенство (1) в виде
Множество решений неравенства (2) есть серия интервалов
поэтому все решения неравенства (1) найдем, решив двойное неравенство
откуда получим
то есть множество решений неравенства (1) состоит из серии интервалов
Пример 2. Решим неравенство
Решение. Перепишем неравенство (3) в виде
Обозначим. Так как неравенство имеет множество решений, то решения неравенства (3) найдем, решив двойное неравенство.
Неравенство
Справедливо для любых x, а множество решений неравенства есть серия промежутков
Она и является множеством решений неравенства (3).
Пример 3. Определим все, при каждом их которых неравенство
имеет хотя бы одно решение.
Решение. Разделим неравенство (4) на число, получим неравенство
равносильное неравенству (4).
Так как, то существует такой угол, что и. Перепишем неравенство (5) в виде
Последнее неравенство, а значит, и неравенство (4), имеет хотя бы одно решение при каждом таком, что, то есть при каждом.
1.1. Зарождение и развитие тригонометрии.
1.2. Сферическая тригонометрия.
1.3. Тригонометрия в Европе до Эйлера.
1.4. Вклад Эйлера в развитие тригонометрии.
1.5. Последователи Эйлера в развитии тригонометрии.
1.1. ЗАРОЖДЕНИЕ И РАЗВИТИЕ ТРИГОНОМЕТРИИ.
Тригонометрия возникла и развивалась в древности как один из разделов астрономии, как ее вычислительный аппарат, отвечающий практическим нуждам человека.
Тригонометрия – слово греческое и в
буквальном переводе означает измерение
треугольников (trigwnon — треугольник, а
metrew — измеряю).
В данном случае измерение треугольников следует понимать как решение треугольников, т.е. определение сторон, углов и других элементов треугольника, если даны некоторые из них. Большое количество практических задач, а также задач планиметрии, стереометрии, астрономии и других приводятся к задаче решения треугольников.
Возникновение тригонометрии связано с землемерением, астрономией и строительным делом. Хотя название науки возникло сравнительно недавно, многие относимые сейчас к тригонометрии понятия и факты были известны ещё 2000 лет назад.
Впервые способы решения треугольников, основанные на зависимостях между сторонами и углами треугольника, были найдены древнегреческими астрономами Гиппархом (2 в. до н. э.) и Клавдием Птолемеем (2 в. н. э.). Позднее зависимости между отношениями сторон треугольника и его углами начали называть тригонометрическими функциями.
Значительный вклад в развитие тригонометрии
внесли арабские ученые Аль-Батани
(850-929) и Абу-ль-Вафа, Мухамед-бен Мухамед
(940-998), который составил таблицы синусов
и тангенсов через 10’с
точностью до 1/60 4 . Теорему синусов
уже знали индийский ученый Бхаскара
(р. 1114, год смерти неизвестен) и
азербайджанский астроном и математик
Насиреддин Туси Мухамед (1201-1274). Кроме
того, Насиреддин Туси в своей работе
«Трактат о полном четырехстороннике»
изложил плоскую и сферическую тригонометрию
как самостоятельную дисциплину.
Теорему синусов
уже знали индийский ученый Бхаскара
(р. 1114, год смерти неизвестен) и
азербайджанский астроном и математик
Насиреддин Туси Мухамед (1201-1274). Кроме
того, Насиреддин Туси в своей работе
«Трактат о полном четырехстороннике»
изложил плоскую и сферическую тригонометрию
как самостоятельную дисциплину.
Длительную историю имеет понятие синус. Фактически различные отношения отрезков треугольника и окружности (а по существу, и тригонометрические функции) встречаются уже в IIIвеке до н.э. в работах великих математиков Древней Греции – Евклида, Архимеда, Апполония Пергского. В римский период эти отношения достаточно систематично исследовались Менелаем (Iвек н.э.), хотя и не приобрели специального названия. Современный синус, например, изучался как полухорда, на которую опирается центральный угол величиной, или как хорда удвоенной дуги.
Слово косинус намного моложе. Косинус
– это сокращение латинского выражения
completelysinus,
т. е. “дополнительный синус” (или иначе
“синус дополнительной дуги”;cos=sin(90-)).
Тангенсы возникли в связи с решением задачи об определении длины тени. Тангенс (а также котангенс) введен в Xвеке арабским математиком Абу-ль-Вафой, который составил и первые таблицы для нахождения тангенсов и котангенсов. Однако эти открытия долгое время оставались неизвестными европейским ученым, и тангенсы были заново открыты лишь вXIVвеке немецким математиком, астрономом Регимонтаном (1467 г.). Он доказал теорему тангенсов. Региомонтан составил также подробные тригонометрические таблицы; благодаря его трудам плоская и сферическая тригонометрия стала самостоятельной дисциплиной и в Европе.
Название «тангенс», происходящее от латинского tanger(касаться), появилось в 1583 г.Tangensпереводится как «касающийся» (линия тангенсов – касательная к единичной окружности).
Дальнейшее развитие тригонометрия
получила в трудах выдающихся астрономов
Николая Коперника (1473-1543) – творца
гелиоцентрической системы мира, Тихо
Браге (1546-1601) и Иогана Кеплера (1571-1630), а
также в работах математика Франсуа
Виета (1540-1603), который полностью решил
задачу об определениях всех элементов
плоского или сферического треугольника
по трем данным.
Долгое время тригонометрия носила чисто геометрический характер, т. е. Факты, которые мы сейчас формулируем в терминах тригонометрических функций, формулировались и доказывались с помощью геометрических понятий и утверждений. Такою она была еще в средние века, хотя иногда в ней использовались и аналитические методы, особенно после появления логарифмов. Пожалуй, наибольшие стимулы к развитию тригонометрии возникали в связи с решением задач астрономии, что представляло большой практический интерес (например, для решения задач определения местонахождения судна, предсказания затемнения и т. д.). Астрономов интересовали соотношения между сторонами и углами сферических треугольников. И надо заметить, что математики древности удачно справлялись с поставленными задачами.
Начиная с XVIIв.,
тригонометрические функции начали
применять к решению уравнений, задач
механики, оптики, электричества,
радиотехники, для описания колебательных
процессов, распространения волн, движения
различных механизмов, для изучения
переменного электрического тока и т. д. Поэтому тригонометрические функции
всесторонне и глубоко исследовались,
и приобрели важное значение для всей
математики.
д. Поэтому тригонометрические функции
всесторонне и глубоко исследовались,
и приобрели важное значение для всей
математики.
Аналитическая теория тригонометрических функций в основном была создана выдающимся математиком XVIIIвеке Леонардом Эйлером (1707-1783) членом Петербургской Академии наук. Громадное научное наследие Эйлера включает блестящие результаты, относящиеся к математическому анализу, геометрии, теории чисел, механике и другим приложениям математики. Именно Эйлер первым ввел известные определения тригонометрических функций, стал рассматривать функции произвольного угла, получил формулы приведения. После Эйлера тригонометрия приобрела форму исчисления: различные факты стали доказываться путем формального применения формул тригонометрии, доказательства стали намного компактнее проще,
Таким образом, тригонометрия, возникшая как наука о решении треугольников, со временем развилась и в науку о тригонометрических функциях.
1.2. СФЕРИЧЕСКАЯ ТРИГОНОМЕТРИЯ.
Сферическая тригонометрия — раздел
тригонометрии, в котором изучаются
зависимости между величинами углов и
длинами сторон сферических треугольников. Применяется для решения различных
геодезических и астрономических задач.
Применяется для решения различных
геодезических и астрономических задач.
Основы сферической тригонометрии были заложены греческим математиком и астрономом Гиппархом во II веке до н. э. Важный вклад в её развитие внесли такие античные учёные, как Менелай Александрийский и Клавдий Птолемей. Сферическая тригонометрия древних греков опиралась на применение теоремы Менелая к полному четырёхстороннику на сфере. Древнегреческие математики излагали условие теоремы Менелая не на языке отношений синусов, а на языке отношений хорд. Для выполнения требуемых расчётов применялись таблицы хорд, аналогичные последующим таблицам синусов.
Как самостоятельная дисциплина
сферическая тригонометрия сформировалась
в работах средневековых математиков
стран ислама. Наибольший вклад в её
развитие в эту эпоху внесли такие учёные,
как Сабит ибн Корра, Ибн Ирак, Кушьяр
ибн Лаббан, Абу-л-Вафа, ал-Бируни, Джабир
ибн Афлах, ал-Джайяни, Насир ад-Дин
ат-Туси. В их работах были введены
основные тригонометрические функции,
сформулирована и доказана сферическая
теорема синусов и ряд других теорем,
применявшихся в астрономических и
геодезических расчётах, ведено понятие
полярного треугольника, позволявшее
вычислять стороны сферического
треугольника по трём его данным углам.
История сферической тригонометрии в Европе связана с трудами таких учёных, как Региомонтан, Николай Коперник, Франческо Мавролико.
Замена хорд синусами стала главным достижением Средневековой Индии. Такая замена позволила вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом, в Индии было положено начало тригонометрии как учению о тригонометрических величинах.
Индийские учёные пользовались различными тригонометрическими соотношениями. Тригонометрия необходима для астрономических расчётов, которые оформляются в виде таблиц. Первая таблица синусов имеется в «Сурья-сиддханте» и у Ариабхаты. Позднее учёные составили более подробные таблицы: например, Бхаскара приводит таблицу синусов через 1°.
Южноиндийские математики в 16 веке
добивались больших успехов в области
суммирования бесконечных числовых
рядов. По-видимому, они занимались этими
исследованиями, когда искали способы
вычисления более точных значений числа
π. Никаланта словесно приводит правила
разложения арктангенса в бесконечный
степенной ряд. А в анонимном трактате
«Каранападдхати» («Техника вычислений»)
даны правила разложения синуса и косинуса
в бесконечные степенные ряды. Нужно
сказать, что в Европе к подобным
результатам подошли лишь в 17-18 вв. Так,
ряды для синуса и косинуса вывел Исаак
Ньютон около 1666 г., а ряд арктангенса
был найден Дж. Грегори в 1671 г. и Г. В.
Лейбницем в 1673 г.
А в анонимном трактате
«Каранападдхати» («Техника вычислений»)
даны правила разложения синуса и косинуса
в бесконечные степенные ряды. Нужно
сказать, что в Европе к подобным
результатам подошли лишь в 17-18 вв. Так,
ряды для синуса и косинуса вывел Исаак
Ньютон около 1666 г., а ряд арктангенса
был найден Дж. Грегори в 1671 г. и Г. В.
Лейбницем в 1673 г.
В 8 в. учёные стран Ближнего и Среднего Востока познакомились с трудами индийских математиков и астрономов и перевели их на арабский язык. В середине 9 века среднеазиатский учёный аль-Хорезми написал сочинение «Об индийском счёте». После того как арабские трактаты были переведены на латынь, многие идеи индийских математиков стали достоянием европейской, а затем и мировой науки.
1.1 Этапы развития тригонометрии как науки
Тригонометрия является одним из наиболее молодых отделов элементарной математики, получивших окончательное оформление лишь в XVIII в., хотя отдельные идеи её относятся к глубокой древности, к античному миру и к математическому творчеству индусов (К. Птолемей, II в., Аль Баттани, IX в., и др.). Европейские математики достигли высокой степени совершенства в вычислении таблиц натуральных синусов и тангенсов (Региомонтанус, XV в., Ретикус и Питискус, XVI в., и др.).
Птолемей, II в., Аль Баттани, IX в., и др.). Европейские математики достигли высокой степени совершенства в вычислении таблиц натуральных синусов и тангенсов (Региомонтанус, XV в., Ретикус и Питискус, XVI в., и др.).
Само название «тригонометрия» греческого происхождения, обозначающее «измерение треугольников»: (тригонон) – треугольник, (метрейн) – измерение.
Научная разработка тригонометрии осуществлена Л. Эйлером в его труде «Jntroductio in analysis infinitorum» (1748). Он создал тригонометрию как науку о функциях, дал ей аналитическое изложение, вывел всю совокупность формул из немногих основных формул. Обозначение сторон малыми буквами и противолежащих углов — соответствующими большими буквами позволило ему упростить все формулы, внести в них ясность и стройность. Эйлеру принадлежит мысль рассматривать тригонометрические функции как отношения соответствующих линий к радиусу круга, т. е. как числа, причём радиус круга как «полный синус» он принял за единицу. Эйлер получил ряд новых соотношений, установил связь тригонометрических функций с показательными, дал правило знаков функций для всех четвертей, получил обобщённую формулу приведения и освободил тригонометрию от многих ошибок, которые допускались почти во всех европейских учебниках математики.
Сочинение Л. Эйлера в дальнейшем послужило фундаментом для учебников тригонометрии. Одно из первых руководств, «Сокращённая математика» С. Румовского (1760), отдел «Начальные основания плоской тригонометрии», начинает изложение следующим образом: «Тригонометрия плоская есть знание через Арифметические выкладки сыскивать треугольники, которые геометрия черченьем находит». Всё изложение сводится к решению треугольников (самые простые случаи), вычисления проводятся весьма сложным путём, учение о функциях отсутствует.
Таким образом, тригонометрия возникла на геометрической основе, имела геометрический язык и применялась к решению геометрических задач. Развитие алгебраической символики позволило записывать тригонометрические соотношения в виде формул; применение отрицательных чисел позволило рассматривать направленные углы и дуги и распространить понятие тригонометрических линий (определенных отрезков в круге) для любых углов. В этот период создалась база для изучения тригонометрических функций как функций числового аргумента, основа аналитической теории тригонометрических (круговых) функций. Аналитический аппарат, позволяющий вычислять значения тригонометрических функций с любой степенью точности, был разработан Ньютоном.
Аналитический аппарат, позволяющий вычислять значения тригонометрических функций с любой степенью точности, был разработан Ньютоном.
Современный вид тригонометрия получила в трудах великого ученого, члена Российской академии наук Л. Эйлера (1707 – 1783). Эйлер стал рассматривать значения тригонометрических функций как числа – величины тригонометрических линий в круге, радиус которого принят за единицу («тригонометрический круг» или «единичная окружность»). Эйлер дал окончательное решение о знаках тригонометрических функций в разных четвертях, вывел все тригонометрические формулы из нескольких основных, установил несколько неизвестных до него формул, ввел единообразные обозначения. Именно в его трудах впервые встречаются записи . Он также открыл связь между тригонометрическими и показательной функциями от комплексного аргумента. На основании работ Л. Эйлера были составлены учебники тригонометрии, излагавшие ее в строгой научной последовательности.
Аналитическое (не зависящее от геометрии) построение теории тригонометрических функций, начатое Эйлером, получило завершение в трудах великого русского ученого Н. И. Лобачевского.
И. Лобачевского.
Современная точка зрения на тригонометрические функции как на функции числового аргумента во многом обусловлена развитием физики, механики, техники. Эти функции легли в основу математического аппарата, при помощи которого изучаются различные периодические процессы: колебательные движения, распространение волн, движения механизмов, колебание переменного электрического тока. Как показал Ж. Фурье (1768 – 1830), всякое периодическое движение с любой степенью точности можно представить в виде суммы простейших синусоидальных (гармонических) колебаний. Если в начале развития тригонометрии соотношение лишь выражало зависимость между площадями квадратов, построенных на сторонах переменного прямоугольного треугольника с гипотенузой равной 1, то в последующем это отношение стало отражать также сложение двух колебательных движений с происходящей при этом интерференцией.
Таким образом, на первоначальных стадиях своего развития тригонометрия служила средством решения вычислительных геометрических задач. Ее содержанием считалось вычисление элементов простейших геометрических фигур, то есть треугольников. Но в современной тригонометрии самостоятельное и столь же важное значение имеет изучение свойств тригонометрических функций. Этот период развития тригонометрии был подготовлен всем ходом развития механики колебательных движений, физики звуковых, световых и электромагнитных волн.
Ее содержанием считалось вычисление элементов простейших геометрических фигур, то есть треугольников. Но в современной тригонометрии самостоятельное и столь же важное значение имеет изучение свойств тригонометрических функций. Этот период развития тригонометрии был подготовлен всем ходом развития механики колебательных движений, физики звуковых, световых и электромагнитных волн.
В этот период даны обобщения многим терминам тригонометрии и, в частности, выведены соотношения для , где n – натуральное число, и др. Функции и рассматриваются теперь как суммы степенных рядов:
Почти также изложен и учебник В. Никитина и П. Суворова.
Вполне научное изложение тригонометрии даёт акад. М. Е. Головин в своём учебнике «Плоская и сферическая тригонометрия с алгебраическими доказательствами», 1789. В этой книге можно найти все важнейшие формулы тригонометрии почти в том виде, в каком принято излагать их в XIX в. (за исключением обратных тригонометрических функций). Автор не нашёл нужным загромождать изложение введением секанса и косеканса, так как эти функции в редких случаях применяются на практике.
В 1804 г. выходит учебник Н. Фусса. Книга предназначена для гимназий. «Плоская тригонометрия,- говорит автор,- есть наука, имеющая предметом из трёх данных и числами изображённых частей прямолинейного треугольника определять три прочие его части». Учебник состоит из 4 равных частей. Общие понятия, решение треугольников, приложение тригонометрии к практической геометрии и геодезии и, наконец, теорема сложения. Учебник Н. Фусса отмежёвывается от сферической тригонометрии.
Шаг вперёд делает академик М. В. Остроградский в 1851 г. В своём конспекте по тригонометрии для руководства в военно-учебных заведениях он выступает как сторонник определения тригонометрических функций, на первом этапе их изучения, как отношений сторон в прямоугольном треугольнике с последующим обобщением их определения и распространением его на углы любой величины.
Комплект под редакцией А.Г. Мордковича, хотя оставлять без внимания остальные учебники тоже не стоит. § 3. Методика преподавания темы «Тригонометрические функции» в курсе алгебры и начал анализа В изучении тригонометрических функций в школе можно выделить два основных этапа: ü Первоначальное знакомство с тригонометрическими функциями. ..
..
Учащихся, школьную документацию, сделать выводы о степени усвоения данного понятия. Подвести итог об исследовании особенностей математического мышления и процесса формирования понятия комплексного числа. Описание методов. Диагностические: I этап. Беседа проводилась с учителем математики, которая в 10Є классе преподает алгебру и геометрию. Беседа состоялась по истечении некоторого времени с начала…
История возникновения тригонометрии. Тригонометрия в природе
История тригонометрии
Тригонометрия – слово греческое и в буквальном переводе означает измерение треугольников ( — треугольник, а - измеряю).
В данном случае измерение треугольников следует понимать как решение треугольников, т.е. определение сторон, углов и других элементов треугольника, если даны некоторые из них. Большое количество практических задач, а также задач планиметрии, стереометрии, астрономии и других приводятся к задаче решения треугольников.
Возникновение тригонометрии связано с землемерением, астрономией и строительным делом.
Хотя название науки возникло сравнительно недавно, многие относимые сейчас к тригонометрии понятия и факты были известны ещё две тысячи лет назад.
Впервые способы решения треугольников, основанные на зависимостях между сторонами и углами треугольника, были найдены древнегреческими астрономами Гиппархом (2 в. до н. э.) и Клавдием Птолемеем (2 в. н. э.). Позднее зависимости между отношениями сторон треугольника и его углами начали называть тригонометрическими функциями.
Значительный вклад в развитие тригонометрии внесли арабские ученые Аль-Батани (850-929) и Абу-ль-Вафа, Мухамед-бен Мухамед (940-998), который составил таблицы синусов и тангенсов через 10
’
с точностью до 1/60
4
. Теорему синусов уже знали индийский ученый Бхаскара (р. 1114, год смерти неизвестен) и азербайджанский астроном и математик Насиреддин Туси Мухамед (1201-1274). Кроме того, Насиреддин Туси в своей работе «Трактат о полном четырехстороннике» изложил плоскую и сферическую тригонометрию как самостоятельную дисциплину.
Длительную историю имеет понятие синус. Фактически различные отношения отрезков треугольника и окружности (а по существу, и тригонометрические функции) встречаются уже в III веке до н.э. в работах великих математиков Древней Греции – Евклида, Архимеда, Апполония Пергского. В римский период эти отношения достаточно систематично исследовались Менелаем (I век н.э.), хотя и не приобрели специального названия. Современный синус , например, изучался как полухорда, на которую опирается центральный угол величиной , или как хорда удвоенной дуги.
М
A
А’
Рис. 1
В
IV
—
V
веках появился уже специальный термин в трудах по астрономии великого индийского учёного Ариабхаты, именем которого назван первый индийский спутник Земли. Отрезок АМ (рис. 1) он назвал ардхаджива (ардха – половина, джива – тетива лука, которую напоминает хорда). Позднее появилось более краткое название джива. Арабскими математиками в
IX
веке это слово было заменено на арабское слово джайб (выпуклость). При переводе арабских математических текстов в веке оно было заменено латинским синус (sinus
– изгиб, кривизна).
При переводе арабских математических текстов в веке оно было заменено латинским синус (sinus
– изгиб, кривизна).
Слово косинус намного моложе. Косинус – это сокращение латинского выражения completely sinus , т. е. “дополнительный синус” (или иначе “синус дополнительной дуги”; cos = sin (90 — )).
Тангенсы возникли в связи с решением задачи об определении длины тени. Тангенс (а также котангенс) введен в X веке арабским математиком Абу-ль-Вафой, который составил и первые таблицы для нахождения тангенсов и котангенсов. Однако эти открытия долгое время оставались неизвестными европейским ученым, и тангенсы были заново открыты лишь в XIV веке немецким математиком, астрономом Регимонтаном (1467 г.). Он доказал теорему тангенсов. Региомонтан составил также подробные тригонометрические таблицы; благодаря его трудам плоская и сферическая тригонометрия стала самостоятельной дисциплиной и в Европе.
Название «тангенс», происходящее от латинского
tanger
(касаться), появилось в 1583 г. Tangens
переводится как «касающийся» (линия тангенсов – касательная к единичной окружности).
Tangens
переводится как «касающийся» (линия тангенсов – касательная к единичной окружности).
Дальнейшее развитие тригонометрия получила в трудах выдающихся астрономов Николая Коперника (1473-1543) – творца гелиоцентрической системы мира, Тихо Браге (1546-1601) и Иогана Кеплера (1571-1630), а также в работах математика Франсуа Виета (1540-1603), который полностью решил задачу об определениях всех элементов плоского или сферического треугольника по трем данным.
Долгое время тригонометрия носила чисто геометрический характер, т. е. Факты, которые мы сейчас формулируем в терминах тригонометрических функций, формулировались и доказывались с помощью геометрических понятий и утверждений. Такою она была еще в средние века, хотя иногда в ней использовались и аналитические методы, особенно после появления логарифмов. Пожалуй, наибольшие стимулы к развитию тригонометрии возникали в связи с решением задач астрономии, что представляло большой практический интерес (например, для решения задач определения местонахождения судна, предсказания затемнения и т.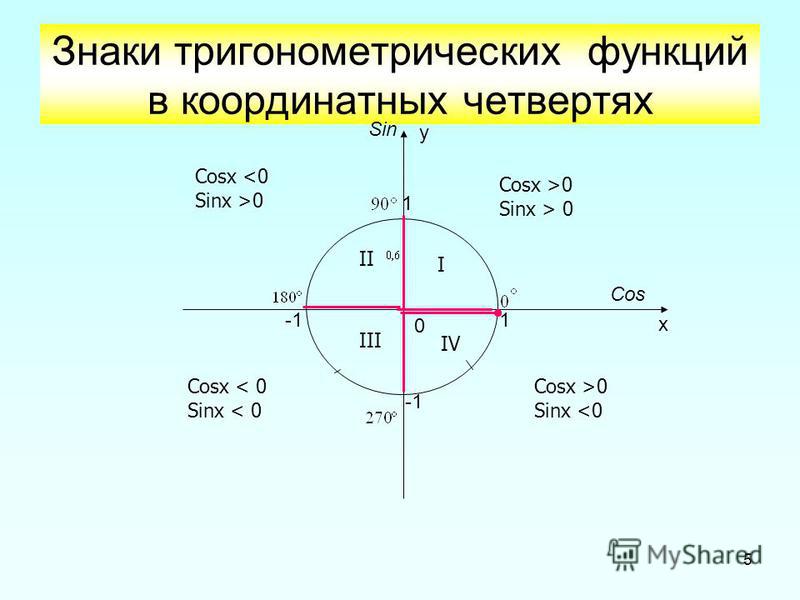 д.). Астрономов интересовали соотношения между сторонами и углами сферических треугольников. И надо заметить, что математики древности удачно справлялись с поставленными задачами.
д.). Астрономов интересовали соотношения между сторонами и углами сферических треугольников. И надо заметить, что математики древности удачно справлялись с поставленными задачами.
Начиная с XVII в., тригонометрические функции начали применять к решению уравнений, задач механики, оптики, электричества, радиотехники, для описания колебательных процессов, распространения волн, движения различных механизмов, для изучения переменного электрического тока и т. д. Поэтому тригонометрические функции всесторонне и глубоко исследовались, и приобрели важное значение для всей математики.
Аналитическая теория тригонометрических функций в основном была создана выдающимся математиком
XVIII
веке Леонардом Эйлером (1707-1783) членом Петербургской Академии наук. Громадное научное наследие Эйлера включает блестящие результаты, относящиеся к математическому анализу, геометрии, теории чисел, механике и другим приложениям математики. Именно Эйлер первым ввел известные определения тригонометрических функций, стал рассматривать функции произвольного угла, получил формулы приведения. После Эйлера тригонометрия приобрела форму исчисления: различные факты стали доказываться путем формального применения формул тригонометрии, доказательства стали намного компактнее проще,
После Эйлера тригонометрия приобрела форму исчисления: различные факты стали доказываться путем формального применения формул тригонометрии, доказательства стали намного компактнее проще,
Таким образом, тригонометрия, возникшая как наука о решении треугольников, со временем развилась и в науку о тригонометрических функциях.
Позднее часть тригонометрии, которая изучает свойства тригонометрических функций и зависимости между ними, начали называть гониометрией (в переводе – наука об измерении углов, от греческого — угол, - измеряю). Термин гониометрия в последнее время практически не употребляется.
История тригонометрии неразрывно связана с астрономией, ведь именно для решения задач этой науки древние ученые стали исследовать соотношения различных величин в треугольнике.
На сегодняшний день тригонометрия является микроразделом математики, изучающим зависимость между значениями величин углов и длин сторон треугольников, а также занимающимся анализом алгебраических тождеств тригонометрических функций.
Термин «тригонометрия»
Сам термин, давший название этому разделу математики, впервые был обнаружен в заголовке книги под авторством немецкого ученого-математика Питискуса в 1505 году. Слово «тригонометрия» имеет греческое происхождение и означает «измеряю треугольник». Если быть точнее, то речь идет не о буквальном измерении этой фигуры, а об её решении, то есть определении значений её неизвестных элементов с помощью известных.
Общие сведения о тригонометрии
История тригонометрии началась более двух тысячелетий назад. Первоначально ее возникновение было связано с необходимостью выяснения соотношений углов и сторон треугольника. В процессе исследований выяснилось, что математическое выражение данных соотношений требует введения особых тригонометрических функций, которые первоначально оформлялись как числовые таблицы.
Для многих смежных с математикой наук толчком к развитию стала именно история тригонометрии. Происхождение единиц измерения углов (градусов), связанное с исследованиями ученых Древнего Вавилона, опирается на шестидесятиричную систему исчисления, которая дала начала современной десятиричной, применяемой во многих прикладных науках.
Предполагается, что изначально тригонометрия существовала как часть астрономии. Затем она стала использоваться в архитектуре. А со временем возникла целесообразность применения данной науки в различных областях человеческой деятельности. Это, в частности, астрономия, морская и воздушная навигация, акустика, оптика, электроника, архитектура и прочие.
Тригонометрия в ранние века
Руководствуясь данными о сохранившихся научных реликвиях, исследователи сделали вывод, что история возникновения тригонометрии связана с работами греческого астронома Гиппарха, который впервые задумался над поиском способов решения треугольников (сферических). Его труды относятся ко 2 веку до нашей эры.
Также одним из важнейших достижений тех времен является определение соотношения катетов и гипотенузы в прямоугольных треугольниках, которое позже получило название теоремы Пифагора.
История развития тригонометрии в Древней Греции связана с именем астронома Птоломея — автора геоцентрической господствовавшей до Коперника.
Греческим астрономам не были известны синусы, косинусы и тангенсы. Они пользовались таблицами, позволяющими найти значение хорды окружности с помощью стягиваемой дуги. Единицами для измерения хорды были градусы, минуты и секунды. Один градус приравнивался к шестидесятой части радиуса.
Также исследования древних греков продвинули развитие сферической тригонометрии. В частности, Евклид в своих «Началах» приводит теорему о закономерностях соотношений объемов шаров различного диаметра. Его труды в этой области стали своеобразным толчком в развитии еще и смежных областей знаний. Это, в частности, технология астрономических приборов, теория картографических проекций, система небесных координат и т. д.
Средневековье: исследования индийских ученых
Значительных успехов достигли индийские средневековые астрономы. Гибель античной науки в IV веке обусловила перемещение центра развития математики в Индию.
История возникновения тригонометрии как обособленного раздела математического учения началась в Средневековье. Именно тогда ученые заменили хорды синусами. Это открытие позволило ввести функции, касающиеся исследования сторон и углов То есть именно тогда тригонометрия начала обосабливаться от астрономии, превращаясь в раздел математики.
Именно тогда ученые заменили хорды синусами. Это открытие позволило ввести функции, касающиеся исследования сторон и углов То есть именно тогда тригонометрия начала обосабливаться от астрономии, превращаясь в раздел математики.
Первые таблицы синусов были у Ариабхаты, они была проведены через 3 о, 4 о, 5 о. Позже появились подробные варианты таблиц: в частности, Бхаскара привел таблицу синусов через 1 о.
Первый специализированный трактат по тригонометрии появился в X—XI веке. Автором его был среднеазиатский учёный Аль-Бируни. А в своем главном труде «Канон Мас‘уда» (книга III) средневековый автор еще более углубляется в тригонометрию, приводя таблицу синусов (с шагом 15″) и таблицу тангенсов (с шагом 1°).
История развития тригонометрии в Европе
После перевода арабских трактатов на латынь (XII-XIII в) большинство идей индийских и персидских ученых были заимствованы европейской наукой. Первые упоминания о тригонометрии в Европе относятся к XII веку.
По мнению исследователей, история тригонометрии в Европе связана с именем англичанина Ричарда Уоллингфордского, который стал автором сочинения «Четыре трактата о прямых и обращенных хордах». Именно его труд стал первой работой, которая целиком посвящена тригонометрии. К XV веку многие авторы в своих трудах упоминают о тригонометрических функциях.
Именно его труд стал первой работой, которая целиком посвящена тригонометрии. К XV веку многие авторы в своих трудах упоминают о тригонометрических функциях.
История тригонометрии: Новое время
В Новое время большинство ученых стало осознавать чрезвычайную важность тригонометрии не только в астрономии и астрологии, но и в других областях жизни. Это, в первую очередь, артиллерия, оптика и навигация в дальних морских походах. Поэтому во второй половине XVI века эта тема заинтересовала многих выдающихся людей того времени, в том числе Николая Коперника, Франсуа Виета. Коперник отвел тригонометрии несколько глав своего трактата «О вращении небесных сфер» (1543). Чуть позже, в 60-х годах XVI века, Ретик — ученик Коперника — приводит в своем труде «Оптическая часть астрономии» пятнадцатизначные тригонометрические таблицы.
В «Математическом каноне» (1579) дает обстоятельную и систематическую, хотя и бездоказательную, характеристику плоской и сферической тригонометрии. А Альбрехт Дюрер стал тем, благодаря кому на свет появилась синусоида.
А Альбрехт Дюрер стал тем, благодаря кому на свет появилась синусоида.
Заслуги Леонарда Эйлера
Придание тригонометрии современного содержания и вида стало заслугой Леонарда Эйлера. Его трактат «Введение в анализ бесконечных» (1748) содержит определение термина «тригонометрические функции», которое эквивалентно современному. Таким образом, этот ученый смог определить Но и это еще не все.
Определение тригонометрических функций на всей числовой прямой стало возможным благодаря исследованиям Эйлера не только допустимых отрицательных углов, но и углов боле 360°. Именно он в своих работах впервые доказал, что косинус и тангенс прямого угла отрицательные. Разложение целых степеней косинуса и синуса тоже стало заслугой этого ученого. Общая теория тригонометрических рядов и изучение сходимости полученных рядов не были объектами исследований Эйлера. Однако, работая над решением смежных задач, он сделал много открытий в этой области. Именно благодаря его работам продолжилась история тригонометрии. Кратко в своих трудах он касался и вопросов сферической тригонометрии.
Кратко в своих трудах он касался и вопросов сферической тригонометрии.
Области применения тригонометрии
Тригонометрия не относится к прикладным наукам, в реальной повседневной жизни ее задачи редко применяются. Однако этот факт не снижает ее значимости. Очень важна, например, техника триангуляции, которая позволяет астрономам достаточно точно измерить расстояние до недалеких звезд и осуществлять контроль за системами навигации спутников.
Также тригонометрию применяют в навигации, теории музыки, акустике, оптике, анализе финансовых рынков, электронике, теории вероятностей, статистике, биологии, медицине (например, в расшифровке ультразвуковых исследований УЗИ и компьютерной томографии), фармацевтике, химии, теории чисел, сейсмологиии, метеорологии, океанологии, картографии, многих разделах физики, топографии и геодезии, архитектуре, фонетике, экономике, электронной технике, машиностроении, компьютерной графике, кристаллографиии и т. д. История тригонометрии и ее роль в изучении естественно-математических наук изучаются и по сей день. Возможно, в будущем областей ее применения станет еще больше.
Возможно, в будущем областей ее применения станет еще больше.
История происхождения основных понятий
История возникновения и развития тригонометрии насчитывает не один век. Введение понятий, которые составляют основу этого раздела математической науки, также не было одномоментным.
Так, понятие «синус» имеет очень долгую историю. Упоминания о различных отношениях отрезков треугольников и окружностей обнаруживаются еще в научных трудах, датируемых III веком до нашей эры. Работы таких великих древних ученых, как Евклид, Архимед, Апполоний Пергский, уже содержат первые исследования этих соотношений. Новые открытия требовали определенных терминологических уточнений. Так, индийский учёный Ариабхата дает хорде название «джива», означающее «тетива лука». Когда арабские математические тексты переводились на латынь, термин заменили близким по значению синусом (т. е. «изгиб»).
Слово «косинус» появилось намного позже. Этот термин является сокращенным вариантом латинской фразы «дополнительный синус».
Возникновение тангенсов связано с расшифровкой задачи определения длины тени. Термин «тангенс» ввел в X веке арабский математик Абу-ль-Вафа, составивший первые таблицы для определения тангенсов и котангенсов. Но европейские ученые не знали об этих достижениях. Немецкий математик и астроном Регимонтан заново открывает эти понятия в 1467 г. Доказательство теоремы тангенсов — его заслуга. А переводится этот термин как «касающийся».
Тригонометрия возникла и развивалась в древности как один из разделов астрономии, как ее вычислительный аппарат; отвечающий практическим нуждам человека. Именно астрономия определила тот факт, что сферическая тригонометрия возникла раньше плоской.
Некоторые тригонометрические сведения были известны древним вавилонянам и египтянам, но основы этой науки заложены в Древней Греции, Древнегреческие астрономы успешно решали отдельные вопросы из тригонометрии, связанные с астрономией. Однако они рассматривали не линии синуса, косинуса и др., а хорды. Роль линии синусов угла ее у них выполняла хорда, стягивающая дугу, равную 2а.
Роль линии синусов угла ее у них выполняла хорда, стягивающая дугу, равную 2а.
Греческий астроном Гиппарх во II в. до н. э. составил таблицу числовых значений хорд в зависимости от величин стягиваемых ими дуг. Более полные сведения из тригонометрии содержатся в известном «Альмагесте» Птолемея.
Птолемей делилокружностьна360 градусов, а диаметр — на 120 частей. Он считал радиус равным 60 частям (60Ч). Каждую, из частей он делил на 60″, а каждую минуту на 60″, секунду — на 60 терций (60″») и т. д. Говоря иными словами, он воспользовался шестидесятеричной системой счисления, по всей вероятности, позаимствованной им от вавилонян. Применяя указанное деление, Птолемей выражал сторону правильного вписанного шестиугольника или хорду, стягивающую дугу в 60° в виде 60 частей радиуса (60 Ч), а сторону вписанного квадрата или хорду в 90° приравнивал числу 84 Ч 5110″. Хорду в 120° — сторону вписанного равностороннего треугольника — он выражал числом 103 Ч 55″23″и т.д.
Применив известные из геометрии теоремы, ученый нашел зависимости, которые равнозначны следующим современным формулам при условии:
Воспользовавшись этими соотношениями и выраженными в частях радиуса значениями хорд 60°» и 72°, он вычислил хорду, стягивающую дугу в 6°, затем 3°; 1,5° и, наконец, —0,75°. (Значение хорды в Г он выражал приближенно.)
(Значение хорды в Г он выражал приближенно.)
Сделанные расчеты позволили Птолемею составить таблицу, которая содержала хорды от 0 до 180°, вычисленные с точностью до 1″ радиуса.
Эта таблица, сохранившаяся до нашего времени, равнозначна таблице синусов от 0 до 90° с шагом 0, 25° с пятью верными десятичными знаками.
Названия линий синуса и косинуса впервые были введены индийскими учеными. Они же составили первые таблицы синусов, хотя и менее точные, чем птолемеевы. В Индии и начинается по существу учение о тригонометрических величинах, названное позже гониометрией (от «гониа», — угол и «мехрио» — измеряю).
Дальнейшее развитие учение о тригонометрических величинах получило в IX—XV вв. в странах Среднего и Ближнего Востока в трудах ряда математиков, которые не только воспользовались существовавшими в то время достижениями в этой области, но и сделали свой значительный вклад в науку.
Известный Мухаммад ибн Муса ал-Хорезми (IX в.) составил таблицы синусов и котангенсов. Ал-Хабаш или (Ахмед ибн Абдаллах ал-Марвази) вычислил таблицы для тангенса, котангенса и косеканса.
Ал-Хабаш или (Ахмед ибн Абдаллах ал-Марвази) вычислил таблицы для тангенса, котангенса и косеканса.
Важное значение в развитии тригонометрии имели труды ал-Баттани (ок. 850—929) и Абу-л-Вафы ал-Бузджани (940—998). Последний вывел теорему синусов сферической тригонометрии, вычислил для синусов таблицу с интервалом в 15″, значения в которой приведены с точностью до 8-го десятичного знака, нашел отрезки, соответствующие секансу и косекансу.
Абу Райхан Мухаммад ибн Ахмад-ал-Беруни (по другой транскрипции Бируни (973—1048)) обобщил и при этом уточнил результаты, которых достигли его предшественники в области тригонометрии. В труде «Канон Мас»уда» он изложил все известные в то время положения из тригонометрии и существенно дополнил их. Важное нововведение, предпринятое Абу-л-Вафой, подтвердил и ал-Беруни. Вместо деления радиуса на части, сделанного Птолемеем, они брали единичный радиус. Ал-Беруни подробно объяснил причину этой замены, показав, что все вычисления с единичным радиусом значительно проще.
Насир ад-Дин Мухаммад ат-Туси (1201—1274) в «Трактате о полном четырехстороннике» впервые изложил тригонометрические сведения как самостоятельный отдел математики, а не придаток к астрономии. Его трактат впоследствии оказал большое влияние на работы Региомонтана (1436—1476).
В первой половине XV в. Джемшид ибн Масуд ал-Каши вычислил с большой точностью тригонометрические таблицы с шагом в. Г, которые на протяжении 250 лет оставались непревзойденными.
В Европе XII—XV вв., после того как были переведены с арабского и греческого языков на латинский некоторые классические математические и астрономические произведения, развитие тригонометрии продолжалось. При решении плоских треугольников широко применялась теорема синусов, вновь открытая жившим в Южной Франции Львом Герсонидом (1288—1344), тригонометрия которого была в 1342 г. переведена на латинский язык. Самым видным европейским представителем этой эпохи в области тригонометрии был Региомонтан. Его обширные таблицы синусов через Г с точностью до 7-й значащей цифры и его мастерски изложенный тригонометрический труд «Пять книг о треугольниках всех видов» имели большое значение для дальнейшего развития, тригонометрии в XVI—XVII вв.
На пороге XVII в. в развитии тригонометрии намечается новое направление — аналитическое. Если до этого главной целью тригонометрии считалось решение треугольников, вычисление элементов геометрических фигур и учение о тригонометрических функциях строилось на геометрической основе, то в XVII—XIX вв. тригонометрия постепенно становится одной из глав математического анализа. Она находит широкое применение в механике, физике и технике, особенно при изучении колебательных движений и других периодических процессов. О свойстве периодичности тригонометрических функций знал еще Виет, первые математические исследования которого относились к тригонометрии. Швейцарский математик Иоганн Бернулли (1642—1727) уже применял символы тригонометрических функций. И если развитие алгебраической символики, введение отрицательных чисел и направленных отрезков содействовали расширению понятия угла и дуги, то развитие учения о колебательных движениях, о звуковых, световых и электромагнитных волнах привело к тому, что основным содержанием тригонометрии стало изучение и описание колебательных процессов. Из физики известно, что уравнение гармонического колебания (например, колебания маятника, переменного электрического тока) имеет вид:
Из физики известно, что уравнение гармонического колебания (например, колебания маятника, переменного электрического тока) имеет вид:
Графиками гармонических колебаний являются синусоиды, поэтому в физике и технике сами гармонические колебания часто называют синусоидальными колебаниями.
В первой половине XIX в. французский ученый Ж. Фурье доказал, что всякое периодическое движение может быть представлено (с любой степенью точности) в виде суммы простых гармонических колебаний.
Расширение представлений о тригонометрических функциях привело к обоснованию их на новой, аналитической базе: тригонометрические функции определяются независимо от геометрии при помощи степенных рядов и других понятий математического анализа.
Развитию аналитической теории тригонометрических функций содействовали И. Ньютон и Л. Эйлер. Основоположником этой теории следует считать Л. Эйлера. Он придал всей тригонометрии современный вид. Дальнейшее развитие теории было продолжено в XIX в. Н.И. Лобачевским и другими учеными. В наше время тригонометрия больше не рассматривается как самостоятельная ветвь математики. Важнейшая ее часть — учение о тригонометрических функциях,— является частью более общего, построенного с единой точки зрения учения о функциях, изучаемых в математическом анализе; другая же часть — решение.треугольников — рассматривается как глава геометрии (плоской и сферической).
Лобачевским и другими учеными. В наше время тригонометрия больше не рассматривается как самостоятельная ветвь математики. Важнейшая ее часть — учение о тригонометрических функциях,— является частью более общего, построенного с единой точки зрения учения о функциях, изучаемых в математическом анализе; другая же часть — решение.треугольников — рассматривается как глава геометрии (плоской и сферической).
Тригонометрия возникла и развивалась в древности как один из разделов астрономии, как ее вычислительный аппарат; отвечающий практическим нуждам человека. Именно астрономия определила тот факт, что сферическая тригонометрия возникла раньше плоской.
Некоторые тригонометрические сведения были известны древним вавилонянам и египтянам, но основы этой науки заложены в Древней Греции, Древнегреческие астрономы успешно решали отдельные вопросы из тригонометрии, связанные с астрономией. Однако они рассматривали не линии синуса, косинуса и др., а хорды. Роль линии синусов угла ее у них выполняла хорда, стягивающая дугу, равную 2а.
Греческий астроном Гиппарх во II в. до н. э. составил таблицу числовых значений хорд в зависимости от величин стягиваемых ими дуг. Более полные сведения из тригонометрии содержатся в известном «Альмагесте» Птолемея.
Птолемей делилокружностьна360 градусов, а диаметр — на 120 частей. Он считал радиус равным 60 частям (60Ч). Каждую, из частей он делил на 60″, а каждую минуту на 60″, секунду — на 60 терций (60″») и т. д. Говоря иными словами, он воспользовался шестидесятеричной системой счисления, по всей вероятности, позаимствованной им от вавилонян. Применяя указанное деление, Птолемей выражал сторону правильного вписанного шестиугольника или хорду, стягивающую дугу в 60° в виде 60 частей радиуса (60 Ч), а сторону вписанного квадрата или хорду в 90° приравнивал числу 84 Ч 5110″. Хорду в 120° — сторону вписанного равностороннего треугольника — он выражал числом 103 Ч 55″23″и т.д.
Применив известные из геометрии теоремы, ученый нашел зависимости, которые равнозначны следующим современным формулам при условии:
Воспользовавшись этими соотношениями и выраженными в частях радиуса значениями хорд 60°» и 72°, он вычислил хорду, стягивающую дугу в 6°, затем 3°; 1,5° и, наконец, -0,75°. (Значение хорды в Г он выражал приближенно.)
(Значение хорды в Г он выражал приближенно.)
Сделанные расчеты позволили Птолемею составить таблицу, которая содержала хорды от 0 до 180°, вычисленные с точностью до 1″ радиуса.
Эта таблица, сохранившаяся до нашего времени, равнозначна таблице синусов от 0 до 90° с шагом 0, 25° с пятью верными десятичными знаками.
Названия линий синуса и косинуса впервые были введены индийскими учеными. Они же составили первые таблицы синусов, хотя и менее точные, чем птолемеевы. В Индии и начинается по существу учение о тригонометрических величинах, названное позже гониометрией (от «гониа», — угол и «мехрио» — измеряю).
Дальнейшее развитие учение о тригонометрических величинах получило в IX-XV вв. в странах Среднего и Ближнего Востока в трудах ряда математиков, которые не только воспользовались существовавшими в то время достижениями в этой области, но и сделали свой значительный вклад в науку.
Известный Мухаммад ибн Муса ал-Хорезми (IX в.) составил таблицы синусов и котангенсов.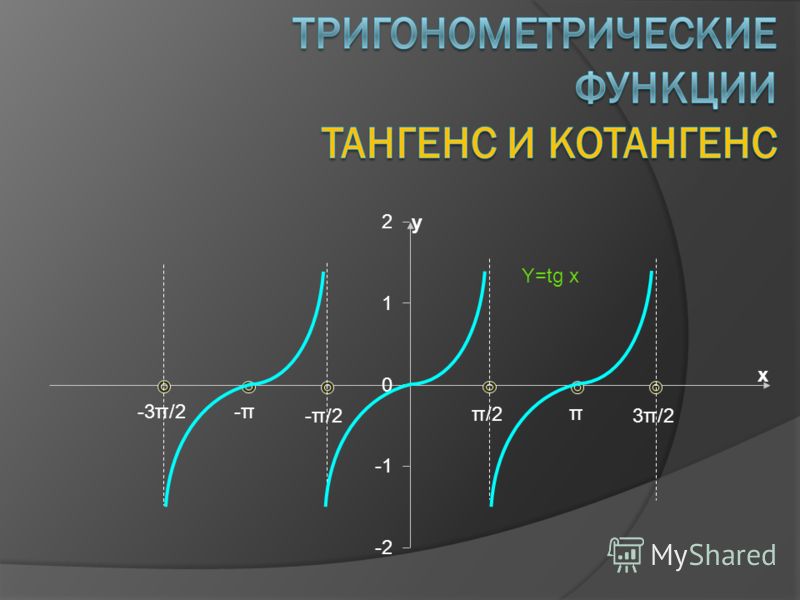 Ал-Хабаш или (Ахмед ибн Абдаллах ал-Марвази) вычислил таблицы для тангенса, котангенса и косеканса.
Ал-Хабаш или (Ахмед ибн Абдаллах ал-Марвази) вычислил таблицы для тангенса, котангенса и косеканса.
Важное значение в развитии тригонометрии имели труды ал-Баттани (ок. 850-929) и Абу-л-Вафы ал-Бузджани (940-998). Последний вывел теорему синусов сферической тригонометрии, вычислил для синусов таблицу с интервалом в 15″, значения в которой приведены с точностью до 8-го десятичного знака, нашел отрезки, соответствующие секансу и косекансу.
Абу Райхан Мухаммад ибн Ахмад-ал-Беруни (по другой транскрипции Бируни (973-1048)) обобщил и при этом уточнил результаты, которых достигли его предшественники в области тригонометрии. В труде «Канон Мас»уда» он изложил все известные в то время положения из тригонометрии и существенно дополнил их. Важное нововведение, предпринятое Абу-л-Вафой, подтвердил и ал-Беруни. Вместо деления радиуса на части, сделанного Птолемеем, они брали единичный радиус. Ал-Беруни подробно объяснил причину этой замены, показав, что все вычисления с единичным радиусом значительно проще.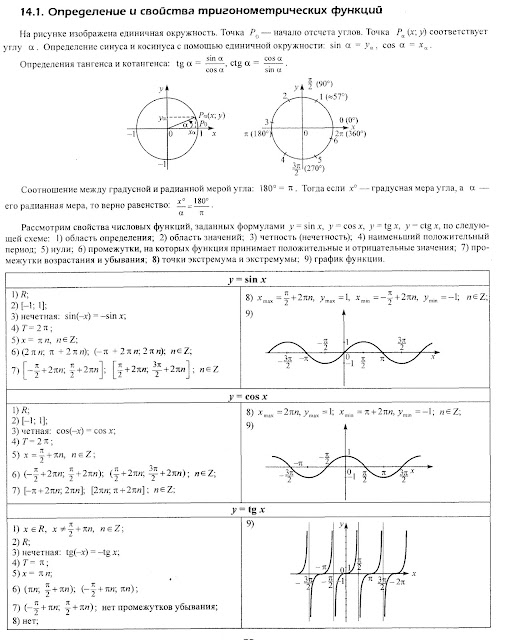
Насир ад-Дин Мухаммад ат-Туси (1201-1274) в «Трактате о полном четырехстороннике» впервые изложил тригонометрические сведения как самостоятельный отдел математики, а не придаток к астрономии. Его трактат впоследствии оказал большое влияние на работы Региомонтана (1436-1476).
В первой половине XV в. Джемшид ибн Масуд ал-Каши вычислил с большой точностью тригонометрические таблицы с шагом в. Г, которые на протяжении 250 лет оставались непревзойденными.
В Европе XII-XV вв., после того как были переведены с арабского и греческого языков на латинский некоторые классические математические и астрономические произведения, развитие тригонометрии продолжалось. При решении плоских треугольников широко применялась теорема синусов, вновь открытая жившим в Южной Франции Львом Герсонидом (1288-1344), тригонометрия которого была в 1342 г. переведена на латинский язык. Самым видным европейским представителем этой эпохи в области тригонометрии был Региомонтан. Его обширные таблицы синусов через Г с точностью до 7-й значащей цифры и его мастерски изложенный тригонометрический труд «Пять книг о треугольниках всех видов» имели большое значение для дальнейшего развития, тригонометрии в XVI-XVII вв.
На пороге XVII в. в развитии тригонометрии намечается новое направление — аналитическое. Если до этого главной целью тригонометрии считалось решение треугольников, вычисление элементов геометрических фигур и учение о тригонометрических функциях строилось на геометрической основе, то в XVII-XIX вв. тригонометрия постепенно становится одной из глав математического анализа. Она находит широкое применение в механике, физике и технике, особенно при изучении колебательных движений и других периодических процессов. О свойстве периодичности тригонометрических функций знал еще Виет, первые математические исследования которого относились к тригонометрии. Швейцарский математик Иоганн Бернулли (1642-1727) уже применял символы тригонометрических функций. И если развитие алгебраической символики, введение отрицательных чисел и направленных отрезков содействовали расширению понятия угла и дуги, то развитие учения о колебательных движениях, о звуковых, световых и электромагнитных волнах привело к тому, что основным содержанием тригонометрии стало изучение и описание колебательных процессов. Из физики известно, что уравнение гармонического колебания (например, колебания маятника, переменного электрического тока) имеет вид:
Из физики известно, что уравнение гармонического колебания (например, колебания маятника, переменного электрического тока) имеет вид:
Графиками гармонических колебаний являются синусоиды, поэтому в физике и технике сами гармонические колебания часто называют синусоидальными колебаниями.
В первой половине XIX в. французский ученый Ж. Фурье доказал, что всякое периодическое движение может быть представлено (с любой степенью точности) в виде суммы простых гармонических колебаний.
Расширение представлений о тригонометрических функциях привело к обоснованию их на новой, аналитической базе: тригонометрические функции определяются независимо от геометрии при помощи степенных рядов и других понятий математического анализа.
Развитию аналитической теории тригонометрических функций содействовали И. Ньютон и Л. Эйлер. Основоположником этой теории следует считать Л. Эйлера. Он придал всей тригонометрии современный вид. Дальнейшее развитие теории было продолжено в XIX в. Н.И. Лобачевским и другими учеными. В наше время тригонометрия больше не рассматривается как самостоятельная ветвь математики. Важнейшая ее часть — учение о тригонометрических функциях,- является частью более общего, построенного с единой точки зрения учения о функциях, изучаемых в математическом анализе; другая же часть — решение.треугольников — рассматривается как глава геометрии (плоской и сферической).
Лобачевским и другими учеными. В наше время тригонометрия больше не рассматривается как самостоятельная ветвь математики. Важнейшая ее часть — учение о тригонометрических функциях,- является частью более общего, построенного с единой точки зрения учения о функциях, изучаемых в математическом анализе; другая же часть — решение.треугольников — рассматривается как глава геометрии (плоской и сферической).
Конец работы —
Эта тема принадлежит разделу:
Доклад история возникновения тригонометрических функций
Доклад.. история возникновения тригонометрических функций.. краткий обзор развития тригонометрии тригонометрия возникла и развивалась в..
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ:
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
Отправить свою хорошую работу в базу знаний просто.
 Используйте форму, расположенную ниже
Используйте форму, расположенную нижеСтуденты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
Департамент образования города Москвы
Государственное бюджетное образовательное учреждение
Среднего Профессионального Образования
Строительный колледж №38
Доклад по математике
На тему: «История развития тригонометрии»
Выполнила студентка:
Удалова Евгения
Группы: 1-Т-1
Москва 2012
Слово тригонометрия впервые встречается в 1505 году в заглавии книги немецкого математика Питискуса.
Тригонометрия — слово греческое и в буквальном переводе означает измерение треугольников (trigwnon — треугольник, а metrew- измеряю).
В данном случае измерение треугольников следует понимать как решение треугольников, т. е. определение сторон, углов и других элементов треугольника, если даны некоторые из них. Большое количество практических задач, а также задач планиметрии, стереометрии, астрономии и других приводятся к задаче решения треугольников.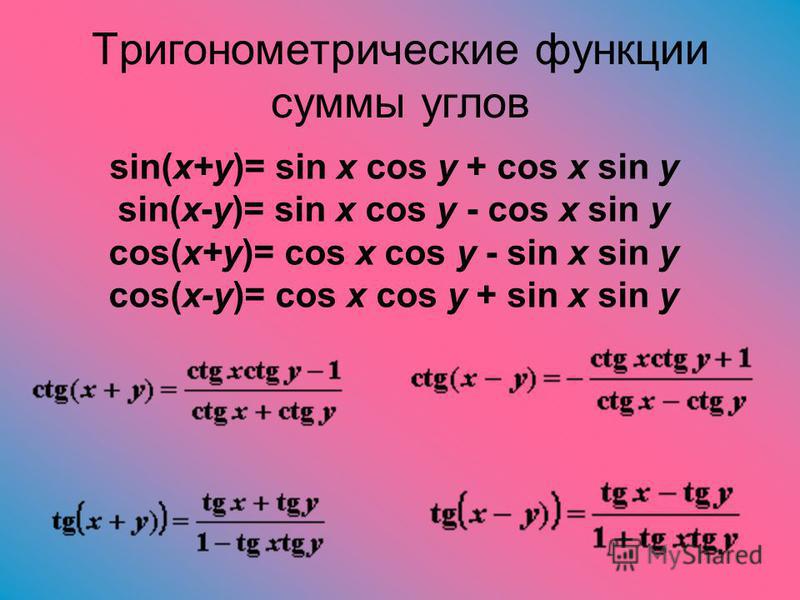
Возникновение тригонометрии связано с землемерением, астрономией и строительным делом.
Хотя название науки возникло сравнительно недавно, многие относимые сейчас к тригонометрии понятия и факты были известны ещё две тысячи лет назад.
Впервые способы решения треугольников, основанные на зависимостях между сторонами и углами треугольника, были найдены древнегреческими астрономами Гиппархом (2 в. до н. э.) и Клавдием Птолемеем (2 в. н. э.). Позднее зависимости между отношениями сторон треугольника и его углами начали называть тригонометрическими функциями
Значительный вклад в развитие тригонометрии внесли арабские ученые Аль-Батани (850-929) и Абу-ль-Вафа, Мухамед-бен Мухамед (940-998), который составил таблицы синусов и тангенсов через 10″ с точностью до 1/604. Теорему синусов уже знали индийский ученый Бхаскара (р. 1114, год смерти неизвестен) и азербайджанский астроном и математик Насиреддин Туси Мухамед (1201-1274). Кроме того, Насиреддин Туси в своей работе «Трактат о полном четырехстороннике» изложил плоскую и сферическую тригонометрию как самостоятельную дисциплину.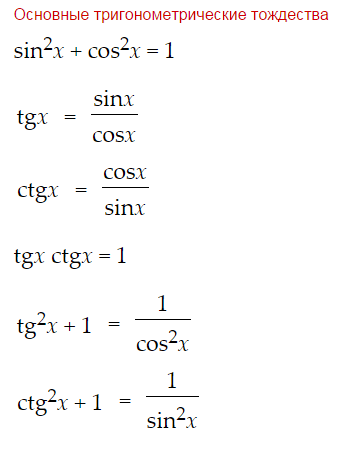
Длительную историю имеет понятие синус. Фактически различные отношения отрезков треугольника и окружности (а по существу, и тригонометрические функции) встречаются уже в III веке до н. э. в работах великих математиков Древней Греции — Евклида, Архимеда, Апполония Пергского. В римский период эти отношения достаточно систематично исследовались Менелаем (I век н. э.), хотя и не приобрели специального названия. Современный синус a, например, изучался как полухорда, на которую опирается центральный угол величиной a, или как хорда удвоенной дуги.
В IV-V веках появился уже специальный термин в трудах по астрономии великого индийского учёного Ариабхаты, именем которого назван первый индийский спутник Земли. Отрезок АМ он назвал ардхаджива (ардха — половина, джива — тетива лука, которую напоминает хорда). Позднее появилось более краткое название джива. Арабскими математиками в IX веке это слово было заменено на арабское слово джайб (выпуклость). При переводе арабских математических текстов в веке оно было заменено латинским синус (sinus — изгиб, кривизна).
Тангенсы возникли в связи с решением задачи об определении длины тени. Тангенс (а также котангенс) введен в X веке арабским математиком Абу-ль-Вафой, который составил и первые таблицы для нахождения тангенсов и котангенсов. Однако эти открытия долгое время оставались неизвестными европейским ученым, и тангенсы были заново открыты лишь в XIV веке немецким математиком, астрономом Регимонтаном (1467 г.). Он доказал теорему тангенсов. Региомонтан составил также подробные тригонометрические таблицы; благодаря его трудам плоская и сферическая тригонометрия стала самостоятельной дисциплиной и в Европе.
Название «тангенс», происходящее от латинского tanger (касаться), появилось в 1583 г. Tangens переводится как «касающийся» (линия тангенсов — касательная к единичной окружности).
Дальнейшее развитие тригонометрия получила в трудах выдающихся астрономов Николая Коперника (1473-1543) — творца гелиоцентрической системы мира, Тихо Браге (1546-1601) и Иогана Кеплера (1571-1630), а также в работах математика Франсуа Виета (1540-1603), который полностью решил задачу об определениях всех элементов плоского или сферического треугольника по трем данным.
Долгое время тригонометрия носила чисто геометрический характер, т. е. Факты, которые мы сейчас формулируем в терминах тригонометрических функций, формулировались и доказывались с помощью геометрических понятий и утверждений. Такою она была еще в средние века, хотя иногда в ней использовались и аналитические методы, особенно после появления логарифмов. Пожалуй, наибольшие стимулы к развитию тригонометрии возникали в связи с решением задач астрономии, что представляло большой практический интерес (например, для решения задач определения местонахождения судна, предсказания затемнения и т. д.). Астрономов интересовали соотношения между сторонами и углами сферических треугольников. И надо заметить, что математики древности удачно справлялись с поставленными задачами.
Начиная с XVII в., тригонометрические функции начали применять к решению уравнений, задач механики, оптики, электричества, радиотехники, для описания колебательных процессов, распространения волн, движения различных механизмов, для изучения переменного электрического тока и т._10-500x500.jpg) д. Поэтому тригонометрические функции всесторонне и глубоко исследовались, и приобрели важное значение для всей математики.
д. Поэтому тригонометрические функции всесторонне и глубоко исследовались, и приобрели важное значение для всей математики.
Аналитическая теория тригонометрических функций в основном была создана выдающимся математиком XVIII веке Леонардом Эйлером (1707-1783) членом Петербургской Академии наук. Громадное научное наследие Эйлера включает блестящие результаты, относящиеся к математическому анализу, геометрии, теории чисел, механике и другим приложениям математики. Именно Эйлер первым ввел известные определения тригонометрических функций, стал рассматривать функции произвольного угла, получил формулы приведения. После Эйлера тригонометрия приобрела форму исчисления: различные факты стали доказываться путем формального применения формул тригонометрии, доказательства стали намного компактнее проще.
Таким образом, тригонометрия, возникшая как наука о решении треугольников, со временем развилась и в науку о тригонометрических функциях.
Позднее часть тригонометрии, которая изучает свойства тригонометрических функций и зависимости между ними, начали называть гониометрией (в переводе — наука об измерении углов, от греческого gwnia — угол, metrew- измеряю). Термин гониометрия в последнее время практически не употребляется.
Термин гониометрия в последнее время практически не употребляется.
тригонометрия математика питискус
Размещено на Allbest.ru
…
Подобные документы
Понятие тригонометрии, ее сущность и особенности, история возникновения и развития. Структура тригонометрии, ее элементы и характеристика. Создание и развитие аналитической теории тригонометрических функций, роль в нем академика Леонарда Эйлера.
творческая работа , добавлен 15.02.2009
Знакомство с особенностями возникновения тригонометрии, рассмотрение этапов развития. Анализ способов решения треугольников, основанных на зависимостях между сторонами и углами треугольника. Характеристика аналитической теории тригонометрических функций.
презентация , добавлен 24.06.2014
Математика Древнего и Средневекового Китая. Правило двух ложных положений. Системы линейных уравнений со многими неизвестными. Начальные этапы развития тригонометрии. Создание позиционной десятичной нумерации. Арифметика натуральных чисел и дробей.
Арифметика натуральных чисел и дробей.
дипломная работа , добавлен 22.12.2012
Развитие аналитического, логического, конструктивного мышления учащихся и формирование их математической зоркости. Изучение тригонометрии в курсе геометрии основной школы, методы решения нестандартных задач из курса 8 класса и из альтернативных учебников.
курсовая работа , добавлен 01.03.2014
Европейская математика эпохи Возрождения. Создание буквенного исчисления Франсуа Виет и метода решения уравнений. Усовершенствование вычислений в конце XVI – начале XVII веков: десятичные дроби, логарифмы. Установление связи тригонометрии и алгебры.
презентация , добавлен 20.09.2015
Понятия сферической геометрии, соответствие между сферической геометрией и планиметрией. Применение сферической тригонометрии в навигации. Углы сферического многоугольника, анализ планиметрических аксиом. Теорема косинусов для сферических треугольников.
курсовая работа , добавлен 06. 12.2011
12.2011
История развития тригонометрии, характеристика ее основных понятий и формул. Общие вопросы, цели изучения и способы определения тригонометрических функций числового аргумента в школьном курсе. Рекомендации и методы решения тригонометрических уравнений.
курсовая работа , добавлен 19.10.2011
Перестройка структуры и содержания учебного курса математики в процессе проведения реформ математического образования. Определения косинуса, синуса и тангенса острого угла. Основные тригонометрические формулы. Понятие и основные свойства векторов.
дипломная работа , добавлен 11.01.2011
Особенности периода математики постоянных величин. Создание арифметики, алгебры, геометрии и тригонометрии. Общая характеристика математической культуры Древней Греции. Пифагорейская школа. Открытие несоизмеримости, таблицы Пифагора. «Начала» Евклида.
презентация , добавлен 20.09.2015
История возникновения и развития арабских цифр, особенности их написания, удобство по сравнению с другими системами.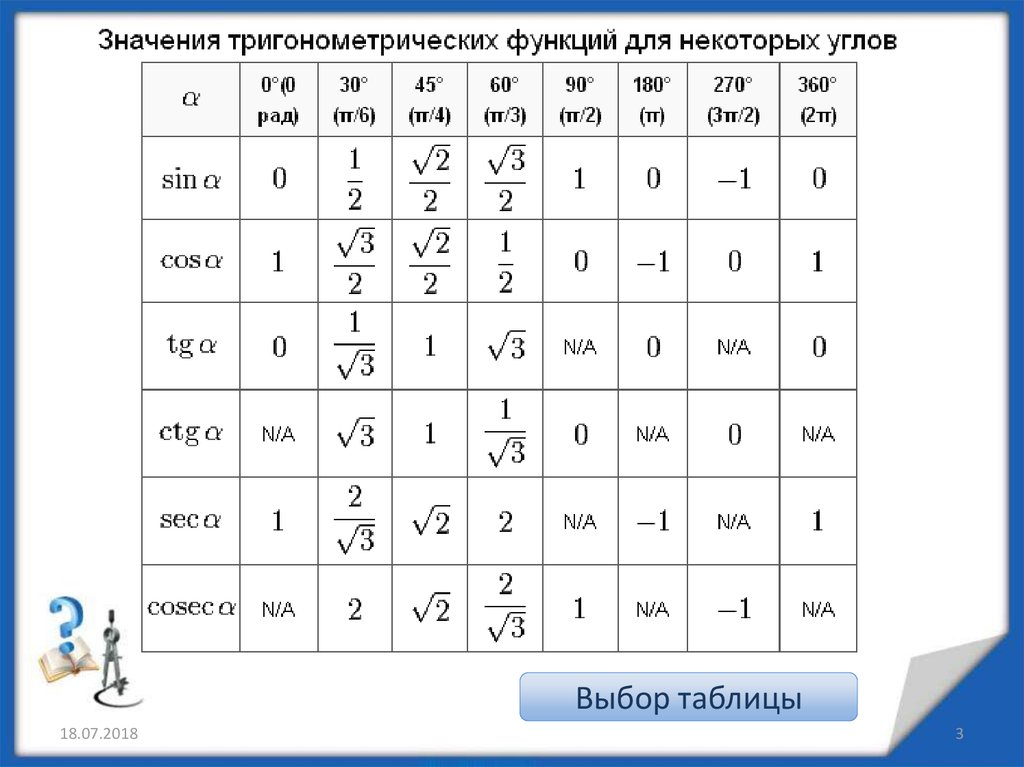 Знакомство с цифрами разных народов: системой счисления Древнего Рима, китайскими, деванагари и их развитием от древности, до наших дней.
Знакомство с цифрами разных народов: системой счисления Древнего Рима, китайскими, деванагари и их развитием от древности, до наших дней.
История развития тригонометрии
- История развития тригонометрии.
Тригонометрия, как и любая другая научная дисциплина, возникла из потребностей практической деятельности человека. Различные задачи астрономии, мореплавания, землемерия, архитектуры привели к необходимости разработки способа вычисления элементов геометрических фигур по известным значениям других их элементов, найденных путем непосредственных измерений. Само название «тригонометрия» греческого происхождения, обозначающее «измерение треугольников»: (тригонон) – треугольник, (метрейн) – измерение.
Зарождение
тригонометрии относится к  Это позволяет сделать
вывод о том, что им были известны
некоторые простейшие сведения из тригонометрии.
Постепенно в геометрии и астрономии установились
понятия синуса, косинуса и тангенса угла.
По существу, ими оперировали еще древние
математики, рассматривая отношение отрезков
в треугольниках и окружностях.
Это позволяет сделать
вывод о том, что им были известны
некоторые простейшие сведения из тригонометрии.
Постепенно в геометрии и астрономии установились
понятия синуса, косинуса и тангенса угла.
По существу, ими оперировали еще древние
математики, рассматривая отношение отрезков
в треугольниках и окружностях.
Накопившийся
материал астрономических наблюдений
потребовал математической обработки.
Одним из основоположников тригонометрии
считается древнегреческий 
Эти таблицы, говоря современным языком, являются таблицами значений удвоенного синуса половины соответствующего центрального угла. В них были даны значения хорд для всех углов (через каждые полградуса) от 00 до 1800. Однако надо иметь в виду, что в древней Греции тригонометрия не выделялась в самостоятельную науку, а считалась частью астрономии.
Важный
вклад в развитие тригонометрии
был внесен индийской математикой в период
V – XII вв. н.э. Индийские математики стали
вычислять не полную хорду, как это делали
греки, а ее половину (то есть «линию синусов»).
Линия синусов именовалась ими «архаджива»,
что буквально означало «половина тетивы
лука». Индийцы составилди таблицу синусов,
в которой были даны значения полухорд,
измеренных частями (минутами) окружности
для всех углов от 00 до 900 (через каждые
). Эти таблицы были точнее таблиц Птолемея.
Об их высокой точности говорит тот факт,
что для синуса и косинуса
были вычислены значения
и
, отличающиеся от истинных менее чем на
.
Индийским
математикам были известны соотношения,
которые в современных обозначениях пишутся
так:
.
В
XI – XIII вв. в трудах математиков Средней
Азии, Закавказья, Ближнего Востока
и Индии началось формирование тригонометрии
как отдельной науки. И в дальнейшем
потребности географии, геодезии, военного
дела способствовали развитию тригонометрии
как науки. Особенно усиленно тригонометрия
развивалась в средние века, в первую очередь
на юго-востоке: в Индии (Ариабхата, Брамагупта,
Бхаскара), в Узбекистане, Азербайджане
и Таджикистане (Насирад-Дин ат-Туси, ал-Каши,
ал-Бируни), в Арабии (Ахмад, ибн-Абдаллах,
ал-Баттани). Большая заслуга в формировании
тригонометрии как отдельной науки принадлежит
азербайджанскому ученому Насирад-Дину
Муххамаду ат-Туси (1201 – 1274), написавшему
«Трактат о полном четырехугольнике».
Работы ученых этого периода привели к
выделению тригонометрии как нового самостоятельного
раздела математики. Однако в их трудах
еще не было необходимой символики, и поэтому
развитие тригонометрии происходило медленно.
Однако в их трудах
еще не было необходимой символики, и поэтому
развитие тригонометрии происходило медленно.
С XV в. и в Европе появляются работы, посвященные вопросам тригонометрии. Немецкий ученый Иоганн Мюллер (1436 – 1476), известный в науке под именем Региомонтан, издал труд «Пять книг о треугольниках всех видов», сыгравший важную роль в развитии тригонометрии. В нем дано систематическое изложение тригонометрии как самостоятельной научной дисциплины. Региомонтан составил таблицы синусов с точностью уже до . В его таблицах радиус круга принимался за вместо числа кратного 60, то есть по сути был совершен переход от шестидесятиричной системы измерения к десятичной. В 1595 г. появился труд Варфоломея Питискуса «Тригонометрия, или Краткий обзорный трактат о решении треугольников».
В
XV – XVII в. в Европе было составлено и
издано несколько тригонометрических
таблиц. Над их составлением работали
крупнейшие ученые: Н. Коперник (1473 – 1543),
и. Кеплер (1571 – 1630), Ф. Виет (1540 – 1603) и др.
В России первые тригонометрические таблицы
были изданы в 1703 г. при участии Л.Ф. Магницкого.
Коперник (1473 – 1543),
и. Кеплер (1571 – 1630), Ф. Виет (1540 – 1603) и др.
В России первые тригонометрические таблицы
были изданы в 1703 г. при участии Л.Ф. Магницкого.
Таким образом, тригонометрия возникла на геометрической основе, имела геометрический язык и применялась к решению геометрических задач. Развитие алгебраической символики позволило записывать тригонометрические соотношения в виде формул; применение отрицательных чисел позволило рассматривать направленные углы и дуги и распространить понятие тригонометрических линий (определенных отрезков в круге) для любых углов. В этот период создалась база для изучения тригонометрических функций как функций числового аргумента, основа аналитической теории тригонометрических (круговых) функций. Аналитический аппарат, позволяющий вычислять значения тригонометрических функций с любой степенью точности, был разработан Ньютоном.
Современный
вид тригонометрия получила в
трудах великого ученого, члена Российской
академии наук Л. Эйлера (1707 – 1783). Эйлер
стал рассматривать значения тригонометрических
функций как числа – величины тригонометрических
линий в круге, радиус которого принят
за единицу («тригонометрический круг»
или «единичная окружность»). Эйлер дал
окончательное решение о знаках тригонометрических
функций в разных четвертях, вывел все
тригонометрические формулы из нескольких
основных, установил несколько неизвестных
до него формул, ввел единообразные обозначения.
Именно в его трудах впервые встречаются
записи
. Он также открыл связь между тригонометрическими
и показательной функциями от комплексного
аргумента. На основании работ Л. Эйлера
были составлены учебники тригонометрии,
излагавшие ее в строгой научной последовательности.
Эйлера (1707 – 1783). Эйлер
стал рассматривать значения тригонометрических
функций как числа – величины тригонометрических
линий в круге, радиус которого принят
за единицу («тригонометрический круг»
или «единичная окружность»). Эйлер дал
окончательное решение о знаках тригонометрических
функций в разных четвертях, вывел все
тригонометрические формулы из нескольких
основных, установил несколько неизвестных
до него формул, ввел единообразные обозначения.
Именно в его трудах впервые встречаются
записи
. Он также открыл связь между тригонометрическими
и показательной функциями от комплексного
аргумента. На основании работ Л. Эйлера
были составлены учебники тригонометрии,
излагавшие ее в строгой научной последовательности.
Аналитическое (не зависящее от геометрии) построение теории тригонометрических функций, начатое Эйлером, получило завершение в трудах великого русского ученого Н.И. Лобачевского.
Современная
точка зрения на тригонометрические
функции как на функции числового аргумента
во многом обусловлена развитием физики,
механики, техники. Эти функции легли в
основу математического аппарата, при
помощи которого изучаются различные
периодические процессы: колебательные
движения, распространение волн, движения
механизмов, колебание переменного электрического
тока.
Эти функции легли в
основу математического аппарата, при
помощи которого изучаются различные
периодические процессы: колебательные
движения, распространение волн, движения
механизмов, колебание переменного электрического
тока.
- Содержание и анализ материала по тригонометрии в различных школьных учебниках
Тригонометрия традиционно является одной из важнейших составных частей школьного курса математики. Анализ материала, посвящённого решению тригонометрических уравнений и неравенств, в учебнике «Алгебра и начала анализа» для 10-11 классов под ред. А.Н.Колмогорова и в учебнике «Алгебра и начала анализа» для 10-11 классов авторов Ш.А. Алимова и др. свидетельствует, что различные виды тригонометрических задач представлены в пособиях по математике для средней школы.
Рассмотрим
содержание материала по тригонометрии
изложенного в различных 
Мордкович А.Г. Алгебра и начала анализа. 10-11
Учебник
разбит на 8 глав. В конце изучения
каждой главы чётко обозначены основные
результаты изучения. Курс изучения математики
в 10 классе начинается с изучения главы
«Тригонометрические функции». Здесь
автор вводит понятия тригонометрической
окружности на координатной плоскости,
понятия синус и косинус, основные тригонометрические
соотношения с ними связанные, решения
простейших уравнений по тригонометрической
окружности. Как таковые формулы приведения
вводятся после изучения тригонометрических
функций углового аргумента. Далее рассматриваются
свойства и графики тригонометрических
функций. Во второй главе «Тригонометрические
уравнения» подробно рассматривается
решение каждого простейшего тригонометрического
уравнения, на основе ранее введенных
понятий арксинуса, арккосинуса, арктангенса.
В этой же главе рассмотрены такие методы
решения: разложение на множители и введение
новой переменной; метод решения однородных
тригонометрических уравнений.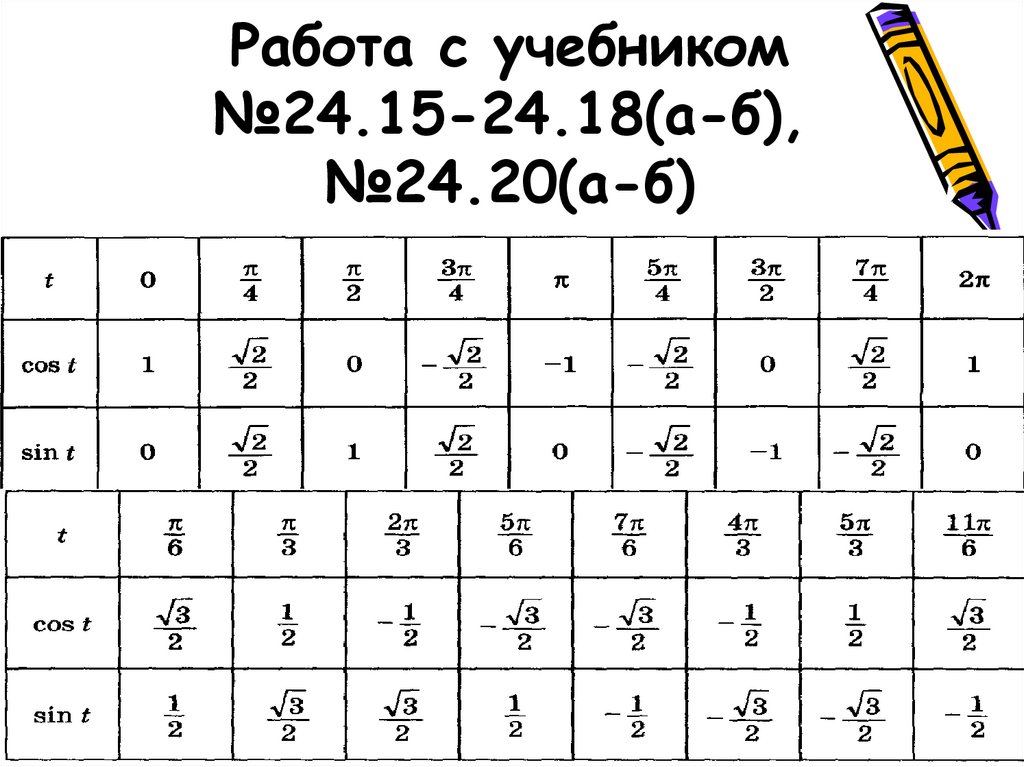 Другие
методы решения рассматриваются после
изучения третьей главы «Преобразование
тригонометрических выражений».
Другие
методы решения рассматриваются после
изучения третьей главы «Преобразование
тригонометрических выражений».
Здесь
схема изучения выглядит следующим
образом: функция → уравнения → преобразования.
С
точки зрения применения учебник
Мордковича удобен для самостоятельного
изучения учащимися, т.к. он содержит сильную
теоретическую базу. Изложение теоретического
материала ведётся очень
Колмогоров А.Н. Алгебра и начала анализа
Учебник
содержит 4 главы. Схема изучения радикально
отличается от предыдущих, т.к. сначала
рассматриваются  В этой же первой главе, но несколько
позже, рассматриваются основные свойства
тригонометрических функций, их графики
и их исследование. После этого вводятся
понятия арксинус, арккосинус, арктангенс,
арккотангенс и «параллельно» с этим решение
простейших тригонометрических уравнений
и неравенств.
В этой же первой главе, но несколько
позже, рассматриваются основные свойства
тригонометрических функций, их графики
и их исследование. После этого вводятся
понятия арксинус, арккосинус, арктангенс,
арккотангенс и «параллельно» с этим решение
простейших тригонометрических уравнений
и неравенств.
Таким образом, схема изучения выглядит так: преобразования → функции → уравнения.
Легко
заметить, что материал, относящийся
к тригонометрии, изучается не единым
блоком, учащиеся не представляют себе
весь спектр применения тригонометрического
материала, дробление на отдельные темы
приводит к тому, что тригонометрия изучается
в течение нескольких лет. Вместе с тем,
количество задач по тригонометрии в ЕГЭ,
олимпиадах различного уровня увеличивается
год от года. Именно по этой причине каждому
учителю необходимо обратить особое внимание
на подготовку учащихся к решению задач
из этого раздела математики. Для удобства
работы, предлагаю ввести классификацию
задач по тригонометрии на основании тем
в школьной программе.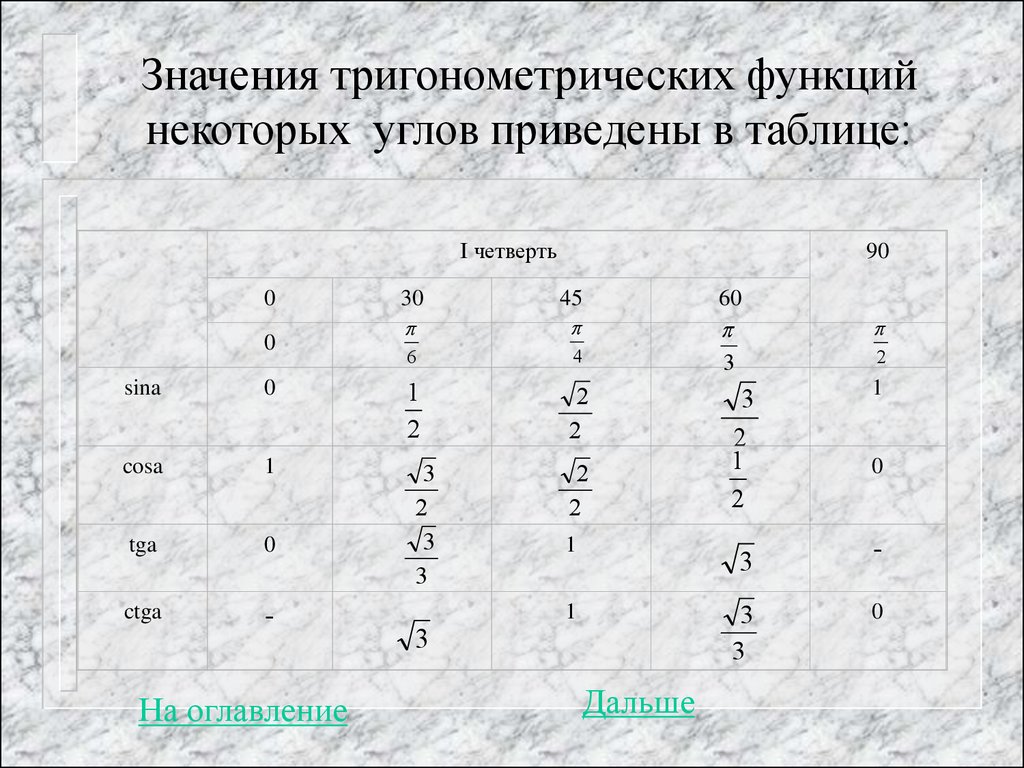
- Классификация задач по тригонометрии. Примеры решения задач.
3.1.Преобразование
тригонометрических выражений. Нахождение
значений выражений.
- Каково максимальное значение выражения
sin a cos b + sin b cos c + sin c cos d + sin d cos a для действительных a, b, c, d?
Решение:
Выражение
sin a cos b + sin b cos c + sin c cos d + sin d cos a можно
рассмотреть как скалярное
Применив теперь неравенство между средним геометрическим и средним арифметическим, получим:
Ответ:
2
2. Найти
значение выражения (
Найти
значение выражения (
Решение: Воспользуемся формулами и , где
, , тогда , , так как угол принадлежит первой четверти, а . Найдем (=, == .Сложив результаты получаем ответ +
Ответ: +
3. Найдите значение выражения , если .
Решение: Разделим и числитель, и знаменатель дроби на .Получим
Ответ: -1
4. Найдите значение выражения , если
Решение: -1= 99, =
Ответ: —
5. Какое
наименьшее значение может принять выражение
cos(2x) – 2cos(x)?
Решение: преобразуем выражение из условия задачи
где t = cos(x).
Квадратный трехчлен относительно t имеет положительный старший коэффициент
и, следовательно, принимает свое наименьшее
значение при t = – координата вершины. Вычислим . Подставим в , получим . Итак, выражение из условия задачи
при cos(x) = принимает свое наименьшее значение,
равное .
Вычислим . Подставим в , получим . Итак, выражение из условия задачи
при cos(x) = принимает свое наименьшее значение,
равное .
Ответ: -3/2
6.
Вычислите .
Решение: рассмотрим функцию f(x) = arccos(cos(x)). Заметим, что f(x) периодична с периодом , т.к. .
Вычислим несколько первых слагаемых требуемой суммы.
Сумма этих шести слагаемых равна . Далее слагаемые будут повторятся, т.к. arccos(cos(x)) периодичная функция. Всего в сумме 300 слагаемых, период состоит из 6 слагаемых, т.о. слагаемые разбиваются на 300/6 = 50 периодов. Сумма слагаемых в каждом периоде . Итого ответ .
Проектная работа по математике на тему «Тригонометрические функции»(1 курс)
Кировское областное государственное профессиональное образовательное автономное учреждение Вятский торгово-промышленный техникум
Проектная работа
по математике
Тригонометрические функции в окружающем мире, их значение для человека
Автор работы: Юркина Кристина, обучающаяся 1 курса группы П-11
Руководитель
проекта: Сысолятина Е. Ю., преподаватель математики
Ю., преподаватель математики
г.Кирс, 2020г
1 Аннотация
В данном проекте по математике «Тригонометрические функции в окружающем мире, их значение для человека» освещается история тригонометрии, связь тригонометрических функций с различными науками и сферами жизни и деятельности человека.
При изучении темы выявлена проблема: а существует ли связь между тригонометрическими функциями, изучаемыми на уроках математики и жизнью человека?
При раскрытии темы была поставлена следующая цель:
Выяснить распространение и роль тригонометрических функций, показать, что тригонометрические функции имеют широкое применение в различных сферах жизни и деятельности человека.
Работа будет интересна в качестве дополнительного материала на уроках при
изучении темы «Тригонометрические функции», а также внеклассных мероприятиях по
математике.
2 Содержание
Введение 4
1 Исследование теоретического вопроса применения тригонометрических функций
1.1 История тригонометрических функций 5
1.2 Тригонометрические функции в астрономии 6
1.3 Тригонометрические функции в физике 7
1.4 Тригонометрические функции и биоритмы человека 8
1.5 Тригонометрические функции в медицине 11
1.6 Тригонометрические функции в музыке, искусстве, архитектуре 14
2 Практическое исследование применения
тригонометрических функций. 17
17
2.1 Опрос о применении тригонометрических функций в жизни человека
2.2 Результаты опроса
Заключение 18
Список используемых источников 19
Введение
Тригонометрия – раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии. Слово тригонометрия состоит из двух греческих слов: trigwnon — треугольник и metrew — измерять и в буквальном переводе означает измерение треугольников. Тригонометрия возникла в результате человеческой практики в процессе решения конкретных практических задач.
Приступая к написанию
данной работы, обнаружено противоречие между имеющимися теоретическими знаниями
по данной теме и отсутствием понимания того, где в реальной жизни можно
встретиться с функциональной моделью, и как человек использует свойства
тригонометрических функций в своей практической деятельности. Поэтому
актуальным и полезным будет рассмотреть сферы применения тригонометрических
функций в жизни человека.
Поэтому
актуальным и полезным будет рассмотреть сферы применения тригонометрических
функций в жизни человека.
Объект исследования–тригонометрические функции; предмет исследования — области их практического применения.
Цель: Выявить связь тригонометрических функций с явлениями окружающего мира и практической деятельностью человека, показать, что данные функции находит широкое применение в жизни.
Выбрав тему исследовательской работы и определив цель, необходимо было решить следующие задачи:
1. Изучить литературу и ресурсы удаленного доступа по теме проекта.
2. Выяснить, какие законы природы выражаются тригонометрическими функцией.
3. Найти примеры применения тригонометрических функций в окружающем мире.
4. Проанализировать и систематизировать имеющийся материал.
Для решения этих задач можно использовать следующие методы:
— теоретические: изучение литературы, ресурсов удалённого доступа по вопросу нашего проекта;
— логический анализ:
метод систематизации накопленного материала.
1 Исследование теоретического вопроса применения тригонометрических функций
1.1 История тригонометрических функций
Первые тригонометрические знания можно найти ещё в рукописях древнего Египта, Вавилона и древнего Китая. Например, в Вавилоне использовалась градусная мера измерения углов. Тригонометрические соотношения в треугольнике появились в Древней Греции. Но в то время тригонометрия ещё не была отдельной наукой, она была тогда частью астрономии.
Несколько теорем тригонометрии попали в книги «Начала» Евклида (4 век до н.э.), включая теорему косинусов, о сумме углов треугольника и др.
В Древней Греции развивалась Плоская и Сферическая геометрии.
Появление тригонометрических функций было много позже- в средние века.
Рисунок 1-График синусоиды в книге Альбрехта Дюрера (1525г).
В 18 веке – после открытия математического анализа
Джеймс Грегори, а затем Исаак Ньютон получили разложение тригонометрических
функций ( а также обратных им) в бесконечные ряды.
Австрийский математик Карл Шерфер и Лагранж обозначили обратные тригонометрические функции приставкой arc: arcsin ,arccos ,arctg.
Современный вид тригонометрии придал Леонард Эйлер. В трактате «Введение в анализ бесконечных» (1748г.) Эйлер дал определение тригонометрических функций и определил обратные тригонометрические функции в современном виде. До него sin и прочие понятия понимали геометрически, то есть как линии в круге или треугольнике. Эйлер же стал рассматривать их как аналитические функции действительного и комплексного переменных.
В России первые сведения о тригонометрии были опубликованы в сборнике «Таблицы логарифмов, синусов и тангенсов к изучению мудролюбивых тщателей» в 1703 году. В 1714 году появился первый русский учебник по тригонометрии с прикладными задачами по артиллерии, навигации и геодезии.
В 1789 году вышел фундаментальный учебник академика
Головина – ученика Эйлера «Плоская и сферическая тригонометрия с
алгеброическими доказательствами». В конце 18 века в Петербурге возникла
авторитетная тригонометрическая школа, которая внесла большой вклад в плоскую и
сферическую тригонометрию.
В конце 18 века в Петербурге возникла
авторитетная тригонометрическая школа, которая внесла большой вклад в плоскую и
сферическую тригонометрию.
1.2 Тригонометрические функции в астрономии
Потребность решения треугольников раньше всего обнаружилась в астрономии, поэтому долгое время тригонометрия включалась в астрономию. Значительных высот она достигла у индийских средневековых астрономов. Их главным достижением стала замена хорд синусами, что позволило вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом в Индии было положено начало тригонометрии как учению о тригонометрических величинах.
В 3 веке до н.э. Аристарх Самосский в трактате «О величинах и расстояниях Солнца и Луны» ставил задачу определить расстояние до небесных тел. Задача решалась вычислением соотношения прямоугольного треугольника при заданном угле.
В результате астрономических наблюдений появилась необходимость
определения углового расстояния до звёзд с помощью всё того же прямоугольного
треугольника.
Рисунок 2 – Тригонометрический метод определения расстояния до звёзд.
Гиппарх впервые стал использовать в астрономии методы сферической тригонометрии. Он повысил точность наблюдений, применив для наведения на светило крест нитей в угломерных инструментах — секстантах и квадрантах. Составленные Гиппархом таблицы положений Солнца и Луны позволили предвычислять моменты наступления затмений (с ошибкой 1—2 ч).
1.3 Тригонометрические функции в физике
В окружающем мире приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Эти процессы называются колебательными. Колебательные явления различной физической природы подчиняются общим закономерностям и описываются одинаковыми уравнениями. Существуют разные виды колебательных явлений, происходящий по закону sin или cos:
1)Гармонические колебания: X(t)=A sin(ωt+φ)
или X(t)=A cos(ωt+φ),
где х-изменяющаяся величина, t-время,
(ωt+φ)-полная
фаза колебаний, А-амплитуда колебаний.
Рисунок 3 – График гармонических колебаний.
2)Механические колебания математического маятника или груза на пружине являются периодическими изменениями, происходящими по закону тригонометрических функций.
а) математический маятник:
Рисунок 4 – Колебания математического маятника.
б) груз на пружине:
Рисунок 5 – колебания груза на пружине.
3)Переменный электрический ток — это ток, который через равные промежутки времени повторяет полный цикл своих изменений, возвращаясь к своей исходной величине:
Рисунок 6 – Развёрнутая диаграмма периодического переменного тока.
1.4 Тригонометрические функции и биоритмы человека
Одно из фундаментальных
свойств живой природы — это цикличность большинства происходящих в ней
процессов. Между движением небесных тел и живыми организмами на Земле
существует связь. Живые организмы не только улавливают свет и тепло Солнца и
Луны, но и обладают различными механизмами, точно определяющими положение
Солнца, реагирующими на ритм приливов, фазы Луны и движение нашей планеты.
Биологические ритмы, биоритмы, — это более или менее регулярные изменения характера и интенсивности биологических процессов. Способность к таким изменениям жизнедеятельности передается по наследству и обнаружена практически у всех живых организмов. Их можно наблюдать в отдельных клетках, тканях и органах, целых организмах и популяциях.
Биоритмы подразделяют на физиологические, имеющие периоды от долей секунды до нескольких минут и экологические, по длительности совпадающие с каким либо ритмом окружающей среды. К ним относят суточные, сезонные, годовые, приливные и лунные ритмы. Основной земной ритм – суточный, обусловлен вращением Земли вокруг своей оси, поэтому практически все процессы в живом организме обладают суточной периодичностью.
Множество экологических
факторов на нашей планете, в первую очередь световой режим, температура,
давление и влажность воздуха, атмосферное и электромагнитное поле, морские
приливы и отливы, под влиянием этого вращения закономерно изменяются.
Мы на семьдесят пять процентов состоим из воды, и если в момент полнолуния воды мирового океана поднимаются на 19 метров над уровнем моря и начинается прилив, то вода, находящаяся в нашем организме так же устремляется в верхние отделы нашего тела. И у людей с повышенным давлением часто наблюдаются обострения болезни в эти периоды, а натуралисты, собирающие лекарственные травы, точно знают в какую фазу луны собирать «вершки – (плоды)», а в какую – «корешки».
Вы замечали, что в определенные периоды
ваша жизнь делает необъяснимые скачки? Вдруг откуда не возьмись — бьют через
край эмоции. Повышается чувствительность, которая внезапно может смениться
полной апатией. Творческие и бесплодные дни, счастливые и несчастные моменты,
резкие скачки настроения. Подмечено, что возможности человеческого организма
меняются периодически. Эти знания лежат в основе «теории трех биоритмов».
Физический биоритм – регулирует
физическую активность. В течение первой половины физического цикла человек
энергичен, и достигает лучших результатов в своей деятельности (вторая половина
– энергичность уступает лености).
Эмоциональный ритм – в периоды его активности повышается чувствительность, улучшается настроение. Человек становится возбудимым к различным внешним катаклизмам. Если у него хорошее настроение, он строит воздушные замки, мечтает влюбиться и влюбляется. При снижении эмоционального биоритма происходит упадок душевных сил, пропадает желание, радостное настроение.
Интеллектуальный биоритм — он распоряжается памятью, способностью к обучению, логическому мышлению. В фазе активности наблюдается подъем, а во второй фазе спад творческой активности, отсутствуют удача и успех.
Теория трех ритмов:
Предположению о существовании трёх биоритмах около 100 лет. Её авторами стали 3 человека: психолог Герман Свобода, отоларинголог Вильгельм Флисс, открывшие эмоциональный и физический биоритмы, и преподаватель Фридрих Тельчер, исследовавший интеллектуальный ритм. Одинаковые результаты они получили независимо друг от друга.
Доктора Вильгельма
Флисса, который жил в Берлине, заинтересовала сопротивляемость организма
человека болезням. Почему дети с одинаковыми диагнозамив одно время имеют
иммунитет, а в другое –умирают? Собрав данные о начале болезни, температуре и
смерти, он связал их с датами рождения. Расчёты показали, что изменения
иммунитета можно прогнозировать с помощью 23-дневного физического и 28-дневного
эмоционального биоритмов. Герман Свобода работал в Вене. Анализируя поведение
своих пациентов, он заметил, что их мысли, идеи, импульсы к действию
повторяются с определённой периодичностью. Он начал анализировать начало и
развитие болезней, особенно цикличность сердечных и астматических приступов.
Результатом этих исследований стало открытие ритмичности физических и
психических процессов.
Почему дети с одинаковыми диагнозамив одно время имеют
иммунитет, а в другое –умирают? Собрав данные о начале болезни, температуре и
смерти, он связал их с датами рождения. Расчёты показали, что изменения
иммунитета можно прогнозировать с помощью 23-дневного физического и 28-дневного
эмоционального биоритмов. Герман Свобода работал в Вене. Анализируя поведение
своих пациентов, он заметил, что их мысли, идеи, импульсы к действию
повторяются с определённой периодичностью. Он начал анализировать начало и
развитие болезней, особенно цикличность сердечных и астматических приступов.
Результатом этих исследований стало открытие ритмичности физических и
психических процессов.
Фридрих Тельчер заметил, что желание и способность студентов воспринимать, систематизировать и использовать информацию, генерировать идеи время от времени изменятся, то есть имеет ритмический характер. Сопоставив даты рождения студентов, экзаменов, их результаты, он открыл интеллектуальный ритм с периодам 33 суток.
Пусковым механизмом
этих ритмов является только момент рождения человека, при котором возникают
ритмы с периодом 23, 28, 33 суток, определяющие уровень его эмоциональной, и интеллектуальной
активности.
Считается, что физический биоритм формируется за счёт магнитного поля самой Земли при вращении расплавленного жидкого металлического ядра Земли вокруг своей оси, длительностью примерно 23 дня. Физический цикл характеризует жизненные силы человека, то есть его физическое состояние, энергию, силу, выносливость, координацию движения.
Второй, эмоциональный биоритм равен 28 дням и обуславливает состояние нервной системы и настроение человека. Он зависит от влияния двух Лунных циклов, от так называемого сидерического, длительностью 27,3 земных суток, возникающего за счёт периода вращения Луны вокруг Земли и второго, синодического месяца, длительностью примерно 29,5 суток –это время необходимо для возврата Луны на своё первоначальное место относительно Солнца. Именно этот ритм по своей выраженности преобладает у известных артистов, художников, писателей и поэтов.
Третий биоритм —
интеллектуальный. Он зависит от вращения Солнца по своей орбите относительно
Земли и его взаимодействия с зодиакальными созвездиями и Луной. Он самый
длительный — составляет 33 дня и характеризует работу полушарий головного
мозга, мыслительные способности человека, его интуицию и интеллект. Именно этот
биоритм доминирует у известных учёных, шахматистов, математиков и бухгалтеров.
Он самый
длительный — составляет 33 дня и характеризует работу полушарий головного
мозга, мыслительные способности человека, его интуицию и интеллект. Именно этот
биоритм доминирует у известных учёных, шахматистов, математиков и бухгалтеров.
Рисунок 7 – Цикличность биоритмов человека.
Физический цикл -23 дня. Определяет энергию, силу, выносливость,
координацию движения
Эмоциональный цикл — 28 дней. Состояние нервной системы и настроение
Интеллектуальный цикл — 33 дня. Определяет творческую способность личности.
1.5 Тригонометрические функции в медицине
С помощью тригонометрии иранские учёные открыли формулу сердца — комплексное алгебраически — тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчётов в случае аритмии.
Биение сердца относится к колебательному процессу. В
течение минуты оно выбрасывает в аорту около 4 литров крови. Сердце человека в
среднем сокращается 100тыс раз в сутки. За 70 лет жизни оно сокращается 2млр
600млн раз и прокачивает при этом 250млн литров крови.
Сердце человека в
среднем сокращается 100тыс раз в сутки. За 70 лет жизни оно сокращается 2млр
600млн раз и прокачивает при этом 250млн литров крови.
Использование кардиограммы в медицине – это возможность получить наиболее точный диагноз в случае заболеваний сердца.
Кардиограмма — кривая, получаемая на бумаге или фотопленке при регистрации деятельности сердца специальными приборами (электрокардиографом, баллистокардиографом и др.).
Электрокардиограмма – это кривая, которая отражает биоэлектрическую работоспособность сердца. В момент возбуждения сердца с его внешней, а также внутренней стороны происходит разность потенциалов, которая постепенно меняет свою величину и направление. Эти изменения становятся результатом внедрения в возбуждение иных частей сердца.
Рисунок 8 – Электрокардиограмма человека.
Выполнения кардиограммы заключается в том, что от
нашего сердца через весь организм проходят электрические линии напряжения,
которые соединяют доли сердца, имеющие разную полярность. Эти линии проходят по
всему организму и их можно «сканировать» с поверхности тела. Изучив состояние
этих линий, можно сделать выводы о состоянии сердца. Поэтому конечный результат
– то есть кардиограмма и, конечно же, то, как ее расшифруют, зависит и от того,
на какие именно участки тела прикладываются электроды. Процедура, применяемая
при снятии электрокардиограммы, называется отведением потенциалов от
конечностей.
Эти линии проходят по
всему организму и их можно «сканировать» с поверхности тела. Изучив состояние
этих линий, можно сделать выводы о состоянии сердца. Поэтому конечный результат
– то есть кардиограмма и, конечно же, то, как ее расшифруют, зависит и от того,
на какие именно участки тела прикладываются электроды. Процедура, применяемая
при снятии электрокардиограммы, называется отведением потенциалов от
конечностей.
Пульс (лат. pulsus удар, толчок)- периодические, связанные с сокращениями сердца колебания объема сосудов, обусловленные динамикой их кровенаполнения и давления в них в течение одного сердечного цикла.
рисунок 9 – Измерение пульса человека, кривая.
Сравнивая график кардиограммы сердца и пульса с синусоидой и пришли к выводу, что кардиограмма сердца и пульс являются искривленной синусоидой:
Рисунок 10 – График синусоиды Рисунок 11- Кардиаграмма сердца.
Ультразву́к — звуковые волны, имеющие частоту выше воспринимаемых человеческим ухом, обычно, под ультразвуком понимают частоты
выше 20 000 герц.
Рисунок 12 – Вид и график ультразвука.
Помимо широкого использования в диагностических целях, ультразвук применяется в медицине (в том числе регенеративной) в качестве инструмента лечения.
Ультразвук обладает следующими эффектами:
· противовоспалительным, рассасывающим действиями;
· анальгезирующим, спазмолитическим действием;
· кавитационным усилением проницаемости кожи.
Фонофорез — комбинированный метод лечения, при котором на ткани вместо обычного геля для ультразвуковой эмиссии (применяемого, например, при УЗИ) наносится лечебное вещество (как медикаменты, так и вещества природного происхождения). Предполагается, что ультразвук помогает лечебному веществу глубже проникать в ткани.
1.6 Тригонометрические функции в музыке, искусстве, архитектуре
Звуковые волны — это волны, воспринимаемые человеческим ухом в диапазоне от 16 Гц до 20 кГц.
Согласно дошедшим из
древности преданиям, первыми, кто пытался использовать тригонометрию в музыке,
были Пифагор и его ученики: частоты, соответствующие одной и той же ноте в 1, 2
и т. д. октавах относятся как 1:2:4:8…..
д. октавах относятся как 1:2:4:8…..
С помощью тригонометрии можно вычислить расстояние между ладами на гитаре.
В музыке существует метод, который тесно связан с тригонометрией.
Этот метод анализа музыкальных произведений получил название «геометрическая теория музыки». С его помощью основные музыкальные структуры и преобразования переводятся на язык современной геометрии.
Каждая нота в рамках новой теории представляется как логарифм частоты соответствующего звука (нота «до» первой октавы, к примеру, соответствует числу 60, октава – числу 12). Аккорд, таким образом, представляется как точка с заданными координатами в геометрическом пространстве. Аккорды сгруппированы в различные «семейства», которые соответствуют различным типам геометрических пространств.
Тетраэдр из различных типов аккордов четырёх звуков:
Синий цвет- это малые интервалы,
Более тёплые тона – более «разряжённые» звуки аккорда,
Красная сфера – наиболее гармоничный аккорд с равными
интервалами между нотами.
Рисунок 13 – тетраэдр из различных типов аккордов.
В архитектуре с древности при создании статуй и зданий применялась тригонометрия.
рисунок 14 – Применение метода треугольников для определения высоты здания.
Современные здания, мосты и другие сооружения также строятся с использованием знаний о тригонометрии и тригонометрических функциях:
рисунок 15 – Мост с арками в виде синусоиды.
Культовые здания во всем мире были спроектированы благодаря математике, которая может считаться гением архитектуры. При проектировании этих зданий не обошлось без тригонометрии.
Рисунок 16 – жилой комплекс, Вайле, Дания.
Рисунок 17 – г.Баку центр Гейдара Алиева
Винодельня «Бодегас Исиос»
2 Практическое
исследование тригонометрических функций.
2.1 Опрос «О применении тригонометрических функций в жизни человека»
При изучении данной темы был проведён опрос среди обучающихся. Респондентам был задан вопрос: «В каких отраслях жизни и деятельности человека встречаются или используются тригонометрические функции?»
2.2 Результаты опроса
В опросе приняли участие 22 человека. Ответы распределились следующим образом:
12 человек- в физике — колебания,
5 — в медицине — звук,
3 – в быту — вазы, посуда, абажуры,
2 человека затруднились ответить.
Заключение
В настоящее время
тригонометрические вычисления применяются практически во всех областях
геометрии, физики и инженерного дела. Большое значение имеет техника триангуляции,
позволяющая измерять расстояния до недалёких звёзд в астрономии, между
ориентирами в географии, контролировать системы навигации спутников.
Также следует отметить применение тригонометрии в таких областях, как теория музыки, акустика, оптика, анализ финансовых рынков, электроника, теория вероятностей, статистика, медицина, фармацевтика, химия, теория чисел, сейсмология, метеорология, океанология, картография, многие разделы физики, топография и геодезия, архитектура, экономика, электронная техника, машиностроение, компьютерная графика, кристаллография и многие другие отрасли науки и техники.
В главе 1 были проанализированы сферы применения тригонометрических функций. Выяснилось, что тригонометрия появилась в жизни человека с необходимостью производить измерения углов и решения треугольников, но со временем развилась и в науку о тригонометрических функциях. Установлено, что тригонометрия тесно связана с физикой, астрономией, встречается в природе, музыке и искусстве, применяется в медицине, архитектуре и других отраслях.
Во 2 главе выписаны
результаты опроса «В каких отраслях жизни и деятельности
человека встречаются или используются тригонометрические функции?
По результатам опроса можно сделать вывод, что обучающиеся знают о
тригонометрических функциях, об их применении в деятельности человека. Проектная работа поможет расширить кругозор обучающихся о тригонометрических
функциях, истории их появления, использования в современной науке и
технологиях.
Проектная работа поможет расширить кругозор обучающихся о тригонометрических
функциях, истории их появления, использования в современной науке и
технологиях.
Таким образом, цель заявленного проекта: выяснить роль тригонометрических функций в жизни человека, их связь с окружающим миром и показать, что тригонометрические функции имеют широкое применение в различных сферах жизни и деятельности человека, достигнута, задачи по исследованию сфер применения выполнены.
Список используемых источников
1. Алимов Ш.А. и др. «Алгебра и начала математического анализа» Учебник для 10-11 классов общеобразовательных учреждений, М., Просвещение, 2018г.
2. Виленкин Н.Я. Функции в природе и
техники: Кн. для внеклассного чтения IX-X кл. – 2-е изд.,: Просвещение, 1985.
для внеклассного чтения IX-X кл. – 2-е изд.,: Просвещение, 1985.
3. https://lyna.info/biotheory/
4. http://artsintrygonometry.blogspot.com/2015/01/blog-post.html
5.https://ru.wikipedia.org/wiki/%D0%A3%D0%BB%D1%8C%D1%82%D1%80%D0%B0%D0%B7%D0%B2%D1%83%D0%BA
«Тригонометрия в окружающем мире и жизни человека»
Российская Федерация
УПРАВЛЕНИЕ ОБРАЗОВАНИЯ АДМИНИСТРАЦИИ МУНИЦИПАЛЬНОГО ОБРАЗОВАНИЯ ГУСЬ-ХРУСТАЛЬНЫЙ РАЙОН (МУНИЦИПАЛЬНЫЙ РАЙОН) ВЛАДИМИРСКОЙ ОБЛАСТИ
МУНИЦИПАЛЬНОЕ КАЗЕННОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ДЕМИДОВСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА
(МКОУ ДЕМИДОВСКАЯ СОШ)
Проект по математике
«Тригонометрия в окружающем мире и жизни человека»
Автор проекта: Терехова Кристина,
ученица 10 класса
Руководитель проекта: Серегина Людмила Александровна,
учитель математики высшей квалификационной категории
2015 г.
АННОТАЦИЯ:
В представленном исследовательском проекте по математике «Тригонометрия в окружающем мире и жизни человека» автор изучает историю тригонометрии, а также адаптацию точной математической науки в абсолютно разных сферах человеческой жизнедеятельности.
В процессе работы над исследовательским проектом по математике «Тригонометрия в окружающем мире и жизни человека» ученицей 10 класса были поставлены цели выявить связь тригонометрических функций с явлениями окружающего мира и практической деятельностью человека, а также показать, что данные функции находят широкое применение в жизни.
В основе исследовательской работы по математике «Тригонометрия в окружающем мире и жизни человека» лежит анализ теоретических сведений о тригонометрии и выявление этого направления в практической и творческой жизни человека.
В предложенном проекте по математике «Тригонометрия в окружающем мире и жизни человека» автор приходит к выводу, что тригонометрия тесно связана с физикой, биологией, встречается в природе, архитектуре и медицине.
Содержание
Введение
1. История тригонометрии
2. Тригонометрия в физике
3. Тригонометрия в астрономии
4. Тригонометрия в медицине
5. Тригонометрия в музыке
6. Применение тригонометрии в искусстве и архитектуре
Заключение
Вывод
Литература
Введение
Реальные процессы окружающего мира обычно связаны с большим количеством переменных и зависимостей между ними.
Описать эти зависимости можно с помощью функций. Понятие «функция» сыграло и поныне играет большую роль в познании реального мира. Знание свойств функций позволяет понять суть происходящих процессов, предсказать ход их развития, управлять ими. Изучение функций является актуальным всегда.
Мир функций богат и разнообразен. В различных науках и областях человеческой деятельности возникают функциональные зависимости, которые могут касаться самых разнообразных явлений природы и окружающей среды.
В нашем информационно-исследовательском проекте «Тригонометрия в окружающем мире и жизни человека» рассматривается практическое применение тригонометрических функций.
Тригонометрия – раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии. Слово тригонометрия состоит из двух греческих слов: trigwnon — треугольник и metrew — измерять и в буквальном переводе означает измерение треугольников. Как и всякая другая наука, тригонометрия возникла в результате человеческой практики в процессе решения конкретных практических задач.
Приступая к написанию данной работы, я столкнулась с противоречием между имеющимися теоретическими знаниями по данной теме и отсутствием понимания того, где в реальной жизни можно встретиться с функциональной моделью, и как человек использует свойства тригонометрических функций в своей практической деятельности.
Объект исследования – тригонометрические функции; предмет исследования — области их практического применения.
Цели:
1. Выявить связь тригонометрических функций с явлениями окружающего мира и практической деятельностью человека.
2. Показать, что данные функции находят широкое применение в жизни.
Выбрав тему исследовательской работы и определив цель, необходимо было решить следующие задачи:
1. Изучить литературу и ресурсы удаленного доступа по теме проекта.
2. Выяснить, какие законы природы выражаются тригонометрическими функцией.
3. Найти примеры применения тригонометрических функций в окружающем мире.
4. Проанализировать и систематизировать имеющийся материал.
Для решения этих задач настоящей проектной деятельности использованы следующие методы:
- теоретические: изучение литературы, ресурсов удалённого доступа по вопросу нашего проекта;
- логический анализ: метод систематизации накопленного материала.
1. История тригонометрии
Сам термин, давший название этому разделу математики, впервые был обнаружен в заголовке книги под авторством немецкого ученого-математика Питискуса в 1505 году. Слово «тригонометрия» имеет греческое происхождение и означает «измеряю треугольник».
Древние люди вычисляли высоту дерева, сравнивая длину его тени с длиной тени от шеста, высота которого была известна. По звездам вычисляли местонахождение корабля в море.
2. Тригонометрия в физике
В технике и окружающем нас мире часто приходится сталкиваться с периодическими (или почти периодическими) процессами, которые повторяются через одинаковые промежутки времени. Такие процессы называют колебательными. Колебательные явления различной физической природы подчиняются общим закономерностям.
Например, колебания тока в электрической цепи и колебания математического маятника могут описываться одинаковыми уравнениями. Общность колебательных закономерностей позволяет рассматривать колебательные процессы различной природы с единой точки зрения. Наряду с поступательными и вращательными движениями тел в механике значительный интерес представляют и колебательные движения.
Механическими колебаниями называют движения тел, повторяющиеся точно (или приблизительно) через одинаковые промежутки времени. Закон движения тела, совершающего колебания, задается с помощью некоторой периодической функции времени x = f(t). Графическое изображение этой функции дает наглядное представление о протекании колебательного процесса во времени. Примером волны такого рода могут служить волны, бегущие по натянутому резиновому жгуту или по струне.
Примерами простых колебательных систем могут служить груз на пружине или математический маятник (рис.1).
Рис.1. Механические колебательные системы.
Механические колебания, как и колебательные процессы любой другой физической природы, могут быть свободными и вынужденными. Свободные колебания совершаются под действием внутренних сил системы, после того, как система была выведена из состояния равновесия. Колебания груза на пружине или колебания маятника являются свободными колебаниями. Колебания, происходящие под действием внешних периодически изменяющихся сил, называются вынужденными.
3.Тригонометрия в астрономии
Составленные Гиппархом таблицы положений Солнца и Луны позволили пред вычислять моменты наступления затмений (с ошибкой 1—2 ч). Гиппарх впервые стал использовать в астрономии методы сферической тригонометрии. Он повысил точность наблюдений, применив для наведения на светило крест нитей в угломерных инструментах — секстантах и квадрантах.
4. Тригонометрия в медицине
Одно из фундаментальных свойств живой природы — это цикличность большинства происходящих в ней процессов. Между движением небесных тел и живыми организмами на Земле существует связь. Живые организмы не только улавливают свет и тепло Солнца и Луны, но и обладают различными механизмами, точно определяющими положение Солнца, реагирующими на ритм приливов, фазы Луны и движение нашей планеты.
Живые организмы не только улавливают свет и тепло Солнца и Луны, но и обладают различными механизмами, точно определяющими положение Солнца, реагирующими на ритм приливов, фазы Луны и движение нашей планеты.
Биологические ритмы, биоритмы, — это более или менее регулярные изменения характера и интенсивности биологических процессов. Способность к таким изменениям жизнедеятельности передается по наследству и обнаружена практически у всех живых организмов. Их можно наблюдать в отдельных клетках, тканях и органах, целых организмах и популяциях.
Биоритмы подразделяют на физиологические, имеющие периоды от долей секунды до нескольких минут и экологические,по длительности совпадающие с каким либо ритмом окружающей среды. К ним относят суточные, сезонные, годовые, приливные и лунные ритмы. Основной земной ритм – суточный, обусловлен вращением Земли вокруг своей оси, поэтому практически все процессы в живом организме обладают суточной периодичностью.
Множество экологических факторов на нашей планете, в первую очередь световой режим, температура, давление и влажность воздуха, атмосферное и электромагнитное поле, морские приливы и отливы, под влиянием этого вращения закономерно изменяются.
Мы на 75% состоим из воды, и если в момент полнолуния воды мирового океана поднимаются на 19 метров над уровнем моря и начинается прилив, то вода, находящаяся в нашем организме так же устремляется в верхние отделы нашего тела. И у людей с повышенным давлением часто наблюдаются обострения болезни в эти периоды, а натуралисты, собирающие лекарственные травы, точно знают в какую фазу луны собирать «вершки – (плоды)», а в какую – «корешки».
Вы замечали, что в определенные периоды ваша жизнь делает необъяснимые скачки? Вдруг откуда не возьмись — бьют через край эмоции. Повышается чувствительность, которая внезапно может смениться полной апатией. Творческие и бесплодные дни, счастливые и несчастные моменты, резкие скачки настроения. Подмечено, что возможности человеческого организма меняются периодически. Эти знания лежат в основе «теории трех биоритмов».
Физический биоритм – регулирует физическую активность. В течение первой половины физического цикла человек энергичен, и достигает лучших результатов в своей деятельности (вторая половина – энергичность уступает лености).
Эмоциональный ритм – в периоды его активности повышается чувствительность, улучшается настроение. Человек становится возбудимым к различным внешним катаклизмам. Если у него хорошее настроение, он строит воздушные замки, мечтает влюбиться и влюбляется. При снижении эмоционального биоритма происходит упадок душевных сил, пропадает желание, радостное настроение.
Интеллектуальный биоритм — он распоряжается памятью, способностью к обучению, логическому мышлению. В фазе активности наблюдается подъем, а во второй фазе спад творческой активности, отсутствуют удача и успех.
Теория трех ритмов
Физический цикл -23 дня. Определяет энергию, силу, выносливость, координацию движения
Эмоциональный цикл — 28 дней. Состояние нервной системы и настроение
Интеллектуальный цикл — 33 дня. Определяет творческую способность личности.
Тригонометрия встречается и в природе. Движение рыб в воде происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения. При плавании тело рыбы принимает форму кривой, которая напоминает график функции y=tgx.
При плавании тело рыбы принимает форму кривой, которая напоминает график функции y=tgx.
При полёте птицы траектория взмаха крыльев образует синусоиду.
Американские ученые утверждают, что мозг оценивает расстояние до объектов, измеряя угол между плоскостью земли и плоскостью зрения. В результате исследования, проведенного студентом иранского университета Шираз Вахидом-Резой Аббаси,медики впервые получили возможность упорядочить информацию, относящуюся к электрической активности сердца или, другими словами, электрокардиографии.
Формула представляет собой комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии. Как утверждают медики, эта формула в значительной степени облегчает процесс описания основных параметров деятельности сердца, ускоряя, тем самым, постановку диагноза и начало собственно лечения.
Тригонометрия в музыке
Каждая нота в рамках новой теории представляется как логарифм частоты соответствующего звука (нота «до» первой октавы, к примеру, соответствует числу 60, октава–числу12).
Аккорд, таким образом, представляется как точка с заданными координатами в геометрическом пространстве. Аккорды сгруппированы в различные «семейства», которые соответствуют различным типам геометрических пространств.
6. Применение тригонометрии в искусстве и архитектуре
С того времени как человек стал существовать на земле, основой улучшения быта и других сфер жизни стала наука. Основы всего, что создано человеком – это различные направления в естественных и математических науках. Одна из них – геометрия.
Архитектура не единственная сфера науки, в которой используются тригонометрические формулы. Большинство композиционных решений и построений рисунков проходило именно с помощью геометрии. Но теоретические данные мало что значат. Рассмотрим пример на построение одной скульптуры французского мастера Золотого века искусства.
Пропорциональное соотношение в построении статуи было идеально. Однако при поднятии статуи на высокий пьедестал, она смотрелась уродливой. Скульптором не было учтено, что в перспективе к горизонту уменьшаются многие детали и при взгляде снизу вверх уже не создается впечатления ее идеальности.
Скульптором не было учтено, что в перспективе к горизонту уменьшаются многие детали и при взгляде снизу вверх уже не создается впечатления ее идеальности.
Велось множество расчетов, чтобы фигура с большой высоты смотрелась пропорционально. В основном они были основаны на методе визирования, то есть приблизительного измерения, на глаз. Однако коэффициент разности тех или иных пропорций позволили сделать фигуру более приближенной к идеалу.
Таким образом, зная примерное расстояние от статуи до точки зрения, а именно от верха статуи до глаз человека и высоту статуи, можно рассчитать синус угла падения взгляда с помощью таблицы. Культовые здания во всем мире были спроектированы благодаря математике, которая может считаться гением архитектуры. Некоторые известные примеры таких зданий:Детская школа Гауди в Барселоне, Ресторан в Лос-Манантиалесе в Аргентине, мост в Сингапуре. При проектировании этих зданий не обошлось без тригонометрии.
Заключение
В настоящее время тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела. Большое значение имеет техника триангуляции, позволяющая измерять расстояния до недалёких звёзд в астрономии, между ориентирами в географии, контролировать системы навигации спутников.
Большое значение имеет техника триангуляции, позволяющая измерять расстояния до недалёких звёзд в астрономии, между ориентирами в географии, контролировать системы навигации спутников.
Также следует отметить применение тригонометрии в таких областях, как теория музыки, акустика, оптика, анализ финансовых рынков, электроника, теория вероятностей, статистика, медицина (включая ультразвуковое исследование (УЗИ) и компьютерную томографию), фармацевтика, химия, теория чисел, сейсмология, метеорология, океанология, картография, многие разделы физики, топография и геодезия, архитектура, экономика, электронная техника, машиностроение, компьютерная графика, кристаллография.
Вывод:
1). Я выяснила, что тригонометрия была вызвана к жизни необходимостью производить измерения углов, но со временем развилась и в науку о тригонометрических функциях.
2). Я доказала, что тригонометрия тесно связана с физикой, биологией, встречается в природе, архитектуре и медицине.
3). Я думаю, что тригонометрия нашла отражение в нашей жизни, и сферы, в которых она играет важную роль, будут расширяться.
Литература
1. Алимов Ш.А. и др. «Алгебра и начала анализа» Учебник для 10-11 классов общеобразовательных учреждений, М., Просвещение, 2010.
2. Виленкин Н.Я. Функции в природе и техники: Кн. для внеклассного чтения IX-X кл. – 2-е изд., испр.-М: Просвещение, 1985.
3. Глейзер Г.И. История математики в школе: IX-X кл. — М.: Просвещение, 1983.
4. Маслова Т.Н. «Справочник школьника по математике»
5. Рыбников К.А. История математики: Учебник. — М.: Изд-во МГУ, 1994.
6. Учеба.ru
7. Math.ru «библиотека»
2. Основы тригонометрии. Основы тригонометрических вычислений
Основы тригонометрических вычислений
реферат
Вот одни из самых основных понятий и правил тригонометрии:
Основы тригонометрии: тригонометрический круг, синус (sin), косинус (cos), тангенс (tg), котангенс (ctg) угла. Основное тригонометрическое тождество.
Синусом острого угла в прямоугольном треугольнике называется отношение катета этого треугольника, лежащего против угла, к гипотенузе треугольника.
Тригонометрические функции угла и внутри единичной окружности
Косинусом острого угла б в прямоугольном треугольнике называется отношение катета, прилежащего к углуб, к гипотенузе треугольника.
Радианной мерой угла называется отношение длины дуги окружности, заключенной между сторонами угла ис центром в вершине угла, к радиусу этой окружности.
Тангенсом острого угла в прямоугольном треугольнике называется отношение катета этого треугольника,лежащего против угла, к катету треугольника, прилежащему к углу.
Первоначально тригонометрические функции были связаны с соотношениями сторон в прямоугольном треугольнике. Их единственным аргументом является угол (один из острых углов этого треугольника).
· Синус — отношение противолежащего катета к гипотенузе.
· Косинус — отношение прилежащего катета к гипотенузе.
· Тангенс — отношение противолежащего катета к прилежащему.
· Котангенс — отношение прилежащего катета к противолежащему.
· Секанс — отношение гипотенузы к прилежащему катету.
· Косеканс — отношение гипотенузы к противолежащему катету.
Данные определения позволяют вычислить значения функций для острых углов, то есть от 0° до 90° (от 0 до радиан). В XVIII веке Леонард Эйлер дал современные, более общие определения, расширив область определения этих функций на всю числовую ось. Рассмотрим в прямоугольной системе координатокружность единичного радиуса (см. рисунок) и отложим от горизонтальной оси угол (если величина угла положительна, то откладываем против часовой стрелки, иначе по часовой стрелке). Точку пересечения построенной стороны угла с окружностью обозначим A. Тогда:
· Синус угла определяется как ордината точки A.
· Косинус — абсцисса точки A.
· Тангенс — отношение синуса к косинусу.
· Котангенс — отношение косинуса к синусу (то есть величина, обратная тангенсу).
· Секанс — величина, обратная косинусу.
· Косеканс — величина, обратная синусу.
Для острых углов новые определения совпадают с прежними.
Возможно также чисто аналитическое определение этих функций, которое не связано с геометрией и представляет каждую функцию её разложением в бесконечный ряд.
Делись добром 😉
Анализ различных подходов к определению тригонометрических функций
Глава 1. Из истории тригонометрии
…
Анализ различных подходов к определению тригонометрических функций
1.1 3арождение тригонометрии
Термин «тригонометрия» был впервые введен в 1595 году немецким богословом — математиком Бартоломеем Питиском (1561 — 1613), известным в то время автором учебника тригонометрии и тригонометрических таблиц…
Анализ различных подходов к определению тригонометрических функций
1.3 Развитие тригонометрии в Средневековье
…
Логарифмическая функция в задачах
§7. Логарифмические уравнения с применением тригонометрии
Пример 35. Решите уравнение
.
Решение
Найдем область допустимых значений:
Рис. 6
Решением системы неравенств является объединение промежутков:
и , или . По свойству логарифмической функции, получим:
.
Поскольку…
По свойству логарифмической функции, получим:
.
Поскольку…
Математика в средние века
1.8 Начальные этапы развития тригонометрии
Древнекитайский прием измерения высоты недоступного предмета.Из математического трактата о морском острове Лю Хуэя (??? в.). Задача. Наблюдают морской остров. Для этого установили пару шестов одинаковой высоты в…
Методика формирования умений решать тригонометрические уравнения и неравенства в курсе алгебры и начал анализа
1.1 Этапы развития тригонометрии как науки
Тригонометрия является одним из наиболее молодых отделов элементарной математики, получивших окончательное оформление лишь в XVIII в., хотя отдельные идеи её относятся к глубокой древности…
Основы тригонометрических вычислений
1. Стадии развития тригонометрии
тригонометрия синус косинус тангенс 1. Тригонометрия была вызвана к жизни в раннюю пору разумной деятельности людей, необходимостью производить измерения углов. 2…
Различные подходы к определению тригонометрических функций
Глава 1.
 Из истории тригонометрии
Из истории тригонометрии…
Различные подходы к определению тригонометрических функций
1.1 3арождение тригонометрии
Термин «тригонометрия» был впервые введен в 1595 году немецким богословом — математиком Бартоломеем Питиском (1561 — 1613), известным в то время автором учебника тригонометрии и тригонометрических таблиц…
Различные подходы к определению тригонометрических функций
1.3 Развитие тригонометрии в Средневековье
1.3.1 Тригонометрия на Ближнем и Среднем Востоке. Плоская тригонометрия Важнейший период истории тригонометрии связан с деятельностью учёных Ближнего и Среднего Востока. Начало его можно датировать VIII в….
Тригонометрические уравнения
ГЛАВА I. Роль тригонометрии в школьном курсе математики
…
Тригонометрические уравнения
1.1 История развития тригонометрии
Термин «тригонометрия» дословно означает «измерение треугольников».
Понятие «тригонометрия» ввел в употребление в 1595 году немецкий математик и богослов Варфоломей Питиск, автор учебника по тригонометрии и тригонометрических таблиц. ..
..
Тригонометрические уравнения
1.4 Основные понятия и формулы тригонометрии
В тригонометрии угол рассматривается как мера вращения, при котором один луч, вращаясь вокруг вершины угла, переходит в положение другого луча. При этом первый луч называют начальной стороной угла…
Тригонометрические функции
7. Основные формулы тригонометрии
7.1. Основные тождества и их следствия 1 cos2б+sin2б=1 5 2 6 Tgбctgб=1 3 7 4 8 7.2. Формулы понижения степени 9 cos2б =2cos2б — 1 10 cos2б =1-2sin2б 7.3…
Тригонометрические функции
Основные формулы тригонометрии.
…
Краткий обзор истории тригонометрии
Краткий обзор истории тригонометрии То есть, если вы хотите
чтобы узнать оставшийся угол и оставшиеся две стороны, все, что вам нужно сделать, это
выложите данную сторону и два угла на ее концах, продлите два других
стороны, пока они не встретятся, и у вас есть треугольник. Никаких численных расчетов
вовлеченный.
То есть, если вы хотите
чтобы узнать оставшийся угол и оставшиеся две стороны, все, что вам нужно сделать, это
выложите данную сторону и два угла на ее концах, продлите два других
стороны, пока они не встретятся, и у вас есть треугольник. Никаких численных расчетов
вовлеченный.Но тригонометрическая версия другая. Если у вас есть измерения двух углов и длины стороны между ними, то задача чтобы вычислить оставшийся угол (что легко, просто вычтите сумму двух углы из двух прямых) и оставшиеся две стороны (что сложно). Современное решение последнего вычисления с помощью закона синусов. Подробности у Дейва Короткий триггерный курс, косые треугольники.
Все тригонометрические вычисления требуют измерения углов и вычисление некоторой тригонометрической функции. Современная тригонометрическая функциями являются синус, косинус, тангенс и их обратные функции, но в древних Использовалась греческая тригонометрия, аккорд, более интуитивная функция.
Тригонометрия, конечно же, зависит от геометрии. Закон косинусов, для
Например, следует из предложения синтетической геометрии, а именно из предложения
II.12 и II.13 Элементов . Итак, задачи по тригонометрии имеют
потребовали новых разработок в синтетической геометрии. Примером может служить Птолемей.
теорема, которая дает правила для хорд суммы и разности углов,
которые соответствуют формулам суммы и разности для синусов и косинусов.
Закон косинусов, для
Например, следует из предложения синтетической геометрии, а именно из предложения
II.12 и II.13 Элементов . Итак, задачи по тригонометрии имеют
потребовали новых разработок в синтетической геометрии. Примером может служить Птолемей.
теорема, которая дает правила для хорд суммы и разности углов,
которые соответствуют формулам суммы и разности для синусов и косинусов.
Основное применение тригонометрии в культурах прошлого, а не только в древних
Греческий, к астрономии. Вычисление углов на небесной сфере требует
другой вид геометрии и тригонометрии, чем на плоскости.
геометрия сферы называлась «сферикой» и составляла часть
квадривиум учебы. Различные авторы, в том числе Евклид, написали книги по
сферики. Нынешнее название предмета — «эллиптическая геометрия».
Тригонометрия, по-видимому, возникла для решения задач, поставленных в сфере, а не
задачи, поставленные в плоской геометрии. Таким образом, сферическая тригонометрия стара как мир.
плоская тригонометрия.
Вавилоняне и измерение углов
Вавилоняне где-то до 300 г. до н. э. использовали градусное измерение для углы. Вавилонские цифры были основаны на числе 60, поэтому можно предположить, что они взяли за единицу измерения то, что мы называем 60°, а затем разделили это в 60 градусов. Возможно, за единицу взято 60°, потому что хорда 60° равняется радиусу окружности, см. ниже о хордах. Измерение градусов было позже принято Гиппархом. Вавилоняне первыми дали координаты звезд. Они использовали
эклиптика как их базовый круг на небесной сфере, то есть кристалл
сфера звезд. Солнце движется по эклиптике, планеты движутся вблизи
эклиптика, созвездия зодиака расположены вокруг эклиптики,
а северная звезда, Полярная звезда, равна 9.0° от эклиптики. Небесный
сфера вращается вокруг оси через северный и южный полюса.
Вавилоняне измеряли долготу в градусах против часовой стрелки от весенней
точка, если смотреть с северного полюса, и измеряли широту в градусах
к северу или югу от эклиптики.
Гиппарх Никейский (ок. 180 — ок. 125 до н. э.)
Гиппарх был прежде всего астрономом, но начало тригонометрии видимо с него и началось. Конечно, вавилоняне, египтяне и более ранние Греки знали много астрономии до Гиппарха, и они также определили положения многих звезд на небесной сфере перед ним, но это Гиппарха, которому приписывают первую таблицу аккордов. Это было выдвинули гипотезу, что Аполлоний и даже Архимед построили таблицы аккордов до него, но нет ссылки на какую-либо такую более раннюю таблицу.Некоторые достижения Гиппарха в астрономии включают вычисление среднего лунный месяц, оценки размеров и расстояний до солнца и луны, варианты по эпициклическим и эксцентрическим моделям движения планет, каталог 850 звезд (долгота и широта относительно эклиптики), а также открытие прецессии равноденствий и измерения этой прецессии.
Согласно Теону, Гиппарх написал 12-книжный труд об аккордах в круге,
так как потерял. Это будет первая известная работа по тригонометрии. Поскольку
работа больше не существует, почти все о ней является спекуляцией. Но несколько
вещи известны из различных упоминаний о нем в других источниках, включая другой
Его личное. Он включал в себя несколько длин хорд, соответствующих различным дугам
круги, возможно таблица аккордов. Помимо этих обрывков информации,
другие могут быть выведены из знаний, которые он считал общеизвестными.
преемники.
Поскольку
работа больше не существует, почти все о ней является спекуляцией. Но несколько
вещи известны из различных упоминаний о нем в других источниках, включая другой
Его личное. Он включал в себя несколько длин хорд, соответствующих различным дугам
круги, возможно таблица аккордов. Помимо этих обрывков информации,
другие могут быть выведены из знаний, которые он считал общеизвестными.
преемники.
Аккорды как основа тригонометрии
В современном представлении тригонометрии синус и косинус угла и — это и — и x -координаты точки на устройстве круг, точка которого является пересечением единичного круга и одной стороны угол и ; другая сторона угла является положительной осью x . Греки, индийцы, арабы и ранние европейцы использовали круг некоторых других удобный радиус. Для этого описания тригонометрии мы оставим радиус не указан как р и это двойное, диаметр мы обозначим д . Хорда угла AOB где O — центр окружности и A и B две точки на окружности, это просто прямая линия АБ . Аккорды связаны с современными синусом и косинусом по формулам
Аккорды связаны с современными синусом и косинусом по формулам
| crd a = d sin ( a /2) sin a = (1/ d ) crd 2 и | crd (180° — a ) = d cos ( a /2) cos a = (1/ d ) crd (180° — 2 a ) |
где a — угол, d — диаметр, а crd — сокращение от аккорд.
Некоторые свойства хорд не могли ускользнуть от внимания Гиппарха, особенно
в 12-книжном труде на эту тему. Например, формула дополнительного угла гласила бы, что если АОБ и BOC являются дополнительными углами, тогда теорема Фалеса утверждает, что треугольник ABC верно, поэтому по теореме Пифагора квадрат на хорде AB плюс квадрат хорды BC равно квадрату хорды
диаметр АС . Обобщено с использованием современных алгебраических обозначений.
где д — это диаметр круга.
Гиппарх, вероятно, построил свою таблицу аккордов, используя полуугол Формула и формула дополнительного угла. Формула половинного угла через аккорды
где r — радиус окружности, а t — угол. Начиная с crd 60° = r , Гиппократ мог с помощью этого Формула половинного угла находит хорды 30°, 15° и 7 1/2°. Он мог составить таблицу аккордов за 7 1/2° шагов, используя crd 90°, формула половинного угла и формула дополнительного угла.
Какие еще отношения между хордами различных углов, которые Гиппократ знал бы остается домыслами.
Менелай (ок. 100 г. н.э.)
Самой ранней работой по сферической тригонометрии была « Spherica » Менелая. Это включала то, что сейчас называется теоремой Менелая, которая связывает дуги больших круги на сферах. Конечно, Менелай сформулировал свой результат в терминах аккордов.
но в терминах современных синусов его теорема гласит
Конечно, Менелай сформулировал свой результат в терминах аккордов.
но в терминах современных синусов его теорема гласит| sin CE sin EA | = | sin CF sin FD | sin BD sin BA |
| sin CA sin EA | = | sin CD sin FD | sin BF sin BE |
Он доказал этот результат, сначала доказав плоскую версию, а затем «спроецировав» ее обратно.
к сфере. Версия самолета говорит
| CE EA | = | CF FD | БД БА |
| CA EA | = | КД ФД | BF BE |
Птолемей (ок.
 100–178 гг. н. э.) Знаменитой математической работой Клавдия Птолемея был « Математический синтаксис ».
( Mathematical Collection ) обычно известный как Альмагест. это
в первую очередь работа по астрономии, которая включала математическую теорию, относящуюся к
астрономия. Она включала тригонометрическую таблицу, таблицу хорд для углов от
от 1/2° до 180° с шагом 1/2°, хорды были округлены до двух
шестидесятеричных разрядов, с точностью до пяти знаков. Он также включил
геометрия, необходимая для построения таблицы. Он вычислил хорду 72°,
центральный угол пятиугольника, конструктивный угол. Вместе с аккордом
60° (радиус, который Птолемей считал равным 60), что дает crd 12°, тогда
crd 6°, crd 3°, crd 1 1/2° и crd 3/4°. Он использовал
интерполяция для нахождения crd 1° и crd 1/2°.
100–178 гг. н. э.) Знаменитой математической работой Клавдия Птолемея был « Математический синтаксис ».
( Mathematical Collection ) обычно известный как Альмагест. это
в первую очередь работа по астрономии, которая включала математическую теорию, относящуюся к
астрономия. Она включала тригонометрическую таблицу, таблицу хорд для углов от
от 1/2° до 180° с шагом 1/2°, хорды были округлены до двух
шестидесятеричных разрядов, с точностью до пяти знаков. Он также включил
геометрия, необходимая для построения таблицы. Он вычислил хорду 72°,
центральный угол пятиугольника, конструктивный угол. Вместе с аккордом
60° (радиус, который Птолемей считал равным 60), что дает crd 12°, тогда
crd 6°, crd 3°, crd 1 1/2° и crd 3/4°. Он использовал
интерполяция для нахождения crd 1° и crd 1/2°.Теорема Птолемея
Птолемей доказал теорему, которая дает формулы суммы и разности для аккорды.- Теорема. Для вписанного четырехугольника (т. е. четырехугольника, вписанного в
круг), произведение диагоналей равно сумме произведений
противоположные стороны.

где O — центр окружности, а d — диаметр. Если мы возьмем a за угол AOB и b за угол AOC , тогда у нас есть
что дает формулу разности
| crd ( b — a ) = | crd b crd (180° — a ) — crd a crd
(180° — b ) d |
При различной интерпретации a и b формула суммы полученные результаты:
| crd ( b + a ) = | crd b crd (180° — a ) + crd и код
(180° — b ) d |
Они, конечно, соответствуют формулам суммы и разности для синусов.
Вооружившись своей теоремой, Птолемей мог составить свою таблицу аккордов от 1/2°
до 180° с шагом 1/2°.
Тригонометрия
Вычислительную тригонометрию можно было начать только после построения хорошего триггерную таблицу, и так продолжил Птолемей. Хотя систематически он не давал методы решения прямоугольных и косоугольных треугольников, решения задач конкретные проблемы обнаружены в Альмагест. Те решения, которые мы найти синусы или косинусы одинаково легко решить с помощью таблицы хорды, но те, которые мы решили бы касательными, потребовали бы деления хорду дополнительной хордой, что усложняет решение. А типичным примером этого было бы нахождение высоты полюса по длине его тени и угла наклона тени. Основным источником информации в этом обзоре является книга Томаса Хита 9.0003 История
греческой математики , Clarendon Press, Oxford, 1921, в настоящее время переиздается
Довер, Нью-Йорк, 1981 год.
Дэвид Э. Джойс, 90 429
Тригонометрия — Открытая библиотека учебников
Доступные форматы
- ПДФ
Условия использования
Attribution-NonCommercial-ShareAlike
CC BY-NC-SA
отзывов
Узнайте больше об отзывах.
Отзыв Калеба Холлоуэя, доцента Технологического института Университета Западной Вирджинии от 01.04.19
В то время как другие тексты могут включать больше тем, мой опыт показывает, что в семестре никогда не хватает времени, чтобы охватить их все. Этот текст охватывает круговую и прямоугольную тригонометрию, аналитическую тригонометрию (тождества и тригонометрические… читать далее
Отзыв Калеба Холлоуэя, доцента Технологического института Университета Западной Вирджинии от 01.04.19
Полнота рейтинг: 4 видеть меньше
В то время как другие тексты могут включать больше тем, мой опыт показывает, что в семестре никогда не хватает времени, чтобы охватить их все. Этот текст охватывает круговую и прямоугольную тригонометрию, аналитическую тригонометрию (тождества и тригонометрические уравнения) и приложения, и уделяет достаточно времени векторам, комплексным числам и полярным координатам, чтобы аккуратно завершить семестр.
Этот текст охватывает круговую и прямоугольную тригонометрию, аналитическую тригонометрию (тождества и тригонометрические уравнения) и приложения, и уделяет достаточно времени векторам, комплексным числам и полярным координатам, чтобы аккуратно завершить семестр.
Точность содержания рейтинг: 5
При просмотре книги я не обнаружил ошибок.
Актуальность/долговечность рейтинг: 5
Тригонометрия жизненно важна для математики и инженерии, а также для многих естественных наук. Я не вижу, чтобы это изменилось в ближайшее время. Приложения в этой книге (которых немало) относятся к этим дисциплинам.
Ясность рейтинг: 5
Тон этой книги очень приятный, почти разговорный, но при этом не лишен необходимой математической строгости. Он представляет идеи и методы соответствующим образом, не звуча отчужденно. Новые идеи вводятся путем соотнесения их со знакомыми идеями, и учащиеся ориентируются на использование собственных рассуждений и тем самым развивают собственное понимание новых концепций. Каждый раздел обычно начинается с примера или проблемы для мотивации последующего обсуждения.
Каждый раздел обычно начинается с примера или проблемы для мотивации последующего обсуждения.
Последовательность рейтинг: 4
Одной из основных особенностей этой книги являются проверки прогресса, которые, по сути, представляют собой примеры задач, которые учащиеся решают сами. Эти Проверки прогресса обычно строятся таким образом, чтобы направлять учащегося в изучении новой темы. Иногда, однако, проверка успеваемости сводится к одному из двух: либо к повторению техники, которая только что была продемонстрирована в тексте, либо к задаче, в которой ученик должен разработать для себя новую идею при слишком слабом руководстве со стороны учителя. книга. Преподаватель должен знать, где возникают такие проблемы, и соответствующим образом разрабатывать классные инструкции по затрагиваемым темам.
Модульность рейтинг: 4
Я думаю, что эта книга настолько модульна, насколько может быть учебник по тригонометрии. Это, конечно, хорошо организовано. Я бы предостерег от чрезмерной свободы в реорганизации текста. Во-первых, темы в тексте обычно основываются на предыдущих. Это по необходимости. Во-вторых, исследования показывают, что учащиеся развивают более целостное понимание тригонометрии, если круговую тригонометрию изучают до тригонометрии прямоугольного треугольника, и связь между ними становится явной, как это делается в этой книге. Таким образом, независимо от того, насколько модульной может быть или не быть эта книга, я считаю, что в интересах учителя излагать темы в порядке, изложенном в книге, насколько это возможно.
Во-первых, темы в тексте обычно основываются на предыдущих. Это по необходимости. Во-вторых, исследования показывают, что учащиеся развивают более целостное понимание тригонометрии, если круговую тригонометрию изучают до тригонометрии прямоугольного треугольника, и связь между ними становится явной, как это делается в этой книге. Таким образом, независимо от того, насколько модульной может быть или не быть эта книга, я считаю, что в интересах учителя излагать темы в порядке, изложенном в книге, насколько это возможно.
Организация/Структура/Поток рейтинг: 5
Книга начинается с довольно подробного рассмотрения измерения угла, темы, которая часто замалчивается в текстах по тригонометрии. В первых нескольких разделах основное внимание уделяется функциям синуса и косинуса, чтобы учащиеся могли получить полное представление о том, как ведут себя эти функции, прежде чем обратить внимание на другие четыре триггерные функции, каждая из которых может рассматриваться как производная от синуса и косинус.
Круговая тригонометрия описана перед тригонометрией прямоугольного треугольника, что, как упоминалось ранее, способствует более целостному пониманию тригонометрии, чем обратный подход. Во многих учебниках векторы не упоминаются до конца книги, где они объединяются с другими «приложениями» тригонометрии. Здесь они представлены сразу после традиционных тем триггера прямоугольного треугольника, который мне нравится.
Остальные темы — тождества триггеров, уравнения триггеров и комплексные числа — рассматриваются в стандартном порядке. Всесторонний обзор алгебры комплексных чисел представлен до тригонометрии комплексных чисел.
Интерфейс рейтинг: 5
Книга была легко читаема, все графики и диаграммы были четкими и легко читаемыми. В книге много ссылок на внешние апплеты, все (которые я проверял) работали.
Грамматические ошибки рейтинг: 5
Я не заметил грамматических ошибок.
Культурная значимость рейтинг: 5
Эта книга подходит для любого учащегося, независимо от его подготовки.
Во многих отношениях эта книга соответствует современному пониманию обучения тригонометрии. Значительное количество времени тратится на раннее развитие у учащихся понимания углов и меры угла. Студенты изучают не только процесс измерения углов, но и природу самих углов. И радианы, и градусы представлены в виде стягиваемых дуг, так что учащиеся могут плавно перемещаться между двумя мерами.
Позже изучаются преобразования тригонометрических функций (обычно сложная тема для студентов), при этом основное внимание уделяется аргументам функций и обращению к композиции функций. Этот пример типичен для здоровой тенденции книги включать старые концепции в новые, но он также позволяет избежать распространенной ловушки представления преобразований в чисто геометрических терминах, благодаря чему учащиеся начинают понимать графики как «форму», а не как след отношения. . Вместо этого подход этой книги поощряет «процедурное представление» функций, обращая внимание на отношения между вводом и выводом и на то, как эти отношения меняются при составлении двух функций.
Эта книга не идеальна. Я бы хотел, чтобы больше внимания уделялось ковариации между вводом и выводом триггерных функций, особенно когда речь идет о графиках синуса и косинуса и о том, как форма этих графиков определяется способами изменения ввода и вывода. вместе. Но в целом эта книга лучше знакомит студентов с тригонометрией, чем большинство книг, которые я видел, будь то открытые или розничные.
Отзыв Кэролин Гудман, доцента, преподавателя математики, Университет Цинциннати, Клермонтский колледж, 27 марта 2018 г.
Этот текст был создан для трехкредитного курса тригонометрии (MATh223-Тригонометрия) в Государственном университете Гранд-Вэлли. Помимо конических сечений, текст охватывает все, что обычно входит в первый курс тригонометрии. Тем не менее… читать далее
Отзыв Кэролин Гудман, доцента, преподавателя математики, Университет Цинциннати, Клермонтский колледж, 27 марта 2018 г.
Полнота рейтинг: 5 видеть меньше
Этот текст был создан для трехкредитного курса тригонометрии (MATh223-Тригонометрия) в Государственном университете Гранд-Вэлли. Помимо конических сечений, текст охватывает все, что обычно входит в первый курс тригонометрии. Однако полнота этого текста превосходит другие тексты по многим важным параметрам. Тригонометрические концепции разрабатываются очень тщательным, терпеливым и последовательным образом, что наверняка понравится учащимся, развивая при этом их математическое понимание и аналитическое мышление. Требуется время, чтобы вовлечь читателя в мыслительный процесс, используя ссылки на хорошо разработанные и интегрированные диаграммы, апплеты Geogrebra, рабочие листы и видеоролики YouTube (разработанные Государственным университетом Гранд-Вэлли). Начальные обзорные действия, основные вопросы, проверки прогресса и сводки по разделам задают направление и поддерживают активное и глубокое обучение. Ответы и подсказки к выбранным упражнениям и геометрическим фактам о кругах и треугольниках включены в приложения.
Помимо конических сечений, текст охватывает все, что обычно входит в первый курс тригонометрии. Однако полнота этого текста превосходит другие тексты по многим важным параметрам. Тригонометрические концепции разрабатываются очень тщательным, терпеливым и последовательным образом, что наверняка понравится учащимся, развивая при этом их математическое понимание и аналитическое мышление. Требуется время, чтобы вовлечь читателя в мыслительный процесс, используя ссылки на хорошо разработанные и интегрированные диаграммы, апплеты Geogrebra, рабочие листы и видеоролики YouTube (разработанные Государственным университетом Гранд-Вэлли). Начальные обзорные действия, основные вопросы, проверки прогресса и сводки по разделам задают направление и поддерживают активное и глубокое обучение. Ответы и подсказки к выбранным упражнениям и геометрическим фактам о кругах и треугольниках включены в приложения.
В этом тексте используется очень интересный обратный хронологический подход к тригонометрии. Тригонометрические функции вводятся как циклические функции, а затем как тригонометрические функции. Теперь я убежден, что это обеспечивает более целостную перспективу тригонометрии и лучше проясняет многие понятия, такие как безразмерная природа радианов.
Тригонометрические функции вводятся как циклические функции, а затем как тригонометрические функции. Теперь я убежден, что это обеспечивает более целостную перспективу тригонометрии и лучше проясняет многие понятия, такие как безразмерная природа радианов.
Точность содержания рейтинг: 5
Ошибок или предвзятости в содержании книги я не заметил.
Актуальность/долговечность рейтинг: 5
Учебник начинается с наиболее актуальных применений тригонометрии, но написан не таким образом, чтобы требовать необходимых обновлений. При необходимости его можно было легко обновить. Автор приглашает обратную связь, особенно от студентов, использующих текст.
Ясность рейтинг: 5
Текст делает даже самые сложные тригонометрические понятия понятными и доступными для учащихся. Он разрабатывает концепции и определения терминологии, чтобы учащиеся могли их понять и запомнить. Он включает в себя проверку прогресса для студентов, чтобы проверить их понимание. В резюме раздела перечислены важные определения и результаты, подтвержденные в разделе.
Дисциплинированный и целеустремленный ученик может самостоятельно выучить тригонометрию по этому тексту. Некоторым учащимся может потребоваться дополнительное разъяснение прочитанного.
Последовательность рейтинг: 5
Текст внутренне непротиворечив с точки зрения терминологии и структуры. Каждое из начальных заданий рассматривает предшествующую математическую работу, необходимую для нового раздела. Ответы на эти начальные действия разрабатываются в материале далее в этом разделе. В каждом разделе есть проверки прогресса с ответами на эти проверки в Приложении A. Каждый раздел обобщается с перечислением важных определений и результатов, подтвержденных в разделе.
Модульность рейтинг: 5
Этот текст лучше всего читать от начала до конца, чтобы полностью понять, как развиваются идеи. Однако каждая глава может стоять сама по себе. Каждый раздел для чтения довольно небольшой, и текст в каждом разделе разбит на небольшие фрагменты, чтобы читатель был вовлечен, активен и заинтересован.
Организация/Структура/Поток рейтинг: 5
Этот текст очень организован, хорошо структурирован и очень хорошо течет. Он особенно силен своим четким и логичным развитием тем. Есть правильное количество ритма и разнообразия, чтобы удерживать внимание читателя. Он использует более разговорный и доступный язык, чем большинство математических текстов.
Интерфейс рейтинг: 5
Там было несколько ссылок на цифры, которые, кажется, не привели меня точно к цифре, но, по крайней мере, близко к ним. В остальном я не заметил никаких проблем с интерфейсом, проблем с навигацией, искажения изображений или каких-либо других отвлекающих или сбивающих с толку особенностей отображения.
Грамматические ошибки рейтинг: 5
Я заметил только пару грамматических ошибок в Progress Check 1.2 и на странице 168, где пропущено одно или два слова.
Культурная значимость рейтинг: 5
Этот текст никоим образом не является культурно нечувствительным. Скорее, разнообразие ресурсов и начальных видов деятельности привлекают учащихся с разным стилем обучения и математическим образованием.
Я считаю этот текст превосходным. Он использует управляемый подход и имеет разговорный, интересный и увлекательный тон, который обещает эффективно охватить всех учащихся, от серьезных студентов-математиков до тех, у кого математическая тревога.
Я обязательно сделаю этот текст доступным для своих учеников, чтобы получить их отзывы, и надеюсь использовать его в качестве основного текста в будущем. Это может значительно облегчить преподавание и обучение как на онлайн-курсах, так и на традиционных курсах.
Содержание
- Примечание для студентов
- Предисловие
- Тригонометрические функции
- Графики тригонометрических функций
- Треугольники и векторы
- Тригонометрические тождества и уравнения
- Комплексные числа и полярные координаты
- Приложение A: ответы для проверки выполнения
- Приложение B: ответы и советы для избранных упражнений
- Приложение C: Некоторые геометрические факты о треугольниках и параллелограммах
- Индекс
Вспомогательный материал
О книге
Этот учебник по тригонометрии отличается от других книг по тригонометрии тем, что его можно загрузить бесплатно, и ожидается, что читатель сделает больше, чем просто прочитает книгу, и должен изучить материал в книге, разрабатывая примеры, а не просто читая о них. . Так что эта книга не только о математическом содержании, но и о процессе изучения и выполнения математических действий. То есть эта книга рассчитана не на простое чтение, а на занятие.
. Так что эта книга не только о математическом содержании, но и о процессе изучения и выполнения математических действий. То есть эта книга рассчитана не на простое чтение, а на занятие.
Поскольку это может быть сложной задачей, в книге есть несколько особенностей, призванных помочь учащимся в этом стремлении. В частности, большинство разделов книги начинаются с начального задания, в котором рассматривается предыдущая математическая работа, необходимая для нового раздела, или вводятся новые понятия и определения, которые будут использоваться позже в этом разделе. Каждый раздел также содержит несколько проверок прогресса, которые представляют собой короткие упражнения или действия, призванные помочь читателям определить, понимают ли они материал. Кроме того, текст содержит ссылки на несколько интерактивных апплетов или рабочих листов Geogebra. Эти апплеты обычно являются частью начального задания или проверки прогресса и предназначены для использования как часть учебника.
Об участниках
Авторы
Тед Сандстром — профессор математики в Государственном университете Гранд-Вэлли в Аллендейле, штат Мичиган.
Стивен Шликер — профессор математики в Государственном университете Гранд-Вэлли в Аллендейле, штат Мичиган.
Внести вклад в эту страницу
Предложить изменение этой записи книгиMath Sux, автор уроков математики
Что такое тригонометрия?
Что такое тригонометрия? Тригонометрия – это изучение углов и сторон треугольников в математике. Применяя правила тригонометрии, мы можем найти неизвестные углы и длины сторон в треугольниках и других формах, которые можно разбить на треугольники.
Какая разница? Зачем нам знать углы треугольника или длину стороны? Это справедливый вопрос! Хотя на бумаге тригонометрия может показаться бесполезной, это отличный инструмент для решения реальных проблем в архитектуре, астрономии, инженерии и даже в дизайне видеоигр! Например, что, если бы мы захотели узнать меру угла между линией нашего взгляда и расстоянием до Луны? Или что, если нужно найти идеальный угол для крыши здания? На все эти вопросы можно было бы ответить, используя прекрасный предмет тригонометрии.
Точно так же, как слово tri угол, tri гонометрия включает префикс « tri », означающий три. Три, магическое число в тригонометрии, так как есть также три основные тригонометрические функции (синус, косинус и тангенс) вместе с их инверсиями (секанс, косеканс и котангенс соответственно). Синус, косинус и тангенс являются основными функциями триггера, которые позволяют нам находить значения углов и/или сторон прямоугольного треугольника.
История тригонометрии
Откуда взялась тригонометрия? Слово тригонометрия восходит к Греции, от греческого слова « trignon », означающего треугольника , и слова « метрон », что означает для измерения . Ясно, что история тригонометрии в Греции восходит к 3 веку до н.э. Хотя это имеет корни в греческой истории, этот предмет также можно проследить до Индии в 5 веке нашей эры. Каждая культура независимо изобретала тригонометрию сначала для астрономических целей.
Базовая тригонометрия прямоугольного треугольника
Мы вкратце затронули основные тригонометрические функции (синус, косинус и тангенс), теперь давайте углубимся и посмотрим, как каждая функция работает с прямоугольным треугольником!
Синус, косинус и тангенс, известные как Sin, Cos и Tan, являются тригонометрическими функциями, которые можно использовать для нахождения углов и сторон прямоугольных треугольников (треугольников с углом 90º). Sin, Cos и Tan можно описать очень запоминающейся аббревиатурой SOH CAH TOA 9.0605 :
Греческая буква θ, произносимая как «тета», используется для обозначения неизвестных углов в тригонометрии и может быть соединена с каждым тригонометрическим отношением (sin θ, cos θ, tan θ), что именно то, что вы видите выше.
Чтобы использовать наши триггерные функции, нам нужно определить различные части прямоугольного треугольника на основе положения угла. Всегда будет сторона , противоположная стороне , противоположной углу θ, и сторона , примыкающая к стороне , которая находится рядом с углом θ. И последняя оставшаяся сторона, единственная сторона, которая всегда будет помечена одинаково (независимо от угла θ), — это самая длинная сторона прямоугольного треугольника, которая называется 9.0604 гипотенуза .
И последняя оставшаяся сторона, единственная сторона, которая всегда будет помечена одинаково (независимо от угла θ), — это самая длинная сторона прямоугольного треугольника, которая называется 9.0604 гипотенуза .
Давайте попробуем Пример:
Учитывая следующий прямоугольный треугольник, найдите sin30º .
Шаг 1: Поскольку мы собираемся найти sin30º, давайте запишем наше отношение для синуса на основе нашей аббревиатуры SOH CAH TOA.
Шаг 2: Теперь мы должны определить нашу противоположность и гипотенузу на основе нашего угла θ. Помните, что противоположность — это длина противоположной стороны по отношению к нашему углу θ, который в данном случае равен 1,
. Гипотенуза — это всегда самая длинная сторона, которая в данном случае равна 2,9.0006
(Смежная ветвь радикальная 3, но в случае нахождения синуса это значение нам не нужно).
Шаг 3: Теперь, когда у нас есть значения противоположности (1) и гипотенузы (2), давайте подставим их в наш коэффициент греха для для нашего ответа.
Если вы ищете больше правильных треугольников и практических вопросов SOH CAH TOA, подобных приведенному выше, пожалуйста, посмотрите видео и ссылку здесь.
Обратные тригонометрические функции:
Обратные тригонометрические отношения являются обратными обычными тригонометрическими функциями (sin, cos и tan), которые мы только что рассмотрели! Проверьте это ниже:
Решаем обратные тригонометрические функции точно так же, как и обычные тригонометрические функции, давайте рассмотрим пример ниже:
Найдите точное значение csc45º
Шаг 1: Мы знаем, что CSC является обратным значением sin , что равно 1/sin , поэтому давайте воспользуемся действием SOH CAH TOA, чтобы найти sin45º как обычно, а затем перевернем наш ответ, чтобы найти значение csc45º.
Шаг 2: Теперь все, что нам нужно сделать, это «перевернуть» ответ, который мы получили на шаге 1, чтобы получить обратное значение, которое будет значением csc45º.
Единичный круг:
Единичный круг является важным справочным инструментом, используемым в тригонометрии для получения всевозможных формул и в первую очередь объясняет, как работает тригонометр!
Почему он называется единичным кругом?
Обратите внимание, что каждая точка на окружности находится на расстоянии одной единицы от начала координат ниже.
Почему градусы идут против часовой стрелки?
Круг имеет 360º, поэтому мы можем перемаркировать ось с помощью 0º, 90°, 180°, 270° и 360°. Заметили, что числа идут против часовой стрелки? Это основано на движении Земли вокруг Солнца, так как оно тоже движется против часовой стрелки. Забавный факт: Астрономия и изучение движения Солнца и Земли — истоки тригонометрии!
Другие сведения об окружности единиц:
1. Градусы следуют схеме против часовой стрелки от 0 до 360 градусов.
Градусы следуют схеме против часовой стрелки от 0 до 360 градусов.
2. Значения косинуса представлены x-координатами .
3. Значения синуса представлены y-координатами .
4. Используя единичный круг, мы можем найти градус и значение в радианах тригонометрических функций (SOH CAH TOA).
Триггерные функции и квадранты:
Основываясь на нахождении углов с помощью теоремы Пифагора, используя эталонные треугольники в каждом квадранте, мы можем определить, какие триггерные функции (sin, cos, tan) положительны в каком квадранте. Давайте посмотрим, как шаг за шагом с доказательством!
Шаг 1: Чтобы доказать, почему некоторые триггерные функции положительны в определенных квадрантах, нарисуйте единичный круг и добавьте треугольники в каждом квадранте. Обратите внимание, что это похоже на галстук-бабочку, и мы также добавили угол θ внутри каждого треугольника, это пригодится позже!
Шаг 2: Теперь найдем тригонометрические функции (синус, косинус, тангенс) относительно θ для каждого треугольника в каждом квадранте. Давайте закроем наш треугольник в квадранте I.
Давайте закроем наш треугольник в квадранте I.
Обратите внимание, что гипотенуза имеет значение 1, потому что это единичный круг, а «1» — это значение радиуса.
Нам неизвестны значения x и y для этого треугольника, но мы знаем, что и x, и y будут положительными значениями.
Если бы мы нашли sinθ, мы бы получили:
Что, если бы мы нашли cosθ и tanθ для нашего эталонного треугольника Квадранта I?
Мы только что доказали, что все наши триггерные функции положительны в квадранте I! Проверьте ниже, чтобы узнать о квадрантах II, III и IV:
На что обратить внимание:
Обратите внимание, что все положительные функции выделены зеленым цветом.
Точно так же, как мы доказали, что квадрант I положителен для всех функций триггера, приведенная выше диаграмма показывает, что только sin положителен в QII, только tan положителен в QIII и только cos в QIV.
Мы получили каждое, используя SOH CAH TOA для каждого эталонного прямоугольного треугольника относительно θ.
О единичном круге можно узнать гораздо больше. Если вам интересно узнать больше, посмотрите видео ниже и дайте ссылку здесь!
Графические функции триггеров:
Мы видели единичный круг, теперь я должен задаться вопросом, как выглядят триггерные функции (sin, cos, tan), когда они графически изображены на координатной плоскости? Приготовьтесь, потому что они выглядят довольно круто, а визуализация этих триггерных функций может вас удивить!
Вы когда-нибудь слышали о синусоиде? Радиоволна? Именно так выглядят графики триггерных функций, потому что они такие!
Sin Graph : Синусоидальные кривые создают то, что выглядит как S-образная форма. Как говорится « S ”для S ine, это самый простой способ запомнить, как выглядит функция синуса, посмотрите ниже!
Как говорится « S ”для S ine, это самый простой способ запомнить, как выглядит функция синуса, посмотрите ниже!
График косинуса: При построении графика косинуса вы можете заметить, что функция косинуса создает нечто похожее на букву «V». Как говорится, «V» — для победы, но, конечно, в данном случае — для косинуса!
Диаграмма тангенса: Функция тангенса выглядит совершенно иначе на графике по сравнению с синусоидой и косинусом. Вы можете заметить пунктирные вертикальные линии ниже, они называются асимптоты и здесь не может быть никаких значений, проверьте это ниже!
Почему графики тригонометрических функций выглядят именно так? Получите и узнайте, почему отношения триггеров на графиках выглядят уникальными и многое другое здесь. И если вы хотите узнать, как преобразовать триггерный граф, перейдите по этой ссылке здесь.
youtube.com/embed/VqLx0xYP8fY?version=3&rel=1&showsearch=0&showinfo=1&iv_load_policy=1&fs=1&hl=en-US&autohide=2&start=5&wmode=transparent» allowfullscreen=»true» sandbox=»allow-scripts allow-same-origin allow-popups allow-presentation»>Специальные треугольники:
Специальные треугольники, также известные как супергерои тригонометрии, являются ценным справочным инструментом для решения тригонометрических функций. Специальные треугольники включают 30 60 9треугольник 0 и треугольник 45 45 90. Каждый из прямоугольных треугольников, которые вы сейчас увидите, может быть получен из единичного круга.
Зная приведенные ниже специальные треугольники, мы можем ответить на такие вопросы, как «найти значение sin 45º и cos 45º без использования калькулятора». Специальные треугольники помогут найти неизвестные значения углов в треугольнике. Теперь давайте посмотрим на наши очень необычные треугольники ниже:
Специальные треугольники помогут найти неизвестные значения углов в треугольнике. Теперь давайте посмотрим на наши очень необычные треугольники ниже:
Нахождение углов и сторон в непрямоугольных треугольниках:
Как найти неизвестный угол или сторону треугольника, если треугольник НЕ является прямоугольным? Ответ заключается в использовании закона синусов или закона косинусов. Как я узнаю, когда использовать закон синусов против закона косинусов? Конечно, все зависит от информации о треугольнике, которая нам дана! См. различия ниже:
различия ниже:
Закон синусов: Использовать при наличии ASA , AAS и неоднозначный случай SSA треугольника.
Закон косинусов: Используйте, когда заданы SSS или SAS треугольника.
A 2 = B 2 + C 2 -2BCCOSA
B 2 = A 2 + C 2 -2ACCOSB
C 2 = 2 2 = = = = = = = = = = = = = = = = = = = = = = 2 = 2 . 2 -2abCosC
Остались вопросы? Есть любимая часть тригонометрии, которой вы хотите поделиться? Не стесняйтесь писать по электронной почте или комментировать ниже! Кроме того, не забудьте подписаться на нас в социальных сетях, чтобы получать самые свежие и лучшие уроки MathSux, видео, вопросы и многое другое. Удачных расчетов!
Удачных расчетов!
Facebook ~ Twitter ~ TikTok ~ Youtube
Автор Math SuxОпубликовано Рубрики Без рубрики2 Комментарии к записи Что такое тригонометрия Приветствую друзей-математиков и добро пожаловать в MathSux! В сегодняшней статье мы рассмотрим закон косинусов ! Также известная как правило косинусов, это отличная формула для нахождения информации об отсутствующем угле и стороне треугольника, который равен , а НЕ является прямоугольным треугольником , когда у нас есть SAS или SSS информация о рассматриваемом треугольнике. Эта формула гораздо более прямолинейна по сравнению с законом синусов, поэтому, если вы уже освоили эту формулу, закон косинусов должен быть легким! Кроме того, не забудьте проверить практические вопросы в конце этого поста, чтобы проверить свои знания закона косинусов. Удачных расчетов!
Удачных расчетов!
Закон косинусов позволяет нам найти недостающие стороны и углы любого непрямоугольного треугольника (также известного как косой треугольник), где нам дано SAS или SSS информация о рассматриваемом треугольнике.
Если вы возьмете пик ниже по закону косинусов, обратите внимание, что его можно вывести из теоремы Пифагора, поскольку он напоминает классическую формулу, которую мы все знаем и любим, a 2 + b 2 = c 2 .
Кроме того, обратите внимание, что каждый угол находится напротив противоположной стороны (угол A противоположен стороне a, угол B противоположен стороне b, а угол C противоположен стороне C).
а 2 = B 2 + C 2 -2BCCOSA
B 2 = A 2 + C 2 -2ACCOSB
C 2 = A 2 + B + + 2 + + + + + + + + + + + + + + + + + 2 . 2abCosC
2abCosC
Чтобы найти Углов , мы также можем вывести и использовать следующие формулы, основанные на законе косинусов, приведенном выше:
Пример #1: SAS Найдите значение отсутствующей стороны.Мы можем использовать закон косинусов, чтобы найти недостающие стороны, когда нам дан косой треугольник, у которого есть сторона, угол и сторона ( SAS ) информация.
Шаг 1: Во-первых, давайте определим, какой тип информации предоставляет нам наш треугольник. Обратите внимание, что нам даны сторона, угол и сторона для SAS . Поскольку наш треугольник содержит SAS, мы знаем, что можем применить правило косинуса, чтобы найти значение неизвестной стороны c.
SAS
Шаг 2: Далее, давайте напишем нашу формулу закона косинусов, чтобы найти значение длины c, и подставим полученную информацию для решения c. В этом случае мы можем подключить сторону a=10, сторону b=8, а противоположную сторону c имеем угол c=40º.
Не забудьте взять квадратный корень из обеих частей уравнения, чтобы получить решение для неизвестной стороны c!
Пример #2: SSS Найдите значение недостающего угла .Когда мы хотим найти значение отсутствующего угла и получаем SSS информацию о треугольнике, мы можем либо использовать исходную формулу закона косинусов и использовать наши знания алгебры и тригонометрии для нахождения неизвестного угла, либо , мы также можем использовать другую версию правила косинусов, показанную ниже. Любой метод работает и даст вам правильный ответ, выбор за вами!
Шаг 1: Во-первых, давайте определим, какой тип информации предоставляет нам наш треугольник. Обратите внимание, что нам дана сторона, сторона и еще одна сторона для SSS . Поскольку наш треугольник содержит SSS, мы знаем, что можем применить правило косинуса, чтобы найти значение недостающего угла C.
SSS
Шаг 2: Далее, давайте напишем нашу формулу закона косинусов, а затем подставим полученную информацию. . В этом примере я буду использовать исходную формулу, а затем использовать алгебру и тригонометрию, чтобы найти правильный ответ, но вы можете применить одну из приведенных выше формул угла и посмотреть, получите ли вы тот же ответ!
. В этом примере я буду использовать исходную формулу, а затем использовать алгебру и тригонометрию, чтобы найти правильный ответ, но вы можете применить одну из приведенных выше формул угла и посмотреть, получите ли вы тот же ответ!
Поскольку мы хотим найти значение угла C, мы будем использовать формулу, которая установлена равной C 2 :
Думаете, вы готовы к большему!? Попробуйте самостоятельно ответить на следующие практические вопросы по правилу косинусов, чтобы по-настоящему освоить эту формулу! Затем сравните свои ответы с приведенными ниже решениями.
Практические вопросы:1) Найдите значение недостающей стороны c с точностью до сотых.
2) Найдите значение пропущенной стороны a с точностью до сотых по формуле косинуса.
3) Найдите угловую меру неизвестного угла A с точностью до градуса по теореме косинусов.
4) Найдите значение недостающего угла B с точностью до сотых по теореме косинусов.
Решение:
Остались вопросы по закону косинусов? Хотели бы вы увидеть, как правило косинусов может быть получено из теоремы Пифагора? Не стесняйтесь комментировать любые вопросы! Если вы хотите проверить ответы на домашнюю работу, вы также можете проверить калькулятор закона косинусов здесь! А если вы ищете дополнительную информацию о тригонометрии, ознакомьтесь с соответствующими статьями ниже. Удачных вычислений! 🙂
Facebook ~ Twitter ~ Tiktok ~ YouTube
Связанные тригонометрические посты:
.
Преобразование триггерных функций
Факторинг тригонометрических функций
Триггерные тождества
Автор Math SuxОпубликовано Категории Без категорийОставить комментарий к Закону косинусов Приветствую друзей-математиков и добро пожаловать в MathSux! В сегодняшней статье мы рассмотрим закон синусов! Это отличная формула для нахождения информации об отсутствующем угле и стороне треугольника, который НЕ является прямоугольным треугольником , то есть только если нам дано ASA (Угол, Сторона, Угол) или AAS (Угол, Угол, сторона) информация об указанном треугольнике.
Существует также нечто, называемое «неоднозначным случаем», когда у нас есть SSA (Side, Side, Angle) информация о треугольнике, и это так же загадочно, как и звучит. Мы можем использовать закон синуса в случае SSA, чтобы найти информацию об отсутствующем угле и стороне треугольника, но в этом случае может быть 0 треугольников, 1 треугольник или даже 2 треугольника!
Звучит непонятно? Не бойтесь, потому что в этом посте мы расскажем обо всем, включая практические вопросы, которые можно найти повсюду и в конце этой статьи. Удачных расчетов!
Закон синусов:
Закон синусов говорит нам, что в любом треугольнике (включая непрямоугольные треугольники!), отношение греха угла к значению его соответствующей стороны одинаково для всех трех сторон треугольника. треугольник. Посмотрите на приведенную ниже формулу:
Пример №1: AAS Найдите значение недостающей стороны Шаг 1: Во-первых, давайте определим, какой тип информации предоставляет нам наш треугольник. Обратите внимание, что нам даны угол A, угол B и сторона b для ААС . Поскольку наш треугольник содержит AAS, мы знаем, что можем применить закон синусов, чтобы найти недостающую сторону.
Обратите внимание, что нам даны угол A, угол B и сторона b для ААС . Поскольку наш треугольник содержит AAS, мы знаем, что можем применить закон синусов, чтобы найти недостающую сторону.
Шаг 2: Далее, давайте напишем нашу формулу закона синусов, а затем подставим предоставленную информацию. Обратите внимание, что мы настроили нашу формулу, где каждая сторона (a и b) и синус ее противоположного угла (Sin A и Sin B) представляют знаменатель и числитель соответственно.
Шаг 3: Пришло время использовать некоторые из наших основных навыков алгебры и тригонометрии и найти неизвестную длину стороны a путем перекрестного умножения.
* Совет ! Помните, что когда вы вводите sin, sin -1 и все другие тригонометрические функции в свой калькулятор, убедитесь, что вы находитесь в режиме градусов !
Пример #2: ASA Найдите значение недостающей стороны Шаг 1: Во-первых, давайте определим, какой тип информации предоставляет нам наш треугольник. Обратите внимание, что нам дан угол A, сторона c и угол B для ASA . Поскольку наш треугольник содержит ASA, мы знаем, что можем применить закон синусов, чтобы найти недостающую сторону.
Обратите внимание, что нам дан угол A, сторона c и угол B для ASA . Поскольку наш треугольник содержит ASA, мы знаем, что можем применить закон синусов, чтобы найти недостающую сторону.
Шаг 2: Взглянув на углы нашего треугольника, обратите внимание, что сторона a находится между углами B и C. У нас есть угол B, но обратите внимание, что значение угла C отсутствует! Итак, сначала нам нужно найти угол C. Мы можем найти значение угла C, зная, что сумма внутренних углов треугольника всегда равна 180º.
Угол C : 180º – (40º +60º) = 80º
Шаг 3: Теперь, когда у нас есть недостающее значение угла, мы можем найти длину стороны a. Давайте напишем нашу формулу закона синусов, а затем подставим предоставленную информацию. Затем мы можем скрестить, умножить и использовать наши знания алгебры и тригонометрии, чтобы найти правильный ответ.
* Совет ! Помните, что когда вы вводите sin, sin -1 и все другие тригонометрические функции в свой калькулятор, убедитесь, что вы находитесь в режиме градусов !
Думаете, вы готовы самостоятельно освоить закон синусов для треугольников AAS и ASA? Попробуйте самостоятельно ответить на следующие практические вопросы, чтобы проверить свои знания закона синусов!
Практические вопросы: 1) Найдите значение отсутствующей стороны b с точностью до десятых.
2) Найдите значение пропущенной стороны с с точностью до десятых.
3) Найдите значение отсутствующей стороны b с точностью до десятых.
4) Найдите значение отсутствующей стороны с с точностью до десятых.
Решения:
Неоднозначный случай — SSA и закон синусовДо сих пор мы видели, как найти недостающую сторону, используя закон синуса, при заданных ASA или AAS треугольника. Но сейчас мы увидим особый сценарий, иначе известный как 9-й.0604 Неоднозначный случай, , где нам дано SSA (сторона, сторона, угол) треугольника, и мы должны использовать закон синусов, чтобы увидеть, есть ли потенциально 0, 1 или 2 треугольника, которые потенциально могут существовать.
Неоднозначный случай является «неоднозначным», потому что SSA содержит недостаточно информации для нахождения неизвестных углов и сторон , , поскольку может быть более одного возможного треугольника с разными величинами углов . Хотя информации недостаточно, SSA сообщает нам достаточно, чтобы вывести все потенциальные треугольники (0, 1 или 2), выяснив, какие потенциальные углы могут существовать, а могут и не существовать.
Хотя информации недостаточно, SSA сообщает нам достаточно, чтобы вывести все потенциальные треугольники (0, 1 или 2), выяснив, какие потенциальные углы могут существовать, а могут и не существовать.
Есть много правил и визуализаций, связанных с неоднозначным случаем, которые я не буду здесь затрагивать. Если вы хотите увидеть больше информации и визуализаций неоднозначного случая, сообщите мне об этом в комментариях. Давайте посмотрим, как это работает на следующем примере:
Пример неоднозначного случаяШаг 1: Сначала нарисуем треугольник и заполним предоставленную нам информацию, зная, что угол A равен 30º, сторона a равно 10, а сторона b имеет длину 15,
Шаг 2: Далее давайте определим, какой тип информации предоставляет нам наш треугольник. Обратите внимание, что нам даны сторона, сторона и угол для SSA . Поскольку наш треугольник содержит SSA, мы знаем, что можем применить закон синусов и что это будет неоднозначный случай, то есть может быть ноль, один или два потенциальных треугольника.
Шаг 3: Теперь мы можем начать, используя закон синуса, чтобы найти значение угла b. Мы хотим найти угол B, потому что у нас уже есть значение длины стороны b, противоположной нашему неизвестному углу B.
* Совет ! Помните, что когда вы вводите sin, sin -1 и все другие тригонометрические функции в свой калькулятор, убедитесь, что вы находитесь в режиме градусов !
Шаг 4: Но подождите! Мы нашли то, что кажется значением неизвестного угла B, но так как это неоднозначный случай SSA, мы не уверены на 100% в нашей величине угла из-за слишком большого количества неизвестных!
Почему угол b может иметь более одного значения?
Так как нам задан SSA нашего треугольника, остается слишком много неизвестных значений не только для угла B, но также для неизвестных значений угла C и длины AB. Это приводит к тому, что мы имеем более одного возможного значения угла для угла B.
Существует ли один треугольник? Да!
Мы можем видеть, что один треугольник существует, используя наш найденный угол, угол b=49º. Исходя из этого, мы можем сделать вывод, каким будет угол С, зная, что сумма внутренних углов треугольника составляет 180º.
Угол C = 180º – (49º+30º) = 101º
Существуют ли два треугольника? Да!
Поскольку наш угол B технически может иметь два значения, мы можем еще раз взглянуть на единичный круг и вспомнить, что sin положителен в квадранте 2 (sin должен быть положительным, поскольку мы имеем дело с законом синусов и треугольников). Зная это, мы можем использовать наш эталонный угол 180º – θ, чтобы найти потенциальное значение бонуса для угла b, подставив значение угла, которое мы нашли ранее для угла B = 49.º для θ.
Альтернативное значение угла B = 180º – θ = 180º – 49º = 131º
Исходя из этого, мы можем сделать вывод, каким будет угол c, зная, что сумма внутренних углов треугольника составляет 180º.
Альтернативное значение угла C = 180º – (30º + 131º) = 19º
Примечание! В этом случае есть два треугольника, но обратите внимание, что это не всегда так, и способ узнать это — убедиться, что все углы вашего второго треугольника в сумме составляют 180º и ничего больше!
Думаете, вы готовы попробовать неоднозначный случай и правило синусов? Попробуйте самостоятельно ответить на следующие практические вопросы!
Практические вопросы:
Сколько треугольников можно построить с заданными размерами?
Решения:
- 2 треугольника
- 1 треугольника
- 2 треугольника
- 1 треугольника
Остались вопросы по закону синуса? Без проблем! Не стесняйтесь оставлять комментарии с любыми вопросами или смотреть видео выше. Удачных расчетов! Если вы хотите проверить ответы на домашнюю работу, посмотрите калькулятор закона синусов здесь! 🙂
Facebook ~ Twitter ~ Tiktok ~ YouTube
Блок Круг
Основные правые треугольные тригонометрические соотношения (SOH CAH TOA)
4545 90 СПЕЦИАЛЬНЫЕ ТРИНГЛИ
30 60 90 ТРИНГИ
Графические функции
.
Факторинг триггерных функций
Закон косинусов
Триггерные тождества
Автор Math SuxОпубликовано Рубрики Без категорий3 Комментарии к записи Закон синусовТак много книг, так мало времени! У меня возникла опасная идея собрать все лучшие книги математической вселенной. История математики и эволюция этого глобального предмета преодолевают языковые барьеры во времени и во всем мире!
Прежде чем сбрасывать со счетов математику как сухой предмет, лишенный чего-либо интересного, помните, что за каждым математическим открытием стоят люди и истории.
Помните, что история математики включает в себя все, что вы можете себе представить, начиная с истоков математики и развития числа ноль и заканчивая более современными истоками STEM и компьютеров!
Применения математики и логики также могут быть применены ко многим различным предметам (наука, техника, технология, химия, физика, искусство и т. д.), что математическая история также может быть найдена в историях этих предметов.
д.), что математическая история также может быть найдена в историях этих предметов.
История математики — это больше, чем просто сама математика, поскольку она включает в себя историю людей, культуры и мотивации того, почему мы, люди, нуждались в математике в первую очередь!
Приведенный ниже список книг по истории математики перенесет нас в приключения от древних цивилизаций до более современных историй и фильмов, таких как «Скрытые фигуры».
Лучшие книги по математике разбиты на три основные категории:
1) Лучшие книги по истории математики — узнайте в хронологическом порядке математические концепции и философию, как и откуда они появились
2) Биографии — узнайте подробно о людях, стоящих за ними предмет математики
2) Лучшие книги по истории математики для детей. Этот сборник книг, предназначенных для всех, но в основном написанный для детей, познакомит вас с математикой как с легкой, интересной и увлекательной игрой!
Книги по истории математики
Краткая история:
Первый раздел предназначен для всех, кто хочет углубиться в историю математики на академическом уровне. Отлично подходит для любителей математики, которые хотят знать историю и историю математики, этот раздел отлично подходит для справки в качестве учителя, профессора или просто отлично подходит для всех, кто хочет узнать больше о математике и людях, стоящих за ней.
Отлично подходит для любителей математики, которые хотят знать историю и историю математики, этот раздел отлично подходит для справки в качестве учителя, профессора или просто отлично подходит для всех, кто хочет узнать больше о математике и людях, стоящих за ней.
1) История математики Карла Бойера и Уты С. Мерцбах. Исследуйте историю математики через древние цивилизации по всему миру и свяжите их с современными теоремами, с которыми мы все лучше знакомы. Эта книга покажет вам истоки математики в классе, которую мы все делаем, и забудет, почему мы это делаем в первую очередь! Хотя, честное предупреждение, это толстая книга, и ее можно читать как учебник, но это отличная информация и отличный источник для справки или если вы хотите прочитать что-то более интенсивное!
2) Неизвестное количество: реальная и воображаемая история алгебры Джона Дербишира. Откройте для себя истории и истории, лежащие в основе предмета алгебры, охватывающие место и время! Посмотрите истоки и развитие математической мысли от прошлого до наших дней. В этой книге по математике вы познакомитесь со многими математиками, узнаете об их вкладе в предмет, а также их истории. Если вы когда-нибудь хотели ответить на такие вопросы, как, почему мы изучаем это в первую очередь? а откуда взялись квадратные уравнения, это вам учебник по математике!
В этой книге по математике вы познакомитесь со многими математиками, узнаете об их вкладе в предмет, а также их истории. Если вы когда-нибудь хотели ответить на такие вопросы, как, почему мы изучаем это в первую очередь? а откуда взялись квадратные уравнения, это вам учебник по математике!
3) Мужчины математики Эрик Темпл Белл. Это математическая классическая (но, возможно, устаревшая) книга по истории математики. Я только говорю, что она может быть датирована, потому что она была написана в 1937 году. Хотя она относится к 30-м годам, мы все должны признать, что древняя история математики до более современной исчисления девятнадцатого века с Исааком Ньютоном не изменилась, и именно поэтому она еще в этом списке. Просто будьте готовы мало слышать о развитии технологий, но будьте готовы узнать о достижениях в математике от нескольких известных математиков на протяжении веков.
Биография:
Математика — предмет изобретенный. Изобретен людьми во все времена по всему миру. Узнайте подробно, кем были эти люди, их борьба, их открытия и, конечно же, их вклад в математику.
Узнайте подробно, кем были эти люди, их борьба, их открытия и, конечно же, их вклад в математику.
1) Скрытые фигуры: американская мечта и нерассказанная история чернокожих женщин-математиков, которые помогли выиграть космическую гонку Марго Ли Шеттерли. Фильм, который мы все знаем и любим, сначала был книгой! Всегда интересно читать книгу, если вы еще не видели никаких различий. А для тех из вас, кто не знает, о чем эта книга, скажу, что она основана на реальной истории и рассказывает о группе чернокожих женщин, работающих в НАСА в качестве математиков, известных как «человеческие компьютеры». Хотя в то время их вклад в НАСА был очень важен, в начале XIX века они столкнулись с дискриминацией на рабочем месте.60-е годы.
2) Человек из будущего: фантастическая жизнь Джона фон Неймана Ананьо Бхаттачарьи. Это биография о Джоне фон Неймане, вундеркинде математики, родившемся в Будапеште, Венгрия, который вырос, чтобы создать первый в истории цифровой компьютер и теоретизировал будущее существование нанотехнологий. Известный как умнее Альберта Эйнштейна, он также внес свой вклад в логику/множества, квантовую механику, теорию игр, ядерную стратегию, искусственный интеллект и многое другое! Эта книга знакомит нас с жизнью и идеями фон Неймана и представляет интерес для всех, кто хочет узнать больше об этом гениальном ученом начала XIX века.00-х.
Известный как умнее Альберта Эйнштейна, он также внес свой вклад в логику/множества, квантовую механику, теорию игр, ядерную стратегию, искусственный интеллект и многое другое! Эта книга знакомит нас с жизнью и идеями фон Неймана и представляет интерес для всех, кто хочет узнать больше об этом гениальном ученом начала XIX века.00-х.
3) Алан Тьюринг: Загадка Эндрю Ходжеса. Еще одна книга, которая в конечном итоге стала фильмом, который вы, возможно, знаете как «Игра в имитацию». Эта книга — история Алана Тьюринга, британского математика, который помог спасти союзников от нацистов во Второй мировой войне с помощью своей универсальной машины, основы современного компьютера, каким мы его знаем! Тьюринг создает свою машину и использует для взлома загадки, немецкого кода, чтобы раскрыть их секреты и в конечном итоге выиграть Вторую мировую войну. Интересно найти различия между книгой и фильмом, чтобы увидеть реальную и воображаемую историю, так как в книге гораздо больше математически насыщенного и технического материала по сравнению с историей фильма. Полезно прочитать тем, кто хочет узнать больше о Тьюринге и математике, лежащей в основе его машины!
Полезно прочитать тем, кто хочет узнать больше о Тьюринге и математике, лежащей в основе его машины!
4) Logicomix: Эпический поиск истины Апостолос Доксиадис и Христос Х. Пападимитриу, иллюстрации Алекос Пападатос и Энни Ди Донна. Это графический роман и биография о философе Бертране Расселе, который ищет логические основы математики и общается с другими математиками. Эта книга отправляет нас в путешествие во времени в Европу во время Первой мировой войны и показывает жизнь Рассела, включая его умственную и профессиональную борьбу. С красивыми иллюстрациями, это интересное чтение для всех, кто хочет узнать больше о Бертране Расселе.
История математики для детей
Список лучших книг по математике для детей отлично подходит для классных комнат, библиотек и кого мы шутим, взрослым тоже понравятся эти книги! Это отличный способ узнать больше о математике в удобной и понятной для детей форме. Многие из этих книг снабжены отличными иллюстрациями, которые идеально подходят для визуализации историй, а также для математических расчетов.
1) Краткая история математики: от подсчета пещерных людей до компьютеров (Краткие истории) Клайва Гиффорда, иллюстрации Майкла Янга. Эта книга предназначена для детей в возрасте 8-12 лет и изобилует иллюстрациями, которые красиво представляют математику визуально для лучшего понимания предмета. Идеально подходит для дома или в классе, так как делает историю математики увлекательной для детей в 3-7 классах. Будьте готовы весело провести время за чтением и погрузиться в древнюю историю математики, в том числе об изобретении нуля и теореме Пифагора, попутно получая забавные математические советы и хитрости!
2) Девушка с умом на математику: История Рэй Монатегю Джулия Финли Моска, иллюстрированная Дэниелом Рили. История о маленькой девочке, которая бросает вызов всем преградам, чтобы осуществить свою мечту стать инженером! Ее способности к математике и STEM удивительны, но ее решительность, бесстрашие и юмор лежат в основе этой истории математики! Это удивительная и вдохновляющая книга с техническими и биографическими материалами в конце. Я упоминал, что эта книга основана на реальной истории жизни Рэя Монтегю?! Монтегю была первой женщиной-менеджером программы кораблей в ВМС США. Отлично подходит для классной или библиотечной книги для обсуждения.
Я упоминал, что эта книга основана на реальной истории жизни Рэя Монтегю?! Монтегю была первой женщиной-менеджером программы кораблей в ВМС США. Отлично подходит для классной или библиотечной книги для обсуждения.
3) Какой смысл в математике? ДК. Написанная для детей от 4 до 7 классов, я искренне думаю, что эта книга могла бы выйти за рамки этого, поскольку она может понравиться детям младшего возраста и даже взрослым. Все возрасты должны быть в состоянии наслаждаться книгой, которая делает математику простой и легкой для понимания, используя иллюстрации. Узнайте, как возникают математические концепции, такие как последовательности, распознавание образов и тригонометрия, и узнайте, как эти темы влияют на нашу жизнь в наше время. Читая эту книгу, наслаждайтесь математическими головоломками, головоломками, играми, математическими фокусами и забавными фактами! Развивайте математическое мышление своих детей, своих учеников или, может быть, только себя!
Вы читали какие-либо из перечисленных книг? Ваше мнение? Есть ли книга по математике, которой, по вашему мнению, не хватает в списке? Позвольте мне знать в комментариях ниже!
Также не забудьте подписаться на нас в социальных сетях ниже. Спасибо, что заглянули и счастливых вычислений!
Спасибо, что заглянули и счастливых вычислений!
Facebook ~ Twitter ~ TikTok ~ Youtube
Автор Math SuxОпубликовано Рубрики Без рубрикиДобавить комментарий к записи Лучшие книги по истории математики Всем привет и добро пожаловать в MathSux! В сегодняшнем посте мы собираемся погрузиться в Trig Identities! Существует множество тригонометрических тождеств, но шесть триггерных функций, которые вам нужно знать для доказательства тригонометрического тождества, к счастью, большинство из них связаны с тригонометрическими функциями, с которыми вы, вероятно, уже знакомы! Тригонометрические доказательства включают в себя работу с тригонометрическими функциями, с которыми мы уже знакомы (sin θ, cos θ, tan θ), но их разбивку, инвертирование каждой тригонометрической функции и применение правил, которые всегда верны (иначе известные как тригонометрические тождества).
Поначалу доказательства могут показаться немного сложными, но после некоторой практики они станут казаться более нормальными! Ключ в том, чтобы всегда оставлять одну часть уравнения в покое, работая с другой частью уравнения и манипулируя ею, пока она не совпадет с другой.
Это отличная тема для более подробного ознакомления с триггерами без необходимости работать с какими-либо треугольниками. Если вы знакомы с приведенными ниже тождествами триггеров, вы должны чувствовать себя уверенно, отвечая на вопросы такого типа. Ниже вы также найдете шпаргалку по тригонометрическим тождествам и список еще большего количества тригонометрических тождеств, которые могут вам понадобиться! Кроме того, не забудьте посмотреть видео и попрактиковаться в вопросах ниже, чтобы освоить тригонометрические тождества. Удачных расчетов!
Триг-функции идентификационная шпаргалка:
Триг-идентичность-чат-лист-3download
. и любовь (sin θ, cos θ, tan θ). Когда мы возьмем инверсию sin θ, cos θ, tan θ, мы получим эти новые триггерные функции: csc θ=1/sin θ, sec θ=1/cos θ и cot θ=1/tan θ! Триггерные функции и их обратные функции должны выглядеть знакомыми, так что их запоминание не составит труда! Простой? Да! Это большой ключ к решению многих триггерных доказательств личности.
и любовь (sin θ, cos θ, tan θ). Когда мы возьмем инверсию sin θ, cos θ, tan θ, мы получим эти новые триггерные функции: csc θ=1/sin θ, sec θ=1/cos θ и cot θ=1/tan θ! Триггерные функции и их обратные функции должны выглядеть знакомыми, так что их запоминание не составит труда! Простой? Да! Это большой ключ к решению многих триггерных доказательств личности.Тождества тригонометрических отношений
: Тождества тригонометрических отношений отлично подходят для разложения tan θ и cot θ на tan θ=sin θ/cos θ и cot θ=cos θ/sin θ. Обратите внимание, что tan и cot взаимно обратны друг другу. Все, что нам нужно сделать, это запомнить следующее: и единичный круг. Главное уравнение, которое нужно знать для всех перечисленных пифагорейских тождеств, это sin 2 θ+cos 2 θ=1 . Знание этого уравнения позволяет нам получить еще 8 связанных пифагорейских функций тождества, которые в конечном итоге помогут нам при анализе тригонометрических функций в наших тригонометрических доказательствах тождества. Внизу спереди выделено жирным шрифтом наше основное пифагорейское тождество:
Внизу спереди выделено жирным шрифтом наше основное пифагорейское тождество:
Теперь, когда у нас есть все необходимое для доказательства истинности тригонометрических тождеств, давайте применим наши новые знания и посмотрим на пример ниже:
Пример:
Шаг 1: Во-первых, мы сосредоточимся только на левой части уравнения, пытаясь сделать ее равной правой части, оставив csc θ+cot θ без изменений.
Шаг 2: Обратите внимание, мы можем расширить левую часть уравнения, отделив sinθ в знаменателе под каждым членом числителя. Это основано на основных правилах сложения и вычитания дробей… пока ничего нового или связанного с триггерными функциями!
Шаг 3: Теперь, глядя на наши тригонометрические обратные тождества и соотношения, мы можем видеть, что 1/sin θ можно переписать как обратную тождество тригонометрических функций, csc θ, и что cos θ/sin θ можно переписать -записывается как тождество тригонометрических соотношений как кроватка θ. Давайте перепишем их и заполним ниже, чтобы получить правильный ответ и доказать истинность нашего уравнения тригонометрических функций:
Давайте перепишем их и заполним ниже, чтобы получить правильный ответ и доказать истинность нашего уравнения тригонометрических функций:
Готовы к большему количеству примеров, чтобы испытать себя!? Ознакомьтесь с практическими задачами ниже:
Практическими задачами:Докажите, что каждое из следующих утверждений верно, затем проверьте свой ответ, используя приведенное ниже доказательство подлинности каждой из триггерных функций.
Решения:
Ищете больше тригонометрических тождеств ? Проверьте это ниже для справки! Приведенные ниже тригонометрические тождества используются для конкретных вопросов отдельно от примеров доказательства, показанных ранее в этом посте. Но придет время, когда они понадобятся, так что держите их пока и дайте мне знать, если вы хотите увидеть несколько примеров!
Идентичности кофункций : Каждая из идентификаций кофункций ниже представляет каждую базовую триггерную функцию и соответствующий им дополнительный угол, что означает, что каждая из них добавляется к 90º (или в радианах π/2).
Сумма и
разницы идентичности:также также известны как идентификаторы, а также разница и разница.
Остались вопросы? Есть любимое тригонометрическое тождество? Не стесняйтесь писать по электронной почте или оставлять комментарии ниже с любыми вопросами, чтобы прояснить ситуацию! Удачных расчетов!
Кроме того, не забудьте подписаться на нас в социальных сетях, чтобы получать самые свежие и лучшие уроки MathSux, видео, вопросы и многое другое!
Facebook ~ Twitter ~ TikTok ~ Youtube
Единичный круг
Тригонометрические отношения основного прямоугольного треугольника (SOH CAH TOA)
4545 90 Особые треугольники
30 60 90 Особые треугольники
Графики тригонометрических функций
Преобразование тригонометрических функций
Факторизация тригонометрических функций
Закон косинусов
Закон синусов
Автор Math SuxОпубликовано Категории Без категорий4 Комментарии к Trig IdentitiesПриветствую и добро пожаловать в MathSux! В сегодняшней статье мы рассмотрим все, что вам нужно знать о кругах. Мы начнем с рассмотрения различных частей круга, включая центр круга, радиус, хорду, касательную и секущую. Затем мы разберем различные формулы круга, чтобы узнать, которые включают площадь, окружность, площадь сектора и несколько различных теорем о кругах, используемых для нахождения недостающих углов и дуг.
Ниже приведена шпаргалка, которая суммирует все в этом посте, но если вы продолжите читать, мы более подробно рассмотрим, как работают эти теоремы, с различными примерами и объяснениями. Так что продолжайте прокручивать, продолжайте читать, оставайтесь позитивными и удачных вычислений!
Шпаргалка по теореме о круге для бесплатного скачивания:
Шпаргалка по теоремам о круге-4 Скачать
Части круга:
Круг состоит из множества разных частей! Давайте подробнее рассмотрим каждую часть ниже со следующими определениями:
- Диаметр: Линия, которая делит круг пополам через его центр.

- Радиус : Линия, идущая от центральной точки к краю круга. (Иначе называется половиной длины диаметра).
- Центр: Все точки окружности равноудалены от этой точки.
- Хорда: Отрезок с концами на окружности, но не пересекающий ее центр.
- Касательная: Непрерывная линия, которая касается только внешней части окружности.
- Секущая: Линия, пересекающая окружность в двух точках.
Окружность окружности:
Окружность окружности измеряет длину окружности по всей окружности. Это похоже на то, что мы проходим по кругу и измеряем, как далеко мы пройдем по пути, пока не вернемся к тому, с чего начали.
Площадь круга:
Площадь круга позволяет нам найти «площадь» или общее значение, найденное в контуре круга.
Площадь сектора:
Мы уже знаем, как найти площадь круга, но как насчет площади сектора? Что вообще означает сектор? Сектор — это кусок круга, вроде как кусок пирога. Посмотрите пример здесь, чтобы получить более четкое представление.
Посмотрите пример здесь, чтобы получить более четкое представление.
Дуги, углы и меры окружности:
Дуга круга является частью окружности круга. Думайте о дуге как о контуре куска пирога, ням!
Что с градусами и дугой AB обозначения ? Есть ли разница?
Дуга измеряется в градусах значением ее центрального угла (называется мерой дуги). Дуга и измеряется по длине в таких единицах измерения, как дюймы или сантиметры. Давайте посмотрим на разницу между каждым ниже:
Мера : Мерой дуги является размер ее центрального угла в градусах. В приведенном ниже примере мы видим, что значение градуса дуги AB равно 90º (выделено зеленым)
Длина: Длина дуги — это длина окружности окружности, и ее можно измерять в таких единицах, как футы, дюймы, сантиметры и т. д. (выделено розовым цветом)
Существуют ли разные типы дуг?
Существует два основных типа дуг: большая дуга и малая дуга. Как вы можете догадаться, один больше, а другой меньше. Смотрим на Пример:
Как вы можете догадаться, один больше, а другой меньше. Смотрим на Пример:
Большая дуга: Дуга со значением измерения больше 180º (больше половины окружности). В приведенном ниже примере мы видим, что главная дуга может быть представлена дугой AB (выделена зеленым цветом).
Малая дуга: Дуга со значением измерения менее 180º (меньше половины окружности). В приведенном ниже примере мы видим, что малая дуга может быть представлена дугой AB (выделена розовым цветом).
Как рассчитать длину и меру дуг?
Определение длины дуги: Чтобы найти длину дуги, нам нужна только одна формула!
Определение меры дуги: Вычисление меры дуги зависит от наличия секущих, касательных, хорд и радиусов. На самом деле существует семь различных возможных ситуаций для нахождения меры дуги! Удивительно, я знаю, но давайте рассмотрим каждый тип по отдельности:
- Центральный угол (два радиуса): Если провести два радиуса из центра окружности, они образуют центральный угол .
 Центральный угол равен длине дуги. В приведенном ниже примере мы видим, что дуга AB имеет длину 90 º и имеет дуговую меру 90 º. Они равны!
Центральный угол равен длине дуги. В приведенном ниже примере мы видим, что дуга AB имеет длину 90 º и имеет дуговую меру 90 º. Они равны!
Чтобы узнать больше о центральных углах, ознакомьтесь с постом, посвященным практическим вопросам, и видео ниже:
2. I nscribed Угол: Когда две хорды соединяются, чтобы коснуться контура круга, они что-то создают. называется угол вписанный . Вписанный угол равен половине значения длины дуги.
Чтобы узнать больше о вписанных углах, ознакомьтесь с постом и практическими вопросами здесь, а также видео ниже!
youtube.com/embed/k6MCm9-BnaA?version=3&rel=1&showsearch=0&showinfo=1&iv_load_policy=1&fs=1&hl=en-US&autohide=2&wmode=transparent» allowfullscreen=»true» sandbox=»allow-scripts allow-same-origin allow-popups allow-presentation»>3. Пересекающиеся хорды: При пересечении двух хорд образуются четыре дуги и два набора вертикальных углов. Каждое множество вертикальных углов конгруэнтно. Чтобы найти значение одного вертикального угла, сложите длины двух дуг и разделите на 2.
4. Касательная и хорда: Когда касательная и хорда соединяются, они образуют угол, который касается контура окружности. Образующийся угол равен половине длины дуги.
5. Два касательных: Когда два касательных касаются внешнего края круга, образуется угол. Угол равен разности длин пересекаемых дуг, деленной на два.
6. Две секущие: Когда две секущие пересекаются вне круга, получается один угол и две длины пересекаемой дуги. Угол равен разности длин пересекаемых дуг, деленной на два.
Угол равен разности длин пересекаемых дуг, деленной на два.
Чтобы узнать больше о пересекающихся секущих, посмотрите видео ниже и ссылку здесь для практических вопросов!
7. Секущая и тангенс: Когда угол образован секущей и касательной, получается один угол и две длины пересекаемой дуги. Угол равен разности длин пересекаемых дуг, деленной на два.
Дополнительный обзор Secant & Tangent смотрите в видео ниже!
Теоремы о кругах:
Теорема 1: В окружности, когда угол образован касательной и радиусом, получается угол. Это происходит всегда и каждый раз!
Это происходит всегда и каждый раз!
Теорема 2: Вписанные в окружность углы, опирающиеся на одну дугу, равны. Эти типы перекрывающихся дуг также могут быть известны как «углы, опирающиеся на дугу». В приведенном ниже примере угол A и угол B являются углами, опирающимися на дугу CD.
Теорема 3 : Вписанный угол в полуокружность является прямым углом.
Теорема 4: Когда четырехугольник вписан в окружность, противоположные углы являются дополнительными (прибавьте к 180º). Обратите внимание, что ниже противоположные углы A и C являются дополнительными и составляют 180º.
*Забавный факт! Четырехугольник, вписанный в окружность, называется циклическим четырехугольником !
Теорема 5: В окружности конгруэнтные центральные углы имеют конгруэнтные дуги (или наоборот).
Теорема 6: В окружности конгруэнтные центральные углы имеют конгруэнтные хорды (или наоборот).
Вот и все, что нам нужно знать о кругах, ура! Хотя мы закончили с обзором того, что нам нужно знать, мы должны подготовиться к вопросам, которые применимы к нашему новому круговому знанию. Один Пример может выглядеть примерно так:
Данная окружность R имеет дугу BC=95º, две касательные AB и AC и два радиуса RB и RC, найдите следующие углы и дуги .
Прежде чем мы просто рассмотрим решение, обязательно попробуйте его самостоятельно! Вспомните все ответы на нахождение дуг и углов окружности 9.0622 R основаны на теоремах о окружности и семи различных способах нахождения углов, которые мы только что рассмотрели в этом посте. Так что возвращайтесь, если вам нужно, я знаю, что мне нужно!
А теперь о долгожданном Решение :
Пояснение:
Остались вопросы? Без проблем! Посмотрите видео выше или прокомментируйте ниже любые вопросы и следите за последними бесплатными уроками математики, видео и практическими вопросами! Удачных расчетов! 🙂
Facebook ~ Twitter ~ TikTok ~ Youtube
Совет! Кроме того, не забудьте проверить ссылки, найденные в этом посте, для каждого связанного урока по центральным углам, теоремам о вписанных углах, теореме о пересекающихся секущих и площади сектора, чтобы еще больше погрузиться в практические вопросы, видео и более!
Автор Math SuxОпубликовано Рубрики Без рубрикиДобавить комментарий к записи Теоремы кругаПриветствую вас, друзья-математики! Сегодня мы рассмотрим вопрос, который мне часто задают: «Как вы изучаете математику?» Как изучать математику, что за вопрос! На самом деле есть только один способ, который я когда-либо знал, — это практиковать вопросы снова и снова. Это основной совет, который я обычно даю, потому что это быстрый и простой ответ (и это правда), но, конечно же, это еще не все! Есть советы и рекомендации по отработке вопросов, чтобы освоить не только математику, но и любой предмет при подготовке к тесту. В этом посте нет ничего сдерживаемого, и я собираюсь раскрыть все свои секреты подготовки к экзаменам! Надеюсь, эта статья пригодится, когда наступит решающий момент, и надеюсь, что, может быть, просто возможно, это учебное пособие по учебе может сделать математику немного веселее (никогда не знаешь)! В любом случае, я надеюсь, что это поможет, когда вам это нужно больше всего, удачи и удачных вычислений!
Решение математических задач:
Математика является активным предметом обучения, и ключом к освоению любой математической темы является решение одних и тех же математических задач снова и снова.
Итак, чтобы сделать это, конечно, нам понадобятся практические вопросы. Но какие практические вопросы? Как узнать, на какие вопросы смотреть?
Здесь мы собираемся собрать и найти все возможные вопросы по теме, с которых можно начать:
1) Математика Заметки для занятий – Повторите и проверьте себя, отвечая на вопросы из урока математики.
2) Проблемы с домашним заданием – Повторите домашнее задание, обратите внимание на те сложные вопросы, которые вы не смогли решить с первого раза. Посмотрите, как вы справляетесь с ними сейчас, проверяя, получили ли вы правильный ответ.
3) Вопросы викторины – Вы уже проходили викторину перед большим тестом? Как ты это сделал? Просмотрите и узнайте, если вы получили неправильный ответ. Просмотрите и узнайте, получили ли вы правильный ответ!
Теперь, когда у нас есть все вопросы, давайте посмотрим, что нам делать дальше!
Памятка:
Что я забыл? Нужно ли запоминать какие-то формулы и что они означают? Что снова представляет это обозначение? Занесите все это в шпаргалку!
Некоторые учителя математики даже разрешают вам принести шпаргалку, если да, то вам повезло! Если нет, то это все еще отличный инструмент, который можно использовать для самостоятельного изучения.
Вот некоторые вещи, которые вы, возможно, захотите включить в свой шпаргалку:
1) Математика Формулы – Мы никогда не хотим произносить слово «запоминать» на уроках математики, но когда в вашем тесте по математике будут формулы, мы знаем, что это именно то, что нам нужно сделать!
2) Математический словарь – Какие новые слова вы не можете вспомнить? Поместите их сюда с определением для каждого нового слова.
3) Практические вопросы — Иногда мы можем забыть, как задать определенный тип вопроса, если это произойдет, поместите здесь полностью решенный вопрос, чтобы мы могли вспомнить, как это делается.
Не хотите писать шпаргалку? Взгляните на эти бесплатные шпаргалки по алгебре, геометрии, алгебре 2/триггерной системе и производным!
Теперь, когда мы сделали все, что могли, давайте посмотрим, что у меня остались вопросы по математике. Что мне теперь делать?
Учись с друзьями!
Организация учебной группы с друзьями — отличный способ заполнить пробелы в математике. То, что знают ваши друзья, может быть именно тем, чего вам не хватает, когда дело доходит до изучения математики, и наоборот.
То, что знают ваши друзья, может быть именно тем, чего вам не хватает, когда дело доходит до изучения математики, и наоборот.
Учебные группы также отлично подходят для объяснения тем, которые вы уже знаете, так как это еще больше улучшит ваше понимание! Так что, даже если вы знаете больше, чем ваши друзья на уроке математики, вы можете учить и становиться еще сильнее в этой теме и стать супергероем математической темы!
Изучать математику в компании друзей может быть весело, так как вы можете быть более расслабленными, чем в классе, и более открыты для вопросов.
Слушайте музыку:
Вы учитесь один? Отличный способ самостоятельного изучения математических понятий во время решения практических вопросов — включить тихую расслабляющую музыку на заднем плане. Это может помочь с концентрацией и оставить некоторое свободное пространство для решения проблем и математического мышления. Это также может помочь нам расслабиться и избавиться от ненужной болтовни в голове.
Будьте позитивны!
Позитивное отношение к любой математической задаче так важно для изучения математики. Убедитесь, что вы можете это сделать, вы способны понимать концепции и способны освоить курс математики. Если у вас есть какие-либо вопросы, вы всегда можете обратиться к доступным вам ресурсам.
Ресурсы по математике:
1) Математический класс — Напишите или поговорите с учителем математики или репетитором по любым конкретным вопросам перед тестом.
2) Одноклассники/Друзья – Как упоминалось ранее, используйте свой круг друзей, чтобы заполнить любые пробелы в понимании!
3) MathSux / YouTube и другие онлайн-ресурсы по математике — бесплатно и быстро!
Математические тесты могут быть сложными, но готовиться к ним необязательно! Как только вы войдете в поток обучения, процесс изучения математики станет намного проще. Есть ли у вас другие советы по обучению или метод изучения математики, отличный от перечисленных здесь? Что работает для вас? Дайте мне знать в комментариях и счастливых вычислений!
Facebook ~ Twitter ~ TikTok ~ Youtube
youtube.com/embed/Ac-POCNHG88?version=3&rel=1&showsearch=0&showinfo=1&iv_load_policy=1&fs=1&hl=en-US&autohide=2&wmode=transparent» allowfullscreen=»true» sandbox=»allow-scripts allow-same-origin allow-popups allow-presentation»> Автор Math SuxОпубликовано Рубрики Без рубрикиДобавить комментарий к записи Как изучать математику Привет всем и добро пожаловать на еще одну неделю MathSux! В сегодняшней статье мы рассмотрим все различные типы преобразования формы в математике, с которыми мы столкнемся в геометрии! В частности, мы увидим, как переводить, отражать, поворачивать или расширять фигуру, линию или точку. Существуют также определенные правила координат, которые применяются к каждому типу преобразования, но не беспокойтесь, потому что каждое правило также может быть легко получено (за исключением этих хитрых вращений, следите за этими парнями!). Если вам нравится искусство или рисование, это отличная тема, где нам придется использовать наш художественный взгляд и наше воображение, чтобы найти правильный ответ. Мы также рассмотрим, где вы могли бы использовать и увидеть преобразования в вашей повседневной жизни! Надеюсь, вы готовы, посмотрите ниже и счастливых вычислений! 🙂
Если вам нравится искусство или рисование, это отличная тема, где нам придется использовать наш художественный взгляд и наше воображение, чтобы найти правильный ответ. Мы также рассмотрим, где вы могли бы использовать и увидеть преобразования в вашей повседневной жизни! Надеюсь, вы готовы, посмотрите ниже и счастливых вычислений! 🙂
Что такое преобразование в математике?
Математические Преобразования включают широкий спектр «вещей». И под «вещами» я подразумеваю 90 622 отражения, перемещения, повороты 90 623 и 90 622 расширения 90 623; Каждое падение под зонтиком известно как «трансформация». В одиночку любой из них нетрудно освоить, но смешайте их вместе и добавьте тест и викторину или два, и это может запутать. Даже слова «трансформация» и «перевод» могут сбить нас с толку, поскольку звучат очень похоже. Но это две разные вещи. перевод это тип преобразования . Давайте разберем каждое из наших новых слов, прежде чем наши мозги взорвутся:
Преобразования: Когда мы берем форму или линию и переворачиваем ее , поворачиваем ее, сдвигаем, увеличиваем или уменьшаем . По сути, когда у нас есть форма или линия, и мы немного возимся с ней, это трансформация. Рассматриваемая форма или линия обычно изображается на координатной плоскости. Преобразования включают:
По сути, когда у нас есть форма или линия, и мы немного возимся с ней, это трансформация. Рассматриваемая форма или линия обычно изображается на координатной плоскости. Преобразования включают:
(1) Переводы (Slide IT)
(2) Отражения (Flip It)
(3) Вращается (вращение IT)
(4) Dill Dilles 9062 или Make Filar 906. Dilles 9066. )
Преобразование формы:
1) Переводы — Когда мы берем форму, линию или точку и перемещаем их вверх, вниз, влево или вправо.
2) Отражения – Когда точка, отрезок линии или фигура отражается на линии, создается зеркальное отражение.
3) Повороты – Когда мы берем точку, линию или форму и поворачиваем их по часовой стрелке или против часовой стрелки, обычно на 90º, 180º, 270º, -90º, -180º или -270º.
4) Расширение – Когда мы берем точку, линию или фигуру и делаем ее больше или меньше, в зависимости от Масштабного коэффициента .
Жесткие преобразования:
Прежде чем мы углубимся в наш первый тип преобразования, давайте сначала определим и исследуем, что это значит, когда преобразование поддерживает Жесткое движение . Когда линия или форма трансформируются, а длина, площадь и углы линии и/или формы не затрагиваются преобразованием, считается, что они имеют жесткое движение . Жесткие преобразования включают перемещения , отражения и повороты (но не расширения) .
Теперь, когда мы знаем, какие типы преобразований поддерживают жесткое движение, давайте рассмотрим каждый тип преобразования более подробно!
Переводов:
Переводы: Когда мы берем форму, линию или точку и перемещаем их вверх, вниз, влево или вправо. Помните, что этот тип преобразования является жестким преобразованием, то есть линия или фигура переводятся, длина, площадь и углы линии и/или формы не затрагиваются преобразованием.
В приведенном выше примере перевода мы начинаем с квадрата ABCD и переводим каждую координату исходного квадрата ABCD на 6 единиц вправо и на 2 единицы вверх, чтобы получить наш новый преобразованный квадрат изображения A | Б | С | Д | .
Формула перевода:P(x,y) -> P| (x+h, y+k)
где….
h=Горизонтальный сдвиг (прибавить (+) при перемещении вправо, вычесть (-) при перемещении влево)
k= Вертикальный сдвиг (прибавить (+) при перемещении вверх, вычесть (-) при перемещении вниз)
Горизонтальное перемещение :
Когда мы переводим точку, линию или фигуру влево или вправо , он подвергается горизонтальному смещению по оси x. Любой тип движения влево или вправо на координатной плоскости является горизонтальным переносом.
Как это влияет на координату x? Если фигура смещается вправо, то мы добавляем единицы к координате x, а если фигура смещается влево, мы вычитаем единицы из x-координаты.
Вертикальный перевод:
Когда мы переводим точку, линию или фигуру вверх или вниз , он подвергается вертикальному перемещению вдоль оси Y. Любой тип движения вверх и вниз на координатной плоскости является вертикальным переносом.
Как это влияет на координату y? Если фигура смещается вверх, то мы прибавляем единицы к координате y, а если фигура смещается вниз, то вычитаем из y-координаты.
Несмотря на то, что сдвиг по горизонтали или по вертикали может произойти, когда мы перемещаем форму, линию или точку, многие переводы имеют комбинацию из двух!
Как меняются координаты после переноса? Правда в том, что для переводов не существует единого уникального правила, но числа всегда будут добавляться или вычитаться из значений координат x и/или y. Если что-то переводится вправо, то мы добавляем единицы к x-значению. С другой стороны, если что-то переводится влево, мы вычитаем единицы из значения x. То же самое можно сказать и о перемещении фигуры вверх: затем мы добавляем единицы к значению y, а если фигура перемещается вниз, мы вычитаем единицы из значения y. Это дает нам следующую формулу перевода ниже:
То же самое можно сказать и о перемещении фигуры вверх: затем мы добавляем единицы к значению y, а если фигура перемещается вниз, мы вычитаем единицы из значения y. Это дает нам следующую формулу перевода ниже:
Если мы посмотрим на наш пример, когда мы переводим исходный квадрат ABCD в квадрат A|B|C|D| в итоге мы переводим каждую координату исходного квадрата ABCD на 6 единиц вправо и на 2 единицы вверх. На самом деле, когда мы переводим, мы добавляем 6 единиц к каждой координате x, а также добавляем 2 единицы к каждой координате y исходного квадрата фигуры ABCD. Посмотрите его ниже:
Чтобы узнать больше о переводах, посмотрите видео ниже и отработайте вопросы здесь.
Отражения:
Отражения на координатной плоскости — это именно то, что вы думаете! Когда точка, отрезок линии или фигура отражается на линии, создается зеркальное отражение. Представьте себе крылья бабочки, сложенную пополам страницу или любое другое место, где существует идеальная симметрия. Посмотрите, как мы решаем приведенный ниже пример отражения, шаг за шагом!
Представьте себе крылья бабочки, сложенную пополам страницу или любое другое место, где существует идеальная симметрия. Посмотрите, как мы решаем приведенный ниже пример отражения, шаг за шагом!
Шаг 1: Сначала нарисуем линию x=-2.
Шаг 2: Найдите расстояние от каждой точки до линии x=-2 и отразите его на другой стороне, измерив такое же расстояние или зеркальное отображение каждой точки. Во-первых, давайте посмотрим на точку C, заметим, что она находится на расстоянии 1 единицы от линии x=-2, чтобы отразить ее, мы отсчитаем 1 единицу (то же самое расстояние) слева от линии x=-2 и пометим нашу новую точка, С | .
Шаг 3: Далее мы отражаем точку А почти таким же образом! Обратите внимание, что точка A находится в 2 единицах слева от линии x=-2, затем мы отмеряем 2 единицы вправо от нашей линии и отмечаем нашу новую точку, A | .
Шаг 4: Наконец, мы отражаем точку B. На этот раз точка B находится на расстоянии 1 единицы справа от линии x=-2, затем мы отмеряем 1 единицу до противоположной стороны нашей линии и отмечаем новая точка, B | .
На этот раз точка B находится на расстоянии 1 единицы справа от линии x=-2, затем мы отмеряем 1 единицу до противоположной стороны нашей линии и отмечаем новая точка, B | .
Шаг 5: Наконец, теперь мы можем соединить все наши новые точки для нашего полностью отраженного треугольника A | Б | С | .
Если вы хотите узнать больше об отражениях, посмотрите приведенные ниже видеоролики и практические вопросы прямо здесь.
Повороты:
Повороты — это тип преобразования в геометрии, когда мы берем точку, линию или форму и поворачиваем их по часовой стрелке или против часовой стрелки, обычно на 90º, 180º, 270º, -90º, -180º или -270º.
Положительное вращение на градуса выполняется против часовой стрелки , а отрицательное вращение на градуса выполняется по часовой стрелке . Давайте посмотрим на разницу в типах вращения ниже и заметим разные направления каждого вращения:
Как мы поворачиваем фигуру?Есть несколько способов сделать это, взгляните на наши варианты ниже:
- Мы можем визуализировать вращение или использовать кальку, чтобы наметить его и повернуть вручную.
- С помощью транспортира измерьте необходимый угол поворота.
- Знайте правила ротации, указанные ниже. Да, это запоминание, но если вам нужно больше вариантов, проверьте номера 1 и 2 выше!
Чтобы вывести наши правила вращения, мы можем взглянуть на наш первый пример, когда мы повернули треугольник ABC на 90º против часовой стрелки вокруг начала координат. Если мы сравним нашу координатную точку для треугольника ABC до и после поворота, мы увидим закономерность, проверьте ее ниже:
Если мы сравним нашу координатную точку для треугольника ABC до и после поворота, мы увидим закономерность, проверьте ее ниже:
Приведенные выше правила вращения применяются только к тем, которые вращаются вокруг начала координат (точки (0,0)) на координатной плоскости. Но точки, линии и фигуры можно вращать в любой точке (а не только в начале координат)! Когда это происходит, нам нужно использовать наш транспортир и/или знание вращений, чтобы найти ответ. Давайте посмотрим на пример ниже:
Шаг 1: Во-первых, давайте посмотрим на нашу точку вращения, обратите внимание, что это не начало координат, вокруг которого мы вращаемся, а точка k! Чтобы понять, где находится наш треугольник относительно точки k, давайте проведем оси x и y, начиная с этой точки:
Шаг 2: Теперь давайте посмотрим на точку координат нашего треугольника, используя наши новые оси, которые начинаются в точке k.
Шаг 2: Далее, давайте посмотрим на наше правило поворота координаты на -90º и применим его к координатам вновь повернутых треугольников: треугольник .
Шаг 4: Наконец, давайте соединим все наши новые координаты, чтобы сформировать наше решение:
Дополнительные примеры и практические вопросы см. в видео ниже и по ссылке здесь.
Расширения:
Расширения — это тип преобразования в геометрии, при котором мы берем точку, линию или форму и делаем их больше или меньше в зависимости от масштабного коэффициента .
Мы всегда умножаем значение коэффициента масштабирования на длину исходной фигуры или координатную точку (точки), чтобы получить увеличенное изображение фигуры. Масштабный коэффициент больше единицы делает фигуру больше, а масштабный коэффициент меньше единицы делает фигуру меньше. Давайте посмотрим, как различные значения коэффициентов масштабирования влияют на расширение ниже:
Давайте посмотрим, как различные значения коэффициентов масштабирования влияют на расширение ниже:
Масштабный коэффициент >1 Больше
Масштабный коэффициент <1 Меньше
Масштабный коэффициент=2На приведенной ниже диаграмме исходный треугольник ABC расширяется с коэффициентом масштабирования, равным 2. Обратите внимание, что треугольник становится больше , и что каждая длина исходного треугольника умножается на 2.
Коэффициент масштабирования=1/2Здесь исходный треугольник ABC расширяется с коэффициентом масштабирования 1/2. Обратите внимание, что треугольник получает меньше , и что каждая длина исходного треугольника умножается на 1/2 (или делится на 2).
Свойства расширения:
Есть несколько вещей, которые происходят, когда форма и/или линия подвергаются расширению. Давайте рассмотрим каждое свойство расширения ниже:
1. Значения углов остаются прежними.
Значения углов остаются прежними.
2. Параллельные и перпендикулярные линии остаются прежними.
3. Длина, площадь и периметр нет остаются прежними.
*Внимание Расширение не является жесткой трансформацией!
Теперь, когда мы немного познакомились с тем, как работают расширения, давайте посмотрим на несколько примеров на координатной плоскости:
Шаг 1: Сначала давайте посмотрим на две соответствующие стороны нашего треугольника и измерим их длину.
Шаг 2: Теперь давайте посмотрим на разницу между двумя длинами и спросим себя, как мы перешли от 3 единиц к 1 единице?
Помните, мы всегда умножаем коэффициент масштабирования на исходные значения длины, чтобы увеличить изображение. Следовательно, мы знаем, что должны были умножить первоначальную длину на 1/3, чтобы получить новую длину 1. расширения, обратите внимание, что это не в начале! В этом вопросе мы распространяемся о точке м ! Чтобы понять, где находится наш треугольник по отношению к точке м , давайте нарисуем новые оси X и Y, исходящие из этой точки, синим цветом ниже.
Шаг 2: Теперь давайте посмотрим на координатную точку K по отношению к нашим новым осям.
Шаг 3: Давайте используем масштабный коэффициент 2 и правило преобразования для расширения, чтобы найти значение его новой точки координат. Помните, чтобы выполнить расширение, мы 90 622 умножаем 90 623 каждой координатной точки на масштабный коэффициент.
Шаг 4: Наконец, давайте построим увеличенное изображение координатной точки K. Помните, что мы изображаем точку (6,4) относительно осей x и y, которые исходят из точки 9.0622 м .
Если вы хотите узнать больше о дилатации, посмотрите видео ниже и попрактикуйтесь в вопросах прямо здесь!
Трансформации в реальном мире?
Если вы думаете, что никогда не увидите реального использования трансформаций, подумайте еще раз! Играя в милую игру Тетрис, мы вращаем фигуры, чтобы получить четкие линии, трансформируя каждую фигуру по ходу дела.
Помимо игры в тетрис, Преобразования в математике можно найти внутри самой игры, внутри ее кода. Разработчики игр должны быть знакомы с правилами координат, чтобы перевернуть и повернуть фигуру в своем коде для Tetris или любой другой игры!
Вы также можете подумать о реальных объектах для преобразования (в отличие от только цифровых, упомянутых выше). Это может быть что угодно: от парковки автомобиля до строительства дома и посадки самолета. Можете ли вы подумать о трансформациях, которые вы используете в своей повседневной жизни? Дайте нам знать об этом в комментариях!
Остались вопросы о математических преобразованиях? Без проблем! Не стесняйтесь комментировать любые вопросы ниже. Хотите больше математических преобразований? Не забудьте просмотреть видеоролики и практические вопросы для каждой из ссылок в этой статье. Спасибо, что заглянули и удачных расчетов! 🙂
Facebook ~ Twitter ~ TikTok ~ Youtube
Автор Math SuxОпубликовано Рубрики Без рубрикиДобавить комментарий к записи Преобразования фигур в математикеПриветствую вас, друзья-математики! В сегодняшнем посте мы рассмотрим несколько геометрических построений, которые вам нужно знать, чтобы сдать геометрию! Мы рассмотрим каждый вид геометрического построения шаг за шагом с помощью циркуля и линейки. Геометрические построения могут доставить массу удовольствия и стать важной частью математики, о которой вы, возможно, никогда не знали! Надеюсь, вы готовы развить свои математические и художественные навыки, так что держите под рукой компас и линейку, пока мы занимаемся следующими геометрическими построениями.
Геометрические конструкции:
Бисек. Сегмент линии
Перпендикулярная линия через точку
Угол бисектор
Стадии конструкции угла 45 градусов
. Квадрат, вписанный в окружность
Разделение отрезка пополам (с помощью циркуля и линейки):
Биссектриса действительно делит линию пополам в ее середине, создавая две равные половины. Это создаст четыре 9углы 0º вокруг линии.
Это создаст четыре 9углы 0º вокруг линии.
Как разделить отрезок пополам шаг за шагом:
Шаг 1: Сначала мы отмерим чуть больше половины линии AB с помощью циркуля.
Шаг 2: Далее мы поместим компас в точку А и качнем его выше и ниже линии АВ, чтобы получился полукруг.
Шаг 3: Сохраняя то же расстояние по компасу, мы затем поместим точку компаса в точку B и повторим тот же шаг, что и в точке A, нарисовав полукруг.
Шаг 4: Обратите внимание на пересечения выше и ниже линии AB!? Теперь мы хотим соединить эти две точки, нарисовав линию с помощью линейки или линейки.
Шаг 5: Ура! Теперь у нас есть серединный перпендикуляр! Это разрезает линию AB точно посередине, разделяя линию AB на две равные половины. Он также создает четыре угла 90º.
Посмотрите полное видео с объяснением ниже и оригинальный пост здесь.
youtube.com/embed/GY9Iuy7Brwo?version=3&rel=1&showsearch=0&showinfo=1&iv_load_policy=1&fs=1&hl=en-US&autohide=2&wmode=transparent» allowfullscreen=»true» sandbox=»allow-scripts allow-same-origin allow-popups allow-presentation»>Перпендикулярная линия через точку Построение:
A Перпендикулярная линия, проходящая через точку очень похожа на биссектрису, но на этот раз вместо того, чтобы «разрезать» отрезок прямо посередине, мы создаем перпендикулярную линию через любую точку на нашем отрезке. Перпендикулярная линия в этом случае также создаст четыре угла 90º. Посмотрите, как это работает ниже:
Шаг 1: Сначала мы собираемся собрать материалы, для этой конструкции нам понадобится циркуль, линейка и маркеры.
Шаг 2: Обратите внимание, что нам нужно провести перпендикулярную линию, проходящую через точку B, указанную на нашей линии.
Шаг 3: Откройте наш компас на любое расстояние (желательно что-то короткое, но чтобы оно соответствовало нашей точке и линии).
Шаг 4: Поместите конечную точку компаса в точку B и нарисуйте полукруг вокруг нашей точки, убедившись, что она пересекает заданную линию.
Шаг 5: Откройте компас (любого размера) и наведите острие компаса на пересечение нашей полуокружности и заданной линии. Затем поверните наш компас над линией.
St ep 6: Сохраняя ту же длину компаса, идем на другую сторону от нашей точки, где соединяются заданная линия и полуокружность. Поверните компас над линией, чтобы она пересеклась с дугой, которую мы сделали в предыдущем шаге.
St ep 7: Отметьте точку пересечения, созданную этими двумя пересекающимися дугами, которые мы только что сделали, и нарисуйте перпендикулярную линию, проходящую через точку B!
Посмотрите полное видео с объяснением ниже и оригинальный пост здесь.
Биссектриса угла Строение:
Биссектриса угла — это линия, которая равномерно делит угол на две равные половины, образуя два равных угла. Биссектрисы углов великолепны, потому что они каждый раз разрезают любой угол пополам! Взгляните на процесс построения ниже:
Биссектрисы углов великолепны, потому что они каждый раз разрезают любой угол пополам! Взгляните на процесс построения ниже:
Шаг 1: Поместите точку компаса на вершину угла.
Шаг 2: Нарисуйте дугу, пересекающую обе линии, образующие угол, который нужно разделить пополам.
Шаг 3: Направьте циркулем точку пересечения линий и дуги, затем нарисуйте дугу к центру угла.
Шаг 4: Теперь, сохраняя то же расстояние по компасу, возьмите острие компаса и поместите его в другую точку, где пересекаются линия и дуга, и нарисуйте еще одну дугу по направлению к центру угла.
Шаг 5: Обратите внимание, мы сделали перекресток!? Там, где эти две дуги пересекаются, отметьте точку и с помощью линейки соедините ее с центром исходного угла.
Шаг 6: Мы официально разделили наш угол на две равные половины по 35º.
Посмотрите полное видео с объяснением ниже и оригинальный пост здесь.
Этапы построения угла 45 градусов:
Время построить угол 45 градусов! Ключом к правильной конструкции является знание того, что 45º — это половина 90º. Давайте посмотрим, как эта конструкция делается с помощью циркуля и линейки шаг за шагом ниже!
Шаг 1: Используя линейку, начертите прямую линию, обозначив каждую точку A и B.
Шаг 2: Используя циркуль, поместите острие компаса на край точки A и начертите окружность.
Шаг 3: Сохраняя ту же длину компаса, переместите острие компаса в точку пересечения окружности и линии AB. Затем поверните циркуль и сделайте новую дугу на окружности.
Затем поверните циркуль и сделайте новую дугу на окружности.
Шаг 4: Сохраняя ту же длину компаса, перейдите к новому перекрестку, который мы только что сделали, и отметьте еще одну дугу вдоль окружности.
Шаг 5: Теперь возьмите новый отрезок компаса (подойдет любой) и поднесите его к одному из пересечений, которые мы сделали на окружности. Затем создайте новую дугу над кругом, вращая циркуль.
Шаг 6: Держите компас той же длины и поднесите его к другому пересечению, которое мы сделали на нашем круге. Затем создайте новую дугу над кругом.
Шаг 7: Отметьте точку, где эти две линии пересекаются, и с помощью линейки соедините это пересечение с точкой A. Обратите внимание, что это образует 9угол 0º.
Шаг 8: Теперь, чтобы разделить пополам наш только что сделанный угол 90º, мы собираемся сфокусироваться на выделенных розовым цветом точках, где исходный круг пересекается с линией AB и нашей новой линией.
Шаг 9: С помощью компаса (любой длины) наведите его на одну из этих выделенных точек и начертите дугу.
Шаг 10: Сохраняя ту же длину компаса, перейдите к другой выделенной точке и сделайте еще одну дугу.
Шаг 11: 906:05 Теперь с помощью линейки проведите линию от точки А до нового пересечения дуг, которые мы только что сделали.
Шаг 12: Обратите внимание, что мы разделили угол 90° пополам и теперь имеем два равных угла 45°?!
Посмотрите полное видео с объяснением ниже и оригинальный пост здесь.
Конструкция равностороннего треугольника:
Равносторонний треугольник : Треугольник с тремя равными сторонами. Нелегко забыть, что равносторонний треугольник очень легко построить с помощью правильных инструментов (циркуль + линейка). Посмотрите ниже:
Нелегко забыть, что равносторонний треугольник очень легко построить с помощью правильных инструментов (циркуль + линейка). Посмотрите ниже:
1. С помощью компаса измерьте расстояние до отрезка .
2. Направив компас в точку A, начертите дугу, имеющую такое же расстояние, как .
3. Направив компас в точку B, нарисуйте дугу, имеющую такое же расстояние, как .
4. Заметили, где пересекаются дуги? Используя линейку, соедините точки A и B с новой точкой пересечения. Это создаст две новые равные стороны нашего треугольника!
Посмотрите полное видео с объяснением ниже и оригинальный пост здесь.
Построение высот треугольника (острого, тупоугольного, прямого):
Высота — это перпендикулярная линия, проведенная из вершины треугольника к противоположной стороне, образующая угол 90º.
Посмотрите, как найти высоты острого, тупоугольного и прямоугольного треугольника, в видео ниже и опубликуйте здесь.
В видео выше мы рассмотрим, как найти высоту острого тупоугольного и прямоугольного треугольников. Мы также найдем что-то под названием ортоцентр , который поясняется ниже.
Как найти ортоцентр треугольника с помощью компаса:
Ортоцентр — это точка, в которой встречаются все три высоты внутри треугольника.
Чтобы найти ортоцентр с помощью компаса, все, что нам нужно сделать, это найти высоту каждой вершины. Точка, в которой они встречаются, является ортоцентром. Посмотрите видео выше, чтобы увидеть, как это работает шаг за шагом.
Посмотрите видео выше, чтобы увидеть, как это работает шаг за шагом.
Квадрат, вписанный в круг Конструкция:
Шаг 1: Нарисуйте круг с помощью циркуля.
Шаг 2: С помощью линейки начертите диаметр по длине круга, проходящий через его середину.
Шаг 3: Откройте компас по кругу. Затем поднесите острие циркуля к одному из концов диаметра и поверните циркуль над кругом, сделав отметку.
Шаг 4: Сохраняя ту же длину компаса, перейдите к другой стороне диаметра и снова качайтесь над кругом, делая еще одну отметку, пока две дуги не пересекутся.
Шаг 5: Повторите шаги 3 и 4, на этот раз создавая метки под кругом.
Шаг 6: Соедините точки пересечения над и под кругом с помощью линейки. Это создает перпендикулярную биссектрису , , сокращающую диаметр пополам и образующую углы 90º.
Шаг 7: Наконец, используйте линейку, чтобы соединить каждую угловую точку друг с другом, создавая квадрат.
Посмотрите полное видео с объяснением ниже и оригинальный пост здесь.
Лучшие инструменты для геометрии!
Ищете лучшие строительные инструменты? Подойдет любой компас и линейка, но лично я предпочитаю использовать мой любимый мини-математический набор инструментов от Staedler. У Stadler есть геометрический математический набор, который поставляется с мини-линейкой, циркулем, транспортиром и ластиком в красивой дорожной упаковке, которая идеально подходит для студентов в пути и для поддержания порядка… я упоминал, что это всего 7,99 долларов США на Amazon? ! Это тот же набор, который я использую для каждого строительного видео в этом посте. Проверьте ссылку ниже и дайте мне знать, что вы думаете!
Проверьте ссылку ниже и дайте мне знать, что вы думаете!
Остались вопросы? Ищете другие конструкции, которых вы не видите здесь? Без проблем! Не стесняйтесь комментировать с любыми вопросами и комментариями ниже. Удачных расчетов! 🙂
Facebook ~ Twitter ~ TikTok ~ Youtube
Автор Math SuxОпубликовано Рубрики Без рубрики6 комментариев к записи Geometry Constructions Приветствую вас, математические выглядки! Сегодня мы поговорим о переводе математики применительно к преобразованиям и геометрии! Перемещения — это тип преобразования, при котором мы берем точку, линию или форму и перемещаем их вверх, вниз, влево или вправо на координатной плоскости. Фигура сохраняет свои углы, длину и направление после перемещения, все, что мы делаем, это просто перемещаем ее по координатной плоскости. Думаете, вы готовы освоить тему!? Продолжайте читать для получения дополнительных объяснений, видео урока и пошаговых примеров. Удачных расчетов!
Думаете, вы готовы освоить тему!? Продолжайте читать для получения дополнительных объяснений, видео урока и пошаговых примеров. Удачных расчетов!
P(x,y) -> P | (x+h, y+k)
где….
h=Сдвиг по горизонтали (прибавить (+) при движении вправо, вычесть (-) при движении влево)
k= Сдвиг по вертикали (прибавить (+) при движении вверх, вычесть (-) при движении вниз)
Что такое переводы? Переводы — это тип преобразования в геометрии, при котором мы берем точку, линию или форму и перемещаем их вверх, вниз, влево или вправо на координатной плоскости. Давайте посмотрим, как выглядит перевод ниже.
Давайте посмотрим, как выглядит перевод ниже.
В приведенном выше примере перевода мы переходим от квадрата ABCD к квадрату A | Б | С | Д | перевод каждой координаты исходного квадрата на 6 единиц вправо и на 2 единицы вверх.
Свойства перемещения + жесткого движения:Когда фигура, линия или точка перемещаются, форма сохраняет жесткое движение , то есть ее длина, площадь и углы не затрагиваются преобразованием, а также , сохраняя прежнее направление.
- Значения углов остаются прежними.
- Параллельные и перпендикулярные линии остаются прежними. (форма/линия сохраняет то же направление)
- Длина, площадь и периметр остаются прежними.
Существует два основных типа переводов: горизонтальные переводы и вертикальные переводы , давайте посмотрим, что каждый из них означает ниже.
Горизонтальное смещение:
Когда мы смещаем точку, линию или фигуру влево или вправо , он подвергается горизонтальному перемещению по оси x. Любой тип движения влево или вправо на координатной плоскости является горизонтальным переносом.
Как это влияет на координату x? Если фигура смещается вправо, то мы добавляем единицы к координате x, а если фигура смещается влево, мы вычитаем единицы из x-координаты.
Вертикальное перемещение:
Когда мы перемещаем точку, линию или фигуру вверх или вниз , они подвергаются вертикальному перемещению вдоль оси Y. Любой тип движения вверх и вниз на координатной плоскости является вертикальным переносом.
Как это влияет на координату y? Если фигура смещается вверх, то мы прибавляем единицы к координате y, а если фигура смещается вниз, то вычитаем из y-координаты.
Несмотря на то, что при перемещении фигуры, линии или точки может произойти сдвиг по горизонтали или по вертикали, во многих переводах используется сочетание этих двух факторов!
Как меняются координаты после переноса?Правда в том, что для переводов не существует единого уникального правила, но числа всегда будут добавляться или вычитаться из значений координат x и/или y. Если что-то переводится вправо, то мы добавляем единицы к x-значению. С другой стороны, если что-то переводится влево, мы вычитаем единицы из значения x. То же самое можно сказать и о перемещении фигуры вверх: затем мы добавляем единицы к значению y, а если фигура перемещается вниз, мы вычитаем единицы из значения y. Это дает нам следующую формулу перевода ниже:
Если мы посмотрим на наш пример, когда мы переводим исходный квадрат ABCD в квадрат A | Б | С | Д | мы переместим каждую координату исходного квадрата ABCD на 6 единиц вправо и на 2 единицы вверх. На самом деле, когда мы переводим, мы добавляем 6 единиц к каждой координате x, а также добавляем 2 единицы к каждой координате y исходного квадрата фигуры ABCD. Проверьте это ниже:
На самом деле, когда мы переводим, мы добавляем 6 единиц к каждой координате x, а также добавляем 2 единицы к каждой координате y исходного квадрата фигуры ABCD. Проверьте это ниже:
Теперь, когда мы больше понимаем переводы, давайте перейдем к некоторым примерам!
Математические примеры перевода
Пример 1. Перемещение треугольниковПлан игры: Чтобы решить эту задачу, нам нужно сравнить две соответствующие точки координат до и после перемещения. Мы можем посмотреть на любую из следующих пар, чтобы найти ответ A & A | , B & B | , С&С | . Все еще в замешательстве? Если это так, не беспокойтесь, потому что мы будем делать это шаг за шагом!
Шаг 1: Определите пару координат для сравнения до и после переноса. В этом случае мы сравниваем точки A и A | .
Шаг 2: Теперь нам нужно измерить, сколько единиц вправо и сколько единиц вверх Точка A | от точки A .
Мы разобрались с переводом фигур, увы, переводить можно не только фигуры. Забавный сюрприз: строки тоже можно переводить! К переводу линий применяются те же правила, что и к фигурам. Преимущество переноса линии по сравнению с фигурой заключается в том, что теперь у нас еще меньше работы (поскольку точек для перевода меньше).
Пример №2: Перевод строкПлан игры: В этом вопросе нам предлагается найти перевод строки RT в строку R | Т | . Нам нужно будет сравнить соответствующие точки координат до и после перевода. Мы можем посмотреть набор точек до и после перевода, включая Point R&R | или Point T&T | . Ничего, с чем мы не можем справиться! Давай сделаем это!
Шаг 1: Определите пару соответствующих точек до и после переноса, для этой задачи сосредоточимся на точке R и точке R | .
Шаг 2: Теперь измерим, сколько единиц влево и сколько единиц вниз Точка R | от точки R .
Решение:
Другие преобразования:
Если вы ищете больше Преобразований помимо математики перевода, которую вы видите здесь, ознакомьтесь с этими уроками ниже! Или нажмите на эту ссылку здесь!
Размышления
Вращения
Расширения
Кроме того, следите за последними уроками MathSux и советами по изучению на Twitter, Facebook, YouTube и TikTok! Удачных расчетов!
Математика перевода
Facebook ~ Twitter ~ TikTok ~ Youtube
Автор Math SuxОпубликовано Рубрики Без рубрики3 Комментарии к переводу Math75 лучших книг по тригонометрии всех времен (обновлено в 2021 г.)
1
Мэри Джейн Стерлинг | 5.00
Простое руководство по основам тригонометрии посвящено отношениям между сторонами и углами треугольников. .. в основном прямоугольных треугольников. На практике тригонометрия является другом астрономов, которые используют триангуляцию для измерения расстояния между звездами. Trig также имеет приложения в таких широких областях, как финансовый анализ, теория музыки, биология, медицинская визуализация, криптология, разработка игр и сейсмология.
.. в основном прямоугольных треугольников. На практике тригонометрия является другом астрономов, которые используют триангуляцию для измерения расстояния между звездами. Trig также имеет приложения в таких широких областях, как финансовый анализ, теория музыки, биология, медицинская визуализация, криптология, разработка игр и сейсмология.
От синусов и косинусов до логарифмов, конических сечений и полиномов, это удобное руководство избавляет от мучений тригонометрии, объясняя основные понятия в… more
См. другие рекомендации для этой книги…
Купить на Amazon
2
Книги для отслеживания номеров для детей в возрасте от 3 до 5 лет, Рабочая тетрадь для отслеживания номеров, Книга для практики написания номеров, Книга для отслеживания номеров. Учим простую математику для детей
Рабочая тетрадь для рукописного ввода | 4.94
См. дополнительные рекомендации по этой книге…
Купить на Amazon
3
Геометрия, алгебра, тригонометрия
Джордж Ф. Симмонс | 4.83
Симмонс | 4.83
Геометрия — очень красивый предмет, чьи качества элегантности, порядка и определенности на протяжении многих веков оказывали сильное влияние на человеческий разум. . . Важность алгебры заключается в будущем студента. . . как необходимая подготовка к серьезному изучению естественных наук, техники, экономики или более продвинутых видов математики. . . Основное значение тригонометрии заключается не в ее приложениях к геодезии и навигации или в расчетах треугольников, а скорее в математическом описании вибраций, вращений и периодических явлений всех видов,… далее
См. другие рекомендации по этой книге…
Купить на Amazon
4
Серия «Улучшите свои математические навыки»
Крис Макмаллен | 4.82
АВТОР Крис Макмаллен получил докторскую степень. получил степень бакалавра физики в Государственном университете Оклахомы и в настоящее время преподает физику в Северо-Западном государственном университете Луизианы. Он разработал серию рабочих тетрадей Improve Your Math Fluency , чтобы помочь учащимся лучше освоить базовые математические навыки.
Он разработал серию рабочих тетрадей Improve Your Math Fluency , чтобы помочь учащимся лучше освоить базовые математические навыки.
ЧЕГО ОЖИДАТЬ Это учебное пособие предназначено для отработки основных навыков. Это не учебник, предназначенный для обучения тригонометрии , а рабочая тетрадь, предназначенная для дополнения обучения студентов тригонометрии. Примеры и краткое описание концепций приведены… more
См. дополнительные рекомендации по этой книге…
Купить на Amazon
5
W. Michael Kelley | 4.82
Единственный способ выучить алгебру — решать задачи по алгебре. Много их. Извиняюсь!
И это то, что вы получаете здесь — больше задач по алгебре, чем ваш самый страшный кошмар — но с БОЛЬШОЙ разницей. Я просмотрел всю книгу и сделал кучу заметок, так что вы получите…
* Очень подробные ответы (больше никаких пропущенных шагов)
* Дополнительные пояснения, которые делают непонятное совершенно ясным
* Указатели на другие задачи, которые показывают навыки, которые вам нужны
Тысячи задач, все основные игроки здесь: линейные уравнения и неравенства, многочлены,. .. больше
.. больше
См. другие рекомендации по этой книге…
Купить на Amazon
6
Питер Х. Селби | 4.80
Введение в тригонометрию, плоскостную и аналитическую геометрию с заключительной главой о пределах, чтобы учащийся был хорошо подготовлен к началу исчисления и высшей математики. Основное внимание в нем уделяется графическому представлению задач и их решению комбинированными аналитическими методами геометрии и алгебры. меньше
Посмотреть больше рекомендаций по этой книге…
Купить на Amazon
7
В. Майкл Келли | 4.80
Большинство учебных пособий по математике и естественным наукам являются отражением профессоров колледжей, которые их пишут, — сухими, трудными и претенциозными. Огромная книга задач по тригонометрии является исключением. Автор Майк Келли взял типичную рабочую тетрадь по тригонометрии, битком набитую решенными задачами — более 750! — и делал пометки на полях, добавляя пропущенные шаги и упрощая концепции и решения, чтобы то, что могло сбить с толку студентов, стало совершенно ясным. Сбитые с толку студенты больше не будут задаваться вопросом, откуда взялся тот или иной ответ, или полагаться на метод проб и ошибок, чтобы решить… подробнее
Сбитые с толку студенты больше не будут задаваться вопросом, откуда взялся тот или иной ответ, или полагаться на метод проб и ошибок, чтобы решить… подробнее
См. другие рекомендации по этой книге…
Купить на Amazon
8
Симпозиум 1977 года по чистой математике, Университет штата Орегон | 4.79
Содержит разделы об автоморфных представлениях и L-функциях, а также об арифметической алгебраической геометрии и L-функциях. меньше
Посмотреть другие рекомендации по этой книге…
Купить на Amazon
9
И. М. Гельфанд | 4.78
В некотором смысле тригонометрия находится в центре школьной математики. Он возникает при изучении геометрии, когда мы исследуем отношения сторон в подобных прямоугольных треугольниках или когда мы смотрим на соотношение между хордой окружности и ее дугой. Это ведет к гораздо более глубокому изучению периодических функций и так называемых трансцендентных функций, которые не могут быть описаны с помощью конечных алгебраических процессов. Он также имеет множество приложений в физике, астрономии и других областях науки. Это очень старая тема. Многие из геометрических результатов, которые мы теперь формулируем в тригонометрических терминах… больше
Он также имеет множество приложений в физике, астрономии и других областях науки. Это очень старая тема. Многие из геометрических результатов, которые мы теперь формулируем в тригонометрических терминах… больше
Посмотреть другие рекомендации по этой книге…
Купить на Amazon
10
Книга-2 Тригонометрия
Мистер Раджеш Сарсват | 4.77
КАК ЗАПОМНИТЬ МАТЕМАТИЧЕСКИЕ ФОРМУЛЫ
Вы когда-нибудь не спали всю ночь, пытаясь запомнить формулы для экзамена по математике, но без изменений?
или
Вы запоминаете список формул сегодня и забываете почти все о них на следующий день?
или
Кажется, это самый сложный аспект изучения математики, который тянет вас назад, вместо того, чтобы двигаться дальше?
Если ответ на любой из вышеперечисленных вопросов положительный, эта книга » Как запоминать формулы в… подробнее
Посмотреть другие рекомендации по этой книге. ..
..
Купить на Amazon
Нет времени читать лучшие книги по тригонометрии всех времен? Читать краткую форму резюмеКраткое изложение поможет вам учиться в 10 раз быстрее:
- Быть всесторонним: вы узнаете наиболее важных пункта в книге
- Избавитесь от лишнего: вы сосредоточите свое время на том, что важно знать
- Интерактивные упражнения: примените идеи книги в своей жизни под руководством наших педагогов.
Подпишитесь на бесплатные обзоры книг
11
Э. Ричард Хайнеман, Дж. Далтон Таруотер | 4,76
Седьмое издание этого учебника по тригонометрии для студентов содержит краткое изложение в сочетании с градуированными упражнениями. Основные изменения включают усиление акцента на использование калькуляторов и упражнений, связанных с калькулятором, сведение к минимуму использования таблиц, отказ от использования логарифмов для решения треугольников и упор на построение графиков. меньше
меньше
См. другие рекомендации по этой книге…
Купить на Amazon
12
Самоучитель
Тим Хилл | 4,76
Это серьезное руководство предоставляет студентам и самостоятельным ученикам ясное и понятное изучение наиболее важных идей тригонометрии. Подход Тима Хилла, не отвлекающий внимание, сочетает в себе многолетний опыт репетиторства с методами его старых русских учителей математики. Результат: узнайте за несколько дней то, на что в обычных школах уходят месяцы.
Обучает общим принципам, которые можно применять к широкому кругу задач. Избегает бессмысленных и чрезмерных рутинных вычислений, характерных для обычных учебников. Рассматривает тригонометрию как логически связную дисциплину, а не как… more
См. другие рекомендации по этой книге…
Купить на Amazon
13
Чарльз П. МакКег | 4.75
Получите четкое представление о принципах тригонометрии и о том, как эти понятия применяются в реальной жизни, с помощью тригонометрии МакКега/Тернера. В книге представлены современные концепции в виде кратких, понятных разделов с использованием текущих подробных примеров и интересных приложений. Увлекательные иллюстрации, такие как езда на велосипеде, колесо обозрения и человеческое пушечное ядро, демонстрируют тригонометрию в действии. Уникальные исторические виньетки предлагают захватывающий взгляд на то, как многие из центральных идей в тригонометрии зародились. Текст легко читается, а важные теоремы и определения заключены в рамки, чтобы их можно было быстро найти… подробнее
В книге представлены современные концепции в виде кратких, понятных разделов с использованием текущих подробных примеров и интересных приложений. Увлекательные иллюстрации, такие как езда на велосипеде, колесо обозрения и человеческое пушечное ядро, демонстрируют тригонометрию в действии. Уникальные исторические виньетки предлагают захватывающий взгляд на то, как многие из центральных идей в тригонометрии зародились. Текст легко читается, а важные теоремы и определения заключены в рамки, чтобы их можно было быстро найти… подробнее
См. другие рекомендации по этой книге…
Купить на Amazon
14
C. V. Durell and A. Robson | 4.75
Этот том является долгожданным ресурсом для преподавателей, которые ищут текст для студентов бакалавриата по продвинутой тригонометрии. Этот текст, идеально подходящий для самостоятельного изучения, предлагает четкое и логичное изложение таких тем, как свойства треугольника и четырехугольника; дольные углы и обратные функции; гиперболические, логарифмические и экспоненциальные функции; намного больше. 1930 издание. Включает 79 фигурок.
1930 издание. Включает 79 фигурок.
меньше
Посмотреть другие рекомендации по этой книге…
Купить на Amazon
15
Мэри Джейн Стерлинг | 4.74
От углов к функциям и тождествам — легко решайте тригонометрические уравнения
Вы разобрались в терминах и понятиях, которые вам нужно знать, но заблудились на полпути к задаче или, что еще хуже, не знаете, с чего начать? Не бойтесь — это практическое руководство направлено на то, чтобы помочь вам решать многие типы тригонометрических уравнений, с которыми вы сталкиваетесь, целенаправленно, шаг за шагом. Имея достаточно пояснений перед каждым набором задач, вы отточите свои навыки и улучшите свою производительность. Вы увидите, как работать с углами, окружностями, треугольниками, графиками, функциями, законами синусов и косинусов,… еще
См. другие рекомендации по этой книге…
Купить на Amazon
16
В. Майкл Келли | 4.73
Теперь студентам нечего бояться!
Учебники по математике могут быть такими же непонятными, как и предмет, который они преподают. Уже нет. Автор бестселлера The Complete Idiot’s Guide® to Calculus взял типичную рабочую тетрадь по математическому анализу, битком набитую решенными математическими задачами, и сделал разборчивые пометки на полях, добавив недостающие шаги и упростив решения. Наконец, все становится совершенно ясно. Учащиеся будут готовы решать непонятные задачи, которые никогда не обсуждались в классе, но, кажется, всегда попадаются на экзаменах.
Уже нет. Автор бестселлера The Complete Idiot’s Guide® to Calculus взял типичную рабочую тетрадь по математическому анализу, битком набитую решенными математическими задачами, и сделал разборчивые пометки на полях, добавив недостающие шаги и упростив решения. Наконец, все становится совершенно ясно. Учащиеся будут готовы решать непонятные задачи, которые никогда не обсуждались в классе, но, кажется, всегда попадаются на экзаменах.
more
См. другие рекомендации по этой книге…
Купить на Amazon
17
Решение x и выяснение почему
Артур Бенджамин | 4.73
Величайший в мире волшебник-математик берет нас в завораживающее путешествие по чудесам чисел (и не только)
«Артур Бенджамин … с радостью показывает вам, как заставить числа природы танцевать.» — Билл Най (ученый)
Магия математики — учебник по математике, который вы хотели бы иметь в школе. Используя восхитительный набор примеров — от шариков мороженого и комбинаций в покере до измерения гор и составления магических квадратов — эта книга упивается ключевыми математическими областями, включая арифметику, алгебру, геометрию и исчисление, а также числа Фибоначчи,. .. подробнее
.. подробнее
См. другие рекомендации для этой книги…
Купить на Amazon
18
MCDOUGAL LITTEL | 4.73
Этот учебник представляет собой подробное введение в «современную» или «абстрактную» алгебру на уровне, подходящем для студентов старших курсов и начинающих аспирантов.
Книга посвящена общепринятым темам: группам, кольцам, полям и линейной алгебре, причем объединяющей темой является симметрия. Эта тема занимает центральное место и широко распространена в современной математике и в приложениях
. Самая важная цель этой книги — вовлечь учащихся в активную математическую практику. Студентам предоставляется возможность участвовать и исследовать, начиная с первой страницы. Упражнения… подробнее
Посмотреть другие рекомендации по этой книге…
Купить на Amazon
19
SparkNotes | 4.72
SparkCharts™:
Необходимая информация — кратко, удобно и точно. Эти учебные пособия и справочные материалы, созданные студентами Гарварда для студентов во всем мире, охватывают широкий спектр предметов колледжей и аспирантов, от бизнеса и компьютерного программирования до медицины, права и языков. Они дадут вам все необходимое, чтобы добиться успеха в школе и за ее пределами. Планы и резюме охватывают ключевые моменты, а диаграммы и таблицы упрощают понимание сложных концепций. Эта четырехстраничная диаграмма содержит обзоры:
Они дадут вам все необходимое, чтобы добиться успеха в школе и за ее пределами. Планы и резюме охватывают ключевые моменты, а диаграммы и таблицы упрощают понимание сложных концепций. Эта четырехстраничная диаграмма содержит обзоры:
Определения тригонометрии, углов и функций далее
См. дополнительные рекомендации по этой книге…
Купить на Amazon
20
CommonCore Math Workbook
Ace Academic Publishing | 4.72
5-й класс Common Core Math: Практическая рабочая тетрадь — Практические вопросы, ответы и пояснения — Рекомендовано учителями — Ace Academic Publishing — на основе общих базовых государственных стандартов: аналогично стандартному экзамену, вы можете найти вопросы всех типов, в том числе несколько — выбор, заполнение пробела, правда или ложь, соответствие правильному ответу и вопросы со свободным ответом. — Высокие стандарты вопросов: каждый из этих вопросов разделен на главы и подтемы. Содержимое этой рабочей тетради по математике включает в себя несколько глав и разделов, охватывающих все необходимые общие базовые стандарты для этого класса. .. далее
.. далее
Посмотреть другие рекомендации по этой книге…
Купить на Amazon
Нет времени читать лучшие книги по тригонометрии всех времен? Читайте краткие резюме.Краткое изложение поможет вам учиться в 10 раз быстрее:
- Быть исчерпывающим: вы узнаете наиболее важных пункта в книге применить идеи книги в своей жизни под руководством наших преподавателей.
Подпишитесь на бесплатную сводку книг
21
Майкл Салливан | 4.71
ПРИМЕЧАНИЕ. Перед покупкой уточните у своего преподавателя, что вы выбрали правильный ISBN. Для каждого наименования существует несколько версий продуктов Pearson MyLab & Mastering, и регистрация не подлежит передаче. Чтобы зарегистрироваться и использовать продукты Pearson MyLab & Mastering, вам также может понадобиться идентификатор курса , , который предоставит ваш инструктор. Подержанные книги, взятые напрокат и приобретенные за пределами Pearson При покупке или аренде у компаний, отличных от Pearson, коды доступа к продуктам Pearson MyLab & Mastering могут быть не включены, могут быть неверными или. .. подробнее
.. подробнее
Подробнее рекомендации для этой книги…
Купить на Amazon
22
Выражения, уравнения и
Paul A. Foerster | 4.70
См. дополнительные рекомендации по этой книге…
Купить на Amazon
23
Мэри Джейн Стерлинг | 4.69
Повысьте свои шансы на получение более высоких баллов по Алгебре II
Алгебра II знакомит учащихся со сложными понятиями алгебры для подготовки к тригонометрии и исчислению. В этом новом издании «Рабочая тетрадь по алгебре II для чайников» учащиеся старших классов и колледжей будут решать задачи по алгебре II, которые они увидят в классе, включая системы уравнений, матрицы, графики и конические сечения. Кроме того, книга теперь поставляется с бесплатным годовым доступом к викторинам по главам онлайн!
Недавний отчет ACT показывает, что более четверти выпускников средних школ 2012 года, прошедших тестирование ACT, не… more
См. дополнительные рекомендации по этой книге…
дополнительные рекомендации по этой книге…
Купить на Amazon
24
Earl W , Своковски и Джеффри А. Коул | 4.67
В этом пособии содержатся решения к упражнениям с нечетными разделами, избранным упражнениям на обзор глав, нечетным упражнениям на обсуждение и всем тестовым упражнениям по главам, что дает учащимся возможность проверить свои ответы и убедиться, что они предприняли правильные шаги для достижения Ответ. меньше
См. другие рекомендации по этой книге…
Купить на Amazon
25
SL Loney’s Original Classic
Сидни Лакстон Лони | 4.67
Полное издание, включая все цифры за вычетом
См. дополнительные рекомендации по этой книге…
Купить на Amazon
26
Забытое искусство сферической тригонометрии
Глен Ван Браммелен | 4.67
Беспрецедентно иллюстрированная история сферической тригонометрии с древности до наших дней
Heavenly Mathematics прослеживает богатую историю сферической тригонометрии, раскрывая, как культуры классической Греции, средневекового ислама и современного Запада использовали это забытое искусство для построения карт небес и Земли. Когда-то на протяжении двух тысячелетий эта дисциплина лежала в основе астрономии и океанской навигации, а на протяжении столетий она также была основой математического образования и широко преподавалась до 1950-х годов. Глен Ван Браммелен исследует эту изысканную область математики и ее роль в… подробнее
Когда-то на протяжении двух тысячелетий эта дисциплина лежала в основе астрономии и океанской навигации, а на протяжении столетий она также была основой математического образования и широко преподавалась до 1950-х годов. Глен Ван Браммелен исследует эту изысканную область математики и ее роль в… подробнее
Посмотреть другие рекомендации по этой книге…
Купить на Amazon
27
Титу Андрееску | 4.66
Сокровища математической олимпиады направлены на то, чтобы построить мост между обычными школьными упражнениями и более сложными, запутанными и абстрактными понятиями математики для студентов. Книга содержит стимулирующий сборник задач по предметам алгебры, геометрии, тригонометрии, теории чисел и комбинаторики. Хотя его можно считать продолжением «Задачи олимпиады по математике», основное внимание уделяется привлечению более широкой аудитории к применению методов и стратегий для решения реальных задач.
На протяжении всей книги учащимся предлагается высказывать свои идеи, предположения,. .. подробнее
.. подробнее
См. дополнительные рекомендации по этой книге…
Купить на Amazon
28
Robert Moyer | 4.64
Сложные тестовые вопросы? Пропущенные лекции? Недостаточно времени? Учебник слишком дорогой?
К счастью, есть Шаум. Этот комплексный пакет включает более 600 полностью решенных задач, примеров и практических упражнений для оттачивания навыков решения задач. Кроме того, у вас будет доступ к 20 подробным видеороликам с участием преподавателей математики, которые объяснят, как решать наиболее часто тестируемые задачи — это все равно, что иметь собственного виртуального репетитора! Вы найдете все, что вам нужно, чтобы укрепить уверенность, навыки и знания для максимально возможного результата.
Более 40 миллионов… more
Просмотреть другие рекомендации по этой книге…
Купить на Amazon
29
Ронда Хюттенмюллер | 4.64
Примечание издателя. Издатель не гарантирует качество, подлинность или доступ к каким-либо онлайн-разрешениям, включенным в продукт, для продуктов, приобретенных у сторонних продавцов.
Издатель не гарантирует качество, подлинность или доступ к каким-либо онлайн-разрешениям, включенным в продукт, для продуктов, приобретенных у сторонних продавцов.
Ваше пошаговое решение для освоения предварительного исчисления Понимание предварительного исчисления часто открывает двери для изучения более сложных и практических математических предметов, а также может помочь выполнить требования колледжа. Precalculus Demystified , второе издание — ваш ключ к освоению этого иногда сложного предмета.
В этом пособии для самообучения сначала представлены общие концепции предварительного исчисления, чтобы вы могли легко… more
См. дополнительные рекомендации по этой книге…
Купить на Amazon
30
Steven Demme | 4.64
Посмотреть другие рекомендации по этой книге…
Купить на Amazon
Нет времени читать лучшие книги по тригонометрии всех времен? Читайте краткие резюме.Краткое изложение поможет вам учиться в 10 раз быстрее:
- Быть исчерпывающим: вы узнаете наиболее важных пункта в книге
- Избавитесь от лишнего: вы сосредоточите свое время на том, что важно знать
- Интерактивные упражнения: примените идеи книги в своей жизни под руководством наших педагогов.

Подпишитесь на бесплатные обзоры книг
31
Структура и метод, Книга 1
Ричард Г. Браун | 4,64
См. дополнительные рекомендации по этой книге…
Купить на Amazon
32
Рабочая тетрадь CommonCore Math
Ace Academic Publishing | 4.64
Common Core Math для 8-го класса: практическая рабочая тетрадь — практические вопросы, ответы и пояснения — рекомендовано учителями — Ace Academic Publishing — на основе общих базовых государственных стандартов: аналогично стандартному экзамену, вы можете найти вопросы всех типов, в том числе несколько — выбор, заполнение пробела, правда или ложь, соответствие правильному ответу и вопросы со свободным ответом. — Высокие стандарты вопросов: каждый из этих вопросов разделен на главы и подтемы. Содержимое этой рабочей тетради по математике включает в себя несколько глав и разделов, охватывающих все необходимые общие базовые стандарты для этого класса… далее
См. другие рекомендации по этой книге. ..
..
Купить на Amazon
33
Дэвид Кей | 4.63
Справочники по курсам CliffsQuickReview охватывают основы ваших самых сложных занятий. Получите твердое представление об основных концепциях и ключевом материале и проверьте свои новые знания с помощью контрольных вопросов. CliffsQuickReview Trigonometry предоставляет вам все, что вам нужно знать, чтобы понять основные концепции тригонометрии, независимо от того, нужны ли вам дополнение к учебнику и курсам или краткий справочник. Тригонометрия — это не просто измерение углов; он имеет множество применений в реальном мире, например, в навигации, геодезии, строительстве и многих других областях науки, включая математику и… далее
См. другие рекомендации по этой книге…
Купить на Amazon
34
Майкл Салливан | 4.63
Восьмое издание этой весьма надежной книги сохранило свои лучшие черты — точность, точность, глубину и множество наборов упражнений — при существенном обновлении содержания и педагогики. Стремясь преподавать математику как образ жизни, Салливан предлагает понятные, реалистичные приложения, соответствующие способностям большинства читателей. Темы глав включают графики; тригонометрические функции; Экспоненциальные и логарифмические функции; Аналитическая геометрия; Аналитическая тригонометрия; Подсчет и вероятность; и более. Для тех, кто интересуется изучением алгебры и тригонометрии, так как… подробнее
Стремясь преподавать математику как образ жизни, Салливан предлагает понятные, реалистичные приложения, соответствующие способностям большинства читателей. Темы глав включают графики; тригонометрические функции; Экспоненциальные и логарифмические функции; Аналитическая геометрия; Аналитическая тригонометрия; Подсчет и вероятность; и более. Для тех, кто интересуется изучением алгебры и тригонометрии, так как… подробнее
См. дополнительные рекомендации по этой книге…
Купить на Amazon
35
Общая базовая математическая рабочая тетрадь
Ace Academic Publishing | 4.63
См. дополнительные рекомендации по этой книге…
Купить на Amazon
36
Функции и приложения
PRENTICE HALL | 4.62
В этом тексте алгебра и тригонометрия представлены как изучение специальных классов функций. В процессе тщательно исследуются отношения между теорией и реальными приложениями, воплощая материал в жизнь. Подходит для курса второго года обучения, курса тригонометрии или курса предварительного исчисления. меньше
меньше
См. другие рекомендации по этой книге…
Купить на Amazon
37
Общая основная математическая рабочая тетрадь
Ace Academic Publishing | 4.62
Посмотреть другие рекомендации по этой книге…
Купить на Amazon
38
Маргарет Л. Лиал | 4.62
Для курсов по тригонометрии.
Постоянная поддержка вашего развивающегося курса Серия College Algebra , написанная Лиал, Хорнсби, Шнайдером и Дэниэлсом, объединяет опыт ведущих учителей, чтобы помочь учащимся развить как концептуальное понимание, так и аналитические навыки, необходимые для успеха в математике. . В этом последнем издании авторы отвечают на вызовы, связанные с новыми ожиданиями учащихся и новыми моделями обучения. Команда Lial теперь предлагает новый набор ресурсов для поддержки современных преподавателей и студентов. Примечание: Вы приобретаете отдельную книгу… подробнее
См. другие рекомендации по этой книге. ..
..
Купить на Amazon
39
Практические занятия по алгебре, геометрии и тригонометрии
Джим Либби | 4.62
«Где мы это будем использовать?» Каждый школьник-математик задавался этим вопросом. Часто сами учителя не знают, как реагировать. Один из ответов заключается в том, что высшая математика, которую изучают в старшей школе, будет необходима для дальнейшего обучения в колледже. Более удовлетворительный ответ требует понимания того, как математика применяется во многих конкретных областях. Эта книга, написанная в первую очередь для учителей, представляет сотни практических приложений математики — от бейсбольной статистики до теории относительности, — которые могут понять все, кто знаком со школьной алгеброй,… подробнее
Посмотреть другие рекомендации по этой книге…
Купить на Amazon
40
Джеймс Стюарт | 4.61
Эта команда авторов бестселлеров объясняет концепции просто и ясно, не замалчивая сложные моменты. Решение задач и математическое моделирование вводятся с самого начала и закрепляются на протяжении всего курса, обеспечивая учащимся прочную основу в принципах математического мышления. Всеобъемлющая и с равномерным темпом, книга обеспечивает полное освещение концепции функции и объединяет значительное количество материалов по графическому калькулятору, чтобы помочь учащимся лучше понять математические идеи. Внимание авторов к деталям и четкость — такие же, как у Джеймса Стюарта… подробнее
Решение задач и математическое моделирование вводятся с самого начала и закрепляются на протяжении всего курса, обеспечивая учащимся прочную основу в принципах математического мышления. Всеобъемлющая и с равномерным темпом, книга обеспечивает полное освещение концепции функции и объединяет значительное количество материалов по графическому калькулятору, чтобы помочь учащимся лучше понять математические идеи. Внимание авторов к деталям и четкость — такие же, как у Джеймса Стюарта… подробнее
Посмотреть другие рекомендации по этой книге…
Купить на Amazon
Нет времени читать лучшие книги по тригонометрии всех времен? Читайте краткие резюме.Краткое изложение поможет вам учиться в 10 раз быстрее:
- Быть исчерпывающим: вы узнаете наиболее важных пункта в книге применить идеи книги в своей жизни под руководством наших преподавателей.
Подпишитесь на бесплатные обзоры книг
41
Как ваши учителя хотели бы преподавать математику. . (Чему бы они вас научили, если бы у них было время Книга 2)
. (Чему бы они вас научили, если бы у них было время Книга 2)
Кевин Беннетт | 4.61
См. дополнительные рекомендации по этой книге…
Купить на Amazon
42
Essential Skills (пошаговые уроки по математике)
Chris McMullen | 4.61
ЧЕГО ОЖИДАТЬ : В этой книге рассматриваются основные концепции тригонометрии, идеи и навыки. Темы включают основные триггерные функции, специальные углы, опорный угол, единичный круг, выход за пределы квадранта I, обратные триггерные функции и радианы. Несколько глав предназначены для того, чтобы помочь учащимся запомнить триггерные функции обычных углов, таких как 30, 150 или 315 градусов, что будет особенно полезно для учащихся, которые могут сдавать экзамены без калькулятора (это касается MCAT и многих математических и естественных наук). курсы). В каждой главе приведены примеры с пошаговыми решениями и пояснениями…. далее
См. другие рекомендации по этой книге…
Купить на Amazon
43
Earl W. Swokowski | 4.60
Swokowski | 4.60
Четкие объяснения, лаконичный и привлекательный макет, а также примеры и упражнения с различными практическими приложениями сделали эту книгу год за годом популярной среди студентов. Это последнее издание книги Своковски и Коула «АЛГЕБРА И ТРИГОНОМЕТРИЯ С АНАЛИТИЧЕСКОЙ ГЕОМЕТРИЕЙ» сохраняет эти особенности. Задачи постоянно хвалили за то, что они находятся на правильном уровне для студентов, изучающих предварительный анализ. В книге также приведены примеры калькуляторов, в том числе конкретные нажатия клавиш, которые показывают, как использовать различные графические калькуляторы для более быстрого решения задач. Пожалуй, самое главное — эта книга… еще
См. другие рекомендации по этой книге…
Купить на Amazon
44
Мэри Джейн Стерлинг | 4.60
Продвинуться вперед в изучении математического анализа
Курсы предварительного исчисления становятся все более популярными: 35 процентов учащихся в США проходят этот курс в средней или старшей школе. Часто завершение такого курса является обязательным условием для математических расчетов и других математических курсов более высокого уровня.
Часто завершение такого курса является обязательным условием для математических расчетов и других математических курсов более высокого уровня.
Предварительный расчет для чайников — бесценный ресурс для студентов, обучающихся на подготовительных курсах по математическому анализу. Представляя основные темы в ясной и краткой форме, книга помогает учащимся улучшить свое понимание предварительного исчисления и подготовиться к курсам математики более высокого уровня.
подробнее
Посмотреть другие рекомендации по этой книге…
Купить на Amazon
45
John H. Saxon Jr. | 4.60
Посмотреть другие рекомендации по этой книге…
Купить на Amazon
46
Линда Дэвис, Линда П. Дэвис | 4.59
См. другие рекомендации по этой книге…
Купить на Amazon
47
Гунтрам Мюллер и Рональд И. Брент | 4.59
Эта книга предназначена для нынешних студентов, изучающих математику, для ознакомления с навыками алгебры и тригонометрии, которые так важны для успеха в математике. Организованный в соответствии с типичным курсом математического анализа, соответствующие темы алгебры и тригонометрии представлены так, как они нужны студентам, с предупреждениями о подводных камнях и наборами упражнений для практики. Независимо от того, используется ли этот текст в качестве справочного материала или для наверстывания, он окажется бесценным для всех студентов, изучающих математический анализ.
Организованный в соответствии с типичным курсом математического анализа, соответствующие темы алгебры и тригонометрии представлены так, как они нужны студентам, с предупреждениями о подводных камнях и наборами упражнений для практики. Независимо от того, используется ли этот текст в качестве справочного материала или для наверстывания, он окажется бесценным для всех студентов, изучающих математический анализ.
Примечание: другая версия этой книги доступна специально для курсов раннего трансцендентального исчисления. меньше
См. другие рекомендации по этой книге…
Купить на Amazon
48
P. Abbott, M.E. Wardle | 4.58
Этот краткий текст «Учись сам» обеспечивает тщательное практическое обоснование фундаментальных принципов тригонометрии, которые любой читатель может применить в своей области. Текст исследует использование калькуляторов и содержит рабочие примеры и упражнения (с ответами) в каждой главе. меньше
См. другие рекомендации по этой книге. ..
..
Купить на Amazon
49
Синтия Янг | 4.58
3-е издание «Тригонометрии» Синтии Янг сосредоточено на исправлениях и дополнениях, включая сотни новых упражнений, больше возможностей для использования технологий и проекты тематического моделирования, которые помогают связать контент с реальными проблемами. Текст основывается на предыдущих двух изданиях с более глубоким и расширенным освещением способов помочь преодолеть общие барьеры в обучении тригонометрии и укрепить доверие читателей. Текст отличается поистине уникальной, сильной педагогикой и, как и в предыдущих двух номерах, написан четким, монотонным голосом. меньше
См. другие рекомендации по этой книге…
Купить на Amazon
50
Margaret L. Lial, John Hornsby, et al. | 4.58
Этот учебник вовлекает и поддерживает учащихся в процессе обучения, развивая как концептуальное понимание, так и аналитические навыки, необходимые для успеха в математике. меньше
Посмотреть другие рекомендации по этой книге. ..
..
Купить на Amazon
Нет времени читать лучшие книги по тригонометрии всех времен? Читайте краткие резюме.Краткое изложение поможет вам учиться в 10 раз быстрее:
- Быть исчерпывающим: вы узнаете наиболее важных пункта в книге
- Избавитесь от лишнего: вы сосредоточите свое время на том, что важно знать
- Интерактивные упражнения: примените идеи книги в своей жизни под руководством наших педагогов.
Подпишитесь на бесплатную сводку книг
51
Джерри Р. Шипман | 4.57
Решатель задач по алгебре и тригонометрии REA
Каждый набор Problem Solver представляет собой содержательное и необходимое руководство по изучению и решению, наполненное четкими и лаконичными решениями задач. Ответы на все ваши вопросы можно найти в одном удобном источнике от одного из самых надежных имен в справочных руководствах по решениям. Более полезные, более практичные и более информативные, эти учебные пособия являются лучшими из доступных обзоров и компаньонов учебников. Они идеально подходят для обучения в бакалавриате и магистратуре.
Более полезные, более практичные и более информативные, эти учебные пособия являются лучшими из доступных обзоров и компаньонов учебников. Они идеально подходят для обучения в бакалавриате и магистратуре.
Этот очень полезный справочник является лучшим обзором… more
См. дополнительные рекомендации по этой книге…
Купить на Amazon
52
Мэри П. Дольчиани | 4.57
Эта книга находится в приемлемом состоянии, однако она пользуется всеобщим признанием и неподвластна времени. Легко понять, поэтому он так популярен — математика стала проще. меньше
Посмотреть другие рекомендации по этой книге…
Купить на Amazon
53
Предварительное исчисление и геометрия
Дебра Энн Росс | 4.56
Master Math: Basic Math and Pre-Algebra в очень удобной и доступной форме обучает вас принципам и формулам для создания прочной математической основы. меньше
Посмотреть другие рекомендации по этой книге…
Купить на Amazon
54
Robert F. Blitzer | 4.56
Blitzer | 4.56
В этой книге традиционное содержание Precalculus представлено таким образом, что отвечает на извечный вопрос: «Когда я когда-нибудь буду этим пользоваться?» Выделяя действительно актуальные приложения, эта книга представляет материал в удобном для преподавания/легком для обучения подходе. КЛЮЧЕВЫЕ ТЕМЫ» Темы главы включают уравнения, неравенства и математические модели, функции и графики, полиномиальные и рациональные функции, экспоненциальные и логарифмические функции, тригонометрические функции, аналитическую тригонометрию, системы уравнений и неравенств, конические сечения и аналитическую геометрию, а также последовательности, индукцию. ,… еще
См. другие рекомендации по этой книге…
Купить на Amazon
55
Дуглас Даунинг | 4.55
Всегда учитесь с самой последней подготовкой! Ищите Barron’s Algebra: The Easy Way , Sixth Edition, ISBN 9781438012131, поступит в продажу 3 сентября 2019 г.
Примечание издателя. Издатель не гарантирует качество, подлинность или доступ к любым онлайн-правам, включенным в продукт. меньше
См. другие рекомендации по этой книге…
Купить на Amazon
56
Bernd Sturmfels | 4.54
См. другие рекомендации по этой книге…
Купить на Amazon
57
С тригонометрией и аналитической геометрией
John H. Saxon | 4.54
См. другие рекомендации по этой книге…
Купить на Amazon
58
Майкл Салливан | 4.53
В девятом издании этого надежного учебника сохранены его лучшие черты — точность, четкость, глубина, мощная поддержка учащихся и множество упражнений, но при этом существенно обновлено содержание и педагогика. меньше
Посмотреть другие рекомендации по этой книге…
Купить на Amazon
59
Stan Gibilisco | 4.52
Примечание издателя: Продукты, приобретенные у сторонних продавцов, не гарантируются издателем в отношении качества, подлинности или доступа к каким-либо онлайн-разрешениям, включенным в продукт.
DeMYSTiFieD — решение для таких сложных вопросов, как тригонометрия. Если вы думаете, что декартова координата — это что-то из научной фантастики, а гиперболический тангенс — сильное преувеличение, вам нужно Trigonometry DeMYSTiFieD , Second Edition, чтобы разгадать фундаментальные концепции и теории этой темы в своем собственном темпе.
Это практическое руководство облегчит вам задачу, начиная с углов и… подробнее
См. дополнительные рекомендации по этой книге…
Купить на Amazon
60
Louis Leithold | 4.52
Посмотреть другие рекомендации по этой книге…
Купить на Amazon
Нет времени читать лучшие книги по тригонометрии всех времен? Читайте краткие резюме.Краткое изложение поможет вам учиться в 10 раз быстрее:
- Быть исчерпывающим: вы узнаете наиболее важных пункта в книге
- Избавитесь от лишнего: вы сосредоточите свое время на том, что важно знать
- Интерактивные упражнения: примените идеи книги в своей жизни под руководством наших педагогов.

Подпишитесь на бесплатные обзоры книг
61
Robert E. Moyer | 4.52
См. дополнительные рекомендации по этой книге…
Купить на Amazon
62
Изольда Фотиева, к.т.н., Дмитрий Фотиев | 4.50
— следует стандартному учебному плану.
— включает как полярные координаты, так и комплексные числа, в отличие от конкурентов. меньше
Просмотреть другие рекомендации по этой книге…
Купить на Amazon
63
Синтия Янг | 4.48
Третье издание «Тригонометрии Синтии Янг» объединяет все элементы, которые позволили преподавателям и учащимся успешно «преодолеть разрыв» между обучением в классе и самостоятельной домашней работой, преодолев распространенные препятствия в обучении и укрепив уверенность в способности учащихся заниматься математикой. Написанная ясным голосом, который говорит со студентами и отражает то, как преподаватели общаются на лекциях, отличительная черта педагогики Янга позволяет студентам стать независимыми и успешными учениками. Разнообразные типы упражнений и моделирующие проекты делают обучение свежим и мотивирующим. Молодой… еще
Разнообразные типы упражнений и моделирующие проекты делают обучение свежим и мотивирующим. Молодой… еще
См. другие рекомендации по этой книге…
Купить на Amazon
64
Дебра Энн Росс | 4.46
Master Math: Trigonometry написана для учащихся, учителей, воспитателей и родителей, а также для ученых и инженеров, которым необходимо найти принципы, определения, объяснения концепций и примеры, относящиеся к области тригонометрии. Тригонометрия — это визуальная и прикладная область математики, которая была разработана ранними астрономами и учеными для понимания, моделирования, измерения и навигации в физическом мире вокруг них. меньше
См. дополнительные рекомендации по этой книге…
Купить на Amazon
65
Графики и модели [с руководством по графическому калькулятору]
Марвин Л. Биттингер, Джудит А. Бичер, Дэвид Дж. Элленбоген, Джудит А. , Пенна | 4.46
Серия «Графики и модели», разработанная Биттингером, Бичером, Элленбогеном и Пенной, известна тем, что помогает учащимся «увидеть математику» за счет сосредоточения внимания на визуализации и технологиях. Эти тексты по-прежнему сохраняют функции, которые помогали учащимся добиваться успеха в течение многих лет: фокус на функциях, визуальный акцент, параллельные алгебраические и графические решения и приложения для работы с реальными данными. В пятом издании визуализация выведена на новый технологический уровень. Авторы также интегрируют приложения для смартфонов, побуждая читателей визуализировать математику. Кроме того, постоянный обзор дополнен новыми… еще
Эти тексты по-прежнему сохраняют функции, которые помогали учащимся добиваться успеха в течение многих лет: фокус на функциях, визуальный акцент, параллельные алгебраические и графические решения и приложения для работы с реальными данными. В пятом издании визуализация выведена на новый технологический уровень. Авторы также интегрируют приложения для смартфонов, побуждая читателей визуализировать математику. Кроме того, постоянный обзор дополнен новыми… еще
Посмотреть другие рекомендации по этой книге…
Купить на Amazon
66
Мэрилин Оккиогроссо | 4.44
Эта простая в использовании рабочая тетрадь полна стимулирующих заданий, которые помогут вашим учащимся прочно познакомиться с тригонометрией! Разнообразные головоломки и форматы самопроверки заставят учащихся мыслить творчески, пока они работают над развитием своих тригонометрических навыков. Каждая страница начинается с четкого объяснения избранной тригонометрической темы, обеспечивая дополнительный обзор и подкрепление. В конце книги есть специальный раздел для оценивания, который поможет учащимся подготовиться к стандартизированным тестам. меньше
В конце книги есть специальный раздел для оценивания, который поможет учащимся подготовиться к стандартизированным тестам. меньше
См. другие рекомендации по этой книге…
Купить на Amazon
67
Майкл Салливан | 4.43
Подготовка, практика, повторение Проверенный временем подход Салливана фокусирует учащихся на основных навыках, необходимых им для изучения курса: «подготовка» к занятиям, «практика» с домашними заданиями и «проверка» понятий. Серия Enhanced with Graphing Utilities была разработана для удовлетворения сегодняшних потребностей курса путем интеграции использования графических калькуляторов, активного обучения и технологий новыми способами, чтобы помочь учащимся добиться успеха в своем курсе, а также в своих будущих начинаниях. В седьмом издании есть несколько новых функций, которые появляются как в тексте, так и в MyMathLab. Сохраняйте свои знания… больше
См. дополнительные рекомендации по этой книге…
Купить на Amazon
68
Концепции и приложения
Paul A. Foerster | 4.42
Foerster | 4.42
См. другие рекомендации по этой книге…
Купить на Amazon
69
The Princeton Review | 4.40
РАСКРОЙТЕ СЕКРЕТЫ АЛГЕБРЫ II с ОБЗОР ПРИНСТОНА.
Алгебра может быть сложным предметом. Вот wh y Наша новая серия High School Unlocked посвящена тому, чтобы дать вам широкий спектр ключевых методов, которые помогут вам справиться с такими предметами, как алгебра II. Если какой-то метод вам не подходит, вы можете использовать альтернативный подход, чтобы понять концепцию или проблему, вместо того, чтобы мучительно пытаться делать одно и то же снова и снова, но безуспешно. Поверьте нам — раскрытие секретов алгебры не причинит вреда !
С помощью этой книги вы откроете для себя связь между… больше
См. дополнительные рекомендации по этой книге…
Купить на Amazon
70
Pearson Education | 4.40
Посмотреть другие рекомендации по этой книге. ..
..
Купить на Amazon
Нет времени читать лучшие книги по тригонометрии всех времен? Читайте краткие резюме.Краткое изложение помогает вам учиться в 10 раз быстрее:
- Быть исчерпывающим: вы узнаёте самых важных пункта в книге
- Избавляетесь от лишнего: вы сосредотачиваете своё время на том, что важно знать
- Интерактивные упражнения: примените идеи книги в своей жизни под руководством наших преподавателей.
Подпишитесь на бесплатные обзоры книг
71
Рон Ларсон | 4.39
Курс АЛГЕБРА И ТРИГОНОМЕТРИЯ Ларсона идеально подходит для двухсеместрового курса и известен тем, что предлагает четкие, последовательно структурированные объяснения и тщательно написанные упражнения. В десятом издании автор продолжает революционизировать способы обучения студентов, используя больше реальных приложений и инновационных технологий. Как вы это видите? упражнения дают учащимся возможность попрактиковаться в применении понятий. Обобщающие и контрольные вопросы укрепляют понимание навыков. MindTap Math, доступная опция для АЛГЕБРЫ И ТРИГОНОМЕТРИИ Ларсона, представляет собой цифровое решение для обучения, которое помогает преподавателям… больше
Обобщающие и контрольные вопросы укрепляют понимание навыков. MindTap Math, доступная опция для АЛГЕБРЫ И ТРИГОНОМЕТРИИ Ларсона, представляет собой цифровое решение для обучения, которое помогает преподавателям… больше
См. другие рекомендации по этой книге…
Купить на Amazon
72
Синтия Янг | 4.38
Любой, кто пытается изучать алгебру и тригонометрию, может думать, что понимает концепцию, но затем не может применить это понимание при выполнении упражнений. Эта новаторская книга помогает им преодолеть распространенные барьеры на пути изучения концепций и укрепляет уверенность в своих способностях заниматься математикой. Во втором издании в конце каждой главы представлены новые разделы по моделированию, а также новый материал по пределам и ранним функциям. Также включены многочисленные примеры, которые предоставляют более подробные аннотации с использованием повседневного языка. Такой подход дает им навыки понимания… more
Посмотреть другие рекомендации по этой книге. ..
..
Купить на Amazon
73
Маргарет Л. Лиал | 4.38
Серия College Algebra , написанная Лиал, Хорнсби, Шнайдером и Дэниэлсом, объединяет опыт ведущих учителей, чтобы помочь учащимся развить как концептуальное понимание, так и аналитические навыки, необходимые для успеха в математике. В этом последнем издании авторы отвечают на вызовы, связанные с новыми ожиданиями учащихся и новыми моделями обучения. Команда Lial теперь предлагает новый набор ресурсов для поддержки современных преподавателей и студентов.
ОСНОВНЫЕ ТЕМЫ: Обзор основных понятий; уравнения и неравенства; Графики и функции; Полиномиальные и… more
См. другие рекомендации по этой книге…
Купить на Amazon
74
Подход по единичному кругу
Майкл Салливан | 4.37
Проверенный временем подход Майка Салливана фокусирует учащихся на основных навыках, необходимых им для изучения курса: «подготовке» к занятиям, «попрактиковании» с домашними заданиями и «повторении» понятий. В девятом издании книга «Тригонометрия: подход единичного круга» эволюционировала, чтобы соответствовать современным потребностям курса, опираясь на эти отличительные черты путем интеграции проектов и других интерактивных средств обучения для использования в классе или в Интернете». меньше
В девятом издании книга «Тригонометрия: подход единичного круга» эволюционировала, чтобы соответствовать современным потребностям курса, опираясь на эти отличительные черты путем интеграции проектов и других интерактивных средств обучения для использования в классе или в Интернете». меньше
См. другие рекомендации по этой книге…
Купить на Amazon
75
Джон Кобурн | 4.37
Три компонента вносят свой вклад в тему, выдержанную на протяжении всей серии Coburn: закладка прочного фундамента, построение прочной основы и обеспечение прочных связей. Мало того, что Коберн представляет надежный процесс решения проблем, чтобы научить студентов распознавать проблему, организовывать процедуру и формулировать решение, текст побуждает студентов смотреть дальше процедур, чтобы лучше понять большие идеи, лежащие в основе математики. концепции. Тригонометрия Коберна, написанная читабельным, но математически зрелым языком, подходящим для студентов колледжа, использует. .. больше
.. больше
Посмотреть другие рекомендации по этой книге…
Купить на Amazon
Нет времени читать лучшие книги по тригонометрии всех времен? Читайте краткие резюме.Краткое изложение поможет вам учиться в 10 раз быстрее:
- Быть исчерпывающим: вы узнаете наиболее важных пункта в книге применить идеи книги в своей жизни под руководством наших преподавателей.
Подпишитесь на бесплатные обзоры книг
Что такое тригонометрия? | Живая наука
Живая наука поддерживается своей аудиторией. Когда вы покупаете по ссылкам на нашем сайте, мы можем получать партнерскую комиссию. Вот почему вы можете доверять нам.
Синус, косинус и тангенс являются основными тригонометрическими функциями. (Изображение предоставлено: ЮрийЗап | Shutterstock ) Тригонометрия — раздел математики, изучающий отношения между сторонами и углами треугольников. Тригонометрия встречается во всей геометрии, поскольку любую форму с прямыми сторонами можно разбить на набор треугольников. Более того, тригонометрия имеет поразительно сложные отношения с другими разделами математики, в частности с комплексными числами, бесконечными рядами, логарифмами и исчислением.
Более того, тригонометрия имеет поразительно сложные отношения с другими разделами математики, в частности с комплексными числами, бесконечными рядами, логарифмами и исчислением.
Слово «тригонометрия» является латинским производным 16-го века от греческих слов «треугольник» ( trigōnon ) и «мера» ( metron ). Хотя эта область возникла в Греции в третьем веке до нашей эры, некоторые из наиболее важных достижений (например, функция синуса) были получены в Индии в пятом веке нашей эры. Поскольку ранние тригонометрические работы Древней Греции были утеряны, неизвестно, были ли индийские ученые разработали тригонометрию независимо или под влиянием Греции. Согласно Виктору Кацу в «Истории математики (3-е издание) (открывается в новой вкладке)» (Пирсон, 2008 г.), тригонометрия возникла в первую очередь благодаря нуждам греческих и индийских астрономов.
Пример: высота мачты парусника
Предположим, вам нужно знать высоту мачты парусника, но вы не можете взобраться на нее, чтобы измерить. Если мачта перпендикулярна палубе, а верхняя часть мачты прикреплена к палубе, то мачта, палуба и такелажный канат образуют прямоугольный треугольник. Если мы знаем, на каком расстоянии от мачты протянута веревка и какой наклон она встречает настил, то все, что нам нужно для определения высоты мачты, — это тригонометрия.
Если мачта перпендикулярна палубе, а верхняя часть мачты прикреплена к палубе, то мачта, палуба и такелажный канат образуют прямоугольный треугольник. Если мы знаем, на каком расстоянии от мачты протянута веревка и какой наклон она встречает настил, то все, что нам нужно для определения высоты мачты, — это тригонометрия.
Для этой демонстрации нам нужно изучить несколько способов описания «наклона». Первый наклон , который представляет собой отношение, сравнивающее, на сколько единиц линия увеличивается по вертикали (ее подъем ) по сравнению с тем, на сколько единиц она увеличивается по горизонтали (ее длина ). Таким образом, уклон рассчитывается как подъем, деленный на пробег. Предположим, мы измеряем точку такелажа на расстоянии 30 футов (9,1 метра) от основания мачты (прогона). Умножив пробег на уклон, мы получили бы подъем — высоту мачты. К сожалению, мы не знаем наклона. Однако мы можем найти угол такелажного каната и используйте его, чтобы найти уклон . Угол – это некоторая часть полного круга, состоящая из 360 градусов. Это легко измерить транспортиром. Предположим, что угол между такелажным канатом и палубой составляет 71/360 окружности или 71 градус.
Угол – это некоторая часть полного круга, состоящая из 360 градусов. Это легко измерить транспортиром. Предположим, что угол между такелажным канатом и палубой составляет 71/360 окружности или 71 градус.
Нам нужен наклон, но у нас есть только угол. Что нам нужно, так это отношения, которые связывают их двоих. Это соотношение известно как «функция касательной », записанная как tan(x). Тангенс угла дает его наклон. Для нашей демонстрации уравнение выглядит так: tan(71°) = 2,9.0. (Позже мы объясним, как мы получили этот ответ.)
Это означает, что наклон нашей такелажной веревки равен 2,90. Поскольку точка крепления находится в 30 футах от основания мачты, мачта должна быть 2,90 × 30 футов или 87 футов в высоту. (В метрической системе это работает так же: 2,90 x 9,1 метра = 26,4 метра.)
Синус, косинус и тангенс
В зависимости от того, что известно о различных длинах сторон и углах прямоугольного треугольника, есть две другие тригонометрические функции что может быть полезнее: « функция синуса », записанная как sin(x), и «функция косинуса », записанная как cos(x). Прежде чем мы объясним эти функции, необходима дополнительная терминология. Соприкасающиеся стороны и углы описываются как смежные . Каждая сторона имеет два смежных угла. Стороны и углы, которые не соприкасаются, описываются как напротив . В прямоугольном треугольнике сторона, противоположная прямому углу, называется гипотенузой (от греческого «протягивающаяся вниз»). Две оставшиеся стороны называются ножки .
Прежде чем мы объясним эти функции, необходима дополнительная терминология. Соприкасающиеся стороны и углы описываются как смежные . Каждая сторона имеет два смежных угла. Стороны и углы, которые не соприкасаются, описываются как напротив . В прямоугольном треугольнике сторона, противоположная прямому углу, называется гипотенузой (от греческого «протягивающаяся вниз»). Две оставшиеся стороны называются ножки .
Обычно нас интересует (как в примере выше) угол, отличный от прямого. То, что мы назвали «подъемом» в приведенном выше примере, принимается за длину стороны, противоположной интересующему углу; аналогичным образом «прогон» принимается за длину соседнего участка. Применительно к измерению угла три тригонометрические функции дают различные комбинации отношений длин сторон.
Другими словами:
- Тангенс угла А = длина противолежащей стороны, деленная на длину прилежащей стороны
- Синус угла A = длина противоположной стороны, деленная на длину гипотенузы
- Косинус угла A = длина противолежащей стороны, деленная на длину гипотенузы
С нашей корабельной мачты В предыдущем примере отношение между углом и его тангенсом можно определить по его графику, показанному ниже. Также включены графики синуса и косинуса.
Также включены графики синуса и косинуса.
Стоит упомянуть, хотя и выходит за рамки этой статьи, что эти функции связаны друг с другом с помощью множества сложных уравнений, известных как тождества, уравнений, которые всегда верны.
Каждая тригонометрическая функция также имеет обратную, которую можно использовать для нахождения угла по отношению сторон. Инверсиями sin(x), cos(x) и tan(x) являются arcsin(x), arccos(x) и arctan(x) соответственно.
Обратные три основные тригонометрические функции. (Изображение предоставлено Робертом Дж. Кулманом)Формы, отличные от прямоугольных треугольников
Тригонометрия не ограничивается только прямоугольными треугольниками. Его можно использовать со всеми треугольниками и всеми фигурами с прямыми сторонами, которые рассматриваются как совокупность треугольников. Для любого треугольника по шести мерам сторон и углов, если известны хотя бы три, остальные три обычно можно определить. Из шести конфигураций трех известных сторон и углов только две из этих конфигураций не могут быть использованы для определения всего о треугольнике: три известных угла (ААА) и известный угол, смежный и противоположный известным сторонам (АСС). Неизвестные длины сторон и углы определяются с помощью следующих инструментов:
Из шести конфигураций трех известных сторон и углов только две из этих конфигураций не могут быть использованы для определения всего о треугольнике: три известных угла (ААА) и известный угол, смежный и противоположный известным сторонам (АСС). Неизвестные длины сторон и углы определяются с помощью следующих инструментов:
- Закон синусов, согласно которому, если известны обе меры одной из трех противолежащих пар угол/сторона, другие могут быть определены только по одному известному: sin(A)/a = sin(B)/b = sin(C)/c
- Закон косинусов, согласно которому неизвестную сторону можно найти по двум известным сторонам и углу между ними. По сути, это теорема Пифагора с поправочным коэффициентом для углов, отличных от 90 градусов: c2 = a2 + b2 – 2ab∙cos(C)
- . Тот факт, что сумма всех углов в треугольнике должна составлять 180 градусов: A + В + С = 180°
История тригонометрии
Тригонометрия идет тем же путем, что и алгебра: она была разработана на древнем Ближнем Востоке и через торговлю и иммиграцию попала в Грецию, Индию, средневековую Аравию и, наконец, в Европу (где, следовательно, колониализм сделал ее версией большинство людей учат сегодня). Хронология тригонометрических открытий усложняется тем фактом, что Индия и Аравия продолжали преуспевать в исследованиях на протяжении столетий после передачи знаний через культурные границы. Например, открытие Мадхавой бесконечной последовательности синусов в 1400 году было неизвестно Европе вплоть до независимого открытия Исаака Ньютона в 1670 году. Из-за этих сложностей мы сосредоточимся исключительно на открытии и прохождении синуса, косинуса и тангенса.
Хронология тригонометрических открытий усложняется тем фактом, что Индия и Аравия продолжали преуспевать в исследованиях на протяжении столетий после передачи знаний через культурные границы. Например, открытие Мадхавой бесконечной последовательности синусов в 1400 году было неизвестно Европе вплоть до независимого открытия Исаака Ньютона в 1670 году. Из-за этих сложностей мы сосредоточимся исключительно на открытии и прохождении синуса, косинуса и тангенса.
Начало на Ближнем Востоке, седьмой век до н.э. ученые Новой Вавилонии определили метод для вычисления времени восхода неподвижных звезд на зодиаке. Для восхода другой неподвижной звезды незадолго до рассвета требуется примерно 10 дней, и в каждом из 12 знаков зодиака есть по три неподвижные звезды; 10 × 12 × 3 = 360. Число 360 достаточно близко к 365,24 дням в году, но с ним гораздо удобнее работать. Почти идентичные деления встречаются в текстах других древних цивилизаций, таких как Египет и долина Инда. Согласно Уте Мерцбах в «Истории математики » (Wiley, 2011), адаптация этой вавилонской техники греческим ученым Гипсиклом из Александрии около 150 г. до н.э. был, вероятно, источником вдохновения для Гиппарха Никейского (19от 0 до 120 г. до н.э.), чтобы начать тенденцию к разрезанию круга на 360 градусов. Используя геометрию, Гиппарх определил тригонометрические значения (для функции, которая больше не используется) для приращений в 7,5 градусов (48 90 115 90 116 круга). Птолемей Александрийский (с 90 по 168 г. н.э.) в своем «Альмагесте» 148 г. н.э. продолжил работу Гиппарха, определив тригонометрические значения для приращений в 0,5 градуса (a 720 th окружности) от 0 до 180 градусов.
до н.э. был, вероятно, источником вдохновения для Гиппарха Никейского (19от 0 до 120 г. до н.э.), чтобы начать тенденцию к разрезанию круга на 360 градусов. Используя геометрию, Гиппарх определил тригонометрические значения (для функции, которая больше не используется) для приращений в 7,5 градусов (48 90 115 90 116 круга). Птолемей Александрийский (с 90 по 168 г. н.э.) в своем «Альмагесте» 148 г. н.э. продолжил работу Гиппарха, определив тригонометрические значения для приращений в 0,5 градуса (a 720 th окружности) от 0 до 180 градусов.
Самое старое упоминание функции синуса происходит из Индии пятого века в работе Арьябхаты (476–550). Стих 1.12 «Арьябхатийя» (499) вместо представления углов в градусах содержит список последовательных разностей синусов двадцать четвертых прямого угла (с шагом 3,75 градуса). Это было отправной точкой для большей части тригонометрии на века вперед.
Следующая группа великих ученых, унаследовавших тригонометрию, принадлежала к Золотому веку ислама. Аль-Мамун (813–833), седьмой халиф Аббасидского халифата и создатель Дома мудрости в Багдаде, спонсировал перевод «Альмагеста» Птолемея и «Арьябхатийя» Арьябхаты на арабский язык. Вскоре после Аль-Хорезми (780 — 850) составил точные таблицы синусов и косинусов в «Зидж аль-Синдхинд» (820). Именно благодаря этой работе знание тригонометрии впервые пришло в Европу. Согласно Джеральду Тумеру в «Словаре научной биографии 7», хотя оригинальная арабская версия была утеряна, она была отредактирована около 1000 г. аль-Маджрити из Аль-Андалуса (современная Испания), который, вероятно, добавил таблицы касательных до Аделара из Бат (в Южной Англии) перевел его на латынь в 1126 году.
Аль-Мамун (813–833), седьмой халиф Аббасидского халифата и создатель Дома мудрости в Багдаде, спонсировал перевод «Альмагеста» Птолемея и «Арьябхатийя» Арьябхаты на арабский язык. Вскоре после Аль-Хорезми (780 — 850) составил точные таблицы синусов и косинусов в «Зидж аль-Синдхинд» (820). Именно благодаря этой работе знание тригонометрии впервые пришло в Европу. Согласно Джеральду Тумеру в «Словаре научной биографии 7», хотя оригинальная арабская версия была утеряна, она была отредактирована около 1000 г. аль-Маджрити из Аль-Андалуса (современная Испания), который, вероятно, добавил таблицы касательных до Аделара из Бат (в Южной Англии) перевел его на латынь в 1126 году.
Дополнительные ресурсы
- Math Is Fun: тригонометрия
- Академия Хана: тригонометрия
- Wolfram MathWorld: тригонометрия
Роберт Кулман, доктор философии, преподаватель и независимый научный писатель, живет в Мэдисоне, штат Висконсин. Он писал для Vice, Discover, Nautilus, Live Science и The Daily Beast. Роберт защитил докторскую диссертацию, превращая опилки в бензиновое топливо и химикаты для материалов, медицины, электроники и сельского хозяйства. Он сделан из химических веществ.
Роберт защитил докторскую диссертацию, превращая опилки в бензиновое топливо и химикаты для материалов, медицины, электроники и сельского хозяйства. Он сделан из химических веществ.
Trigonometry — 1st Edition
Select country/regionUnited States of AmericaUnited KingdomAfghanistanÅland IslandsAlbaniaAlgeriaAmerican SamoaAndorraAngolaAnguillaAntigua and BarbudaArgentinaArmeniaArubaAustraliaAustriaAzerbaijanBahamasBahrainBangladeshBarbadosBelgiumBelizeBeninBermudaBhutanBoliviaBonaire, Sint Eustatius and SabaBosnia and HerzegovinaBotswanaBrazilBritish Indian Ocean TerritoryBritish Virgin IslandsBruneiBulgariaBurkina FasoBurundiCambodiaCameroonCanadaCanary IslandsCape VerdeCayman IslandsCentral African RepublicChadChileChinaChristmas IslandCocos (Keeling) IslandsColombiaComorosCongoCook IslandsCosta RicaCroatiaCubaCuraçaoCyprusCzech RepublicDemocratic Republic of the CongoDenmarkDjiboutiDominicaDominican RepublicEcuadorEgyptEl СальвадорЭкваториальная ГвинеяЭритреяЭстонияЭфиопияФолклендские (Мальвинские) островаФарерские островаФедеративные Штаты МикронезииФиджиФинляндияФранцияФранцузская ГвианаФранцузская ПолинезияГабонГамбияГрузияГерманияГанаГибралтарГрецияГренландияГренадаГуад eloupeGuamGuatemalaGuernseyGuineaGuinea-BissauGuyanaHaitiHondurasHong KongHungaryIcelandIndiaIndonesiaIranIraqIrelandIsle of ManIsraelItalyJamaicaJapanJerseyJordanKazakhstanKenyaKiribatiKuwaitKyrgyzstanLaoLatviaLesothoLiberiaLibyaLiechtensteinLuxembourgMacaoMacedoniaMadagascarMalawiMalaysiaMaldivesMaliMaltaMarshall IslandsMartiniqueMauritaniaMauritiusMayotteMexicoMoldovaMonacoMongoliaMontenegroMontserratMoroccoMozambiqueMyanmarNamibiaNepalNetherlandsNew CaledoniaNew ZealandNicaraguaNigerNiueNorfolk IslandNorth KoreaNorthern Mariana IslandsNorwayOmanPakistanPalauPanamaPapua New GuineaParaguayPeruPhilippinesPitcairnPolandPortugalPuerto RicoQatarRéunionRomaniaRwandaSaint BarthélemySaint HelenaSaint Kitts and NevisSaint LuciaSaint Martin (French part)Saint Pierre and MiquelonSaint Vincent and the GrenadinesSamoaSan MarinoSao Tome and PrincipeSaudi ArabiaSenegalSerbiaSeychellesSierra LeoneSingaporeSint Maarten (Dutch part)SlovakiaSloveniaSolomon IslandsSomaliaSouth AfricaSouth Georgia и т he South Sandwich IslandsSouth KoreaSouth SudanSpainSri LankaSudanSurinameSvalbard and Jan MayenSwazilandSwedenSwitzerlandSyriaTaiwanTajikistanTanzaniaThailandTimor LesteTogoTokelauTongaTrinidad and TobagoTunisiaTurkeyTurkmenistanTurks and Caicos IslandsTuvaluUgandaUkraineUnited Arab EmiratesUruguayUS Virgin IslandsUzbekistanVanuatuVatican CityVenezuelaVietnamWallis and FutunaWestern SaharaYemenZambiaZimbabwe
Варианты покупки недоступны.
Бесплатная доставка по всему миру
Нет минимального заказа
Описание
Тригонометрия посвящена принципам, операциям, формулам и функциям тригонометрии. В публикации сначала рассматриваются шесть тригонометрических функций, тригонометрия прямоугольного треугольника и мера радиана. Обсуждения сосредоточены на освещенности и градусах, единичном круге и четных и нечетных функциях, длине дуги и площади сектора, тригонометрических функциях острого угла, решении прямоугольных треугольников, прямоугольной системе координат, а также углах, градусах и специальных треугольниках. Затем в рукописи рассматриваются графики и обратные функции, тождества, формулы и уравнения. Темы включают решение тригонометрических уравнений, параметрических уравнений и дальнейшее построение графиков, формулы суммы и разности, формулы половинного угла, дополнительные тождества, фазовый сдвиг, амплитуду и период, построение графиков комбинаций функций и обратных тригонометрических функций. В тексте рассматриваются комплексные числа и полярные координаты, треугольники и уравнения, включая закон синусов и косинусов, произведения и частные в тригонометрической форме, корни комплексного числа и полярные координаты. Книга является надежным справочником для студентов и читателей, интересующихся тригонометрией.
В тексте рассматриваются комплексные числа и полярные координаты, треугольники и уравнения, включая закон синусов и косинусов, произведения и частные в тригонометрической форме, корни комплексного числа и полярные координаты. Книга является надежным справочником для студентов и читателей, интересующихся тригонометрией.
Содержание
-
1 Шесть тригонометрических функций I
1.1 Углы, градусы и специальные треугольники
1.2 Прямоугольная система координат
1.3 Определение 1: Тригонометрические функции
Тест
2 Тригонометрия прямоугольного треугольника
2.1 Тригонометрические функции острого угла
2.2 Таблицы и калькуляторы для тригонометрических функций острого угла
2.3 Решение прямоугольных треугольников
2.4 Приложения
2.5 Векторы
Резюме и обзор
Тест
3 Радианная мера
3.1 Базовый угол
3.2 Радианы и градусы
3.3 Единичная окружность, четная и нечетная функции
и площадь сектора
3. 4 Длина дуги
4 Длина дуги
3.5 Скорости
Сводка и обзор
Тест
4 Графики и обратные функции
4.1 Основные графики
4.2 Амплитуда и период
4.3 Фазовый сдвиг
4.4 Графики комбинаций функций
4.5 Обратные тригонометрические отношения
4.6 Обратные тригонометрические функции
Сводная и обзор
Тест
5 Идентификации и формулы
5.1 Доказательные идентичности
5,2 Сумма и разнообразные формы
5.3. Форма с двойным углом
5.4. Обзор
Тест
6 Уравнения
6.1 Решение тригонометрических уравнений
6.2 Дополнительные сведения о тригонометрических уравнениях
6.3 Тригонометрические уравнения с участием нескольких углов
6.4 Параметрические уравнения и построение графиков
Резюме и обзор
Тест
7 Треугольники
7.1 Закон синусов
7.2 Неоднозначный случай
7.3 Закон косинусов
7.4 Площадь треугольника
Резюме и обзор
Комплексные числа
Тест 90 и полярные координаты
8.
