Бинарное отношение: Отношения. Часть II / Хабр

Отношение. Бинарное отношение

Бинарным отношением на множествах А,В называется произвольное подмножество декартовых произведений этих множеств.

Бинарное отношение можно интерпретировать как некоторое свойство, которым обладают пара элементов множества А и В.

Тот факт что элементы аA bB записывается (a,b)или ab.

Если бинарные отношения заданы на паре множ. А,А, то ешл называют бинарным отношением на множ А. 

Симметричная разность А∆В. Симметричной разностью называется множество С, которое состоит из тех и только тех элементов, которые входят в объединеннное множество АиВ и не входят в пересечение.

Бинарное отношение удобно изображать, используя язык теории графов. При этом элементы множества изображаются точками на плоскости, а тот факт, что ab обозначается стрелкой из a в b. Стрелки — это дуги.

Булеан на декартовом произведении АВ множество бинарных отношений на паре множеств А,В 2^(А*В).

(-1), *, то есть применяя эти операции к элементам данного булеана в результате получим элементы этого же булеана.

Свойства бинарных отношений

1.Бинарным отношением на множестве А называется диагональным, если оно состоит из всевозможных пар одинаковых элементов. В графичном изображении диагонального бинарного отношения каждый элемент имеет петлю, других дуг нет.

2.Бинарное отношение на множестве А называется рефлексивным, если каждый элемент этого множества находится в отношении с самим собой.

Для рефлексивного бинарного отношения в графичном изображении возможны кроме петель другие дуги.

3.Бинарное отношение  на множестве А называется транзитивным, если abbc =>ac

Бинарное отношение транзитивно тогда и только тогда, когда из а есть дуга в b из b есть дуга в с

4.Бинарное отношение на множине А называется симметричным, если ab =>ba

5.Бинарное отношение на множине А называется антисимметричным, если ab,ba => a=b

6. Бинарное отношение на множине А называется отношением эквивалентности, если оно одновременно рефлективно, симметрично и транзитивно

7.Бинарным отношением на множине А называется отношением порядка, если оно одновременно рефлективно, антисимметрично и транзитивно.

Два элемента a и b ищ множ. А назыв. Сравнимыми, если справедливо аb и ba.

Бинарное отношение и его свойства

Свойство 1. Умножение бинарного отношения А на положительную  [c.75]

Свойство 2. Ранжирование альтернатив на основе бинарных отношений  [c.75]

Типы бинарных отношений. В зависимости от свойств, которыми обладают бинарные отношения, производят их типизацию. Приведем определения некоторых распространенных типов бинарных отношений.  [c.23]

Рассмотрим ситуацию, когда одно решение предпочтительнее второго, а оно, в свою очередь, предпочтительнее некоторого третьего решения. В таком положении здравомыслящий человек при сравнении первого и третьего решения всегда выберет первое.

Здесь происходит примерно то же самое, что и при сравнении чисел с помощью отношения строгого неравенства. Например, если 5 > 3 и 3 > 1, то непременно выполнено 5 > 1. В терминах возможных решений это свойство может быть сформулировано следующим образом для любой тройки возможных решений х, х», х » из выполнения соотношений х >х х» и х» >х х » обязательно следует справедливость соотношения х >-х х «. На языке бинарных отношений это означает, что отношение предпочтения, используемое в задачах многокритериального выбора, должно быть подчинено требованию транзитивности.  [c.26]

Отношения, инвариантные относительно линейного положительного преобразования. Напомним определение инвариантного отношения, данное в разд. 1.2. Бинарное отношение Ж, заданное на пространстве Rm называют инвариантным относительно линейного положительного преобразования, если для произвольных векторов у, у» / » из выполнения соотношения у Шу» следует соотношение (ау + с) Ж (ау» + с) для любого вектора с е Rm и всякого положительного числа а. Иначе говоря, отношение Ш является инвариантным относительно положительного линейного преобразования, если оно обладает следующими двумя свойствами  [c.51]

Для математического моделирования предпочтений всегда важно знать, какими из свойств бинарных отношений оно обладает. Среди разнообразных свойств бинарных отношений нас прежде всего будут интересовать такие, как реф-  [c.169]

В общем случае для существования функции полезности потребительские предпочтения представляются бинарным отношением — подмножеством прямого произведения пространства благ с самим собой, от которого требуют свойств полноты и транзитивности. Тогда пространство благ разбивается на классы эквивалентных элементов, отражающих факт безразличия выбора потребителя между элементами этих классов, и предпочтения можно представить действительнозначной функцией полезности.  [c.109]

Бинарное отношение и его свойства  [c.16]

Определим теперь некоторые свойства бинарных отношений, которые мы в дальнейшем будем использовать при рассмотрении отношений предпочтения.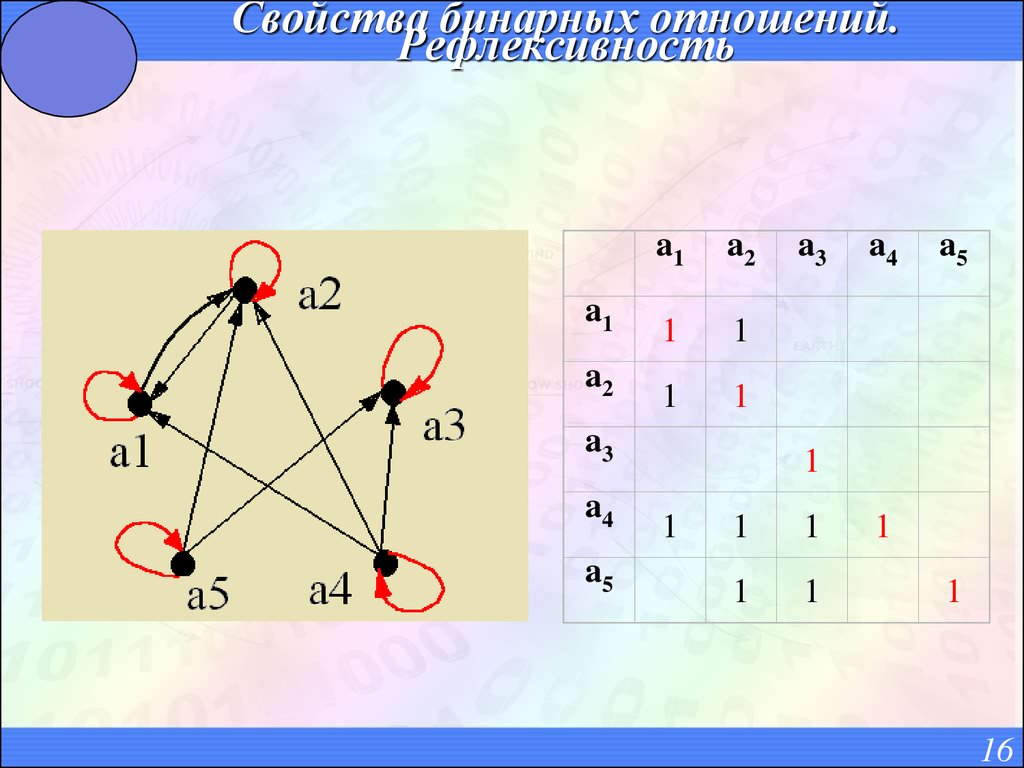  [c.17]

Проиллюстрируем введенные свойства бинарного отношения на примерах. Пример 1.  [c.17]

Выше мы ввели и обсудили ряд часто используемых свойств бинарных отношение. Сейчас рассмотрим взаимосвязь между этими свойствами.  [c.18]

Кстати, а каким свойствам удовлетворяет это бинарное отношение  [c.18]

Приведите пример бинарного отношения, не удовлетворяющего ни свойству симметричности, ни свойству асимметричности.  [c.20]

Не прибегая к исчислению высказываний (т.е. рассуждениям вида ( А => В) (В =>А)), докажите, что для любого бинарного отношения Т свойство  [c.21]

Будем строить теорию потребительского поведения на основе строгого отношения предпочтения >- — бинарного отношения, заданного на множестве допустимых альтернатив. Тот факт, что в случае двух альтернатив х и у из X для некоторого потребителя альтернатива х лучше, чем альтернатива у будет обозначаться как х > у. Традиционным для экономической теории является предположение о том, что строгое отношение предпочтения, на основе которого потребители упорядочивают альтернативы, асимметрично и отрицательно транзитивно. Эти предположения о свойствах отношения >- тесно связаны с понятиями рациональности потребителя, непротиворечивости вкусов, их внутренней состоятельности. В данном контексте свойство асимметричности предпочтения позволяет говорить о непротиворечивости вкусов потребителя. Свойство отрицательной транзитивности, в свою очередь, означает, что если некоторые две альтернативы сравнимы по отношению >-, то любая третья альтернатива сравнима, по крайней мере, с одной из них по этому отношению. Как мы увидим далее, это свойство тоже тесно связано с непротиворечивостью выбора и полнотой предпочтений. Пока же на основе строгого отношения определим нестрогое отношение предпочтения и отношение эквивалентности.  [c.21]

Рассмотрим теперь, каким свойствам удовлетворяют введенные выше бинарные отношения.  [c.22]

Пусть > — нестрогое отношение предпочтения (полное и транзитивное бинарное отношение), заданное на X, а >- (х>у (х>у) и (у>х) ) и (х у (х>у) и (у>х)) — строгое отношение предпочтения и отношение эквивалентности, построенные на его основе.

Каким свойствам будут удовлетворять отношения >- и  [c.27]

Пусть > — нестрогое отношение предпочтения (полное и транзитивное бинарное отношение) заданное на X, а (х у (х >у и (у>х) ) — отношение эквивалентности. Рассмотрим семейство множеств (кривых) безразличия, построенных на основании . Как на основании порядка, задаваемого отношением >, корректно и непротиворечиво ввести порядок на этом семействе Какими свойствами он обладает  [c.28]

ТЕОРИЯ ГРАФОВ [graph theory] — математическая теория, содержание которой формулируется двояко в зависимости от трактовки ее исходного понятия граф теоретико-множественной или геометрической. В первом случае предметом теории являются графы как некие объекты, определяемые двумя множествами — множеством элементов и множеством бинарных отношений между ними. Во втором случае — свойства геометрических схем (графов), образованных множеством точек и соединяющих их линий (подробнее см. в ст. «Граф»).  [c.355]

Теоретико-множественные ММО [11 и др. ]. Эта группа методов основана на использовании теории бинарных отношений. Именно предполагается, что функция выбора ЛПР является бинарной, т. е. описывается бинарным отношением » R на множестве альтернатив (или на множестве критериальных оценок). На основании наблюдений за работой ЛПР или путем опроса экспертов строится набор решающих правил , устанавливающих некоторые свойства и соотношения отношения R. После выявления принадлежности очередного решающего правила RikR помощью ЭВМ выделяется ядро отношения Ri на множестве альтернатив xi, т. е. GRl xi). Далее полагают  [c.73]

Мы будем предполагать, что причинные связи между индивидами можно аксиоматизировать, используя бинарное отношение, которое мы обозначим символом ->. Так, (а->Ь) должно обозначать, что некоторое свойство индивида а (значение некоторого предиката или функции от а) причинно связано с некоторым свойством индивида Ь, и если последнее изменяется, то, вероятно, изменится и первое свойство. Смысл нашего предположения состоит в том, что если мы сможем доказать (а- -Ь) ), то ясно, что любое изменение b не вызовет никакого изменения а.

Это немедленно приводит к правилу вывода. Например, если нам известно, что а не связано отношением -> ни с одним из индивидов, на которые непосредственно влияет действие, то мы можем вывести, что после совершения данного действия все свойства индивида а сохраняются.  [c.444]

В частности, бинарное отношение называют эквивалентностью, если оно обладает свойствами рефлексивности, транзитивности и симметричности. Это отношение играет важную роль при принятии решений, поскольку моделирует факт разбиения множества предъявленных ЛПР элементов на определенные классы одинаковой предпочтительности. Элементы, принадлежащие одному классу эквивалентности, равноценны по предпочтению, а принадлежащие разным классам — резко различаются по предпочтительности при их сравнении с элементами других классов. Эквивалентность между элементами можно понимать как их взаимозаменимость при выборе для ЛПР. При этом свойство транзитивности очень важно для однозначности отнесения объекта к тому или иному классу.

Если отношение предпочтения только лишь симметрично и рефлексивно, то оно будет толерантностью (образовывать класс «похожих» элементов), но не эквивалентностью. Так, например, результаты сортировки в ходе экспертизы могут моделироваться либо как эквивалентность, либо как толерантность — в зависимости от степени уверенности, с которой ЛПР сортировало множество предъявления в соответствии со своими предпочтениями. Обычно ЛПР среди предъявленных ему элементов может уверенно отнести к тому или иному классу лишь элементы субъективно «сильно» различающиеся между собой, а среди оставшихся, «похожих», действует менее уверенно. В результате транзитивность на  [c.170]

Пусть Х- множество студентов учащихся в этом учебном году в Новосибирском Государственном Университете, 91 — отношение выше ростом, чем заданное на X. Посмотрим, каким указанным выше свойствам удовлетворяет данное бинарное отношение. Очевидно, что какого бы мы студента не взяли, его рост не может быть больше его же роста, т. е., например, 175 не может быть больше 175. Таким образом, это отношение является иррефлексивным и не удовлетворяет свойству рефлексивности. Это отношение также является  [c.17]

Часто это свойство также называют нерефлексивностью, но при такой терминологии возникают довольно странные выражения типа — бинарное отношение не является ни рефлексивным, ни нерефлексивным . Что бы избежать этой игры слов, мы и используем выбранный вариант.  [c.17]

Пусть Х=М+, на этом множестве задано отношение 91 по правилу (ж15ж2) T iy y2) х1 + у2 у1+ х2. Перед тем как отвечать на вопрос о том, каким свойствам удовлетворяет данное бинарное отношение, заметим, что xl + у2 yl + х2 xl — х2 yl — у2, т.е. (жьж2) Т у у2) х1 — х2 У у2. Как не сложно догадаться, данное бинарное отношение удовлетворяет тем же свойствам, что и отношение на действительной прямой, т.е. полнота, транзитивность, рефлексивность. Проверьте самостоятельно выполнение/невыполнение условий симметричности/асимметричности и отрицательной транзитивности.  [c.18]

7.1: Бинарные отношения — Математика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

23920

• Дэйв Витте Моррис и Джой Моррис
• Летбриджский университет

Напомним, что по определению любая функция \(f : A \rightarrow B\) представляет собой набор упорядоченных пар. Точнее, каждый элемент \(f\) представляет собой упорядоченную пару \((a, b)\), такую, что \(a \in A\) и \(b \in B\). Следовательно, каждый элемент \(f\) является элементом \(A \times B\), поэтому \(f\) является подмножеством \(A \times B\). \[\text { Каждая функция от } A \text { до } B \text { является подмножеством } A \times B \text {. }\]

Пример \(7.1.1\).

Функция \(\text {мать: ЛЮДИ } \rightarrow \text { ЛЮДИ }\) представлена ​​множеством \[\{(p, m) \in \text { ЛЮДИ } \times \text { ЛЮДИ } \mid m \text { мать } p\} .\]

Многие другие отношения также могут быть представлены подмножествами \(\text {PEOPLE} \times \text {PEOPLE}\), даже если они не являются функциями. Например, сын не является функцией, потому что у некоторых людей есть более одного сына (или потому что у некоторых людей вообще нет сыновей). Однако мы можем представить это отношение множеством

На самом деле любое отношение, которое вы можете определить между двумя людьми (или, говоря так на официальном языке логики, любой бинарный предикат на множестве \(\text {ЛЮДИ}\)) может быть представлено подмножеством \ (\text {ЛЮДИ} \times \text {ЛЮДИ}\). Вот несколько примеров возможных взаимосвязей:

• \(x\) сестра \(y\)
• \(x\) знал \(y\) в старшей школе
• \(x\) выше, чем \(y\)
• \(x\) и \(y\) учатся в одном математическом классе
• и т. д.

Признавая это, математики просто определяют отношение как набор упорядоченных пар; то есть отношение — это любое подмножество \(A \times B\). В отличие от функций здесь нет ограничений — каждое подмножество является отношением.

Определение \(7.1.2\).

Предположим, что \(A\) и \(B\) — множества.

1. Любое подмножество \(A \times B\) называется отношением от \(A\) до \(B\).
2. Для особого случая, когда \(A = B\), любое подмножество \(A \times A\) называется бинарным отношением на \(A\).

В основном нас будут интересовать бинарные отношения, а не отношения от некоторого множества \(A\) к некоторому другому множеству \(B\).

Пример \(7.1.3\).

Некоторые примеры бинарных отношений на \(\text {ЛЮДИ}\): \(\text {брат, сестра, тетя, дядя, мать, отец, дедушка, двоюродный брат и т. д.}\)

Определение \(7.1.4\).

Мы можем нарисовать картинку для представления любого заданного бинарного отношения на любом заданном множестве \(A\):

• Нарисовать точку для каждого элемента \(A\).
• Для \(a, b \in A\) проведите стрелку от \(a\) к \(b\) тогда и только тогда, когда \((a, b)\) является элементом отношения.

Полученная картинка называется 9{2}+y<10\вправо\} .\]

Это бинарное отношение представлено следующим орграфом:

Например, обратите внимание, что \((x, 4) \in R \text { iff } x \in\{1,2\}\), а орграф имеет стрелки от 1 до 4 и от 2 до 4.

Упражнение \(7.1.6\).

Пусть \(B\) будет набором, состоящим из вас, ваших братьев и сестер, ваших родителей, ваших бабушек и дедушек. Нарисуйте орграф, представляющий каждое из следующих бинарных отношений на \(B\).

1. Отношение «когда-либо имело ту же фамилию, что и».
2. Отношение «является потомком».
3. Отношение «когда-либо состояло в браке».

Пример \(7.1.7\).

В этой книге (как и в других учебниках по математике) в основном рассматриваются отношения на множествах математических объектов. Вот несколько хорошо известных примеров:

1. Отношение «меньше чем» «\(<\)» является бинарным отношением на \(\mathbb{R}\).
   То есть для любых действительных чисел \(x\) и \(y\) утверждение \(x < y\) либо истинно, либо ложно.
2. Отношение равенства «\(=\)» — это бинарное отношение ко всей вселенной дискурса \(\mathcal{U}\).
3. Отношение подмножества «\(\subset\)» — это бинарное отношение на наборе всех множеств в \(\mathcal{U}\).
4. Отношение «\(x\) не пересекается с \(y\)» также является бинарным отношением на наборе всех множеств в \(\mathcal{U}\).

Обозначение \(7.1.8\).

Предположим, что \(R\) является бинарным отношением на множестве \(A\). Для \(a_{1}, a_{2} \in A\):

1. Чтобы показать, что \((a_{1}, a_{2}) \in R\), мы можем написать \(a_{1} R a_{2}\).
2. Чтобы обозначить, что \(\left(a_{1}, a_{2}\right) \notin R\), мы можем написать \(a_{1} \not R a_{2}\).

Есть три основных свойства, которыми может обладать или не обладать любое заданное бинарное отношение:

Определение \(7.

1.9\).

Предположим, что \(R\) является бинарным отношением на множестве \(A\).

1. Мы говорим, что \(R\) является рефлексивным тогда и только тогда, когда \(\forall a \in A, (a R a)\).
2. Мы говорим, что \(R\) является -симметричным тогда и только тогда, когда \(\для всех a, b \in A,((a R b) \Rightarrow(b R a))\).
3. Мы говорим, что \(R\) является транзитивным тогда и только тогда, когда \(\для всех a, b, c \in A,(((a R b) \&(b R c)) \Rightarrow(a R c)) \).

Пример \(7.1.10\).

1. «\(=\)» рефлексивно, симметрично и транзитивно».
2. «\(<\)" является транзитивным, но не рефлексивным и не симметричным.
3. «\(\subset\)» является транзитивным и рефлексивным, но не симметричным.

Пример \(7.1.12\).

Рассмотрим следующее бинарное отношение \(R\) на \(\{1, 2, 3\}\): \[R=\{(1,1),(2,2),(3,3) ,(1,2),(2,1),(2,3),(3,2)\}\]

1. \(R\) рефлексивно, так как \(1 R 1,2 R 2,\) и \(3 R 3\).
2. \(R\) симметрично, потому что для каждого \((a, b) \in R\) обращение \((b, a)\) также находится в \(R\).
3. \(R\) есть , а не транзитивно, потому что \(1 R 2\) и \(2 R 3\), а \(1 \не R 3\).

Упражнение \(7.1.12\).

Найдите бинарные отношения на \(\{1, 2, 3\}\), которые являются:

1. симметричными, но ни рефлексивными, ни транзитивными.
2. рефлексивно, но ни симметрично, ни транзитивно.
3. транзитивно и симметрично, но не рефлексивно.
4. ни рефлексивный, ни симметричный, ни транзитивный.

( Представьте каждое отношение в виде набора упорядоченных пар, нарисуйте соответствующий орграф и кратко обоснуйте свои ответы. )

---

Эта страница под названием 7.1: Бинарные отношения распространяется под лицензией CC BY-NC-SA 2.0, автором, ремиксом и/или куратором этой страницы являются Дэйв Витте Моррис и Джой Моррис.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или страница

   Автор

   Дэйв Витте Моррис и Джой Моррис

   Лицензия

   CC BY-NC-SA

   Версия лицензии

   2,0

   Показать страницу TOC

   нет

2. Теги

   На этой странице нет тегов.

бинарное отношение — Викисловарь

Содержание

• 1 Английский
  • 1.1 Существительное
    • 1.1.1 Замечания по использованию
    • 1.1.2 Синонимы
    • 1.1.3 Гипонимы
    • 1.1.4 Переводы
  • 1.2 См. также
  • 1.3 Дополнительная литература

Английский0299

Википедия

Существительное

1. (теория множеств, теория порядка, «на» множестве A) Подмножество декартова произведения A × A (множество упорядоченных пар ( a , b ) элементов A ).
   • 1978 , Джордж Гретцер, Общая теория решеток , Academic Press, стр. 1,

     А частично упорядоченный набор ⟨A,ϱ⟩{\displaystyle \langle A,\varrho \rangle} состоит из непустого набора A{\displaystyle A} и бинарного отношения ϱ{\displaystyle \varrho} на A{\ displaystyle A}, такой, что ϱ{\displaystyle \varrho} удовлетворяет свойствам (P1)–(P3).

   • 1999 , Джеймс С. Мур, Математические методы экономической теории 1 , Springer, стр. 24,

     1.30. Следствие. Если P является бинарным отношением , который является асимметричным и отрицательно транзитивным, то P также транзитивен.

     Следует отметить, что бинарное отношение может быть иррефлексивным и отрицательно транзитивным, не будучи транзитивным; в качестве примера рассмотрим стандартное соотношение неравенства (≠).

   • 2005 , Т. С. Блит, Решетки и упорядоченные алгебраические структуры , Springer, стр. 1,

     Определение Если E непустое множество, то с помощью порядка к E мы имеем в виду бинарное отношение к E , которое является рефлексивным, антисимметричным и транзитивным.

2. (теория множеств, теория порядка, «на» или «между» множествами A и B) Подмножество декартова произведения A × B .

Примечания по использованию , и можно сказать, что a{\displaystyle a} находится в двоичном отношении R{\displaystyle R} к b{\displaystyle b}.

Синонимы[править]

• (теория порядка): соответствие, диадическое отношение, двухместное отношение

  теория порядка

  Чехия: binární relace  f Финский: binäärirelaatio Французский язык: binaire f Венгерский: kétváltozós reláció (hu) Исландский: tvistæð vensl n pl

  Итальянский: relazione binaria f Японский: 二項関係 (ja) (nikō-kankei) Румынский: relație binară (ro)  f Испанский: relación binaria  f

  См.

  

  No related posts.