| |||||||
|
Таблицы истинности — презентация онлайн
Похожие презентации:
Основы логики.
n+1, где n – количество
переменных)
Выяснить количество столбцов = количество
переменных + количество логических операций.
Установит последовательность выполнения
Построить таблицу, указывая названия
столбцов и возможные наборы значений
исходных логических переменных.
Заполнить таблицу истинности по столбцам.
4. Постройте таблицу истинности для выражения F=(A v B) (A v B)
Постройте таблицуистинности для выражения
F=(A v B) ( A v B)
5. Постройте таблицу истинности для выражения F=X v Y Z
Постройте таблицуистинности для выражения
F=X v Y Z
6. Составьте таблицы истинности для следующих логических выражений
1.2.
3.
4.
5.
6.
F=(X Y) v Z
F=X Y v X
F= (X v Y) (Y v X)
F= ((X v Y) (Z v X)) (Z v Y)
F=A B C D
F=(A v B) ( B v A v B)
7. Составьте таблицы истинности для следующих логических выражений и определите значение логического выражения при заданных
значениях переменных1.
2.
3.
4.
5.
F=АvВ С , А=1, В=1, С=1
F= (Аv В С), А=0, В=1, С=1
F= А v В С, А=1, В=0, С=1
F= (А v В) (С v В), А=0, В=1, С=0
F= (A B C), А=0, В=0, С=1
8. Составьте таблицы истинности для следующих логических выражений и определите значение логического выражения при заданных
значениях переменных5.
6.
F= (A B C) v (В Сv А, А=1, В=1,
С=0
F=В А v В А, А=0, В=0
Символом F обозначено одно из указанных
ниже логических выражений от трех
аргументов: X, Y, Z. Дан фрагмент таблицы
истинности выражения:
X
0
0
1
Y
0
1
1
Z
0
0
1
F
0
1
1
Какое выражение соответствует F:
1. XvYvZ
2. X&Y&¬Z
3. ¬X&Y&¬Z
4. Xv¬YvZ
Символом F обозначено одно из указанных
ниже логических выражений от трех
аргументов: X, Y, Z. Дан фрагмент таблицы
истинности выражения:
X
0
0
1
Y
0
1
0
Z
F
1
1
0
0
0
1
Какое выражение соответствует F:
1.
XvYvZ2. X&¬Y&¬Z
3. Xv¬YvZ
4. ¬X&Y&¬Z
Символом F обозначено одно из указанных
ниже логических выражений от трех
аргументов: X, Y, Z. Дан фрагмент таблицы
истинности выражения:
X
0
0
0
Y
1
1
0
Z
F
1
1
0
1
1
1
Какое выражение соответствует F:
1. ¬X&Y&Z
2. Xv¬YvZ
3. ¬XvYv¬Z
4. ¬X&Y&¬Z
English Русский Правила
Пропозициональная логика
Пропозициональная логикаМы можем определить логические выражения, используя рекурсивное определение:
- Пропозициональные переменные (значение которых ИСТИНА или ЛОЖЬ) а пропозициональные константы ИСТИНА и ЛОЖЬ являются логическими выражениями.
- Если LE1 и LE2 являются логическими выражениями, то LE1 AND LE2 — логическое выражение, значение которого равно TRUE, если оба LE1 и LE2 имеют значение TRUE, и FALSE в противном случае.
- Если LE1 и LE2 являются логическими выражениями, то
LE1 ИЛИ LE2 — логическое выражение, значение которого равно TRUE, если
либо LE1, либо LE2 имеют значение TRUE,
и FALSE в противном случае.
- Если LE1 является логическим выражением, то NOT LE1 является логическим выражением, чье значение равно TRUE, если LE1 имеет значение FALSE, и FALSE в противном случае.
Уровни приоритета логических операторов:
- НЕ
- И
- ИЛИ
Присваивая значения переменным в логическом выражении, мы также присваиваем значение самому выражению.
Пример: задано выражение «(p AND q) OR r», если p=TRUE, q=TRUE и r=FALSE, то значение выражения равно TRUE.
Булевы функции и таблицы истинности
Смысл (или значение) логического выражения — это логическое значение. функция из множества возможных присвоений значений истинности для переменных в выражении к значениям {ИСТИНА, ЛОЖЬ}.
Пример: учитывая выражение «(p AND q) OR r», мы можем описать
логическая функция, определяющая значение выражения
путем рассмотрения всех комбинаций присваивания значений для p, q и r.
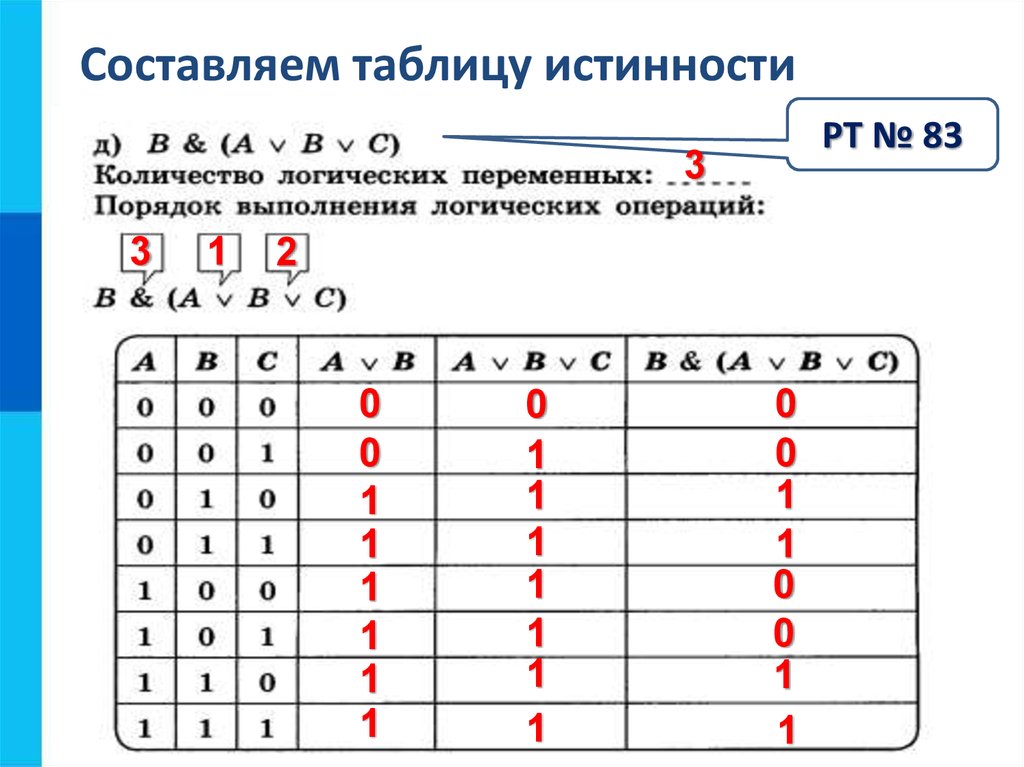
p q r (p AND q) ИЛИ r
------------------------------
Т Т Т Т
Т Т Ф Т
Т Ф Т Т
Т Ф Ф Ф
Ф Т Т Т
Ф Т Ф Ф
Ф Ф Т Т
Ф Ф Ф Ф
Приведенная выше таблица описывает логическую функцию «(p AND q) OR r» называется таблицей истинности . В таблице истинности есть столбец для каждой переменной в выражение, и каждая строка в таблице соответствует присвоение значений переменным. В последнем столбце указано значение выражения для конкретный набор назначений переменных, заданный в строке. 9N различных булевых функций от N переменных.
Вот некоторые дополнительные функции двух переменных, которые часто используются:
p q p->q p==q p И-НЕ q p ИЛИ-НЕ q
-------------------------------------------
0 0 1 1 1 1
0 1 1 0 1 0
1 0 0 0 1 0
1 1 1 1 0 0
Комментарии к этим функциям:
- Значение: «p -> q» или «p подразумевает q»
означает, что всякий раз, когда p истинно, то же самое и q. Единственный способ, которым «p -> q» может быть ЛОЖЬ, — это если p — ИСТИНА, а q — ЛОЖЬ.
- Эквивалентность: «p == q» означает что p и q имеют одинаковое значение.
- НЕ-И: «p НЕ-И q» равнозначно «НЕ (p И q)».
- ИЛИ: «p ИЛИ q» совпадает с «НЕ (p ИЛИ q)».
- Приоритет (от высшего к низшему): НЕ, И-НЕ, НИ, И, ИЛИ, -> , ==.
Единственный способ, которым «p -> q» может быть ЛОЖЬ, — это если p — ИСТИНА, а q — ЛОЖЬ.Вычисление выражений с помощью таблиц истинности
Мы можем вычислить значение выражения, используя таблицы истинности. Мы создаем таблицу для всех возможных значений переменных, и все подвыражения в выражении.
Вычислите значение следующего выражения E для всех возможные назначения истинности: (p -> q) -> (q -> r)
p q r p->q q->r E
---------------------------
0 0 0 1 1 1
0 0 1 1 1 1
0 1 0 1 0 0
0 1 1 1 1 1
1 0 0 0 1 1
1 0 1 0 1 1
1 1 0 1 0 0
1 1 1 1 1 1
Обратите внимание, что столбец для значения q->r тот же
как столбец для значения всего выражения E.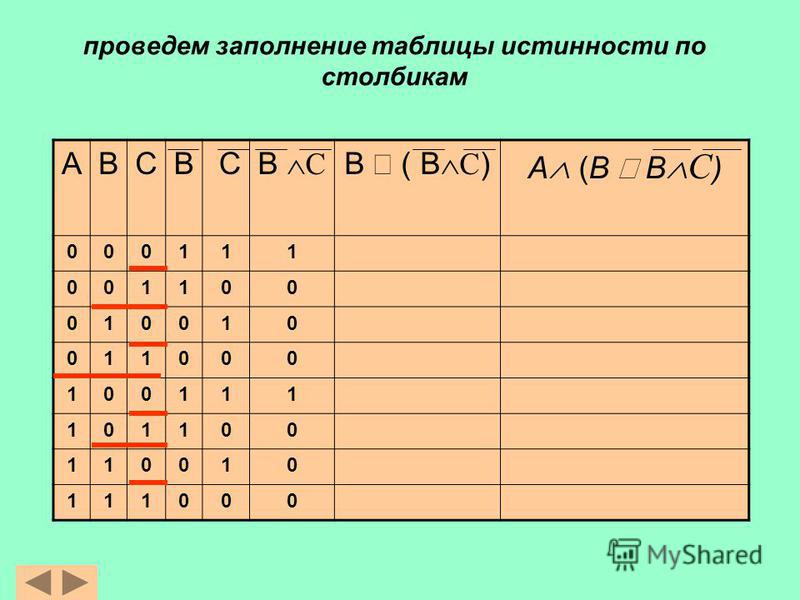
Мы установили эквивалентность этих двух столбцов,
что значит:
(p -> q) -> (q -> r) == q->r.
Создание выражений из функций
Нам часто дают булеву функцию в виде таблицы истинности. и должен вывести соответствующее логическое выражение.
Например, цифровые схемы строятся из цифровых элементы, которые вычисляют основные логические операции (например, НЕ и НЕ-И).
Дана конкретная функция, выраженная в виде результатов присвоения переменной (например, схема, которая добавляет два биты вместе и производит сумму и бит переноса, все который выражается в форме таблицы истинности), мы бы как соответствующее логическое выражение, так что мы можно построить схему для функции.
Мы можем построить такое логическое выражение непосредственно из таблица истинности функции.
В полученном выражении в качестве операторов используются только И, ИЛИ и НЕ.
Эксклюзивное или: Выражение из таблицы истинности
Исключающее ИЛИ (XOR) — еще одна известная функция двух переменных.
Таблица истинности для XOR:
р q исключающее ИЛИ
---------------
0 0 0
0 1 1
1 0 1
1 1 0
Мы можем построить выражение для XOR в терминах AND, OR и НЕ, используя следующие рассуждения:
- Вторая строка говорит нам, что p XOR q ИСТИНА когда p равно FALSE, а q равно TRUE. Другими словами, p XOR q имеет значение TRUE, если NOT p AND q имеет значение TRUE.
- Третья строка говорит нам, что p XOR q ИСТИНА когда р ИСТИНА, а q ЛОЖЬ. Другими словами, p XOR q имеет значение TRUE, если p AND NOT q имеет значение TRUE.
- Другие строки говорят нам, что p XOR q является ЛОЖЬЮ в все остальные случаи.
- Таким образом, p XOR q ИСТИНА, если НЕ p AND q ИСТИНА, или если p AND NOT q истинно.
Из вышеизложенного определяем следующее. логическое выражение для функции p XOR q:
(НЕ p И q) ИЛИ (p И НЕ q)
Конъюнктивные и дизъюнктивные нормальные формы
То есть логическое выражение B находится в дизъюнктивной нормальной форме.
если написано так:
А1 ИЛИ А2 ИЛИ А3 ИЛИ ... Ан
где каждый Ai выражается как
Т1 И Т2 И... И Тм
где каждый Ti является либо простой переменной, либо
или отрицание (НЕ) простой переменной.
Каждое из слагаемых Ai называется минтерм .Логическое выражение находится в конъюнктивной нормальной форме . если оно выражается как произведение (И) сумм (ИЛИ). То есть логическое выражение B находится в конъюнктивной нормальной форме. если написано так:
О1 И О2 И О3 И ... Вкл.
где каждый Oi выражается как
Т1 ИЛИ Т2 ИЛИ ... ИЛИ Тм
где каждый Ti является либо простой переменной, либо
или отрицание (НЕ) простой переменной.
Каждое из слагаемых Oi называется макстерм .Нормальные формы в таблицах истинности
Конъюнктивные и дизъюнктивные нормальные формы
двойственны друг другу;
любой из них может использоваться для создания логического выражения
из таблицы истинности.
С этими нормальными формами мы можем быть более точными о том, как сгенерировать логическое выражение из таблицы истинности.
Чтобы построить логическое выражение в дизъюнктивной нормальной форме из таблица истинности:
- Создайте минтерм для каждой строки таблицы, где функция верна.
- Для каждой переменной, значение которой равно 1 в этой строке, мы включаем переменная в минтерме; если переменная равна 0 в этой строке, мы включаем отрицание переменной в minterm.
- Выражение состоит из ИЛИ всех минтермов.
Мы могли бы, конечно, построить выражение в дизъюнктивном нормальном форма с использованием maxterms и AND.
Логическое выражение для сумматора
Двоичный целочисленный сумматор может быть построен из ряда
одноразрядных сумматоров.
Одноразрядный сумматор принимает два одноразрядных операнда (x и y).
и бит переноса из предыдущего однобитового сумматора (ci),
и производит сумму этих битов,
и выводной бит (co).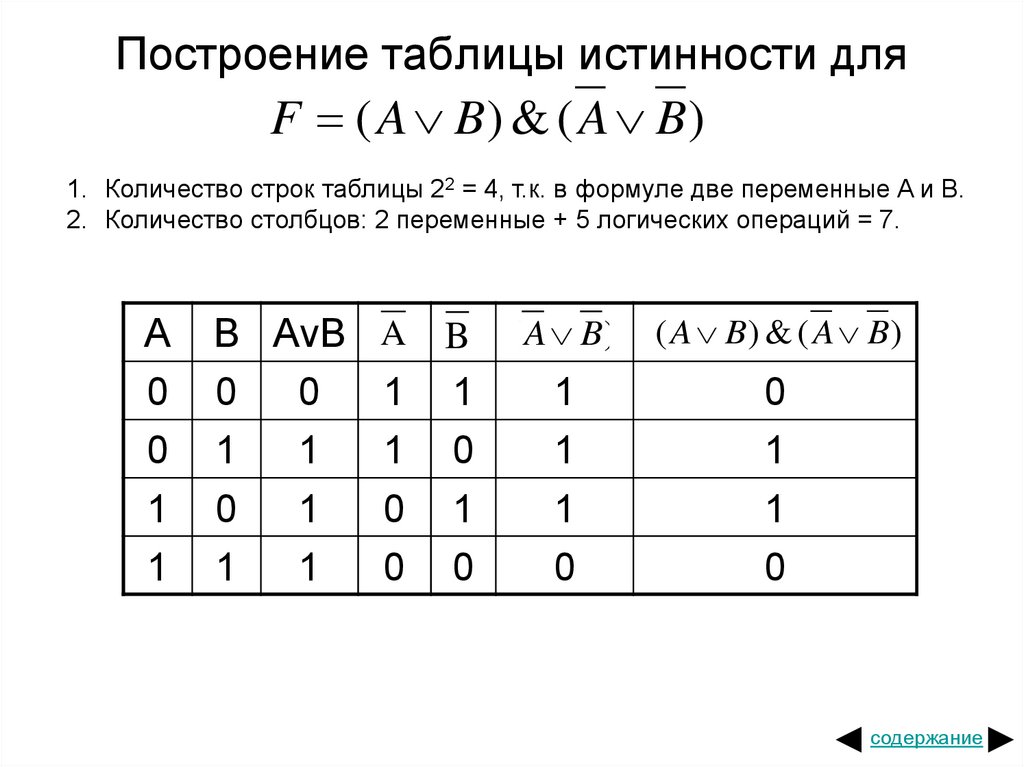
Мы можем определить логическую функцию, соответствующую сумматору в виде таблицы истинности. Затем мы можем построить логические выражения для s и co, из которых мы могли бы построить цепь.
x y ci co s --------------------- 0 0 0 0 0 0 0 1 0 1 s : НЕ x И НЕ y И ci 0 1 0 0 1 с : НЕ x И y И НЕ ci 0 1 1 1 0 co: НЕ x И y И ci 1 0 0 0 1 s : x И НЕ y И НЕ ci 1 0 1 1 0 co: x И НЕ y И ci 1 1 0 1 0 co: x И y И НЕ ci 1 1 1 1 1 co,s: x AND y AND ci
Логическое выражение для s:
(НЕ x И y И ci) ИЛИ (x И НЕ y И ci) ИЛИ (x И y И НЕ ci) ИЛИ (x И y И ci)
Логическое выражение для co:
(НЕ x И НЕ y И ci) ИЛИ (НЕ x И y И НЕ ci) ИЛИ (x И НЕ y И НЕ ci) ИЛИ (x И y И ci)
Полнота булевых операторов
Предыдущее построение логического выражения из
таблица истинности показала, как представить любую булевую функцию
в виде суммы произведений или произведения сумм.
Поскольку мы можем представить любую логическую функцию с помощью И, ИЛИ, и НЕ, эти операторы образуют полный набор для Булевы функции.
Мы можем показать, что одного оператора И-НЕ достаточно. генерировать каждую булеву функцию, показывая, как реализовать И, ИЛИ и НЕ с точки зрения И-НЕ.
p q p НЕ-И 1 q НЕ-И 1 p НЕ-И q E1 E2
--------------------------------------------
0 0 1 1 1 0 0
0 1 1 0 1 0 1
1 0 0 1 1 0 1
1 1 0 0 0 1 1
E1: p И q == ((p НЕ И q) НЕ И ИСТИНА)
E2: p ИЛИ q == ((p НЕ-И ИСТИНА) НЕ-И (q НЕ-И ИСТИНА))
E3: (НЕ p) == (p НЕ И ИСТИНА)
Аналогичную конструкцию можно использовать, чтобы показать, что NOR является также достаточно для генерации каждой булевой функции.
Таким образом, мы можем генерировать цифровые схемы для любой булевой функции. используя только операторы NAND или NOR (или компоненты).
Тавтологии
Тавтология — это логическое выражение, которое всегда ИСТИНА,
независимо от присвоения значений истинности переменным
в выражениях.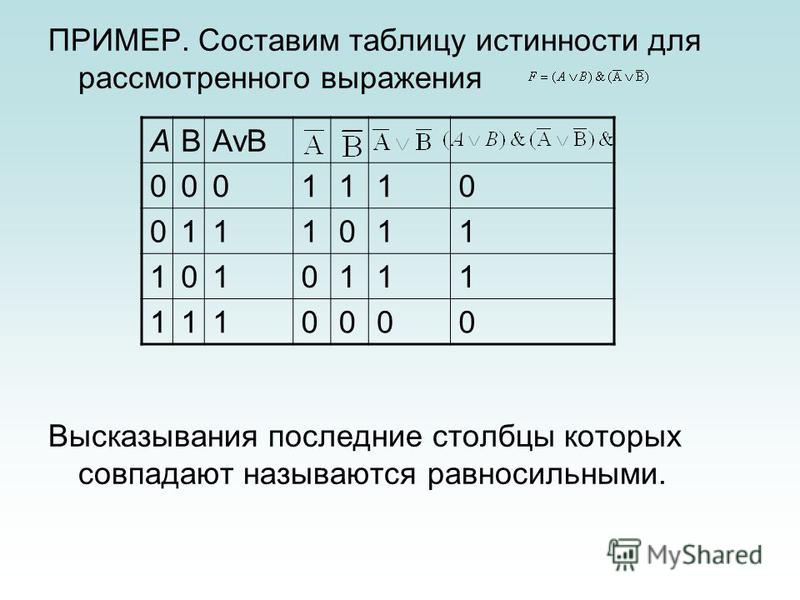
Примеры тавтологии:
- ИСТИНА
- ИСТИНА ИЛИ p
- р ИЛИ НЕ р
- НЕ (р И НЕ р)
- р == р
- (p ИЛИ q) == p ИЛИ (НЕ p И q)
- (р == q) -> (p -> q)
Если мы сможем установить, что «LE1 == LE2» является тавтологией, то независимо от того, какие значения мы присвоим переменным в LE1 и LE2, мы знаем, что «LE1 == LE2» имеет значение TRUE.
Если «LE1 == LE2» является тавтологией, то мы можем заменить LE1 на LE2. (или наоборот) в любом выражении, без изменения значения выражения.
Проблема тавтологии
Интересно задаться вопросом, является ли данная логическая выражение является тавтологией. Этот вопрос известен как «проблема тавтологии».
Для решения задачи тавтологии нам достаточно построить
таблица истинности логического выражения.
Если выражение имеет значение TRUE для всех возможных
значения присвоения для переменных в выражении
(то есть, если весь столбец для выражения в
таблица истинности ИСТИНА), то выражение является тавтологией.
9кн) время, т.е. экспоненциальное время.
Алгоритм решения задачи тавтологии неизвестен. занимает меньше экспоненциального времени. Такие проблемы называются «неразрешимыми», потому что большие экземпляры этих проблем не может быть решена за разумное время.
Еще одна такая неразрешимая проблема — «проблема выполнимости». который спрашивает, есть ли присвоение значений истинности переменные в логическом выражении, которое делает выражение ИСТИННЫМ. Не существует известного алгоритма для этой задачи, более эффективнее, чем циклическое перебор всех возможных комбинаций присваивание истинности переменным.
3: Логические схемы, булева алгебра и таблицы истинности
Загрузить примечания
ТЕМА 1: Логическое представление
Существует три распространенных способа представления логики.
1. Таблицы истинности
2. Логическая схема
3. Логическое выражение
Здесь мы обсудим каждую и продемонстрируем способы преобразования между ними.
3=8 комбинаций входов. (Аудио)
ТЕМА 3: Логическая диаграмма
Логическая диаграмма использует графическое описание логических вентилей в комбинации для представления логического выражения. В приведенном ниже примере показана логическая схема с тремя входами (A, B и C) и одним выходом (Y). Интерпретация этого станет ясной в следующих разделах.
ТЕМА 4: Логическое выражение
Булева алгебра может использоваться для записи логического выражения в форме уравнения. Есть несколько символов, которые вы узнаете, но вам нужно переопределить.
Примечание. Иногда, когда ! используется для обозначения НЕ, оно используется перед буквой, а иногда и после буквы. Следует соблюдать осторожность, чтобы вы понимали, какой метод используется!
Ниже приведен пример логического выражения. Фактически, он представляет ту же логику, что и приведенная выше примерная логическая схема. Эта концепция также станет более ясной, когда мы рассмотрим преобразование из логического выражения и в него ниже.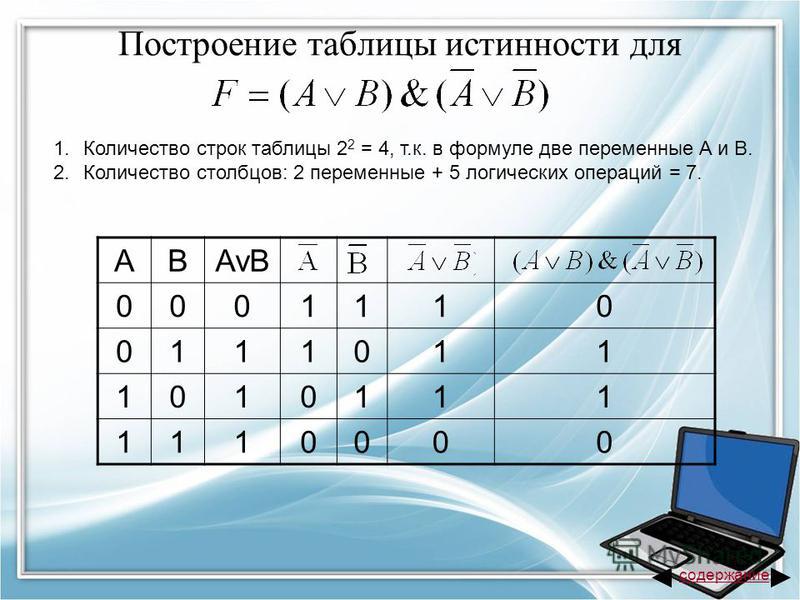
ТЕМА 5: Преобразование логической схемы в истинную таблицу
Это преобразование выполняется путем выбора каждого состояния (или комбинации входов) по одному, замены входов их соответствующими значениями и вычисления значения каждой точки схемы до тех пор, пока не будет достигнут выход. Окончательное выходное значение для каждого состояния затем указывается в таблице истинности рядом со значением каждого входа. Ниже представлена логическая схема с входными значениями. Внимательно изучите его в течение длительного периода времени, это анимированное изображение, и входные и выходные данные будут меняться каждые несколько секунд. (Щелкните изображение, если оно не меняется) Ниже приведены результаты преобразования в форме таблицы истинности.
ТЕМА 6: Преобразование логических схем в логические выражения
Чтобы преобразовать логические схемы в логические выражения, мы начинаем с перечисления наших входных данных в правильном месте и обрабатываем входные данные через логические элементы, по одному вентилю за раз.
, записывая результат на выходе каждого вентиля. Ниже приводится результирующее логическое выражение каждого из вентилей.
А вот пример выполняемого процесса. Тот факт, что результат упрощается до XOR, просто совпадение. (Аудио)
РАЗДЕЛ 7: Преобразование таблиц истинности в логические выражения
Существует два метода преобразования таблиц истинности в логические выражения.
Сумма произведений (аудио)
Произведение сумм (аудио)
ТЕМА 8. Преобразование логических выражений в логические диаграммы
странице, потому что это требует очень хорошего понимания порядка операций. Ниже приведен порядок операций, используемых в этом преобразовании. (Аудио)
Для того, чтобы завершить это преобразование, мы выполним порядок операций. Сначала мы будем искать количества в квадратных скобках или что-то в скобках. Внутри любых скобок мы будем искать дополнительные скобки, а затем НЕ, затем И, затем ИЛИ.
Лучше всего начать с примера.
Аудио
АудиоАудиоАудио ТЕМА 9: Преобразование таблицы истинности в логическую диаграмму
Самый простой способ добиться этого — сначала преобразовать таблицу истинности в логическое выражение, а затем в логическую диаграмму.
Теперь вы должны быть готовы ответить на следующие вопросы. Щелкните здесь для Webct.
1. Логическая система имеет 5 входов. Сколько возможных состояний существует в этой системе?
2. Какой символ используется для обозначения элемента НЕ, когда черта над буквой неудобна для использования?
3. Логическая система имеет 3 входа и, следовательно, 8 возможных состояний. Представление логической схемы показано ниже. Заполните таблицу истинности и преобразуйте выходной столбец в шестнадцатеричный, если состояние 0 является младшим значащим битом, а состояние 7 — старшим значащим битом.
4. Введите логическое выражение из приведенной выше принципиальной схемы.