Ч 2 y ч y 2: Mathway | Популярные задачи

23-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

[PDF] 1.

Частные производные от f (x, y) = xy −… y − xy равны f = y − 2xy − y

Скачать 1. Частные производные от f (x, y) = xy −… y − xy равны f = y − 2xy − y…

1. Частными производными от f (x, y) = xy − x2 y − xy 2 являются fx = y − 2xy − y 2 и fy = x − x2 − 2xy. Критические точки находятся из системы y − 2xy − y 2 = 0 x − x2 − 2xy = 0. Это эквивалентно

y(1 − 2x − y) = 0 x(1 − x − 2y) = 0

Из первого уравнения следует, что либо y = 0, либо 1 − 2x − y = 0. В первом случае второе уравнение принимает вид x(1 − x) = 0, что дает нам два решения (x, y) = (0, 0) и (х, у) = (1, 0). Рассмотрим теперь второй случай 1 − 2x − y = 0, т. е. 2x + y = 1. Из второго уравнения x(1 − x − 2y) = 0 следует, что либо x = 0, либо 1 − x − 2y = 0. В первом случае мы получаем y = 1, так что (x, y) = (0, 1). Во втором случае мы получаем систему 2x + y = 1 x + 2y = 1. Ее решение (x, y) = (1/3, 1/3). Получаем шесть критических точек (0, 0), (1, 0), (0, 1), (1/3, 1/3).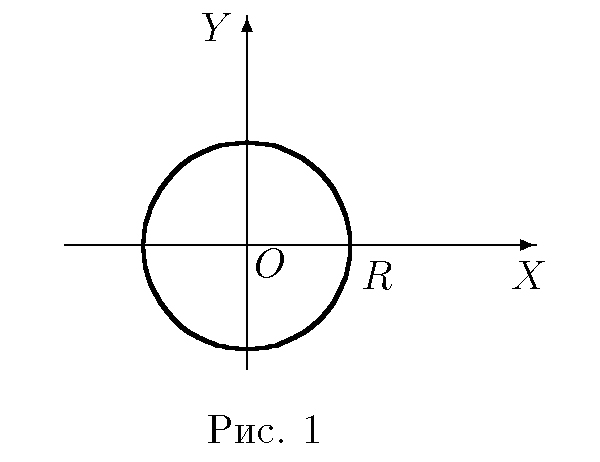

2 . Имеем fxx = −2y, fyy = −2x, fxy = 1 − 2x − 2y. Найдем fxx fyy − fxy 2 Следовательно, fxx fyy − fxy = 4xy − (1 − 2x − 2y)2 . Его значения в точках (0, 0), (1, 0), (0, 1), (1/3, 1/3) равны −1, −1, −1, 4/9.−(1−4/3)2 = 4/9 − 1/9 = 1/3. Отсюда следует, что точки (0, 0), (1, 0) и (0, 1) являются седлами, а точка (1/3, 1/3) — точкой локального максимума, так как fxx (1/3 , 1/3) = −2/3 x2 + 4y 2 = 1 −xy h−ye , −xe−xy i = λh3x, 8yi или

 2  x + 4y 2 −ye−xy  −xe−xy

= 1 = 2λx = 8λy

Из второго уравнения следует, что либо x = 0, либо λ=−

y − xy e . 2x

В случае x = 0 из первого уравнения получаем 4y 2 = 1, но это противоречит тому, что −ye−xy = 2λx = 0, так что это невозможно.

1

Подставив выражение для λ в третье уравнение системы, получим 4y y, x и умножив на x) −xe−xy = −

или (разделив на −e−xy

x2 = 4y 2. √ √ Используя x2 +4y 2 = 1, мы получаем x2 = 4y 2 = 1/2, так что x = ±1/2 и y = ±1/2 2, где возможны все четыре комбинации знаков.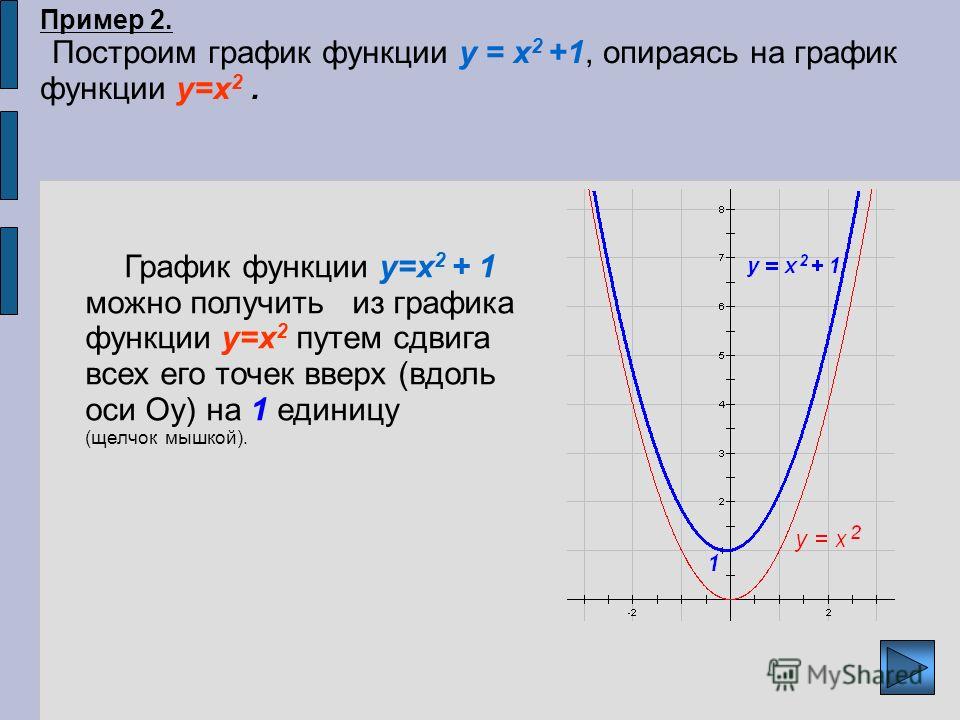 √ Мы тестируем пять особых точек: (0, 0), ±(1/2, 1/2 2) и √ получили √ ±(1/2, −1/2 2). √ соответствующие значения √ функции равны 1, e1/4 и √ √ −1/4 e Отсюда следует, √ что (1/√ 2, 1/2 2) и √ (−1/√ 2, −1/2 2) являются точками точки максимума, а точки минимума (1/ 2, −1/2 2) и (−1/ 2, 1/2 2) RR R e R y4 Re Re Re y4 3. Имеем D 1/x dA = 1 y2 1/x dx dy = 1 ln x|x=y2 dy = 1 (4 ln y − Re e 2 ln y) dy = 1 2 ln y dy = 2y ln y − 2y|1 = (2e − 2e) − (0 − 2) = 2. 4. Областью интегрирования является треугольник с вершинами (0, 0), (3, 0), (3, 1), поэтому интеграл можно записать в виде 3

Z

x/3

Z

0

2

ex dy dx =

0

Z

3

2

xex /3 dx =

0

Z 0

3

3 2 2 e9 − 1 ex /6 dx2 = ex /6 = 6 0

RR p 5. Он равен интегралу D 4×2 + 4y 2 + 1 dA, где D — область, ограниченная окружностью x2 + y 2 = 4 (равно пересечению параболоида с плоскостью xy). Перейдем к полярным координатам для вычисления интеграла.