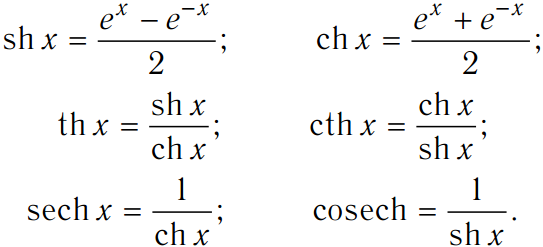Гиперболические функции формулы. Справочные данные по гиперболическим функциям – свойства, графики, формулы
Его можно записать в параметрическом виде, используя гиперболические функции (этим и объясняется их название).
Обозначим y= b·sht , тогда х2 / а2=1+sh3t =ch3t . Откуда x=± a·cht .
Таким образом мы приходим к следующим параметрическим уравнениям гиперболы:
У= в ·sht , –
Рис. 1.
Знак «»+»» в верхней формуле (6) соответствует правой ветви гиперболы, а знак «»– «» — левой (см. рис. 1). Вершинам гиперболы А(– а; 0) и В(а; 0) соответствует значение параметра t=0.
Для сравнения можно привести параметрические уравнения эллипса, использующие тригонометрические функции:
X=а·cost ,
Y=в·sint , 0 t 2p . (7)
3. Очевидно, что функция y=chx является четной и принимает только положительные значения. Функция y=shx – нечетная, т.к. :
Функции y=thx и y=cthx являются нечетными как частные
четной и нечетной функции. Отметим, что в отличие
от тригонометрических, гиперболические функции
не являются периодическими.
Отметим, что в отличие
от тригонометрических, гиперболические функции
не являются периодическими.
4. Исследуем поведение функции y= cthx в окрестности
точки разрыва х=0:
Таким образом ось Оу является вертикальной
асимптотой графика функции y=cthx . Определим
наклонные (горизонтальные) асимптоты:
Следовательно, прямая у=1 является правой горизонтальной асимптотой графика функции y=cthx . В силу нечетности данной функции ее левой горизонтальной асимптотой является прямая у= –1. Нетрудно показать, что эти прямые одновременно являются асимптотами и для функции y=thx. Функции shx и chx асимптот не имеют.
2) (chx)»=shx (показывается аналогично).
4)
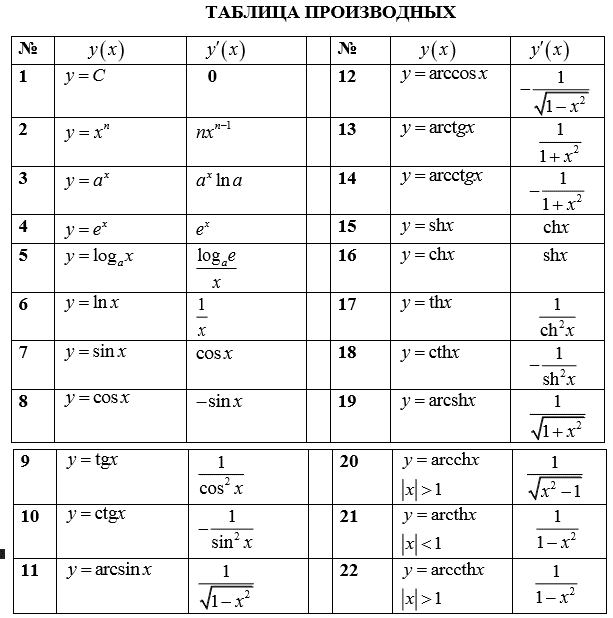
Здесь так же прослеживается определенная аналогия с тригонометрическими функциями. Полная таблица производных всех гиперболических функций приведена в разделе IV.
Тангенс, котангенс
Определения гиперболических функций, их области определений и значений
sh
x
— гиперболический синус
,
-∞ ch
x
— гиперболический косинус
, -∞ cth x — гиперболический котангенс
, x ≠ 0 ; y +1 .
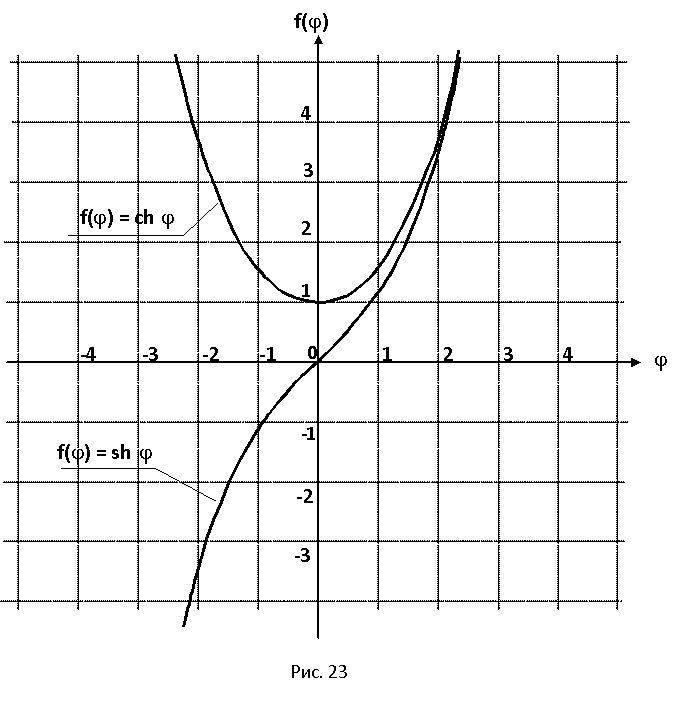
Графики гиперболических функций
График гиперболического синуса y = sh x
График гиперболического косинуса y = ch x
График гиперболического тангенса y = th x
График гиперболического котангенса y = cth x
Формулы с гиперболическими функциями
Связь с тригонометрическими функциями
sin
iz = i sh
z ; cos
iz = ch
z
sh
iz = i sin
z ; ch
iz = cos
z
tg
iz = i th
z ; ctg
iz = — i cth
z
th
iz = i tg
z ; cth
iz = — i ctg
z
Здесь i
— мнимая единица, i 2 = -1
.
Применяя эти формулы к тригонометрическим функциям, получаем формулы, связывающие гиперболические функции.
Четность
sh(-x) = — sh x
;
ch(-x) = ch x
.
th(-x) = — th x
;
cth(-x) = — cth x
.
Разность квадратов
ch 2 x — sh 2 x = 1 .
Формулы суммы и разности аргументов
sh(x ± y) = sh
x ch
y ± ch
x sh
y
,
ch(x ± y) = ch
x ch
y ± sh
x sh
y
,
,
,
sh 2
x = 2 sh
x ch
x
,
ch 2
x = ch 2
x + sh 2
x
= 2 ch 2
x — 1 = 1 + 2 sh 2
x
,
.
Формулы произведений гиперболического синуса и косинуса
,
,
,
,
,
.
Формулы суммы и разности гиперболических функций
,
,
,
,
.
Связь гиперболического синуса и косинуса с тангенсом и котангенсом
,
,
,
.
Производные
,
Интегралы от sh x, ch x, th x, cth x
,
,
.
Разложения в ряды
Обратные функции
Ареасинус
При — ∞ ,
.
Ареакосинус
При 1
≤ x ,
.
Вторая ветвь ареакосинуса расположена при 1 ≤ x .
Ареатангенс
При — 1 ,
В математике и её приложениях к естествознанию и технике находят широкое применение показательные функции. Это, в частности, объясняется тем, что многие изучаемые в естествознании явления относятся к числу так называемых процессов органического роста, в которых скорости изменения участвующих в них функций пропорциональны величинам самих функций.
Если обозначить через функцию, а через аргумент, то дифференциальный закон процесса органического роста может быть записан в виде где некоторый постоянный коэффициент пропорциональности.
Интегрирование этого уравнения приводит к общему решению в виде показательной функции
Если задать начальное условие при, то можно определить произвольную постоянную и, таким образом, найти частное решение которое представляет собой интегральный закон рассматриваемого процесса.
К процессам органического роста относятся при некоторых упрощающих предположениях такие явления, как, например, изменение атмосферного давления в зависимости от высоты над поверхностью Земли, радиоактивный распад, охлаждение или нагревание тела в окружающей среде постоянной температуры, унимолекулярная химическая реакция (например, растворение вещества в воде), при которой имеет место закон действия масс (скорость реакции пропорциональна наличному количеству реагирующего вещества), размножение микроорганизмов и многие другие.
Возрастание денежной суммы вследствие начисления на неё сложных процентов (проценты на проценты) также представляет собой процесс органического роста.
Эти примеры можно было бы продолжать.
Наряду с отдельными показательными функциями в математике и её приложениях находят применение различные комбинации показательных функций, среди которых особое значение имеют некоторые линейные и дробно-линейные комбинации функций и так называемые гиперболические функции. Этих функций шесть, для них введены следующие специальные наименования и обозначения:
(гиперболический синус),
(гиперболический косинус),(гиперболический тангенс),
(гиперболический котангенс),
(гиперболический секанс),
(гиперболический секанс).
Возникает вопрос, почему даны именно такие названия, причём здесь гипербола и известные из тригонометрии названия функций: синус, косинус, и т. д.? Оказывается, что соотношения, связывающие тригонометрические функции с координатами точек окружности единичного радиуса, аналогичны соотношениям, связывающим гиперболические функции с координатами точек равносторонней гиперболы с единичной полуосью.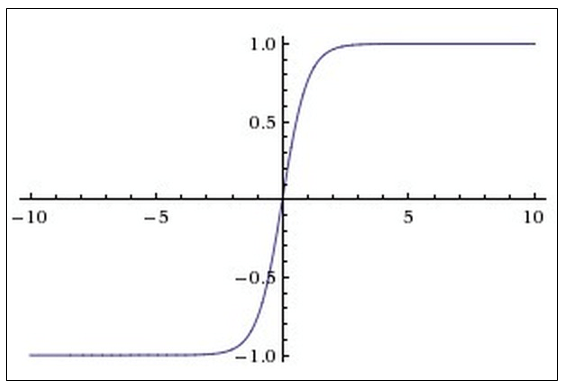 Этим как раз и оправдывается наименование гиперболических функций.
Этим как раз и оправдывается наименование гиперболических функций.
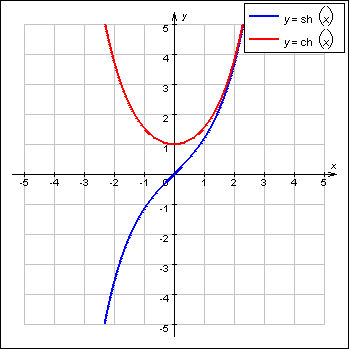
Функции, заданные формулами называют соответственно гиперболическим косинусом и гиперболическим синусом.
Эти функции определены и непрерывны на, причем — четная функция, а — нечетная функция.
Рисунок 1.1 — Графики функций
Из определения гиперболических функций и следует, что:
По аналогии с тригонометрическими функциями гиперболические тангенс и котангенс определяются соответственно формулами
Функция определена и непрерывна на, а функция определена и непрерывна на множестве с выколотой точкой; обе функции — нечетные, их графики представлены на рисунках ниже.
Рисунок 1.2 — График функции
Рисунок 1.3 — График функции
Можно показать, что функции и — строго возрастающие, а функция — строго убывающая. Поэтому указанные функции обратимы. Обозначим обратные к ним функции соответственно через.
Рассмотрим функцию, обратную к функции, т.е. функцию. Выразим ее через элементарные. Решая уравнение относительно, получаем Так как, то, откуда
Решая уравнение относительно, получаем Так как, то, откуда
Заменяя на, а на, находим формулу для функции, обратной для гиперболического синуса.
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ — Гиперболические синус (sh x) и косинус (сh x) определяются следующими равенствами:
Гиперболические тангенс и котангенс определяются по аналогии с тригонометрическими тангенсом и котангенсом:
Аналогично определяются гиперболические секанс и косеканс:
Имеют место формулы:
Свойства гиперболических функций во многом аналогичны свойствам (см.). Уравнения х=соs t, у=sin t определяют окружность х²+у² = 1; уравнения х=сh t, у=sh t определяют гиперболу х² — у²=1. Как тригонометрические функции определяются из окружности единичного радиуса, так и гиперболические функции определяются из равнобочной гиперболы х² — у²=1. Аргумент t есть двойная площадь заштрихованного криволинейного треугольника ОМЕ (рис. 48), аналогично тому как для круговых (тригонометрических) функций аргумент t численно равен удвоенной площади криволинейного треугольника ОКЕ (рис.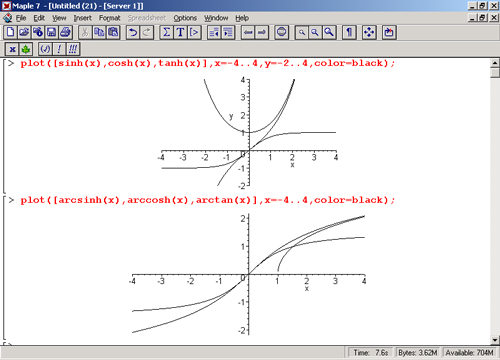 49):
49):
для круга
для гиперболы
Теоремы сложения для гиперболических функций аналогичны теоремам сложения для тригонометрических функций:
Эти аналогии легко усматриваются, если за аргумент х принять комплексное переменное г. Гиперболические функции связаны с тригонометрическими функциями следующими формулами: sh x = — i sin ix, ch x = cos ix,где i — одно из значений корня √-1
. Гиперболические функции sh х, а также и сh x: могут принимать сколько, угодно большие значения (отсюда, естественно, и большие единицы) в отличие от тригонометрических функций sin х, соs х, которые для действительных значений не могут быть по модулю больше единицы.
Гиперболические функции играют роль в геометрии Лобачевского (см. ), используются при изучении сопротивления материалов, в электротехнике и других отраслях знаний. Встречаются в литературе также обозначения гиперболических функций такие sinh x; соsh х; tgh x.
Гиперболический косинус — frwiki.wiki
Для одноименных статей см Косинус (значения) .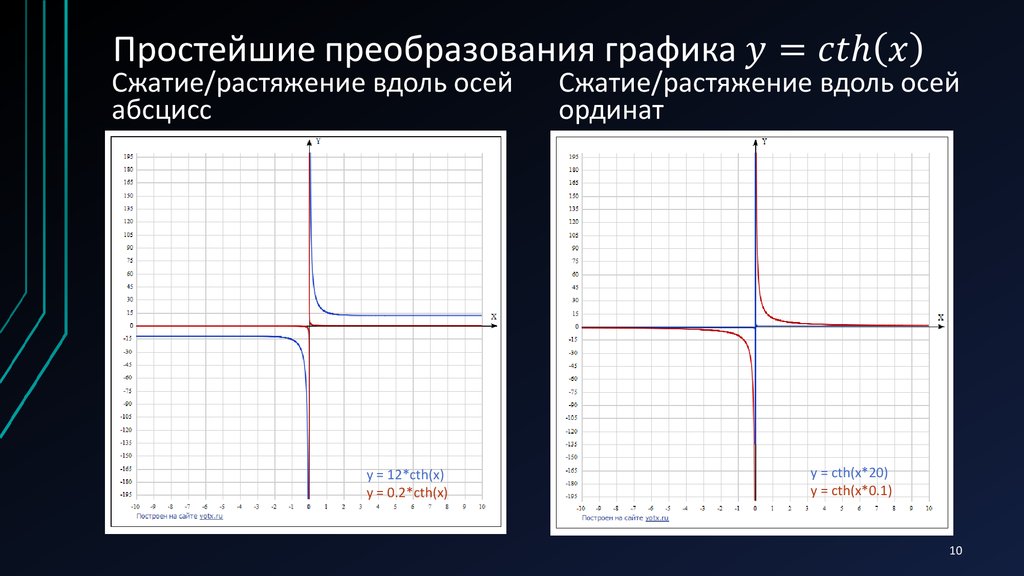
Следовательно, функция гиперболического косинуса является четной частью комплексной экспоненты. Она ограничена на вещественной функции вещественной переменной .
Функция гиперболического косинуса, ограниченная, является в некотором смысле аналогом функции косинуса в гиперболической геометрии .
Обозначение Ch. X был введен Винченцо Риккати в XVIII — го века.
Характеристики
Общие свойства
- сп является непрерывной и даже голоморфна следовательно класса С ∞ ( т.е. бесконечно дифференцируема ). Его производной является функция гиперболического синуса , отмечает sinh .
- сЬ является пара .
- В примитивов из сЬ являются зп + С , где С является постоянная интегрирования.
- ch строго возрастает над ℝ + .
Тригонометрические свойства
Из определений функций гиперболического косинуса и синуса мы можем вывести следующие равенства, справедливые для любого комплекса и аналогичные формулам Эйлера в круговой тригонометрии: z{\ displaystyle z}
- еzзнак равношишz+грехzа такжее-zзнак равношишz-грехz,следовательношиш2z-грех2zзнак равно1.
 {2} +1} {2 \ mathrm {e}}}} ;
{2} +1} {2 \ mathrm {e}}}} ;- шишязнак равнопотому что1{\ Displaystyle \ сп \ mathrm {я} = \ соз 1}.
Нули
Все нули в ch — чистое воображение . Точнее, для любого комплексного числа , z{\ displaystyle z}
- шишzзнак равно0⇔z∈яπ(Z+12).{\ displaystyle \ cosh z = 0 \ Leftrightarrow z \ in \ mathrm {i} \ pi \ left (\ mathbb {Z} + {\ frac {1} {2}} \ right).}
Действительно, либо с реалом. Это было тогда , так zзнак равноИкс+яу{\ Displaystyle г = х + \ mathrm {я} у}Икс,у{\ displaystyle x, y}шишzзнак равношишИкспотому чтоу+ягрехИксгреху{\ Displaystyle \ сш г = \ сш Икс \ соз у + \ mathrm {я} \ зп х \ грех у}
- шишzзнак равно0⇔(потому чтоузнак равно0 а также грехИксзнак равно0)⇔(у∈{π/2+kπ∣k∈Z} а также Иксзнак равно0){\ displaystyle \ cosh z = 0 \ Leftrightarrow \ left (\ cos y = 0 {\ text {et}} \ sinh x = 0 \ right) \ Leftrightarrow \ left (y \ in \ {\ pi / 2 + k \ pi \ mid k \ in \ mathbb {Z} \} {\ text {and}} x = 0 \ right)}.
 {2} -1}}}.}
{2} -1}}}.}использовать
Физический
Репрезентативная кривая функции на описывает цепь , то есть форму однородного троса, закрепленного на обоих концах и подверженного действию силы тяжести. шиш{\ displaystyle \ cosh}
Архитектура
Gateway Arch в Сент — Луисе , штат Миссури .
Гиперболический косинус по архитектуре соответствует дуге цепной передачи, изначально возникшей в результате проектирования подвесных мостов . Антони Гауди был одним из первых, кто широко использовал его в общей архитектуре, в частности, с двумя из его самых известных работ: склепом Колония Гуэль и Саграда Фамилия .
Gateway Arch в Сент — Луисе в Миссури имеет форму перевернутой цепной линии. Он возвышается на 192 м в центре и на 192 м в основании. Точки этой арки приблизительно удовлетворяют уравнению
- узнак равно-39шиш(Икс39)+231{\ displaystyle y = -39 \ cosh \ left ({\ frac {x} {39}} \ right) +231}
для –96 < x <96 .

Примечания и ссылки
- ↑ Международный стандарт ISO / IEC 80000-2 : 2009 рекомендует кос .
Смотрите также
- Гиперболический синус
- Гиперболический тангенс
Тригонометрия
Круговая тригонометрия Тригонометрические функции - Косинус
- Синус
- Касательная
- Котангенс
- Секант
- Косеканс
- синус разливается
Взаимные круговые функции - Арккосинус
- Синусовая дуга
- Касательная дуга
- Котангенс дуги
- Секущая дуга
- Косекансная дуга
Тригонометрические интегралы - Интегральный косинус
- Интегральный синус
Отношения - Тригонометрическая идентичность
- Пифагорейское тригонометрическое тождество
- Закон косинуса
- Закон синусов
- Закон касательных
- Закон котангенсов
Гиперболическая тригонометрия Гиперболическая функция - Гиперболический косинус
- Гиперболический синус
- Гиперболический тангенс
- Гиперболический котангенс
- Гиперболический секанс
- Гиперболический косеканс
Реципрокная гиперболическая функция - Обратный гиперболический косинус
- Реципрокный гиперболический синус
- Взаимный гиперболический тангенс
- Эллиптическая функция / Эллиптическая интегральная функция
- Сферическая тригонометрия
<img src=»https://fr.
{-х}}{2}, \end{уравнение} гиперболический косинус. Гиперболический тангенс \begin{уравнение} \tanh x = \frac{\sinh x}{\cosh x}, \end{уравнение} также иногда рассматривается. Другие обозначения включают: $\operatorname{sh} x$, $\operatorname{Sh} x$, $\operatorname{ch} x$, $\operatorname{Ch} x$, $\operatorname{tgh} x$, $ \operatorname{th} x$, $\operatorname{th} x$. Графики этих функций представлены на рис. а. wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>Рисунок: h048250a
Основными отношениями являются:
70012
14414 70012
4 0002 Рисунок: h048250b
Геометрическая интерпретация гиперболических функций аналогична интерпретации тригонометрических функций (рис.
 б). Параметрические уравнения гипербол
б). Параметрические уравнения гиперболпозволяют интерпретировать абсциссу и ординату точки на равносторонней гиперболе как гиперболические синус и косинус; гиперболический тангенс является отрезком . Параметр точки равен удвоенной площади сектора , где дуга гиперболы. Параметр отрицателен для точки (для ).
Обратные гиперболические функции определяются по формулам
7 являются:
3 Гиперболические функции и также могут быть определены рядом
во всей комплексной плоскости, так что
(3) Доступны обширные табличные значения гиперболических функций.
 Значения гиперболических функций также можно получить из таблиц, содержащих и .
Значения гиперболических функций также можно получить из таблиц, содержащих и .Каталожные номера
[1] Э. Янке, Ф. Эмде, Ф. Лёш, «Tafeln höheren Funktionen», Teubner (1966) , [2] 196 Таблицы круговых и гиперболические синусы и косинусы в мере радиального угла 02 Правые части определяющих соотношений (1), (2) допускают аналитическое продолжение на всю комплексную плоскость. После этого с помощью формул Эйлера видно, что имеет место (3), из которого легко вывести разложения в ряды. Литература
[a1] А. Сегун, М. Абрамовиц, «Справочник по математическим функциям», Прил. Мат. сер. , 55 , физ. Бур. Стандарты (1970) [a2] H.B. Дуайт, «Таблицы интегралов и другие математические данные» , Macmillan (1963) Как цитировать эту запись:
Гиперболические функции. Математическая энциклопедия. URL: http://encyclopediaofmath.org/index.php?title=Hyperbolic_functions&oldid=29142
Математическая энциклопедия. URL: http://encyclopediaofmath.org/index.php?title=Hyperbolic_functions&oldid=29142Эта статья адаптирована из оригинальной статьи В.И. Битюцкова (создатель), которая появилась в Энциклопедии математики — ISBN 1402006098. См. Оригинальную статью
6.9 Исчисление гиперболических функций — Исчисление, том 1
Цели обучения
- 6.9.1 Примените формулы для производных и интегралов гиперболических функций.
- 6.9.2 Примените формулы для производных обратных гиперболических функций и связанных с ними интегралов.
- 6.9.3 Опишите общие прикладные условия контактной кривой.
Мы познакомились с гиперболическими функциями в разделе «Введение в функции и графики» вместе с некоторыми их основными свойствами. В этом разделе мы рассмотрим формулы дифференцирования и интегрирования для гиперболических функций и их обратных функций.
Производные и интегралы гиперболических функций
Напомним, что гиперболический синус и гиперболический косинус определяются как
sinhx=ex-e-x2andcoshx=ex+e-x2.
 sinhx=ex-e-x2andcoshx=ex+e-x2.
sinhx=ex-e-x2andcoshx=ex+e-x2.Другие гиперболические функции затем определяются через sinxsinhx и chx.coshx. Графики гиперболических функций показаны на следующем рисунке.
Рисунок 6,81 Графики гиперболических функций.
Легко вывести формулы дифференцирования для гиперболических функций. Например, глядя на sinxsinhx, мы имеем
.ddx(sinhx)=ddx(ex-e-x2)=12[ddx(ex)-ddx(e-x)]=12[ex+e-x]=coshx.ddx(sinhx)=ddx(ex- e−x2)=12[ddx(ex)−ddx(e−x)]=12[ex+e−x]=chx.
Аналогично, (d/dx)coshx=sinhx.(d/dx)coshx=sinhx. Мы суммируем формулы дифференцирования для гиперболических функций в следующей таблице.
ф(х)ф(х) ddxf(x)ddxf(x) синхсинхх кошхкошх кошхкошх синхсинхх танхтанх sech3xsech3x коткскоткс -csch3x-csch3x sechxsechx −sechxtanx−sechxtanx cschxcschx -cschxcothx-cschxcothx Стол 6.
 2
Производные гиперболических функций
2
Производные гиперболических функцийДавайте на минутку сравним производные гиперболических функций с производными стандартных тригонометрических функций. Сходства много, но и различий тоже. Например, производные функций синуса совпадают: (d/dx)sinx=cosx(d/dx)sinx=cosx и (d/dx)sinhx=coshx.(d/dx)sinhx=coshx. Однако производные функций косинуса различаются по знаку: (d/dx)cosx=-sinx, (d/dx)cosx=-sinx, но (d/dx)chx=sinhx.(d/dx)coshx= синх. Продолжая изучение гиперболических функций, мы должны помнить об их сходствах и различиях со стандартными тригонометрическими функциями.
Эти формулы дифференцирования для гиперболических функций непосредственно приводят к следующим интегральным формулам.
cothu+C∫coshudu=sinhu+C∫sechutanhudu=−sechu+C∫sech3udu=tanhu+C∫cschucothudu=−cschu+C
Пример 6,47
Дифференцирование гиперболических функций
Оценить следующие производные:
- ддх(ш(х2))ддх(ш(х2))
- ddx(кошх)2ddx(кошх)2
Решение
Используя формулы из таблицы 6.
 2 и цепное правило, мы получаем
2 и цепное правило, мы получаем- ddx(sinh(x2))=ch(x2)·2xddx(sinh(x2))=ch(x2)·2x
- ddx(coshx)2=2coshxsinhxddx(coshx)2=2coshxsinhx
Контрольно-пропускной пункт 6,47
Оценить следующие производные:
- ddx(tanh(x2+3x))ddx(tanh(x2+3x))
- ddx(1(sinx)2)ddx(1(sinx)2)
Пример 6,48
Интегралы, включающие гиперболические функции
Вычислите следующие интегралы:
- ∫xcosh(x2)dx∫xcosh(x2)dx
- ∫tanhxdx∫tanhxdx
Решение
Мы можем использовать u -замену в обоих случаях.
- Пусть u=x2.u=x2. Тогда du=2xdxdu=2xdx и
∫xcosh(x2)dx=∫12coshudu=12sinhu+C=12sinh(x2)+C.∫xcosh(x2)dx=∫12coshudu=12sinhu+C=12sinh(x2)+C .
- Пусть u=coshx.u=coshx. Тогда du=sinhxdxdu=sinhxdx и
∫tanhxdx=∫sinhxcoshxdx=∫1udu=ln|u|+C=ln|coshx|+C.
 ∫tanhxdx=∫sinhxcoshxdx=∫1udu=ln|u|+C=ln| кошх|+С.
∫tanhxdx=∫sinhxcoshxdx=∫1udu=ln|u|+C=ln| кошх|+С.
Обратите внимание, что chx>0coshx>0 для всех x,x, поэтому мы можем исключить знаки абсолютного значения и получить∫tanhxdx=ln(chx)+C.∫tanhxdx=ln(chx)+C.
Контрольно-пропускной пункт 6,48
Вычислите следующие интегралы:
- ∫sinh4xcoshxdx∫sinh4xcoshxdx
- ∫sech3(3x)dx∫sech3(3x)dx
Расчет обратных гиперболических функций
Глядя на графики гиперболических функций, мы видим, что при соответствующих ограничениях диапазона все они имеют обратные значения. Большинство необходимых ограничений диапазона можно различить при внимательном рассмотрении графиков. Области и диапазоны обратных гиперболических функций приведены в следующей таблице.
Функция Домен Диапазон sin-1xsin-1x (-∞,∞)(-∞,∞) (-∞,∞)(-∞,∞) кош-1хкош-1х [1,∞)[1,∞) [0,∞)[0,∞) tanh-1xtanh-1x (−1,1)(−1,1) (-∞,∞)(-∞,∞) полотно-1xпокрытие-1x (−∞,−1)∪(1,∞)(−∞,−1)∪(1,∞) (-∞,0)∪(0,∞)(-∞,0)∪(0,∞) сек-1кссек-1х (0, 1] (0, 1] [0,∞)[0,∞) csch-1xcsch-1x (-∞,0)∪(0,∞)(-∞,0)∪(0,∞) (-∞,0)∪(0,∞)(-∞,0)∪(0,∞) Стол 6.
 3
Области и диапазоны обратных гиперболических функций
3
Области и диапазоны обратных гиперболических функцийГрафики обратных гиперболических функций показаны на следующем рисунке.
Рисунок 6,82 Графики обратных гиперболических функций.
Чтобы найти производные обратных функций, мы используем неявное дифференцирование. У нас есть
y=sinh-1xsinhy=xddxsinhy=ddxxcoshydydx=1.y=sinh-1xsinhy=xddxsinhy=ddxxcoshydydx=1.
Напомним, что ch3y-sinh3y=1, cosh3y-sinh3y=1, поэтому coshy=1+sinh3y.coshy=1+sinh3y. Тогда
dydx=1coshy=11+sinh3y=11+x2.dydx=1coshy=11+sinh3y=11+x2.
Аналогичным образом можно вывести формулы дифференцирования для других обратных гиперболических функций. Эти формулы дифференцирования сведены в следующую таблицу.
ф(х)ф(х) ddxf(x)ddxf(x) sin-1xsin-1x 11+x211+x2 кош-1хкош-1х 1×2-11×2-1 tanh-1xtanh-1x 11-x211-x2 полотно-1xпокрытие-1x 11-x211-x2 сек-1кссек-1х −1×1−x2−1×1−x2 csch-1xcsch-1x −1|x|1+x2−1|x|1+x2 Стол 6.
 4
Производные обратных гиперболических функций
4
Производные обратных гиперболических функцийОбратите внимание, что производные от tanh-1xtanh-1x и coth-1xcoth-1x одинаковы. Таким образом, когда мы интегрируем 1/(1−x2),1/(1−x2), нам нужно выбрать правильную первообразную на основе области определения функций и значений x.x. Формулы интегрирования, включающие обратные гиперболические функции, резюмируются следующим образом.
∫11+u2du=sinh−1u+C∫1u1−u2du=−sech−1|u|+C∫1u2−1du=ch−1u+C∫1u1+u2du=−csch−1|u|+C∫ 11−u2du={tanh−1u+Cif|u|<1coth−1u+Cif|u|>1∫11+u2du=sinh−1u+C∫1u1−u2du=−sech−1|u|+C∫1u2 −1du=ch−1u+C∫1u1+u2du=−csch−1|u|+C∫11−u2du={tanh−1u+Cif|u|<1coth−1u+Cif|u|>1
Пример 6,49
Дифференцирование обратных гиперболических функций
Вычисление следующих производных:
- ddx(sinh-1(x3))ddx(sinh-1(x3))
- ddx(tanh-1x)2ddx(tanh-1x)2
Решение
Используя формулы из таблицы 6.4 и цепное правило, мы получаем следующие результаты: =19+x2
- ddx(tanh-1x)2=2(tanh-1x)1-x2ddx(tanh-1x)2=2(tanh-1x)1-x2
Контрольно-пропускной пункт 6,49
Оценить следующие производные:
- ddx(cosh-1(3x))ddx(cosh-1(3x))
- ddx(coth-1x)3ddx(coth-1x)3
Пример 6.
 50
50Интегралы, включающие обратные гиперболические функции
Вычислите следующие интегралы:
- ∫14×2−1dx∫14×2−1dx
- ∫12×1−9x2dx∫12×1−9x2dx
Решение
Мы можем использовать u-подстановкуu-подстановку в обоих случаях.
- Пусть u=2x.u=2x. Тогда du=2dxdu=2dx и имеем
∫14×2−1dx=∫12u2−1du=12cosh−1u+C=12cosh−1(2x)+C.∫14×2−1dx=∫12u2−1du=12cosh−1u+ С=12кош-1(2х)+С.
- Пусть u=3x.u=3x. Тогда du=3dxdu=3dx и мы получаем
∫12×1−9x2dx=12∫1u1−u2du=−12sech−1|u|+C=−12sech−1|3x|+C.∫12×1−9x2dx=12∫1u1 −u2du=−12sech−1|u|+C=−12sech−1|3x|+C.
Контрольно-пропускной пункт 6.50
Вычислить следующие интегралы:
- ∫1×2−4dx,x>2∫1×2−4dx,x>2
- ∫11−e2xdx∫11−e2xdx
приложений
Одно из физических применений гиперболических функций включает подвесные кабели.
 Если кабель одинаковой плотности подвешен между двумя опорами без какой-либо нагрузки, кроме собственного веса, кабель образует кривую, называемую контактной сетью. Высоковольтные линии электропередач, цепи, висящие между двумя столбами, и нити паутины образуют контактную сеть. На следующем рисунке показаны цепи, свисающие с ряда столбов.
Если кабель одинаковой плотности подвешен между двумя опорами без какой-либо нагрузки, кроме собственного веса, кабель образует кривую, называемую контактной сетью. Высоковольтные линии электропередач, цепи, висящие между двумя столбами, и нити паутины образуют контактную сеть. На следующем рисунке показаны цепи, свисающие с ряда столбов.Рисунок 6,83 Цепи между этими столбами имеют форму контактной сети. (кредит: модификация работы OKFoundryCompany, Flickr)
Гиперболические функции могут использоваться для моделирования контактных сетей. В частности, функции вида y=acosh(x/a)y=acosh(x/a) являются контактными. На рис. 6.84 показан график y=2cosh(x/2).y=2cosh(x/2).
Рисунок 6,84 Функция гиперболического косинуса образует контактную сеть.
Пример 6,51
Использование контактной сети для определения длины троса
Предположим, что висящий трос имеет вид 10cosh(x/10)10cosh(x/10) для −15≤x≤15, −15≤x≤15, где xx измеряется в футах.
 Определите длину кабеля (в футах).
Определите длину кабеля (в футах).Решение
Напомним из Раздела 2.42.4, что формула для длины дуги такова:
Длина дуги=∫ab1+[f′(x)]2dx. Длина дуги=∫ab1+[f′(x)]2dx.
Имеем f(x)=10cosh(x/10),f(x)=10cosh(x/10), поэтому f′(x)=sinh(x/10).f′(x)=sinh( х/10). Тогда
Длина дуги=∫ab1+[f′(x)]2dx=∫−15151+sinh3(x10)dx. Длина дуги=∫ab1+[f′(x)]2dx=∫−15151+sinh3(x10)dx .
Теперь вспомним, что 1+sinh3x=cosh3x,1+sinh3x=cosh3x, поэтому мы имеем
Длина дуги=∫−15151+sinh3(x10)dx=∫−1515cosh(x10)dx=10sinh(x10)|−1515 =10[sinh(32)−sinh(−32)]=20sinh(32)≈42,586 футов. Длина дуги=∫−15151+sinh3(x10)dx=∫−1515cosh(x10)dx=10sinh(x10)|− 1515=10[sinh(32)−sinh(−32)]=20sinh(32)≈42,586 фута.
Контрольно-пропускной пункт 6,51
Предположим, что висящий трос имеет форму 15cosh(x/15)15cosh(x/15) для −20≤x≤20,−20≤x≤20. Определите длину кабеля (в футах).
Раздел 6.9 Упражнения
377.

[T] Найдите выражения для coshx+sinhxcoshx+sinhx и coshx-sinhx.coshx-sinhx. Используйте калькулятор, чтобы построить график этих функций и убедиться, что ваше выражение правильное.
378.
Из определений ch(x)ch(x) и sh(x),sinh(x) найдите их первообразные.
379.
Покажите, что ch(x)ch(x) и sh(x)sinh(x) удовлетворяют условию y″=y.y″=y.
380.
Используйте правило частных, чтобы проверить, что tanh(x)′=sech3(x).tanh(x)′=sech3(x).
381.
Выведите ch3(x)+sinh3(x)=ch(2x)cosh3(x)+sinh3(x)=cosh(2x) из определения.
382.
Возьмите производную от предыдущего выражения, чтобы найти выражение для sinh(2x).sinh(2x).
383.
Докажите, что sinh(x+y)=sinh(x)ch(y)+cosh(x)sinh(y)sinh(x+y)=sinh(x)ch(y)+cosh(x)sin(y) ), заменив выражение экспонентами.

384.
Возьмите производную от предыдущего выражения, чтобы найти выражение для cosh(x+y).cosh(x+y).
В следующих упражнениях найдите производные заданных функций и постройте график вместе с функцией, чтобы убедиться, что ваш ответ правильный.
385.
[T] ш(3х+1)ш(3х+1)
386.
[T] ш(х2)ш(х2)
387.
[Т] 1шт(х)1шт(х)
388.
[T] sin(ln(x)) sin(ln(x))
389.
[T] cosh3(x)+sinh3(x)cosh3(x)+sinh3(x)
390.
[T] ch3(x)−sinh3(x)ch3(x)−sinh3(x)
391.
[T] танх(х2+1)танх(х2+1)
392.

[T] 1+tanh(x)1−tanh(x)1+tanh(x)1−tanh(x)
393.
[Т] sin6(x)sin6(x)
394.
[T] пер(сек(х)+танг(х)) пер(сек(х)+танг(х))
Для следующих упражнений найдите первообразные для заданных функций.
395.
кош(2x+1)кош(2x+1)
396.
танх(3x+2)танх(3x+2)
397.
ксош(х2)кскош(х2)
398.
3x3tanh(x4)3x3tanh(x4)
399.
cosh3(x)sinh(x)cosh3(x)sinh(x)
400.
tanh3(x)sech3(x)tanh3(x)sech3(x)
401.
грех(х)1+кош(х)зп(х)1+кош(х)
402.
Кот (х) Кот (х)
403.

кош(х)+шп(х)ш(х)+шп(х)
404.
(ш(х)+шп(х))п(ш(х)+шп(х))п
Для следующих упражнений найдите производные функций.
405.
tanh−1(4x)tanh−1(4x)
406.
sinh-1 (x2) sinh-1 (x2)
407.
sinh−1(ch(x)) sinh−1(ch(x))
408.
кош-1(х3) кош-1(х3)
409.
tanh−1(cos(x))tanh−1(cos(x))
410.
esinh-1(x)esinh-1(x)
411.
пер(танг-1(х)) пер(танг-1(х))
Для следующих упражнений найдите первообразные функций.
412.
∫dx4−x2∫dx4−x2
413.
∫dxa2−x2∫dxa2−x2
414.

∫dxx2+1∫dxx2+1
415.
∫xdxx2+1∫xdxx2+1
416.
∫-dxx1-x2∫-dxx1-x2
417.
∫exe2x-1∫exe2x-1
418.
∫−2xx4−1∫−2xx4−1
В следующих упражнениях используйте тот факт, что падающее тело с трением, равным квадрату скорости, подчиняется уравнению dv/dt=g−v2.dv/dt=g−v2.
419.
Покажите, что v(t)=gtanh((g)t)v(t)=gtanh((g)t) удовлетворяет этому уравнению.
420.
Получите предыдущее выражение для v(t)v(t) путем интегрирования dvg-v2=dt.dvg-v2=dt.
421.
[T] Оцените, как низко упало тело за 1212 секунд, найдя площадь под кривой v(t).v(t).
Для следующих упражнений используйте этот сценарий: Канат, висящий под собственным весом, имеет наклон S=dy/dxS=dy/dx, удовлетворяющий условию dS/dx=c1+S2.
 dS/dx=c1+S2. Константа cc представляет собой отношение плотности троса к натяжению.
dS/dx=c1+S2. Константа cc представляет собой отношение плотности троса к натяжению.422.
Покажите, что S=sinh(cx)S=sinh(cx) удовлетворяет этому уравнению.
423.
Интегрируйте dy/dx=sinh(cx)dy/dx=sinh(cx), чтобы найти высоту троса y(x)y(x), если y(0)=1/c.y(0)=1/c.
424.
Нарисуйте кабель и определите, насколько он провисает при x=0.x=0.
Для следующих упражнений решите каждую задачу.
425.
[T] Цепь свисает с двух столбов на расстоянии 22 м друг от друга, образуя контактную сеть, описываемую уравнением y=2cosh(x/2)−1.y=2cosh(x/2)−1. Найдите уклон контактной сети у левого столба забора.
426.
[T] Цепь свисает с двух столбов на расстоянии четырех метров друг от друга, образуя контактную сеть, описываемую уравнением y=4cosh(x/4)−3.
 y=4cosh(x/4)−3. Найдите общую длину контактной сети (длину дуги).
y=4cosh(x/4)−3. Найдите общую длину контактной сети (длину дуги).427.
[T] Высоковольтная линия электропередачи представляет собой контактную сеть, описываемую формулой y=10cosh(x/10).y=10cosh(x/10). Найдите отношение площади под контактной сетью к длине ее дуги. Что ты заметил?
428.
Телефонная линия — контактная сеть, описываемая формулой y=acosh(x/a).y=acosh(x/a). Найдите отношение площади под контактной сетью к длине ее дуги. Подтверждает ли это ваш ответ на предыдущий вопрос?
429.
Докажите формулу производной y=sinh-1(x)y=sinh-1(x) путем дифференцирования x=sinh(y).x=sinh(y). ( Подсказка: Используйте гиперболические тригонометрические тождества.)
430.
Докажите формулу производной y=ch-1(x)y=ch-1(x) путем дифференцирования x=ch(y).


 {2} +1} {2 \ mathrm {e}}}} ;
{2} +1} {2 \ mathrm {e}}}} ; {2} -1}}}.}
{2} -1}}}.}
 wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>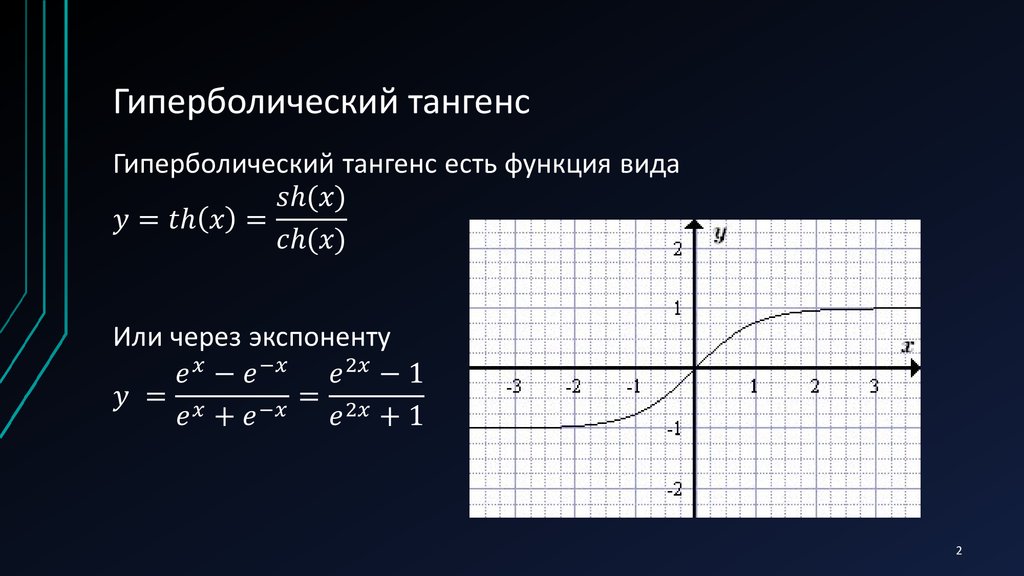 б). Параметрические уравнения гипербол
б). Параметрические уравнения гипербол Значения гиперболических функций также можно получить из таблиц, содержащих и .
Значения гиперболических функций также можно получить из таблиц, содержащих и . Математическая энциклопедия. URL: http://encyclopediaofmath.org/index.php?title=Hyperbolic_functions&oldid=29142
Математическая энциклопедия. URL: http://encyclopediaofmath.org/index.php?title=Hyperbolic_functions&oldid=29142 sinhx=ex-e-x2andcoshx=ex+e-x2.
sinhx=ex-e-x2andcoshx=ex+e-x2.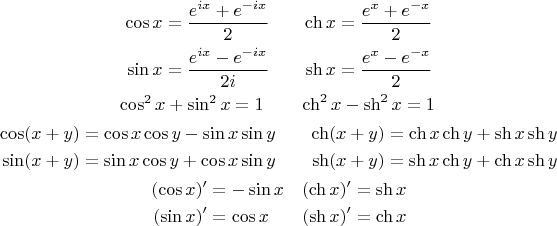 2
Производные гиперболических функций
2
Производные гиперболических функций 2 и цепное правило, мы получаем
2 и цепное правило, мы получаем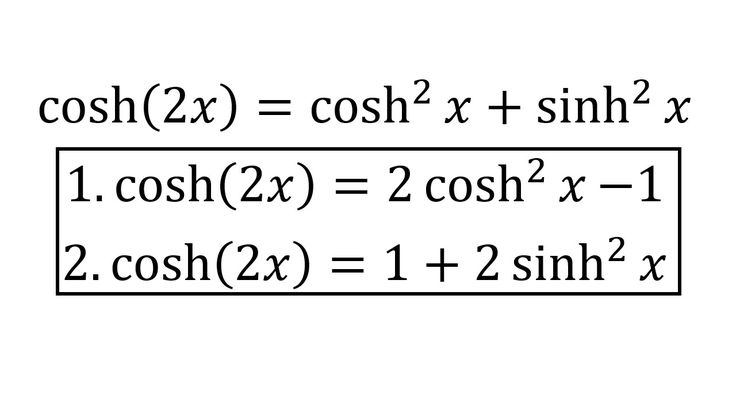 ∫tanhxdx=∫sinhxcoshxdx=∫1udu=ln|u|+C=ln| кошх|+С.
∫tanhxdx=∫sinhxcoshxdx=∫1udu=ln|u|+C=ln| кошх|+С.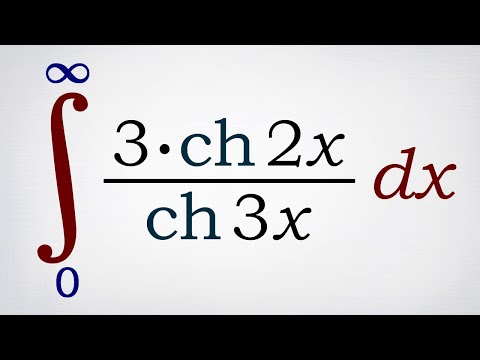 3
Области и диапазоны обратных гиперболических функций
3
Области и диапазоны обратных гиперболических функций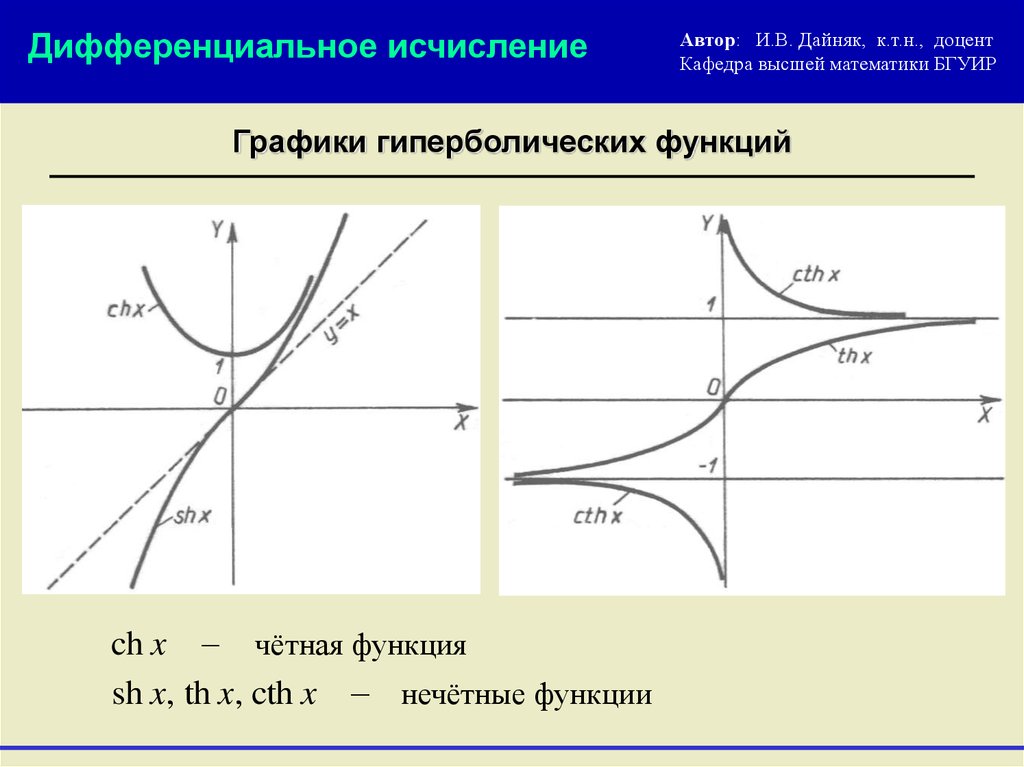 4
Производные обратных гиперболических функций
4
Производные обратных гиперболических функций 50
50 Если кабель одинаковой плотности подвешен между двумя опорами без какой-либо нагрузки, кроме собственного веса, кабель образует кривую, называемую контактной сетью. Высоковольтные линии электропередач, цепи, висящие между двумя столбами, и нити паутины образуют контактную сеть. На следующем рисунке показаны цепи, свисающие с ряда столбов.
Если кабель одинаковой плотности подвешен между двумя опорами без какой-либо нагрузки, кроме собственного веса, кабель образует кривую, называемую контактной сетью. Высоковольтные линии электропередач, цепи, висящие между двумя столбами, и нити паутины образуют контактную сеть. На следующем рисунке показаны цепи, свисающие с ряда столбов.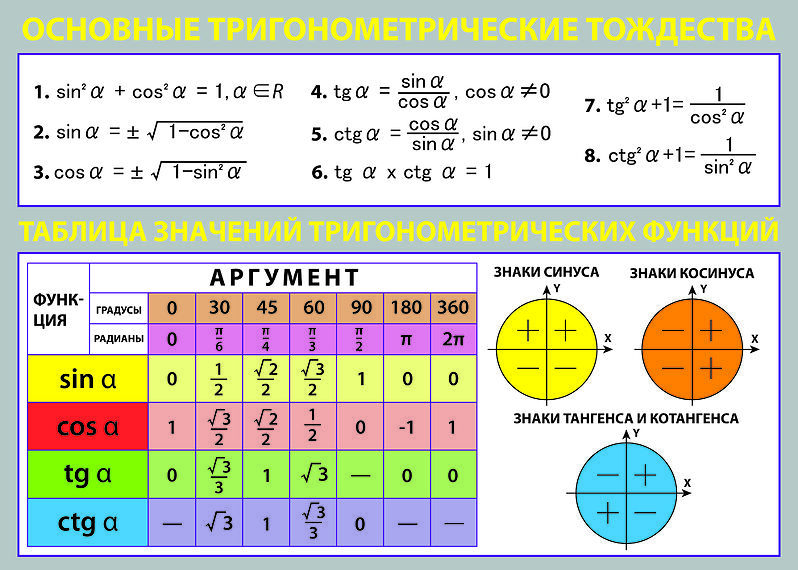 Определите длину кабеля (в футах).
Определите длину кабеля (в футах).
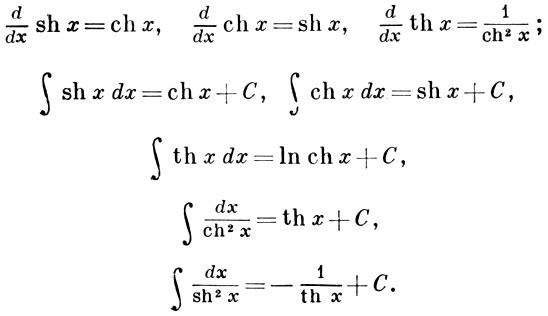
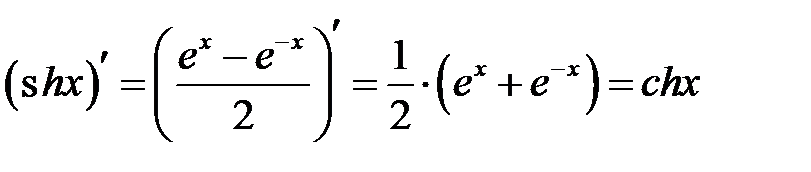


 dS/dx=c1+S2. Константа cc представляет собой отношение плотности троса к натяжению.
dS/dx=c1+S2. Константа cc представляет собой отношение плотности троса к натяжению. y=4cosh(x/4)−3. Найдите общую длину контактной сети (длину дуги).
y=4cosh(x/4)−3. Найдите общую длину контактной сети (длину дуги).