Частица движется по замкнутой траектории в центральном силовом поле: Частица движется по замкнутой траектории в центральном силовом поле, где её потенциальная

Энергия и Момент Импульса (Energy and Angular Momentum)

Общая Физика
Лекция 6
Энергия и Момент Импульса
(Energy and Angular Momentum)
Лектор:
доцент НИЯУ МИФИ, к.ф.-м.н.,
Ольчак Андрей Станиславович(

2. Внешние и внутренние силы. Замкнутая система.

f ik — внутренняя сила
F — внешняя сила
Если на систему не действуют
внешние силы, или ими можно
пренебречь, или их действие
скомпенсировано — такая система
называется замкнутой.
Зако́ны сохране́ния — фундаментальные физические
законы, согласно которым при определённых условиях
некоторые измеримые физические величины,
характеризующие замкнутую физическую систему, не
изменяются с течением времени.

3. Закон сохранения импульса для замкнутой системы частиц

m3
m2
m4
m1
F21
F12
m5
Замкнутая система = совокупность попарно
взаимодействующих материальных точек.
Суммарное изменение импульса а каждой
паре равно нулю => суммарный импульс
всей системы сохраняется:
Pсист = P1 + P2 + P3 + … = Σ Pi = Const
dPсист / dt = Σ Fi = Fвнеш = Mdvc /dt = Md2rc /dt2
Движение составного объекта допустимо рассматривать, не
вникая в его внутреннюю структуру и не учитывая
взаимодействие его частей!
rс = Σ miri /M – радиус-вектор центра масс системы
Дадим определения: Работа. Мощность.
• Элементарная работа силы.
A Fd r
• Работа силы на участке траектории
2
от точки 1 до точки 2 A Fd r
1
• Мгновенная мощность силы
A
Fd r
P
Fv
dt
dt
• Определение работы по известной tзависимости
2
мощности от времени
A Pdt
t1
• Средняя мощность силы
t2
Pdt
A
t1
P
t2 t1 t2 t1

5. Кинетическая энергия.

Элементарную работу суммарной силы, действующей на
материальную точку, можно представить в виде:
mv 2
dv
A F d r mwd r m
d r mvd v d
dt
2
Величину T = mV2/2 называют кинетической энергией материальной
точки. Элементарная работа суммарной силы, действующей на
материальную точку, идет на приращение ее кинетической энергии. И
наоборот: за счет потери кинетической энергии тело может совершить
механическую работу A T
Энергия = мера способности тела произвести работу..

6. Консервативные и неконсервативные силы.

Работа консервативных сил (гравитация, электростатические силы,
упругость) НЕ зависит от формы траектории, а только от начального и
конечного положений частицы. Для консервативных сил можно ввести
понятие потенциальной энергии, зависящей исключительно от
координат точки в поле консервативной силы.
Работа консервативной силы равна разности
потенциальных энергий объекта в начальной и
А12 = U1 — U2
В частности, для 2-х близких точек:
dА12 = U(r) — U (r+dr) = -(dr,dU/dr) =
= -dx(дU/дх)- dy(дU/дy)- dz(дU/дz)
конечной точках траектории:
Физический смысл имеет именно разность значений потенциальной
энергии между разными точками. Абсолютное значение потенциальной
энергии можно отсчитывать от любого уровня, какой удобен

7. Потенциальная энергия частицы во внешнем силовом поле.

Работа консервативной силы не зависит от формы траектории
r2
À12 cons Fdr U r1 U r2
À12cons U
,
r1
….. и может пойти на приращение кинетической энергии точки
dAcons = dT = — dU
=> Сумма потенциальной и кинетической энергии точки,
движущейся в консервативном поле сил, остается неизменной
U + T = Const

8.

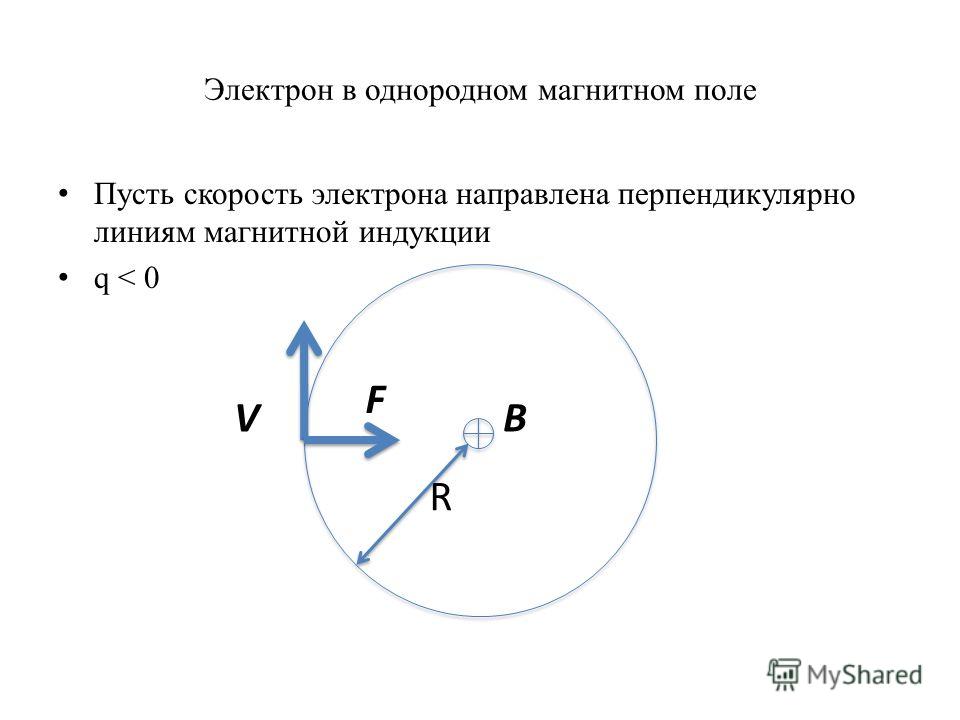НЕ консервативные силы. Сила тренияРабота не консервативных сил зависит от формы траектории.
v
Fтр
v
Fтр
2
Сила трения направлена против скорости
движения материальной точки.
Элементарная работа силы трения равна.
1
dA = (F, dr) = -Fds,
где ds — элемент пройденного пути.
Работа силы трения на пути между точками 1 и 2 (и туда и обратно)
равна.
A12 = — Fds,
.
Работа силы трения всегда отрицательна.
Закон сохранения энергии
Некоторые частные случаи
1. Изолированная частица: T
= Const
2. Частица движется в потенциальном, стационарном поле
консервативных сил:
Е = T +U = Const
3.Тело движется в потенциальном, стационарном поле сил и на
нее действует сила трения – уравнение баланса энергии
Е1 (=U1+T1 ) = Е2 (=U2+T2) + А(против трения)
4. Замкнутая система взаимодействующих материальных точек, в
которой нет НЕ консервативных сил.
T U вз const

10. Связь законов сохранения со свойствами пространства и времени.

Cвойства пространства
и времени
Законы сохранения,
следующие из этих
свойств
Однородность времени
Закон сохранения энергии
Однородность
пространства
Закон сохранения
импульса
Изотропность
пространства
Закон сохранения момента
импульса
Ландау Л.Д., Лифшиц Е.М. «Механика», гл.2
Момент импульса.
Закон сохранения момента импульса
Момент импульса.
Закон сохранения момента импульса
Момент импульса. Плечо импульса
Моментом импульса частицы относительно точки называется
векторное произведение радиус-вектора на импульс частицы:
M p M r
M O r , p r , mv
ex
M r , p x
M rp sin lp
ey
ez
y
z
px p y pz
yp z zp y e x xpz zp x e y xpy yp x e z
Длина перпендикуляра, опущенного из точки O
на прямую, вдоль которой направлен импульс
частицы называется плечом импульса
относительно точки О
l r sin
Момент импульса. Плечо импульса
ПРИМЕРЫ
1.Частица массы m движется по прямой со скоростью v. Момент
импульса частицы может изменяться только по модулю. Модуль
момента импульса равен M = mvl, причем плечо l остается
неизменным.
Если на частицу не действуют силы – ее момент импульса не
меняется ни по величине, ни по направлению:
M = [r, p]
Момент импульса. Плечо импульса
ПРИМЕРЫ
2. Частица движется по окружности радиуса r со скоростью v.
Модуль момента импульса относительно точки O равен M =
pr·sin90° = mvr. Вектор M перпендикулярен плоскости окружности,
причем направление движения частицы и вектор M образуют
правовинтовую систему. Плечо l = r = const и момент импульса
может изменяться только за счет модуля скорости.
Когда частица движется в центральном поле сил, ее момент
импульса не меняется ни по величине, ни по направлению:
M = [r, p].
Момент силы. Плечо силы.
Моментом силы F относительно точки О, из которой проведен
радиус-вектор r точки приложения силы называется псевдовектор:
N [r , F ]
1. Вектор N перпендикулярен векторам r и F, и образует с ними правую тройку.
2. Модуль момента силы можно представить в виде N
= r F·sinα =l·F,
где l= r·sinα – плечо силы относительно точки O (длина перпендикуляра,
опущенного из точки О на прямую, вдоль которой действует сила)
3. Точку приложения силы (в случае твердого тела) можно сдвигать вдоль линии
действия силы: ни l ни N при этом не изменятся. Но величина и направление
зависят от выбора точки О
N
Пара сил.
Пара сил = две равные по модулю противоположно направленные
силы, не действующие вдоль одной прямой. Расстояние
между
прямыми, вдоль которых действуют силы= плечо пары Суммарный
момент сил, образующих пару, равен:
N [r1 , F1 ] [r2 , F2 ]
F1 F2
N [r1 , F2 ] [r2 , F2 ] [ r2 r1 , F2 ]
N [l , F ]
l r2 r1
l = вектор, проведенный из точки приложения силы F1 в точку приложения силы F2
Момент пары сил не зависит от точки отсчета O. Вектор момента пары сил
перпендикулярен к плоскости, в которой лежат силы и численно равен
произведению модуля любой из сил на плечо.
Производная момента импульса по времени
dM d dr dp dp
r , p , p r , v , p r ,
dt
dt
dt dt
dt
dp
p || v [v , p] 0
F
dt
dM
r, F N
dt
Производная по времени момента импульса частицы
относительно некоторой точки равна моменту силы
относительно той же точки.
Момент импульса системы материальных точек
Момент импульса системы относительно точки = векторная сумма
моментов импульса всех частиц, входящих в систему:
M сист M i ri , pi
i
Для каждой частицы:
i
dM i
N i N ij
dt
j , j i
Первое слагаемое – момент внешних сил, действующих на i-ую
частицу, а второе – сумма моментов внутренних сил. Суммируя по всем
частицам, получаем:
dM сист
dM i
N i N ij
dt
dt
i
i
i j , j i
Закон сохранения момента импульса
Закон изменения полного момента импульса системы:
dM сист
dM i
N i N ij
dt
dt
i
i
i j , j i
Двойная сумма в правой части уравнения обращается в нуль, т. 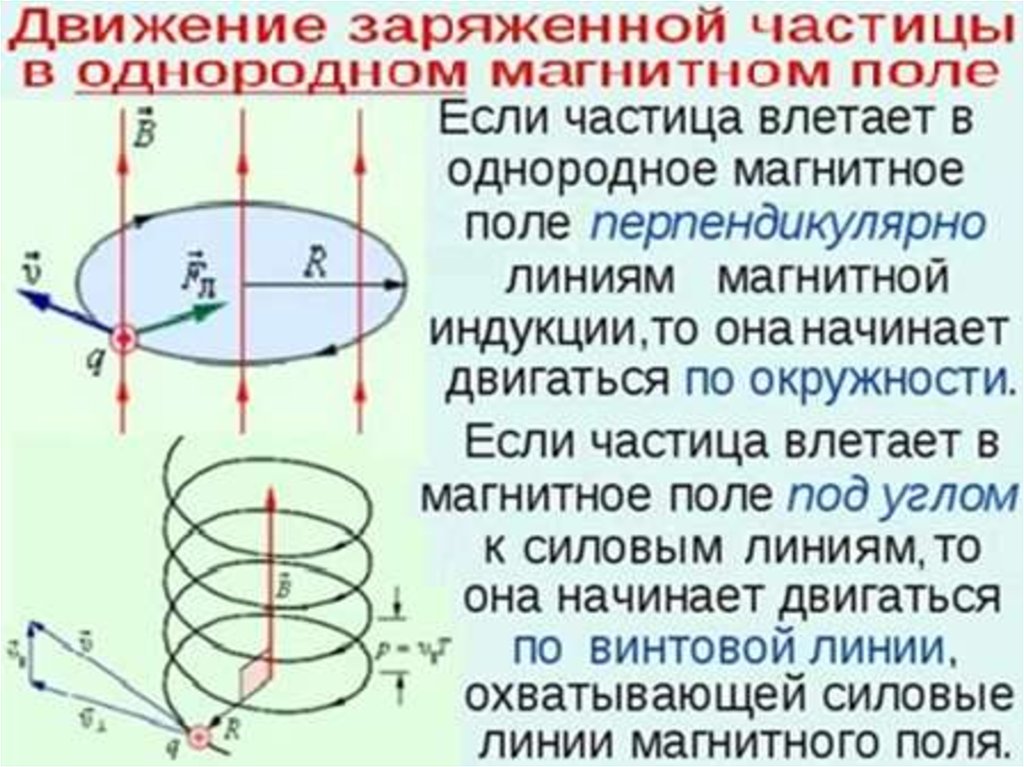к. содержит
парные слагаемые вида:
ri , Fij rj , F ji ri rj , Fij
dM сист
Ni
dt
i
Fij F ji
Скорость изменения момента импульса
системы равна суммарному моменту
внешних сил, днйствующих на систему:
[ri r j , Fij ] 0
Закон сохранения момента импульса
dM сист
Ni
dt
i
Уравнение моментов: производная по времени полного
момента импульса системы равна результирующему моменту
внешних сил.
Пример: падение подпиленного столба
В точке опоры O действует неизвестная и, к тому же,
меняющаяся со временем сила реакции N . Но момент
этой силы относительно точки опоры равен нулю, и в
уравнение моментов войдет только момент известной
силы тяжести:
dM 0
mg l
dt
При отсутствии внешних
сил
dM / dt 0
Для замкнутой
системы M постоянен
Закон сохранения момента импульса
dM сист
Ni
dt
i
При отсутствии внешних
сил
dM / dt 0
Для замкнутой системы
M постоянен
Закон сохранения момента импульса: момент импульса
замкнутой системы материальных точек остается постоянным.
Момент импульса остается постоянным и для незамкнутой
системы при условии, что суммарный момент внешних сил
равен нулю.
Движение в центральном поле сил
В центральном поле силы, действующие на частицу в любой точке
направлены на центр поля, а модуль силы зависит только от
расстояния до этого центра.
r
F f r er f r
r
r
NO r , F r , f r 0 Момент импульса частицы относительно
r
центра (т. 0) будет сохраняться
M O r, mv const
Момент
перпендикулярен
образованной r и p
к
плоскости,
M = const => плоскость движения фиксирована
При движении частицы в центральном поле сил ее радиус-вектор
остается все время в одной плоскости. В этой же плоскости лежит все
время вектор p. Траектория частицы представляет собой плоскую
кривую.
Движение в центральном поле сил.
ПРИМЕР
Силы, обратно пропорциональные квадрату расстояния от центра
f r 2 , const
r
dr
U 2 C, U 0 C 0
r
r
mr 2 mr 2 2
2 2
E
M
mr
z
2
2
r
mr 2 M z const
mr mr 2
2
2
2
2 E const
r
r t , t
Движение в центральном поле сил.
ПРИМЕР
Силы, обратно пропорциональные квадрату расстояния от центра
f r 2 , const
r
mr 2 M z const
2
mr mr
2 E const
r
2
2
2
r t , t
Траектория частицы = коническое сечение, т.е. либо эллипс, либо
параболу, либо гиперболу.
α > 0 (отталкивание): Гипербола. При Mz= 0 вырождается в прямую
α < 0 (притяжение): Эллипс при E < 0, гипербола при E > 0, парабола
при E = 0
Космические скорости
Первой космической скоростью называется скорость, которую надо
сообщить телу, чтобы оно стало спутником планеты. С этой скоростью
оно будет двигаться по круговой орбите радиуса r.
vI2
Mm
m G 2
r
r
M
vI G
r
Космические скорости
Второй космической скоростью
называется минимальная
скорость, которую следует сообщить спутнику, чтобы он двигался
по параболической траектории, т.е. ушел из сферы притяжения
планеты. Ее можно найти из условия:
2
II
M
mv
mM
E
G
0 vII 2G vI 2
r
2
r

27.

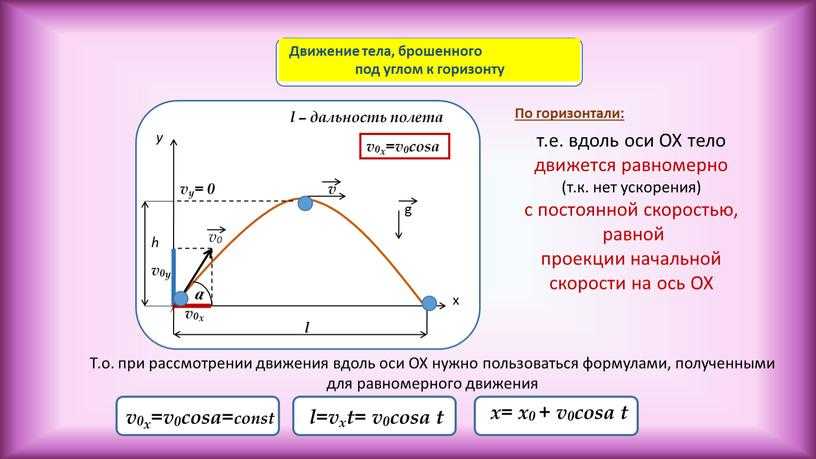Связь законов сохранения со свойствами пространства и времени.Основные свойства
пространства
и времени
Законы сохранения,
вытекающие из этих
свойств
Однородность времени
Закон сохранения энергии
Однородность
пространства
Закон сохранения
импульса
Изотропность
пространства
Закон сохранения момента
импульса
Ландау Л.Д., Лифшиц Е.М. «Механика», гл.2
Курс общей физики НИЯУ МИФИ
Спасибо за внимание!
Продолжение следует.
Закон сохранения момента импульса
dM сист
Ni
dt
i
Уравнение моментов: производная по времени полного
момента импульса системы равна результирующему моменту
внешних сил.
Пример: падение подпиленного столба
В точке опоры O действует неизвестная и, к тому же,
меняющаяся со временем сила реакции N . Но момент
этой силы относительно точки опоры равен нулю, и в
уравнение моментов войдет только момент известной
силы тяжести:
dM 0
mg l
dt
При отсутствии внешних
сил
dM / dt 0
Для замкнутой
системы M постоянен
Курс общей физики НИЯУ МИФИ
M
vI G
r

Белорусский государственный университет транспорта — БелГУТ (БИИЖТ)

Как поступить в БелГУТ:

дневное, заочное полное,
заочное сокращенное

Как получить место

в общежитии БелГУТа

Как поступить иностранному гражданину

События

Все события

Пн	Вт	Ср	Чт	Пт	Сб	Вс
					1	2
3	4 Дата : 2022-10-04	5	6 Дата : 2022-10-06	7	8	9
10	11 Дата : 2022-10-11	12	13 Дата : 2022-10-13	14 Дата : 2022-10-14	15	16
17	18	19	20 Дата : 2022-10-20	21	22	23
24	25	26 Дата : 2022-10-26	27 Дата : 2022-10-27	28	29 Дата : 2022-10-29	30
31

Все анонсы

• Билеты на фестиваль по бальным танцам «GOMEL OPEN». ..
• I международная научно-техническая конференция сту…
• 29 октября — ДЕНЬ ОТКРЫТЫХ ДВЕРЕЙ ФАКУЛЬТЕТА ПГС…
• Вакцинация от гриппа
• 1 тур серии игр «ЧТО? ГДЕ? КОГДА?» среди студентов…
• Открытая лекция Евдокимовича Владислава Евгеньевич…
• Лига дебатов в БелГУТе
• 12 ноября — ДЕНЬ ОТКРЫТЫХ ДВЕРЕЙ ЭЛЕКТРОТЕХНИЧЕСКО…
• Курсы самообороны
• Заседание совета университета …

Анонсы

Университет

Абитуриентам

Студентам

Конференции

Приглашения

Билеты на фестиваль по бальным танцам «GOMEL OPEN»…

I международная научно-техническая конференция сту…

29 октября — ДЕНЬ ОТКРЫТЫХ ДВЕРЕЙ ФАКУЛЬТЕТА ПГС…

Вакцинация от гриппа

Новости

Университет

Международные связи

Спорт

Воспитательная работа

Жизнь студентов

Новости подразделений



• Студенческая жизнь

Лига дебатов в БелГУТе
28 октября 2022

• Университет

Поздравляем с присвоением ученой степени кандидата технических наук! .

..
28 октября 2022

• Университет

Научный семинар оппонирующей организации…
28 октября 2022

• Университет

IV Отчетно-выборная конференция первичной организации РГОО «Белорусск…
28 октября 2022

• Воспитательная работа

Спасибо, Доноры!
27 октября 2022

• Университет

СИЛА ЗАКОНА
27 октября 2022

• Университет

Поздравляем с присвоением степени кандидата технических наук…
27 октября 2022

• Воспитательная работа

Студенты на телепрограмме «Черное и белое» Беларусь-4. ..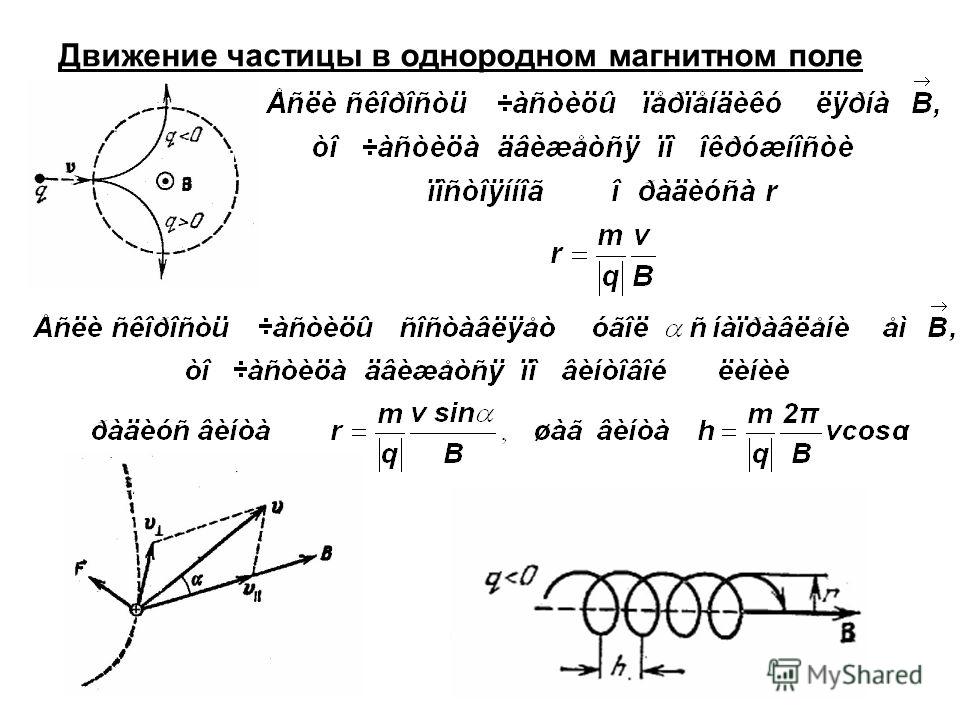
27 октября 2022

• Спорт

Встреча школьников-таможенников со студентами-спортсменами сборной Бел…
27 октября 2022

Другие новости

• Встреча с представителями силового блока…
• «Крылья надежды» в КСУП «Брилево»
• Волшебная неделя ФРАНЦУЗСКОГО ЯЗЫКА
• К 30-летнему юбилею специальности «АВТОМОБИЛЬНЫЕ ДОРОГИ» в УО «БЕЛОРУ…
• Диалоговая площадка с представителями Гомельской таможни…
• Волейбольная встреча БелГУТа и БТЭУ
• Неделя родительской любви глазами участников автопоезда #Беларусь.Моло…
• Курсы самообороны
• В гостях «Золотой голос БелГУТа» Дмитрий Даниленко — выпускник нашего …
• Победа за нами!
• Первый визит Второго секретаря Центрального комитета ОО «БРСМ» Прохоро…

КУДА ПОСТУПАТЬ

Все факультеты

БелГУТ на Доске почета

Достижения университета

Предложения

Все предложения

Видеотека

Все видео

Фотогалерея

Все фото

Движение центральной силы | SpringerLink

В 1687 году Исаак Ньютон сделал замечательное открытие. Ньютон утверждал, что сила, которая удерживает планеты на их орбитах, — это та же самая сила, которая заставляет яблоко падать с дерева. Закон всемирного тяготения Ньютона гласит, что каждая частица во Вселенной притягивает любую другую частицу с силой, прямо пропорциональной произведению масс частиц и обратно пропорциональной квадрату расстояния между ними . Величина этой гравитационной силы равна 9{2} $$

Сила гравитации эффективна, когда одна или обе массы очень велики. Это потому, что G — очень маленькое число. Обратите внимание, что гравитационная сила не является контактной силой; это сила поля, которая может действовать через любую среду. Направление гравитационной силы лежит вдоль линии, соединяющей две частицы.

Таким образом, гравитационная сила является центральной силой, так как ее величина пропорциональна только расстоянию между двумя частицами (где одну из частиц можно считать центром силы), а ее направление лежит вдоль соединяющей их линии ( к центру силы).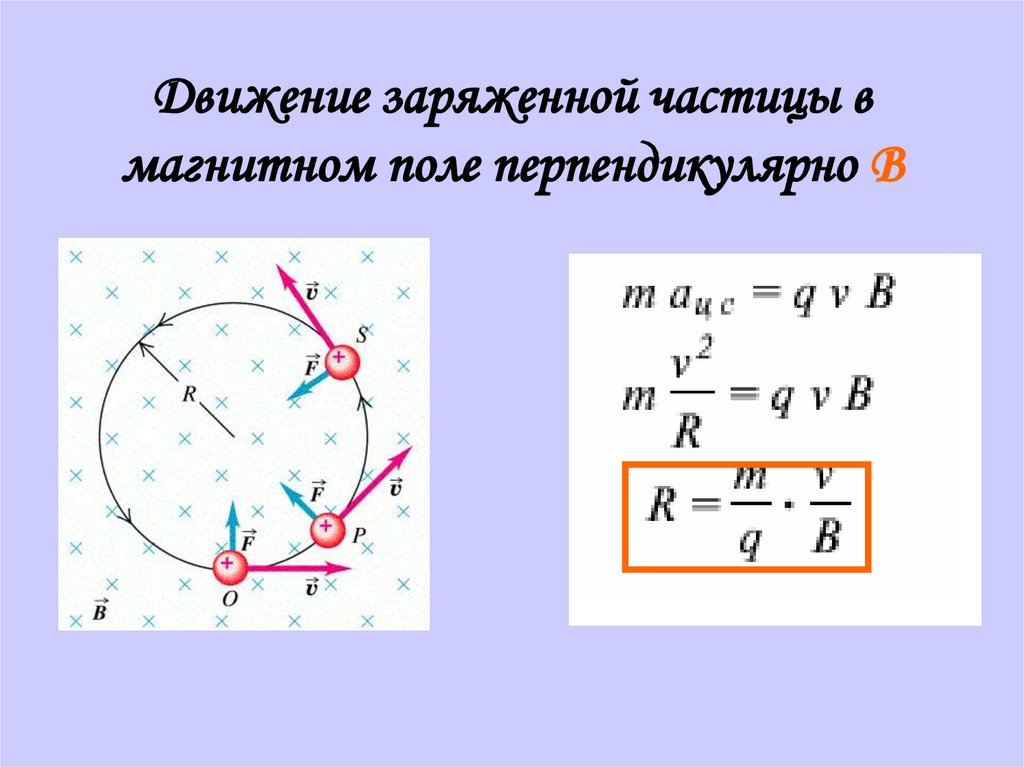

Рис. 9.5

Две частицы с массами \(m_{1}\) и \(m_{2}\). Каждая частица воздействует на другую гравитационно. Каждая частица оказывает гравитационное воздействие на другую. Пусть сила тяжести, действующая на \(m_{2}\) со стороны \(m_{1}\), равна \(\mathbf {F}_{21}\), а сила, действующая на \(m_{1}\ ) на \(m_{2}\) равным \(\mathbf {F}_{12}\). Из третьего закона Ньютона о действии и противодействии имеем 9{2}}\mathbf {r}_{21} $$

где \(\mathrm {r}_{12}\) — единичный вектор, направленный вдоль линии, соединяющей две частицы (направленный от \( m_{1}\) в \(m_{2}\)) и \(\mathbf {r}_{21}\) — единичный вектор, направленный из \(m_{2}\) в \(m_{1 }\). Знак минус указывает на то, что сила притягивает. То есть сила, действующая на \(m_{1}\) со стороны \(m_{2}\), будет двигаться \(m_{1}\) в направлении, противоположном \(\mathrm {r}_{21} \), т. е. в сторону \(m_{2}\). Где сила, действующая на \(m_{2}\) со стороны \(m_{1}\), будет двигаться \(m_{2}\) против \(\mathrm {r}_{12}\) (к \ (м_{1}\)). Если частица \(\mathrm {P}\) массы \(m_{P}\) взаимодействует с системой частиц, результирующая гравитационная сила \(\mathbf {F}_{P}\), действующая на частицу \ (\mathrm {P}\) за счет всех частиц в системе представляет собой векторную сумму отдельных сил, которые каждая частица в системе действует на частицу \(\mathrm {P}\): 9{2}}\mathbf {r}_{iP} $$

где \(\mathbf {r}_{iP}\) — единичный вектор, направленный от i-й частицы в системе к частице \(\mathrm {P}\) и \(\mathbf {F}_{Pi}\) — сила, действующая на частицу \(\mathrm {P}\) со стороны i -й частицы. Если частица \(\mathrm {P}\) массой m взаимодействует с протяженным телом массой M , результирующая гравитационная сила \(\mathbf {F}_{P}\), действующая на частицу \(\ mathrm {P}\) представляет собой векторную сумму отдельных сил \(d\mathbf {F}\), действующих на частицу \(\mathrm {P}\) из-за каждого элемента массы 9{2}}\mathbf {r}_{1} $$

где \(\mathbf {r}_{1}\) — единичный вектор, направленный от элемента массы dM к частице, как показано на рис. . 9.6. Сила гравитации придает планетам и другим тяжелым небесным телам сферическую форму. Это потому, что по мере того, как масса тела становится больше, сила тяжести становится сильнее, и все частицы со всех сторон равномерно притягиваются к центру. В результате тело имеет тенденцию иметь сферическую форму.

Рис. 9.6

Частица \(\mathrm {P}\) массой m взаимодействует с протяженным телом массой M

Изображение в полный размер

Пример 9.2

Две частицы масс \(m_{1}=0,2 \) кг и \(m_{2}=0,3\) кг разделены расстоянием 0,05 \(\mathrm {m}\). Найдите: а) гравитационную силу, с которой каждая частица действует на другую; б) на каком расстоянии третья частица \(m_{3}=0,5\) кг должна быть помещена с другой стороны \(m_{1}\) так, чтобы результирующая сила тяжести на \(m_{1}\ ) равно нулю. (Все частицы лежат на прямой). 9{2} $$

$$ r_{31}=0,064 \; \mathrm {m} $$

9.2.1 Сила гравитации между частицей и однородной сферической оболочкой

Случай I. Частица вне оболочки Рассмотрим частицу массой m , находящуюся вне однородной сферической оболочки на точка \(\mathrm {P}\) как на рис. 9.7. Представьте, что эта оболочка состоит из большого количества тонких колец, каждая из которых имеет внешнюю толщину \(Rd\theta\) и внутреннюю толщину l . Кольцо настолько тонкое (поскольку используется \(d\theta\)), что каждая частица в кольце находится на расстоянии s от P Кроме того, каждая частица в кольце оказывает гравитационное воздействие на частицу в точке P.

Рис. 9.7

Поскольку \(\mathbf {F}_{1}\) и \(\mathbf {F }_{2}\) равны по величине, то их компоненты \(\mathrm {y}\) компенсируют друг друга, а их компоненты \(\mathrm {x}\) составляют в сумме

Полноразмерное изображение

Откуда симметрия кольца, если частица (1) на верхней стороне оказывает гравитационную силу \(\mathbf {F}_{1}\) на м , всегда есть другая частица (2) на противоположной стороне кольца, воздействующего на частицу другой силой (\(\mathbf {F}_{2}\)) . {2}}\bigg)ds=0 $$ 9{2}} \; (r\ge R) $$

$$ F_{g}=0 \; (r

На рис. 9.8 показана сила, действующая на частицу, в зависимости от ее местоположения.

Рис. 9.8

Сила, действующая на частицу, как функция ее \(\mathrm {r}\)

Изображение в натуральную величину

9.2.2 Гравитационная сила между частицей и однородным твердым шаром

Случай I: Частица вне сферы Рассмотрим частицу массой m , находящуюся вне однородной сплошной сферы. Сферу можно считать состоящей из ряда концентрических сферических оболочек. Сила, действующая на частицу каждой оболочкой, равна 9{2}} \end{aligned}$$

(9.18)

Таким образом, твердая сфера ведет себя как частица с массой M , находящаяся в центре сферы.

Рис. 9.9

Если частица массой м находится внутри однородного твердого шара массой м , то сила тяжести, действующая на частицу, обусловлена ​​только частью сферы радиусом \(r

Изображение в полный размер

Случай II: Частица внутри сферы Если частица массой м находится внутри однородной твердой сферы массой м , то сила тяжести, действующая на частицу, обусловлена ​​только частью сферы радиусом \(r рис. 9.9). Остальная часть сферы представляет собой сферическую оболочку, которая не действует на частицу, так как частица находится внутри нее. Из уравнения 9.18, гравитационная сила, действующая на частицу из-за сферы радиусом r 9{3}} $$

, где \(r

$$ F_{g}=0 $$

На рис. 9.10 показана сила, действующая на частицу, в зависимости от ее местоположения.

Рис. 9.10

Сила, действующая на частицу, как функция ее \(\mathrm {r}\)

Изображение в полный размер

Пример 9.3 масса

м , которая находится на расстоянии a от тонкого стержня массой 9{2}}\mathbf {i} $$

То есть стержень можно рассматривать как частицу массой M , находящуюся на расстоянии a от m .

Пример 9.4

Найти силу тяжести, действующую на частицу массой m , находящуюся на расстоянии a от центра однородного твердого диска радиусом R и массой M , как показано на рис. 9.12.

Рис. 9.12

Гравитационная сила, действующая на частицу массой м то есть на расстоянии a от центра однородного сплошного диска радиусом R и массой M

Решение 9.4

Разобьем диск на тонкие концентрические кольца радиус r и толщина dr . В силу симметрии результирующая сила, действующая на частицу, направлена ​​вдоль оси кольца, так как \(\mathrm{y}\)-составляющие сил, действующих на все частицы кольца, будут сокращаться, где их \(\ mathrm {x}\)-компоненты складываются. то есть 9{2}}}\bigg ] $$

Пример 9.5

Однородный твердый шар имеет массу 4,7 кг и радиус 0,05 \(\mathrm {m}\). Найти величину силы тяжести, с которой шар действует на частицу массой 0,02 кг, расположенную на расстоянии а) 0,5 \(\mathrm {м}\) от центра шара; б) 0,03 \(\mathrm {m}\) от центра сферы; в) на поверхности сферы; г) в центре сферы.

Решение 9.5

(a)

$$ F_{1s}=\displaystyle \frac{GmM}{r^{2}}=\frac{(6. {-11} \; \mathrm{N}$$ 9{-9} \; \mathrm {N}$$

(d)

$$ F_{1s}=0 $$

Пример 9.6

Три концентрические сферические оболочки имеют массы \(M_{1}, M_{2}\) и \(M_{3}\) и радиус \(R_{1}, R_{2}\) и \(R_{3}\) соответственно, как на рис. 9.13. Найдите гравитационную силу, действующую на частицу массой м , расположенную в точке (a) \(r=a(\mathrm {b})r=b(\mathrm {c})r=c(\mathrm {d}) r=d.\)

Рис. 9.13

Три концентрические сферические оболочки

Изображение в натуральную величину 9{3}\mathrm {m}/\mathrm {s})}=6968,8\mathrm {s}=116,15\min $$

9.2.3 Вес и гравитационная сила

В гл. 4 мы видели, что вес объекта определяется как гравитационная сила, действующая на объект со стороны Земли (или любого другого астрономического объекта), и она направлена ​​к центру Земли. Вес объекта определяется выражением \(\mathbf {w}=m\mathbf {g}\), где \(\mathbf {g}\) — ускорение свободного падения, а его значение у поверхности земли равно 9,8. {2}\). Точная форма гравитационной силы между любыми двумя объектами была дана ранее в этой главе с помощью закона всемирного тяготения Ньютона.{2}} $$

где \(M_{E}\) — масса Земли, а m — масса частицы, находящейся на расстоянии r от центра Земли. Обратите внимание, что предполагается, что Земля является идеальной сферой с однородным распределением массы и, следовательно, ведет себя как частица. На самом деле Земля не идеальная сфера, а скорее эллипсоид. Кроме того, плотность Земли неоднородна, поскольку она меняется в зависимости от радиуса Земли.

Плотность земли также варьируется на поверхности земли от одного региона к другому. Кроме того, если включить вращение Земли, то результирующая сила, действующая на объект, будет равна его весу плюс центростремительная сила, действующая на объект из-за вращения. Однако этими вариациями часто пренебрегают. Из определения веса имеем 9{2}} $$

Таким образом, вес объекта уменьшается с увеличением высоты. В таблице 9.1 показано изменение g в зависимости от высоты.

Таблица 9.1 Изменение \(\mathrm {g}\) с высотой

Полная таблица

Пример 9.9

Человек может прыгнуть вертикально вверх с поверхности земли и достичь высоты 0,2 \(\mathrm {м }\). Найдите высоту, на которую может подняться человек, прыгнув с той же начальной скоростью на поверхность Луны.

9{2} $$

9.2.4 Гравитационное поле

Как упоминалось ранее, сила гравитации представляет собой силу поля, которая может действовать через пустое пространство, т. е. для действия такой силы не требуется физического контакта между объектами. Альтернативным способом описания гравитационного притяжения является введение понятия гравитационного поля. Предположим, что пробная частица массы \(m_{0}\) находится в разных точках от другой массы M (которая представляет собой центр гравитационной силы). В каждой точке на пробную частицу будет действовать гравитационная сила, которая зависит от ее расстояния от 9{2}}\mathbf {r}_{1} $$

То есть гравитационное поле в точке определяется как гравитационная сила на единицу массы в этой точке. {2}}\mathbf {i} $$ 9{2}}\mathbf {i} $$

Рис. 9.15

Нахождение величины и направления гравитационного поля в точке P

Изображение в полный размер

центральное силовое поле $\vec F =\phi(r) \vec r$

Задавать вопрос

спросил 10 лет, 4 месяца назад

Изменено 9 лет, 11 месяцев назад

Просмотрено 32к раз

$\begingroup$

Проблема, которую я пытаюсь решить, выглядит следующим образом:

Частица движется в силовом поле, определяемом формулой $\vec F =\phi(r) \vec r$. Докажите, что угловой момент частицы относительно начала координат постоянен.

Я настроил так: 92} $

$ \ vec v = \ int {\ frac {\ vec F} {m}} \ dt = \ int {\ frac {\ phi (r) \ vec r} {m}} \ dt $

, что равно:

${\ frac {\phi(r) t \vec r}{m} } + c$

(Я не уверен, что я делаю в этот момент. Правильно ли мое интегрированное выражение ?)

Предполагая, что это так, мы получаем:

Угловой момент $L = m (\vec r \times \vec v) = \vec r \times (\phi(r) t \vec r + c)$

Теперь я не знаю, что делать с постоянным членом, но я знаю, что

$\vec r \times k\vec r = 0$

Однако в задаче указано, что мы должны доказать, что результат является константой, поэтому я думаю, что ошибаюсь. Конкретные места, где кто-то может мне помочь:

(1) Правильно ли моя интеграция? Если нет, то как интегрировать силу (заданную в терминах обозначения вектора положения) по отношению к время?

(2) Что происходит с константой? Перекрестное произведение вектора и скаляра не имеет никакого смысла.

• домашние задания и упражнения
• ньютоновская механика
• угловой момент
• законы сохранения
• крутящий момент

$\endgroup$

1

$\begingroup$

Если вы хотите доказать, что $\vec{L}=\vec{r}\times \vec{p}$ постоянна по времени для частицы в центральном силовом поле $\vec F = \phi( r) \vec r$, просто покажите, что угловой момент не меняется со временем, т. е. $\frac{d}{dt}\vec{L}=0$.

Используя правило произведения, мы получаем два термина:

$\frac{d}{dt}\vec{L}=\frac{d}{dt}(\vec{r}\times \vec{p}) = \frac{d\vec r}{dt} \times \vec p + \vec r \times \frac{d \vec p}{dt}$.

Так как $\vec p = m \frac{d \vec r}{dt}$ и $\frac{d \vec r}{dt}$, очевидно, параллельны, первое слагаемое обращается в нуль. В частном случае центральной силы $\vec F = \phi(r) \vec r$ обращается в нуль и второй член: У нас есть $\frac{d\vec p}{dt} = \vec F \propto \vec r$, поэтому два вектора во втором члене параллельны, в результате чего векторное произведение становится равным нулю.

Следовательно, $\frac{d}{dt}\vec{L}=0$ и $\vec{L}$ является константой по времени.

Чтобы ответить на ваши вопросы:

(1) Нет, так интегрироваться нельзя. Положение частицы $\vec r$ меняется со временем, поэтому вы не можете рассматривать его как константу при интегрировании. Если вы хотите решить этот интеграл, сначала решите уравнения движения $\frac{d \vec p}{dt} = \vec F$.

(2) Если бы ваше интегрирование было правильным (например, если бы положение частицы было постоянным), константа интегрирования тоже была бы вектором. Тогда перекрестное произведение снова имело бы смысл.

$\endgroup$

$\begingroup$

Поскольку $ F = \phi(r) \vec r $, можно найти крутящий момент относительно начала координат.

Крутящий момент $ \tau = \vec F \times \vec r = \phi (r) \vec r \times \vec r$

Но $\vec r \times \vec r$ равен нулю, поэтому крутящий момент вокруг начало также равно нулю.

Поскольку крутящий момент — это просто скорость изменения углового момента $\frac{ d\vec L}{dt}$, угловой момент не меняется, что вы и хотели доказать.

$\endgroup$

0

$\begingroup$

Вы не можете вычислить этот интеграл, потому что мы ожидаем, что $\vec{r}$ изменится со временем.

No related posts.