Чем окружность отличается от круга: Чем отличается окружность от круга

Круг и окружность

Цели:

• Познакомить детей с новым понятием – круг. Помочь детям освоить признаки круга.
• Дать понятие “окружности”, определить место положения окружности по отношению к кругу.
• Освоить с детьми работу с циркулем-помощником.
• Развивать умение логически мыслить, воображение и творческие способности детей.
• Воспитывать интерес к предмету и умение оценивать свой труд.

Оборудование: Бумага, циркули, карандаш, металлическая крышка для консервирования с резинкой, шаблоны треугольника, квадрата, пятиугольника, смайлики, клей, ножницы.

Ход урока

1. Организационный момент.

Долгожданный дан звонок,
Начинается урок.

Возьмём с собой на урок улыбки и хорошее настроение.

Посмотрим, какое оно у вас.

Игра.

У меня два солнышка – грустное и радостное.

Хлопните в ладоши те, у кого грустное настроение. А у кого радостное?

Надеюсь, у кого настроение грустное, станет радостным, а у кого хорошее – станет ещё лучше. Пожелаем друг другу удачи и улыбнёмся. Покажите свои ладошки, потрите их, погладьте себя по голове и скажите: “Какой я замечательный!”

На уроке вас ждут открытия: у кого-то они будут большие, у кого-то маленькие, но у каждого они свои.

2. Повторение изученного материала.

Прежде чем, приступить к новому материалу давайте, повторим то, что нам известно.

Игра “Угадай фигуру”

В конверте фигуры (треугольник, квадрат, пятиугольник). Один ученик описывает фигуру, не называя её, а другие должны отгадать.

Три вершинки, три угла,

Три сторонки – вот и я! (треугольник)

Он давно знаком со мной,
Каждый угол в нём прямой.
Все четыре стороны
Одинаковой длины.
Вам его представить рад,
А зовут его.. (квадрат)

3. Изучение нового материала.

Сегодня мы с вами снова отправимся в страну Геометрию с нашими старыми знакомыми — Линейкой, Карандашом и Резинкой. Они идут по улице и видят, что жители Геометрии рассматривают на стене дома такую картинку:

 — Ну, это я знаю, — сказал Карандаш. – Это кривые.

— Красивый рисунок, хороший мастер его делал, - говорит Линейка, — смотри, Карандаш, здесь есть одна кривая удивительной формы: вся такая одинаково плавная, гладкая..

— Про какую кривую говорит Линейка? Каким инструментом можно начертить такую правильную, всю одинаково плавную кривую?

(Дети называют циркуль. Если не называют, сюжет знакомит их с этим инструментом.)

— Кто же нарисовал эту замечательную кривую? – спросил Карандаш.

— Это мастер Циркуль, — ответили ему жители Геометрии.

Познакомились наши друзья с Циркулем. Спрашивает Линейка:

— Как вам удаётся такие плавные линии рисовать?

— А вот так, — говорит Циркуль. – Встаю на острую ножку и кручусь на ней, как балерина. Р-раз!

Учитель берёт большой циркуль и быстро чертит на доске окружность.

— О, какая красивая линия! – говорит Карандаш. – Что это?

— Это окружность,- говорит Циркуль. – Линию, которую рисует мой грифель называют словом

окружность. Если вы начертите окружность на бумаге и вырежете её, то эта линия останется на границе выреза. А то, что останется у вас в руках, называется круг. (Учитель показывает бумажный круг.)

Окружность – это граница круга.

Пока Циркуль объяснял Линейке, что такое окружность, карандаш наклонился и что-то поднял с тротуара.

— Смотрите! – закричал он. – У меня есть и окружность, и круг.

— И показал всем вот это. (Учитель показывает детям металлическую крышку для консервирования и вынимает из неё круглую резинку).

— Ребята, что здесь окружность, а что — круг?

— Я знаю, как легко запомнить, чем отличается окружность от круга, — говорит Карандаш. – Резинка, иди сюда, прыгай!

Карандаш подставил Резинке то, что держал в одной руке. Резинка весело прыгнула. Но когда Карандаш предложил ей прыгнуть сквозь предмет в другой руке, Резинка обиделась и сказала:

— Ты что, карандаш, думаешь, ты один запомнил разницу между окружностью и кругом?

— Сквозь что прыгнула Резинка? (Сквозь окружность. Сквозь круг прыгнуть нельзя: он сплошной.)

— А что вы ещё умеете, мастер Циркуль? – спросила Линейка.

— О, я могу многое, ответил Циркуль, — смотрите!

(Учитель показывает несколько красивых орнаментов и аппликаций, выполненных с помощью циркуля. )

— Ой, как сложно! – говорит карандаш. – Я, наверное, не смогу так.

— Это совсем не сложно, говорит мастер Циркуль, - и я этому научу очень быстро. Самое главное – научиться правильно, держать меня в руках.

Физкультминутка

Раз, два, три, четыре, пять (шаги на месте)!
Все умеем мы считать (хлопки в ладоши),
Отдыхать умеем тоже (прыжки на месте).
Руки за спину положим (руки за спину),
Голову поднимем выше (поднять голову выше)
И легко-легко подышим (глубокий вдох-выдох).
Подтянитесь на носочках столько раз,
Ровно столько, сколько пальцев (показали, сколько пальцев на руках)
На руке у вас (поднимаемся на носочках 10 раз).

Практическая работа

Возьмите в руки циркуль, рассмотрите его, найдите и потрогайте остриё, на котором циркуль “крутится”, найдите “хвостик”, подвигайте “ноги”.

— Какая ножка циркуля стоит в центре окружности – игла или грифель?

(Центр учитель отмечает и показывает на чертеже.)

— Какой ножкой циркуль рисует? (Грифелем.)

— Ноги циркуля двигаются. Что надо сделать, чтобы нарисовать большую окружность, развести их или сдвинуть ближе?

— Попробуйте нарисовать самую большую окружность, какая поместится на вашем листе.

— А теперь самую маленькую, какая у вас только получится ( на том же листе в любом месте, можно внутри большой).

Физкультминутка для глаз

• Плотно сомкните веки на 5 секунд, затем широко откройте их на такое же время, не морща при этом лоб. Повторите 3-4 раза.
• Сосредоточьте взгляд на отдалённом предмете, затем переведите его на кончик носа. Повторите 4-6 раз.
• Делайте медленные круговые движения глазами, будто следите за большим колесом, вращающимся 2 раза в одну сторону и 2 раза в другую сторону.
  Повторите 2-4 раза.
• Посмотрите на верхний левый угол стены вашей комнаты, переведите взгляд на кончик носа, а затем на верхний правый угол стены и снова на кончик носа. Повторите 5-6 раз.

Игра “Сложи круг”

Из разных деталей сложить круг. Работа выполняется индивидуально. Ребятам предлагается 5 наборов с разными вариантами сборки (в конвертах).

Практическое задание по изготовлению аппликации “Снеговик”.

На листе цветной бумаги дети делают аппликацию “Снеговик”. Используются шаблоны кругов, ведро, метлу, нос, пуговицы, глаза дорисовывают фломастером.

4. Домашнее задание.

Дома доделать аппликацию, оформить снеговика, доделать фон (сделать ночь или день)

5. Итог урока. Рефлексия.

• Что нового вы узнали сегодня?
• Какие открытия вы сделали для себя?

Отгадайте загадки.

Нет углов у меня,
И похож на блюдце я,
На тарелку, и на крышку,
На кольцо, на колесо.
Кто же я такой, друзья? (круг)

У круга есть одна подруга,
Знакома всем её наружность.
Она идёт по краю круга
И называется… (окружность)

У вас на партах фигуры.

— я хорошо понял, что такое круг и окружность

— я не всё понял, у меня были ошибки

— я не понял, что такое круг и окружность

Учащимся предлагается выбрать символ и оценить свою деятельность. Дети сами вывешивают свои символы на магнитную доску.

Использованная литература.

1. Истомина Н.Б. Наглядная геометрия. Тетрадь по математике. 2-й класс. М.: ЛИНКА-ПРЕСС, 2008.
2. Газета “Начальная школа” издательский дом “Первое сентября” № 27-28 июль, 2004
3. Житомирский В.Г., Шеврин Л. Н. Путешествие по стране Геометрии. – М.: Педагогика, 1991.
4. Жильцова Т.В., Обухова Л.А. Поурочные разработки по наглядной геометрии: 1 – 4 класс. – М.: ВАКО, 2004.

Окружность и круг

Устный счет. Определение темы урока

О

Ж

К

Р

У

1.Найдите произведение наибольшего и наименьшего двузначных чисел

2.Найдите площадь земельного участка, если его ширина 800м, а

длина 900м. Результат выразите в га

3. S = a² — формула…?

4 .S кв . = 100 м². Чему равна его сторона?

5. Длина прямоугольника 6см, ширина в 2 раза меньше.

Найдите площадь прямоугольника

Устный счет.

Определение темы урока

У

О

Ж

Н

Ь

К

Р

С

Т

О

6.Сколько кубических сантиметров в одном кубическом метре?

7.Как найти объем прямоугольного параллелепипеда?

8.Чему равен объем куба, длина ребра которого равна 2м?

9.Если фигура разбита на части, то чему равна площадь фигуры?

10.Найдите произведение 24 и 11.

Окружность и круг

О

На уроке я должен:

— получить представление об окружности и круге;

— получить представление об элементах окружности и круга;

— научиться строить окружность и круг с помощью циркуля;

— научиться измерять радиус и диаметр;

— уметь применять полученные знания к решению практических задач;

— воспитывать уверенность в себе и уважение к окружающим

Мой циркач, циркач лихой Чертит круг одной ногой, А другой проткнул бумагу, Уцепился и ни шагу.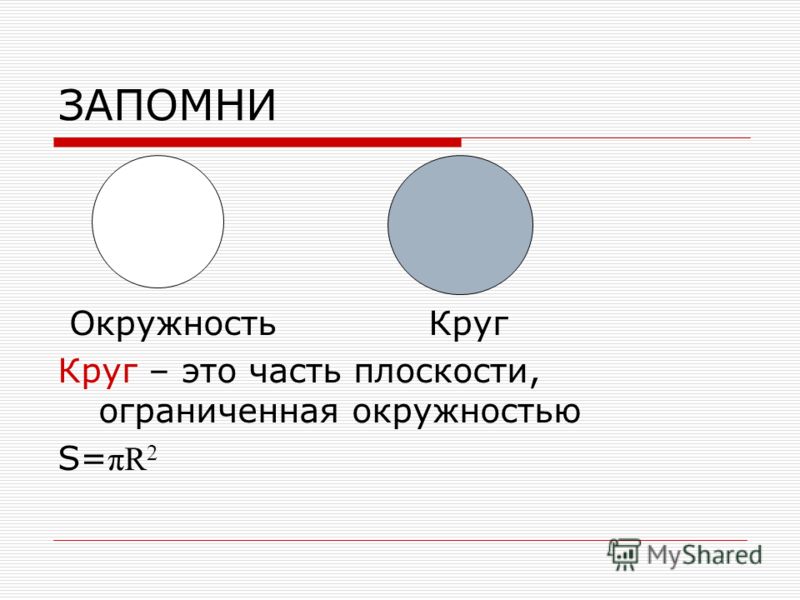

(Циркуль)

Циркуль – это чертежный инструмент. С ним нужно работать осторожно. На одном конце у него — игла, на другом — карандаш. Пользоваться им надо осторожно, чтобы не уколоться и не поломать грифель карандаша. Нельзя подносить циркуль иглой к лицу и нельзя передавать циркуль соседу “иглой вперед”.

1. Поставьте в тетради точку и назовите её буквой О.

2. Возьмите в раствор циркуля отрезок 3 см.

О

3. Поставьте иголку циркуля в точку О, а другой «ножкой» циркуля проведите замкнутую линию.

Точка О называется

центром окружности

О

Задание №1

.

Окружность – это замкнутая линия, все точки которой равноудалены от центра

О

Задание №2

Используя циркуль, построй в тетради две окружности с одинаковым раствором циркуля, равным 2 см, закрась внутреннюю область одной окружности.

Чем отличается окружность и круг друг от друга?

O

O

Круг

Окружность

O

O

Круг

Окружность

Круг – часть плоскости,

ограниченная окружностью

O

O

Круг

Окружность

У круга есть одна подруга,

Знакома всем ее наружность,

Она идет по краю круга,

И называется окружность.

Какие знакомые вам предметы имеют форму круга, а какие форму окружности?

Задание №3

М

Отметим на окружности две точки А и М.

Соединим точки О и М, О и А.

О

Отрезки ОА и ОМ – называются радиусами окружности .

А

Радиус — отрезок, соединяющий центр окружности с точкой, лежащей на окружности.

3

М

Сколько радиусов у окружности?

Что можно сказать про них?

О

Запишите в тетради:

ОА=ОМ

А

3

Задание №4

Продлите отрезок АО до пересечения с окружностью.

М

К

Обозначьте точку пересечения буквой К.

Отрезок АК – называется диаметром окружности.

О

А

Диаметр – это отрезок, соединяющий две точки на окружности и проходящий через её центр.

М

К

Сравните радиус окружности и её диаметр.

О

А

Перечислите все радиусы и диаметры окружности.

С

В

D

O

E

А

L

F

K

3

Задание №5

Нарисуйте окружность с центром в точке О произвольного радиуса.

Р

Отметьте на окружности две точки А и В.

О

А

Точки А и В разделили окружность на две части, которые называются дугами окружности.

Н

Чтобы было понятно о какой дуге идёт речь, возьмём на каждой дуге по одной точке Н и Р.

В

ВНА, ВРА – дуги окружности.

3

С

Назовите все получившиеся дуги на окружности:

O

А

М

Р

K

3

Назовите точки, лежащие на круге:

Назовите точки, лежащие на окружности.

Назовите точки, не лежащие на окружности.

L

K

С

В

D

X

T

О

А

E

Y

Z

P

N

F

S

M

3

Задание №6

(на индивидуальном листе)

Отметьте точки А, В и C , лежащие внутри круга.

Точки Д, Е, и К, лежащие на окружности.

Точки F , М, и N , лежащие вне круга

Задание №7

(на индивидуальном листе)

Измерь радиусы окружностей

Запиши, чему равны диаметры

каждой из фигур

Работа над задачей

№ 868

3

Домашнее задание

№ 853, 854, 878(а)

3

Итог урока:

Опиши свои впечатления о сегодняшнем уроке:

• Спасибо за…
• Я узнал…
• Хорошо, что…
• Мне понравилось…
• Меня удивило…

Не забудь нарисовать нашему «солнышку»

улыбку или огорчение!

3

3

3

Форма: Круг — элементарная математика

Значение

Неформальное значение: Слово «круг» знакомо большинству детей очень рано, но оно имеет не более чем неформальное значение слова «круглый». Мы сидим «в кругу», не особо задумываясь о том, насколько он круглый, и не представляя себе геометрический объект, связанный со словом.

По мере того, как учащиеся изучают геометрию, мы помогаем им уточнить значение из неформального смысла — формы кольца, колеса или фрисби — и принять более формальное математическое значение. Во-первых, круг — это двумерная фигура: то есть фотография мяча может быть круглой, но сам мяч — нет (мяч трехмерен). И «круглого» недостаточно: все приведенные ниже фигуры «круглые», но чтобы что-то было кругом, каждая его точка должна быть на одинаковом расстоянии от центра.

Некоторые точки эллипса и яйцевидной формы находятся дальше от центра (красные), чем другие; все точки окружности находятся на одинаковом расстоянии от центра.

Формальное определение: Окружность — это набор точек на плоскости, которые равноудалены от фиксированной точки (центра окружности). Обратите внимание, что формальное определение исключает «внутреннюю часть» окружности: эти точки ближе к центру, чем точки на самой окружности. Когда студентов просят указать на круг, они часто указывают внутри круга и могут называть круговой «обод» этой формы окружностью. В точном использовании замкнутая кривая сама по себе является окружностью, а термин окружность относится к длине кривой. (Слово «диск» используется для обозначения области, заключенной в круглую границу. Но даже математики могут сказать «разрезать круг пополам» вместо «разрезать диск пополам», когда контекст делает значение достаточно ясным.)

Один из способов прояснить язык — представить картинку, на которой круг и его внутренняя часть окрашены по-разному. На этой картинке круг красный; его внутренняя часть желтая. Внешний вид круга — это вся оставшаяся плоскость, не находящаяся на круге и не заключенная в нем. На этом рисунке показана небольшая квадратная область этой плоскости, а внешняя сторона круга окрашена в синий цвет.

Измерения на окружностях

Для нахождения длины окружности и площади круга можно использовать две важные формулы:

• Окружность: C = πd = 2πr
• Площадь: A = πr ²

В каждой формуле r представляет длину радиуса окружности, а d представляет длину диаметра или удвоенную длину радиуса. Число пи (π) — иррациональное число, определяемое как отношение C/d — отношение длины окружности к длине его диаметра — хотя точные вычисления значения π никогда не основываются на измерениях. Его значение составляет примерно 3,14159.265…

Открытие формулы длины окружности

Поскольку это определение числа пи, «формула» для длины окружности на самом деле не является чем-то новым, это просто переформулировка или повторное использование определения числа пи.

Если , то .

Открытие формулы площади

Мы не можем точно измерить площадь круга, нанеся на него квадраты; они не подойдут, независимо от того, какой размер мы выберем. Итак, чтобы найти формулу площади круга, мы «рассекаем» его, разрезаем на части, площади которых можем измерить. (См. Формулы площади для примеров рассечения параллелограммов и треугольников.)

Сектора круга немного похожи на треугольники, особенно если разделить круг на достаточное количество секторов. Если мы разделим круг на восьмые части (левый круг на рисунке ниже), разница (показана розовым цветом) между полным сектором и треугольником, который он содержит (показан синим цветом), будет довольно существенной. Мы могли бы вычислить площадь этого синего треугольника, умножить на 8, а затем просто удовлетвориться этой заниженной оценкой площади круга.

Но мы могли бы сделать лучше. Если мы разделим круг на двенадцатые части (в центре вверху), ошибка — количество оставшегося розового — будет значительно меньше. А если разрезать круг на 24 части (справа вверху), то остаток будет еще меньше, даже с учетом того, что таких остатков теперь 24.

Что еще более важно, мы замечаем еще кое-что. По мере того, как круг делится на большее количество секторов — и различие между «сектором» и «треугольником» все больше и больше испаряется — размеры каждого треугольника теперь легче соотносить с размерами круга. Если мы разделили круг на 24 сектора, короткая сторона треугольника составляет (почти) 1/24 длины окружности круга, а высота этого треугольника равна (почти) радиусу круга. Итак, используя эти приближения, площадь треугольника равна

Но в круге 24 таких треугольника, поэтому площадь круга будет

и мы знаем, что C = 2πr, поэтому

Еще немного осторожности. Наша окончательная формула предполагала, что основание и высота треугольника равны , ровно , как мы хотели: , ровно , окружности и , ровно , радиуса, что, как мы знали, было неверным. Что спасает рассуждения, так это то, что мы можем сделать приближение сколь угодно точным. Если бы мы разбили круг на 1000 секторов — чертить совершенно бессмысленно — основание и высота треугольника были бы еще ближе к 1/1000 длины окружности круга и точно радиусу. С рассуждения всегда дают один и тот же результат, и мы можем получить приближение, поддерживающее это рассуждение, сколь угодно точное — разрезать круг на миллион секторов или миллион миллион секторов — результат общий.

Еще одно изображение, которое иногда используется, чтобы получить представление о площади круга, показано ниже. Там все сектора раздвинуты, как дольки апельсина.

Затем их можно собрать вместе, чтобы получился параллелограмм.

Опять же, чем больше секторов, тем больше этот параллелограмм приближается к прямоугольнику, размеры которого равны r и . Тот же результат.

Другие измерения окружности

Обобщения формул площади и окружности могут быть использованы для определения длины дуги окружности или площади сектора окружности:

• Площадь сектора:

• Длина дуги:

В каждой формуле x представляет меру дуги в градусах.

Этимология

От латинского circulus, уменьшительного от circus, что означает «кольцо», возможно, от индоевропейского корня ker- или sker- означает поворачиваться или сгибаться.

Индоевропейское слово ker- также дает начало Кривому, Изгибу и короне, коронации, короне солнца и т. д.

Связанные математические термины

Корень окружность- дает начало многим терминам, используемым в математических и случайных значениях.

Окружность, Окружность

Другие родственные слова

циркулировать, цирк, обход, кругосветное плавание, обстоятельство, корона, корона и т. д.

Различия между кругом и сферой

Согласно определению круга и сферы, они оба круглые; однако, в то время как круги являются фигурами, сфера может быть описана как объект. Их можно сравнить с наброском теннисного мяча на бумаге, а затем с самим мячом в реальности. Круг считается 2D-представлением, а сфера — 3D-объектом с объемом. Вы можете определить только поверхность круга, тогда как есть способ определить объем сферы. Земля является примером сферы, присутствующей во Вселенной. В следующих отрывках мы поймем определение круга и сферы, уравнение круга и сферы и разницу между кругом и сферой.

Круг

Круг в буквальном смысле означает кольцо и ведет свое происхождение от греческого слова «киркос». Окружность может быть описана как набор точек и имеет особенность, когда все точки находятся на фиксированном расстоянии от точного местоположения на плоскости. Это петля с закрытыми концами, которая разделяет равнины на две разные части, то есть внутреннюю и внешнюю области. Это двухмерная форма. Круги — очень распространенный объект. Это другой тип эллипса, две точки фокуса которого перекрывают друг друга, а их эксцентриситет равен нулю.

Отличительными характеристиками круглой формы являются ее диаметр, центр касательной, хорда и длина окружности. Круг измеряется по его радиусу. Радиус окружности можно определить как прямую линию, соединяющую центр и окружность окружности. Радиус обозначается буквой «r». Некоторые примеры круга включают диски, часы и так далее.

Сфера

В отличие от кругов, сфера является обычной трехмерной формой. Точки сферы будут равны центру каждой точки. Он обычно используется для быстрого определения площади поверхности, размеров площади поверхности и радиуса. Диаметр сферы — это прямая линия, проходящая через центр и соединяющая два противоположных конца окружности сферы. Сфера представляет собой комбинацию крошечных кругов и полушарий, соединенных вместе. Футбол, апельсины, глазные яблоки и т. д. — вот некоторые примеры сфер.

Различия между кругом и сферой

Согласно определению сфер и кругов, они демонстрируют точную симметрию в своей центральной точке. Края круга и самые удаленные точки сферы точно отделены от их центральной точки (центра). Есть некоторые отличия. Например, круги двумерны, а сфера — это предмет, имеющий три измерения. Величина расстояния между двумя самыми удаленными точками называется диаметром (и в два раза больше его радиуса). В этом разделе мы поймем разницу между сферой и кругом. Кроме того, мы рассмотрим математическое уравнение между кругом и сферой.

Differences between a circle and a sphere
Differentiating Property	Circle	Sphere
Размеры	Круг — это фигура, имеющая два измерения.	Сфера трехмерна.
Формула площади	ПЛОЩАДЬ КРУГА = πr 2 .	Площадь поверхности сферы определяется как 4πr 2 .
Формула объема	Круг не основан на объеме.	Размер сферы равен (4/3) πr 3 .
Формула длины окружности	Длина окружности равна 2πr.	Сфера не имеет окружности.
Уравнение	Уравнение круга равно (x — a) 2 + (y — b) 2 = R 2	9003 ) 2 + (y – k) 2  + (z – l) 2  = r 2

Какое уравнение окружности и сферы?

В этом параграфе мы поймем уравнение круга и сферы. 9Уравнение сферы а) ²  + (y – b) ²  = R ²

Заключение

Согласно определению круга и сферы, круг можно описать как двумерный объект с размерами X и Y , тогда как сфера — это трехмерный объект с размерами X, Y и Z внутри плоскости.