Внеклассный урок — Арккосинус
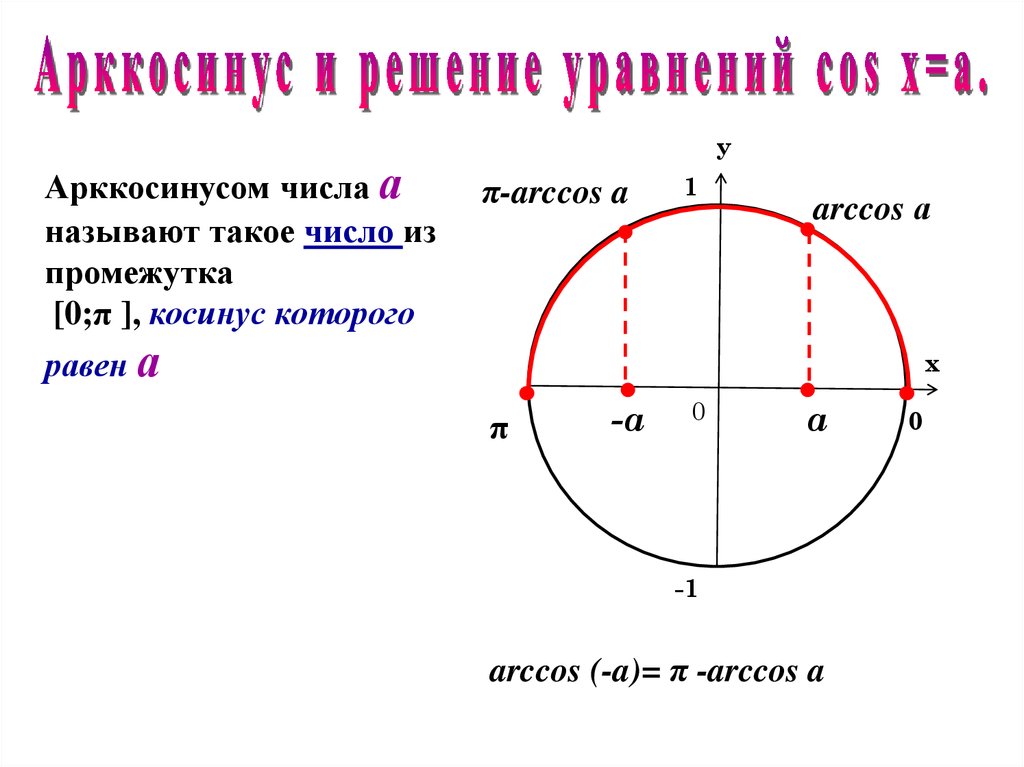
АрккосинусАрккосинус в переводе с латинского означает дуга и косинус. Это обратная функция.
При этом | a | ≤ 1. Обозначается так: arccos a. |
Говоря иначе:
arccos a = t. Следовательно, cos t = a. Условия: модуль а не больше 1; t не меньше 0, но не больше π (| a | ≤ 1; 0 ≤ t ≤ π) |
Пример-пояснение: Найдем arccos √2/2 (см. рисунок).
рисунок).
Решение.
Выражение arccos √2/2 показывает, что косинус угла t равен √2/2 (cos t = √2/2).
Далее просто находим точку этого косинуса на числовой окружности, что и является ответом:
число √2/2, являющееся значением оси х, соответствует точке π/4 на числовой окружности.
Значит, arccos √2/2 = π/4.
Обратите внимание:
если cos π/4 = √2/2, то arccos √2/2 = π/4.
То есть в первом случае по точке на числовой окружности определяем значение косинуса, а во втором – наоборот, по значению косинуса находим точку на числовой окружности. Движение в обратную сторону. Это и есть арккосинус.
Обобщим: косинус – это точка на оси х, а арккосинус – это соответствующая ей точка на окружности.
Формулы:
t = ± arccos a + 2πk, где k – любое целое число arccos (-a) = π – arccos a, где 0 ≤ a ≤ 1 |
Пример 1: Вычислить арккосинус 1/2.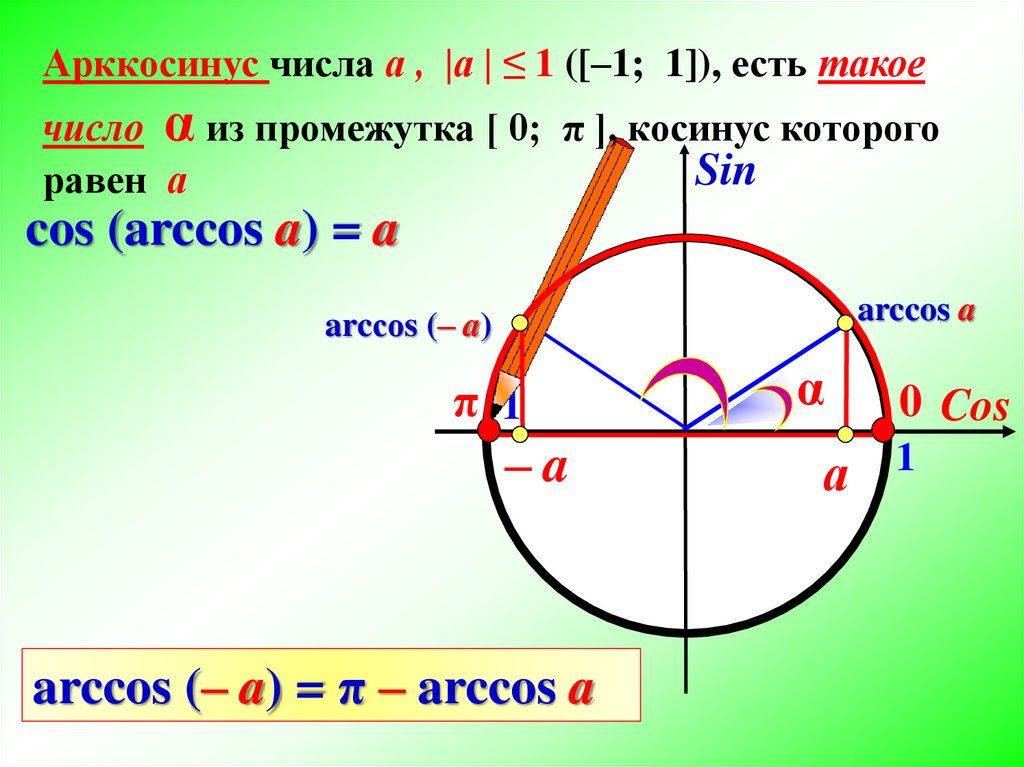
Решение.
Итак, а = 1/2. Значит, наша формула arccos a = t обретает конкретику:
arccos 1/2 = t.
Это означает, что косинус угла t равен 1/2:
cos t = 1/2.
При этом наша точка t находится на отрезке [0; π].
Находим значение t. Для этого смотрим на числовую окружность. Мы видим, что число 1/2 является абсциссой точки π/3 – то есть является косинусом угла π/3. Иначе говоря:
t = π/3.
Подставляем значение t в выражение cos t = 1/2:
cos π/3 = 1/2. При этом π/3 входит в отрезок [0; π].
Совершаем обратное действие: если cos π/3 = 1/2, то:
arccos 1/2 = π/3.
Без объяснений процесс решения будет таким:
arccos 1/2 = t
cos t = 1/2, t ∈ [0; π]
t = π/3, π/3 ∈ [0; π]
arccos 1/2 = π/3
Пример решен.
Обратите внимание: косинусом π/3 является 1/2, а арккосинусом 1/2 является π/3. Движение в обратную сторону. Косинусом числа является точка на оси координат, а арккосинусом – точка на числовой окружности.
√3
Пример 2: Найти arccos – ——
2
Решение.
√3
arccos (– ——) = t
2
√3
cos t = – ——, t ∈ [0; π]
2
√3
cos 5π/6 = – ——, 5π/6 ∈ [0; π]
2
√3 5π
arccos – —— = ——
2 6
Пример решен.
Акцентируем ваше внимание: косинусом 5π/6 является -√3/2, а арккосинусом -√3/2 является 5π/6.
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт.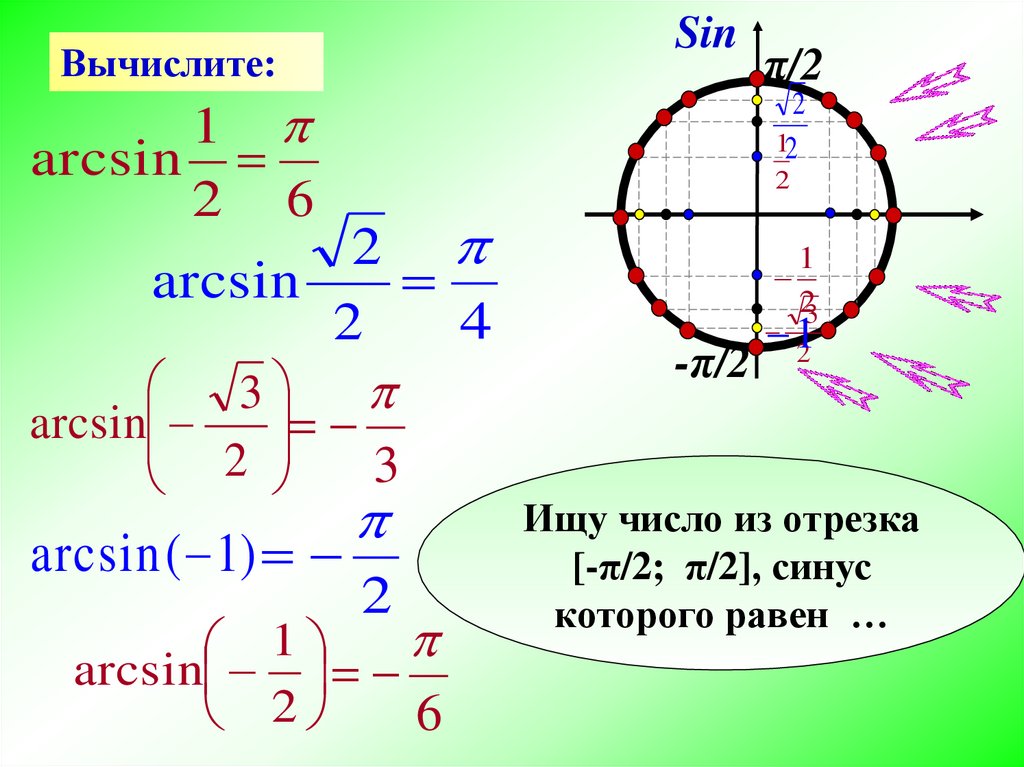 )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | ||
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Калькулятор — arccos(1/2) — Solumaths
Arccos, расчет онлайн
Резюме:
Функция arccos позволяет вычислить арккосинус числа. Функция arccos является обратной функцией функции косинуса.
Функция arccos является обратной функцией функции косинуса.
arccos online
Описание:
Функция арккосинуса является обратной функцией функция косинуса, это вычисляет арккосинус числа онлайн .
Число, к которому вы хотите применить функцию функции арккосинуса, должно принадлежать диапазону [-1,1].
- Расчет арккосинуса
- Таблица замечательных значений
- Арккосинус : arccos.
 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. - Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
- Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
- Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
- Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
- Косеканс: косеканс. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Котангенс : котанг. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
- Тригонометрическое расширение: expand_trigo.

Чтобы вычислить арккосинус числа , просто введите число и примените функция arccos . Таким образом, для , вычисляющего , арккосинус числа, следующего за 0,4, вы должны ввести arccos(`0.4`) или сразу 0.4, если кнопка arccos уже есть, результат 1.1592)`.
| arccos(`-1`) | `pi` | |
| arccos(`-sqrt(3)/2`) | `5*pi/6` | |
| `3*pi/4` | ||
| arccos(`-1/2`) | `2*pi/3` | |
| arccos(`0`) | ``2*pi/3` pi/2` | |
| arccos(`1/2`) | `pi/3` | |
| arccos(`sqrt(2)/2`) | `pi/4` | |
| arccos(`sqrt(3)/2`) | `pi/6` | |
| arccos(`1`) | `5 `0` |


 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.