Решите неравенство cosx 1 2: conf__edu_age }) }) edu_group = edu_age_conf.groups[conf__edu_age] edu_ad = edu_age_conf.ads[edu_group] } $(document).ready(() => { if (typeof KrApi != ‘undefined’) { edu_group = edu_age_conf.pods[KrApi.settings.base_pod] if (typeof edu_group != ‘undefined’) { edu_ad = edu_age_conf.ads[edu_group] } } })

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )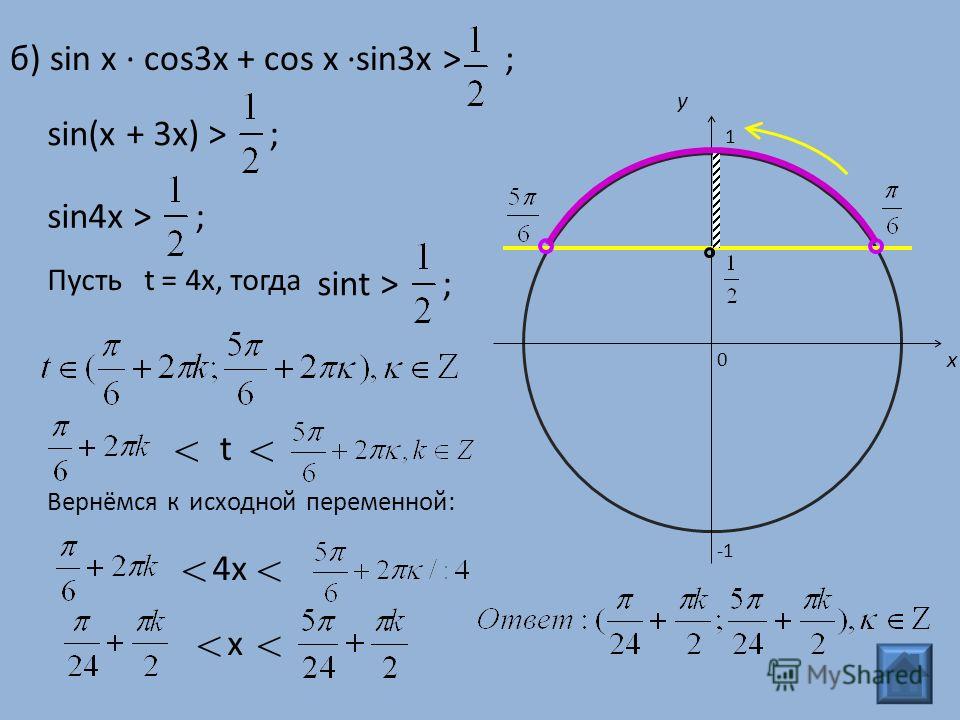
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значениеsin((2pi)/3)
88
Найти точное значение		tan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

cosx меньше a

Рассмотрим решение тригонометрических неравенств вида cosx меньше a (cosx<a) на единичной окружности.

Снова применяем ассоциацию косинус-колобок. Оба кругленькие, оба начинаются с ко-. Колобку, в силу особенности его фигуры, удобнее двигаться влево-вправо, а не вверх-вниз. Влево-вправо на координатной плоскости — движение по оси ox. Значит, косинус — это x. То есть абсцисса,  координата x точки на окружности. Геометрически cosx=a в точках пересечения единичной окружности и прямой x=a (прямая, параллельная оси ox). Соответственно, точки окружности, находящиеся правее этой прямой, соответствуют значениям косинуса, большим a, а cosx меньше a — левее этой прямой. Прямая и окружность могут пересекаться, не пересекаться и касаться. От их взаимного расположения зависит решение тригонометрического неравенства cosx меньше a.

1) cosx<a, при 0<a<1.

 

Первая точка пересечения прямой и окружности находится, как обычно, — это arccos a. Поскольку нам нужны значения, в которых cos x меньше a, из первой точки ко второй мы идем по верхнему пути, против часовой стрелки. При таком направлении обхода угол увеличивается. Вторую точку получили, немного не дойдя до 2п. На сколько не дошли? На тот же угол, который соответствует arccos a. Раз не дошли, то это число вычитаем из 2п. Поэтому вторая точка пересечения прямой с окружностью есть 2п-arccos a. Итак, решением неравенства cos x меньше a является промежуток (arccos a; 2п-arccos a). Поскольку период косинуса равен 2п, к каждому из концов промежутка прибавляем 2пn, где n -целое число (то есть n принадлежит Z). Получаем окончательный вариант ответа: (arccos a+2пn; 2п-arccos a+2пn). Для нестрогого неравенства точки закрашиваем и ставим квадратные скобки.

2) cos x меньше -a, при 0<a<1.

Решение неравенства аналогично первому случаю. Отличие — нужно вычислить арккосинус отрицательного числа (чуть позже я расскажу, как легко запомнить значения arccos (-a) с помощью ассоциации). А пока что arccos (-a)= п-arccos a. Ко второй точке здесь тоже идем против часовой стрелки, то есть значение угла увеличивается. Не доходим до 2п на величину arccos(-a), отсюда вторая точка есть 2п-arccos(-a). Чтобы учесть все решения неравенства, к концам промежутка прибавляем 2пn. Если неравенство нестрогое, точки закрашиваем и включаем в ответ (с квадратной скобкой).

3) cosx<0

То есть ищем, где косинус отрицательный.

В качестве первой точки промежутка, на котором косинус принимает отрицательные значения, берем п/2, вторая точка — 3п/2. Чтобы учесть все промежутки, на которых косинус отрицательный, прибавляем к концам промежутка 2пn. Таким образом, решение тригонометрического неравенства cosx<0 есть промежуток (п/2+2пn; 3п/2+2пn), где n — целое число. Если неравенство нестрогое, то есть ищем неотрицательные значения косинуса, точки закрашиваем, скобки берем квадратные.

4) cosx<1

В этом случае окружность и прямая x=a касаются в одной точке — в нуле. Таким образом, за исключением этой точки, окружность расположена левее прямой. Значит, cosx меньше 1 в любой точке, кроме точек вида 0+2пn. Чтобы записать решение тригонометрического неравенства cosx<1 в виде интервала, в качестве второго конца промежутка берем 2п и к обоим концам прибавляем 2пn.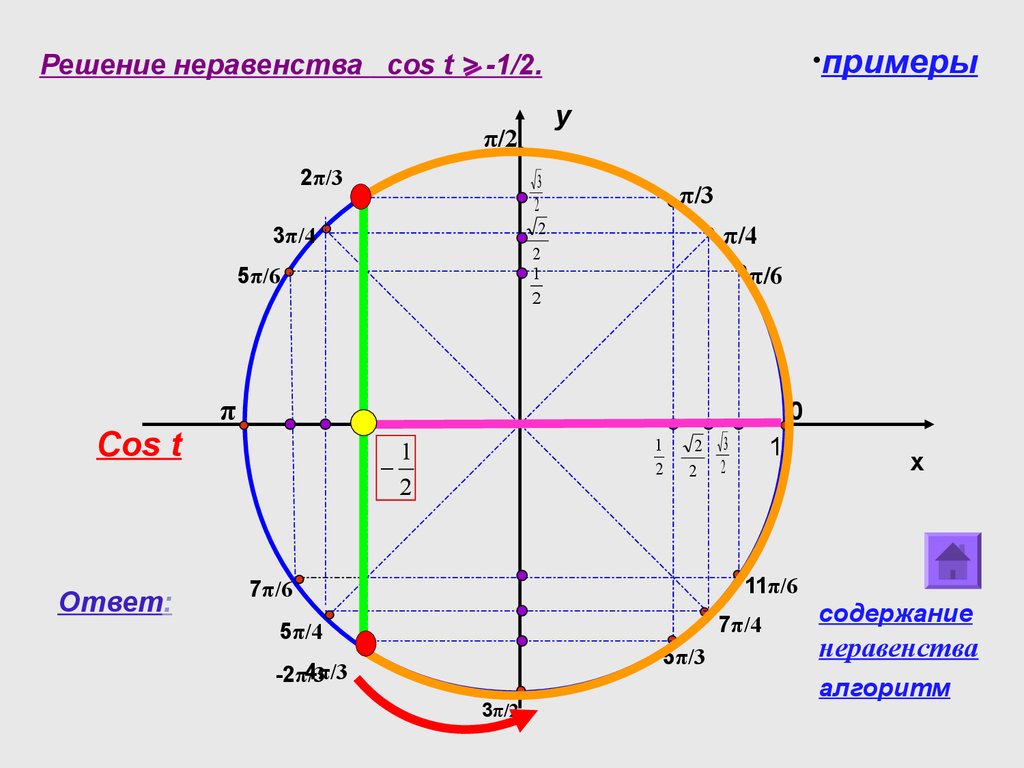 Получаем (2пn; 2п+2пn).

5) cosx<a, при a>1.

В этом случае окружность целиком лежит левее прямой x=a и любое значение x удовлетворяет условию неравенства. Таким образом, в этом случае косинус меньше a на промежутке (-∞;+∞).

6) cosx<-a, при a>1.

При таких a окружность целиком расположена правее прямой x=-a и нет ни одного x, удовлетворяющего требованию cosx меньше -a. Поэтому решений нет.

   

В этом случае точку пересечения окружности и прямой исключать из решения не нужно, значит, x — любое число и решением является вся числовая прямая: (-∞;+∞).

   

Единственным решением этого тригонометрического неравенства является точка п. С учетом периодичности косинуса, решением является множество точек вида п+2пn, где n — целое число.

И в заключении — пример решения тригонометрического неравенства вида cosx меньше a: cosx<-1/2:

 

Найдите набор решений неравенства cosx>= (-1)/2.

  • Курс
    • NCERT
      • Класс 12
      • Класс 11
      • Класс 10
      • Класс 9
      • Класс 8
        • 900 03 Класс 7
      • Класс 6
    • IIT JEE
  • Экзамен
    • JEE MAINS
    • JEE ADVANCED
    • X BOARDS
    • XII BOARDS
    • NEET
      • Neet Предыдущий год (по годам)
      • Физика Предыдущий год
      • Химия Предыдущий год
      • Биология Предыдущий год
      • Нет Все образцы работ
      • Образцы работ Биология
      • Образцы работ Физика
      • Образцы работ Химия
        • 900 21
    • Скачать PDF-файлы
      • Класс 12
      • Класс 11
      • Класс 10
      • Класс 9
      • Класс 8
      • Класс 7
      • Класс 6
    • Экзамен угол
    • Онлайн-класс
    • Викторина
    • Задать вопрос в Whatsapp
    • Поиск Сомнение
      • 900 21
      • Английский словарь
      • Toppers Talk
      • Блог
      • О нас
      • Карьера
      • Скачать
      • Получить приложение

      Вопрос

      Обновлено: 25/02/2018

      Рекомендуемые вопросы

      9 видео

      РЕКЛАМА

      Ab Padhai каро бина объявления ке

      Khareedo DN Про и дехо сари видео бина киси объявление ки рукаават ке!

      Похожие видео

      Найдите множество решений неравенства |x−1|<2.

      51238212

      01:43

      Найдите множество решений неравенства x+1x+2>1.

      51238215

      01:30

      Набор решений для неравенства 1x−2<0 есть-

      277386051

      00:55

      Множество решений неравенства 3|x|+2≤1

      385982705

      02:27

      Найдите множества решений следующих неравенств.
      5х≥3х+1.

      643338277

      01:28

      Найдите множество решений неравенства sinx>12.

      644008248

      02:10

      Найдите множество решений неравенства: 2x+1>3

      644623953

      01:12

      Найдите множество решений неравенства cosx≥12

      645257775

      03:00

      РЕКЛАМА

      • Рекомендуемые вопросы

      • Найдите множество решений неравенства cosx>= (-1)/2.

        07:09

      • Множество решений неравенства |x+1|

        02:18

      • Найдите множество решений неравенства sinx > 1/2.

        01:35

      • Алгоритм решения неравенств вида (ax+b)/(cx+d)

        08:00

      • Найдите множество решений неравенства |(3|x|-2)/(|x|-1)|>=2

        05:55

      • Найдите множество решений неравенства |(3| x | -2)/(| x | -1) |> = 2

        05:55

      • Найдите набор решений по неравенству COSX GE 1/2

        02:21

      • Набор раствора неравенство (-3)/(2) lt 1

        Текст Решение

      • Найдите набор решений неравенства (1)/(x-2)lt0.

        01:31

      1. Ask Unlimited Doubts
      2. Видеорешения на нескольких языках (включая хинди)
      3. Видеолекции экспертов
      4. Бесплатные PDF-файлы (документы за предыдущий год, книжные решения и многое другое)
      5. Посещайте специальные консультационные семинары для IIT- JEE, NEET и Board Exams

      Doubtnut хочет отправлять вам уведомления. Разрешите получать регулярные обновления!

      Слушаю…

      Найдите множество решений неравенства cosx>= (-1)/2.

      • Курс
        • NCERT
          • Класс 12
          • Класс 11
          • Класс 10
          • Класс 9
          • Класс 8
            • 9000 3 Класс 7
          • Класс 6
        • IIT JEE
      • Экзамен
        • JEE MAINS
        • JEE ADVANCED
        • X BOARDS
        • XII BOARDS
        • NEET
          • Neet Предыдущий год (по годам)
          • Physics Предыдущий год
          • Химия Предыдущий год
          • Биология Предыдущий год
          • Нет Все образцы работ
          • Образцы работ по биологии
          • Образцы работ по физике
          • Образцы работ по химии
      • Скачать PDF-файлы
        • Класс 12
        • Класс 11
        • Класс 10
        • Класс 9
        • Класс 8
        • Класс 7
        • Класс 6
      • Экзаменационный уголок
      • Онлайн класс
        • 9 0021
        • Викторина
        • Задать вопрос в Whatsapp
        • Поиск Doubtnut
        • Английский словарь
          9 0003 Toppers Talk
        • Блог
        • О нас
        • Карьера
        • Скачать
        • Получить приложение

        Вопрос

        Обновлено: 28/04/2021 Экзамен за предыдущие 13 лет)

        13 видео

        РЕКЛАМА

        Ab Padhai каро бина объявления ке

        Khareedo DN Про и дехо сари видео бина киси объявление ки рукаават ке!

        Похожие видео

        Множество решений неравенства |x+1|

        124441

        02:18

        Найдите множество решений неравенства sinx>12.

        346759

        01:35

        Алгоритм решения неравенств вида ax+bcx+d

        1339464

        08:00

        Найти решение множество неравенства |(3|x|-2)/( |х|-1)|>=2

        2054237

        05:55

        Найдите множество решений неравенства |(3|x|-2)/(|x|-1)|>=2

        2054324

        05:55

        9 0130 Найдите решение набор неравенств cosx≥12

        8493407

        02:21

        Набор решений неравенства −32<1

        42359917

        Текст Решение

        9013 0 Найдите множество решений неравенства 1x−2<0.

        51238211

        01:31

        Найдите множество решений неравенства |x−1|<2.

        51238212

        01:43

        Найдите множество решений неравенства x+1x+2>1.

        51238215

        01:30

        Набор решений неравенства 1x−2<0 равен 3|x|+2≤1

        385982705

        02 :27

        Найдите наборы решений следующих уравнений.
        5х≥3х+1.

        643338277

        01:28

        Найдите множество решений неравенства sinx>12.

        No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *