Задача, от которой отказался Ричард Фейнман / Хабр
В замечательной книге «Вы, конечно, шутите, мистер Фейнман!» есть эпизод, который привел меня к небольшой практической работе, что и послужило основой для создания данной статьи. А началось все с этого момента:
” Пол проходит по столовой, где все просто стоят на ушах. “Эй, Пол! – кричат они. – Фейнман – просто супер! Мы даем ему задачу, которую можно сформулировать за десять секунд, и он за одну минуту дает ответ с точностью до 10 процентов. Дай ему какую-нибудь задачу!” Почти не останавливаясь, он говорит: “Тангенс 10 градусов в сотой степени”. Я влип: для этого нужно делить на число пи до ста десятичных разрядов! Это было безнадежно!”.
В приведенном фрагменте переводчик ошибся. Пол Олам просит Фейнмана вычислить тангенс числа 10 в сотой степени. И речь идет о радианах, а не градусах. Именно в такой формулировке задача становится неподъемной для будущего нобелевского лауреата.
Я решил рассмотреть более простую задачу. А именно, как узнать сколько будет tg(10°) в сотой степени? Размышление над данным вопросом послужило толчком для проведения небольшого вычислительного эксперимента, результатами которого я и хочу поделиться. А начал я с того, что попросил Googlе вычислить названную величину. Ответ был дан мгновенно – 4,2842727е-76.
Тангенс это синус, деленный на косинус. Поэтому свои исследования я начал с решения более простой задачи. А именно, как найти синус 10 градусов и возвести его в сотую степень. Причем нам надо реализовать два различных метода, чтобы убедиться в правильности полученного результата. Все вычисления проводились на платформе 1С: Предприятие 8.2. Особенностью данной платформы является то, что результаты расчетов хранятся в текстовом виде, что снимает вопрос о количестве знаков после запятой и, как следствие, точности расчетов, по крайней мере, для операций сложения и умножения. Теперь определимся с вариантами расчета.
 Самый простой – это вычислить синус и затем умножить его на себя. Раз степень, в которую мы возводим четная, то вспомним про формулу косинуса двойного угла и запишем:
Самый простой – это вычислить синус и затем умножить его на себя. Раз степень, в которую мы возводим четная, то вспомним про формулу косинуса двойного угла и запишем:Поскольку при проведении расчетов, нам необходимо контролировать точность используемых данных, то косинус 20 градусов будем искать, как корень следующего уравнения:
4*cos³(20°)-3*cos(20°)=0,5
Данное уравнение получается из формулы для косинуса тройного угла. Для численного решения уравнения воспользуемся методом Ньютона. В дальнейшем найденное значение sin²(10°) умножаем само на себя 49 раз (можно, разумеется, сократить количество умножений, это в данном случае неважно).
Приведем таблицу с зависимостью проведенных расчетов от точности определения cos(20°).
Из полученных результатов видно, что точность в 10% достигается, когда входные данные содержат 4 значащих цифры после запятой.
 Я делал расчет четной степени синуса, но использованный подход может быть применен и к тангенсу, просто это увеличит объем излагаемого материала. Заменим исходную функцию ее разложением в ряд Фурье. Разложение получим с использованием следующего тождества:
Я делал расчет четной степени синуса, но использованный подход может быть применен и к тангенсу, просто это увеличит объем излагаемого материала. Заменим исходную функцию ее разложением в ряд Фурье. Разложение получим с использованием следующего тождества:cos(α)*cos(β)=0,5*(cos(α-β)+cos(α+β))
Вот как мы его применяем.
sin²(x)* sin²(x)=(0,5-0,5cos(2x))(0,5-0,5cos(2x))
Раскроем скобки в правой части и затем заменим произведения косинусов их суммой. Затем полученную сумму опять умножим на (0,5-0,5 cos(2x)) опять раскроем скобки и еще раз проведем операцию замены произведения на сумму. Разумеется, изложенную процедуру я проводил с помощью программы на встроенном языке платформы 1С: Предприятие. В результате данных мероприятий было получено разложение исходной функции по базису из функций cos(2ix), где i меняется от 0 до 25. Найденное разложение мы в дальнейшем вычисляем в точке 10°=π/18. Приведем таблицу со значениями базисных функций в данной точке.
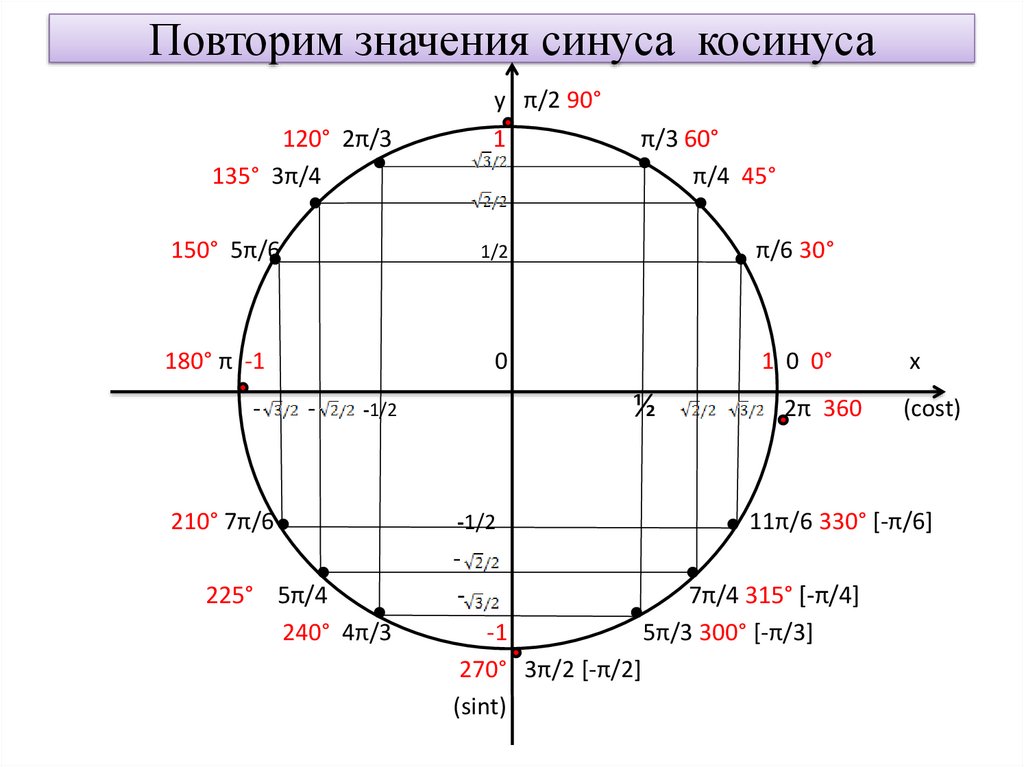
Для углов в диапазоне от 180° до 340° значения базисных функций будут отличаться от приведенных величин только знаком из-за сдвига на «пи». Теперь, когда есть значения базисных функции и есть коэффициенты разложения, можно провести альтернативный расчет. А вот в этом случае точность исходных данных должна быть сопоставима с точностью конечного результат, т.е не меньше чем 10⁻⁷⁷. Впрочем это и понятно. Когда мы складываем какие-то величины, то для получения нужной точности члены суммы должны быть рассчитаны с погрешностью не меньше предполагаемого результата. В следующей таблице приведены результаты расчета по изложенной методике для различной точности входных данных.
Приведенные числа согласуются с нашим замечанием о связи точности входных данных и конечного результата. В тоже время, они подтверждают достоверность предыдущих расчетов.
Ниже приведено изображение формы обработки, которую я применял в своих исследованиях
На данной форме, в частности, приведен спектр разложения в ряд Фурье функции sin¹⁰⁰ (x).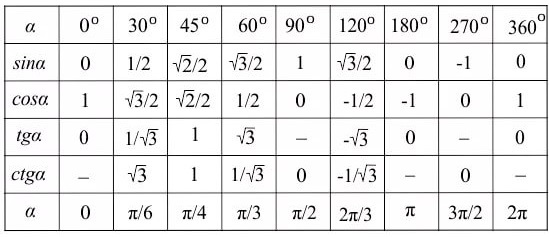
И так, с помощью вычислительной техники, которая стала значительно доступнее со времен атомного проекта, мы задачу решили. Но можно ли ее решить в уме, или хотя бы получить оценку порядка для конечного результата. Приведем возможную последовательность рассуждений.
Вспомним, что разложение функции tg²(x) по степеням sin²(x) имеет вид:
Оценку для sin(10°) получим из тождества:
sin(30°)=3sin(10°)-4sin³(10°)
Если отбросить кубический член, то оценка будет 1/6=0,166666, так как она занижена, то возьмем 0,17, а квадрат тангенса оценим в 0,03. Прологарифмируем искомую величину и получим
Ln(tg²(10°)⁵⁰)=50*(-2*Ln(10)+Ln(3))
Ln(3)=Ln(e*(1+0,3/e))≈1+Ln(1+1/9)=1,1
Вспомним, что Ln(10) ≈2,30.Тогда натуральный логарифм искомой величины будет равен
50*(-4,6+1,1)=-50*3,5=-2,3*50*35/23=2,3*50*(1+12/23)≈-2,3*50*(1+0,5*(1+1/24))=-2,3*50*1,52=-2,3*76.
Возведем e в полученную степень и приходим к результату 10⁻⁷⁶.

Заключение
В данной работе я не смог найти ответ на вопрос, который сформулировал Пол Олам. Тем не менее, приведенный анализ, с моей точки зрения, является неплохой демонстрацией того, как можно применять математические инструменты для решения задач, когда надо дойти до числа. Мне кажется, что изложенный материал можно использовать, как основу для практического занятия по вычислительной математике в старших классах.
%d0%ba%d0%be%d1%81%d0%b8%d0%bd%d1%83%d1%81 in Polish — Russian-Polish Dictionary
Sample translated sentence: Командир отряда 81-го гвардейского бомбардировочного авиационного полка (1-я гвардейская бомбардировочная авиационная дивизия, 6-й гвардейский бомбардировочный авиационный корпус, 2-я воздушная армия, 1-й Украинский фронт) гвардии капитан Пётр Абрамов особенно отличился при выполнении боевых заданий по доставке оружия, боеприпасов и продовольствия партизанам Белоруссии и Украины. ↔ Dowodził oddziałem 81 pułku lotnictwa bombowego 1 Gwardyjskiej Dywizji Lotnictwa Bombowego 6 Gwardyjskiego Korpusu Lotnictwa Bombowego 2 Armii Powietrznej 1 Frontu Ukraińskiego w stopniu kapitana, szczególnie zasłużył się przy dostarczaniu broni, zapasów i żywności dla partyzantów Białorusi i Ukrainy.
Glosbe Translate
Google Translate
+ Add translation Add
Currently we have no translations for %d0%ba%d0%be%d1%81%d0%b8%d0%bd%d1%83%d1%81 in the dictionary, maybe you can add one? Make sure to check automatic translation, translation memory or indirect translations.
ареа-косинус гиперболический
area cosinus hiperboliczny
Интегральный косинус
Sinus i cosinus całkowy
обратный гиперболический косинус
area cosinus hiperboliczny
теорема косинусов
twierdzenie cosinusów
гиперболический косинус
cosinus hiperboliczny · kosinus hiperboliczny
Модифицированное дискретное косинус-преобразование
zmodyfikowana dyskretna transformacja kosinusowa
Add example Add
Declension Stem
Командир отряда 81-го гвардейского бомбардировочного авиационного полка (1-я гвардейская бомбардировочная авиационная дивизия, 6-й гвардейский бомбардировочный авиационный корпус, 2-я воздушная армия, 1-й Украинский фронт) гвардии капитан Пётр Абрамов особенно отличился при выполнении боевых заданий по доставке оружия, боеприпасов и продовольствия партизанам Белоруссии и Украины.
Dowodził oddziałem 81 pułku lotnictwa bombowego 1 Gwardyjskiej Dywizji Lotnictwa Bombowego 6 Gwardyjskiego Korpusu Lotnictwa Bombowego 2 Armii Powietrznej 1 Frontu Ukraińskiego w stopniu kapitana, szczególnie zasłużył się przy dostarczaniu broni, zapasów i żywności dla partyzantów Białorusi i Ukrainy.
WikiMatrixДругой трек этого альбома — «Irresistible (Westside Connection)» поднялся на 81-ю строчку чарта Hot R&B/Hip-Hop Singles & Tracks.
Inna piosenka z tego albumu „Irresistible (Westside Connection)” znalazła się na 81. miejscu Hot R&B/Hip-Hop Singles & Tracks.
WikiMatrixРасчет 81, скорая всё ещё на переезде.
Wóz 81, karetka nadal nie może wyjechać.
OpenSubtitles2018.v3Сейчас мне 83 года, и 63 из них я провела в полновременном служении.
Dziś w wieku 83 lat spoglądam wstecz na ponad 63 lata spędzone w służbie pełnoczasowej.
Расчет 81, Спасатель 3,
/ Wóz 81, ekipa ratunkowa 3,
OpenSubtitles2018.v3she will
— Zaślubi pan kobietę bogatą — rzekła — ale będzie pan miał przez nią wiele zmartwienia…
Literature2-й ЗАВСЕГДАТАЙ: Must be doing a Harry!
STAŁY KLIENT 2: Może się bawi w Harry’ego!
LiteratureВ настоящий 83-й год правления Царства, возглавляемого Иисусом, некоторые, возможно, думают, что сейчас как раз период замедления.
Ponieważ nastał osiemdziesiąty trzeci rok królowania Jezusa, niektórzy mogą odnosić wrażenie, że żyjemy w okresie takiego ‛odwlekania się’.
jw2019Похоже, мы можем поехать по шоссе 81 и дальше через Даллас.
Możemy dojechać do trasy 81 i jechać w kierunku Dallas.
OpenSubtitles2018.v3Она распространяет миллионы [19 миллионов каждого выпуска] экземпляров своего материала примерно на 60 [в настоящее время на 81] языках, в том числе на языках пиджин, хилигайнон и зулу.
Swoją publikację ludzie ci rozpowszechniają w milionach egzemplarzy [19 milionów każdego numeru] i w około 60 językach [ściśle w 81], między innymi w neomelanezyjskim, hiligajno i zuluskim.
jw201983 • Нельсон Ещё толком не очухавшись, он знает — что-то пошло ужасно, ужасно не так.
Nelson Zanim jeszcze odzyskał przytomność, już wie, straszliwie, straszliwie nie tak.
LiteratureДорск 81 кивнул: — Он победил мастера Скайуокера.
Dorsk 81 przytaknął. — On pokonał mistrza Skywalkera.
LiteratureПока не была закончена южная часть D0 Пражской кольцевой дороги, был самым нагруженным элементов в системе улиц Праги (на 2008 год 137000 автомобилей в день).
Przed zakończeniem południowej części obwodnicy Pragi był najbardziej ruchliwym mostem w Pradze i Czech (127 000 pojazdów dziennie, w 2008 roku odnotowano 137 tysięcy pojazdów na dobę).
WikiMatrixЯ хотел бы начать благотворительность, and I think that would be a-a good place to start.
Chciałbym otworzyć fundacje, i myślę, że byłoby to dobre miejsce na start.
OpenSubtitles2018.v3Поскольку я стоял рядом, я прочел это короткое послание: My expectation is that this will be opened after my death.
Stojąc za nim przeczytałem: Oczekuję, że zostanie to otwarte po mojej śmierci.
Literature83:надписание
83:nagłówek
jw2019Задача для расчета 81:
Wóz 81 dostaje zmianę zadania.
OpenSubtitles2018.v3— Только эта парочка даже не знает, что им нужно это сказать, — ответил я. 81.
Dodałem tylko: — Tylko że one dwie nawet nie zdają sobie sprawy, że chciałyby to rzec. 81.
LiteratureГлава 81 – Складывается впечатление, что кто-то охраняет гнездо, – сказал Ганн.
Rozdział 81 – Wygląda na to, że ktoś pilnuje gniazdka — powiedział Gunn.
LiteratureКак же удивлялись эти люди, читая такие библейские стихи, как Псалом 83:18, где сказано: «Ты, чье имя Иегова, ты один Всевышний над всей землей».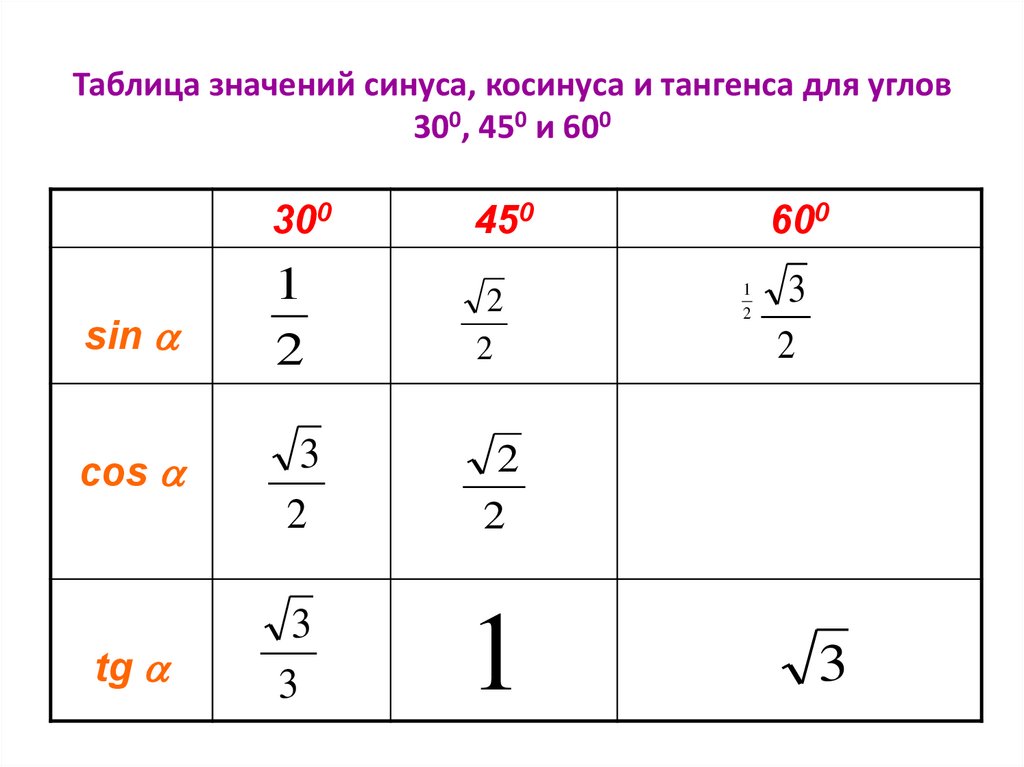
Jakże więc zdziwieni byli ci ludzie, gdy na własne oczy widzieli w Piśmie Świętym na przykład słowa Psalmu 83:18: „Ty, który masz na imię Jehowa, ty sam jesteś Najwyższym nad całą ziemią”!
jw2019Everything’s Gonna Be порядке.
Wszystko będzie w porządku
OpenSubtitles2018.v3Если вы желаете получить новый выпуск «Пробудитесь!», который издается сейчас на 81 языке, обратитесь к Свидетелям Иеговы, живущим с вами по соседству, или напишите по одному из адресов, указанных на странице 5.
Jeżeli chcieliby Państwo otrzymać najnowszy numer Przebudźcie się!, które obecnie wydawane jest w 81 językach, prosimy nawiązać kontakt z mieszkającymi w pobliżu Świadkami Jehowy lub napisać pod odpowiednim z adresów podanych na stronie 5.
jw2019Альбом включает в себя несколько оригинальных песен (среди них «Dummy» и «I Wanna Be», на которые также были сняты видеоклипы, «I Have Arrived», и «This Is Me», которые были написаны совместно с Эммой Робертс), так же как и некоторые песни Эдди из первого сезона (но более поздние их версии), включая «Punch Rocker» и «New Shoes» (обе из серии «The Party»), «94 Weeks (Metal Mouth Freak)» (из серии «The Bar Mitzvah») и «Mexican Wrestler» (которая ранее выходила в альбоме Джилл Собул Pink Pearl в 2000 году и в серии Нетакой «The 66th Day»).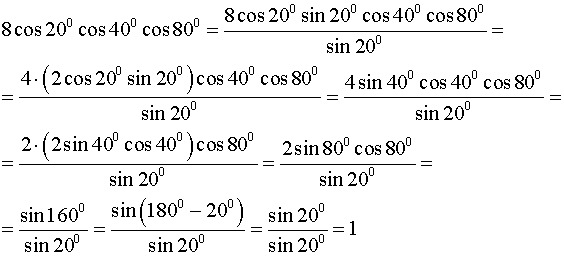
Na płycie znajduje się kilka oryginalnych piosenek, m.in. „I Have Arrived” i „This Is Me”, które zostały napisane wspólnie z Roberts, a także kilka z pierwszego sezonu serialu – „Punch Rocker” i „New Shoes” (odcinek The party), „94 Weeks (Metal Mouth Freak)” (odcinek The Bar Mitzvah), „Mexican Wrestler” (który pojawił się wcześniej na albumie Jill Sobule z 2000 roku a następnie w odcinku The 66th Day).
WikiMatrixГосподь сказал нам: «Каждому предупрежденному человеку надлежит предупредить ближнего своего» (У. и З. 88:81).
Pan powiedział nam: „Przystoi każdemu, kto został ostrzeżony, aby ostrzegł sąsiada swego” (NiP 88:81).
81-й, проверьте грузовик.
81, zajmijcie się ciężarówką.
OpenSubtitles2018.v3 The most popular queries list: 1K, ~2K, ~3K, ~4K, ~5K, ~5-10K, ~10-20K, ~20-50K, ~50-100K, ~100k-200K, ~200-500K, ~1MКалькулятор — cos(20) — Солуматы
Cos, расчет онлайн
Итог:
Тригонометрическая функция cos вычисляет cos угла в радианах,
градусов или градианов.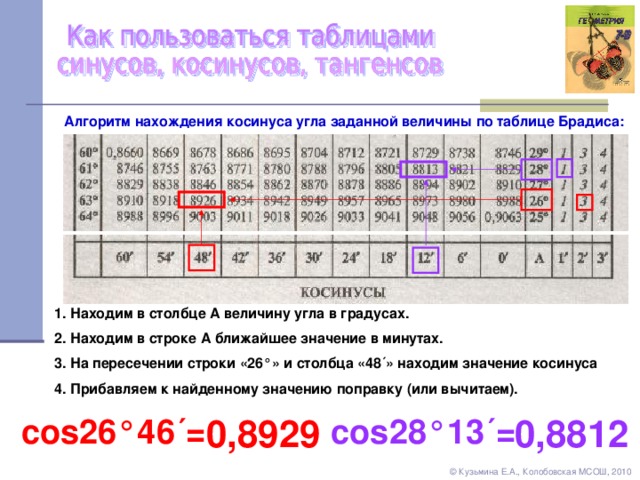
cos online
Описание:
Калькулятор позволяет использовать большинство из тригонометрических функций , есть возможность вычислить косинус , синус и касательная угла через одноименные функции.
Косинус тригонометрической функции отметил cos , позволяет вычислить косинус угла онлайн , можно использовать разные угловые единицы: градусы, грады и радианы, которые по умолчанию являются угловыми единицами.
- Расчет косинуса
- Специальные значения косинуса
- Основные свойства
Расчет косинуса угла в радианах
Калькулятор косинуса позволяет через функцию cos вычислить онлайн косинус угла в радианах, вы должны сначала
выберите нужную единицу, нажав на кнопку параметров расчетного модуля.
После этого можно приступать к расчетам.
Чтобы вычислить косинус онлайн от `pi/6`, введите cos(`pi/6`), после вычисления результат `sqrt(3)/2` возвращается.
Обратите внимание, что функция косинуса способна распознавать некоторые специальные углы и делать расчеты со специальными связанными значениями в точной форме.
Вычислить косинус угла в градусах
Чтобы вычислить косинус угла в градусах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.
Чтобы вычислить косинус 90, введите cos(90). возвращает 0.
Вычислить косинус угла в градусах
Для вычисления косинуса угла в градианах необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.
Чтобы вычислить косинус 50, введите cos(50), после вычисления
возвращается результат `sqrt(2)/2`.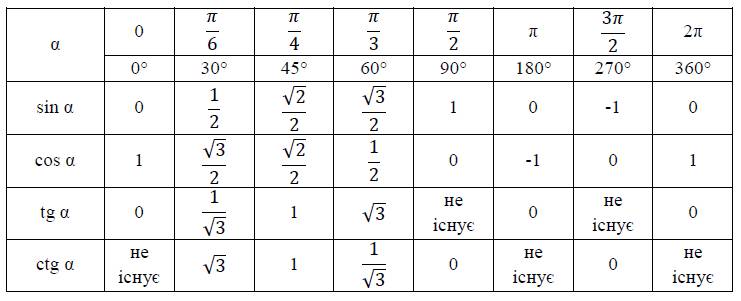
Обратите внимание, что функция косинуса способна распознавать некоторые специальные углы и выполнять исчисление со специальными ассоциированными точными значениями.
Косинус допускает некоторые специальные значения, которые калькулятор может определить в точных формах. Вот список специальные значения косинуса :
| cos(`2*pi`) | `1` | |
| cos(`pi`) | `-1` | |
| cos(`pi/2`) 70 7 7 7 90 90 90 90 | ||
| cos(`pi/4`) | `sqrt(2)/2` | |
| cos(`pi/3`) | `1/2` | |
| `sqrt(3)/2` | ||
| cos(`2*pi/3`) | `-1/2` | |
| cos(`3*pi/4`) | `-sqrt(2)/2` | |
| cos(`5*pi/6`) | `-sqrt(3)/2` | |
| cos(`0`) | `1` | `1` |
| cos(`-pi`) | `-1` | |
| cos(`pi/2`) | 7-7 `09` 90` | pi/4`)`sqrt(2)/2` |
| cos(`-pi/3`) | `1/2` | |
| cos(`-pi/6`) | `sqrt(3)/2` | |
| cos(`-2*pi/3`) | `-1/2` | |
| cos(`-3*pi/4`) | `-sqrt(2)/2` | |
| cos(`-5*pi/6`) | `-sqrt(3)/2` |
`AA x в RR, k в ZZ`,
- `cos(-x)= cos(x)`
- `cos(x+2*k*pi)=cos(x)`
- `cos(pi-x)=-cos(x) `
- `cos(pi+x)=-cos(x)`
- `cos(pi/2-x)=sin(x)`
- `cos(pi/2+x)=-sin(x) )`
Производная косинуса равна -sin(x).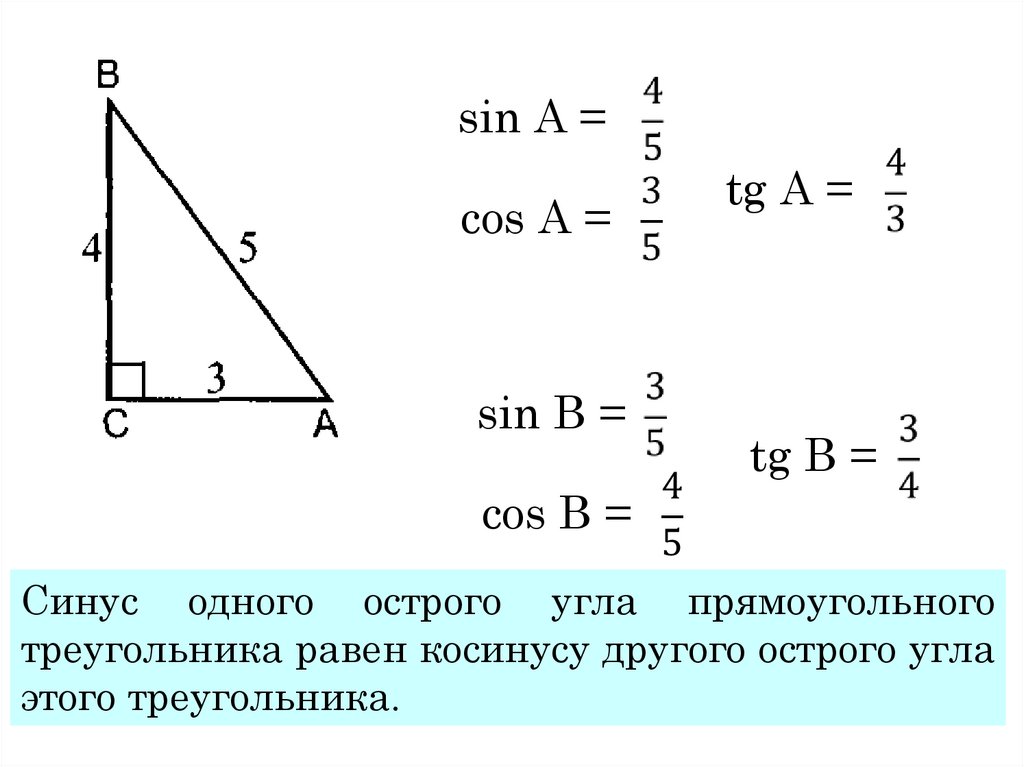
Первообразная косинуса равна sin(x).
Функция косинуса является четной функцией для каждого действительного x, `cos(-x)=cos(x)`. Следствием для кривой, представляющей функцию косинуса, является то, что она допускает ось ординат как ось симметрии.
Калькулятор имеет решатель, который позволяет решать уравнение с косинусом вида cos(x)=a . Расчеты для получения результата детализированы, поэтому можно будет решать уравнения типа `cos(x)=1/2` или `2*cos(x)=sqrt(2)` с этапами расчета.
Синтаксис:
cos(x), где x — мера угла в градусах, радианах или градах.
Примеры:
cos(`0`), возвращает 1
Производная косинуса:
Чтобы дифференцировать функцию косинуса онлайн, можно использовать калькулятор производной, который позволяет вычислить производную функции косинуса
производная от cos(x) is производная(`cos(x)`)=`-sin(x)`
Первообразная косинуса :
Калькулятор первообразной позволяет вычислить первообразную функции косинуса.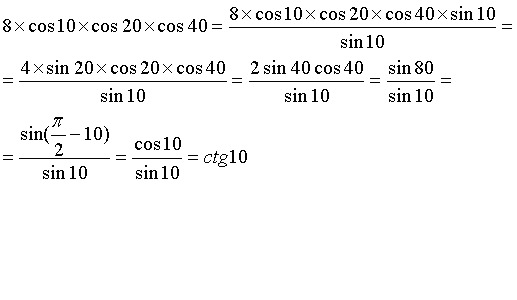
Первопроизводная от cos(x) является первообразной(`cos(x)`)=`sin(x)`
Предельный косинус :
Калькулятор предела позволяет вычислить пределы функции косинуса.
предел cos(x) is limit(`cos(x)`)
Обратная функция косинуса :
обратная функция косинуса является функцией арккосинуса, отмеченной как arccos.
Графический косинус:
Графический калькулятор может отображать функцию косинуса в заданном интервале.
Свойство функции косинуса:
Функция косинуса является четной функцией.
Расчет онлайн с косинусом
См. также
Список связанных калькуляторов:
- Арккосинус : arccos.
 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. - Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
- Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
- Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
- Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
- Косеканс: косеканс Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Котангенс : котан. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
- Тригонометрическое расширение: expand_trigo.
 Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор позволяет получить тригонометрическое разложение выражения. - Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
- Упростить калькулятор: упростить. Калькулятор, который может упростить алгебраическое выражение онлайн.
- Секанс : сек. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Синус : синус. Тригонометрическая функция sin для вычисления греха угла в радианах, градусов или градианов.
- Тангенс: коричневый. Тригонометрическая функция тангенса для вычисления тангенса угла в радианах, градусов или градианов.
Прочие ресурсы
- Исправленные упражнения на числовые функции
- Бесплатные онлайн математические игры про функции — производная — примитив — f(x)=0
- Научитесь считать с помощью обычных математических функций
Видео-урок: Тригонометрия прямоугольного треугольника: нахождение стороны
Стенограмма видео
найти значение длины недостающей стороны в прямоугольном треугольнике, выбрав
соответствующее тригонометрическое соотношение для данного угла. Предположим, у нас есть прямоугольный треугольник
как тот, который показан с одним из непрямых углов, помеченным как 𝜃. Гипотенуза прямоугольного треугольника
это его самая длинная сторона, которая всегда является стороной, прямо противоположной прямому углу. По отношению к углу, который мы
обозначен как 𝜃, сторона, прямо противоположная этому углу, известна как противоположная. И, наконец, другая сторона рядом с
угол 𝜃, не являющийся гипотенузой, называется прилежащим. Это тоже та сторона,
между прямым углом и 𝜃.
Предположим, у нас есть прямоугольный треугольник
как тот, который показан с одним из непрямых углов, помеченным как 𝜃. Гипотенуза прямоугольного треугольника
это его самая длинная сторона, которая всегда является стороной, прямо противоположной прямому углу. По отношению к углу, который мы
обозначен как 𝜃, сторона, прямо противоположная этому углу, известна как противоположная. И, наконец, другая сторона рядом с
угол 𝜃, не являющийся гипотенузой, называется прилежащим. Это тоже та сторона,
между прямым углом и 𝜃.
Мы часто будем видеть названия этих
три стороны, сокращенно opp, adj и hyp или просто O, A и H. Три тригонометрических отношения
синус, косинус и тангенс, которые мы сокращаем до sin, cos и tan, описывают
отношения между различными парами длин сторон в прямоугольном треугольнике. При фиксированном значении 𝜃 соотношение
между каждой парой длина стороны всегда одинакова, независимо от того, насколько большой треугольник
является. Мы можем использовать аббревиатуру SOHCATOA для
помогите нам вспомнить определения трех тригонометрических соотношений. Первая буква в каждой части
относится либо к синусу, либо к косинусу, либо к тангенсу. И затем следующие две буквы относятся
к сторонам, участвующим в отношении, сначала числитель, а затем
знаменатель.
Мы можем использовать аббревиатуру SOHCATOA для
помогите нам вспомнить определения трех тригонометрических соотношений. Первая буква в каждой части
относится либо к синусу, либо к косинусу, либо к тангенсу. И затем следующие две буквы относятся
к сторонам, участвующим в отношении, сначала числитель, а затем
знаменатель.
Итак, SOH говорит нам, что синус отношение, sin данного угла 𝜃, равно длине противолежащей стороны, деленной на длину гипотенузы. cos 𝜃 равен длине прилежащая сторона, деленная на длину гипотенузы. И тангенс 𝜃 равен длина противоположной стороны, деленная на длину соседней. Давайте теперь посмотрим, как мы можем использовать эти тригонометрические отношения для вычисления неизвестной длины в прямоугольном треугольнике.
Найдите 𝑥 на данном рисунке. Дайте ответ с точностью до двух знаков после запятой
места.
В этом прямоугольном треугольнике имеем даны длина одной стороны и мера одного из других углов. Мы хотим рассчитать длину другая сторона. Начнем с обозначения размера треугольник по отношению к углу 68 градусов. Сторона, прямо противоположная Прямой угол всегда является гипотенузой, которую мы будем сокращать до H. Сторона, прямо противоположная Угол 68 градусов — это противоположная сторона, которую мы будем сокращать до O. И, наконец, сторона между прямой угол, а угол 68 градусов является смежным, который мы будем сокращать до A. Мы можем использовать аббревиатуру SOHCATOA, чтобы помогите нам решить, какое из тригонометрических соотношений нам нужно использовать в этом вопрос.
Сторона, которую мы хотим рассчитать, равна
противоположная сторона, а сторона, длину которой мы знаем, является смежной, что говорит нам о том, что мы
будем использовать отношение тангенса.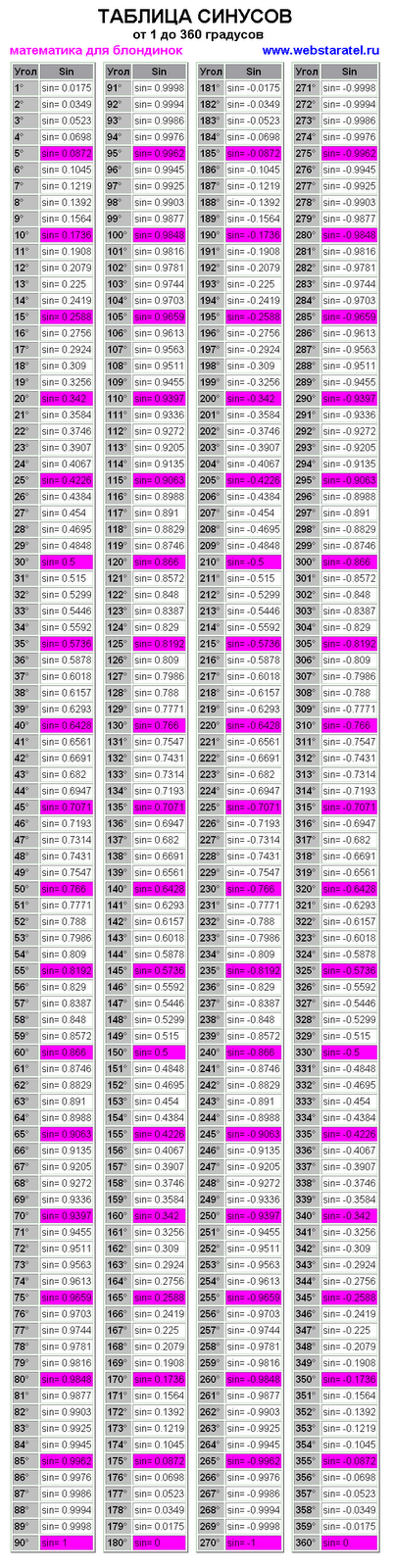 Напомним его определение. В прямоугольном треугольнике тангенс
угол 𝜃 равен длине противоположной стороны, деленной на длину
соседняя сторона. Теперь подставляем значение 𝜃
и значения или выражения для противоположного и смежного в этом треугольнике. 𝜃 составляет 68 градусов. Обратного мы не знаем, но мы
есть выражение 𝑥. А соседний 11 ед. Итак, у нас есть уравнение загара 68
градусов равно 𝑥 больше 11,
Напомним его определение. В прямоугольном треугольнике тангенс
угол 𝜃 равен длине противоположной стороны, деленной на длину
соседняя сторона. Теперь подставляем значение 𝜃
и значения или выражения для противоположного и смежного в этом треугольнике. 𝜃 составляет 68 градусов. Обратного мы не знаем, но мы
есть выражение 𝑥. А соседний 11 ед. Итак, у нас есть уравнение загара 68
градусов равно 𝑥 больше 11,
Чтобы решить это уравнение относительно 𝑥, мы
нужно умножить обе стороны на 11. Это дает 11, умноженное на тангенс
68 градусов равно 𝑥. Или мы могли бы просто написать это как 11
тангенс 68 градусов. Нам не нужно умножение
знак. Теперь мы можем оценить это на нашем
калькуляторы, убедившись, что они находятся в режиме градусов. И это дает 27.225. В вопросе указано, что мы
должен дать наш ответ с точностью до двух знаков после запятой. Таким образом, округляя наш ответ, мы имеем
27.23. Единицы не указаны в
вопрос, так что наш ответ просто 27,23 единиц длины.
Таким образом, округляя наш ответ, мы имеем
27.23. Единицы не указаны в
вопрос, так что наш ответ просто 27,23 единиц длины.
В этом примере неизвестное мы хотел вычислить был в числителе или верхней части дроби. Итак, преобразуя наше уравнение в решить для 𝑥 было довольно просто. Давайте теперь посмотрим на другой пример где неизвестное стоит в знаменателе дроби.
Найдите 𝑥 с точностью до двух знаков после запятой.
В этом прямоугольном треугольнике мы знаем
мера одного из других углов и длины одной стороны. Мы хотим рассчитать длину
другая сторона этого треугольника. Мы можем сделать это, используя
тригонометрия. Начнем с обозначения трех
сторон этого треугольника относительно угла 20 градусов. Сторона, прямо противоположная
прямой угол это гипотенуза треугольника. Сторона, противоположная углу 20
градусов наоборот.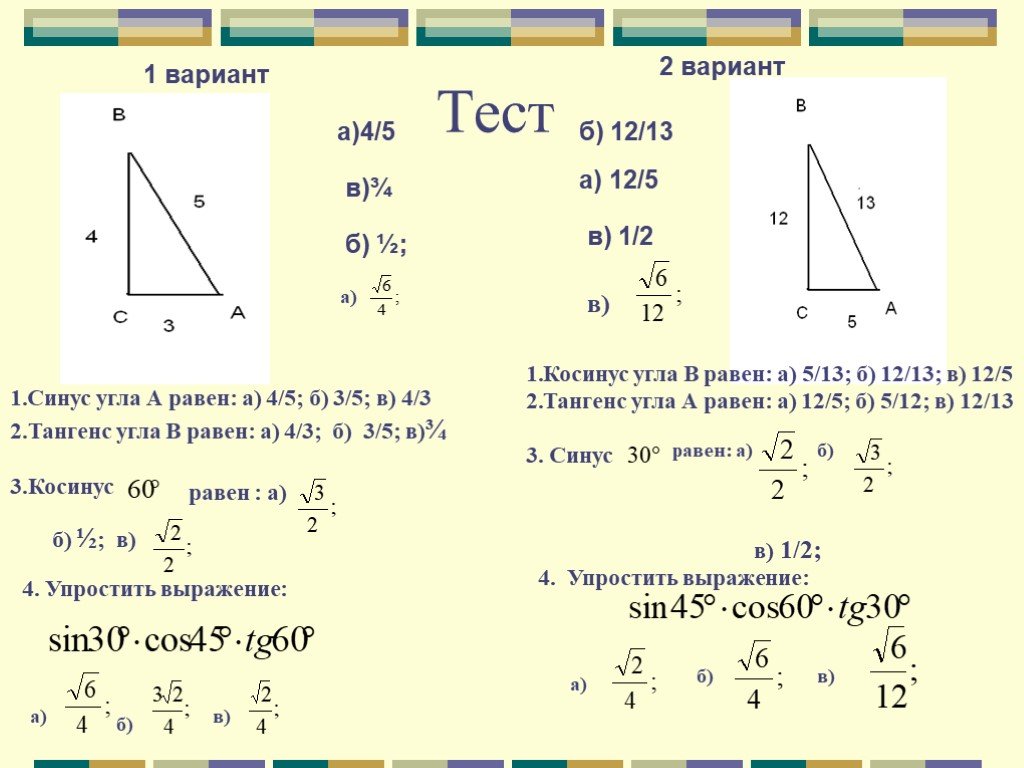 И сторона между правой
угол, а угол 20 градусов является смежным.
И сторона между правой
угол, а угол 20 градусов является смежным.
Далее вспоминаем аббревиатуру SOHCAHTOA, чтобы помочь нам решить, нужны ли нам синус, косинус или тангенс отношения в этот вопрос. Сторона, которую мы знаем, противоположный. И сторону, которую мы хотим вычислить это гипотенуза. Итак, мы собираемся использовать синус соотношение. Для данного угла 𝜃 в прямом треугольник, отношение синуса, sin 𝜃, равно длине противоположной стороны разделить на длину гипотенузы. Мы можем заменить значения для этот треугольник в это определение. 𝜃 равно 20 градусам, напротив 12 единиц, а гипотенуза это неизвестная 𝑥. Итак, у нас есть уравнение sin 20 градусов равно 12 на 𝑥.
Здесь мы должны быть осторожны. Очень распространенная ошибка — думать
что неизвестное, в данном случае 𝑥, всегда должно быть в числителе дроби,
и поэтому записать вместо этого грех 20 градусов равно 𝑥 над 12. Но, конечно, если бы мы это сделали, мы
будет делить длину гипотенузы на длину противоположной, а не
длина противоположного на длину гипотенузы. Это очень распространенная ошибка,
хотя. Так что нам просто нужно не торопиться
при подстановке значений или выражений для каждой стороны треугольника в
определение наших тригонометрических соотношений. Теперь нам нужно решить это уравнение
где 𝑥 стоит в знаменателе дроби, а для этого потребуется два
шаги.
Но, конечно, если бы мы это сделали, мы
будет делить длину гипотенузы на длину противоположной, а не
длина противоположного на длину гипотенузы. Это очень распространенная ошибка,
хотя. Так что нам просто нужно не торопиться
при подстановке значений или выражений для каждой стороны треугольника в
определение наших тригонометрических соотношений. Теперь нам нужно решить это уравнение
где 𝑥 стоит в знаменателе дроби, а для этого потребуется два
шаги.
Сначала умножаем обе части
уравнение нашим неизвестным 𝑥. С левой стороны мы теперь имеем
𝑥 грех 20 градусов и справа, 12 больше 𝑥 умножить на 𝑥 упрощает
до 12. Далее нам нужно разделить обе стороны
уравнения на грех 20 градусов. Помните, что это всего лишь число, поэтому
это абсолютно нормально. Это дает 𝑥 равно 12 больше
грех 20 градусов. Наконец, мы оцениваем на нашем
калькуляторы, дающие 35.085. Помните, мы должны убедиться, что
наши калькуляторы находятся в режиме градусов, чтобы дать правильный ответ. В вопросе указано, что мы
должен дать наш ответ с точностью до двух знаков после запятой. Значит округляем до 35.09. Таким образом, применяя коэффициент синуса в
этого прямоугольного треугольника, мы обнаружили, что значение 𝑥 с точностью до двух знаков после запятой равно
35.09.
Наконец, мы оцениваем на нашем
калькуляторы, дающие 35.085. Помните, мы должны убедиться, что
наши калькуляторы находятся в режиме градусов, чтобы дать правильный ответ. В вопросе указано, что мы
должен дать наш ответ с точностью до двух знаков после запятой. Значит округляем до 35.09. Таким образом, применяя коэффициент синуса в
этого прямоугольного треугольника, мы обнаружили, что значение 𝑥 с точностью до двух знаков после запятой равно
35.09.
Теперь мы видели примеры того, как
вычислить неизвестную длину стороны как тогда, когда она появляется в числителе, так и в
знаменатель дроби. Подведем итоги основных шагов, которые мы
нужно выполнить. Сначала мы обозначаем три стороны
треугольник с использованием букв O, A и H для обозначения противоположного, смежного и
гипотенуза. Далее определяем сторону, чья
длину, которую мы знаем, и сторону, которую мы хотим вычислить.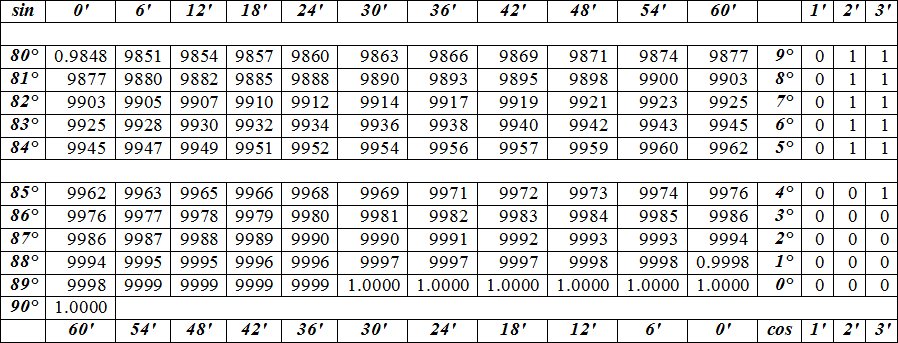 Тогда мы используем аббревиатуру SOHCATOA
чтобы помочь нам решить, какое тригонометрическое соотношение нам нужно использовать.
Тогда мы используем аббревиатуру SOHCATOA
чтобы помочь нам решить, какое тригонометрическое соотношение нам нужно использовать.
Затем мы записываем определение этого тригонометрического отношения и подставьте значения для конкретного треугольника мы работаем с. Наконец, решаем уравнение найдите недостающую длину и оцените с помощью нашего калькулятора. Помните, иногда это требуют более сложной перестановки, если сторона, которую мы должны вычислить, находится в знаменатель дроби.
В каждой из проблем мы рассмотренный до сих пор, у нас есть диаграмма треугольника, который мы должны использовать. Это не всегда может быть случай. Итак, давайте рассмотрим вопрос в который нам сначала нужно нарисовать треугольник из словесного описания.
𝐴𝐵𝐶 — прямоугольный треугольник
в 𝐵, где угол 𝐶 равен 62 градусам, а 𝐴𝐶 равен 17 сантиметрам.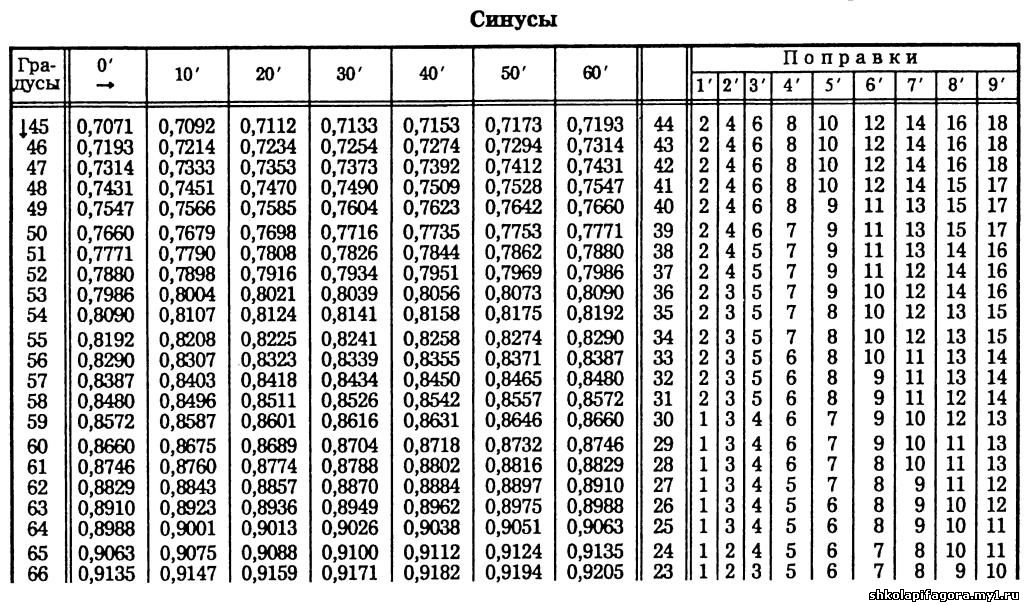 Найдите длины 𝐴𝐵 и 𝐵𝐶
давая ответ с двумя десятичными знаками и мерой угла 𝐴 давая
ответ с точностью до степени.
Найдите длины 𝐴𝐵 и 𝐵𝐶
давая ответ с двумя десятичными знаками и мерой угла 𝐴 давая
ответ с точностью до степени.
Начнем с наброска этот треугольник. Нам говорят, что он прямоугольный. в 𝐵. Итак, 𝐵 — вершина справа угол, а две другие вершины — 𝐴 и 𝐶. Другая информация, которую мы получили состоит в том, что угол 𝐶 равен 62 градусам, а 𝐴𝐶 равен 17 сантиметрам. Нас просят найти длину 𝐴𝐵 и 𝐵𝐶. Это две другие стороны треугольник. Поэтому мы назовем их 𝑥 сантиметрами и 𝑦 сантиметров. И мы также попросим найти мера угла 𝐴.
Теперь, собственно, мы можем вычислить
мера угла 𝐴 сразу, потому что у нас есть треугольник, в котором мы знаем
два других угла. Сумма углов любого треугольника равна
180 градусов, поэтому мы можем вычислить меру третьего угла, вычитая
два других на 180 градусов. Получается 28 градусов. А теперь давайте подумаем, как мы
найдем длины двух других сторон этого треугольника. Начнем с обозначения всех трех
сторон относительно угла 62 градуса. 𝐴𝐶 — гипотенуза, 𝐴𝐵 которая
мы называем 𝑥 сантиметров противоположным, а 𝐵𝐶 соседним.
Получается 28 градусов. А теперь давайте подумаем, как мы
найдем длины двух других сторон этого треугольника. Начнем с обозначения всех трех
сторон относительно угла 62 градуса. 𝐴𝐶 — гипотенуза, 𝐴𝐵 которая
мы называем 𝑥 сантиметров противоположным, а 𝐵𝐶 соседним.
Тогда мы вспомним аббревиатуру
SOHCATOA, чтобы помочь нам решить, какое тригонометрическое соотношение нам нужно для вычисления
длина каждой стороны. Начиная с 𝐴𝐵, прежде всего,
сторона, которую мы хотим вычислить, является противоположной, а сторона, которую мы знаем, является
гипотенуза. Итак, мы собираемся использовать синус
соотношение. Это говорит нам о том, что грех угла
𝜃 равно обратному делению на гипотенузу. Подставляя значения для этого
треугольника, у нас есть грех 62 градусов, равный 𝑥 на 17. Мы находим 𝑥, умножая оба
стороны уравнения на 17, что дает 𝑥 равно 17 грех 62 градусов. Оценка дает 15,0101, что мы
округлить до 15.01.
Оценка дает 15,0101, что мы
округлить до 15.01.
Чтобы вычислить вторую сторону, 𝐵𝐶,
у нас есть выбор. Теперь мы знаем длину двух
стороны в этом прямоугольном треугольнике, мы могли бы вычислить длину третьей стороны как
применение теоремы Пифагора. Но поскольку мы концентрируемся на
здесь тригонометрия, давайте вместо этого рассчитаем 𝐵𝐶, используя тригонометрические отношения. На этот раз сторона, которую мы хотим
вычислить — это соседняя, а сторона, которую мы изначально дали, — это
гипотенуза. Итак, мы собираемся использовать косинус
соотношение. В качестве альтернативы мы могли бы использовать
стороны, которую мы только что рассчитали, что дало бы пару O и A. Таким образом, мы будем использовать отношение тангенса. Но имеет смысл использовать значение
нам изначально дали на случай, если вы допустили ошибки при расчете длины
противоположного.
Замена 62 градусов на 𝜃, 𝑦 для соседнего и 17 для гипотенузы дает потому что 62 градуса равны 𝑦 над 17. Затем мы можем умножить обе части уравнение на 17, чтобы дать 𝑦, равно 17, потому что 62 градуса и оценить на нашем калькуляторы, убедившись, что они находятся в режиме градусов. Затем округляем до двух знаков после запятой места, что дает 7,98. Итак, мы завершили задачу. Длина 𝐴𝐵 составляет 15,01. сантиметры. Длина 𝐵𝐶 равна 7,9.8 сантиметров, каждое с точностью до двух знаков после запятой. А мера угла 𝐴 равна 28 градусов.
Тригонометрия прямоугольного треугольника
действительно полезно, потому что его также можно применять в практических контекстах. Часто проблемы, с которыми мы сталкиваемся,
принимают форму рассказа или описания реальной ситуации и могут быть решены
применяя методы, которые мы практикуем здесь. Если нам не дана схема, то
ключевой первый шаг будет для нас, чтобы нарисовать эскиз на основе информации, которую мы
данный. Давайте рассмотрим последний пример
этот тип.
Если нам не дана схема, то
ключевой первый шаг будет для нас, чтобы нарисовать эскиз на основе информации, которую мы
данный. Давайте рассмотрим последний пример
этот тип.
Воздушный змей, находящийся перпендикулярно высотой 44 метра, прикреплен к струне, наклоненной под углом 60 градусов к горизонтальный. Найдите длину строки с точностью до одного десятичного знака.
Начнем с наброска
Эта проблема. У нас есть воздушный змей, который прикреплен к
строка. Эта струна наклонена под углом
60 градусов к горизонтали и перпендикулярной высоте воздушного змея. Значит, высота
кайт, образующий прямой угол с горизонтом, составляет 44 метра. Теперь мы видим, что имеем право
треугольник, образованный горизонталью, вертикалью и тетивой воздушного змея. Мы хотим рассчитать длину
строка, так что давайте обозначим это как 𝑦 метров. Мы работаем с правом
треугольник, поэтому мы можем подойти к этой проблеме с помощью тригонометрии.
Мы работаем с правом
треугольник, поэтому мы можем подойти к этой проблеме с помощью тригонометрии.
Начнем с обозначения трех сторон треугольника относительно угла 60 градусов. Далее вспомним аббревиатуру SOHCATOA, чтобы помочь нам решить, какое тригонометрическое соотношение нам здесь нужно. Сторона, длину которой мы знаем, равна наоборот, и сторона, которую мы хотим вычислить, является гипотенузой. Итак, мы собираемся использовать синус соотношение. Для угла 𝜃 в прямом треугольника, это определяется как длина противоположного, деленная на длину гипотенуза. Затем мы можем заменить значения для 𝜃, противоположного и гипотенузы, в это уравнение, дающее грех 60 градусов равно 44 больше 𝑦.
Нам нужно быть осторожными, потому что
неизвестное стоит в знаменателе этой дроби. Далее решим это уравнение. Поскольку 𝑦 появляется в знаменателе,
первый шаг — умножить обе части уравнения на 𝑦, что дает 𝑦 sin
60 градусов равно 44. Далее делим обе стороны
уравнение на грех 60 градусов, что дает 𝑦 равно 44 по греху 60 градусов. И затем мы оцениваем на нашем
калькуляторы, которые должны быть в градусном режиме, дают 50.806. Вопрос требует нашего ответа
с точностью до одного десятичного знака. Таким образом, мы округляем это значение и включаем
единицы, которые являются метрами. Длина строки до одного
десятичный разряд 50,8 метра.
Далее делим обе стороны
уравнение на грех 60 градусов, что дает 𝑦 равно 44 по греху 60 градусов. И затем мы оцениваем на нашем
калькуляторы, которые должны быть в градусном режиме, дают 50.806. Вопрос требует нашего ответа
с точностью до одного десятичного знака. Таким образом, мы округляем это значение и включаем
единицы, которые являются метрами. Длина строки до одного
десятичный разряд 50,8 метра.
Давайте теперь суммируем ключевые моменты
из этого видео. При работе с прямоугольными треугольниками
мы используем термины «противоположный», «примыкающий» и «гипотенуза» для обозначения трех сторон
треугольник. Гипотенуза прямо противоположна
прямой угол, и это всегда самая длинная сторона треугольника. Противоположные и примыкающие
помечены по отношению к заданному углу, часто обозначаемому 𝜃. Противоположная сторона прямо
против этого угла, а прилежащая сторона — это сторона между этим углом и
прямой угол.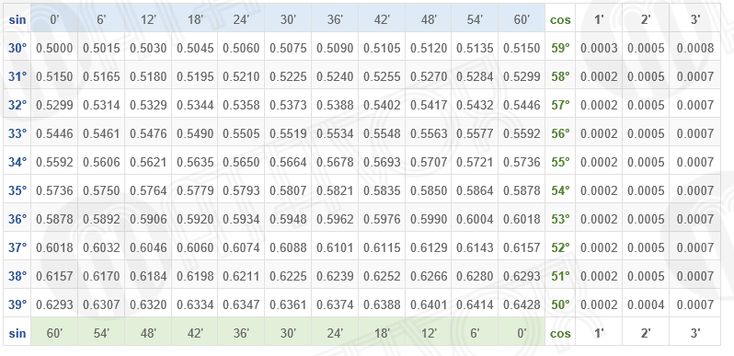 Мы можем использовать аббревиатуру SOHCATOA для
помогите нам определить, какой тригонометрический коэффициент нам нужно использовать для вычисления недостающего
сторона. Грех 𝜃 равен противоположному
над гипотенузой. cos 𝜃 равен соседнему
над гипотенузой. И тангенс 𝜃 равен
противоположное над соседним.
Мы можем использовать аббревиатуру SOHCATOA для
помогите нам определить, какой тригонометрический коэффициент нам нужно использовать для вычисления недостающего
сторона. Грех 𝜃 равен противоположному
над гипотенузой. cos 𝜃 равен соседнему
над гипотенузой. И тангенс 𝜃 равен
противоположное над соседним.
При использовании тригонометрии для нахождения
неизвестная длина стороны в прямоугольном треугольнике, мы работаем через следующие шаги. Сначала мы обозначаем стороны
треугольника относительно известного угла 𝜃. Во-вторых, мы используем SOHCATOA для
выбрать правильное тригонометрическое соотношение. Затем подставляем известный угол
и известной длины стороны. И, наконец, решим уравнение
вычислить неизвестное. Помните, нам нужно взять дополнительные
будьте осторожны при перестановке, если неизвестное находится в знаменателе дроби.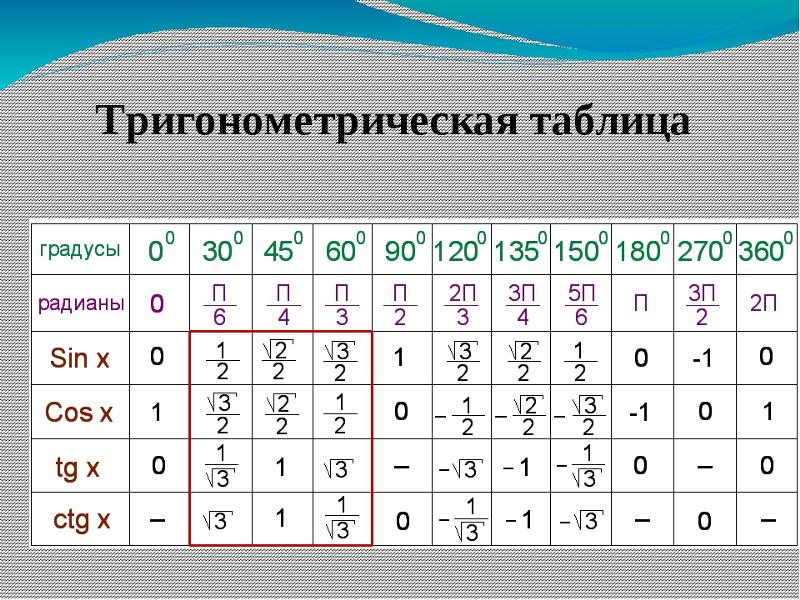

 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор позволяет получить тригонометрическое разложение выражения.