Четная и нечетная одновременно функция: Чётные и нечётные функции — урок. Алгебра, 9 класс.

y=0 единственная и чётная и нечётная функция? : Школьная алгебра

Сообщения без ответов | Активные темы | Избранное

Правила форума

В этом разделе нельзя создавать новые темы.

Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».

Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.

Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.

Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.

Pripyat	y=0 единственная и чётная и нечётная функция? 28. 09.2012, 22:09
22/11/07 87	Здравствуйте, уважаемые математики. Верно ли, что y=0 единственная и чётная и нечётная функция. Или вернее говорить, о том, что любая функция с симметричной областью определения и множеством значений E={0} является и чётной и нечётной?

chessar	Re: y=0 единственная и чётная и нечётная функция? 28. 09.2012, 22:28
03/12/08 351 Букачача	Ну если такие функции рассматриваются над произвольным полем характеристики не равной 2, то верно.

Munin	Re: y=0 единственная и чётная и нечётная функция? 28. 09.2012, 22:34
Заслуженный участник 30/01/06 72407	А вы не можете это вывести? Берёте определения: и решаете систему.

Toucan	Posted automatically 28. 09.2012, 23:08
Админ форума 19/03/10 8952	i  Тема перемещена из форума «Математика (общие вопросы)» в форум «Помогите решить / разобраться (М)»

Pripyat	Re: y=0 единственная и чётная и нечётная функция? 28. 09.2012, 23:09
22/11/07 87	Функции и являются и чётными и нечётными одновременно на своей области определения. Считать их разными или одинаковыми? Всё таки области определения не совпадают…

Someone	Re: y=0 единственная и чётная и нечётная функция? 29. 09.2012, 00:16
Заслуженный участник 23/07/05 17973 Москва	Разными. Но одна может быть продолжением другой (или, наоборот, ограничением на часть области определения).

Pripyat	Re: y=0 единственная и чётная и нечётная функция? 29. 09.2012, 08:59
22/11/07 87	Это понятно. Значит y=0 — не единственная?! Как минимум две, а верней — их бесконечно много? Потому что везде пишут одна!

Cash	Re: y=0 единственная и чётная и нечётная функция? 29.09. 2012, 09:10
Заслуженный участник 12/09/10 1540	Непорядок!!! Срочно писать в Академию наук и ЮНЕСКО!!!

Esp_	Re: y=0 единственная и чётная и нечётная функция? 29. 09.2012, 10:27
22/01/11 309	Pripyat в сообщении #624592 писал(а): Это понятно. Значит y=0 — не единственная?! Как минимум две, а верней — их бесконечно много? Потому что везде пишут одна! Формально — бесконечно много. а в каком учебнике написано, что она одна?

zhoraster	Re: y=0 единственная и чётная и нечётная функция? 29. 09.2012, 12:01
Модератор 30/06/10 980	!  Cash, устное замечание за бессодержательное сообщение

Someone	Re: y=0 единственная и чётная и нечётная функция? 29. 09.2012, 12:24
Заслуженный участник 23/07/05 17973 Москва	Pripyat в сообщении #624592 писал(а): Потому что везде пишут одна! Ну, имеется такое стремление — при не очень строгом обсуждении отождествлять функции, из которых одна является ограничением другой на часть области определения. Но в аккуратных рассуждениях приходится их различать — вплоть до введения различных обозначений.

ewert	Re: y=0 единственная и чётная и нечётная функция? 29. 09.2012, 19:56
Заслуженный участник 11/05/08 32139	Pripyat в сообщении #624515 писал(а): Или вернее говорить, о том, что любая функция с симметричной областью определения и множеством значений E={0} является и чётной и нечётной? Формально — вернее. Но если в формулировке не сделано никаких спецоговорок насчёт областей определения, то по умолчанию в подобных случаях подразумевается, что функция задана на всей оси.

Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию

Страница 1 из 1

[ Сообщений: 12 ]

Модераторы: Модераторы Математики, Супермодераторы

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения

Найти:

Ряды Фурье.

Теория поля. Аналитические и специальные функции. Преобразование Лапласа Ряды Фурье. Теория поля. Аналитические и специальные функции. Преобразование Лапласа

Романовский П.И. Ряды Фурье. Теория поля. Аналитические и специальные функции. Преобразование Лапласа Небольшое по объему учебное пособие.В сжатой, конспективной, доступной для студентов форме излагается основное содержание дополнительных глав курса математики: ряды Фурье и интеграл Фурье; теория поля; теория аналитических функций; некоторые специальные функции; операционное исчисление. Представляет интерес также для аспирантов, инженеров, преподавателей. Оглавление ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ ГЛАВА 1. РЯДЫ ФУРЬЕ И ИНТЕГРАЛ ФУРЬЕ § 2. 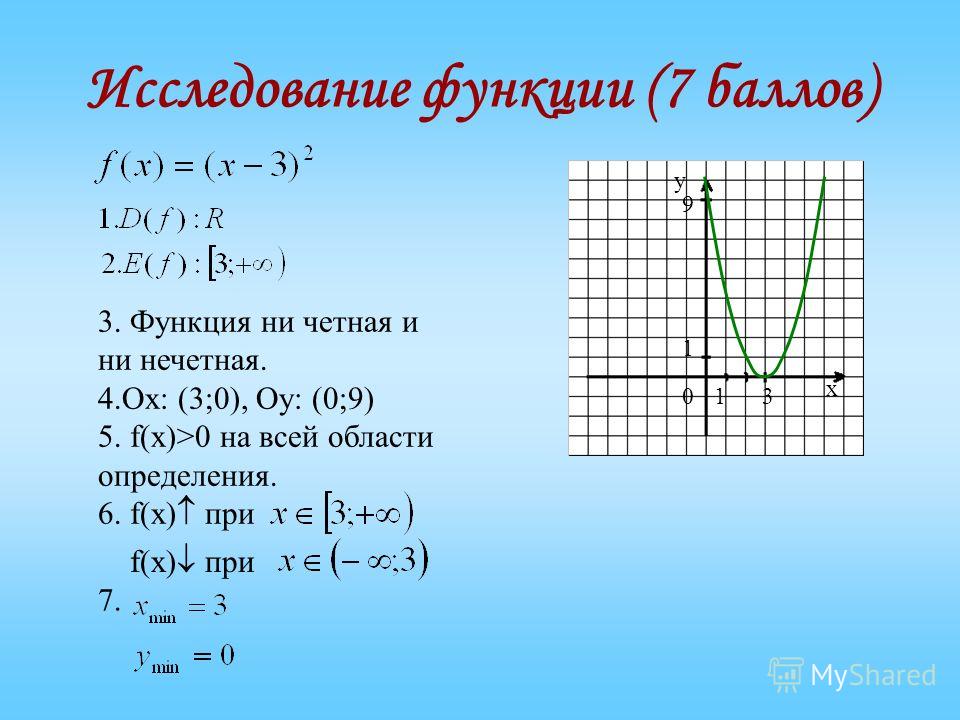РЯДЫ ФУРЬЕ ДЛЯ ФУНКЦИЙ С ПЕРИОДОМ 2pi § 3. КОМПЛЕКСНАЯ ФОРМА РЯДА ФУРЬЕ ДЛЯ ФУНКЦИЙ С ПЕРИОДОМ 2pi § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ § 5. РЯДЫ ФУРЬЕ ДЛЯ ЧЕТНЫХ И НЕЧЕТНЫХ ФУНКЦИЙ С ПЕРИОДОМ 2pi § 6. РЯДЫ ФУРЬЕ ДЛЯ ФУНКЦИИ С ЛЮБЫМ ПЕРИОДОМ § 7. УРАВНЕНИЕ СВОБОДНЫХ МАЛЫХ КОЛЕБАНИЙ СТРУНЫ И ЕГО РЕШЕНИЕ МЕТОДОМ ФУРЬЕ § 8. ИНТЕГРАЛ ФУРЬЕ § 9. КОМПЛЕКСНАЯ ФОРМА ИНТЕГРАЛА ФУРЬЕ § 10. ИНТЕГРАЛ ФУРЬЕ ДЛЯ ЧЕТНЫХ И НЕЧЕТНЫХ ФУНКЦИЙ § 11. ОРТОГОНАЛЬНЫЕ СИСТЕМЫ ФУНКЦИЙ § 12. МИНИМАЛЬНОЕ СВОЙСТВО КОЭФФИЦИЕНТОВ ФУРЬЕ ГЛАВА II. ОСНОВЫ ТЕОРИИ ПОЛЯ § 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ВЕКТОРНОЙ АЛГЕБРЫ § 2. ВЕКТОРНЫЕ ФУНКЦИИ СКАЛЯРНОГО ПЕРЕМЕННОГО § 3. СОПРОВОЖДАЮЩИЙ ТРЕХГРАННИК ПРОСТРАНСТВЕННОЙ КРИВОЙ § 4. СКАЛЯРНОЕ ПОЛЕ. ГРАДИЕНТ СКАЛЯРНОГО ПОЛЯ § 5. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ § 6. ВЕКТОРНОЕ ПОЛЕ § 7. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ § 8. ФОРМУЛА ОСТРОГРАДСКОГО § 9 ВЕКТОРНАЯ ЗАПИСЬ ФОРМУЛЫ ОСТРОГРАДСКОГО. ДИВЕРГЕНЦИЯ ВЕКТОРНОГО ПОЛЯ § 10. ФОРМУЛА СТОКСА § 11. 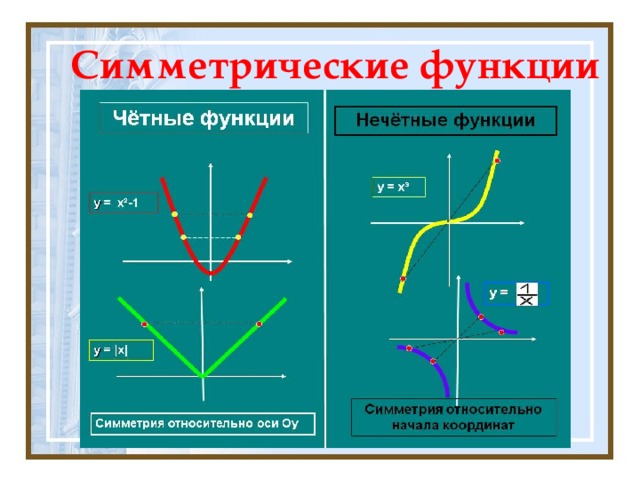ВЕКТОРНАЯ ЗАПИСЬ ФОРМУЛЫ СТОКСА. ВИХРЬ ВЕКТОРНОГО ПОЛЯ § 12. ОПЕРАЦИИ ВТОРОГО ПОРЯДКА § 13. СИМВОЛИКА ГАМИЛЬТОНА § 14. ВЕКТОРНЫЕ ОПЕРАЦИИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ ГЛАВА III. НАЧАЛЬНЫЕ СВЕДЕНИЯ ОБ АНАЛИТИЧЕСКИХ ФУНКЦИЯХ § 1. КОМПЛЕКСНЫЕ ЧИСЛА § 2. РЯДЫ С КОМПЛЕКСНЫМИ ЧЛЕНАМИ § 3. СТЕПЕННЫЕ РЯДЫ § 4. ПОКАЗАТЕЛЬНЫЕ, ГИПЕРБОЛИЧЕСКИЕ И ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО § 5. НЕКОТОРЫЕ МНОГОЗНАЧНЫЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО § 6. ПРОИЗВОДНАЯ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО § 7. АНАЛИТИЧЕСКИЕ И ГАРМОНИЧЕСКИЕ ФУНКЦИИ § 8. ИНТЕГРАЛ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО § 9. ОСНОВНАЯ ТЕОРЕМА КОШИ § 10. ИНТЕГРАЛЬНАЯ ФОРМУЛА КОШИ § 11. ИНТЕГРАЛ ТИПА КОШИ § 12. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ ОТ АНАЛИТИЧЕСКОЙ ФУНКЦИИ § 13. ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ АНАЛИТИЧЕСКИХ ФУНКЦИЙ § 14. РЯД ТЕЙЛОРА § 15. РЯД ЛОРАНА § 16. ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ АНАЛИТИЧЕСКОЙ ФУНКЦИИ § 17. ВЫЧЕТЫ § 18. ПРИНЦИП АРГУМЕНТА § 19. 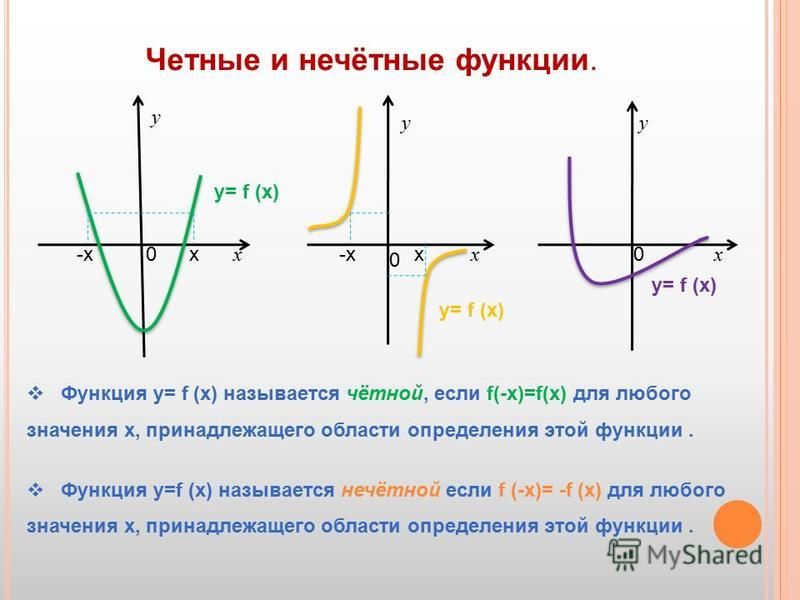ДИФФЕРЕНЦИРУЕМЫЕ ОТОБРАЖЕНИЯ Отображение, конформное в данной точке § 20. КОНФОРМНЫЕ ОТОБРАЖЕНИЯ ОБЛАСТЕЙ Конформное отображение области на область Линейные преобразования Конформные отображения односвязных областей ГЛАВА IV. О НЕКОТОРЫХ СПЕЦИАЛЬНЫХ ФУНКЦИЯХ § 1. ГАММА-ФУНКЦИЯ § 2. БЕССЕЛЕВЫ ФУНКЦИИ С ЛЮБЫМ ИНДЕКСОМ § 3. ФОРМУЛЫ ПРИВЕДЕНИЯ ДЛЯ БЕССЕЛЕВЫХ ФУНКЦИЙ § 4. БЕССЕЛЕВЫ ФУНКЦИИ С ПОЛУЦЕЛЫМ ИНДЕКСОМ § 5. ИНТЕГРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ БЕССЕЛЕВЫХ ФУНКЦИЙ С ЦЕЛЫМ ИНДЕКСОМ § 6. АСИМПТОТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БЕССЕЛЕВЫХ ФУНКЦИЙ С ЦЕЛЫМ ИНДЕКСОМ ДЛЯ БОЛЬШИХ ЗНАЧЕНИЙ АРГУМЕНТА § 7. ИНТЕГРАЛЬНЫЙ ЛОГАРИФМ, ИНТЕГРАЛЬНЫЙ СИНУС, ИНТЕГРАЛЬНЫЙ КОСИНУС ГЛАВА V. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА § 2. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА § 3. ПРОСТЕЙШИЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА § 4. СВЕРТКА ФУНКЦИЙ § 5. ОРИГИНАЛЫ С РАЦИОНАЛЬНЫМИ ИЗОБРАЖЕНИЯМИ § 6. ПРИЛОЖЕНИЯ К РЕШЕНИЮ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ И СИСТЕМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ § 7. ПРИЛОЖЕНИЕ К РЕШЕНИЮ ЛИНЕЙНЫХ УРАВНЕНИЙ В КОНЕЧНЫХ РАЗНОСТЯХ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ § 8. ОРИГИНАЛЫ С ИЗОБРАЖЕНИЯМИ, РЕГУЛЯРНЫМИ В БЕСКОНЕЧНОСТИ § 9. ИЗОБРАЖЕНИЯ НЕКОТОРЫХ СПЕЦИАЛЬНЫХ ФУНКЦИЙ 2. Изображения функций, связанных с интегралом вероятностей 3. Изображения интегрального синуса и интегрального косинуса 4. Изображения интегралов Френеля § 10. ФОРМУЛЫ ОБРАЩЕНИЯ § 11. ДОСТАТОЧНОЕ УСЛОВИЕ ДЛЯ ТОГО, ЧТОБЫ АНАЛИТИЧЕСКАЯ ФУНКЦИЯ БЫЛА ИЗОБРАЖЕНИЕМ

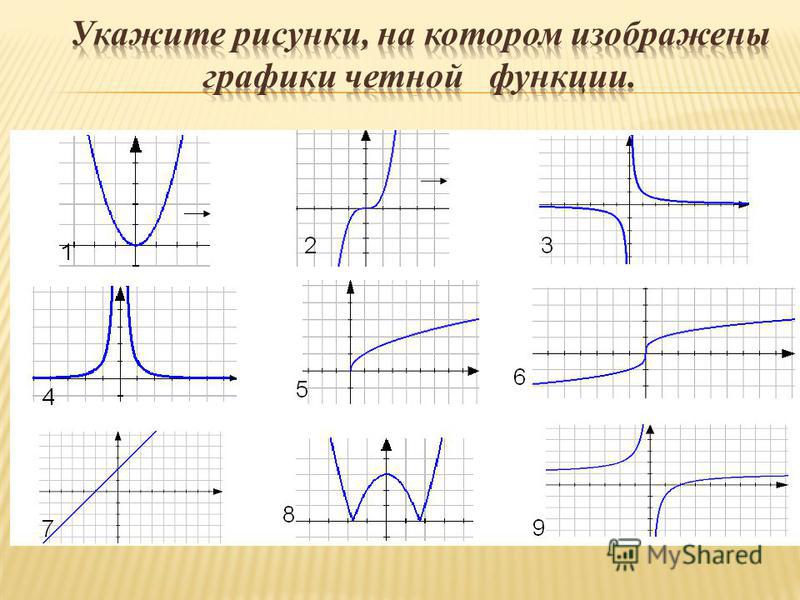
Четные и нечетные функции | Математика

Как определить, является ли функция четной, нечетной или ни одной?

Функция y = f(x) является

четной функцией x, если f(-x) = f(x)

нечетной функцией x, если f(-x) = -f(x)

для каждого x в области определения функции.

Имена четных и нечетных происходят от степеней \boldsymbol{x}.

Четная функция:

Если y является четной степенью x, как в y = x^{2} и y = x^{4} , это четная функция x, потому что 9{3}

Характеристики четной функции:

1. График четной функции симметричен относительно оси \boldsymbol{y}.

Это потому, что в случае четной функции значение y одинаково для x и -x.

2. График четной функции не изменится, если отразить его поперек оси \boldsymbol{y}.

Характеристики нечетной функции:

1. График нечетной функции симметричен относительно начала координат.

Это связано с тем, что в случае нечетной функции значение y в точке -x равно отрицательному значению y в точке x.

2. График нечетной функции не изменится, если его повернуть на \boldsymbol{180º} вокруг начала координат.

 

3. Нечетная функция всегда принимает значение \boldsymbol{0} при \boldsymbol{x = 0}.

Это потому, что для нечетной функции f(-x) = -f(x) .

При x = 0 f(-0) = -f(0)

 \ подразумевает f(0) = -f(0)

\ подразумевает 2f(0) = 0 \ подразумевает f(0) = 0

Следовательно, если функция нечетная, f(0) всегда равно 0, но f(0) = 0 не означает, что функция нечетная.

4. График нечетной функции всегда проходит через начало координат. 9{2}+1 = f(x)

Поскольку \boldsymbol{f(-x) = f(x)}, данная функция четна.

Ниже приведен график этой функции, и мы видим, что он симметричен относительно оси Y.

Пример 2: Рассмотрим функцию \boldsymbol{f(x) = x + 1}. Определите, является ли эта функция четной, нечетной или ни одной из них.

Решение:

Как обсуждалось ранее, сначала нам нужно определить f(-x) .

f(-x) = (-x) + 1 = -x + 1 9{3} + x) = -f(x)

Поскольку \boldsymbol{f(-x) = -f(x)}, данная функция нечетна.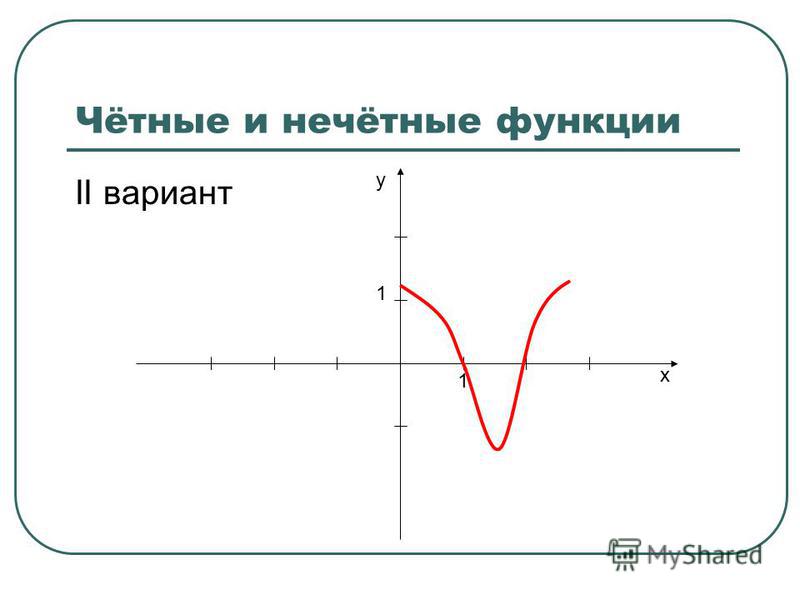

Ниже приведен график этой функции, и мы видим, что он симметричен относительно начала координат.

Пример 4: Рассмотрим функцию \boldsymbol{f(x) = 0}. Определите, является ли эта функция четной, нечетной или ни одной из них.

Решение:

Сначала нам нужно определить f(-x) .

Поскольку f(x) — постоянная функция, следовательно, f(-x) также равно 0 .

f(-x) = 0

Кроме того, -f(x) = 0

Ясно, что f(-x) = f(x) и f(-x) = -f(x)

Поэтому , данная функция является как четной, так и нечетной функцией.

График этой функции расположен вдоль оси x и симметричен как относительно начала координат, так и относительно оси y.

\boldsymbol{f(x) = 0} — единственная действительная функция, которая одновременно является и четной, и нечетной функцией.

Некоторые другие свойства:

1. Сумма двух или более четных функций также является четной функцией.

2. Сумма двух или более нечетных функций также является нечетной функцией.

3. Сумма четной функции и нечетной функции не является ни четной, ни нечетной функцией, если только одна из функций не равна нулю.

4. Произведение двух или более четных функций также является четной функцией.

5. Произведение двух нечетных функций есть четная функция.

6. Произведение трех нечетных функций является нечетной функцией.

7. Произведение четной функции на нечетную есть нечетная функция.

Наши продукты:

Название продукта: Классическая футболка с длинным рукавом Mathematics Be Positive

Покрой: стандартный крой, унисекс

Нажмите здесь, чтобы посмотреть эту футболку.

Предыдущий

Следующий

Название продукта: Классический пуловер с капюшоном Mathematics Be Positive

Покрой: стандартный крой, карман-кенгуру, унисекс

Нажмите здесь, чтобы посмотреть эту толстовку с капюшоном.

Предыдущая

Следующая

Теги: Четные и нечетные функции    Четные функции    Функции    Математика    Математика    Нечетные функции

Разложение функции на четную и нечетную части

Как я уже говорил, я не внезапное озарение человек. Время от времени это случается, но обычно мой стиль мышления таков: внимательно изучить большое количество примеров, а затем постепенно сделать вывод о них. Я проницательный, но медленный мыслитель. Но в моей жизни было несколько случаев, когда решение проблемы пришло мне в голову внезапно ни с того ни с сего.

Один из таких случаев был в первый день моего второго курса по физике с отличием. в 1987 году. Это был один из лучших уроков, которые я посещал в колледже. карьера. Он был дан профессором Стивеном Неттелом, и речь шла о явления резонанса. Мне нравится, когда курс имеет единую всеобъемлющую тему и приступает к ее подробному изучению; это все слишком редко. я глубоко сожалею, что оставил свою копию конспектов курса в ресторане в 1995.

Курс был очень сложным, но и очень удовлетворительным. Это также волосы встают дыбом из-за привычки профессора Неттела говорить: на протяжении всей второй половины «Не волнуйтесь, если вам кажется, что это не в любом случае, все это сложится для вас во время выпускного экзамена». Это не успокаивало. Но он был прав! Это все пришли вместе во время выпускного экзамена.

На экзамене было два набора задач. Проблемы с левой стороны экзаменационная работа касалась какой-то механической системы, я думаю, что стержень закреплен на одном конце и свободный на другом, или что-то в этом роде. Этот набор задачи просили нас вычислить резонансную частоту стержня, его степень демпфирования на различных частотах движения и связанные с этим вопросы. Правые задачи касались электрической системы, включающей резистор, конденсатор и катушка индуктивности. Вопросы были те же, и ответы были формально идентичными, отличаясь лишь деталями: на слева ответы включали длину, массу и жесткость стержня, а справа — сопротивление, емкость и индуктивность электрические компоненты.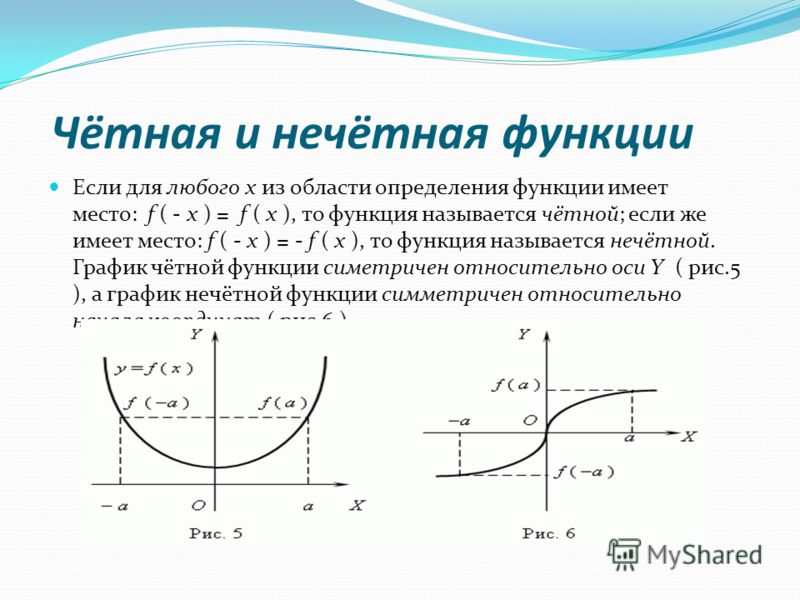 Это был блестящий экзамен, и я никогда узнал так много о предмете 93}{20}!!, показано внизу справа.)

Я нашел это заявление очень удивительным, и мы понятия не имели, как решить это. Ну, не совсем нет идеи : я знал, что функции могут быть расширены в Ряд Фурье как сумма синуса ряд и косинусный ряд, причем часть синуса была нечетной, а косинус часть была ровной. Но это казалось большим молотком, чем было требовалось, особенно потому, что новые второкурсники не должны были знать о рядах Фурье.

Я имел честь быть в этом классе с Рон Бакмайр и я помнишь, мы стояли у здания класса под осенним солнцем и обсудили проблему. Я мог подумать, что, возможно, был какой-то способ заменить отрицательную часть !!f!! с отраженная копия положительной части, чтобы сделать четную функцию, и может быть, что !!f(x) + f(-x)!! всегда был даже, когда меня ударили из синий с раствором:

$$ \начать{выравнивать} f_e(x) & = \frac{f(x) + f(-x)}2 \text{четно},\\ f_o(x) & = \frac{f(x) — f(-x)}2 \text{ нечетно, а}\\ f(x) &= f_e(x) + f_o(x) \end{выравнивание} $$

Вот и решилась проблема. остальные три не помню проблемы в домашнем задании того дня, но я помню, что когда-либо с.

Но почему-то до сегодняшнего дня мне не приходило в голову подумать о как на самом деле выглядели эти функции. Конечно, если !!f!! четно, то !!f_e = f!! и !!f_o = 0!!, и аналогично, если !!ф!! странно. Но большинство функций не являются ни четными, ни нечетными. 93}3 + х!!:

Мне нравится смотреть на них и видеть, как четная синяя линия и нечетная фиолетовая линия объединяется, чтобы сделать любую красную линию, которую я захочу.

Я все время хотел попробовать знакомые простые функции, например !!\frac1x!!, но многие из них либо четные, либо нечетные, и поэтому не представляют интереса для это приложение. Но вы можете превратить четную или нечетную функцию в ни четная, ни нечетная функция, просто переместив ее по горизонтали, что вы делаете, заменяя !!x!! с !!х-с!!. Итак, следующая функция I пытался было !!\frac1{x+1}!!, что является переводом !!\frac 1x!!. Тут меня ждал сюрприз. Я знал это !!\frac1{x+1}!! был undefined при !!x=-1!!, поэтому я изобразил его только для !!x>-1!!. Но четная составляющая !!\frac12\left(\frac1{1+x}+\frac1{1-x}\right)!!, который не определен в обоих !!x=-1!! и при !!x=+1!!. Точно так же нечетное компонент не определен в двух точках. Итак, !!f = f_o + f_e!! формула работает не совсем корректно, не дает правильного значение в !!x=1!!, хотя !!f!! там определяется. В общем, если !!ф!! не определена при некотором !!x=c!!, то разложение на четные и нечетные компоненты выходят из строя при !!x=-c!! также. Предел $$\lim_{x\to -c} f(x) = \lim_{x\to -c} \left(f_o(x) + f_e(x)\right)$$, однако. график ниже показывает разложение !!\frac1{x+1}!!.

Вертикальные переводы неинтересны: уходят !!f_o!! неизменный и перевести !!f_e!! на ту же сумму, как можно проверить алгебраически или просто подумав об этом.

Следуя той же стратегии, я попробовал косинусоидальную волну. ровность функция косинуса является одним из его основных свойств, поэтому я перевел его и использовал !!\cos (x+1)!!. График ниже на самом деле для !!5\cos(x+1)!! чтобы детали не были слишком сжаты:

Это напомнило мне о времени, когда мне было четырнадцать, и я нарисовал график !!\sin x + \cos х!! и был удивлен, увидев, что это был еще один идеальный синусоида. Но я понял, что есть простой способ понять этот. Я уже знал, что !!\cos(x + y) = \sin x\cos y + \sin y \cos Икс!!. Если взять !!y=\frac\pi4!! и умножить все на !!\sqrt 2!!, вы получаете $$\sqrt2\cos\left(x + \frac\pi4\right) = \sqrt2\sin x\cos\frac\pi4 + \sqrt2\cos x\sin\frac\pi4 = \sin x + \cos x$$, так что !!\sin x + \cos x!! это просто сдвинутый масштабированный косинус изгиб. Разложение !!\cos(x+1)!! еще проще, потому что вы можно работать вперед, а не назад, и обнаружить, что !!\cos(x+1) = \sin x\cos 1 + \cos x \sin 1!!, и первый член нечетный, а второй член четный, так что !!\cos(x+1)!! разлагается как сумма четного и нечетная синусоида, как вы видите на графике выше. 9\lambda}{x!}!!, для некоторой константы !!\lambda!!. !!Икс! !! в знаменателе определяется только для неотрицательного целого числа !!x!!, но вы можете расширить его до дробного и отрицательного !!x!! в обычным способом, используя !!\Gamma(x+1)!! вместо этого, где !!\Gamma!! это Гамма-функция. !!\Гамма!! функция не определена в нуле и отрицательных целых числах, но, к счастью, то, что нам нужно здесь, это обратная гамма-функция !!\frac1{\Gamma(x)}!!, который отлично себя ведет. Результаты впечатляющие. На приведенном ниже графике !!\лямбда = 0,8!!.

Часть этого с !!x\ge 0!! мне самое интересное, потому что распределение Пуассона имеет очень характерную форму, и еще раз мне нравится видеть синий и фиолетовый !!\Gamma!! функции работать вместе, чтобы сделать это. Я думаю, это просто здорово, как красная линия мягко стремится к нулю как !!x!! увеличивается, несмотря на то, что даже и нечетные компоненты сходят с ума. (!!x!!! !! быстро увеличивается с !!x!!, поэтому обратное !!\Gamma!! функция быстро стремится к нулю. Но четные и нечетные компоненты также имеют !!\frac1{\Gamma(-x)}!! часть, и это то, что доминирует над синими и фиолетовыми линиями, когда !!x >4!!.)

На !!x\lt 0!! сторона для меня не имеет значения, и это просто шевеление линии. Раньше мне и в голову не приходило, что можно продлить функция распределения Пуассона к отрицательному !!x!!, и я все еще не могу представить, что бы это могло значить, но я полагаю, почему бы и нет. Вероятно, некоторые статистик мог бы объяснить мне, что такое распределение Пуассона о том, когда !!x<0!!.

Вы также можете рассмотреть функцию !!\sqrt x!!, которая разбивает полностью, потому что либо !!\sqrt x!! или !!\sqrt{-x}!! не определено за исключением случаев, когда !!x=0!!. Итак, утверждение, что каждая функция является суммой четная и нечетная функции здесь также не работают. За исключением, пожалуй, нет! Ты вероятно, можно было бы рассмотреть расширение функции извлечения квадратного корня на комплексной плоскости, и взять одну из ее ветвей, и я предполагаю, что это работает просто отлично.