Презентация на тему: Разность противолежащих углов
трапеции равнаПовторение68°. Найти больший угол.
(2)
А+ В=180°В+ С
Если А=х°, тох+х+68=180В=х°+68°
2х=180-68 х=12
В=12°+68°=80°
Ответ: 80.
22
В равнобедренном треугольнике углы при основании равны.
Сумма углов, прилежащих боковой стороне трапеции равна 180°.
D |
| О |
|
| С | Найдите угол между |
|
|
| биссектрисами углов | |||
|
|
|
|
|
| параллелограмма, прилежащих |
А | 4 | 3 | 2 | 1 | В | к одной стороне. |
|
| (3) |
ПовторениеDАВ+ АВС=180°
Так как 1= 2 и 3= 4, то
3+ 2=90°О=180°-( 3+ 2)=90
Ответ: 90.
Сумма соседних углов параллелограмма равна 180
В треугольнике сумма углов равна 180°
В 47 |
|
| Найдите угол между | |
? | D | гипотенузой и медианой, | ||
| проведенной из прямого угла. | |||
|
|
|
| Повторение |
С |
|
| А | (3) |
А+ В=90°
Так как С= А+ В, то В= ВСD, А=АCD ВCD=47°
ВDC=180°-2∙47 =86
Ответ: 86.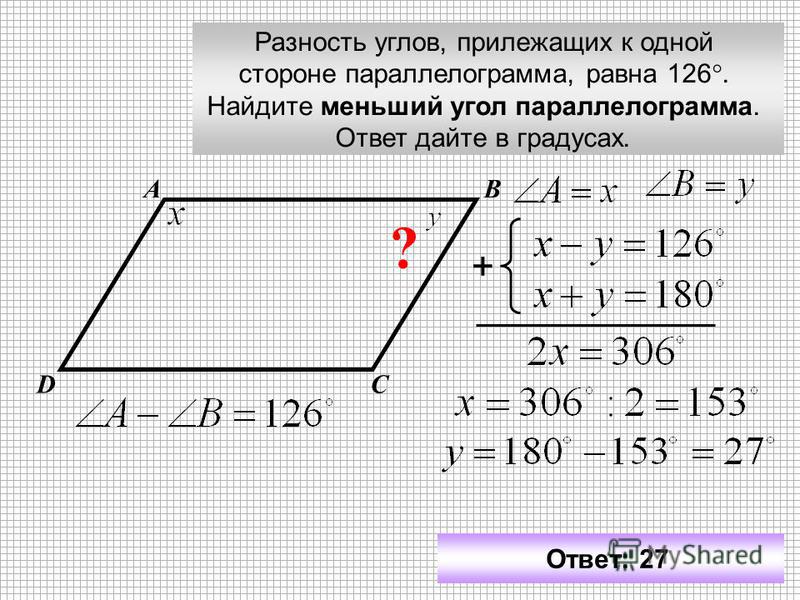
В прямоугольном треугольнике сумма острых углов равна 90
В равнобедренном треугольнике углы при основании равны
Сумма углов треугольника равна 180
|
| С | ? | Найдите внешний угол при | |
| N | О | L | вершине С. | Повторение |
|
| (3) | |||
В | 4 | 100 | 1 | А |
|
3 | 2 |
|
| ||
Так как 1= 2, 3= 4, то 2+ 3=1/2( А + В)2+ 3=180°-100 =80
А+ В=80 ∙2=160 Внешний угол при вершине С равен 160
Ответ: 160.
28
Биссектриса – это луч, который делит угол пополам
В треугольнике сумма углов равна 180°
Внешний угол треугольника – это угол, смежный с углом треугольника и он равен сумме углов треугольника, не смежных с ним.
С | H |
| Повторение |
| 26 | L | (3) |
|
|
В ∆HLF H=90, HАL+ HLA=90°
HLA=90°-26 =64
HLA внешний для ∆АLВ, HLA= LАВ+ В
∆АLВ — равнобедренный, LАВ= В
В=½ HLA= ½ ∙ 64 =32
Ответ: 32.
В прямоугольном треугольнике сумма острых углов равна 90°
Внешний угол треугольника равен сумме углов треугольника, не смежных с ним
В равнобедренном треугольнике углы при основании равны
31
|
| А | Повторение |
| Y | ? | (2) |
|
| O | X | |
В |
| ||
| 119 | С |
ВОС= XOY как вертикальные
XOY =119
YOX+ OYA+ A+ AXO =360°, гдеOYAА=360AXO=90-2∙90 — 119 =61
Ответ: 61.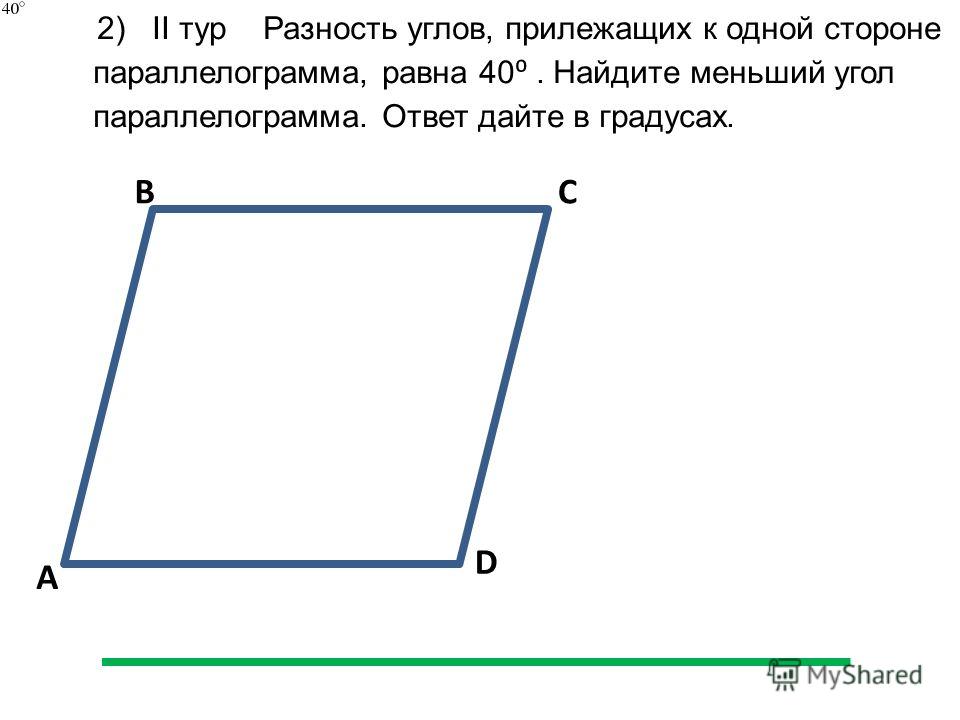
Разность углов прилежащих к одной стороне параллелограмма… -reshimne.ru
Новые вопросы
Ответы
Разность углов прилежащих к одной стороне параллелограмма равна 28°. Найти меньший угол.Разность углов прилежащих к одной стороне параллелограмма равна 28°. Найти меньший угол.Разность углов прилежащих к одной стороне параллелограмма равна 28°. Найти меньший угол.Разность углов прилежащих к одной стороне параллелограмма равна 28°. Найти меньший угол.
Сумма углов прилежащих к одной стороне равна 180 градусов
(180-28):2=76 градусов меньший угол
если захочешь найти больший то 76+28=104
Похожие вопросы
√3 с чертежом пожалуйста…
Решите пожалуйста щадачу с чертежом…
Запиши формулу для нахождения координат вектора по координатам его начала и конца.
..
Периметр квадрата равен (в первое окошко введи число, во второе — единицу измерения):
…
В равнобедренной трапеции высота делит большее основание на отрезки равные 14 и 3 см. Найдите среднюю линию трапеции….
Вычисли острый угол ромба, если сумма двух углов этого ромба равна 272°…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
Обществознание
Окружающий мир
География
Українська мова
Українська література
Қазақ тiлi
Беларуская моваИнформатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
Что такое формулы разности углов? Примеры
Формулы разности углов используются для нахождения тригонометрических отношений некоторых конкретных нестандартных углов путем записи их в виде разности двух стандартных углов.
Они также известны как тождества разности углов. Наряду с формулами разности углов у нас также есть формулы суммы углов.
Что такое формула разницы углов?
Мы уже знаем значения тригонометрических функций стандартных углов из тригонометрической таблицы. т. е. мы можем напрямую указать точные значения sin 90°, cos 45°, cosec 30° и т. д. с помощью тригонометрической таблицы. Но каковы значения sin 75°, cos 15°, tan 105° и т. д.? Их можно найти, используя формулы разности углов и формулы суммы углов. Вот формулы разности углов.
sin (A — B) = sin A cos B — cos A sin B
cos (A — B) = cos A cos B + sin A sin B
тангенс (A — B) = (тангенс A — тангенс B) / (1 + тангенс A тангенс B)
Вы можете увидеть формулы разности углов и суммы углов ниже.
Рассмотрим применение формул разности углов в следующем разделе.
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы.
С Cuemath находите решения простыми и легкими шагами.
Запись на бесплатный пробный урок
Примеры использования формулы разности углов
Пример 1: Найдите точное значение sin 15°.
Решение:
Найти: Значение sin 15°.
Используя одну из формул разности углов (от sin),
sin (A — B) = sin A cos B — cos A sin B
Подставьте A = 45° и B = 30° в приведенную выше формулу,
sin (45° — 30°) = sin 45° cos 30° — cos 45° sin 30°
sin 15° = (1 / √2) (√3 / 2) — ( 1/ √2) ( 1 / 2)
= √3 / 2√2 — 1 / 2√2
= (√3 — 1) / 2√2
Ответ: sin 15° = (√3 — 1) / 2√2
Пример 2: Найдите точное значение cot 15°.
Решение:
Найти: Значение кроватки 15°.
Используя одну из формул разности углов (тангенса),
тангенс (А — В) = (тангенс А — тангенс В) / (1 + тангенс А тангенс В)
Замените А = 45° и В = 30 ° в приведенной выше формуле
тангенс (45° — 30°) = (тангенс 45° — тангенс 30°) / (1 + тангенс 45° тангенс 30°)
tan 15° = (1 — (√3 / 3)) / ( 1 + 1 × (√3 / 3))
= ( (3 — √3) / 3) / ( (3 + √3) /3 )
= (3 — √3) / (3 + √3)
Но мы хотим найти кроватку 15°.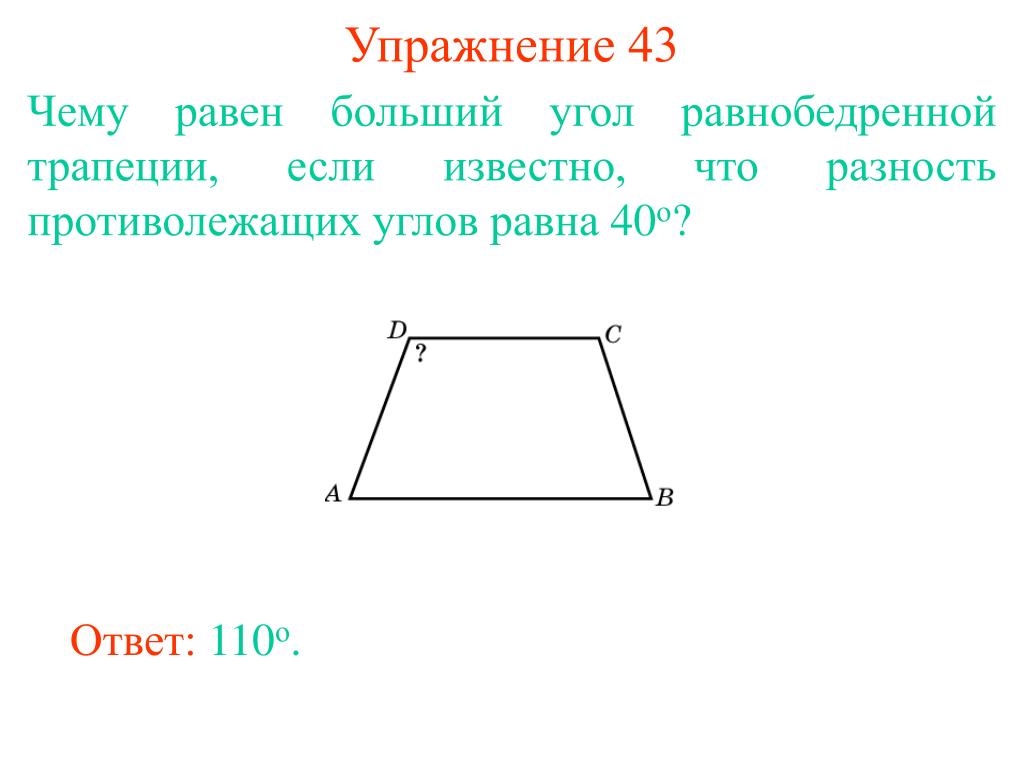
Мы знаем, что кроватка и загар являются взаимозаменяемыми.
cot 15° = 1 / (tan 15°)
Применяя формулу разности углов, tan (A — B) = (tan A — tan B) / (1 + tan A tan B)
tan 15° = (tan 45° — tan 30°)/(1+ tan 45° tan 30°)
cot 15° = (1+ tan 45° tan 30°)/(tan 45° — tan 30°)
= (1+ 1 . 1/√3)/ (1- 1/√3)
= (1+ 1/√3)/ (1- 1/√3)
= (√3 + 1 )/ (√3 — 1)
Рационализируя знаменатель,
cot 15° = (1 + √3) / (1 — √3) × (1 + √3) / (1 + √3)
= (1+ √3) 2 / (3-1)
= (1 + 3 + 2 √3)/2
= (4+ 2 √3)/2
= 2 + √3.
Ответ: кроватка 15° = 2 + √3.
Тождества суммы и разности углов
Главная > Математика > Тригонометрия > Тождества суммы и разности углов
Тождества суммы углов и тождества разности углов можно использовать для нахождения значений функций любых углов, однако наиболее практичным применением является нахождение точных значений угла, которые можно записать в виде суммы или разности, используя знакомые значения синуса, косинуса.
и тангенс углов 30°, 45°, 60° и 90° и их кратные.
Тождества суммы углов | Разность углов тождества |
sin(A + B) = sin A · cos B + cos A · sin B | sin(A — B) = sin A · cos B — cos A · sin B |
cos (A + B) = cos A · cos B — sin A · sin B | Cos(A — B) = cos A · cos B + sin A · sin B |
загар (А + В) = |
Пример : найдите точное значение cos 75°, используя формулу суммы .
Поскольку 75 является суммой 30 и 45, можно использовать формулу кос-суммы.
cos (A + B) = cos A · cos B — sin A · sin B
cos (30 + 45) = cos 30 · cos 45 — sin 30 · sin 45
=
=
Следовательно, cos 75° =
Пример: Найдите точное значение синуса 15°, используя формулу разности.
Поскольку 15 — это разность 45 и 30, можно использовать формулу разности синусов.
sin(A — B) = sin A · cos B — cos A · sin B
sin(45 — 30) = sin 45 · cos 30 — cos 45 · sin 30
=
=
Следовательно, sin 15° =
3 специальных примечания:
1) У вас может быть более одного варианта. Например, найдите синус 120°
sin(90 + 30) с использованием формулы суммы
или
sin(180 — 60) с использованием формулы разности
обе формулы дадут один и тот же результат.
2) Не забудьте определить, в каком квадранте будет лежать угол.