Сколько радиан составляет угол в 120 градусов
Статьи › Находится › Найдите радианную меру углов и укажите в какой четверти находится угол 150 200
2,093 рад.
Ответ: 120° составляет 2,093 рад.
- Чему равна Радианная мера угла 210 градусов
- Как найти значение угла в радианах
- Как найти Радианную меру угла выраженного в градусах
- Как перевести из градусной меры в Радианную
- Чему равна Радианная мера угла 270 градусов
- Чему равна градусная мера в 1 рад
- Сколько градусов составляет угол в 1 радиан
- Чему равен угол 90 по радианной мере угла
- Что такое угол в один радиан
- Чему равна Радианная мера угла в 240 градусов
- Какой угол в радианах соответствует углу 75
- Как найти Радианную меру угла 60 градусов
- Чему равна Радианная мера угла 18 градусов
- Чем отличается радиан от градуса
- Как перевести в радианы число
- Чему равна Радианная мера угла 315 градусов
- Какая мера угла 30 градусов
- Какой угол в радианах соответствует углу 36
- Зачем переводить градусы в радианы
- Сколько радиан в одном круге
- Как найти градусную меру
- Чему равна градусная мера угла
- Что такое Радианная мера радиан
Чему равна Радианная мера угла 210 градусов
210° = -210 * пи / 180 = 7 * пи / 6. Ответ: 7*пи / 6.
Ответ: 7*пи / 6.
Как найти значение угла в радианах
Ответы1. Чтобы перевести градусы в радианы необходимо воспользоваться формулой, связывающей их. Выглядит она так: х° = (х° * Пи)/180°.
Как найти Радианную меру угла выраженного в градусах
Для того, чтобы найти радианную меру угла, выраженного в градусах, как 15°, умножим 15 на π и разделим результат на 180. Имеем: 15° = (15 * π / 180) радиан = (π / 12) радиан.
Как перевести из градусной меры в Радианную
1 рад = (180 / П)°. Тогда, воспользовавшись данной формулой, получим: 2П/3 рад = (2П/3) * (180 / П)° = 2П * 180° / 3П = 2 * 180° / 3 = 2 * 60° = 120°.
Чему равна Радианная мера угла 270 градусов
270° = 270 * П/180 радиан = 3П/2 радиан = 270 * 0,0174 = 4,7 радиан.
Чему равна градусная мера в 1 рад
Для его измерения рассмотрим единичную окружность, где вершина угла совпадает с его центром. Затем нарисуем дугу, равную радиусу окружности и соединим концы дуги с центром. Это и есть один радиан, один градус равен π180 радиан и 1 радиан равен 180π градусов.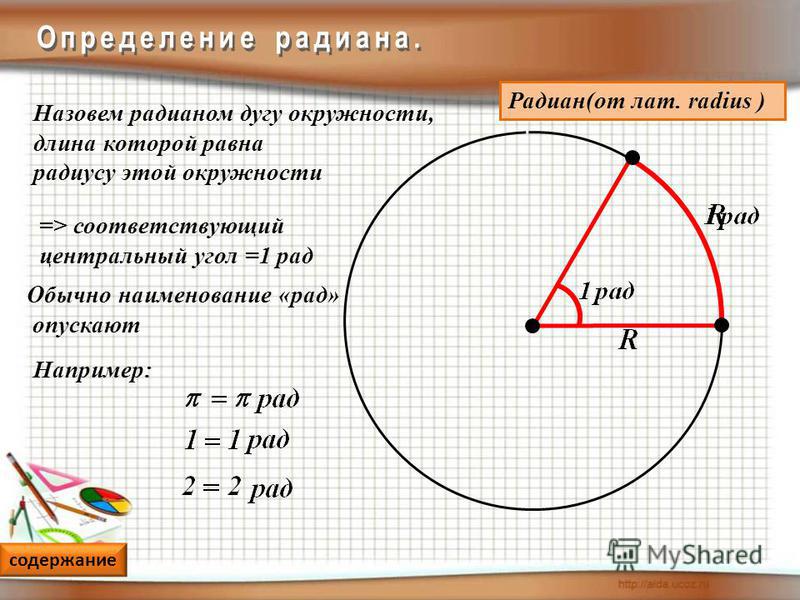
Сколько градусов составляет угол в 1 радиан
Радианная мера угла принимает за единицу измерения острый угол, под которым видна из центра окружности ее дуга, равная по длине радиусу окружности. Такой угол называется — радиан. Радианы, Радианная мера угла — Измерение углов, 1 радиан равен 57 градусов 17 минут 45 секунд.
Чему равен угол 90 по радианной мере угла
90° = 90п/180 = п/2 = 1,57 рад.
Что такое угол в один радиан
Углом в 1 радиан называют центральный угол тригонометрического круга, которому соответствует дуга окружности тригонометрического круга длиной 1.
Чему равна Радианная мера угла в 240 градусов
Ответ: 240° = (4п/3) рад ≈ 4,187 рад.
Какой угол в радианах соответствует углу 75
Ответ: 75 градусов в радианной мере равно 5/12 * pi.
Как найти Радианную меру угла 60 градусов
60° = 60 × π/180 = π/3. Чаще всего при вычислении меры угла в радианах наименование «рад» не указывают.
Чему равна Радианная мера угла 18 градусов
Следовательно, а) 18° = 18 * (π/180) радиан = (18 * π) / 180 радиан = π/10 радиан; б)- 250° = -250 * (π/180) радиан = (-250 * π) / 180 радиан = -25 * π/18 радиан; в) -360° = -360 * (π/180) радиан = (-360 * π) / 180 радиан = -2 * π радиан; г) 225° = -225 * (π/180) радиан = (-225 * π) / 180 радиан = -5 * π/4 радиан.
Чем отличается радиан от градуса
Главное — помнить, что 2П радиан — это 360 градусов. Отсюда П радиан равно 180 градусам. И из этого выражения мы всегда можем выразить хоть 1 радиан, хоть 1 градус. И совсем необязательно запоминать, что 1 радиан — это 180/П градусов, а 1 градус — это П/180 радиан.
Как перевести в радианы число
Формула перевода проста — градусы * Пи/180.
Чему равна Радианная мера угла 315 градусов
315° = (315 * π)/180 ≈ 5,495 радиан. Ответ: угол α = 315°=5,495 радиан.
Какая мера угла 30 градусов
Выразим в радианах: 30° = 30 * (π / 180) радиан = π/6 радиан ≈ 0,5236 радиан.
Какой угол в радианах соответствует углу 36
Ответы1. Ответ: 45º ≈ 0,79 рад; 36º ≈ 0,63 рад; 180º ≈ 3,14 рад.
Зачем переводить градусы в радианы
Запись величины углов в радианах удобнее, компактнее и целесообразнее для вычислений
Сколько радиан в одном круге
В полной окружности содержится 2π радиан, или 360 градусов.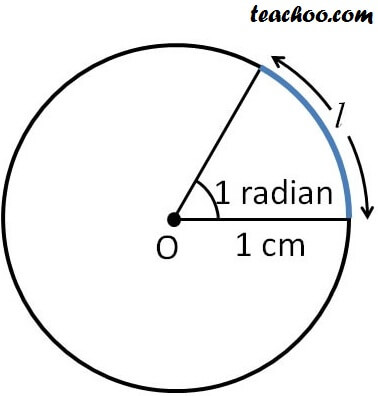 Таким образом: 2π радиан = 360° 1 радиан = (360/2π) градусов = (180/π) градусов
Таким образом: 2π радиан = 360° 1 радиан = (360/2π) градусов = (180/π) градусов
Как найти градусную меру
Как мы помним, для того, чтобы определить, какой величине будет равняться градусная мера угла правильного многоугольника возможно воспользоваться нижеследующей формулой: 180 * (n — 2) = a * n, где n — это количество сторон многоугольника, a — это градусная мера угла.
Чему равна градусная мера угла
Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
Что такое Радианная мера радиан
Радианная мера — угловая мера, в которой за единицу принимается угол в 1 радиан. То есть, радианная мера любого угла — это отношение этого угла к радиану. Из определения следует, что величина полного угла равна 2π радиан (см.
Что называется углом в 1 рад?
Что называется углом в 1 рад?
1 радиан — центральный угол, длина дуги которого равна радиусу окружности.
Как выразить величину угла в радианах?
. Формула перевода градусов в радианы имеет вид . То есть, если известна величина угла в градусах, то умножив ее на пи и разделив на 180, получим величину этого угла в радианах.
Сколько Радиан содержит полный оборот?
Соответственно, в полном обороте, в 360 градусах содержится 6,28 радиан.
Как посчитать в радианах?
Чтобы вычислить радианную меру этого угла необходимо длину дуги разделить на длину радиуса окружности. Рассматриваемому углу соответствует длина дуги, равная половине длины окружности π⋅r . Разделим длину дуги на радиус и получим радианную меру угла: π⋅rr=π π · r r = π рад. Итак, рассматриваемый угол равен π радиан.
Сколько Радиан в прямом угле?
1 радиан=57°19мин.
Чем отличается Радиан от градуса?
1 Rad = 180/π градуса. Таким образом, π радианов = 180°, а 1° = π/180 радиана. Радианная мера угла – это такая мера угла, при которой за 1 Rad принимается угол дуги, равной радиусу этой дуги.
Как перевести из радиан в градусы на калькуляторе?
Чтобы перевести из радиан в градусы, надо 180 поделить на Пи и умножить на количество радиан, получится число с дробной частью, где целое — это количество градусов.
Зачем нужна Радианная мера угла?
Для описания непрерывного вращения градусная мера угла поворота становится неудобной – с ней трудно связывать другие характеристики движения, например, скорость или соединять вращательное движение с иными движениями. Поэтому вводят другую меру угла поворота, так называемую радианную меру.
Почему 180 градусов это пи?
Если угол задан в радианах с числом «пи«, то всё очень просто. Мы знаем, что «пи» радиан — это 180 градусов. Вот и подставляем вместо «пи» радиан — число 180. Сокращаем всё что сокращается и получаем угол в градусах.
Как пишется градусная мера?
1). Градусной мерой угла называется положительное число, которое показывает, сколько раз градус и его части — минута и секунда — укладываются в данном угле, то есть градусная мера — величина, отражающая количество градусов, минут и секунд между сторонами угла.
Что измеряется в радианах в секунду?
В случае вращательного движения угловая частота равна модулю вектора угловой скорости. В Международной системе единиц (СИ) и системе СГС угловая частота выражается в радианах в секунду, её размерность обратна размерности времени (радианы безразмерны).
Что такое Омега т?
OmegaT — это свободная система автоматизированного перевода, поддерживающая память переводов, написанная на языке программирования Java.
Что показывает циклическая частота?
Циклической (угловой, радиальной круговой) частотой называют скалярную физическую величину, которая служит мерой вращательного или колебательного движения. Угловая скорость при равномерном движении по окружности является постоянной величиной, в этом случае ее называют циклической частотой.
Чему равна Омега?
Циклическая частота колебний (ω) — число колебаний за 2π секунд. — связь циклической частоты с частотой колебаний и периодом.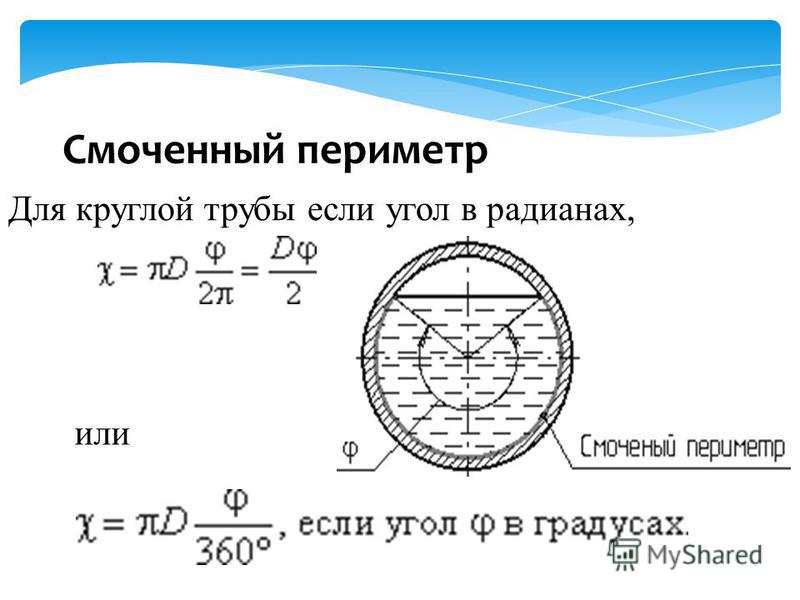 Циклическая частота в уравнениях колебаний: — циклическая частота колебаний математического маятника.
Циклическая частота в уравнениях колебаний: — циклическая частота колебаний математического маятника.
Что значит Омега человек?
Омега — стопроцентный «ничегонеделатель», никаких задач, целей и стремлений. Ипостаси могут быть две — либо вечная жертва, либо осознанный иждивенец, паразитирующий на своем партнере. Минусы Омег…. сам факт их существования.
Как найти Омега в физике?
А угловая, или циклическая, частота ω — то же самое, только выраженное не в оборотах, а в радианах. Так как 1 оборот=2*π радиан, то отсюда и вытекает формула ω=2*π*f. То есть ω показывает величину угла (в радианах), проходимого телом за 1 секунду. 2) По определению, f=1/T.
Что такое течка у Омеги?
В процессе течки происходит большее выделение смазки, чем в обычное время. Помимо этого омега выделяет в момент течки специфический запах, на который реагируют все альфы, а также гаммы и беты. Если у омеги нет постоянного партнера (или точнее своей половинки), то он становится приманкой для других альф.
Кто такой Омега в Лгбт?
Во главе стаи всегда вожак – самый сильный, ловкий и выносливый самец. Его-то и называют альфа-самцом. Далее, ниже в иерархии – бета-самцы. Омега-самцы – самые слабые и нежизнеспособные самцы, которые чаще являются изгоями.
Кто такой Омега в волчьей стае?
В любой волчьей стае царит строгая иерархия, на высшей ступени которой находятся альфа-самец и альфа-самка. За вожаками стаи следуют волки из группы «бета», и на самой низшей ступени иерархии располагаются так называемые омега—волки. … Если говорить простым человеческим языком, то омега—волк — это «груша для битья».
Как часто у омег течка?
Следует сказать, что (если сравнивать с волками) течка у омеги может происходить каждые четыре месяца. Но некоторые авторы или уменьшают этот срок (чаще всего до двух месяцев), или наоборот увеличивают (раз в шесть месяцев).
Кто такие Альфы и Омеги в Фанфиках?
Теперь о том, почему же гаммы именно гибрид альфы и омеги. Дело в том, что гамма совмещает в себе все главные прелести одного и другого. От омеги они берут матку, развитую гормональную систему, а от альфы — активные сперматозоиды и сильный детородный орган в виде члена и вместе с узлом. То есть два в одном.
Дело в том, что гамма совмещает в себе все главные прелести одного и другого. От омеги они берут матку, развитую гормональную систему, а от альфы — активные сперматозоиды и сильный детородный орган в виде члена и вместе с узлом. То есть два в одном.
Откуда взялся омегаверс?
Так всё-таки, откуда появился омегаверс? Официально — из фандома сериала «Сверхъестественное». Точнее из фанфиков, где Сэм и Дин были вервольфами. Этим можно объяснить некоторые особенности физиологии альфа-самцов.
Что такое блокаторы в Омегаверсе?
Блокаторы альфа- и бета-адренорецепторов являются подклассом бета-блокаторов, которые обычно используют для лечения высокого артериального давления (АД). К этому классу лекарств относятся карведилол (Coreg), лабеталол (Trandate) и дилевалол (Unicard).
Что такое Гон в Омегаверсе?
Гон – поиск свободным альфой свободной омеги/женщины-альфы, готовой к вязке и рождению потомства.
Кто такая гамма в Омегаверсе?
Гамма – нераспространенный тип в омегаверсе. Не часто о нем вспоминают, но это большое упущение. Ведь гамма уникальное создание: человек совместивший в себе суть и альфы и омеги. Гамма является гибридом двух противоположностей, перестраиваясь и адаптируюсь к ситуации или партнеру.
Не часто о нем вспоминают, но это большое упущение. Ведь гамма уникальное создание: человек совместивший в себе суть и альфы и омеги. Гамма является гибридом двух противоположностей, перестраиваясь и адаптируюсь к ситуации или партнеру.
Что блокируют бета блокаторы?
Бета—блокаторы — это лекарства, которые блокируют действие адреналина и норадреналина на сердце. Бета—блокаторы могут замедлить работу сердца и снизить кровяное давление, и это может снизить риск серьезных событий.
2.5.1: Измерение в радианах — K12 LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4233
Измерение угла в окружности, где длина дуги равна радиусу.
Во время проведения эксперимента в школьной научной лаборатории учитель просит вас включить детектор, повернув ручку на \(\dfrac{\pi}{2}\) радиан. Вы сразу озадачены, так как не знаете, что такое 9{th}}\) полного оборота вокруг окружности. Радиан — альтернативная единица измерения углов в тригонометрии. Как это ни звучит, радиан основан на радиусе круга. Один радиан (сокращенно рад) — это угол, образованный изгибанием длины радиуса вокруг дуги окружности. Поскольку радиан основан на фактической части окружности, а не на произвольном делении, это гораздо более естественная единица измерения угла для математики верхнего уровня.
Рисунок \(\PageIndex{1}\) Что, если бы мы вращались по всей окружности? Продолжая складывать длины радиусов, мы обнаруживаем, что для завершения поворота требуется чуть больше 6 из них.
Напомним из геометрии, что длина дуги полного оборота равна длине окружности, где формула равна \(2\pi\), умноженному на длину радиуса. \(2\pi\) примерно равно 6,28, поэтому длина окружности чуть больше 6 длин радиуса. Или, если говорить о радианах, полный оборот (360 градусов) равен \(2\pi\) радианам. 9{\circ}\), в радианах:
Рисунок \(\PageIndex{4}\)Обратите внимание, что все дополнительные углы на чертеже имеют исходные углы 45 градусов, а все их измерения в радианах кратны \(\dfrac{ \пи}{4}\). Все четные кратные являются квадрантными углами и уменьшаются, как и любая другая дробь.
Давайте решим несколько задач, связанных с радианными измерениями.
1. Найдите значение этих углов в радианах.
| Угол в градусах | Угол в радианах |
|---|---|
| 90 | \(\dfrac{\pi}{2}\) |
| 45 | |
| 30 |
Поскольку 45 — это половина 90, половина \(\dfrac{1}{2}\pi\) равна \(\dfrac{1}{4}\pi\).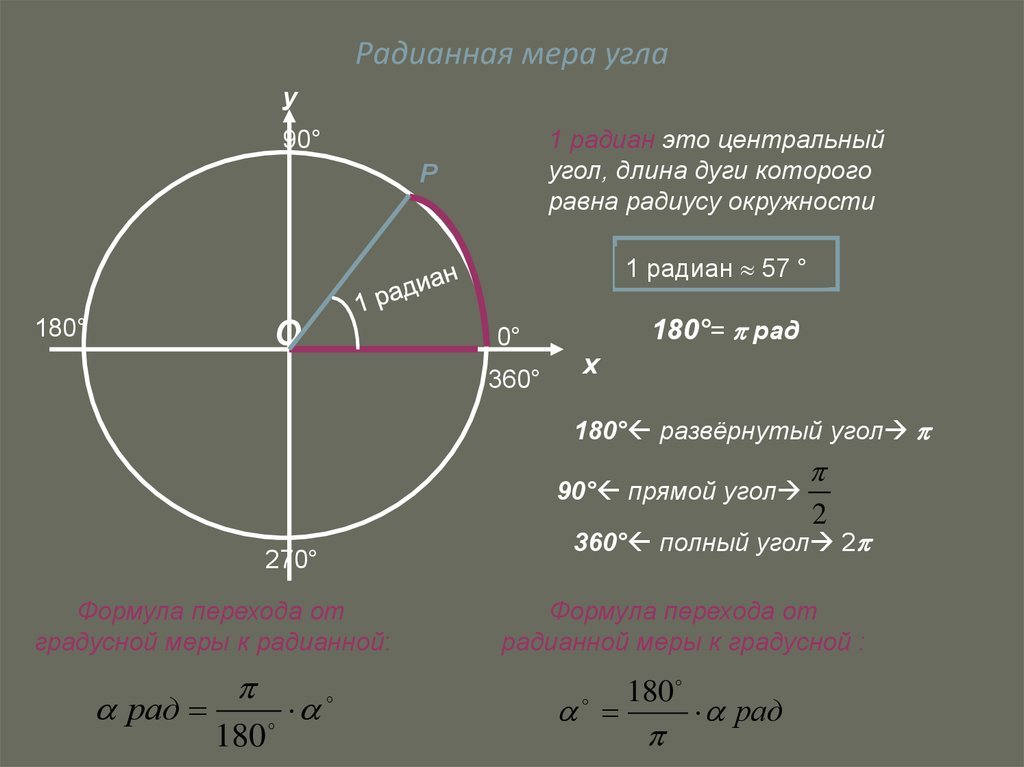 30 — это треть прямого угла, поэтому умножение дает:
30 — это треть прямого угла, поэтому умножение дает:
\(\dfrac{\pi}{2}\times \dfrac{1}{3}=\dfrac{\pi}{6}\)
и поскольку 60 вдвое больше 30:
\ (2\times \dfrac{\pi}{6}=\dfrac{2\pi}{6}=\dfrac{\pi}{3}\)
Вот заполненная таблица:
| Угол в градусах | |
|---|---|
| 90 | \(\dfrac{\pi}{2}\) |
| 45 | \(\dfrac{\pi}{4}\) |
| 30 | \(\dfrac{\pi}{6}\) |
Существует формула для преобразования радианов в градусы, которую вы, возможно, уже узнали, выполняя этот пример. Однако многие широко используемые углы можно легко найти по значениям в этой таблице.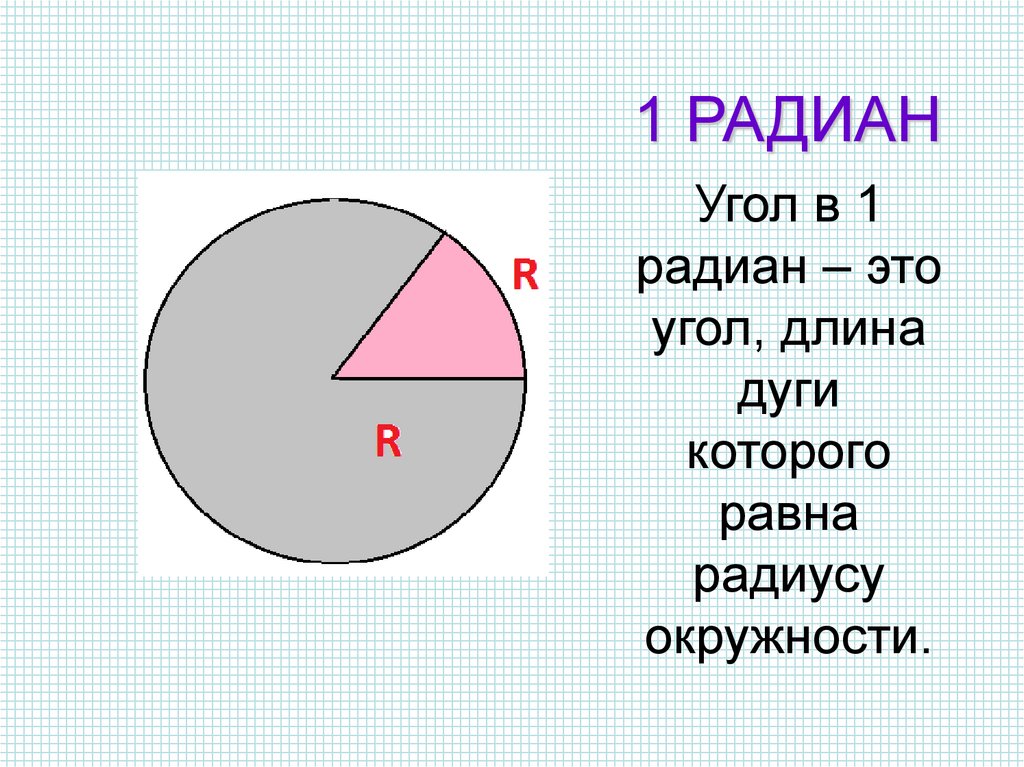 Например, большинству учащихся легко запомнить числа 30 и 60. 30 — это \(\pi\) больше 6 , а 60 — это \(\pi\) больше 9.0026 3
Например, большинству учащихся легко запомнить числа 30 и 60. 30 — это \(\pi\) больше 6 , а 60 — это \(\pi\) больше 9.0026 3
2. Выполните следующие измерения в радианах, считая числа, кратные \(\dfrac{\pi}{3}\) и \(\dfrac{\pi}{6}\):
Рисунок \(\PageIndex{5 }\)Рисунок \(\PageIndex{6}\)Обратите внимание, что все углы с опорными углами 60 градусов кратны \(\dfrac{\pi}{3}\), а все углы с 30- опорные углы в градусах кратны \(\dfrac{\pi}{6}\). Счет в этих терминах на основе этого шаблона, а не обратное преобразование в градусы, поможет вам лучше понять радианы.
3. Найдите значение этих углов в радианах.
| Угол в градусах | Угол в радианах |
|---|---|
| 120 | |
| 180 | |
| 240 | |
| 270 | |
| 300 |
Поскольку 30 — это одна треть прямого угла, умножение дает:
\(\dfrac{\pi}{2}\times 13=\dfrac{\pi}{6}\)
сложение этого к известному значению для девяноста градусов \(\dfrac{\pi}{2}\):
\(\dfrac{\pi}{2}+\dfrac{\pi}{6}=3\dfrac{ \pi}{6}+\dfrac{\pi}{6}=4\dfrac{\pi}{6}=\dfrac{2 \pi}{3}\)
Вот заполненная таблица:
| Угол в градусах | Угол в радианах |
|---|---|
| 120 | \(\dfrac{2\pi}{3}\) |
| 180 | \(\пи\) |
| 240 | \(\dfrac{4\pi}{3}\) |
| 300 | \(\dfrac{5\pi}{3}\) |
Найдите градусную меру каждого угла.
- \(\dfrac{3\pi}{2}\)
- \(\dfrac{5\pi}{4}\)
- \(\dfrac{7\pi}{6}\)
- \(\dfrac{\pi}{6}\)
- \(\dfrac{5\pi}{3}\)
- \(\пи\)
- Объясните, почему если вам дан угол в градусах и умножить его на \(\dfrac{\pi}{180}\), вы получите тот же угол в радианах.
- Объясните, почему если вам дан угол в радианах и вы умножите его на \(\dfrac{180}{\pi}\), вы получите тот же угол в градусах.
- Объясните своими словами, почему в круге есть \(2\pi\) радиан.
Обзор (ответы)
Чтобы просмотреть ответы на обзор, откройте этот PDF-файл и найдите раздел 2.1.
Словарь
| Срок | Определение |
|---|---|
| радиан | Радиан — это единица измерения угла, равная углу, образованному в центре окружности, длина дуги которой равна радиусу. |
Дополнительные ресурсы
Интерактивный элемент
Видео: Измерение угла — Обзор
Практика: Измерение радиана
Эта страница под названием 2.5.1: Radian Measure распространяется под лицензией CK-12 и была создана, изменена и/или курирована Фондом CK-12 с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
ПОД ЛИЦЕНЗИЕЙ
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- СК12
- Лицензия
- СК-12
- Программа OER или Publisher
- СК-12
- Показать оглавление
- нет
- Теги
- источник@https://www.
 ck12.org/c/trigonometry
ck12.org/c/trigonometry
- источник@https://www.
Предварительное исчисление по алгебре — Путаница в связи с отношением, которое включает меру в радианах.
На евклидовой плоскости круговой сектор с радиусом r и длиной дуги s имеет угол при вершине, тета, пропорциональный s и обратно пропорциональный r — это следует из аксиом, определяющих евклидово пространство. Таким образом, мы имеем:
тета = const (s/r)
Поскольку размерность тета представляет собой плоский угол, скажем, A, а s/r безразмерна, размерность const равна A, т.е. const — это угол. Мы можем легко вычислить const, установив s = 2 pi r, что соответствует тета = rev (угол, состоящий из одного полного оборота, что легко представить):
rev = const (2 pi r)/r = (2 pi) const
Итак:
const = rev/(2 pi)
обратите внимание, что это размерное соответствие — уравнение имеет размерность A.
Мы даем этой важной константе специальное имя: один радиан, символ рад.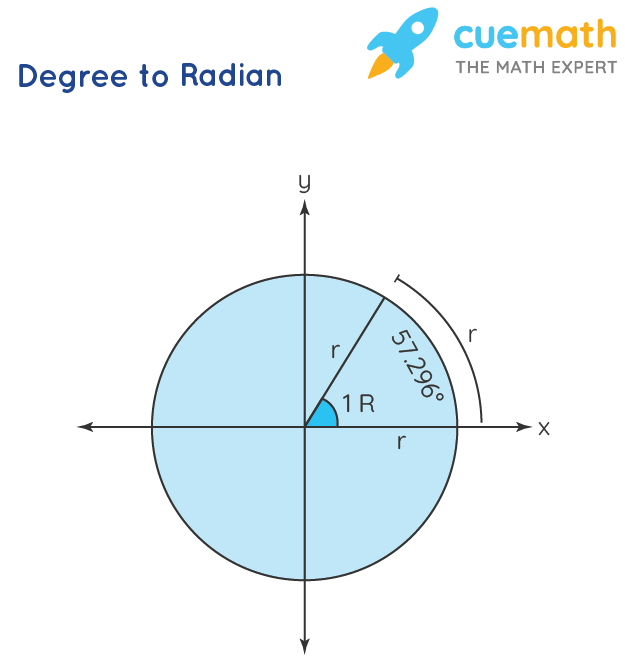 Таким образом:
Таким образом:
рад = оборот/(2 pi)
и теперь мы имеем (ФУНДАМЕНТАЛЬНОЕ УРАВНЕНИЕ):
тета = (s/r) рад,
Мы можем получить представление об угле, представленном рад, установив s = r:
тета (s = r) = (r/r) рад = рад
т. е. один радиан — это угол при вершине кругового сектора, в котором длина дуги равна радиусу (хорошо известное определение — с известной диаграммой).
То, что обычно называют «углом в радианах» или «радианной мерой угла», на самом деле является числом радиан в тета , тета/рад:
радиан мера (тета) = тета/рад = s/r
число радиан в тета (будучи числом) безразмерно — опять же, уравнение размерностно согласовано. Мы можем переписать фундаментальное уравнение «тета = (s/r) рад» двумя другими способами:
(1): s/тета = r/рад
или
(2): s/(тета/рад) = r/1
Прописью:
(1): (длина дуги)/ (угол) = (радиус)/(один радиан)
Обратите внимание, что знаменатель слева — это угол, а НЕ «угол в радианах».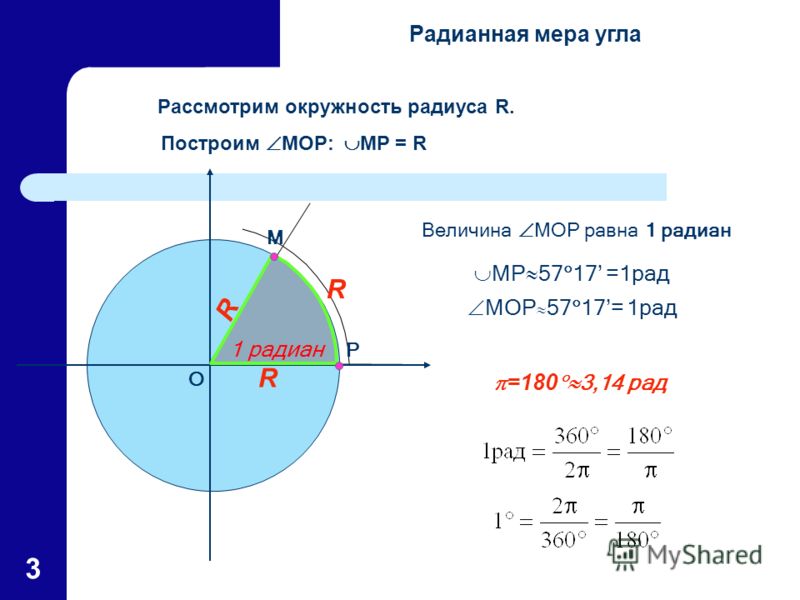
(2): (длина дуги)/(«угол в радианах») = (радиус)/(один)
Обратите внимание, что знаменатель справа равен единице, а НЕ одному радиану.
К сожалению, во многих учебниках (и в определении СИ) безразмерная величина тета/рад называется (плоскостным) «углом». Это (очевидно) вовсе не угол — это число радиан в углу тета. Если мы обозначаем тета/рад символом тета*, фундаментальное уравнение принимает следующий вид:
тета* = s/r
Это форма, которую можно увидеть в (большинстве) учебников и онлайновых учебных пособий, где тета* называется «углом» (и без предупредительной звездочки), но с оговоркой, что « угол» должен быть «выражен в радианах» или в «радианах». Первое неполное: «угол должен быть выражен в радианах, и мы должны взять его числовое значение, тета/рад». Термин «радианная мера», конечно, означает то же самое, но (обычно) никогда не разъясняется.
Еще одна проблема заключается в том, что «радиан» в системе СИ определяется как тета*, когда s = r, т.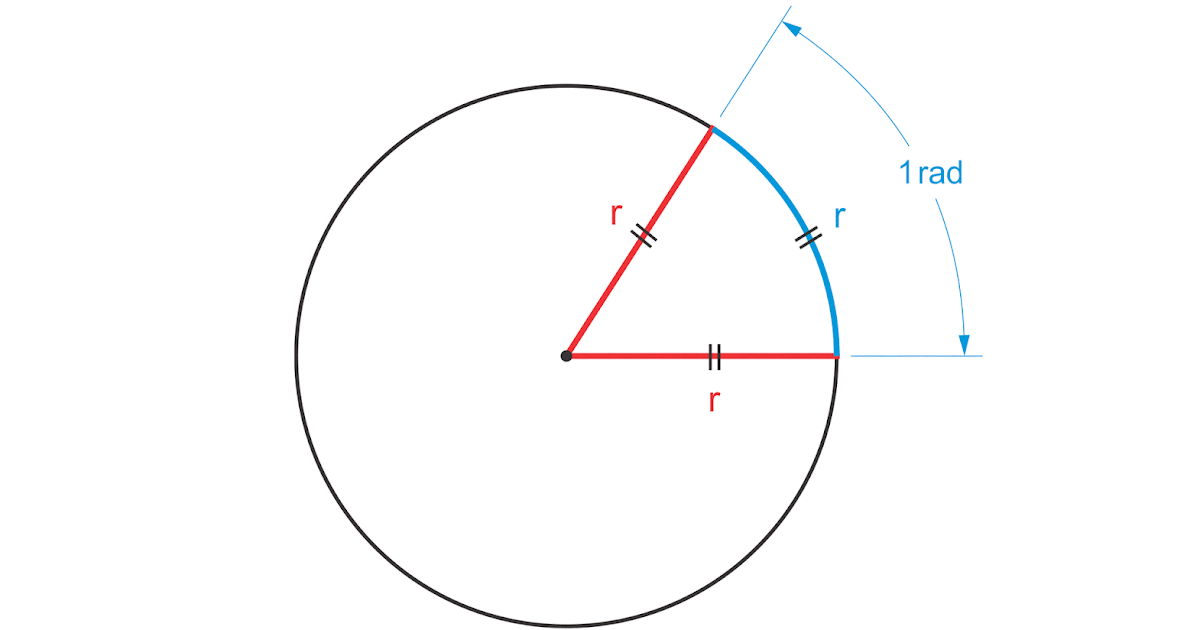

 ck12.org/c/trigonometry
ck12.org/c/trigonometry