Что значит прямой угол: Что такое прямой угол? Ответ на webmath.ru

определение, фигуры с ним, пример задачи

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

В данной публикации мы рассмотрим, что такое прямой угол, перечислим основные геометрические фигуры, в которых он встречается, а также разберем пример задачи по этой теме.

• Определение прямого угла
• Фигуры с прямыми углами
• Пример задачи

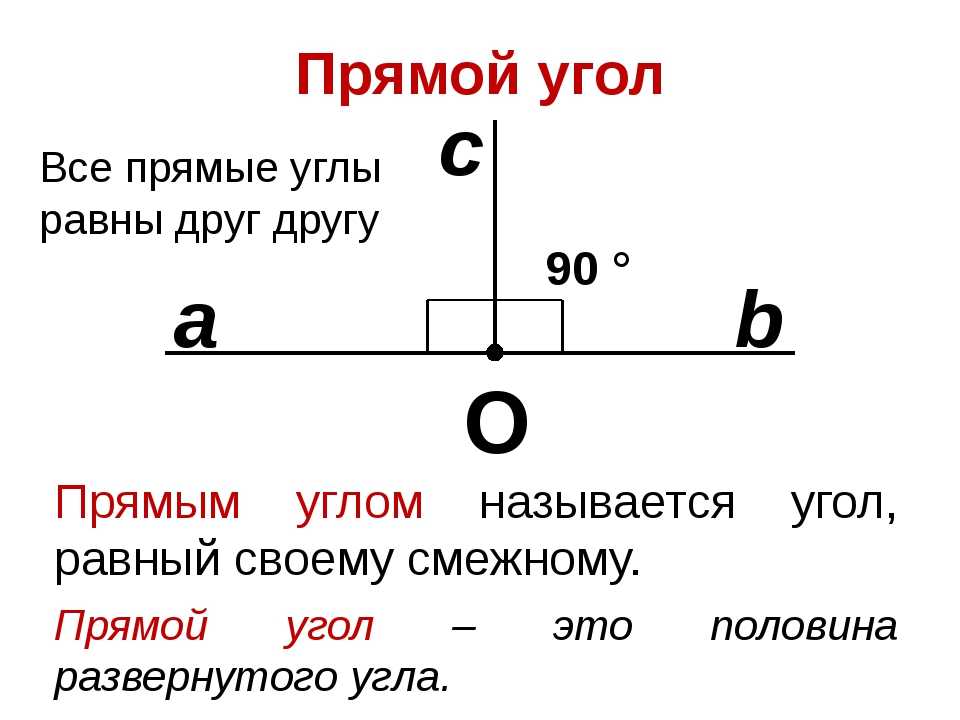
Определение прямого угла

Угол является прямым, если его градусная мера равняется 90 градусам.

На чертежах для обозначения такого угла используется не круглая дуга, а квадратная.

Прямой угол составляет половину развернутого угла (180°) и в радианах равняется π/2.

Фигуры с прямыми углами

1. Квадрат – ромб, все углы которого равны 90°.

2. Прямоугольник – параллелограмм, все углы которого, также, являются прямыми.

3. Прямоугольный треугольник – один из его углов прямой.

4. Прямоугольная трапеция – хотя бы один из углов равняется 90°.

Пример задачи

Известно, что в треугольнике один из углов является прямым, а два остальных равны между собой. Найдем неизвестные значения.

Решение

Как мы знаем из теоремы о сумме углов треугольника, она равняется 180°.

Следовательно, на два неизвестных угла приходится 90° (180° – 90°). Значит каждый из них равняется 45° (90° : 2).

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Что такое угол? Определение, виды, как обозначают, примеры

Поможем понять и полюбить математику

Начать учиться

116. 6K

Знания школьной геометрии пригодятся в самых неожиданных ситуациях: во время ремонта, при рисовании граффити или чтобы нарезать пирог. В этой статье узнаем все про углы.

Определение угла

Угол — это простая геометрическая фигура. Определение угла напрямую связано с понятием луча.

Луч — прямая линия, у которой есть начало, но нет конца, и продолжается она только в одну сторону.

Если нам дана прямая a на плоскости, и на ней есть некоторая точка O — выходит, что прямая разделена точкой на две части, каждая из которых является лучом с началом в точке O.

Луч можно обозначить одной строчной буквой латинского алфавита или двумя прописными. Например, вот так:

Угол — часть плоскости между двумя линиями, исходящими из одной точки. Каждая сторона угла является лучом, а вершина — общим началом сторон.

Что такое вершина и стороны угла

В математике существует специальный символ для обозначения угла, вот он: ∠.

Если стороны угла названы малыми латинскими буквами, то их записывают после символа. Например, так: ∠ab или ∠ba.

Если стороны угла названы большими буквами, то обозначение угла будет состоять из символа и трех букв, при этом вершина всегда записывается в центре. При сторонах угла OA и OB название угла запишем так: ∠AOB и ∠BOA. Также можно назвать угол одной большой буквой, которая указывает на его вершину, например: ∠O.

Иногда встречается обозначение в виде цифр — так тоже можно.

Для наглядности — все способы обозначения углов:

Так как угол делит плоскость на две части, одна будет внутренней областью угла, а другая — внешней областью угла.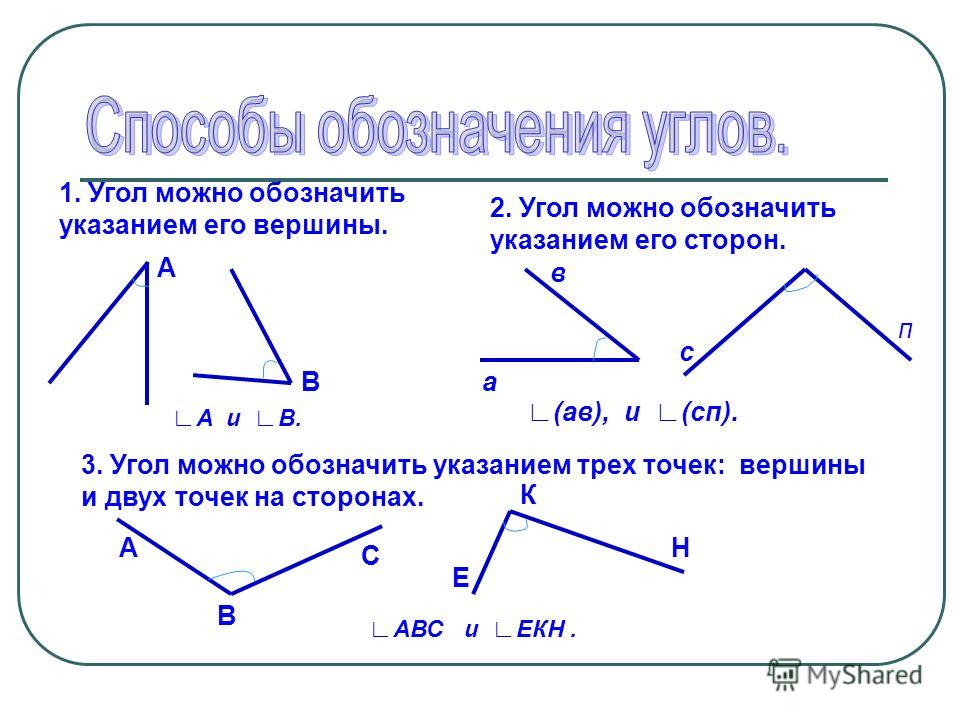 Вот так:

Единица измерения углов — градусы. Символ для обозначения градуса угла: °.

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

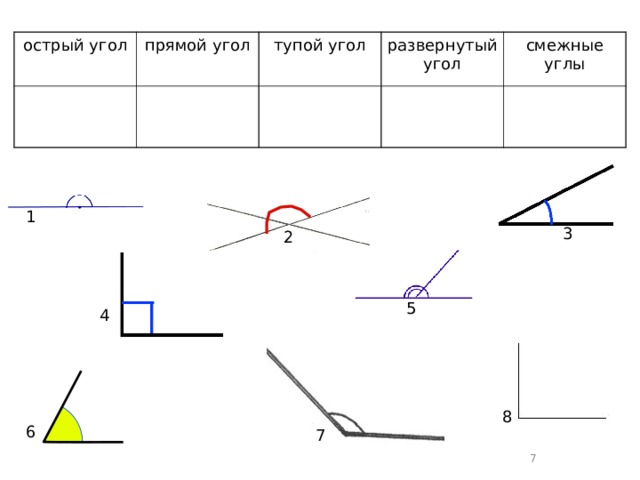
Виды углов

Есть разные типы углов и у каждого своё название:

• острый
• прямой
• тупой
• развернутый
• выпуклый
• полный

Различать виды углов в геометрии важно. Определять можно на глаз или с помощью линейки.

Прямой угол — это угол, стороны которого перпендикулярны друг другу. Прямой угол всегда равен 90°.

Если два смежных угла равны между собой, то каждый из них является прямым. Для удобства прямой угол обозначается уголком. Вот так:

На картинке изображены два прямых угла ∠AOC и ∠COB. Общая сторона OC перпендикулярна прямой AB, а точка O — основание перпендикуляра.

Острый угол — это угол, который меньше прямого угла, то есть < 90°.

Развернутый угол — это открытый угол, который образован двумя лучами и равен сумме двух прямых углов. Развернутый угол равен 180°. Как выглядит развернутый угол, показано на первой картинке.

При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.

Неразвернутый угол — это любой угол, который не является развернутым, то есть не равен 180°.

Тупой угол — это угол, который больше прямого угла, но меньше развернутого:
90° < тупой угол < 180°.

Выпуклый угол — это угол, который больше развернутого угла, но меньше полного:
180° < выпуклый угол < 360°.

Полный угол — это угол, обе стороны которого совпадают с одним лучом. Он равен сумме четырех прямых углов, то есть = 360°.

Прилежащие углы — это пара углов с общей вершиной и стороной, другие стороны при этом лежат по разные стороны от общей стороны.

На картинке мы видим два прилежащих угла ∠AOB и ∠BOC, общую вершину O и общую сторону OB.

Можно сформулировать определение по-другому: если из вершины любого угла провести луч, разделяющий угол на два, то образованные углы будут прилежащими.

Чтобы найти угол, который разделен лучом, нужно сложить полученные углы: ∠AOB = ∠AOC + ∠COB. Из этого можно выделить следующие верные разности:

• ∠AOC = ∠AOB − ∠COB,
• ∠COB = ∠AOB − ∠AOC.

Запоминаем!

Угол называется прямым, если он равен 90°, острым, если он меньше 90°, тупым, если он больше 90°, но меньше 180°. Развернутый угол равен 180°.

Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!

Сравнение углов

Для сравнения углов можно использовать самый простой способ из программы 4 класса — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны заданных углов совпадут, значит углы равные. Если нет, то угол, который лежит внутри другого, будет меньшим. Здесь два наглядных примера с равными и неравными углами:

При этом развернутые углы всегда являются равными.

Совмещение углов ∠𝐴𝐵𝐶 и ∠𝑀𝑁𝐾 происходит следующим образом:

 

1. Вершину 𝐵 одного угла совмещаем с вершиной 𝑁 другого угла.


2. Сторону 𝐵𝐴 одного угла накладываем на сторону 𝑁𝑀 другого угла так, чтобы стороны 𝐵𝐶 и 𝑁𝐾 располагались в одном направлении.

Если совпадут и другие стороны, то углы равны: ∠𝐴𝐵𝐶 = ∠𝑀𝑁𝐾.

Если нет, то один угол — меньше другого: ∠𝐴𝐵𝐶<∠𝑀𝑁𝐾.

Сравнить углы можно также, измерив их величины. Для этого понадобится специальный инструмент для построения и измерения углов — транспортир. Вот как он выглядит:

Как правильно измерять углы

Измерение углов похоже на измерение отрезков: нужно сравнить их с углом, принятым за единицу измерения. В геометрии обычно за единицу измерения принимают градус — угол, равный 1/180 части развернутого угла. Он обозначается так: °.

Градусная мера угла — положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.

Есть еще две возможные меры угла: минуты и секунды. Они позволяют выполнять более точные расчеты, особенно, когда величина не является целым обозначением градуса.

Минута — 1/60 часть градуса. Обозначается ´.

Секунда — 1/60 часть минуты. Обозначается ´´.

Градус состоит из 3600 секунд, то есть: 1° = 60´ = 3600´´.

Как происходит измерение угла: сначала измеряют стороны угла, а после — его внутреннюю область. Всегда нужно считать количество уложенных углов, так как они предопределяют меру измеряемого угла.

Когда луч делит угол на два или более углов, градусная мера всего угла равна сумме градусных мер этих углов.

На рисунке изображен угол АОВ, он состоит из углов АОС, СОD и DОВ. Можно записать так: ∠AOB = ∠AOC + ∠COD + ∠DOB = 45° + 30° + 60° = 135 °.

Равные углы имеют равную градусную меру.

Обозначение углов на чертеже

Чертеж помогает решать задачки по геометрии в разы быстрее. Чтобы наглядно изображать углы и прочие фигуры, придумали даже отдельное направление — геометрический чертеж.

Задачи с углами могут быть разными, и не всегда есть возможность правильно изобразить и отметить угол. Вот что важно запомнить при обозначении лучей и углов:

• Равные углы обозначают одинаковым количеством дуг.
• Неравные углы обозначают разным количеством дуг, чтобы они отличались между собой.

На чертеже отмечены три неравных угла:

Для обозначения на чертеже более трех углов используем разные виды дуг: волнистые, зубчатые.

Обозначать углы можно разными цветами. Главное, чтобы было просто и броско. При этом не обязательно отмечать все-все углы — достаточно только тех, которые нам нужны для решения задачки.

 

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Лидия Казанцева

Автор Skysmart

К предыдущей статье

257. 5K

Наибольший общий делитель (НОД), свойства и формулы

К следующей статье

Неполные квадратные уравнения

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Прямой угол — определение, примеры

Прямой угол — это угол, равный 90 градусам. Это наиболее часто встречающийся ракурс в нашей повседневной жизни. Его можно увидеть в углах комнаты, краях ящиков, на экране мобильного телефона и так далее. Стороны квадрата и прямоугольника всегда образуют прямой угол друг с другом. В радианах это представлено как π/2. Давайте обсудим больше об определении прямого угла

, форме прямого угла вместе с 9Примеры 0003 прямого угла в этой статье.

1.	Что такое прямой угол?
2.	Прямоугольные формы
3.	Калькулятор прямого угла
4.	Треугольник с прямым углом
5.	Часто задаваемые вопросы о прямом угле

Что такое прямой угол?

Прямой угол равен 90°. Когда два луча пересекаются и образуют угол 90° или перпендикулярны друг другу в точке пересечения, говорят, что они образуют прямой угол.

Определение прямого угла

Угол, образованный двумя перпендикулярными друг другу прямыми, называется прямым углом. Прямой угол равен 90° и имеет форму буквы «L».

Градус прямого угла

Градус прямого угла равен 90°. Именно по этой причине 90° известен как прямой угол. На следующем рисунке АВ и ВС образуют прямой угол АВС.

Прямоугольные формы

Прямой угол похож на букву L.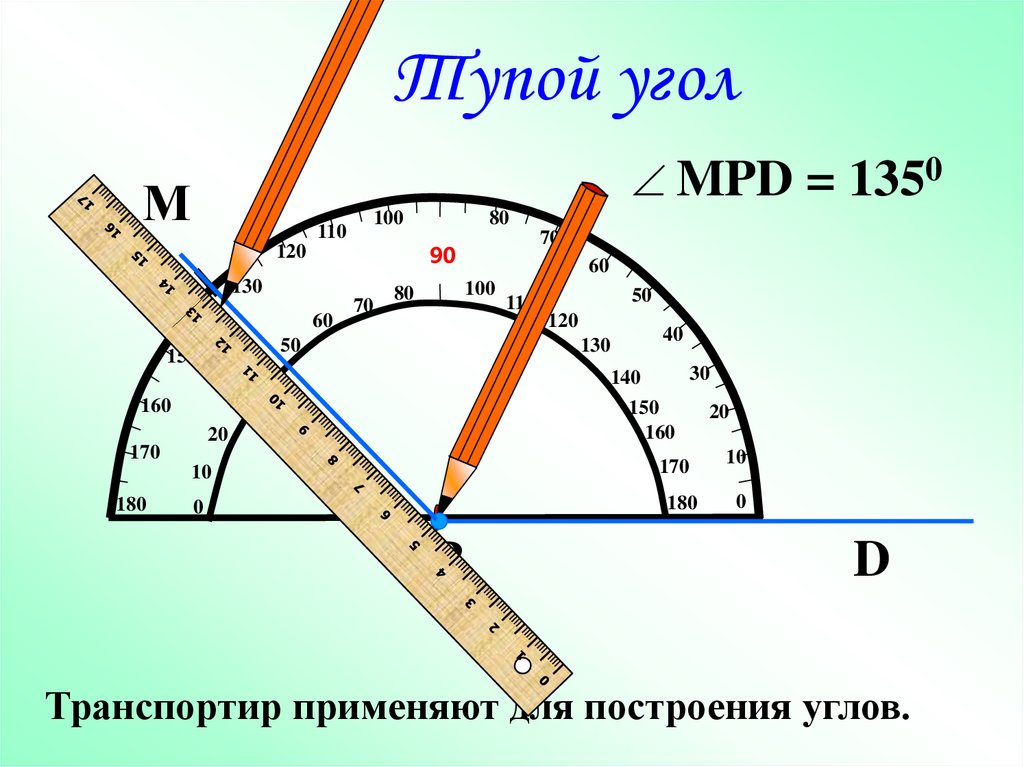 Его можно наблюдать во многих формах, например, угол, образуемый стрелками часов в 15:00. Давайте посмотрим на несколько примеров прямого угла в реальной жизни.

Примеры прямых углов в реальной жизни

Мы можем видеть много примеров прямых углов в реальной жизни. Некоторые из них приведены ниже.

• Края двери образуют прямой угол.
• Четыре грани телевизора.
• Угол стула.
• Края мобильного экрана.

Попробуйте определить и заметить прямые углы в следующих формах.

Калькулятор прямого угла

Некоторыми устройствами, используемыми для измерения прямого угла, являются транспортиры, угольники и угольники. Калькуляторы прямых углов используются для проверки, является ли данный угол прямым углом или нет. Мы выравниваем стороны заданных квадратов с заданным углом и проверяем, совпадает ли угол со сторонами заданных квадратов. Точно так же мы используем пробный квадрат, чтобы проверить, соответствует ли заданный угол форме сторон пробного квадрата.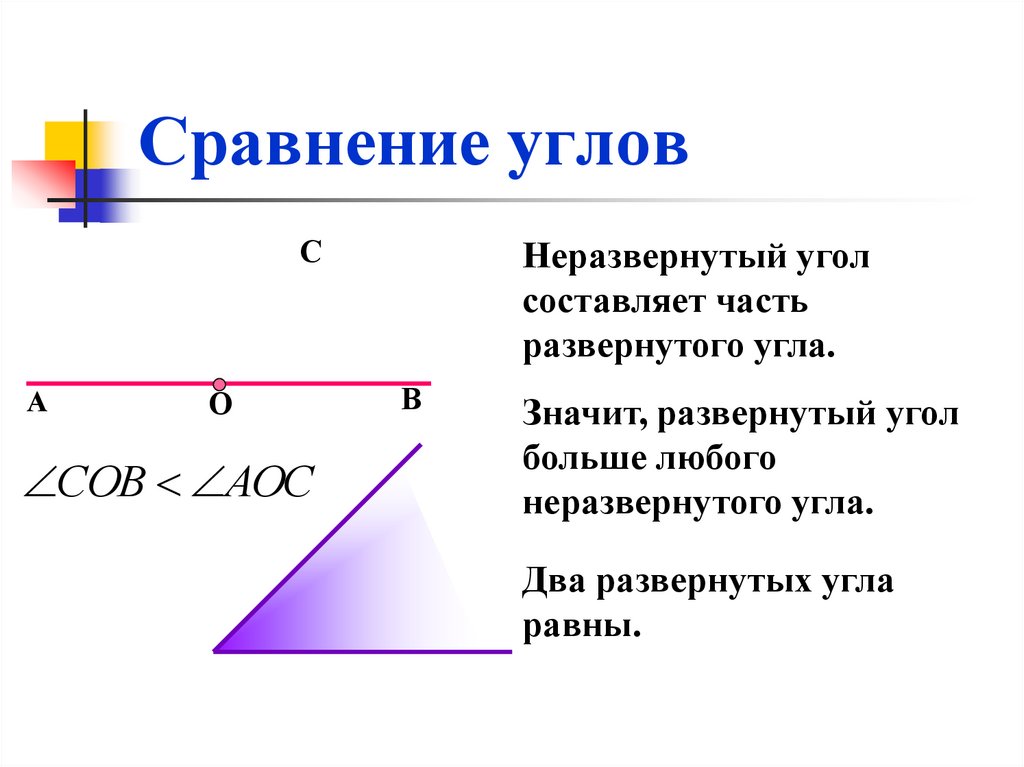 Базовая линия транспортира должна совпадать с основанием данного неизвестного угла, а затем мы проверяем, проходит ли другой луч угла точно из 9Отметка 0 градусов на транспортире или нет. Если луч проходит через отметку 90 градусов, то это прямой угол, иначе нет.

Наиболее часто используемые калькуляторы прямых углов показаны ниже:

Треугольник с прямым углом

Есть еще одно место, где используется прямой угол, и это прямоугольный треугольник. Если среди трех углов треугольника один угол равен 90°, то такой треугольник называется прямоугольным. Так как три внутренних угла прямоугольного треугольника в сумме дают 180°, и если один угол всегда равен 90°, то два других угла всегда должны составлять 90°.

Советы и подсказки по прямому углу:

Вот несколько моментов, которые следует помнить при изучении прямого угла:

• квадраты.
• Наиболее распространенными примерами прямых углов являются края двери, четыре края телевизора, 9:30 аналоговых часов и угол ноутбука.

☛ Статьи по теме

• Калькулятор прямоугольного треугольника
• Формулы прямоугольного треугольника
• Полный угол
• Прямоугольный
• Угол рефлекса

 

Примеры прямых углов

1. Пример 1: Укажите истинное или ложное отношение к прямым углам.

   а.) У квадрата 4 прямых угла.

   b.) Чтобы получить 180°, необходимо 2 прямых угла.

   c.) Буква «S» английского алфавита обозначает прямой угол.

   Решение:

   а.) Верно, у квадрата 4 внутренних угла, и все они прямые.

   b.) Верно, чтобы получить 180°, нужно 2 прямых угла, потому что 90° + 90° = 180°

   c.) Неверно, буква «S» в английском алфавите не образует прямого угла. Однако несколько букв с прямыми углами — это T, L, H и E.

   .

2. Пример 2: Найдите угол между стрелками часов в 15:00. и 21:00

   Решение:

   На рисунке видно, что две стрелки часов образуют L-образный угол, который является прямым углом.

   Ответ: Угол, образованный часами в 15:00. и 21:00 является прямым углом.

3. Пример 3: Если сумма двух углов ∠1 и ∠2 является прямым углом, а ∠2 составляет 30°, какова будет величина ∠1?

   Решение:

   Дано, что ∠2 = 30°, а ∠1 + ∠2 = 90°. Подставив значение ∠2 в уравнение, мы получим ∠1 + 30° = 90°.

   ⇒ ∠1 = 90° — 30°

   ⇒ ∠1 = 60°

   Следовательно, значение ∠1 равно 60°.

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы по прямому углу

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о прямом угле

Что такое прямой угол в математике?

Прямой угол — это угол со значением, равным 90°.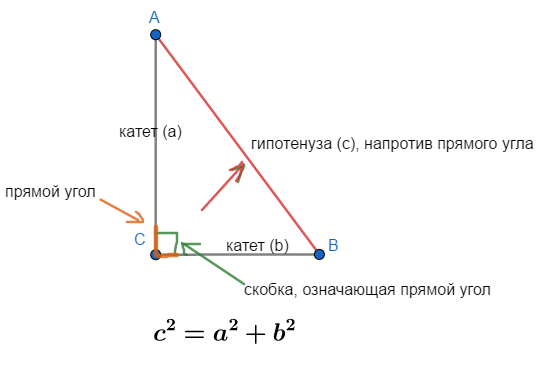 Когда два луча пересекаются и образуют в точке пересечения угол 90°, говорят, что они образуют прямой угол. Это наиболее часто встречающийся ракурс в нашей повседневной жизни. Мы можем видеть его во многих местах, таких как углы окна, края шкафа, экран мобильного телефона и так далее.

Сколько градусов у прямого угла?

Прямой угол равен 90 градусам. Он образуется, когда две линии пересекаются друг с другом под углом 90 градусов.

Какой угол прямой?

Когда два луча встречаются под углом 90°, они образуют прямой угол. В радианах это представлено как π/2.

Как определить прямой угол?

Прямой угол легко идентифицировать по букве L. Это угол между ногой и плечом буквы L. Если букву L можно образовать в любом месте данной формы, ее можно назвать прямым углом.

Прямой угол только 90 градусов?

Да, прямой угол всегда равен 90°. Он никогда не может быть иным, чем этот угол, и может быть представлен как π/2 в радианах. Любой угол меньше 90° является острым, а угол больше 90°, но меньше 180° — тупым.

Как измерить прямой угол?

Мы можем использовать транспортиры, квадраты или квадраты для измерения прямого угла. Нам просто нужно разместить их правильно и проверить размер и положение.

Что такое прямоугольный треугольник?

Прямоугольный треугольник — это треугольник, в котором один угол равен 90°. Поскольку угол в 90 градусов называется прямым углом, треугольник с прямым углом называется прямоугольным треугольником или прямоугольным треугольником.

Как выглядит прямой угол?

Прямой угол напоминает форму буквы «L». Его можно увидеть во многих реальных объектах вокруг нас, таких как края мобильного телефона, четыре края телевизора и так далее.

Прямой угол — определение, свойства, форма, примеры

В геометрии, когда два луча встречаются в одной точке, они образуют угол. Место встречи двух лучей называется вершиной.

Углы измеряются в градусах (символ: °) 

Некоторые распространенные типы углов: острые, прямые и тупые.

Прямой угол 

Когда две прямые пересекаются друг с другом под углом 90˚ или перпендикулярны друг другу в точке пересечения, они образуют прямой угол. Прямой угол обозначается символом ∟.

На данном изображении показаны различные образования прямого угла.

Мы умеем находить прямые углы в фигурах.

Квадрат или прямоугольник имеет четыре угла с прямыми углами.

Примеры прямых углов окружают нас повсюду. Мы можем видеть прямые углы в углах комнаты, книги, куба, окна и в некоторых других местах.

Вертикальная и горизонтальная линии составляют наиболее распространенные прямые углы. Однако пересекающиеся друг с другом диагональные линии также образуют прямые углы. Если провести диагонали квадрата, ромба или воздушного змея, угол при пересечении будет равен 90 градусов и, следовательно, угол прямой.

Связанные игры

Как нарисовать прямой угол с помощью транспортира?

1. Начните с рисования горизонтальной линии.

2. Теперь поместите транспортир на горизонтальную линию.

3. Измерьте угол 90° и отметьте его точкой.

4. Теперь с помощью масштаба проведите прямую линию от этой точки до горизонтальной линии.

Связанные рабочие листы

Интересные факты 

1. Все прямые углы одинаковы.
2. Все прямые углы соответствуют четверти полного оборота.
3. Все треугольники с одним прямым углом называются прямоугольными.

Решенные примеры

1. Найдите количество прямых углов на рисунке ниже.

Решение: Фигура выше представляет собой прямоугольник. Количество прямых углов на приведенном выше рисунке равно 4. Каждая сторона на рисунке встречается с соседней стороной в 90°.

2. Если две линии PQ и RS перпендикулярны, какова мера ∠SOT ?

Solution:

               Since, line PQ ⟂ line RS, m∠SOQ=90°

Moreover, m∠SOQ=m∠QOT+m∠SOT

90°=30°+м∠SOT

Следовательно, м∠SOT=90°-30°=60°

3. Сколько прямых углов на данной фигуре?

Решение:

На данном рисунке изображены 3 прямых и 2 тупых угла.

Практические задачи

1

Сколько прямых углов в квадрате?

4

2

3

1

Правильный ответ: 4
Пояснение: В квадрате 4 угла, и все они равны 90°.

2

Сколько прямых углов на данной фигуре?

2

4

3

Правильный ответ: 2
Пояснение: На данном рисунке изображен четырехугольник с двумя прямыми углами.

3

В прямоугольном треугольнике один угол равен 90°. Чему равна сумма мер двух других углов?

$\lt$ 90°

$\gt$ 90°

= 90°

$\gt$ 180°

Правильный ответ: = 90°
Пояснение: сумма трех внутренних углов любого треугольника до 180°. Так как один из внутренних углов прямоугольного треугольника равен 90°, сумма двух других внутренних углов должна составлять 90°.

4

Сколько прямых углов нужно, чтобы получить угол 180°?

3

6

5

2

Правильный ответ: 2
Пояснение: Два прямых угла вместе образуют угол 180°.