Cos 330 градусов: Чему равен косинус 330° градусов

2

Формулы приведения как определить знак. Формулы приведения

Тригонометрия.Формулы приведения.

Формулы приведения не нужно учить их нужно понять. Понять алгоритм их вывода. Это очень легко!

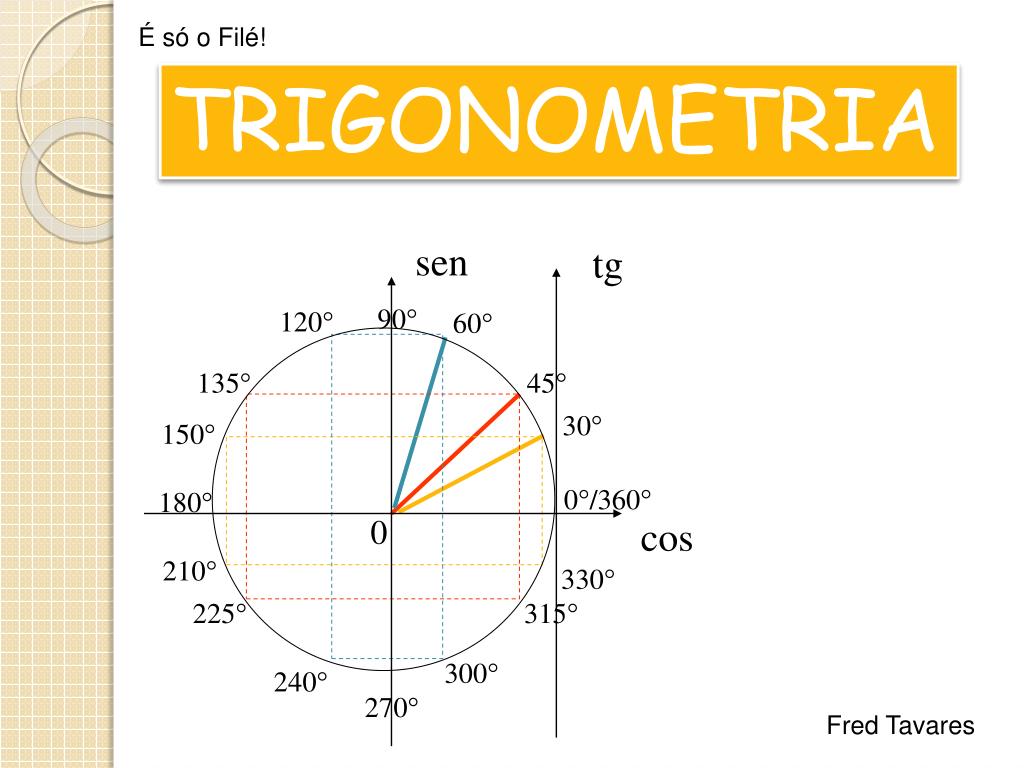
Возьмем единичную окружность и расставим все градусные меры (0°; 90°; 180°; 270°; 360°) на ней.

Разберем в каждой четверти функции sin(a) и cos(a).

Запомним, что функцию sin(a) смотрим по оси Y, а функцию cos(a) по оси X.

В первой четверти видно, что функция sin(a)>0
И функция cos(a)>0
Первую четверть можно описать через градусную меру, как (90-α) или (360+α).

Во второй четверти видно, что функция sin(a)>0 , потому что ось Y положительна в этой четверти.
А функция cos(a) , потому что ось X отрицательна в этой четверти.
Вторую четверть можно описать через градусную меру, как (90+α) или (180-α).

В третьей четверти видно, что функции sin(a) Третья четверть можно описать через градусную меру, как (180+α) или (270-α).

В четвертой четверти видно, что функция sin(a) , потому что ось Y отрицательна в этой четверти.
А функция cos(a)>0 , потому что ось X положительна в этой четверти.
Четвертую четверть можно описать через градусную меру, как (270+α) или (360-α).

Теперь рассмотрим сами формулы приведения.

Запомним простой алгоритм :
1. Четверть. (Всегда смотрите в какой вы четверти находитесь).
2. Знак. (Относительно четверти смотрите положительны или отрицательный функции косинуса или синуса).
3. Если у вас есть в скобочках (90° или π/2) и (270° или 3π/2), то функция меняется .

И так начнем разбирать по четвертям данный алгоритм.

Выясни чему будет равно выражение cos(90-α)
Рассуждаем по алгоритму:
1. Четверть первая.

Будет cos(90-α) = sin(α)

Выясни чему будет равно выражение sin(90-α)

Рассуждаем по алгоритму:
1. Четверть первая.

Будет sin(90-α) = cos(α)

Выясни чему будет равно выражение cos(360+α)
Рассуждаем по алгоритму:
1. Четверть первая.
2. В первой четверти знак у функции косинуса положительный.

Будет cos(360+α) = cos(α)

Выясни чему будет равно выражение sin(360+α)
Рассуждаем по алгоритму:
1. Четверть первая.
2. В первой четверти знак у функции синуса положительный.
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет sin(360+α) = sin(α)

Выясни чему будет равно выражение cos(90+α)
Рассуждаем по алгоритму:
1. Четверть вторая.

3. В скобочках есть (90° или π/2), то функция меняется с косинуса на синус.
Будет cos(90+α) = -sin(α)

Выясни чему будет равно выражение sin(90+α)
Рассуждаем по алгоритму:
1. Четверть вторая.

3. В скобочках есть (90° или π/2), то функция меняется с синуса на косинус.
Будет sin(90+α) = cos(α)

Выясни чему будет равно выражение cos(180-α)
Рассуждаем по алгоритму:
1. Четверть вторая.
2. Во второй четверти знак у функции косинуса отрицательный.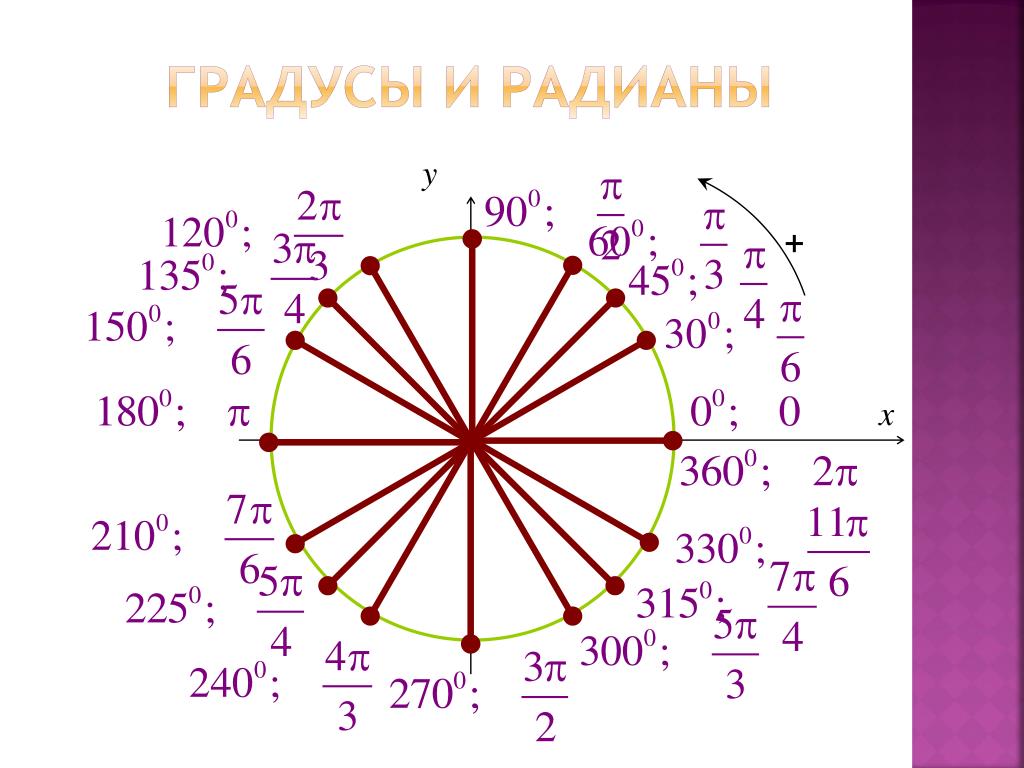
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет cos(180-α) = cos(α)

Выясни чему будет равно выражение sin(180-α)
Рассуждаем по алгоритму:
1. Четверть вторая.
2. Во второй четверти знак у функции синуса положительный.
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет sin(180-α) = sin(α)

Рассуждаю про третью и четвертую четверть подобным образом составим таблицу:

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

Определение. Формулами приведения называют формулы, которые позволяют перейти от тригонометрических функций вида к функциям аргумента . С их помощью синус, косинус, тангенс и котангенс произвольного угла можно привести к синусу, косинусу, тангенсу и котангенсу угла из интервала от 0 до 90 градусов (от 0 до радиан). Таким образом, формулы приведения позволяют нам переходить к работе с углами в пределах 90 градусов, что, несомненно, очень удобно.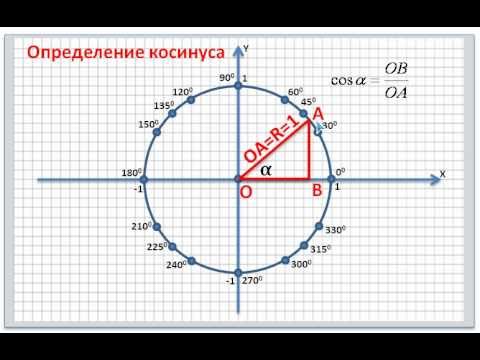

Формулы приведения:

Для использования формул приведения существует два правила.

1. Если угол можно представить в виде (π/2 ±a) или (3*π/2 ±a), то название функции меняется sin на cos, cos на sin, tg на ctg, ctg на tg. Если же угол можно представить в виде (π ±a) или (2*π ±a), то

название функции остается без изменений.

Посмотрите на рисунок ниже, там схематично изображено, когда следует менять знак, а когда нет

2. Знак приведенной функции остается прежним. Если исходная функция имела знак «плюс», то и приведенная функция имеет знак «плюс». Если исходная функция имела знак «минус», то и приведенная функция имеет знак «минус».

На рисунке ниже представлены знаки основных тригонометрических функций в зависимости от четверти.

Пример:

Вычислить

Воспользуемся формулами приведения:

Sin(150˚) находится во второй четверти, по рисунку видим что знак sin в этой четверти равен «+».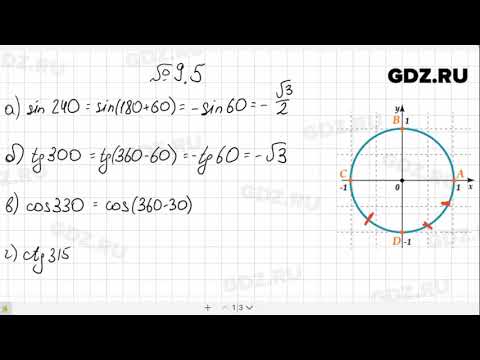 Значит у приведенной функции тоже будет знак «+». Это мы применили второе правило.

Теперь 150˚ = 90˚ +60˚. 90˚ это π/2. То есть имеем дело со случаем π/2+60, следовательно по первому правилу меняем функцию с sin на cos. В итоге получаем Sin(150˚) = cos(60˚) = ½.

Формулы приведения — это соотношения, которые позволяют перейти от синус, косинус, тангенс и котангенс с углами `\frac {\pi}2 \pm \alpha`, `\pi \pm \alpha`, `\frac {3\pi}2 \pm \alpha`, `2\pi \pm \alpha` к этим же функциям угла `\alpha`, который находится в первой четверти единичной окружности. Таким образом, формулы приведения «приводят» нас к работе с углами в пределе от 0 до 90 градусов, что очень удобно.

Всех вместе формул приведения есть 32 штуки. Они несомненно пригодятся на ЕГЭ, экзаменах, зачетах. Но сразу предупредим, что заучивать наизусть их нет необходимости! Нужно потратить немного времени и понять алгоритм их применения, тогда для вас не составит труда в нужный момент вывести необходимое равенство. \circ \pm \alpha`):

`sin(2\pi — \alpha)=-sin \ \alpha;` ` sin(2\pi + \alpha)=sin \ \alpha`

`cos(2\pi — \alpha)=cos \ \alpha;` ` cos(2\pi + \alpha)=cos \ \alpha`
`tg(2\pi — \alpha)=-tg \ \alpha;` ` tg(2\pi + \alpha)=tg \ \alpha`
`ctg(2\pi — \alpha)=-ctg \ \alpha;` ` ctg(2\pi + \alpha)=ctg \ \alpha`

Часто можно встретить формулы приведения в виде таблицы, где углы записаны в радианах:

Чтобы воспользоваться ею, нужно выбрать строку с нужной нам функцией, и столбец с нужным аргументом. Например, чтобы узнать с помощью таблицы, чему будет равно ` sin(\pi + \alpha)`, достаточно найти ответ на пересечении строки ` sin \beta` и столбца ` \pi + \alpha`. Получим ` sin(\pi + \alpha)=-sin \ \alpha`.

И вторая, аналогичная таблица, где углы записаны в градусах:

Мнемоническое правило формул приведения или как их запомнить

Как мы уже упоминали, заучивать все вышеприведенные соотношения не нужно. Если вы внимательно на них посмотрели, то наверняка заметили некоторые закономерности.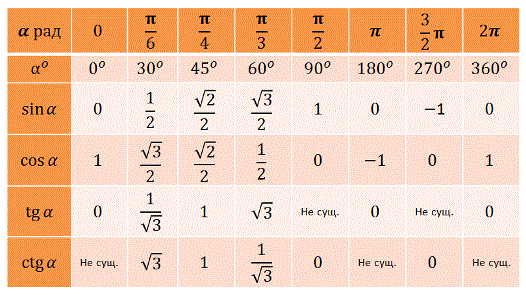

Они позволяют нам сформулировать мнемоническое правило (мнемоника — запоминать), с помощью которого легко можно получить любую с формул приведения.

Сразу отметим, что для применения этого правила нужно хорошо уметь определять (или запомнить) знаки тригонометрических функций в разных четвертях единичной окружности.
Само привило содержит 3 этапа:

1. 1. Аргумент функции должен быть представлен в виде `\frac {\pi}2 \pm \alpha`, `\pi \pm \alpha`, `\frac {3\pi}2 \pm \alpha`, `2\pi \pm \alpha`, причем `\alpha` — обязательно острый угол (от 0 до 90 градусов).
   2. Для аргументов `\frac {\pi}2 \pm \alpha`, `\frac {3\pi}2 \pm \alpha` тригонометрическая функция преобразуемого выражения меняется на кофункцию, то есть противоположную (синус на косинус, тангенс на котангенс и наоборот). Для аргументов `\pi \pm \alpha`, `2\pi \pm \alpha` функция не меняется.
   3. Определяется знак исходной функции. Полученная функция в правой части будет иметь такой же знак.

Чтобы посмотреть, как на практике можно применить это правило, преобразим несколько выражений:

1. \circ`, их значения не изменятся, если на эти величины увеличить или уменьшить аргумент.

Исходя из этого, наше выражение можно записать следующим образом: `cos (\pi+(\frac{\pi}2-\alpha)`. Применив два раза мнемоническое правило, получим: `cos (\pi+(\frac{\pi}2-\alpha)= — cos (\frac{\pi}2-\alpha)= — sin \alpha`.

Ответ: `cos(\frac {7\pi}2 — \alpha)=- sin \alpha`.

Лошадиное правило

Второй пункт вышеописанного мнемонического правила еще называют лошадиным правилом формул приведения. Интересно, почему лошадиным?

Итак, мы имеем функции с аргументами `\frac {\pi}2 \pm \alpha`, `\pi \pm \alpha`, `\frac {3\pi}2 \pm \alpha`, `2\pi \pm \alpha`, точки `\frac {\pi}2`, `\pi`, `\frac {3\pi}2`, `2\pi` — ключевые, они располагаются на осях координат. `\pi` и `2\pi` на горизонтальной оси абсцисс, а `\frac {\pi}2` и `\frac {3\pi}2` на вертикальной оси ординат.

Задаем себе вопрос: «Меняется ли функция на кофункцию?». Чтобы ответить на этот вопрос, нужно подвигать головой вдоль оси, на которой расположена ключевая точка.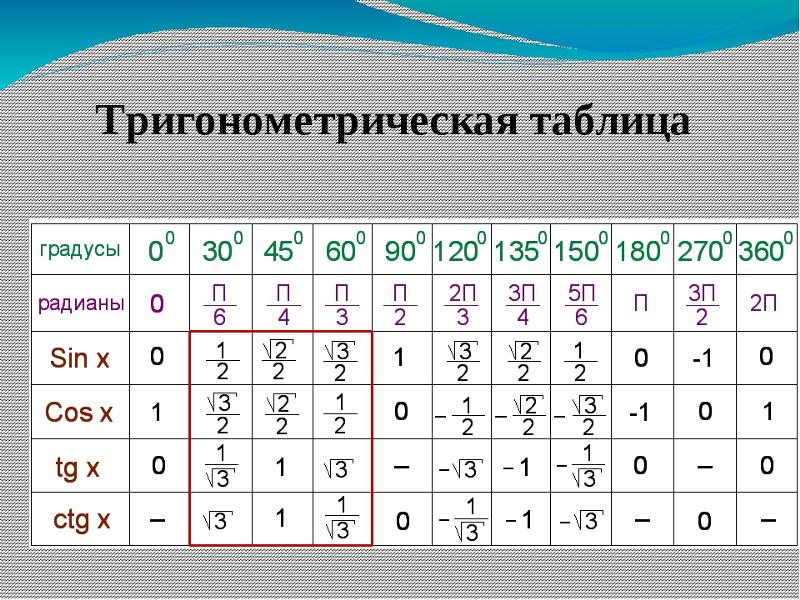 \circ=-\frac{\sqrt 3}2`.

Пример 2. Выразив косинус через синус по формулам приведения, сравнить числа: 1) `sin \frac {9\pi}8` и `cos \frac {9\pi}8`; 2) `sin \frac {\pi}8` и `cos \frac {3\pi}10`.

Решение: 1)`sin \frac {9\pi}8=sin (\pi+\frac {\pi}8)=-sin \frac {\pi}8`

`cos \frac {9\pi}8=cos (\pi+\frac {\pi}8)=-cos \frac {\pi}8=-sin \frac {3\pi}8`

`-sin \frac {\pi}8> -sin \frac {3\pi}8`

`sin \frac {9\pi}8>cos \frac {9\pi}8`.

2) `cos \frac {3\pi}10=cos (\frac {\pi}2-\frac {\pi}5)=sin \frac {\pi}5`

`sin \frac {\pi}8

`sin \frac {\pi}8

Докажем сначала две формулы для синуса и косинуса аргумента `\frac {\pi}2 + \alpha`: ` sin(\frac {\pi}2 + \alpha)=cos \ \alpha` и` cos(\frac {\pi}2 + \alpha)=-sin \ \alpha`. Остальные выводятся из них.

Возьмем единичную окружность и на ней точку А с координатами (1,0). Пусть после поворота на угол `\alpha` она перейдет в точку `А_1(х, у)`, а после поворота на угол `\frac {\pi}2 + \alpha` в точку `А_2(-у,х)`.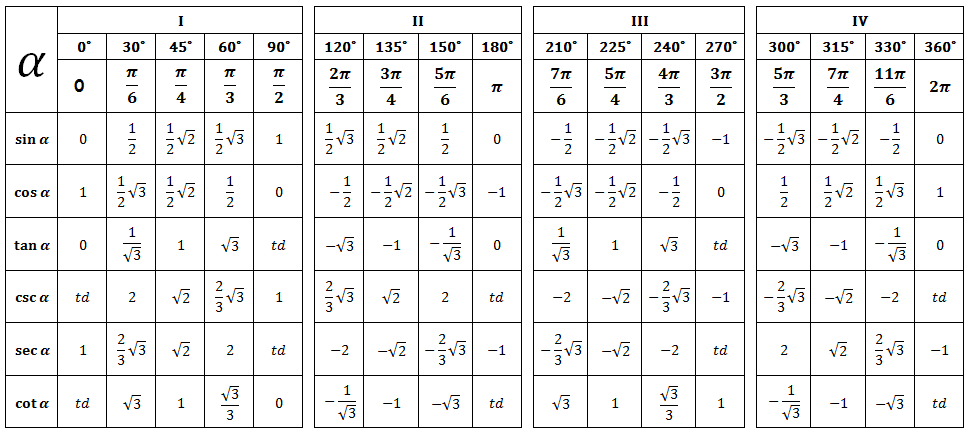 Опустив перпендикуляры с этих точек на прямую ОХ, увидим, что треугольники `OA_1H_1` и `OA_2H_2` равны, поскольку равны их гипотенузы и прилежащие углы. Тогда исходя из определений синуса и косинуса можно записать `sin \alpha=у`, `cos \alpha=х`, ` sin(\frac {\pi}2 + \alpha)=x`, ` cos(\frac {\pi}2 + \alpha)=-y`. Откуда можно записать, что ` sin(\frac {\pi}2 + \alpha)=cos \alpha` и ` cos(\frac {\pi}2 + \alpha)=-sin \alpha`, что доказывает формулы приведения для синуса и косинуса угла `\frac {\pi}2 + \alpha`.

Выходя из определения тангенса и котангенса, получим ` tg(\frac {\pi}2 + \alpha)=\frac {sin(\frac {\pi}2 + \alpha)}{cos(\frac {\pi}2 + \alpha)}=\frac {cos \alpha}{-sin \alpha}=-ctg \alpha` и ` сtg(\frac {\pi}2 + \alpha)=\frac {cos(\frac {\pi}2 + \alpha)}{sin(\frac {\pi}2 + \alpha)}=\frac {-sin \alpha}{cos \alpha}=-tg \alpha`, что доказывает формулы приведения для тангенса и котангенса угла `\frac {\pi}2 + \alpha`.

Чтобы доказать формулы с аргументом `\frac {\pi}2 — \alpha`, достаточно представить его, как `\frac {\pi}2 + (-\alpha)` и проделать тот же путь, что и выше. Например, `cos(\frac {\pi}2 — \alpha)=cos(\frac {\pi}2 + (-\alpha))=-sin(-\alpha)=sin(\alpha)`.

Углы `\pi + \alpha` и `\pi — \alpha` можно представить, как `\frac {\pi}2 +(\frac {\pi}2+\alpha)` и `\frac {\pi}2 +(\frac {\pi}2-\alpha)` соответственно.

А `\frac {3\pi}2 + \alpha` и `\frac {3\pi}2 — \alpha` как `\pi +(\frac {\pi}2+\alpha)` и `\pi +(\frac {\pi}2-\alpha)`.

Урок и презентация на тему: «Применение формул приведения при решении задач»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса
1С: Школа. Интерактивные задания на построение для 7-10 классов
1С: Школа. Решаем задачи по геометрии. Интерактивные задания на построение в пространстве для 10–11 классов

Что будем изучать:
1. Немного повторим.
2. Правила для формул приведения.
3. Таблица преобразований для формул приведения.
4. Примеры.

Повторение тригонометрических функций

Ребята, с формулами привидения вы уже сталкивались, но так их еще не называли. Как думаете: где?

Посмотрите на наши рисунки. Правильно, когда вводили определения тригонометрических функций.

Правило для формул приведения

Давайте введем основное правило: Если под знаком тригонометрической функции содержится число вида π×n/2 + t, где n – любое целое число, то нашу тригонометрическую функцию можно привести к более простому виду, которая будет содержать только аргумент t. Такие формулы и называют формулами привидения.

Вспомним некоторые формулы:

• sin(t + 2π*k) = sin(t)
• cos(t + 2π*k) = cos(t)
• sin(t + π) = -sin(t)
• cos(t + π) = -cos(t)
• sin(t + π/2) = cos(t)
• cos(t + π/2) = -sin(t)
• tg(t + π*k) = tg(x)
• ctg(t + π*k) = ctg(x)

формул привидения очень много, давайте составим правило по которому будем определять наши тригонометрические функции при использовании формул привидения :

• Если под знаком тригонометрической функции содержатся числа вида: π + t, π — t, 2π + t и 2π — t, то функция не изменится, то есть, например, синус останется синусом, котангенс останется котангенсом.
• Если под знаком тригонометрической функции содержатся числа вида: π/2 + t, π/2 — t,
  3π/2 + t и 3π/2 — t, то функция изменится на родственную, т. е. синус станет косинусом, котангенс станет тангенсом.
• Перед получившийся функцией, надо поставить тот знак, который имела бы преобразуемая функция при условии 0

Эти правила применимы и когда аргумент функции задан в градусах!

Так же мы можем составить таблицу преобразований тригонометрических функций:

Примеры применения формул приведения

1.Преобразуем cos(π + t). Наименование функции остается, т.е. получим cos(t). Далее предположим, что π/2

2. Преобразуем sin(π/2 + t). Наименование функции изменяется, т.е. получим cos(t). Далее предположим что 0 sin(t + π/2) = cos(t)

3. Преобразуем tg(π + t). Наименование функции остается, т.е. получим tg(t). Далее предположим, что 0

4. Преобразуем ctg(270 0 + t). Наименование функции изменяется, то есть получим tg(t). Далее предположим что 0

Задачи с формулами приведения для самостоятельного решения

Ребята, преобразуйте самостоятельно, используя наши правила:

1) tg(π + t),
2) tg(2π — t),
3) ctg(π — t),
4) tg(π/2 — t),
5) ctg(3π + t),
6) sin(2π + t),
7) sin(π/2 + 5t),
8) sin(π/2 — t),
9) sin(2π — t),
10) cos(2π — t),
11) cos(3π/2 + 8t),
12) cos(3π/2 — t),
13) cos(π — t).

И еще одна задача B11 на ту же тему — из реального ЕГЭ по математике.

Задача. Найдите значение выражения:

В этом коротком видеоуроке мы узнаем, как применять формулы приведения для решения реальных задач B11 из ЕГЭ по математике. Как вы видите, перед нами — два тригонометрических выражения, каждое из которых содержит синусы и косинусы, а также довольно зверские числовые аргументы.

Прежде чем решать эти задачи, давайте вспомним, что такое формулы приведения. Итак, если у нас есть выражения вида:

То мы можем избавиться от первого слагаемого (вида k · π/2) по специальным правилам.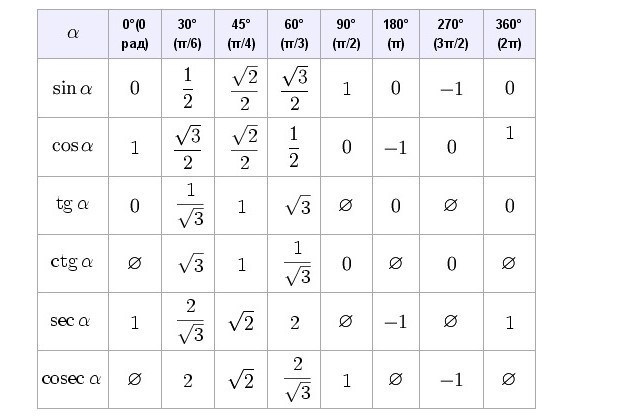 Начертим тригонометрическую окружность, отметим на ней основные точки: 0, π/2; π; 3π/2 и 2π. Затем смотрим на первое слагаемое под знаком тригонометрической функции. Имеем:

1. Если интересующее нас слагаемое лежит на вертикальной оси тригонометрического круга (например: 3π/2; π/2 и т.д.), то исходная функция заменяется на ко-функцию: синус заменяется косинусом, а косинус — наоборот, синусом.
2. Если же наше слагаемое лежит на горизонтальной оси, то исходная функция не меняется. Просто убираем первое слагаемое в выражении — и все.

Таким образом, мы получим тригонометрическую функцию, не содержащую слагаемых вида k · π/2. Однако на этом работа с формулами приведения не заканчивается. Дело в том, что перед нашей новой функцией, полученной после «отбрасывания» первого слагаемого, может стоять знак плюс или минус. Как определить этот знак? Вот сейчас и узнаем.

Представим, что угол α, оставшийся внутри тригонометрической функции после преобразований, имеет очень малую градусную меру.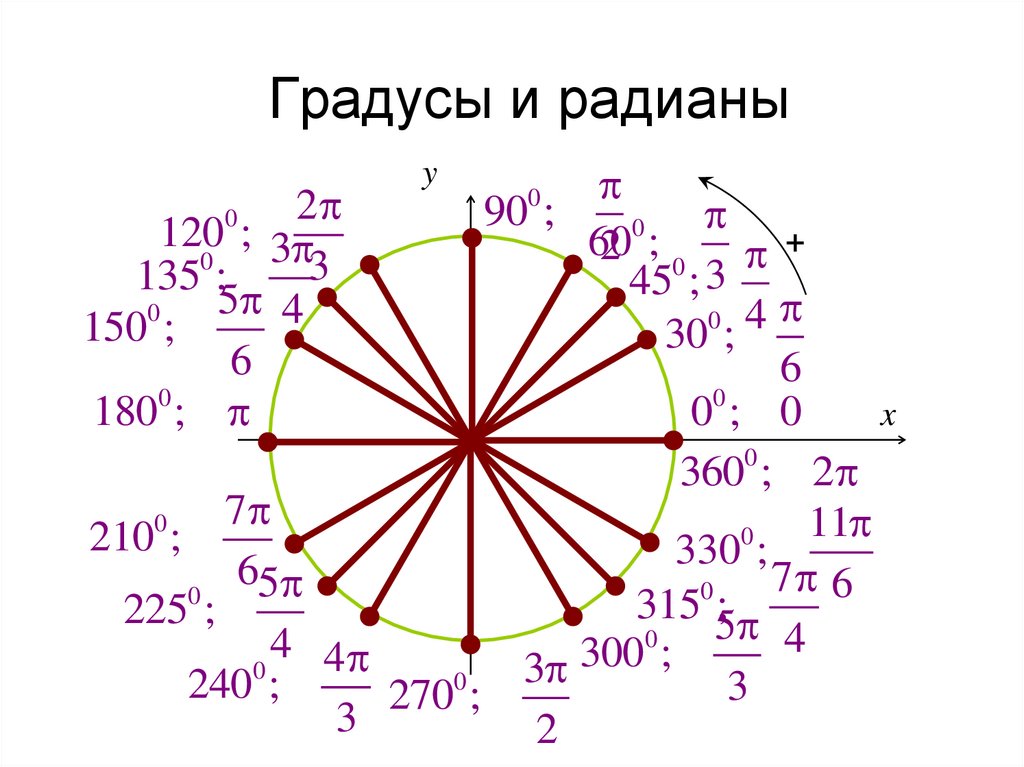 Но что значит «малая мера»? Допустим, α ∈ (0; 30°) — этого вполне достаточно. Рассмотрим для примера функцию:

Тогда, следуя нашим предположениям, что α ∈ (0; 30°), заключаем, что угол 3π/2 − α лежит в третьей координатной четверти, т.е. 3π/2 − α ∈ (π; 3π/2). Вспоминаем знак исходной функции, т.е. y = sin x на этом интервале. Очевидно, что синус в третьей координатной четверти отрицателен, поскольку по определению синус — это ордината конца подвижного радиуса (короче синус — это координата y ). Ну, а координата y в нижней полуплоскости всегда принимает отрицательные значения. Значит, и в третьей четверти y тоже отрицателен.

На основании этих размышлений мы можем записать окончательное выражение:

Задача B11 — 1 вариант

Вот эти же самые приемы вполне подходят для решения задачи B11 из ЕГЭ по математике. Разница лишь в том, что во многих реальных задачах B11 вместо радианной меры (т.е. чисел π, π/2, 2π и т.д.) используется градусная мера (т.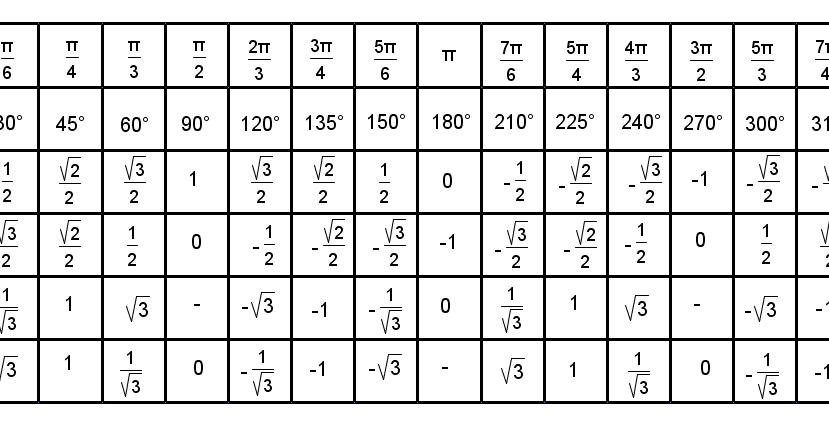 е. 90°, 180°, 270° и т.д.). Давайте посмотрим на первую задачу:

Сначала разберемся с числителем. cos 41° — это нетабличное значение, поэтому мы ничего не можем сделать с ним. Пока так и оставим.

Теперь смотрим на знаменатель:

sin 131° = sin (90° + 41°) = cos 41°

Очевидно, что перед нами формула приведения, поэтому синус заменился на косинус. Кроме того, угол 41° лежит на отрезке (0°; 90°), т.е. в первой координатной четверти — именно так, как требуется для применения формул приведения. Но тогда 90° + 41° — это вторая координатная четверть. Исходная функция y = sin x там положительна, поэтому мы и поставили перед косинусом на последнем шаге знак «плюс» (другими словами не поставили ничего).

Осталось разобраться с последним элементом:

cos 240° = cos (180° + 60°) = −cos 60° = −0,5

Здесь мы видим, что 180° — это горизонтальная ось. Следовательно, сама функция не поменяется: был косинус — и останется тоже косинус. Но вновь возникает вопрос: плюс или минус будет стоять перед полученным выражением cos 60°? Заметим, что 180° — это третья координатная четверть.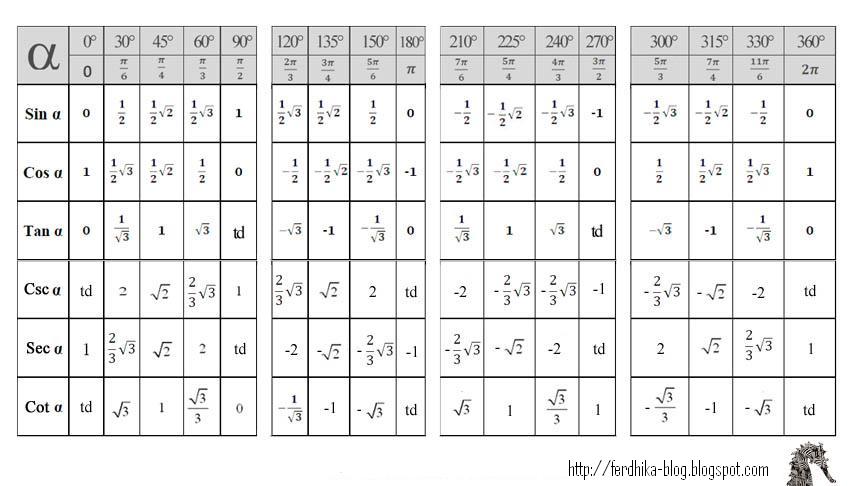 Косинус там отрицательный, следовательно, перед косинусом в итоге будет стоять знак «минус». Итого, получаем конструкцию −cos 60° = −0,5 — это табличное значение, поэтому все легко считается.

Теперь подставляем полученные числа в исходную формулу и получаем:

Как видим, число cos 41° в числителе и знаменателе дроби легко сокращается, и остается обычное выражение, которое равно −10. При этом минус можно либо вынести и поставить перед знаком дроби, либо «держать» рядом со вторым множителем до самого последнего шага вычислений. Ответ в любом случае получится −10. Все, задача B11 решена!

Задача B14 — 2 вариант

Переходим ко второй задаче. Перед нами снова дробь:

Ну, 27° у нас лежит в первой координатной четверти, поэтому здесь ничего менять не будем. А вот sin 117° надо расписать (пока без всякого квадрата):

sin 117° = sin (90° + 27°) = cos 27°

Очевидно, перед нами снова формула приведения : 90° — это вертикальная ось, следовательно, синус поменяется на косинус.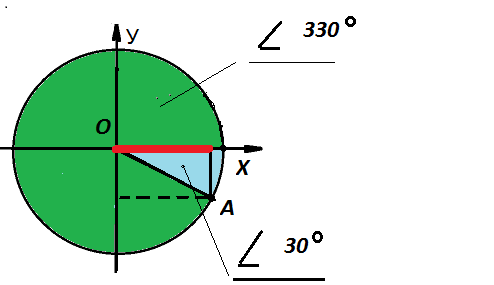 Кроме того, угол α = 117° = 90° + 27° лежит во второй координатной четверти. Исходная функция y = sin x там положительна, следовательно, перед косинусом после всех преобразований все равно остается знак «плюс». Другими словами, там ничего не добавляется — так и оставляем: cos 27°.

Возвращаемся к исходному выражению, которое требуется вычислить:

Как видим, в знаменателе после преобразований возникло основное тригонометрическое тождество: sin 2 27° + cos 2 27° = 1. Итого −4: 1 = −4 — вот мы и нашли ответ ко второй задаче B11.

Как видите, с помощью формул приведения такие задачи из ЕГЭ по математике решаются буквально в пару строчек. Никаких синусов суммы и косинусов разности. Все, что нам нужно помнить — это только тригонометрический круг.

Cos 330 градусов — Найдите значение Cos 330 градусов

LearnPracticeDownload

Значение cos 330 градусов равно 0,8660254. . . . Cos 330 градусов в радианах записывается как cos (330° × π/180°), то есть cos (11π/6) или cos (5,759586.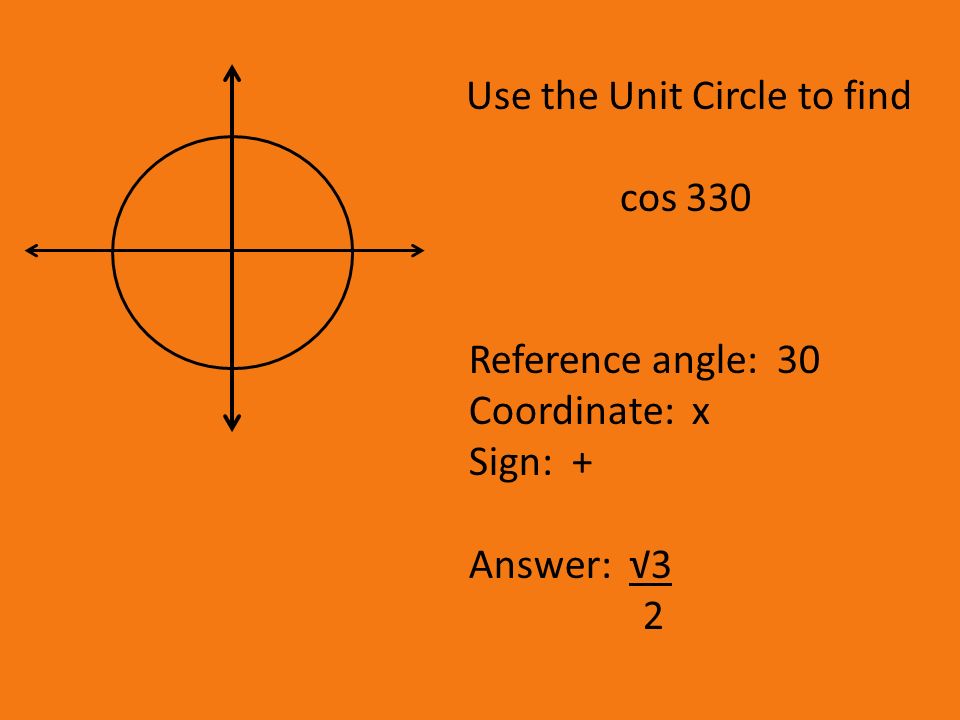 ..). В этой статье мы обсудим способы нахождения значения cos 330 градусов на примерах.

• Cos 330°: 0,8660254. . .
• Cos 330° в дробях: √3/2
• Cos (-330 градусов): 0,8660254. . .
• Cos 330° в радианах: cos (11π/6) или cos (5,7595865 . . .)

Каково значение Cos 330 градусов?

Значение cos 330 градусов в десятичной системе равно 0,866025403. . .. Cos 330 градусов также можно выразить с помощью эквивалента заданного угла (330 градусов) в радианах (5,75958 . . .)

Мы знаем, используя преобразование градусов в радианы, что θ в радианах = θ в градусах × (pi/ 180°)
⇒ 330 градусов = 330° × (π/180°) рад = 11π/6 или 5,7595. . .
∴ cos 330 ° = cos (5,7595) = √ 3/2 или 0,8660254. . .

Объяснение:

Для cos 330 градусов угол 330° лежит между 270° и 360° (четвертый квадрант). Поскольку функция косинуса положительна в четвертом квадранте, значение cos 330° = √3/2 или 0,8660254. . .
Поскольку функция косинуса является периодической функцией, мы можем представить cos 330° как cos 330 градусов = cos(330° + n × 360°), n ∈ Z.
⇒ cos 330° = cos 690° = cos 1050° и так далее.
Примечание: Поскольку косинус — четная функция, значение cos(-330°) = cos(330°).

Методы определения значения Cos 330 градусов

Функция косинуса положительна в 4-м квадранте. Значение cos 330° равно 0,86602. . .. Мы можем найти значение cos 330 градусов по:

• Используя Unit Circle
• Использование тригонометрических функций

Cos 330 градусов с использованием единичной окружности

Чтобы найти значение cos 330 градусов, используя единичную окружность:

• Поверните ‘r’ против часовой стрелки, чтобы образовать угол 330° с положительной осью x.
• Космос 330 градусов равен координате x (0,866) точки пересечения (0,866, -0,5) единичной окружности и r.

Следовательно, значение cos 330° = x = 0,866 (приблизительно)

Cos 330° в терминах тригонометрических функций

Используя формулы тригонометрии, мы можем представить cos 330 градусов как:

• ± √(1-sin²(330°))
• ± 1/√(1 + tan²(330°))
• ± кроватка 330°/√(1 + кроватка²(330°))
• ±√(косек²(330°) — 1)/косек 330°
• 1/сек 330°

Примечание. Поскольку 330° лежит в 4-м квадранте, окончательное значение cos 330° будет положительным.

Мы можем использовать тригонометрические тождества для представления cos 330° как

• -cos(180° — 330°) = -cos(-150°)
• -cos(180° + 330°) = -cos 510°
• sin(90° + 330°) = sin 420°
• sin(90° — 330°) = sin(-240°)

☛ Также проверьте:

• cos 90 градусов
• кос 20 градусов
• потому что 1 градус
• потому что 61 градус
• потому что 80 градусов
• потому что 68 градусов

Примеры использования Cos 330 градусов

1. Пример 1: Используя значение cos 330°, решите: (1-sin²(330°)).

   Решение:

   Мы знаем, (1-sin²(330°)) = (cos²(330°)) = 0,75
   ⇒ (1-sin²(330°)) = 0,75

2. Пример 2: Найдите значение cos 330°, если sec 330° равно 1,1547.

   Решение:

   Так как cos 330° = 1/сек 330°
   ⇒ cos 330° = 1/1,1547 = 0,866

3. Пример 3. Найдите значение 2 cos(330°)/3 sin(-240°).

   Решение:

   Используя тригонометрические тождества, мы знаем, что cos(330°) = sin(90° — 330°) = sin(-240°).
   ⇒ cos(330°) = sin(-240°)
   ⇒ Значение 2 cos(330°)/3 sin(-240°) = 2/3

перейти к слайдуперейти к слайдуперейти к слайду

 

Готовы увидеть мир глазами математика?

Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.

Запишитесь на бесплатный пробный урок

Часто задаваемые вопросы о Cos 330 Degrees

Что такое Cos 330 Degrees?

Cos 330 градусов — значение тригонометрической функции косинуса для угла, равного 330 градусам. Значение cos 330° равно √3/2 или 0,866 (приблизительно)

Как найти значение cos 330 градусов?

Значение cos 330 градусов можно рассчитать, построив угол 330° с осью x и затем найдя координаты соответствующей точки (0,866, -0,5) на единичной окружности. Значение cos 330° равно координате x (0,866). ∴ cos 330° = 0,866.

Как найти Cos 330° с точки зрения других тригонометрических функций?

Используя формулу тригонометрии, значение cos 330° может быть выражено через другие тригонометрические функции следующим образом:

• ± √(1-sin²(330°))
• ± 1/√(1 + tan²(330°))
• ± кроватка 330°/√(1 + кроватка²(330°))
• ± √(косек²(330°) — 1)/косек 330°
• 1/сек 330°

☛ Также проверьте: таблицу тригонометрии

Каково значение Cos 330° в пересчете на Sec 330°?

Поскольку функция секанса является обратной функцией косинуса, мы можем записать косинус 330° как 1/сек (330°). Значение sec 330° равно 1,154700.

Каково значение Cos 330 градусов по отношению к Cot 330°?

Мы можем представить функцию косинуса в терминах функции котангенса, используя тригонометрические тождества, cos 330° можно записать как -cot 330°/√(1 + cot²(330°)). Здесь значение cot 330° равно -1,73205.

 

Скачать БЕСПЛАТНЫЕ учебные материалы

Тригонометрия

Рабочие листы по математике и
визуальная программа

Как найти точное значение шести тригонометрических функций 330 градусов?

Подсказка: В этом вопросе нам дается значение степени, т. е. 330 градусов, и нас просят найти все остальные тригонометрические отношения. Сначала мы узнаем основные тригонометрические функции, т. е. sin, cos и Теперь, когда у нас есть значения $\sin\theta$ и $\cos\theta$, по этим значениям можно вычислить $\tan\theta$, и другие тригонометрические отношения можно рассчитать, найдя обратную величину этих тригонометрических отношений.