| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град.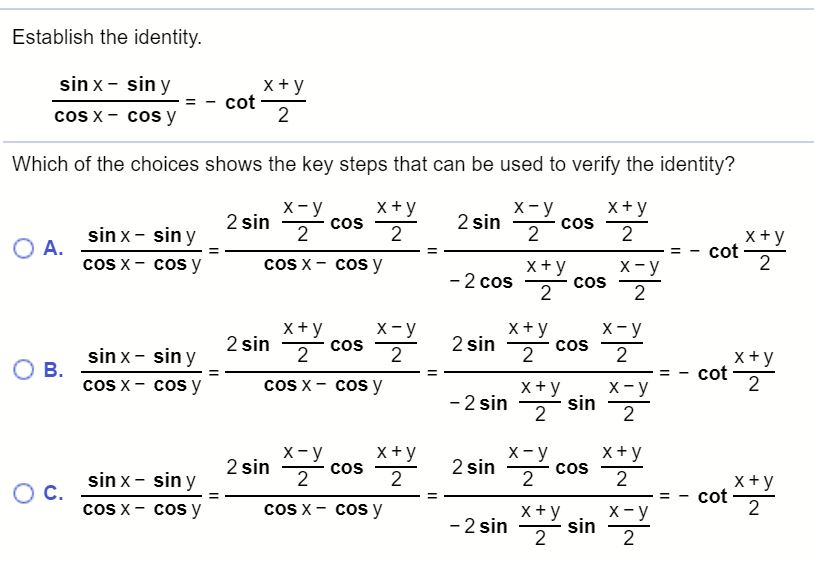 ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Формулы тригонометрии — презентация онлайн
Похожие презентации:
Формулы понижения степени
Решение уравнения cosx = a. Понятие арккосинуса числа
Тригонометрические формулы. (10 класс)
Итоговое повторение по курсу «Алгебра и начала анализа» 10 класс
Тождественные преобразования тригонометрических выражений. 9 класс
9 класс
Формулы сложения
Формулы сложения. Синус, косинус, тангенс суммы и разности аргументов
Задание В7, открытого банка ЕГЭ по математике
Формулы приведения
Решение уравнения cosx = a. Понятие арккосинуса числа
Формулы тригонометрии
Синус и косинус разности
аргументов
sin( x y ) sin x cos y cos x sin y
cos( x y ) cos x cos y sin x sin y
cos( x y ) cos x cos y sin x sin y
Пример 1
Вычислить : sin 75
sin 75 sin( 30 45 )
sin 30 cos 45 cos 30 sin 45
1 2
3 2
2 2
2 2
2
6
4
4
2 6
4
Пример 2
Вычислить : cos15
cos15 cos( 45 30 )
cos 45 cos 30 sin 45 sin 30
2 3
2 1
2 2
2 2
6
2
4
4
6 2
4
Пример 3
Вычислить : sin 48 cos12 cos 48 sin 12
sin 48 cos12 cos 48 sin 12
3
sin( 48 12 ) sin 60
2
Пример 4
Вычислить : cos(
3
y ), если
II
3
cos y , y
5 2
1
3
cos( y ) cos cos y sin sin y cos y
sin y
3
3
3
2
2
1
3
3 4
( )
3 4 3 3 4 3
22
5 2 2 5
10
10 10
sin у cos у 1
9
1
25
9
sin 2 у 1
25
sin 2 у
16
25
4
sin у
5
sin 2 у
Тангенс суммы и разности
аргументов
tgx tgy
tg ( x y )
1 tgx tgy
tgx tgy
tg ( x y )
1 tgx tgy
Котангенс суммы и разности
аргументов
ctgx ctgy 1
ctg ( x y )
ctgx ctgy
ctgx ctgy 1
ctg ( x y )
ctgx ctgy
Пример 1
Вычислить : tg 75
tg
30
tg
45
tg 75 tg (30 45 )
1 tg30 tg 45
1 3
1
1
3
1 3
3 1 3 3 1 1 3
3
:
1
3 1
3
3
3
3 1
3 1
1
1
3
3
Пример 2
II
3
Вычислить : tg ( x), если cos x , x
5 2
4
tgx
4
4
1
1 tgx
4
1
3 3 7
tg ( x)
: ( ) 7
4
1
1
tgx
4
3
3
1 tg tgx
1
3
3
4
sin 2 x cos 2 x 1
9
2
sin x
1
25
9
sin 2 x 1
sin x
4
3
4
25
tgx
: ( )
tg
16
sin x
25
4
sin x
5
2
1
cos x
5
5
3
Формулы двойного аргумента
sin 2x 2 sin x cos x cos 2 x cos x sin x
2
2tg x
tg 2 x
1 tg 2 x
2
ctg x 1
ctg 2 x
2ctgx
2
Пример 1
Доказать тождество : 1 sin 2 x (cos x sin x) 2
1 sin 2 x
sin 2 x cos 2 x 2 sin x cos x
sin 2 x 2 sin x cos x cos 2 x (sin x cos x )2
Пример 2
1
sin
2
x
дробь
:
Сократить
cos 2 x
2
2
sin
x
cos
x 2 sin x cos x
1 sin 2 x
2
2
cos 2 x
cos x sin x
(sin x cos x)
sin x cos x
(cos x sin x) (cos x sin x)
cos x sin x
2
Пример 3
Вычислить : cos
cos
2
8
sin
2
2
8
sin
2
8
cos( 2 ) cos
8
8
4
2
2
Пример 4
Зная, что сosx 3 , x 3 ;2 , вычислить cos 2 x :
5
2 IV
2
2
3
4
сos2x cos x sin x 9 16 7
25
25 25
5 5
sin 2 x cos 2 x 1
2
9
1
25
9
2
sin x 1
25
sin 2 x
16
25
4
sin x
5
sin
2
x
2
Формулы понижения степени.

x 1 cos x
cos
2
2
x 1 cos x
sin
2
2
x 1 cos x
tg
2 1 cos x
x 1 cos x
ctg
2 1 cos x
2
2
2
2
Пример 2
5
x
, x ; , вычислите cos
Зная, что cos x
13
2
2 II
5
1
8
8 1
4
x
1
cos
x
2
13
:2
cos
13
13 2
13
2
2
2
x
cos
2
4
13
x
cos 2
2
13
Разложение суммы и разности на
множители
sin x sin y 2 sin x y cos x y
2
2
x y
x y
sin x sin y 2 sin
cos
2
2
x y
x y
cos x cos y 2 cos
cos
2
2
x y
x y
sin
cos x cos y 2 sin
2
2
Формулы представления
произведения в виде суммы
cos( x y ) cos( x y )
sin x sin y
2
cos( x y ) cos( x y )
cos x cos y
2
sin( x y ) sin( x y )
sin x cos y
2
English Русский Правила
тригонометрия — $\cos(x+y)=\cos x + \cos y$?
спросил
Изменено 11 месяцев назад
Просмотрено 5к раз
$\begingroup$
Найдите значение с помощью калькулятора: $\cos 75°$
Сначала я думал, что все, что мне нужно, это разделить более простые известные значения следующим образом: 9\circ = \cos 30°+\cos45° = {\sqrt3}/{2} + {\sqrt2}/{2} $
$= {(\sqrt3+\sqrt2)}/{2} $ Это мой ответ, который переводится на калькуляторе
как = $1,5731$ Однако, когда я использовал калькулятор непосредственно на $\cos 75°$, я получил $0,2588$.
Где я ошибаюсь?
- тригонометрия
$\endgroup$
6
$\begingroup$
Вы использовали формулу $\cos(x+y) = \cos(x) + \cos(y)$, которая неверна. Правильная формула: $$\cos(x+y)=\cos(x)\cos(y)-\sin(x)\sin(y)$$
$\endgroup$
$\begingroup$
Ответ прост: Нет, и чтобы увидеть, что это возьмет $y=0$, мы находим $$\cos(x)=\cos(x)+1$$ что явно неверно.
$\endgroup$
0
$\begingroup$
Вы можете просто построить график $cos(x+y)-(cos(x)+cos(y))$, чтобы получить ответ:
$\endgroup$
1
$\begingroup$
Альтернативно: cos(A+B) = cosAcosB-sinAsinB, где A = 45, а B равно 30
$\endgroup$
1
$\begingroup$
Как упоминалось в других ответах, $\cos(x+y)=\cos(x)\cos(y)-\sin(x)\sin(y)$.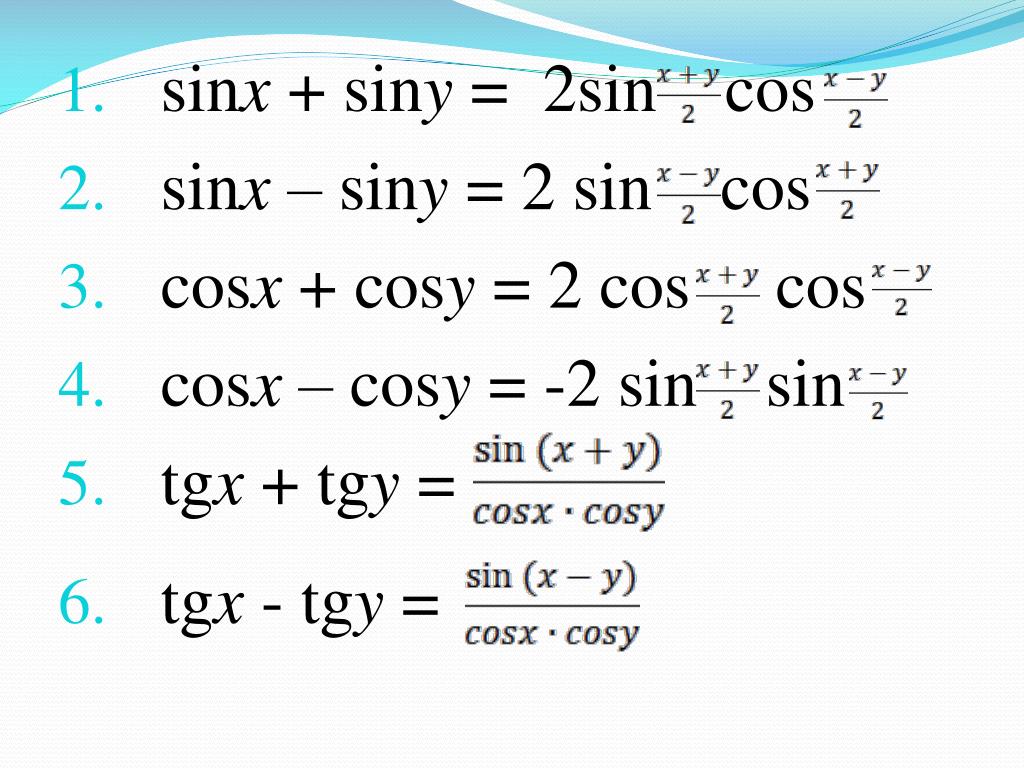
У нас также есть $\cos(x)+\cos(y)=2\cos\left(\frac{x+y}{2}\right)\cos\left(\frac{x-y}{2} \справа)$.
Поскольку $\cos(0)=1$, мы получаем $\cos(0+0)=1\ne2=\cos(0)+\cos(0)$.
$\endgroup$
$\begingroup$
Максимальное значение cos(x+y)=1.
Максимальные значения cos(x) и cos(y) равны 1.
Поскольку cos(x)+cos(y)=2cos(x+y) для некоторых значений x и y, это не может быть так что cos(x)+cos(y)=cos(x+y), за исключением особых значений x и y.
$\endgroup$
$\begingroup$
Если вы рассмотрите все $x,y$ в $\mathbb R$, такие что $\cos(x+y)=\cos(x)+\cos(y)$ верно, вы получите это.
$\endgroup$
1
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
тригонометрия — Докажите, что $ \cos x — \cos y = -2 \sin ( \frac{x-y}{2} ) \sin ( \frac{x+y}{2} ) $
спросил
Изменено 6 лет, 4 месяца назад
Просмотрено 4к раз 92 x = 1 $
Мне удалось доказать это с помощью приведенных выше фактов, но я только что понял, что я не могу их использовать. Теперь я хожу по кругу некоторое время.
Теперь я хожу по кругу некоторое время.
Есть идеи, как это доказать или хотя бы приблизиться к этому?
Спасибо!
- тригонометрия
$\endgroup$
2
$\begingroup$
Запомните этот трюк на всю жизнь: напишите $x = a+b$ и $y = a-b$. Итак: $$\begin{cases} x&= a+b \\ y &= a-b \end{cases} \ подразумевает \begin{cases} a &= \frac{x+y}{2}\\ b &= \frac{x-y}{2} \end{case}.$$
Тогда: $$\begin{align} \cos x — \cos y &= \cos(a+b)-\cos(a-b) \\ &= \cos a \cos b — \sin a \sin b — (\cos a \cos b + \sin a \sin b) \\ &= -2 \sin a \sin b \\ &= -2 \sin \left(\frac{x+y}{2}\ справа) \sin\left(\frac{x-y}{2} \right).\end{align}$$
$\endgroup$
$\begingroup$
Вы можете использовать комплексное определение функций sin и cos, полученное из формулы Эйлера.
