| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | ||
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град.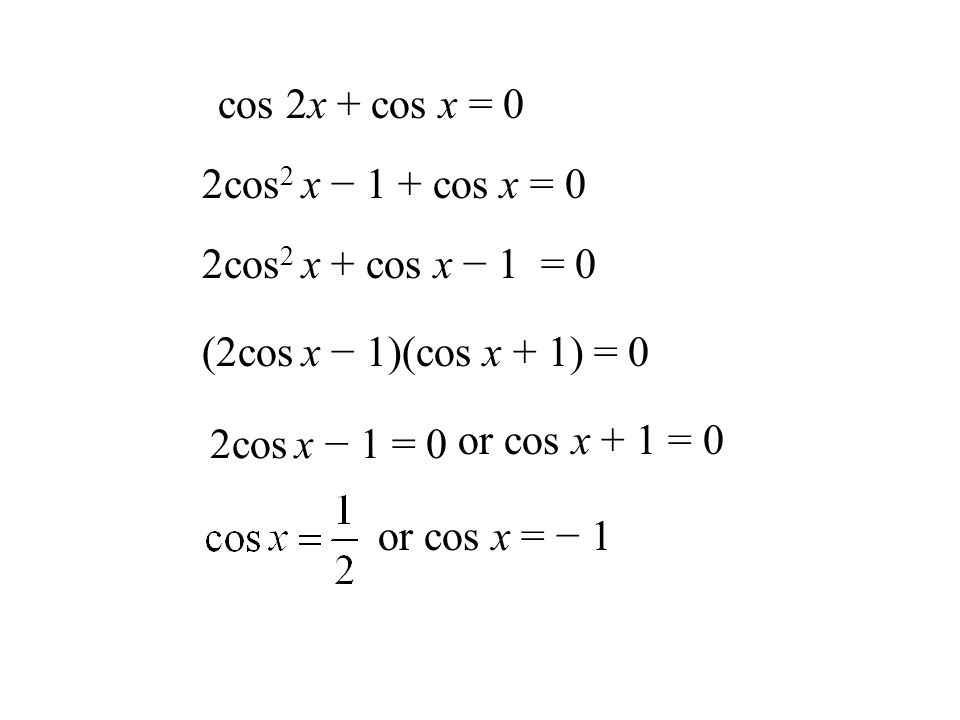 ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | arcsin(0) | ||
| 95 | Найти точное значение | sin(120 град.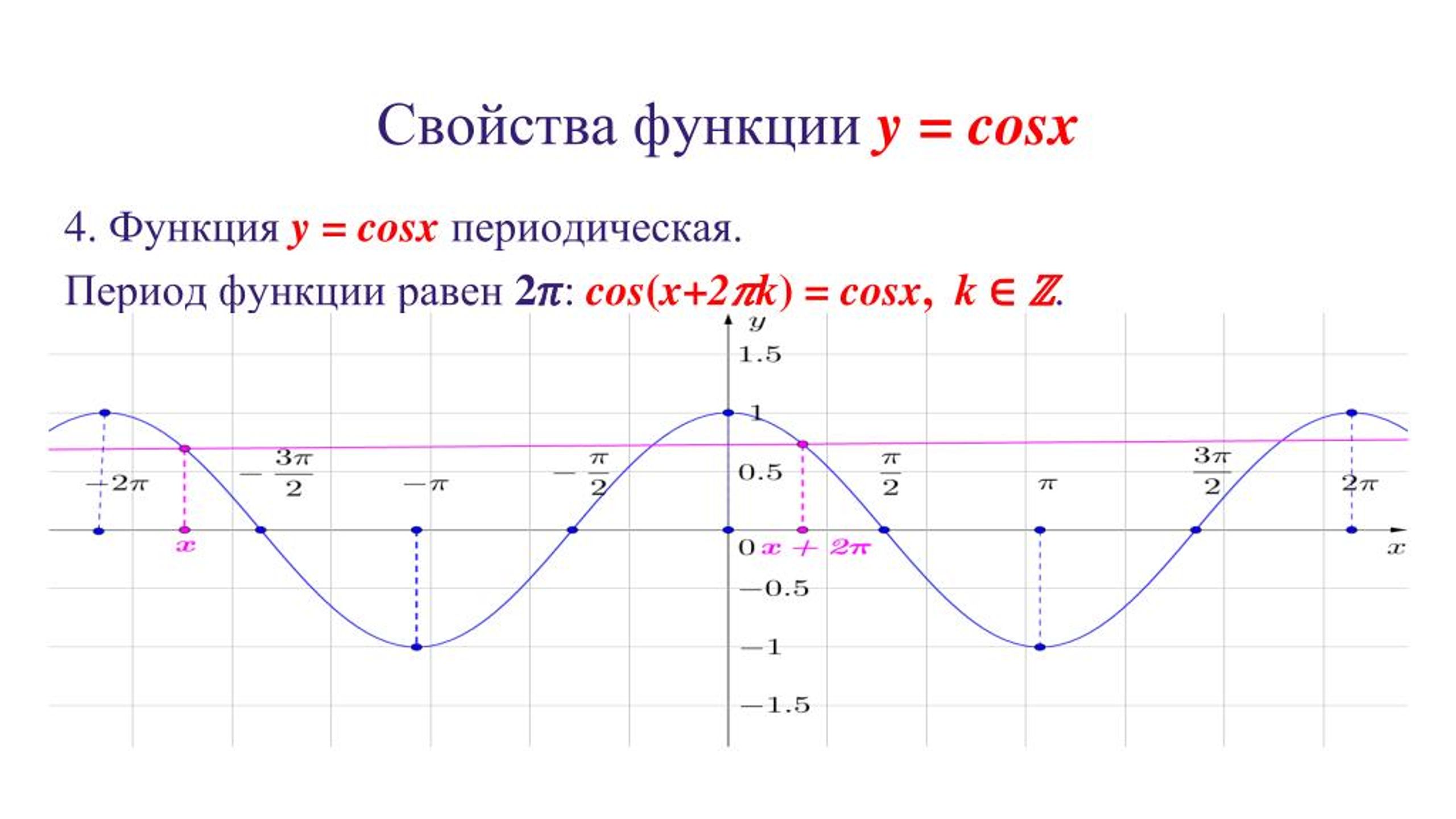 ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
заказ решений на аукционе за минимальную цену с максимальным качеством
Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:
- решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
- написание лабораторных, рефератов и курсовых
- выполнение заданий по литературе, русскому или иностранному языку.

Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.
Объединение сервисов в одну систему
Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:
- Форум, где посетители обмениваются идеями и помогают друг другу
- Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
- Аукцион, где цена за товар или услугу определяется в результате торгов
- Система рейтингов, где участники могут оценивать ответы друг друга. Причем, чем больше рейтинг пользователя, тем более значимым становится его голос
Принцип работы
Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.
Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.
Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.
Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте). Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т. к. можно учитывать и другие факторы – см. выше).
к. можно учитывать и другие факторы – см. выше).
Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.
За счет чего будет развиваться сервис
Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.
Второе – удобный сервис для заказчиков и для желающих заработать на решениях.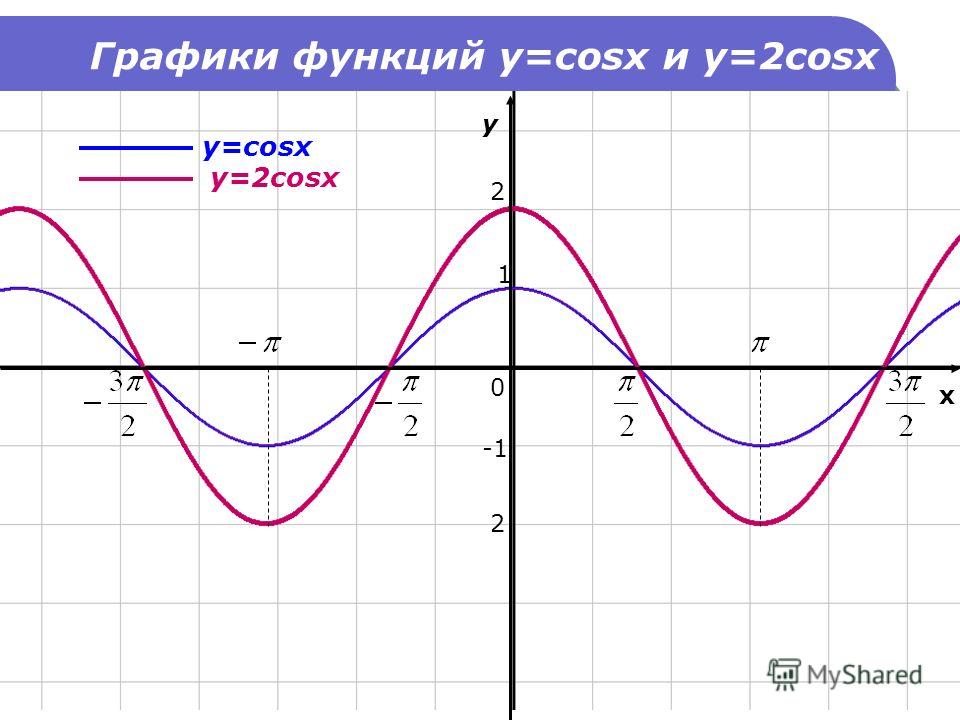
Преимущества для заказчиков
Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.
Преимущества для решающих задания
Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.
Преимущества для владельца сервиса
Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике. И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.
И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.
В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.
Что необходимо для создания сервиса
- Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.
Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.

- Выбрать платежную систему.
- Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
- Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.
Урок 3. свойства и график функции y=cosx — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №3. Свойства и график функции y=cos x
Перечень вопросов, рассматриваемых в теме
- Изучение свойств функции ;
- Построение графика функции;
- Расположение промежутков монотонности функции ;
- Определение свойств и положения графика тригонометрических функций вида и ;
- демонстрирование уверенного владения свойствами функции ;
- объяснение зависимости свойств и положения графика функции вида и ,от значения коэффициентов a, k, b.

Глоссарий по теме
Амплиту́да — максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении.
Функция y=f(x) возрастает на интервале X, если для любых и , выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.
Функция y=f(x) убывает на интервале X, если для любых и , выполняется неравенство . Другими словами – большему значению аргумента соответствует меньшее значение функции.
Точку х0 называют точкой максимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство . Значение функции в точке максимума называют максимумом функции и обозначают ymax.
Точку х0 называют точкой минимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство . Значение функции в точке минимума называют минимумом функции и обозначают ymin.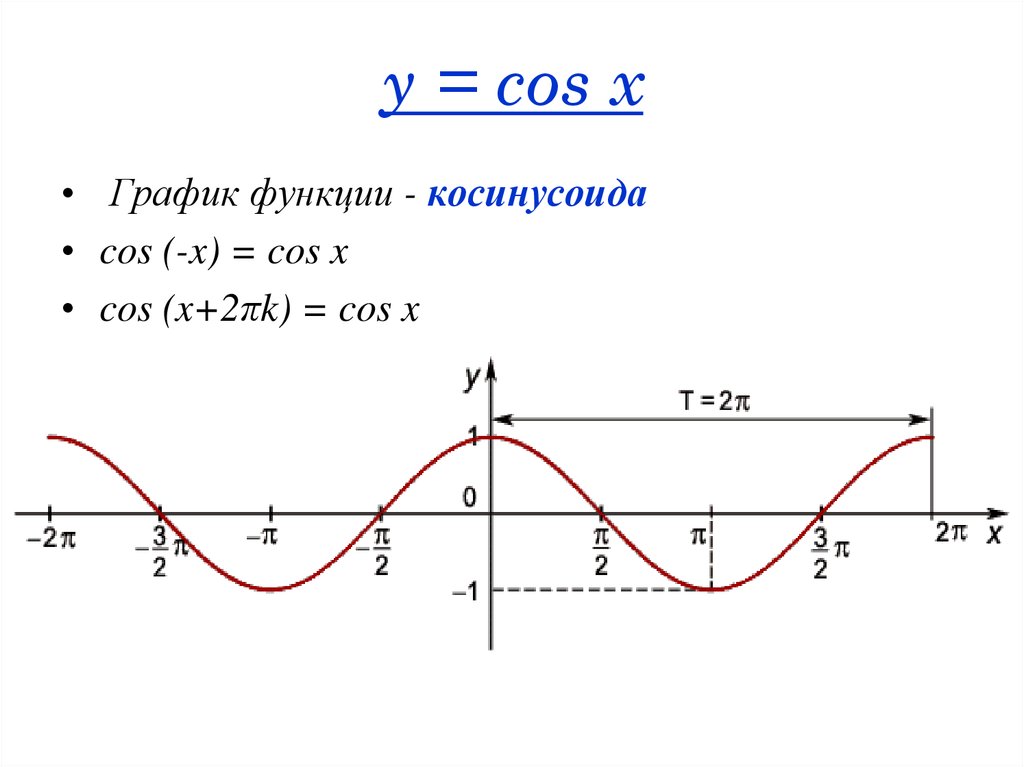
Основная литература:
Колягин М.В. Ткачева Ю.М., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. М.: Просвещение, 2010.–336 с.
Дополнительная литература:
Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.
Открытые электронные ресурсы:
Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].– Режим доступа: http://ege.fipi.ru/
Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс]. – Режим доступа: https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
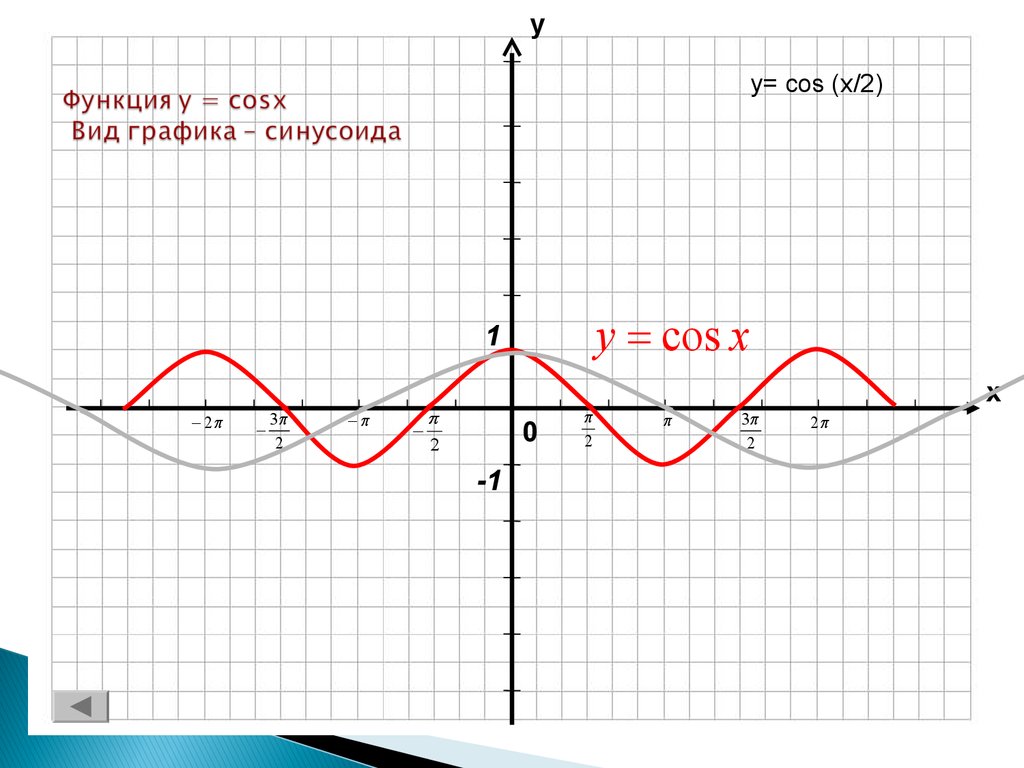
Напомним, что все тригонометрические функции являются периодическими функциями. Функции и повторяются через каждые 360° (или 2π радиан), поэтому 360° называется периодом этих функций (рис.1).
Рис. 1 – графики функций и .
Функции и повторяются через каждые 180° (или π радиан), поэтому 180° — это период для данных функций (рис.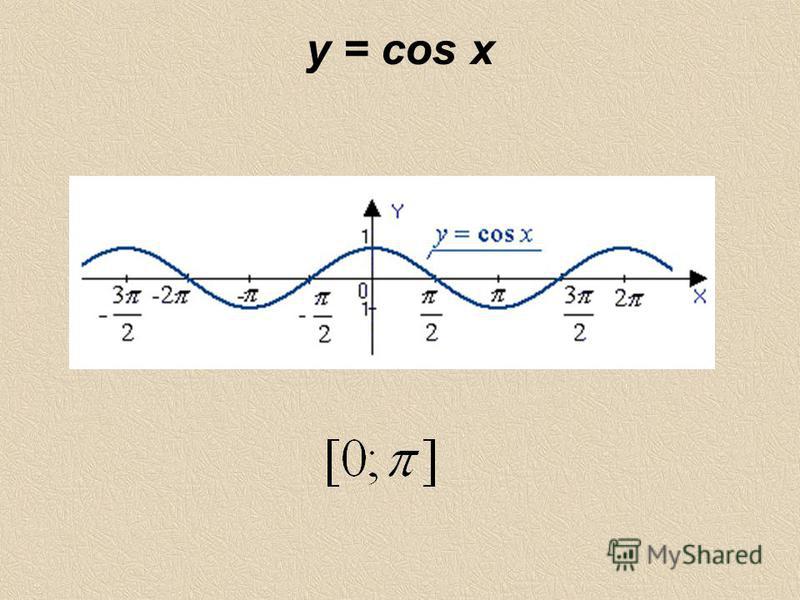 2).
2).
Рис. 2 – графики функций и .
В общем случае если и (где — константа), то период функции равен (или радиан). Следовательно, если , то период этой функции равен , если , то период этой функции равен .
Амплитудой называется максимальное значение синусоиды. Каждый из графиков 1-4 имеет амплитуду +1 (т.е. они колеблются между +1 и -1).
Рис. 3 – изображение амплитуды графиков и .
Однако, если , каждая из величин умножается на 4, таким образом, максимальная величина амплитуды — 4. Аналогично для амплитуда равна 5, а период — .
Рис. 4 – график функции .
Свойства функции :
- Область определения — множество R всех действительных чисел.
- Множество значений — отрезок [−1;1].
- Функция периодическая, Т=2π.
- Функция — чётная
- Функция принимает:
- значение, равное 0, при
- наибольшее значение, равное 1, при
- наименьшее значение, равное −1, при ;
- положительные значения на интервале и на интервалах, получаемых сдвигами этого интервала на ;
- отрицательные значения на интервале и на интервалах, получаемых сдвигами этого интервала на .

- Функция
- возрастает на отрезке [π;2π] и на отрезках, получаемых сдвигами этого отрезка на ;
- убывает на отрезке [0;π] и на отрезках, получаемых сдвигами этого отрезка на .
Интересно, что графиками тригонометрических функций –косинус и синус описываются многие процессы в нашей жизни. Например, работа сердца. Сделанная электрокардиограмма (ЭКГ) представляет собой график синусоиды, отражающую биоэлектрическую активность сердца. Или еще пример, электромагнитные волны к ним относятся: мобильные телефоны, беспроводная связь, радио, СВЧ-печи тоже распространяются по закону синуса или косинуса. Их существование было предсказано английским физиком Дж.Максвеллом в 1864 году.
Актуализация знаний
Напомним, что множество значений функции y=cosx принадлежит отрезку [–1;1], определена данная функция на всей числовой прямой и, следовательно, функция ограничена и график её расположен в полосе между прямыми y=–1 и y=1.
Так как функция периодическая с периодом , то достаточно построить её график на каком-нибудь промежутке длиной , например на отрезке Тогда на промежутках, полученных сдвигами выбранного отрезка на , график будет таким же.
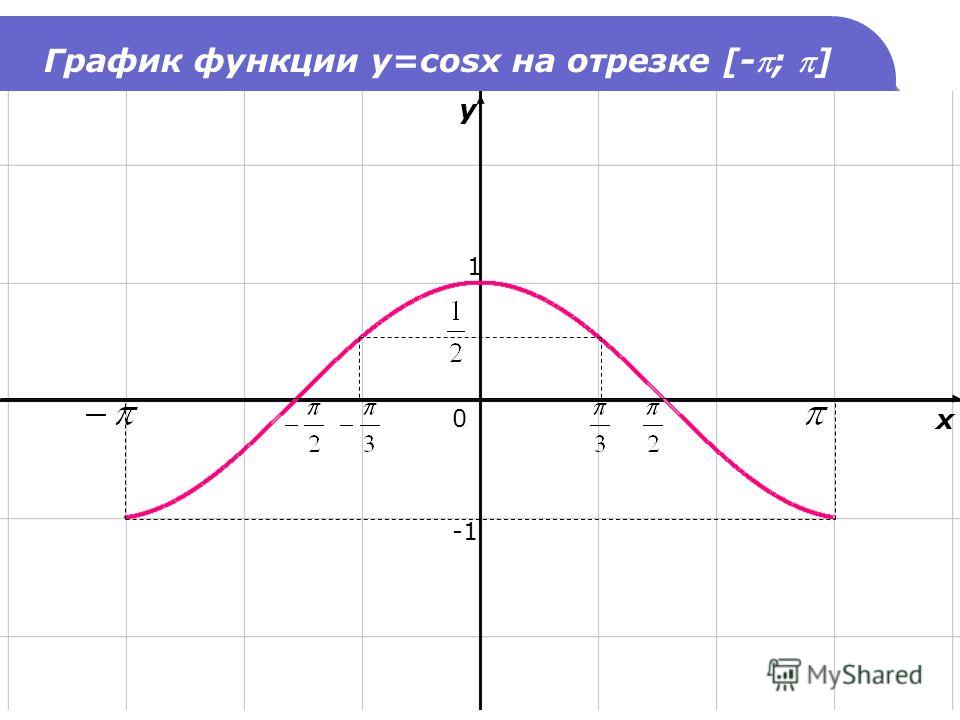
Функция является чётной. Поэтому её график симметричен относительно оси Оу. Для построения графика на отрезке достаточно построить для а затем симметрично отразить его относительно оси Оу (рис. 5)
Рис. 5 – график функции .
Примеры и разборы решения заданий тренировочного модуля:
Пример 1. Найдем все корни уравнения , принадлежащие отрезку .
Построим графики функций и (рис. 6)
Рис. 6 – графики функций и .
Графики пересекаются в трёх точках, абсциссы которых являются корнями уравнения . На отрезке от корнем уравнения является число . Из рисунка видно, что точки х1 и х2 симметричны относительно оси Оу, следовательно . А .
Пример 2.Найти все решения неравенства , принадлежащие отрезку .
Из рисунка 6 видно, что график функции лежит ниже графика функции на промежутках и
Ответ: , .
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт.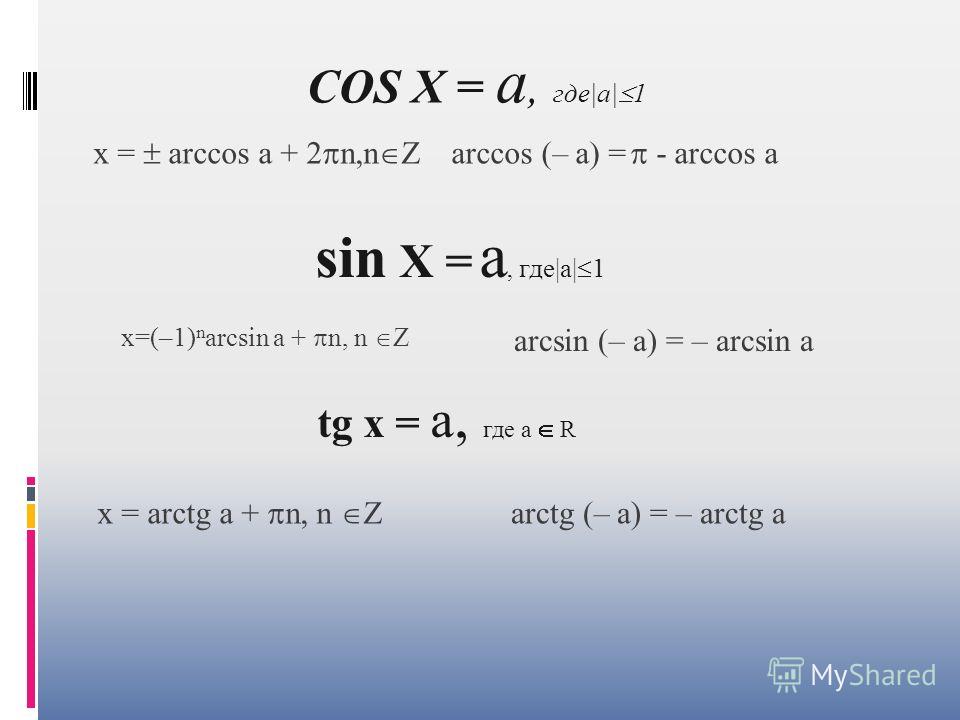 )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Тригонометрические тождества и формулы
Тригонометрические тождества и формулы Ниже приведены некоторые из наиболее важных определений, тождеств и формул в тригонометрии.
Тригонометрические функции острых углов
sin X = opp / hyp = a / c , csc X = hyp / opp = c / a
tan X = opp / adj = a / b , cot X = adj / opp = b / a
cos X = прил / hyp = b / c , сек X = hyp / прил = c / b ,Тригонометрические функции произвольных углов
грех X = b / r , csc X = r / b
загар X = b/a, раскладушка X = a/b
cos X = a / r , сек X = r / aОсобые треугольники
С помощью специальных треугольников можно найти тригонометрические функции особых углов: 30, 45 и 60 градусов. 
Законы синусов и косинусов в треугольниках
В любом треугольнике имеем:
1 — Закон синусов
грех А / а = грех В / б = грех С / с
2 — Законы косинусов
а 2 = б 2 + в 2 — 2 b c cos A
b 2 = a 2 + c 2 — 2 a c cos B
c 2 = a 2 + b 2 — 2 a b cos CОтношения между тригонометрическими функциями
cscX = 1/sinX
sinX = 1/cscX
секХ = 1/cosX
cosX = 1/секX
tanX = 1 / cotX
cotX = 1 / tanX
tanX = sinX / cosX
cotX = cosX / sinXПифагорейские тождества
sin 2 X + cos 2 X = 1
1 + тангенс 2 X = сек 2 X
1 + детская кроватка 2 X = csc 2 XТождества с отрицательным углом
sin(-X) = — sinX , нечетная функция
csc(-X) = — cscX , нечетная функция
cos(-X) = cosX , четная функция
sec(-X) = secX , четная функция
tan(-X) = — tanX , нечетная функция
cot(-X) = — cotX , нечетная функцияКофункции Идентичности
грех (π/2 — X) = cosX
cos(π/2 — X) = sinX
тангенс(π/2 — X) = cotX
раскладушка(π/2 — X) = tanX
сек(π/2 — X) = cscX
csc(π/2 — X) = secXФормулы сложения
cos(X + Y) = cosX уютный — sinX sinY
cos(X — Y) = cosX cosy + sinX sinY
sin(X + Y) = sinX cosy + cosX sinY
sin(X — Y) = sinX cos — cosX sinY
tan(X + Y) = [ tanX + tanY ] / [ 1 — tanX tanY]
tan(X — Y) = [ tanX — tanY ] / [ 1 + tanX tanY]
раскладушка (X + Y) = [ раскладушка X раскладушка Y — 1 ] / [ раскладушка X + раскладушка Y]
раскладушка(X — Y) = [ раскладушкаX раскладушка Y + 1 ] / [раскладушкаY — раскладушкаX]Суммировать формулы произведения
cosX + уют = 2cos[ (X + Y) / 2 ] cos[ (X — Y) / 2 ]
sinX + sinY = 2sin[ (X + Y) / 2 ] cos[ (X — Y) / 2 ]Отличие от формул продукта
cosX — уютный = — 2sin[ (X + Y) / 2 ] sin[ (X — Y) / 2 ]
sinX — sinY = 2cos[ (X + Y) / 2 ] sin[ (X — Y) / 2 ]Произведение в формулы суммы/разности
cosX уютный = (1/2) [ cos (X — Y) + cos (X + Y) ]
sinX cosy = (1/2) [ sin (X + Y) + sin (X — Y) ]
cosX sinY = (1/2) [ sin (X + Y) — sin [ (X — Y) ]
sinX sinY = (1/2) [ cos (X — Y) — cos (X + Y) ]Формулы разности квадратов
sin 2 X — sin 2 Y = sin(X + Y)sin(X — Y)
cos 2 X — cos 2 Y = — sin(X + Y)sin(X — Y)
cos 2 X — sin 2 Y = cos(X + Y)cos(X — Y)Формулы двойного угла
sin(2X) = 2 sinX cosX
cos(2X) = 1 — 2sin 2 X = 2cos 2 X — 1
тангенс (2X) = 2тангенс X / [ 1 — тангенс 2 X ]Формулы множественных углов
sin(3X) = 3sinX — 4sin 3 X
cos(3X) = 4cos 3 X — 3cosX
sin(4X) = 4sinXcosX — 8sin 3 XcosX
cos(4X) = 8cos 4 X — 8cos 2 X + 1Формулы половинного угла
sin (X/2) = + или — √ ((1 — cosX) / 2)
cos (X/2) = + или — √ ((1 + cosX) / 2)
тангенс (X/2) = + или — √ ((1 — cosX) / (1 + cosX))
= sinX / (1 + cosX) = (1 — cosX) / sinXФормулы для снижения мощности
sin 2 X = 1/2 — (1/2)cos(2X))
cos 2 X = 1/2 + (1/2) cos(2X))
sin 3 X = (3/4)sinX — (1/4)sin(3X)
cos 3 X = (3/4)cosX + (1/4)cos(3X)
sin 4 X = (3/8) — (1/2)cos(2X) + (1/8)cos(4X)
cos 4 X = (3/8) + (1/2) cos(2X) + (1/8)cos(4X)
грех 5 Х = (5/8)sinX — (5/16)sin(3X) + (1/16)sin(5X)
cos 5 X = (5/8)cosX + (5/16)cos(3X) + (1/16)cos(5X)
sin 6 X = 5/16 — (15/32)cos(2X) + (6/32)cos(4X) — (1/32)cos(6X)
cos 6 X = 5/16 + (15/32) cos(2X) + (6/32)cos(4X) + (1/32)cos(6X)Периодичность тригонометрических функций
sin (X + 2π) = sin X , период 2π
cos (X + 2π) = cos X , период 2π
сек (X + 2π) = сек X , период 2π
csc (X + 2π) = csc X , период 2π
тангенс (X + π) = тангенс X , период π
раскладушка (X + π) = раскладушка X , период π- Тригонометрические таблицы.

- Свойства шести тригонометрических функций. График, домен, диапазон, асимптоты (если есть), симметрия, точки пересечения x и y, а также точки максимума и минимума каждой из 6 тригонометрических функций.
Дополнительные ссылки по тригонометрии
Тригонометрия.
Решение задач по тригонометрии .
бесплатных вопросов по тригонометрии с ответами.
сообщите об этом объявлении
| Популярные страницы |
|---|
|
Math Scene — Тригонометрические функции — Более сложные уравнения и неравенства
Math Scene — Тригонометрические функции — Более сложные уравнения и неравенства — Урок 5 2008 Расмус Эхф | Печать |
Пример 1
Решить уравнение sin x = cos x и затем неравенство
грех x > cos x на интервале 0 x < 2,
Из единичного круга мы видим, что sin x и cos x
может иметь одинаковое значение только в двух местах, в x = /4
и х = 5/4
(45 и 225 ).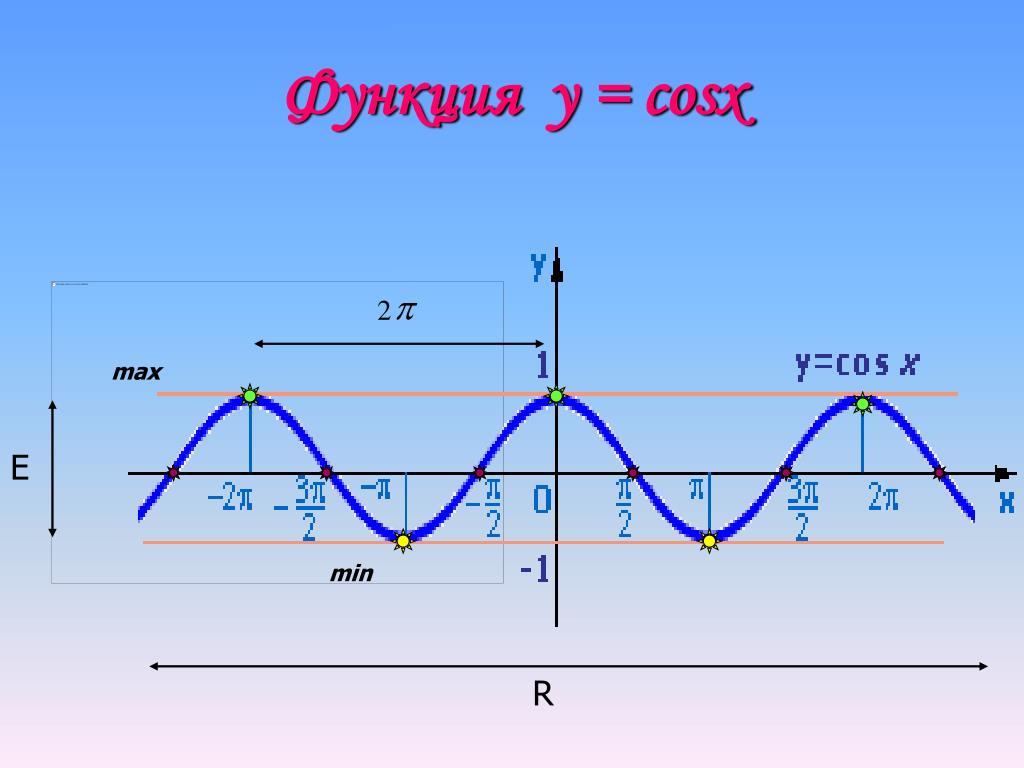
Уравнение sin x = cos x также можно решить путем деления на cos x.
тангенс х = 1
x = тангенс −1 (1)
х = 45 ∙ /180 + к∙
x = /4 + k∙ (k — любое целое число, положительное или отрицательное)
Если положить k = 0 и k = 1, получим решения /4 (45 ) и /4 + = 5/4 (45 + 180 = 225 ).
Чтобы решить неравенство sin x > cos x, нам нужно увидеть, что больше sin x или cos x на интервалах между решениями /4 и 5/4. Решения можно увидеть, если мы нарисуем графики f(x) = sin x и g(x) = cos Икс. График sin x лежит над графиком cos x на интервале /4 x 5x/4 (см. заштрихованную область на диаграмме).
sin x cos x на интервале /4 x 5x/4.
Пример 2
Решить уравнение sin x ∙ cos x = 0 и затем неравенство
sin x ∙ cos x > 0 на интервале 0 x < 2.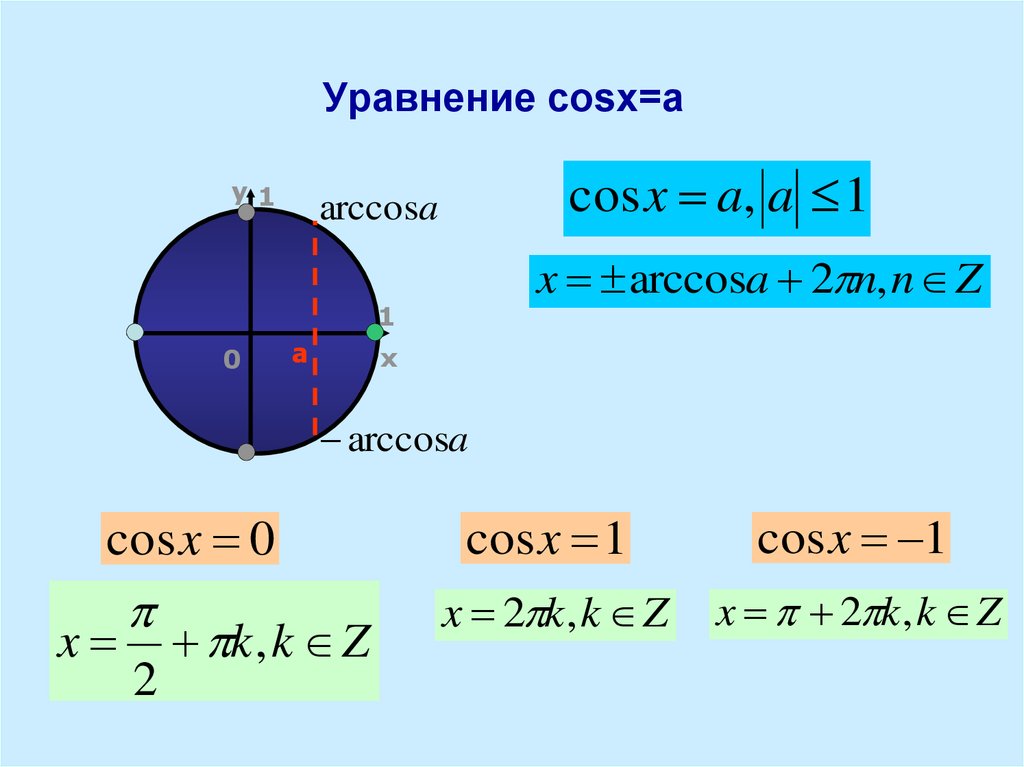
Неравенство не имеет решение, когда sin x или cos x принимают значение 0. Это происходит с интервалом 90.
Решения уравнение sin x ∙ cos x = 0 на интервале 0 x < 2, поэтому 0, /2 и 3/2 (0 , 90 , 180 и 270 ).
Решение sin x
∙ cos x > 0 можно найти, взглянув на единичный круг. Нам нужно найти
где sin x, умноженный на cos x, является положительным. Другими словами, sin x и cos x имеют
иметь один и тот же знак, оба должны быть
положительный или оба отрицательные. Это происходит в первом и третьем квадранте.
поэтому решения
0 < х < /2 и р < х < 3/2.
Мы также можем увидеть это по
построение графика
f(x) = sin x ∙ cos x.
Пример 3
Решите уравнение sin x ∙ cos x − sinx = 0 и тогда неравенство sin x ∙ cos x − sin x > 0 на интервале 0 x < 2,
sin x ∙ cos x − sinx = 0 sin x (cos x − 1) = 0 | Нам нужно
чтобы разложить уравнение на множители, взяв sin x за скобки. |
У уравнения есть решения когда sin x = 0 или скобка (cos x − 1) = 0,
sin x = 0
x = 0 или (180 ).
или
потому что х — 1 = 0
потому что х = 1
х = 0
Единственные решения уравнение поэтому 0 и .
Неравенство sin x ∙ cos x − sin x > 0 можно переписать как sin x (cos x − 1) > 0,
Теперь полезно сделать таблицу знаков и посмотрите на знаки sin x и cos x − 1.
Решение
Мы видим, что оба фактора
отрицательно на интервале
< x < 2,
Теперь давайте посмотрим, как это подходит
в с графиком
f(x) = sin x ∙ cos x − sin x
Заштрихованная область над крестиком
ось показывает, где
sin x (cos x − 1) > 0, что согласуется с нашими расчетами.
Пример 4
Найдите все решения уравнения cos 2 x − cos x = 0,
cos 2 x − cos х = 0
cos x∙(cos x − 1) = 0
Решения можно найти, когда cos x = 0 или cos x − 1 = 0
потому что х = 0
x =/ 2 или 3/2 (90 или 270 )
x = / 2 + k∙
или
потому что х — 1 = 0
потому что х = 1
x = 0 + k∙2 = k∙2
Все решения соответствуют шаблону x = /2 + к∙
Пример 5
Найти все решения уравнения sin 2 x − 5 sin x + 4 = 0,
Это квадратное уравнение с sin x в качестве
переменная. Поэтому мы можем найти sin x, используя квадратичную формулу. а = 1, б = -5 или с = 4,
Поэтому мы можем найти sin x, используя квадратичную формулу. а = 1, б = -5 или с = 4,
Для синуса мы не можем взять значение 4, поэтому нам не нужно рассматривать sin x = 4. Другая возможность — sin x = 1, решение которой /2 (90 ). Таким образом, полное решение:
.х = / 2 + к∙2
Пример 6
Решить уравнение sin 5x = грех х .
Возможно, положение 5x на единичном круге совпадает с позицией x и поскольку эта позиция повторяется с интервалом в 360, мы получаем следующее уравнение:
1) 5x = x + к∙360
4x = к∙360
х = к∙90
Мы показываем эту возможность в диаграмма.
Появляется вторая возможность
от того что
грех х = грех (180 − х ). Это дает нам следующее решение:
5 х = 180 — х + к∙360
6x = 180 + к∙360
х = 30 + к∙60
Это решение показано на
схему справа.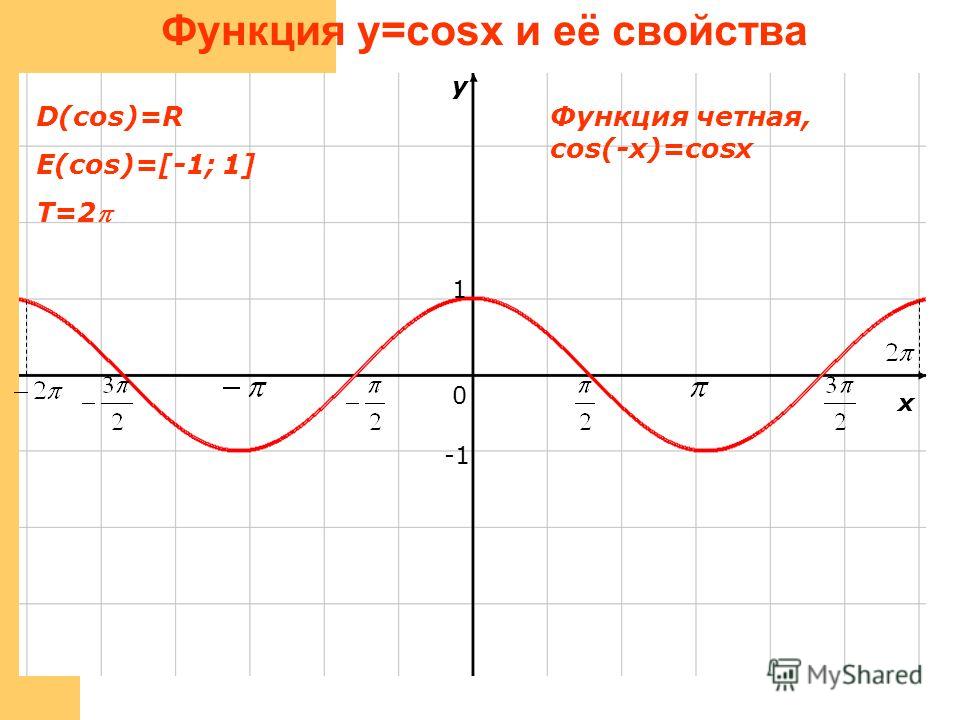
Но мы замечаем, что первое решение содержится в второе решение, поэтому достаточно дать второе решение
х = 30 + к∙60
Пример 7
Решите уравнение cos 2x = cos x на интервале 0 x < 2,
1) Сначала рассмотрим вероятность того, что x и 2x находятся в одном и том же месте на единичной окружности.
2x = x + k∙2 x = k∙2 х = 0 | Вычесть x из обеих частей уравнения, а затем выберите k = 0 (k = 1 дает 2, которое находится вне интервала |
2) Второй вариант.
по факту
потому что v = cos (-v). Тогда решение будет следующим:
2x = −x + к∙2
3x = k∙2
x = k∙2/ 3
Это дает решения 2/3 (120 )
для k = 1 и 4/3 (240 ) для k = 2.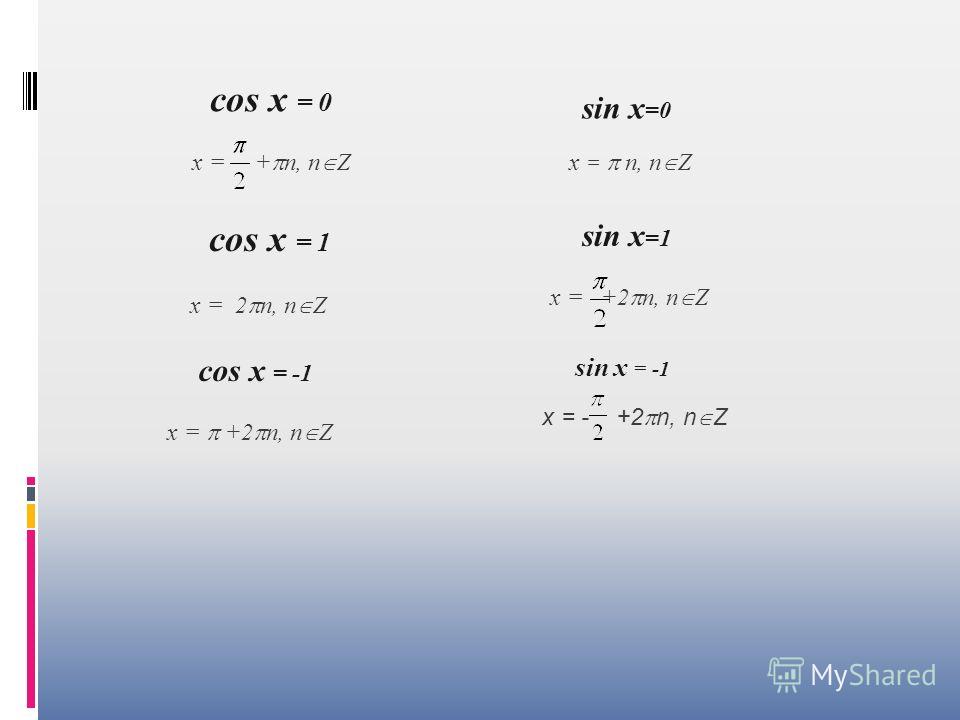 поэтому полное решение:
поэтому полное решение:
0, 2/3 или 4/3.
Пример 8
Решите уравнение tan 3x = загар 2x.
Уравнения Тана во многих способов самое простое из тригонометрических уравнений, так как есть только возможность считать, что повторяется с интервалом 180 .
3x = x + k∙180
2x = к∙180
х = к∙90
или в радианах
х = к∙/ 2
Попробуйте викторину 5 по триггерным функциям.
Не забывайте использовать контрольный список, чтобы отслеживать свою работу.
Các Công Thức lượng giác toán 10 ầy ủ nhất
trong cuối chương trình lớp 10, các em học sinh sẽc làm vớp chương lượg ghác. Trong chương này, cac em sẽ học cac kiến thức về cung và góc lượng giac. Để làm tốt cac dạng bài tập về lượng giác yêu cầu cac em phai nắm vững cac cong thức. До đ, Чунг Той, бион Соун Как Кона, это я.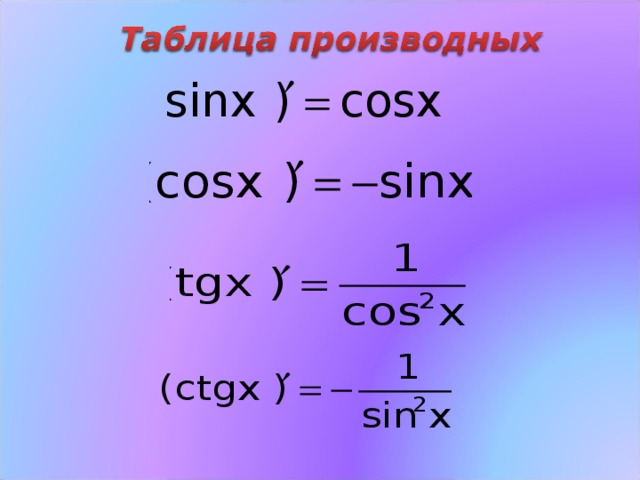
ặc biệt, ể giúp các em học thuộc các công thức này một cách dễ dàng, trong phần 3 chúng tôi còn giới thiệu thêm một số ghá nhang scá nhang shá nhang nhang nha nhang nha nhang nha nha nhang nha nhan gha nhangha nhan gha nhan giới thêu thê nh nha nha giới thệu thê nh nha nha giới thệu thộ nh nha nha giới thệu thuộc cô Hy vọng, đây sẽ la một tài liệu giúp cac em học lượng giác một cách thú vị hơn.
I. Các Công thức lượng giác toán 10 Cơ Bản
>>> nắm bắt toàn bộng kiến thức fron -phú về nắm toán bộng kiến thức wrú về về về nắn 10. тиу как
công thức lượng giác toán 10 cơ bản nằm trong chương trình sách giáo khoa lớp 10. Đây là những công thức bắt buộc các em học sinh lớp 10 cần phải học thuộc lòng thì mới có thể làm được những bài tập lượng giác cơ Бан Нат. 1. Bảng giá trị lượng giác của một số cung hay góc đặc biệt :
2.
 Hệ thức cơ bản :
Hệ thức cơ bản :Đăng ký học ngay lớp Toán thầy Mạnh lớp 10
3. CUNG LIên KếT:(Cách NHớ: Cose Bù, Sin Bù, Tan Hơn Kém Pi, Phụ Chéo )
444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444. những góc có mối liên hệ đặc biệt với nhau như : đối nhau, phụ nhau, bù nhau, hơn kém pi, hơn kém pi/2
• Hai góc đối nhau
cos(–x) = cosx
sin(–x) = – sinx
tan(–x) = – tanx
cot(–x) = – cotx
• Hai góc bù nhau
sin (π – x) = sinx
cos (π – x) = -cosx
tan (π – x) = -x cotx
sin (π + x) = -sinx
cos (π + x) = -cosx
tan (πcot + x) = tanx
t π + x) = cotx
• hai góc phụ nhau 4. Công thức cộng:
Công thức cộng: (cô nhớ ì ì ì ì ì ì ì ì ì ì ì ì ì ì ì ì ì ì ì ì ì ì ì ì ì ì ì ì ì ì ì ì ì ì ì ì ì ì ì ì ì ì ì ì ì nh ì ừ ì ừ ì nh ì ừ ừ ừ ừ ừ nh ức: cos. , tan thì tan nọ tan kia chia cho mẫu số một trừ tan tan) :
sin3x = 3sinx – 4sin 3 x
cos3x = 4cos 3 x – 3cosx
7. Công thức hạ bậc: . Cac công thức lượng giác lớp 10 nâng cao Trong phần 2, ngoài cac Công thức lượng giác toán 10 Cơ Bản, Chúng tôoi Sẽ giới thiệu thêm Cho các bạn học sinh các công thức lượng giác lớp 10 nâng cao . Đây là những công thức lượng giác hoàn toàn không có trong sách giáo khoa nhưng rất thường xuyên gặp phải trong các bài toán rút gọn biểu thức, chứng minh biểu thức, giải phương trình lượng giác. Cac em học sinh kha, giỏi có thể thể khảo để vận dụng trong cac bài tập nâng cao.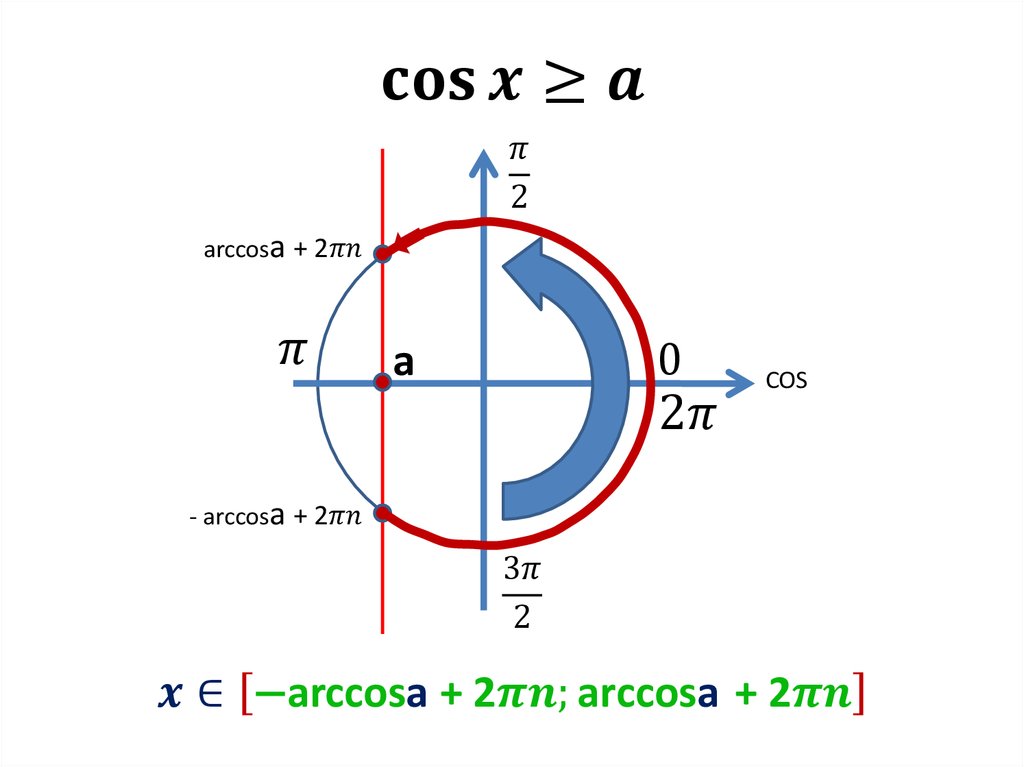 Cac công thức được bien soạn thành 4 dạng:
Cac công thức được bien soạn thành 4 dạng:
908
. Cách ghi nhớ công thức lượng giác toán 10ối với nhiều em học sinh việc học các công thức lượng giác toán 10 ược xem làt khin. Do đó, chung tôi sẽ giới thiệu một số cách ghi nhớ công thức lượng giác nhanh và hiệu quả.
Кач Ги Нхо Конг Тхок Конг Cos + cos = 2 cos cos
cos – cos = trừ 2 sin sin
Sin + sin = 2 sin cos
sin – sin = 2 cos sin.
Sin thì sin cos cos sin
Cos thì cos cos sin sin rồi trừ
Tang tổng thì lấy tổng tang
Chia 1 trừ với tích tang, dễ mà.
TAN (x+y) =
bài thơ: tan 2 tổng 2 tầng cao rộng
thượng tầng tang cộng cùng tang
Hạ tầng Số 1 rấng TNG Tang
Hạ Tầng Số 1 rấng TNG
Hạ Tầng Số 1 rừng Tang
Hạ TầNG.
cos ối, sin bù, phụ chéo, tan hơn kém pi
cách ghi nhớ công thức biến ổ ổi tích thành tổng cos-cos-cos-cos-trừ +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, +, а trừ cos-+
sin cos nửa sin-++ sin-trừ
tính tổng típ tổng sin cro cro
còn tính tan tử + đôi tan (hay là: tan tổng lập tổng 2 tan)
1 trừ tan tích mẫu mang thương rầu
nếu gặp hiệu ta chớ lo âu,
ổi trừ thành cộng ghi sâu trong lòng
một cách nhớ khác của câu tang mình + với tang. tình mình cộng lại tình ta, sinh ra hai ứa con mình con ta
tangx — tang y: tình mình trừ với tình ta sinh raệu chúng, con ta conhnh
4. cáng, con ta conh44. Cáng, Con nhớnhnh44. Cáng. VD: sin2x= 2sinxcosx (Tương tự cac loại cong thức như vậy)
Cáng, Con nhớnhnh44. Cáng. VD: sin2x= 2sinxcosx (Tương tự cac loại cong thức như vậy)Cách ghi nhớ: Sin gấp đôi bằng 2 sin cos
Cos gấp đôi bằng bình phương cos trừ đi bình sin
Bằng trừ 1 cộng hai bình cos
Bằng cộng 1 trừ hai bình sin
(Chúng ta chỉ việc nhớ công thức nhân đôi của cos bằng câu nhớ trên rồi từ đó có thể suy ra công thức hạ bậc.)
Tan gấp đôi bằng Tan đôi ta lấy đôi tan (2 tan)
Chia một trừ lừ lại, bình
Mỗi bạn sẽ suy nghĩ cho mình những cách ghi nhớ công thức lượng giác toán 10 khác nhau nhưng kết quả cuối cùng là sự dễ thuộc, dễ hiểu và khả năng áp dụng được vào mọi bài toán mình gặp
Trên đay la cac cong thức lượng giác toán 10 cơ bản và nâng cao. Ể có thể làm tốt các bài tập rút gọn biểu thức hay chứng minh biểu thức lượng giác các em cần phải học thuộc lòng các công thức lượng giác trên. Việc học các công thức lượng giác này nhuẫn nhuyễn còn giúp các em rất nhiều khi lên 11, ặc biệt là phục vụ những bài toán giải phương trìng. Có thể noi lượng giác đối với cac bạn học sinh rất mới mẻ và phức tạp. Tuy nhiên но chỉ khó với những ai lười học cong thức và sẽ đơn giải nếu ta học thuộc và vận dụng khéo leo cac côcong thọng thẽ đơn giải Cuối cùng, xin chúc cac bạn học thuộc cac công thức này thành công và đạt điểm tốt trong cac bài kiem tra lượng giác. 92 x -cosx=0 thỏa man điều kiện
Có thể noi lượng giác đối với cac bạn học sinh rất mới mẻ và phức tạp. Tuy nhiên но chỉ khó với những ai lười học cong thức và sẽ đơn giải nếu ta học thuộc và vận dụng khéo leo cac côcong thọng thẽ đơn giải Cuối cùng, xin chúc cac bạn học thuộc cac công thức này thành công và đạt điểm tốt trong cac bài kiem tra lượng giác. 92 x -cosx=0 thỏa man điều kiện
Кау Хой:
25.04.2020 1098
Nghiệm của phương trình cos2x -cosx=0 thỏa man điều kiện 0 А. x=π2
Чап ан Чинххак
Б. x=-π2
x=-π2
С. x=π6
D. x=π4
Xem lời giải
Câu hỏi trong đề: Tổng hợp đề thi thử thptqg môn Toán có lời giải !!
Куанг Као
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Một đoàn đại biểu gồm 5 người được chọn ra từ một tổ gồm 8 nam và 7 nữ để tham dự hội nghị. Xac suất để chọn được đoàn đại biểu có đúng 2 người nữ là:
А. 56143
56143
Б. 140429
С. 1143
Д. 28715
Ксем Джап » 25.04.2020 8 941
Кау 2:
một loại vi khuẩn sau mỗi phút số lượng tăng gấp đôi biết rằng sau 5 phút người ta ếm ược cou 64000 con hỏi sau bao nhiê phút thì có ược 2048000 con.
А. 10.
Б. 11
К. 26
Д. 50
Ксем Джап » 25.04.2020 8 474
Кау 3:
Тим Тет Ка Сак Нгим Куа Пхонг Трин cos3x+sin2x-sin4x=0
A. x=π6+k2π3, k∈ℤ
x=π6+k2π3, k∈ℤ
Б. x=π6+kπ3, k∈ℤ
C. x=kπ3 hoặc x=π6+k2π hoặc x=5π6+k2π(k∈ℤ)
D. x=π6+kπ3 hoặc x=π3+k2π (k∈ℤ)
Ксем Джап » 25.04.2020 8 308
Кау 4:
Đường thẳng d: y=x+4 cắt đồ thị ham số y=x3+2mx2+(m+3)x+4 tại 3 điểm phân biệt A(0;4),
6 C
B
và và diện tích tam giác MBC bằng 4, với M(1;3). Mệnh đề nào sau đay là đúng ?
Mệnh đề nào sau đay là đúng ?А. m∈-∞;0
Б. m∈0;2
С. m∈2;4
г.
Д. m∈4;+∞
Ксем Джап »
25. 04.2020
6 545
04.2020
6 545
Кау 5:
Phương trình 1+8+15+22+…+x=7944 có nghiệm x bằng bao nhiêu?
А. х=330
Б. х=220
С. х=351
Д. х=407
Ксем Джап »
25. 04.2020
6 473
04.2020
6 473
Кау 6:
Cho khối nón có bán kính đay r=1 và góc ở đỉnh 60°. Diện tích xung quanh Sxq của hình nón bằng bao nhiêu?
А. №
Б. 2π
г.
С. 3π
Д. 2π
2π
Ксем Джап » 25.04.2020 6 180
Кау 7:
Cho lập phương có cạnh bằng a và một hình trụ có hai đay là hai hình tròn nội tiếp hai mặt đối lối diện hƒn cện Gọi S 1 là diện tích 6 mặt của hình lập phương, S 2 là diện tích xung quanh của hủa hủnh. Hãy tính tỉ số S2/S1.
А. S2S1=12
Б. S2S1=π2
С. S2S1=π
S2S1=π
г.
Д. S2S1=π6
Ксем Джап » 25.04.2020 6 128
Хайбай
Гои 084 283 45 85
Hỗ trợ đăng ký khóa học tại Vietjack
Derivada de Coseno, cos(x) — Fórmula, Demostración y Gráficas
Demostración de la Derivada de la Función Coseno
La función trigonométrica coseno de un ángulo se define como la relación entre un lado adyacente a un ángulo en un triángulo rectángulo y la hipotenusa. Ilustrándolo a través de una figura, tenemos
donde C es 90°. Para el triángulo de la derecha de la muestra, obtener el coseno del ángulo A se puede evaluar como
Para el triángulo de la derecha de la muestra, obtener el coseno del ángulo A se puede evaluar como
$latex \cos{(A)} = \frac{b}{c}$
donde A es el ángulo, b es su lado adyacente y c es la hipotenusa del triángulo rectángulo de la figura.
Antes de aprender la prueba de la derivada de la coseno, se le recomienda aprender el teorema de Pitagorean, Soh-Cah-Toa y Cho-Sha-Cao, y el primer principio de los limites como requisitos previos.
Recordemos que cualquier función se puede derivar igualándola al límite de
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{f(x+h) -f(x)}{h}}$$
Supongamos que nos piden obtener la derivada de
$latex f(x) = \cos{(x)}$
tenemos
$$\frac{d}{dx} f(x) = \lim \ limit_{h \to 0} {\frac{\cos{(x+h)} – \cos{(x)} }{h}}$$
Анализ нуэстра ecuación, podemos observar que el primer término en el numerador del límite es un coseno de la suma de dos ángulos x y h . Con Esta observación, podemos tratar de aplicar las identidades de suma y diferencia para coseno y seno, también llamadas identidades de Ptolomeo. Апликандо Эсто, Тенемос
Апликандо Эсто, Тенемос
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{\cos{(x+h)} – \cos{(x)}}{ h}}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ (\cos{(x)}\cos{(h) } – \sin{(x)}\sin{(h)}) – \cos{(x)} }{h}}$$
Intentemos reorganizar el numerador,
$$\frac{d}{dx } f(x) = \lim \limits_{h \to 0} {\frac{ \cos{(x)}\cos{(h)} — \cos{(x)} — \sin{(x)} \sin{(h)} }{h}}$$
Teniendo en cuenta el primer y segundo términos de nuestro numerador reorganizado, tenemos
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ \cos{(x)}(\cos{(h)} – 1) – \sin{(x)}\sin{(h)}) }{h}}$$
Haciendo algunos arreglos arreglos, tenemos
$$\frac{d}{dx} f(x) = \lim \ limit_{h \to 0} {\ frac{\cos{(x)} (-(1-\cos{(h)})) — \sin{(x)}\sin{(h)}}}{h }}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} {\frac{ -\cos{(x)} (1-\cos{( h)}) – \sin{(x)}\sin{(h)} }{h}}$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \ на 0} { \left( \frac{ -\cos{(x)} (1-\cos{(h)}) }{h} – \frac{ \sin{(x)}\sin{(h) } }{h} \right) }$$
$$\frac{d}{dx} f(x) = \lim \limits_{h \to 0} { \frac{ -\cos{(x)} (1-\cos{(h)}) }{h} } – \lim \limits_{h \to 0} { \frac{ \sin{(x)}\sin{(h)} }{h} }$$
Como estamos calculando el límite en términos de h , todas las funciones que no sean h se считает постоянными. Reorganizando, tenemos
Reorganizando, tenemos
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \frac{ (1-\cos {(h)}) }{h} } \right) – \sin{(x)} \left( \lim \limits_{h \to 0} { \frac{ \sin{(h)} }{h} } \справа)$$
Ограничение тригонометрических функций $latex \cos(\theta)$ a $latex \theta$ a medida que $latex \theta $ tiende a cero es igual uno. Миссия, которую вы можете применить к $latex \cos(h)$, содержит $latex H$. Апликандо, tenemos
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \frac{ (1-\cos {(h)}) }{h} } \right) – \sin{(x)} \cdot 1$$
$$\frac{d}{dx} f(x) = -\cos{(x )} \left( \lim \limits_{h \to 0} { \frac{ (1-\cos{(h)}) }{h} } \right) – \sin{(x)}$$
Ya hemos evaluado el límite del ultimo término. Грех эмбарго, el Primer término aún es imposible de ser Evaluado definitivamente debido al denominador $latex H $. Intentemos usar otra identidad trigonometrica ver si el truco funcionará.
Подемос намерен использовать ла identidad де medio ángulo en el numerador del Primer término. {2}{\left(\frac{h}{2}\right)}\right) }{h} } \right) – \sin{(x)}$$ 9{2}{\left(\frac{h}{2}\right)} }{ \frac{h}{2} }} \right) – \sin{(x)}$$
{2}{\left(\frac{h}{2}\right)}\right) }{h} } \right) – \sin{(x)}$$ 9{2}{\left(\frac{h}{2}\right)} }{ \frac{h}{2} }} \right) – \sin{(x)}$$
$$\frac {d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \frac{ \sin{\left(\frac{h}{2} \right)} \cdot \sin{\left(\frac{h}{2}\right)} }{ \frac{h}{2} }} \right) — \sin{(x)}$$
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \sin{\left(\frac{h}{ 2}\right)} \cdot \left( \frac{\sin{\left(\frac{h}{2}\right)} }{\frac{h}{2} } \right) }\right) – \sin{(x)}$$
Como notará una vez más, tenemos un seno de una variable sobre esa misma variable. En este caso, es $latex \sin{\left(\frac{h}{2}\right)}$ sobre $latex \frac{h}{2}$. Por lo tanto, podemos aplicar nuevamente los limites de las funciones trigonométricas de $latex \frac{\sin{(\theta)}}{\theta}$.
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \sin{\left(\frac{h} {2}\right)} \cdot 1} \right) – \sin{(x)}$$
Finalmente, hemos logrado Evaluar el límite del primer término. Оценка, подтверждающая аппроксимацию $латекса h$, тенемос
Оценка, подтверждающая аппроксимацию $латекса h$, тенемос
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0 } { \sin{\left(\frac{h}{2}\right)} }\right) — \sin{(x)}$$
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \sin{\left(\frac{0}{2}\right)}} \right) — \sin{( х)}$$
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} { \sin{(0)}} \right) – \sin{(x)}$$
$$\frac{d}{dx} f(x) = -\cos{(x)} \left( \lim \limits_{h \to 0} {0 } \right) – \sin(x)$$
$$\frac{d}{dx} f(x) = -\cos{(x)} \cdot 0 – \sin{(x)}$$
$$\frac{d}{dx} f(x) = -\sin{(x)}$$
Порт, производная тригонометрической функции ‘coseno’, es:
$$\frac{ d}{dx} (\cos{(x)}) = -\sin{(x)}$$
¿Cómo производная функция coseno?
El proceso de derivación de una función coseno es muy sencillo, suponiendo que ya haya aprendido los conceptos detrás del uso de la función coseno y cómo llegamos a su fórmula derivada.
МЕТОД 1: Деривада-дель-Козено-де-Куалькиер-Ангуло
x на концах ангуло x| $latex \frac{d}{dx} \left(\cos{right) = -\sin{(x)}$ |
Paso 1: Аналитика си эль косено де ун ангуло эс уна функция де эти миссмо ангуло. Por ejemplo, si el lado derecho de la ecuación es $latex \cos(x)$, verifique si es una función del mismo ángulo x 91 602 или 91 599 f 91 602 ( 91 599 x 91 602 ).
Por ejemplo, si el lado derecho de la ecuación es $latex \cos(x)$, verifique si es una función del mismo ángulo x 91 602 или 91 599 f 91 602 ( 91 599 x 91 602 ).
NOTA: Si $ LATEX \ COS (X) $ ES UNA FUNCIón de un ángulo o variable difbreente F ( T ) O F ( T ) O F ( T ) O F ( T ) O F ( T ). está fuera del alcance de este artículo.
Пасо 2: Прямая аппликационная формула, производная от функции coseno
0908
Si nada se va a simplificar más, entonces esa sería la respuesta final.
MÉTODO 2: Производное Coseno de cualquier función
u en terminos de x| $latex \frac{d}{dx} \left( \cos{(u)} \right) = \sin{(u)} \cdot \frac{d}{dx} (u)$ |
Paso 1: Выражение функции x ($) \cos(u)$, donde $latex u$ представляет собой дополнительную функцию, не связанную с морем х .
Paso 2: Рассмотрим $latex \cos{(u)}$ как внешнюю функцию $latex f(u)$ y $latex u$ (внутреннюю функцию $latex x)$ вычисляет функцию $latex F(x)$. Por lo tanto, tenemos
$latex f(u) = \cos{(u)}$
y también
$latex g(x) = u$
9 Пасо Получение производной внешней функции $latex f(u)$, которая используется для производной функции coseno, на концах $latex u$.
$латекс \frac{d}{du} \left( \cos{(u)} \right) = -\sin{(u)}$
Пасо 4: Получение производной внутренней функции $latex g(x) = u$. Используйте la regla de derivada apropiada que se aplica a $latex u$.
Paso 5: Аппликация формулы регламента кадены базовая мультипликаторная алгебраическая производная от внешней функции $latex $(u)$ )$
$латекс \frac{dy}{dx} = \frac{d}{du} (f(u)) \cdot \frac{d}{dx} (g(x))$
$latex \frac {dy}{dx} = -\sin{(u)} \cdot \frac{d}{dx} (u)$
Paso 6: Substituye $latex u$ en $latex f'(u)$
Paso 7: Simplifique y aplique cualquier ley de función cuando matcha para finalizar la respuesta.
Графико де Косено де
x по сравнению с производной от xФункция
$latex f(x) = \cos{(x)}$
el graphic se ilustra como
Y al comemos производная $latex f(x) = \cos{(x)}$, полученная
$latex f'(x) = -\sin{(x)}$
, которая иллюстрирует графику вместе с
Ilustrando ambas graficas en una, tenemos
Анализ различий между функциями и графиками, возможность наблюдения за оригинальной функцией $latex f(x) = \cos(x)$ tiene un dominio de
$latex (-\infty,\infty)$ или todos los números reales
y exists dentro del rango de
$latex [-1,1]$
mientras que la derivada $latex f ‘(x) = -\sin(x)$ есть в доме по номеру
$latex (-\infty,\infty)$ или по всем числовым объектам
и существует в центре ранго
$latex [-1,1]$
Ejemplos
A continuación se muestran algunos ejemplos del uso del primer o segundo método para derivar una función coseno.
EJEMPLO 1
Производное: $latex f(\beta) = \cos{(\beta)}$
Решение: Анализ функции прикосновения, $ vemos que es solo un coseno gulo de un латекс \бета $. Por lo tanto, podemos usar el primer método para derivar este Problema.
Paso 1: Анализ $latex \beta$ является функцией $latex \beta$. En este problema, lo es. Por lo tanto, продолжение с el paso 2.
92$
Paso 3: Получение производной внешней функции $latex f(u)$, которую нужно использовать для производной функции coseno, en términos de $latex u$.
$latex \frac{d}{du} \left( \cos{(u)} \right) = -\sin{(u)}$
Paso 4: Обтенга ла производная от внутренней функции $latex g(x)$ или $latex u$. Dado Que Nuestra $latex u$ en Este Problema Es una Function polinomial, usaremos la regla de la potencia y la suma/diferencia de derivadas para derivard $latex u$.