Ответ: Наша производная будет выглядеть так f(x)’ = 2 * (соs (x)) * (sin (x)) – 2 * (sin (x)) * (соs (x)) = 0.
[email protected] Выход
Этот математический калькулятор онлайн поможет вам если нужно найти производную функции. Программа решения производной не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения производной функции.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Вы можете посмотреть теорию о производной функции и правила дифференцирования и таблицу производных, т.е. список формул для нахождения производных от некоторых элементарных функций.
Если вам нужно найти уравнение касательной к графику функции, то для этого у нас есть задача Уравнение касательной к графику функции.
Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите выражение функции Найти производную функции f(x)
В решении ошибка
Если вы считаете, что задача решена не правильно, то нажмите на эту кнопку.
Определение производной
Определение. Пусть функция ( y = f(x) ) определена в некотором интервале, содержащем внутри себя точку ( x_0 ). Дадим аргументу приращение ( Delta x ) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции ( Delta y ) (при переходе от точки ( x_0 ) к точке ( x_0 + Delta x ) ) и составим отношение ( frac). Если существует предел этого отношения при ( Delta x
Найдем соответствующее приращение функции ( Delta y ) (при переходе от точки ( x_0 ) к точке ( x_0 + Delta x ) ) и составим отношение ( frac). Если существует предел этого отношения при ( Delta x
ightarrow 0 ), то указанный предел называют производной функции ( y=f(x) ) в точке ( x_0 ) и обозначают ( f'(x_0) ).
Для обозначения производной часто используют символ y’. Отметим, что y’ = f(x) — это новая функция, но, естественно, связанная с функцией y = f(x), определенная во всех точках x, в которых существует указанный выше предел. Эту функцию называют так: производная функции у = f(x).
Геометрический смысл производной состоит в следующем. Если к графику функции у = f(x) в точке с абсциссой х=a можно провести касательную, непараллельную оси y, то f(a) выражает угловой коэффициент касательной:
( k = f'(a) )
Поскольку ( k = tg(a) ), то верно равенство ( f'(a) = tg(a) ) .
А теперь истолкуем определение производной с точки зрения приближенных равенств.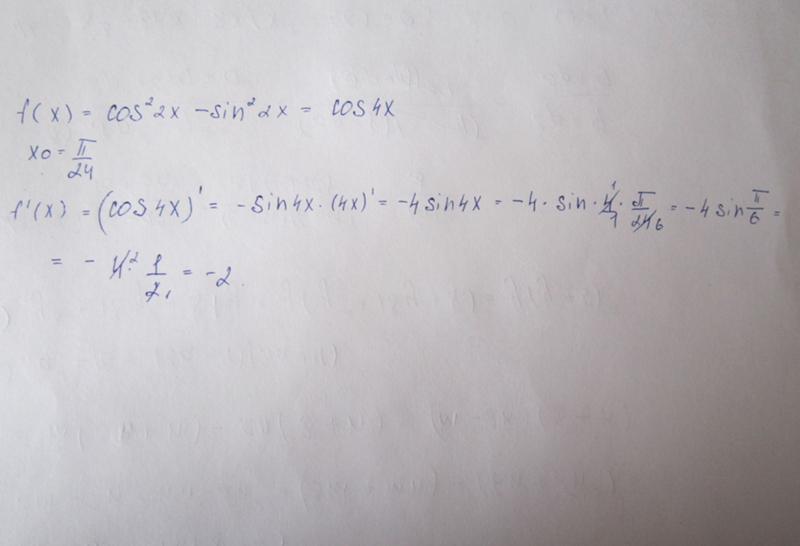 2 ) справедливо приближенное равенство ( Delta y approx 2x cdot Delta x ). Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.
2 ) справедливо приближенное равенство ( Delta y approx 2x cdot Delta x ). Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.
Как найти производную функции у = f(x) ?
1. Зафиксировать значение ( x ), найти ( f(x) )
2. Дать аргументу ( x ) приращение ( Delta x ), перейти в новую точку ( x+ Delta x ), найти ( f(x+ Delta x) )
3. Найти приращение функции: ( Delta y = f(x + Delta x) — f(x) )
4. Составить отношение ( frac)
5. Вычислить $$ lim_ frac$$
Этот предел и есть производная функции в точке x.
Если функция у = f(x) имеет производную в точке х, то ее называют дифференцируемой в точке х. Процедуру нахождения производной функции у = f(x) называют дифференцированием функции у = f(x).
Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.
Пусть функция у = f(x) дифференцируема в точке х. Тогда к графику функции в точке М(х; f(x)) можно провести касательную, причем, напомним, угловой коэффициент касательной равен f'(x). Такой график не может «разрываться» в точке М, т. е. функция обязана быть непрерывной в точке х.
Такой график не может «разрываться» в точке М, т. е. функция обязана быть непрерывной в точке х.
Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция у = f(x) дифференцируема в точке х, то выполняется приближенное равенство ( Delta y approx f'(x) cdot Delta x ). Если в этом равенстве ( Delta x ) устремить к нулю, то и ( Delta y ) будет стремиться к нулю, а это и есть условие непрерывности функции в точке.
Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке.
Обратное утверждение неверно. Например: функция у = |х| непрерывна везде, в частности в точке х = 0, но касательная к графику функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой точке не существует производная.
Еще один пример. Функция ( y=sqrt[3] ) непрерывна на всей числовой прямой, в том числе в точке х = 0. И касательная к графику функции существует в любой точке, в том числе в точке х = 0. Но в этой точке касательная совпадает с осью у, т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид х = 0. Углового коэффициента у такой прямой нет, значит, не существует и ( f'(0) )
Но в этой точке касательная совпадает с осью у, т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид х = 0. Углового коэффициента у такой прямой нет, значит, не существует и ( f'(0) )
Итак, мы познакомились с новым свойством функции — дифференцируемостью. А как по графику функции можно сделать вывод о ее дифференцируемости?
Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.
Правила дифференцирования
Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу. Если C — постоянное число и f=f(x), g=g(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
Если C — постоянное число и f=f(x), g=g(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
Решение
Применим правило производной частного:
Производная косинус есть минус синус:
Затем примените цепочку правил. Умножим на :
Производная произведения константы на функцию есть произведение этой константы на производную данной функции.
В силу правила, применим: получим
Таким образом, в результате:
В результате последовательности правил:
Производная синуса есть косинус:
Затем примените цепочку правил. Умножим на :
Производная произведения константы на функцию есть произведение этой константы на производную данной функции.
В силу правила, применим: получим
Таким образом, в результате:
В результате последовательности правил:
В силу правила, применим: получим
Теперь применим правило производной деления:
Линейные дифференциальные уравнения с постоянными коэффициентами.
 Специальная часть cos(x),sin(x)
Пример 1.
Специальная часть cos(x),sin(x)
Пример 1.
y» +4y’ — 12y = 8sin(2x)
Решение уравнения будем искать в виде y = erx находим с помощью калькулятора. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r2 +4 r — 12 = 0
D = 42 — 4 • 1 • (-12) = 64
Корни характеристического уравнения:
r1 = 2
r2 = -6
Следовательно, фундаментальную систему решений составляют функции:
Общее решение однородного уравнения имеет вид:
Рассмотрим правую часть:
f(x) = 8•sin(2•x)
Поиск частного решения.
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида:
R(x) = eαx(P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы
y(x) = xkeαx(R(x)cos(βx) + S(x)sin(βx))
где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).

Здесь P(x) = 0, Q(x) = 8, α = 0, β = 2.
Следовательно, число α + βi = 0 + 2i не является корнем характеристического уравнения .
Уравнение имеет частное решение вида:
y* = Acos(2x) + Bsin(2x)
Вычисляем производные:
y’ = 2•B•cos(2x)-2•A•sin(2x)
y» = -4(A•cos(2x)+B•sin(2x))
которые подставляем в исходное дифференциальное уравнение:
y» + 4y’ -12y = (-4(A•cos(2x)+B•sin(2x))) + 4(2•B•cos(2x)-2•A•sin(2x)) -12(Acos(2x) + Bsin(2x)) = 8•sin(2•x)
или
-8•A•sin(2x)-16•A•cos(2x)-16•B•sin(2x)+8•B•cos(2x) = 8•sin(2•x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
-8A -16B = 8
-16A + 8B = 0
Решая ее, методом Гаусса находим:
A = -1/5;B = -2/5;
Частное решение имеет вид:
y* = —1/5cos(2x) —2/5sin(2x)
Таким образом, общее решение дифференциального уравнения имеет вид:
Пример 2.
4y’’ -8y’ + 5y = 5cos(x)
Решение уравнения будем искать в виде y = erx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
4 r2 -8 r + 5 = 0
D = (-8)2 — 4 • 4 • 5 = -16
Корни характеристического уравнения:
(комплексные корни):
r1 = 1 + 1/2i
r1 = 1 — 1/2i
Следовательно, фундаментальную систему решений составляют функции:
y1 = excos(1/2x)
y2 = exsin(1/2x)
Общее решение однородного уравнения имеет вид:
Рассмотрим правую часть:
f(x) = 5cos(x)
Поиск частного решения.
Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида:
R(x) = eαx(P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы
имеет частное решение
y(x) = xkeαx(R(x)cos(βx) + S(x)sin(βx))
где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
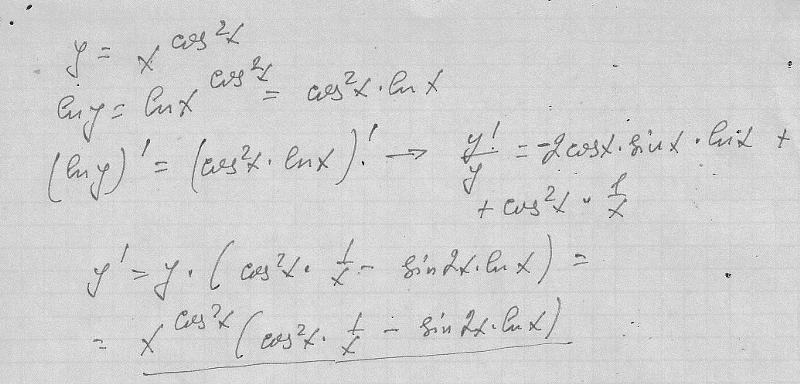
Здесь P(x) = 5, Q(x) = 0, α = 0, β = 1.
Следовательно, число α + βi = 0 + 1i не является корнем характеристического уравнения .
Уравнение имеет частное решение вида:
y* = Acos(x) + Bsin(x)
Вычисляем производные:
y’ = Bcos(x)-Asin(x)
y» = -Acos(x)-Bsin(x)
которые подставляем в исходное дифференциальное уравнение:
4y» -8y’ + 5y = 4(-Acos(x)-Bsin(x)) -8(Bcos(x)-Asin(x)) + 5(Acos(x) + Bsin(x)) = 5cos(x)
или
8Asin(x)+Acos(x)+Bsin(x)-8Bcos(x) = 5cos(x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
8A + B = 0
A -8B = 5
Решая ее методом Гаусса, находим:
A =
Частное решение имеет вид:
y* = 1/13cos(x) + -8/13sin(x)
Таким образом, общее решение дифференциального уравнения имеет вид:
Перейти к онлайн решению своей задачи
Пример 3. 2)’= 2 * (соs (x)) * (sin (x)) – 2 * (sin (x)) * (соs (x)) = 0.
2)’= 2 * (соs (x)) * (sin (x)) – 2 * (sin (x)) * (соs (x)) = 0.
Ответ: Наша производная будет выглядеть так f(x)’ = 2 * (соs (x)) * (sin (x)) – 2 * (sin (x)) * (соs (x)) = 0.
[email protected] Выход
Этот математический калькулятор онлайн поможет вам если нужно найти производную функции. Программа решения производной не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения производной функции.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Вы можете посмотреть теорию о производной функции и правила дифференцирования и таблицу производных, т.е. список формул для нахождения производных от некоторых элементарных функций.
Если вам нужно найти уравнение касательной к графику функции, то для этого у нас есть задача Уравнение касательной к графику функции.
Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите выражение функции Найти производную функции f(x)
В решении ошибка
Если вы считаете, что задача решена не правильно, то нажмите на эту кнопку.
Определение производной
Определение. Пусть функция ( y = f(x) ) определена в некотором интервале, содержащем внутри себя точку ( x_0 ). Дадим аргументу приращение ( Delta x ) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции ( Delta y ) (при переходе от точки ( x_0 ) к точке ( x_0 + Delta x ) ) и составим отношение ( frac<Delta y> <Delta x>). Если существует предел этого отношения при ( Delta x
ightarrow 0 ), то указанный предел называют производной функции ( y=f(x) ) в точке ( x_0 ) и обозначают ( f'(x_0) ).
Для обозначения производной часто используют символ y’. Отметим, что y’ = f(x) — это новая функция, но, естественно, связанная с функцией y = f(x), определенная во всех точках x, в которых существует указанный выше предел. Эту функцию называют так: производная функции у = f(x).
Геометрический смысл производной состоит в следующем. Если к графику функции у = f(x) в точке с абсциссой х=a можно провести касательную, непараллельную оси y, то f(a) выражает угловой коэффициент касательной:
( k = f'(a) )
Поскольку ( k = tg(a) ), то верно равенство ( f'(a) = tg(a) ) .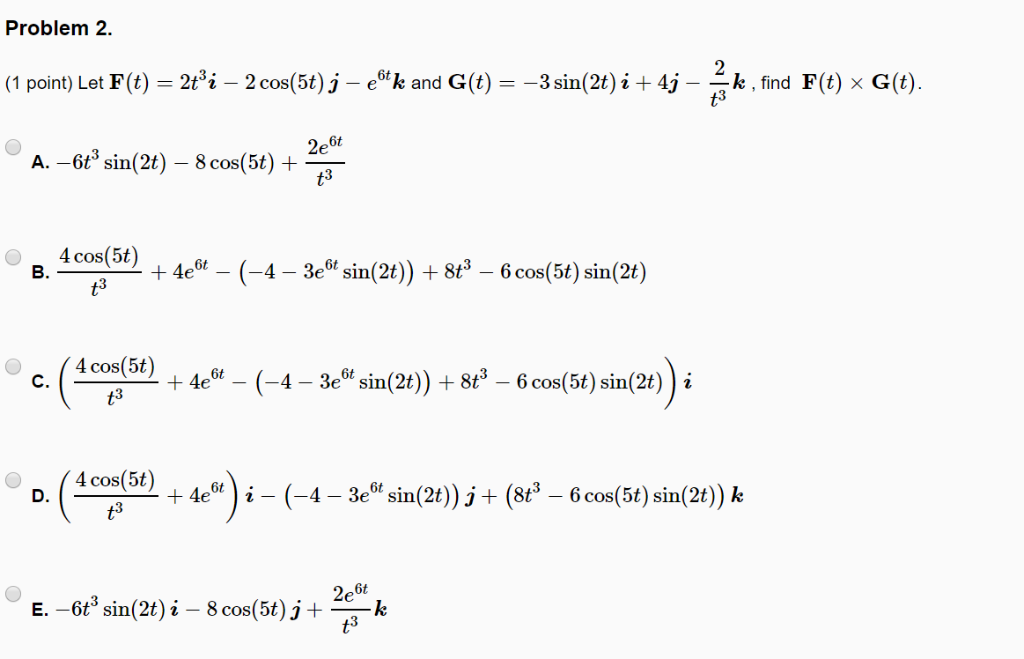 2 ) справедливо приближенное равенство ( Delta y approx 2x cdot Delta x ). Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.
2 ) справедливо приближенное равенство ( Delta y approx 2x cdot Delta x ). Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.
Как найти производную функции у = f(x) ?
1. Зафиксировать значение ( x ), найти ( f(x) )
2. Дать аргументу ( x ) приращение ( Delta x ), перейти в новую точку ( x+ Delta x ), найти ( f(x+ Delta x) )
3. Найти приращение функции: ( Delta y = f(x + Delta x) — f(x) )
4. Составить отношение ( frac<Delta y> <Delta x>)
5. Вычислить $$ lim_ <Delta x o 0>frac<Delta y> <Delta x>$$
Этот предел и есть производная функции в точке x.
Если функция у = f(x) имеет производную в точке х, то ее называют дифференцируемой в точке х. Процедуру нахождения производной функции у = f(x) называют дифференцированием функции у = f(x).
Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.
Пусть функция у = f(x) дифференцируема в точке х. Тогда к графику функции в точке М(х; f(x)) можно провести касательную, причем, напомним, угловой коэффициент касательной равен f'(x). Такой график не может «разрываться» в точке М, т. е. функция обязана быть непрерывной в точке х.
Тогда к графику функции в точке М(х; f(x)) можно провести касательную, причем, напомним, угловой коэффициент касательной равен f'(x). Такой график не может «разрываться» в точке М, т. е. функция обязана быть непрерывной в точке х.
Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция у = f(x) дифференцируема в точке х, то выполняется приближенное равенство ( Delta y approx f'(x) cdot Delta x ). Если в этом равенстве ( Delta x ) устремить к нулю, то и ( Delta y ) будет стремиться к нулю, а это и есть условие непрерывности функции в точке.
Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке.
Обратное утверждение неверно. Например: функция у = |х| непрерывна везде, в частности в точке х = 0, но касательная к графику функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой точке не существует производная.
Еще один пример. Функция ( y=sqrt[3] ) непрерывна на всей числовой прямой, в том числе в точке х = 0.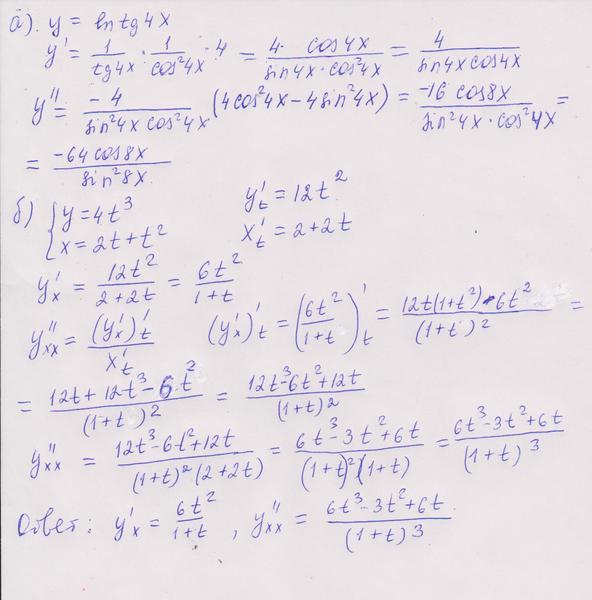 И касательная к графику функции существует в любой точке, в том числе в точке х = 0. Но в этой точке касательная совпадает с осью у, т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид х = 0. Углового коэффициента у такой прямой нет, значит, не существует и ( f'(0) )
И касательная к графику функции существует в любой точке, в том числе в точке х = 0. Но в этой точке касательная совпадает с осью у, т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид х = 0. Углового коэффициента у такой прямой нет, значит, не существует и ( f'(0) )
Итак, мы познакомились с новым свойством функции — дифференцируемостью. А как по графику функции можно сделать вывод о ее дифференцируемости?
Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.
Правила дифференцирования
Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу. Если C — постоянное число и f=f(x), g=g(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу. Если C — постоянное число и f=f(x), g=g(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
Решение
Применим правило производной частного:
Производная косинус есть минус синус:
Затем примените цепочку правил. Умножим на :
Производная произведения константы на функцию есть произведение этой константы на производную данной функции.
В силу правила, применим: получим
Таким образом, в результате:
В результате последовательности правил:
Производная синуса есть косинус:
Затем примените цепочку правил. Умножим на :
Производная произведения константы на функцию есть произведение этой константы на производную данной функции.
В силу правила, применим: получим
Таким образом, в результате:
В результате последовательности правил:
В силу правила, применим: получим
Теперь применим правило производной деления:
Найти производную функции y = cos2x ?
Алгебра, 2020-11-14 15:34:25, zlooo2
Ответ
Ответ разместил: Kisa2Mary
Производная — f'(x)=-2sin(2x)
Ответ
Ответ разместил: Vania54
1)y=cos2x
=y’=-2sin2x
2) y'()=
ответ:-1
Ответ
Ответ разместил: Zepstro
функция y=cos2x + 4x
производная y’=-2sin2x+4
значение производной функции y=cos2x + 4x в точке x0=Pi/2
y'(pi/2)=-2*sin2*(pi/2)+4=-2*sin pi + 4=-2*0+4=4
ответ:y'(pi/2)=4
Ответ
Ответ разместил: adamabiev
Y’= -sin2x*(2x)’+3=3-2sin2x
Ответ
Ответ разместил: lehakharitonov
Y’=-2sin(2x)
y'(pi/4)=-2sin(pi/2)=-2
Ответ
Ответ разместил: ВероникаФардзинова
Y=cos2x+3x
y’=(cosz)'(2x)’+3(x)’=-2sin2x+3 z=2x
Ответ
Ответ разместил: Фадиля
Y=cos2x
y’=-sin2x·(2x)’=-2sin2x
Ответ
Ответ разместил: qwertyqwerty1233
Y`=[(-2sin2x*(4x-3)+4cos2x)*2x³-6x²*cos2x*(4x-3)]/4x^6 +
+3x²*cosx³*ctg(3x/4) + 3/4*sinx³*[-1/sin²(3x/4)]=
=(-2xsin2x*(4x-3)+4cos2x- 3cos2x*(4x-3)]/2x^64 +3x²*cosx³*ctg(3x/4) -3sinx³/sin²(3x/4)
Ответ
Ответ разместил: Tara8808
ответ ответ ответ ответ ответ ответ
Ответ
Ответ разместил: kirillBruchov
У меня получилось так
Ответ
Ответ разместил: lilulurens
внизу на красном фоне ответ. 2-45x-2 на отрезке: [-6; -1]…
2-45x-2 на отрезке: [-6; -1]…
Ответов: 3
Опубликовано: 01.03.2019 15:40
Велосипедист выехал из пункта а. когда он был на расстоянии 200м от него , за ним вдогонку отправился мотоциклист. скорость мотоциклиста в 2 раза больше скорости велосипедиста . на…
Ответов: 3
Опубликовано: 01.03.2019 15:50
Примеры различных видов движения клеток. сравните механизм движения у разных видов клеток….
Ответов: 2
Опубликовано: 01.03.2019 19:10
1)структурная формула 2 2 3- триметилпентан 2)определите число первичных, вторичных, третичных и четвертичных атомов углерода 3)напишите уравнения реакции галогенирования этого сое…
Ответов: 2
Опубликовано: 01.03.2019 19:40
Дано: a=30 см b=20 см c=25 см определить массу воды в аквариуме. побыстрее!. ..
..
Ответов: 1
Опубликовано: 02.03.2019 02:50
Вразные эпохи у молодёжи были свои кумиров(люди, которым молодёжь хотела поражать)кого можно назвать идеалом современной молодёжи ? почему?…
Ответов: 2
Популярные вопросы
Опубликовано: 28.02.2019 20:00
Автобус выехал в 8 часов утра и ехал три часа со скоростью 60км/ч. за это время было пройдено 3/4 всего расстояния. с какой скоростью автобусу надо проехать оставшуюся часть пути,…
Ответов: 2
Опубликовано: 28.02.2019 21:20
Двое рабочих выполнили вместе некоторую работу за 12 часов. если бы сначалапервый рабочий сделал половину этой работы, а затем другой остальную часть, то вся работа была бы выполне…
Ответов: 2
Опубликовано: 01.03.2019 05:10
Составьте молекулярные и ионные уровнения гидролиза солей k3po4 и k2hpo4 раствор какой из этих двух солей имеет большое значение ph? почему?. ..
..
Ответов: 3
Опубликовано: 02.03.2019 18:50
Выполнить действия: а) 12 мин 23 с + 7 мин 52 с б) 6 ч 18 мин — 3 ч 49 мин…
Ответов: 3
Опубликовано: 03.03.2019 14:40
В1-й день турист половину всего пути, во 2-й день две третьи его оставшейся части. какую часть осталось пройти за 3-й день?…
Ответов: 2
Опубликовано: 04.03.2019 08:00
425 рабочих заводов изготавливают по 236 деталей в день. двадцать пятая часть деталей идет на продажу, половину оставшихся деталей закупает автомобильный завод. сколько деталей зак…
Ответов: 2
Опубликовано: 07.03.2019 16:00
Основание пирамиды – прямоугольник со сторонами 6см и 8 см. высота пирамиды равна 12 см и проходит через точку пересечения диагоналей основания. найдите боковые ребра пирамиды.. ..
..
Ответов: 1
Опубликовано: 08.03.2019 00:01
Два туриста вышли навстречу друг другу из двух поселков. первый шел со скоростью 5 км/ч. второй вышел на 2 часа позже первого и шел со скоростью 6 км/ч. сколько времени до встречи…
Ответов: 3
Опубликовано: 08.03.2019 02:30
Какое число атомов содержится в аммиаке nh4объёмом11,2 дм3…
Ответов: 1
Опубликовано: 08.03.2019 03:20
Втреугольнике авс медиана аd и бессектриса ве пересекаются в точке о. если ad перпердикулярно ве и s(aoe)=2,то площадь треугольника авс равна если можно с рисунком…
Ответов: 2
Больше вопросов по предмету: Алгебра Случайные вопросы
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Производная от Sin2x | Шаги, poof, правила, вычисление
Дифференциация тригонометрических признаков также является математическим подходом к получению побочного продукта тригонометрической характеристики или ее платы за экстрадицию по отношению к переменной. Тем не менее, тригонометрические функции нередко занимают места sin (x), cos (x) и tan (x) (x). Например, f ′(a) = cos(x) является побочным продуктом f(x) = sin(x) (a). Плата за выдачу sin(x) при определенном коэффициенте обозначается через f ′(a).
Тем не менее, тригонометрические функции нередко занимают места sin (x), cos (x) и tan (x) (x). Например, f ′(a) = cos(x) является побочным продуктом f(x) = sin(x) (a). Плата за выдачу sin(x) при определенном коэффициенте обозначается через f ′(a).
Однако sin(x) и cos(x) могут быть использованы для получения производных всех тригонометрических признаков округления. Однако, чтобы дифференцировать последующее выражение, соблюдайте правило отношения. Затем, используя неявное дифференцирование и сквозную торговлю правильными тригонометрическими признаками, необходимо обнаружить производные обратных тригонометрических признаков.
Давайте оценим некоторые статистические данные приблизительно в 2 раза раньше, чем сразу перейдем к поиску побочного продукта. 2x — это двойная перспектива, а sin 2x = 2 sin x cos x — одна из формул двойной перспективы. Поскольку sin 2x имеет двойную перспективу, его побочный продукт также имеет двойную перспективу. Однако, используя многочисленные методы, мы можем показать, что побочным продуктом sin 2x в этой статье является два cos 2x.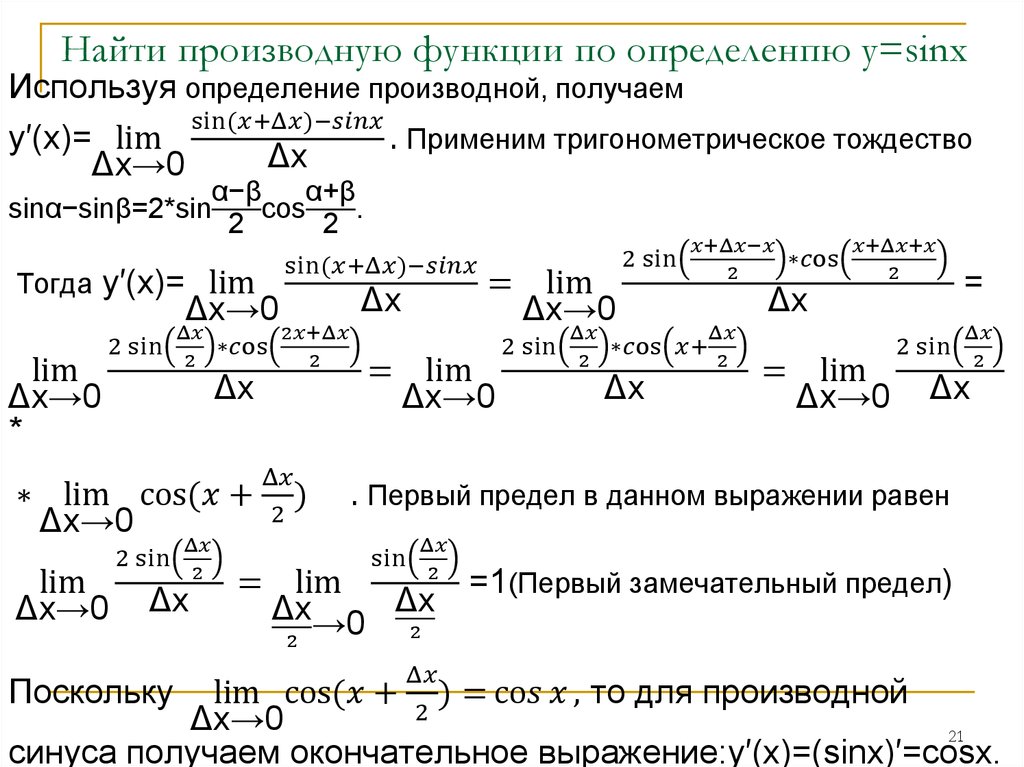
Давайте рассмотрим некоторые необычные подходы к получению побочного продукта sin 2x и используем его для прояснения некоторых случаев. Кроме того, не забывайте о различиях между производными sin 2x и sin2x.
Содержание
Что такое производная от Sin2x2 cos 2x является побочным продуктом sin2x. Однако в математике это записывается как d/dx (sin 2x) = 2 cos 2x (или) (sin 2x)’ = 2 cos 2x. Тогда синусоидальная характеристика в двойной перспективе равна f(x) = sin 2x. Однако дифференциация sin 2x может быть проведена множеством подходов, в том числе:
- Используя первичное правило
- Затем, используя цепное правило
- Затем, используя правило произведения
. В результате производные необходимы для решения задач исчисления и дифференциальных уравнений. В общем, ученые изучают системы преобразования (динамические системы), чтобы определить плату за экстрадирование интересующей переменной, затем подставляют эти данные прямо в дифференциальное уравнение и используют стратегии интегрирования, чтобы получить характеристику, которая может быть использована для того, чтобы ожидать, как уникальные машина будет вести себя в различных условиях.
Читайте также: Калькулятор интервала сходимости — значение, использование, серия
Характеристика, которая не всегда непрерывна, не может быть дифференцируемой, поскольку каждая дифференцируемая характеристика должна быть непрерывной. Характеристика также может быть дифференцируемой, а может и не быть дифференцируемой, даже если она проходит много миль без остановок.
Производная формулы Sin2x2 cos 2x является производной от sin 2x. Его можно представить как d/dx (sin 2x) = 2 cos 2x (sin 2x) = 2 cos 2x (sin 2x)’ = 2 cos 2x
Производная Sin2x с использованием первого принципаПервый принцип используется для дифференциации sin 2x. Предположим, что в этом случае f(x) = sin 2x. Тогда sin 2(x + h) = sin (2x + 2h) = f(x + h) = f(x + h) = f(x + h) = f(x + h) = f(x +). основная заповедь, замена этих чисел в формуле побочного продукта (определение ограничения побочного продукта),
f'(x) = limₕ→₀ [f(x + h) – f(x)] / h
Тогда f'(x) = limₕ→₀ [sin (2x + 2h) – sin 2x] / h
Точно так же мы можем упростить этот предел двумя способами.
По одной из тригонометрических формул sin C – sin D = 2 cos [(C + D)/2] sin [(C – D)/2]. Однако, применяя это, мы получаем
f'(x) = limₕ→₀ [2 cos[(2x + 2h + 2x)/2] sin[(2x +2h – 2x)/2] ] / h
Тогда f'(x) = limₕ→₀ [2 cos[(4x + 2h)/2] sin (h) ] / h
Тогда f'(x) = 2 limₕ→₀ [cos[(4x + 2h)/2] · limₕ→₀ [sin h / h]
Однако, используя предельные формулы, lim ₓ→₀ (sin x/x) = 1. Итак,
f'(x) = 2 [cos[(4x + 0)/2] · (1) = 2 cos (4x/2) = 2 cos 2x
Таким образом, мы доказали, что производная от sin 2x равна 2 кос 2х.
Метод 2По формулам суммы и разности,
sin (A + B) = sin A cos B + cos A sin B
Используя это,
f'(x) = limₕ→₀ [sin 2x cos 2h + cos 2x sin 2h – sin 2x] / h
Тогда f'(x) = limₕ→₀ [ – sin 2x (1- cos 2h) + cos 2x sin 2h] / h
Тогда f ‘(x) = limₕ→₀ [- sin 2x (1 — cos 2h)]/h + limₕ→₀ (cos 2x sin 2h)/h
Аналогично, f'(x) = -sin 2x limₕ→₀ (1 – cos 2h)/h + (cos 2x) limₕ→₀ sin 2h/h
Однако, используя формулы двойного угла, 1 – cos(2h ) = 2 sin2(h).
Следовательно, f'(x) = -sin 2x limₕ→₀ (2 sin2(h))/h + (cos 2x) limₕ→₀ sin 2h/h
= -2sin 2x [limₕ→₀ sin (h ) / (h) · limₕ→₀ sin h] + (cos 2x) (limₕ→₀ sin 2h/h)
Однако по одной из предельных формул lim ₓ→₀ (sin x/x) = 1 и lim ₓ→₀ (sin ax/x) = a.
Итак, f'(x) = -2sin 2x (1 · sin 0) + cos 2x (2)
Тогда f'(x) = -2sin 2x(0) + 2 cos 2x (Из тригонометрической таблицы sin 0 = 0)
Следовательно, f'(x) = 2 cos 2x
В результате имеем способны сделать вывод, что побочным продуктом sin 2x является два cos 2x.
Первая заповедь используется для обнаружения побочного продукта sin 2x.
Производная Sin2x с использованием правила произведенияПроизводная Sin 2x Доказательное правило произведения
Чтобы получить производную f(x) = sin 2x с использованием правила произведения, мы должны выразить sin 2x как произведение двух функций. Используя формулу двойного угла для греха, мы получаем Sin 2x = 2 sin x cos x. Рассмотрим уравнения v = cos x и u = 2 sin x. Затем вычисляются v’ = -sin x и u’ = 2 cos x. По общему правилу 9Производная от Sin2x
Рассмотрим уравнения v = cos x и u = 2 sin x. Затем вычисляются v’ = -sin x и u’ = 2 cos x. По общему правилу 9Производная от Sin2x
Производная от sin 2x, полученная итеративным дифференцированием sin 2x n раз, называется n-й производной. Найдите первую производную, вторую производную и так далее, пока не будет определена n-я производная от sin 2x, чтобы понять тренд/паттерн.
2 cos 2x — первая производная от sin 2x.
Тогда вторая производная sin 2x становится -4 sin 2x.
Тогда третья производная sin 2x равна -8 cos 2x.
Точно так же четвертая производная sin 2x равна 16 sin 2x.
Аналогично, 5-я производная sin 2x равна 32 cos 2x, и наоборот.
Тогда 6-я производная sin 2x равна -64 sin 2x.
Точно так же седьмая производная sin 2x равна -128 cos 2x.
Точно так же 8-я производная от sin 2x, например, равна 256 sin 2x и так далее.
Используя эту тенденцию, n-я производная от sin 2x может быть рассчитана следующим образом:
(sin 2x)(n) = (sin 2x)(n)(n)
Производная от Sin2x с использованием цепного правилаПроизводное от Sin 2x Цепное правило доказательства
В этом примере мы попробуем применить Цепное правило к трем функциям, которые вложены друг в друга. Это тоже первая и самая главная роль. После этого следует функция sin, за которой следует функция cos. Создавайте каждую из них, как если бы она была единственной в своем роде, используя правило цепочки (независимо от аргумента). В качестве наглядного пособия мы также перемножим каждую производную по отдельности. Чтобы различать каждую производную, мы можем использовать красно-сине-зеленую цветовую схему.
Это тоже первая и самая главная роль. После этого следует функция sin, за которой следует функция cos. Создавайте каждую из них, как если бы она была единственной в своем роде, используя правило цепочки (независимо от аргумента). В качестве наглядного пособия мы также перемножим каждую производную по отдельности. Чтобы различать каждую производную, мы можем использовать красно-сине-зеленую цветовую схему.
Цепное правило, с другой стороны, представляет собой формулу исчисления, которая вычисляет производную набора двух или более функций. Это верно только в том случае, если f и g являются обеими функциями. В результате производная составной функции fg выражается по цепному правилу как производная от f и g.
Однако, если g дифференцируема в точке x и f в g(x), составная функция F = f g, определяемая формулой F(x) = f(g(x)) дифференцируема в точке x, а F’ определяется произведение F'(x) = f'(g(x)).g'(x)
Если y = f (u) и u = g(x) являются дифференцируемыми функциями в системе обозначений Лейбница, то dy/dx = dy/du. du/dx
du/dx
Цепное правило может быть записано либо в простом, либо в не- простое обозначение (f g)'(x) = f'(g(x))g’ или в составном обозначении f(g)'(x) = f'(g(x)g'(x)
f'( x) = 4 sin(2x) cos(2x)
Эту функцию можно сжать, используя тригонометрическое тождество (получив: 2sin(4x)), но мы не хотим усложнять ситуацию.
Производная Sin2x относительно до хSin2 x имеет производную.
Производная sin2x не совпадает с производной sin2x. Производная от sin2x равна sin2x. Давайте посмотрим, что мы можем придумать. Предположим, что f(x) равно sin2x. Формулу для f(x) = (sin x)2 можно найти здесь. Чтобы найти его производную, мы можем использовать комбинацию степенного правила и цепного правила. В результате f'(x) = 2(sin x) d/dx(sin x) = 2 sin x cos x = sin 2x (при использовании формулы двойного угла для sin)
В результате производная sin2x это грех 2x.
Важные моменты, которые следует помнить о производной sin 2x:
Производная sin 2x равна 2 cos 2x.
Ось cos обычно является производной от оси sin.
Sin 2x и sin2x не имеют одинаковых производных.
d/dx (sin 2x) = 2 cos 2x
d/dx (sin2x) = sin 2x
Производная от Sin2x cos2xЗначение sin2x Cos 2x вычисляется с использованием тригонометрических формул двойного угла. При выводе используются значения sin 2x и cos 2x.
Из тригонометрических формул двойного угла выводятся тригонометрические формулы двойного угла.
Sin 2x = 2 sin x cos x ————(i)
И,
Cos 2x = Cos2x − Sin2x
= 2 cos2x − 1 ————(ii) [Поскольку Sin2 x + Cos2 x = 1]
= 1 − 2Sin2x ————(iii)
Теперь, чтобы получить значение Sin 2x Cos 2x, умножьте уравнение (i) на (ii) или (i)
Рассмотрим уравнение (i) и (ii)
Sin 2x = 2 sin x cos x
And,
Cos 2x = 2 cos2x − 1
Умножьте их, чтобы получить 2 Cos x (2 Sin x Cos2 x − Sin x)
Теперь рассмотрим уравнения (i) и (iii),
Sin 2x = 2 sin x cos x
And,
Cos 2x = 1 − 2 Sin2x
Умножьте их, чтобы получить Грех3 х)
So,
Sin 2x Cos 2x = 2 Cos x (2 Sin x Cos2 x − Sin x)
Или,
Sin 2x Cos 2x = 2 Cos x (Sin x – 2 Sin3 x)
Производная 9 of Sin 2x Cos 2x
d/dx (Sin 2x Cos 2x) = 2Cos(4x)
Доказательство:
Sin(2x)cos(2x)
= ½(2sin(2x)cos(2x))
Или, ½Sin(4x)
Теперь продифференцируем данную функцию по x:
d/dx [½ Sin (4x)]
= ½[ d/dx (Sin(4x) ) ]
9cos x относительно x,dz/dx = d(ecos x)/dx
= ecos x × d(cos x)/dx
= ecos x × (-sinx)
= -sinx . ecos x
ecos x
В результате dz/dx = -sinx является дифференцированием e cos x по x.
Мы получаем дифференцирование sin2x относительно e cos x путем деления (dy/dx) на (dz/dx).
В результате (dy/dx) / (dz/dx) = (2 sinx.cosx) / (-sinx.cos x), или dy/dz = -2 cos x/e cos x.
Производная от Sin2x /1+cosxПроизводная sin2x/ (1 + cosx)
Пусть y = sin2x/(1 + cosx)
Таким образом, используя правило частных,
dy/dx = {(1 + cosx) × d/dx (sin2x) – sin2x × d/dx (1+cosx)} / (1+cosx)2
Следовательно, dy/dx = {(1+cosx) * sinx.cosx – sin2x(-sinx)} / (1+cosx) 2
Тогда dy/dx = {sin2x + sinx.cosx + sin3x} / (1+cosx)2
Производная от Sin2x Cos3xПроизводная от sin2x cos3x
92ddxcos3x) = (sin2x) × d/dx (cos3x)+(cos3x) × d/dx (sin2x)
Таким образом, d/ dx (sin 2x.cos 3x) = (sin 2x) × d/dx (cos 3x)+(cos 3x) × d/dx (sin 2x)
Тогда d/ dx (sin 2x .cos 3x) = (sin 2x) × (−sin 3x) × 3+(cos 3x) × (cos 2x) × 2
= (sin 2x) × (-sin 3x) × 3+(cos 3x) × (cos 2x) × 2
[Мы используем цепное правило]
= (−3 sin 2x sin3x + 2 cos3x cos2x)
Следовательно, d/ dx (sin 2x.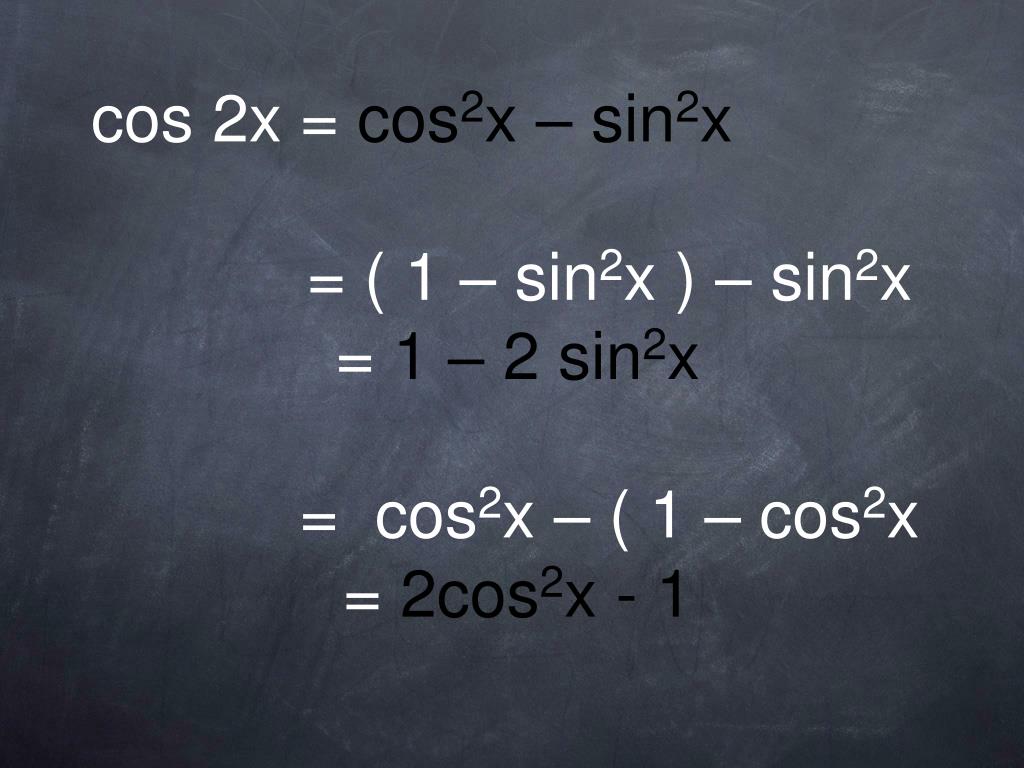 cos 3x) = (-3 sin 2x sin 3x + 2 cos 3x cos 2x)
cos 3x) = (-3 sin 2x sin 3x + 2 cos 3x cos 2x)
Производная Sin2x относительно cos2x
Мы уже знаем, что sin 2x равно 2sinxcosx и (uv)’=u’v+v’u. Это называется правилом дифференциации продукта.
d/dx (sin2x) = d/dx(2 sinx cosx) = 2 d/dx (sinx cosx) является результатом.
d/dx sin2x = 2sinx.d/dx cosx + 2cosx.d/dx sinx — правило произведения дифференцирования.
Теперь мы знаем, что производная sin равна cos, а производная cos x равна -sin x.
Отсюда имеем
d/dx sin 2x = 2 sin x (−sinx) + 2 cos x × cos x = 2(cos 2x − sin 2x) 9(2-1) × d/dz ( cos z )
Аналогично, dy/dx = 2 × sin x × cos z + 2 cos z (- sinz)
Тогда dy/dx = 2 × sin z × cos z – 2 × sin z × cos z
Тогда dy/dx = 0
Производная от ln sin2xВоспользуйтесь цепным правилом.
Ваша функция может быть разложена на логарифмическую, квадратную и синусоидальную составляющие следующим образом: )
Теперь необходимо вычислить три производные этих трех функций (и ввести соответствующие значения u и v):
f'(u)=1/u=1/v²=1/sin²x
u'(v)=2v=2sinx
v'(x)=cos(x)
Все, что осталось сделать сейчас умножить эти три производные:
f'(x) = f'(u) × u'(v) × v'(x) = 1/ sin² x 2 sin x cos x
= ( 2 cos x ) / sin x
Производная Sin2x при x=π/2sin 2x при x = π/2 Дано: f (x) = sin 2x Используя формулу производной,
f(a) = limₕ→₀ [ { f (a+h) – f (a) } / h], где h – положительное целое число небольшого размера.
Производная sin2x при x = π/2 задается как
f’ ( π/2 ) = limₕ→₀ [ { f ( π/2 + h ) – f (π/2) } / h ]
=limₕ→₀ [sin {2 × (π/2 + h)} – sin2 × π/2]/h
=limₕ→₀ {sin (π + 2h) – sin π}/h. [Следовательно, sin (π+x) = – sinx и sin π = 0]
=limₕ→₀ (-sin 2h – 0)/ h
=limₕ→₀ sin 2h / h
[Потому что неоднозначный характер. Чтобы определить предел, воспользуемся теоремой о сэндвиче.]
Умножив числитель и знаменатель на два, мы получим
= – limₕ→₀ (sin 2h / 2h ) × 2 = – 2 limₕ→₀ ( sin 2h / 2h)
Используя формулу lim x→₀ sinx / x = 1, получаем
f’ ( π/2 ) = – 2 × 1 = -2
Следовательно, производная sin 2x при x = π/2 равна (-2).
Найдите dy/dx, если y = sin2xЧтобы решить эту проблему, вы примените цепное правило. Для этого вам нужно выяснить, что такое «внешняя» функция, а также «внутренняя» функция, являющаяся частью внешней функции.
В этой ситуации sin(x) является внутренней функцией, являющейся частью функции sin2 (x). 2 x= 2sin x cos x= sin2x
2 x= 2sin x cos x= sin2x
В частности, dy/dx= 2*cos (2x). Помните цепное правило: сначала различайте внешнюю функцию, затем различайте внутреннюю функцию. Производная sin(x) по x равна cos(x), тогда как производная 2x по x равна только 2.
Является ли sin2x таким же, как 2sinx?2 — это синус 2, умноженный на х, или удвоенный угол х, тогда как 1 умножается на. В результате мы также получили два очень разных результата. Поскольку синус — это периодический (повторяющийся) сигнал, эти графики будут пересекаться через равные промежутки времени, давая один и тот же ответ для обоих уравнений! 9в 2 раза значит?
Техническое машиностроение, Институт инженерии и менеджмента. Между тем, 13 мая 2017 года я получил ответ на свой запрос. Поскольку это «синус (x в квадрате)», Sin x2 является обычной синусоидальной функцией. Функция синуса отличается от функции Sin2x, что означает «квадрат синуса от х».
Чтобы сложить cos2 x, выполните следующие действия:
- Используя тождество половинного угла для косинуса, перепишите интеграл через cos 2x. 92(х)?
Sin2x нельзя интегрировать напрямую (x). Затем для решения задачи используйте тригонометрические тождества и процедуры подстановки исчисления. Однако подставьте 1/2 интеграла от (1 – cos(2x)) dx в интеграл, используя формулу половинного угла sin2(x) = 1/2*(1 – cos(2x)).
Что такое цепное правило в исчислении?Производная от f(g(x)) равна f'(g(x))g’ в соответствии с цепным правилом (x). Иными словами, это помогает в дифференциации *составных функций*. Sin(x2), например, является составной функцией, поскольку ее можно записать как f(g(x)) для f(x)=sin(x) и g(x)=x². 92 раза?
Техническое машиностроение, Институт инженерии и менеджмента. Между тем, 13 мая 2017 года я получил ответ на свой запрос.
Что означает Cos 2x? Поскольку это «синус (x в квадрате)», Sin x2 является обычной синусоидальной функцией. Функция синуса отличается от функции Sin2x, что означает «квадрат синуса от х».
Поскольку это «синус (x в квадрате)», Sin x2 является обычной синусоидальной функцией. Функция синуса отличается от функции Sin2x, что означает «квадрат синуса от х».Триггерная функция Cos(2x) представляет собой триггерную функцию «двойного угла». На калькуляторе нечего «делать», если только мы не пытаемся вычислить косинус для значения 2x. В этом случае x — это угол, а 2x — удвоенная мера этого угла.
Является производной от sin2x sin²x?Производная sin 2x равна 2 cos 2x. Однако мы запишем это математически как d/dx (sin 2x) = 2 cos 2x (или) (sin 2x)’ = 2 cos 2x. Точно так же здесь f(x) = sin 2x — функция синуса с двойным углом.
Какие формулы двойного угла?Формулы суммы, где α=β, являются частным случаем формул двойного угла. Однако формула суммы используется для получения формулы синуса двойного угла. sin(α+β)=sinαcosβ+cosαsinβ. sin(θ+θ)=sinθ cosθ+cos θ sin θ sin(2θ)=2sinθcosθ.
 {n-1}}\], чтобы найти значение нашей данной задачи.
{n-1}}\], чтобы найти значение нашей данной задачи.Полный пошаговый ответ:
У нас есть y = sin 2x – cos 2x, нам нужно найти производную этой функции. Прежде чем мы начнем, мы узнаем кое-что о деривативах и изучим некоторые правила. Во-первых, мы видим, что если мы найдем производную разности двух функций, то их производная будет такой же, как дифференцирование этих функций по отдельности, а затем нахождение разности. Если A(x) и B(x) две функции, то
\[\dfrac{d\left( A\left( x \right)-B\left( x \right) \right)}{dx}= \dfrac{d\left( A\left( x \right) \right)}{dx}-\dfrac{d\left( B\left( x \right) \right)}{dx}\] 9{‘}}\left( x \right).\] Мы будем использовать их для решения нашей задачи, поэтому у нас есть as y = sin 2x – cos 2x. При дифференцировании получаем
\[\dfrac{dy}{dx}=\dfrac{d\left( \sin 2x-\cos 2x \right)}{dx}\]
При упрощении с помощью \[\dfrac{ d\left( A-B \right)}{dx}=\dfrac{dA}{dx}-\dfrac{dB}{dx},\] получаем
\[\Rightarrow \dfrac{d\left( \sin \ left( 2x \right) \right)}{dx}-\dfrac{d\left( \cos \left( 2x \right) \right)}{dx}\]
Теперь применим цепное правило к этим двум чтобы решить, мы будем находить производную один за другим. Как мы видим, sin 2x образован суммой sin x и 2x, поэтому пусть f(x) = sin x и g(x) = 2x. Итак, получаем
Как мы видим, sin 2x образован суммой sin x и 2x, поэтому пусть f(x) = sin x и g(x) = 2x. Итак, получаем
\[\dfrac{d\left( \sin \left( 2x \right) \right)}{dx}=\cos \left( 2x \right).2\]
[As f'(g(x) ) = cos 2x и g'(x) = 2]
И аналогично,
\[\dfrac{d\left( \cos \left( 2x \right) \right)}{dx}=-\sin \left( 2x \right).2\]
[Поскольку производная cos x равна – sin x, а производная 2x равна 2]
Таким образом, используя приведенное выше, мы получаем,
\[\Rightarrow \dfrac{dy}{dx}=2\ cos \left( 2x \right)-\left[ -2\sin \left( 2x \right) \right]\]
\[\Стрелка вправо \dfrac{dy}{dx}=2\cos \left( 2x \ вправо)+2\sin\влево( 2x\вправо)\] 9{n-1}},\] простая ошибка, которая может возникнуть при расчете.Недавно обновленные страницы
Значения электроотрицательности Полингса для элементов относятся к 11 классу химии CBSE
Для частицы, совершающей простое гармоническое движение, физика 11 класса CBSE
Дальнозоркий человек, потерявший очки, читает 10 класс физики JEE_Main
7
иметь класс высокой устойчивости 12 по физике CBSEЕсли альфа и бета альфа и гамма альфа и дельта относятся к классу 10 по математике JEE_Main
Значение p, для которого оба корня уравнения класс 10 по математике JEE_Main
Значения электроотрицательности Полингса для элементов относятся к классу 11 по химии CBSE
Для частицы, совершающей простое гармоническое движение, класс 11 по физике CBSE
Дальновидный человек, который потерял очки читает физику 10 класса JEE_Main
Обладает ли нихром высоким сопротивлением 12 класс физики CBSE
Если альфа и бета альфа и гамма альфа и дельта соответствуют 10 классу математики JEE_Main
Значение p, для которого оба корня уравнения класса 10 математики JEE_Main
Тенденции сомнения
Производная от Sin2x | Формула, доказательство, правила и примеры
Дифференцирование тригонометрических функций также является математическим методом для получения производной тригонометрической функции или скорости ее изменения по отношению к переменной.
 Однако распространенными тригонометрическими функциями являются sin(x), cos(x) и tan(x)(x). Например, f ′(a) = cos(x) является производной от f(x) = sin(x) (a). Скорость изменения sin(x) в определенной точке обозначается через f ′(a).
Однако распространенными тригонометрическими функциями являются sin(x), cos(x) и tan(x)(x). Например, f ′(a) = cos(x) является производной от f(x) = sin(x) (a). Скорость изменения sin(x) в определенной точке обозначается через f ′(a).Однако sin(x) и cos(x) можно использовать для получения производных всех круговых тригонометрических функций. Однако, чтобы отличить результирующее выражение, примените правило частного. Затем требуется использование неявного дифференцирования и побочных продуктов обычных тригонометрических функций для нахождения производных обратных тригонометрических функций.
Прежде чем перейти к поиску производной, рассмотрим несколько фактов о sin 2x. 2x — двойной угол, а sin 2x = 2 sin x cos x — одна из формул двойного угла. Поскольку sin 2x имеет двойной угол, его производная также имеет двойной угол. Однако, используя несколько методов, в этой статье мы покажем, что производная от sin 2x равна 2 cos 2x.
Давайте рассмотрим несколько различных способов получить производную от sin 2x и использовать ее для решения нескольких задач.
 Также рассмотрим разницу между производными sin 2x и sin2x.
Также рассмотрим разницу между производными sin 2x и sin2x.Содержание
Определение производнойПроизводная — это скорость изменения функции по отношению к переменной в математике. В результате производные имеют решающее значение при решении задач исчисления и дифференциальных уравнений. Как правило, ученые наблюдают за изменяющимися системами (динамическими системами), чтобы определить скорость изменения интересующей нас переменной, затем подставляют эту информацию в дифференциальное уравнение и используют методы интегрирования для получения функции, которую можно использовать для предсказания поведения исходной системы. вести себя в различных условиях.
Читайте также: Понимание концепции прошедшего времени: обновление 2021
Функция, которая не является непрерывной, не может быть дифференцируемой, поскольку каждая дифференцируемая функция должна быть непрерывной. Функция может быть дифференцируемой, а может и не быть дифференцируемой, даже если она непрерывна.
Какая производная от Sin2x
2 cos 2x является производной от sin2x. Однако в математике это записывается как d/dx (sin 2x) = 2 cos 2x (или) (sin 2x)’ = 2 cos 2x. Тогда синусоидальная функция с двойным углом равна f(x) = sin 2x. Однако дифференцировать sin 2x можно разными способами, в том числе:
- Использование первого принципа
- Затем, используя цепное правило
- Затем, используя правило продукта
2 cos 2x является производной от sin 2x. Его можно представить как d/dx (sin 2x) = 2 cos 2x (sin 2x) = 2 cos 2x (sin 2x)’ = 2 cos 2x
Производная от Sin2x с использованием первого принципаИспользуется первый принцип дифференцировать грех 2x. Предположим, что в этом случае f(x) = sin 2x. Тогда sin 2(x + h) = sin (2x + 2h) = f(x + h) = f(x + h) = f(x + h) = f(x + h) = f(x +). первый принцип, подставьте эти числа в формулу производной (предельное определение производной),
f'(x) = limₕ→₀ [f(x + h) – f(x)] / h
Тогда f'(x) = limₕ→₀ [sin (2x + 2h) – sin 2x] / h
Точно так же мы можем упростить этот предел двумя способами.
Метод 1
По одной из тригонометрических формул sin C – sin D = 2 cos [(C + D)/2] sin [(C – D)/2]. Однако, применяя это, мы получаем
f'(x) = limₕ→₀ [2 cos[(2x + 2h + 2x)/2] sin[(2x +2h – 2x)/2] ] / h
Тогда f'(x) = limₕ→₀ [2 cos[(4x + 2h)/2] sin (h) ] / h
Тогда f'(x) = 2 limₕ→₀ [cos[(4x + 2h)/2] · limₕ→₀ [sin h / h]
Однако, используя предельные формулы, lim ₓ→₀ (sin x/ x) = 1. Таким образом,
f'(x) = 2 [cos[(4x + 0)/2] · (1) = 2 cos (4x/2) = 2 cos 2x
Таким образом, мы доказали, что производная от sin 2x равна 2 cos 2x.
Метод 2По формулам суммы и разности,
sin (A + B) = sin A cos B + cos A sin B
Используя это,
f'(x) = limₕ→₀ [sin 2x cos 2h + cos 2x sin 2h – sin 2x] / h
Тогда f'(x) = limₕ→₀ [ – sin 2x (1- cos 2h) + cos 2x sin 2h] / h
Тогда f'(x) = limₕ→₀ [ – sin 2x (1 – cos 2h)]/h + limₕ→₀ (cos 2x sin 2h)/h
Аналогично, f'(x) = -sin 2x limₕ→₀ (1 – cos 2h)/h + (cos 2x) limₕ→ ₀ sin 2h/h
Однако, используя формулы двойного угла, 1 – cos(2h) = 2 sin2(h).

Следовательно, f'(x) = -sin 2x limₕ→₀ (2 sin2(h))/h + (cos 2x) limₕ→₀ sin 2h/h
= -2sin 2x [limₕ→₀ sin (h ) / (h) · limₕ→₀ sin h] + (cos 2x) (limₕ→₀ sin 2h/h)
Однако по одной из предельных формул lim ₓ→₀ (sin x/x) = 1 и lim ₓ→₀ (sin ax/x) = a.
Итак, f'(x) = -2sin 2x (1 · sin 0) + cos 2x (2)
Тогда f'(x) = -2sin 2x(0) + 2 cos 2x (Из тригонометрической таблицы, sin 0 = 0)
Следовательно, f'(x) = 2 cos 2x
В результате мы можем сделать вывод, что производная sin 2x равна 2 cos 2x.
Первый принцип используется для нахождения производной sin 2x.
Производная от Sin2x с использованием цепного правилаЦепное правило Производная от Sin 2x Proof
В этом примере мы попробуем применить Цепное правило к трем функциям, которые вложены друг в друга. Это также самая важная и первая функция. За ней следует функция sin, за которой следует функция cos. Используя Цепное правило, создайте каждое из них так, как если бы оно было уникальным (независимо от аргумента).
 Мы дополнительно умножим каждую отдельную производную вместе в качестве наглядного пособия. Однако мы можем использовать красно-сине-зеленую цветовую схему, чтобы различать каждую производную.
Мы дополнительно умножим каждую отдельную производную вместе в качестве наглядного пособия. Однако мы можем использовать красно-сине-зеленую цветовую схему, чтобы различать каждую производную.Однако в математическом анализе цепное правило — это формула, которая вычисляет производную набора из двух или более функций. Это верно только в том случае, если f и g являются функциями. В результате цепное правило выражает производную составной функции f g как производную от f и g.
Однако, если g дифференцируема в точке x и f в g(x), составная функция F = f g, определяемая формулой F(x) = f(g(x)) дифференцируема в точке x, а F’ определяется произведение F'(x) = f'(g(x)).g'(x)
Если y = f (u) и u = g(x) являются дифференцируемыми функциями в системе обозначений Лейбница, то dy/dx = dy/du.du/dx
Цепное правило может быть записано как в простых, так и в непростых числах. обозначение (f g)'(x) = f'(g(x))g’ или в составном обозначении f(g)'(x) = f'(g(x)g'(x)
f'(x ) = 4 sin(2x) cos(2x)
Для сокращения этой функции можно использовать тригонометрическое тождество (получив: 2sin(4x)), но мы не хотим путать подход
Производная от Sin2x с использованием правило продуктаПравило произведения Производная от Sin 2x Доказательство
Однако, чтобы использовать правило произведения для получения производной f(x) = sin 2x, мы должны выразить sin 2x как произведение двух функций.
 Точно так же мы видим Sin 2x = 2 sin x cos x, используя формулу двойного угла для греха. Затем рассмотрим уравнения u = 2 sin x и v = cos x. Тогда v’ = -sin x и u’ = 2 cos x. Как правило,
Точно так же мы видим Sin 2x = 2 sin x cos x, используя формулу двойного угла для греха. Затем рассмотрим уравнения u = 2 sin x и v = cos x. Тогда v’ = -sin x и u’ = 2 cos x. Как правило,f ‘(x) = uv’ + vu’
= (2 sin x) (- sin x) + (cos x) (2 cos x)
= 2 (cos2x – sin2x) )
= 2 cos 2x
Это потому, что по формуле двойного угла cos cos 2x = cos2x – sin2x.
Итак, мы нашли производную от sin 2x, используя правило произведения.
N th Производная от Sin2xN-я производная от sin 2x является производной от sin 2x, полученной итеративным дифференцированием sin 2x n раз. Чтобы понять тренд/паттерн, найдите первую производную, вторую производную и так далее, пока не будет найдена n-я производная от sin 2x.
1-я производная sin 2x равна 2 cos 2x
Тогда 2-я производная sin 2x равна -4 sin 2x
Тогда 3-я производная sin 2x равна -8 cos 2x
Аналогично, 4-я производная sin 2x равна 16 sin 2x
Тогда 5-я производная sin 2x равна 32 cos 2x
Тогда 6-я производная sin 2x равна -64 sin 2x
Аналогично, 7-я производная sin 2x равна -128 cos 2x
Тогда 8-я производная производная от sin 2x равна 256 sin 2x и так далее.

n-я производная sin 2x может быть определена следующим образом, используя этот тренд:
(sin 2x)(n) = (sin 2x)(n) = (sin 2x)(n)
Если n кратно 4, 2n sin 2x; если n меньше кратного 4, -2n cos 2x
Если n на 2 меньше кратного 4, то -2n sin 2x. Если n на 3 меньше, чем кратное 4, то 2n коснется 2x.
Другой способ записать это следующим образом:
Производная Sin2x по xSin2 x имеет производную.
Производная Sin2x не совпадает с производной sin 2x. Sin 2x является производной от sin2x. Давайте посмотрим, что мы можем сделать. Предположим, что f(x) = sin2x. f(x) = (sin x)2 можно представить в виде формулы. Мы можем использовать комбинацию правила мощности и правила цепи, чтобы обнаружить его производную. Тогда f'(x) = 2(sin x) d/dx(sin x) = 2 sin x cos x = sin 2x получается (используя формулу двойного угла для sin)
В результате производная sin2x равна sin 2x.
Важные примечания относительно производной sin 2x:
2 cos 2x является производной от sin 2x.

Производная от sin ax обычно представляет собой cos axe.
Например, sin (-3x) имеет производную от -3 cos(-3x), sin 5x имеет производную от 5 cos 5x и так далее.
Sin 2x и sin2x не имеют одинаковых производных.
d/dx (sin 2x) = 2 cos 2x
d/dx (sin2x) = sin 2x
Производная от Sin2x /1+cosxПроизводная sin2x/ (1 + cosx)
Пусть y = sin2x/(1 + cosx)
Таким образом, используя правило частных,
dy/dx = {(1 + cosx) × d/dx (sin2x) – sin2x × d/dx (1+cosx)} / (1+cosx)2
Следовательно, dy/dx = {(1+cosx) * sinx.cosx – sin2x(-sinx)} / (1+cosx) 2
Тогда dy/dx = {sin2x + sinx.cosx + sin3x} / (1+cosx)2
Производная от Sin2x Cos3xПроизводная от sin2x cos3x
92ddxcos3x) = (sin2x) × d/dx (cos3x)+(cos3x) × d/dx (sin2x)
Таким образом, d/ dx (sin 2x.cos 3x) = (sin 2x) × d/dx (cos 3x)+(cos 3x) × d/dx (sin 2x)
Тогда d/ dx (sin 2x .
 cos 3x) = (sin 2x) × (−sin 3x) × 3+(cos 3x) × (cos 2x) × 2
cos 3x) = (sin 2x) × (−sin 3x) × 3+(cos 3x) × (cos 2x) × 2= (sin 2x) × (-sin 3x) × 3+(cos 3x) × (cos 2x) × 2
[Мы используем цепное правило]
= (−3 sin 2x sin3x + 2 cos3x cos2x)
Следовательно, d/ dx (sin 2x.cos 3x) = (-3 sin 2x sin 3x + 2 cos 3x cos 2x)
Производная от Sin2x cos2xТригонометрические формулы двойного угла используются для получения значения sin2x Cos 2x. При выводе используются значения sin 2x и cos 2x.
Формулы тригонометрических двойных углов получены из формул тригонометрических двойных углов.
Sin 2x = 2 sin x cos x ————(i)
И,
Cos 2x = Cos2x − Sin2x
= 2 cos2x − 1 ————(ii) [Поскольку Sin2 x + Cos2 x = 1]
= 1 − 2Sin2x ————(iii)
Теперь, чтобы получить значение Sin 2x Cos 2x, умножьте уравнение (i) на (ii) или (i)
Рассмотрим уравнение (i) и (ii)
Sin 2x = 2 sin x cos x
And,
9Sin 2x Cos 2x = 2 Sin x Cos x (2 cos2x — 1)
= 4 Sin x Cos 3x — 2 Sin x Cos x
= 2 Cos x (2 Sin x Cos2 x − Sin x)
Теперь рассмотрим уравнения (i) и (iii),
Sin 2x = 2 sin x cos x
And,
Cos 2x = 1 − 2 Sin2x
Умножьте их, чтобы получить Грех3 х)
So,
Sin 2x Cos 2x = 2 Cos x (2 Sin x Cos2 x − Sin x)
Or,
Sin 2x Cos 2x = 2 Cos x (Sin x – 2 Sin3 x)
Производная
of Sin 2x Cos 2xd/dx (Sin 2x Cos 2x) = 2Cos(4x)
Доказательство:
Sin(2x)cos(2x)
= ½(2sin(2x)cos(2x))
Или, ½Sin(4x)
Теперь продифференцируем данную функцию по x:
d/dx [½ Sin (4x)]
= ½[ d/dx (Sin(4x) ) ]
9cos x относительно x,dz/dx = d(ecos x)/dx
= ecos x × d(cos x)/dx
= ecos x × (-sinx)
= -sinx .
 ecos x
ecos xВ результате dz/dx = -sinx является дифференцированием e cos x по x.
Мы получаем дифференцирование sin2x относительно e cos x путем деления (dy/dx) на (dz/dx).
В результате (dy/dx) / (dz/dx) = (2 sinx.cosx) / (-sinx.cos x), или dy/dz = -2 cos x/e cos x.
Производная Sin2x относительно Cos2xПроизводная Sin2x относительно cos2x
Мы уже знаем, что sin 2x равен 2sinxcosx и (uv)’=u’v+v’u. Это называется правилом дифференциации продукта.
d/dx (sin2x) = d/dx(2 sinx cosx) = 2 d/dx (sinx cosx) является результатом.
d/dx sin2x = 2sinx.d/dx cosx + 2cosx.d/dx sinx — правило произведения дифференцирования.
Теперь мы знаем, что производная sin равна cos, а производная cos x равна -sin x.
Отсюда имеем
d/dx sin 2x = 2 sin x (−sinx) + 2 cos x × cos x = 2(cos 2x − sin 2x)
Мы знаем, что cos 2x = cos2x − sin2x
Следовательно, имеем
d /dx sin2x= 2(cos 2x)= 2 cos2x
Производная Sin2x при x=π/2sin 2x при x = π/2 Дано: f (x) = sin 2x Используя формулу производной,
f(a) = limₕ→₀ [ { f (a+h) – f (a) } / h], где h — положительное целое число небольшого размера.

Производная sin2x при x = π/2 задается как
f’ ( π/2 ) = limₕ→₀ [ { f ( π/2 + h ) – f (π/2) } / h ]
= limₕ→₀ [ sin { 2 × ( π/2 + h )} – sin2 × π/2 ] / ч
= limₕ→₀ {sin ( π + 2h ) – sin π}/ ч. [Следовательно, sin (π+x) = – sinx и sin π = 0]
=limₕ→₀ (-sin 2h – 0)/ h
=limₕ→₀ sin 2h / h
[Потому что неоднозначный характер. Для определения предела воспользуемся теоремой о сэндвиче.]
Умножая числитель и знаменатель на два, получаем
= – limₕ→₀ (sin 2h / 2h ) × 2 = – 2 limₕ→₀ ( грех 2ч / 2ч) 9(2-1) × d/dz ( cos z )
Аналогично, dy/dx = 2 × sin x × cos z + 2 cos z (- sinz)
Тогда dy/dx = 2 × sin z × cos z – 2 × sin z × cos z
Тогда dy/dx = 0
Производная от ln sin2xИспользуйте цепное правило в своих интересах.
Вы можете разложить свою функцию на логарифмическую, квадратную и синусоидальную составляющие следующим образом: x)
Теперь вы должны вычислить три производные этих трех функций (и затем подставить соответствующие значения u и v): 92 x= 2sin x cos x= sin2x
Какая производная от sin2x?В частности, dy/dx= 2*cos (2x).
Является ли sin2x таким же, как 2sinx? Помните цепное правило: «Дифференцируйте внешнюю функцию, оставив внутреннюю функцию в покое, затем дифференцируйте внутреннюю функцию». cos(x) — это производная от sin(x) по x, а производная от 2x по x равна всего 2.
Помните цепное правило: «Дифференцируйте внешнюю функцию, оставив внутреннюю функцию в покое, затем дифференцируйте внутреннюю функцию». cos(x) — это производная от sin(x) по x, а производная от 2x по x равна всего 2.1 умножается на, тогда как 2 есть синус 2, умноженный на х, или удвоенный угол х. В результате мы имеем два совершенно разных результата. Поскольку синус — это периодический (повторяющийся) сигнал, эти графики будут пересекаться через равные промежутки времени, что приведет к одному и тому же результату для обоих уравнений!
Какова формула sin2x?- Формулы двойного угла: sin 2x = 2sin x cos x, cos 2x = cos2x − sin2x = 2cos2x − 1=1 − 2sin2x.
Институт инженерии и менеджмента, Техническое машиностроение. 13 мая 2017 года я получил ответ на свой вопрос.
Как интегрировать Cos 2x? Sin x2 — это обычная синусоидальная функция, поскольку она представляет собой «синус (x в квадрате)». Sin2x означает «квадрат синуса от x», что не совпадает с функцией синуса.
Sin x2 — это обычная синусоидальная функция, поскольку она представляет собой «синус (x в квадрате)». Sin2x означает «квадрат синуса от x», что не совпадает с функцией синуса.Вот как сложить cos2 x:
- Перепишите интеграл через cos 2x, используя тождество половинного угла для косинуса.
- Чтобы перенести знаменатель вне интеграла, используйте правило постоянного множителя.
- Распределите функцию и разделите ее на множество интегралов, используя правило сумм.
- Вычислить два интеграла по отдельности.
Sin2x нельзя интегрировать напрямую (x). Для решения задачи используйте тригонометрические тождества и процедуры подстановки исчисления. Подставьте 1/2 интеграла от (1 – cos(2x)) dx в интеграл, используя формулу половинного угла sin2(x) = 1/2*(1 – cos(2x)).
Что такое цепное правило в исчислении?Производная от f(g(x)) равна f'(g(x))g’ в соответствии с цепным правилом (x).
Что означает производная от sin 2 x? Иными словами, это помогает в дифференциации *составных функций*. Sin(x2), например, является составной функцией, поскольку ее можно записать как f(g(x)) для f(x)=sin(x) и g(x)=x².
Иными словами, это помогает в дифференциации *составных функций*. Sin(x2), например, является составной функцией, поскольку ее можно записать как f(g(x)) для f(x)=sin(x) и g(x)=x².Институт инженерии и менеджмента, Техническое машиностроение. 13 мая 2017 года я получил ответ на свой вопрос. Sin x2 — это обычная синусоидальная функция, поскольку она представляет собой «синус (x в квадрате)». Sin2x означает «квадрат синуса от x», что не совпадает с функцией синуса.
Что означает Cos 2x?Триггерная функция Cos(2x) — это просто триггерная функция «двойного угла». Если только мы не пытаемся вычислить косинус для значения 2x, где x — угол, а 2x — удвоенная мера этого угла, на калькуляторе нечего «делать». 92(2x) – Дифференцирование тригонометрических функций – это математический процесс нахождения производной тригонометрической функции или скорости ее изменения по отношению к переменной.
 Общие тригонометрические функции включают sin(x), cos(x) и tan(x). Например, производная от f(x) = sin(x) представлена как f ′(a) = cos(a). f ′(a) – скорость изменения sin(x) в конкретной точке a.
Общие тригонометрические функции включают sin(x), cos(x) и tan(x). Например, производная от f(x) = sin(x) представлена как f ′(a) = cos(a). f ′(a) – скорость изменения sin(x) в конкретной точке a.Все производные круговых тригонометрических функций можно найти, используя производные функций sin(x) и cos(x). Затем применяется правило частного, чтобы дифференцировать полученное выражение. Нахождение производных обратных тригонометрических функций включает использование неявного дифференцирования и производных обычных тригонометрических функций. 92x
В данном случае sin(x) – это внутренняя функция, составляющая часть sin²(x). Чтобы взглянуть на это с другой стороны, давайте обозначим u=sin(x) так, чтобы u²=sin²(x). Вы заметили, как здесь работает составная функция? Внешняя функция u² возводит в квадрат внутреннюю функцию u=sin(x). Не позволяйте вам сбить вас с толку, это просто показать вам, как одна функция является составной частью другой. Как только вы это поймете, вы сможете это вывести.

Итак, математически цепное правило:
Производная составной функции F(x):
F'(x)=f'(g(x))(g'(x)) Или, прописью:
производная внешней функции (без внутренней функции!) умноженная на производную внутренней функции.1) Производная внешней функции (без внутренней функции) равна:
d/dx(u²)=2u
(пока я оставляю u, но вы можете подставить u=sin(x), если хотите, пока выполняете шаги. Помните, что это всего лишь шаги, фактическая производная вопроса показана внизу) 2) производная внутренней функции: 92(2x)Здесь я попытался бы применить Цепное правило к трем функциям, вложенным одна в другую:
первая и всеобъемлющая функция ()2; следующая — функция sin, а последняя — функция 2x.Я буду использовать цепное правило, выводя каждое из них как отдельное (независимо от аргумента), и я буду перемножать каждую отдельную производную вместе, используя в качестве наглядной помощи последовательность красно-сине-зеленых цветов для идентификации каждой производной:
дача: 92x)Используйте цепное правило.

Вы можете разбить свою функцию на логарифм, квадрат и функцию синуса следующим образом:
f(u)=ln(u)
u(v)=v²(x)
v(x)=sin(x)Теперь вам нужно вычислить три производные этих трех функций (а затем подставить соответствующие значения u и v):
f'(u)=1/u=1/v²=1/sin²x
u'(v)=2v=2sinx
v'(x)=cos(x)Теперь осталось только перемножить эти три производные: Надеюсь, это помогло! 92 x= 2sin xcos x= sin2x
Какая производная от sin2x?А именно, dy/dx= 2*cos(2x). Помните, что цепное правило гласит, что человек «дифференцирует внешнее, оставляя нетронутым внутреннее, а затем различает внутреннюю функцию». Производная sin(x) по отношению к x равна cos(x), а производная от 2x по отношению к x равна просто 2.
Является ли sin2x таким же, как 2sinx?Говоря простым языком, 1 умножается на , тогда как 2 — это синус 2, умноженный на x, или удвоенный угол x.
Как интегрировать Cos 2x? Итак, два очень разных результата. Интересно, что синус — это периодический (повторяющийся) сигнал, поэтому эти графики будут периодически пересекаться, и два выражения будут оцениваться как 9. 2 x — это «квадрат синуса от x», который является функцией, отличной от функции синуса.
Итак, два очень разных результата. Интересно, что синус — это периодический (повторяющийся) сигнал, поэтому эти графики будут периодически пересекаться, и два выражения будут оцениваться как 9. 2 x — это «квадрат синуса от x», который является функцией, отличной от функции синуса.Вот как интегрировать cos 2 x:
- Используйте тождество половинного угла для косинуса, чтобы переписать интеграл через cos 2x:
- Используйте правило постоянного множителя, чтобы переместить знаменатель за пределы интеграла:
- Распределите функцию и с помощью правила сумм разделите ее на несколько интегралов: 9 2 (x) = 1/ 2 *(1 – cos(2x)) и подставить в интеграл, чтобы он стал 1/ 2 умножить на интеграл от (1 – cos(2x)) dx.
 Что такое цепное правило в исчислении?
Что такое цепное правило в исчислении? Цепное правило утверждает, что производная от f(g(x)) равна f'(g(x))⋅g'(x). Другими словами, это помогает нам различать *составные функции*. Например, sin(x²) является составной функцией, поскольку ее можно построить как f(g(x)) для f(x)=sin(x) и g(x)=x². 9 2 x — это «квадрат синуса от x», который является функцией, отличной от функции синуса.
Что означает Cos 2x?Cos ( 2x ) — это просто триггерная функция «двойного угла»… нет ничего, что могло бы « сделать » на калькуляторе, если только мы не пытались вычислить косинус для некоторого значения 8x где x — угол, а 2x — удвоенная мера этого угла.

Производная от sin2x: доказательство, расчет, цепное правило и примеры
Математический метод определения производной тригонометрической функции или скорости ее изменения относительно переменной представляет собой дифференцирование тригонометрических функций. sin(x), cos(x) и tan(x) являются примерами общих тригонометрических функций (x). Например, производная от f(x) = sin(x) обозначается как f ′(a) = cos(x) (a). f ′(a) обозначает скорость изменения sin(x) в определенном месте a.
Однако производные всех круговых тригонометрических функций можно вычислить с помощью sin(x) и cos(x). Кроме того, используйте правило отношения, чтобы отличить результирующее выражение. Нахождение производных обратных тригонометрических функций требует использования неявного дифференцирования и побочных продуктов обычных тригонометрических функций.
Если вы хотите узнать больше об этой теме, то вам сюда. Продолжайте читать, пока мы исследуем факты о происхождении sin 2 x.

Содержание
В математике производная — это скорость изменения функции по отношению к переменной. Таким образом, производные необходимы при решении задач исчисления и дифференциальных уравнений. Как правило, ученые наблюдают за изменяющимися системами (динамическими системами), чтобы определить скорость изменения некоторой интересующей нас переменной, затем подставляют эту информацию в дифференциальное уравнение и используют методы интегрирования, чтобы получить функцию, которую мы можем использовать для предсказания поведения исходной переменной. системы в различных условиях.
Поскольку каждая дифференцируемая функция должна быть непрерывной, непрерывная функция не может быть дифференцируемой. Однако, даже если функция непрерывна, она может быть или не быть дифференцируемой.
Производная sin 2 x по первому принципуЧтобы решить это, вам нужно будет использовать цепное правило.
 Таким образом, чтобы сделать это, вы должны сначала определить «внешнюю» функцию и «внутреннюю» функцию, состоящую из внешней функции. В этом примере sin(x) — это внутренняя функция, являющаяся частью функции sin 9.1722 2 функция (х).
Таким образом, чтобы сделать это, вы должны сначала определить «внешнюю» функцию и «внутреннюю» функцию, состоящую из внешней функции. В этом примере sin(x) — это внутренняя функция, являющаяся частью функции sin 9.1722 2 функция (х).Аналогично, другими словами, обозначим u = sin(x) так, чтобы u 2 = sin 2 (x). Однако вы заметили, как в этом случае используется составная функция? Внутренняя функция u = sin возводит в квадрат внешнюю функцию u 2 (x). Не позволяйте этому сбить вас с толку; это просто для демонстрации того, как одна функция является составной частью другой. Тем не менее, вы можете сделать вывод, как только вы это поймете.
Расчет:Использование производной определения функции f′(x) = lim h→0 f(x+h)f(x)h.
Воспользуйтесь тем фактом, что sin x.sin y = 2 cos(x+y 2 ) sin(xy 2 ).
Используйте формулу lim h→0 sin(h)h=1.

В результате определите производную sin 2 x.
Вместо этого используйте цепное правило дифференцирования, т. е. d/dx(f(g(x))=dd(g(x))f((g(x))d/dxg (x)
Используйте тот факт, что d/dx(sinx) = cosx и d/dx(x) = 1,
Пусть f(x) = sin 2x.
Отсюда имеем
f′(x)=lim h→0 f(x+h) − f(x)h
f(x+h) = sin 2 (x+h)
Отсюда имеем
f′(x)=lim h→0 sin 2 (x+h) − sin 2 xh
Мы знаем, что sin x − sin y = 2 cos(x+ y 2 ) sin(x−y 2 )
Замените x на 2x+2h и y на 2x, мы получим
sin (2x+2h) − sin 2x = 2 cos (2x+2h+2x 2 ) грех (2x+2h−2x 2 ) = 2 cos (2x+h) sin h
Отсюда имеем
f′(x) = lim h→0 2 cos (2x+h) sin (h)h = lim h→ 2 cos (2x+h) × lim h→0 sin(h)h
Мы знаем, что lim x→0 sin x = 1.
Используя приведенный выше результат, мы получаем
f′( x) = 2 cos (2x+0)1 = 2 cos 2x
Отсюда имеем
d/dx(sin2x) = 2 cos 2x
Альтернативно имеем
Пусть f(x) = sinx и г (х) = 2х.

Тогда мы имеем h(x) = туман(x) = sin 2x.
Мы знаем, что d/dx f(g(x)) = d(g(x)) туман(x) d/dx g(x). Это известно как цепное правило дифференцирования.
Теперь мы знаем, что d/dx(sin x) = cos x
Отсюда имеем
d/dx (2x) sin (2x) = cos 2x
Также имеем d/dx 2x = 2
Следовательно, из цепного правила дифференцирования мы имеем
d/dxsin2x=d/dx(2x)sin(2x)
d/dx 2x=cos 2x(2)=2 cos 2x.
Это то же самое, что мы получили выше.
Производная sin 2 x относительно cos 2 xМы знаем, что sin 2x = 2sinxcosx и (uv)’=u’v+v’u {Это известно как правило дифференцирования произведения}
Следовательно, мы имеем ,
d/dx (sin2x) = d/dx(2 sinx cosx) = 2 d/dx (sinx cosx)
Используя правило дифференцирования произведения, мы имеем
d/dx sin2x = 2sinx.d/dx cosx + 2cosx.d/dx sinx
Теперь мы знаем, что производная sin равна cos, а производная cos x равна -sin x.

Отсюда имеем
d/dx sin 2x = 2 sin x(−sinx) + 2 cos x.cos x = 2(cos 2x−sin 2x)
Мы знаем, что cos 2x = cos 2 x − sin 2 x
Следовательно, мы имеем
D/DX SIN 2 x = 2 (COS 2x) = 2 COS 2 X
Деривативность SIN 2 . x.sure. В этом случае мы попытаемся применить цепное правило к трем функциям, вложенным друг в друга. Это также первая и самая важная функция. Далее следует функция sin, за которой следует функция cos. Используя цепное правило, получая каждое из них, как если бы оно было само по себе (независимо от аргумента). Кроме того, в качестве наглядного пособия мы также будем перемножать каждую производную в отдельности. Однако, чтобы различать каждую производную, мы можем использовать последовательность цветов красный-синий-зеленый.
Цепное правило также является формулой в исчислении, которая вычисляет производную комбинации двух или более функций.
 Однако это если f и g обе функции. В результате цепное правило описывает производную составной функции f g в терминах f и вывода g.
Однако это если f и g обе функции. В результате цепное правило описывает производную составной функции f g в терминах f и вывода g.- Если g также дифференцируема в точке x и f дифференцируема в точке g(x), то составная функция F = f g, определяемая равенством F(x) = f(g(x)) дифференцируема в точке x, и F’ обеспечивается произведением F'(x) = f'(g(x)).g'(x)
- Если y = f (u) и u = g(x) являются дифференцируемыми функциями в системе обозначений Лейбница, то dy/dx = dy/du.du/dx
- Цепное правило также может быть выражено в любой простой записи ( f g)'(x) = f'(g(x))g’ или в составной записи f(g)'(x) = f'(g(x)g'(x)
f'(x) = 4 sin(2x) cos(2x)
Эту функцию можно сжать (получив: 2sin(4x)) с помощью тригонометрического тождества, но мы не хотим запутать процедуру
Производная от sin 2 xПри вычислении производной функции мы должны продифференцировать ее по независимой переменной.
Итак, давайте разберемся, как мы можем прийти к нашему решению.
Объяснение:
Пусть, y = sin 2x
Дифференцируя обе стороны относительно x,
dy/dx = d[sin2(x)]/dx
= 2 sin(x) × d (x)] /dx [с использованием цепного правила]
= 2 sin(x) × cos(x)
= sin(2x) [так как, 2 sin(x) cos(x) = sin(2x)]
Мы также можем проверить ваш ответ на онлайн-калькуляторе производных.
Derivative of sin 2 x/ (1+cosx)Let y = sin 2 x/(1+cosx)
Thus using quotient rule ,
dy/ dx =
{(1+cosx) × d/dx(sin 2 x) – sin 2 x × d/dx(1+cosx)} / (1+cosx) 2
=> dy/dx = {(1+cosx) * sinx.cosx – sin 2 x(-sinx)} / (1+cosx) 2
=> dy/dx = {sin2x + sinx.cosx + sin 3 x} / (1 + cosx) 2
Производное SIN 2 X COS 3 xв этом вопросе, 907
9292929292.  9072. 9072. 9072. 9072. 9072. 9072. 9072. 9072. 9072. 9072. 9072.
9072. 9072. 9072. 9072. 9072. 9072. 9072. 9072. 9072. 9072. 9072.9072. 9072. x . cos 3 х) = (sin 2 х).
d/dx (cos 3 x)+(cos 3 x).
ддх (грех 2 х)
Таким образом,
ddx (sin 2x.cos 3x)
= (sin 2x).ddx(cos 3x)+(cos 3x).ddx(sin 2x)
= (sin 2x).(−sin 3x) ).3+(cos 3x).(cos 2x).2
= (sin 2x).(-sin 3x).3+(cos 3x).(cos 2x).2
[Мы используем цепное правило ]
= (−3 sin 2x sin3x + 2 cos3x cos2x)
= (-3 sin 2x sin 3x + 2 cos 3x cos 2x)
Производная sin 2 x по отношению к e22 cos xДифференцировать, y = sin²x относительно x, 9 cos x относительно x,
dz/dx = d(e cos x )/dx
= e cos x × d(cos x)/dx
= e
x
2 cos x (-sinx)= -sinx . e cos x
Таким образом, дифференцирование e cos x по x равно dz/dx = -sinx .


 Поскольку это «синус (x в квадрате)», Sin x2 является обычной синусоидальной функцией. Функция синуса отличается от функции Sin2x, что означает «квадрат синуса от х».
Поскольку это «синус (x в квадрате)», Sin x2 является обычной синусоидальной функцией. Функция синуса отличается от функции Sin2x, что означает «квадрат синуса от х». {n-1}}\], чтобы найти значение нашей данной задачи.
{n-1}}\], чтобы найти значение нашей данной задачи. Как мы видим, sin 2x образован суммой sin x и 2x, поэтому пусть f(x) = sin x и g(x) = 2x. Итак, получаем
Как мы видим, sin 2x образован суммой sin x и 2x, поэтому пусть f(x) = sin x и g(x) = 2x. Итак, получаем  Однако распространенными тригонометрическими функциями являются sin(x), cos(x) и tan(x)(x). Например, f ′(a) = cos(x) является производной от f(x) = sin(x) (a). Скорость изменения sin(x) в определенной точке обозначается через f ′(a).
Однако распространенными тригонометрическими функциями являются sin(x), cos(x) и tan(x)(x). Например, f ′(a) = cos(x) является производной от f(x) = sin(x) (a). Скорость изменения sin(x) в определенной точке обозначается через f ′(a). Также рассмотрим разницу между производными sin 2x и sin2x.
Также рассмотрим разницу между производными sin 2x и sin2x.


 Мы дополнительно умножим каждую отдельную производную вместе в качестве наглядного пособия. Однако мы можем использовать красно-сине-зеленую цветовую схему, чтобы различать каждую производную.
Мы дополнительно умножим каждую отдельную производную вместе в качестве наглядного пособия. Однако мы можем использовать красно-сине-зеленую цветовую схему, чтобы различать каждую производную. Точно так же мы видим Sin 2x = 2 sin x cos x, используя формулу двойного угла для греха. Затем рассмотрим уравнения u = 2 sin x и v = cos x. Тогда v’ = -sin x и u’ = 2 cos x. Как правило,
Точно так же мы видим Sin 2x = 2 sin x cos x, используя формулу двойного угла для греха. Затем рассмотрим уравнения u = 2 sin x и v = cos x. Тогда v’ = -sin x и u’ = 2 cos x. Как правило,

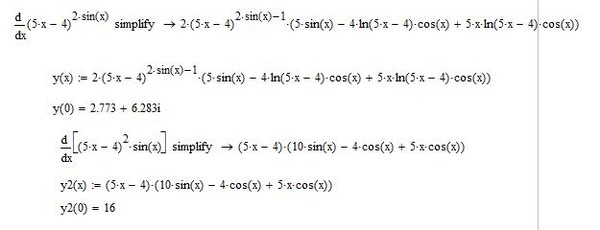 cos 3x) = (sin 2x) × (−sin 3x) × 3+(cos 3x) × (cos 2x) × 2
cos 3x) = (sin 2x) × (−sin 3x) × 3+(cos 3x) × (cos 2x) × 2 ecos x
ecos x
 Помните цепное правило: «Дифференцируйте внешнюю функцию, оставив внутреннюю функцию в покое, затем дифференцируйте внутреннюю функцию». cos(x) — это производная от sin(x) по x, а производная от 2x по x равна всего 2.
Помните цепное правило: «Дифференцируйте внешнюю функцию, оставив внутреннюю функцию в покое, затем дифференцируйте внутреннюю функцию». cos(x) — это производная от sin(x) по x, а производная от 2x по x равна всего 2. Sin x2 — это обычная синусоидальная функция, поскольку она представляет собой «синус (x в квадрате)». Sin2x означает «квадрат синуса от x», что не совпадает с функцией синуса.
Sin x2 — это обычная синусоидальная функция, поскольку она представляет собой «синус (x в квадрате)». Sin2x означает «квадрат синуса от x», что не совпадает с функцией синуса. Иными словами, это помогает в дифференциации *составных функций*. Sin(x2), например, является составной функцией, поскольку ее можно записать как f(g(x)) для f(x)=sin(x) и g(x)=x².
Иными словами, это помогает в дифференциации *составных функций*. Sin(x2), например, является составной функцией, поскольку ее можно записать как f(g(x)) для f(x)=sin(x) и g(x)=x². Общие тригонометрические функции включают sin(x), cos(x) и tan(x). Например, производная от f(x) = sin(x) представлена как f ′(a) = cos(a). f ′(a) – скорость изменения sin(x) в конкретной точке a.
Общие тригонометрические функции включают sin(x), cos(x) и tan(x). Например, производная от f(x) = sin(x) представлена как f ′(a) = cos(a). f ′(a) – скорость изменения sin(x) в конкретной точке a.
 Итак, два очень разных результата. Интересно, что синус — это периодический (повторяющийся) сигнал, поэтому эти графики будут периодически пересекаться, и два выражения будут оцениваться как 9. 2 x — это «квадрат синуса от x», который является функцией, отличной от функции синуса.
Итак, два очень разных результата. Интересно, что синус — это периодический (повторяющийся) сигнал, поэтому эти графики будут периодически пересекаться, и два выражения будут оцениваться как 9. 2 x — это «квадрат синуса от x», который является функцией, отличной от функции синуса. Что такое цепное правило в исчислении?
Что такое цепное правило в исчислении? 

 Таким образом, чтобы сделать это, вы должны сначала определить «внешнюю» функцию и «внутреннюю» функцию, состоящую из внешней функции. В этом примере sin(x) — это внутренняя функция, являющаяся частью функции sin 9.1722 2 функция (х).
Таким образом, чтобы сделать это, вы должны сначала определить «внешнюю» функцию и «внутреннюю» функцию, состоящую из внешней функции. В этом примере sin(x) — это внутренняя функция, являющаяся частью функции sin 9.1722 2 функция (х).


 Однако это если f и g обе функции. В результате цепное правило описывает производную составной функции f g в терминах f и вывода g.
Однако это если f и g обе функции. В результате цепное правило описывает производную составной функции f g в терминах f и вывода g.
 9072. 9072. 9072. 9072. 9072. 9072. 9072. 9072. 9072. 9072. 9072.
9072. 9072. 9072. 9072. 9072. 9072. 9072. 9072. 9072. 9072. 9072.