Cosx четная или нечетная: Свойства функции y = cosx и её график — урок. Алгебра, 11 класс.

Применим правила четная функция. Четность и нечетность функции

— (матем.) Функция у = f (x) называется чётной, если она не меняется, когда независимое переменное изменяет только знак, то есть, если f (x) = f (x). Если же f (x) = f (x), то функция f (x) называется нечётной. Например, у = cosx, у = x2… …

F(x) = x пример нечётной функции. f(x) = x2 пример чётной функции. f(x) = x3 … Википедия

Функция, удовлетворяющая равенству f (x) = f (x). См. Чётные и нечётные функции … Большая советская энциклопедия

F(x) = x пример нечётной функции. f(x) = x2 пример чётной функции. f(x) = x3 … Википедия

Специальные функции, введённые французским математиком Э. Матье (E. Mathieu) в 1868 при решении задач о колебании эллиптической мембраны. М. ф. применяются также при изучении распространения электромагнитных волн в эллиптическом цилиндре … Большая советская энциклопедия

Запрос «sin» перенаправляется сюда; см. также другие значения. Запрос «sec» перенаправляется сюда; см. также другие значения. Запрос «Синус» перенаправляется сюда; см. также другие значения … Википедия

. Для этого воспользуйтесь миллиметровкой или графическим калькулятором. Выберите несколько любых числовых значений независимой переменной x {\displaystyle x} и подставьте их в функцию, чтобы вычислить значения зависимой переменной y {\displaystyle y} . Найденные координаты точек нанесите на координатную плоскость, а затем соедините эти точки, чтобы построить график функции.

В функцию подставьте положительные числовые значения x {\displaystyle x} и соответствующие отрицательные числовые значения. Например, дана функция f (x) = 2 x 2 + 1 {\displaystyle f(x)=2x^{2}+1} . Подставьте в нее следующие значения x {\displaystyle x} :

Проверьте, симметричен ли график функции относительно оси Y. Под симметрией подразумевается зеркальное отображение графика относительно оси ординат. Если часть графика справа от оси Y (положительные значения независимой переменной) совпадает с частью графика слева от оси Y (отрицательные значения независимой переменной), график симметричен относительно оси Y. Если функция симметрична относительно оси ординат, такая функция четная.

Проверьте, симметричен ли график функции относительно начала координат. Начало координат – это точка с координатами (0,0). Симметрия относительно начала координат означает, что положительному значению y {\displaystyle y} (при положительном значении x {\displaystyle x} ) соответствует отрицательное значение y {\displaystyle y} (при отрицательном значении x {\displaystyle x} ), и наоборот. Нечетные функции обладают симметрией относительно начала координат.

Проверьте, имеет ли график функции какую-нибудь симметрию. {2}} . Будучи записанной в такой форме, функция кажется четной, потому что присутствует четный показатель степени. Но этот пример доказывает, что вид функции нельзя быстро определить, если независимая переменная заключена в скобки. В этом случае нужно раскрыть скобки и проанализировать полученные показатели степени.

Четная функция.

Четной называется функция, знак которой не меняется при изменении знака x .

x выполняется равенство f (–x ) = f (x ). Знак x не влияет на знак y .

График четной функции симметричен относительно оси координат (рис.1).

Примеры четной функции:

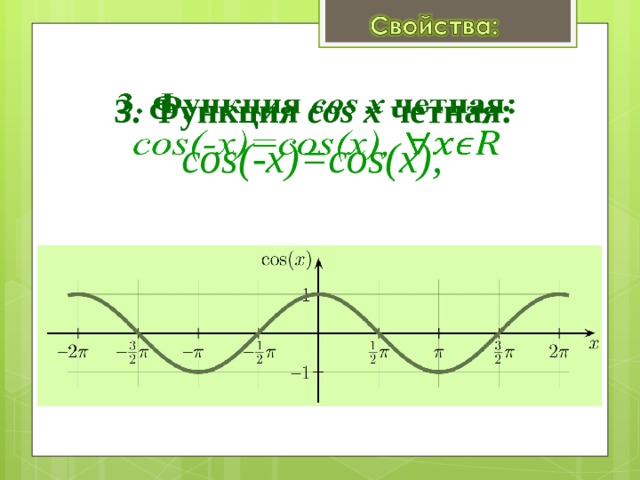
y = cos x
y = x 2
y = –x 2
y = x 4
y = x 6
y = x 2 + x
Пояснение:
Возьмем функцию y = x 2 или y = –x 2 .
При любом значении x функция положительная.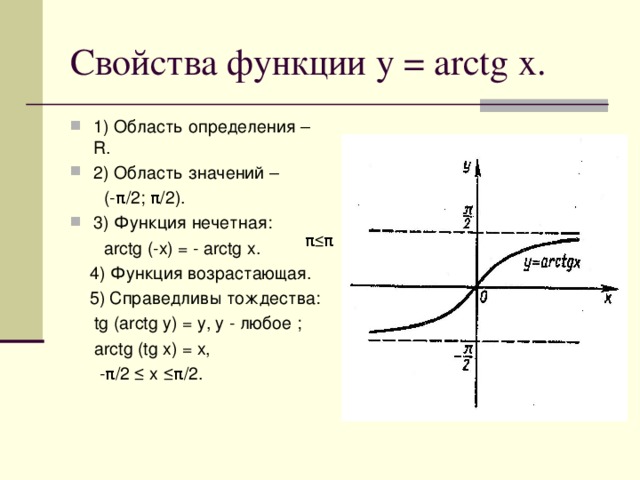 Знак x не влияет на знак y . График симметричен относительно оси координат. Это четная функция.
Нечетная функция.
Нечетной называется функция, знак которой меняется при изменении знака x .
Говоря иначе, для любого значения x выполняется равенство f (–x ) = –f (x ).
График нечетной функции симметричен относительно начала координат (рис.2).
Примеры нечетной функции:
y = sin x
y
= x 3
y = –x 3
Пояснение:
Возьмем функцию y = –x 3 .
Все значения у в ней будут со знаком минус. То есть знак x влияет на знак y . Если независимая переменная – положительное число, то и функция положительная, если независимая переменная – отрицательное число, то и функция отрицательная: f (–x ) = –f (x ).
График функции симметричен относительно начала координат. Это нечетная функция.
Свойства четной и нечетной функций:
ПРИМЕЧАНИЕ:
Не все функции являются четными или нечетными. Есть функции, которые не подчиняются такой градации. К примеру, функция корня у = √х не относится ни к четным, ни к нечетным функциям (рис.3). При перечислении свойств подобных функций следует давать соответствующее описание: ни четна, ни нечетна.
Периодические функции.

Как вы знаете, периодичность – это повторяемость определенных процессов с определенным интервалом. Функции, описывающие эти процессы, называют периодическими функциями . То есть это функции, в чьих графиках есть элементы, повторяющиеся с определенными числовыми интервалами.
Которые в той или иной степени были вам знакомы. Там же было замечено, что запас свойств функций будет постепенно пополняться. О двух новых свойствах и пойдет речь в настоящем параграфе.
Определение 1.
Функцию у = f(x), х є Х, называют четной, если для любого значения х из множества X выполняется равенство f (-х) = f (х).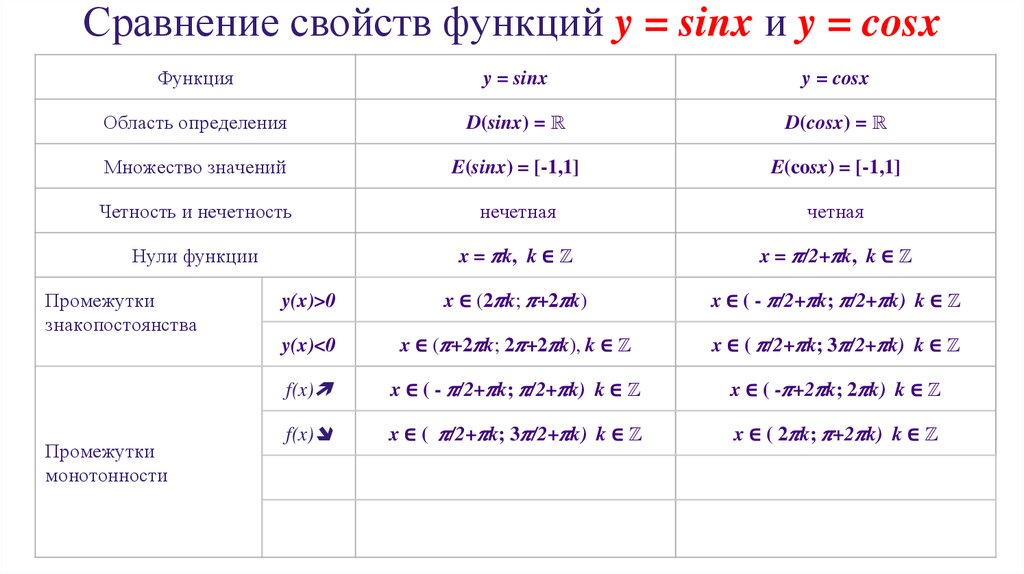
Определение 2.
Функцию у = f(x), х є X, называют нечетной, если для любого значения х из множества X выполняется равенство f (-х) = -f (х).
Доказать, что у = х 4 — четная функция.

Решение. Имеем: f(х) = х 4 , f(-х) = (-х) 4 . Но (-х) 4 = х 4 . Значит, для любого х выполняется равенство f(-х) = f(х), т.е. функция является четной.
Аналогично можно доказать, что функции у — х 2 ,у = х 6 ,у — х 8 являются четными.
Доказать, что у = х 3 ~ нечетная функция.
Решение. Имеем: f(х) = х 3 , f(-х) = (-х) 3 . Но (-х) 3 = -х 3 . Значит, для любого х выполняется равенство f (-х) = -f (х), т.е. функция является нечетной.
Аналогично можно доказать, что функции у = х, у = х 5 , у = х 7 являются нечетными.
Мы с вами не раз уже убеждались в том, что новые термины в математике чаще всего имеют «земное» происхождение, т.е. их можно каким-то образом объяснить. Так обстоит дело и с четными, и с нечетными функциями. Смотрите: у — х 3 , у = х 5 , у = х 7 — нечетные функции, тогда как у = х 2 , у = х 4 , у = х 6 — четные функции. И вообще для любой функции вида у = х» (ниже мы специально займемся изучением этих функций), где n — натуральное число , можно сделать вывод: если n — нечетное число, то функция у = х» — нечетная; если же n — четное число, то функция у = хn — четная.

Существуют и функции, не являющиеся ни четными, ни нечетными. Такова, например, функция у = 2х + 3. В самом деле, f(1) = 5, а f (-1) = 1. Как видите, здесь Значит, не может выполняться ни тождество f(-х) = f (х), ни тождество f(-х) = -f(х).
Итак, функция может быть четной, нечетной, а также ни той ни другой.
Изучение вопроса о том, является ли заданная функция четной или нечетной, обычно называют исследованием функции на четность.
В определениях 1 и 2 речь идет о значениях функции в точках х и -х. Тем самым предполагается, что функция определена и в точке х, и в точке -х. Это значит, что точка -х принадлежит области определения функции одновременно с точкой х. Если числовое множество X вместе с каждым своим элементом х содержит и противоположный элемент -х, то X называют симметричным множеством.

2\,1 \end{cases} \quad\Leftrightarrow\quad \begin{cases} x=0\\ \mathrm{tg}\,(\cos x)=\mathrm{tg}\,1 \end{cases}\quad\Leftrightarrow\quad x=0\] Следовательно, значение \(a=-\mathrm{tg}\,1\) нам подходит.
Ответ:
\(a\in \{-\mathrm{tg}\,1;0\}\)
Задание 2 #3923
Уровень задания: Равен ЕГЭ
Найдите все значения параметра \(a\) , при каждом из которых график функции \
симметричен относительно начала координат.
Если график функции симметричен относительно начала координат, то такая функция является нечетной, то есть выполнено \(f(-x)=-f(x)\) для любого \(x\) из области определения функции. Таким образом, требуется найти те значения параметра, при которых выполнено \(f(-x)=-f(x).\)
\[\begin{aligned} &3\mathrm{tg}\,\left(-\dfrac{ax}5\right)+2\sin \dfrac{8\pi a+3x}4= -\left(3\mathrm{tg}\,\left(\dfrac{ax}5\right)+2\sin \dfrac{8\pi a-3x}4\right)\quad \Rightarrow\quad -3\mathrm{tg}\,\dfrac{ax}5+2\sin \dfrac{8\pi a+3x}4= -\left(3\mathrm{tg}\,\left(\dfrac{ax}5\right)+2\sin \dfrac{8\pi a-3x}4\right) \quad \Rightarrow\\ \Rightarrow\quad &\sin \dfrac{8\pi a+3x}4+\sin \dfrac{8\pi a-3x}4=0 \quad \Rightarrow \quad2\sin \dfrac12\left(\dfrac{8\pi a+3x}4+\dfrac{8\pi a-3x}4\right)\cdot \cos \dfrac12 \left(\dfrac{8\pi a+3x}4-\dfrac{8\pi a-3x}4\right)=0 \quad \Rightarrow\quad \sin (2\pi a)\cdot \cos \frac34 x=0 \end{aligned}\]

Последнее уравнение должно быть выполнено для всех \(x\) из области определения \(f(x)\) , следовательно, \(\sin(2\pi a)=0 \Rightarrow a=\dfrac n2, n\in\mathbb{Z}\) . 2\) .
1) Пусть \(a>0\) . Тогда график функции \(f(x)\) будет выглядеть следующим образом:

Тогда для того, чтобы уравнение имело 4 решения, нужно, чтобы график \(g(x)=|a+2|\cdot \sqrtx\) проходил через точку \(A\) :

Следовательно, \[\dfrac{64}9a=|a+2|\cdot \sqrt8 \quad\Leftrightarrow\quad \left[\begin{gathered}\begin{aligned} &9(a+2)=32a\\ &9(a+2)=-32a \end{aligned} \end{gathered}\right. \quad\Leftrightarrow\quad \left[\begin{gathered}\begin{aligned} &a=\dfrac{18}{23}\\ &a=-\dfrac{18}{41} \end{aligned} \end{gathered}\right.\] Так как \(a>0\) , то подходит \(a=\dfrac{18}{23}\) .
2) Пусть \(a

Нужно, чтобы график \(g(x)\) прошел через точку \(B\) : \[\dfrac{64}9a=|a+2|\cdot \sqrt{-8} \quad\Leftrightarrow\quad \left[\begin{gathered}\begin{aligned} &a=\dfrac{18}{23}\\ &a=-\dfrac{18}{41} \end{aligned} \end{gathered}\right.\] Так как \(a
3) Случай, когда \(a=0\) , не подходит, так как тогда \(f(x)=0\) при всех \(x\) , \(g(x)=2\sqrtx\) и уравнение будет иметь только 1 корень.
{\log_{\sqrt2} t_1}\) , то первое уравнение совокупности перепишется в виде \ Как мы уже говорили, любое кубическое уравнение имеет не более трех решений, следовательно, каждое уравнение из совокупности будет иметь не более трех решений. А значит и вся совокупность будет иметь не более шести решений.
Значит, чтобы исходное уравнение имело шесть решений, квадратное уравнение \((*)\) должно иметь два различных решения, а каждое полученное кубическое уравнение (из совокупности) должно иметь три различных решения (причем ни одно решение одного уравнения не должно совпадать с каким-либо решением второго!)
Очевидно, что если квадратное уравнение \((*)\) будет иметь одно решение, то мы никак не получим шесть решений у исходного уравнения.
Таким образом, план решения становится ясен. Давайте по пунктам выпишем условия, которые должны выполняться.
1) Чтобы уравнение \((*)\) имело два различных решения, его дискриминант должен быть положительным: \

2) Также нужно, чтобы оба корня были положительными (так как \(t>0\) ). 2+2}\cdot \ln 2\cdot 2x\) . Ноль производной: \(x=0\) . При \(x0\) , при \(x>0\) : \(g» Функция \(f(x)\) при \(x>0\) является возрастающей, а при \(x Действительно, при \(x>0\) первый модуль раскроется положительно (\(|x|=x\) ), следовательно, вне зависимости от того, как раскроется второй модуль, \(f(x)\) будет равно \(kx+A\) , где \(A\) – выражение от \(a\) , а \(k\) равно либо \(13-10=3\) , либо \(13+10=23\) . При \(x Найдем значение \(f\) в точке минимума: \
Для того, чтобы уравнение имело хотя бы одно решение, нужно, чтобы графики функций \(f\) и \(g\) имели хотя бы одну точку пересечения. Следовательно, нужно: \ Решая данную совокупность систем, получим ответ: \\]
Ответ:
\(a\in \{-2\}\cup\)
Введение в математику — тест 4
Введение в математику — тест 4
Решение тестов Intuit
игра брюс 2048
Главная / Математика / Введение в математику / Тест 4
Упражнение 1:
Номер 1
Если X=[–2;5], Y=[0;2], то будет:
Ответ:
&nbsp(1) числовой функцией&nbsp
&nbsp(2) множеством&nbsp
&nbsp(3) областью&nbsp

Номер 2
Функция y=sin(x)+cos(x) на промежутке :
Ответ:
&nbsp(1) нечетная&nbsp
&nbsp(2) монотонно убывающая&nbsp
&nbsp(3) ни четна, ни нечетна, ни монотонна&nbsp

Номер 3
Соответствие – это:
Ответ:
&nbsp(1) порядок&nbsp
&nbsp(2) отображение&nbsp
&nbsp(3) множество&nbsp

Упражнение 2:
Номер 1
Функции задаются:
Ответ:
&nbsp(1) аналитически, таблично и графически&nbsp
&nbsp(2) графически и таблично&nbsp
&nbsp(3) аналитически, таблично, графически, словесно&nbsp

Номер 2
Если X=[0;3], Y=[3;0], то будет:
Ответ:
&nbsp(1) числом&nbsp
&nbsp(2) отображением&nbsp
&nbsp(3) множеством&nbsp

Номер 3
В списке: y=|x|, y=1+х+x², y=x, y=х+cos(x–90°), y=x³ число четных и нечетных функций равно, соответственно:
Ответ:
&nbsp(1) 1 и 3&nbsp
&nbsp(2) 3 и 2&nbsp
&nbsp(3) 2 и 3&nbsp

Упражнение 3:
Номер 1
В списке: y=sinx, y=x², y=x, y=cosx, y=x³ число четных и нечетных функций равно, соответственно:
Ответ:
&nbsp(1) 2 и 3&nbsp
&nbsp(2) 3 и 2&nbsp
&nbsp(3) 4 и 1&nbsp

Номер 2
Функция y=sin(x/5) на промежутке :
Ответ:
&nbsp(1) четная и непериодическая&nbsp
&nbsp(2) нечетная и монотонно убывающая&nbsp
&nbsp(3) нечетная и монотонно возрастающая&nbsp

Номер 3
Период функции y=tgx равен:
Ответ:
&nbsp(1) &nbsp
&nbsp(2) &nbsp
&nbsp(3) &nbsp

Упражнение 4:
Номер 1
Период функции y=sinx равен:
Ответ:
&nbsp(1) &nbsp
&nbsp(2) &nbsp
&nbsp(3) &nbsp

Номер 2
Верно утверждение:
Ответ:
&nbsp(1) график функции z(x)=f(x)+g(x) имеет область определения &nbsp
&nbsp(2) график z(x)=f(x)+g(x) получаем умножением отрезков у₁=f(x1), у₂=f(x2)&nbsp
&nbsp(3) график z(x)=f(x)–g(x) имеет область определения D(z)=D(f) &nbsp

Номер 3
В списке функций: y=10cosx, y=1+x+x³, y=x–3, y=e^x монотонных на [0;1] функций всего:
Ответ:
&nbsp(1) 4&nbsp
&nbsp(2) 3&nbsp
&nbsp(3) 2&nbsp

Упражнение 5:
Номер 1
В списке функций: y=sinx, y=ctgx, y=x, y=e^x монотонных на [0;1] функций всего:
Ответ:
&nbsp(1) 4&nbsp
&nbsp(2) 3&nbsp
&nbsp(3) 2&nbsp

Номер 2
Неверно утверждение
Ответ:
&nbsp(1) график у=f(x)+а получается из графика у=f(x) сдвигом вдоль оси Оу на |а| единиц&nbsp
&nbsp(2) график у=аf(x) получаем из графика у=f(x) растяжением в а раз по оси Оу (|а| > 1)&nbsp
&nbsp(3) график у=f(ax) получаем из графика у=f(x) растяжением в а раз по оси Оу (|а|<1)&nbsp

Номер 3
Верно утверждение:
Ответ:
&nbsp(1) график функции z(x)=f(x)–g(x) имеет область определения &nbsp
&nbsp(2) график z(x)=f(x)g(x) получаем умножением отрезков у₁=f(x1), у₂=f(x2)&nbsp
&nbsp(3) график z(x)=f(x)g(x) получаем умножением отрезков у₁=f(x1), у₂=f(x2)&nbsp

Главная / Математика / Введение в математику / Тест 4
3 6 Решить для ? cos(x)=1/2 7 Найти x sin(x)=-1/2 8 Преобразование градусов в радианы 225 9 Решить для ? cos(x)=(квадратный корень из 2)/2 10 Найти x cos(x)=(квадратный корень из 3)/2 11 Найти x sin(x)=(квадратный корень из 3)/2 92=9 14 Преобразование градусов в радианы 120 градусов 15 Преобразование градусов в радианы 180 16 Найти точное значение желтовато-коричневый(195) 92-4 38 Найти точное значение грех(255) 39 Оценить лог база 27 из 36 40 Преобразовать из радианов в градусы 2 шт. 92-3sin(x)+1=0 43 Найти x tan(x)+ квадратный корень из 3=0 44 Найти x sin(2x)+cos(x)=0 45 Упростить (1-cos(x))(1+cos(x)) 92=25 59 График f(x)=- натуральный логарифм x-1+3 60 Найдите значение с помощью единичного круга угловой синус(-1/2) 61 Найти домен квадратный корень из 36-4x^2 92=0 66 Найти x cos(2x)=(квадратный корень из 2)/2 67 График у=3 68 График f(x)=- логарифмическая база 3 x-1+3 92 71 Найти x квадратный корень из x+4+ квадратный корень из x-1=5 72 Решить для ? cos(2x)=-1/2 73 Найти x логарифмическая база x из 16=4 9х 75 Упростить (cos(x))/(1-sin(x))+(1-sin(x))/(cos(x)) 76 Упростить сек(х)sin(х) 77 Упростить кубический корень из 24 кубический корень из 18 92=0 96 Найти x 3x+2=(5x-11)/(8г) 97 Решить для ? sin(2x)=-1/2 98 Найти x (2x-1)/(x+2)=4/5 93 6 Решить для ? cos(x)=1/2 7 Найти x sin(x)=-1/2 8 Преобразование градусов в радианы 225 9 Решить для ? cos(x)=(квадратный корень из 2)/2 10 Найти x cos(x)=(квадратный корень из 3)/2 11 Найти x sin(x)=(квадратный корень из 3)/2 92=9 14 Преобразование градусов в радианы 120 градусов 15 Преобразование градусов в радианы 180 16 Найти точное значение желтовато-коричневый(195) 92-4 38 Найти точное значение грех(255) 39 Оценить лог база 27 из 36 40 Преобразовать из радианов в градусы 2 шт.
No related posts.