Калькулятор дробей онлайн
Если вам необходимо произвести математические операции с дробями воспользуйтесь нашим онлайн калькулятором:
+−×÷
=
Просто заполните необходимые поля и получите ответ и подробное решение.
Данный калькулятор может работать как с положительными, так и с отрицательными дробями.
При этом нужно помнить, что:
− ac = a− c = − ac
Всегда нужно использовать только последний вариант.
Сложение дробей
С одинаковыми знаменателями
При сложении дробей с одинаковыми знаменателями складываются только числители, а знаменатель остаётся прежним.
Формула
ac + bc = a + bc
Пример
Для примера сложим следующие дроби с равными знаменателями:
27 + 47 = 2 + 47 = 67
С разными знаменателями
При сложении дробей с разными знаменателями для начала необходимо привести дроби к общему знаменателю. А затем сложить числители.
А затем сложить числители.
Формула (универсальная)
ac + bd = a⋅d + b⋅cc⋅d
Пример №1
Для примера сложим следующие дроби с разными знаменателями:
12+13=1⋅32⋅3+1⋅23⋅2=36+26=3+26=56
Пример №2
Существуют также частные случаи, когда знаменатель одной дроби можно привести к знаменателю второй. Например:
12+14=1⋅22⋅2+14=24+14=2+14=34
Этот же пример можно решить и применяя вышеуказанную универсальную формулу:
12+14=1⋅42⋅4+1⋅24⋅2=48+28=4+28=68=34
Обратите внимание, что мы сократили дробь:
68=3 ⋅ 24 ⋅ 2=34
Сложение смешанных чисел
Смешанные числа — это такие числа, у которых есть как дробная часть, так и целая.
Преобразуя в неправильную дробь
Для начала смешанное число (дробь) нужно преобразовать в неправильную дробь, а потом можно складывать как в предыдущих примерах.
Формула
a bc + d ef = b + a ⋅ cc + e + d ⋅ ff
Пример
Для примера сложим два смешанных числа:
312+123=1+3⋅22+2+1⋅33=72+53=7⋅32⋅3+5⋅23⋅2=216+106=21+106=316=5⋅6+16=5⋅
+ 16=516
Обратите внимание, что из полученной неправильной дроби мы выделили целую часть:
316=5⋅6+16=5⋅66 + 16=516
Складывая целую и дробную части отдельно
Целую и дробную части смешанных чисел можно складывать по отдельности.
Формула
a bc + d ef = (a + d) + (bc + ef)
Пример
Решим предыдущий пример этим способом:
3 12 + 1 23 = (3+1)+(12+23) = 4+1⋅32⋅3+2⋅23⋅2=4+36+46=4+3+46=4+76=4+116 = 516
Вычитание дробей
Вычитание дробей происходит по тем же принципам, что и сложение.
С одинаковыми знаменателями
Формула
ac − bc = a − bc
Пример
Для примера вычтем одну дробь из другой с равными знаменателями:
35−25=3−25=15
С разными знаменателями
Тут также, как и при сложении, дроби нужно подвести под общий знаменатель, а затем вычитать.
Формула
ac − bd = a⋅d − b⋅cc⋅d
Пример
Для примера вычтем одну дробь из другой, с разными знаменателями:
34−13=3⋅34⋅3−1⋅43⋅4=912−412=9−412=512
Вычитание смешанных чисел
Для начала смешанные числа преобразуем в неправильные дроби, потом приводим полученные дроби к общему знаменателю, а затем вычтем одну из другой. Далее выделяем целую часть если она есть.
Формула
a bc − d ef = b + a ⋅ cc − e + d ⋅ ff
Пример
312−123=1+3⋅22−2+1⋅33=72−53=7⋅32⋅3−5⋅23⋅2=216−106=21−106=116=1⋅6+56=1⋅+ 56=156
Умножение дробей
При умножении дробей неважно одинаковые или разные у них знаменатели. Числитель одной дроби умножается на числитель другой, а знаменатели тоже перемножаются между собой.
Формула
ac ⋅ be = a ⋅ bc ⋅ e
Давайте рассмотрим несколько примеров:
Пример №1
Умножим дроби с одинаковыми знаменателями:
13⋅23=1⋅23⋅3=29
Пример №2
Умножим дроби с разными знаменателями:
13⋅24=1⋅23⋅4=212=1⋅
6⋅
=16
Пример №3
Умножим смешанные числа:
112⋅223=1+1⋅22⋅2+2⋅33=32⋅83=3⋅82⋅3=246=4
Деление дробей
При делении одной дроби на другую также неважно одинаковые или разные у них знаменатели. Чтобы разделить одну дробь на другую нужно перемножить числитель первой дроби и знаменатель второй, а знаменатель первой умножить на числитель второй.
Чтобы разделить одну дробь на другую нужно перемножить числитель первой дроби и знаменатель второй, а знаменатель первой умножить на числитель второй.
Формула
ac : be = a ⋅ ec ⋅ b
Давайте рассмотрим несколько примеров:
Пример №1
Разделим одну дробь на другую с таким же знаменателем:
23:13=23⋅31=2⋅33⋅1=63=2
Пример №2
Делим дроби с разными знаменателями:
Пример №3
Деление смешанных чисел:
412:223=1+4⋅22:2+2⋅33=92:83=92⋅38=9⋅32⋅8=2716=1⋅16+1116=1⋅
+ 1116=11116
См. также
Онлайн калькулятор дробей. Вычисления с дробями. Сложение, вычитание, умножение и деление дробей — Справочник
Математика дробь
Используя этот Онлайн калькулятор с дробями, вы сможете Сложить, вычесть, умножить, разделить или возвести в степень обыкновенные дроби, смешанные числа (дроби с целой частью), десятичные дроби и целые числа, соответственно найти их сумму, разность, произведение или частное.
Воспользовавшись онлайн калькулятором дробей, вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения задач с дробями и закрепить пройденный на уроках материал.
Калькулятор дробей
| | | 1 | 2 | 3 | ÷ | |
| ( | ) | 4 | 5 | 6 | × | С |
| A 2 | 7 | 8 | 9 | — | | |
| A b | . | 0 | + |
Инструкция использования калькулятора дробей
Для решения вашей задачи выполните следующие действия:
- введите ваш пример в калькулятор; нажмите кнопку для выполнения вычислений.
Ввод данных в калькулятор дробей
В калькулятор дробей можно вводить: целые числа, десятичные дроби, обыкновенные дроби и смешанные числа.
Целые числа. Для ввода целых чисел используйте цифровые клавиши калькулятора или цифровые клавиши вашего компьютера. 3)
3)
N. B. Калькулятор поддерживает только целые степени!
N. B. Буквенные выражения, операции извлечения корня калькулятор не поддерживает!
Калькулятор дробей
| | | 1 | 2 | 3 | ÷ | |
| ( | ) | 4 | 5 | 6 | × | С |
| A 2 | 7 | 8 | 9 | — | | |
| A b | . | 0 | + |
Для решения вашей задачи выполните следующие действия:
- введите ваш пример в калькулятор; нажмите кнопку для выполнения вычислений.
Целые числа.
Ru. onlinemschool. com
04.10.2017 4:14:43
2017-10-04 04:14:43
Источники:
Https://ru. onlinemschool. com/math/assistance/fraction/fraction_calc/
Обыкновенные дроби — Определение, Примеры, Действия, Доли, Числитель и Знаменатель » /> » /> .keyword { color: red; }
Математика дробь
С 5 класса редкий урок математики проходит без дробей. Тема непростая и объемная, поэтому лучше начать разбираться сейчас, чтобы дальше было проще решать задачки. В этой статье расскажем про обыкновенные дроби.
Тема непростая и объемная, поэтому лучше начать разбираться сейчас, чтобы дальше было проще решать задачки. В этой статье расскажем про обыкновенные дроби.
О чем эта статья:
Доля целого
Доля это каждая из равных частей, на которые поделено целое.
Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.
У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.
- Половина — одна вторая доля предмета или 1/2. Треть — одна третья доля предмета или 1/3. Четверть — одна четвертая доля предмета или 1/4.
Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.
Как устроена обыкновенная дробь
Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.
Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.
Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.
Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.
Черта между числителем и знаменателем — символ деления.
Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.
Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.
Как устроена десятичная дробь
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т. д. Выходит, что Десятичная дробь — это то, что получается, если разделить числитель на знаменатель.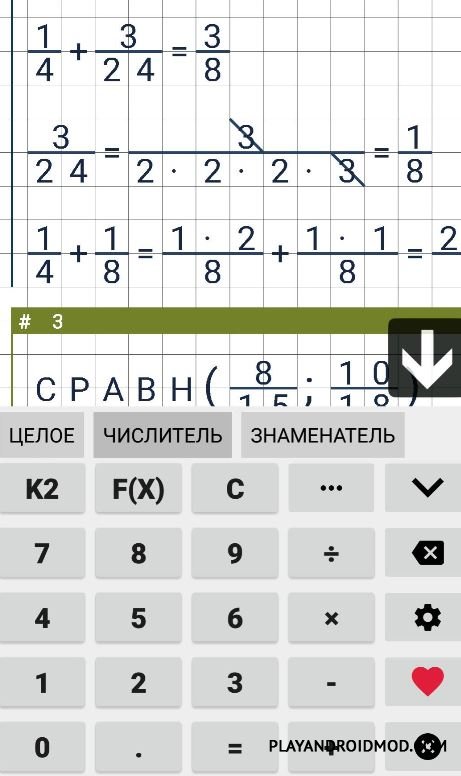 Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства дробей
Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:
где a, b, k — натуральные числа.
Дробь не имеет значения, если знаменатель равен нулю. Дробь равна нулю, если числитель равен нулю, а знаменатель — нет. Две дроби a/b и c/d называются равными, если a * d = b * c.
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
- Целая часть десятичной дроби равна целой части смешанной дроби.
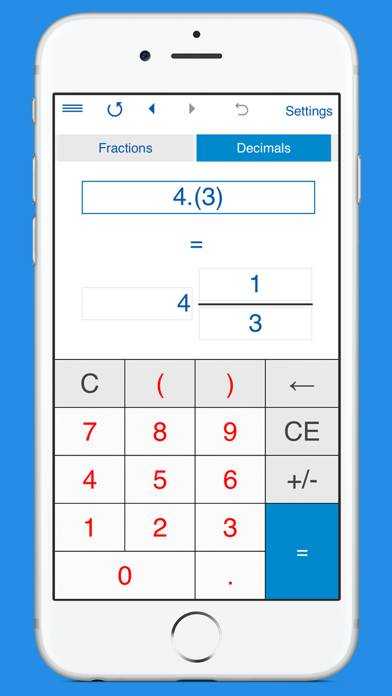 Если числитель меньше знаменателя, то целая часть равна нулю. Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде, если в знаменателе обыкновенной дроби числа 10, 100, 1000 и т. д. Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби, если в знаменателе обыкновенной дроби числа 10, 100, 1000 и т. д. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Если числитель меньше знаменателя, то целая часть равна нулю. Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде, если в знаменателе обыкновенной дроби числа 10, 100, 1000 и т. д. Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби, если в знаменателе обыкновенной дроби числа 10, 100, 1000 и т. д. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.У нас есть отличные курсы по математике для учеников с 1 по 11 классы, записывайтесь!
Действия с дробями
С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.
Сравнение дробей
Из двух дробей с Одинаковыми знаменателями больше та, у которой числитель больше.
Сравним 1/5 и 4/5. Как рассуждаем:
В обеих дробях знаменатель равен 5.
В первой дроби числитель равен 1, во второй дроби равен 4.
Из двух дробей с Одинаковыми числителями
Сравним 1/2 и 1/8. Как рассуждаем:
Представим, что у нас есть торт. Так как знаменатель первой дроби равен 2, то делим торт на две части и забираем себе одну, то есть половину торта.
Знаменатель второй дроби равен 8, делим торт на восемь частей и забираем крохотный кусочек. Половина торта больше больше маленького кусочка.
Таким образом 1/2 > 1/8.
Чтобы Сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.
Пример. Сравнить 2/7 и 1/14.
Важно запомнить: Любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.
Чтобы сравнить дроби с разными числителями и знаменателями, нужно:
- привести дроби к общему знаменателю; сравнить полученные дроби.

Чтобы привести дроби к общему знаменателю, нужно:
Найти общее кратное знаменателей дробей, которое станет их общим знаменателем.
Разделить общий знаменатель на знаменатель данных дробей, то есть найти для каждой дроби дополнительный множитель.
Умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Сокращение дробей
Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81.
Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число.
В этом примере делим обе части дроби на двойку.
Можно никуда не спешить и сокращать дроби последовательно, в несколько действий.
Сложение и вычитание дробей
При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.
Не забудьте проверить, можно ли сократить дробь и выделить целую часть.
При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).
Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.
НОК (15, 18) = 3 * 2 * 3 * 5 = 90
Полученные числа запишем справа сверху над числителем.
- если числитель больше знаменателя, нужно преобразовать дробь в смешанное число; если есть что сократить, нужно выполнить сокращение.
Ход решения одной строкой:
Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:
Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.
Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.
Умножение и деление дробей
Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:
Не забываем про сокращение. Это может облегчить вычисления.
Чтобы Умножить два смешанных числа, надо:
преобразовать смешанные дроби в неправильные;
перемножить числители и знаменатели дробей;
сократить полученную дробь;
если получилась неправильная дробь, преобразовать в смешанную.
Чтобы Разделить дробь на дробь нужно выполнить следующую последовательность действий:
- числитель первой умножить на знаменатель второй, результат произведения записать в числитель новой дроби; знаменатель первой умножить на числитель второй, результат произведения записать в знаменатель новой дроби.
Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.
Числа, произведение которых равно 1, называют Взаимно обратными.
Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше.
- если числитель больше знаменателя, нужно преобразовать дробь в смешанное число; если есть что сократить, нужно выполнить сокращение.
где a, b, k — натуральные числа.
Бесконечная десятичная дробь это когда после запятой количество цифр бесконечно.
Skysmart. ru
08.03.2018 21:12:03
2018-03-08 21:12:03
Источники:
Https://skysmart. ru/articles/mathematic/obyknovennye-drobi
Математика дробь » /> » /> .keyword { color: red; }
Математика дробь
Дроби это тема об которую спотыкается половина жителей нашей планеты. Если спросить у людей с какой темы у них начались проблемы с математикой, то большинство из них ответят — с дробей.
Этих людей нельзя упрекнуть. Дроби действительно тема не из простых. Тема дробей требует много терпения и внимания, особенно если человек изучает её впервые.
Но есть и хорошие новости. Если вы наберётесь терпения и освоите дроби, то уверяем, что дальнейшее изучение математики станет для вас простым и интересным.
А если вы ещё хорошо изучили предыдущий урок, который назывался деление, то можете быть уверены, что дроби вы освоили уже наполовину.
Что такое дробь?Если говорить простым языком, то дробь это часть чего-либо. Это «чего-либо» может быть чем угодно — едой, деньгами, числом. В народе дробь называют долей. Само слово «дробь» тоже говорит за себя — дробь означает дробление, деление, разделение.
Рассмотрим пример из жизни. Мы купили себе пиццу, чтобы съесть её в течении дня. Допустим мы решили разделить её на четыре части, чтобы съедать постепенно по одному кусочку.
Посмотрите на этот рисунок. Представьте, что это наша пицца, разделённая на четыре куска. Каждый кусок пиццы это и есть дробь, потому что каждый кусок по отдельности это часть пиццы.
Каждый кусок пиццы это и есть дробь, потому что каждый кусок по отдельности это часть пиццы.
Допустим мы съели один кусок. Как его записать? Очень просто. Сначала рисуется маленькая линия:
Внизу этой линии записывается на сколько кусков пицца была разделена. Пицца была разделена на четыре куска. Значит внизу линии записывается четвёрка:
А сверху этой линии записывается сколько кусков пиццы было съедено. Съеден был один кусок, значит сверху записываем единицу:
Такие записи называют Дробями. Дробь состоит из числителя и знаменателя.
Число, которое записывается сверху, называется Числителем дроби.
Число, которое записывается снизу, называется Знаменателем дроби.
В нашем примере числитель дроби это единица, а знаменатель дроби — четвёрка. Эту дробь можно прочитать так: «одна четвёртая» либо «один кусок из четырёх» либо «одна четвёртая доля» либо «четверть» — в сё это синонимы.
Теперь представьте, что мы съели ещё один кусок той же самой пиццы, которая была разделена на четыре куска. Как записать такую дробь?
Как записать такую дробь?
Очень просто. Сверху записываем 2 (поскольку уже съедено два куска), а внизу записываем 4 (поскольку всего кусков было 4):
Эта дробь читается так: «две четвёртых» либо «два куска из четырёх» либо «две четвёртые доли» .
Теперь представьте, что пиццу мы разделили не на четыре части, а на три.
Допустим мы съели один кусок этой пиццы. Как записать такую дробь?
Очень просто. Опять же рисуется маленькая линия. Внизу этой линии записывается число 3, поскольку пицца разделена на три части, а сверху этой линии записывается число 1, поскольку съеден один кусок:
Эта дробь читается так: «Одна третья» либо «Один кусок из трёх» либо «Одна третья доля» либо «Треть» .
Если мы съедим два куска пиццы, то такая дробь будет называться «две третьих» и записываться следующим образом:
Теперь представьте, что пиццу мы разделили на две части, или как говорят в народе: «Пополам» :
Допустим, из этих двух кусков мы съели один кусок. Как записать такую дробь?
Как записать такую дробь?
Опять же рисуем линию. Внизу этой линии записываем число 2, поскольку пицца разделена на две части, а вверху записываем число 1, поскольку съеден один кусок:
Эта дробь читается так: «одна вторая» либо «один кусок из двух» либо «одна вторая доля» либо «половина».
Дроби, которые мы сейчас рассмотрели, называют Обыкновенными.
Вообще, дроби бывают двух видов: Обыкновенные и Десятичные. На данный момент мы рассматриваем Обыкновенные Дроби. Обыкновенная дробь это дробь, которая состоит из числителя и знаменателя. Десятичные дроби рассмотрим немного позже.
Знаменатель дроби — это число, которое показывает на сколько равных частей можно что-либо разделить. Вернёмся к нашей пицце. Поровну эта пицца может быть разделена и на 2 части и на 3, и на 4, и на 5, и на 6. В зависимости от того, на сколько частей мы будем делить пиццу, знаменатель будет меняться.
На следующем рисунке представлены три пиццы, которые разделены по разному. У первой пиццы знаменателем будет 2. У второй пиццы знаменателем будет 3. У третьей пиццы знаменателем будет 4.
Числитель же показывает сколько частей взято от чего-либо. К примеру, если разделить пиццу на две части, как на первом рисунке, и взять одну часть для трапезы, то получится что мы взяли ( одну часть из двух ), или как говорят в народе «половину» пиццы.
С помощью переменных дробь можно записать так:
где a — это числитель, b — знаменатель.
Следующая вещь, которую важно знать это то, что обыкновенные дроби бывают Правильными и Неправильными.
Правильная дробь — это дробь, у которой числитель меньше знаменателя. Например, следующие дроби являются правильными:
Почему такие дроби называют правильными? Вспомним, что дробь это часть чего-либо. Ведь будет логичнее, если эта часть будет меньше того, откуда эта часть была взята. Например, если пицца разделена на четыре части, и мы возьмём ( одну четвёртую ), то наш кусок будет меньше, чем все четыре куска вместе взятые ( чем одна целая пицца ). Поэтому такие дроби называют правильными.
Например, если пицца разделена на четыре части, и мы возьмём ( одну четвёртую ), то наш кусок будет меньше, чем все четыре куска вместе взятые ( чем одна целая пицца ). Поэтому такие дроби называют правильными.
С неправильной дробью всё с точностью наоборот. Неправильная дробь — это дробь, у которой числитель больше знаменателя. Например, следующие дроби являются неправильными:
Видно, что у этих дробей числитель больше знаменателя. Почему же такие дроби называют неправильными? Вспомним, что дробь это часть чего-либо. Знаменатель показывает на сколько частей это чего-либо разделено. А числитель показывает сколько этого чего-либо взяли.
Теперь возьмём к примеру неправильную дробь и применим её к нашей пицце. В знаменателе стоит 2, значит пицца разделена на две части, а в числителе стоит 9. Получается, что взято девять кусков из двух. Но как можно взять девять кусков, если их всего два? Ответ — никак. Поэтому такие дроби называют неправильными.
Дробь, у которой числитель и знаменатель одинаковые, тоже называют неправильной. Например:
Например:
Вообще, такие дроби даже не должны называться дробями. И вот почему. Рассмотрим к примеру дробь. Применим её к нашей пицце.
Допустим, мы хотим съесть пиццы. В знаменателе стоит число 2, значит пицца разделена на две части. И в числителе стоит 2, значит взято две части. По сути, взята вся целая пицца, и если мы съедим эту пиццы, то съедим не часть пиццы, а всю пиццу целиком. Иными словами, съедим не дробь, а целую часть пиццы. Поэтому дробь, у которой числитель и знаменатель одинаковые, называют неправильной.
Дробь означает делениеЧерта в дроби, которая отделяет числитель от знаменателя, означает деление. Она говорит, что числитель можно разделить на знаменатель.
Например, рассмотрим дробь. Дробная черта говорит, что четвёрку можно разделить на двойку. Мы знаем, что четыре разделить на два будет два. Ставим знак равенства (=) и записываем ответ:
Можно сделать вывод, что любое деление чисел можно записать с помощью дробей. Например:
Например:
Это простейшие примеры. Видно, что у них отсутствует остаток. С остатком немного сложнее, зато интереснее. Поговорим об этом в следующей теме, которая называется «выделение целой части дроби».
Выделение целой части дроби
Вычислим дробь. Пять разделить на два будет два и один в остатке:
5 : 2 = 2 (1 в остатке)
Проверка: (2 × 2) + 1 = 4 + 1 = 5
Но сейчас мы имеем дело с дробями, значит и отвечать надо в дробном виде. Чтобы хорошо понять, как это делается, рассмотрим пример из жизни.
Представьте, что у вас есть 5 яблок и вы решили поделиться ими со своим другом. Причём поделиться по-честному, чтобы каждому досталось поровну. Как разделить эти 5 яблок?
Очевидно, что каждому из вас достанется по два яблока, а оставшееся одно яблоко вы разрежете ножом пополам и тоже разделите между собой:
Посмотрите внимательно на этот рисунок. На нём показано, как пять яблок разделены между вами и вашим другом. Очевидно, что каждому досталось по два целых яблока и по половинке яблока.
Очевидно, что каждому досталось по два целых яблока и по половинке яблока.
Теперь возвращаемся к дроби и отвечаем на её вопрос. Сколько будет пять разделить на два? Смотрим на наш рисунок и отвечаем: если пять яблок разделить на двоих, то каждому достанется два целых яблока и половинка яблока. Так и записываем:
Схематически это выглядит так:
Процедуру, которую мы сейчас провели, называют Выделением целой части дроби.
В нашем примере мы выделили целую часть дроби и получили новую дробь. Такую дробь называют Смешанной. Смешанная дробь — это дробь, у которой есть Целая часть и Дробная.
В нашем примере целая часть это 2, а дробная часть это
Обязательно запомните эти понятия! А лучше запишите в свою рабочую тетрадь.
Выделить целую часть можно только у неправильных дробей. Напомним, что неправильная дробь это дробь, у которой числитель больше знаменателя. Например, следующие дроби являются неправильными, и у них выделена целая часть:
Чтобы выделить целую часть, достаточно знать, как делить числа уголком.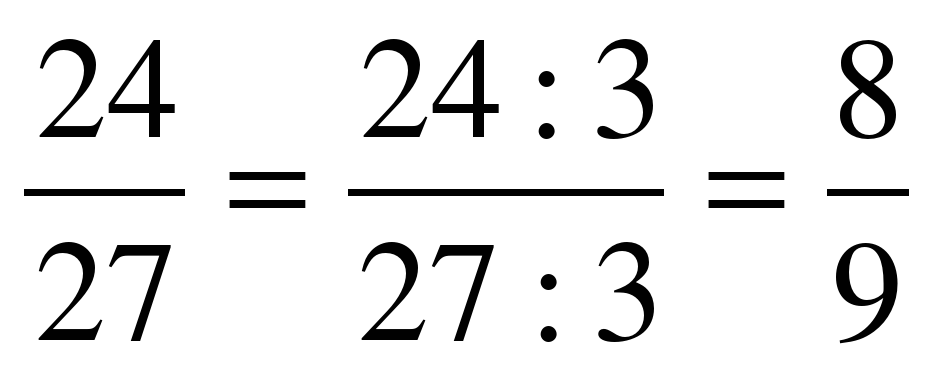 Например, выделим целую часть у дроби. Записываем уголком данное выражение и решаем:
Например, выделим целую часть у дроби. Записываем уголком данное выражение и решаем:
После того, как решение примера завершается, новую дробь собирают подобно детскому конструктору. Важно понимать, что куда относить. Частное относят к целой части, остаток относят в числитель дробной части, делитель относят в знаменатель дробной части.
В принципе, если вы хорошо знаете таблицу умножения, и можете быстро в уме выполнять элементарные вычисления, то можно обойтись без записей уголком. В школах кстати, именно этого и требуют — чтобы учащиеся не тратили время на простые операции, а сразу записывали ответы.
Но если вы только начинаете изучать математику, советуем записывать каждую мелочь.
Рассмотрим ещё один пример на выделение целой части. Пусть требуется выделить целую часть дроби
Записываем уголком данное выражение и решаем. Потом собираем смешанную дробь:
Получили:
Перевод смешанного числа в неправильную дробьЛюбое смешанное число получается в результате выделения целой части в неправильной дроби. Например, рассмотрим неправильную дробь. Если выделить в ней целую часть, то получается
Например, рассмотрим неправильную дробь. Если выделить в ней целую часть, то получается
Но возможен и обратный процесс — любое смешанное число можно перевести в неправильную дробь. Для этого целую часть надо умножить на знаменатель дробной части и полученный результат прибавить к числителю дробной части. Полученный результат будет числителем новой дроби, а знаменатель останется без изменений.
Например, переведём смешанное число в неправильную дробь. Умножаем целую часть 2 на знаменатель дробной части:
Затем к 6 прибавляем числитель дробной части:
Полученная семёрка будет числителем новой дроби, а знаменатель 3 останется без изменений:
Подробное решение выглядит так:
А с помощью переменных перевод смешанного числа в неправильную дробь можно записать так:
Пример 2. Перевести смешанное число в неправильную дробь.
Умножаем целую часть смешанного числа на знаменатель дробной части и прибавляем к числителю дробной части, а знаменатель оставляем без изменений:
Основное свойство дробиОсновное свойство дроби говорит о том, что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь. Это означает, что значение дроби не изменится.
Это означает, что значение дроби не изменится.
Например, рассмотрим дробь. Умножим её числитель и знаменатель на одно и то же число, например на число 2
Получили новую дробь. Если верить основному свойству дроби, то дроби и равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:
Посмотрите внимательно на эти два рисунка. Первый рисунок иллюстрирует дробь (один кусок из двух) , а второй иллюстрирует дробь (два куска из четырёх) . Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на два куска, и с неё взяли один кусок. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.
Поэтому между дробями и можно поставить знак равенства (=), поскольку они равны одному и тому же значению:
Теперь испытаем основное свойство дроби, разделив числитель и знаменатель на одно и то же число.
Рассмотрим дробь. Давайте разделим её числитель и знаменатель на одно и то же число, например на число 2
Давайте разделим её числитель и знаменатель на одно и то же число, например на число 2
Получили новую дробь. Если верить основному свойству дроби, то дроби и равны между собой. Так ли это? Давайте проверим, нарисовав эти дроби в виде кусочков пиццы:
Посмотрите внимательно на эти два рисунка. Первый рисунок иллюстрирует дробь (четыре куска из восьми) , а второй иллюстрирует дробь (два куска из четырёх) . Если хорошо присмотреться на эти куски, то можно убедиться, что у них одинаковые размеры. Различие лишь в том, что разделаны они по-разному. Первая пицца была разделана на восемь кусков, и с неё взяли четыре куска. А вторая пицца была разделана на четыре куска, и с неё взяли два куска.
Поэтому между дробями и можно поставить знак равенства (=), поскольку они равны одному и тому же значению:
Теперь мы полностью проверили, как работает основное свойство дроби, и убедились, что работает оно замечательно.
Число, на которое умножается числитель и знаменатель, называется Дополнительным множителем. Запомните это обязательно!
Запомните это обязательно!
Дроби можно сокращать. Сократить — значит сделать дробь короче и проще для восприятия. Например, дробь выглядит намного проще и красивее, чем дробь.
Если при решении примеров получается большая и некрасивая дробь, то нужно попытаться её сократить.
Сокращение дроби опирается на основное свойство дроби. Поэтому, прежде чем изучать сокращение дробей, обязательно изучите основное свойство дроби.
Деление числителя и знаменателя на их наибольший общий делитель называется Сокращением дроби.
Пример 1. Сократить дробь
Итак, нужно разделить числитель и знаменатель дроби на наибольший общий делитель чисел 2 и 4.
В данном случае дробь простая и для неё НОД ищется легко. НОД чисел 2 и 4 это число 2. Значит, числитель и знаменатель дроби надо разделить на 2
В результате дробь обратилась в более простую дробь. Значение исходной дроби при этом не изменилось, поскольку сокращение подразумевает деление числителя и знаменателя на одно и то же число. А это действие, как было указано ранее, не меняет значение дроби.
А это действие, как было указано ранее, не меняет значение дроби.
На рисунке представлены дроби и в виде кусочков пиццы. До сокращения и после сокращения они имеют одинаковые размеры. Разница лишь в том, что раздéланы они по-разному.
Пример 2. Сократим дробь
Чтобы сократить дробь, нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 20 и 40.
НОД чисел 20 и 40 это число 20. Поэтому делим числитель и знаменатель дроби на 20
Пример 3. Сократим дробь
Чтобы сократить дробь, нужно числитель и знаменатель этой дроби разделить на наибольший общий делитель чисел 32 и 36.
НОД чисел 32 и 36 это число 4. Поэтому делим числитель и знаменатель дроби на 4
Если в числителе и знаменателе располагаются простые числа, то такую дробь сократить нельзя — она не сокращается. Такие дроби называют Несократимыми. Например, следующие дроби являются несократимыми:
Напомним, что простыми называются числа, которые делятся только на единицу и самих себя.
Второй способ сокращения дроби
Второй способ является короткой версией первого способа. Суть его заключается в том, что пропускается подробное разъяснение того, на что был разделён числитель и знаменатель.
К примеру, вернёмся к дроби. Эту дробь мы сократили на 4, то есть разделили числитель и знаменатель этой дроби на число 4
Теперь представьте, что в данном выражении отсутствует конструкция, и сразу записан ответ. Получится следующее выражение:
Суть в том что число, на которое разделили числитель и знаменатель, хранят в уме. В нашем случае числитель и знаменатель делят на 4 — это число и будем хранить в уме.
Сначала делим числитель на число 4. Полученный ответ записываем рядом с числителем, предварительно зачеркнув его:
Затем таким же образом делим знаменатель на число 4. Полученный ответ записываем рядом со знаменателем, предварительно зачеркнув его:
Затем собираем новую дробь. В числитель отправляем новое число 8 вместо 32, а в знаменатель отправляем новое число 9 вместо 36
Происходит своего рода замена одной дроби на другую. Значение новой дроби равно значению предыдущей дроби, поскольку срабатывает основное свойство дроби, которое говорит о том что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь.
Значение новой дроби равно значению предыдущей дроби, поскольку срабатывает основное свойство дроби, которое говорит о том что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то получится равная ей дробь.
Также, дроби можно сокращать, предварительно разложив на простые множители числитель и знаменатель.
Например, сократим дробь, предварительно разложив на простые множители числитель и знаменатель:
Итак, мы разложили числитель и знаменатель дроби на множители. Теперь применяем второй способ сокращения. В числителе и в знаменателе выбираем по множителю и делим выбранные множители на НОД этих множителей.
Давайте сократим по тройке в числителе и в знаменателе. Для этого разделим эти тройки на 3 (на их наибольший общий делитель). Получим следующее выражение:
Сократить можно ещё по тройке в числителе и в знаменателе:
Дальше сокращать больше нéчего. Последнюю тройку в знаменателе просто так сократить нельзя, поскольку в числителе нет множителя, который можно было бы сократить вместе с этой тройкой.
Записываем новую дробь, в числителе и в знаменателе которой будут новые множители.
Получили ответ. Значит, при сокращении дроби получается новая дробь.
Не рекомендуется пользоваться вторым способом сокращения дроби и способом разложения на простые множители числителя и знаменателя, если человек только нáчал изучать математику. Практика показывает, что это оказывается сложным на первых этапах.
Поэтому, если испытываете затруднения при использовании второго способа, то пользуйтесь старым добрым способом сокращения: делите числитель и знаменатель дроби на их наибольший общий делитель. Выражение в таком случае получается простым, понятным и красивым. Так, предыдущий пример может быть решён старым способом и будет выглядеть так:
Сравните это выражение с выражением, которое мы получили, когда пользовались вторым способом:
Умножаем целую часть смешанного числа на знаменатель дробной части и прибавляем к числителю дробной части, а знаменатель оставляем без изменений:
Съеден был один кусок, значит сверху записываем единицу.
Spacemath. xyz
25.02.2020 12:03:49
2020-02-25 12:03:49
Источники:
Http://spacemath. xyz/drobi/
Калькулятор дробей онлайн с решением!
Удобный и простой онлайн калькулятор дробей с подробным решением может:
- Складывать, вычитать, умножать и делить дроби онлайн,
- Получать готовое решение дробей картинкой и удобно его переносить.
Результат решения дробей будет тут…
У нашего онлайн калькулятора дробей быстрый ввод. Чтобы получить решение дробей, к примеру , просто напишите 1/2+2/7 в калькулятор и нажмите кнопку «Решать дроби«.
Калькулятор напишет вам подробное решение дробей и выдаст удобную для копирования картинку.
Знаки используемые для записи в калькуляторе
| Знак | Расшифровка | Пример записи |
| / | Знак дроби(для операции деления не используется) | Дробь одна третья 1/3 |
| + | Знак плюс для сложения дробей | 1/2+3/5 |
| — | Минус для вычитания дробей | 3/5-2/7 |
| *, × или · | Знак умножения дробей | 2/3*5/8 |
| : или ÷ | Деление дробей (знак дроби «/» не используется!) | 1/3:7/8 |
Набирать пример для решения вы можете как, с клавиатуры, так и используя кнопки.
Возможности онлайн калькулятора дробей
Калькулятор дробей может выполнить операции только с 2-мя простыми дробями. Они могут быть как правильными(числитель меньше знаменателя), так и неправильными(числитель больше знаменателя). Числа в числителе и знаменатели не могут быть отрицательными и больше 999.
Наш онлайн калькулятор решает дроби и приводит ответ к правильному виду — сокращает дробь и выделяет целую часть, если потребуется.
Если вам нужно решить отрицательные дроби, просто воспользуйтесь свойствами минуса.
При перемножении и делении отрицательных дробей минус на минус дает плюс. То есть произведение и делении отрицательных дробей, равно произведению и делению таких же положительных. Если одна дробь при перемножении или делении отрицательная, то просто уберите минус, а потом добавьте его к ответу.
При сложении отрицательных дробей, результат будет таким же как если бы вы складывали такие же положительные дроби. Если вы прибавляете одну отрицательную дробь, то это тоже самое, что вычесть такую же положительную.
При вычитании отрицательных дробей, результат будет таким же, как если бы поменяли их местами и сделали положительными. То есть минус на минус в данном случае дает плюс, а от перестановки слагаемых сумма не меняется. Этими же правилами мы пользуемся при вычитании дробей одна из которых отрицательная.
Для решения смешанных дробей (дробей, в которых выделена целая часть) просто загоните целую часть в дробь. Для этого умножьте целую часть на знаменатель и прибавьте к числителю.
Если вам нужно решить онлайн 3 и более дроби, то решать их следует по очереди. Сначала посчитайте первые 2 дроби, потом с полученным ответом прорешайте следующую дробь и так далее. Выполняйте операции по очереди по 2 дроби, и в итоге вы получите верный ответ.
Примеры решения дробей в калькуляторе.
Ссылки на решение дробей с числителями и знаменателями от 1 до 5:
1/2+1/3, 1/2-1/3, 1/2*1/3, 1/2:1/3, 1/2+1/4, 1/2-1/4, 1/2*1/4, 1/2:1/4, 1/2+1/5, 1/2-1/5, 1/2*1/5, 1/2:1/5, 1/2+2/3, 1/2-2/3, 1/2*2/3, 1/2:2/3, 1/2+2/4, 1/2-2/4, 1/2*2/4, 1/2:2/4, 1/2+2/5, 1/2-2/5, 1/2*2/5, 1/2:2/5, 1/2+3/4, 1/2-3/4, 1/2*3/4, 1/2:3/4, 1/2+3/5, 1/2-3/5, 1/2*3/5, 1/2:3/5, 1/2+4/5, 1/2-4/5, 1/2*4/5, 1/2:4/5, 1/3+1/4, 1/3-1/4, 1/3*1/4, 1/3:1/4, 1/3+1/5, 1/3-1/5, 1/3*1/5, 1/3:1/5, 1/3+2/4, 1/3-2/4, 1/3*2/4, 1/3:2/4, 1/3+2/5, 1/3-2/5, 1/3*2/5, 1/3:2/5, 1/3+3/4, 1/3-3/4, 1/3*3/4, 1/3:3/4, 1/3+3/5, 1/3-3/5, 1/3*3/5, 1/3:3/5, 1/3+4/5, 1/3-4/5, 1/3*4/5, 1/3:4/5, 1/4+1/5, 1/4-1/5, 1/4*1/5, 1/4:1/5, 1/4+2/3, 1/4-2/3, 1/4*2/3, 1/4:2/3, 1/4+2/5, 1/4-2/5, 1/4*2/5, 1/4:2/5, 1/4+3/5, 1/4-3/5, 1/4*3/5, 1/4:3/5, 1/4+4/5, 1/4-4/5, 1/4*4/5, 1/4:4/5, 1/5+2/3, 1/5-2/3, 1/5*2/3, 1/5:2/3, 1/5+2/4, 1/5-2/4, 1/5*2/4, 1/5:2/4, 1/5+3/4, 1/5-3/4, 1/5*3/4, 1/5:3/4, 2/3+2/4, 2/3-2/4, 2/3*2/4, 2/3:2/4, 2/3+2/5, 2/3-2/5, 2/3*2/5, 2/3:2/5, 2/3+3/4, 2/3-3/4, 2/3*3/4, 2/3:3/4, 2/3+3/5, 2/3-3/5, 2/3*3/5, 2/3:3/5, 2/3+4/5, 2/3-4/5, 2/3*4/5, 2/3:4/5, 2/4+2/5, 2/4-2/5, 2/4*2/5, 2/4:2/5, 2/4+3/5, 2/4-3/5, 2/4*3/5, 2/4:3/5, 2/4+4/5, 2/4-4/5, 2/4*4/5, 2/4:4/5, 2/5+3/4, 2/5-3/4, 2/5*3/4, 2/5:3/4, 3/4+3/5, 3/4-3/5, 3/4*3/5, 3/4:3/5, 3/4+4/5, 3/4-4/5, 3/4*4/5, 3/4:4/5
Для чего предназначен онлайн решатель дробей.
Делать решения в калькуляторе следует с целью научиться решать дроби.
Калькулятор не несет цели решить дроби за вас. Это не универсальный решебник, а обучающий инструмент.
Он поможет вам разобраться в решении, чтобы вы умели сами легко решать дроби. Помимо калькулятора для обучения мы также рекомендуем изучить наш материал: «Как решать дроби. Решение дробей.»
Если вы заметили какую то ошибку или неудобство в использовании калькулятора, обязательно напишите нам в комментариях. По мере возможностей мы будем дорабатывать калькулятор под Вас!
калькулятор дробей — Рассчитать фракции онлайн
Опытные сотрудники калькулятора онлайн всегда здесь, чтобы предоставить эффективный и надежный образовательный инструмент для простоты расчетов. Да, недавно они обновили калькулятор значительных дробей, который помогает понимать дробные и дробные дроби, умножение и деление дробей, упрощение дробей и преобразование между дробями и десятичными дробями.
На этой платформе вы можете найти калькулятор четырех фракций, с помощью которого вы можете легко выполнять определенные фракции.
Что ж, прежде чем узнавать о нашем калькуляторе с дробями, давайте начнем с термина «дробь».
Что такое фракция?Дробь – это число, которое говорит нам, сколько частей целого у нас есть, значит, это число, представляющее целое число, которое делится на равные части. Фракция записывается косой чертой между двумя числами. Верхнее число называется числителем, оно представляет часть целого числа, а нижнее число называется знаменателем и представляет целое число, из которого сделаны части. Попадание в более подробные дроби далее классифицируется как:
Правильные дробиК этим дробям относятся те, в которых числитель, который является верхней цифрой, меньше знаменателя, а нижняя цифра, например 4/9, 6/9 2/6 во всех этих числовых дробях, меньше знаменателя.
Неправильные дробиЭто те дроби, в которых числитель больше знаменателя, например, 6/3, 9/5, 7/2 во всех этих числителях больше знаменателя.
Это такие же дроби, как, например, 2/4, 1/2, они похожи на дроби, потому что 2/4 в упрощенном виде будет ½. Еще один пример, который поможет вам понять, что 2/3 и 6/9 также являются одинаковыми дробями, потому что если мы упростим 6/9 с тем же числом, получится 2/3
В отличие от дробиЭто дроби, которые не одинаковы или не упрощены, чтобы быть одинаковыми, например, 2/3, а 6/9 отличаются от дробей.
О фракции калькулятор:Наш калькулятор фракций специально разработан для выполнения основных и сложных операций с фракциями; он работает как конвертер дробей. Да, этот калькулятор для дробей помогает выполнять сложение, вычитание, умножение и деление дробей. Кроме того, этот калькулятор с дробью помогает рассчитать упрощенные дроби и даже перевод между дробными и десятичными числами.
Инструкция / Как:Как добавить дроби с помощью калькулятора дробей:- Прежде всего, вы должны ввести правильные и неправильные дроби
- Затем выберите операцию (+) и нажмите кнопку «Рассчитать» в калькуляторе добавления дроби, чтобы получить результат дроби.

- Вам просто нужно ввести каждую фракцию в указанных полях
- Затем выберите операцию (-)
- Сразу после этого нажмите кнопку расчета этой доли калькулятора, чтобы получить результат
- Сначала введите значения каждой дроби в данное поле
- Затем выберите операцию (*)
- Когда закончите, нажмите кнопку расчета этого множителя дроби, чтобы получить результат
- Вы должны ввести значения каждой дроби в обоих заданных полях
- Затем выберите операцию (/)
- Наконец, нажмите кнопку расчета этого калькулятора деления фракций, чтобы получить значение деления дроби
- Вы просто вводите оба значения в приведенном выше расчете доли
- И, нажмите кнопку расчета, чтобы получить значение дроби упрощения
Вам просто нужно ввести значение дроби в приведенном выше калькуляторе, а остальные расчеты можно выполнить с помощью нашего десятичного калькулятора дроби.
Просто введите десятичное значение в данное поле и нажмите кнопку вычисления, чтобы преобразовать десятичное значение в дробное значение
Формулы фракций:Эти формулы дроби помогут вам раскрыть несколько вопросов, таких как:
Как вы добавляете дроби?Вы можете легко добавлять дроби с простотой данной формулы:
a / b + c / d = (ad + bc) / bd
Например:
2/6 + 1/4 = ((2 * 4) + (6 * 1)) / ((6 * 4)) = 14/24 = 7/12
Наш калькулятор добавления фракций также использовал ту же формулу для добавления фракций.
Как вы вычитаете дроби?Вычитание дроби становится легче с помощью следующей формулы:
a / b – c / d = (ad-bc) / bd
Например:
2/6 – 1/4 = ((2 * 4) – (6 * 1)) / ((6 * 4)) = 2/24 = 1/12
Наш калькулятор вычитания фракций также учитывает ту же формулу для вычитания фракций.
Получите простое умножение дроби с помощью приведенной ниже формулы:
a / b × c / d = ac / bd
Например:
2/6 × 1/4 = (2 × 1) / (6 × 4) = 2/24 = 1/12
Наш калькулятор умножения долей также учитывает ту же формулу, выполняя вычисления умножения долей.
Как вы делите фракции?Следующая формула помогает раскрыть этот вопрос:
a / b ÷ c / d = ad / bc
Например:
2/6 ÷ 1/4 = (2 × 4) / (6 × 1) = 8/6 = 4/3 = 1 1/3
Наш калькулятор деления фракций выполняет вычисление деления фракций, используя ту же формулу деления фракций.
Использование фракций в повседневной жизниФракции используются в вашей повседневной жизни во многих задачах. Вы можете воспользоваться помощью фракций в управлении временем для различных задач или, если вам придется готовить или печь снова, делите общее время на фракции, тем самым предоставляя подходящее время для каждой задачи. Фракции также широко используются для приготовления пищи, в которой различные ингредиенты определяются фракциями, такими как 1/4 стакана молока, ½ стакана сахара и аналогичным образом. Точно так же ученые и химики используют часть своих экспериментов.
Фракции также широко используются для приготовления пищи, в которой различные ингредиенты определяются фракциями, такими как 1/4 стакана молока, ½ стакана сахара и аналогичным образом. Точно так же ученые и химики используют часть своих экспериментов.
Да, этот онлайн-калькулятор фракций использует продвинутый алгоритм для решения уравнений дробей. Не стесняйтесь использовать этот эффективный удобный инструмент и получите желаемые результаты!
Other Languages: Fraction Calculator, Kalkulator Ułamków, Kesir Hesap Makinesi, Bruchrechnen, Kalkulator Pecahan, 分数の計算, 분수 계산기, Kalkulačka Zlomky, Calculadora De Fração, Calculatrice Fraction, Calculadora De Fracciones, Calcolatrice Frazioni, حاسبة الكسور, Fraktiolaskin
Онлайн калькулятор дробей с решением
Произвести {$ main.types[data.type] $}
Первая дробь
Вторая дробь
Результат расчёта
{$ result $}
Обыкновенная дробь — это способ представления рациональных чисел. На деле дробные числа используются для работы с частями целого, поэтому находят широкое применение не только в чистой математике или прикладных науках, но и в повседневной жизни.
На деле дробные числа используются для работы с частями целого, поэтому находят широкое применение не только в чистой математике или прикладных науках, но и в повседневной жизни.
Что такое дробь
Простая дробь — это рациональное число, в числителе которого стоит натуральное число, а в знаменателе — целое число. Любое рациональное число можно представить в виде дроби: 1/2, 2/3 или 22/7 — все это рациональные числа. Иррациональные объекты, такие как квадратные корни, числа Пи, е или фи нельзя выразить в виде отношения двух чисел, так как эти числа бесконечные и непериодические.
Виды дробей
Дробное число, у которого по модулям числитель меньше знаменателя, называется правильным. К таким математическим объектам относятся правильные дроби 1/3, 5/8 иди 14/27. Если по модулям числитель больше знаменателя, то дробь считается неправильной. Например, 22/7 — неправильная дробь. Неправильные дроби удобны для проведения вычислений, однако сложны для восприятия. Именно поэтому после арифметических операций с дробями правила хорошего тона требуют преобразования неправильных дробей в смешанные.
Смешанная дробь — это представление рационального числа в виде целой и дробной части. То же число 22/7 можно представить в виде 3 + 1/7, что гораздо проще для восприятия. Кроме того, существуют составные и цепные дроби, которые представляют собой «многоэтажные» выражения для записи приблизительных значений иррациональных чисел.
Арифметические операции с дробями
Еще в античные времена людям приходилось работать с частями целого. Торговцы и ремесленники постоянно оперировали дробями в своей повседневной деятельности, и хотя древние дроби отличались от современных, смысл был тот же. Рассмотрим основные правила работы с дробными числами.
Сложение и вычитание дробей
Для начала уясним, что одно и то же число можно представить множеством различных дробей. К примеру, очевидно, что число 0,5 — это 1/2. Если прочитать значение 0,5 вслух, мы получим пять десятых и соответствующую дробь — 5/10. Это же число можно записать и как 2/4, 3/6, 9/18 или 50/100 — список можно продолжать бесконечно. Это важное свойство дробей и его понимание необходимо для успешного сложения и вычитания рациональных чисел.
Это важное свойство дробей и его понимание необходимо для успешного сложения и вычитания рациональных чисел.
Сложение и вычитание дробей с одинаковыми знаменателями не требует никаких дополнительных преобразований: для совершения операции достаточно сложить или вычесть числители. Например:
- 1/5 + 2/5 = 3/5;
- 12/17 − 4/17 = 8/17.
Если же у дробей знаменатели разные, требуется привести все члены выражения к общему знаменателю. Для этого используется метод поиска наименьшего общего кратного или разложение знаменателей на множители. Например, если вы хотите сложить или вычесть 1/5, 1/12 и 1/15, то все дроби должны иметь одинаковый знаменатель. Каждую из этих дробей мы можем увеличить на произвольное число, и ее значение при этом не изменится. Так, 1/5 — это все равно, что 2/10, 3/15 или 10/50.
НОК (5, 12, 15) = 60, следовательно, требуется умножить каждую дробь таким образом, чтобы в знаменателе получить 60:
- 1/5 умножим на 12 и получим 12/60;
- 1/12 умножим на 5, что равно 5/60;
- 1/15 умножим на 4 и получим 4/60.
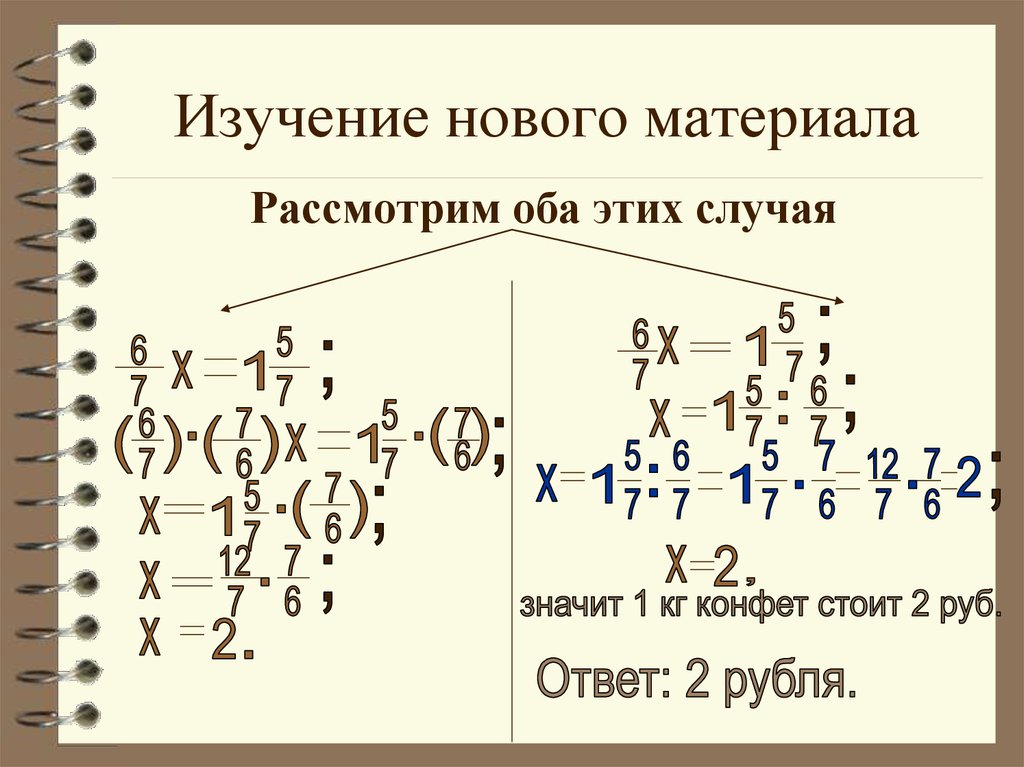
Теперь мы легко можем сложить или вычесть эти числа, оперируя только числителями:
- 12/60 + 5/60 + 4/60 = 21/60;
- 12/60 − 5/60 − 4/60 = 3/60 = 1/20.
Если в задаче требуется сложить или вычесть смешанные дроби, то их необходимо преобразовать в неправильные, после чего привести слагаемые к общему знаменателю и выполнить необходимые расчеты. Например:
2 12/15 + 3 2/30 = 42/15 + 92/30 = 84/30 + 92/30 = 176/30 = 5 26/30 = 5 13/15.
Произведение и деление дробей
С этим все проще. Для произведения дробных чисел не требуется проводить дополнительные преобразования — достаточно выполнить операции между числителями и между знаменателями. Для произведения правильных и неправильных дробей, а также рациональных чисел с разными знаменателями операция умножения осуществляется по формуле:
a/b × c/d = a × c / b × d.
На практике это выглядит следующим образом:
- 1/2 × 1/2 = 1/4;
- 2/3 × 4/5 = 8/15;
- 5/10 × 3/12 = 15/120.
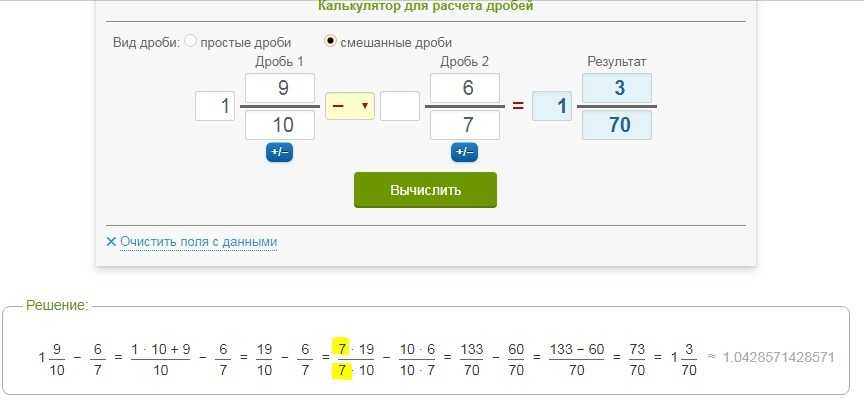
Деление — это действие, обратное умножению. В случае с дробями это определение приобретает буквальный смысл. Если требуется разделить первую дробь на вторую, то достаточно первую умножить на дробь, обратную второй. Математическим языком правило записывается так:
a/b / c/d = a/b × d/c = a × d / b × c.
Рассмотрим численные примеры:
- 1/2 / 1/2 = 1/2 × 2/1 = 2/2 = 1;
- 2/3 / 4/5 = 2/3 × 5/4 = 10/12 = 5/6;
- 5/10 / 3/12 = 5/10 × 12/3 = 60/30 = 2.
Наша программа представляет собой полноценный калькулятор для решения дробных выражений. Меню калькулятора предлагает выбор одного из четырех арифметических действий (сложение, вычитание, умножение и деление), а поля программы рассчитаны на ввод составных или обыкновенных дробей. Результирующую дробь программа автоматически представит в виде правильной дроби с выделением целой части. Интуитивно понятный интерфейс калькулятора позволит вам решать любые примеры на тему арифметических операций с дробными числами.
Заключение
Во время изучения школьного курса математики нам кажется, что полученные знания нам никогда не пригодятся в жизни. Однако операции с дробями мы производим постоянно на интуитивном уровне, даже когда просим в магазине половинку хлеба или 300 грамм сыра, когда готовим пищу или занимаемся сборкой моделей. Дроби пронизывают человеческую реальность, а наша программа позволит вам научиться быстро оперировать частями целого.
Онлайн калькулятор для сокращения дробей.
Разработка калькулятора для сайта
Наши контакты:
+375 29 1898322 (whatsapp, viber, telegram)
skype: dev_calc
e-mail: Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра.
У нас Вы можете заказать разработку онлайн калькулятора для сайта. Онлайн-калькулятор представляет собой программный модуль, встраиваемый в Ваш сайт, и позволяет посетителям Вашего сайта оперативно вычислить стоимость предлагаемых на сайте услуг, продаваемых товаров и т. д. Мы разрабатываем индивидуальные онлайн калькуляторы любой тематики и сложности.
д. Мы разрабатываем индивидуальные онлайн калькуляторы любой тематики и сложности.
Разработанные нами онлайн калькуляторы легко устанавливаются и корректно работают на сайтах, работающих под управлением любых CMS (сокр. от «Система управления контентом»), например, таких как: Joomla, WordPress, Drupal, 1С-Битрикс, CMS-S3 («Мегагрупп») и другие. Все калькуляторы разрабатываются с учетом дизайна и структуры сайта, на который будут устанавливаться, что позволяет калькулятору органично вписаться в Ваш сайт и выглядеть как неотъемлемая часть сайта.
Примеры онлайн калькуляторов разработанных нами
Мы готовы разработать онлайн калькулятор для сайта под заказ любой сложности. Оценить уровень нашей работы Вы можете на примерах выполненных нами калькуляторов.
Калькулятор скинали
Калькулятор кровли
Калькулятор имплантатов
Калькулятор фотокниг
Калькулятор бытовок
Калькулятор авиаперевозок
Калькулятор заборов
Калькулятор такси
Калькулятор ремонта
санузла
Калькулятор оконной
фурнитуры
Калькулятор кухонной
столешницы
Калькулятор сухой
стяжки
Посмотреть более подробный список разработанных нами онлайн калькуляторов для сайта можно в разделе Примеры наших работ
Отзывы клиентов о нашей работе
Как заказать у нас разработку онлайн калькулятора для сайта
Для того, чтобы заказать у нас разработку калькулятора для сайта свяжитесь с нами любым удобным для Вас способом:
- оставьте заказ на разработку онлайн калькулятора для сайта через форму:
- напишите нам на e-mail: Этот адрес электронной почты защищён от спам-ботов.
 У вас должен быть включен JavaScript для просмотра.;
У вас должен быть включен JavaScript для просмотра.; - позвоните нам по телефону: +375 (29) 189-83-22;
- закажите обратный звонок (укажите в заявке или письме Ваш номер телефона и удобное время звонка).
Если у Вас возникли какие-либо вопросы – напишите или позвоните нам!
Сколько стоит разработка онлайн калькулятора для сайта под заказ
Стоимость разработки онлайн калькулятора под заказ индивидуальна и зависит от сложности расчетов, дизайна калькулятора, наличия дополнительных функций и т.д. Чтобы узнать ориентировочную стоимость разработки интересующего Вас онлайн-калькулятора, оставьте заявку через форму обратной связи или напишите Нам письмо, где опишите функционал калькулятора.
Изменение цен на услуги, виды работ и товары в онлайн калькуляторе
Вы сможете самостоятельно изменять цены на услуги, виды работ, товары и т.д. в Вашем онлайн-калькуляторе. Все цены будут храниться в файле, который можно редактировать в Excel.
По желанию заказчика Мы можем разработать панель администрирования для управления онлайн калькулятором. Панель администрирования представляет собой веб-интерфейс, с помощью которого владелец сайта может менять цены на услуги и товары в калькуляторе, а также добавлять новые виды товаров или услуг.
Установка онлайн калькулятора на сайт заказчика
Установку калькулятора на сайт заказчика мы выполняем бесплатно. Если по каким-либо соображениям заказчик пожелает установить калькулятор на свой сайт самостоятельно, то в этом случае к калькулятору будет приложена подробная инструкция по установке.
5 преимуществ разработки онлайн калькулятора для сайта
Обновляя сайт или заказывая «с нуля» хочется сделать что-то интересное, чтобы привлекло внимание заказчиков и, конечно же, повысило уровень продаж — онлайн-калькулятор под заказ – вот, что Вам нужно! Как калькулятор для сайта может сделать Вашу страничку реально продающей и постоянно интересной покупателям?
Предлагаем Вам ознакомится с пятью основными преимуществами разработки индивидуального онлайн-калькулятора под заказ.
1. Первое, что обеспечит разработка калькулятора — постоянный поток клиентов на сайт.
Почему это важно:
Больше потенциальных покупателей узнают о вашей компании, а каждый десятый может стать реальным клиентом. Чем больше заказчиков – больше продаж, тем выше прибыль – эта формула понятна даже современным детям.
2. Второе:
Если разработка индивидуального онлайн-калькулятора выполняется под заказ, то калькулятор на сайте — уникальный сервис. Сайт становится не просто страничкой, на которой можно глянуть интересные картинки и прочитать информацию. Его значение изменяется моментально. С онлайн-калькулятором он уже незаменимое средство, упрощающее ежедневные расчеты для посетителей. Ваша страничка для заказчиков становится как родная, а значит, при необходимости, будьте уверены, что они обратится именно к Вам и, обязательно (абсолютно бескорыстно) порекомендует друзьям и знакомым. Не стоит забывать, что теперь сайт исполняет роль мощнейшего оружия для борьбы с конкурентами.
Конкуренты нервно ищут способы Вас обойти, но – безуспешно!
Такой результат принесет разработка онлайн-калькулятора!
3. Третье:
Разработка онлайн-калькулятора под заказ помогает снизить расходы на рекламу. Страничка в интернете, как рекламный инструмент, может полноценно заменить менее эффективные (чаще, и более дорогие) рекламные площади.
4. Четвертое:
Создание калькулятора упрощает работу персонала. Специалисты по продажам смогут:
- Сберечь время, которое они тратят на расчет стоимости для покупателей. Если клиента не устраивает цена, которую предоставил калькулятор на сайте, он не станет звонить и отвлекать менеджера.
- Ускорить цикл заключения сделки, ведь покупатель, просчитавший цену с помощью разработанного калькулятора, позвонив вам, с ценой уже согласился. В продажах убеждение клиента в адекватности цены – не самый легкий этап.
- Направить свои силы на изучение новых продуктов и технологий продаж.
 Даже таким образом создание калькулятора помогает увеличить число продаж.
Даже таким образом создание калькулятора помогает увеличить число продаж.
5. Пятое:
Онлайн-калькулятор под заказ рассказывает (возможно, и показывает), из чего складывается цена на товар или услугу. Клиент понимает, что его не обманывают, видит, за что платит. Повышается доверие к фирме. Покупатель с удовольствием и позитивом с Вами сотрудничает. Повышается престиж компании – в Вашей компании ничего не скрывают от клиента, и он это обязательно оценит.
Важный момент – чтобы все свойства онлайн-калькулятора раскрыли себя на все 100%, калькулятор должен:
- располагаться на самом видном месте. Не нужно прятать далеко удобный сервис, каждый посетитель его должен найти без труда
- быть интуитивно понятным для любого из ваших клиентов. Стоит заметить, что Вы — специалист в своей области, а посетитель, который захочет воспользоваться калькулятором для сайта, совсем не обязательно.
И самое главное, просто необходимо связаться с нами и заказать разработку индивидуального онлайн-калькулятора под заказ!
Ведь если этого не сделать сейчас, то все вышеперечисленные выгоды от онлайн-калькулятора для сайта под заказ достанутся Вашим конкурентам!
Чтобы заказать калькулятор для своего сайта, свяжитесь с нами, используя форму обратной связи.
Онлайн калькулятор дробей с решением со степенями со скобками с буквами
Данный онлайн калькулятор дробей предназначен для сложения, вычитания, деления и умножения между собой обыкновенных дробей. А так же дробей с целой частью и десятичных дробей.
Основные возможности:
- Сложение, вычитание, деление и умножение дробей.
- Расчет дробей с подробнейшим решением.
- Расчет дробей со степенями, скобками и буквами.
- Сокращение дробей.
- Поддержка до трех дробей онлайн.
На данном калькуляторе можно посчитать сложение вычитание деление или умножение дробей.
Калькулятор умеет:
- Вносить целую часть дроби в числитель для смешанных дробей.
- Расчет дробей со скобками- поддержка до двух уровней вложенности скобок.
- Расчет дробей со степенями — степенью может быть только число.
- Расчет дробей с буквами — любые анг. буквы или символы. (-2) +1.
- При сложении дробей состоящих только из чисел калькулятор вычисляет НОД и НОК.

- При расчете сразу трех дробей сначала выполняется операция умножение(деления), затем сложения(вычитания). Для изменения этого порядка поставьте галочку в поле «Большие скобки» и выберите нужный порядок расчета. В этом случае первой будет выполняться операция в больших скобках.
Калькулятор дробей онлайн | Сложение, вычитание, умножение, деление
Дробный калькулятор онлайн расчитывает произведение, разность, сумму и частное для двух дробей с выводом подробного решения, которое поволяет понять последовательность выполненния арифметических операций с дробями.
при просмотре на смартфоне — поверните экран
Выполнение решения
проверка возможности выполнения решения дробей
1) Перевод смешанных дробей в неправильные дроби
перевод смешанных дробей в неправильные дроби
2) Приведение дробей к общему знаменателю
приведение смешанных дробей к общему знаменателю
3) Выполнение операции с дробями
выполнение арифметической операции
4) Определение наибольшего общего делителя (НОД) числителя и знаменателя дроби
определение наибольшего общего делителя (НОД) числителя и знаменателя
5) Сокращение числителя и знаменателя дроби
сокращение числителя и знаменателя
6) Выделение целой части дроби
выделение целой части
7) Перевод алгебраической дроби в десятичную дробь
перевод алгебраической дроби в десятичную дробь
Помощь на развитие проекта premierdevelopment. ru
ru
Send mail и мы будем знать, что движемся в правильном направлении.
Спасибо, что не прошели мимо!
I. Порядок действий при расчете калькулятором для дробей онлайн:
- Чтобы выполнить сложение, вычитание, умножение или деление дробей введите в соответствующие поля значения числителя, знаменателя для двух дробей и выберите необходимую арифметическую операцию из выпадающего списка. Если дробь смешанная, то также заполните поле, соответствующее целой части дроби. Если дробь простая, то оставьте поле целой части пустым.
- Чтобы задать отрицательную дробь, поставьте знак минус в целой части дроби.
- В зависимости от задаваемых калькулятору дробей и арифметической операции автоматически выполняется следующая последовательность действий:
- перевод смешанных дробей в неправильные дроби, т.е. избавление от целой части дроби: для обеих дробей целая часть умножается на ее знаменатель и суммируется с ее числителем;
- приведение дробей к общему знаменателю: числитель и знаменатель первой дроби умножается на знаменатель второй дроби, а числитель и знаменатель второй дроби умножается на знаменатель первой дроби;
- выполнение заданной арифметической операции с дробями:
- сложение — сложение числителей дробей,
- вычитание — вычитание из числителя первой числителя второй дроби,
- умножение — умножить числитель первой дроби на числитель второй дроби и знаменатель первой дроби на знаменатель второй,
- деление — умножить числитель первой дроби на знаменатель второй дроби, а знаменатель первой дроби на числитель второй дроби;
- определение наибольшего общего делителя (НОД) числителя и знаменателя дроби;
- сокращение числителя и знаменателя дроби на НОД;
- выделение целой части дроби, если числитель итоговой дроби больше знаменателя.

- перевод итоговой алгебраической дроби в десятичную дробь с округлением до сотых.
II. Для справки:
- сокращение дроби
- — замена дроби другой равной дробью, но с меньшими значением числителя и знаменателя.
Сложение дробей | Онлайн калькулятор
Сложение дробей с одинаковыми знаменателями:
Определение: Суммой дробей с одинаковыми знаменателями называют дробь,числитель которой равен сумме числителей исходных дробей,и со знаменателем равным знаменателю обеих дробей.
Формула
Сложим две дроби с одинаковым с одинаковыми знаменателями
По формуле складываем числители, а знаменатель оставляем исходный
Важно: Если есть возможность сократить дробь, то в конечный ответ мы записываем сокращенную дробь.
Пример: При сокращении дроби у нас получится число 1/2
Сложение дробей с разными знаменателями:
Определение: Для того, чтобы найти сумму дробей с разными знаменателями сначала нужно дроби привести к общему знаменателю, а затем сложить их как дроби с одинаковыми знаменателями.
Задача:
Ход решения:
1) Приводим дроби к общему знаменателю.
Для этого ищем НОК — наименьшее общее кратное, для знаменателей 7 и 6 это число 42.
Делим число 42 на знаменатели дробей 3/7 и 2/6
Так мы нашли дополнительные множители.
Дальше домножаем дроби на дополнительные множители и получаем выражение:
2) Складываем дроби.
В нашем случае дробь можно сократить на 2 , и в конечный ответ записываем число 16/21
Сложение дроби и целого числа:
Определение: Для того, чтобы сложить дробь с целым числом, нужно сначала представить целое число как дробь со знаменателем равным 1.
Алгоритм расчета:
1) Приводим дроби к общему знаменателю.
2) Складываем дроби
3) Если есть возможность, то сокращаем полученную дробь.
4) Если же получилась неправильная дробь, то вычисляем из нее целую часть.
Пример:
Решение:
Вычисляем целую часть, и получаем ответ
Сложение смешанных дробей:
Определение: Для того, чтобы сложить смешанные дроби нужно отдельно сложить целые части, и отдельно сложить дробные части.
Формула
Пример:
Подставляем цифры в формулу:
Получаем:
Из дроби вычисляем целую часть т.к она неправильная,и получаем выражение 7+2=9.
Сложение дробей с помощью онлайн калькулятора:
Смотрите также
деление, умножение, вычитание и сложение обыкновенных дробей.
Как работать с калькулятором обыкновенных дробей?
Калькулятор предназначен для решения простых дробей и дробей с целыми числами (смешанных). В будущем, планируется внедрение функции решения десятичных дробей, но в данный момент она отсутствует.
Для начала работы с дробным калькулятором необходимо понять очень простой принцип ввода данных. Все целые числа вводятся с помощью больших кнопок, расположенных слева. Все числители вводятся с помощью маленьких белых кнопок, расположенных в правом верхнем блоке цифр. Все знаменатели, соответственно, вводятся путем нажатия на кнопки в правом нижнем углу. Данный способ ввода данных является в некотором роде инновационным, поскольку четко разграничивает целое, числитель и знаменатель, что облегчает вычисления, экономит время и делает взаимодействие с приложением более эффективным.
Допустим, вам требуется сложить квадратный корень из двух пятых и одну целую две девятых в шестой степени. Начните вводить пример с кнопки корня. После этого нажмите на цифру 2 в области числителя и на цифру пять в области знаменателя. Первое слагаемое готово. Теперь нажмите на знак «+» — это действие сложения. Далее введите целое число один на основной клавиатуре, потом число два в области числителя и девять в области знаменателя.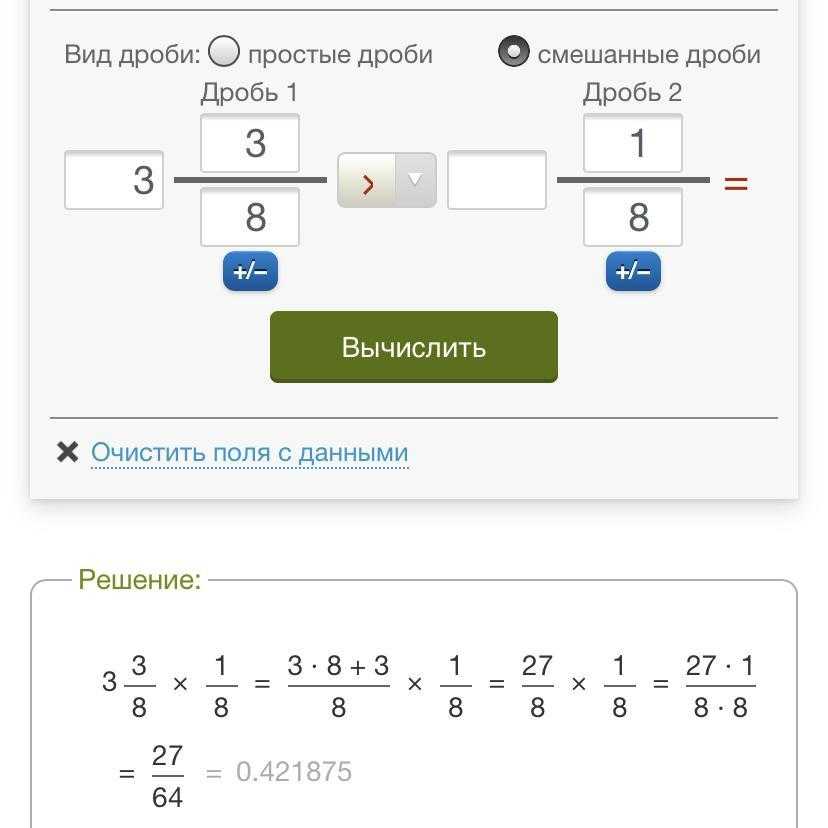 », после чего на цифру шесть на основной клавиатуре. В результате, получится готовый пример:
», после чего на цифру шесть на основной клавиатуре. В результате, получится готовый пример:
Теперь нажмите на кнопку равно и получите результат калькуляции. В примере выше проиллюстрирован практически весь арсенал возможностей калькулятора дробей. Точно таким же образом, вы можете осуществлять умножение, деление и вычитание дробей, как простых, так и алгебраических, с одинаковыми и разными знаменателями, целыми числами и т.д. Также, калькулятор может вычислить проценты от дробей, что требуется не так часто, но тем не менее очень важно для решения многих актуальных задач.
Если вам требуется сделать положительное число отрицательным, то сначала введите число, а потом нажмите на кнопку «+/-». После этого число или дробь автоматически обернется в скобки с отрицательным значением или наоборот (в зависимости от изначального статуса числа). Если необходимо удалить число, числитель или знаменатель, то воспользуйтесь соответствующей стрелкой Backspace, которая есть в блоке и числителя и знаменателя. Стрелки работают одинаково и по очереди стирают числа или знаки, находящиеся на дисплее калькулятора.
Стрелки работают одинаково и по очереди стирают числа или знаки, находящиеся на дисплее калькулятора.
Управление калькулятором дробей с клавиатуры.
Использовать калькулятор дробей онлайн можно не только с помощью компьютерной мыши, но и с помощью клавиатуры. Здесь логика очень проста:
- Все целые числа вводятся как обычно, нажатиями на клавиши чисел.
- Все числители вводятся с добавлением клавиши CTRL (например, CTRL+1).
- Все знаменатели вводятся с добавлением клавиши ALT (например, ALT+2).
Действия умножения, деления, сложения и вычитания так же инициируются соответствующими кнопками клавиатуры, если они есть (обычно располагаются в правой части, в так называемой области Numpad). Удаление производится нажатием на клавишу Backspace. Действие очистки (красная кнопка «C») вызывается нажатием на клавишу «C». Квадратный корень – нажатием на соседнюю клавишу «V» . Удаление производится нажатием на клавишу Backspace.
Зачем нужен калькулятор дробей онлайн?
Калькулятор дробей онлайн предназначен для решения обыкновенных и смешанных дробей (с целыми числами). Решение дробей часто требуется школьникам и студентам, а также инженерам и аспирантам. Наш калькулятор предоставляет возможность производить с дробями следующие действия: деление дробей, умножение дробей, сложение дробей и вычитание дробей. Также, калькулятор умеет работать с корнями и степенями, а еще с отрицательными числами, благодаря чему он многократно превосходит аналогичные онлайн приложения.
Решение дробей часто требуется школьникам и студентам, а также инженерам и аспирантам. Наш калькулятор предоставляет возможность производить с дробями следующие действия: деление дробей, умножение дробей, сложение дробей и вычитание дробей. Также, калькулятор умеет работать с корнями и степенями, а еще с отрицательными числами, благодаря чему он многократно превосходит аналогичные онлайн приложения.
Калькулятор простых дробей онлайн поможет вам решить примеры с дробями и при этом вам не надо беспокоиться о том, как предварительно сократить дробь. Здесь это сделается автоматически, т.к. приложение само вычисляет общий знаменатель и выдает вам готовый результат на экран.
В чем преимущества такого способа решения дробей?
Калькулятор поддерживает работу со скобками, что позволяет решать дроби даже в сложных математических примерах. В частности, действия со скобками часто требуются при вычислении алгебраических дробей или отрицательных дробей, над которыми постоянно приходится корпеть всем школьникам средних классов. Дополнительно, вы можете использовать этот калькулятор для сокращения дробей или решения дробей с разными знаменателями. Более того, в отличии от многих других бесплатных сервисов, данный калькулятор умеет работать с двумя, тремя, четырьмя и вообще с любым количеством дробей и чисел.
Дополнительно, вы можете использовать этот калькулятор для сокращения дробей или решения дробей с разными знаменателями. Более того, в отличии от многих других бесплатных сервисов, данный калькулятор умеет работать с двумя, тремя, четырьмя и вообще с любым количеством дробей и чисел.
Калькулятор обыкновенных дробей полностью бесплатный и не требует регистрации. Вы можете использовать его в любое время дня и ночи. Работать можно с помощью мыши или прямо с клавиатуры (это касается как чисел, так и действий). Мы постарались реализовать максимально удобный интерфейс дробных вычислений, благодаря чему сложные математические калькуляции превратятся для вас в одно удовольствие! 🙂
Онлайн калькулятор дробей с решением
Обыкновенная дробь — это способ представления рациональных чисел. На деле дробные числа используются для работы с частями целого, поэтому находят широкое применение не только в чистой математике или прикладных науках, но и в повседневной жизни.
Что такое дробь
Простая дробь — это рациональное число, в числителе которого стоит натуральное число, а в знаменателе — целое число. Любое рациональное число можно представить в виде дроби: 1/2, 2/3 или 22/7 — все это рациональные числа. Иррациональные объекты, такие как квадратные корни, числа Пи, е или фи нельзя выразить в виде отношения двух чисел, так как эти числа бесконечные и непериодические.
Любое рациональное число можно представить в виде дроби: 1/2, 2/3 или 22/7 — все это рациональные числа. Иррациональные объекты, такие как квадратные корни, числа Пи, е или фи нельзя выразить в виде отношения двух чисел, так как эти числа бесконечные и непериодические.
Виды дробей
Дробное число, у которого по модулям числитель меньше знаменателя, называется правильным. К таким математическим объектам относятся правильные дроби 1/3, 5/8 иди 14/27. Если по модулям числитель больше знаменателя, то дробь считается неправильной. Например, 22/7 — неправильная дробь. Неправильные дроби удобны для проведения вычислений, однако сложны для восприятия. Именно поэтому после арифметических операций с дробями правила хорошего тона требуют преобразования неправильных дробей в смешанные.
Смешанная дробь — это представление рационального числа в виде целой и дробной части. То же число 22/7 можно представить в виде 3 + 1/7, что гораздо проще для восприятия. Кроме того, существуют составные и цепные дроби, которые представляют собой «многоэтажные» выражения для записи приблизительных значений иррациональных чисел.
Арифметические операции с дробями
Еще в античные времена людям приходилось работать с частями целого. Торговцы и ремесленники постоянно оперировали дробями в своей повседневной деятельности, и хотя древние дроби отличались от современных, смысл был тот же. Рассмотрим основные правила работы с дробными числами.
Сложение и вычитание дробей
Для начала уясним, что одно и то же число можно представить множеством различных дробей. К примеру, очевидно, что число 0,5 — это 1/2. Если прочитать значение 0,5 вслух, мы получим пять десятых и соответствующую дробь — 5/10. Это же число можно записать и как 2/4, 3/6, 9/18 или 50/100 — список можно продолжать бесконечно. Это важное свойство дробей и его понимание необходимо для успешного сложения и вычитания рациональных чисел.
Сложение и вычитание дробей с одинаковыми знаменателями не требует никаких дополнительных преобразований: для совершения операции достаточно сложить или вычесть числители. Например:
- 1/5 + 2/5 = 3/5;
- 12/17 − 4/17 = 8/17.

Если же у дробей знаменатели разные, требуется привести все члены выражения к общему знаменателю. Для этого используется метод поиска наименьшего общего кратного или разложение знаменателей на множители. Например, если вы хотите сложить или вычесть 1/5, 1/12 и 1/15, то все дроби должны иметь одинаковый знаменатель. Каждую из этих дробей мы можем увеличить на произвольное число, и ее значение при этом не изменится. Так, 1/5 — это все равно, что 2/10, 3/15 или 10/50.
НОК (5, 12, 15) = 60, следовательно, требуется умножить каждую дробь таким образом, чтобы в знаменателе получить 60:
- 1/5 умножим на 12 и получим 12/60;
- 1/12 умножим на 5, что равно 5/60;
- 1/15 умножим на 4 и получим 4/60.
Теперь мы легко можем сложить или вычесть эти числа, оперируя только числителями:
- 12/60 + 5/60 + 4/60 = 21/60;
- 12/60 − 5/60 − 4/60 = 3/60 = 1/20.
Если в задаче требуется сложить или вычесть смешанные дроби, то их необходимо преобразовать в неправильные, после чего привести слагаемые к общему знаменателю и выполнить необходимые расчеты. Например:
Например:
2 12/15 + 3 2/30 = 42/15 + 92/30 = 84/30 + 92/30 = 176/30 = 5 26/30 = 5 13/15.
Произведение и деление дробей
С этим все проще. Для произведения дробных чисел не требуется проводить дополнительные преобразования — достаточно выполнить операции между числителями и между знаменателями. Для произведения правильных и неправильных дробей, а также рациональных чисел с разными знаменателями операция умножения осуществляется по формуле:
a/b × c/d = a × c / b × d.
На практике это выглядит следующим образом:
- 1/2 × 1/2 = 1/4;
- 2/3 × 4/5 = 8/15;
- 5/10 × 3/12 = 15/120.
Деление — это действие, обратное умножению. В случае с дробями это определение приобретает буквальный смысл. Если требуется разделить первую дробь на вторую, то достаточно первую умножить на дробь, обратную второй. Математическим языком правило записывается так:
a/b / c/d = a/b × d/c = a × d / b × c.
Рассмотрим численные примеры:
- 1/2 / 1/2 = 1/2 × 2/1 = 2/2 = 1;
- 2/3 / 4/5 = 2/3 × 5/4 = 10/12 = 5/6;
- 5/10 / 3/12 = 5/10 × 12/3 = 60/30 = 2.

Наша программа представляет собой полноценный калькулятор для решения дробных выражений. Меню калькулятора предлагает выбор одного из четырех арифметических действий (сложение, вычитание, умножение и деление), а поля программы рассчитаны на ввод составных или обыкновенных дробей. Результирующую дробь программа автоматически представит в виде правильной дроби с выделением целой части. Интуитивно понятный интерфейс калькулятора позволит вам решать любые примеры на тему арифметических операций с дробными числами.
Заключение
Во время изучения школьного курса математики нам кажется, что полученные знания нам никогда не пригодятся в жизни. Однако операции с дробями мы производим постоянно на интуитивном уровне, даже когда просим в магазине половинку хлеба или 300 грамм сыра, когда готовим пищу или занимаемся сборкой моделей. Дроби пронизывают человеческую реальность, а наша программа позволит вам научиться быстро оперировать частями целого.
Решение дробей онлайн с примерами и разъяснениями!
Сложение дробей онлайн, вычитание дробей, умножение дробей, деление дробей. Наш онлайн вычисляет дроби с пошаговым решением. Это очень удобно чтобы понять весь алгоритм. На этой станице вы найдете все ответы для решения дробей.
Как решать обыкновенные дроби? Что такое числитель дроби? Что такое знаменатель дроби?
Что такое правильные дроби? Что такое неправильные дроби? Как сократить дробь? Составные дроби.
Онлайн калькулятор сложение и вычитание дробей с одинаковыми знаменателями.
Умножение простых дробей. Умножение дроби на натуральное число.
Умножение, деление смешанных дробей.
Короче говоря наш онлайн калькулятор дробей умеет все!!!
Наш онлайн вычисляет дроби с пошаговым решением. Это очень удобно чтобы понять весь алгоритм. На этой станице вы найдете все ответы для решения дробей.
Как решать обыкновенные дроби? Что такое числитель дроби? Что такое знаменатель дроби?
Что такое правильные дроби? Что такое неправильные дроби? Как сократить дробь? Составные дроби.
Онлайн калькулятор сложение и вычитание дробей с одинаковыми знаменателями.
Умножение простых дробей. Умножение дроби на натуральное число.
Умножение, деление смешанных дробей.
Короче говоря наш онлайн калькулятор дробей умеет все!!!
Введите числа в калькулятор:
Рубли Рубли с НДС Калькулятор-календарь Дроби
Шпаргалка, сложение и вычитание дробей с одинаковыми знаменателями.
В этом примере разберем сложение дробей с одинаковыми знаменателями. Для примера начертим единичный отрезок и разделим его на девять частей.
Вычислим выражение
Отметим три части на отрезке, это и будет
Затем отметим еще две части на отрезке, это будет
Запишем полное решение
Откуда получился ответ пять девятых?
- Мы взяли отрезок и разделили его на девять частей.

- Отметили на отрезке три части и получили дробь три девятых.
- Затем отметили на отрезке еще две части и получили дробь две девятых.
- Прибавляем к трем частям еще две. Получаем ответ пять девятых.
Вычитание дробей с общим знаменателем.
Вычитание дробей происходит очень просто, так же как и сложение. Рассмотрим выражение дробей:
Как получит правила вычитания? Необходимо знаменатель оставить тот же а из числителя уменьшаемого, вычесть числитель вычитаемого. Семь минус четыре равняется три девятых.
При вычитании дробей с одинаковым числителем и знаменателем ответ всегда будет «0» .
Шпаргалка, сложение и вычитание дробей с разными знаменателями.
Запишем выражение:
Как видим в данном выражении разные знаменатели.
Сначала на нужно привести дроби к общему знаменателю.
Для этого нам нужно до множить эти дроби на какие то числа и числитель и знаменатель
так, чтобы в результате мы получили в знаменателе обоих дробей одно и тоже число.
Если дробь одну третью до множить на 2 и числитель и знаменатель, мы получим результат две шестых.
Пример: Дробь две шестых будет равняться дроби одной третьей
Теперь знаменатель у наших дробей одинаковый. Берем дробь одну шестую и прибавляем две шестых. Складываем числители: 1 + 2 = 3, знаменатель остается тот же.
Пример:
Полученный результат необходимо сократитьРезультат три шестых необходимо разделить на максимальное делимое число, в нашем случае это три.
Запишем решение полностью
Ответ:
Вычитание дробей с разными знаменателями происходит так же как и сложение, сначала приводим дроби к общему знаменателю методом до множить. Когда знаменатели у нас одинаковые, отнимаем числители а знаменатель остается тот же.
Решить дроби в онлайн калькуляторе
Умножение простых дробей
Решить дроби в онлайн калькуляторе
Умножить натуральное число на простую дробь или простую дробь умножить на натуральное число.
Тут все очень просто, чтобы умножить натуральное число на простую дробь, нужно натуральное число умножить на числитель а знаменатель перенести.
Пример:
Таким же способом происходит умножение дроби на натуральное число.
ДУМАЮ НЕТ СМЫСЛА ДАЛЬШЕ ПРИВОДИТЬ ПРИМЕРЫ РЕШЕНИЯ ДРОБЕЙ, ТАК КАК НАШ ОНЛАЙН КАЛЬКУЛЯТОР В НАЧАЛЕ СТРАНИЦЫ, РЕШАЕТ ЛЮБЫЕ ДРОБИ С ПОДРОБНЫМ РАЗЪЯСНЕНИЕМ В АВТОМАТИЧЕСКОМ РЕЖИМЕ.
Поделитесь пожалуйста в соцсетях!
Калькулятор сложения дробей
| ||
|
Как складывать или вычитать дроби?
Это очень просто, когда дроби имеют одинаковый знаменатель. Затем вы просто добавляете числители.
Примеры:
И так далее.
А если дроби не одного знаменателя?
Поместите их в один и тот же знаменатель. Вы можете использовать разложение на простые множители, чтобы узнать кгВ, или просто попытайтесь найти число, делящееся на оба знаменателя.
Пример: мы хотим посчитать. Возможный общий знаменатель. Итак, вычисляем:
.
Другой пример: мы хотим посчитать. Конечно, мы могли бы использовать в качестве знаменателя, но если мы присмотримся, мы поймем, что это килограммы.Итак, нам просто нужно вычислить
.
Если вы хотите увидеть еще больше примеров, просто введите свой пример выше. Он будет рассчитан немедленно и бесплатно.
Калькулятор сложения дробей
Наш калькулятор сложения дробей поможет вам сложить любые две дроби или смешанные числа.
В этом калькуляторе замечательно то, что он также покажет вам все тренировки на этом пути!
Если вы хотите сложить две дроби, пожалуйста, используйте калькулятор выше.
Чтобы ввести дробь, вы должны ввести числитель с последующим знаком «/». за которым следует знаменатель. Например. 4/5 или 23/7
за которым следует знаменатель. Например. 4/5 или 23/7
Чтобы ввести смешанную дробь, сначала введите целое число, а затем пробел. за которым следует числитель, за которым следует ‘/’, за которым следует знаменатель.Например. 3 1/4 (3 с четвертью).
Если вам нужна помощь, чтобы узнать, как складывать дроби, на этой странице есть дополнительная помощь!
Здесь вы найдете простые советы и поддержку. чтобы помочь вам научиться складывать две дроби вместе.
Кроме этого, есть также видео и несколько рабочих примеров, показывающих, что делать на каждом этапе.
Прежде чем вы начнете учиться складывать дроби с помощью разные знаменатели, вы должны быть уверены с использованием эквивалентных дробей.
Взгляните на еще несколько наших ресурсов, похожих на эти.
У нас есть ряд калькуляторов дробей, которые помогут вам решить все ваши проблемы с дробями.
Если вы хотите сложить или вычесть, умножить или разделить, упростить или преобразовать дроби, у нас есть калькулятор для вас.
Здесь вы найдете подборку рабочих листов дроби разработан, чтобы помочь вашему ребенку понять и практиковать как сложить и вычесть 2 дроби.
Прежде чем ваш ребенок начнет складывать и вычитать дроби, они должны быть уверены в эквивалентных дробях.
Использование этих листов поможет вашему ребенку:
- применяют свое понимание эквивалентных дробей;
- сложить 2 дроби с разными знаменателями;
- отнимите 2 дроби с разными знаменателями.
Все листы с добавлением вычитания дробей в этом разделе Поддержите контрольные показатели по элементарной математике для пятого класса.
Наша страница поддержки вычитания дробей поможет вам овладеть навыком вычитания дробей.
Есть видео вместе с отработанными примерами и практическими листами, а также множество пошаговых советов.
Здесь вы найдете бесплатную онлайн-справку по математике Math Salamanders о дробях.
Существует широкий спектр справочных страниц, в том числе справка по следующим вопросам:
- определения фракций;
- эквивалентных фракций;
- преобразование неправильных дробей;
- как складывать и вычитать дроби;
- как переводить дроби в десятичные дроби и проценты;
- как упростить дроби.

Саламандры по математике надеются, что вам понравятся эти бесплатные распечатываемые рабочие листы по математике. и все другие наши математические игры и ресурсы.
Мы приветствуем любые комментарии о нашем сайте или рабочие листы в поле для комментариев Facebook внизу каждой страницы.
Калькулятор сложения множественных дробей
Как найти сумму множественных дробей типа «нравится» и «не равно»?
Сумма двух чисел не зависит от их порядка. Другими словами, он удовлетворяет свойству коммутативности. Сумма чисел не зависит от того, как числа сгруппированы. Это свойство называется ассоциативным свойством. Когда мы имеем дело с дробями, есть два типа сложения:
- Когда все дроби похожи на дроби
Когда знаменатели дробей равны, их сумма будет суммой числителей над общим знаменателем. При необходимости результат можно упростить. Это можно выразить алгебраически: $$ \ frac {a_1} {b_1} + \ frac {a_2} {b_1} + \ ldots + \ frac {a_n} {b_1} = \ frac {a_1 + a_2 + \ ldots a_n} {b_1}, \ quad \ mbox { для} \; b_1 \ ne0 $$
- Когда некоторые дроби отличаются от дробей
Если знаменатели дробей разные, для сложения двух и более таких дробей необходимо выполнить следующие действия:
- Найдите НОК знаменателей;
- Перепишите дроби над НОК;
- Добавить новые числители;
- Результат — сумма числителей по НОК;
- При необходимости упростите результат.

Этот метод можно выразить алгебраически: $$ \ begin {align} & \ frac {a_1} {b_1} + \ frac {a_2} {b_2} + \ ldots + \ frac {a_n} {b_n} = \ frac {a_1 \ times \ frac {LCM (b_1, b_2, \ ldots, b_n)} {b_1} + a_2 \ times \ frac {LCM (b_1, b_2, \ ldots, b_n)} {b_2} + \ ldots + a_n \ times \ frac {LCM (b_1, b_2, \ ldots, b_n)} {b_n}} {LCM (b_1, b_2, \ ldots, b_n)} \ end {align} $$ для $ b_1, b_2 \ ldots, b_n \ ne0. $
Если $ LCM (b_1, b_2, \ ldots, b_n) = b_1 \ times b_2 \ times \ ldots \ times b_n $, то предыдущая формула принимает вид
$$ \ begin {align} & \ frac {a_1} {b_1} + \ frac {a_2} {b_2} + \ ldots + \ frac {a_n} {b_n} = \ frac {a_1 \ times b_2 \ times \ ldots \ times b_n + a_2 \ times b_1 \ times \ ldots \ times b_n + \ ldots + a_n \ times b_1 \ times b_2 \ times \ ldots \ times b_ {n-1}} {b_1 \ times b_2 \ times \ ldots \ times b_n} \ конец {align} $$ для $ b_1, b_2 \ ldots, b_n \ ne0.$
Например, найдем сумму для $ \ frac 27, \ frac 64, \ frac 85 $ и $ \ frac 87 $. Поскольку $ LCM (7,4,5,7) = 140 $, то
\ begin {align}
\ frac 27+ \ frac 64+ \ frac 85+ \ frac 87 & = \ frac {2 \ times 20} {140} + \ frac {6 \ times 35} {140} + \ frac {8 \ times 28} { 140} + \ frac {8 \ times 20} {140} \\
& = \ frac {40} {140} + \ frac {210} {140} + \ frac {224} {140} + \ frac {160} {140} \\
& = \ frac {634} {140}
\ end {align}
Чтобы записать сумму в простейшей форме, найдите ОКФ числителя и знаменателя числа
сумма. Поскольку $ GCF (634,140) = 2 $, окончательный результат будет
$$ \ frac {634 \ div2} {140 \ div2} = \ frac {317} {70} $$
Обратите внимание, что часть дроби может быть отрицательной дробью.Аналогичное соображение может применяться к добавлению двух или более смешанных чисел или двух или более алгебраических дробей. Чтобы сложить два или более смешанных числа, преобразуйте смешанные числа в соответствующие неправильные дроби и примените описанную выше процедуру.
Поскольку $ LCM (7,4,5,7) = 140 $, то
\ begin {align}
\ frac 27+ \ frac 64+ \ frac 85+ \ frac 87 & = \ frac {2 \ times 20} {140} + \ frac {6 \ times 35} {140} + \ frac {8 \ times 28} { 140} + \ frac {8 \ times 20} {140} \\
& = \ frac {40} {140} + \ frac {210} {140} + \ frac {224} {140} + \ frac {160} {140} \\
& = \ frac {634} {140}
\ end {align}
Чтобы записать сумму в простейшей форме, найдите ОКФ числителя и знаменателя числа
сумма. Поскольку $ GCF (634,140) = 2 $, окончательный результат будет
$$ \ frac {634 \ div2} {140 \ div2} = \ frac {317} {70} $$
Обратите внимание, что часть дроби может быть отрицательной дробью.Аналогичное соображение может применяться к добавлению двух или более смешанных чисел или двух или более алгебраических дробей. Чтобы сложить два или более смешанных числа, преобразуйте смешанные числа в соответствующие неправильные дроби и примените описанную выше процедуру.
Работа по сложению нескольких дробей с пошаговыми инструкциями показывает полное пошаговое вычисление для нахождения суммы четырех дробей $ \ frac 27, \ frac 64, \ frac 85 $ и $ \ frac 87 $ с использованием правила сложения нескольких дробей. Для любых других дробей просто укажите две или более правильных или неправильных дробей и нажмите кнопку «СОЗДАТЬ РАБОТУ».Учащиеся начальной школы могут использовать этот калькулятор сложения нескольких одинаковых и непохожих дробей для создания работы, проверки результатов сложения двух или более чисел, полученных вручную, или для эффективного выполнения домашних заданий.
Для любых других дробей просто укажите две или более правильных или неправильных дробей и нажмите кнопку «СОЗДАТЬ РАБОТУ».Учащиеся начальной школы могут использовать этот калькулятор сложения нескольких одинаковых и непохожих дробей для создания работы, проверки результатов сложения двух или более чисел, полученных вручную, или для эффективного выполнения домашних заданий.
Калькулятор дробей
Ниже приведены несколько калькуляторов дробей, способных выполнять сложение, вычитание, умножение, деление, упрощение и преобразование дробей и десятичных дробей. Поля над сплошной черной линией представляют числитель, а поля ниже — знаменатель.
Калькулятор смешанных чисел
Калькулятор упрощенных дробей
Калькулятор десятичных дробей
Калькулятор дробей в десятичную
Калькулятор дробей большого числа
Используйте этот калькулятор, если числители или знаменатели являются очень большими целыми числами.
В математике дробь — это число, которое представляет собой часть целого. Он состоит из числителя и знаменателя.В числителе указано количество равных частей целого, а в знаменателе — общее количество частей, составляющих это целое. Например, в дроби
Он состоит из числителя и знаменателя.В числителе указано количество равных частей целого, а в знаменателе — общее количество частей, составляющих это целое. Например, в дроби
числитель равен 3, а знаменатель — 8. Более наглядный пример может включать пирог с 8 ломтиками. 1 из этих 8 кусочков будет составлять числитель дроби, а всего 8 кусочков, составляющих весь пирог, будут знаменателем. Если бы человек съел 3 ломтика, оставшаяся часть пирога была бы такой, как показано на изображении справа.Обратите внимание, что знаменатель дроби не может быть 0, так как это сделает дробь неопределенной. Дроби могут подвергаться множеству различных операций, некоторые из которых упомянуты ниже.
Дополнение:
В отличие от сложения и вычитания целых чисел, таких как 2 и 8, дроби требуют общего знаменателя для выполнения этих операций. Один из методов нахождения общего знаменателя заключается в умножении числителей и знаменателей всех участвующих дробей на произведение знаменателей каждой дроби. Умножение всех знаменателей гарантирует, что новый знаменатель обязательно будет кратным каждому отдельному знаменателю. Числители также необходимо умножить на соответствующие коэффициенты, чтобы сохранить значение дроби в целом. Это, пожалуй, самый простой способ убедиться, что дроби имеют общий знаменатель. Однако в большинстве случаев решения этих уравнений не будут представлены в упрощенной форме (предоставленный калькулятор вычисляет упрощение автоматически). Ниже приведен пример использования этого метода.
Умножение всех знаменателей гарантирует, что новый знаменатель обязательно будет кратным каждому отдельному знаменателю. Числители также необходимо умножить на соответствующие коэффициенты, чтобы сохранить значение дроби в целом. Это, пожалуй, самый простой способ убедиться, что дроби имеют общий знаменатель. Однако в большинстве случаев решения этих уравнений не будут представлены в упрощенной форме (предоставленный калькулятор вычисляет упрощение автоматически). Ниже приведен пример использования этого метода.
Этот процесс можно использовать для любого количества фракций. Просто умножьте числители и знаменатели каждой дроби в задаче на произведение знаменателей всех остальных дробей (не включая соответствующий знаменатель) в задаче.
Альтернативный метод нахождения общего знаменателя состоит в том, чтобы определить наименьшее общее кратное (НОК) для знаменателей, а затем сложить или вычесть числители, как если бы это было целое число. Использование наименьшего общего кратного может быть более эффективным и с большей вероятностью приведет к дроби в упрощенной форме. В приведенном выше примере знаменатели были 4, 6 и 2. Наименьшее общее кратное — это первое общее кратное этих трех чисел.
В приведенном выше примере знаменатели были 4, 6 и 2. Наименьшее общее кратное — это первое общее кратное этих трех чисел.
| Кратное 2: 2, 4, 6, 8 10, 12 |
| Кратное 4: 4, 8, 12 |
| Кратное 6: 6, 12 |
Первое кратное, которое они все разделяют, равно 12, так что это наименьшее общее кратное. Чтобы выполнить задачу сложения (или вычитания), умножьте числители и знаменатели каждой дроби в задаче на любое значение, которое сделает знаменатели 12, а затем сложите числители.
Вычитание:
Вычитание фракции по сути то же самое, что и сложение фракции. Для выполнения операции требуется общий знаменатель. Обратитесь к разделу добавления, а также к приведенным ниже уравнениям для пояснения.
Умножение:
Умножение дробей довольно просто. В отличие от сложения и вычитания, нет необходимости вычислять общий знаменатель для умножения дробей. Просто числители и знаменатели каждой дроби умножаются, и результат образует новый числитель и знаменатель. По возможности решение следует упростить. Обратитесь к приведенным ниже уравнениям для пояснения.
По возможности решение следует упростить. Обратитесь к приведенным ниже уравнениям для пояснения.
Дивизион:
Процесс деления дробей аналогичен процессу умножения дробей. Чтобы разделить дроби, дробь в числителе умножается на величину, обратную дроби в знаменателе. Число , обратное , — это просто
. Когда a является дробью, это, по сути, включает в себя замену числителя и знаменателя местами.Следовательно, величина, обратная дроби. Обратитесь к приведенным ниже уравнениям для пояснения.
Упрощение:
Часто проще работать с упрощенными дробями. Таким образом, фракционные растворы обычно выражаются в их упрощенных формах.
например, более громоздкий, чем. Предоставленный калькулятор возвращает входные дроби как в неправильной форме дроби, так и в форме смешанных чисел. В обоих случаях дроби представлены в их низшей форме путем деления числителя и знаменателя на их наибольший общий множитель.
Преобразование дробей в десятичные дроби:
Преобразование десятичных дробей в дроби выполняется просто. Однако это требует понимания того, что каждый десятичный разряд справа от десятичной точки представляет собой степень 10; первый десятичный разряд — 10 1 , второй — 10 2 , третий — 10 3 и т. д. Просто определите, до какой степени 10 распространяется десятичная дробь, используйте эту степень 10 в качестве знаменателя, введите каждое число справа от десятичной точки в качестве числителя и упростите. Например, если посмотреть на число 0,1234, число 4 находится в четвертом десятичном разряде, что составляет 10 4 или 10 000. Это сделает дробь
, что упрощается до, поскольку наибольший общий делитель между числителем и знаменателем равен 2.
Точно так же дроби со знаменателями, которые являются степенями 10 (или могут быть преобразованы в степени 10), могут быть переведены в десятичную форму, используя те же принципы. Возьмем, к примеру, дробь
Возьмем, к примеру, дробь
. Чтобы преобразовать эту дробь в десятичную, сначала преобразуйте ее в дробь.Зная, что первый десятичный разряд представляет 10 -1 , можно преобразовать в 0,5. Если бы вместо этого была дробь, десятичная дробь была бы 0,05 и так далее. Помимо этого, преобразование дробей в десятичные требует операции деления в столбик.
Преобразование общей инженерной дроби в десятичную дробь
В машиностроении дроби широко используются для описания размеров таких компонентов, как трубы и болты. Наиболее распространенные дробные и десятичные эквиваленты перечислены ниже.
| 64 -й | 32 -й | 16 -й | 8 -й | 4 -й | 2 -й | десятичный | 1 (десятичный) 1 (десятичный) 1||
| 1/64 | 0,015625 | 0,396875 | ||||||
| 2/64 | 1/32 | 03125 | 0,79375 | |||||
| 3/64 | 0,046875 | 1,1 | ||||||
| 4/64 | 2/32 | 04 1/160 | 0,0625 | 1,5875 | ||||
| 5/64 | 0,078125 | 1. 984375 984375 | ||||||
| 6/64 | 60 | 0. 09375 | 2.38125 | |||||
| 7/64 | 0.109375 | 2.778125 | ||||||
| 8/64 9004 | 4/32 | 2/32 | 2 | 0,125 | 3,175 | |||
| 9/64 | 0,140625 | 3,571875 | ||||||
| 10/64 | 10/64 | 60.15625 | 3.96875 | |||||
| 11/64 | 0.171875 | 4.365625 | ||||||
| 12/64 | 6/32 | 0,1875 | 4,7625 | |||||
| 13/64 | 0. 203125 203125 | 5.159375 | ||||||
| 14/64 | 640. 21875 | 5,55625 | ||||||
| 15/64 | 0,234375 | 5,953125 | ||||||
| 16/64 | 8/32 | 4/32 | 1/4 | 0,25 | 6,35 | |||
| 17/64 | 0,265625 | 6,746875 | ||||||
| 0.28125 | 7,14375 | |||||||
| 19/64 | 0,296875 | 7,540625 | ||||||
| 20/64 | 10/32 | 0,3125 | 7,9375 | |||||
| 21/64 | 0,328125 | 8,334375 | ||||||
| 22/64 | 640 | 0. 34375 34375 | 8.73125 | |||||
| 23/64 | 0,359375 | 9.128125 | ||||||
| 24/64 | 12/32 | 60,375 | 9,525 | |||||
| 25/64 | 0,3 | 9.921875 | ||||||
| 0.40625 | 10,31875 | |||||||
| 27/64 | 0,421875 | 10.715625 | ||||||
| 28/64 9004 | 14/32 | 70004 | 0,4375 | 11,1125 | ||||
| 29/64 | 0,453125 | 11,509375 | ||||||
| 30/64 | 64 15/320 | 0. 46875 46875 | 11. | |||||
| 31/64 | 0,484375 | 12.303125 | ||||||
| 32/64 9004 | 16/32 | 80004 | 2/4 | 1/2 | 0,5 | 12,7 | ||
| 33/64 | 0,515625 | 13.096875 | ||||||
| 34/64 900 | 0.53125 | 13.49375 | ||||||
| 35/64 | 0.546875 | 13.8 | ||||||
| 36/64 9004 | 18/32 | 0,5625 | 14,2875 | |||||
| 37/64 | 0,578125 | 14,684375 | ||||||
| 38/64 | 0 9/320404 | 0 | 0. 59375 59375 | 15.08125 | ||||
| 39/64 | 0.609375 | 15.478125 | ||||||
| 40/64 9004 | 20/32 | /0,625 | 15,875 | |||||
| 41/64 | 0,640625 | 16.271875 | ||||||
| 0.65625 | 16,66875 | |||||||
| 43/64 | 0,671875 | 17.065625 | ||||||
| 44/64 9004 | 22/32 | 110004 110004 | 0,6875 | 17,4625 | ||||
| 45/64 | 0,703125 | 17,859375 | ||||||
| 46/64 | 04 | 9324 | 0. 71875 71875 | 18,25625 | ||||
| 47/64 | 0,734375 | 18,653125 | ||||||
| 48/64 9004 | 24/32 | /3/4 | 0,75 | 19,05 | ||||
| 49/64 | 0,765625 | 19,446875 | ||||||
| 0.78125 | 19.84375 | |||||||
| 51/64 | 0,796875 | 20.240625 | ||||||
| 52/64 | 26/32 | 130004 130004 | 0,8125 | 20,6375 | ||||
| 53/64 | 0,828125 | 21,034375 | ||||||
| 54/64 | 0 | 04 27/320 | 0. 84375 84375 | 21,43125 | ||||
| 55/64 | 0,859375 | 21,828125 | ||||||
| 56/64 | 28/32 14/32 | 60,875 | 22,225 | |||||
| 57/64 | 0,8 | 22,621875 | ||||||
| 0. | 23.01875 | |||||||
| 59/64 | 0,921875 | 23.415625 | ||||||
| 60/64 | 30/32 | 150004 150004 | 0,9375 | 23,8125 | ||||
| 61/64 | 0,953125 | 24.209375 | ||||||
62/640166404 | 0 | 0. 96875 96875 | 24.60625 | |||||
| 63/64 | 0,984375 | 25.003125 | ||||||
| 64/64 | 32/32 | 169004 | 4/4 | 2/2 | 1 | 25,4 |
Сложение двух дробей — WebMath
Быстро! Мне нужна помощь с: Выберите пункт справки по математике…Calculus, DerivativesCalculus, IntegrationCalculus, Quotient RuleCoins, CountingCombrations, Finding allComplex Numbers, Adding ofComplex Numbers, Calculating withComplex Numbers, MultiplyingComplex Numbers, Powers ofComplex NumberConversion, SubtractingConversion, TemperatureConversion, FindConversion, MassConversion, Mass анализ AverageData, поиск стандартного отклонения, анализ данных, гистограммы, десятичные числа, преобразование в дробь, электричество, стоимость факторинга, целые числа, наибольшие общие факторы, наименьшие общие фракции, добавление фракций, сравнение фракций, преобразование фракций, преобразование в десятичные дроби, дробление фракций, умножение фракций, уменьшение дробных фракций, умножение фракций , BoxesGeometry, CirclesGeometry, CylindersGeometry, RectanglesGeometry, Right TrianglesGeometry, SpheresGeometry, SquaresGraphing, LinesGraphing, Любая функцияGraphing, CirclesGraphing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, The Equation from point and slopeLines, Equation from slope и y-intLines, The Equation from two pointsLodsottery Практика многочленов Математика, Практика основ , Факторинг разности квадратов многочленов, разложение на множители трехчленов, многочленов, разложение на множители с GCF, многочлены, умножение многочленов, возведение в степень ns, Решить с помощью факторинга Радикалы, Другие корни Радикалы, Отношения квадратного корня, Что они собой представляют, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, Умножение форм, ПрямоугольникиУпрощение, Все, что угодноУпрощение, Образцы, Образцы, Упрощение, Упрощение, Методы Правые треугольники, Ветер, рисунок
| Параметр | Описание |
|---|---|
| Неправильное преобразование | Если дробь смешанная, отображаются шаги для преобразования в неправильную дробь. |
| Неправильная фракция | Если дробь смешанная, значения последней неправильной дроби. |
| Добавить | Показывает фактические шаги сложения. |
| наименьшее общее кратное (LCM) | Показывает вычисленное наименьшее общее кратное. Это наименьшее число, при котором обе дроби делятся поровну. |
| Ответ | Показывает решение. Обратите внимание, это решение не упрощено. |
| Наибольший общий делитель | Используется для упрощения ответа. Наибольшее или наибольшее целое число, которое разделит числитель и знаменатель без получения дроби. |
| Разделить на GCD | Показывает числитель и знаменатель, разделенные на НОД для уменьшения дроби. |
| Ответ (упрощенный) | Решение в правильном или неправильном формате. |
| Ответ (смешанный) | Если раствор является неправильной дробью, отображается преобразованная смешанная дробь. Смешанная фракция показывает дробь с целой частью в дополнение к оставшейся части фракции. Смешанная фракция показывает дробь с целой частью в дополнение к оставшейся части фракции. |
Калькулятор дробей — Сайт калькулятора
Используйте этот популярный калькулятор дробей, чтобы складывать, вычитать, умножать и делить дроби, включая смешанные дроби. Калькулятор дает объяснение задействованных рабочих шагов и упрощает результат, используя наибольший общий знаменатель.
Нравится? Пожалуйста, поделитесь
Пожалуйста, помогите мне распространить информацию, поделившись этим с друзьями или на своем веб-сайте / в блоге. Спасибо.
Ссылка на сайт
Заявление об ограничении ответственности: несмотря на то, что для создания этого калькулятора были приложены все усилия, мы не должны
несет ответственность за любой ущерб или денежные убытки, возникшие в результате или в связи с его использованием.Этот инструмент предназначен исключительно в качестве услуги для вас, пожалуйста, используйте его на свой страх и риск. Полный отказ от ответственности. Не используйте расчеты для чего-либо, где неточные расчеты могут привести к гибели людей, денег, имущества и т. Д.
Не используйте расчеты для чего-либо, где неточные расчеты могут привести к гибели людей, денег, имущества и т. Д.
Как складывать дроби
- Проверьте, совпадают ли ваши знаменатели (нижние числа).
- Они делают? Отлично. Переходите к шагу 5.
- Нет? ОК. Умножьте ваши разные знаменатели вместе…
- … И пропорционально скорректируйте обоих ваших номинаторов (верхние числа).Например. если вы удвоили знаменатель, то удвоите его числитель.
- Сложите номинаторы и положите полученную сумму над общим знаменателем.
- Упростите дробь до наименьшего возможного знаменателя, при этом знаменатель также уменьшится пропорционально.
Быстрая формула
\ (\ dfrac {a} {b} + \ dfrac {c} {d} = \ dfrac {ad + bc} {bd} \)
Пример того, как складывать дроби
\ (\ dfrac {2} {3} + \ dfrac {1} {4} = \ dfrac {(2 \ times4) + (3 \ times1)} {3 \ times4} = \ dfrac {11} {12} \)
Как вычесть дроби
- Проверьте, совпадают ли ваши знаменатели (нижние числа).

- Они делают? Отлично. Переходите к шагу 5.
- Нет? ОК. Умножьте ваши разные знаменатели вместе…
- … И пропорционально скорректируйте обоих ваших номинаторов (верхние числа). Например. если вы удвоили знаменатель, то удвоите его числитель.
- Вычтите второй знаменатель из первого и положите полученную сумму над общим знаменателем.
- Упростите дробь до наименьшего возможного знаменателя, при этом знаменатель также уменьшится пропорционально.
Быстрая формула
\ (\ dfrac {a} {b} — \ dfrac {c} {d} = \ dfrac {ad — bc} {bd} \)
Пример того, как вычитать дроби
\ (\ dfrac {2} {3} — \ dfrac {1} {4} = \ dfrac {(2 \ times4) — (3 \ times1)} {3 \ times4} = \ dfrac {5} {12} \)
Вы можете узнать о том, как складывать и вычитать дроби в нашей статье, как складывать, вычитать, умножать и делить дроби.
Рекламное объявление
Как умножать дроби
- Умножьте числители (верхние числа) вместе, чтобы получить ответ числителя.

- Умножьте знаменатели (нижние числа) вместе, чтобы получить ответ знаменателя.
- Упростите дробь до наименьшего возможного знаменателя, при этом знаменатель также уменьшится пропорционально.
Быстрая формула
\ (\ dfrac {a} {b} \ times \ dfrac {c} {d} = \ dfrac {ac} {bd} \)
Пример умножения дробей
\ (\ dfrac {2} {3} \ times \ dfrac {1} {4} = \ dfrac {(2 \ times1)} {(3 \ times4)} = \ dfrac {2} {12} = \ dfrac {1} {6} \)
Как делить дроби
- Выпишите всю сумму, НО замените ÷ на ×
- Переверните вторую дробь вверх дном, поменяв местами знаменатель (верхнее число) и знаменатель (второе число).
- Завершите сумму, умножив первую дробь на обратную вторую дробь.
- Упростите дробь до наименьшего возможного знаменателя, при этом знаменатель также уменьшится пропорционально.
Быстрая формула
\ (\ dfrac {a} {b} \ div \ dfrac {c} {d} = \ dfrac {ad} {bc} \)
Пример как делить дроби
\ (\ dfrac {2} {3} \ div \ dfrac {1} {4} = \ dfrac {(2 \ times4)} {(3 \ times1)} = \ dfrac {8} {3} \)
Если вам нужна помощь с преобразованием десятичных знаков в дроби, см.
Калькулятор дробей. Пошаговое решение
Создано Ханной Памула, кандидатом наук
Отредактировано Домиником Черня, кандидатом наук и Джеком Боуотером
Последнее обновление: 08 июня 2022 г.
Содержание:- Как делить дроби?
- Как делить дроби с целыми числами?
- Как разделить целое число на дробь?
- Как делить смешанные дроби?
- Пример 1: 3/4 разделить на 2 в виде дроби
- Пример 2: Деление трех дробей
Ищете инструмент, который может делить любую комбинацию дробей, смешанных и целых чисел? Если это так, не ищите дальше — этот калькулятор дробей для вас! Этот калькулятор может помочь вам со многими различными вопросами:
✔️ Как разделить дроби с целыми числами ?
✔️ Как разделить целое число на дробь ?
✔️ Как разделить смешанные дроби ?
❌ Как сложить две дроби? А как перевести дроби в десятичные и десятичные в дроби?
Последний пункт не является целью этого инструмента. Лучше ознакомьтесь с нашим калькулятором сложения дробей, чтобы получить советы и рекомендации по сложению дробей, а также два отличных конвертера дробей в десятичные и десятичные в дроби, разработанные для того, чтобы развеять любые сомнения относительно преобразования дробей. А для тех, кто ищет комплексное решение, у нас есть кое-что особенное — универсальный калькулятор дробей. Попробуй!
Лучше ознакомьтесь с нашим калькулятором сложения дробей, чтобы получить советы и рекомендации по сложению дробей, а также два отличных конвертера дробей в десятичные и десятичные в дроби, разработанные для того, чтобы развеять любые сомнения относительно преобразования дробей. А для тех, кто ищет комплексное решение, у нас есть кое-что особенное — универсальный калькулятор дробей. Попробуй!
Как делить дроби?
Деление дробей очень похоже на умножение дробей. Вам просто нужно выполнить следующие шаги, чтобы разделить две дроби (например, 4 / 5 на 2 / 3 ):
Найдите обратную второй дроби — делитель (дробь, на которую нужно разделить). Чтобы найти обратную величину, просто переверните число вверх ногами так, чтобы верхнее число оказалось внизу, а нижнее — над чертой: 9{3}/ _{2}2/3→ 3/2
Помните, что есть одно число, для которого не имеет обратной величины — 0 .
 Таким образом, наша вторая дробь не может иметь верхнее число, равное 0, и мы надеемся, что нам не нужно напоминать вам, что вы не можете делить на ноль, поэтому нижнее число дроби также никогда не может быть равно нулю.
Таким образом, наша вторая дробь не может иметь верхнее число, равное 0, и мы надеемся, что нам не нужно напоминать вам, что вы не можете делить на ноль, поэтому нижнее число дроби также никогда не может быть равно нулю.Умножьте дроби . Напоминаем, что для умножения двух дробей нужно умножить числитель на другой числитель и знаменатель на другой знаменатель: 9{6}/ _{5}12/10= 6/5
И все! Это было не так сложно, не так ли? 😉 Наш калькулятор деления дробей покажет вам пошаговое решение выбранного вами примера, если у вас все еще есть проблемы с пониманием того, как делить дроби.
Подводя итог, вы только что узнали общие правила деления дробей. Если вы ищете более конкретные инструкции, такие как деление смешанных дробей или деление дробей на целые числа, продолжайте читать!
Как делить дроби с целыми числами?
Когда дело доходит до деления дробей на целые числа, это почти то же самое, что и выше: вам нужно умножить вашу дробь на обратное — но на этот раз это обратное целого числа . Давайте рассмотрим пример, разделив 1 / 2 на 3:
Давайте рассмотрим пример, разделив 1 / 2 на 3:
- Найдите обратную величину вашего целого числа . Так как вы можете записать каждое целое число как , это число больше 1 , тогда 3 равно 3 / 1 . Тогда его обратное значение равно 91/ _6
\end{align*}31/2=3/11/2= 1/2× 1/3= (1×1)/(2×3)= 1/6
Другими словами, вы можете сказать, что знаменатель вашей дроби умножается на целое число.
Давайте подумаем о текстовой задаче для приведенного выше примера, чтобы помочь вам интуитивно понять деление дробей на целые числа.
На следующий день после Хэллоуина 🎃 двое твоих друзей пришли в гости. Вы бы хотели предложить им немного еды, но у вас в доме только половинка тыквенного пирога 😱. Какую долю всего пирога должен иметь каждый кусочек, если вы хотите разделить его поровну? Не забывайте о себе, вы тоже хотите съесть этот вкусный пирог 🥧.
Верно! Каждому достанется одна шестая часть пирога.

Как разделить целое число на дробь?
Деление целого числа на дробь должно быть для вас пустяком (или кусочком тыквенного пирога?🤔). Протокол действительно похож, давайте проверим, как разделить 2 на 1 / 6 :
- Найдите обратную величину делителя – вторую дробь.
16↗↘61\qquad \frac{\textcolor{#ff8000}1}{\textcolor{#5c85d6}6} \nearrow\kern{-1em} \searrow \frac{\textcolor{#5c85d6}6}{ \textcolor{#ff8000}1}61↗↘16 9{12}/_1 = 12 \end{align*}2/1× 6/1= (2×6)/(1×1)= 12/1=12
И это все, в данном случае вы не нужно сделать какое-то упрощение.
Возвращаясь к тыквенному пирогу, вы можете представить эту задачу как вопрос «Сколько кусочков, составляющих одну шестую часть пирога, помещается в два пирога🥧🥧?»
Да, именно! Если разделить два пирога на 1/6 кусочков, всего получится 12 таких кусочков.
Как делить смешанные дроби?
Мы уверены, что вы уже догадались, как делить смешанные дроби.
 Вам нужен только один дополнительный шаг – 9{17}/ _{18}
\end{align*} 7/2× 5/9= (7×5)/(2×9)= 35/18=117/18
Вам нужен только один дополнительный шаг – 9{17}/ _{18}
\end{align*} 7/2× 5/9= (7×5)/(2×9)= 35/18=117/18Конечно, наш калькулятор деления дробей может разобраться с делением смешанных дробей 💪
Пример 1: 3/4 разделить на 2 в форме дроби
Поскольку вы прочитали абзац о том, как делить дроби на целые числа, мы уверены, что это будет прогулка в парке для тебя. Давайте проверим, как рассчитать 3 / 4 разделить на 2 как дроби, используя этот калькулятор деления дробей:
- Выберите форму дроби . Давайте выберем вариант смешанное число , так как вы хотите ввести целое число (однако форма простой дроби также подойдет, тогда вы должны написать целое число как число больше 1).
- Введите первую дробь . В выбранном примере поставьте 3 в числителе (верхнее число) и 4 в знаменателе (это нижнее число). Вы можете игнорировать все числовое поле или ввести 0.
- Введите второе значение .
 Введите 2 в поле для целых чисел и оставьте остальные поля пустыми.
Введите 2 в поле для целых чисел и оставьте остальные поля пустыми. - И все — калькулятор делящихся дробей выдал ответ! Теперь вы знаете, что 3 / 4 разделить на 2 в дробной форме будет 3 / 8 .
Если вам нужны дополнительные сведения о расчетах для вашего примера, ознакомьтесь с пошаговым решением.
Пример 2: Деление трех дробей
Наконец, давайте обсудим несколько более необычный случай — деление трех дробей. Чтобы сделать это еще более сложным, давайте выберем дроби в разных формах: две дроби в их простой форме (одна отрицательная) и одна дробь, представляющая собой смешанное число:
7 1 / 4 : 5 / 6 : — 2 / 3 = ?
- Выберите правильную форму дроби . Вам нужен вариант смешанный номер , так как у вас есть одна смешанная дробь.

- Введите дроби :
- 1 ст дробь: 7 — целое число, 1 — числитель, 4 — знаменатель;
- 2 й дробь: пустой или 0 как целое число, 5 как числитель, 6 как знаменатель; и
- 3 rd дробь: пусто или 0 как целое число, -2 как числитель, 3 как знаменатель.
- Проверьте, как разделить 3 дроби с помощью пошагового решения . Результат операции — 261 / 20 = -13 1 / 20
Ханна Памула, кандидат наук
Форма дроби
Для деления дробей и целых чисел выберите форму дроби «смешанное число».
Values (you can enter up to 5 fractions)
1 st fraction
Numerator (n₁)
Denominator (d₁)
2 nd fraction
Numerator (n₂)
Знаменатель (d₂)
Показать пошаговое решение?
Посмотрите 17 похожих калькуляторов дробей 🍕
Сложение дробейСравнение дробейДесятичная дробь… Еще 14
Калькулятор дробей — CalcuNation.
 com
comТеперь вы можете складывать дроби, вычитать дроби, умножать дроби и делить дроби онлайн. Найдите ответ в самом простом с помощью этого онлайн-калькулятора дробей.
Первая дробь /
(+, -, x, ÷)
Доля секунды /Сложение дробей
Вычитание дробей
Умножение дробей
Разделение дробейЧтобы привести дробь к простейшей форме, попробуйте наш калькулятор упрощения дробей
Как складывать дроби?
Есть два случая относительно знаменателей, когда мы складываем обыкновенные дроби, которые показаны следующим образом:
Сложение дробей с одинаковыми знаменателями:
• Просто добавьте числители дробей.
• Знаменатель полученной дроби будет общим знаменателем дробей.
• Уменьшить полученную дробь.
Например: а/б + г/б = (а + г)/б
или
7/17 + 9/17 = (7 + 9)/17Сложение дробей с разными знаменателями:
• Если знаменатели не совпадают, перемножьте знаменатели вместе.
• Отрегулируйте свои числители (верхние числа) соответствующим образом. Например. если удвоить знаменатель, то удвоить и числитель.
• Сложите числители и поднесите эту сумму к общему знаменателю.
• Упростите дробь до наименьшего возможного знаменателя, при этом числители также будут пропорционально уменьшены.
Пример: a/b + c/d = (ad + cb)/bd
Для сложения дробей 1/3 и 1/5,
1/3 + 1/5 = (1*5 + 1*3)/3*5 = 5+3/15 = 8/15
Сумма 8/15 уже в простейшем виде.Как вычитать дроби?
Есть два случая относительно знаменателей, когда мы вычитаем обыкновенные дроби, которые показаны следующим образом с шагами:
Вычитание дробей с одинаковыми знаменателями:
• Просто вычтите числители дробей.
• Знаменатель полученной дроби будет общим знаменателем дробей.
• Уменьшить полученную дробь.
Пример
• а/г — в/д = (а-в)/д
• 4/18 — 3/18 = ( 4 — 3)/18 = 1/18Вычитание дробей с разными знаменателями:
• Если знаменатели не совпадают, перемножьте знаменатели вместе.
• Отрегулируйте свои числители (верхние числа) соответствующим образом. Например. если удвоить знаменатель, то удвоить и числитель.
• вычтите числители и поднесите эту сумму к общему знаменателю.
• Упростите дробь до наименьшего возможного знаменателя, при этом числитель также уменьшится пропорционально.
a/b — c/d = (ad — cb)/bd
Для вычитания дробей 1/3 и 1/5,
1/3 — 1/5 = (1*5 — 1*3)/3*5 = 5-3/15 = 2/15
Пример: для вычитания дробей 10/15 и 1/5,
10/15 — 1/5 = (10*5 — 1*15)/15*5 = 50-15/75 = 35/75 = 7/15Как умножать дроби?
Умножать дроби довольно просто.
 В отличие от сложения и вычитания, нет необходимости вычислять
общий знаменатель для умножения дробей, умножение дробей показано в следующем порядке:
В отличие от сложения и вычитания, нет необходимости вычислять
общий знаменатель для умножения дробей, умножение дробей показано в следующем порядке:• Просто умножаются числители и знаменатели каждой дроби.
• Результат формирует новый числитель и знаменатель.
• Если возможно, решение должно быть упрощено. Обратитесь к приведенным ниже уравнениям для пояснений.
а/б × с/д = а*с/б*д
Пример: Перемножьте дроби 10/15 и 1/5.
10/15 × 1/5 = 10/75
или =2/15
Ответ 2/15 уже в простейшем виде.Как вы делите дроби?
Для деления дробей используются следующие шаги:
• Сначала вы находите обратную величину второй дроби.
• Затем умножьте обе дроби, чтобы получить результат.
Пример:
Для деления дроби a/b и c/d величина, обратная c/d, равна d/c.
Затем вы умножаете первую дробь на обратную величину второй дроби.
a/b ÷ c/d =a/b x d/c = a*d / b*c
Пример 2: Для деления дробей 1/5 и 15/4.
1/5 ÷ 15/4 = 1/5 х 4/15 = 4/75
Ответ 4/75. Этот ответ уже в простейшей форме.Лучшее 21 1/12 Делится на 7 в виде дроби Interconex
Wiki
5 дней назад
1 8 минут чтения
Ниже представлена лучшая информация и знания о 1/12, разделенные на 7 в виде дроби , собранные и собранные командой interconex.edu.vn , наряду с другими связанными темами, такими как: 7/12, разделенное на 7 в виде дроби. дробь, 1/12 разделить на 8, Калькулятор дробей, Десятичная дробь, Десятичная дробь, 12 разделить на 1/2, Калькулятор смешанных дробей, Рабочий лист дроби
Изображение для ключевого слова: 1/12 разделить на 7 в виде дроби
Самые популярные статьи о 1/12 разделить на 7 в виде дроби
Содержание
- 1 1. Калькулятор дробей 9 0 9001 , Запишите дробь в простейшей форме (1/12)÷7 – Mathway
- 3 3.
 Сколько 7 разделить на 1/12 – Visual Fractions
Сколько 7 разделить на 1/12 – Visual Fractions - 4 4. Разделить 1/12 на 7/12 – Ответы на каждый день. com
- 5 5. Калькулятор дробей – Бесплатный онлайн калькулятор – Byju’s
- 6 6. 12 разделить на 7 в виде дроби – онлайн-калькулятор
- 7 7. 12/7 разделить на 7 в виде дроби – getcalc.com
- 8 8. Простой в использовании калькулятор дробей | День Пи
- 9 9. Деление дробей
- 10 10. Калькулятор дробей
- 11 11. Калькулятор дробей. Все операции с объяснением
- 12 12. Сколько 7/12 разделить на 1/6? – Quora
- 13 13. Калькулятор дробей – CalcuNation.com
- 14 14. Чему равно 7, деленное на 12, как дробь? – Ответы
- 15 15. Сколько 7 разделить на 12 как дробь? – Ответы
- 16 16. 1/9 разделить на 7/12 в виде дроби – NUMBER.ROCkS
- 17 17. Сложение, вычитание, деление и умножение дробей – Calculators.org
- 18 18. Справка по математике: как работать Из дроби — Owlcation
- 19 19.
 Деление дробей 5/7 и 1/12 — OnlineCalculator.Guru
Деление дробей 5/7 и 1/12 — OnlineCalculator.Guru - 20 20. Умножение и деление дробей — GCFGlobal
- 21 21. Что такое 12/7 как Смешанный номер? [Решено] — Куэмат
1. Калькулятор дробей
Автор: www.calculator.net
Оценить 3 ⭐ (8196 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Сводка: Статьи о калькуляторе дробей Этот бесплатный калькулятор дробей поддерживает сложение, вычитание, умножение, деление и преобразование дробей.
Совпадение с результатами поиска: В отличие от сложения и вычитания целых чисел, таких как 2 и 8, дроби требуют общего знаменателя для выполнения этих операций. Один из методов нахождения общего знаменателя включает умножение числителей и знаменателей всех дробей на произведение знаменателей каждой дроби…
Цитата из источника: …
2.
 Запишите дробь в простейшей форме (1/12)÷7 – Mathway
Запишите дробь в простейшей форме (1/12)÷7 – MathwayАвтор: www.mathway.com
Оценить 4 ⭐ (31164 Оценки)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о Запишите дробь в простейшей форме (1/12)÷7 – Mathway Перепишите деление в виде дроби. … Умножьте числитель на обратную величину знаменателя. … Умножьте 112⋅17 1 12 ⋅ 1 7 .
Совпадение с результатами поиска: Пожалуйста, убедитесь, что ваш пароль состоит не менее чем из 8 символов и содержит каждый из следующих символов:
Цитата из источника: …
3. Сколько 7 разделить на 1/12 – Visual Fractions
Автор: visualfractions.com
Оценить 4 ⭐ (29547 оценок)
Лучшие оценки: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о том, что 7 разделить на 1/12 – наглядные дроби Если у вас есть целое число 7 и вы хотите разделить его на дробь 1/12, то вы нашли идеальную статью.

Совпадение с результатами поиска: «Сколько будет 7 разделить на 1/12». VisualFractions.com. По состоянию на 12 сентября 2022 г. http://visualfractions.com/calculator/whole-divided-by-fraction/what-is-7-divided-by-1-12/.
Цитата из источника: …
4. Разделите 1/12 на 7/12 – Answers by Everydaycalculation.com
Автор: answer.everydaycalculation.com
Оценить 3 ⭐ (4031 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Итого: Статьи о делении 1/12 на 7/12 – ответы Everydaycalculation.com 1/12 разделить на 7/12 равно 1/7. Получите пошаговую инструкцию по делению дробных чисел. … Этапы деления дробей. Найдите обратную величину делителя
.Совпадение с результатами поиска: Связанные: 2/12÷7/12 1/12÷14/12 1/24÷7/12 1/12÷7/24 3/12÷7/12 1/12÷21 /12 1/36÷7/12 1/12÷7/36 5/12÷7/12 1/12÷35/12 1/60÷7/12 1/12÷7/60 7/12÷7/ 12 1/12÷49/12 1/84÷7/12 1/12÷7/84
Цитата из источника: …
5.
 Калькулятор дробей – Бесплатный онлайн калькулятор – Byju’s
Калькулятор дробей – Бесплатный онлайн калькулятор – Byju’sАвтор: byjus.com
Оценить 4 ⭐ (22405 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о Калькуляторе дробей — Бесплатный онлайн-калькулятор — Byju’s Используя алгебраические формулы для сложения, вычитания, умножения и деления дробей, этот калькулятор будет складывать, вычитать, умножать или делить …
Совпадение с результатами поиска: В математике дробь представляет собой часть целого числа. Он состоит из числителя и знаменателя, где числитель представляет собой количество равных частей, а знаменатель представляет собой общую сумму, которая составляет целое.
Например, 5/6 — дробь, где 5 — числитель, а 6 — номинал…Цитата из источника: …
6.
 12 разделить на 7 как дробь – онлайн-калькулятор
12 разделить на 7 как дробь – онлайн-калькуляторАвтор: online-calculator.org
Оценить 4 ⭐ (27043 Оценки)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о делении 12 на 7 в виде дроби – Онлайн-калькулятор 12, разделенных на 7 в виде дроби; Ответ: 12/7 = 1, 5. 7 …
Совпадение с результатами поиска: Сколько будет 12 разделить на 7? – 12 разделить на 7 равно 1,7142857142857 в виде десятичной дроби. Следуйте приведенным ниже инструкциям о том, как вычислить, что 12 разделить на 7 равно чему.
Цитата из источника: …
7. 12/7 разделить на 7 в виде дроби – getcalc.com
Автор: getcalc.com
Оценить 3 ⭐ (9994 рейтинга)
Лучшие оценки: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о делении 12/7 на 7 в виде дроби — getcalc.
 com найти что …
com найти что …Сопоставьте результаты поиска:
шаг 1 Адресуйте входные параметры, значения и наблюдайте, что нужно найти: Входные параметры и значения: дробь A = 12/7целое число B = 7Что нужно найти:Найти, что делится на 12/7 на 7 в дроби. 12/7 ÷ 7 = ?
Шаг 2 Найдите обратную величину целого числа 7:
Обратная часть целого числа 7 равна 1…Цитата из источника: …
8. Простой в использовании калькулятор дробей | День Пи
Автор: www.piday.org
Оценить 4 ⭐ (28622 Оценки)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о простом калькуляторе дробей | День числа Пи Калькулятор дробей будет складывать, вычитать, умножать и делить дроби с одинаковыми.
 .. Поскольку знаменатель обеих дробей равен 5, сложите 3 и 4, чтобы получить 7.
.. Поскольку знаменатель обеих дробей равен 5, сложите 3 и 4, чтобы получить 7.Совпадение с результатами поиска: Это дает нам \(\frac{68}{100}\). Теперь мы можем упростить дробь, найдя общий множитель. Если вы не знаете наибольший общий делитель, вы можете начать с деления на любой общий делитель. Обратите внимание, что 68 и 100 делятся на 2. Это уменьшает дробь до 34/50. Отсюда обратите внимание, что …
Цитата из источника: …
9. Деление дробей
Автор: www.math-only-math.com
Оценить 4 ⭐ (29049 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о делении дробей Здесь мы обсудим деление дробей на целое число, … Например: 1. 710 ÷ 5 = 710 ÷ 51. = 710 × 15.
 = 7×110×5. = 750…3/5×1/12.
= 7×110×5. = 750…3/5×1/12.Совпадение с результатами поиска: При сравнении дробей с одинаковыми числителями следующие прямоугольные фигуры одинаковой длины разделены на разные части, чтобы показать разные знаменатели. 3/10 3/5 > 3/10 В дробях с одинаковым числителем эта дробь равна
Цитата из источника: …
10. Калькулятор дробей
Автор: www.calculatorsoup.com
Оценить 3 ⭐ (6511 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о калькуляторе дробей Используйте этот калькулятор дробей, чтобы складывать, вычитать, умножать и делить дроби. … Итак, если одна из ваших дробей равна -6/7, вставьте -6 в числитель и 7 в …
.Совпадение с результатами поиска: Фьюри, Эдвард «Калькулятор фракций» на https://www.
 calculatorsoup.com/calculators/math/fractions.php от CalculatorSoup,
calculatorsoup.com/calculators/math/fractions.php от CalculatorSoup,
https://www.calculatorsoup.com – онлайн-калькуляторыЦитата из источника: …
11. Калькулятор дробей. Все операции с объяснением
Автор: www.omnicalculator.com
Оценка 3 ⭐ (7616 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о калькуляторе дробей. Объяснение всех операций с объяснением дробей: Деление целого торта на 2,3 и 6 кусочков. … 7 частей апельсина из целого апельсина, которые мы разрезаем на 8.
Совпадение с результатами поиска: А при умножении дроби на целое число помните, что целое число можно записать как само деленное на 1:
Цитата из источника: …
12.
 Сколько 7/12 разделить на 1/6? – Квора
Сколько 7/12 разделить на 1/6? – КвораАвтор: www.quora.com
Оценить 3 ⭐ (12380 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о том Сколько 7/12 разделить на 1/6? — Quora 3 câu trả lời
Совпадение с результатами поиска: Что-то пошло не так. Подождите немного и повторите попытку.
Цитата из источника: …
13. Калькулятор дробей – CalcuNation.com
Автор: www.calcunation.com
Оценить 4 ⭐ (21571 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о калькуляторе дробей – CalcuNation.
 com Итак, если одна из ваших дробей равна -9/7, вставьте -9 в числитель и 7 в знаменатель. Вы можете складывать, вычитать, умножать и делить отрицательные дроби на этом …
com Итак, если одна из ваших дробей равна -9/7, вставьте -9 в числитель и 7 в знаменатель. Вы можете складывать, вычитать, умножать и делить отрицательные дроби на этом …Сопоставьте результаты поиска: Для деления дробей выполните следующие шаги:
• Сначала вы находите обратную величину второй дроби.
• Затем перемножьте обе дроби, чтобы получить результат.Пример:
Для деления дроби a/b и c/d обратная величина c/d равна d/c.
Затем вы умножаете первую дробь на обратную …Цитата из источника: …
14. Сколько 7 разделить на 12 как дробь? – Ответы
Автор: math.answers.com
Оценить 3 ⭐ (15836 оценок)
Лучшие оценки: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о том, сколько 7 разделить на 12 как дробь? – Ответы 1/12.
 Учебные пособия… 1/12. Этот ответ: 👍 Полезно (1) 👎 Бесполезно (0). Добавить комментарий … Что такое -12 разделить на -7 как дробь?
Учебные пособия… 1/12. Этот ответ: 👍 Полезно (1) 👎 Бесполезно (0). Добавить комментарий … Что такое -12 разделить на -7 как дробь?Совпадение с результатами поиска: Минни Крист ∙
Цитата из источника: …
15. Сколько 7 разделить на 12 как дробь? – Ответы
Автор: math.answers.com
Оценить 3 ⭐ (20356 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о том, сколько 7 разделить на 12 как дробь? – Ответы 1/12. Учебные пособия… 1/12. Этот ответ: 👍 Полезно (1) 👎 Бесполезно (0). Добавить комментарий … Что такое -12 разделить на -7 как дробь?
Совпадение с результатами поиска: Минни Крист ∙
Цитата из источника: …
16.
 1/9 разделить на 7/12 в виде дроби – NUMBER.ROCKS
1/9 разделить на 7/12 в виде дроби – NUMBER.ROCKSАвтор: номер.рокс
Оценить 4 ⭐ (33288 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о делении 1/9 на 7/12 в виде дроби – КОЛИЧЕСТВО КАМЕНЕЙ Здесь мы покажем вам пошаговое подробное решение деления 1/9 на 7/12 (часто записывается как 1/9 ÷ 7 /12), с ответами в форме дроби, …
Совпадение с результатами поиска: Чтобы разделить дроби, найдите обратную вторую дробь (переверните ее вверх дном), затем перемножьте числители и знаменатели.
Обратное число 712 равно 127Цитата из источника: …
17. Сложение, вычитание, деление и умножение дробей – Calculators.org
Автор: www.
 calculators.org
calculators.orgОценить 4 ⭐ (34358 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о сложении, вычитании, делении и умножении дробей – Логотип мини-калькулятора Calculators.org. Калькулятор дробей · Введите ваши дроби в приведенном выше калькуляторе. · Найдите наименьший общий знаменатель путем умножения каждого …
Совпадение с результатами поиска: В Греции практика использования дробных значений в виде сумм
единичных дробей была довольно распространена до средневековья. Например, Liber
Abbaci итальянского математика Фибоначчи является
известным текстом 13-го века. Он широко использовал дроби, описывая
различных способов преобразования других дробей…Цитата из источника: …
18.
 Математическая помощь: как вычислить дробную часть числа – Owlcation
Математическая помощь: как вычислить дробную часть числа – OwlcationАвтор: owlcation.com
Оценить 4 ⭐ (25681 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи по математике Помощь: Как вычислить дробь числа – Owlcation Ответ: Нужно делить на большее, а умножать на меньшее. 12 разделить на 3 равно 4, а 4 умножить на 4 равно 16. Вопрос: Какая часть 5 3/5 составляет 7/ …
Совпадение с результатами поиска: Помните: чтобы вычислить дробь от числа, все, что вам нужно сделать, это разделить это число на знаменатель дроби, а затем умножить результат на числитель дроби. Давайте сделаем несколько примеров задач для практики.
Цитата из источника: …
19. Деление дробей 5/7 и 1/12 – OnlineCalculator.
 Guru
GuruАвтор: onlinecalculator.guru
Оценить 3 ⭐ (11734 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о делении дробей 5/7 и 1/12 – OnlineCalculator.Guru Калькулятор деления дробей поможет вам определить деление дробей 5/7 и 1/12, т.е. 60/7 с пошаговым объяснением того, как ответ прибыли.
Сопоставьте результаты поиска: И таким же образом знаменатель второй дроби, т.е. 12, придет в числитель первой дроби и умножится:
Цитата из источника: …
20. Умножение и деление дробей – GCFGlobal
Автор: edu.gcfglobal.org
Оценить 3 ⭐ (1274 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи об умножении и делении дробей — GCFGlobal 1 умножить на 7 равно 7, поэтому мы напишем 7 справа от числителя.
 Когда мы складывали дроби, знаменатели оставались прежними. Но когда мы умножаем, …
Когда мы складывали дроби, знаменатели оставались прежними. Но когда мы умножаем, …Совпадение с результатами поиска: Дробь является частью целого. На прошлом уроке вы научились складывать и вычитать дроби. Но это не единственный вид математики, который вы можете делать с дробями. Бывают случаи, когда полезно будет умножать и дроби.
Цитата из источника: …
21. Что такое 12/7 как смешанное число? [Решено] — Куэмат
Автор: www.cuemath.com
Оценить 3 ⭐ (2853 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о том, что такое 12/7 как смешанное число? [Решено] — Cuemath Сначала мы делим числитель данной неправильной дроби на знаменатель. А теперь сохраните частное как отдельное.
 Частное 12 разделить на 7 равно …
Частное 12 разделить на 7 равно …Совпадение с результатами поиска: 12/7 — неправильная дробь. Представим его как целое число, а также дробную часть, называемую смешанным числом.
Цитата из источника: …
Видеоуроки о делении 1/12 на 7 в виде дроби
Статьи по теме
Лучшее 20 1/5 Делить на 7/15 в виде дроби
Wiki
2 дня назадПоследнее обновление: 15/09/2022
1 8 минут чтения
Ниже представлена лучшая информация и знания о 1/5, деленная на 7/15 в виде дроби , собранная и составленная командой hocdientu.net , а также другие связанные темы, такие как:
Изображение для ключевого слова: 1 /5 разделить на 7/15 в виде дроби
Самые популярные статьи о 1/5 разделить на 7/15 в виде дроби
Содержание
- 1 1.
 Вычислить (1/5)÷(7/15) – Mathway
Вычислить (1/5)÷(7/15) – Mathway - 2 2. Разделить 7/15 на 1/5 – Answers by Everydaycalculation.com
- 3 3. Калькулятор дробей
- 4 4. Калькулятор дробей – CalcuNation.com
- 5 5. Как складывать дроби 7/15+1/5 = ? Результат записывается как положительный …
- 6 6. Калькулятор дробей – Бесплатный онлайн калькулятор – BYJU’S
- 7 7. Сколько 5 разделить на 7/15 – Наглядные дроби
- 8 8. Разработать 4 /5 ÷ 7 /15 Дать ваш ответ как смешанное число в …
- 9 9. Умножение и деление дробей – GCFGlobal
- 10 10. Калькулятор дробей. Все операции с объяснением
- 11 11. Справка по математике: как вычислить дробную часть числа – Owlcation
- 12 12. Решения NCERT для 6-го класса по математике Глава 5 – Дроби
- 13 13. На что делится 3/5 1/7? – Калькулятор дробей
- 14 14. Преобразуйте каждое из следующих чисел в неправильную дробь: i) 7 1/4 …
- 15 15. 7/15 умножить на 9 в виде дроби – calculate.
 name
name - 16 16. Калькулятор смешанных чисел в процентах
- 17 17. Как делить дроби — KS3 Maths — BBC Bitesize
- 18 18. Деление дробей
- 19 19. Как вычислять дроби: пошаговое руководство 90
- 20 20. Деление дробей на 1 – / – 7 и 5 – OnlineCalculator.Guru
1. Вычисление (1/5)÷(7/15) – Mathway
Автор: www.mathway.com
Оценить 4 ⭐ (29823 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Сводка: Статьи о Evaluate (1/5)÷(7/15) – Mathway Чтобы разделить на дробь, умножьте на ее обратную величину. 15⋅157 1 5 ⋅ 15 7. Шаг 2. Сокращение общего множителя 5 5 . Нажмите, чтобы увидеть больше шагов.
Совпадение с результатами поиска: Пожалуйста, убедитесь, что ваш пароль состоит не менее чем из 8 символов и содержит каждый из следующих символов:
Цитата из источника: …
2.
 Разделите 7/15 на 1/5 – Answers by Everydaycalculation.com
Разделите 7/15 на 1/5 – Answers by Everydaycalculation.comАвтор: answer.everydaycalculation.com
Оценить 3 ⭐ (10133 Оценки)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Итого: Статьи о делении 7/15 на 1/5 – ответы Everydaycalculation.com 7/15 разделить на 1/5 равно 7/3. Получите пошаговую инструкцию по делению дробных чисел.
Совпадение с результатами поиска: Загрузите наше мобильное приложение и научитесь работать с дробями в удобное время:
Android и iPhone/iPadЦитата из источника: …
3. Калькулятор дробей
Автор: www.calculator.net
Оценить 3 ⭐ (2266 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Сводка: Статьи о калькуляторе дробей Этот бесплатный калькулятор дробей поддерживает сложение, вычитание, умножение, деление и преобразование дробей.

Совпадение с результатами поиска: Процесс деления дробей аналогичен процессу умножения дробей. Чтобы разделить дроби, дробь в числителе умножается на обратную дробь в знаменателе. Обратное число а равно
.Цитата из источника: …
4. Калькулятор дробей – CalcuNation.com
Автор: www.calcunation.com
Оценить 4 ⭐ (33399 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о Калькуляторе дробей – CalcuNation.com Используйте этот Калькулятор дробей, чтобы складывать, вычитать, умножать или делить дроби… Пример 2: Для деления дробей 1/5 и 15/4.
Совпадение с результатами поиска: Для деления дробей шаги следующие:
• Сначала найдите обратную величину второй дроби.
• Затем перемножьте обе дроби, чтобы получить результат.Пример:
Для деления дроби a/b и c/d обратная величина c/d равна d/c.
Затем вы умножаете первую дробь на обратную …Цитата из источника: …
5. Как сложить дроби 7/15+1/5 = ? Результат написан как положительный …
Автор: www.fractii.ro
Оценить 3 ⭐ (16856 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Сводка: Статьи о том, как складывать дроби 7/15+1/5 = ? Результат записывается как положительный … Сократите (упростите) дроби до их эквивалентов с наименьшими членами: Чтобы уменьшить дробь: разделите числитель и знаменатель на их наибольший общий множитель, …
Совпадение с результатами поиска: Есть два случая относительно знаменателей при сложении обыкновенных дробей:
Цитата из источника: …
6.
 Калькулятор дробей – Бесплатный онлайн калькулятор – BYJU’S
Калькулятор дробей – Бесплатный онлайн калькулятор – BYJU’SАвтор: byjus.com
Оценить 4 ⭐ (33870 оценок)
Лучшие оценки: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о Калькуляторе дробей — Бесплатный онлайн-калькулятор — BYJU’S Дроби можно складывать, вычитать, умножать и делить, как и все другие числа. Используя алгебраические формулы сложения, вычитания, умножения и …
Совпадение с результатами поиска: В математике дробь представляет собой часть целого числа. Он состоит из числителя и знаменателя, где числитель представляет собой количество равных частей, а знаменатель представляет собой общую сумму, которая составляет целое.
Например, 5/6 — дробь, где 5 — числитель, а 6 — номинал…Цитата из источника: …
7.
 Сколько 5 разделить на 7/15 – Visual Fractions
Сколько 5 разделить на 7/15 – Visual FractionsАвтор: visualfractions.com
Оценить 4 ⭐ (22774 Оценки)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о том, что 5 разделить на 7/15 – наглядные дроби Если у вас есть целое число 5 и вы хотите разделить его на дробь 7/15, то вы нашли идеальную статью.
Совпадение с результатами поиска: Если у вас есть целое число 5 и вы хотите разделить его на дробь 7/15, то вы нашли идеальную статью. В этом кратком уроке по математике мы покажем вам, как можно разделить любое целое число на дробь. Если вам нравится делить числа на дроби, читайте дальше, друг мой!
Цитата из источника: …
8. Решите 4 /5 ÷ 7 /15 Дайте ответ в виде смешанного числа в …
Автор: brainly.
 in
inОценить 3 ⭐ (19245 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о тренировках 4/5 ÷ 7/15 Дайте ответ в виде смешанного числа в … 1 5/7. Пошаговое объяснение: 4/5÷7/15=? Разделить две дроби — это то же самое, что умножить первую дробь на обратную (обратную) …
Совпадение с результатами поиска: Включите JS и отключите любой блокировщик рекламы
Цитата из источника: …
9. Умножение и деление дробей – GCFGlobal
Автор: edu.gcfglobal.org
Оценить 4 ⭐ (25243 Оценки)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи об умножении и делении дробей — GCFGlobal 1 умножить на 5 равно 5, поэтому 5 — знаменатель нашего ответа.
 Итак, 4/1 умножить на 1/5 равно 4/5.
Итак, 4/1 умножить на 1/5 равно 4/5.Совпадение с результатами поиска: Дробь является частью целого. На прошлом уроке вы научились складывать и вычитать дроби. Но это не единственный вид математики, который вы можете делать с дробями. Бывают случаи, когда полезно будет умножать и дроби.
Цитата из источника: …
10. Калькулятор дробей. Все операции с объяснением
Автор: www.omnicalculator.com
Оценить 3 ⭐ (14525 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о калькуляторе дробей. Все операции с объяснением Как умножать дроби ✖️; Как делить дроби ➗; Как упростить дроби? Как преобразовать десятичную дробь в дробь? Как превратить …
Совпадение с результатами поиска: Добро пожаловать в наш калькулятор дробей, действительно универсальный инструмент.
 Он может:
Он может:
➕ складывать,
➖ вычитать,
✖️умножать и
➗ делить любые две дроби. Более того, в нем есть возможность упростить дробь (он же уменьшить), а также подсказать, как дробь превратить в десятичную и наоборот. Если вы все еще не впечатлены…Цитата из источника: …
11. Математическая помощь: как вычислить дробную часть числа – Owlcation
Автор: owlcation.com
Оценить 4 ⭐ (34050 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи по математике Помощь: Как вычислить дробную часть числа – Owlcation Ответ: Чтобы вычислить 1/5 любого числа, разделите число на 5. Таким образом, 240 разделить на 5 равно 48. Вопрос: Что такое 4/11 из 66? Ответ: Используйте метод …
Совпадение с результатами поиска: Помните: чтобы вычислить дробь от числа, все, что вам нужно сделать, это разделить это число на знаменатель дроби, а затем умножить результат на числитель дроби.
 Давайте сделаем несколько примеров задач для практики.
Давайте сделаем несколько примеров задач для практики.Цитата из источника: …
12. Решения NCERT для математики класса 6 Глава 5 – Дроби
Автор: www.meritnation.com
Оценить 3 ⭐ (6113 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о NCERT Решения для 6 класса Математика Глава 5 – Дроби Данный прямоугольник не делится на четыре равные части. … (vi) 12715 = (12 × 15) + 715 = 18715 … Вопрос 23: Что нужно прибавить к 6715, чтобы получить 815?
Совпадение с результатами поиска: (i) 23 =2×23×2 = 2×33×3= 2×43×4= 2×53×5 = 2×63×6
∴ 23 = 46 = 69 = 812 = 1015 = 1218
Следовательно, пять дробей эквивалентны …
Цитата из источника: …
13.
 Сколько 3/5 разделить на 1/7? – Калькулятор дробей
Сколько 3/5 разделить на 1/7? – Калькулятор дробейАвтор: multifractions.com
Оценка 4 ⭐ (21513 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о том, сколько 3/5 делится на 1/7? – Калькулятор дробей Калькулятор дробей для деления дробей определяет деление дробей между дробями 3/5 и 1/7, т.е. 21/5 … Пример: 2/5÷5/10 (или) 4/9÷6/22 (или) 5/34÷ 15 7 …
Сопоставьте результаты поиска: И таким же образом знаменатель второй дроби, т.е. 7, придет в числитель первой дроби и умножится:
Цитата из источника: …
14. Преобразуйте каждое из следующих чисел в неправильную дробь: i) 7 1/4 …
Автор: www.doubtnut.com
Оценить 4 ⭐ (33889 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о Преобразуйте каждое из следующих чисел в неправильную дробь: i) 7 1/4 … Преобразуйте каждое из следующих чисел в неправильную дробь: i) 7 1/4 (ii) \ 8 5/7 (iii ) 5 3/(10) (iv) 12 7/(15)
Совпадение с результатами поиска: привет ученикам вопрос заключается в преобразовании каждого из следующих чисел в неправильную дробь первая 7 1 на 4 вторая 857 третья 53 на 10 и 12 7 так что давайте поймем первая часть 7 1 на 4 здесь одна остаток 4 — это делитель, а 7 — это вопрос, поэтому, чтобы преобразовать смешанную дробь в неправильную дробь…
Цитата из источника: …
15.
 7/15 умножить на 9 в виде дроби – calculate.name
7/15 умножить на 9 в виде дроби – calculate.nameАвтор: калькулятор.имя
Оценить 4 ⭐ (21811 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о 7/15 умножить на 9 в виде дроби – calculate.name 7/15 умножить на 9 в виде дроби равно 21/5 … общий делитель 63 и 15 равен 3, упростите дробь, разделив оба числителя а знаменатель на 3,
Совпадение с результатами поиска: Числитель дроби больше знаменателя, она называется неправильной дробью, поэтому мы также можем преобразовать это 21/5 в смешанное число. Таким образом,
Цитата из источника: …
16. Калькулятор смешанных чисел в процентах
Автор: www.calculatorsoup.com
Оценить 4 ⭐ (27809Рейтинги)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о Калькуляторе смешанных чисел в процентах Затем разделите числитель на знаменатель и умножьте на 100, чтобы получить процентное значение.
. Пример. Преобразуйте смешанное число 7 1/5 в проценты, используя дробь …
Пример. Преобразуйте смешанное число 7 1/5 в проценты, используя дробь …Совпадение с результатами поиска: Вы также можете преобразовать смешанное число в процентное сложение дробей. Сначала преобразуйте целую числовую часть смешанного числа в неправильную дробь и прибавьте ее к дробной части смешанного числа. Затем разделите числитель на знаменатель и умножьте на 100, чтобы получить процентное значение.
Цитата из источника: …
17. Как делить дроби — KS3 Maths — BBC Bitesize
Автор: www.bbc.co.uk
Оценить 3 ⭐ (19559 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о том, как делить дроби — KS3 Maths — BBC Bitesize Чтобы разделить дробь на дробь, используйте обратный метод.
 Это значит перевернуть вторую дробь вверх ногами и умножить. Иногда расчеты могут быть …
Это значит перевернуть вторую дробь вверх ногами и умножить. Иногда расчеты могут быть …Совпадение с результатами поиска: Подсказка: Понимание того, как преобразовывать смешанные числа в неправильные дроби, может быть полезно при делении дробей. Было бы полезно иметь ручку и бумагу, чтобы помочь вам в работе.
Цитата из источника: …
18. Деление дробей
Автор: www.math-only-math.com
Оценить 4 ⭐ (31810 оценок)
Лучшие по рейтингу: 4 ⭐
Самый низкий рейтинг: 2 ⭐
Резюме: Статьи о делении дробей Здесь мы обсудим деление дробей на целое число, на дробное число или на другую смешанную дробь… Шаг I: Найдите обратную величину 1/5.
Совпадение с результатами поиска: Существуют три типа дробей: Правильная дробь, Неправильная дробь, Смешанная дробь, Правильная дробь: Дроби, числители которых меньше знаменателей, называются правильными дробями.
 (Числитель
(ЧислительЦитата из источника: …
19. Как считать дроби: пошаговое руководство
Автор: Psychometric-success.com
Оценить 3 ⭐ (3320 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о том, как считать дроби: пошаговое руководство Задачи на дроби часто встречаются в тестах по математике или счету. … Обратные числа используются при делении и умножении дробей (5 ÷ 1/5 — это …
Совпадение с результатами поиска: Правильная дробь – Правильная дробь – это дробь, в которой числитель меньше знаменателя. 1/2, 10/15 и 85/100 — все это примеры правильных дробей. Общее значение правильной дроби всегда меньше единицы.
Цитата из источника: …
20.
 Деление дробей на 1 – / – 7 и 5 – OnlineCalculator.Guru
Деление дробей на 1 – / – 7 и 5 – OnlineCalculator.GuruАвтор: onlinecalculator.guru
Оценить 3 ⭐ (2428 оценок)
Лучшие по рейтингу: 3 ⭐
Самый низкий рейтинг: 1 ⭐
Резюме: Статьи о делении дробей на 1 – / – 7 и 5 – OnlineCalculator.Guru Калькулятор деления дробей поможет вам определить деление дробей 1/7 и 5/7 т.е. 1/5 с пошаговым объяснением того, как пришел ответ.
Сопоставьте результаты поиска: И таким же образом знаменатель второй дроби, т.е. 7, придет в числитель первой дроби и умножится:
Цитата из источника: …
Видеоуроки о делении 1/5 на 7/15 в виде дроби
Похожие статьи
Калькулятор дробей (÷) | Простобесплатные инструменты
Калькулятор дробей онлайн.

Введите дроби и нажмите кнопку =.
Введите простые дроби с косой чертой (/).
Например: 1/2 ÷ 1/3
Введите смешанные числа с пробелом.
Например: 2 1/2 ÷ 1 1/3
Пример деления дробей
1/2 ÷ 1/3 = 1/2 × 3/1 = (1×3) / (2×1) = 3 / 2 = 1 1/2
В настоящее время у нас есть около 5611 калькуляторов, таблиц преобразования и полезных онлайн-инструментов и программных функций для студентов, преподавателей и преподавателей, дизайнеров и просто для всех.
Вы можете найти на этой странице финансовые калькуляторы, ипотечные калькуляторы, калькуляторы для кредитов, калькуляторы автокредита и калькуляторы лизинга, калькуляторы процентов, калькуляторы выплат, пенсионные калькуляторы, калькуляторы амортизации, инвестиционные калькуляторы, калькуляторы инфляции, калькуляторы финансов, калькуляторы подоходного налога , калькуляторы сложных процентов, калькулятор зарплаты, калькулятор процентной ставки, калькулятор налога с продаж, калькуляторы фитнеса и здоровья, калькулятор ИМТ, калькуляторы калорий, калькулятор жировых отложений, калькулятор BMR, калькулятор идеального веса, калькулятор темпа, калькулятор беременности, калькулятор зачатия беременности, срок родов калькулятор, математические калькуляторы, научный калькулятор, калькулятор дробей, калькулятор процентов, генератор случайных чисел, калькулятор треугольника, калькулятор стандартного отклонения, другие калькуляторы, калькулятор возраста, калькулятор даты, калькулятор времени, калькулятор часов, калькулятор среднего балла, калькулятор оценок, конкретный калькулятор, подсеть калькулятор, генерация пароля или калькулятор преобразования и многие другие инструменты, а также для редактирования и форматирования текста, загрузки видео с Facebook (мы создали один из самых известных онлайн-инструментов для загрузки видео с Facebook).
 Мы также предоставляем вам онлайн-загрузчики для YouTube, Linkedin, Instagram, Twitter, Snapchat, TikTok и других сайтов социальных сетей (обратите внимание, что мы не размещаем видео на своих серверах. Все видео, которые вы загружаете, загружаются с Facebook, YouTube, Linkedin, CDN в Instagram, Twitter, Snapchat, TikTok. Мы также специализируемся на сочетаниях клавиш, ALT-кодах для Mac, Windows и Linux и других полезных советах и инструментах (как написать смайлики онлайн и т. д.)
Мы также предоставляем вам онлайн-загрузчики для YouTube, Linkedin, Instagram, Twitter, Snapchat, TikTok и других сайтов социальных сетей (обратите внимание, что мы не размещаем видео на своих серверах. Все видео, которые вы загружаете, загружаются с Facebook, YouTube, Linkedin, CDN в Instagram, Twitter, Snapchat, TikTok. Мы также специализируемся на сочетаниях клавиш, ALT-кодах для Mac, Windows и Linux и других полезных советах и инструментах (как написать смайлики онлайн и т. д.)Есть много очень полезных бесплатных онлайн-инструментов, и мы будем рады, если вы поделитесь нашей страницей с другими или пришлете нам какие-либо предложения по другим инструментам, которые придут вам на ум. Также, если вы обнаружите, что какой-либо из наших инструментов не работает должным образом или нуждается в лучшем переводе, сообщите нам об этом. Наши инструменты сделают вашу жизнь проще или просто помогут вам выполнять свою работу или обязанности быстрее и эффективнее.
Ниже перечислены наиболее часто используемые многими пользователями по всему миру.

- Бесплатные онлайн-калькуляторы и инструменты
- Калькуляторы часовых поясов/часов/дат
- Бесплатные онлайн-калькуляторы перевода единиц
- Бесплатные онлайн-инструменты для веб-дизайна
- Бесплатные онлайн-инструменты для электричества и электроники
- Математика 1 Инструменты Онлайн-инструменты
Текст - Инструменты PDF
- Код
- Экология
- Прочее
- Бесплатные онлайн-загрузчики для социальных сетей
- Бесплатные онлайн-калькуляторы и инструменты для электротехники
- Бесплатные онлайн финансовые калькуляторы и инструменты
- Бесплатные онлайн калькуляторы оценок и инструменты
- Бесплатные онлайн калькуляторы освещения и инструменты
- Бесплатные онлайн математические калькуляторы и инструменты
- Бесплатные онлайн калькуляторы проводов и инструменты
- Бесплатные онлайн детские калькуляторы и инструменты
- Бесплатные онлайн-калькуляторы тела и инструменты
- Калькулятор преобразования переменного тока в постоянный
- Сложение дробей бесплатный онлайн-калькулятор
- Сложение бесплатный онлайн-калькулятор
- Antilog бесплатный онлайн калькулятор
- Arccos бесплатный онлайн калькулятор
- Arcsin бесплатный онлайн калькулятор
- Arctan бесплатный онлайн калькулятор
- Average бесплатный онлайн калькулятор
- Base бесплатный онлайн калькулятор
- Binary 09 бесплатный онлайн калькулятор 90 бесплатно 90 90 Косинус онлайн калькулятор
- Деление дробей онлайн бесплатный онлайн калькулятор
- Деление бесплатный онлайн калькулятор
- Калькулятор формулы экспоненциального роста/убывания
- Калькулятор степени
- Калькулятор множителей
- Калькулятор дробей
- Калькулятор наибольшего общего множителя
- Калькулятор наименьшего общего кратного
- Калькулятор логарифмов9 Математический бесплатный онлайн калькулятор
- Умножение бесплатный онлайн калькулятор
- Умножение дробей бесплатный онлайн калькулятор
- Калькулятор натурального логарифма онлайн
- Калькулятор процентов без ошибок
- Калькулятор процентного изменения бесплатный онлайн калькулятор
- Радикалы и корни бесплатный онлайн калькулятор
- Бесплатный онлайн генератор случайных чисел
- Генератор случайных чисел 0-1
- Генератор случайных чисел 0-10
- Генератор случайных чисел 0-100
- Генератор случайных чисел 0-9
- Генератор случайных чисел 0-99
- Генератор случайных чисел 1-10 00009 90-10 Генератор случайных чисел Генератор случайных чисел 1-2
- Генератор случайных чисел 1-20
- Генератор случайных чисел 1-3
- Генератор случайных чисел 1-4
- Генератор случайных чисел 1-5
- Генератор случайных чисел 1-6
- Калькулятор пропорций
- Калькулятор научного представления
- Калькулятор упрощения дробей
- Калькулятор синуса
- Квадратный корень
- Калькулятор стандартного отклонения
- Калькулятор вычитания Вычитание0 Калькулятор вычитания0 онлайн калькулятор
- Тангенс бесплатный онлайн калькулятор
- Тригонометрия бесплатный онлайн калькулятор
- Бесплатный онлайн-калькулятор дисперсии
- Бесплатный онлайн-калькулятор средневзвешенного значения
И мы все еще разрабатываем больше. Наша цель — стать универсальным сайтом для людей, которым нужно быстро рассчитать или найти быстрый ответ для основных конверсий.
Наша цель — стать универсальным сайтом для людей, которым нужно быстро рассчитать или найти быстрый ответ для основных конверсий.
Кроме того, мы считаем, что Интернет должен быть источником бесплатной информации. Поэтому все наши инструменты и сервисы абсолютно бесплатны и не требуют регистрации. Мы кодировали и разрабатывали каждый калькулятор индивидуально и подвергали каждый из них строгому всестороннему тестированию. Однако, пожалуйста, сообщите нам, если вы заметите малейшую ошибку — ваш вклад чрезвычайно ценен для нас. Хотя большинство калькуляторов на Justfreetools.com предназначены для универсального использования во всем мире, некоторые из них предназначены только для определенных стран.
Нашли ошибку? Дайте нам знать!
Мы получили ваше сообщение, мы свяжемся с вами в ближайшее время.
Ой! Что-то пошло не так, обновите страницу и повторите попытку.
Идентификатор страницы: 113
Простой в использовании калькулятор дробей
Калькулятор дробей
| + — x / | = | ? | ||
? |
Калькулятор упрощения дробей
Калькулятор десятичных дробей
Калькулятор дробей
Вернуться на страницу «Калькуляторы» Это также позволит нам упростить дроби, преобразовать дроби в десятичные и десятичные дроби.
Сначала просто введите значения a,b,c,d для дробей \(\frac{a}{b}\) и \(\frac{c}{d}\), затем математическую операцию, которую вы хотите выполнить (+, -, х, /). Калькулятор моментально и точно выполнит операцию и выдаст ответ в самой простой форме. Вы также можете использовать калькулятор, чтобы проверить свою работу, которую вы сделали вручную.
Сложите или вычтите числители, оставив знаменатели одинаковыми.
Пример: \(\frac{3}{5} + \frac{4}{5}\)
Поскольку в обеих дробях знаменатель равен 5, прибавьте 3 и 4, чтобы получить 7. В знаменателе остается 5, поэтому ответ 7/5.
\(\frac{7}{6} – \frac{5}{6}\)
Поскольку знаменатель обеих дробей равен 6, вычтите 5 из 7, чтобы получить 2. Тогда дробь будет \( \фракция{2}{6}\).
Тогда дробь будет \( \фракция{2}{6}\).
Но теперь мы можем упростить \(\frac{2}{6}\). Для упрощения найдите общий множитель. Обратите внимание, что 2 делится без остатка и на 2, и на 6. Поэтому разделите и числитель, и знаменатель на 2, чтобы получить \(\frac{1}{3}\). Теперь дробь упрощена.
Разные знаменателиЧтобы сложить и вычесть разные знаменатели, сначала вычислите общий знаменатель. Самый простой способ сделать это — умножить два знаменателя. Это не всегда дает наименьший общий знаменатель, но вы можете упростить после сложения и вычитания.
Пример: \(\frac{2}{5} + \frac{4}{7}\)
Общий знаменатель равен 5(7) = 35. Поскольку знаменатель первой дроби умножается на 7, числитель также должен быть умножен на 7, чтобы получить \(\frac{14}{35}\). Поскольку знаменатель во второй дроби умножается на 5, числитель должен быть таким же, чтобы получить \(\frac{20}{35}\).
Теперь добавьте \(\frac{14}{35}+\frac{20}{35}=\frac{34}{35}\)
Вычитание выполняется таким же образом, просто вычтите две дроби после перезаписи дроби с общими знаменателями. Если вам нужно упростить, не забудьте разделить на наибольший общий множитель.
Если вам нужно упростить, не забудьте разделить на наибольший общий множитель.
При умножении дробей просто перемножайте числители и знаменатели. Тогда упрости. Вы также можете сначала упростить перед умножением.
Пример: \(\frac{2}{9}\times\frac{4}{7}\)
Умножьте 2 и 4, чтобы получить 8. Затем умножьте 9 и 7, чтобы получить 63. Результат: \( \фракция{8}{63}\). Упрощение не требуется, поскольку наибольший общий делитель равен 1,9.0003
Теперь предположим, что мы хотим разделить \(\frac{2}{9} \div \frac{4}{7}\).
При делении дроби возьмите первую дробь и умножьте на обратную величину второй. Обратное — это просто замена числителя и знаменателя местами. Задача деления превращается в задачу умножения.
\(\frac{2}{9} \times \frac{7}{4}\)
2 × 7 = 14 и 9 × 4 = 36. Таким образом, ответ равен \(\frac{14 {36}\). Но заметьте, это не в простейшей форме. Наибольший общий множитель равен 2, поэтому деление обоих на 2 дает упрощенный ответ \(\frac{7}{18}\).
Но заметьте, это не в простейшей форме. Наибольший общий множитель равен 2, поэтому деление обоих на 2 дает упрощенный ответ \(\frac{7}{18}\).
Калькулятор преобразования дробей в десятичные принимает любую дробь и преобразует ее в десятичную.
Способ преобразования дроби в десятичную довольно прост. Просто разделите числитель на знаменатель.
Изменить \(\frac{14}{25}\) на десятичную дробь.
Разделите 14 на 25, чтобы получить 0,56. Вы можете сделать это на калькуляторе или вручную с помощью деления в большую сторону. С некоторыми дробями не так просто работать вручную, особенно с неконечными. На этом калькуляторе намного проще работать.
Но если вы решите решать вручную, калькулятор станет отличным инструментом для мгновенной проверки вашей работы.
Преобразование десятичных дробей в дроби является обратным преобразованию дробей в десятичные. Калькулятор быстро выполнит это с точными результатами, просто введя десятичное значение.
Калькулятор быстро выполнит это с точными результатами, просто введя десятичное значение.
Чтобы преобразовать вручную, возьмите десятичную дробь и преобразуйте ее в целое число, затем разделите на 10, возведя число десятичных разрядов вправо, чтобы преобразовать число. Оттуда вы можете упростить дробь, если это необходимо.
Пример:
Преобразование 0,68 в дробь. Чтобы преобразовать 0,68 в целое число, переместите запятую на 2 знака вправо, чтобы получить 68. Поскольку мы переместили 2 знака после запятой, разделите 68 на 10, возведенное во вторую степень, что равно 100.
Это дает нам \(\ гидроразрыв{68}{100}\). Теперь мы можем упростить дробь, найдя общий множитель. Если вы не знаете наибольший общий делитель, вы можете начать с деления на любой общий делитель. Обратите внимание, что 68 и 100 делятся на 2. Это уменьшает дробь до 34/50. Отсюда обратите внимание, что и 34, и 50 делятся на 2. Это сводится к \(\frac{17}{25}\), что является упрощенным ответом.
