Умножение и деление обыкновенных дробей. Проект. Реализация требований ФГОС ООО при обучении учащихся 5 класса
1. ПРОЕКТ Реализация требований ФГОС ООО при обучении учащихся_5_ класса теме: «Умножение и деление обыкновенных дробей»
ПРОЕКТРеализация требований ФГОС ООО
Выполнил:
при обучении
учащихся_
5_ класса
учитель математики МБОУ СОШ №8
Трошина Т. А.
теме:
«Умножение
и деление
Руководитель курса: профессор кафедры математических
дисциплин
обыкновенных
Боженкова Л. И.дробей»
Цель проекта:
Реализация требований ФГОС ООО при изучении темы: «Умножение и деление
обыкновенных дробей»
Для достижения поставленной цели необходимо решение следующих задач.
Задачи исследования.
1. Выявить теоретические основы обучения теме, связанные с реализацией ФГОС
ООО.
2. Выполнить отбор средств обучения теме, в том числе средства ИКТ
3. Разработать таблицу целей и карту обучения теме.
4. Составить учебную рабочую программу «Тематическое и почасовое планирование
образовательных результатов освоения математики.

5. Разработать методические рекомендации обучения теме и применить их в учебном
процессе (фрагментов двух – трёх уроков, иллюстрирующих развитие и
формирование УУД при обучении данной теме школьного курса математики).
Требования ФГОС ООО к школьному курсу математики при изучении темы
«Умножение и деление обыкновенных дробей».
1) формирование представлений о математике как о методе познания действительности, позволяющем описывать и
изучать реальные процессы и явления;
2) развитие умений работать с учебным математическим текстом (анализировать, извлекать необходимую
информацию), точно и грамотно выражать свои мысли с применением математической терминологии и
символики, проводить классификации, логические обоснования, доказательства математических утверждений;
3) овладение символьным языком алгебры, умения моделировать реальные ситуации на языке алгебры, исследовать
построенные модели с использованием аппарата алгебры, интерпретировать полученный результат;
4) овладение системой функциональных понятий, развитие умения использовать функционально-графические
представления для решения различных математических задач, для описания и анализа реальных зависимостей;
5) овладение геометрическим языком; развитие умения использовать его для описания предметов окружающего
мира; развитие пространственных представлений, изобразительных умений, навыков геометрических
построений;
6) развитие умений применять изученные понятия, результаты, методы для решения задач практического характера
и задач из смежных дисциплин с использованием при необходимости справочных материалов, компьютера,
пользоваться оценкой и прикидкой при практических расчётах;
4.
 Развитие познавательных УУД при обучении теме «Умножение и деление обыкновенных дробей»:информационный поиск для формулировки алгоритма, самостоятельная
Развитие познавательных УУД при обучении теме «Умножение и деление обыкновенных дробей»:информационный поиск для формулировки алгоритма, самостоятельнаяформулировка гипотезы умножения и деления обыкновенных дробей,
выбор наиболее эффективных способов умножения и деления
обыкновенных дробей, самостоятельная формулировка гипотезы
нахождения дроби от числа и числа по его дроби, выбор наиболее
эффективных способов решения задач на нахождение дроби от числа
и числа по его дроби, анализ примеров с выделением существенных
признаков, синтез как формулировка алгоритма решения примеров,
применение алгоритма , самостоятельное решение примеров,
построение логической цепи рассуждения, нформационный поиск для
решения задач, выбор наиболее эффективных способов решения
задач, анализ задач с выделением существенных отличительных
признаков, а значит различных способов их решения, осознанное
построение устного и письменного речевого высказывания,
извлечение информации при чтении условии задач, установление
причинно- следственных связей в условиях задач.
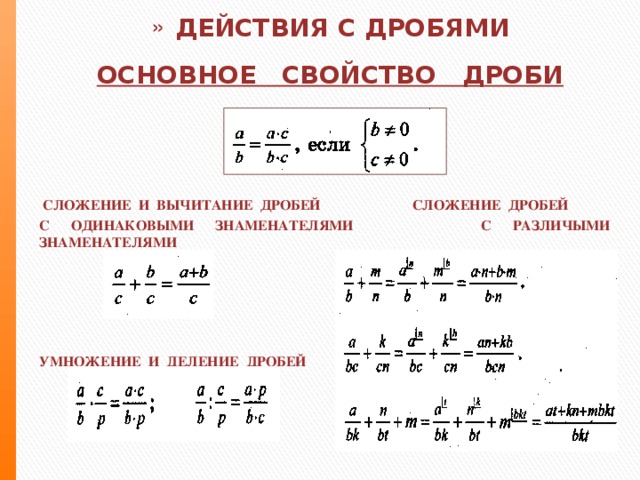
5. Развитие регулятивнвных УУД при обучении теме «Умножение и деление обыкновенных дробей»:
целеполагание(постановка учебной задачи умножения и деленияобыкновенных дробей на основе соотнесения того, что известно и
усвоено учащимися — замена умножения сложением, составление
алгоритма умножения и деления обыкновенных дробей, составление
плана решения примеров по алгоритму и последовательное его
выполнение, контроль(сверка своего решения с работой у доски),
коррекция(внесение необходимых изменений с записью на доске),
самоконтроль с ответами на доске, коррекция ответов, оценка своей
деятельности, волевая саморегуляция, постановка учебной задачи на
нахождение дроби от числа и числа по его дроби на основе соотнесения
усвоенных действий умножения и деления обыкновенных дробей,
составление алгоритма нахождение дроби от числа и числа по его дроби,
постановка учебной цели на решение задач на нахождение дроби от числа
и числа по его дроби на основе соотнесения усвоенных действий
умножения и деления обыкновенных дробей, составление алгоритма
нахождение дроби от числа и числа по его дроби, постановка учебной
цели на решение задач на нахождение дроби от числа и числа по его дроби
на основе соотнесения усвоенных действий умножения и деления
обыкновенных дробей.

6. Развитие коммуникативных УУД при обучении теме «Умножение и деление обыкновенных дробей»:
проверка в парах – согласование действий спартнером; планирование учебного
сотрудничества; построение речевых
высказываний при решении примеров и задач,
постановка вопросов к изучаемому материалу,
лидерство и согласование действий с соседом по
парте или в группе.
7. Развитие личностных УУД при обучении теме «Умножение и деление обыкновенных дробей»:
самопознание и самоопределение(«понялли я алгоритм», оценивание своей
работы, самопознание и
самоопределение.
8. Учебный план темы
№Тема урока
Страница в
учебнике
Основные понятия и задания
1
2
Умножение обыкновенных дробей
§ 10 стр.170
№795-797
Правило умножения обыкновенных дробей. Составление
алгоритма.
Умножение смешанных чисел
§ 10 стр.171
№798-801
3
Умножение дроби на натуральное
число
§ 10 стр.172
№802-809
Алгоритм умножения дроби на натуральное число, решение
подготовительных задач на нахождения целого по его
части.

4
5
6
Закрепление пройденного
§ 10 стр.173
№810-813
Умножение обыкновенных дробей с помощью алгоритма,
решение примеров и задач.
Умножение смешанных чисел на
натуральное число
§ 10 стр.173
814-818
Алгоритм умножения смешенных чисел на натуральное число
различными способами.
7
8
9
Решение задач на умножение
обыкновенных дробей.
§ 10 стр.174
№819, задача в
рабочей
тетради №5-9
Алгоритм умножения смешанных чисел, возведение
обыкновенных дробей в натуральную степень, сравнение
выражений без вычислений.
Работа со схемами и чертежами при решении задач на
нахождение дроби от числа. Самостоятельная работа
контролирующего характера.
Деление дроби на натуральное
число
§ 10 стр.175
№820-822
Алгоритм деления дроби на натуральное число, решение
примеров и задач.
Взаимно обратные числа
§ 10 стр.177
№823-827
Введение понятия взаимно обратных чисел, решение примеров
на умножение и деление обыкновенных дробей.

Правило деления обыкновенных
дробей
§ 10 стр.178
№828-831
Введение алгоритма деления обыкновенных дробей.
10
Деление смешанных чисел
§ 10 стр.178
№832-835
Введение алгоритма деления смешанных чисел, решение
задач.
11
Введение понятия «движение
по реке» при решении задач
§ 10 стр.180
№835, задача по
тетради №2 №1015
Формирование понятия «скорость по течению» и
«скорость против течения», решение примеров.
12
Деление целого числа на
натуральную дробь
§ 10 стр.180
№836, 837
Алгоритм деления целого числа на натуральную дробь,
решение примеров в рабочей тетради №2 «Обыкновенные
дроби»
13
Решение задач на нахождение
части от числа и числа по его
части
§ 10 стр.181
№838-841
Формирование умения различать два типа задач на
нахождение дроби от числа и числа по его дроби.
14
Решение примеров и задач
§ 10 стр.182
№842-845
Формирование умений и навыков по решению примеров и
задач по данной теме.

15
Решение примеров и задач
§ 10 стр.184
№846-852
Формирование умений и навыков по решению примеров и
задач по данной теме. Работа в группах.
16
Решение примеров и задач
§ 10 стр.186
№853-858
Формирование умений и навыков по решению примеров и
задач по данной теме. Самостоятельная работа
контролирующего характера.
17
Решение примеров и задач
§ 10 стр.187
№859-868
Формирование умений и навыков по решению примеров и
задач по данной теме. Обобщение по теме.
18
Контрольная работа №10 по
теме «Умножение и деление
обыкновенных дробей»
19
Работа над ошибками
Коррекция
№871-875
Корректировка знаний по данной теме.
Карта целей при обучении теме «Умножение и деление обыкновенных дробей»
1
Умножение
обыкновен
ных дробей
Урок
Ц 1: Приобретение учебной информации и развитие интеллектуальных умений при
изучении правила умножения обыкновенных дробей и решение типовых задач,
используя основное свойство дроби.

Ц 5: Введение в тему, постановка и формулирование целей своей учебной
деятельности, формулировка алгоритма умножения обыкновенных дробей,
работа по алгоритму.
2
Алгоритм
умножения
смешанных
чисел на
дробь и на
смешанное
число
Урок
Ц 1: Приобретение учебной информации и развитие интеллектуальных умений при
изучении правила умножения смешанных чисел на обыкновенную дробь и
умножение смешанных чисел, возведение обыкновенных дробей в степень
путем умножения, сравнение выражений не вычисляя их значений.
Ц 2: Контроль усвоения теоретических знаний алгоритма умножения обыкновенных
дробей.
Ц 3: Применение знаний интеллектуальных умений при решении текстовых задач.
Ц4:
Ц4: Развитие коммуникативных умений через: включение в групповую работу;
взаимопомощь, рецензирование ответов; организацию взаимоконтроля и
взаимопроверки на всех этапах УПД
3
Умножение
дроби на
натурально
е число
Урок
смешанног
о типа
Фронтальноиндивидуал
ьная форма
обучения
Ц 1: Приобретение учебной информации и развитие интеллектуальных умений при
изучении правила умножения обыкновенной дроби на натуральное число,
решение подготовительных задач на наглядном материале на нахождение
целого по его части.

Ц 3: Применение знаний интеллектуальных умений при решении текстовых задач.
Ц4: Развитие коммуникативных умений через: включение в групповую работу;
взаимопомощь, рецензирование ответов; организацию взаимоконтроля и
взаимопроверки на всех этапах УПД.
УПД.
Ц 5: Введение в тему, постановка и формулирование целей своей учебной
деятельности, формулировка алгоритма умножения обыкновенной дроби на
натуральное число, работа по алгоритму.
смешанног
о типа
Фронтальноиндивидуал
ьная форма
обучения
смешанног
о типа
Фронтальноиндивидуал
ьная форма
обучения
4
Закрепление
пройденного.
Решение примеров
и задач.
Практикум.
Фронтальная
и групповая
форма работы
Ц 1: Приобретение учебной информации и развитие интеллектуальных умений
при изучении свойств умножения для дробных чисел.
Ц 2: контроль усвоения изученного материала в процессе решения примеров на
умножение обыкновенных дробей.

Ц 3: Применение знаний интеллектуальных умений при решении текстовых
задач.
Ц4: Развитие коммуникативных умений через: включение в групповую работу;
взаимопомощь, рецензирование ответов; организацию взаимоконтроля и
взаимопроверки на всех этапах УПД.
УПД.
5
Умножение
смешанных чисел
на натуральное
число
Урок
Смешанного
типа
Фронтальная
и групповая
форма работы
Постановка и решение проблемы (познавательные УУД)
Ц 1:составление
1:составление алгоритма умножения смешанного числа на натуральное
различными способами.
Ц 2: контроль усвоения изученного материала в процессе самостоятельной
работы.
Ц 3: Применение знаний интеллектуальных умений при решении текстовых
задач.
Ц4: Развитие коммуникативных умений через: включение в групповую работу;
взаимопомощь, рецензирование ответов; организацию взаимоконтроля и
взаимопроверки на всех этапах УПД.
УПД.
Ц 5: Введение в тему, постановка и формулирование целей своей учебной
деятельности, формулировка алгоритма умножения смешанных чисел на
натуральное число, работа по алгоритму.

6
Использование
Свойств
умножения и
сложения при
Сравнении
выражений.
Решение задач
различных видов,
используя схему
Практикум:
Парное
Взаимообуче
ие
Ц 2:
2: а1) использует определения свойств умножения для сравнения
выражений; б1)решение задач , используя схемы и планы решения ; в1)
находит ошибки в решении задач своего уровня сложности; решает задачи
своего уровня сложности, используя готовый план или схему поиска;
решает задачи второго и третьего уровня сложности, составляя схемы
поиска и план;
Ц4: Развитие коммуникативных умений через: включение в групповую работу;
взаимопомощь, рецензирование ответов; организацию взаимоконтроля и
взаимопроверки на всех этапах УПД.
УПД.
Ц 5: Введение в тему, постановка и формулирование целей своей учебной
деятельности, планирование решения задач, работа по плану.
7
Алгоритм
деления дроби на
Натуральное
число
Урок
Смешанного
типа
Фронтальная
и групповая
Форма
работы
Ц 1:составление
1:составление алгоритма деления дроби на натуральное число.

Ц 2: контроль усвоения изученного материала в процессе самостоятельной работы.
Ц 3: Применение знаний интеллектуальных умений при решении текстовых задач.
Ц4: Развитие коммуникативных умений через: включение в групповую работу;
взаимопомощь, рецензирование ответов; организацию взаимоконтроля и
взаимопроверки на всех этапах УПД.
УПД.
Ц 5: Введение в тему, постановка и формулирование целей своей учебной
деятельности, формулировка алгоритма деления дроби на натуральное число,
работа по алгоритму
8
Введение понятия
Взаимно
обратных чисел.
Решение задач.
Практикум.
Фронтальная
и групповая
Форма
работы
Ц 1:Введение
1:Введение понятия взаимно обратных чисел.
Ц 2: контроль усвоения изученного материала в процессе самостоятельной работы.
Ц 3: Применение знаний интеллектуальных умений при решении текстовых задач:
решает задачи своего уровня сложности, составляет задачи по готовой схеме,
составляет обратные задачи и решает их, осуществляет самопроверку или
проверку в парах.

Ц4: Развитие коммуникативных умений через: включение в групповую работу;
взаимопомощь, рецензирование ответов; организацию взаимоконтроля и
взаимопроверки на всех этапах УПД.
УПД.
Ц 5: Введение в тему, постановка и формулирование целей своей учебной
деятельности.
9
Правило деления
дробей (введение
алгоритма)
Урок
Смешанного
типа
Фронтальная
и
Индивидуаль
ная формы
обучения
Ц 1:составление
1:составление алгоритма деления обыкновенных дробей .
Ц 3: Применение знаний интеллектуальных умений при решении примеров
различного уровня.
Ц4: Развитие коммуникативных умений через: включение в групповую работу;
взаимопомощь, рецензирование ответов; организацию взаимоконтроля и
взаимопроверки на всех этапах УПД.
УПД. (анализирует ошибки в парах или
группах, оказывает помощь, работающим на предыдущих уровнях).
10
Деление
Смешанных
чисел,
Решение
задач.
Урок
смешанного
типа
Ц 1:составление
1:составление алгоритма деления смешанных чисел, решение задач различного вида.

Ц 2: Использует предписания для решения типов задач своего уровня сложности.
Ц 3: Применение знаний интеллектуальных умений при решении примеров различного
уровня.
Ц4: Развитие коммуникативных умений через: включение в групповую работу;
взаимопомощь, рецензирование ответов; организацию взаимоконтроля и
взаимопроверки на всех этапах УПД.
УПД. (анализирует ошибки в парах или группах,
оказывает помощь, работающим на предыдущих уровнях).
11
Формирован
е понятия
«скорость по
течению» и
«скорость
Против
течения»
Урок
Смешанного
типа
Ц 1:Формирование
1:Формирование понятия «движение по реке».
Ц 2: Контроль усвоения изученного материала в процессе самостоятельной работы.
Ц 3: Применение знаний интеллектуальных умений при решении задач различного
уровня.
Ц4: Развитие коммуникативных умений через: включение в групповую работу;
взаимопомощь, рецензирование ответов; организацию взаимоконтроля и
взаимопроверки на всех этапах УПД.

УПД. (анализирует ошибки в парах или группах,
оказывает помощь, работающим на предыдущих уровнях).
12
Деление
целого числа
на
Обыкновенную
дробь
Урок
Смешанного
типа
Ц 1:составление
1:составление алгоритма деления целого числа на обыкновенную дробь .
Ц 3: Применение знаний интеллектуальных умений при решении примеров различного
уровня.
Ц4: Развитие коммуникативных умений через: включение в групповую работу;
взаимопомощь, рецензирование ответов; организацию взаимоконтроля и
взаимопроверки на всех этапах УПД.
УПД. (анализирует ошибки в парах или группах,
оказывает помощь, работающим на предыдущих уровнях).
13
Деление
целого числа
на
Обыкновенную
дробь
Практикум
Ц2:
Ц2: а1) использует алгоритмы умножения и деления обыкновенных дробей, решает
примеры различного уровня сложности; б1)решает задачи , используя схемы и
планы решения в1) находит ошибки в решении задач своего уровня сложности;
решает задачи своего уровня сложности, используя готовый план или схему
поиска; решает задачи второго и третьего уровня сложности, составляя схемы
поиска и план;
Ц4: Развитие коммуникативных умений через: включение в групповую работу;
взаимопомощь, рецензирование ответов; организацию взаимоконтроля и
взаимопроверки на всех этапах УПД.

УПД.
14
Решение задач
на
Нахождения
части от числа
и числа по его
части
Урок
смешанного
типа
Ц1: Приобретение учебной информации и развитие интеллектуальных умений при
изучении различных типов задач части от числа и числа по его части.
Составление плана и схем решения задач, выделение признаков различия типов
задач.
Ц3: Применение знаний интеллектуальных умений при решении текстовых задач:
решает задачи различного уровня сложности, составляет задачи по готовой схеме,
составляет обратные задачи и решает их, осуществляет самопроверку или
проверку в парах.
Ц4: Развитие коммуникативных умений через: включение в групповую работу;
взаимопомощь, рецензирование ответов; организацию взаимоконтроля и
взаимопроверки на всех этапах УПД.
УПД.
15
Решение задач
на
Нахождения
части от числа
и числа по его
части
Урок
сешанного
типа
Ц1: Приобретение учебной информации и развитие интеллектуальных умений при
изучении различных типов задач части от числа и числа по его части.

Составление плана и схем решения задач, выделение признаков различия типов
задач.
Ц3: Применение знаний интеллектуальных умений при решении текстовых задач:
решает задачи различного уровня сложности, составляет задачи по готовой схеме,
составляет обратные задачи и решает их, осуществляет самопроверку или
проверку в парах.
Ц4: Развитие коммуникативных умений через: включение в групповую работу;
взаимопомощь, рецензирование ответов; организацию взаимоконтроля и
взаимопроверки на всех этапах УПД.
УПД.
16
Решение
примеров и
задач
Практикум.
Парное
Взаимообучен
е.
Ц2: Использует предписания для решения типов задач своего уровня сложности.
Ц3:
Ц3: а1) использует планы и схемы решения различных типов задач, решает задачи
различного уровня сложности; б1) находит ошибки в решении задач своего
уровня сложности; решает задачи своего уровня сложности, используя готовый
план или схему поиска; решает задачи второго и третьего уровня сложности,
составляя схемы поиска и план;
Ц4: Развитие коммуникативных умений через: включение в групповую работу;
взаимопомощь, рецензирование ответов; организацию взаимоконтроля и
взаимопроверки
17
Решение
примеров и
задач
Практикум.

Фронтально
Индивидуальн
я форма
обучения.
Ц2: Использует предписания для решения типов задач своего уровня сложности.
Ц3:
Ц3: а1) использует планы и схемы решения различных типов задач, решает
задачи различного уровня сложности; б1) находит ошибки в решении задач
своего уровня сложности; решает задачи своего уровня сложности,
используя готовый план или схему поиска; решает задачи второго и
третьего уровня сложности, составляя схемы поиска и план;
Ц4: Развитие коммуникативных умений через: включение в групповую работу;
взаимопомощь, рецензирование ответов; организацию взаимоконтроля и
взаимопроверки
18
Контрольная
работа
Практикум.
Индивидуальн
я форма
работы.
Ц 2, 3, 5: выбирает задачи своего уровня сложности , решает их, осуществляет
самопроверку; делает выводы о качестве собственных знаний,
необходимых для выполнения контрольной работы
19
Урок
коррекции и
рефлексии
Ц2, Ц4: анализирует собственные ошибки с помощью товарища и исправляет
их;
Ц5: вспоминает планируемые цели своей учебной деятельности; оценивает свою
итоговую деятельность по данным объективным критериям; по
собственным критериям, сравнивая их с объективными критериями; е)
делает выводы о результатах своей деятельности, дальнейших действиях,
планирует коррекцию учебной познавательной деятельности
16.
 Примерные контрольные работы
Примерные контрольные работы18. Фрагмент урока в 5 классе по теме: «Умножение обыкновенной дроби на натуральное число» Цель: ввести алгоритм умножения дроби на
натуральное число, закрепить алгоритм решения задачи примеров.
Деятельность учителя
Слайд 1 на доске. Задача по
Маша.
чертежу.
1.Как можно найти расстояние,
пройденное черепахой?
2.Но мы не умеем умножать
обыкновенную дробь на
натуральное число.(проблемная
ситуация).
3.Как можно вычислить?
Деятельность ученика
2
4
9
Заменить умножение сложением и
вычислить.
2
2 2 2 2 2 2 2 2 2 4 8
4
9
9 9 9 9
9
9
9
По мере ответов учащихся
открывается слайд 1
Работа с учебником. №802.
1.
Кто из детей рассуждал так
же как и мы?
2.
А как рассуждал Миша?
3.
Кто считал быстрее?
4.
Попытайтесь
сформулировать правило
умножения дроби на
натуральное
число( выдвижение
гипотезы).

5.
Сравните свою гипотезу с
правилом в учебнике.
Миша.
3
3 3 3 3 3 3 3 3 3 3 3 5
5
4
4 4 4 4 4
4
4
3
3 5 3 5 3 5
5
4
4 1 4 1
4
Чтобы умножить дробь на натуральное
число, надо ее числитель умножить
на это число, а знаменатель оставит
без изменения.
Стр. 172 учебника.
Реализация целей и УУД
Ц 1: Приобретение учебной информации и
развитие интеллектуальных умений при
изучении правила умножения
обыкновенной дроби на натуральное число.
Ц 5: Введение в тему, постановка и
формулирование целей своей учебной
деятельности, формулировка алгоритма
умножения обыкновенной дроби на
натуральное число, работа по алгоритму.
Регулятивные УУД:
целеполагание(постановка учебной задачи
умножение обыкновенной дроби на
натуральное число на основе соотнесения
того, что известно и усвоено учащимися замена умножения сложением.
Общеучебные УУД: информационный
поиск для формулировки алгоритма.

Ц4: Развитие коммуникативных умений
через: включение в групповую работу;
взаимопомощь, рецензирование
ответов; организацию взаимоконтроля
и взаимопроверки на всех этапах УПД.
УПД.
Регулятивные УУД: составление алгоритма
умножение обыкновенной дроби на
натуральное число.
Общеучебные УУД: самостоятельная
формулировка гипотезы умножение
обыкновенной дроби на натуральное
число, выбор наиболее эффективных
способов умножения.
Логические общепознавательные действия:
анализ примеров с выделением
существенных признаков, синтез как
формулировка алгоритма умножения.
Работа с учебником.
№803 (работа
у доски и в
тетрадях)
Стр. 173 №803
Ц 3: Применение знаний интеллектуальных умений при решении
примеров на умножение обыкновенной дроби на натуральное
число.
Личностные УУД: самопознание и самоопределение(«понял ли я
алгоритм».
Регулятивные УУД: составление плана решения примеров по
алгоритму и последовательное его выполнение,
контроль(сверка своего решения с работой у доски),
коррекция(внесение необходимых изменений с записью на
доске).

Работа с учебником.
№809 (работа
у доски и в
тетрадях)
Стр. 173 №809. Учащиеся
выполняют номер
самостоятельно, ответы
проверяют с ответами на
доске(ответы написаны заранее
на переносных досках).
Учащиеся самостоятельно
оценивают свою работу и
ставят себе оценку.
Ц 5: Введение в тему, постановка и формулирование целей своей
учебной деятельности, формулировка алгоритма умножения
обыкновенной дроби на натуральное число, работа по
алгоритму.
Общепознавательные УУД: анализ примеров, применение
алгоритма , самостоятельное решение примеров.
Регулятивные УУД: самоконтроль с ответами на доске, коррекция
ответов, оценка своей деятельности, волевая саморегуляция.
Личностные УУД: оценивание своей работы
Слайд 3.
Математический
диктант(5
примеров)
Учащиеся решают,
проверяют ответы
в парах,
выставляют
оценку соседу по
парте.
Ц 2: Контроль усвоения теоретических
знаний алгоритма умножения
обыкновенных дробей.

Ц4: Развитие коммуникативных умений
через: включение в групповую работу;
взаимопомощь, рецензирование ответов;
организацию взаимоконтроля и
взаимопроверки на всех этапах УПД.
Коммуникативные УУД: проверка в парах –
согласование действий с партнером.
Общепознавательные УУД: построение
логической цепи рассуждения.
Регулятивные УУД: самоконтроль с ответами
на доске, коррекция ответов, оценка
своей деятельности, волевая
саморегуляция.
25. Спасибо за внимание!
Умножение обыкновенных дробей
Тема урока. Умножение обыкновенных дробей.
Цели урока:
— Обеспечить применение учащимися теоретических знаний об умножении обыкновенных дробей при выполнении практических заданий.
— Создать условия для формирования умения решать задачи на нахождение дроби от числа; применять распределительное свойство умножения при упрощении выражений и вычислений.
— Организовать деятельность учащихся по самостоятельному применению знаний в стандартной и изменённой ситуации.
— Создать условия для развития мышления, активности, памяти и внимания.
— Создать условия для воспитания культуры общения, аккуратности, организованности.
Оборудование: графопроектор, плёнки, маркер, карточка с заданиями д/м, сборник тестовых заданий.
Девиз урока: « Решай, ищи, твори и мысли»
Ход урока.
I.Организационный момент.
1) Приветствие учителя.
2) Проверка подготовленности учащихся и урока.
3) Сообщить тему урока. Вместе с учащимися сформулировать цели урока.
II. Повторение изученного материала.
1) Фронтальный опрос учащихся по вопросам:
1. Как умножить дробь на натуральное число?
2. Как выполнить умножение двух дробей?
3. Как выполнить умножение смешанных чисел?
4. Сформулировать правило нахождения дроби от числа. Прочитать стихотворение.
5. Расскажите, как найти несколько процентов от числа.
6. Расскажите, как можно умножить смешанное число на натуральное число, применяя распределительное свойство умножения.
2) Математический диктант (используем плёнку и графопроектор )
| 1 в | 2 в | |
| Вычислите: | ||
| 1. | | |
| 2. | | |
| 3. | | |
| Найдите: | ||
| 4. | от 42 | от 54 |
| 5. | 35% от 40 | 40% от 35 |
| Вычислите: | ||
| 6. | | |
3) В это время один ученик выполняет задание на доске.
Упростите и найдите значение выражения:
у — у + у при у = 0,4
Ш. Выполнить упражнения:
1) решите уравнение (самостоятельно с последующей проверкой):
Гимнастика для глаз.
2) Вы можете назвать любое значение х, а я сразу же назову значение данного произведения. Кто сможет сделать то же самое?
3) Кто быстрее решит задачу в стихах.
«Синички – воробьиные сестрички».
На рябину сели птицы: воробьишки и синицы.
Всех пернатых 220,
птиц – синички – воробьиные сестрички.
Сколько в стае воробьёв?
4) Проверьте равенства:
1.
2.
3.
4.
IV. Самостоятельная работа.
1 группа – тесты ( для слабых ), ( стр. 14 – 1в; стр. 15 – 2в. )
2 группа – ( для сильных ).
1в. 2в.Д/м, стр. 12 Д/м, стр. 39
№ 127, № 128, № 129, № 130. – любые 3
задания на « 5 »
V. Д/З. « Идеальное »
Д/З. « Идеальное »
повт. п. 13 -15.
VΙ. Рефлексия.
« Человек подобен дроби,
числитель, которой есть то,
что человек представляет
собой, а знаменатель – то,
что он думает о себе »
А. Толстой.
открытых учебников | Siyavula
Загрузите наши открытые учебники в различных форматах, чтобы использовать их так, как вам удобно. Нажмите на обложку каждой книги, чтобы увидеть доступные для загрузки файлы на английском и африкаанс. Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! См. различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.
Математика
- Читать онлайн
Учебники
Английский
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
Африкаанс
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
Африкаанс
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
Африкаанс
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
-
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
Наука
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 7А
- PDF (CC-BY-ND)
Класс 7Б
- PDF (CC-BY-ND)
Африкаанс
Граад 7А
- PDF (CC-BY-ND)
Граад 7Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 8А
- PDF (CC-BY-ND)
Класс 8Б
- PDF (CC-BY-ND)
Африкаанс
Граад 8А
- PDF (CC-BY-ND)
Граад 8Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 9А
- PDF (CC-BY-ND)
Класс 9Б
- PDF (CC-BY-ND)
Африкаанс
Граад 9А
- PDF (CC-BY-ND)
Граад 9Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 4А
- PDF (CC-BY-ND)
Класс 4Б
- PDF (CC-BY-ND)
Африкаанс
Граад 4А
- PDF (CC-BY-ND)
Граад 4Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 5А
- PDF (CC-BY-ND)
Класс 5Б
- PDF (CC-BY-ND)
Африкаанс
Граад 5А
- PDF (CC-BY-ND)
Граад 5Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 6А
- PDF (CC-BY-ND)
Класс 6Б
- PDF (CC-BY-ND)
Африкаанс
Граад 6А
- PDF (CC-BY-ND)
Граад 6Б
- PDF (CC-BY-ND)
Лицензирование наших книг
Эти книги не только бесплатны, но и имеют открытую лицензию! Один и тот же контент, но разные версии (фирменные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий. Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите сайт Creative Commons Attribution-NoDerivs 3.0 Unported.
Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите сайт Creative Commons Attribution-NoDerivs 3.0 Unported.
Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (версии без торговой марки)
Эти версии одного и того же контента без торговой марки доступны для вас, чтобы вы могли делиться ими, адаптировать, преобразовывать, изменять или развивать их любым способом, при этом единственным требованием является предоставление соответствующей ссылки на Siyavula. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Класс 5 | СС | Виртуальный ботаник
Дополнительные темы
для 5 классаПопулярные учебные пособия
для 5 классаКаковы коммутативные свойства сложения и умножения?
Свойство коммутативности является фундаментальным строительным блоком математики, но оно работает только для сложения и умножения. В этом руководстве определяется свойство коммутативности и приводятся примеры его использования.
Каковы ассоциативные свойства сложения и умножения?
Ассоциативность — одно из тех фундаментальных свойств математики, благодаря которым математика работает. Вы, вероятно, принимаете это свойство как должное, потому что оно настолько укоренилось, но важно увидеть, как работают нутро математики, поэтому ознакомьтесь с учебным пособием и убедитесь, что вы твердо знаете свои основы!
Что такое дивиденд и что такое делитель?
Когда вы решаете задачи на деление, вам нужно знать словарный запас, который люди используют, чтобы описать, какое число делится и какое число выполняет деление.
 Этот учебник поможет вам сохранить этот словарный запас!
Этот учебник поможет вам сохранить этот словарный запас!Как умножать дроби?
Работа с дробями может быть пугающей, но если вы вооружитесь нужными инструментами, вы обнаружите, что работать с дробями не сложнее, чем с простыми числами. В этом уроке вы увидите процесс умножения 3 очень простых дробей. Наслаждаться!
Как складывать дроби с разными знаменателями?
Пытаетесь складывать дроби с разными знаменателями? Сначала вам понадобится общий знаменатель! Следуйте этому руководству и посмотрите, что вам нужно сделать, чтобы сложить эти дроби вместе.
Как умножить целое число на дробь?
Умножение целого числа на дробь может сбить с толку, но это руководство поможет разобраться. Проверьте это!
Каково происхождение?
Координатная плоскость имеет две оси: горизонтальную и вертикальную.
 Эти две оси пересекаются друг с другом в точке, называемой началом координат. Узнайте об упорядоченной паре, которая указывает начало координат и ее положение в координатной плоскости, посмотрев этот урок!
Эти две оси пересекаются друг с другом в точке, называемой началом координат. Узнайте об упорядоченной паре, которая указывает начало координат и ее положение в координатной плоскости, посмотрев этот урок!Что такое координатная плоскость?
Вы не можете построить график функции или построить упорядоченные пары без координатной плоскости! Узнайте о координатной плоскости, посмотрев этот урок.
Что такое координата X?
Упорядоченные пары являются важной частью построения графика, но вам нужно знать, как определить координаты в упорядоченной паре, если вы собираетесь нанести ее на координатную плоскость. В этом уроке вы увидите, как определить координату x в упорядоченной паре!
Что такое координата Y?
Упорядоченные пары являются важной частью построения графика, но вам нужно знать, как определить координаты в упорядоченной паре, если вы собираетесь нанести ее на координатную плоскость.
 В этом уроке вы увидите, как определить координату Y в упорядоченной паре!
В этом уроке вы увидите, как определить координату Y в упорядоченной паре!Что такое ось X?
Чтобы построить график функции или построить упорядоченную пару, вам нужно использовать координатную плоскость, поэтому вы должны изучить все это! В этом уроке вы узнаете об оси x и увидите, где она расположена в координатной плоскости.
Что такое ось Y?
Чтобы построить график функции или построить упорядоченную пару, вам нужно использовать координатную плоскость, поэтому вы должны изучить все это! В этом уроке вы узнаете об оси Y и увидите, где она расположена в координатной плоскости.
Что такое оси координат?
Координатная плоскость имеет две оси: горизонтальную и вертикальную. Узнайте об этих осях и названиях их точек пересечения, посмотрев этот урок!
Как вы делите целые числа?
Division — это строительный блок математики.
 В этом учебном пособии показано, как выполнить деление в длинное число, выполняя процесс по одному шагу за раз.
В этом учебном пособии показано, как выполнить деление в длинное число, выполняя процесс по одному шагу за раз.Как решить текстовую задачу, разделив целые числа?
Словесные задачи — отличный способ увидеть математику в реальном мире! Математика может помочь нам ответить на повседневные вопросы. Посмотрите этот урок, чтобы узнать, как деление используется для решения задачи со словами.
Как найти значение цифры в целом числе?
Понимание разрядности является строительным блоком понимания чисел. Следуйте этому руководству, чтобы узнать, как найти значение цифры для заданного числа!
Как упростить выражение, используя порядок операций?
Вы не можете упростить выражение без полного понимания порядка операций! Следуйте этому руководству, чтобы узнать, как использовать порядок операций для упрощения выражения.
Как умножить трехзначное число на однозначное?
Если вы хотите умножить трехзначное число на однозначное, может оказаться полезным выровнять умножение по вертикали.
 Этот урок проведет вас через процесс умножения!
Этот урок проведет вас через процесс умножения!Как умножить двузначное число на однозначное?
Умножение — это строительный блок математики, поэтому важно уметь с ним работать! В этом уроке вы потренируетесь умножать однозначное число на двузначное.
Как умножить двузначное число на двузначное?
Когда вы умножаете двузначное число на двузначное число, важно правильно расположить разряды. Этот учебник поможет вам попрактиковаться в умножении, сохраняя при этом порядок!
Как умножить двузначное число на двузначное с помощью частичных произведений?
Вы можете использовать частичные произведения для умножения двух чисел! Следуйте инструкциям в этом руководстве, чтобы увидеть, как частичные произведения могут упростить задачу на умножение!
Что такое разрядное значение для целых чисел?
Значение разряда — это строительный блок чисел.
 Без разрядности мы не смогли бы упорядочить все наши числа! В этом руководстве представлена местная стоимость и показаны части диаграммы разрядной стоимости.
Без разрядности мы не смогли бы упорядочить все наши числа! В этом руководстве представлена местная стоимость и показаны части диаграммы разрядной стоимости.Какие операции выполняются в первую очередь в выражении?
Невозможно упростить задачу без порядка действий. В этом уроке вы узнаете об этом особом порядке и увидите, как использовать его для решения проблемы!
Как конвертировать чашки в пинты?
Может быть полезно увидеть емкость, указанную в разных единицах измерения. В этом уроке показано, как измерить мерки в чашках и преобразовать их в пинты!
Как перевести кварты в галлоны?
Если вы идете в магазин, чтобы купить определенное количество литров молока, а в магазине молоко продается только в галлонах, что вы делаете? Вам нужно преобразовать эти кварты в галлоны! Следуйте этому руководству, чтобы узнать, как это сделать.
Как перевести миллилитры в литры?
Миллилитры и литры — это две единицы измерения вместимости.
 В этом уроке вы увидите, как взять заданное количество миллилитров и преобразовать его в литры!
В этом уроке вы увидите, как взять заданное количество миллилитров и преобразовать его в литры!Как округлить десятичную дробь с помощью числовой строки?
Округление — важная часть математики! В этом руководстве вы увидите, как использовать числовую линию, чтобы помочь вам округлить десятичную дробь до выбранного разрядного значения.
Как использовать предварительную оценку для оценки суммы нескольких десятичных знаков?
Предварительная оценка может быть отличным способом приблизить сумму. В этом руководстве вы увидите, как использовать предварительную оценку для приблизительной стоимости школьных принадлежностей!
Как вы оцениваете сумму десятичных знаков с помощью кластеризации?
Если вы хотите найти приблизительную сумму десятичных знаков, вы можете сначала округлить эти числа! В этом руководстве показано, как округлить десятичные дроби и посмотреть, к каким числам они близки, чтобы упростить сложение.

Как перегруппировать числа, чтобы мысленно складывать десятичные дроби?
Складывать числа в уме проще, чем вы думаете! Это может быть быстрый и интересный навык! Этот урок покажет вам, как брать десятичные дроби и складывать их мысленно.
Как умножить десятичную дробь на целое число?
Если вы хотите умножить десятичную дробь на целое число, просто игнорируйте десятичную точку и умножайте как обычно! Затем верните десятичную точку для ответа. Этот учебник показывает вам весь процесс шаг за шагом.
Как умножить десятичную дробь на целое число, используя оценку для размещения десятичной дроби?
Когда вы умножаете десятичное и целое число, удаление десятичной точки может упростить умножение, но куда девается десятичная точка, когда вы хотите получить ответ? В этом уроке вы увидите, как оценить положение десятичной точки после умножения!
Как решить задачу со словами, разделив десятичные дроби и округлив ответ в большую сторону?
Никогда не знаешь, где может появиться дивизия! Эта задача со словами — отличный пример использования деления на длинные числа для решения задачи.

Как упорядочить дроби и десятичные дроби от наибольшего к наименьшему?
Если вы хотите сравнить различные типы чисел, начните с преобразования их всех в один тип числа! В этом уроке показан пример использования дробей и десятичных знаков!
Как сложить две дроби с разными знаменателями?
Если вы складываете дроби с разными знаменателями, вам сначала нужно сделать эти знаменатели одинаковыми! В этом руководстве показано, как записывать дроби, чтобы у них были общие знаменатели, а затем показано, как складывать эти дроби.
Как вычесть две дроби с разными знаменателями?
Чтобы вычитать дроби, у них должны быть одинаковые знаменатели. Чтобы получить одинаковые знаменатели, вы можете найти эквивалентные дроби! В этом уроке показано, как вычитать дроби с разными знаменателями.
Какова формула объема прямоугольной призмы?
Найдите объем прямоугольной призмы с помощью формулы! Посмотрите этот урок, чтобы узнать больше!
Как вы делаете длинное умножение?
Умножение больших чисел? Без проблем! В этом уроке вы увидите, как выполнить длинное умножение, чтобы найти ответ (без использования калькулятора!).
 Взглянем!
Взглянем!Как вы переводите фразы в числовые выражения?
Превратить фразу из слов в математическую задачу может быть сложно, но практика может облегчить этот процесс! В этом уроке вы увидите, как искать ключевые слова, которые могут помочь вам перевести фразу в математику.
Что такое эквивалентные дроби?
Нахождение эквивалентных дробей является важной частью таких операций, как сложение, вычитание и сравнение дробей. Но что это такое? В этом уроке вы узнаете, что эквивалентные дроби — это просто дроби, которые имеют одинаковое значение, даже если они могут выглядеть очень по-разному! Взгляните на эквивалентные дроби, посмотрев этот урок!
Как складывать смешанные дроби с разными знаменателями путем преобразования в неправильные дроби?
Добавление смешанных фракций? Вы можете сначала преобразовать каждую в неправильную дробь. Если у них нет общих знаменателей, найдите общий знаменатель и используйте его, чтобы переписать каждую дробь.
 Затем сложите дроби вместе и упростите. В этом уроке вы узнаете, как сложить смешанные дроби с разными знаменателями!
Затем сложите дроби вместе и упростите. В этом уроке вы узнаете, как сложить смешанные дроби с разными знаменателями!Как вычитать смешанные дроби с разными знаменателями путем перегруппировки?
Вычитание смешанных дробей с разными знаменателями? Вы можете сначала найти общий знаменатель и использовать его, чтобы переписать каждую дробь. Затем вычтите целые числа и дроби отдельно. В этом уроке вы познакомитесь с вычитанием смешанных дробей с разными знаменателями!
Как вычитать смешанные дроби с разными знаменателями путем преобразования в неправильные дроби?
Вычитание смешанных дробей? Вы можете сначала преобразовать каждую в неправильную дробь. Если у них нет общих знаменателей, найдите общий знаменатель и используйте его, чтобы переписать каждую дробь. Затем вычтите дроби и упростите. В этом уроке вы познакомитесь с вычитанием смешанных дробей с разными знаменателями!
Как округлить десятичную дробь до заданного разрядного значения?
Иногда десятичные дроби бывают такими длинными, что вам нужен способ оценить десятичную дробь.
 В других случаях вам может понадобиться только определенная точность, чтобы получить ответ. Вот где округление десятичных долей до выбранного места может быть очень полезным! Посмотрите этот урок, чтобы узнать, как округлить десятичную дробь до выбранного разряда.
В других случаях вам может понадобиться только определенная точность, чтобы получить ответ. Вот где округление десятичных долей до выбранного места может быть очень полезным! Посмотрите этот урок, чтобы узнать, как округлить десятичную дробь до выбранного разряда.Что такое разрядное значение?
Знаете ли вы, что у чисел есть разрядность? В этом учебном пособии вы познакомитесь с термином «место» и покажете некоторые из наиболее часто встречающихся мест. Взглянем!
Как классифицировать четырехугольники?
Есть фигура с четырьмя сторонами? Тогда у вас есть четырехугольник! Но есть много специальных типов четырехугольника. Следуйте инструкциям, поскольку этот учебник покажет вам, как определить возможные имена для данного четырехугольника!
Что такое прямоугольник?
Прямоугольник — одна из многих основных фигур, встречающихся в математике.
 Прямоугольники обладают особыми свойствами, которые могут быть очень полезны при решении проблемы. В этом уроке вы познакомитесь с прямоугольниками и объясните их интересные свойства!
Прямоугольники обладают особыми свойствами, которые могут быть очень полезны при решении проблемы. В этом уроке вы познакомитесь с прямоугольниками и объясните их интересные свойства!Что такое четырехугольник?
Термин «четырехугольник» — это действительно причудливо звучащее название для определенного типа многоугольника. Знаете ли вы, что существуют особые типы четырехугольников? Посмотрите этот урок, чтобы узнать о четырехугольниках и их особых типах.
Что такое квадрат?
Квадрат — одна из многих основных фигур, встречающихся в математике. Квадраты обладают особыми свойствами, которые могут быть очень полезны при решении проблемы. В этом уроке вы познакомитесь с квадратами и объясните их интересные свойства!
Что такое ромб?
Ромб — это особый вид четырехугольника. Знание особых свойств ромба важно для идентификации и использования этих специальных многоугольников.


 Этот учебник поможет вам сохранить этот словарный запас!
Этот учебник поможет вам сохранить этот словарный запас! Эти две оси пересекаются друг с другом в точке, называемой началом координат. Узнайте об упорядоченной паре, которая указывает начало координат и ее положение в координатной плоскости, посмотрев этот урок!
Эти две оси пересекаются друг с другом в точке, называемой началом координат. Узнайте об упорядоченной паре, которая указывает начало координат и ее положение в координатной плоскости, посмотрев этот урок! В этом уроке вы увидите, как определить координату Y в упорядоченной паре!
В этом уроке вы увидите, как определить координату Y в упорядоченной паре! В этом учебном пособии показано, как выполнить деление в длинное число, выполняя процесс по одному шагу за раз.
В этом учебном пособии показано, как выполнить деление в длинное число, выполняя процесс по одному шагу за раз.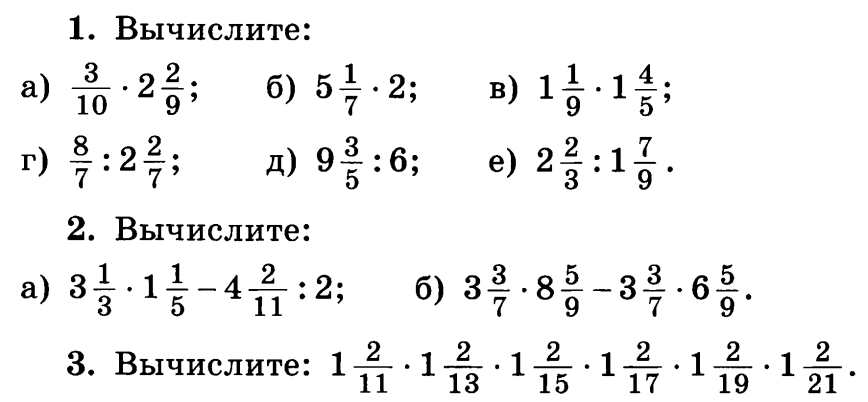 Этот урок проведет вас через процесс умножения!
Этот урок проведет вас через процесс умножения! Без разрядности мы не смогли бы упорядочить все наши числа! В этом руководстве представлена местная стоимость и показаны части диаграммы разрядной стоимости.
Без разрядности мы не смогли бы упорядочить все наши числа! В этом руководстве представлена местная стоимость и показаны части диаграммы разрядной стоимости. В этом уроке вы увидите, как взять заданное количество миллилитров и преобразовать его в литры!
В этом уроке вы увидите, как взять заданное количество миллилитров и преобразовать его в литры!

 Взглянем!
Взглянем! Затем сложите дроби вместе и упростите. В этом уроке вы узнаете, как сложить смешанные дроби с разными знаменателями!
Затем сложите дроби вместе и упростите. В этом уроке вы узнаете, как сложить смешанные дроби с разными знаменателями! В других случаях вам может понадобиться только определенная точность, чтобы получить ответ. Вот где округление десятичных долей до выбранного места может быть очень полезным! Посмотрите этот урок, чтобы узнать, как округлить десятичную дробь до выбранного разряда.
В других случаях вам может понадобиться только определенная точность, чтобы получить ответ. Вот где округление десятичных долей до выбранного места может быть очень полезным! Посмотрите этот урок, чтобы узнать, как округлить десятичную дробь до выбранного разряда. Прямоугольники обладают особыми свойствами, которые могут быть очень полезны при решении проблемы. В этом уроке вы познакомитесь с прямоугольниками и объясните их интересные свойства!
Прямоугольники обладают особыми свойствами, которые могут быть очень полезны при решении проблемы. В этом уроке вы познакомитесь с прямоугольниками и объясните их интересные свойства!