структура и изменения ⋆ MAXIMUM Блог
Никогда не программировал, но хочешь сдать ЕГЭ по информатике? Тогда знай: к экзамену можно подготовиться за год, если грамотно организовать учебный процесс. Из этой статьи ты узнаешь все о структуре ЕГЭ по информатике в 2023 году, изменениях и типах заданий.
Структура и изменения ЕГЭ 2023 по информатикеИзменения в ЕГЭ по информатике 2023
Последние 2 года ЕГЭ по информатике проводился в компьютерной форме, что предоставляло сдающим большое право выбора, как решать то или иное задание, благодаря чему появлялись лазейки, упрощающие решения некоторых номеров из экзамена.
В связи с этим, ФИПИ ежегодно вносят изменения в КИМ по информатике, чтобы внести больше разнообразия и избавиться от шаблонных решений. В 2023 году полностью претерпят структуру 2 задания, но это не все изменения, что ФИПИ представили в новой демоверсии ЕГЭ.
Долой переборное решение!
В блоке «Программирование» даже после перехода на компьютерную форму было два задания, в которых программа уже представлена в условии, а задача сдающего — проанализировать ее — задания №6 и 22. Но многие справедливо подумали – зачем анализировать код, если я могу его переписать и запустить переборное решение. Благодаря этому, почти все, кто знал о таком варианте решения заданий, законно получали 2 балла за них. ФИПИ такой способ решения вряд ли понравился.
Но многие справедливо подумали – зачем анализировать код, если я могу его переписать и запустить переборное решение. Благодаря этому, почти все, кто знал о таком варианте решения заданий, законно получали 2 балла за них. ФИПИ такой способ решения вряд ли понравился.
Официальный список изменений выглядит следующим образом:
ФИПИ об изменениях в ЕГЭ по информатике 2023Задание №6 теперь мы будем относить к блоку «Алгоритмизация», так как теперь оно предоставляет нам работу с исполнителем и анализом алгоритма. В демоверсии вам предлагают проанализировать «Черепашку», которая многим знакома из ОГЭ по информатике:
Задание 6, демоверсия ЕГЭ по информатике 2023Задание №22 пополняет ряды блока «Информационные модели», а также заданий, к которым прилагаются дополнительные файлы, если быть точнее — электронная таблица. В условии затрагивается новая для экзамена тема – многопоточность (довольно важная тема для многих IT-специалистов и затрагивается на определенных предметах в университете), а решение требует анализа таблицы и зависимостей процессов:
Задание 22, демоверсия ЕГЭ по информатике 2023Кроме двух новых заданий, некоторые номера также претерпели изменения:
Задание №14 все еще направлено на работу с системами счисления, но теперь нужно искать неизвестную цифру числа. Такого прототипа ранее на ЕГЭ мы не видели:
Такого прототипа ранее на ЕГЭ мы не видели:
Задание №12, судя по демоверсии, станет сложнее — это уже знакомый для экзамена исполнитель «Редактор», но с необычным вопросом (раньше, в основном, требовалось назвать получившуюся после обработки программой строку/сумму цифр строки):
Задание 12, демоверсия ЕГЭ по информатике 2023Задание №16 на рекурсию из демоверсии намекает нам на то, что не стоит забывать про аналитическое решение. Это происходит из-за больших аргументов у функции, гораздо проще поразмыслить, что же считает функция:
Задание 16, демоверсия ЕГЭ по информатике 2023Как видите, ЕГЭ по информатике в 2023 году изменился заметно. Все эти обновления нужно учитывать. Если вы не знаете, чего от вас ждут составители экзамена, даже незначительное изменение в формулировке может стоить вам нескольких баллов. А в условиях, когда от ЕГЭ зависит поступление в хороший вуз и качество образования, каждый балл важен.
Поэтому на своих занятиях по подготовке к ЕГЭ по информатике я всегда разбираю с учениками самые свежие обновления ФИПИ. Мы выясняем, как именно надо понимать задание, изучаем разные алгоритмы решения и тренируем лучшие способы их оформления — в соответствии со всеми критериями. Именно поэтому мои ученики сдают экзамен на высокий балл и поступают в тот вуз, в который изначально хотели. Помочь с этим я могу и вам — записывайтесь на курс и начните подготовку к ЕГЭ на 80+ 💪
О структуре экзамена
В ЕГЭ по-прежнему осталось 27 заданий с кратким ответом. За задания 1-25 можно получить по 1 первичному баллу, а за задания 26 и 27 — по 2 балла. Максимальный возможный результат — 29 первичных баллов.
Все задания школьникам нужно решить за 3 часа 55 минут.
На экзамене встретятся задания по программированию, логике, алгоритмизации, на работу с информационными моделями, а также на кодирование информации.
В каждом блоке есть определенные темы, которые нужно знать.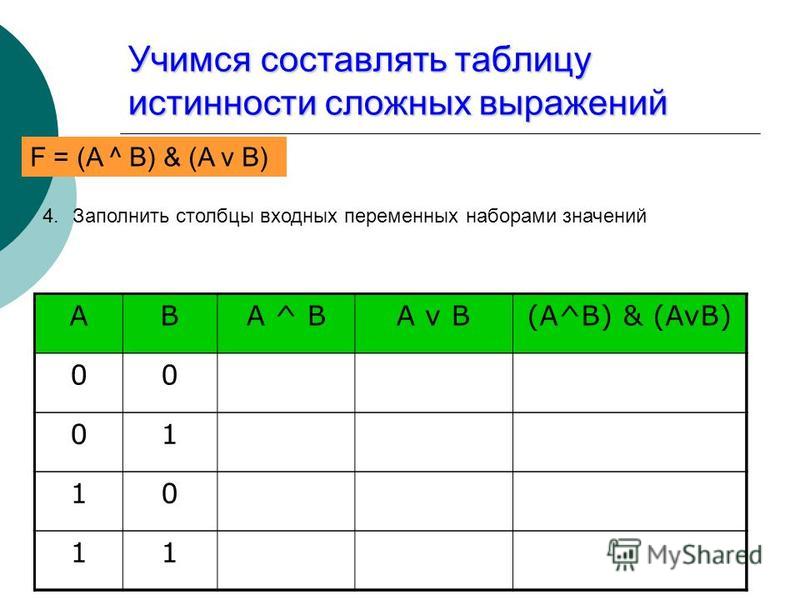 Давайте посмотрим, что именно надо учить.
Давайте посмотрим, что именно надо учить.
Программирование
Программирование встречается в шести заданиях — а именно в 16, 17, 24, 25, 26 и 27. Чтобы справиться с ними достаточно хорошо знать только один язык программирования. Нужно уметь работать с массивом, строками, файлами, знать алгоритмы сортировки и другие не менее важные алгоритмы работы с числами.
Задание 24, демоверсия ЕГЭ по информатике 2023Логика
Логика встречается в заданиях 2 и 15. Чтобы успешно справиться с этими заданиями, нужно знать основные логические операции и их таблицы истинности, уметь преобразовывать и анализировать выражения.
Алгоритмизация
В данный блок входят семь заданий (5, 6, 12, 19, 20, 21 и 23). Для решения этих заданий нужно уметь работать с различными алгоритмами и исполнителями. Важно понимать теорию игр — определять выигрывающего игрока, выигрышную позицию, различать понятия заведомо проигрышной и выигрышной позиций.
Благодаря возможности использовать инструменты компьютера, многие из этих заданий также можно решать с помощью написания программы или построения электронной таблицы.
Информационные модели
С заданиями 1 и 13 ученики обычно справляются хорошо. Чтобы их решить, нужно уметь работать с графами и таблицами и знать пару простых методов. С заданием 10 проблемы возникают редко, так как от вас требуется найти количество определенных слов в текстовом документе. Задания 3, 9 и 18 требуют работы с электронными таблицами, при решении вам помогут знания про ссылки, функции и фильтры. К этому же блоку добавляется новое задание 22.
Задание 9, демоверсия ЕГЭ по информатике 2023Информация и ее кодирование
Задания этого блока достаточно разнообразны. Вы встретите алгоритмы перевода чисел в различные системы счисления, условие Фано, формулы, единицы измерения информации и комбинаторику. Все это разнообразие встречается в заданиях 4, 7, 8, 11, 14, а также может пригодится в заданиях на программирование. А новый прототип задания 14 на работу с системами счисления и вовсе можно решить с помощью программы.
Шкала оценивания
На самом деле шкала перевода баллов составляется после проведения экзаменов, так как в формуле есть параметр «среднее значение». То есть то, что мы называем шкалой — это результат перевода баллов прошлого года. ФИПИ переводит баллы по формуле, а не по шкале. Поэтому шкала меняется, если меняется экзамен или массово меняются результаты его прохождения. Мы полагаем, что в 2023 году проходной балл будет 40 вторичных баллов, но это может измениться.
То есть то, что мы называем шкалой — это результат перевода баллов прошлого года. ФИПИ переводит баллы по формуле, а не по шкале. Поэтому шкала меняется, если меняется экзамен или массово меняются результаты его прохождения. Мы полагаем, что в 2023 году проходной балл будет 40 вторичных баллов, но это может измениться.
Какие типы заданий встретятся на ЕГЭ по информатике 2023?
На ЕГЭ 2023, как и в 2021 году, все задания будут с кратким ответом, больше не нужно писать подробные объяснения по теории игр и сдавать программный код на проверку на бумаге. Но это не значит, что все задания идентичны. Посмотрим, какие именно типы заданий встретятся на экзамене.
Задания, которые можно решить «вручную»
Хотя ЕГЭ по информатике и проходит в компьютерной форме, в КИМах по-прежнему остаются задания, которые можно решать, как на бумаге, так и на компьютере. Это задания 1, 2, 4-8, 11-15, 19-23, в них необходимо получить число или последовательность букв в ответе. Ты можешь написать программу на компьютере или использовать электронные таблицы, а затем записать в ответ получившееся значение. За каждое задание можно получить 1 балл.
Ты можешь написать программу на компьютере или использовать электронные таблицы, а затем записать в ответ получившееся значение. За каждое задание можно получить 1 балл.
Задания, которые решаются с помощью компьютера
Все такие задания бывают трех типов:
- Работа с предложенным файлом
- Создание программы
- Написание программы и получение ответа, используя предложенный файл
Разберемся с каждым типом отдельно.
Работать только с предложенным файлом нужно в заданиях 3, 9, 10, 18 и 22. Чтобы решить эти задания, нужно знать, какие функции есть у текстовых редакторов и редакторов электронных таблиц, а также теория по реляционным базам данных. За каждое задание можно получить по 1 баллу.
Создать программу понадобится в задании 25. Задача в том, чтобы написать код и получить на выходе какой-то ответ. Начальные данные, при которых нужно получить ответ, уже указаны в самом задании. За оба задания можно получить по 1 баллу.
Задания, где нужно написать программу и считать информацию из файла — это 17, 24, 26 и 27. Эффективность и способ решения, который вы использовали, не проверяется. Главное — получить верный численный ответ. За задания 17 и 24 вы можете получить по 1 баллу, а за задания 26 и 27 — по 2 первичных балла.
Эффективность и способ решения, который вы использовали, не проверяется. Главное — получить верный численный ответ. За задания 17 и 24 вы можете получить по 1 баллу, а за задания 26 и 27 — по 2 первичных балла.
Обрати внимание, что в некоторых прототипах заданий 17, 24, 25, 26 и 27 программу можно не писать, если ты знаешь, как решить эти задания другим способом — это не запрещено.
Как подготовиться к ЕГЭ по информатике 2023?
Лучший способ — разобраться в каждой теме и выучить все необходимое. Как это сделать?
- Для начала оцените текущий уровень знаний. Можно пройти диагностическое тестирование или попробовать решить последнюю демоверсию экзамена. Таким образом вы поймете, что вы уже знаете, а над чем нужно еще поработать.
- Если вы не умеете программировать, советуем заняться этим с самого начала учебного года. Задания на программирование приносят минимум 8 первичных баллов из 29, это достаточно много.
- Подумайте, смогут ли вас хорошо подготовить в школе.
 Оцените, что из школьной программы вы уже знаете, а что предстоит изучить в течение года.
Оцените, что из школьной программы вы уже знаете, а что предстоит изучить в течение года. - Решите, как вам комфортнее заниматься: лично с преподавателем, в группе или онлайн.
- Регулярно занимайтесь, уделяя время и теории, и практике!
Именно по такой схеме проходят мои занятия по подготовке к ЕГЭ по информатике в MAXIMUM Education. Но вдобавок к этому я еще показываю ученикам разные ловушки экзамена: как в формулировках заданий, так и в критериях и правилах оформления решений. Я помогаю распознавать эти ловушки и обходить их стороной — только так можно гарантированно получить максимальный балл за каждое задание.
Помимо этого, я знаю много разных лайфхаков решения ЕГЭ по информатике. С их помощью найти правильный ответ можно намного быстрее — а это очень важно на экзамене, когда время ограничено. Всеми этими лайфхаками я делюсь со своими учениками и показываю, как применять на практике каждый способ.
Так что на экзамен мои ученики приходят абсолютно спокойные и уверенные в своих силах. И результаты ЕГЭ у них соответствующие: намного выше среднего балла по стране. Если и вы хотите получить 80+ на экзамене по информатике, записывайтесь на курс подготовки к ЕГЭ. Я научу вас всему, что я знаю!
И результаты ЕГЭ у них соответствующие: намного выше среднего балла по стране. Если и вы хотите получить 80+ на экзамене по информатике, записывайтесь на курс подготовки к ЕГЭ. Я научу вас всему, что я знаю!
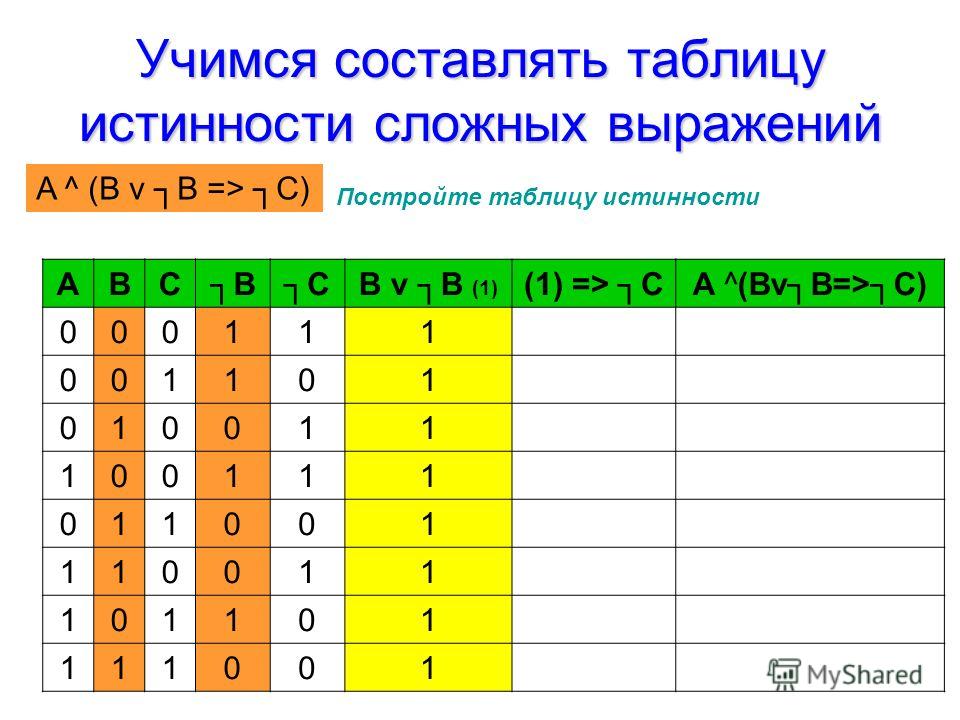
Таблица истинности. Базовые логические элементы.
Главная » Справочник » Таблица истинности. Базовые логические элементы.
admin
Categories Справочник
Так же, как и стандартные Булевы выражения, информация на входах и выходах различных логических элементов или логических схем может быть собрана в единую таблицу – таблицу истинности.
Таблица истинности дает наглядное представление о системе логических функций. В таблице истинности отображаются сигналы на выходах логических элементов при всех возможных комбинациях сигналов на их входах.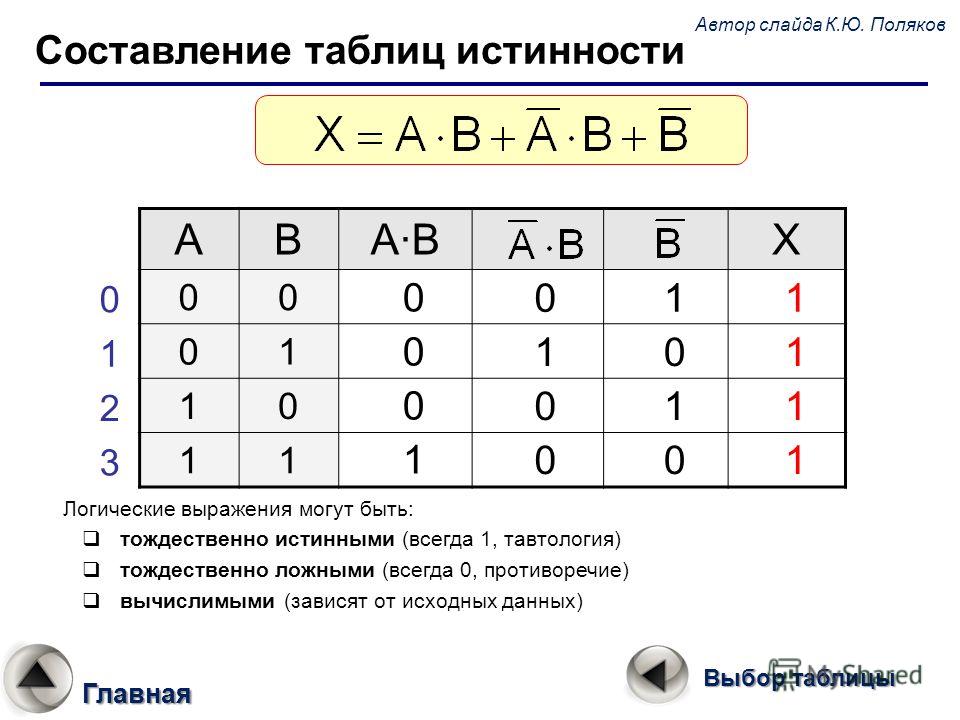
В качестве примера, рассмотрим логическую схему с двумя входами и одним выходом. Входные сигналы отметим как «А» и «В», а выход «Q». Есть четыре (2²) возможных комбинаций входных сигналов, которые можно подать на эти два входа («ON — наличие сигнала» и «OFF — отсутствие сигнала»).
Однако, когда речь идет о логических выражениях и, особенно о таблице истинности логических элементов, вместо общего понятия «наличие сигнала» и «отсутствие сигнала» используют битные значения, которые представляют собой логический уровень «1» и логический уровень «0» соответственно.
Тогда четыре возможные комбинации «А» и «В» для 2-входного логического элемента можно представить в следующем виде:
- «OFF» — «OFF» или (0, 0)
- «OFF» — «ON» или (0, 1)
- «ON» — «OFF» или (1, 0)
- «ON» — «ON» или (1, 1)
Следовательно, у логической схемы имеющей три входа будет восемь возможных комбинаций (2³) и так далее. Для обеспечения легкого понимания сути таблицы истинности, мы будем изучать ее только на простых логических элементах с числом входов не превышающим двух.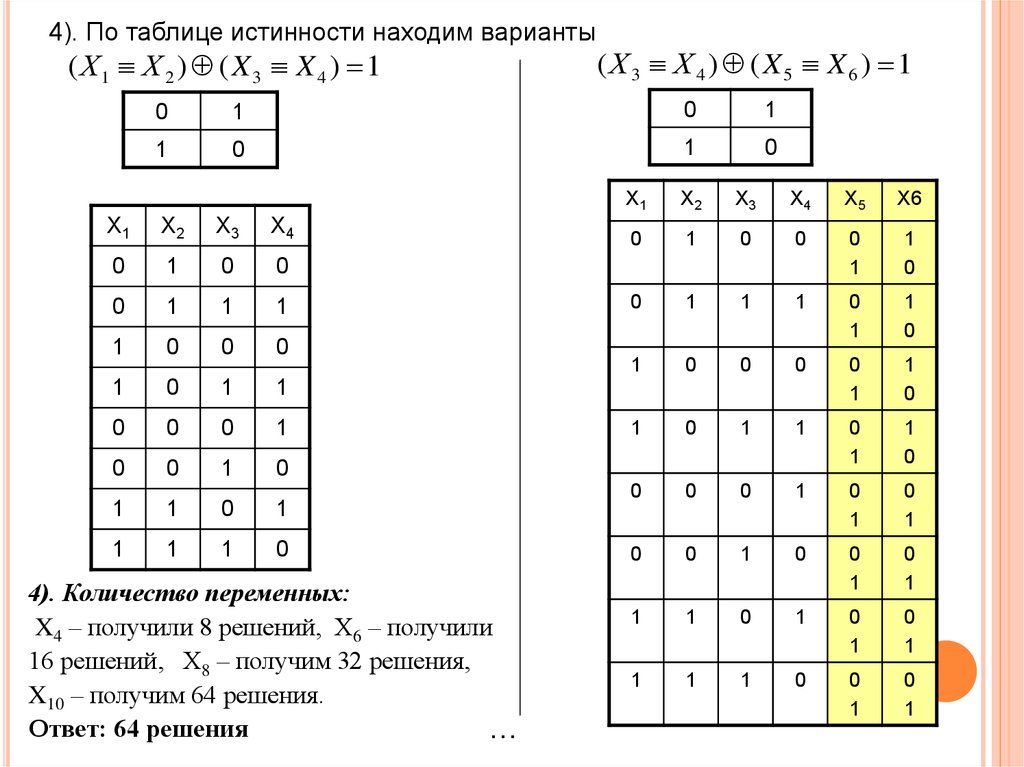
Практически, таблица истинности состоит из одного столбца для каждой из входных переменных (например, А и В), и один последний столбец для всех возможных результатов логической операции (Q). Следовательно, каждая строка таблицы истинности содержит один из возможных вариантов входных переменных (например, A = 1, B = 0), и результат операции с этими значениям.
Элемент «И»
Для логического элемента «И» выход Q будет содержать лог.1, только если на оба входа («А» и «В») будет подан сигнал лог.1
Микросхемы, содержащие логический элемент «И»:
- К155ЛИ1, аналог SN7408N
- К155ЛИ5 с открытым коллектором, аналог SN74451N
- К555ЛИ1, аналог SN74LS08N
- К555ЛИ2 с открытым коллектором, аналог SN74LS09N
Элемент «ИЛИ»
Выход Q, элемента «ИЛИ», будет иметь лог.1, если на любой из двух входов или же на оба входа сразу подать лог.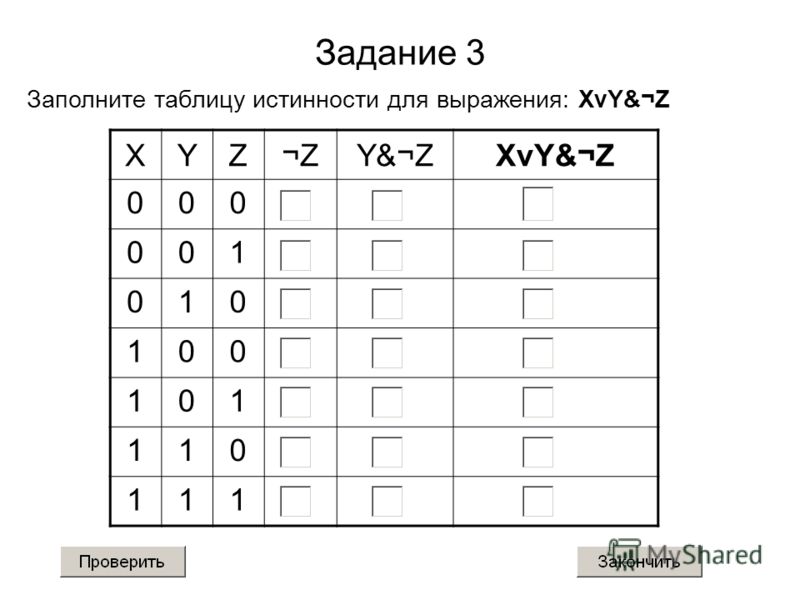 1
1
Микросхемы, содержащие логический элемент «ИЛИ»:
Блок питания 0…30В/3A
Набор для сборки регулируемого блока питания…
Подробнее
- К155ЛЛ1, аналог SN7432N
- К155ЛЛ2 с открытым коллектором, аналог SN75453N
- К555ЛЛ1, аналог SN74LS32N
Элемент «НЕ»
В данном случае выход Q, логического элемента «НЕ», будет иметь сигнал противоположный входному сигналу.
Микросхемы, содержащие логический элемент «НЕ»:
- К155ЛН1, аналог SN7404N
- К155ЛН2 с открытым коллектором, аналог SN7405N
- К155ЛН3, аналог SN7406N
- К155ЛН5 с открытым коллектором, аналог SN7416N
- К155ЛН6, аналог SN7466N
Элемент «И-НЕ»
На выходе Q элемента «И-НЕ» будет лог.1 если на обоих входах одновременно отсутствует сигнал лог.1
Микросхемы, содержащие логический элемент «И-НЕ»:
- К155ЛА3, аналог SN7400N
- К155ЛА8, аналог SN7401N
- К155ЛА9 с открытым коллектором, аналог SN7403N
- К155ЛА11 с открытым коллектором, аналог SN7426N
- К155ЛА12 с открытым коллектором, аналог SN7437N
- К155ЛА13 с открытым коллектором, аналог SN7438N
- К155ЛА18 с открытым коллектором, аналог SN75452N
Элемент «ИЛИ-НЕ»
Только если на оба входа логического элемента «ИЛИ-НЕ» подать лог. 0 мы получим на его выходе Q сигнал соответствующий лог.1
0 мы получим на его выходе Q сигнал соответствующий лог.1
Микросхемы, содержащие логический элемент «ИЛИ-НЕ»:
- К155ЛЕ1, аналог SN7402N
- К155ЛЕ5, аналог SN7428N
- К155ЛЕ6, аналог SN74128N
Элемент «Исключающее ИЛИ»
В данном случае выход Q будет содержать лог.1, если на вход элемента «Исключающее ИЛИ» поданы два противоположных друг другу сигнала.
Микросхемы, содержащие логический элемент «Исключающее ИЛИ»:
- К155ЛП5, аналог SN7486N
Подведем итог, собрав все полученные ранее результаты работы логических элементов в единую таблицу истинности:
Инвертор 12 В/ 220 В
Инвертор с чистой синусоидой, может обеспечивать питание переменно…
Подробнее
Categories Справочник
Отправить сообщение об ошибке.
Генератор таблиц истинности — онлайн-калькулятор логической алгебры для таблиц
Генератор таблиц истинности
Логическое/логическое выражениеОтображение
Полная таблица истинности (входные переменные + выходные значения)
Таблица истинности с этими переменными
Только выходные значения (список 0 и 1)
Соответствующие minterms $ Σm(…) $ (0-индексированные)
Соответствующие Maxterms $ ΣM(…) $ (0-индексированные)
См. также: Калькулятор логических выражений — Boolean Minterms и Maxterms
также: Калькулятор логических выражений — Boolean Minterms и Maxterms
Найти уравнение по таблице истинности
Указывать только выходные значения функции (последний столбец из булевой таблицы истинности)
Выходные значения (список 0 и 1)| Таблица упорядочена (входные значения) | От 0,…,0 до 1,…,1 От 1,…,1 до 0,…,0 |
| Булева запись | Литеральная (И, ИЛИ, НЕ) Логическая (∧, ∨, ¬) Программирование (&&, ||, ~) Алгебраическая (*, +, !) |
См. также: Калькулятор логических выражений
Ответы на вопросы (FAQ)
Что такое таблица истинности? (Определение)
Таблица истинности представляет собой таблицу, представляющую выходные логические значения логического выражения на основе их записей. Таким образом, таблица отображает все возможные комбинации $n$ входных логических переменных (обычно 0/FALSE и 1/TRUE по $n$ столбцам) и результат уравнения в качестве вывода (последний столбец).
Пример: Таблица функции логического НЕ с 1 входом А (1-й столбец) и выходным значением НЕ А (последний столбец):
| А | НЕ А | 01 |
|---|---|
| 1 | 0 |
Каждая электронная схема связана с таблицей истинности , которая описывает ее.
Обычно массив начинается с входных значений в $ 0 $ и заканчивается входными значениями в $ 1 $, но иногда это наоборот.
Как работает калькулятор таблицы истинности?
dCode Генератор таблицы истинности интерпретирует булевское логическое выражение и вычисляет (используя булеву алгебру) все возможные комбинации 0 и 1 для каждой переменной (среди запрошенных логических переменных), чтобы составить таблицу истинности .
dCode также позволяет найти булеву логическую функцию/выражение из таблицы истинности .
Как найти уравнение из таблицы истинности?
Единственным важным столбцом таблицы истинности является последний, который описывает выходные значения (первые столбцы всегда идентичны для заданного количества входных данных) и который позволяет преобразовать в логическое выражение.
Существует 2 метода нахождения логического уравнения из таблицы истинности : либо с использованием выходных значений 0 (расчет Maxterms), либо с использованием выходных значений 1 (расчет Minterms).
Пример: Выходные значения: 0,1,1,0 , (и таблица упорядочена от 00 до 11), поэтому таблица истинности :
X
Вот различные вычисления (которые дают тот же результат для данного примера) 1 , запишите соответствующие входные значения, разделенные логическими И , затем сгруппируйте эти результаты с помощью логических ИЛИ .
Пример: Строки 2 и 3 равны 1 , строка 2 записывается как A AND NOT(B) (поскольку A равно 1 , а B равно 0 ), строка 3 записывается как NOT(A) AND B , поэтому уравнение равно (A AND NOT (B)) OR (NOT(A) AND B) , что, возможно, упрощается до A XOR B
Вычисление на основе выходных значений 0 таблицы истинности (Maxterms): для каждого 0 напишите соответствующие входные значения, разделенные логическим ИЛИ , затем сгруппируйте эти результаты с помощью логического И .
Пример: Строки 1 и 4 равны 0 , строка 1 записывается как A ИЛИ B , строка 4 записывается как НЕ(А) ИЛИ НЕ(В) и поэтому уравнение равно (A OR B) AND (NOT(A) OR NOT(B)) , что, возможно, упрощается до A XOR B
Какая таблица истинности для логического И?
Таблица истинности для функции И:
| A | B | A AND B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Что такое таблица истинности для логического ИЛИ?
Таблица истинности для функции ИЛИ:
| A | B | A OR B |
|---|---|---|
| 0 | 0032 0||
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
What is the truth table for logical XOR?
The truth table for the XOR function is:
| A | B | A XOR B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
What The Prame Table Table Tabil Talecil?
The truth table for the NAND function is:
| A | B | A NAND B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Какая таблица истинности для логического НЕ-ИЛИ?
The truth table for the NOR function is:
| A | B | A NOR B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Какая таблица истинности для логического ИСТИНА?
The truth table for the TRUE (=1) function is:
| A | TRUE |
|---|---|
| 0 | 1 |
| 1 | 1 |
What is the таблица истинности для логического FALSE?
Таблица истинности для функции ЛОЖЬ (=0):
| A | ЛОЖЬ | ||||
|---|---|---|---|---|---|
| 0 | 0 | ||||
| 1 | 0 |
| Таблица упорядочена (входные значения) | От 0,…,0 до 1,…,1 От 1,…,1 до 0,…,0 |
| Булева запись | Литеральная (И, ИЛИ, НЕ) Логическая (∧, ∨, ¬) Алгебраическая (*, 7 3 6 9 003 | 4 | 4 | 4 | 4 |
См. также: Калькулятор логических выражений
Ответы на вопросы (FAQ)
Что такое таблица истинности? (Определение)
Таблица истинности представляет собой таблицу, представляющую выходные логические значения логического выражения на основе их записей.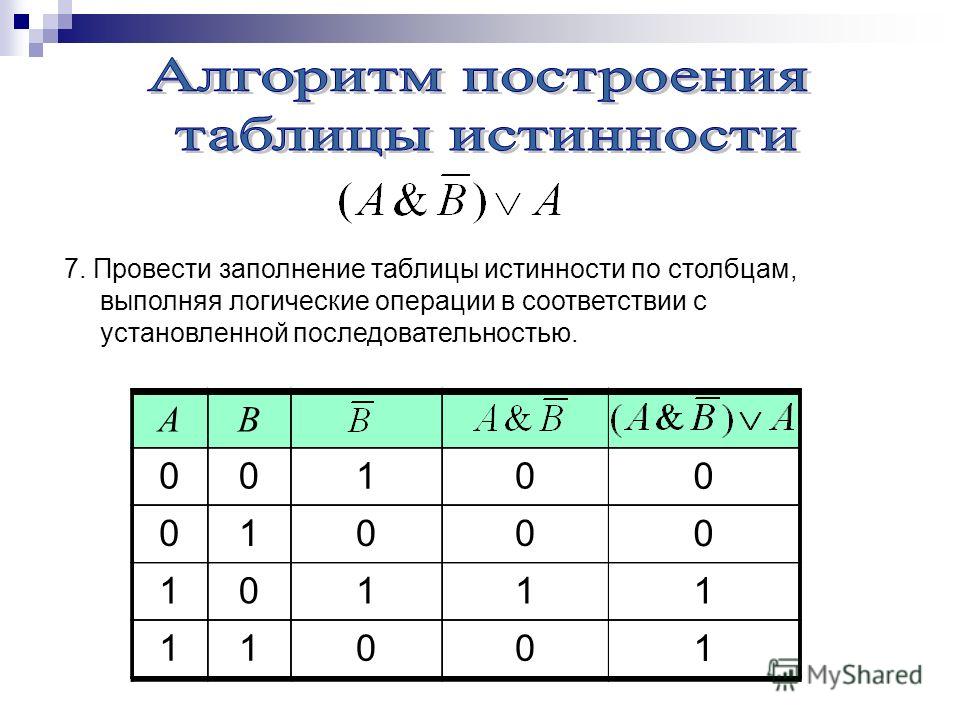 Таким образом, таблица отображает все возможные комбинации $n$ входных логических переменных (обычно 0/FALSE и 1/TRUE по $n$ столбцам) и результат уравнения в качестве вывода (последний столбец).
Таким образом, таблица отображает все возможные комбинации $n$ входных логических переменных (обычно 0/FALSE и 1/TRUE по $n$ столбцам) и результат уравнения в качестве вывода (последний столбец).
Пример: Таблица логической функции НЕ с 1 входом A (1-й столбец) и выходным значением NOT A (last column):
| A | NOT A |
|---|---|
| 0 | 1 |
| 1 | 0 |
Every electronic circuit is associated with a truth table , который описывает это.
Обычно массив начинается с входных значений в $ 0 $ и заканчивается входными значениями в $ 1 $, но иногда это наоборот.
Как работает калькулятор таблицы истинности?
дКод 9Генератор таблицы истинности 0060 интерпретирует логическое выражение логического типа и вычисляет (используя алгебру логики) все возможные комбинации 0 и 1 для каждой переменной (среди запрошенных переменных логического характера), чтобы составить таблицу истинности .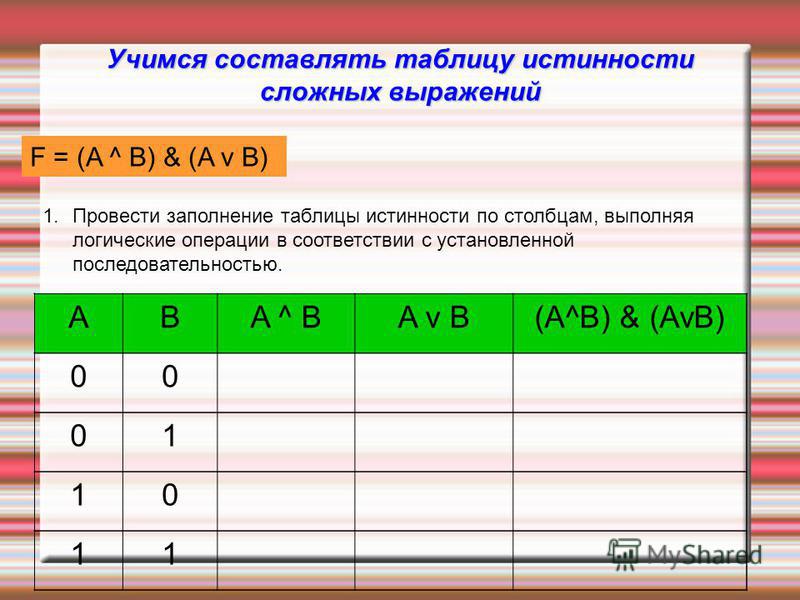
dCode также позволяет найти булеву логическую функцию/выражение из таблицы истинности .
Как найти уравнение из таблицы истинности?
Единственный важный столбец таблицы истинности является последним, который описывает выходные значения (первые столбцы всегда идентичны для заданного количества входных данных) и который позволяет преобразовать в логическое выражение.
Существует 2 метода нахождения логического уравнения из таблицы истинности : либо с использованием выходных значений 0 (расчет Maxterms), либо с использованием выходных значений 1 (расчет Minterms).
Пример: Выходные значения: 0,1,1,0 , (and the table is ordered from 00 to 11), so the truth table is:
| input A | input B | output X |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Вот различные вычисления (которые дают тот же результат для данного примера)
Расчет на основе выходных значений 1 таблицы истинности (Minterms): для каждого 1 запишите соответствующие входные значения отдельно логическими И , затем сгруппируйте эти результаты с логическими ИЛИ .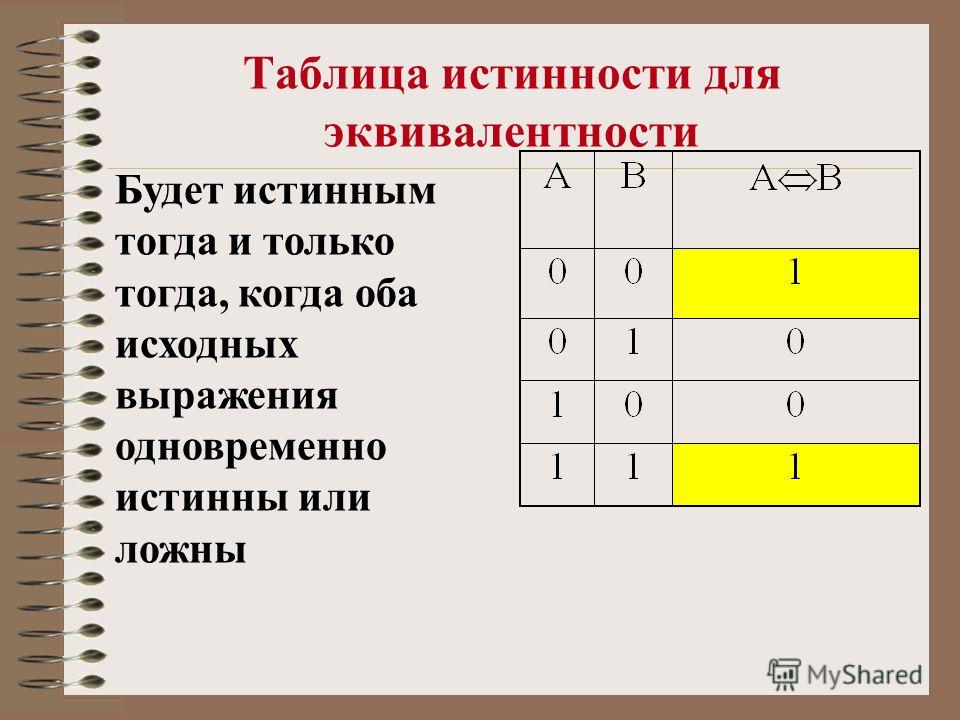
Пример: Строки 2 и 3 равны 1 , строка 2 записывается как A И НЕ(B) (потому что A равно 1 и B равно 0 ), строка 3 записывается как НЕ(А) И В и, следовательно, уравнение имеет вид (А И НЕ(В)) ИЛИ (НЕ(А) И B) , который, возможно, упрощается до A XOR B
Вычисление на основе выходных значений 0 таблицы истинности (Maxterms): для каждого 0 запишите соответствующие входные значения, разделенные логическим ИЛИ , затем сгруппируйте эти результаты с логической И .
Пример: Строки 1 и 4 равны 0 , строка 1 записывается как A ИЛИ B , строка 4 записывается как НЕ(А) ИЛИ НЕ(В) и поэтому уравнение равно (A OR B) AND (NOT(A) OR NOT(B)) , что, возможно, упрощается до A XOR B
Какая таблица истинности для логического И?
Таблица истинности для функции И:
| A | B | A AND B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Что такое таблица истинности для логического ИЛИ?
Таблица истинности для функции ИЛИ:
| A | B | A OR B |
|---|---|---|
| 0 | 0032 0||
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
What is the truth table for logical XOR?
The truth table for the XOR function is:
| A | B | A XOR B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
What The Prame Table Table Tabil Talecil?
The truth table for the NAND function is:
| A | B | A NAND B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Какая таблица истинности для логического НЕ-ИЛИ?
The truth table for the NOR function is:
| A | B | A NOR B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Какая таблица истинности для логического ИСТИНА?
The truth table for the TRUE (=1) function is:
| A | TRUE |
|---|---|
| 0 | 1 |
| 1 | 1 |
What is the таблица истинности для логического FALSE?
Таблица истинности для функции ЛОЖЬ (=0):
| A | ЛОЖЬ |
|---|---|
| 0 | 0 |
| 1 | 0 |

 Оцените, что из школьной программы вы уже знаете, а что предстоит изучить в течение года.
Оцените, что из школьной программы вы уже знаете, а что предстоит изучить в течение года.

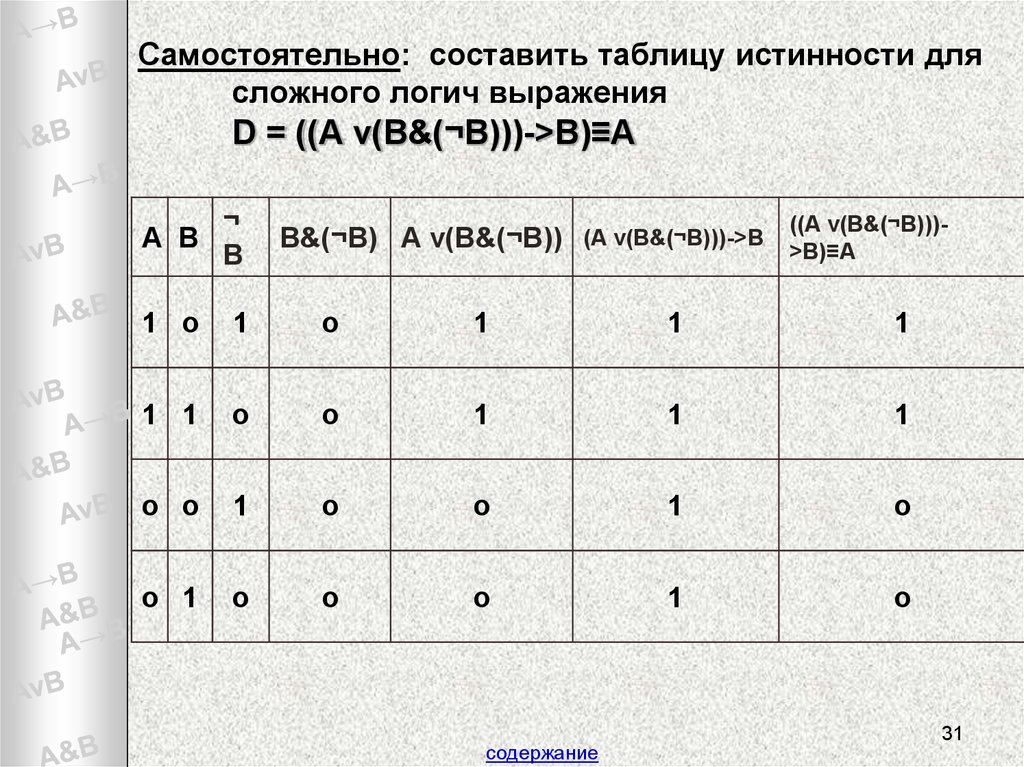 также: Калькулятор логических выражений — Boolean Minterms и Maxterms
также: Калькулятор логических выражений — Boolean Minterms и Maxterms